-
近年来, 光激发作用下分子与金属纳米复合结构之间的相互作用、相关的光学响应及其潜在的应用引起了广泛关注. 随着纳米技术的发展, 实验室可以制备出多种分子团簇与金属纳米复合结构[1], 促进了分子与金属纳米结构相互作用机理的研究. 在外场激发作用下, 金属纳米结构能够激发等离激元形成局域电磁场, 从而提高分子团簇与金属纳米材料之间的能量转移效率. 等离激元场的局域和增强效应在光伏电池[2,3]、光学传感[4–6]、全光开关及量子计算[7]等多个领域均有广泛应用. 在弱场激发作用下, 分子团簇可以近似认为形成单激子态, 与等离激元的耦合称为单模耦合[8,9]. 而在强场和金属纳米粒子的共同作用下, 分子团簇出现多激子态同时金属纳米结构出现等离激元的高阶模式, 导致多模耦合, 进而出现诸多新的物理现象, 对多模耦合机理的理论研究将对新型功能器件的制备、有机光电器件性能的优化提供思路.
基于分子团簇和金属纳米复合结构的多尺度和多样性特性, 目前已经发展了多种理论模型和方法来模拟分子团簇与金属纳米复合结构间的耦合动力学行为, 包括分子动力学方法[10]、弗仑克尔激子模型[11]、非线性光学响应理论[12]等. 分子动力学作为一种广泛应用的模拟方法, 在研究材料的微观结构和力学性能方面具有重要价值. 弗仑克尔激子模型常用于描述分子团簇和金属纳米结构中的电子激发及能量转移过程, 尤其适合具有紧密堆积结构的有机染料和量子点系统[11]. 非线性光学响应理论能够探讨金属纳米复合结构在强场下的非线性光学行为, 如二次谐波产生和三阶非线性效应等[12], 对于设计新型光学材料和超快光开关具有重要意义. 我们在金属纳米粒子与分子团簇耦合方面也开展了一些研究, 例如, 金属纳米粒子(MNPs)对分子激发态的等离激元增强效应, 分析了多个MNPs通过等离激元杂化改变其与单个分子的相互作用, 进而影响分子的光激发效率的物理过程[13]; 研究了如何通过金属纳米粒子产生的局部增强场控制分子链中的光诱导激发能量转移[14]等. 但这些工作主要关注单模耦合, 对分子团簇在强场激发下产生的多激子态与等离激元的相互作用即多模耦合效应研究较少.
MB分子作为一种有机染料, 在与金属纳米粒子作用时展现出丰富的光物理特性, 比如与等离激元的强耦合产生的Rabi劈裂. 由于MB分子具有较大的偶极矩, 与金属纳米结构有较强的相互作用, 且在一定条件下可以形成二聚体及单体与二聚体的混合物, MB分子也可用来分析多模耦合效应. 为了深入研究团簇与金属表面等离激元的多模耦合[15,16], 本文在密度矩阵的理论框架下, 采用半经典模型处理外场与分子及等离激元的耦合, 结合实验数据探讨分子团簇的多激子动力学过程及其与等离激元耦合的动力学行为[17–19]. 在结果与相关实验定性一致的前提下, 进一步揭示MB分子在多模耦合效应中的物理机理. 本文第2部分介绍所采用的模型和理论方法, 第3部分是结果与讨论, 最后给出简要的结论.
-
在研究MB分子在不同溶液中的聚集行为的实验中[20], MB分子可以形成单体、二聚体及单体和二聚体的混合物. MB分子单体及二聚体能级特征如图1所示. 当MB分子形成二聚体时, 在能量表象上会产生能级劈裂形成对光激发的明暗能级, 若忽略激子-激子湮灭现象对动力学过程的影响, 我们仍可以将其当作二能级体系处理. 由于二聚体形成后具有相对稳定结构, 不易解体, 也不易形成多聚体, 随着MB染料浓度增大, 可以形成单体、二聚体混合物[20,21]. 本文将单体、二聚体视为独立结构进行处理(忽略更高聚集形态), 分子部分的哈密顿量可以写为
式中
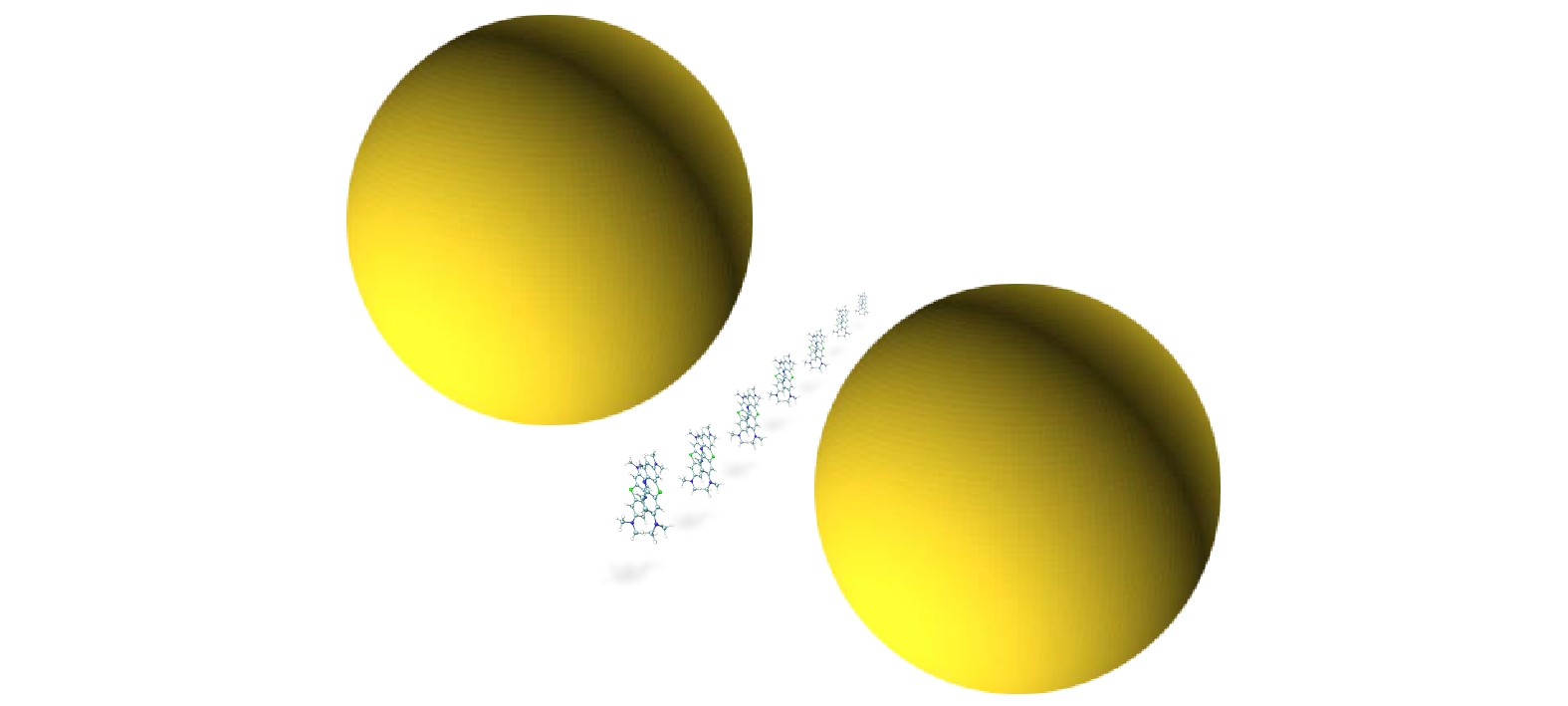
$ {H_{{\text{mon(dimer)}}}} $ 表示单体或二聚体哈密顿量;${H_{{\text{mon-dimer}}}}$ 表示单体与二聚体的耦合项; m(d)和n(f )为单体(二聚体)分子编号;$B_{m(d)}^ + $ 表示单体(二聚体)分子从基态到激发态的跃迁偶极算符, 满足费米子对易条件;$ {E_{m(d)}} $ 表示单体(二聚体)第1激发态能量;$ {J_{m(d)n(f)}} $ ,$ {U_{md}} $ 分别表示不同单体(二聚体)分子间、单体和二聚体间的耦合项. 我们考虑的二聚体中分子间距离大于1 nm, 可以忽略电子云重叠和直接的电子交换效应, 仅考虑分子整体电荷的分布不均匀性, 即偶极近似下计算其相互作用引起的分子间能量转移和相互影响.对于由MB单体、二聚体以及两个金属纳米粒子组成的复合体系, 其结构示意图如图2所示. 这里金属纳米粒子的引入构建了类似纳米腔的环境(两粒子中间区域视为纳米尺度腔体), 通过调整其尺寸、形状和相对位置模拟金属纳米腔, 从而调控复合体系光学性质.
在激光脉冲场作用下, 该复合结构的系统哈密顿量可描述为
设金属纳米结构为两个金属纳米粒子, 等离激元的哈密顿量
${H_{{\text{pl}}}}$ 可写为式中,
${E_N}$ 表示第N (N = 1, 2)个金属纳米粒子上产生的等离激元激发能;${J_{NM}}$ 表示不同金属纳米间等离激元的耦合;$C_N^ + $ 表示等离激元从其基态到激发态的跃迁算符:$ C_N^+=\left|\varphi_{\text{Ne}}\right\rangle\left\langle\varphi_{\text{Ng}}\right| $ , 其中$ \varphi_{\text{Ng}} $ 代表基态,$ \varphi_{\text{Ne}} $ 代表激发态, 满足玻色子对易条件.$ {H_{{\text{mol-pl}}}} $ 表示分子与等离激元耦合, 可写为式中,
$ {V_{mN}} $ 和$ {V_{dN}} $ 分别表示单体分子、二聚体分子和等离激元的耦合. 在偶极近似下, 单分子间、二聚体间的耦合均可以写为:$ V = \dfrac{{{\kappa _{m(d)N}}{\mu _{m(d)}}{\mu _N}}}{{R_{m(d)N}^3}} $ , 其中$ {\kappa _{m(d)N}} $ 是取向因子,$ {\mu _{m(d)}} $ 是分子单体或二聚体的偶极矩,$ {\mu _N} $ 是等离激元的等效偶极矩,$ {R_{m(d)N}} $ 是两个偶极子中心之间的距离. 取向因子$ {\kappa _{m(d)N}} $ 具体为式中,
$ {{{\boldsymbol{e}}}_{m(d)}} $ 和$ {{{\boldsymbol{e}}}_N} $ 分别是分子m(d)和等离激元N的过渡偶极矩方向的单位向量,$ {{{\boldsymbol{n}}}_{m(d)N}} $ 是连接两者质心的单位向量.外场与激子的耦合项
${H_{{\text{field}}}}(t)$ 可写为式中
$ {\boldsymbol{E}}(t) $ 为脉冲场;$ {\boldsymbol d}_m, {\boldsymbol d}_d,{\boldsymbol d}_N $ 是单体、二聚体、金属纳米粒子的跃迁偶极矩;$ {R_m}(t) $ ,$ {R_d}(t) $ ,${R_N}(t)$ 分别表示单体分子、二聚体分子、等离激元激发的Rabi能量, 具体形式可写为在密度矩阵理论框架下, 采用马尔科夫近似[22], 系统的量子主方程为
耗散项主要由分子耗散与等离激元耗散两部分组成, 其中, 分子耗散主要为分子退相干耗散, 可写为
式中,
$ \gamma _m^{\left( {{\text{pd}}} \right)} $ 为分子基态激发态间的退相干速率. 等离激元耗散可表示为式中,
${\gamma _N}$ 为等离激元的耗散速率.采用双格点近似[23], 引入
$ {\tilde \omega _{m(d)}} = {E_{m(d)}}/ \hbar + {\text{i}}{\gamma _{m(d)}} $ ,${\tilde \varOmega _{M(N)}} = {E_{M(N)}}/\hbar + {\text{i}}{\gamma _{M(N)}}/2$ , 得到以下动力学方程:式中m, n, k用于描述单体分子; d, f, p用于描述二聚体分子; N, M, K用于描述等离激元.
分子团簇处于稳态时激发态的电子占据数为
其中
$P_m^{\left( {{\text{ss}}} \right)}$ 是第m个单体分子达到稳态时的激发态布居,$P_d^{\left( {{\text{ss}}} \right)}$ 是第d个二聚体分子达到稳态时的激发态布居, 布居数随入射光频率的变化图像可以反映分子的吸收谱特征[24]. -
将金属纳米腔中的MB分子单体和二聚体作为研究对象, 相关参数如分子个数N、偶极矩d、耗散系数γ和外场强度E等列于表1中, 其中单体、二聚体激发态能量, 金属纳米粒子偶极矩取自文献[21,25]. 由于所研究的动力学过程在皮秒范围, 而分子单体及二聚体的寿命通常在纳秒量级, 所以文中取激发态到基态的衰变率
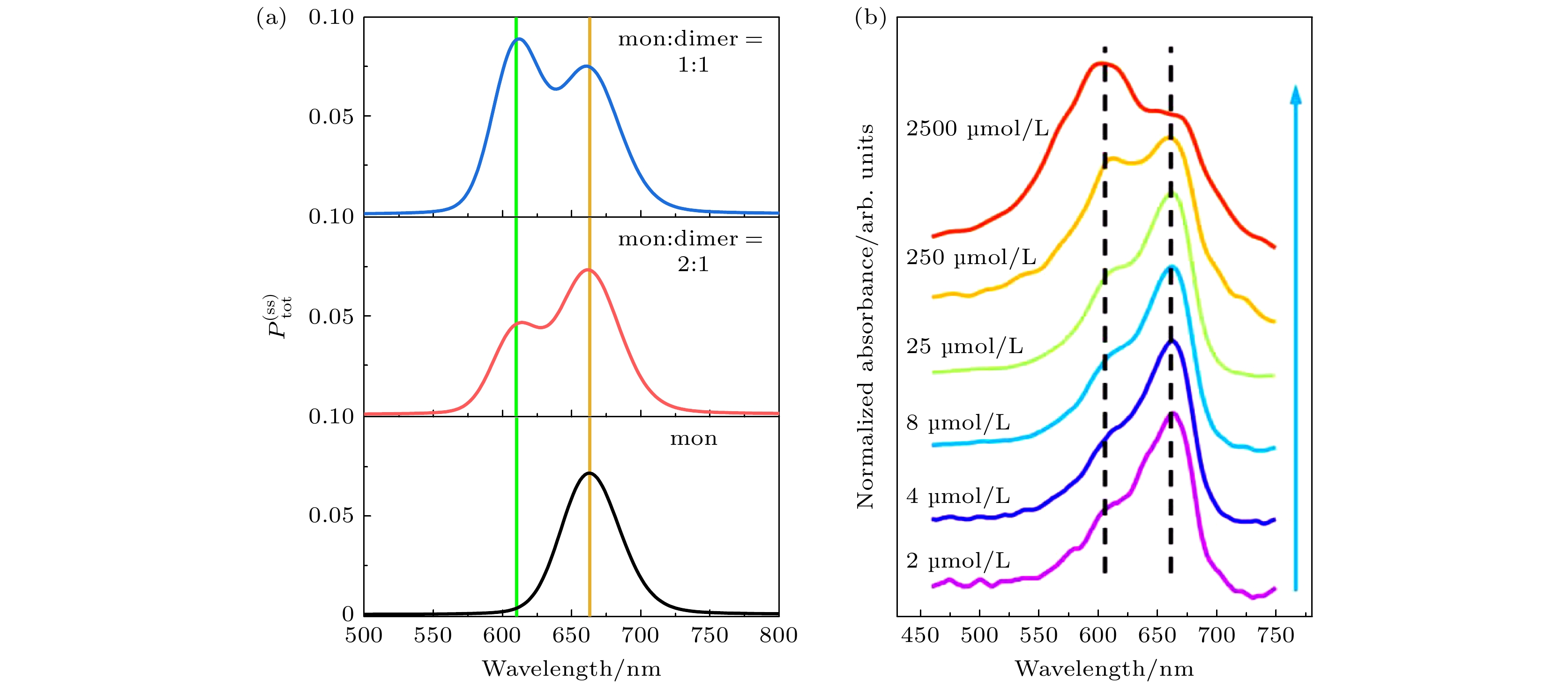
$ {k_m} = {k_d} = 0 $ . 在研究MB溶液中形态共存及其比例变化的实验中[26], MB溶液同时包含单体和二聚体形态. 通过调节其溶度, 可以获得分子聚集体中不同比例的单体与二聚体分布. 在我们的计算中, 设MB分子单体和二聚体的总数保持一定(设$ {N_{{{\mathrm{mon}}}}}{+}{N_{{{\mathrm{dimer}}}}} = 12 $ ), 用单体和二聚体数量的比例来表示溶液的浓度. 溶液中MB染料的单体偶极矩为3.5 D, 在分子间距为2.67 Å的间距下, 二聚体偶极矩约为3.8 D. 如图3(a)所示, 在强脉冲电场(激发光脉冲面积$ a_{\text{p}}= E_0\tau_{\text{p}}= 10^6\; \text{ps}\cdot\text{V/m}, $ 激发光脉冲宽度$\tau_{\text{p}}=20\; \text{fs} $ )的激发下, 研究了不同组成比例的MB分子聚集体对波长的响应, 计算了其光脉冲的动态响应过程. 可以看到在单体形态下, MB分子仅在663 nm (橙色竖线)处有明显的吸收峰; 随着二聚体分子比例的增大, 610 nm (绿色竖线)附近出现了新的吸收峰, 且其强度显著增强. 这表明在激光脉冲场的作用下, 单体和二聚体分子同时被激发. 由于二聚体的明能级偶极矩大于单体分子, 其比例的增加导致相应频率的吸收峰发生显著变化, 变化趋势和峰值比例与不同浓度下MB染料的光吸收光谱一致[21] (图3(b)). 采用不同组成比例的单分子和H型二聚体组合, 可以有效模拟MB分子聚集体在溶液中的吸收行为.为了研究不同浓度的MB溶液与杂化纳米结构的耦合效应, 选用单体分子表示低浓度MB溶液, 单体与二聚体以1∶1组成的分子团簇表示高浓度溶液. 将由两个金属纳米粒子组成的复合体看作杂化纳米结构, 把单体及单体与二聚体的复合体置于两个金属纳米粒子中间. 在强场短脉冲(
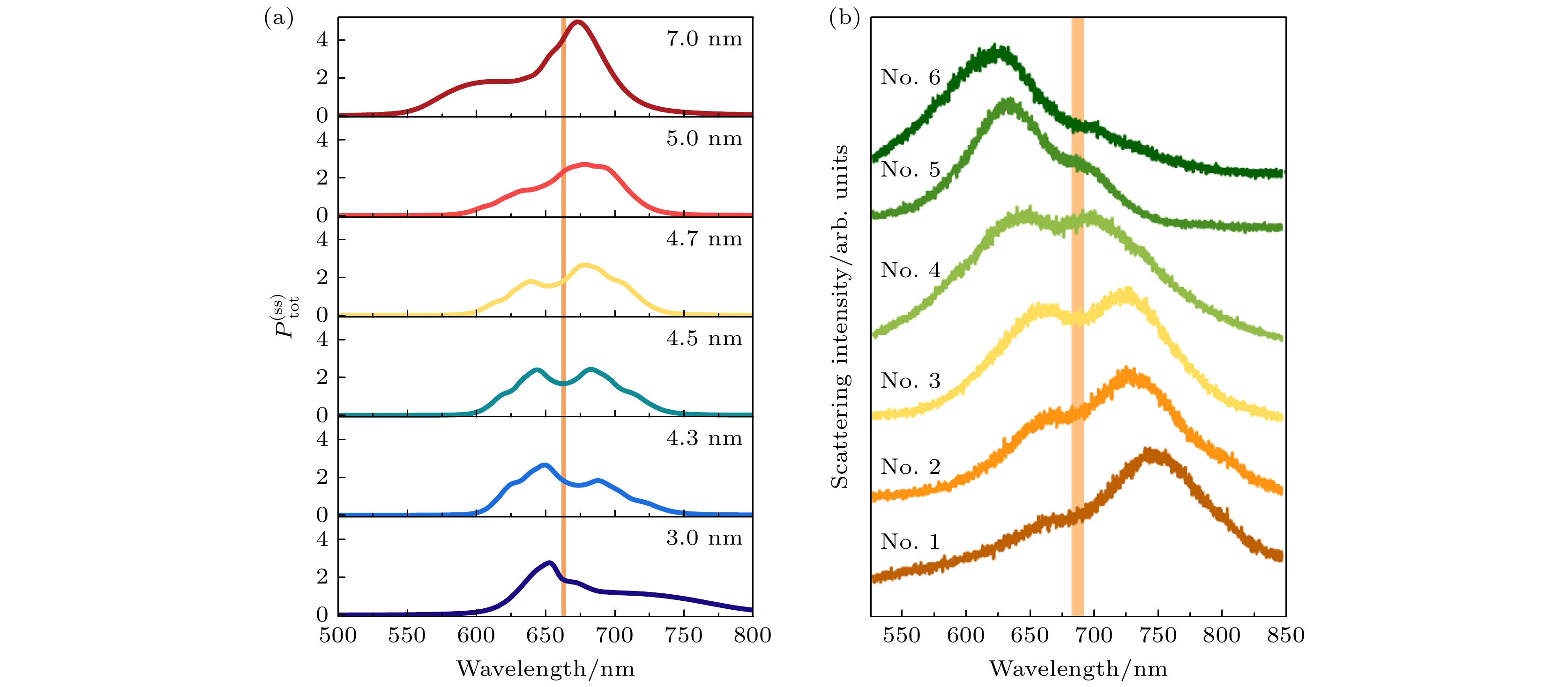
$ {a}_{\text{p}}= {10}^{6}\;\text{ps}\cdot \text{V/m}, \text{ }{\tau }_{\text{p}}=20\;\text{fs} $ )作用下, 图4(a)给出了不同间距的双金属纳米粒子(两个金属纳米粒子最近邻表面间的间距分别为3.0, 4.3, 4.5, 4.7, 5.0, 7.0 nm)与MB单体复合结构的稳态激发态布居$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化. 可以看到, 单体分子与不同间距的双金属纳米粒子均在663 nm (橙色竖线)附近发生耦合劈裂, 形成两个新的光学响应峰, 特别是当两个金属纳米粒子表面间距为4.5 nm时, 复合体的光学响应峰呈明显的对称性. 这是因为在4.5 nm的间距下, 两个金属纳米粒子共振耦合形成的等离激元耦合态与MB单体激子态能级共振, 导致能级耦合劈裂. 随着金属纳米粒子间距的增大, 等离激元的共振耦合态发生蓝移, 不再与单体激子态共振, 导致复合体的耦合杂化态发生变化, 表现为共振峰对称性的减弱. 通过计算不同波长下的稳态激发态布居$ P_{{\text{tot}}}^{{\text{(ss)}}} $ , 可以实现对光学吸收谱的模拟. 图4(b)给出了低浓度MB染料与银纳米腔构成的杂化纳米结构的光学散射谱[21]. 我们发现$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 的峰值与实验观测到的散射谱的峰值呈现对称性特征, 符合实验规律. 这证明我们采用的双金属纳米粒子复合结构模型能够模拟实验中的银纳米腔体系, 且分子复合体与纳米腔中的等离激元耦合形成了杂化态.下文采用两个金属纳米粒子模拟金属纳米腔, 进一步研究高浓度MB溶液与双金属纳米粒子间的耦合行为. 这里涉及到多模耦合, 多模耦合是指多个不同模式(单体的激子态、二聚体的激子态、等离激元态)之间的同时相互作用. 图5给出了不同间距(分别为3.0, 4.3, 4.5, 4.7, 5.0, 7.0 nm)的双金属纳米粒子与MB分子团簇(单体∶二聚体 = 1∶1)所组成的复合体系(下文简称为MB-双金属复合体)在不同波长下的稳态激发态布居
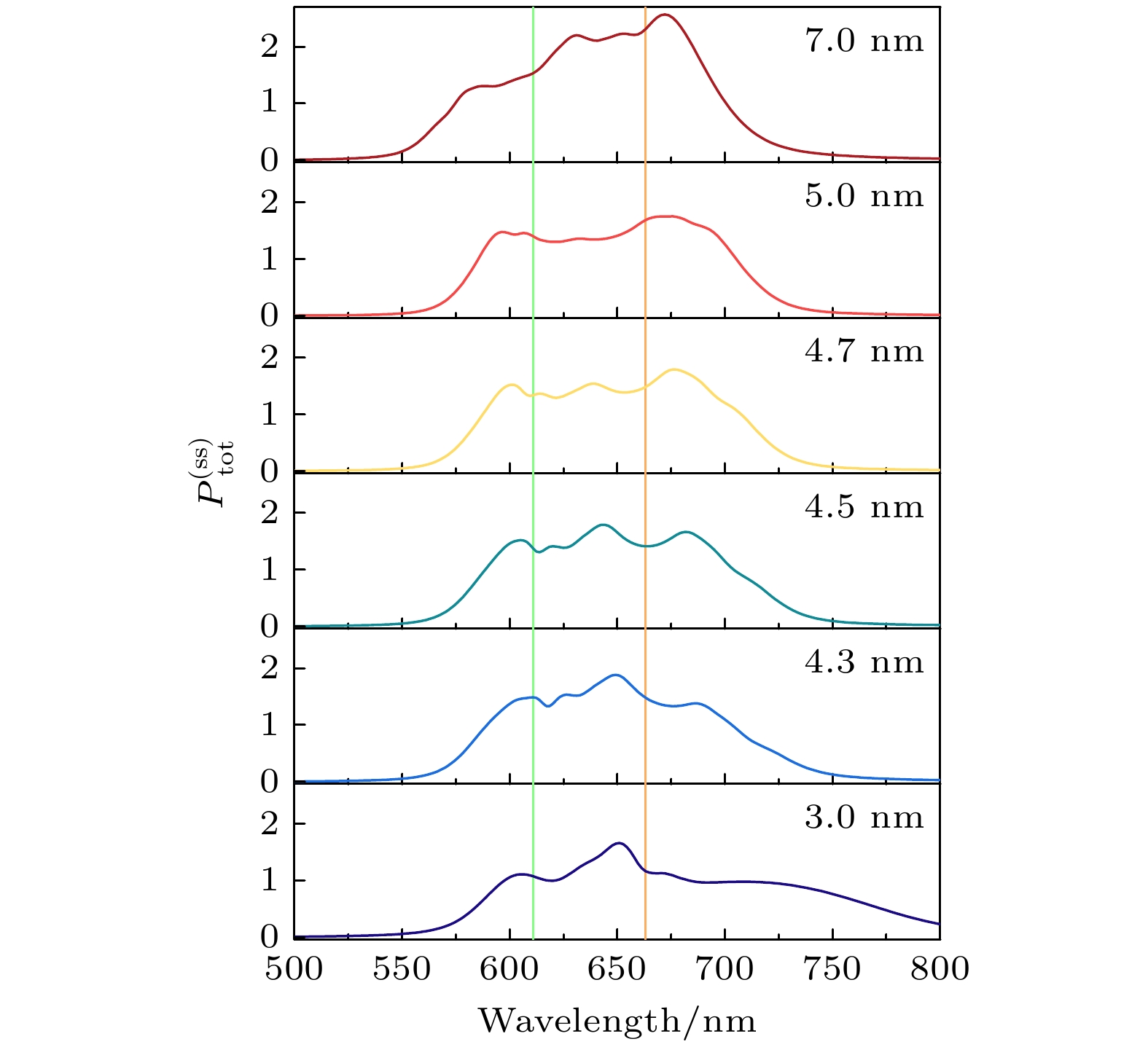
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ . 在波长663 nm (橙色竖线)和610 nm (绿色竖线)处, 观察到单体和二聚体混合体系与双金属纳米粒子间发生了耦合劈裂, 形成了多个光学响应峰. 值得注意的是, 随着金属纳米粒子间距的增大, 光学响应峰向短波方向移动. 这一现象的产生机制在于双金属纳米粒子共振形成的等离激元态与MB单体激子态和二聚体激子态发生耦合作用, 且随着金属纳米粒子间距的增大, 等离激元共振吸收峰发生蓝移, 导致MB单体和二聚体与双金属纳米粒子耦合产生的杂化态也蓝移, 从而形成了一种可调谐的多模耦合态.为深入研究MB分子团簇在金属纳米腔中不同激发脉冲下的动力学过程, 采用脉宽为20 fs的短脉冲激发MB分子团簇与双金属纳米粒子的复合体系, 并计算不同光学响应频率下团簇内分子激发态布居
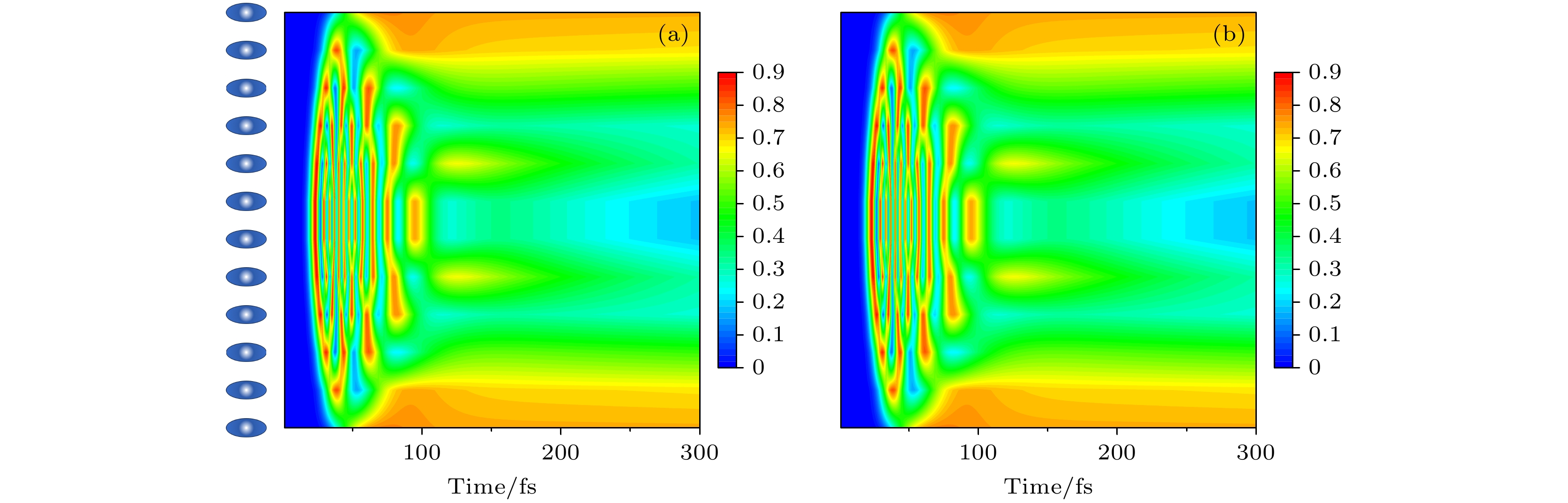
$ {P_m} $ 和$ {P_d} $ 随时间的演变. 图6中蓝色彩球表示MB单体, 图中的纵坐标表示分子数, 彩色图代表的是分子激发态布居. 由于间距为4.5 nm的双金属纳米粒子与MB单体共振, 计算了此条件下($ \hbar {\omega _0} = 1.82 \;{{\mathrm{eV}}} $ (图6(a))和$ \hbar {\omega _0} = 1.93\; {{\mathrm{eV}}} $ (图6(b)))外场激发时分子单体激发态布居$ {P_m} $ 随时间的演变. 可以发现, 在这两个共振能量下, 激发态布居呈对称性分布, 分子链中心的分子产生较强的Rabi振荡, 并迅速达到稳态, 而两侧分子的激发态布居随时间变化缓慢减小. 说明当MB分子中的激子与纳米腔中的等离激元的不同模式处于共振态时, 其杂化态特征类似. 具体而言, 邻近双金属纳米粒子的激子耦合作用强, 促进了能量转移, 加速了激子耗散过程, 而随着金属纳米粒子与分子间距离的增大, 耦合强度减弱, 激子的耗散速率降低.图7进一步给出了3种不同共振能量
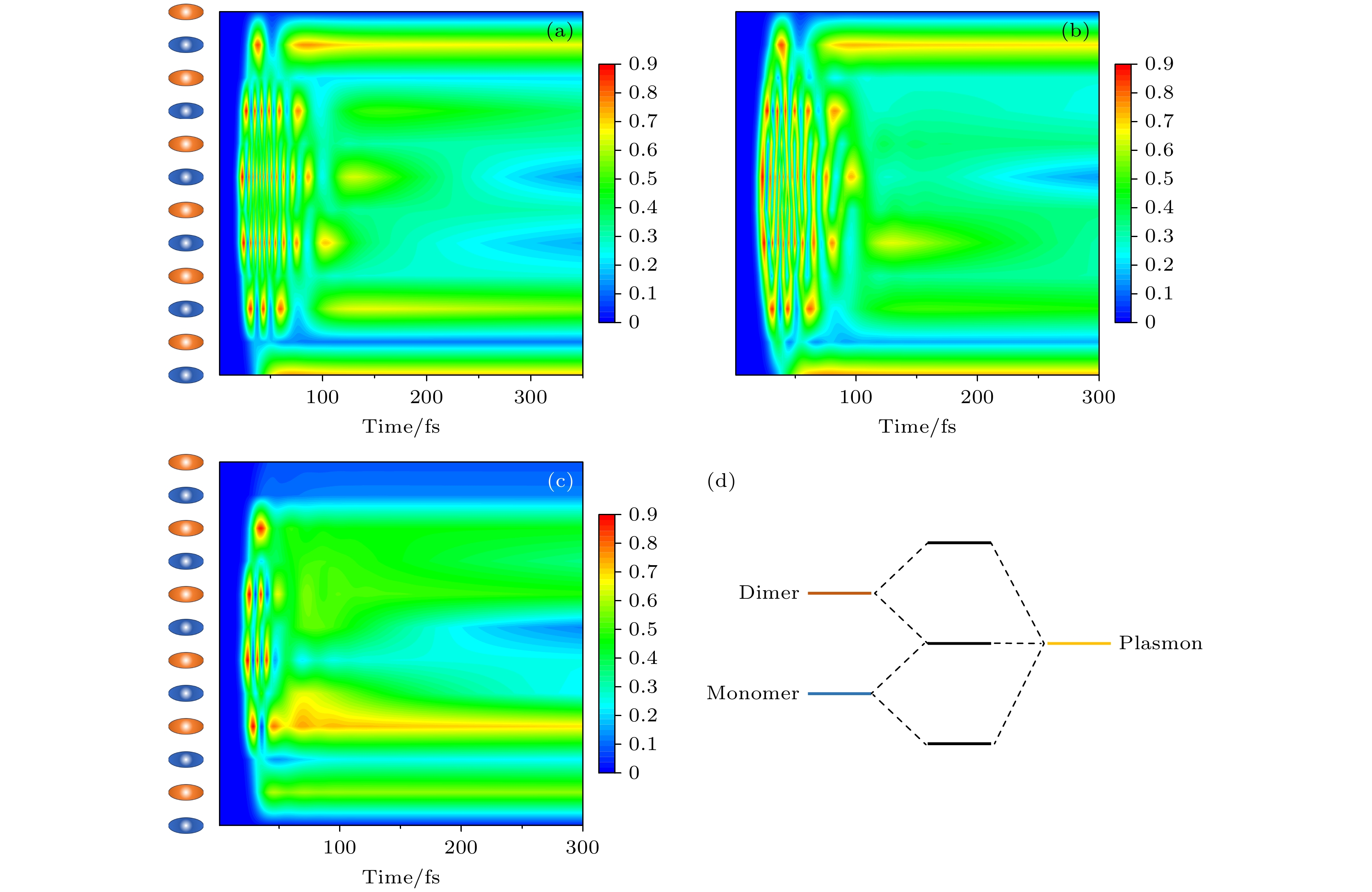
$( \hbar {\omega _0} = 1.82 \;{{\mathrm{eV}}} $ ,$ \hbar {\omega _0} = 1.93 \;{{\mathrm{eV}}} $ ,$ \hbar {\omega _0} = 2.05 \;{{\mathrm{eV}}}$ )下, MB-双金属复合体中分子激发态布居$ {P_m} $ 和$ {P_d} $ 随时间的演变. 图中的红色和蓝色彩球代表MB分子团簇(单体∶二聚体 = 1∶1), 纵坐标表示分子数, 彩色图代表的是分子激发态布居. 结果发现, 在$ \hbar {\omega _0} = 1.82 \;{{\mathrm{eV}}} $ 的脉冲激发下, 金属纳米等离激元仅与MB单体发生耦合, 表现出明显的Rabi振荡现象, 当能量为$ \hbar {\omega _0} = 2.05 \;{{\mathrm{eV}}} $ (图7(c))时, 单体分子不再表现出Rabi振荡, 此时金属纳米等离激元仅与MB二聚体发生耦合. 而在$ \hbar {\omega _0} = 1.93 \;{{\mathrm{eV}}} $ 的脉冲激发下时, 单体和二聚体分子均显示出明显的耦合振荡现象. 表明单体激子态、二聚体激子态及等离激元态形成了多模杂化态, 其能级杂化示意图如图7(d)所示.比较图7(b)与图6(b)能够发现, 图7(b)中分子激发态布居的对称性分布不如图6(b)显著, 且图7(b)中单体分子的激发态占据数高于二聚体激子, Rabi振荡现象也更加明显. 这主要是因为双金属纳米粒子形成的等离激元与MB单体激子态之间有较好的共振, 因此等离激元态与单体激子态间的耦合作用更强, 从而提高了能量转移效率.
为深入探究MB分子团簇与双金属纳米粒子间的耦合行为与激光脉冲场的关系. 针对确定的脉冲场能量
$ {a_{\text{p}}} = {10^6}\;{{\mathrm{ps}}} \cdot {{\mathrm{V/m}}} $ ($ {a_{\text{p}}} = {E_0}{\tau _{\text{p}}} $ ), 计算了不同脉冲宽度$ {\tau _{\text{p}}} $ 激发下复合结构的稳态激发态布居$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 的变化. 图8(a)所示为不同脉冲宽度(10, 20, 50 fs)对MB单体分子与金属纳米粒子的复合结构光学响应的影响. 随着脉冲宽度的增大, 光学响应峰的宽度变窄. 这是因为长脉冲具有较窄的激发频域, 减少了与等离激元耦合的激子数目, 从而减弱了耦合强度. 而在单体分子和二聚体与金属纳米粒子的复合体系中, 如图8(b)所示, 当使用$ {\tau _{\text{p}}} = 50{\text{ fs}} $ 脉冲激光激发时, 仅在663 nm (橙色竖线)处观察到耦合劈裂现象, 形成新的光学响应峰, 然而随着脉冲宽度的减小, 610 nm (绿色竖线)附近也出现了耦合劈裂, 产生了更多光学响应峰. 说明$ {\tau _{\text{p}}} = {\text{ }}50{\text{ fs}} $ 的脉冲激发下, 由于激发频域展宽很窄, 二聚体激子态与等离激元态间没有发生耦合; 反之, 随着脉冲宽度的减小, 激发频域变大, 出现了多模耦合态. 从图8(a)可以看到, 在不同脉冲宽度下, 单体和二聚体混合体系与双金属纳米粒子耦合劈裂所形成峰谷都小于单体与金属纳米粒子耦合产生的峰谷. 这是因为单体与金属纳米粒子之间的直接耦合作用较强, 而二聚体分子的激子态与等离激元态之间的耦合受到内部相互作用的影响, 导致耦合效率相对较低.此外, 考虑到等离激元具有超短寿命, 复合系统耗散性质对耦合行为也会有显著影响, 图9给出了短脉冲强场(
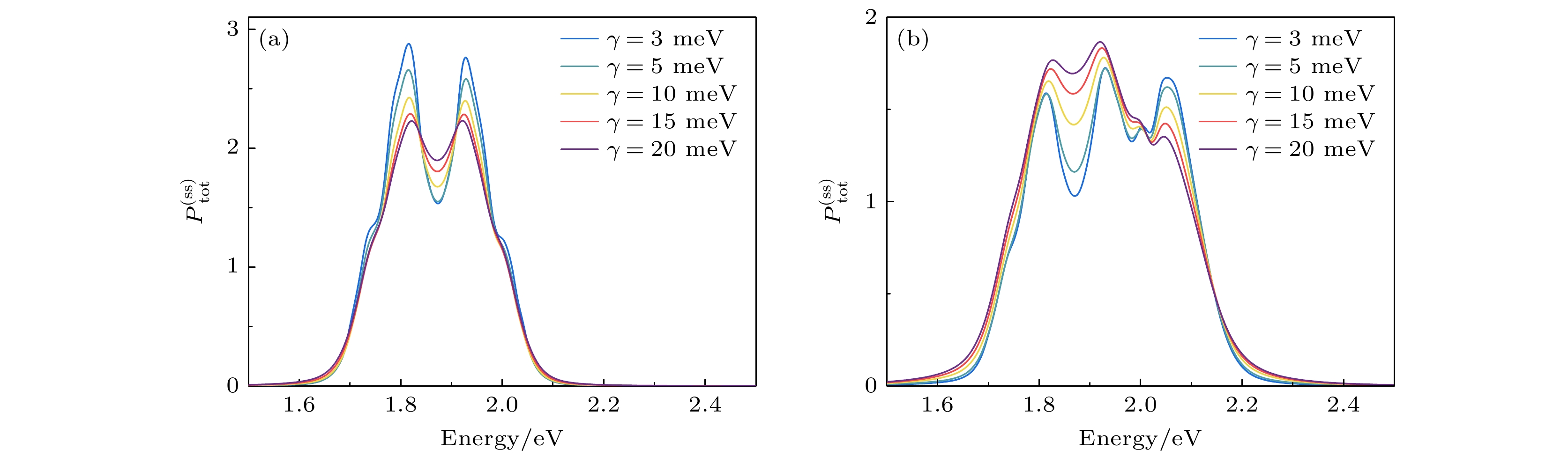
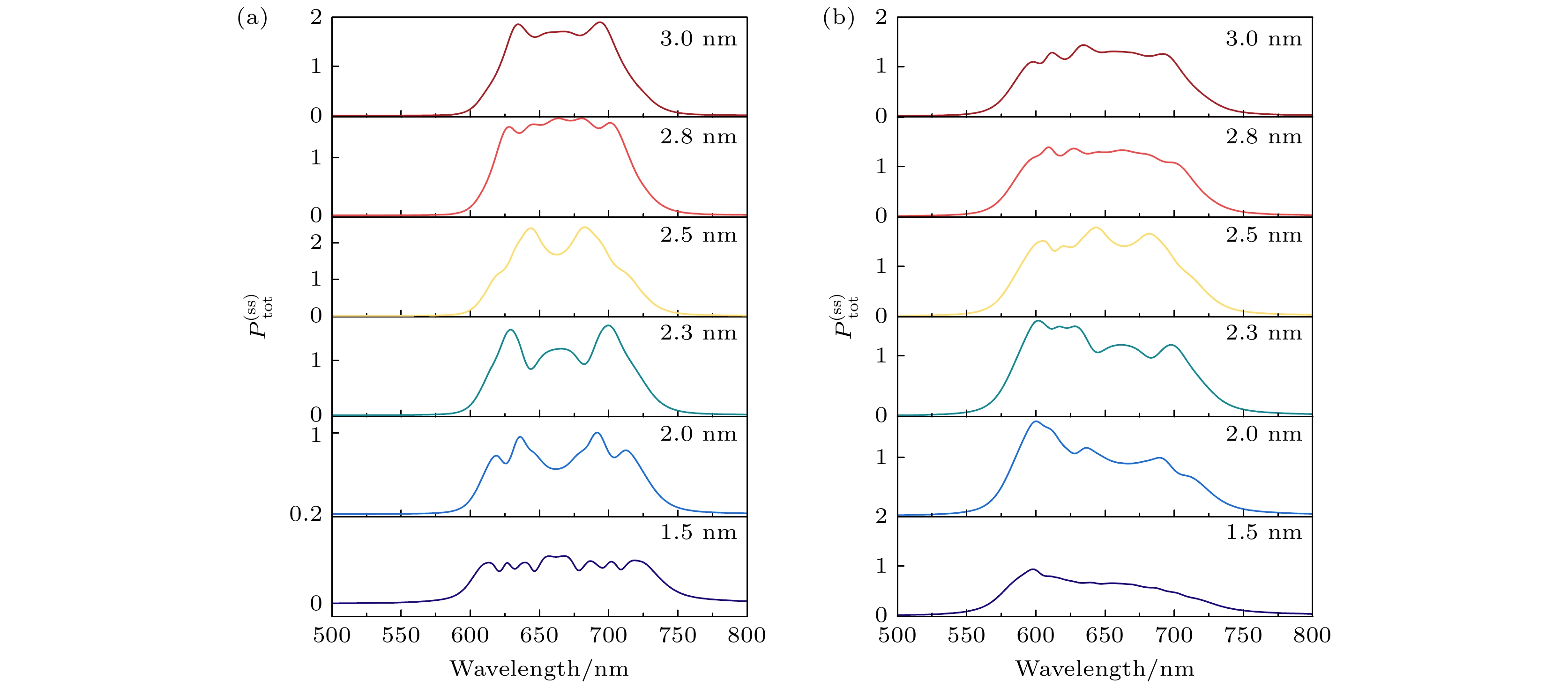
$ {a}_{\text{p}}={10}^{6}\;\text{ps}\cdot \text{V/m}, \text{ }{\tau }_{\text{p}}=20\;\text{fs} $ )条件下, 不同激子退相干速率对耦合体系的影响. 可以看到, 对于单体复合体, 激子的退相干速率越小, 激子态寿命越长, 耦合强度越大, 表现为耦合峰高越大. 对于MB-双金属复合体, 随着激子寿命的增大($ \gamma $ 减小), 等离激元与单体耦合劈裂峰峰值增大, 但与二聚体激子耦合劈裂峰峰值则减小. 说明在激子寿命较大时(小$ \gamma $ 值)多模耦合现象更显著.值得注意的是, 激子-激子耦合是影响分子团簇与等离激元耦合的重要因素之一, 在我们的偶极模型中, 分子或二聚体间间距越小, 耦合越强. 在单体与金属纳米粒子的复合体系中, 分子间距减小, 光学响应峰数量增多(图10(a)). 在间距为1.5 nm时其光学响应峰的峰值大幅减小, 大约是其他分子间距下峰值的十分之一, 表明在这个耦合强度下激子间的能量转移大大增强, 杂化态的数量也随之增加, 形成了离域的激子态与等离激元耦合. 离域激子与等离激元进一步耦合作用下, 激子的耗散速率明显加快, 导致光学响应峰的峰值大幅减小. 对于混合体系与金属纳米粒子的复合体系中(图10(b)), 在与单体相同分子间距下, MB二聚体的激子共振态附近表现出明显的光学响应峰. 随着分子间距离的减小, 单体与等离激元耦合的光学响应峰峰值相对增加, 相较于单体激子态, 二聚体激子态的耗散速率随分子间距变化缓慢, 因此在相应的波长下, 光学响应峰的峰值变化不大.
-
本文将MB分子单体、H型二聚体简化为二能级模型, 并将两个金属纳米粒子之间的间隙视为纳米腔, 应用密度矩阵和平均场近似方法, 基于量子主方程, 深入探讨了MB分子团簇在纳米腔中的复合体系耦合动力学行为. 研究表明, 在强短脉冲场的激发下, MB单体与纳米腔产生单模耦合, 形成新的杂化态; 而当分子团簇由单体和二聚体混合构成时, 则与纳米腔形成多模耦合态, 从而扩展激子的激发频域, 这与实验中不同浓度MB染料与金属纳米腔所组成的纳米杂化结构的散射光谱相吻合. 同时对不同杂化能级下的耦合动力学行为进行了分析, 揭示了多模耦合态的形成是单体激子态、二聚体激子态及等离激元态共同作用的结果. 在不同脉冲场的激发下, 随着脉冲宽度的减小, 更多的激子态和等离激元态被激发, 增强了耦合作用并进一步扩展了激子的激发频域. 在短脉冲激励下, 等比例的单体、二聚体与双金属纳米粒子组成的复合体系明显表现出多模耦合现象. 研究还发现, 激子退相干速率直接影响MB分子团簇与双金属纳米粒子间的耦合效应, 耦合强度随激子退相干速率的减小而增大. 当分子团簇包含多种激子态时, 受等离子态共振频率的影响, 不同耦合杂化态的光学响应峰会呈现相反的变化趋势. 此外, 分子间距是影响分子团簇与双金属纳米粒子耦合行为的重要因素, 分子间距较小时, 激子间耦合作用增强, 导致杂化能级劈裂增大, 促进更多激子与等离激元的耦合. 在激子-激子耦合与激子-等离激元耦合共同作用下, 激子耗散速率加快, 当激子态与等离激元态共振时, 该现象尤为明显.
亚甲基蓝分子团簇与双金属纳米结构的多模耦合效应
Multimodal coupling effect between methylene blue molecular clusters and dual metal nanoparticles
-
摘要: 基于亚甲基蓝(methylene Blue, MB)-银纳米腔体系的双拉比分裂实验, 建立了MB分子团簇和双金属纳米粒子结构模型, 在密度矩阵理论框架下, 应用偶极近似方法, 计算了MB分子团簇与双金属纳米粒子形成的杂化态的耦合动力学过程, 研究了多激子态-等离激元相互作用下的多模耦合效应, 得到了与实验定性一致的结果. 通过短脉冲激发, 在更大的激发频域下研究激子态和等离激元的耦合态. 探讨了激子退相干速率和分子间距离对耦合过程的影响、分子与等离激元的耦合强度随激子退相干时间缩短而增强的现象, 由于团簇内离域激子与等离激元耦合相互作用, 复合体系内可以产生更多杂化能级, 使得光学响应峰发生相应变化. 通过对分子团簇与金属纳米结构的多模耦合的机理研究, 为设计高效光捕获和转换材料提供了理论依据和思路.Abstract: Methylene blue (MB), as an organic dye, exhibits rich photophysical properties when interacting with metal nanoparticles. Based on the double Rabi splitting experiment of MB molecular clusters and dual metal nanoparticles in a silver nanocavity, a cluster model composed of MB molecular monomers and dimers is developed and placed in a nanocavity environment consisting of two metal nanoparticles in this work. The density matrix theory framework combined with dipole approximation is used to calculate the coupling dynamics of the hybrid state formed between MB molecular clusters and dual metal nanoparticles. The semi-classical model is used to deal with the coupling of external fieldsand molecules and plasmons, and the multi-mode coupling effect caused by the interaction between multi-exciton states and plasmons is discussed. The results are qualitatively consistent with experimental results. The research results show that under the excitation of strong short pulse fields, single-mode coupling occurs mainly between MB monomers and nanocavities, forming new hybrid states. When the molecular cluster is composed of a mixture of monomers and dimers, it forms a multi-mode coupling state with the nanocavity. As the pulse width decreases, more exciton states and plasmon states are activated, which not only enhances the coupling effect but also further expands the excitation range of excitons. The effects of exciton decoherence rate and intermolecular distance on the coupling process are explored. The results show that the coupling strength increases with the exciton decoherence rate decreasing, that is, the longer the exciton decoherence time, the greater the coupling strength will be. This is because a longer decoherence time means that the exciton state has a longer lifetime and can more effectively couple with the plasmonic state. Meanwhile, molecular spacing is also an important factor affecting coupling behaviors. When the intermolecular distance is small, the coupling between excitons is enhanced, which leads to an increase of the splitting of hybrid energy levels, thereby promoting more excitons to couple with plasmons. The study of the multi-mode coupling mechanism between MB molecular clusters and dual metal nanoparticle structures reveals that under the interaction between multi-exciton states and plasmons, more hybrid energy levels can be generated in the composite system, leading the optical response peak to change accordingly. This work not only deepens our understanding of the coupling between molecules and plasmons but also provides theoretical insights for designing efficient light harvesting and conversion materials.
-
Key words:
- methylene blue molecular clusters /
- metal nanoparticles /
- optical response /
- multimode coupling .
-

-
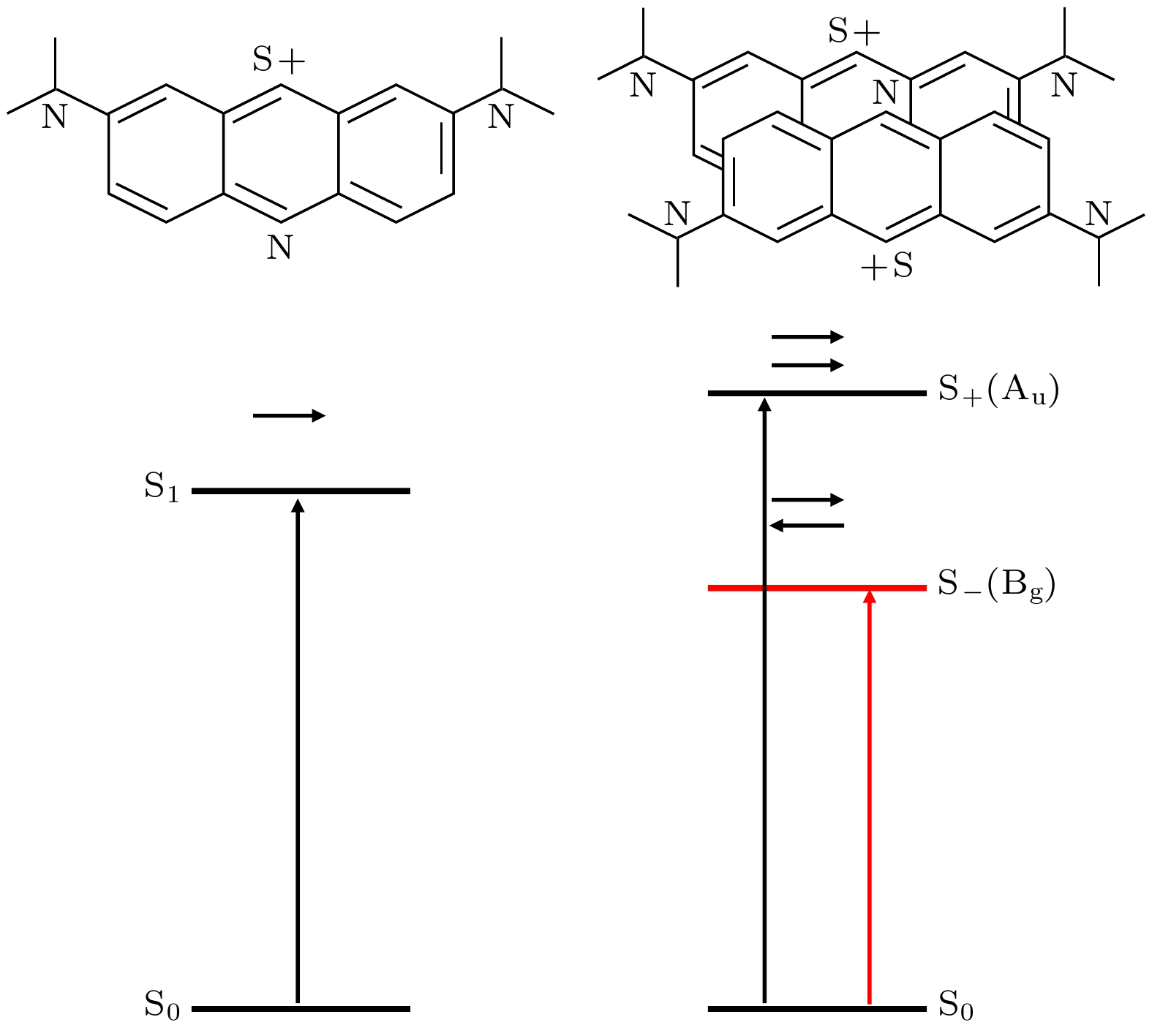
图 1 MB分子单体、H型二聚体的分子结构图及其能级图(横向箭头表示偶极的方向, S0表示单体或二聚体的基态, S1表示单体的第1激发态, S+和S–分别表示二聚体的两个劈裂态)
Figure 1. Molecular structure diagram and energy level diagram of MB monomer and H-dimer (The horizontal arrow indicates the direction of the dipole, S0 represents the ground state of the monomer or dimer, S1 represents the first excited state of the monomer, and S+ and S– represent the two splitting states of the dimer, respectively).
图 3 (a) 不同数值比例的MB分子团簇的稳态激发态布居
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化; (b)不同数值比例的MB分子团簇吸收谱, 蓝色箭头表示染料浓度增大[21]Figure 3. (a) Steady-state excited state population of MB molecular clusters with different numerical ratios as a function of wavelength; (b) absorption spectra of MB clusters at different numerical ratios, with blue arrows indicating increased dye concentrations[21]
图 4 (a) 不同间距的双金属纳米粒子与MB单体所组成的复合结构的稳态激发态布居
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化; (b) 不同尺寸的银纳米立方体与低浓度MB溶液所组成的杂化纳米结构的散射光谱[21]Figure 4. (a) Steady-state excited state population of composite structures composed of dual metal nanoparticles with different spacing and MB monomers as a function of wavelength; (b) scattering spectra of hybrid nanostructures composed of silver nanocubes of different sizes and low-concentration MB solution[21].
图 5 不同间距的MB-双金属复合体的稳态激发态布居
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化(绿色和橙色的竖线分别表示610 nm和663 nm处光学响应峰)Figure 5. Steady-state excited state population of MB and dual metal nanoparticles complex with different spacing varies with wavelength (The green and orange vertical lines represent the optical response peaks at 610 nm and 663 nm, respectively).
图 6 MB单体与双金属纳米粒子所组成的复合结构的分子激发态布居
$ {P_m} $ 随时间的演变 (a)$ \hbar {\omega _0} = 1.82\; {{\mathrm{eV}}} $ ; (b)$ \hbar {\omega _0} = 1.93 \; {{\mathrm{eV}}} $ Figure 6. Evolution of molecular excited state population over time in the composite structure composed of MB monomer and dual metal nanoparticles: (a)
$ \hbar {\omega _0} = 1.82 \; {{\mathrm{eV}}} $ ; (b)$ \hbar {\omega _0} = 1.93 \; {{\mathrm{eV}}} $ .图 7 MB-双金属复合体的分子激发态布居
$ {P_m} $ 和$ {P_d} $ 随时间的演变, 其中(a)$ \hbar {\omega _0} = 1.82\; {{\mathrm{eV}}} $ , (b)$ \hbar {\omega _0} = 1.93 \; {{\mathrm{eV}}} $ , (c)$ \hbar {\omega _0} = 2.05\; {{\mathrm{eV}}} $ ; (d)复合体系的杂化能级示意图Figure 7. Evolution of molecular excited state population of MB and dual metal nanoparticles complex over time: (a)
$ \hbar {\omega _0} = 1.82\; {{\mathrm{eV}}} $ ; (b)$ \hbar {\omega _0} = 1.93\; {{\mathrm{eV}}} $ ; (c)$ \hbar {\omega _0} = 2.05\; {{\mathrm{eV}}}$ . (d) Schematic diagram of hybrid energy levels in composite systems.图 8 (a)不同脉冲宽度下, MB单体与双金属纳米粒子所组成的复合结构的稳态激发态布居
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化; (b)不同脉冲宽度下, MB-双金属复合体系的稳态激发态布居$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化Figure 8. (a) Steady-state excited state population of the composite structure composed of MB monomer and dual metal nanoparticles as a function of wavelength under different pulse widths; (b) the steady-state excited state population of MB and dual metal nanoparticles complex as a function of wavelength under different pulse widths.
图 9 (a)不同激子退相干速率下, MB单体与双金属纳米粒子所组成复合结构的稳态激发态布居
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随光子能量的变化; (b)不同激子退相干速率下, MB-双金属复合体的稳态激发态布居$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随光子能量的变化Figure 9. (a) Steady-state excited state population of the composite structure composed of MB monomer and dual metal nanoparticles as a function of photon energy at different exciton decoherence rates; (b) the steady-state excited state population of MB and dual metal nanoparticles complex as a function of photon energy at different exciton decoherence rates.
图 10 (a)不同分子间距下, MB单体与双金属纳米粒子所组成的复合结构的稳态激发态布居
$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化; (b)不同分子间距下, MB-双金属复合体的稳态激发态布居$ P_{{\text{tot}}}^{{\text{(ss)}}} $ 随波长的变化Figure 10. (a) Steady-state excited state population of the composite structure composed of MB monomer and dual metal nanoparticles as a function of wavelength at different molecular spacings; (b) the steady-state excited state population of MB and dual metal nanoparticles complex as a function of wavelength at different molecular spacings.
表 1 激子-等离激元耦合研究参数设置
Table 1. Parameter settings for exciton plasmon coupling research.
参数名称 数值 $ {N_{{{\mathrm{mon}}}}} $ 12, 8, 6 $ {N_{{{\mathrm{dimer}}}}} $ 0, 4, 6 $ {E_{{{\mathrm{mon}}}}} $ /eV1.87[21] $ {E_{{{\mathrm{dimer}}}}} $ /eV2.03[21] $ {E_{{{\mathrm{pl}}}}} $ /eV2.60 $ {d_{{{\mathrm{mon}}}}} $ /D3.5 $ {d_{{{\mathrm{dimer}}}}} $ /D3.8 $ {d_{{{\mathrm{pl}}}}} $ /D2925[25] $ \gamma $ / meV3, 5, 10, 15, 20 $ {\gamma _{{{\mathrm{pl}}}}} $ / meV57 $ {E_0} $ /(V·m–1)105—107 $ {\tau _{\text{p}}} $ /fs10, 20, 50 -
[1] Jose D, Matthiesen J E, Parsons C, Sorensen C M, Klabunde K J 2012 J. Phys. Chem. Lett. 3 885 doi: 10.1021/jz201640e [2] Jiang X X, Dai J G, Wang H B, Geng Y H, Yan D H 2007 Chem. Phys. Lett. 446 329 doi: 10.1016/j.cplett.2007.08.042 [3] Winder C, Andreev A, Sitter H, Matt G, Sariciftci N S, Meissner D 2003 Synthetic Met. 139 573 doi: 10.1016/S0379-6779(03)00287-X [4] Mousavizadegan M, Shalileh F, Mostajabodavati S, Mohammadi J, Hosseini M 2024 TRAC 177 117794 doi: 10.1016/j.trac.2024.117794 [5] Liu J W, Wu D, Wu Y N, Shi Y H, Liu W Q, Sun Z W, Li G L 2024 TRAC 177 117793 doi: 10.1016/j.trac.2024.117793 [6] Mohan B, Sasaki Y, Minami T 2024 Anal. Chim. Acta 1313 342741 doi: 10.1016/j.aca.2024.342741 [7] Sasikala V, Chitra K 2018 J. Opt. 47 307 doi: 10.1007/s12596-018-0452-3 [8] Bratati D, Resmi M, Elaganuru B, Ramachandrarao Y 2023 Proc. SPIE 12638 126380Y doi: 10.1117/12.2670075 [9] Xiong C X, Li H J, Xu H, Zhao M Z, Zhang B H, Liu C, Wu K 2019 Opt. Express 27 17718 doi: 10.1364/OE.27.017718 [10] 赵珂, 刘朋伟, 韩广超 2011 物理学报 60 124216 doi: 10.7498/aps.60.124216 Zhao K, Liu P W, Han G C 2011 Acta Phys. Sin. 60 124216 doi: 10.7498/aps.60.124216 [11] Gil E S, Giustini A, Accomasso D, Granucci G 2024 J. Chem. Theory Comput. 20 8437 doi: 10.1021/acs.jctc.4c00886 [12] Zhang Y X, Wang Y H 2017 RSC Adv. 7 45129 doi: 10.1039/C7RA07551K [13] Chang K N, Gao J, Wang L X 2016 Org. Electron. 32 83 doi: 10.1016/j.orgel.2016.02.015 [14] Wang L X, Volkhard M 2017 J. Phys. B: At. Mol. Opt. 50 154003 doi: 10.1088/1361-6455/aa77a5 [15] Zhang P C, Jin W J, Liang W Z 2018 J. Phys. Chem. C 122 10545 doi: 10.1021/acs.jpcc.8b02450 [16] Sun J, Ding Z L, Yu Y Q, Liang W Z 2020 J. Chem. Phys. 152 224708 doi: 10.1063/5.0009549 [17] 范旭阳, 陈瀚超, 王鹿霞 2021 物理学报 70 227302 doi: 10.7498/aps.70.20211242 Fan X Y, Chen H C, Wang L X 2021 Acta Phys. Sin. 70 227302 doi: 10.7498/aps.70.20211242 [18] Veljko J, Tomáš M 2020 J. Chem. Phys. 153 244122 doi: 10.1063/5.0029914 [19] Huang X K, Liang W Z 2024 J. Phys. Chem. Lett. 15 6592 doi: 10.1021/acs.jpclett.4c01337 [20] Dean J C, Oblinsky D G, Rafiq S, Scholes G D 2016 J. Phys. Chem. B 120 440 doi: 10.1021/acs.jpcb.5b11847 [21] Han X B, Li F, He Z C, Liu Y H, Hu H T, Wang K, Lu P X 2022 Nanophotonics 11 603 doi: 10.1515/nanoph-2021-0697 [22] Garrahan J P 2018 Physica A 504 130 doi: 10.1016/j.physa.2017.12.149 [23] Fan X Y, Wei A, Klamroth T, Zhang Y, Gao K, Wang L X 2023 Phys. Rev. B 107 134301 doi: 10.1103/PhysRevB.107.134301 [24] Chernikov A, Ruppert C, Hill H M, Rigosi A F, Heinz T F 2015 Nat. Photonics 9 466 doi: 10.1038/nphoton.2015.104 [25] 高静, 常凯楠, 王鹿霞 2015 物理学报 64 147303 doi: 10.7498/aps.64.147303 Gao J, Chang K N, Wang L X 2015 Acta Phys. Sin. 64 147303 doi: 10.7498/aps.64.147303 [26] Tafulo P, Queirós R, González-Aguilar G 2009 Spectrochim. Acta A 73 295 doi: 10.1016/j.saa.2009.02.033 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: