-
水下高压脉冲放电可分为完全放电和局部放电[1–3]: 完全放电是指放电通道贯通正负电极, 电极间的液体水介质完全击穿; 局部放电是指放电只发生在电极附近的液体水介质中, 放电通道没有贯通正负电极. 水下高压脉冲流光放电是一种常见的水下局部放电, 产生紫外线、OH、H和O等自由基以及H2、H2O2、O3等分子化学活性种[4–6]. 近年来, 水下放电在纤维素材料改性[7]、水中有机污染物降解处理[8–10]、植物基因转录[11]、农作物种子处理[12]等方面展现出良好的应用前景.
通常, 水下流光放电采用针-板电极结构来实现, 针电极附近可以观察到两种不同模式的流光放电, 依据流光传播速度和放电形貌分为第一模式流光(primary streamer)和第二模式流光(second streamer)[13–17]. 第一模式流光用ICCD相机几乎无法观测到发光图像, 主要采用阴影成像技术进行观测研究. 已经发现第一模式流光从针尖附近预先形成的气泡[14]或气泡团簇突起[18]产生, 传播速度为~2 km/s, 形态呈以针尖为中心的扇形气态丝丛, 扇形半径小于500 μm[13,15,18]. 第一模式流光的持续时间大约在400 ns [14,15], 对应的放电电流仅有数十毫安, 往往被测量噪声淹没难以辨别[18]. 第二模式流光从第一模式流光形成的丝丛中产生[15,18], 传播速度为~30 km/s[13–16], 形态呈树枝结构. 第二模式流光在水中跳跃式传播, 每跳一步流光头部发射一个球形冲击波[14,19,20], 流光丝的最大长度能够发展到数毫米或数厘米[21,22].
综合水下流光放电模式的文献报道可以发现: 过去的放电形态模式研究大都是在电导率小于800 µS/cm的条件下进行的, 比如, An等[13]在水电导率2—800 µS/cm范围内、Ceccato等[14]在水电导率0.1—500 µS/cm范围内、Fujita等[15]在水电导率0.8 µS/cm以及Li等[17]在水电导率20—320 µS/cm对两种放电模式进行研究. 这些研究对认识水下高压脉冲流光放电的物理过程很有意义, 但是在实际应用中, 水电导率往往大于800 µS/cm, 比如处理电镀工业废水中的氯代多氟醚基磺酸, 溶液电导率大于1000 µS/cm[23]; 处理石油石化行业废水中的醋酸, 溶液初始电导率为1500 μS/cm[24]; 处理水产养殖废水中的盐酸环丙沙星, 溶液电导率为~2000 µS/cm[25]; 处理含氯苯的工业废水, 初始电导率范围在500—1000 μS/cm[26]. 为了促进水下流光放电的工业规模化应用, 研究高水电导率条件下高压脉冲流光放电形态模式十分必要.
本文利用四分幅超高速相机在水电导率200—1400 µS/cm的范围内观测不同水电导率、外加电压条件下水下微秒脉冲流光放电演化过程, 基于发光图像和阴影图像研究水电导率对水下微秒脉冲流光放电形态的影响; 研究水电导率对流光传播速度、单个脉冲的放电延迟时间以及注入的放电能量的影响.
-
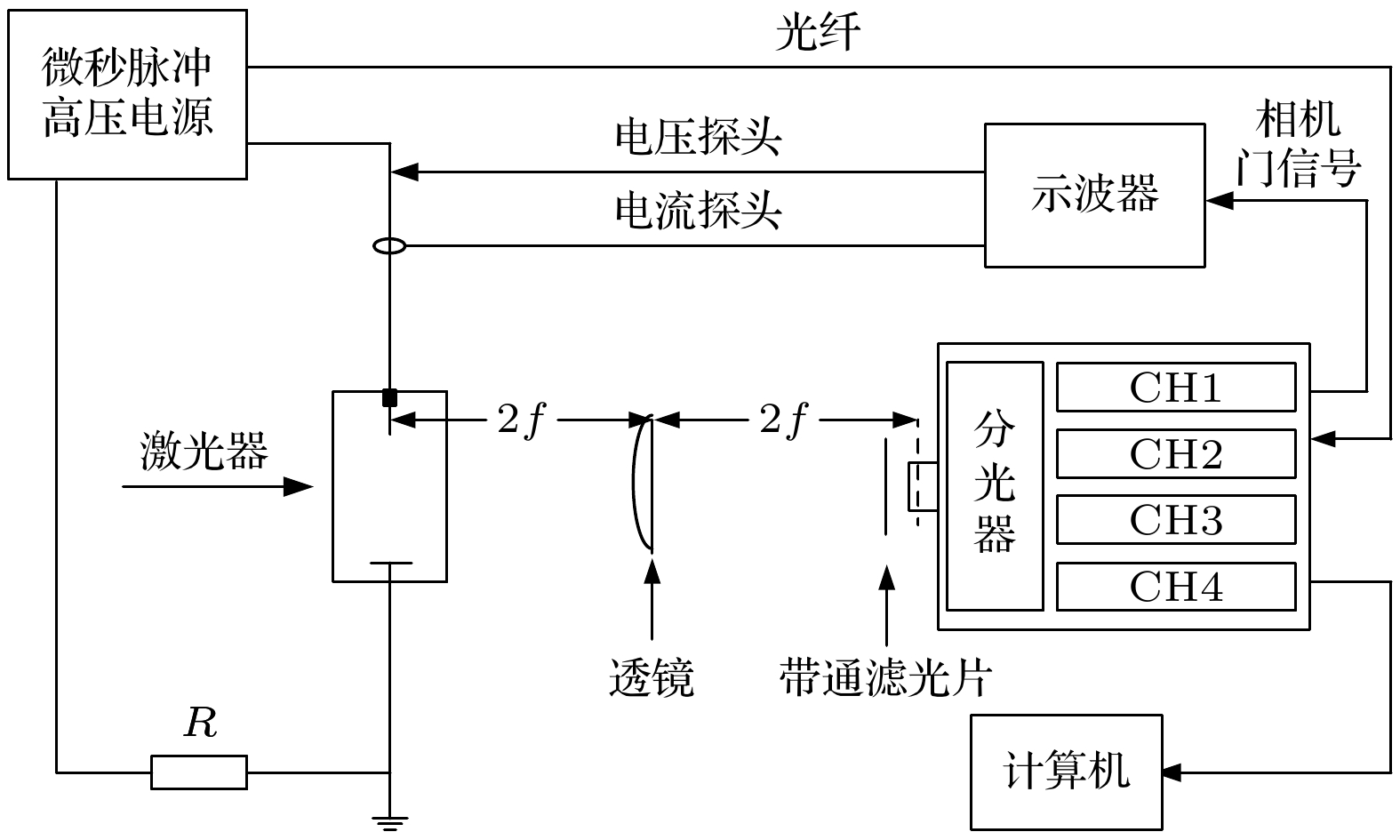
图1是实验电路与光路示意图. 实验采用针-板电极构型, 电极材料为不锈钢, 针尖曲率半径约40 μm, 针、板电极间距40 mm. 针-板电极安装在尼龙水槽中, 两侧设有石英玻璃窗以便观测放电过程. 水槽内分别注入电导率为200, 400, 600, 800, 1000, 1200和1400 µS/cm的水进行实验. 微秒脉冲高压电源以1 Hz的重复频率向针-板电极施加脉宽2 µs高电压脉冲在针-板电极间产生水下流光放电, 其中针尖电极为正极. 实验过程中外加电压分别为22, 26, 30, 34和38 kV, 在同一水电导率和电压条件下重复30个脉冲. 放电电压用高压探头(Tektronix P6015 A)探测, 放电电流用电流探测器(Pearson 6585)探测, 电压和电流波形用数字存储示波器(Yokogawa DLM2054)记录保存.
利用四分幅超高速ICCD相机分别拍摄水下流光放电的发光图像和阴影图像. 四分幅超高速ICCD相机有4个ICCD通道, 采用DOUBLE模式, 每个通道在一次外触发条件下可曝光两次, 通过适当设定4个ICCD通道的曝光时序在一个放电脉冲过程中可以依次获得8幅图像. 实验中相机的外触发信号由高压脉冲电源提供, 相机曝光时输出一个快门信号, 该门信号接入示波器作为示波器的触发信号, 使得示波器记录存储与图像一一对应的放电电压、电流波形, 根据相机的设定时序可以确定相机图像在电压、电流波形上的对应时刻. 在拍摄流光放电阴影图像时, 使用波长532.8 nm激光作为背光, 并在相机入口处放置(532.8±10) nm带通滤光片滤除放电本身的发光, 相机的曝光时间设定为20 ns, 时间间隔设定为180 ns. 拍摄流光放电发光图像时, 关闭激光背光, 相机的曝光时间设定为20 ns, 为在一个脉冲放电过程中同时观察放电早期和后期的演化过程, 根据不同的实验条件, 前四幅图像的时间间隔设定为20或40或 80 ns, 后4幅图像则不管什么实验条件下, 时间间隔都设定为200 ns. 由于水电导率大于600 µS/cm以后流光丝发光很强导致ICCD饱和, 考虑到流光丝主要光谱成分是Hα[13], 实验中在ICCD相机入口处放置(656±10) nm带通滤光片获取Hα发光图像.
-
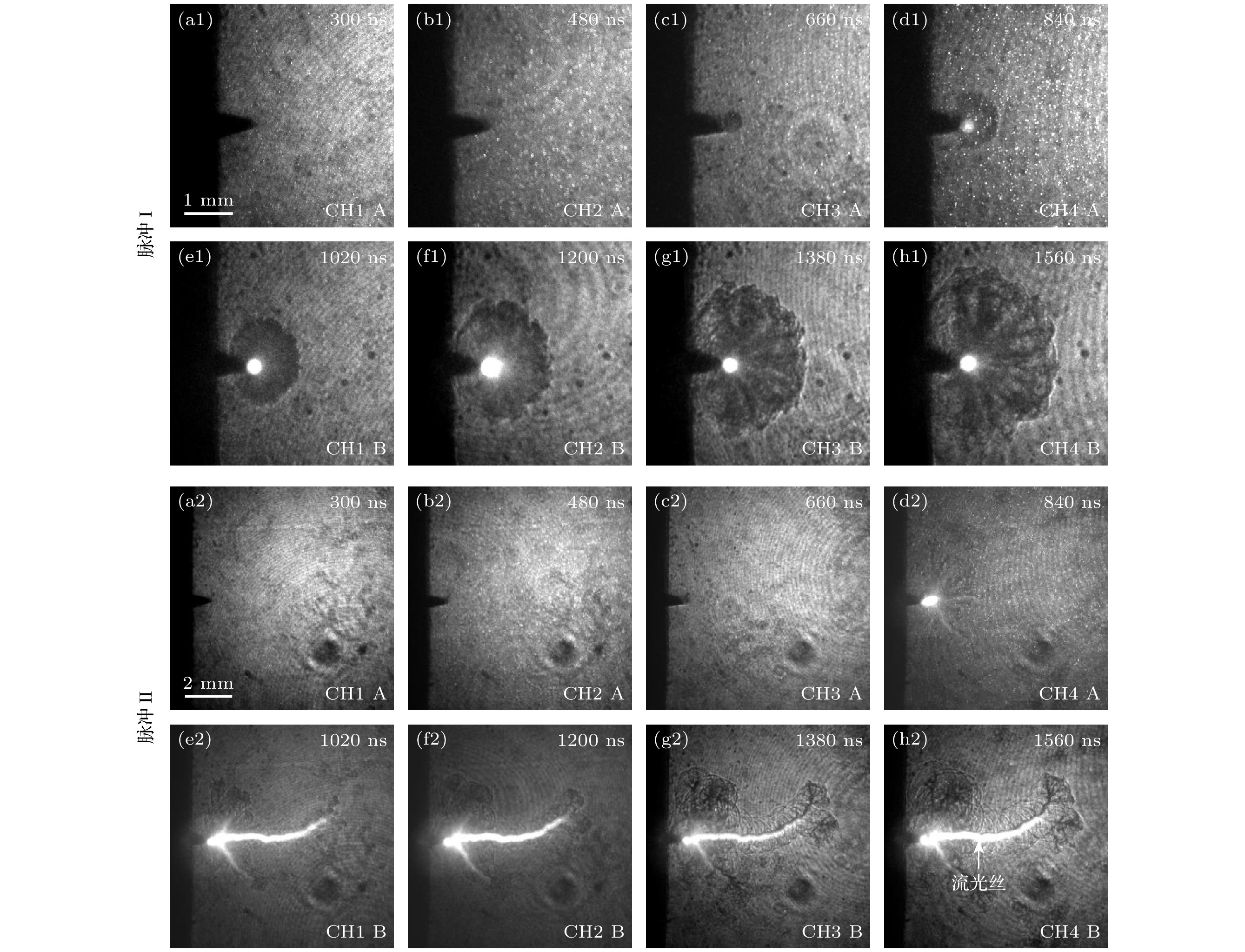
在200, 400, 600, 800, 1000, 1200, 1400 µS/cm 7个不同的水电导率下进行了实验. 在同一个水电导率下, 外加电压分别设定为22, 26, 30, 34, 38 kV. 在同一水电导率和外加电压条件下拍摄了30个放电脉冲的水下流光放电发光图像, 发现当水电导率大于800 µS/cm时同一实验条件下存在两种不同的放电形态, 典型发光图像如图2所示. 图2是在水电导率1200 µS/cm, 外加电压38 kV条件下两个不同放电脉冲观测到的水下流光放电时间演化发光图像, 可以看出同一条件下的两个脉冲放电的形态显著不同: 脉冲I的放电产生几根发光较弱的流光丝, 且长度几乎相同, 同步变长; 而脉冲II的放电产生一根流光丝随时间逐步变长, 其长度显著比脉冲I的流光丝长.
为了进一步研究上述两种形态的区别, 分别在200, 400, 600, 800, 1000, 1200, 1400 µS/cm 7个不同的水电导率条件下拍摄了放电的阴影图像, 图3是水电导率1000 µS/cm、外加电压38 kV条件下的典型阴影图像.
拍摄阴影图像时采用波长532.8 nm的激光为背光, 相机镜头前加了(532.8±10) nm带通滤光片以滤除流光丝本身的发光. 尽管加了(532.8±10) nm带通滤光片, 阴影图像上仍然可以看到很强的流 光丝发光. 根据文献[3,27–30]报道的水下放电发 射光谱诊断结果, 流光丝在(532.8±10) nm附近 没有特征谱线, 考虑到流光丝温度可达3600— 7000 K[13,30,31], 图3的阴影图像上观测到的流光丝发光应为532.8 nm附近的热辐射发光.
图3(c1)中可以看到放电脉冲I在针尖附近形成了一个直径约0.5 mm的阴影, 推测是初期形成的小气泡, 经过180 ns后图3(d1)放电脉冲I以 针尖为中心形成一个扇形的阴影区域, 针尖附近 出现热辐射发光, 而扇形区域没有明显的热辐射发光, 表明扇形区域的温度比针尖附近温度低很多. 图3(e1), (f1) 脉冲I放电(1020—1560 ns)的形貌与图3(d1)相似, 但扇形半径随时间增大, 扇形阴影中可以看到多根丝, 每一根丝都没有出现明显的热辐射发光, 表明这个过程中丝的温度仍然比针尖附近的温度低很多. 放电脉冲I的最显著特征是在1020—1560 ns过程中没有出现一根发光长丝, 本文中将形如放电脉冲I (图2和图3)的放电形态称为扇形丝丛形态.
脉冲II图3(c2)中, 针尖附近可以看到一个直径约0.2 mm的阴影, 应为初期形成的小气泡. 经过180 ns后脉冲II图3(d2)中, 可以看到从针尖生长出多根流光丝, 丝的根部(针尖附近)有约0.4 mm长度的强烈的热辐射发光, 丝的其他部分的热辐射发光微弱, 表明此时针尖附近温度与流光丝内的温度差别很大, 热源集中在针尖附近. 脉冲II图3(e2), (f2)可以看到图3(c2)中出现的流光丝中只有一根继续发展形成一根长流光丝, 且这根长流光丝从根部(针尖)到头部的热辐射发光强度都很强, 表明1020—1560 ns这个过程中整根流光丝的温度大致相同. 本文中将形如放电脉冲II (图2和图3)的放电形态称为单根长丝形态.
-
基于不同实验条件下获得的发光图像和阴影图像, 分别统计了同一实验条件下出现扇形丝丛形态、单根长丝形态的放电脉冲个数, 求出每种放电形态的出现比率(简称出现率), 研究两种放电形态的出现率与水电导率、外加电压的关系.
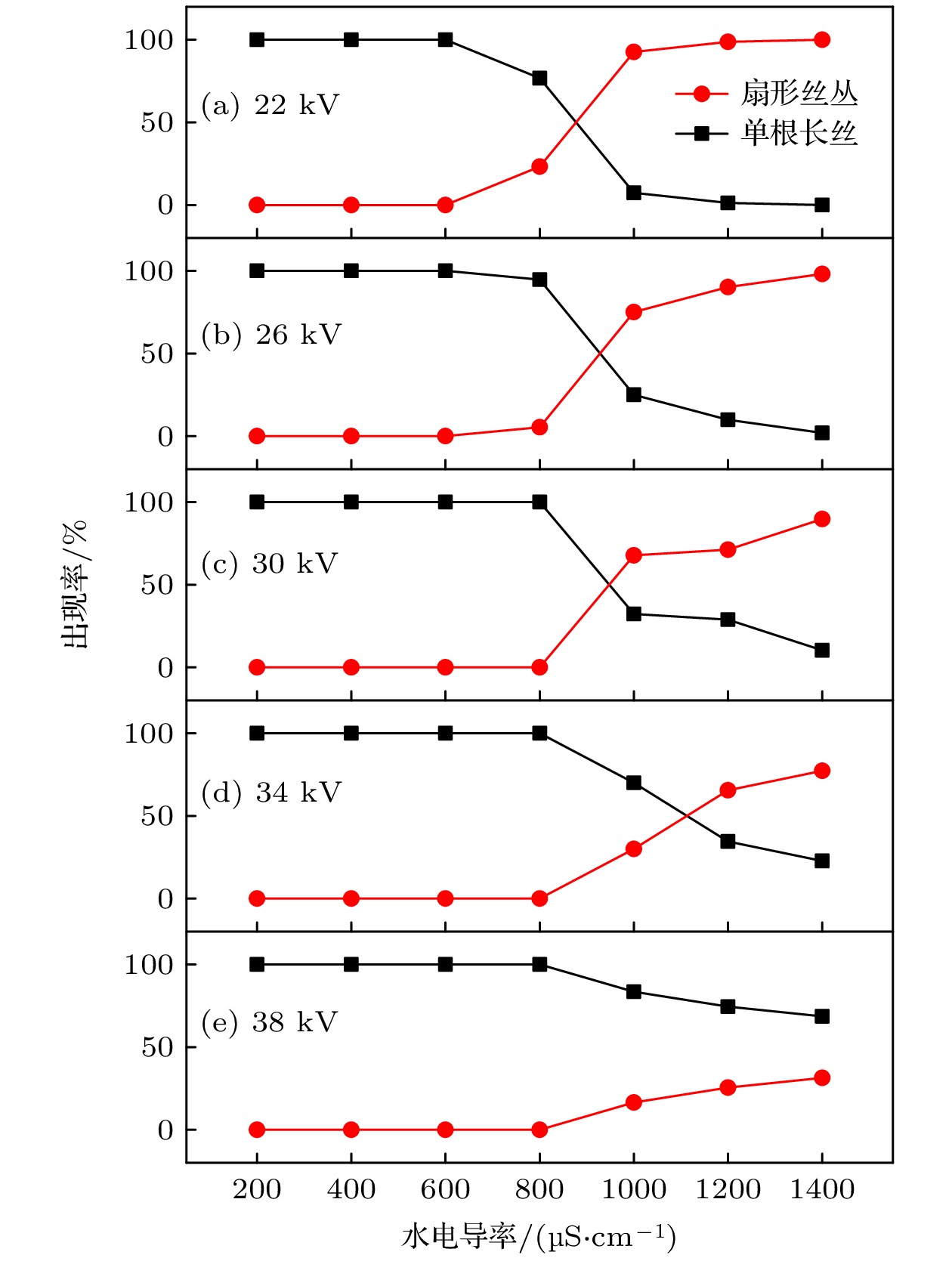
图4是水电导率对两种放电形态出现率的影响, 可以看出, 不论外加电压如何变化, 水电导率800 µS/cm是一个明显的分界点, 水电导率小于800 µS/cm时, 扇形丝丛形态的出现率为零, 而单根长丝形态出现率为100%; 当水电导率大于800 µS/cm, 扇形丝丛形态的出现率随水电导率的增大而增大, 单根长丝形态的出现率随电导率增大而减小.
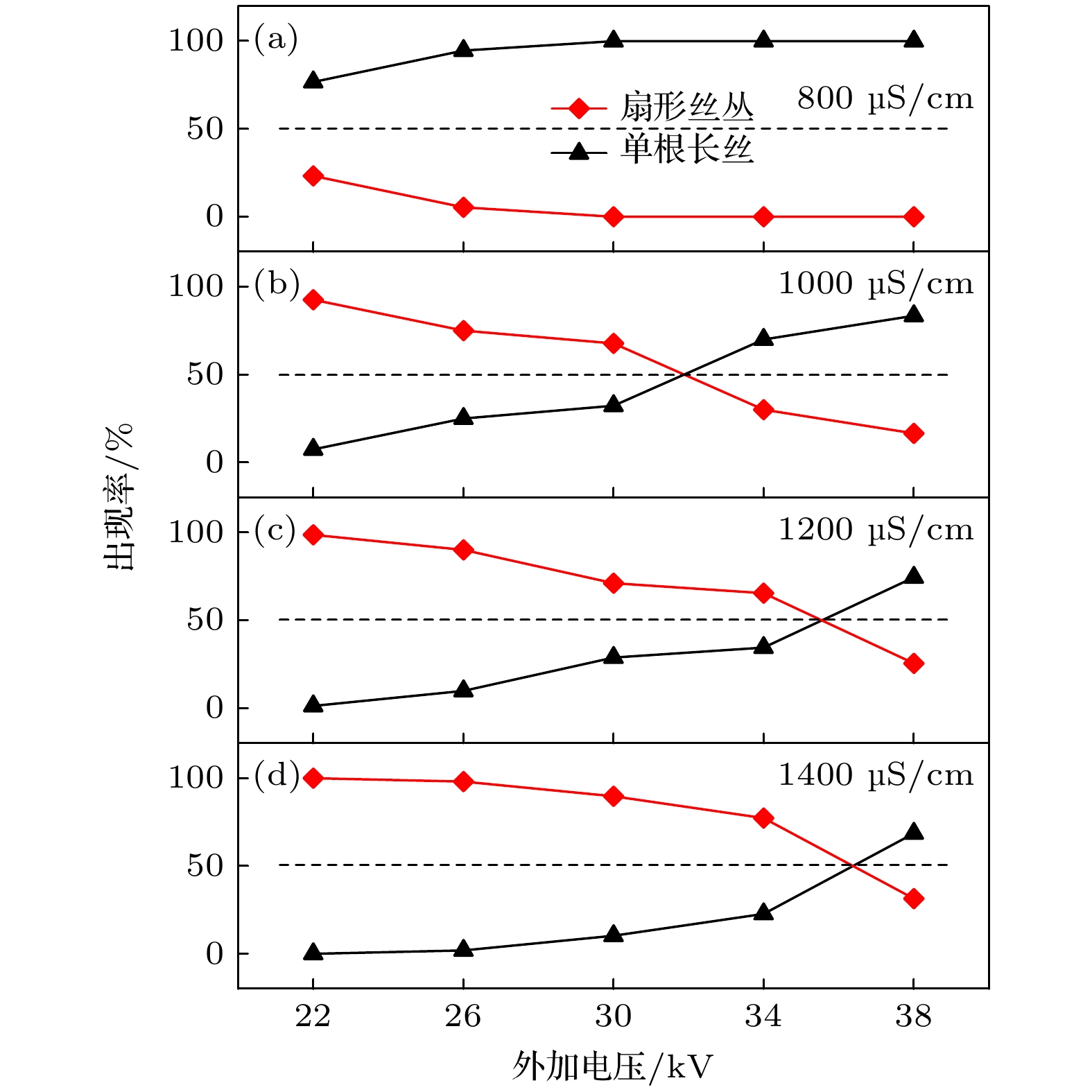
图5是两种放电形态出现率随外加电压的变化. 由于水电导率200—600 µS/cm时, 不同外加电压条件下只出现单根长丝形态(见图4), 因此图5中只给出了水电导率800—1400 µS/cm时外加电压对两种形态出现率的影响. 从总体看, 在各个相同的水电导率下, 随着外加电压升高扇形丝丛形态的出现率减小, 单根长丝形态的出现率增大. 水电导率为800 µS/cm时, 不管电压如何, 单根长丝形态都是主导性的放电形态. 水电导率大于1000 µS/cm以后, 主导放电形态为扇形丝丛形态, 要使两种放电形态的出现率发生反转, 所需的电压随水电导率的增大而增大.
-
基于同一脉冲放电过程中获得的8幅时间演化发光图像和阴影图像, 通过测量扇形丝丛形态的扇形阴影半径的时间演化、测量单根长丝形态的丝长度的时间演化, 分别得到扇形丝丛形态和单根长丝形态的水中传播速度, 研究了水电导率和外加电压对传播速度的影响.
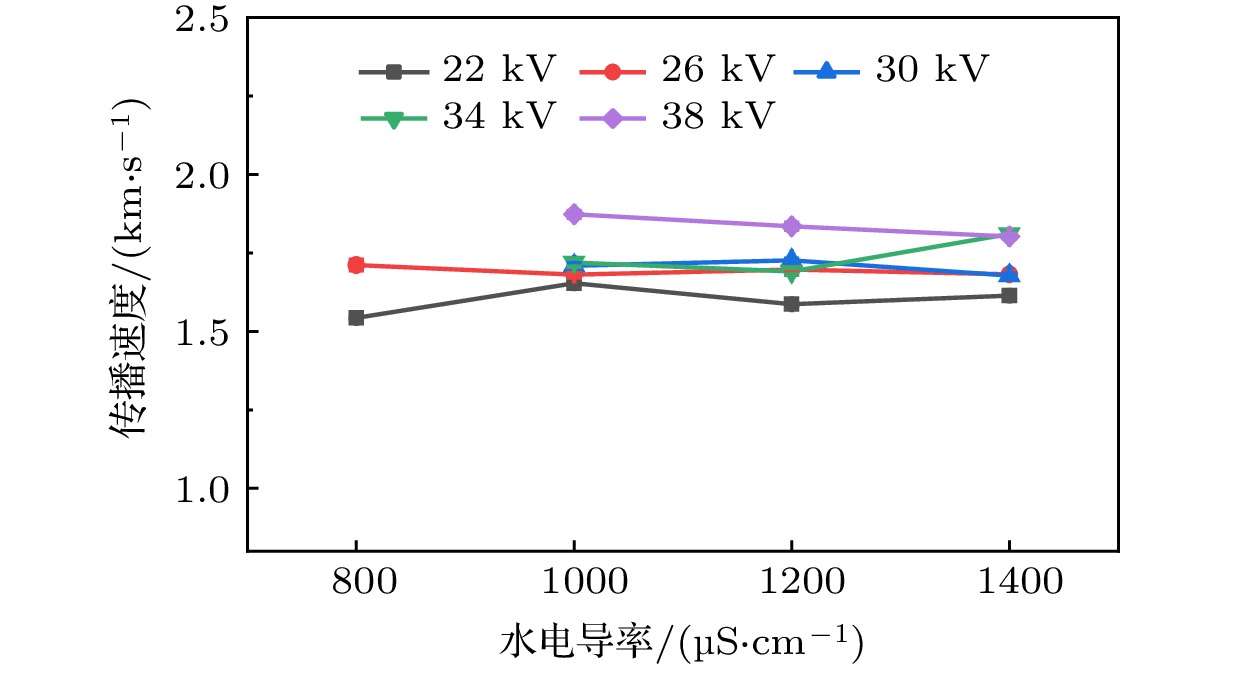
水电导率≥ 800 µS/cm后出现扇形丝丛形态, 图6是不同水电导率和外加电压条件下测得的扇形丝丛形态在水中的传播速度. 总体上扇形丝丛形态的传播速度为~1.7 km/s, 几乎不受水电导率和外加电压的影响.
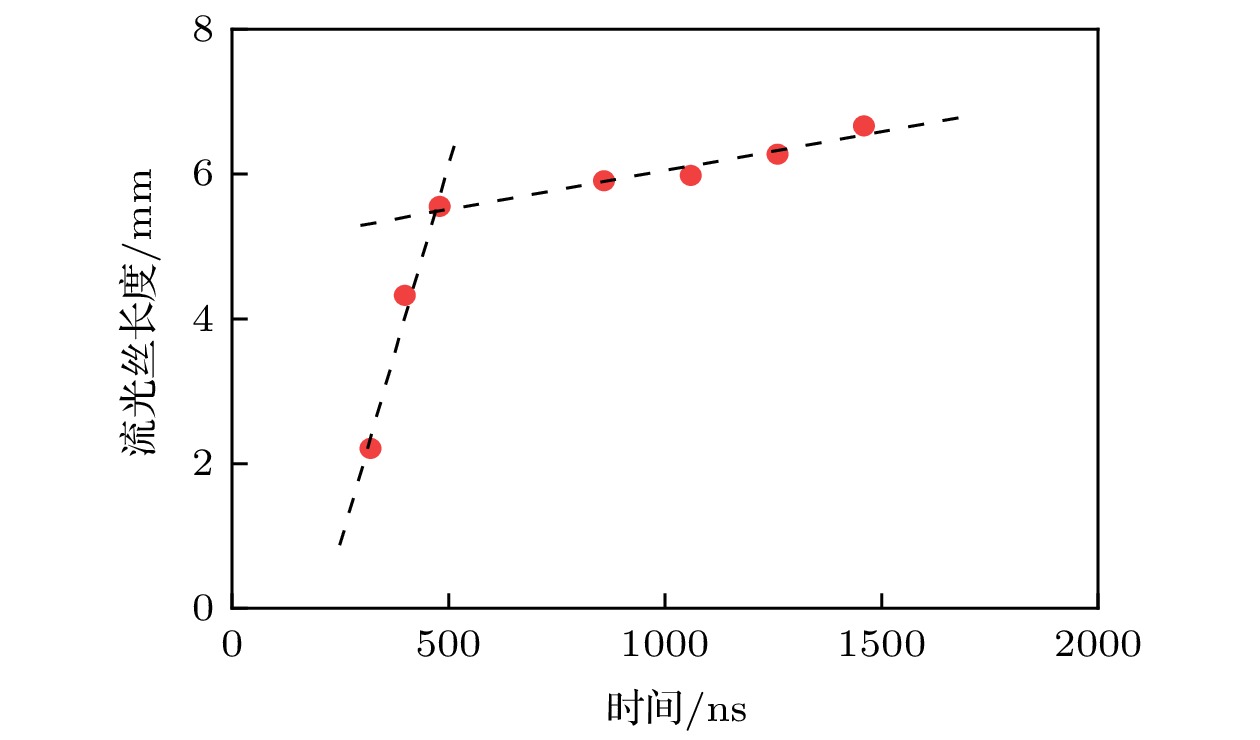
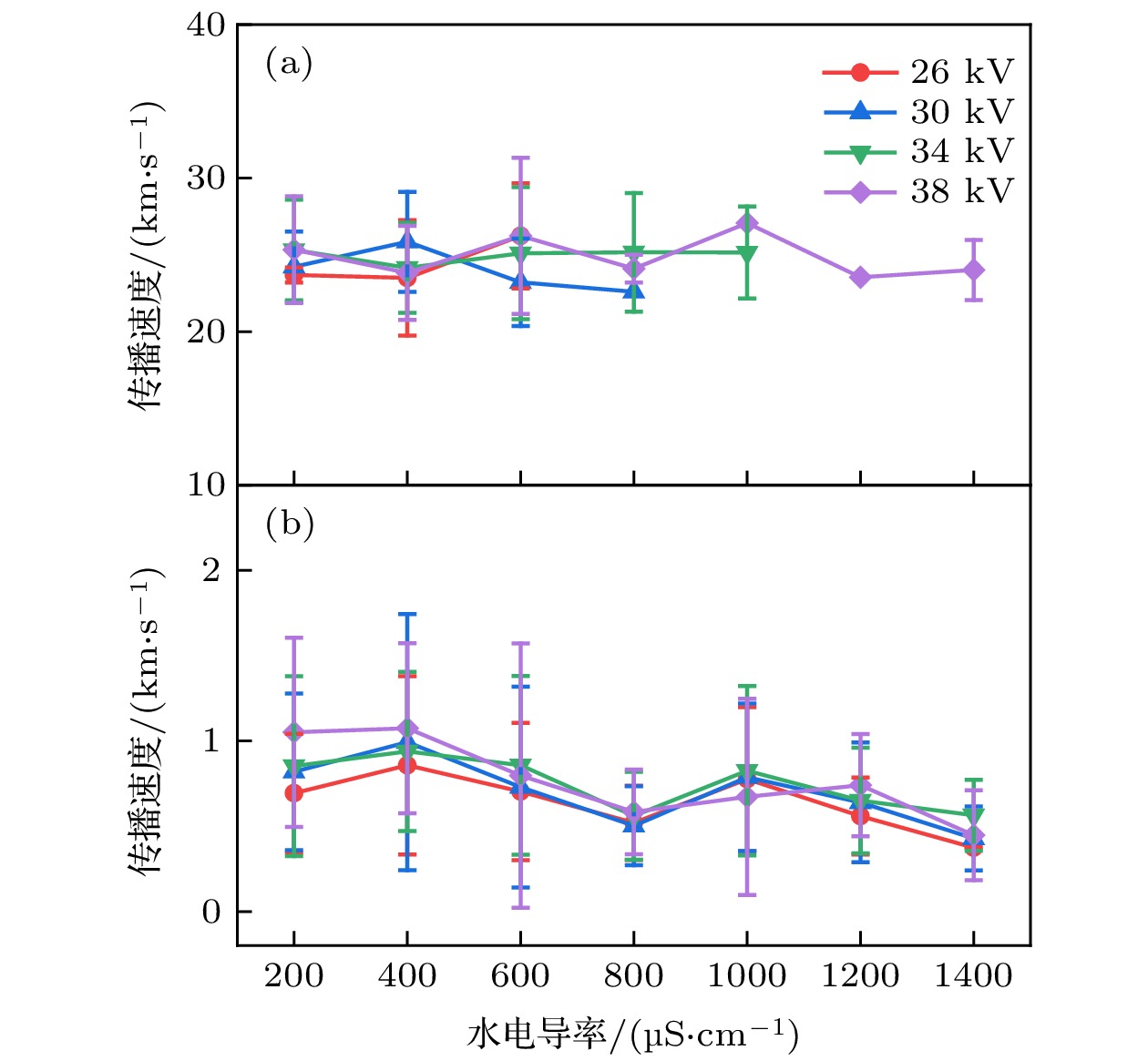
图7所示为一个放电脉冲下单根长丝的长度随时间的变化, 可以看出单根长丝形态的传播速度在整个脉冲放电过程中不是恒定不变的, 早期传播速度很快, 后期传播速度显著放慢. 图8(a)是在不同的水电导率和外加电压下测得的单根长丝早期的传播速度, 可以看到早期单根长丝的传播速度为~25 km/s, 总体上外加电压和水电导率对早期传播速度的影响不显著, 这个结果和文献[14,18,32,33]报道的水下流光放电第二模式单根丝传播速度的结果是一致的, 本文观测到的单根长丝形态从形态上和传播速度上可归属为水下流光放电的第二模式. 图8(b)是不同水电导率和外加电压时测得的单根丝后期的传播速度, 可以看出后期单根流光丝的速度为~0.8 km/s, 显著低于前期的传播速度, 总体上看, 随着水电导率的增大单根流光丝后期传播速度略有降低的趋势, 电压对后期传播速度几乎没有影响. 后期传播速度减小是由流光丝暂停和再激活现象导致的[20,34].
-
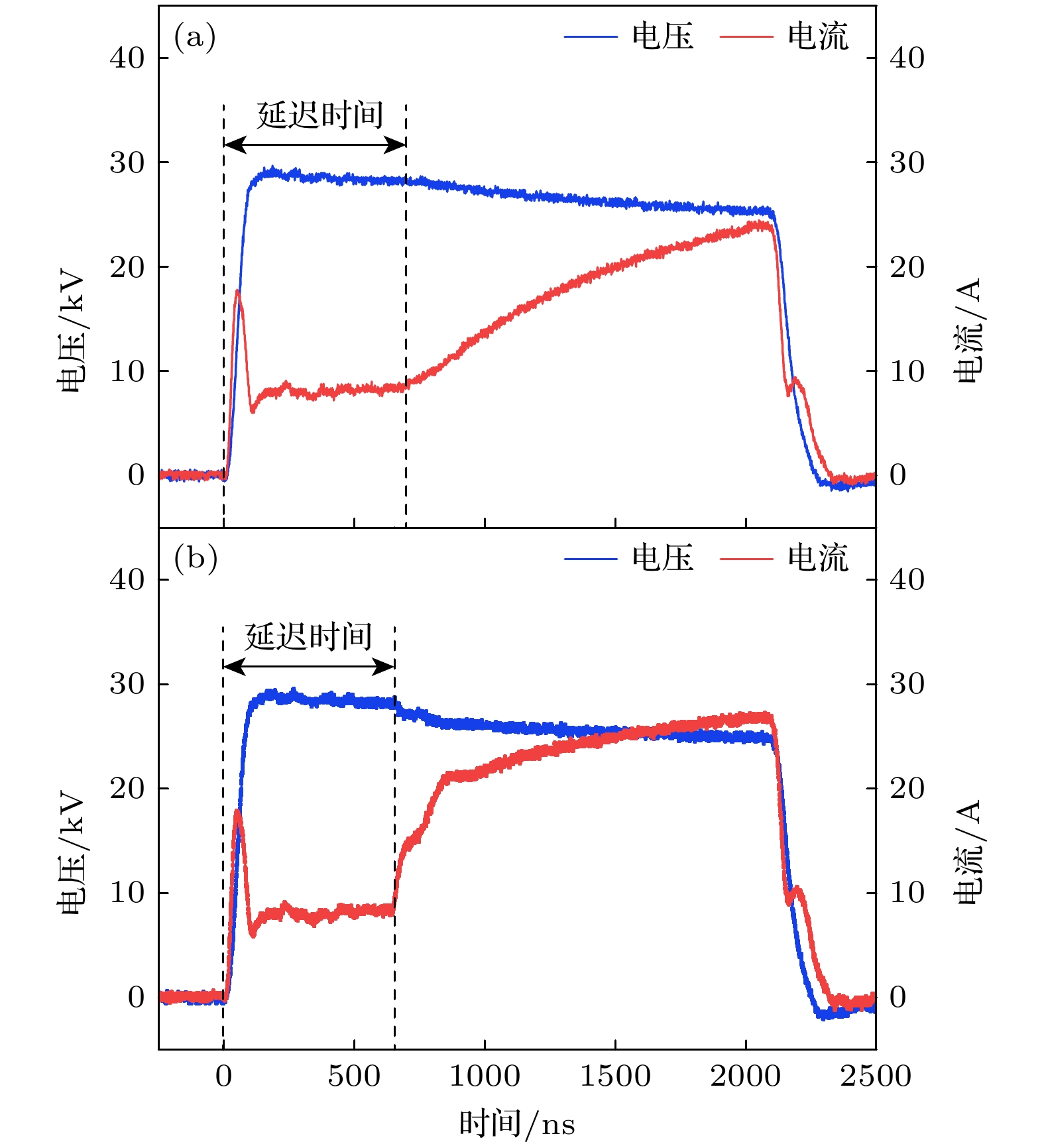
实验得到的两种放电形态的典型电压、电流波形如图9所示, 两种放电形态的电流波形中都有一个平台区, 是由高电导率水中的传导电流引起的[35,36]. 开始放电后, 可以看到两种放电形态的电流波形的升高方式显著不同: 扇形丝丛形态的放电电流相对缓慢地从平台区升起, 而单根长丝形态的电流从平台区激烈跳跃升起, 随后转为缓慢升高.
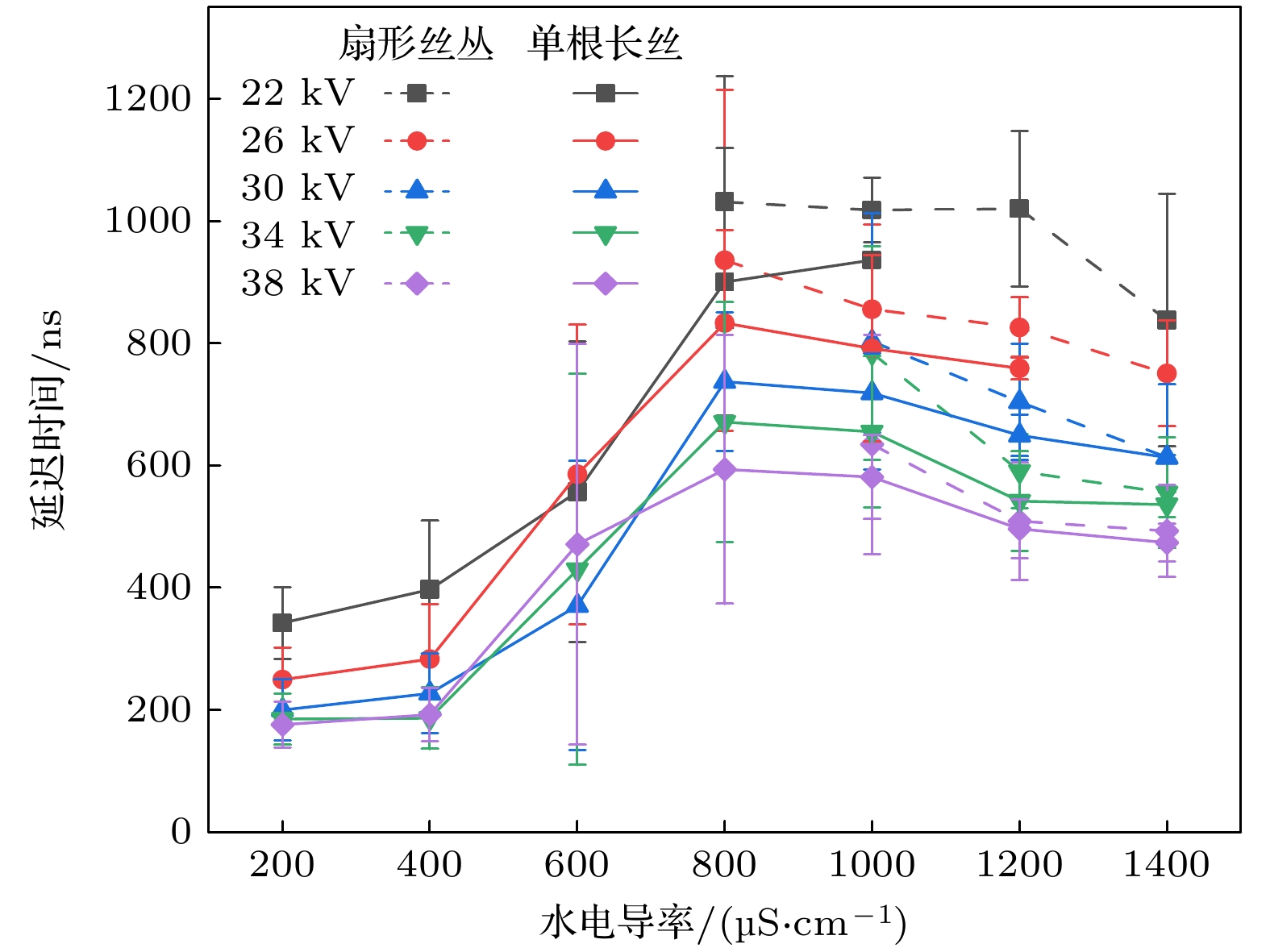
水下流光放电是水的部分击穿, 流光通道未连通正负两个电极, 此时的放电延迟时间是指高电压脉冲开始时刻到流光放电起始时刻之间的时间差, 如图9所示. 基于实验得到的不同条件下的放电电压、电流波形, 分别测量了两种放电形态的放电延迟时间, 研究了外加电压和水电导率对两种放电形态的放电延迟时间的影响, 结果如图10所示. 可以看出, 水电导率800 µS/cm是一个转折点, 水电导率小于800 µS/cm时单根长丝形态的放电延迟时间随水电导率的增大而增大; 水电导率大于800 µS/cm后两种形态的放电延迟时间随水电导率的增大而减小, 无论外加电压和水电导率如何变化, 扇形丝丛形态的放电延迟时间总是比单根长丝形态的放电延迟时间大8%左右.
单个放电脉冲过程的注入能量E可由下式计算:
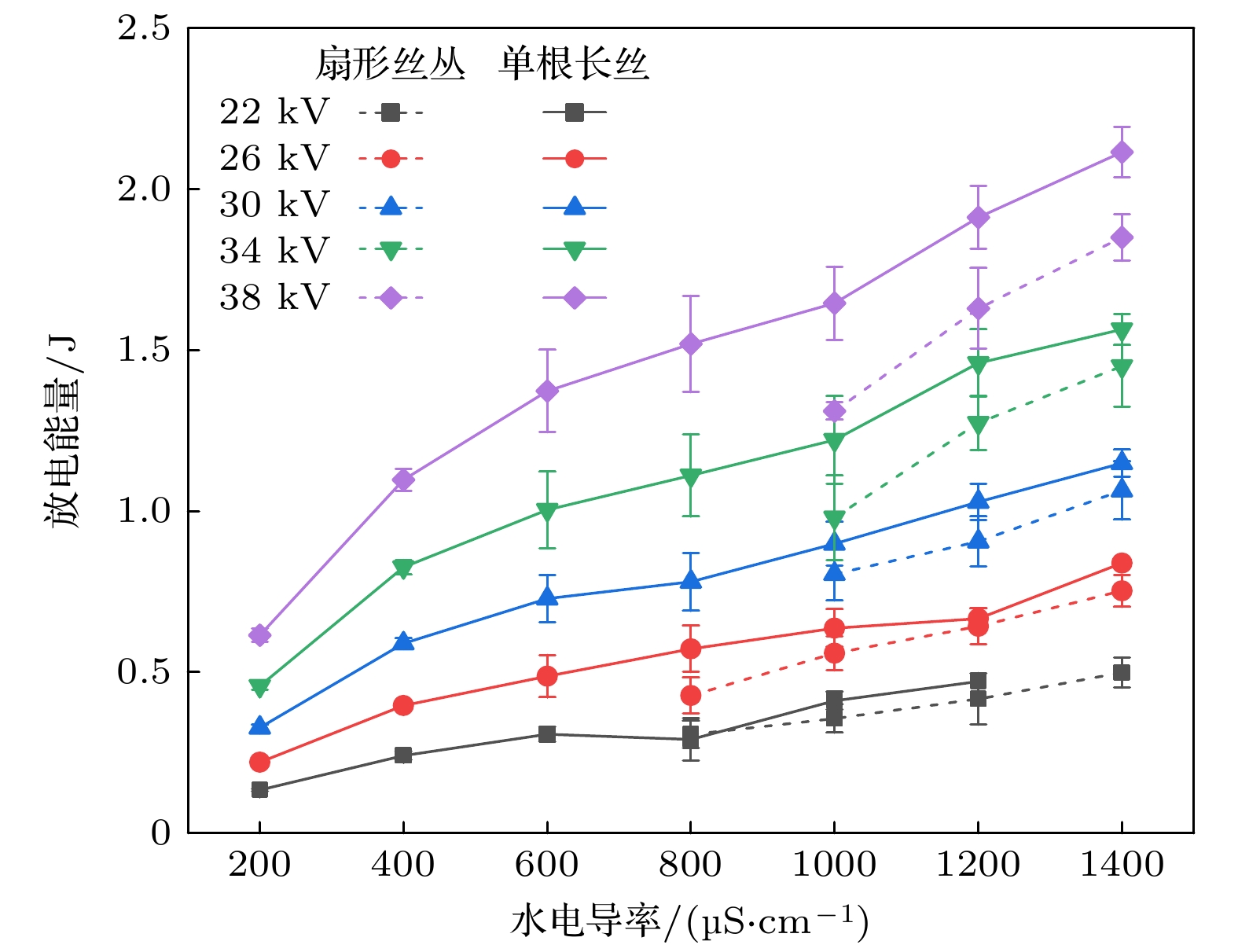
其中U, I分别为放电电压、电流, t0, T分别为放电起始时刻和电压脉宽. 根据实验测得的放电电压、电流波形, 按(1)式分别计算了两种放电形态单个放电脉冲的注入能量, 研究了水电导率和外加电压对单个放电脉冲注入能量的影响, 结果如图11. 根据实验条件的不同, 两种放电形态的单脉冲注入能量为0.1—2 J, 两种放电形态单脉冲注入能量都是随着水电导率和外加电压的增大而增大, 但是两种放电形态单脉冲注入能量有显著的差异: 扇形丝丛形态的单脉冲注入能量总是比单根长丝形态的小20%左右.
-
文献[13–18,33]报道了关于水下流光放电第一放电模式的研究. 图12(a)是本课题组过去拍摄的水下流光放电第一模式的典型阴影图像[17], 图12(b)是本研究的扇形丝丛形态的典型阴影图像. 从阴影图像看水下流光放电第一模式的形态与本研究的扇形丝丛形态十分的相似; 从传播速度上看文献报道的第一模式传播速度为1.5—4 km/s, 与本研究的扇形丝丛形态的传播速度1.7 km/s大致也是相当. 但是, 水下流光放电第一模式和本研究的扇形丝丛形态之间存在十分显著差异: 1)出现的条件不同, 水下流光放电第一模式出现在相对较低水电导率(≤800 µS/cm)较低电压(≤20 kV)的情形[13–15,17], 而本研究的扇形丝丛形态出现在较高水电导率(≥800 µS/cm)较高外加电压(≥22 kV)的情形; 2)扇形半径显著不同, 水下流光放电第一模式的扇形半径小于500 μm[13,15,17], 而本研究的扇形丝丛形态的半径达到1600 μm以上; 3)放电持续时间不同, 水下流光放电第一模式的持续时间约400 ns[14,17], 而本研究的扇形丝丛形态的持续时间可以达到1500 ns以上; 4)放电电流不同, 水下流光放电第一模式电流大小只有数十毫安, 往往被背景噪声淹没难以辨识[14,15], 而本研究的扇形丝丛形态的电流大小可超过30 A. 从目前的结果来看, 本研究的扇形丝丛形态无法归属为水下流光放电第一模式.
本研究观测发现: 一个放电脉冲过程中要么出现扇形丝丛形态, 要么出现单根长丝形态. 导致这种现象的物理机理尚不清楚, 可能与两个因素有关: 一个是施加高电压脉冲后到实际放电之间这段时间内针尖附近形成的气泡(见图3), 气泡的体积、内部水蒸气的密度、形状及其与外加电场之间的取向等都可能导致放电形态的不同. 另一个是水中的带电离子, 高电导率的水中带电离子浓度较大, 针尖附近形成气泡的过程中水中的带电离子向气-水界面运动形成一个与气泡表面形状相似的带电离子富集层, 这个带电离子富集层对气泡内的电场产生影响.
从图3可以看出, 扇形丝丛形态几乎没有(532.8±10) nm热辐射发光, 而单根长丝形态的整根丝有强烈的(532.8±10) nm热辐射发光. 这意味着扇形丝丛形态中的流光丝热辐射温度比单根长丝的要低得多, 扇形丝丛形态中的等离子体状态和单根长丝中的显著不同. 这也意味着单个放电脉冲过程中扇形丝丛形态放电生成的OH, H和O等自由基以及H2, H2O2, O3等分子化学活性种的产额与单根长丝形态放电生成的这些化学活性种的产额可能显著不同. 今后对这两种放电形态产生的等离子体进行甄别诊断, 对高电导率水环境中有机污染物降解和农作物种子处理等实际应用具有重要意义: 如果扇形丝丛形态对应用目的有利则选择扇形丝丛放电主导, 如果单根长丝形态对应用目的有利则选择单根长丝形态放电主导. 图5的结果对实际应用给出了一个参考指导, 在同一水电导率条件下可以通过调节外加电压选择扇形丝丛形态主导或者是单根长丝形态主导.
-
利用四分幅超高速相机观测了不同水电导率和外加电压条件下水下微秒脉冲流光放电演化过程, 发现在高水电导率条件下水下微秒流光放电存在两种不同的放电形态: 扇形丝丛形态和单根长丝形态. 根据流光放电发光图像和阴影图像统计了两种形态的出现率, 发现在本文研究范围内, 水电导率800 µS/cm是一个明显的分界点: 水电导率小于800 µS/cm时, 单根长丝形态的出现率为100%, 而扇形丝丛形态的出现率为零; 当水电导率大于800 µS/cm, 单根长丝形态的出现率随水电导率增加而降低, 扇形丝丛形态的出现率随水电导率的增加而增大. 水电导率大于1000 µS/cm以后, 主导放电形态为扇形丝丛形态, 随着水电导率的增大要使两种放电形态的出现率发生反转所需的电压增大. 扇形丝丛形态的传播速度为~1.7 km/s, 单根长丝形态的早期传播速度~25 km/s, 后期传播速度下降至~0.8 km/s, 水电导率和外加电压对两种形态的传播速度没有显著影响. 在放电延迟时间上, 水电导率800 µS/cm也是一个明显的转折点, 水电导率小于800 µS/cm时, 单根长丝形态的放电延迟时间随水电导率的增大而增大, 水电导率大于800 µS/cm时扇形丝丛形态和单根长丝形态的放电延迟时间都随水电导率的增大而减小, 扇形丝丛形态的放电延迟时间总是比单根长丝形态的大~8%. 扇形丝丛形态的单脉冲注入能量比单根长丝形态的小~20%.
水电导率对水下微秒脉冲流光放电形态的影响
Effect of water conductivity on underwater microsecond pulsed streamer discharge type
-
摘要: 水下流光放电在降解水中有机污染物、改良农作物种子等方面有良好的应用前景, 其放电形态对实际应用效果有重要影响. 本文利用四分幅超高速相机观测了不同水电导率、外加电压条件下水下微秒脉冲流光放电过程, 发现在高水电导率条件下存在两种不同的放电形态: 扇形丝丛和单根长丝. 在本文研究范围内水电导率800 µS/cm是两种形态出现率的分界点: 水电导率小于800 µS/cm时, 单根长丝形态的出现率为100%; 水电导率大于800 µS/cm时, 随着水电导率的增大, 单根长丝形态的出现率降低, 扇形丝丛形态的出现率增大; 水电导率大于1000 µS/cm后, 主导放电形态为扇形丝丛形态, 随水电导率的增大反转两种放电形态的出现率所需的电压增大. 扇形丝丛流光传播速度~1.7 km/s, 单根长丝流光早期传播速度~25 km/s, 后期传播速度下降至~0.8 km/s, 水电导率和外加电压对两种形态的传播速度没有显著影响. 扇形丝丛形态的放电延迟时间总是比单根长丝形态的大~8%, 单脉冲注入能量比单根长丝形态的小~20%.
-
关键词:
- 水下微秒脉冲流光放电 /
- 水电导率 /
- 扇形丝丛形态 /
- 单根长丝形态
Abstract: Underwater streamer discharges have various potential applications in the fields of wastewater treatment, crop seed processing, etc. The underwater streamer discharge types have an important effect on the practical applications. In this work, the underwater microsecond pulsed streamer discharges are investigated by using an ultra-high-speed frame camera system at different water conductivities and applied voltages. It is found that there exist two different types of discharge under the same experimental conditions: the fan-shaped bush type and the long-single filament type. The water conductivity of 800 µS/cm marks the boundary point for the occurrence rates of the two discharge types: when the water conductivity is less than 800 µS/cm, the occurrence rate of the long-single filament type is 100%; when the water conductivity is larger than 800 µS/cm, the occurrence rate of the long-single filament type decreases, but the occurrence rate of the fan-shaped bush type increases with water conductivity increasing. When the water conductivity is larger than 1000 µS/cm, the dominant discharge type is the fan-shaped bush type, and the voltage required to reverse the appearance rates of the two discharge types increases as the water conductivity increases. The fan-shaped bush type streamer has a propagation velocity of ~1.7 km/s, and the long-single filament streamer has a propagation velocity of ~25 km/s in the early stage and a propagation velocity of ~0.8 km/s in the later stage. Neither of water conductivity and applied voltage has significant influence on the propagation velocities of the two types of streamers. The time lag of the fan-shaped bush-type discharge is about 8% larger than that of the long-single filament-type discharge. The injection energy per pulse of the fan-shaped bush-type discharge is about 20% smaller than that of the single filament-type discharge. -

-
图 2 水电导率1200 µS/cm、电压38 kV条件下单一放电脉冲过程中依次获得的8幅时间演化Hα发光图像, 放电脉冲I和放电脉冲II的相机设定完全相同. (a1)—(d1), (a2)—(d2)为放电早期阶段, 相邻两幅图像的时间间隔为80 ns; (e1)—(h1), (e2)—(h2)为放电后期阶段, 相邻两幅图像的时间间隔为200 ns, 所有图像的相机曝光时间为20 ns
Figure 2. Eight successive Hα emission images acquired during a single pulse discharge at water conductivity of 1200 µS/cm and applied voltage of 38 kV, the camera settings for Pulse I and Pulse II are identical: (a1)–(d1), (a2)–(d2) Correspond to the early stage of the streamer discharge, and the time interval between two adjacent images is 80 ns; (e1)–(h1), (e2)–(h2) correspond to the later stage of the streamer discharge, and the time interval is 200 ns, the gating time of each image is 20 ns.
图 3 水电导率1000 µS/cm、电压38 kV条件下的单一放电脉冲过程中依次获得的8幅时间演化阴影图像, 放电脉冲I和放电脉冲II的相机设定完全相同 图中相邻两幅图像之间的时间间隔为180 ns, 每幅图像的曝光时间为20 ns
Figure 3. Eight successive shadow images obtained during a single pulse discharge at water conductivity of 1000 µS/cm and applied voltage of 38 kV, the camera time settings for Pulse I and Pulse II are identical: The time interval between two neighboring images in images is 180 ns, and the exposure time for each image is 20 ns.
-
[1] Locke B R, Sato M, Sunka P, Hoffmann M R, Chang J S 2006 Ind. Eng. Chem. Res. 45 882 doi: 10.1021/ie050981u [2] Kolb J F, Joshi R P, Xiao S, Schoenbach K H 2008 J. Phys. D: Appl. Phys. 41 234007 doi: 10.1088/0022-3727/41/23/234007 [3] Bruggeman P, Leys C 2009 J. Phys. D: Appl. Phys. 42 053001 doi: 10.1088/0022-3727/42/5/053001 [4] Sato M, Ohgiyama T, Clements J S 1996 IEEE. Trans. Ind. Appl. 32 106 doi: 10.1109/28.485820 [5] Lukes P, Clupek M, Babicky V, Sunka P 2008 Plasma Sources Sci. Technol. 17 024012 doi: 10.1088/0963-0252/17/2/024012 [6] Akiyama H 2000 IEEE Trans. Dielectr. Electr. Insul. 7 646 doi: 10.1109/94.879360 [7] Titova Y V, Stokozenko V G, Maximov A I 2010 IEEE Trans. Plasma Sci. 38 933 doi: 10.1109/TPS.2010.2042181 [8] Sharma A K, Locke B R, Arce P, Finney W C 1993 Hazard. Waste Hazard. Mater. 10 209 doi: 10.1089/hwm.1993.10.209 [9] Sun B, Sato M, Clements J S 1999 J. Phys. D: Appl. Phys. 32 1908 doi: 10.1088/0022-3727/32/15/319 [10] Wang H J, Li J, Quan X 2006 J. Electrostat. 64 416 doi: 10.1016/j.elstat.2005.11.004 [11] Wang D Y, Lin X F, Hirayama K, Li Z, Ohno T, Zhang W B, Namihira T, Katsuki S, Takano H, Takio S, Akiyama H 2010 IEEE Trans. Plasma Sci. 38 39 doi: 10.1109/TPS.2009.2035126 [12] Sivachandiran L, Khacef A 2017 RSC Adv. 7 1822 doi: 10.1039/C6RA24762H [13] An W, Baumung K, Bluhm H 2007 J. Appl. Phys. 101 053302 doi: 10.1063/1.2437675 [14] Ceccato P, Guaitella O, Shaper L, Graham B, Rousseau A 2009 IEEE Pulsed Power Conference Washington. D C, USA, June 28–July 2, 2009 p866 [15] Fujita H, Kanazawa S, Ohtani K, Komiya A, Sato T 2013 J. Appl. Phys. 113 113304 doi: 10.1063/1.4795765 [16] Lesaint O 2016 J. Phys. D: Appl. Phys. 49 144001 doi: 10.1088/0022-3727/49/14/144001 [17] Li J S, Wen X Q, Liu X H, Zhou Y B 2019 IEEE Trans. Plasma Sci. 47 1514 doi: 10.1109/TPS.2019.2895698 [18] Fujita H, Kanazawa S, Ohtani K, Komiya A, Kaneko T, Sato T 2014 J. Appl. Phys. 116 213301 doi: 10.1063/1.4902862 [19] Katsuki S, Tanaka K, Fudamoto T, Namihira T, Akiyama H, Bluhm H 2006 Jpn. J. Appl. Phys. 45 239 doi: 10.1143/JJAP.45.239 [20] Wen X Q, Xue X D, Liu X H, Li J S, Zhou Y B 2019 J. Appl. Phys. 125 133302 doi: 10.1063/1.5088193 [21] Katsuki S, Akiyama H, Abou-Ghazala A, Schoenbach K H 2002 IEEE Trans. Dielectr. Electr. Insul. 9 498 doi: 10.1109/TDEI.2002.1024426 [22] Wen X Q, Liu G S, Ding Z F 2012 IEEE Trans. Plasma Sci. 40 438 doi: 10.1109/TPS.2011.2176516 [23] Zhang H, Zhang Y Y, Zhu L X, Liu Y N 2024 J. Hazard. Mater. 476 135069 doi: 10.1016/j.jhazmat.2024.135069 [24] Takeuchi N, Ishibashi N, Sugiyama T, Kim H H 2018 Plasma Sources Sci. Technol. 27 055013 doi: 10.1088/1361-6595/aac0ea [25] Liu S, Kang Y 2024 Environ. Pollut. 348 123891 doi: 10.1016/j.envpol.2024.123891 [26] Jose J, Philip L 2019 J. Environ. Chem. Eng. 7 103476 doi: 10.1016/j.jece.2019.103476 [27] 牛志文, 晏现峰, 李书翰, 温小琼, 刘金远 2015 光谱学与光谱分析 35 2911 doi: 10.3964/j.issn.1000-0593(2015)10-2911-05 Niu Z W, Yan X F, Li S H, Wen X Q, Liu J Y 2015 Spectroscopy Spectral Analy. 35 2911 doi: 10.3964/j.issn.1000-0593(2015)10-2911-05 [28] Sun B, Sato M, Clements J S 1997 J. Electrostat. 39 189 doi: 10.1016/S0304-3886(97)00002-8 [29] Šimek M, Člupek M, Babický V, Lukeš P, Šunka P 2012 Plasma Sources Sci. Technol. 21 055031 doi: 10.1088/0963-0252/21/5/055031 [30] Marinov I, Starikovskaia S, Rousseau A 2014 J. Phys. D: Appl. Phys. 47 224017 doi: 10.1088/0022-3727/47/22/224017 [31] Salazar J N, Bonifaci N, Denat A, Lesaint O 2005 IEEE International Conference on Dielectric Liquids Coimbra, Portugal, June 26–July 1, 2005 p91 [32] Ceccato P H, Guaitella O, Gloahec Le M R, Rousseau A 2010 J. Phys. D: Appl. Phys. 43 175202 doi: 10.1088/0022-3727/43/17/175202 [33] Marinov I, Guaitella O, Rousseau A, Starikovskaia S M 2013 J. Phys. D: Appl. Phys. 46 464013 doi: 10.1088/0022-3727/46/46/464013 [34] 王雪, 温小琼, 王丽茹, 杨元天, 薛晓东 2022 物理学报 71 015203 doi: 10.7498/aps.71.20211162 Wang X, Wen X Q, Wang L R, Yang Y T, Xue X D 2022 Acta Phys. Sin. 71 015203 doi: 10.7498/aps.71.20211162 [35] Wang L R, Wen X Q, Yang Y T, Wang X 2023 J. Appl. Phys. 134 013302 doi: 10.1063/5.0152105 [36] 杨双越, 温小琼, 杨元天, 李霄 2024 物理学报 73 075203 doi: 10.7498/aps.73.20231881 Yang S Y, Wen X Q, Yang Y T, Li X 2024 Acta Phys. Sin. 73 075203 doi: 10.7498/aps.73.20231881 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: