在地磁场的作用下, 地球辐射带会俘获大量能量低于10 MeV的高能电子, 常被称为“杀手电子”^[1]. 这些电子入射航天器后, 会发生单粒子、总剂量和充放电等效应, 严重影响航天器的在轨安全运行^[2]. 根据地球辐射带环境模型AE-8和AE-9, 累计后的空间电子能谱结构呈近指数型分布, 具有宽能谱的特点^[3,4]. 然而, 基于传统加速器的空间辐射环境地面模拟装置产生的电子束通常是单能的, 因此存在空间辐射损伤等效性问题, 难以准确表征空间粒子的辐射效应^[5–7]. 激光等离子体加速器的快速发展为宽能谱近指数型电子束的产生提供了有效的方法, 当聚焦功率密度为10¹⁸—10²⁰ W/cm²的超强激光辐照厚度为几个微米的固体靶时, 激光加热电子, 能够有效地产生指数型宽能谱电子束^[8,9]. 2010年, Hidding等^[8]首次提出利用激光等离子体加速器模拟空间辐射环境的方案^[7], 并对实验进行了初步设计. 随后, 利用功率为150 TW超强激光辐照厚度为280 μm的铝靶, 获得了能够模拟GPS轨道电子辐射的指数型宽能谱电子束, 验证了基于激光的粒子加速技术模拟空间带电粒子辐射的可行性^[9]. 近年来, 研究表明, 基于激光加速器的空间辐射环境模拟装置也能模拟深空辐射环境(如金星)的电子和质子辐射, 进一步拓展了激光粒子加速器的应用范围^[10].

在激光驱动电子加速的研究中, 不同激光强度和等离子体参数对应着不同的加速机制, 也决定了电子束的能谱结构和截止能量. 当前, 激光驱动电子加速使用的靶材主要包括气体靶、固体靶以及近临界密度靶^[11,12], 涉及的主要加速机制为激光尾波场加速^[13–15]、激光直接加速^[16–18]、有质动力加速^[19–21]、J×B加热^[22–24]、真空加热^[25–27]等. 激光驱动固体靶加速具有能量转化效率高等优点, 是产生强流高能电子束的重要途径, 也是产生宽能谱指数型电子束的有效方案. 然而, 对于激光直接辐照高密度固体靶, 获得匹配GPS轨道的指数型宽能谱电子束 (最大电子能量为7 MeV和有效电子温度为0.65 MeV)需要的激光强度为4.5×10¹⁹ W/cm², 且根据Haines等^[28]的电子温度定标$ {T_{\text{e}}} = 0.511[ ( {1 + \sqrt 2 {a_0}} )^{1/2} - 1 ]~ {\text{MeV}} $, 其中${a_0}$为驱动激光归一化强度, 能够得到理论上的指数谱电子温度. 为了进一步提高能量转化效率, 优化能谱结构, 研究人员也提出了多种靶构型操控电子加速和辐射^[29–31], 如双层等离子体靶、纳米阵列靶等, 这些特殊靶结构能够增强激光能量吸收效率、优化加速粒子束品质, 已广泛应用于许多研究领域, 如离子加速、THz辐射、X射线辐射等.

针对近地空间电子辐射环境模拟需求, 本文利用二维粒子模拟方法研究了激光驱动双平面复合靶产生指数型宽能谱电子束的方案. 研究结果表明, 组合靶可以获得与空间电子辐射环境能谱结构相一致的电子束, 并给出了能谱匹配的评价方法, 随后分析不同垂直平面靶密度对电子加速机制的影响. 同时, 进行垂直平面靶的长度与密度的参数扫描发现, 获得电子束温度与之存在一定的线性关系, 可以通过贝叶斯优化获得最优的靶参数条件, 以获得匹配效果更优的电子束. 相比于单平面固体靶, 该方案能谱可调谐性更强, 所需激光强度更低, 研究结果为不同轨道空间电子辐射环境模拟实验研究提供了理论参考.

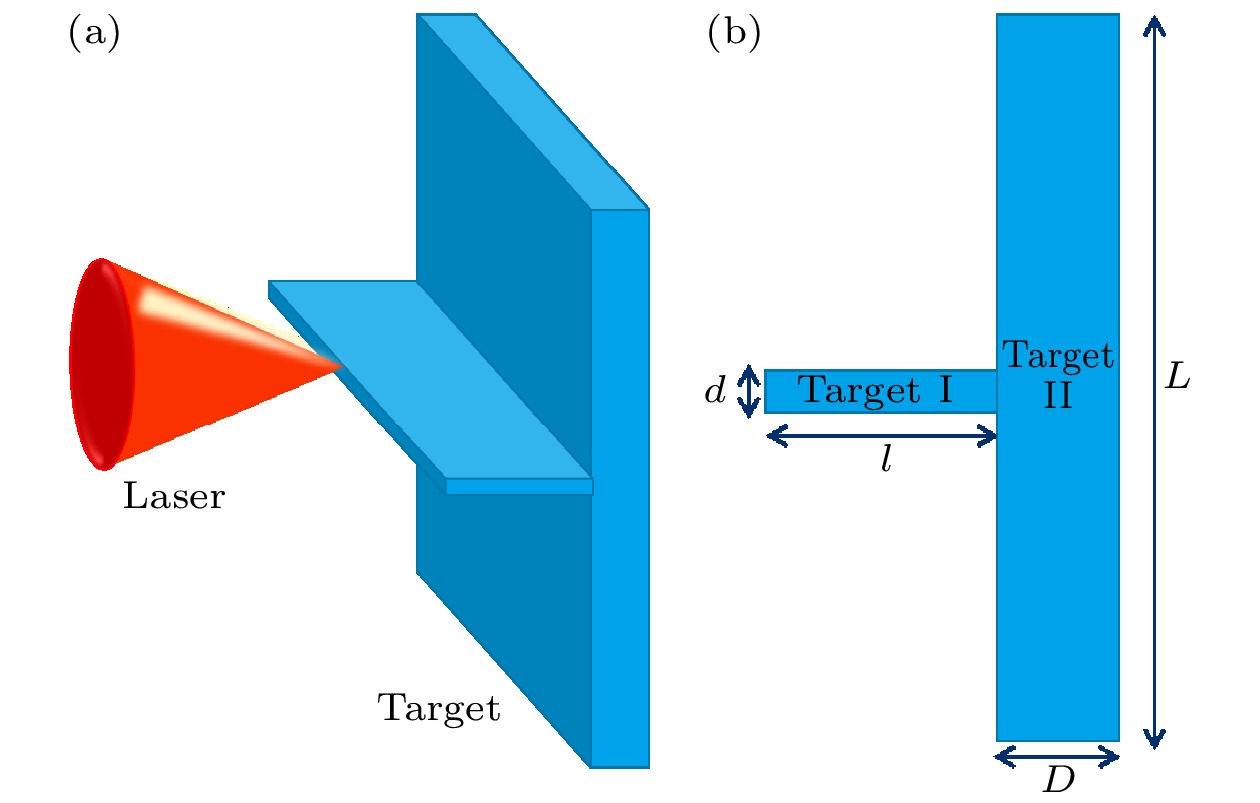
为了研究激光驱动双平面复合靶产生指数型宽能谱电子束的方案, 利用二维粒子模拟程序LAPINE^[32,33]开展了一系列数值模拟研究. 模拟参数如下: 一束沿着y方向偏振的线极化激光从模拟盒子左边界沿x轴正方向入射, 激光时间和空间波形均为高斯型, 激光波长为$ {\lambda _0} = 1\;{\text{μm}} $, 归一化强度${a_0} = 3.2$, 对应峰值强度${I_0} = 1.4 \times {10^{19}}\;{\text{W}}/{\text{c}}{{\text{m}}^2}$, 脉冲宽度为40 fs, 焦斑半径为5 μm. 靶型设置如图1所示, 高密度平面固体靶Ⅱ电子密度为${n_{{\text{e}}2}} = 60\;{n_{\text{c}}}$, 其中$n_{\rm c} = 1.1 \times 10^{21}\text{ cm}^{-2}$为激光传输临界密度, 厚度D = 10 μm, 横向宽度L = 30 μm, 垂直平面靶Ⅰ放置在靶Ⅱ中心轴, 电子密度为$ {n_{{\text{e}}1}} $, 长度l = 3 μm, 横向宽度d = 1 μm. 模拟盒子大小为40 μm × 30 μm, 网格划分为8000 × 2000, 靶Ⅰ与靶Ⅱ分别设置为完全电离的C和Al. 考虑到预脉冲引起等离子体膨胀问题, 在靶Ⅱ表面设置0.01 μm密度呈幂指数上升的预等离子体^[16], 通过控制预脉冲和主脉冲时间间隔, 可以实现较小的预等离子体膨胀长度. 对于方案中使用的垂直平面靶Ⅰ, 能够通过醋酸纤维素TAC或石墨烯气凝胶进行3D打印实现, 其密度可低至$0.05{n_{\text{c}}}$, 尺寸可较易达到微米级别^[34,35].

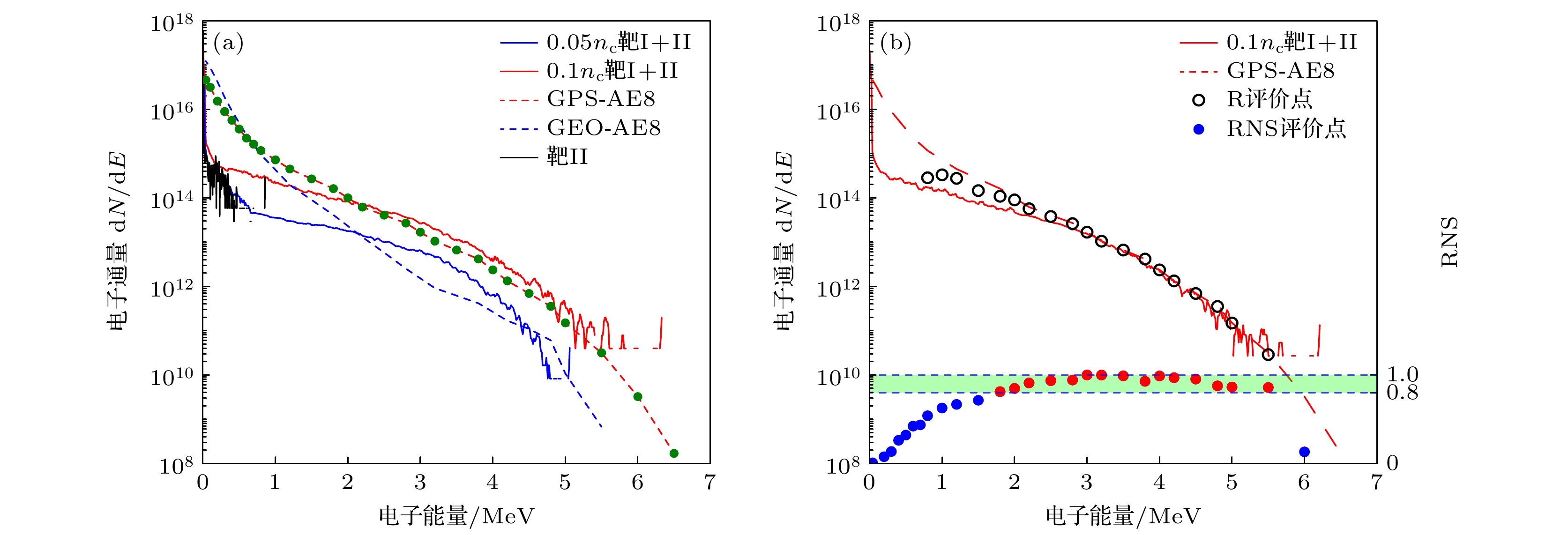
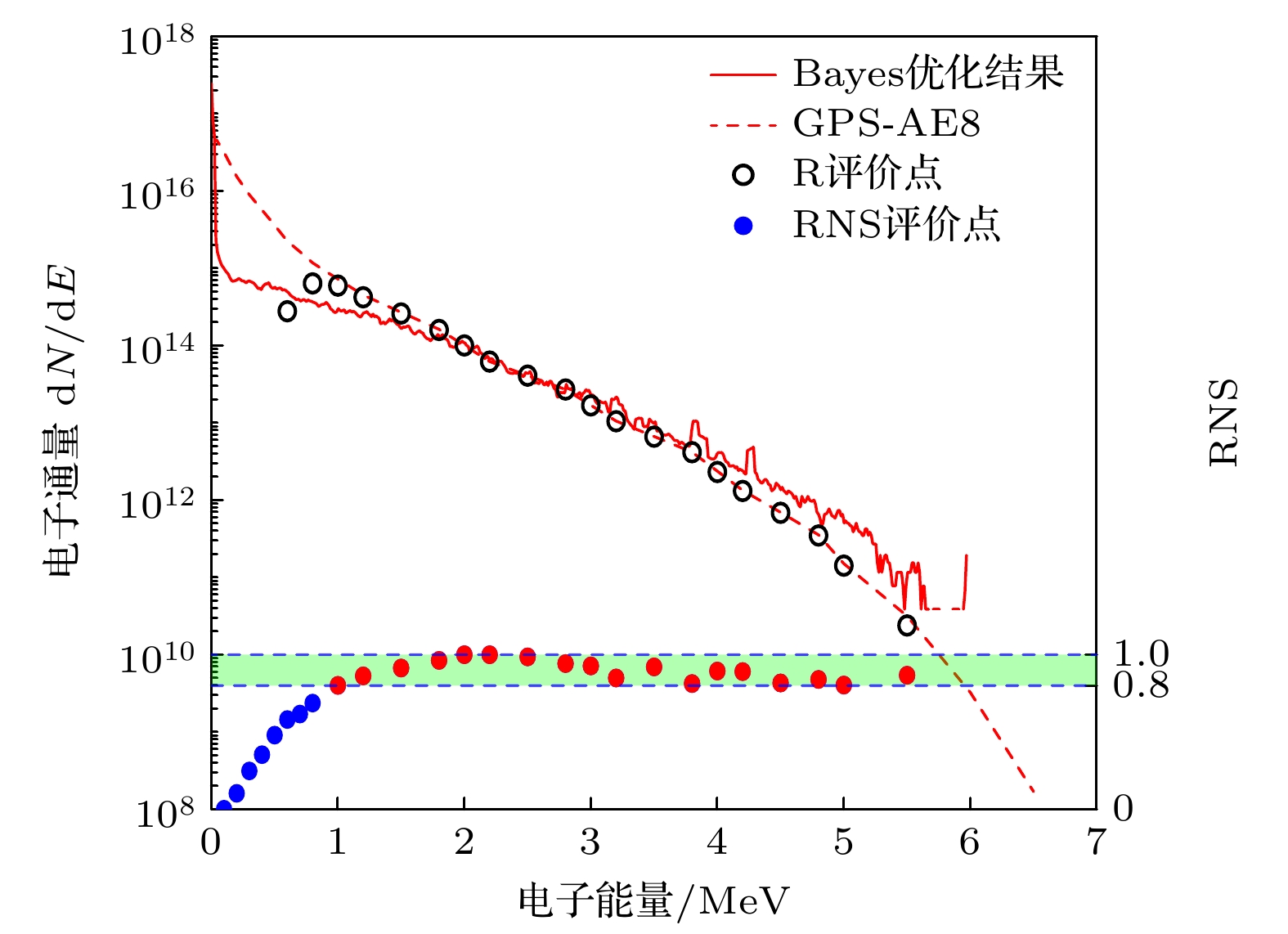
图2(a)给出了$t = 48\;{T_{0}}$时刻不同密度垂直平面靶Ⅰ情况的电子能谱分布, 其中${T_0}$为激光周期, 虚线为典型轨道GPS和GEO累积15年的电子积分能谱 (AE-8模型^[3]). 可以看到, 不同垂直平面靶Ⅰ密度对应的有效电子温度和截止能量不同(激光参数和其他靶参数相同), 靶Ⅰ密度越高, 电子束截止能量越大. 当靶Ⅰ密度为$0.05{n_{\text{c}}}$时, 最大电子能量为5.06 MeV, 根据麦克斯韦分布的近指数型能谱的电子温度$T = \dfrac{{{E_1} - {E_2}}}{{\ln ({n_2} - {n_1})}}$^[34], 能够得到获得高能端(大于1 MeV)有效电子温度为0.69 MeV, 其中$E$和$n$取自电子能谱分布. 而当靶Ⅰ密度为$0.1{n_{\text{c}}}$时, 高能端能谱结构和电子温度与GPS轨道电子辐射相一致, 最大电子能量为5.8 MeV, 高能端有效电子温度约为0.63 MeV. 同时, 我们给出了仅有高密度平面固体靶Ⅱ的电子能谱分布 (黑色实线), 此时电子能谱为单温分布, 且电子截止能量仅为0.85 MeV, 与靶Ⅰ密度为$0.05{n_{\text{c}}}$情况的低能端几乎相同, 这也证明了靶Ⅰ主要提供少量的高能电子, 而高密度固体靶Ⅱ则提供了大量低能电子. 因此, 利用双平面复合靶能够有效匹配空间轨道的指数型宽能谱结构, 并能通过优化靶密度与尺寸实现电子能谱的调节.

为了评价电子能谱局部匹配程度, 提出一种基于AE8模型7 MeV以内30个数据点(图2(a)中绿色实心点)的拟合计算评价方法, 并以GPS轨道为例展示了我们的计算结果. 评价两条曲线拟合程度的方法有很多, 常用的有RMSE方法与决定系数R², RMSE方法主要用于评价两条曲线之间的差值^[36], R²的优势在于评价两条曲线整体趋势上的匹配程度^[37]. 根据模型的特点, 对其差值(电子通量差异)与整体趋势(电子能量分布)均有相应要求, 需要基于两种方法分别计算并评价, 将改进后的两种方法分别称为局部(RMSE-normalized score) RNS评价和整体R评价. RNS评价方法计算流程如下. 首先根据均方根误差公式${\text{RMSE}} = \sqrt {\displaystyle\frac{1}{n}\sum\nolimits_{i = 1}^n {({y_{1 i}}} - {y_{2 i}}{)^2}} $计算出各数据点处的平均误差, 其中${y_{1 i}}$为模型计算的各通量值, ${y_{2 i}}$为模拟计算的各通量值. 同时, 为了提高计算精度, 以数据点附近0.1 MeV能量范围划分100个数据作为该点处RMSE评价值. 然后根据

对均方根值进行归一化, 可以称为RMSE归一化处理 (RMSE-normalized score, RNS), 得到最终的RNS评价点. 这里$S$为RNS计算结果, ${M_i}$为各点处均方根误差, ${M_{\max }}$与${M_{\min }}$为各点均方根误差最大值与最小值^[34], 计算结果如图2(b)中实心点所示. 其中, 我们以模拟结果与AE8模型结果电子通量差值在1个数量级以内表示能谱匹配程度较好, 此时RNS值在0.8—1之间. 因此定义RNS值在0.8—1之间时(图2(b)中位于两条蓝色虚线中间的绿色带状部分的红色点), 能谱匹配度满足要求, 而蓝色点代表RNS值小于0.8的点, 表示匹配程度较差. 可以看到, 能谱高能端1.8—5.5 MeV范围内, 模拟值与理论模型匹配较好, 共产生15个可信点, 在大于1 MeV区间内占比达到71.4%.

进一步使用基于决定系数R²的整体R评价方法对能谱整体的匹配程度进行评价, 同样采用数据点附近区间进行计算, 具体计算方法为

其中$\overline {{y_1}} $和$\overline {{y_2}} $分别为模型值与模拟值在数据点左右区间的均值^[37], 该区间取相邻两个数据点分别与该数据点的均值作为上下界, 边界点的上下界取其本身. 根据R²的计算特点, 计算值越接近1表明拟合程度越高, 利用计算获得的R值与GPS轨道该能量对应的通量相乘即可得到能谱整体匹配程度的评价点, 计算结果如图2(b)中空心点所示(舍弃计算结果为负的点). 可以看到, 模拟结果整体匹配较好, 统计偏差在1个数量级内的R值计算结果为大于0.7, 对应能量点范围在高能端1.8—5.5 MeV. 统计局部RNS评价与整体R评价匹配效果为优的重合点, 最终得到拟合结果为优的能量区间为1.8—5.5 MeV, 占比达到71.4%.

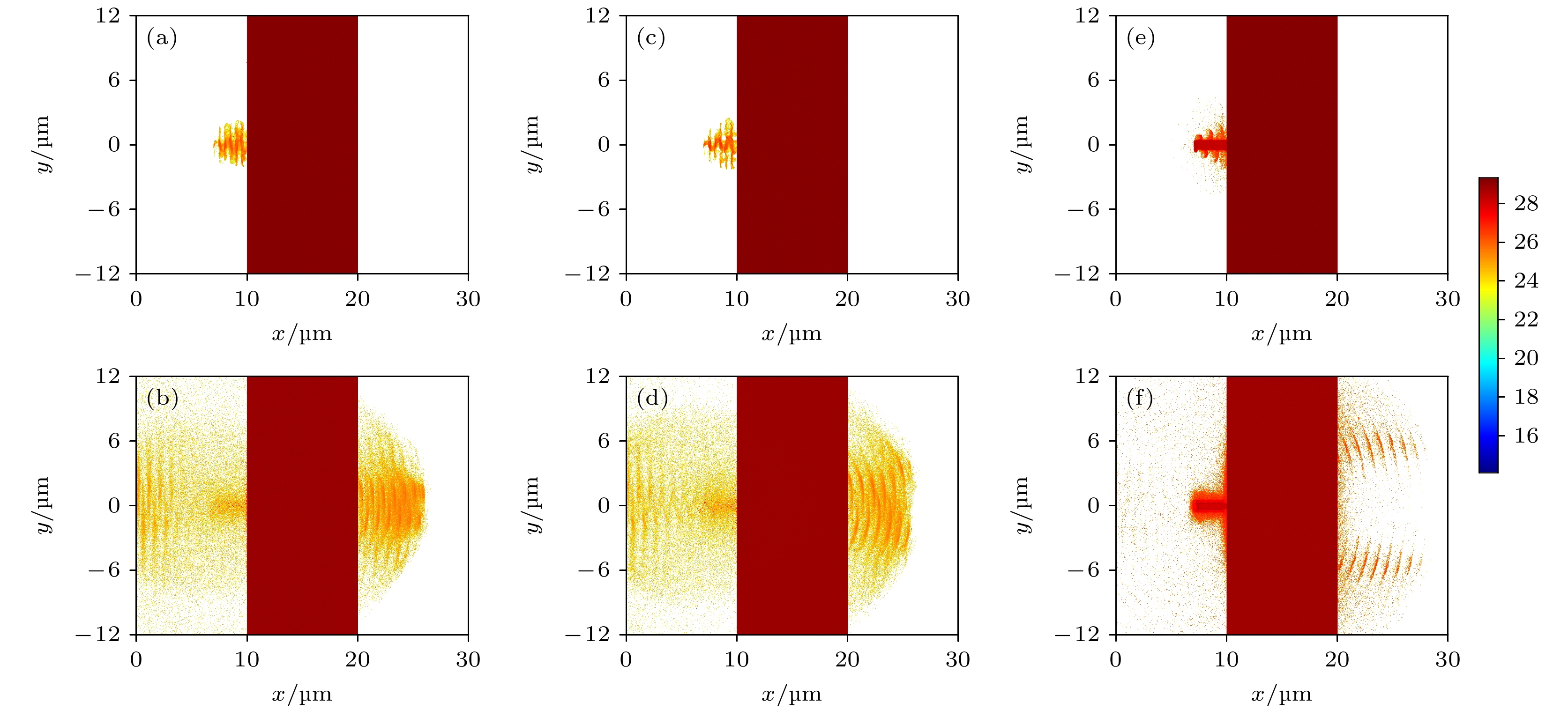
图3给出了$ t = 18{T_0} $和$t = 34{T_0}$时刻垂直平面靶Ⅰ密度为$0.05{n_{\text{c}}}$, $0.1{n_{\text{c}}}$, $10{n_{\text{c}}}$时的电子密度空间分布. 可以看到, 3种情况靶Ⅰ的电子密度分布演化差异较大. 在垂直平面靶Ⅰ密度为$0.05{n_{\text{c}}}$时, 靶Ⅰ的电子呈现振荡加速, 振荡波长为激光波长的一半, 如图3(a)所示, 这源于线极化激光的有质动力振荡项$ - ({e^{2}}/4{m_{\text{e}}}\omega _0^2)\cos (2{\omega _0}t)\nabla {E^2}(x) $, 加速机制为激光有质动力加速^[33], 其中, $e$为电子电荷量, ${\omega _0}$为激光角频率, ${m_{\text{e}}}$为电子质量, $E(x)$为激光电场振幅. 根据低密度丝靶有质动力加速模型^[38], 加速电子的最大能量可以表示为$ E = 1.6{a_0}\times \exp ( - \lambda _0^2/16{\sigma ^2}){\text{ MeV}} $, 其中$ \sigma $为激光焦斑半径. 因此, 在当前参数下, 理论计算的最大电子能量为5.1 MeV, 与模拟结果的最大电子能量4.9 MeV相一致. 当驱动激光和垂直平面靶Ⅰ被加速的高能电子到达高密度平面固体靶Ⅱ时, 高能电子直接穿过靶, 而垂直入射的驱动激光仍保持垂直入射至靶Ⅱ, 无法满足真空锁相加热以及随机加热的条件^[27]. 因此, 激光脉冲主要通过J×B机制加速大量高密度平面固体靶Ⅱ前表面电子, 继而在靶后产生指数型能谱电子束, 且电子束准直性较好, 如图3(b)所示.

当靶Ⅰ密度增大到$0.1{n_{\text{c}}}$时, 靶Ⅰ的电子仍呈振荡加速, 但振荡波长除了半波长分量, 还出现了波长分量, 且最大电子能量提高到5.7 MeV. 这是因为靶Ⅰ的电子加速机制不仅有激光有质动力 加速, 还伴随着表面有质动力加速^[39], 如图3(c) 所示. 驱动激光和靶Ⅰ的高能电子与高密度平面固体靶Ⅱ的相互作用与低密度情况一致, 且在此参数条件下, 电子加速机制逐渐由激光有质动力加速主导向表面有质动力加速主导过渡.

当靶Ⅰ密度增大到$10{n_{\text{c}}}$时, 电子加速由表面有质动力加速主导, 大量电子首先被驱动激光拉出靶表面, 其运动方向在洛伦兹力作用下迅速变化为激光传输方向, 并在靶Ⅰ的上下表面形成了电子片状结构^[31,38,39], 如图3(e)所示. 根据表面有质动力加速模型^[39], 电子获得的最大能量可以表示为$ {E_{\max }} = 2\eta {m_{\text{e}}}{a_0}{c^2}\sqrt {{\omega _0}t} $, 其中ƞ为自生电场最大振幅与激光纵向电场的比值, $t$为电子在激光场中运动的时间. 取靶Ⅰ上表面0.1 μm位置处自生电场的最大值, 得$\eta \approx 0.76$, 电子在激光场中运动的最大距离即为靶Ⅰ长度. 因此, 运动的时间为$t = 3{\lambda _0}/c$, 理论计算的电子最大能量为10.8 MeV, 与模拟结果的10.3 MeV接近(未在图中展示).

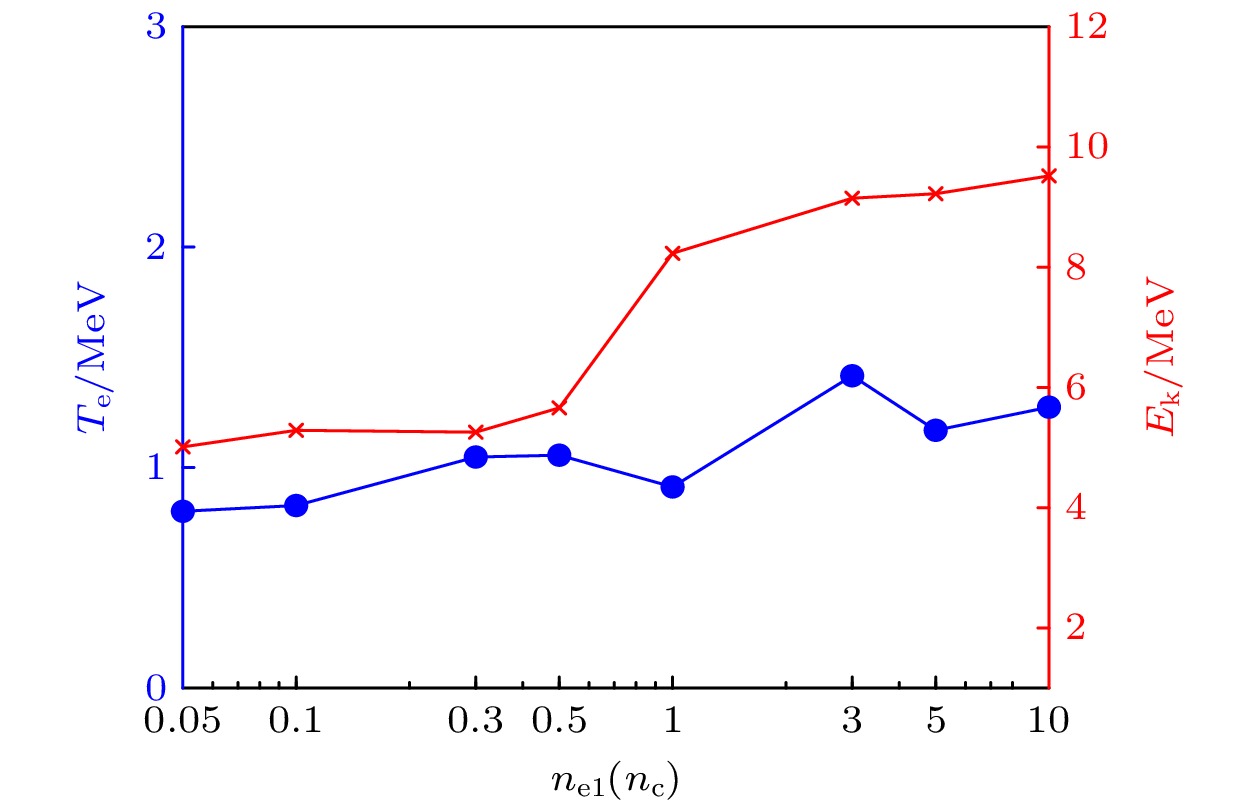
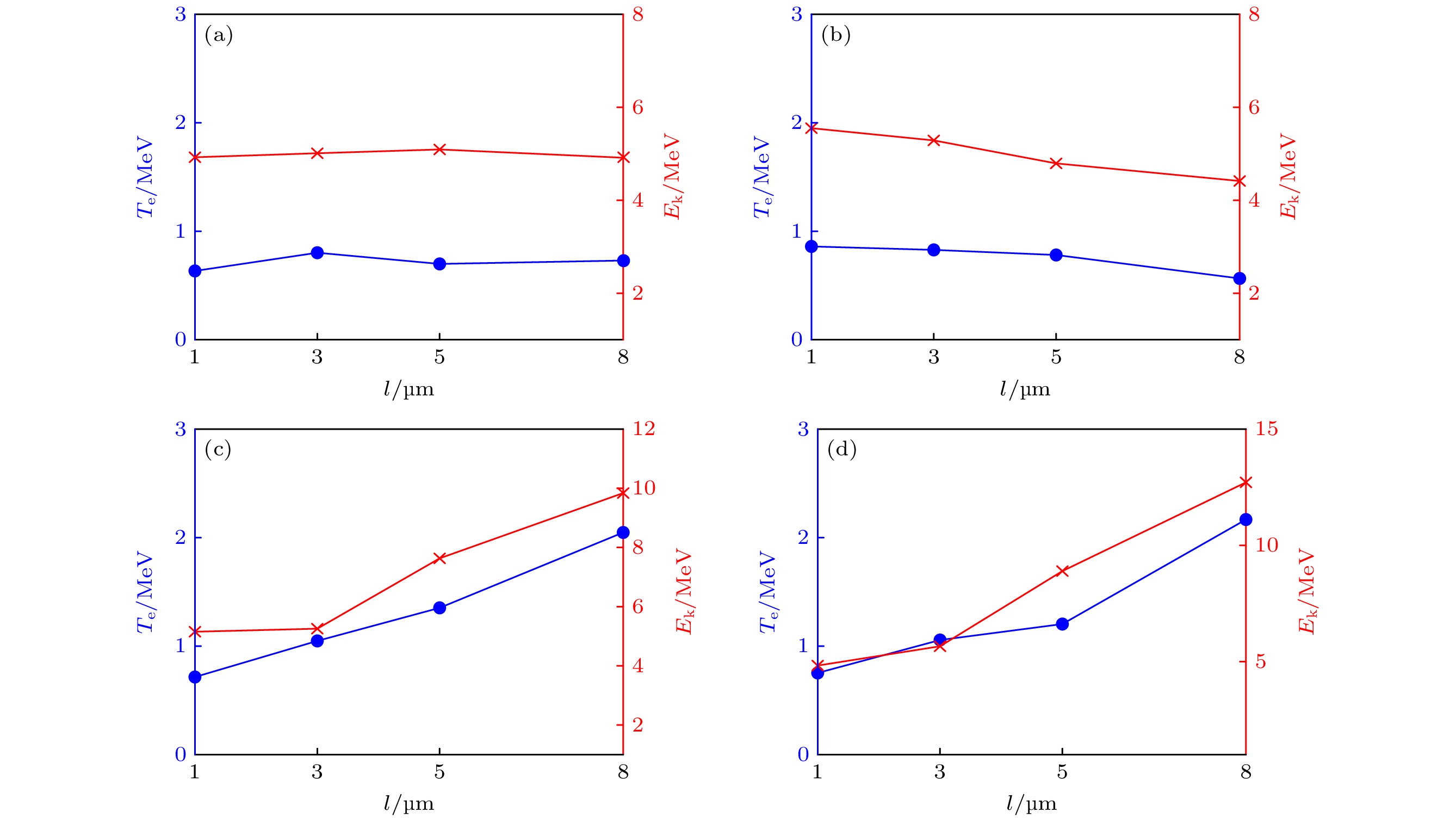
为了详细研究复合靶对电子束能谱的调控, 对靶Ⅰ进行参数扫描. 图4给出了不同密度靶Ⅰ的电子最大能量和高能端(能量大于1 MeV)电子温度演化. 可以看到, 加速电子的最大能量随靶Ⅰ密度增大而升高, 同时, 在临界密度以下最大能量增幅较为平缓, 临界密度以上最大能量在一定范围内增长迅速, 这是由于电子加速机制发生变化. 另外, 当靶Ⅱ密度达到数十至上百${n_{\text{c}}}$时, 由于激光的能量转化效率区域饱和, 电子最大能量不会明显升高^[40]. 高能端电子温度随靶Ⅰ密度的增大也缓慢增长, 这与最大电子能量的升高相对应.

图5给出了4种密度靶Ⅰ情况下的电子最大能量(红线)与高能端电子温度(蓝线)随靶Ⅰ长度的演化. 从图5(a), (b)可以看到, 由于靶Ⅰ密度较低, 激光有质动力主导电子加速, 电子最大能量仅与激光强度、焦斑半径和激光波长相关^[39], 电子最大能量被限制在6 MeV以下, 电子温度在1 MeV以下. 从图5(c), (d)可以看到, 随着靶Ⅰ密度升高, 电子加速机制逐渐变为表面有质动力加速, 电子最大能量提高至10 MeV以上, 随着高能量电子数目的增多, 电子温度不断升高, 最高可达2 MeV.

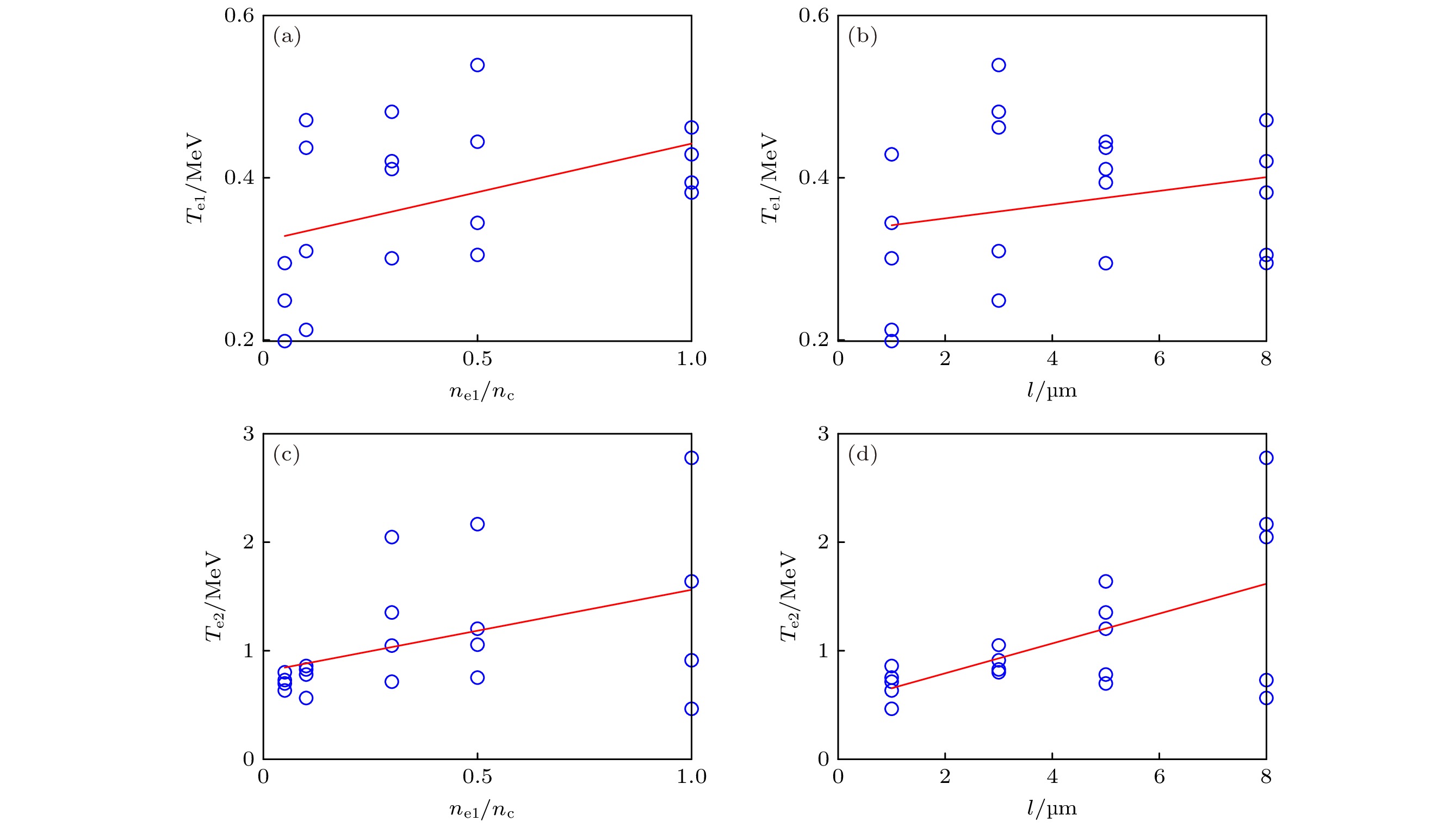
以上研究表明, 靶Ⅰ的密度和长度与电子温度之间存在复杂的线性关系, 根据目标轨道电子温度, 寻找匹配该轨道电子能谱的靶Ⅰ参数需要大量模拟计算. 为了优化计算效率, 可以采用贝叶斯优化算法优化靶设计, 以较小的计算资源获得匹配能谱的最优解. 图6给出了电子束能谱的低能端(小于1 MeV)电子温度T_e1和高能端(大于1 MeV)电子温度T_e2随靶Ⅰ密度${n_{{\text{e}}1}}$和长度$l$演化, 蓝色散点为模拟数据, 红色实线为线性回归模型拟合直线. 可以看到, 高能端电子温度T_e2更接近拟合直线, 说明高能端电子温度与靶Ⅰ密度${n_{{\text{e}}1}}$和长度$l$有较强的线性关系, 而低能端电子温度的线性关系较弱. 为更准确表示靶Ⅰ参数对电子温度的影响程度, 使用假设检验方法对参数进行计算, 由于样本数量小于30, 采用F检验方法进行计算^[41], 其中统计量$F = \dfrac{{{\text{MSR}}}}{{{\text{MSE}}}}$. 这里, ${\text{MSR}} = \dfrac{{{\text{SSR}}}}{{{\text{dfR}}}}$为回归平方和, 其中${\text{SSR}} = {\displaystyle\sum {(\widehat {{y_i}} - \overline y )} ^2}$为预测值与平均观测值误差的平方和, ${\text{dfR}}$为预测变量的数量; ${\text{MSE = }} \dfrac{{{\text{SSE}}}}{{{\text{dfE}}}}$为误差平方和, 其中${\text{SSE}} = {\displaystyle\sum {({y_i} - \widehat {{y_i}})} ^2}$为观测值与预测值误差的平方和, ${\text{dfE}}$为误差自由度. 可以得到, 靶Ⅰ密度${n_{{\text{e}}1}}$对低能端电子温度T_e1的F检验统计量为4.46, 查表得到对应p值为0.049, 表明靶Ⅰ密度${n_{{\text{e}}1}}$对低能端电子温度T_e1影响较大 (p值小于显著性水平0.05) ^[40]. 靶Ⅰ密度${n_{{\text{e}}1}}$对高能端电子温度T_e2的F检验统计量为4.25, 对应p值为0.054, 表明靶Ⅰ密度${n_{{\text{e}}1}}$对高能端电子温度T_e2影响较小. 同样计算长度$l$分别对低能端和高能端电子温度的F检验统计量为1.06和10.1, 对应p值为0.316和0.0053, 表明长度$l$对低能端电子温度T_e1影响较小, 对高能端电子温度T_e2影响较大.

根据靶参数与高能端电子温度之间的线性关系, 采用二维贝叶斯优化算法对数据进行整合并预测^[42,43]. 选取靶Ⅰ密度和长度为输入参数, 高能端电子温度作为目标响应, 以GPS轨道为目标轨道, 高能端电子温度约为0.62 MeV, 贝叶斯代理函数使用高斯代理函数, 取目标电子温度作为采集函数的一个常量, 迭代1000次计算靶Ⅰ密度和长度参数, 输入粒子模拟程序LAPINE进行检验, 计算得到新的数据后导入原始数据中再次进行迭代, 最终得到靶Ⅰ密度为0.82n_c和长度为2.4 μm时, 获得高能端电子温度0.62 MeV, 与目标电子温度一致. 图7给出了贝叶斯优化参数后的粒子模拟电子束能谱及R和RNS评价方法结果. 可以看到, 最优点匹配能量区间由1.8—5.5 MeV扩展到1—5.5 MeV, 大于1 MeV的拟合点占比达到85.7%, 高能端能谱结构更加符合GPS轨道电子辐射.

面向空间辐射环境模拟应用, 利用二维粒子模拟方法研究了激光驱动双平面复合靶电子加速模拟近地空间轨道电子辐射的方案. 研究结果表明, 高密度平面固体靶能够提供大量低能电子, 而其前表面放置的垂直平面靶则提供少量高能电子, 使得电子束能谱结构与空间辐射环境相一致, 有效地降低了驱动激光强度, 并给出了能谱匹配的评价方法. 同时发现, 随着垂直平面靶密度的增大, 加速机制由有质动力加速逐渐过渡到表面有质动力加速, 进而增大了电子束最大能量和电子温度. 最后, 利用贝叶斯优化方法对垂直平面靶的密度和长度进行了优化设计, 获得了能谱结构与空间辐射环境更加匹配的电子束. 该方案能谱可调谐性更强, 可为不同轨道空间电子辐射环境模拟实验研究提供理论参考.