-
核物质状态方程(equation of states, EoS)描述了核物质体系在不同热力学条件(如温度、压强)、同位旋不对称度、强外场(如磁场、涡旋等)下宏观量之间的依存关系. 主导核物质体系的相互作用是强相互作用, 描述强相互作用的基本理论是量子色动力学(QCD). 核物质体系的宏观量之间的关联实际上是核物质体系微观相互作用的最终体现, 因此研究EoS对理解强相互作用的基本理论——QCD在不同能标和外部条件下的性质, 以及理解由强相互作用主导的体系的性质和演化过程, 如早期宇宙的演化、原子核性质、重离子碰撞动力学、致密天体内部结构、双中子星合并等都具有重要意义. 类似地, 比如水存在气相、液相和固相, 这些相之间的转化是外部条件改变导致水分子之间微观自由度改变而引起的宏观表现. 分子之间的相互作用力是范德瓦耳斯力, 它是电磁相互作用的剩余相互作用, 研究分子(原子)的相结构推动了人们对电磁相互作用的理解. 在核物质中核子之间的相互作用通常被称为核力, 核力是强相互作用的剩余相互作用. 强相互作用的一个基本性质是其耦合常数(
$ \alpha_{\mathrm{s}} $ )随着能标的降低而变大, 这就是强相互作用的渐进自由特性. 在低能标下如原子核中的核子-核子相互作用, 强相互作用的耦合常数很大, 传统的微扰方法不再有效, 即从QCD出发计算核力和核核相互作用的方法不再可行. Wilson[1]在1974年提出了格点量子色动力学(lattice QCD, LQCD)研究强相互作用的理论框架, LQCD通过将连续的时空离散化为一个个有限的格点网格, 从而使得量子色动力学可用于低能标下的计算. LQCD对基于SU(3)对称性的重子-重子相互作用势能够给出较好的描述[2–4], 但是在计算有限密度核物质体系性质时受所谓符号问题限制遇到了很大挑战[5]. 20世纪80年代, Weinberg[6,7]基于核力的介子交换理论指出在低能标强相互作用中的基本自由度是核子和π介子, 提出了手征有效场论(chiral effective field theory, ChEFT), 该方法在计算核子-核子散射问题中取得了巨大的成功. 多体的核子-核子相互作用可以将ChEFT的拉氏量按动量展开来计算, 关于ChEFT的理论综述详见参考文献[8,9]. ChEFT的低能量标定义为系统中核子动量或者π介子的质量小于ChEFT失效的能标($ \varLambda_{\text{ChEFT}}\approx 1\;{\mathrm{GeV}} $ ), 对应的核物质体系的密度范围大致为$ \rho<3\rho_0 $ 区域, 其中$ \rho_0\;{\approx}\;0.17\;{\mathrm{fm}}^{-3} $ 为原子核饱和密度. 2016年, Drischler等[10]基于ChEFT计算得到了同位旋依赖的单核子能量, 趋势上该计算结果与唯象理论结果一致. 同位旋是核物质状态方程的重要自由度, 同位旋是基于粒子物理标准模型中u, d夸克相关的量子数, 比如质子和中子是同位旋I = 1/2的粒子, 它们同位旋第三分量$ I_3 $ 分别为1/2和–1/2. 同位旋不对称度定义为核物质体系内中子数($ N_{\mathrm{n}} $ )和质子数($ N_{\mathrm{p }}$ )的差与总核子数的比例, 即$ \delta = (N_{\mathrm{n}}-N_{\mathrm{p}})/(N_{\mathrm{n}}+N_{\mathrm{p}}) $ , δ的数值分布范围为0—1, δ = 0对应同位旋对称核物质(symmetric nuclear matter, SNM), δ = 1对应纯中子核物质(pure neutron matter, PNM).近年结合手征有效场论与格点量子蒙特卡罗方法发展出了格点有效场论(nuclear lattice effective field theory, NL-EFT), 它能够在统一的理论框架下构建核力和求解量子多体问题[11]. NL-EFT能给出质量数A = 3—58各稳定同位素的质量, 并且在N3LO阶次考虑2体和3体相互作用后, 能够给出与现有EoS唯象理论一致的结果[12]; 近期基于NL-EFT的N3LO核力的计算, 成功给出了4He, 12C与16O等原子核的电荷半径[13]. 通常, 输运模型/唯象模型采用参数化形式来定义EoS, 核物质状态方程的参数通过比较实验结果和模型模拟结果来获取. 基于第一性原理计算给出的EoS对温度、密度、同位旋不对称度、奇异成分等的依赖, 是输运模型/唯象模型和强子输运模型中状态方程的重要依据, 更重要的是这建立了状态方程的参数表达和微观相互作用的之间关联.
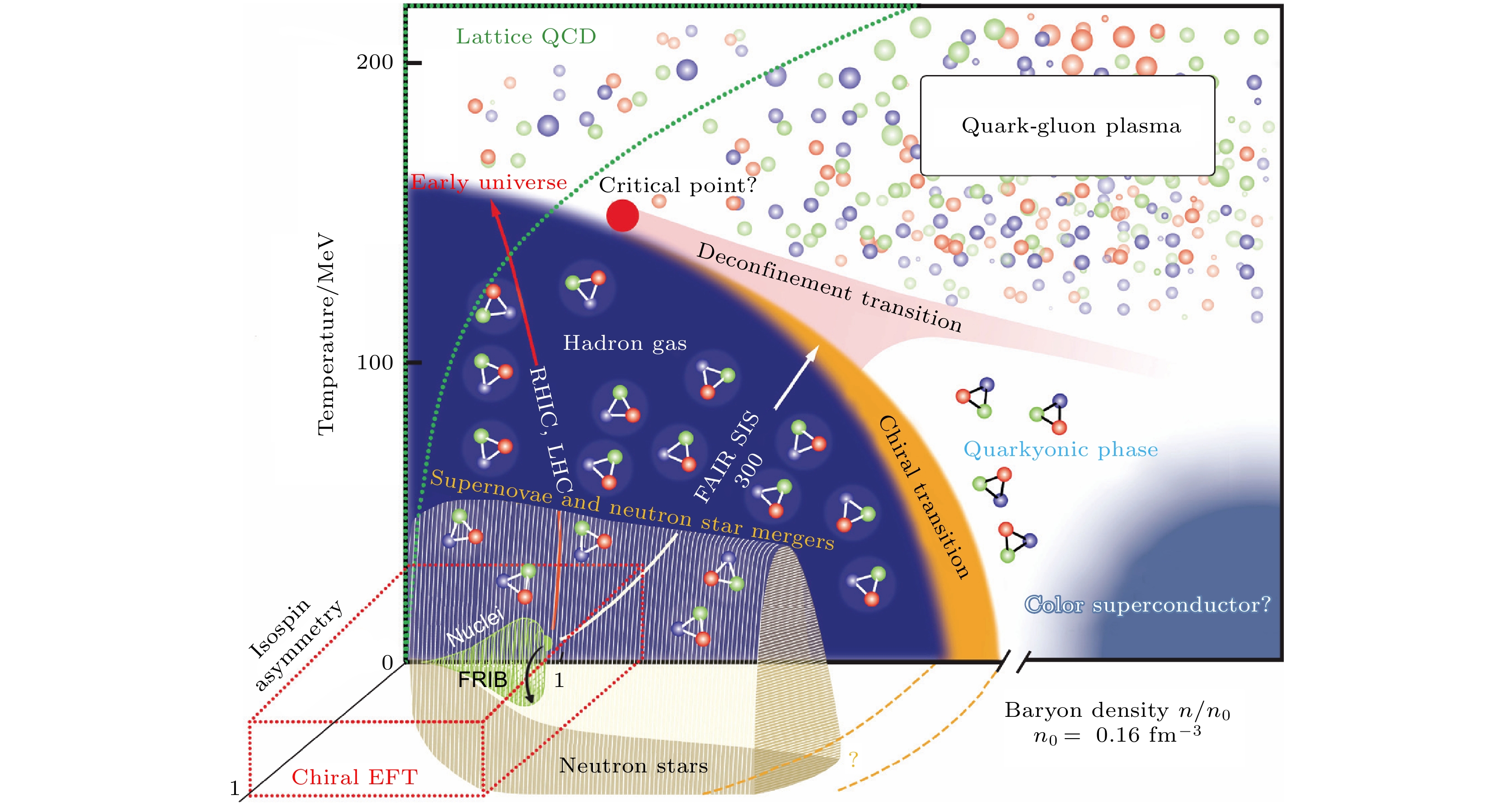
图1所示为用温度(T)、重子密度和同位旋不对称度(δ)所表示的核物质相结构示意图[8], 其中ChEFT理论适用的大致范围对应图中左下角的立方体区域. 由于核物质体系的密度与重子化学势之间存在单调关联, 核物质相图的横轴文献中也常见用重子化学势(
$ \mu_{\mathrm{B}} $ )表示[14], 重子化学势表示在核物质体系中增加或者移除一个核子时体系能量的改变. 图1中垂直于温度和重子密度平面的轴为同位旋不对称度δ. 本文用ρ表示密度,$ \rho_0 $ 表示原子核饱和密度, 本文引用的一些图中核物质密度用n表示, 请读者注意对照图解来理解图中符号所代表的物理量. 图1中的不同区域可以对应到宇宙演化过程中存在的实体或者场景, 核物质状态方程直接决定这些实体或者过程的演化行为、内部结构、热力学性质以及相应实验可观测量的行为. 在极端高密、高温的情况下, 核物质体系中的强子会发生夸克解禁闭, 核物质以夸克胶子等离子体(quark-gluon plasma, QGP)的形式存在, 这被认为是宇宙大爆炸之初物质的存在形态; LQCD预言在重子化学势$ \mu_{\mathrm{B}} $ = 0时强子气体到QGP的相变是一个平滑过渡, 且给出临界温度$ T_{\mathrm{c}} = (158\pm 0.6) $ MeV[15], 这个结果与相对论性重离子碰撞数据中提取的化学冻出温度一致[16]. 极高温、高能量密度极限对应宇宙大爆炸的早期状态——QGP; 目前, 强子气体到QGP的相变类型尚不清楚, 如果这个相变是一级相变, 则存在相变临界点(critical end point, CEP). 因为CEP是定义强相互作用物质形态的基本参考量, 实验上寻找相边界和可能存在的CEP是高能核物理的研究前沿[14]. 在低温高密区, 理论预言了更加丰富的核物质存在形式, 如夸克素物质(quarkyonic matter)[17]、色超导态[18]等, 这些理论预言的核物质相有待实验的进一步证实.在低温、高密区(高重子密度区)对应致密天体, 如中子星. 中子星是由大质量恒星(约5—20倍太阳质量)晚期塌缩形成的星体, 它的质量是1—2倍太阳质量、近似零温、半径约12 km, 其内部密度可以达到
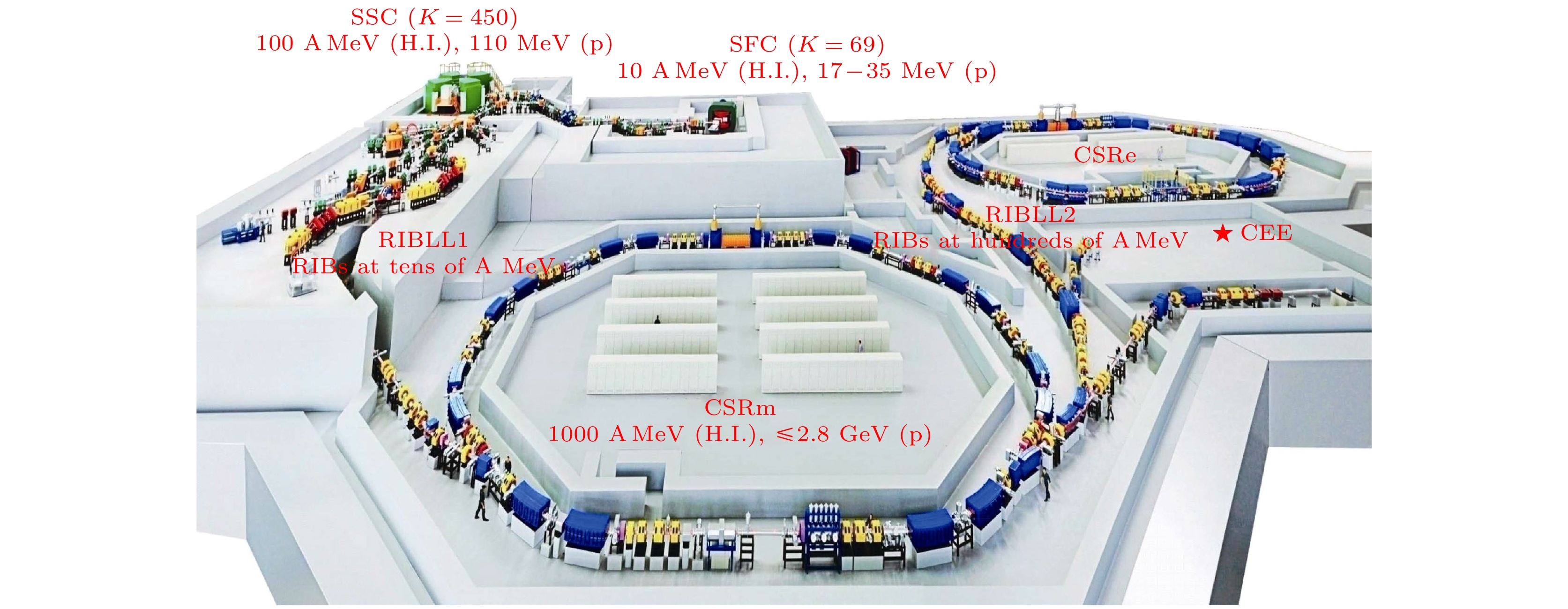
$ 4\rho_0 —8\rho_0 $ . 由于中子星是天然存在的大尺度中子物质, 因此天文观测中得到的中子星性质、双中子星并合的数据对研究PNM状态方程具有极其重要的意义. 在中子星的性质研究中, 不同的EoS模型可以给出中子星质量和半径的依赖关系. 天文观测中测量中子星的半径和质量, 对现在EoS的类型和参数就显得尤为重要. 2010年, 利用Shapiro效应天文观测中发现了1.97 ± 0.04倍太阳质量($ M_{\odot} $ )[19]的中子星; 2022年基于同样的办法观测到(2.17 ± 0.17)$ M_{\odot} $ 的中子星[20], 这些超大质量中子星的发现, 可以排除高密区软EoS. 对于中子星半径的测量近年来也取得突破性进展, NICER合作组[21,22]通过双星系统中子星热斑辐射的办法同时测量到质量约为1.4$ M_{\odot} $ 和2.08$ M_{\odot} $ 的中子星的半径分别为(12.45 ± 0.65) km和(12.35 ± 0.75) km. 2017年8月17日, LIGO/VIRGO合作组[23]观测到首个具有里程碑意义的双中子星合并产生引力波的事件GW170817, 两个中子星在靠近的过程中由于引力作用导致中子星发生潮汐形变, 基于潮汐形变参数提取到质量为1.4$ M_{\odot} $ 中子星的半径R1.4 = 12.42 km, 这个测量的误差下限和上限分别为10.95 km和13.21 km[24]. 在给定引力强度的情况下, 潮汐形变的程度依赖于EoS的软和硬. 而潮汐形变又可以通过引力波的振荡频率来测量, 这就为研究纯中子物质EoS提供了非常直接的天文观测的输入[25–27]. 基于这些天文观测得到的EoS的参数值与地面实验中提取的一致, 详细参数的比较见本文第2节. 理论模拟显示, GW170817事件中的双中子星合并的中心会产生高温高密核物质(密度会达到$ 2\rho_0 $ 以上, 且温度约为70 MeV)[28], 在并合过程中除了引力波, 天文观测中还同时观测到了X射线、γ射线、中微子等可观测信号, 这也将天文观测带入所谓的多信使时代. 这些天文观测将为研究中子核物质在不同热力学条件下的性质提供强有力的实验限制.本文主要介绍利用中高能重离子碰撞实验来研究核物质状态方程的进展. 第2节介绍核物质状态方程的基本概念, 以及综合重离子碰撞实验和天文观测相结合状态方程研究现状; 第3节介绍中高能重离子碰撞的基本动力学, 以及对状态方程敏感的运动学变量; 第4节介绍中高能重离子碰撞研究核物质状态方程的典型实验和实验结果; 第5节主要讨论包含奇异强子的致密核物质状态方程的实验和理论研究进展; 最后, 介绍高重子密度区在运行或在建的重离子加速器, 以及相关实验的最新进展, 并简要介绍我国已经建成的兰州重 离子加速器-冷却储存环(HIRFL-CSR)、低温高密核物质测量谱仪(CEE) 建造进展和在建大科学装置——强流重离子加速器装置(HIAF)上核物质状态方程相关的研究机遇和挑战.
-
核物质体系的能量与体系的热力学条件和同位旋不对称度相关. 在近似零温情况下, 核物质体系的状态方程可以用(1)式表达:
其中,
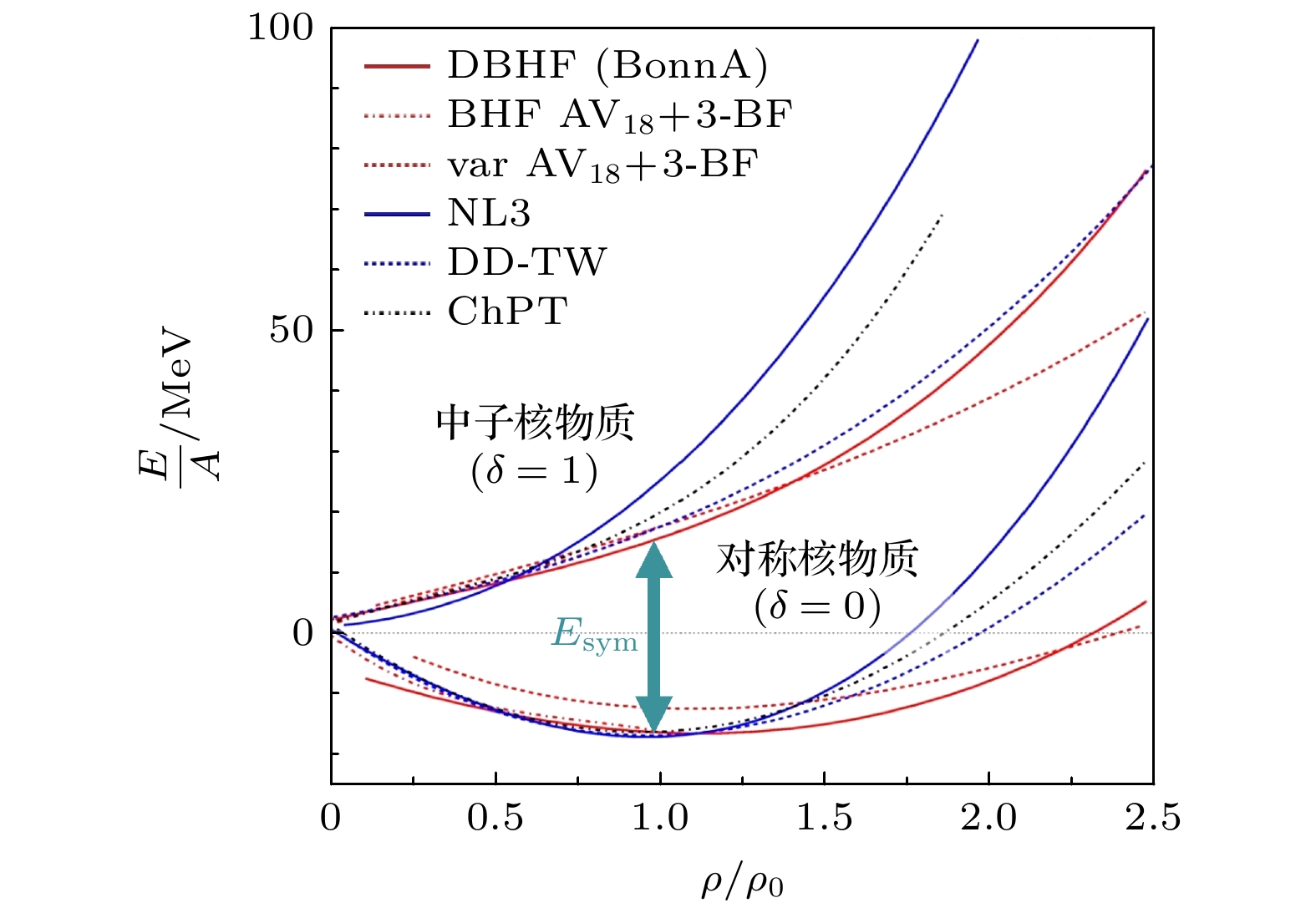
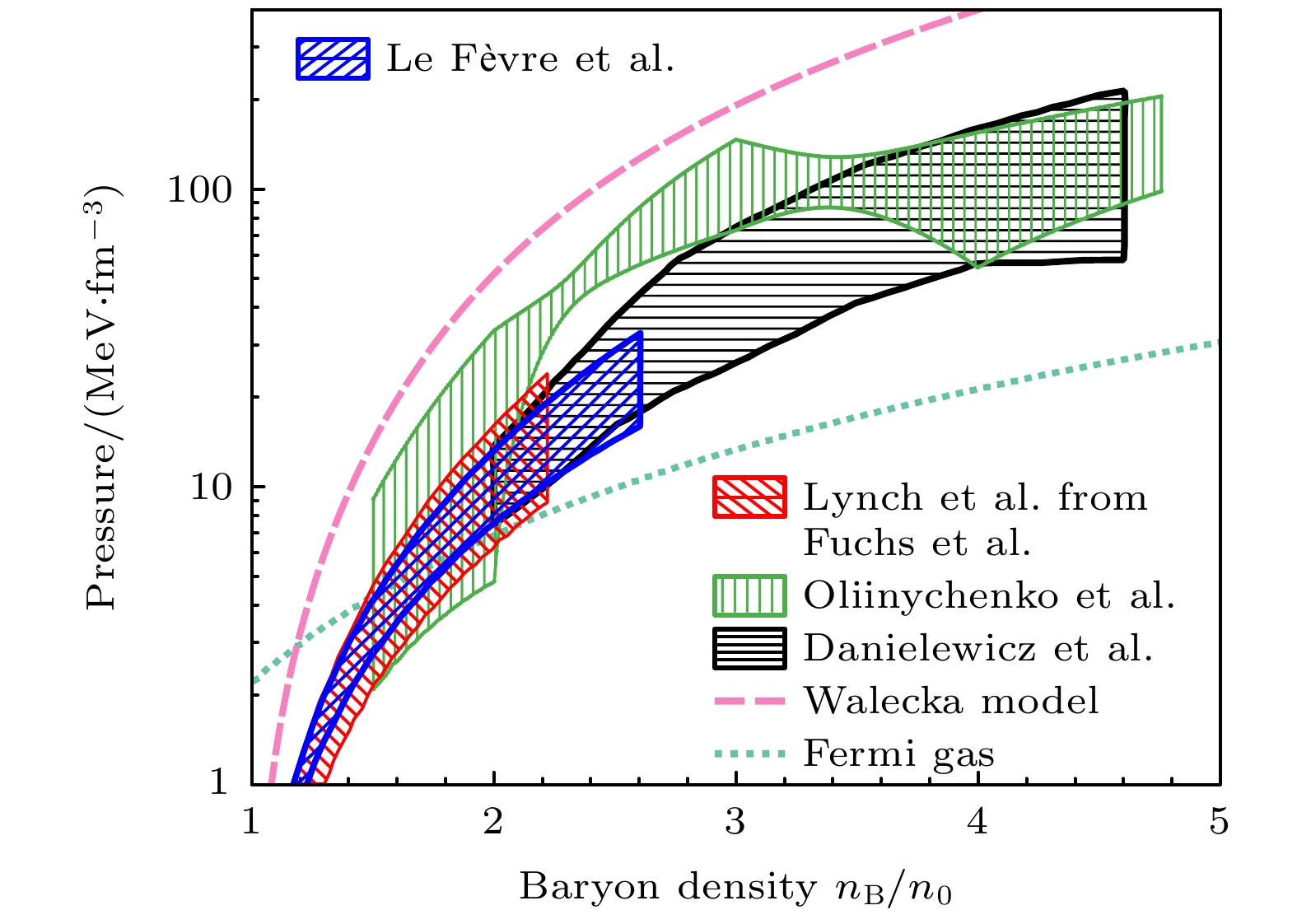
$ \rho = \rho_{\text{n}}+\rho_{\text{p}} $ 为所有核子总密度, δ为体系的同位旋不对称度,$ E_0(\rho) $ 为对称核物质的单核子能量,$ E_{\text{sym}}(\rho) $ 为同位旋不对称度相关的能量系数, 也被称为对称能. 通常EoS对密度做泰勒展开假设级数是收敛的, 高阶项的贡献随着阶数的增加而迅速减小, 高阶项的贡献相对较小, 因此忽略高阶项不会显著影响结果的准确性. 另外, 目前的实验数据主要集中在低密度区域, 高阶项的贡献难以通过实验测量, 忽略高阶项可以使理论更好地与实验数据匹配.图2所示为几个理论模型给出的对称核物质和中子核物质的状态方程与体系密度的关系[29], 其中SNM在饱和密度处的能量约为–16 MeV, 且随着密度的升高单核子能量随之增大; 纯中子物质由于泡利不相容原理的限制, 单核子能量都是大于0, 且随着密度逐渐上升. 对称能是SNM EoS与PNM EoS之间的差异, 由于SNM和PNM在不同密度处行为存在差异, 导致对称能亦具有密度依赖. 对于同位旋不对称度0 < δ < 1系统的EoS, 体系总能量由(1)式给出. 相应地, 核物质体系的压强P和不可压缩系数K分别正比于系统能量
$E( \rho, \delta) $ 对密度的1阶和2阶导数, 如(2)式和(3)式所示:自然存在的原子核是在饱和密度附近的核体系, 基于原子核性质的研究, 人们对核物质在饱和点处的认识比较丰富. 为了研究在亚饱和密度和超饱和密度区间核物质的性质, 把核物质状态方程按变量
$ \chi = (\rho-\rho_0)/3\rho_0 $ 在饱和密度附近做泰勒展开, 则可以写成如下形式:其中, 斜率L、曲率K和偏度J分别为能量对χ变量的1, 2和3阶导数的系数. 依照以上形式, 对称核物质和纯中子物质在饱和密度处的状态方程在忽略高阶项时, 可分别写成
因为在更高阶的展开项中会产生发散的问题, 目前的研究中这些系数一般考虑到3阶项. 这里首先给出对称核物质和纯中子物质状态方程的表达式, 以及这些参数当前的取值范围, 然后在第4节中具体讨论提取这些参数的典型实验.
对称核物质状态方程即(5)式中的
$ E_0(\rho_0) $ 约为–16 MeV, 为饱和密度处单核子的能量, (5)式中没有出现1阶系数$ L_0 $ , 是因为在饱和密度处核子的能量$ E_0 $ 达到极小值使得$ L_0 = \dfrac{\text{d}E(\rho)}{{\mathrm{d}}\chi}\Big|_{\rho = \rho_0} = 0 $ ,$ K_0 $ 表示核物质在饱和密度附近的不可压缩性(文献中也常用κ表示), 它表示对体系压缩单位体积时所需要的能量. 当$ K_0\approx 200 $ MeV时, 状态方程被称为软EoS, 反之在$ K_0\approx350 $ MeV时则被称为硬EoS, 如图2所示. 根据原子核巨共振[30]和基于中能重离子加速器SIS18上的重离子碰撞实验数据, Margueron等[31]提取到对称核物质EoS的不可压缩系数$ K_0 $ 的范围为(230 ± 20) MeV; 第3阶系数$ J_0 $ 的范围为(200 ± 200) MeV, 这里$ J_0 $ 参数仍具有较大的不确定性, 理论预言这是由于在高密区对核子-核子三体相互作用的理解不足[32].对称能
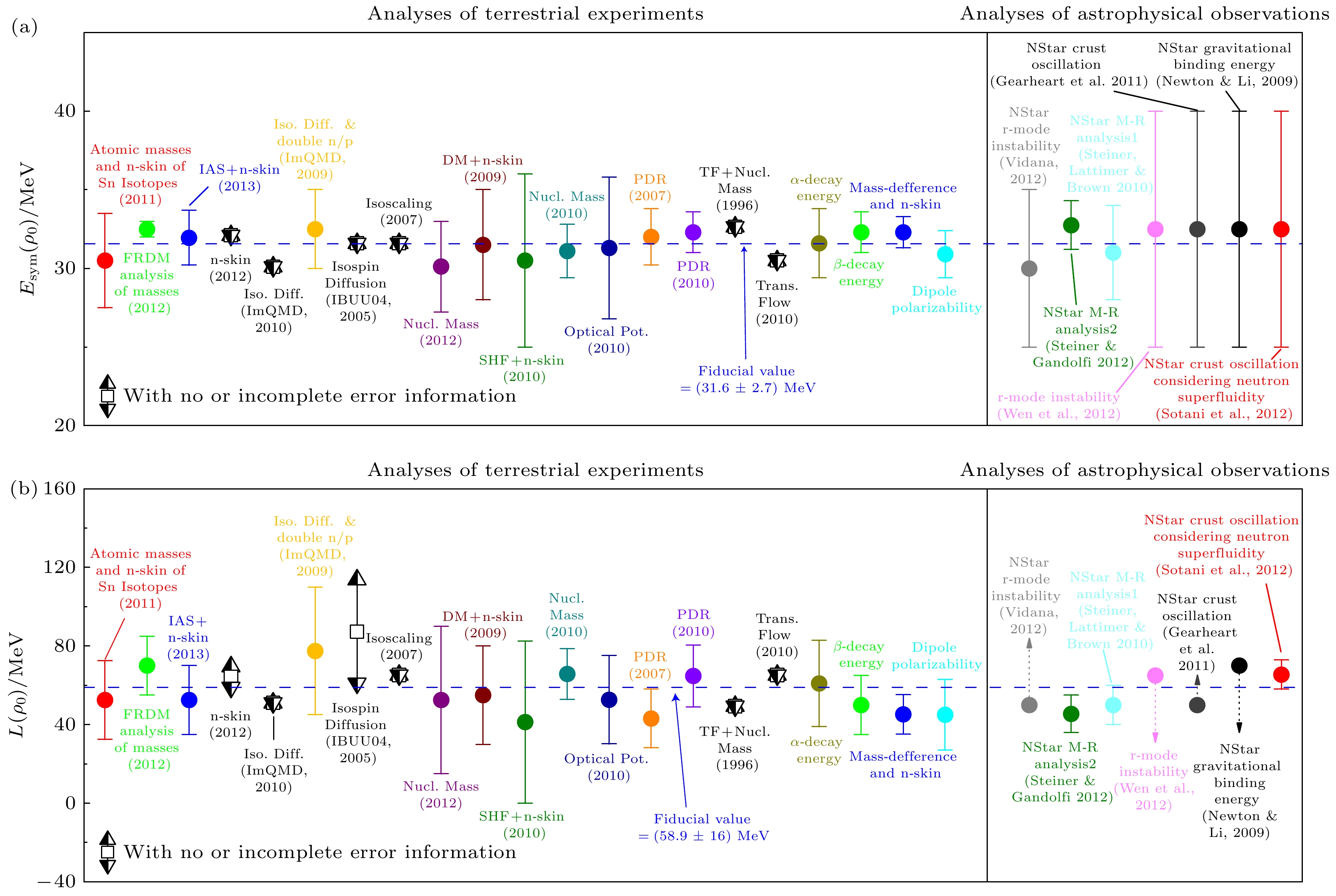
$ E_\text{sym}(\rho) $ 与原子核束缚能、稀有同位素存在、原子核中子皮厚度等原子核性质密切相关. 另外, 宇宙中的致密天体——中子星内部中子物质占主导, 因此对称能对中子星的质量、半径、中子星自转频率突变(neutron star glitch)、双中子星并合、中子星-黑洞合并过程中发射的引力波模式等都具有决定性作用. 对于(6)式在饱和密度处 的参数, 李宝安等结合中高能重离子碰撞实验 结果、天文观测中给出的中子星质量和半径、双中子星并合事件中提取的潮汐形变参数等实验数据, 给出了饱和密度处对称能参数$ E_\text{sym}(\rho_0) = (31.6\pm 2.7)\;{\mathrm{MeV}} $ [24],$ L_\text{sym} = (58.9\pm 16) \;{\mathrm{MeV}}$ [24]和$ K_\text{sym} = (-107\pm88)\;{\mathrm{MeV}} $ (68%置信度水平)[27]. 不同测量给出的$ E_\text{sym}(\rho_0) $ 和$ L_\text{sym}(\rho_0) $ 的限制如图3所示[24]. -
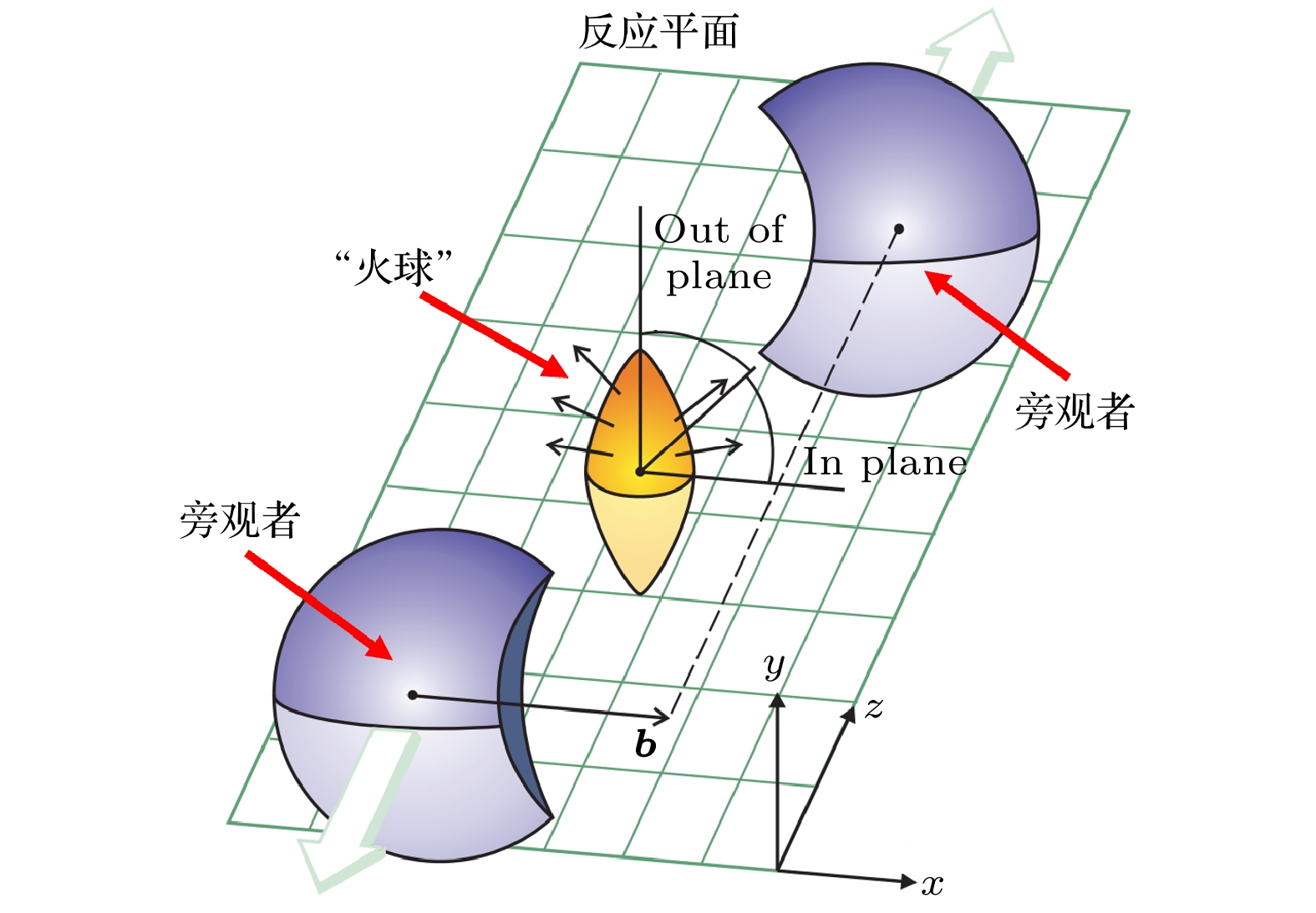
中高能重离子碰撞是实验室产生高温高密核物质的唯一手段. 重离子碰撞中, 在垂直于弹核动量方向上, 弹核和靶核中心的最短距离称为碰撞参数b (impact parameter). 如图4所示, 碰撞参数和弹核动量方向矢量所定义的平面称为反应平面, 在碰撞中两个核重叠区域会形成被称为“火球”的高温高密核物质, 没有参与形成火球的部分称为“旁观者”.
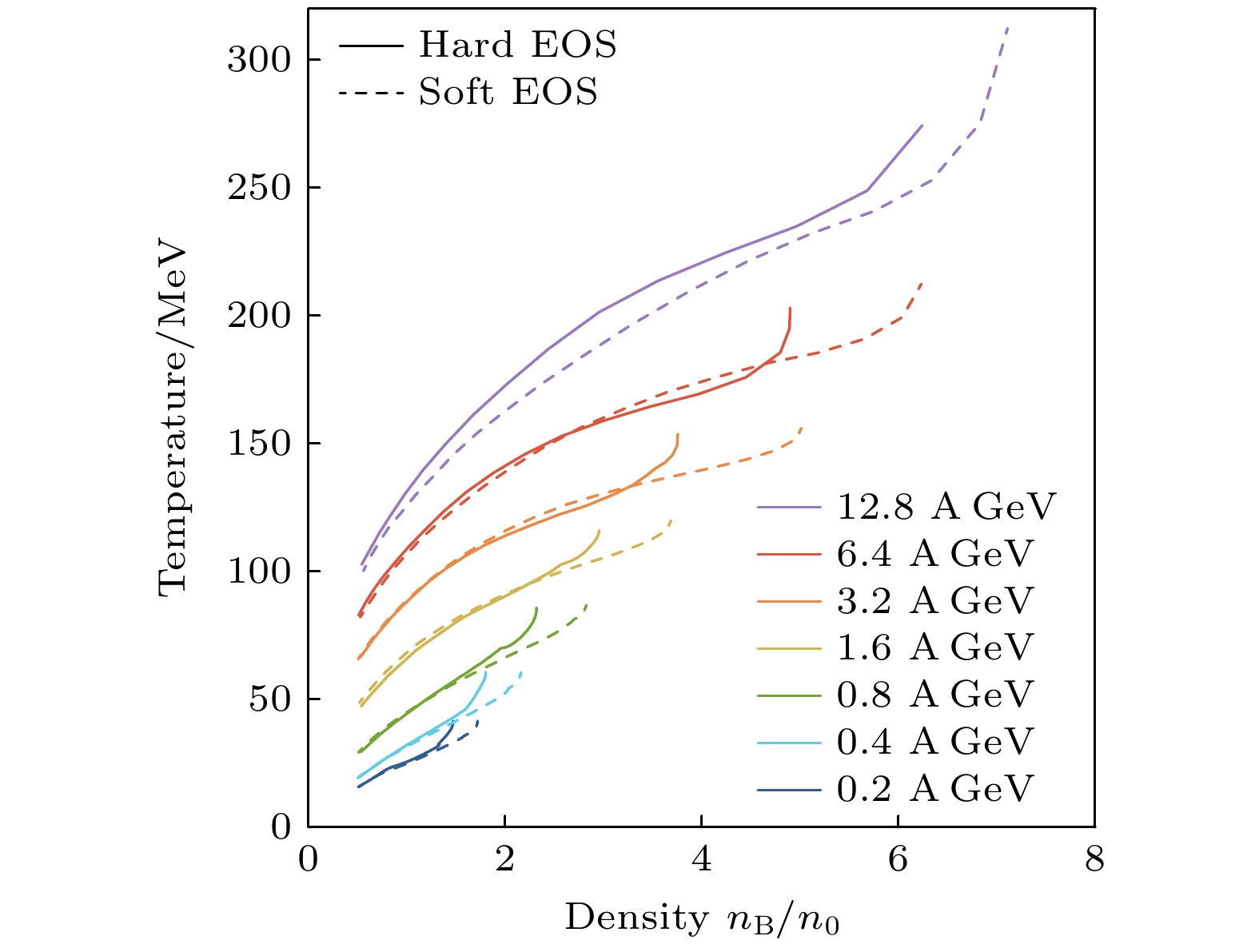
随着重离子碰撞能量的升高, 火球中的能量密度和温度都会随之上升. 给定能量的核核碰撞, 火球中心的最大重子密度与EoS的不可压缩性(状态方程中的第二阶系数)直接相关. 图5所示为UrQMD模型[33]模拟0.2—12.8 GeV/u (对应质心系能量
$ \sqrt{s_{{\mathrm{NN}}}} $ 为1.97—5.25 GeV)的Au + Au对心碰撞(碰撞参数b = 0 fm)中纯强子相(不考虑QGP)下的温度和密度关联图, 其中实线和虚线 分别表示硬和软的核物质状态方程[34]. 由于非对心核核碰撞的初始几何效应, 所产生高温高密的火球内部会建立向外的压强梯度, 随着时间的演化高温高密火球会向外膨胀. 在压强梯度大的区域粒子会获得更大的向外的推力, 最终使得火球内部压强梯度最终转化为出射粒子在动量空间的不对称性. 最终产生的粒子在方位角分布上呈现一定集体运动的行为, 这也被称为集体流(collective flow).不同的核物质状态方程(如硬和软的EoS)会导致火球内部压强和压强梯度的不同, 导致粒子集体运动行为的不同, 因此集体流是核核碰撞中探测EoS的敏感实验探针.
1996年, Voloshin和Zhang[35]提出, 中高能重离子碰撞末态粒子在方位角平面上的分布可以写成傅里叶级数的形式:
等式的左侧为不变截面, 其中E和p为粒子能量和动量,
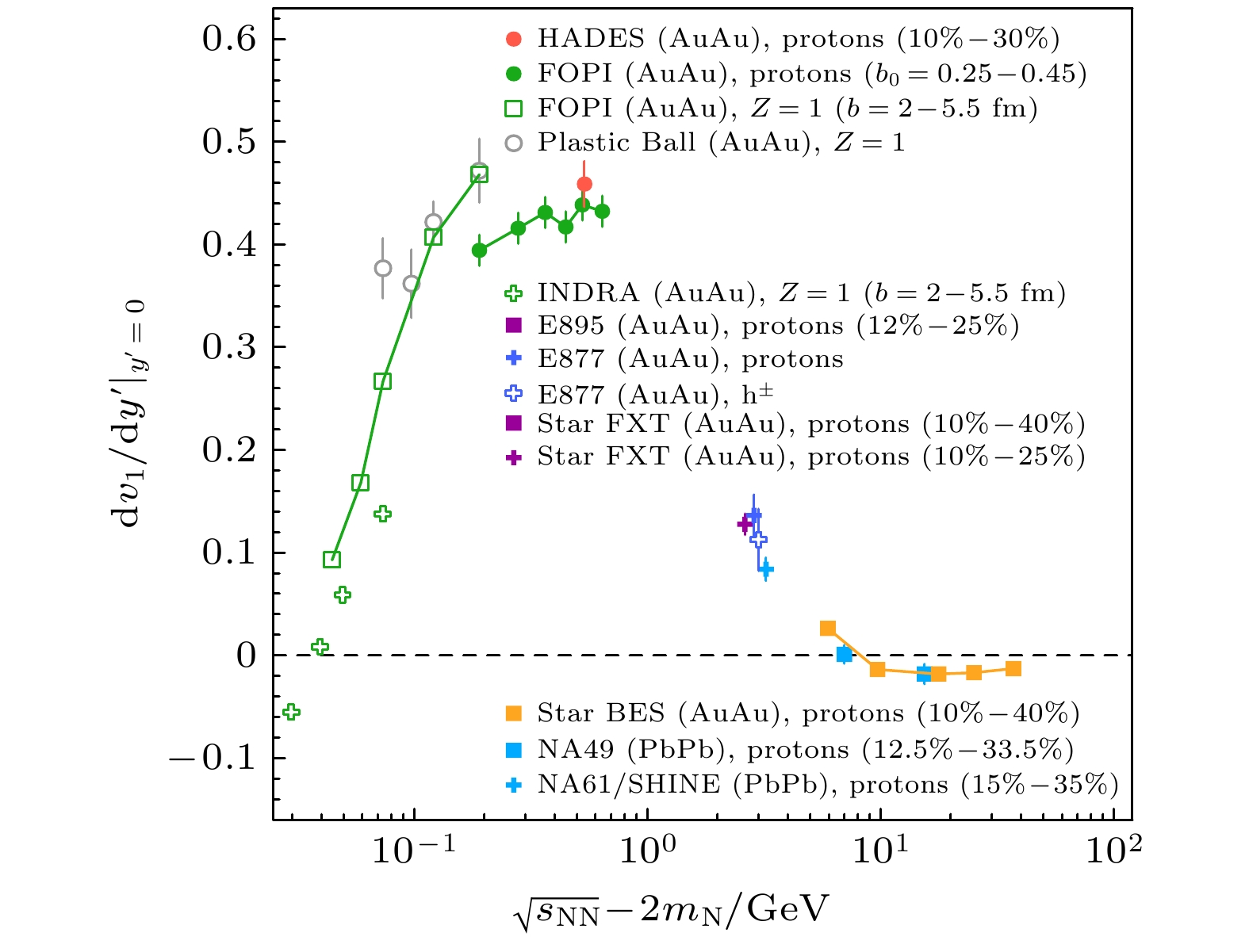
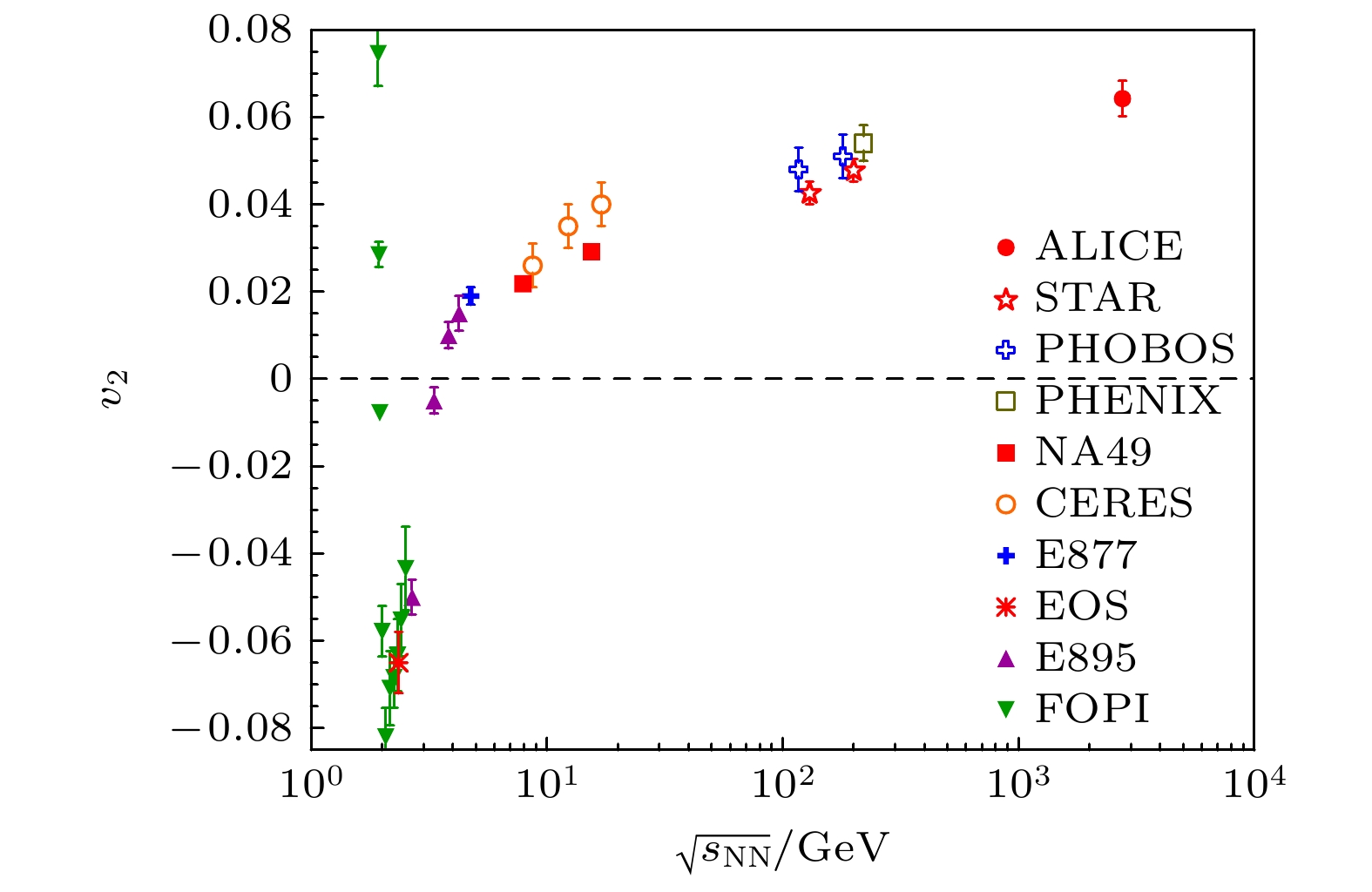
$ p_{\mathrm{t}} = \sqrt{p^2_x+p^2_y} $ 为横动量, 快度$ y = \dfrac{1}{2}\ln\Big(\dfrac{E+p_z}{E-p_z}\Big) $ ,$ v_n $ 为n阶谐波系数, ϕ为粒子的方位角,$ \varPsi_n $ 为n阶反应平面. 其中, 一阶系数$ v_1 $ 称为直接流(directed flow), 二阶系数$ v_2 $ 称为椭圆流(elliptic flow). 等价地,$ v_1 $ 和$ v_2 $ 可以分别写成动量相关比值的平均值, 即$ v_1 = {\langle}p_x/p_{\mathrm{t}}{\rangle} $ 和$ v_2 = {\langle}(p^2_x-p^2_y)/p_{\mathrm{t}}^2{\rangle} $ , 这里的$ {\langle}\cdots{\rangle} $ 表示对所有碰撞事件求平均. 常见地, 粒子的$ v_1 $ 和$ v_2 $ 与粒子横动量($ p_{\mathrm{t}} $ )、快度(y)、碰撞中心度以及碰撞体系的能量关联在一起, 来提取不同维度上系统演化的信息. 在对称重离子碰撞(弹核和靶核是同样的核)中,$ v_1 $ 与y关联满足$ v_1(y) = -v_1(-y) $ ,$ v_1 $ 在中心快度区$ y_{{\mathrm{cm}}} = 0 $ 的斜率$ {\mathrm{d}}v_1/{\mathrm{d}}y _{{\mathrm{cm}}}|_{y_{{\mathrm{cm}}} = 0} $ , 可以表示该粒子受到火球推力的累计效应. 由于直接流携带碰撞早期系统演化的性质, 因此$ {\mathrm{d}}v_1/{\mathrm{d}}y _{{\mathrm{cm}}}|_{y_{{\mathrm{cm}}} = 0} $ 是研究核物质在不同热力学条件下, 尤其是高重子密度区状态方程和核核碰撞动力学的重要实验可观测量.图6[36]和图7[37]分别为质心系能量在1.9—14000 GeV重离子碰撞中的质子
$ {\mathrm{d}}v_1/{\mathrm{d}}y _{{\mathrm{cm}}}|_{y_{{\mathrm{cm}}} = 0} $ 和$ v_2 $ 随碰撞能量的变化. 可见, 斜率$ {\mathrm{d}}v_1/{\mathrm{d}}y _{{\mathrm{cm}}}|_{y_{{\mathrm{cm}}} = 0} $ 随着系统碰撞能量升高, 约在$ \sqrt{s_{{\mathrm{NN}}}}> $ 2.8 GeV后单调下降;$ v_2 $ 则从低能的正值迅速变为负值, 随着能量升高在$ \sqrt{s_{{\mathrm{NN}}}}\approx $ 3.2 GeV由负值转为正值. 重离子碰撞中的这些集体流整体行为, 可以用基本核核碰撞动力学来解释. 在非对心核核碰撞过程中, 存在两个演化时间的竞争: 一个是火球从压缩到膨胀的时间, 另一个是旁观者通过火球区域的时间. 火球的碰撞时间实验上不能直接测量, 给定束流能量的情况下通过时间$ t = (R_{\mathrm{p}}+ R_{\mathrm{t}})/{\gamma}v_\text{beam} $ , 这里的$ R_{\mathrm{p}} $ 和$ R_{\mathrm{t}} $ 分别为弹核和靶核的半径,$ v_\text{beam} $ 是束流的速度. 中高能重离子碰撞中(典型质心系能量范围$ \sqrt{s_{\mathrm{NN}}} < $ 3.2 GeV), 旁观者通过火球区域的时间要慢于火球膨胀时间, 旁观者在通过火球区域时会感受到来自火球膨胀的横向推力, 这就导致原本只有沿着z方向(束流方向)动量的旁观者获得了横向的动量, 从而形成侧向流, 也就是这里说的直接流. 同时, 由于旁观者的存在, 火球在旁观者区域的膨胀被阻挡和挤压, 这导致火球膨胀行为发生变化, 部分火球物质沿垂直于反应平面的方向出射($ v_2 $ 为负值), 这在文献中被称为挤出流(squeeze-out). 旁观者引起的这个效应, 有时候也被称为遮蔽效应(shadowing effect). 在高能和相对论性重离子碰撞中(典型质心系能量范围$ \sqrt{s_{{\mathrm{NN}}}} $ >7 GeV), 旁观者通过火球的速度远快于火球的膨胀速度, 火球的膨胀按其内部的压力梯度和温度膨胀, 此时椭圆流$ v_2 $ 为正值. 可见末态粒子的集体流是极端核物质内部温度和压强分布的体现. 因此, 集体流是实验上测量EoS的敏感实验观测量. 关于重离子碰撞动力学效应的详细情况, 请参考相关的综述文献[38]. 2002年, Danielewichz等[39]综合碰撞能量为0.1—10 GeV/u重离子碰撞中的$ v_1 $ 和$ v_2 $ 数据, 结合BUU输运模型模拟表明, 在$ \rho< 3\rho_0 $ 区域排除了非常硬和非常软的对称核物质状态方程. 实 验上利用集体流测量结果来提取EoS参数的过 程中, 需要和输运模型的计算结果做比较, BUU模型模拟中不能用一套参数来描述所有实验数据, 这就给实验测量和理论模型同时提出了挑战. 在实 验方面, 为了消除不同实验组在测量上可能存在的差异, 就需要不同实验组来重复测量这些实验结果. 随着实验探测手段和实验方法的发展, 实验上可以给出高精度的集体流与碰撞中心度、横动量、快度等变量依赖关系; 对同一碰撞体系, 实验上也能给出不同碰撞能量下的横动量谱、微分产额分布(dN/dy)、产额与中心度等的高质量数据. 这些数据为模型自洽描述实验观测量提供了极大限 制. 当前在高重子密度区, 世界上有好几个实验室都在建造高精度重离子碰撞实验谱仪, 以便开展 实验, 如德国FAIR装置上的CBM/HADES实 验[40]、俄罗斯NICA装置上的MPD实验[41]、中国HIRFL-CSR装置的CEE实验[42]、美国密西根 大学的FRIB上的EoS实验[43]、日本理化学研究所 (RIKEN)的RIBF上的SπRIT实验[44]、韩国RAON装置上的LAMPS实验[45]. 这些实验对集体流的测量结果, 将能够对限制高密区核物质状态方程提供强有力的数据支持. 随着探测手段的发展, 未来几年相同能段不同实验之间测量结果的不一致性或将显著降低.另一方面, 在理论研究上, 由于重离子碰撞输运过程的复杂性, 基于相同的实验观测量, 不同的输运模型可能给出完全相反的结论. 同时, 为了能够描述实验数据, 输运模型中引入了一些尚未被实验限制的物理机制, 如强子的介质效应(比如有效质量的改变)、动量依赖的相互作用、短程关联等效应, 而这些效应的引入为检验不同模型的可靠性提出了挑战. 为了减小输运模型之间的差异, 世界范围内的输运模型研究人员已经开始了细致的比较工作, 具体工作进展在下文中详述.
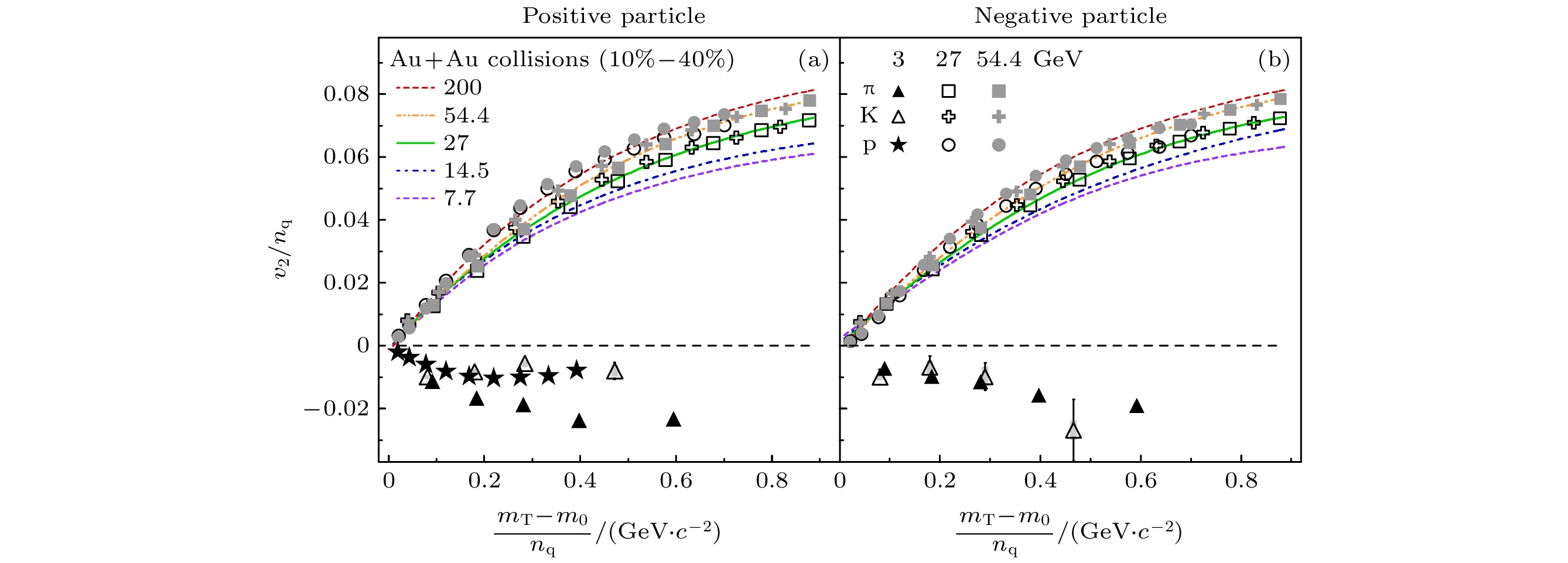
对于核物质状态方程而言, 由于解禁闭的QGP相比强子气体自由度更多, 当能量密度达到强子气体到QGP转换的临界能量密度, 核物质状态方程就会出现软化, 当前具体在哪个能量下的重离子碰撞中会发生这个相变, 或者说强子气体转变为QGP的临界热力学条件尚不明确. 图8所示((a)图为正电荷强子, (b)图为负电荷强子)为STAR实验测量的夸克数约化强子椭圆流(
$ v_2/n_{\mathrm{q}} $ ,$ n_{\mathrm{q}} $ 为强子组分夸克数)与夸克数约化横能量的依赖关系[46]. 由图可见, 在$ \sqrt{s_{{\mathrm{NN}}}} $ = 7.7—200 GeV Au-Au碰撞中强子的$ v_2/n_{\mathrm{q }}$ 符合统一的标度率, 这说明在高能重离子碰撞中, 强子的椭圆流起源于部分子层级分子的集体运动. 同时, 这也意味着强子气体到QGP转变的临界碰撞能量低于$ \sqrt{s_{{\mathrm{NN}}}}<7.7 $ GeV, 而STAR实验$ \sqrt{s_{{\mathrm{NN}}}} = 3.0 $ GeV的Au-Au碰撞中则发现强子椭圆流的组分夸克标度不再适用[46]. 这些结果或建议从强子气体到QGP转变的能量范围为$ 3.0\;{\mathrm{GeV}}<\sqrt{s_{{\mathrm{NN}}}}<7.7\;{\mathrm{GeV}} $ .除了粒子的集体运动, 重离子碰撞中一些特殊粒子的产额或者产额比也是探测高密核物质状态方程的敏感观测量. 粒子产额与核物质状态方程的联系大致可以分为两类: 第一类, 粒子的产生与体系的同位旋不对称度有关, 这些粒子的产额比能够与核物质体系中的同位旋不对称度联系起来, 比如
$ \pi^+/\pi^- $ [47], t/3He[48],$ \Xi^-/\Xi^0 $ [49]等粒子的产额比; 第二类是在强子产生阈值附近, 由于多次散射的效应, 强子产额与核物质状态方程的软硬密切有关, 如果核物质较软, 则碰撞中会产生高密核物质, 反之亦然. 一般, 实验上测量这些对EoS敏感的强子产额比, 如K介子的阈下产生[50], 再与输运模型在软和硬EoS下的计算结果比较来提取EoS方程的参数. -
稳定重原子核内中子比质子多, 但是质子数和中子数相差并不大, 因此在重离子碰撞中更容易确定对称核物质EoS, 而在限制对称能方面相对要困难很多. 本节简要介绍几个与提取对称核物质EoS参数和对称能有关的典型实验, 以及提取EoS参数的方法和实验结果. 为了叙述EoS从低密到高密随密度的依赖完整性, 在4.2.2节介绍中子皮测量实验对提取饱和密度区对称能的进展.
-
对称核物质密度在ρ<4.5ρ0的区域, 基于AGS的加速器的Plastic ball[51], EOS[52], E895[53], E877[54]等实验0.15—10 GeV/u的Au+Au碰撞数据中质子直接流和椭圆流的测量结果, Danielewicz等[39]通过比较实验结果和BUU模型计算结果, 提取的对称核物质不可压缩系数范围为210 MeV
$ < {K_0}< $ 300 MeV. 目前, 基于不同加速器的实验结果, 输运模型所给出的对称核物质的压强随密度的变化如图9所示[34]. 下面简要介绍几个用于提取对称核物质状态方程的典型实验和实验结果. -
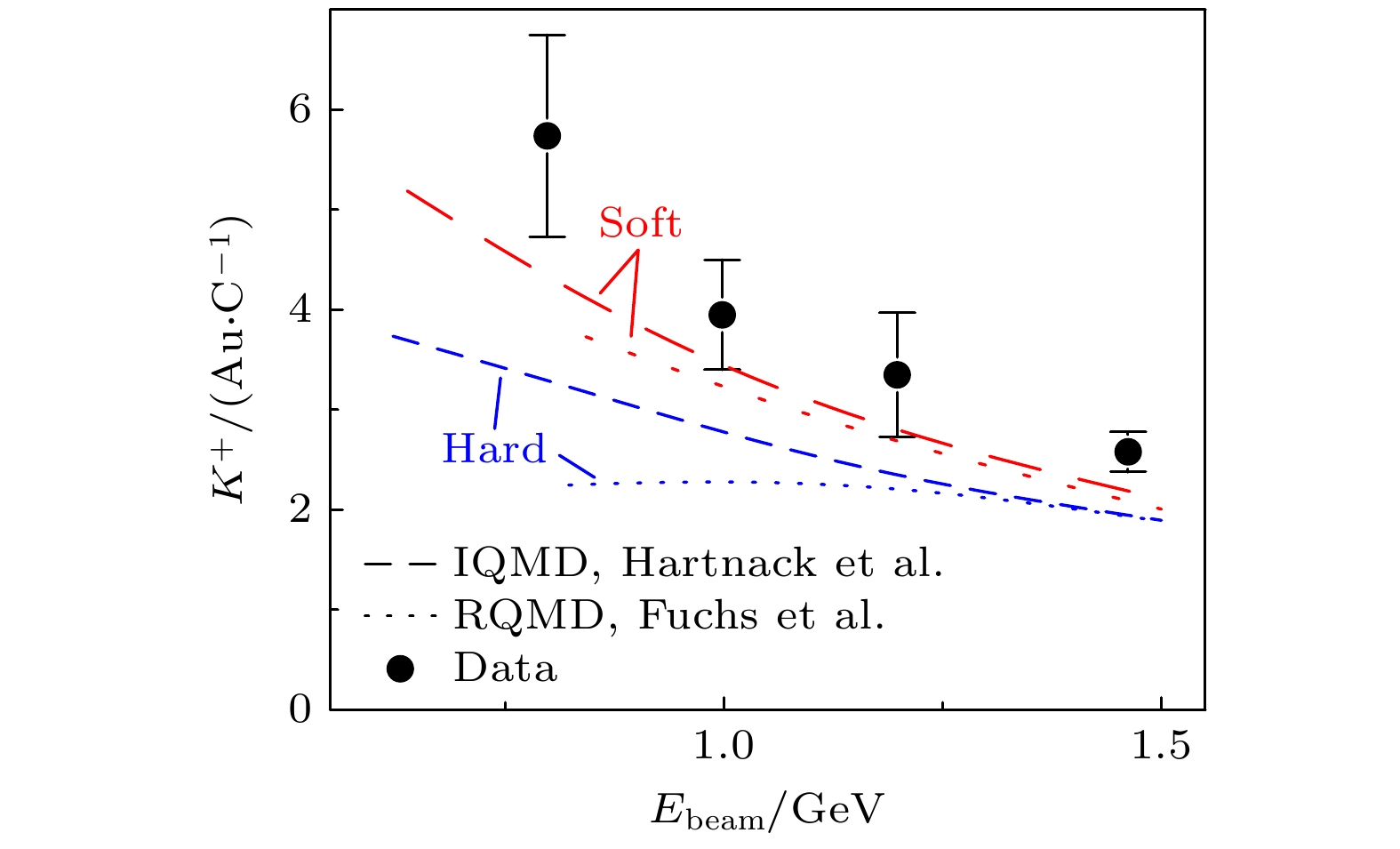
基于德国GSI的SIS18加速器的KaoS实验测量了束流能量600—1500 MeV/u的Au+Au和Cu+Cu重离子碰撞中
$ {\mathrm{K}}^+ $ 介子的产额[50]. 在pp碰撞中产生$ {\mathrm{K}}^+ $ 介子的束流能量阈值为1.57 GeV, 阈下产生的$ {\mathrm{K}}^+ $ 介子是由于在致密核物质中的多步反应, 主要是致密物质中的核子激发态(如Δ)以及核子反应产生Λ超子和$ {\mathrm{K}}^+ $ 的贡献. 在相同单核子束流能量下, 重碰撞系统Au+Au会比轻Cu+Cu系统中产生更致密的核物质, 因此$ {\mathrm{K}}^+ $ 的产额就可以作为探测两个系统中产生致密物质差异的探针. KaoS合作组测量了Au+Au和Cu+Cu碰撞的$ {\mathrm{K}}^+ $ 产额比, 如图10所示, 以此来抵消实验和理论计算中的部分系统误差. 与输运模型IQMD和RQMD比较发现, 在SIS18能区实验数据支持对称核物质的状态方程为软EoS的理论预言. 来自输运模型IQMD和RQMD的硬EoS和软EoS分别用短线和点线表示[50]. -
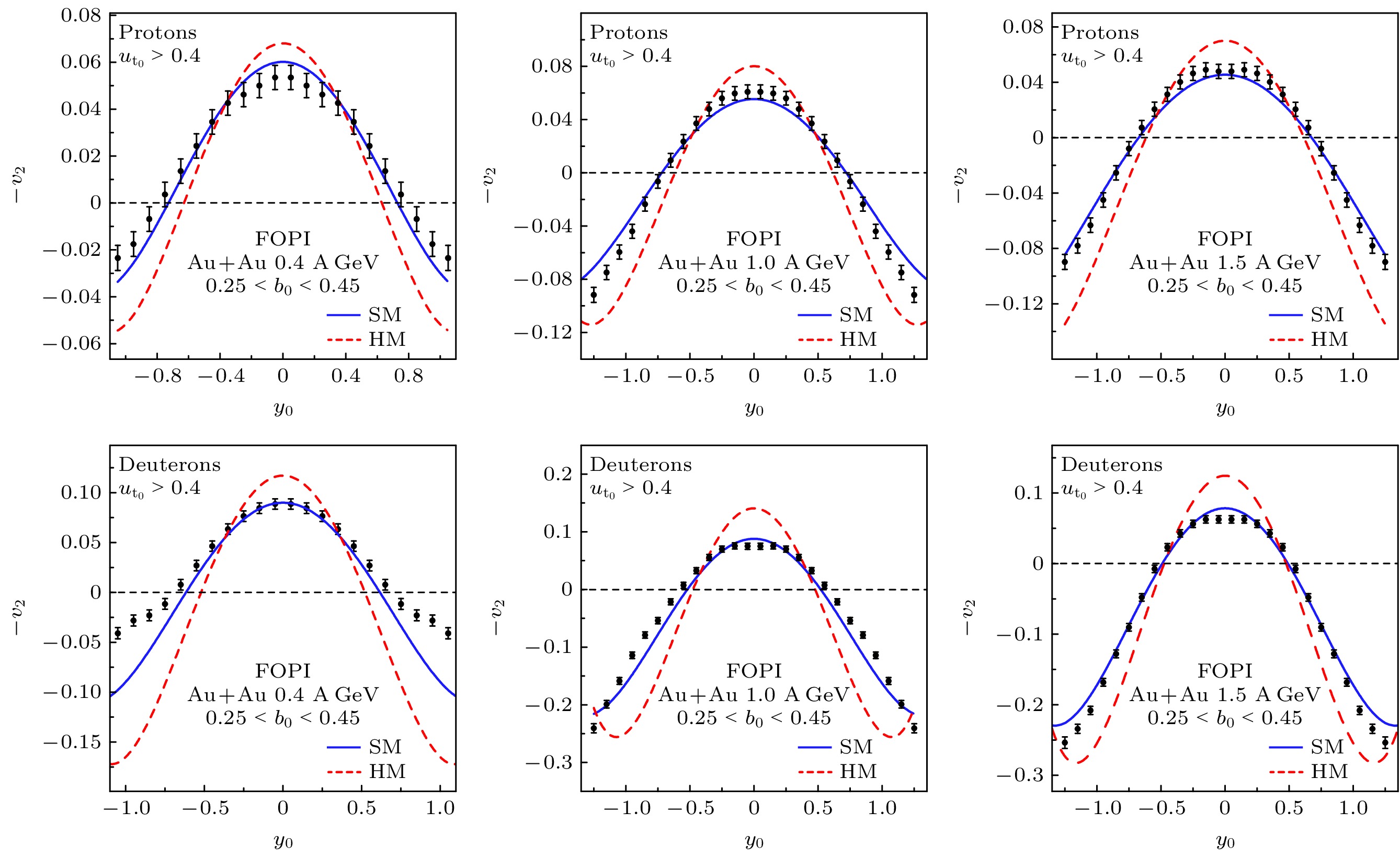
基于SIS18加速器的FOPI实验[55]测量了0.4, 1.0和1.5 GeV/u的Au+Au碰撞中质子和氘核的椭圆流随快度的依赖关系, 如图11所示. 基于IQMD模型(碰撞参数范围
$ 0.25<b_0<0.45 $ )硬EoS(K = 380 MeV)和软EoS(K = 200 MeV)的结果分别用虚线和实线表示, 可以看出, 软EoS的结果比硬EoS的理论结果与实验数据符合得更好. 由于该结果中定义的参数未被广泛使用, 所以这里予以说明. 其中, 约化碰撞参数$ b_0 = b/b_{{\mathrm{max}}} $ , 式中的b为碰撞参数,$ b_{{\mathrm{max}}} $ 是Au+Au碰撞的最大碰撞参数$ b_{{\mathrm{max}}} = 1.15(A^{1/3}_{\mathrm{P}}+A^{1/3}_{\mathrm{T}}) $ ,$ A_{\mathrm{P }}$ 和$ A_{\mathrm{T}} $ 分别为弹核和靶核的半径; 横向速度$ u_{\mathrm{t }}= \beta_{\mathrm{t}}\gamma $ , 约化横向速度和束流速度的比值为$ u_{{\mathrm{t}}0} = u_{\mathrm{t}}/u_{\mathrm{p}} $ , 其中$ u_{\mathrm{t}} $ 为横向速度,$ u_{{\mathrm{p}}} = \beta_{\mathrm{p}}\gamma_{\mathrm{p}} $ 为束流的速度. IQMD输运模型模拟结果表明, 在0.4—1.5 GeV/u的重离子碰撞集体流测量中, 得到$ \rho<2.5\rho_0 $ 区域对称核物质状态方程属于软EoS, 且提取到的不可压缩系数为(190 ± 30) MeV. -
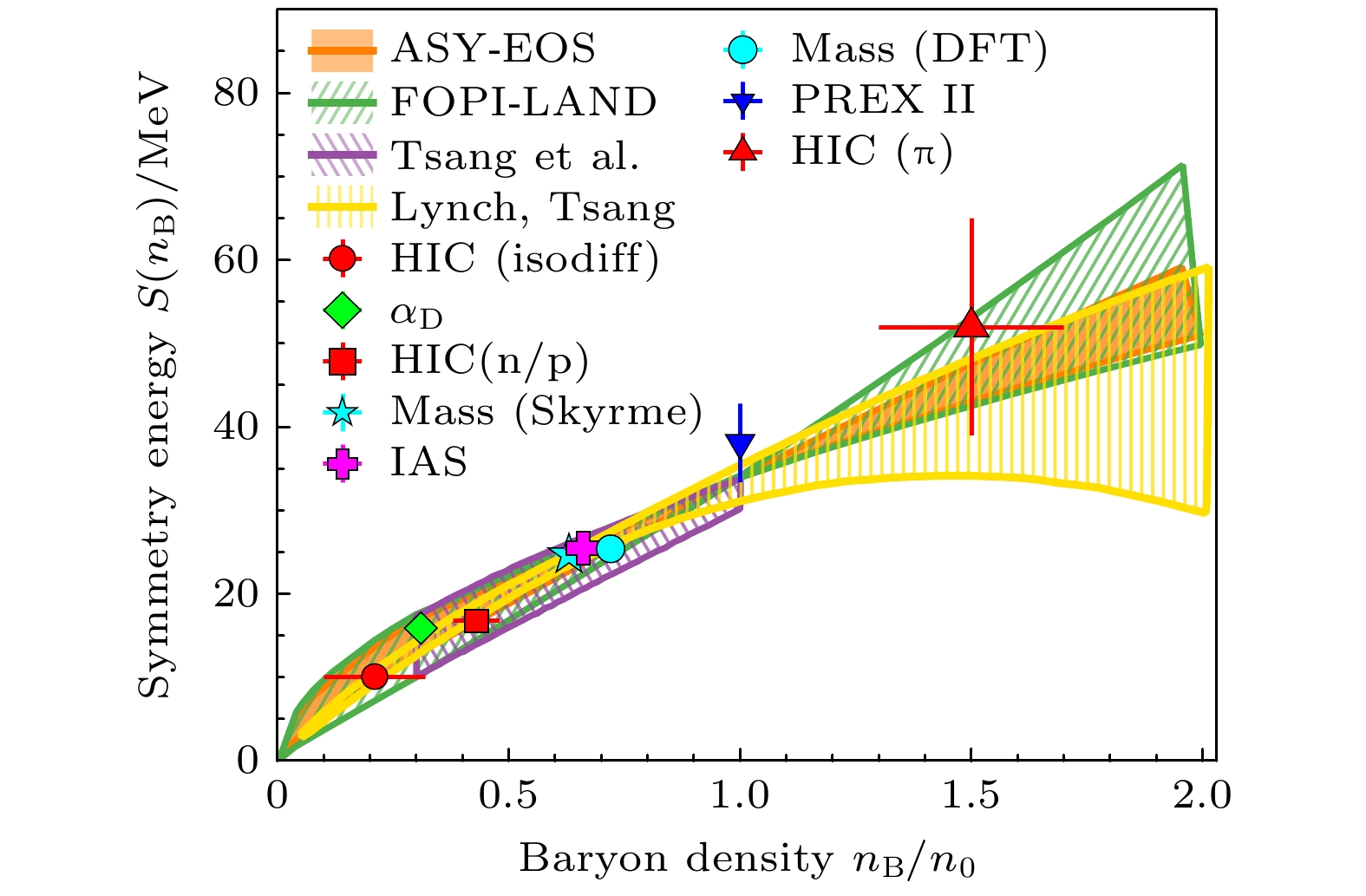
高密区对称能是当前核物质状态方程研究的前沿, 图12所示为当前实验提取到的对称能(
$ E_\text{sym} $ )随密度的依赖关系, 其中不同的点来自不同的实验[34]. 从低密到高密, 提取对称能参数的方法也存在较大差异. 为了较系统讲述对称能与密度的关系, 本节介绍从亚饱和密度、饱和密度和超饱和密度区实验观测量与提取对称能参数的方法和测量结果. 在亚饱和密度区, 即$ 0.3\rho_0<\rho<\rho_0 $ 区域, 对称能的研究主要来自在费米能区(20— 100 MeV/u)的重离子碰撞; 在$ \rho = \rho_0 $ 区域(经过理论延拓后的结果, 中子皮直接测量对应核物质密度$ \rho \approx 2/3\rho_0 $ ), 主要来自对原子核的中子皮的厚度测量实验; 在更高密度区($ \rho>\rho_0 $ ), 对称能参数的限制主要来自少数几个中高重离子碰撞实验. 在能量为100—1500 MeV/u的重离子碰撞中, 根据不同弹靶组合, 可以调节参与形成火球的中子数和质子数. 由于对称核物质是体系能量最低的状态, 因此在中子占主导的核物质中, 就会发生将中子转换为质子或者将中子扩散到低同位旋不对称度的区域, 使得反应$ {\mathrm{n+n}}\rightarrow {\pi}^-+{\mathrm{n}}+{\mathrm{p}} $ 比$ {\mathrm{p+p}}\rightarrow {\pi}^++ {\mathrm{n+p }}$ 更容易发生. 因此, 在这个能区的重离子碰撞中测量, 中子和质子的集体流、$ {\pi}^\pm $ 的产额比, 被认为是测量对称能的理想实验可观测量. 下面, 简要介绍在不同密度区域提取对称能的一些典型实验. -
正如前文所述, 由于对称能的排斥效应, 使得费米能区的重离子碰撞的中子更容易被激发到气相, 而质子则容易停留在液相, 这就是所谓的同位旋蒸馏效应[57]. 在该能区的重离子周边碰撞中, 由于同位旋蒸馏效应, 就会形成低密度丰中子的颈部和近饱和密度亚丰中子旁观者区域. 由于这两个区域之间存在同位旋梯度, 同位旋梯度使得加强质子向颈部区域的迁移. 由于在实验上精确且高效测量低能中子比较困难, 就通过测量类弹/靶区域不同荷质比(N/Z)碎片产物的分布来提取对称能. 其中轻核的产生可以认为是在蒸发阶段与周边核子的并合而产生的, 这就是所谓的并合核子数方法(coalescence invariant, CI), 分别统计轻核中的质子和中子来提取体系中子发射和质子发射的差异.
基于兰州重离子研究装置(HIRFL), 肖志刚等利用一套费米能区实验谱仪(CSHINE), 包括6块有效面积为
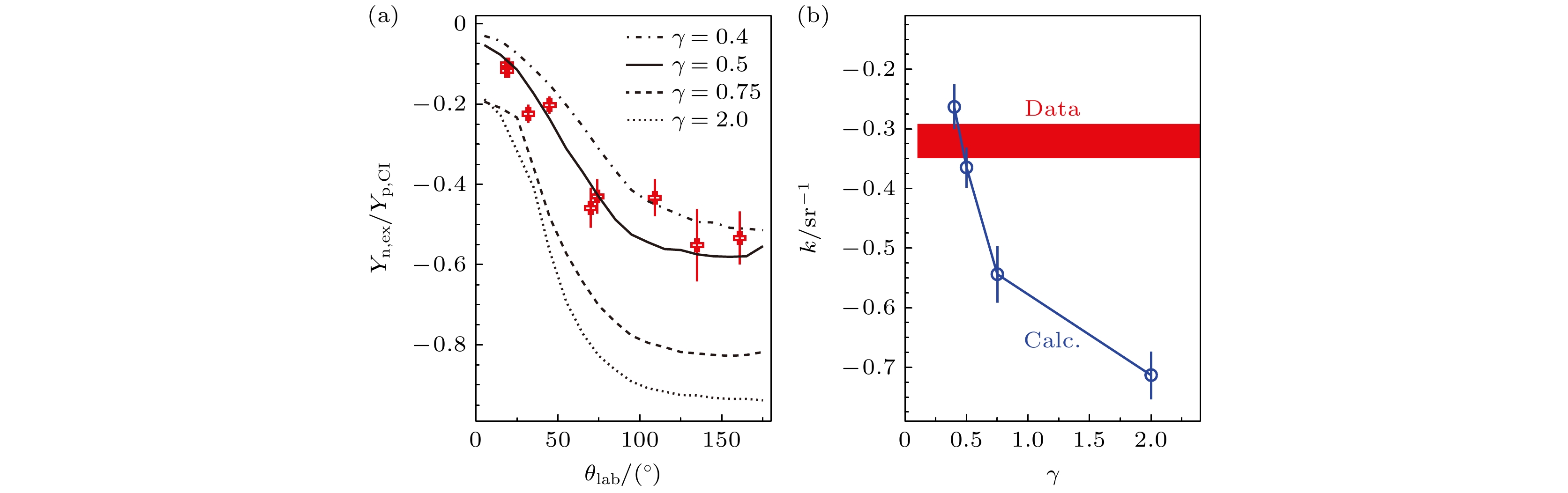
$ 30\;{\mathrm{cm}}{\times}35\; \text{cm} $ 的平行板雪崩计数器(PPAC)和9组望远镜系统($ {\Delta} $ E-$ {\Delta} $ E-CsI(Tl))在9个方向测量了35 MeV/u Ar+Au碰撞中发射的重碎片和轻核的产生截面, 获得了该反应中发射的轻核内中子相对丰度随角度的变化. 提取了如下式定义的约化中子丰度:其中
$ y_i $ 表示Z = 1或Z =2同位素中某种粒子i的产额,$ N_i $ 为中子数,$ Z_i $ 为质子数. 图13所示为该实验中提取的$ {Y_{{\mathrm{n, ex}}}}/{Y_{{\mathrm{p, CI}}}} $ 随出射角度的依赖关系, 其中不同曲线是ImQMD+GEMINI模型在不同对称能密度依赖参数γ下的理论计算结果. 通过比较实验结果和理论模拟结果, 在95%不确定度下, 提取到的在饱和密度附近对称能斜率参数$ L_\text{sym} = (47\pm 14) $ MeV. 误差范围内, 该结果与其他观测中提取到的对称能斜率结果一致. -
重原子核内, 由于质子之间存在库仑排斥, 使得其内部中子数多于质子数. 在饱和密度附近, 对于对称核物质体系, 可以认为每个核子都处于一个势阱中(见图2), 在这个效应的作用下, 即便是质子之间存在库仑排斥, 原子核内质子仍然束缚在原子核内部, 而原子核内盈余的中子, 则由于对称能产生的排斥作用将其推到原子核的外层, 从而形成了中子皮. 中子皮厚度定义为核内中子分布和质子分布的均方根半径的差, 即
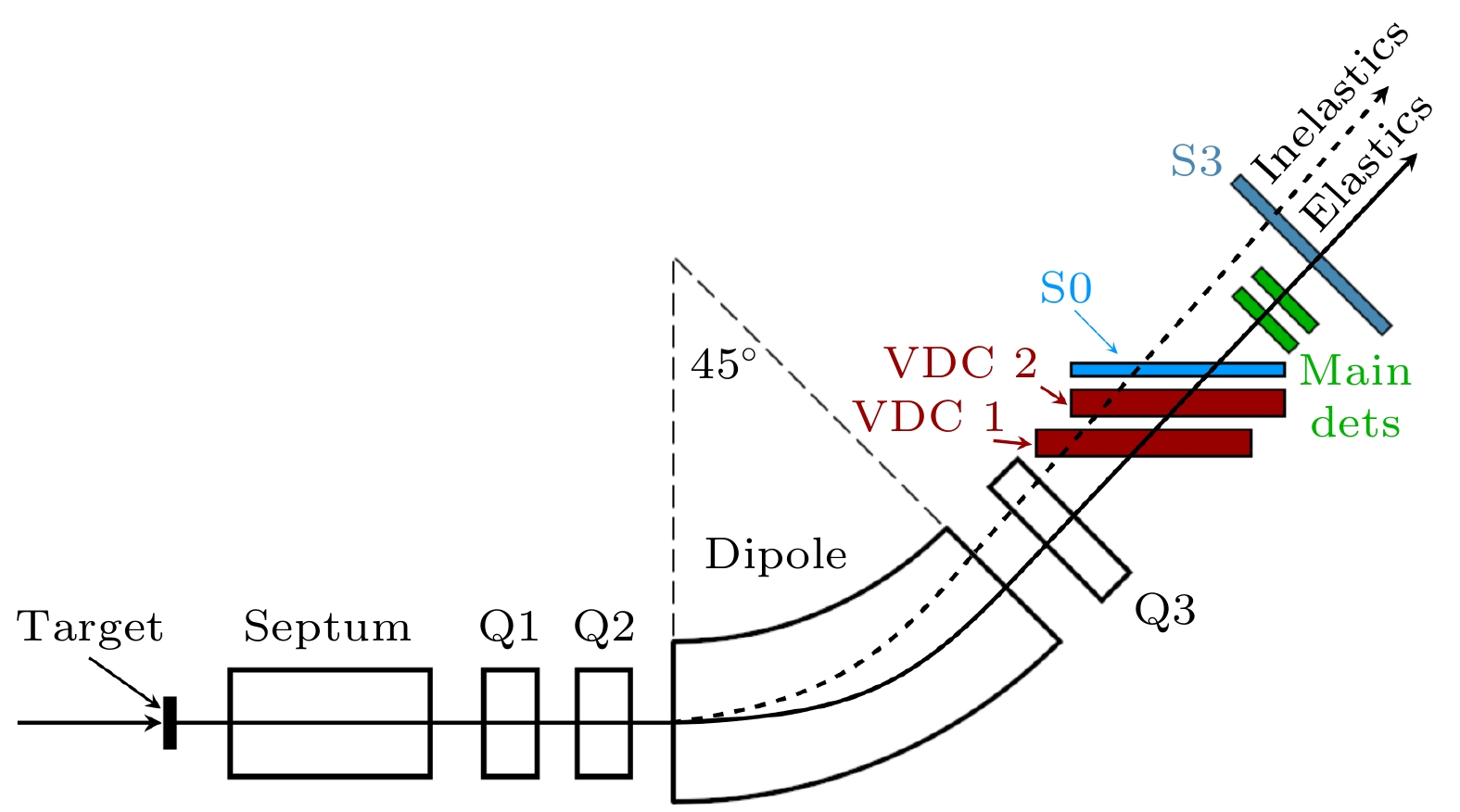
$ {\Delta}r_{{\mathrm{np}}} = \sqrt{{\langle}r^2_{\mathrm{n}}{\rangle}}-\sqrt{{\langle}r^2_{\mathrm{p}}{\rangle}} $ . 中子皮的厚度与饱和密度附近的对称能有直接关系. 由(2)式可以看出, 在饱和密度附近, 中子物质的压强与$ L_\text{sym} $ 的关系可以近似为$ P_0 \approx \rho_0{\times}L_\text{sym}/3 $ . Roca-Maza等[59]基于对不同理论模型结果的分析, 更进一步指出中子皮厚度与对称能斜率$ L_\text{sym} $ 存在的线性关系, 即$ {\Delta}r_{{\mathrm{np}}} = 0.101+0.00147 L_{\text{sym}} $ . 因此, 如果能够精确测量原子核中子皮厚度, 就可以框定饱和密度附近的对称能参数.1989年, Donnelly等[61]提出利用弱相互作 用的宇称不守恒特征, 来测量原子核内中子分布 的方法. 美国杰弗逊实验室(JLab)的PREX (Pb Radius Experiment)合作组利用CEBAF(the continuous electron beam accelerator facility)装置提供的轴向极化和反向极化的953 MeV的电子束流, 开展电子-208Pb核散射实验. PREX-II实验的探测器布局如图14所示, 其中Q1, Q2和Q3为聚焦四极磁铁; VDC1和VDC2为多丝正比室用于测量散射电子的位置; S0和S3为塑料闪烁体探测器用来提供时间测量; 图中标记为Main Dets的是2块完全一样且互为备份的抗辐照熔融石英(fused-silica), 来记录弹性散射电子的流量, 每个熔融石英耦合一个光电倍增管, 读出电子在探测中产生的切伦科夫光信号. 图14中的实线表示弹性散射电子第一个主峰的路径, 虚线表示非弹性散射电子第一个主峰的路径. 实际PREX实验中, 还有3块平面型基于气体电子倍增膜(GEM)的带电粒子位 置探测器, 用于优化束流光学和束流调整, 在该平面图中并没有标记. 该实验中, 测量得到在不同极化方向的散射截面每10亿个事件存在的差异为
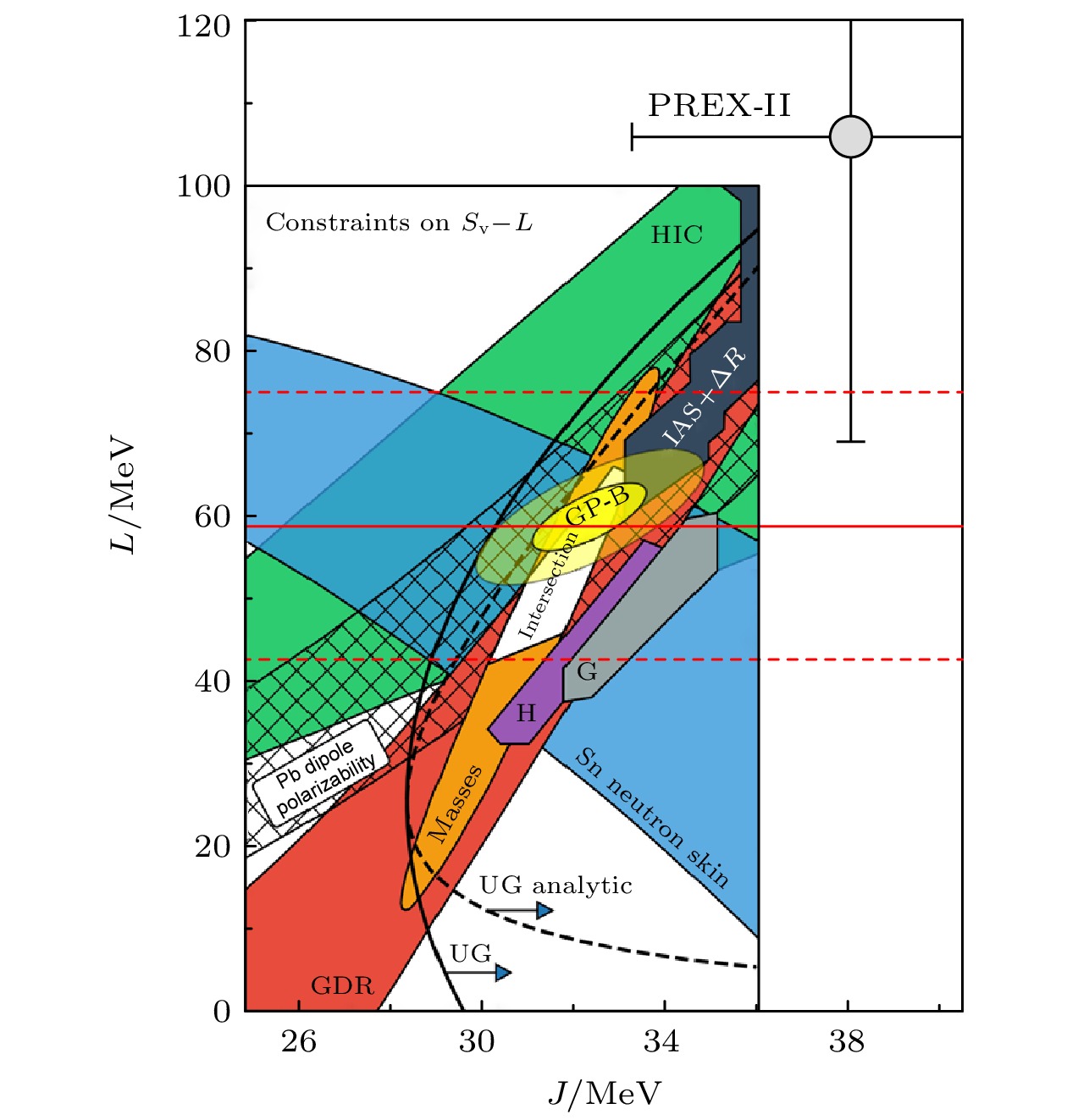
$ A_\text{PV} = 550\pm16(\text{stat})\pm8(\text{sys}) $ , 结合之前实验测量到的208Pb的电荷半径, 得到208Pb核的中子皮厚度为$ (0.283\pm0.071) $ fm[62], 对应对称能斜率$ L_\text{sym} = (106\pm37) $ MeV[63]. 图15为当前对称能参数$ L_\text{sym}-J_\text{sym} $ 的实验结果和理论预言, PREX-II实验结果为黑色空心圈, 李宝安等[24]提取的$ L_\text{sym} = (58.9\pm16 )$ MeV的中心值和误差分别用红色实线和虚线表示. 可见PREX-II提取的对称能参数 的中心值与其他实验的测量结果存在较大差异. 因此, 后续进一步缩小PREX实验的误差, 就成为进一步证实电子散射实验和其他实验是否真的存在测量结果差异的关键. -
中高能重离子碰撞是实验室产生致密核物质的唯一手段. 实验室系能量为200 MeV/u—3000 MeV/u的重离子碰撞的中心区域会产生密度为1.5ρ0—3.5ρ0的核物质. 由于重原子核本身质子数和中子数不同, 在这样高密的环境中可以提取对称能的贡献. 由图12可见, 目前对称能
$ E_{\text{sym}} $ 在高密区的行为尚存在很大不确定性. 本节介绍重离子碰撞实验中提取超饱和密度区对称能的实验和结果.在高密区对称能贡献使得体系对中子产生排斥作用, 而对质子则是吸引作用, 这就可能会导 致体系内中子和质子集体运行的不同, 李宝安[47] 在2002年首先提出中子和质子的集体流的比 值(或两者之间的差)可以作为研究高密区对称 能行为的敏感探针. 由于实验上中子测量的效率 和精度较差, 仅有的中子集体流的实验数据来自 GSI SIS18加速器上的FOPI-LAND实验和ASY-EoS实验.
-
1993年, 德国GSI的FOPI-LAND实验首次测量了400 MeV/u的Au+Au碰撞中中子和氢核(电荷Q = 1粒子)垂直于反应平面方向的发射现象, 在文献中也被称为“挤出流”[64]. 由于集体流的实验方法建立于1997年, 所以该文章中没有提取出中子和氢核的椭圆流
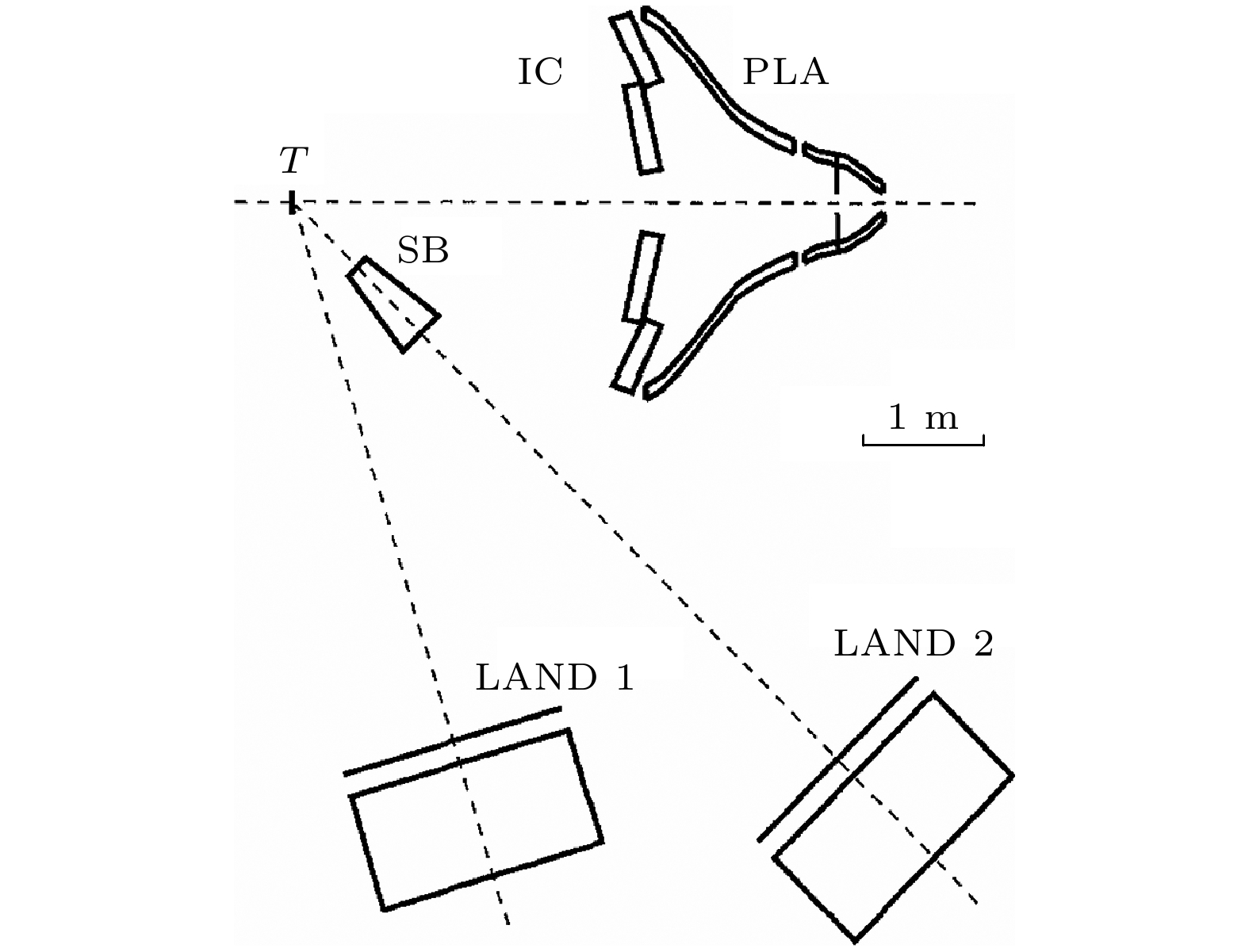
$ v_2 $ 的结果. 直到2011年, 重新分析了实验数据, 得到了中子、质子和氢核素(电荷Q = 1的粒子)直接流和椭圆流与快度的依赖关系. FOPI-LAND实验的探测器布局如图16所示, 沿着束流线放置的IC和PLA为FOPI实验第一阶段探测器, 其中IC为电离室(ionization chamber)探测器, PLA由外圈512根双端由光电倍增管(PMT)读出的塑料闪烁体条和内圈252个单端PMT读出的塑闪片组成, 用于测量粒子的飞行时间和粒子在塑闪中的能损, 双端PMT读出的塑闪条可以通过两端的时间差测量到粒子的击中位置. 为了测量低能粒子的能损信息, 在PLA前放置了IC探测器, 进一步增加粒子电荷的测量. IC和 PLA覆盖$ 0^{\circ}\leqslant\phi\leqslant360^{\circ} $ 方位角和$ 1.2^{\circ}\leqslant \theta\leqslant30^{\circ} $ 极角范围. 结合IC测量的电荷、位置信息和PLA探测器给出的飞行时间, 可以鉴别电荷$ 1\leqslant Q\leqslant10 $ 的核素. 根据IC和PLA上粒子空间分布和击中多重数, 来确定反应平面和碰撞中心度. LAND探测器是长、宽、厚度为$ 2\; \mathrm{m}\times1\; \mathrm{m}\times1\ \mathrm{m} $ 的中子探测器, 为了覆盖不同的相空间区域, 将LAND在厚度方向分为厚度为0.5 m的2个探测器, 分别在图16中标记为LAND1和LAND2. 组成LAND的基本单元是长、宽、厚度为$ 200\;{\mathrm{m}}\times10\;{\mathrm{m}} \times 10\;{\mathrm{m}} $ 的塑料闪烁体探测器, 每个单元由面积为$ 200\;{\mathrm{cm}} \times 10\; \text{cm}$ 的11层铁(外层厚度2.5 mm, 内层厚度5 mm)和10层厚度5 mm的塑闪间隔堆叠而成, 每个塑闪层中的两端耦合光导, 10层塑闪光信号用模块两端的PMT完成时间的测量. 20个这样的探测器单元依次排列, 就组成了一层LAND探测器. LAND探测器包括10个这样的探测器层(LAND1和LAND2分别包括5个探测层), 且间隔层中探测单元沿着长度方向相互垂直. 与FOPI谱仪PLA类似, 每个探测器单元从两端的PMT给出时间信息, 通过信号到达两端的时间差, 可以重建出该入射粒子的位置. 为了区分带电粒子和中子, 在LAND1和LAND2探测器前面分别放置了5 mm的塑闪反符合探测器, 在反符合中子的同时该探测器给出能损测量, 可以区分电荷Q = 1和Q = 2的粒子. 详细关于LAND探测器的设计和性能见文献[65]. LAND1和LAND2分别放置于距离靶点7 m和5 m的位置, 且分别覆盖靶点$ \theta_\text{lab} = 73^{\circ}\pm12^{\circ} $ 和$ \theta_\text{lab} = 45^{\circ}\pm8^{\circ} $ 的张角范围.2011年, Russotto等[66]利用UrQMD输运模型的平均场模式(平均场模式下所有除了核子-核子相互作用, 每一个核子还会受体系平均势能的贡献)模拟了400 MeV/u的Au+Au碰撞数据, 该模拟中对称能使用了如(9)式所示的幂次函数的参数化形式:
其中
$ \gamma = 0.5 $ 和$ \gamma = 1.5 $ 分别对应软和硬对称能. 通过比较实验和模型计算的中子和质子椭圆流的差异, 发现在半中心碰撞事件中(对应碰撞参数范围为:$ 5.5\leqslant{b}\leqslant7.5 $ fm), 提取到$ \gamma = 0.9\pm0.4 $ (包括统计误差和系统误差), 这个值对应饱和密度处对称能斜率$ L_\text{sym} = (83\pm26) $ MeV[66]; 结合实验结果和UrQMD模型模拟结果, 提取到的对称能和密度依赖关系如图12中的蓝斜线区域. 2013年, 输运模型TuQMD (Tübingen QMD model)中的对称能采用了核子动量依赖的Gogny力, 模拟了400 MeV/u的Au+Au碰撞, 并与FOPI-LAND实验比较提取到的中等硬度的对称能参数$ L_\text{sym} = (122\pm57) $ MeV和$ K_\text{sym} =( 229\pm363) $ MeV[67]. 基于FOPI-LAND实验的质子和中子椭圆流数据误差范围, 模型UrQMD和TuQMD给出的限制是一致的. -
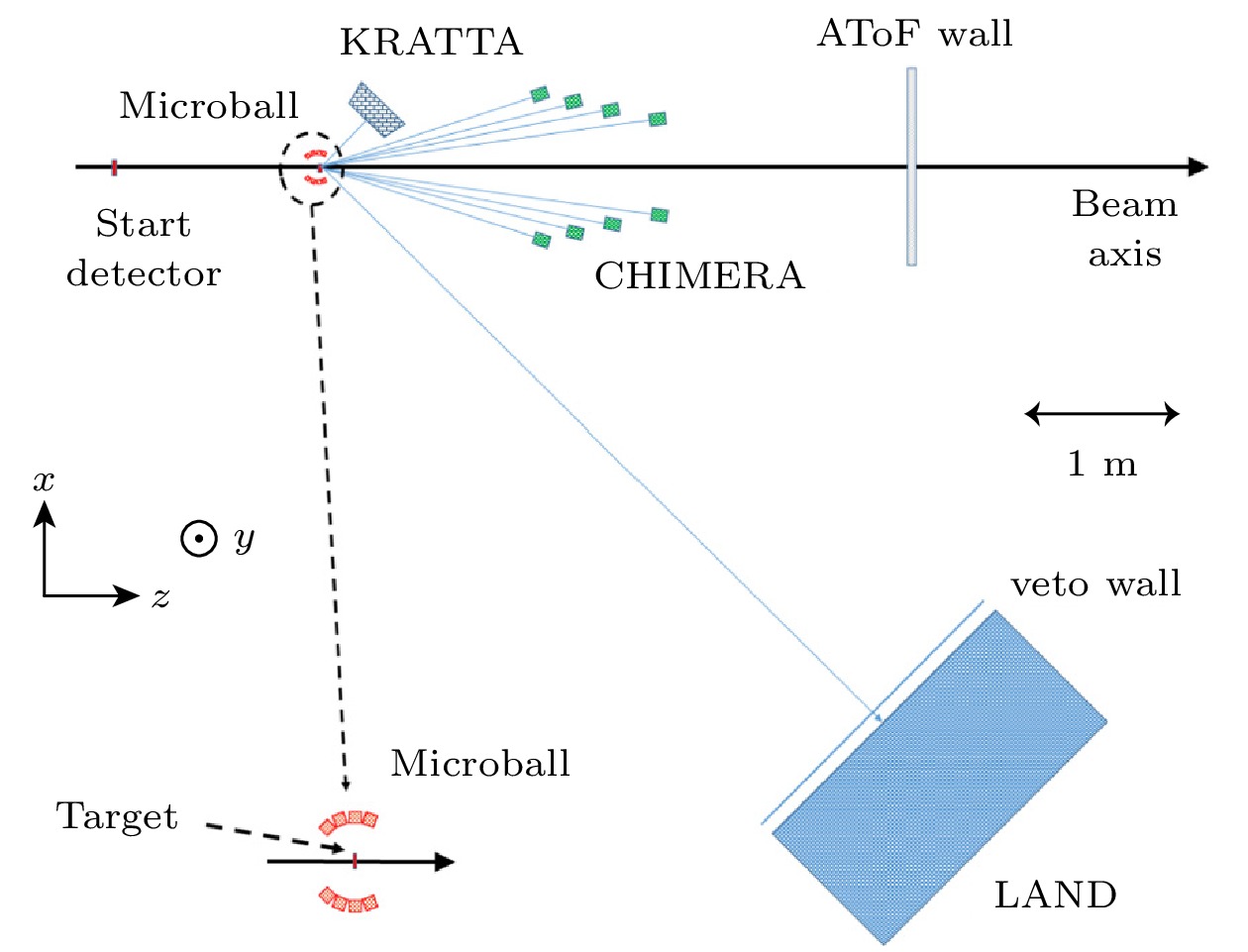
由于FOPI-LAND实验中测量到的是质子和中子的集体流, 在提取高密区对称能方面的独特优势(见本文4.2.3节), 德国GSI于2011年又进行ASY-EOS实验, 其目的在于在实验上累积更多400 MeV/u的Au+Au碰撞数据, 进一步提高该反应中质子和中子的集体流实验精度, 依此来更进一步限制对称能在高密区的参数空间. ASY-EOS实验探测器布局如图17所示.
图17中, 围绕在靶点的探测器为Microball, 它是由50块厚度为3.6—5.6 mm的CsI (Tl)晶体围成的四个环, 覆盖的极角区域为
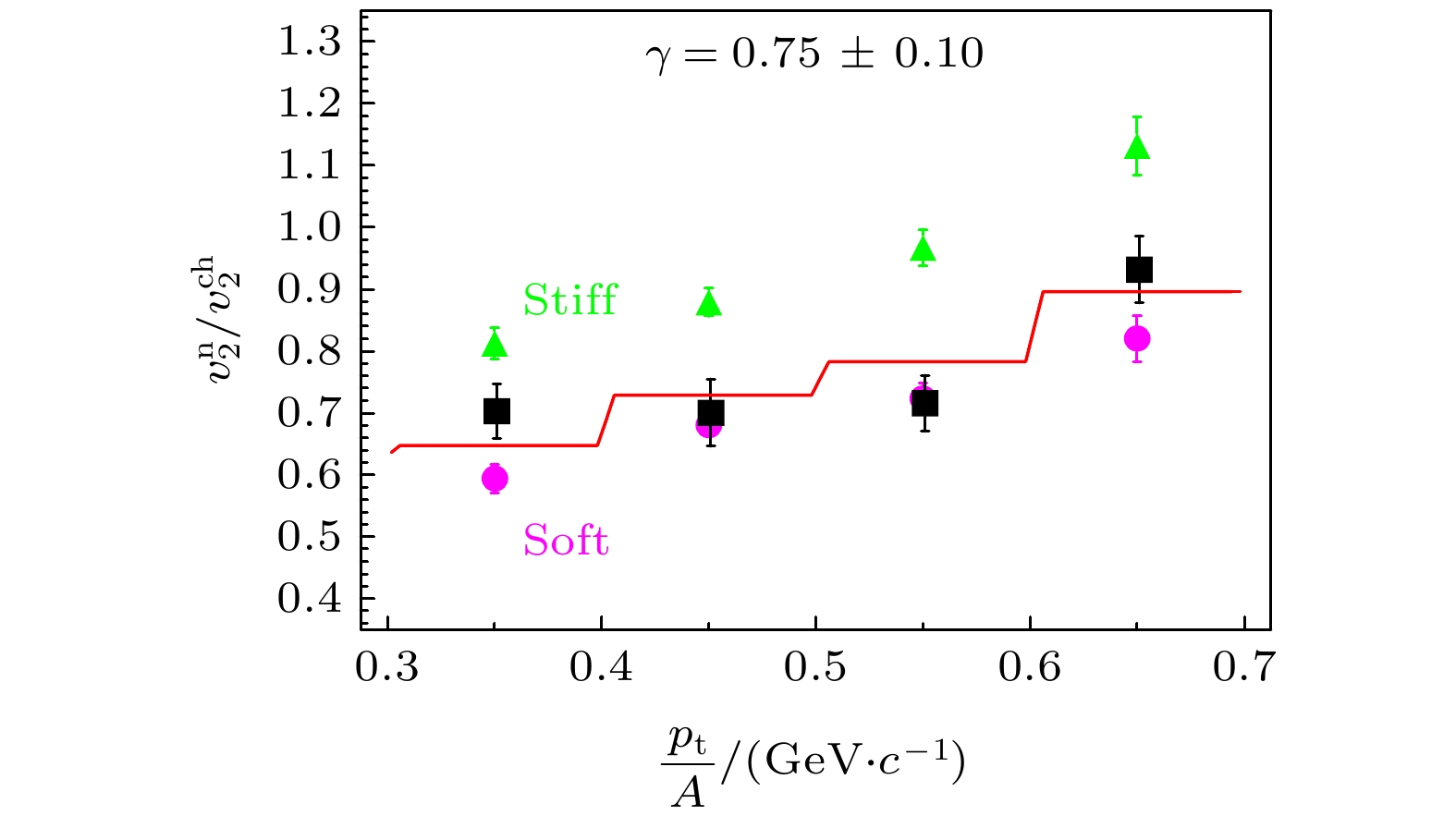
$ 60^{\circ} $ —$ 147^{\circ} $ , 其主要功能是测量后角区出射的粒子以确定反应平面. CHIMERA探测器是由352块CsI (Tl)晶体分为4个双层环组成的阵列探测器, 覆盖的极角范围为$ 7^{\circ}\leqslant{\theta}\leqslant20^{\circ} $ . CHIMERA可以鉴别出A = 1—4的粒子. ATOF墙由2层塑闪板组成, 有效面积约为1 m2放置于靶后3.7 m的位置, 覆盖$ \theta<8^{\circ} $ 范围的空间区域; 每层包括48个塑闪探测单元, 每个探测单元的长、宽、厚度为$ 110\;{\mathrm{cm}}\times2.5\;{\mathrm{cm}}\times 1 \;{\mathrm{cm}}$ , 两端分别耦合1个PMT; ATOF记录粒子的飞行时间, 以及带电粒子在塑闪中的能量损失; 根据飞行时间和沉积能量, ATOF可以分辨电荷 Z < 10的核素, 但是对于更重的离子电荷分辨水平估计为$ {\Delta}Z = 2 $ ; ATOF的时间分辨与离子电荷相关, 对于Li碎片典型时间分辨为300 ps, 对于电荷Q×10的碎片典型时间分辨为100 ps. 根据每个ATOF单元两端的时间差, 可以给出离子在沿条方向的位置, 典型的沿条方向的位置分辨为±2 cm; 由于ATOF前后两层交错放置, 每个Hit在水平方向典型的位置分辨为1.25 cm. LAND探测器在FOPI-LAND实验中已做详细介绍, 有效面积为$ 2\;{\mathrm{m}}\times 2 \;{\mathrm{m}}$ , 厚度为1 m包括10个塑闪探测层(LAND1和LAND2的合并). 由于LAND探测器采用的新的读出电子学性能远低于预期, 导致LAND的反符合探测器(veto)只能分辨中子和带电粒子, 而不能分辨出带电粒子的电荷. 关于ASY-EoS的实验细节, 详见文献[68]. 由于LAND子探测器电子学性能不及预期, 需要对LAND的飞行时间测量进行比较复杂的修正. 同时, 由于束流与非靶物质反应(主要来自束流与空气反应的贡献), 导致在前角区的探测器会记录到背景事件, 由于靶区反应Microball同样可以记录到信息, 分析中利用Micaroball和CHIMERA重建事件平面的反关联, 将背景事件比例压制在20%以下.图18为ASY-EOS实验测量的400 MeV/u的Au+Au碰撞(b < 7.5 fm) 中子和带电粒子椭圆流的比值
$ v_2^{\mathrm{n}}/v_2^{{\mathrm{ch}}} $ 与横动量的关联(黑色方框), 以及理论计算的结果. 图中三角和圆分别代表UrQMD在硬($ \gamma = 1.5 $ )和软($ \gamma = 0.5 $ )对称能时的计算结果, 实线是对理论计算结果做线性延拓, 与实验数据符合得最好时$ \gamma = 0.75\pm0.1 $ , 对应的对称能参数$ L_\text{sym} = (72\pm13 )$ MeV[68]. 这个结果对对称能和密度依赖的限定, 见图12中的黄色竖线区域. -
2002年, 李宝安[47]提出π的产额可以作为研究高密区对称能的实验可观测量, 后有一系列基于输运模型的文章[68–70]研究了
${\pi}^-/{\pi}^+$ 产额比作为研究高密区对称能的有效性, 这些理论研究发现π产生阈值附近的重离子碰撞中, π介子的产额与Δ重子的产生密切相关, 而随着碰撞能量的升高, 核子-核子散射中会产生大量的π介子, 伴随着π介子的吸收、产生和散射导致π趋于热化, 使得${\pi}^-/{\pi}^+ $ 的产额对$ E_\text{sym} $ 的敏感度随着能量升高逐渐降低. 在GeV能区重离子碰撞中, 理论模型中广泛使用的π产额(${\pi}^-/{\pi}^+ $ 产额比)数据主要来自德国GSI的FOPI实验和近期日本理化学研究所的RIBF装置上的SπRIT实验的测量结果, 下面简要介绍这个实验装置、实验结果和相关的理论讨论. -
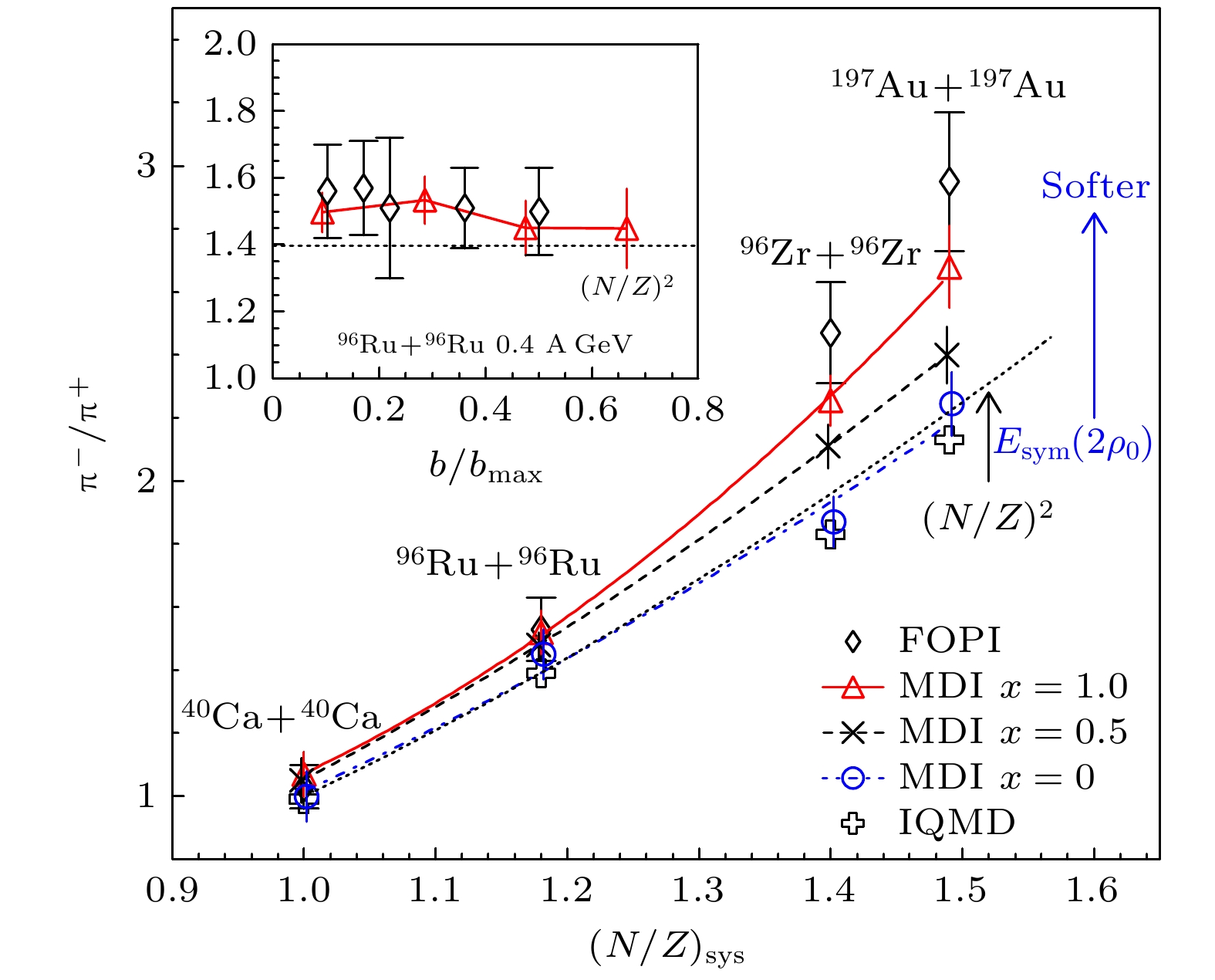
2007年GSI的FOPI实验发表了一系列实验结果: 0.4, 0.6, 0.8, 1.0, 1.5, 1.93 GeV/u的
$ ^{40}\text{Ca}+ ^{40}\text{Ca} $ ; 0.4, 1.0, 1.5 GeV/u的$ ^{96}\text{Ru}+^{96}\text{Ru} $ 和$ ^{96}\text{Zr}+ ^{96}\text{Zr} $ ; 0.4, 0.6, 0.8, 1.0, 1.5 GeV/u的$ ^{197}\text{Au}+ ^{197}\text{Au} $ 等反应系统中${\pi}^\pm $ 的产额、产额比、直接流和椭圆流[71]. 基于FOPI实验的$ {\pi}^-/{\pi}^+ $ 比值测量结果被多个强子输运模型用来提取对称能的参数, 但是由于模型依赖, 不同的输运模型给出了不同甚至相反的对称能参数. 2009年肖志刚等[72]基于同位旋和动量依赖的IBUU04强子输运模型, 计算了400 MeV/u的$ ^{40}\text{Ca} +{}^{40}\text{Ca} $ ,$ ^{96}\text{Ru} +{}^{96}\text{Ru} $ ,$ ^{96}\text{Zr} + {}^{96}\text{Zr} $ 和$ ^{197}\text{Au}+^{197}\text{Au} $ 中心碰撞($ b/b_\text{max}\leqslant 0.15 $ )中的$ {\pi}^-/{\pi}^+ $ 产额比. 图19所示为FOPI实验测量400 MeV/u的核核中心碰撞中${\pi}^-/{\pi}^+ $ 产额比与碰撞系统N/Z的依赖关系(空心菱形). IBUU04模型基于软(x = 1)、中等(x = 0.5)、硬(x = –1)对称能时的$ {\pi}^-/{\pi}^+ $ 产额比, 结果分别用红色三角形、黑色叉号和蓝色圆圈表示. 通过比较实验数据和理论计算结果, 发现x = 1的情况下理论与实验产额符合得最好, 最终得出的结论为在$ \rho>2\rho_0 $ 的区域, 对称能$ E_\text{sym}(\rho) $ 是软的. 然而, 2010年冯兆庆等[73]基于改进的同位旋依赖量子分子动力学模型(ImIQMD), 在该模型中π的产生主要来自$ \Delta(1232) $ 和$ {\mathrm{N}}^*(1440) $ 的衰变, 基于同样的FOPI实验的数据, 却得出高密区对称能是硬EoS. 2013年, 谢文杰等[74]利用改进后的BUU模型计算了$ {\pi}^-/{\pi}^+ $ 的产额比, 与FOPI实验数据比较后, 得出结论, 即在高密区对称能是偏软的. 可见由于理论上的不确定性, 基于FOPI实验测量的${\pi}^-/{\pi}^+ $ 产额比提取高密区对称能参数尚存在困难.基于同样的实验数据, 不同的理论模型给出了不同结论, 促使世界范围内的强子输运模型研究者于2014年启动名为“transport model evaluation project (TMEP)”的计划, 比较在相同的输入和边界条件下, 不同输运模型的计算结果, 以此来促进输运模型发展和计算结果的可靠性, 关于本文提到的输运模型也请参考文献[75]. 最近, TEMP研究了
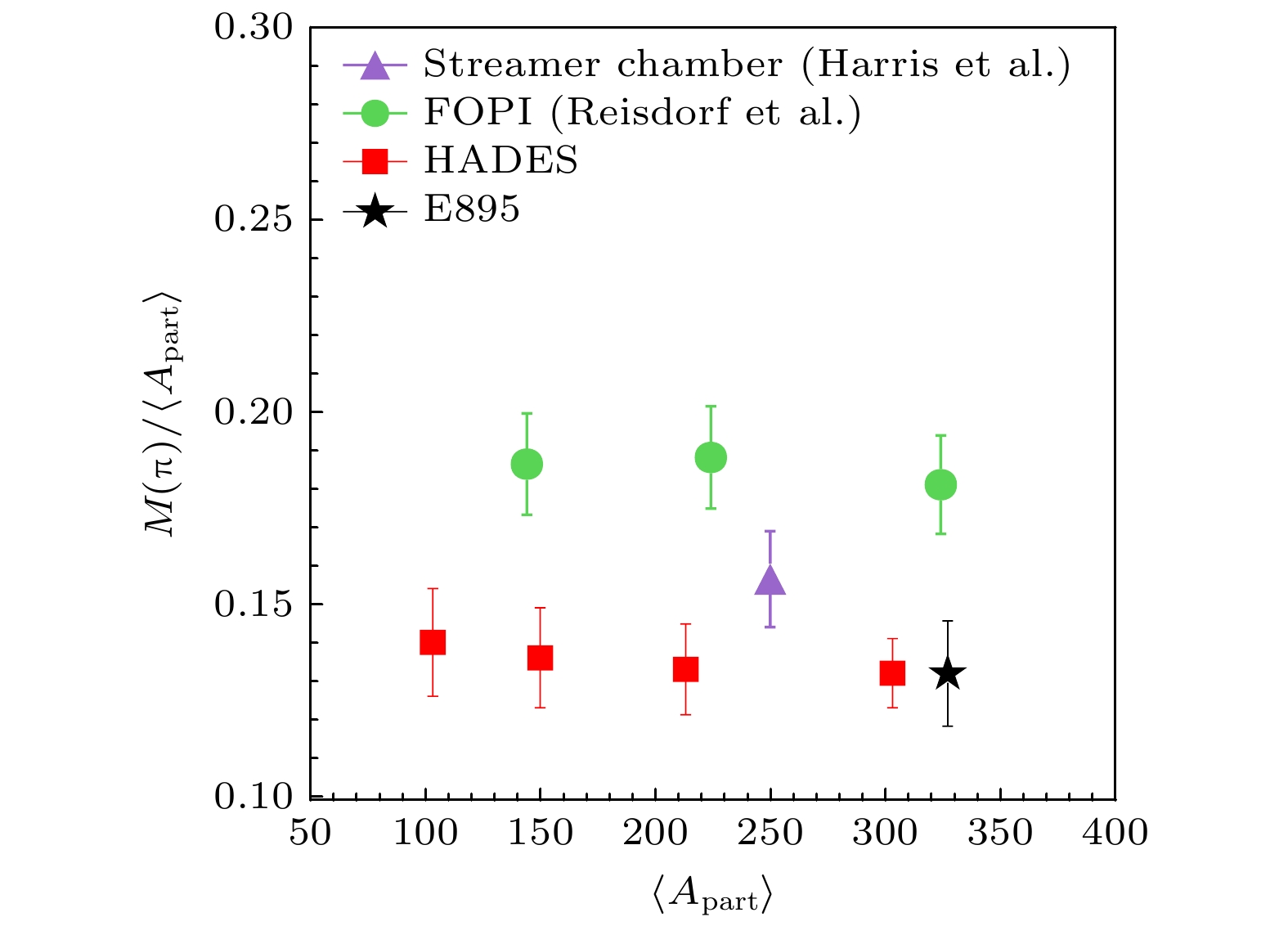
$ {\pi}^- $ 介子在270 MeV/u的重离子碰撞中的产生, 其中包括4个基于Boltzmann-Uehling-Uhlenbeck (BUU)和6个基于量子分子动力学(QMD)模型的比较, 为了简化不同理论的差异, 其中并没有包括动量依赖的相互作用势和π的介质效应[76]. 强子输运模型的这些比较和后续改进, 对于理解中高重离子碰撞中的系统演化、粒子产生机制、提取高密区对称能参数等都是非常重要的. 另外, 在BEVLELOC装置上的E895实验[77], GSI的TAPS实验[78]、KaoS实验[79]、FOPI实验[71]和HADES实验[80]分别测量π的产额, 图20所示为π的产生多重数与参与者($ \langle {A}_\text{part} \rangle $ )之间的关联, 实验上HADES实验和FOPI实验在π的产额上比FOPI实验的测量低约30%[81]. 因此, 在将来的GeV能区的实验中, 澄清这一基本问题对于提取高密区核物质状态方程具有重要作用. -
日本理化学研究所的放射性束流线(RIKEN RI beam factory, RIBF)可提供最高350 MeV/u的重离子束流和放射性束流[82,83]. 该能量下的对心重离子碰撞中, 可以产生约2
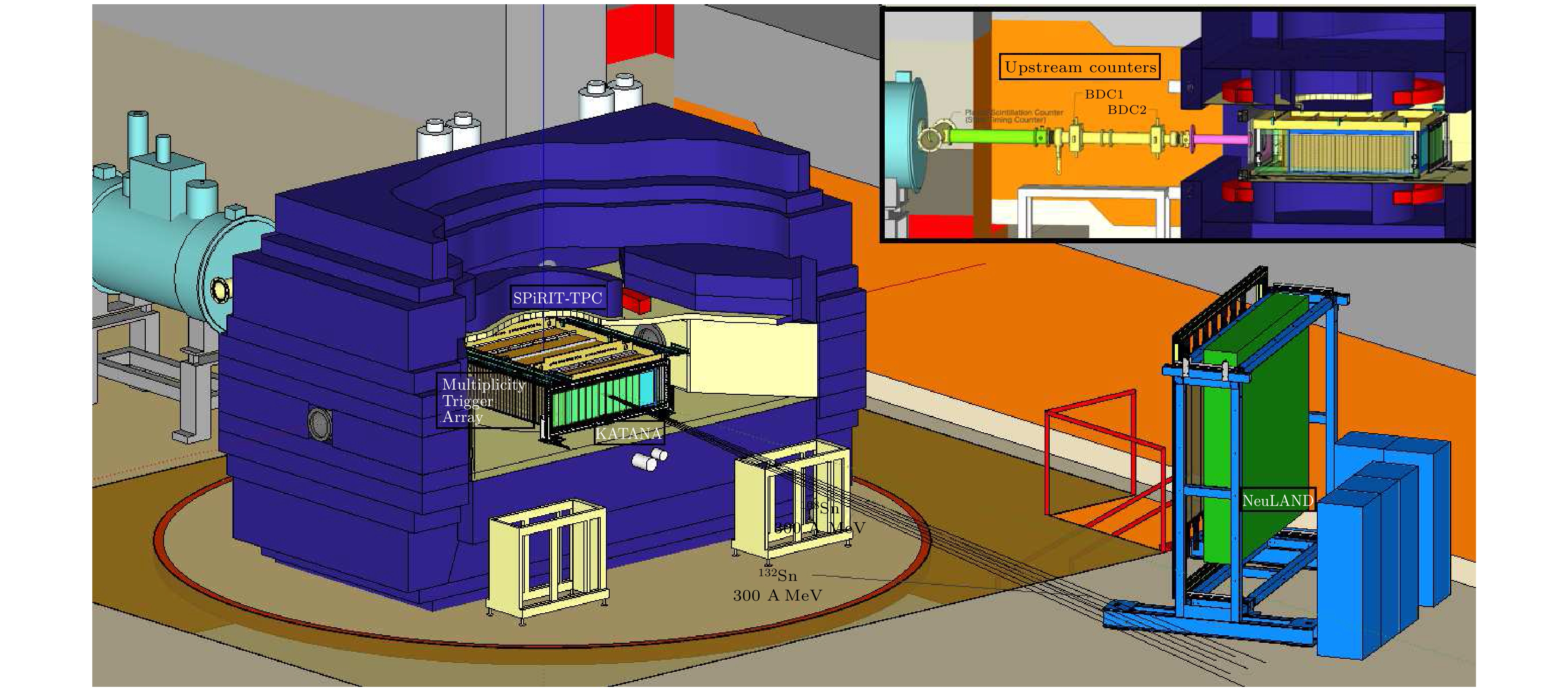
$ \rho_0 $ 的核物质. 同时利用RIBF上的丰中子或者丰质子束流与靶核碰撞, 通过测量$ {\pi}^-/{\pi}^+ $ 产额比可以研究对称能在高密区的行为.SπRIT实验的安排如下: 在一个大接收度、磁场强度为0.5 T的超导二极磁铁(称为SAMURAI)内(如图21所示[84]), 放置了一个灵敏体积为864 mm (宽) × 1344 mm (长) × 505 mm (高)的时间投影室(TPC)[44,85]. 该TPC的工作气体为1个标准大气压的P10气体(90%氩气和10%的甲烷), 典型动量分辨
$ {\Delta}p/p $ = 2%, 利用带电粒子的能损(dE/dx)可以鉴别电荷Q = 1—8的粒子, 通过重建动量和dE/dx的关联图, 可以鉴别$ {\pi}^\pm $ , p, d, t, 3,4He, Li-O. TPC的两个侧面由Tyoto-Array覆盖. Tyoto-Array包括2组30个塑料闪烁体探测器, 每一个塑闪单元的光信号通过波长位移光纤被多像素光子计数器(multi-pixel photon counter, MPPC)记录. TPC的前端由KATANA塑闪阵列覆盖, 它包括3个厚度为1 mm、面积为100 mm (宽) × 400 mm (高)的塑闪板(称为KATANA-Veto, 材料为BC-404), 以及12块厚度为10 mm、面积为100 mm (宽) × 400 mm (高)的塑闪板(称为KATANA-Multi, 材料为BC-408). KATANA-Veto放置于束线上, 由于磁铁对束流的偏转, KATANA-Multi中有7块放置于KATANA-Veto的左侧, 5块放置于KATANA-Veto的右侧. Tyoto-Array和KATANA安装完成后的实物照片如图22所示[86]. 为了筛选中心碰撞事件, 在SπRIT实验中设置的触发条件为: Kyoto-Array击中数 ≥4与KATANA-Veto测得电荷<20 [84].为了产生不同同位旋不对称的碰撞体系, SπRIT实验中, 利用RIBF放射性束流线产生4种270 MeV/u的Sn同位素132Sn, 124Sn, 112Sn和108Sn, 靶为纯度大于95%的112Sn和124Sn. 由于束流124Sn纯度较低, SπRIT实验于2021年仅发表了132Sn+124Sn, 112Sn+124Sn和108Sn+124Sn等系统中心碰撞事件中的
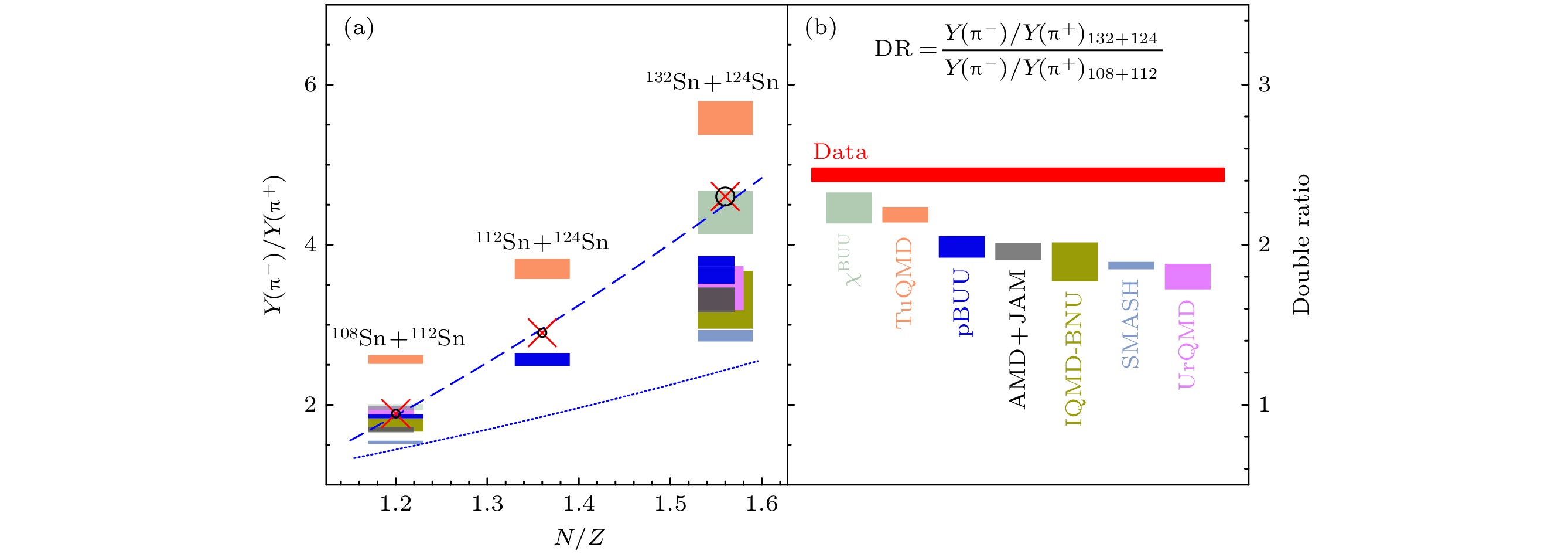
$ {\pi}^-/{\pi}^+ $ 产额比. 图23(a)是SπRIT实验270 MeV/u时, 不同Sn+Sn碰撞系统中${\pi}^-/{\pi}^+ $ 产额比的实验结果[88]; 图23(b)是132Sn+124Sn和108Sn+112Sn系统双${\pi}^-/{\pi}^+ $ 产额比(红色横线); 7个输运模型(包括3个BUU类型和4个QMD类型)在标准设置下, 计算了碰撞参数b = 3 fm时,${\pi}^-/{\pi}^+ $ 产额比和双$ {\pi}^-/{\pi}^+ $ 产额比. 图23(a), (b)中不同模型计算结果用方框表示, 其中方框的上(下)边界分别是该模型中用硬(软)对称能下的计算结果, 方框的高度则代表了该模型中对称能能对${\pi}^-/{\pi}^+ $ 产额比的敏感程度, 可见这些输运模型之间的计算差异非常显著. 不同的理论模型在对模型做一定改进也能成功描述实验结果, 比如雍高产在impBUU输运模型中用软的对称能$ L_\text{sym}(\rho_0) = (66.75\pm24.75) $ MeV和考虑短程关联的贡献后, 可以很好地描述SπRIT实验中测量的π多重数和${\pi}^-/{\pi}^+ $ 产额比[89]. 总之, SπRIT实验测量到得$ {\pi}^-/{\pi}^+ $ 产额比与FOPI实验测量结果面临同样的情形, 即在输运模型之间的分歧没有达成一致的情况下, 利用${\pi}^-/{\pi}^+ $ 产额提取高密区对称能参数尚存在困难. -
前面讨论的核物质状态方程都是基于质子和中子作为基本自由度. 在高密核物质环境中, 比如中子星内部, 早在1982年Glendenning就[90]提出随着核物质密度的增加, 由于中子化学势的升高, 核介质中通过弱过程
$ {\mathrm{NN}}{\rightarrow }{\mathrm{N}}\Lambda $ 将中子转变为Λ超子. 通过对超核(核子和超子的束缚态)束缚能和激发态能级的测量, 提取到Λ超子在饱和密度核物质中的单核子势约为–30 MeV[91,92]. 基于超核实验数据限制的超子-核子相互作用, Schaffner等[93,94]利用相对论平均场理论得出, 当核物质密度$ \rho>2.5\rho_0 $ , 核物质中就会产生Λ超子. 近期基于AMPT输运模型也得到了类似的结论[95]. 这些理论研究都说明在高密区核物质状态方程研究中奇异自由度是必须要考虑的.超子的出现则会导致核物质状态方程EoS的软化, 导致中子星的最大质量降为约1.4
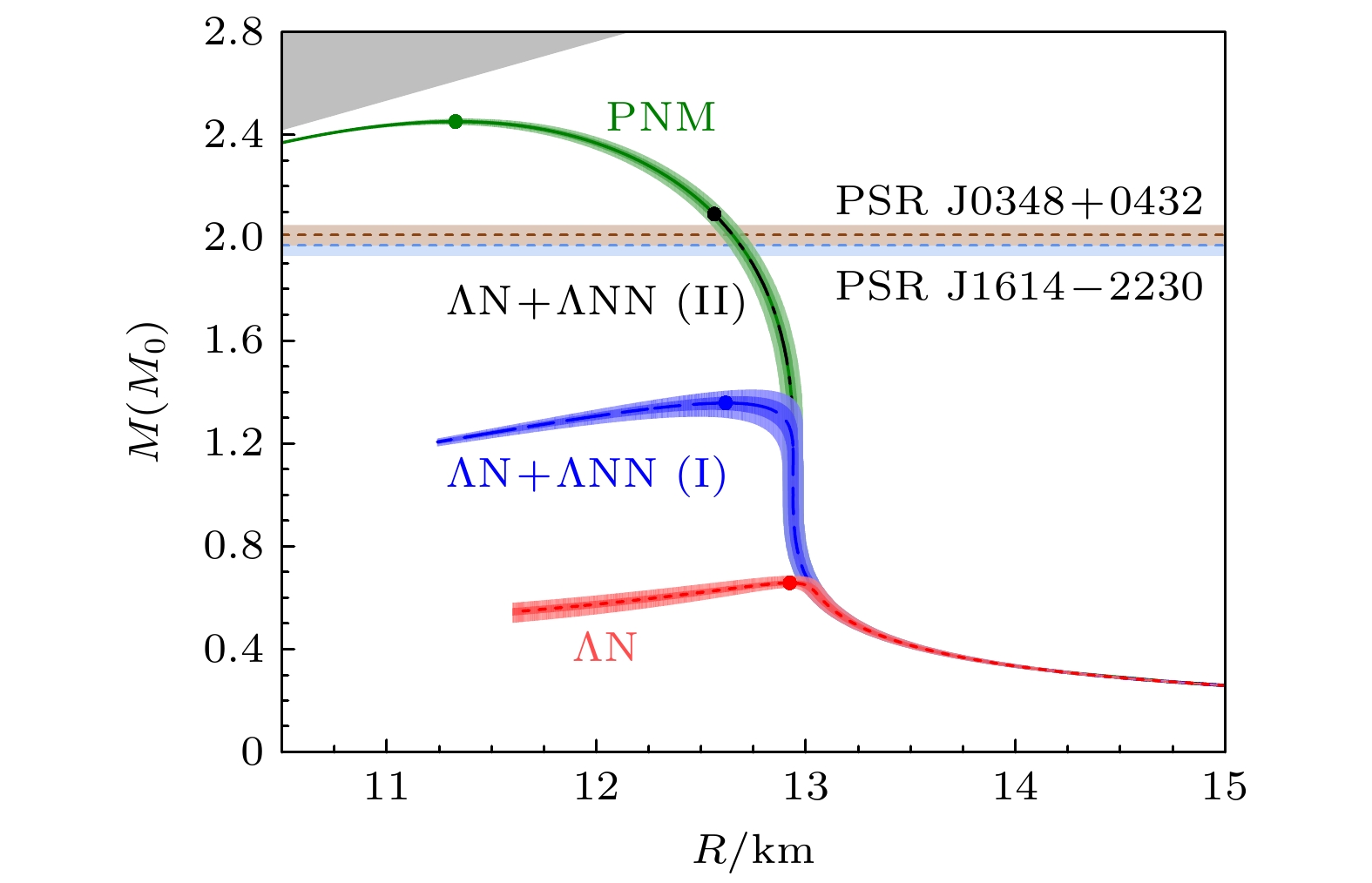
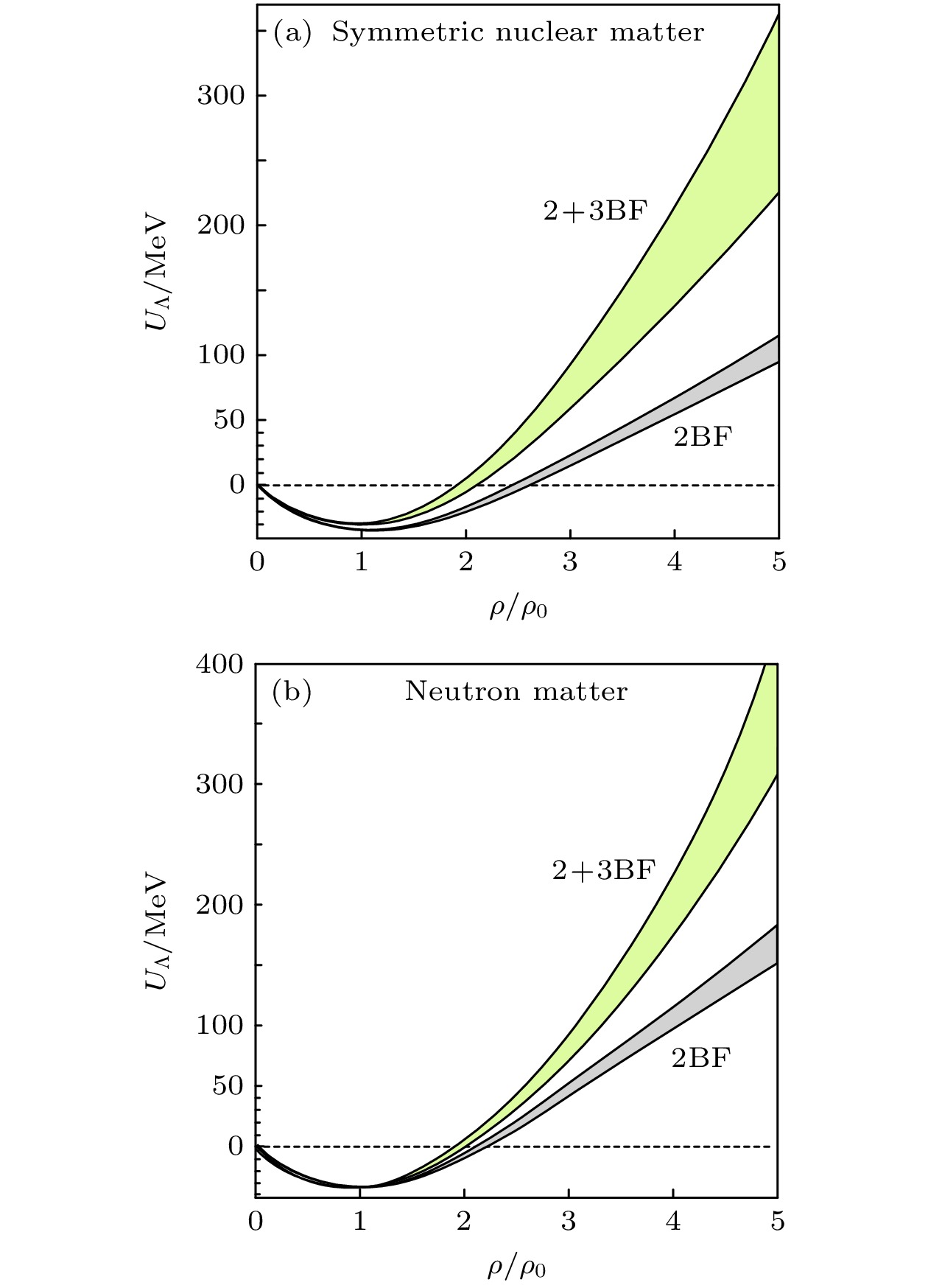
$ M_\odot $ . 自2010年天文观测上利用Shapiro效应, 在脉冲星和白矮星双星系统中发现了$ (1.97\pm0.04 )M_\odot $ 中子星PSRJ1614-2230[19], 后面陆续发现了质量为$ (2.01\pm 0.04) M_\odot $ 的中子星PSR J3048+0432以及$ (2.08\pm 0.07) M_\odot $ 的中子星PSR J0740-6620[97], 近期还发现了质量为$ (2.35 \pm 0.17 ) M_\odot $ 的最重中子星PSR J0952–0607[20]. 这些中子星的观测数据都要求硬的中子核物质状态方程才能支撑这样的大质量中子星. 在中子星研究中, 核物质状态方程中包括奇异强子后的理论, 与实际天文观测的数据不一致, 这就是所谓中子星研究中的“超子谜题(hyperon puzzle)”[98]. 理论上提出了很多解决超子谜题的办法, 其中比较主流的解决办法是考虑三体相互作用等机制对物态方程的贡献[96], 来平衡由于超子出现对EoS软化的贡献. 作为一个例子, Lonardoni等[96]基于辅助场扩散蒙特卡罗算法, 提出了超子-核子-核子(YNN)相互作用对核物质状态方程的影响. 图24所示为中子星质量(M)和半径(R)的关系, 其中绿色区域为核物质, 红色区域代表在核物质基础上再加入$ {\Lambda}{\mathrm{N}} $ 相互作用后中子星的M-R关系, 其中考虑了两种都可以描述超核数据的YNN相互作用, 发现三体相互作用确实可以硬化EoS, 但是两种YNN相互作用硬化EoS的程度具有很大差异, 意味着研究高密区的YN相互作用的强度对于理解“超子谜题”的基本输入量非常重要.基于SU(3)对称性的有效场论, Gerstung等[99]得出了超子-核子(YN)和三体超子-核子-核子(YNN)相互作用与对称核物质体系和中子核物质体系的密度依赖关系, 分别如图25所示. 可以看出, 在高密度区, 两体YN相互作用和三体YNN相互作用都是排斥势. 这里问题的关键就变成了在实验上如何提取核物质密度依赖的YN和YNN相互作用.
前面已经讨论了高能重离子碰撞是实验室产生高密核物质的唯一手段, 在重离子碰撞中会产生大量的超子(包括Λ, Σ, Ξ等). 根据YN相互作用的理论, 在核介质中由于单Λ势与密度的依赖关系, 会导致超核产额和集体流行为的改变[100]. 实验上, STAR实验第二阶段能量扫描实验(BES-II)的数据采集已经完成. 在固定靶实验中可以覆盖能量为
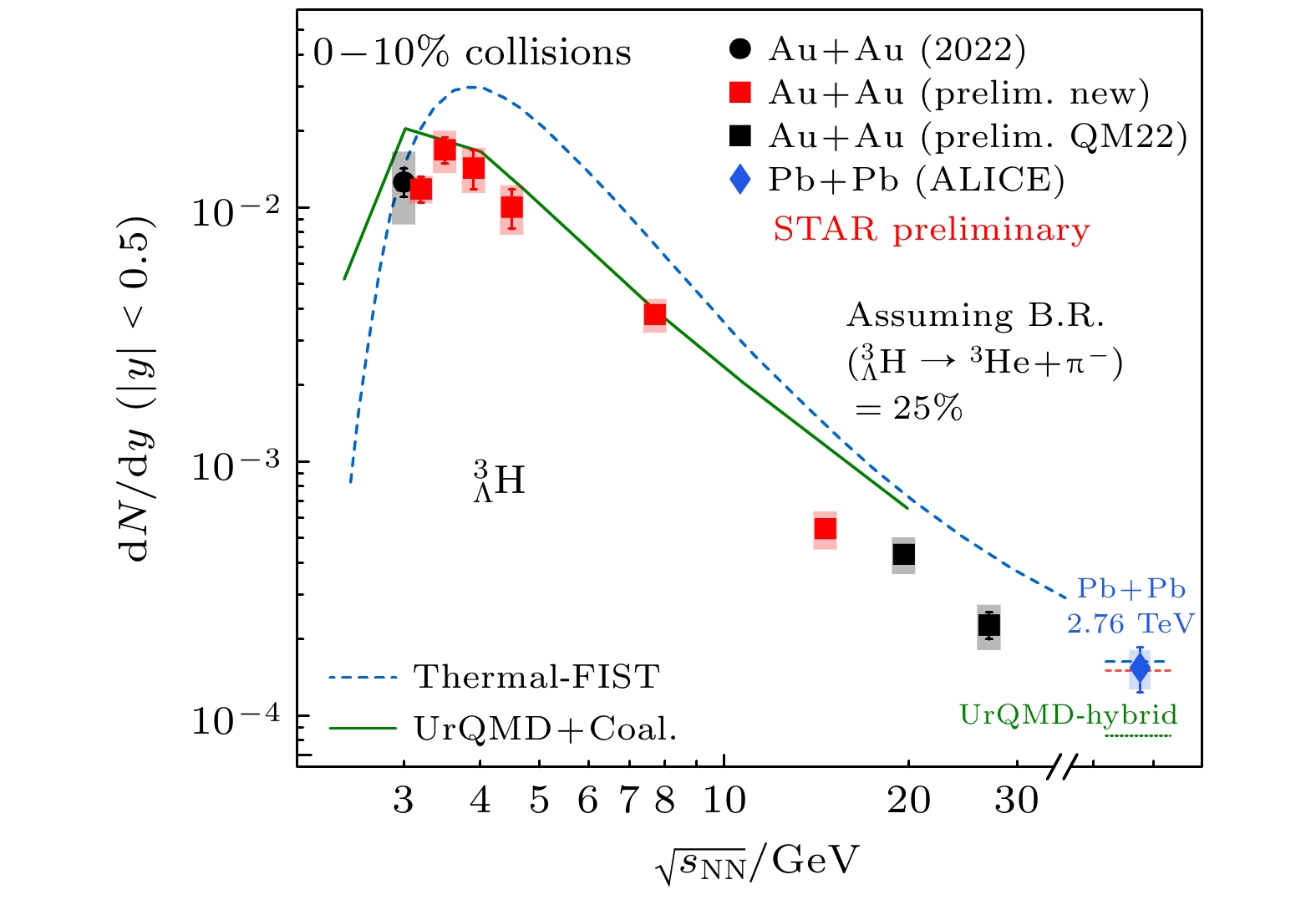
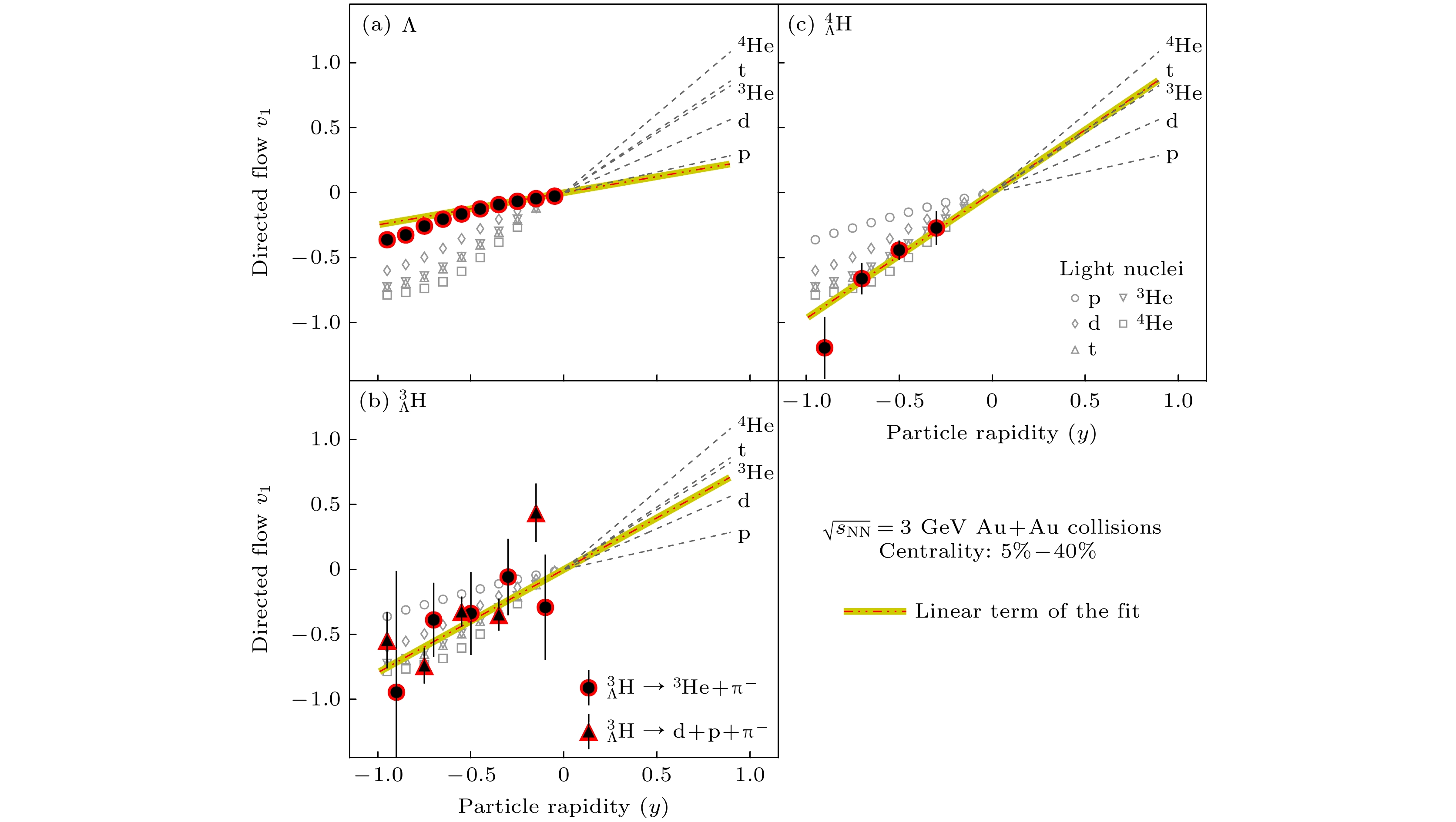
$ \sqrt{s_{{\mathrm{NN}}}} = $ 3.0—7.7 GeV的区域. 从能量区间的数据中可以系统性地获得超子(如Λ, Ξ)和轻超核(如$ ^3_{\Lambda}\text{H} $ ,$ 4_{\Lambda}\text{H} $ ,$ ^4_{\Lambda}\text{He} $ 等)产额随碰撞能量、碰撞中心度、快度的分布; 同时也可以获得这些粒子集体流的测量结果. 这些高精度的数据为研究核介质密度依赖的超子-核子相互作用提供重要依据. 图26所示为超氚$ ^3_{\Lambda}\text{H} $ 产额随碰撞能量的关系[101], 其中可以看到在$ \sqrt{s_{{\mathrm{NN}}}} = $ 3.0—4.0 GeV的区域,$ ^3_{\Lambda}\text{H} $ 产额达到最大值, 然后随能量单调下降. UrQMD计算结果再结合末态的并合模型, 能够定性描述3—7 GeV区间在中心快度区域$ ^3_{\Lambda}\text{H} $ 的产额, 而热力学模型能够定性描述$ ^3_{\Lambda}\text{H} $ 产额的趋势, 整体上高估$ ^3_{\Lambda}\text{H} $ 产额.正是由于在
$ \sqrt{s_{{\mathrm{NN}}}} = $ 3—4 GeV的Au+Au碰撞中具有较高的超核产生截面, 这样就能测量超核集体流. 2023年, STAR实验在3 GeV的5%—40%中心度的Au+Au碰撞中, 首次测量到了超核$ ^3_{\Lambda}\text{H} $ 和$ ^4_{\Lambda}\text{H} $ 直接流随快度的分布, 如图27所示. 同时, 比较了Λ超子与质子,$ ^3_{\Lambda}\text{H} $ 和$ ^4_{\Lambda}\text{H} $ 与相同重子数的轻核直接流的差异, 发现超子和超核直接流斜率($\text{d}v_1/\text{d}y_{y = 0} $ )与质量数呈线性关联, 并且该斜率与轻核直接流斜率随质量数变化中的斜率是一致的[102], 并且轻核和超核的$ v_1 $ 随快度的依赖, 可以用JAM模型+末态并合模型来描述. 这里可以看出, 输运模型+末态并合模型可以较好地描述轻核、超核的产额和集体流.但是如果考察输运模型+末态并合过程来构造集团过程, 其局限性也是显而易见的. 该过程中, 首先需要基于输运模型给出在特定冻出时间(freeze-out time), 系统中所有重子(包括核子、超子等)的坐标空间和动量, 然后把坐标空间和动量空间中距离足够近的2个或者多个重子合并为一个集团. 如果这个集团中含有超子, 则这个集团就是超核. 输运模型中在粒子冻出之后, 其动量可以认为是不变的, 但是粒子的坐标空间(或者说粒子之间的距离)随着体系演化时间的增加在不断变大. 基于这个简单的原因就可以知道, 用统一的并合参数来描述所有实验数据是非常困难的. 由于中高能核核碰撞的中心温度可以达到40—100 MeV, 而一般集团(包括轻核、超核)的束缚能约为几个MeV, 在环境高温比集团束缚能高1个量级的情况下, 一般认为在火球内部不存在这些集团, 这些集团是在系统膨胀到一定程度, 或者在火球的表面粒子在出射时凝结而形成的, 这个过程完全符合并合过程的图像.
自2021年, SMASH模型中首先提出高温系统中弱束缚集团的产额是在动态演化的, 是各种集团的产生道和解离道之间的动态竞争. 该模型中考虑了氘核产生道
$ {{\pi}}{\mathrm{pn}}{\rightarrow }{{\pi}}{\mathrm{d }}$ 和氘核解离道$ {{\pi}}{\mathrm{d}}{\rightarrow }{{\pi}}{\mathrm{pn}} $ 后, 能够成功描述能量为3—200 GeV的Au-Au碰撞实验中观测到的氘和反氘的产额[103]. 2022年, Neidig等[104]基于同样的思路, 考虑了更多轻核和超核的产生和解离的反应道, 发现如果系统在温度为155 MeV的环境中, 轻集团(如d, t, 3He等)产生很快就达到化学平衡, 这也能够解释为什么基于实验测量粒子产额数据的热力学模型所提取的冻出温度是155 MeV, 而不是在体系膨胀末期的温度(一般认为系统演化末期温度远低于体系中早期的温度). 近期, 孙开佳等[105]基于包括强子再散射效应的相对论量子多体输运方法(kinetic approach), 在系统中考虑了$ {{\pi}}{\mathrm{NNN}}{\Leftrightarrow}{{\pi}}{\mathrm{t }}$ 和$ {{\pi}}{\mathrm{Nd}}{\Leftrightarrow}{{\pi}}{\mathrm{t}} $ 过程, 发现可以很好地描述200 GeV Au-Au碰撞中的氘核和氚核产额. PHQMD模型基于输运过程中集团识别的方法, 发现集团产额在演化后期与体系演化时间关联较弱[106]. 在这些过程中, 集团的产生和集体流行为会受到不同核核物质密度中YN相互作用的影响. 因此, 是否可以从超子、轻核、超核的产额和集体流提取到超子-核子相互作用与核物质密度的依赖关系, 有待更多的实验数据和理论的进一步发展. -
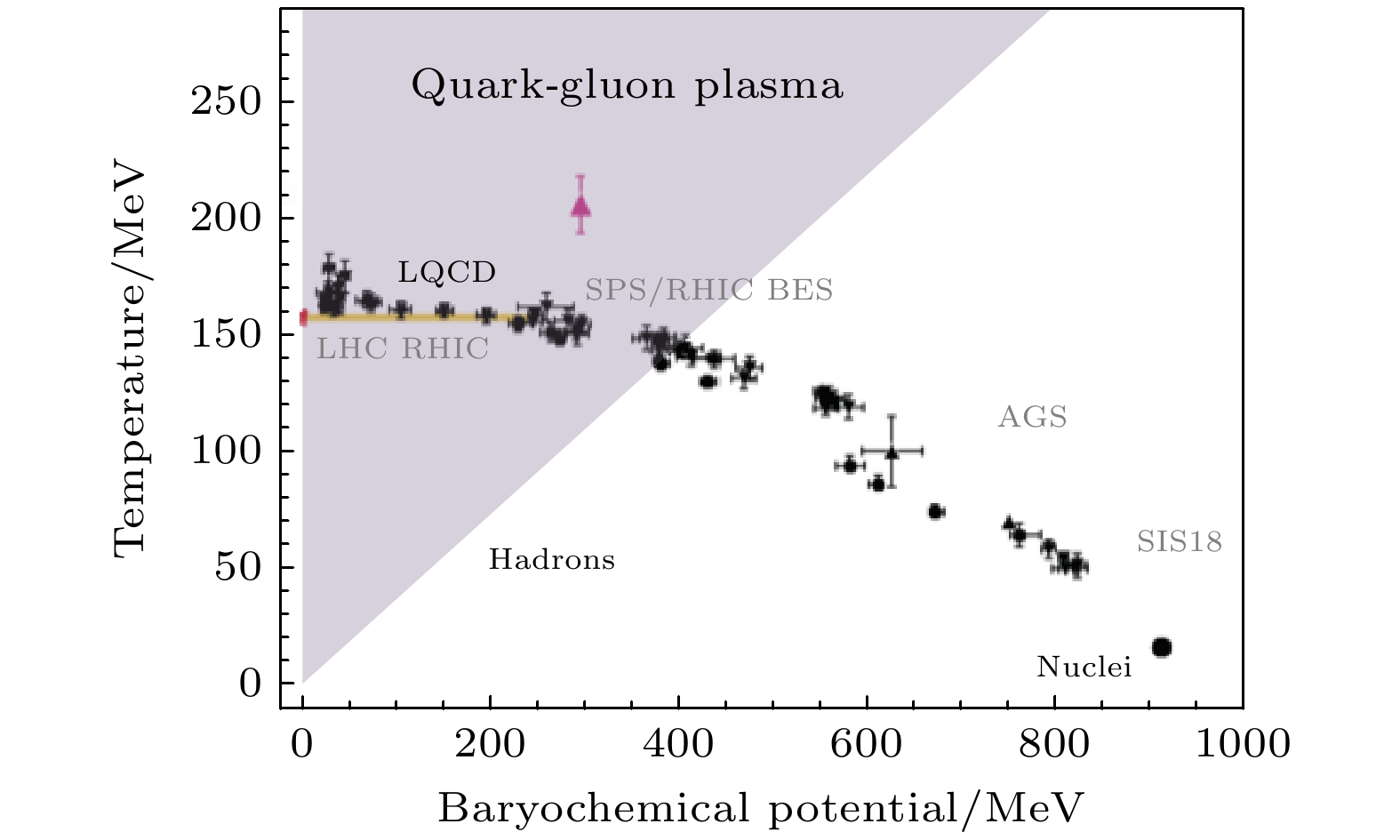
重离子碰撞是实验室产生高温高密核物质的唯一实验手段, 不同能量的重离子碰撞, 可以产生不同温度和密度的核物质, 这就为研究核物质在不同热力学条件下的性质提供了可能. 现有重离子碰撞数据中, 最早来自二十世纪70年代美国劳伦斯伯克利国家实验室(Lawrence Berkeley national laboratory, LBNL)的Bevalac加速器上的最高能量为2 GeV/u的重离子碰撞实验, 该加速器于1993年停止运行; 德国重离子研究中心(GSI)于1990年建成且至今仍然在运行的SIS18加速器, 可以提供0.4—2 GeV/u的重离子束流, 基于SIS18加速器的典型实验有前文已经提到的KaoS, FOPI, Hades等; 1996年, 美国布鲁克海文国家实验室(BNL)建成了可提供约2—10 GeV/u重离子束流的AGS加速器, 之后AGS作为相对论重离子加 速器(RHIC)的注入器; 2009年, RHIC开始提供最高能量为200 GeV/u的重离子束流; 2011年, 欧洲核子中心(CERN)建成了可以提供13— 158 GeV/u的SPS加速器, 之后SPS用作大型强子对撞机(LHC)的注入器, 自2022年起LHC可以提供最高能量为5.36 TeV/u的Pb束流[107]. 图28所示为从SIS18/Bevalac能区到LHC能区的重离子碰撞实验中, 利用粒子产额并基于热力学模型所提取的化学冻出温度(T )和重子化学势(
$ \mu_{\mathrm{B}} $ )的关联图[108]. 可以看出, 碰撞能量越高的重离子碰撞产生的高温越高, 重子化学势越低. 可见, 建造不同能量的重离子加速器设施是定量研究核物质在不同热力学条件下性质的必要条件.这些数据能够反映出重离子碰撞中所创造的极端核物质的整体性质. 但是, 极端核物质性质研究中有几个理解强相互作用的基本问题尚未解决, 比如核物质状态方程在高密区的精确表述、强子气体到QGP的相变是一级相变还是二级相变, 如果是一级相变, 临界点的位置在哪里、如何在实验上提取核介质相关的YN相互作用、强子气体相转变为QGP的临界密度等. 强子气体相在某个临界能量密度会转变为QGP, QGP的出现将软化核物质的EoS, 这个临界密度实验测量对于理解强相互作用的理论、中子星内是否存在夸克物质、双中子并合等具有极为重要的意义. 另外, 不同类型理论研究结果预言[15,109–112], 强子气体到QGP的相变是一级相变, 且相变临界点(
$ \mu^{\mathrm{c}}_{\mathrm{B}}, \;T^{\mathrm{c}} $ )可能存在的范围为495 MeV$ <\mu^{\mathrm{c}}_{\mathrm{B}}< $ 654 MeV和100 MeV$ <T^{\mathrm{c}}< $ 119 MeV, 这个临界区域对应的核核碰撞的质心系能量的范围约为3.5 GeV$ <\sqrt{s_{{\mathrm{NN}}}}< $ 5.0 GeV. 因此, 实验上是否可以给出确切的临界信号就是发现相变临界点的关键. 这就使得积累高重子数密度区的高精度实验数据, 对于核物质状态方程和相结构研究显得尤为重要. 为了能细致研究致密核物质性质与重离子碰撞的能量依赖关系, RHIC装置上的STAR实验在2018—2022年间实施了第一阶段的能量扫描实验(BES-I), 取得了束流能量范围在$ \sqrt{s_{{\mathrm{NN}}}} = 7.7—27 $ GeV的Au-Au碰撞数据; 并于2022—2024年完成了能量扫描二期的实验计划(BES-II), 包括一系列的固定靶实验, BES-II覆 盖了能量$ \sqrt{s_{{\mathrm{NN}}}} = 3—13.7 $ GeV的Au-Au碰撞数据[113].由于上述的一些重要的物理都集中在了高 重子密度区, 国际上该能区实验逐渐成为了焦点, 除了前面已经提到RIKEN的RIBF装置上的SπRIT实验, 还有几个计划实施的实验: 如美国MSU的FRIB上基于放射性束的EoS实验、中国HIRFL-CSR上的低温高密核物质测量谱仪(CEE)实验、德国FAIR装置(SIS100)上的CBM/Hades实验、俄罗斯NICA装置上的MPD实验、中国HIAF装置上的CEE+/CHNS, 韩国RAON装置上的LAMPS实验等. 表1所列为以上提到加速器装置、重离子碰撞质心系能量和相关实验的信息汇总. 下面简要介绍在建重离子加速器及计划实施实验的进展情况.
-
德国FAIR (facility for antiproton and ion research)装置的加速器为SIS100[114], 现有的SIS18作为SISI100的注入器. SIS100能够提供流强为
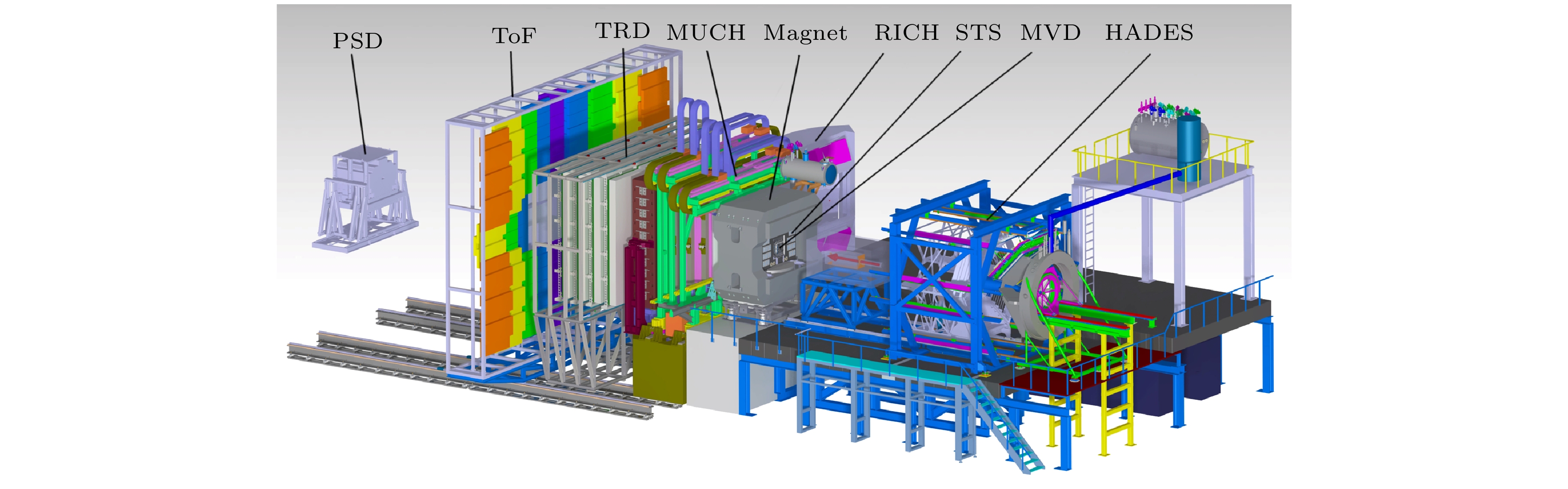
$2.5 \times10^{13} $ ion/cycle, 最高能量为29 GeV的质子束流; 重离子束流(比如Au)流强为$ 1{\times}10^{10} $ ion/cycle, 最高能量到11 A GeV; 轻粒子(比如Ca)的能量为14 A GeV. SIS100加速器于2017年7月正式开建, 预计于2029年开始运行. 在FAIR装置上有2个实验组分别开展高能重离子碰撞实验: CBM (the compressed baryonic matter)实验[40]和HADES (the high acceptance di-electron spectrometer)实验[80]. 这两个实验装置将放置于同一个实验大厅, 图29所示为CBM实验和Hades实验的探测器示意图[40].CBM实验室是一个固定靶综合高能实验平台, 包括一个磁场强度为0.5 T的超导二极磁铁, 探测器子系统按束流方向依次排列. 在磁铁内部放置顶点探测器(MVD)和硅微条径迹探测器(STS); STS的后面是用于电子(正电子)测量的环形成像切伦科夫探测器(RICH)和用于缪子测量的探测器(MUCH), 这两个探测器安装在同一导轨上, 按实验目的来使用相应的探测器; 紧接着是用于鉴别电子和测量径迹的穿越辐射探测器(TRD), TRD的后面是基于多气隙阻性板室(MRPC)的飞行时间探测器(TOF), 最后是用于测量事件平面和碰撞中心度的探测器(PSD). CBM实验设计的最高事件率为10 MHz. 为了实现这样的挑战, CBM的数据获取采用无触发的设计、基于强大计算机集群完成在线粒子鉴别和事件筛选. 由于CBM实验是SIS100加速器的第一个终端, 预计CBM实验将于2028开始实验取数. CBM实验除了高精度测量带电粒子, 另外一个特色的设计是测量HICs中产生的轻子(包括epm和
$ {\text{μ}}^\pm $ ). 由于轻子不参与强相互作用, 在核核碰撞 中产生的轻子可以逃离火球, 这样发射的轻子就携带火球演化的信息. 另外火球中产生的一些粒子如矢量介子会在核介质中衰变, 通过双轻子道来研究这些粒子的性质, 就可能提取到这些粒子的核介质效应. 更多关于CBM实验的物理计划以及相关的理论背景, 强烈推荐参考CBM实验的物理白皮 书[115]. -
1993年, 俄罗斯联合核研究所(JINR)建成了最高可以提供4.5 A GeV重离子束流的Nuclotron加速器, 基于Nuclotron的固定靶实验BM@N[116]于2018年开始, BN@N所能覆盖的能量范围为2.3 GeV
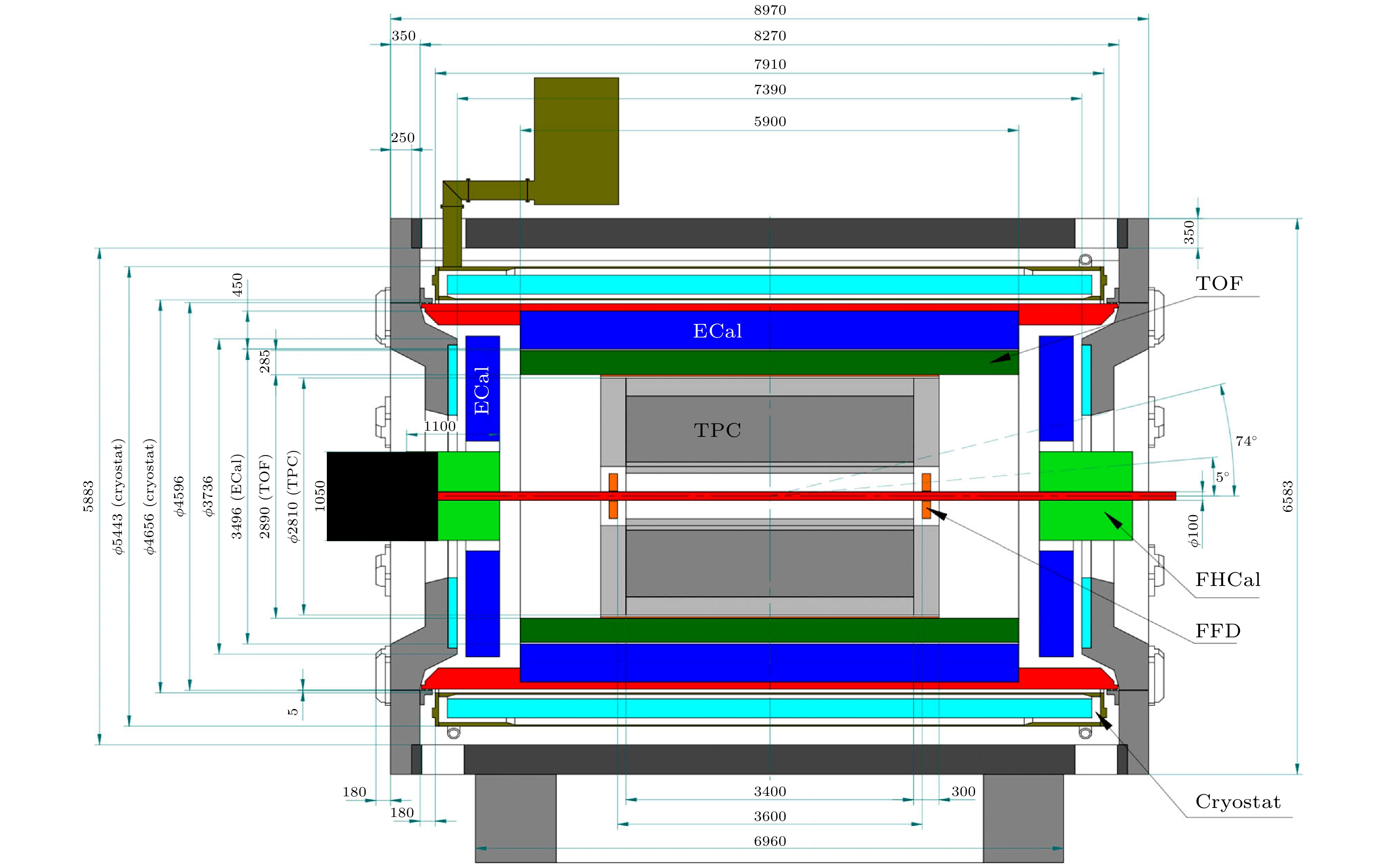
$ <\sqrt{s_{{\mathrm{NN}}}}< $ 3.5 GeV. 2013年, JINR启动新一代研究高重子数密度区核物质性质的加速器NICA (the nuclotron-based ion collider acility)[117]. Nuclotron作为NICA注入器, 粒子继续在新增的2个超导加速器环中加速到最高11 A GeV, 并开展对撞实验. NICA装置上设置了2个对撞点, 其中1个对撞点上的实验谱仪是MPD (multi-purpose detector)[41], MPD实验的主要科学目标就是研究核物质状态方程和核物质相结构. MPD实验的探测器都放置在一个磁场强度为0.5 T的超导螺线管磁铁中. 探测器布局是典型的洋葱式结构, 如图30所示, 最内层是时间投影室(TPC) 用于带电粒子鉴别和测量粒子的动量, TPC的外层是飞行时间探测器(TOF), TOF的外面和端盖部分安装有电磁量能器(ECAL), 主要用来测量电子和光子的能量; 在MPD两端的小角度区域放置前角区强子量能器(FHC), 用来测量反应平面和定义碰撞中心度. MPD实验预计于2025年开始正式运行. -
RAON (the rare isotope accelerator complex for on-line experiments)是韩国正在建造的中能重离子加速器装置[118]. RAON装置可以加速p-U的所有离子, 质子束流的能量为600 MeV, Ar束流能量为300 A MeV, U束流的能量为200 A MeV. 基于RAON的放射性束线可以产生流强为
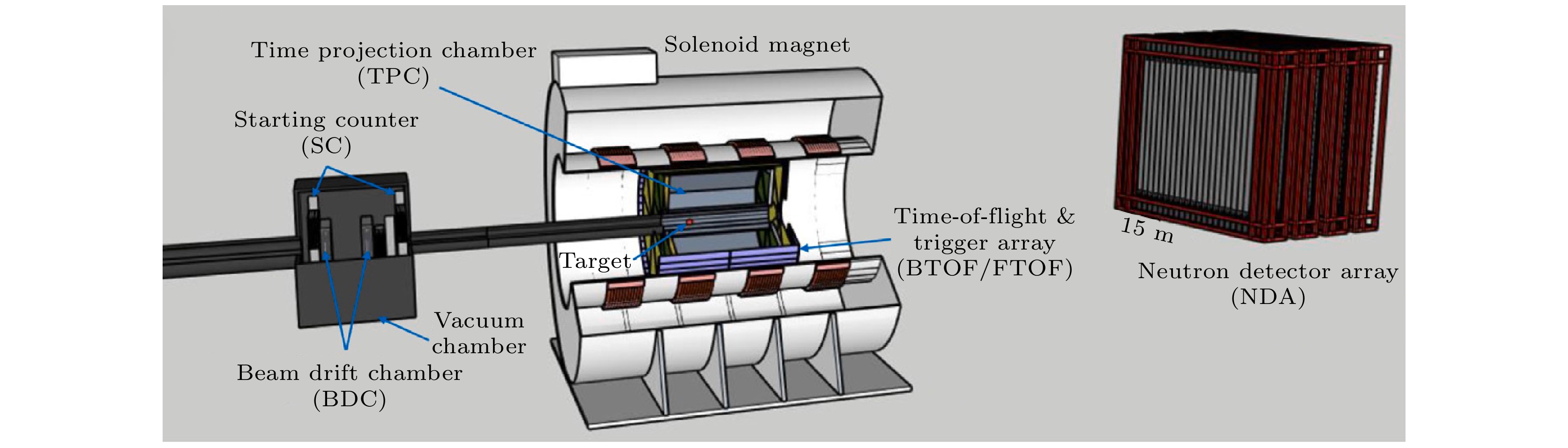
$ 10^8 $ particle/s、能量为250 A MeV的Sn系列同位素, 这样就能够开展类似于SπRIT实验的Sn+Sn 碰撞实验和测量$ {\pi}^-/{\pi}^+ $ 的产额比来提取$ E_\text{sym} $ 参 数. 除了测量带电粒子, LAMPS实验中还包括中子探测器, 在该能区的同类实验中具有一定的独 特性.RAON装置上的LAMPS实验[45]主要是基于以上的物理思路来开展核物质状态方程的实验研究. 图31为LAMPS实验的探测器布局示意图, LAMPS实验的最上游是一组用于束流定位的多丝漂移室(BDC)和时间起点探测器(T0), 靶的周围是时间投影室(TPC), 用来测量带电粒子在工作气体中的能量损失和动量, 最终完成粒子鉴别. TPC的桶部和下端盖安装了由塑料闪烁体探测器组成的飞行时间探测器(TOF), 用于测量粒子的飞行时间, LAMPS的最下游放置效探测面积为
$ 2\;{\mathrm{m}}{\times}2\;{\mathrm{m}} $ 的中子探测器(NDA), NDA包括1层反符合探测器(Veto)和四组中子探测器, 每一组中子探测器包括2层交错的中子飞行时间探测器, 每层中子飞行时间探测器都由20个尺寸为$ 10\;{\mathrm{cm}}{\times}10\;{\mathrm{cm}}{\times}200 \;{\mathrm{cm}}$ 的塑料闪烁体条并排构成, 每个塑闪条的两端分别由1个光电倍增管读出信号. RAON装置于2011年开始建造, 计划于2027年完成高能重离子束线建设, LAMPS实验的计划于2030年开始实验取数据[45]. -
我国于1989年建成兰州重离子加速器研究装置(heavy-ion research facility at Lanzhou, HIRFL), HIRFL能提供小于100 MeV/u的重离子束流. 在HIRFL装置的基础上, 2008年建成的兰州重离子加速器-冷却储存环(HIRFL-CSR)装置, 能够提供最高1.1 GeV/u的重离子束流(U束流最高能量为500 MeV/u), 实现了我国重离子实验研究从中低能向高能的跨越. 到目前为止, HIRFL-CSR仍是亚洲能量最高、国内唯一的中高能重离子加速器. 比如在500 MeV/u的U+U碰撞中, 能产生~2.5饱和密度、温度约为40 MeV的极端核物质, 这就为研究GeV能区的核物质状态方程在高密区的行为、核物质相结构、三体力、短程关联、超核等前沿物理课题提供了契机.
2018年启动建造的强流重离子加速器装置(high intensity heavy-ion accelerator facility, HIAF)能够提供最高能量为9.3 GeV的质子束流和4.25 GeV/u的重离子束流(U束流最高能量为2.6 GeV/u). 基于HIAF装置的重离子碰撞能产生3—5倍饱和密度、温度约为80 MeV的极端核物质. HIAF装置上的重离子束流能量很好地覆盖了奇异强子产生的阈值, 且处于产生超核界面极大的区域(见图26). HIAF装置将于2025年建成, 届时基于HIAF装置的重离子碰撞除了探索更高密、高温区核物质状态方程, 还为探索包含奇异夸克自由度的核物质状态方程、强子的介质效应、超核极化、发现和研究双超子超核等人们认识尚浅的前沿课题提供了绝佳束流条件. 下面简要介绍HIRFL-CSR和HIAF加速器装置的组成, 并介绍基于我国大科学装置的探测器谱仪建设进展和当前的规划.
-
HIRFL装置主要包括电子回旋共振(ECR)离子源、扇聚焦回旋加速器(SFC)、分离扇回旋加速器(SSC), 以及于2007年建成的冷却储存主环(CSRm)和实验环(CSRe)(常见地, 为了体现CSR加速后的高能束流有时也合并称为HIRFL-CSR). HIRFL-CSR装置可以加速He-U的重离子, 其中重核如238U72+最高能量为500 MeV/u, 轻离子如12C6+能量最高为1.1 GeV/u. 连接CSRm和CSRe的是一条长度为55 m称为RIBLL-II的高能放射性束流线. 图32所示为HIRFL-CSR加速器布局示意图.
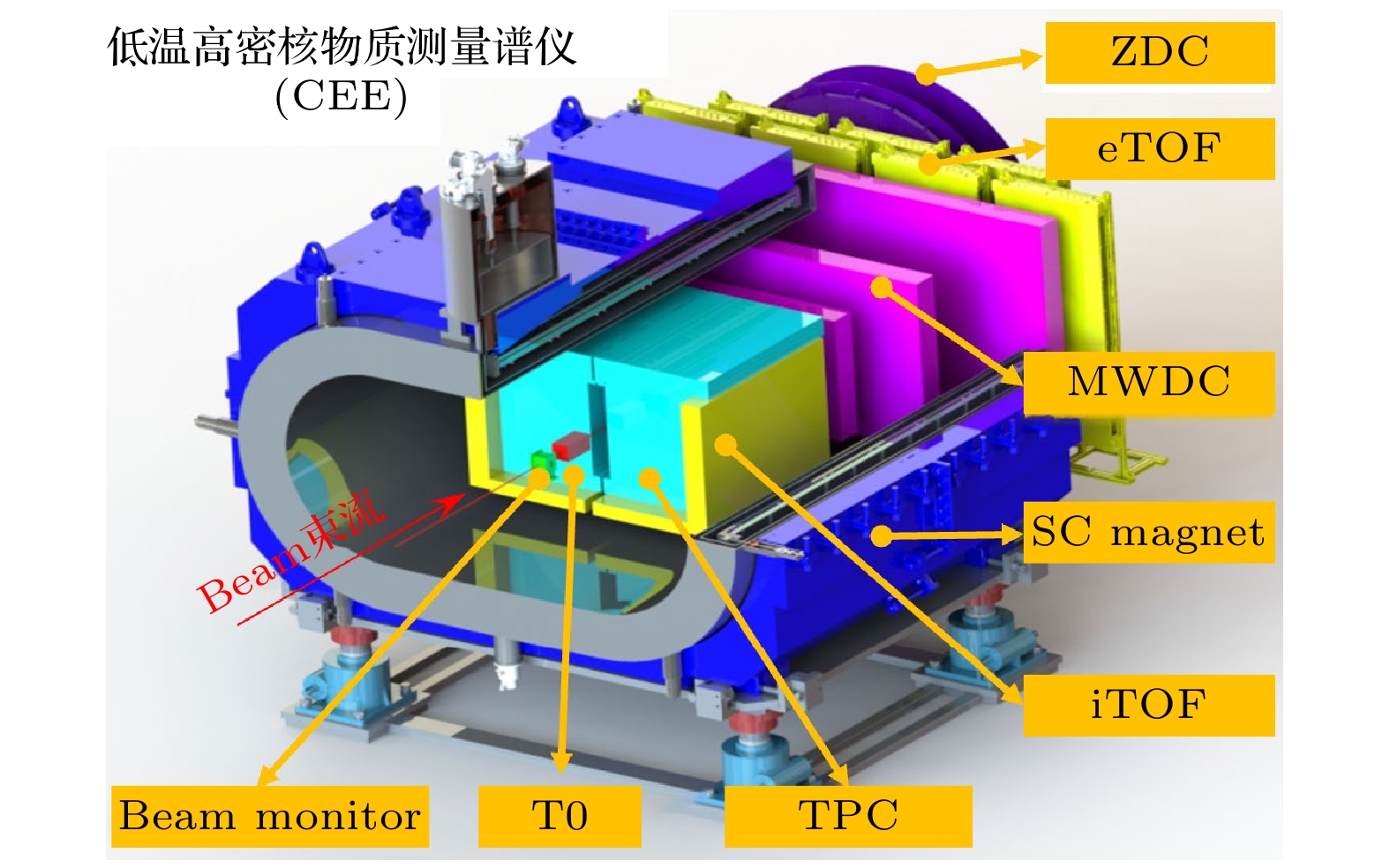
基于这样的物理机遇和背景, 2019年国家自然科学基金委员会批准了基于HIRFL-CSR装置的“低温高密核物质测量谱仪(CEE)”的重大仪器项目. 图33是CEE谱仪探测器布局示意图. CEE谱仪包括一个磁场强度为0.5 T的大接受度超导二极磁铁, CEE谱仪靶的上游安装微像素的束流定位探测器(BM)和起始时间探测器(T0); 磁铁内部放置一个时间投影室(TPC), TPC的3个侧面(TPC的读出电子学在顶端)由基于多层阻性板(MRPC)技术的TOF探测器(iTOF)包围. TPC可以测量带电粒子在气体中的能量损失(dE/dx)和动量, TOF探测器主要是测量带电粒子的飞行时间. 利用测量到的dE/dx-动量的关联和动量-飞行时间, 就可以实现带电粒子的鉴别. 在前角区是三块多丝漂移室阵列和一个基于MRPC技术的TOF探测器(eTOF), 它们用于测量前角区出射粒子的dE/dx、动量和飞行时间, 利用同样的原理实现粒子鉴别和粒子四动量的重建. CEE谱仪的最下游是一个由24个扇区, 每个扇区8块塑闪单元构成的零度角探测器(ZDC), ZDC的主要用途是测量事件平面和定义碰撞中心度. CEE谱仪的设计最大事件率为10 kHz, 典型动量分辨
$ {\Delta}p/p<5{\text{%}} $ . CEE谱仪将于2025年实施探测器组装, 2025年年底开展科学实验. -
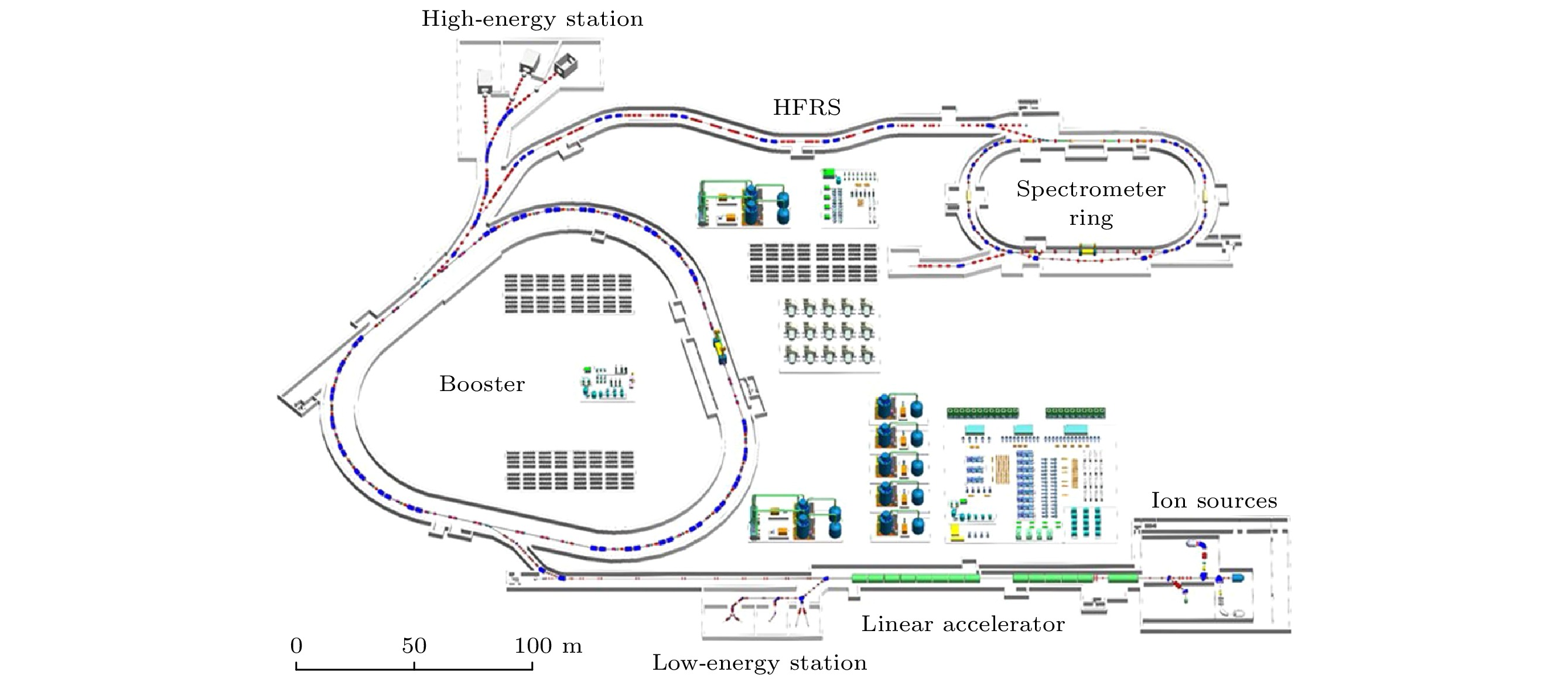
强流重离子加速器装置(HIAF)[120]是中国新一代用于研究极端条件下的核物质性质、核物质状态方程、超核、原子核存在极限和奇特结构、重元素起源等前沿课题的加速器装置[121]. HIAF于2018年开始建设, 预计于2025年投入运行. HIAF包括强流超导离子源(SECR)、超导离子直线加速器(iLinac)、最大磁钢度为34 Tm的同步加速器(BRing)和高精度实验环(SRing), 连接BRing和SRing的是一个最大磁刚度为25 Tm、长192 m的高能碎片分离谱仪(HFRS), HIAF装置的平面布局如图34所示[121]. HIAF装置可以加速p-U的束流, BRing可以将质子加速到最高9.3 GeV, 流强2.0
$ {\times}10^{12} $ ppp (每个束团包括的粒子数目); 轻粒子如12C6+能量为4.25 GeV/u; 重离子238U束流的能量范围为0.8—2.6 GeV/u. 基于HIAF装置的重离子碰撞质心系能量区为$ \sqrt{s_{{\mathrm{NN}}}} = 2.2—2.9 $ GeV. 这个能量区间与NICA装置上的BM@N、FAIR装置上的CBM/Hades有一定重叠, 与STAR BES-II的实验结果形成碰撞能量上的衔接.基于HIAF的核核碰撞可以产生密度为3—5倍饱和密度、温度约80 MeV的核物质, 这对研究核物质状态方程、QCD相结构、超核等提供 了良好的机遇. 在HIAF装置上预留了一个高能 实验大厅(见图34), 其中包括2个高能实验终 端和1个高能粒子束应用实验终端. 这两个高能终端上将开展基于pp, pA和AA的碰撞实验, 开展核物质相结构、状态方程、强子物理、超核等前沿课题的实验研究. 在实验谱仪的规划方面, 升级后的CEE谱仪(CEE+)、中国超核谱仪(CHNS)、由RIKEN的超核团队设计的超核研究装置[122]、基于次级介子束流的实验装置都还处于概念设计阶段.
-
由于核物质状态方程是强相互作用粒子在不同热力学或者外部条件下的系统宏观量之间的表达, 这对于理解强相互作用的理论, 理解EoS相关的物理现象(如种子皮)、过程(如早期宇宙演化)或者对象(如中子星)的性质具有重要意义, 因此核物质状态方程研究是核物理研究的重大前沿课题之一. 重离子碰撞是实验室产生高密核物质的唯一手段, 本文主要从实验者角度介绍了实验室重离子碰撞运动学变量(观测量)与核物质状态方程的联系、核物质状态方程当前的研究现状和一些我们认为重要的结果, 并介绍了未来几年国际上在建实验装置的进展.
基于SIS18加速器和AGS加速器的实验数据给出2—4.5倍饱和密度对称核物质的状态方程偏软, 对应饱和密度处的不可压缩系数
$ K_0 $ 的范围是(230 ± 20) MeV. 对于同位旋不对称核物质, 综合地面实验和天文中子星观测数据后得出的状态方程参数的差别仍然较大. 李宝安等给出在饱和密度处的对称能参数为:$ E_{\text{sym}}(\rho_0) = (31.6\pm2.7 )$ MeV, 斜率$ L_{\text{sym}} = (58.9\pm16 )$ MeV,$ K_{\text{sym}} = (-107\pm88) $ MeV. 基于$ {\pi}^-/{\pi}^+ $ 产额比所提取的对称能参数具有很强的模型依赖性, 有待输运模型发展来消除模型之间的不一致性. 基于Pb中子皮测量结果则要求非对称核物质在饱和密度处是硬的EoS. 实验上唯一中子的集体流测量来自FOPI-LAND实验的400 MeV/u的Au+Au碰撞, 实验结果结合TuQMD模型和UrQMD模型计算, 对于大于饱和密度区的对称能参数给出了一定约束. 在更高密度区, 对称能的限制则来自天文观测数据的中子星质量、中子星半径和双中子星合并中引力波. 因此, 在积累更多天文观测数据的同时, 积累更高质量、大统计量、包括中子测量的高重子密度区重离子碰撞实验数据就显得尤为重要. 实验上就必须要提高精度、计数率和实验效率(如CBM实验和ALICE实验将要采用的无触发系统). 这样的实验可以给出不同粒子的产额和集体流随碰撞中心度、横动量、快度等的变化. 这些多维度的数据自然就对输运模型提出了自洽描述的要求.本文所讨论的研究状态方程的场景中, 比如高重子密度区重离子碰撞和双中子星并合中, 所产生的极端核物质的温度可能会达到约100 MeV, 而(1)式中的展开是在零温近似下的EoS表达, 一个自然的问题就是在有限温情况下核物质状态方程参数的取值, 甚至EoS的表达形式是否有效? 在重离子碰撞提取状态方程参数时, 输运模型中的EoS的行为与(1)式中的形式等价, 体系的温度效应(体系内粒子运动速度的分布)在输运模型中通过粒子之间微观相互作用自动产生. 通常一个合理的输运模型要求能够描述不同粒子的产额(化学温度)以及他们的横动量的分布(动力学温度), 因此本文讨论的EoS的参数在限温体系中的定义是一致的. 而在有些场景, 比如双中子星并合事件中, 采用输运过程来模拟双中子星并合的过程是不现实的, 这就需要在EoS的展开中除了密度、同位旋不对称度, 还需要考虑温度的贡献. 有限温情况下EoS依据密度、同位旋不对称、温度做泰勒展开的数学形式尚未达成共识, 最新关于此类展开尝试还在发展中, 如文献[123]. 除了前文讨论的EoS与密度、同位旋不对称度、温度、超子-核子相互作用的贡献, 核物质状态方程还可能依赖系统所处的外部条件, 如强磁场、强涡旋等, 相关研究的最新进展请参考文献[124]. 另外, 近些年我国研究人员在核核碰撞中粒子自旋效应的理论研究和实验研究中发挥了重要作用[125–127], 这些研究表明, 重离子碰撞演化过程中自旋核手征效应或许能对核物质状态方程的研究提供新的自由度和实验可观测量. 2023年, 国内专家组织了关于高能重离子碰撞过程的自旋与手征效应最新研究进展的专刊[128], 其中文献[129–131]讨论了粒子自旋效应在核物质状态方程中可能存在的效应. 这里需要指出的是, 虽然EoS可有不同的展开形式, 如多阶展开、多变量的展开等, 但是尝试提取所有高阶数的参数展开项系数在实验上是不现实的. 如何基于EoS的参数化形式, 来给出更简洁或者更解析的EoS表达, 将是人们理解强相互作用性质的重大突破, 当前迅速发展的人工智能或许能为解决这个问题发挥关键作用.
未来几年, 在高重子数密度区重离子碰撞研究上会有新的实验数据陆续公布, 比如来自SISI8上运行的HADES实验、NICA装置上的BM@N实验、HIRFL装置上的CEE实验、STAR-BESII的固定靶实验数据等, 这些高精度且多维度(比如产额、集体流等随中心度、快度、横动量等)的实验数据, 将对核物质状态方程在高密区的行为产生强有力的约束. 随着高质量的实验数据陆续公布和TEMP合作组推进的输运模型发展计划, 输运模型之间的差异将逐渐缩小. 这对于提取核物质状态的参数具有至关重要的意义. 我国在建的基于HIRFL-CSR装置的CEE谱仪将于2025年开始运行, 标志着我国可以自主开展1—2倍饱和密度区、温度约为40 MeV的核物质性质研究: 包括核物质状态方程、相结构、短程关联等. 将于2025年建成的HIAF装置, 为研究极端核物质性质相关的前沿课题——包含奇异夸克自由度的核物质状态方程、强子的介质效应、超核极化、发现新超核和多超子超核、核介质依赖YN相互作用、自旋效应等尚未被人们充分认识的领域提供绝佳研究机遇.
中高能重离子碰撞与核物质状态方程研究
Intermediate/high-energy heavy-ion collisions and nuclear matter equation of state
-
摘要: 核物质状态方程是对核物质体系在不同热力学或者外场条件下的宏观性质的描述, 它对理解微观强相互作用的理论——量子色动力学(QCD)、原子核性质、重离子碰撞动力学、致密天体内部结构、双中子星合并等具有重要意义. 重离子碰撞(HICs)是在实验室产生极端条件(如高温、高密、强磁场、强涡旋等)核物质的唯一手段, 不同碰撞能量的HICs为定量研究核物质在不同热力学条件下的性质提供了可能. 本文主要介绍当前核物质状态方程的研究现状, 并介绍HICs中对核物质状态方程敏感的基本可观测量、探索核物质状态的典型实验和结果. 展现包含有奇异强子核物质状态方程的研究进展, 并探讨未来可能的研究方向. 介绍国际上在建和正在运行的重离子加速器和实验谱仪的最新进展, 包括我国已经建成的兰州重离子加速器装置(HIRFL)和兰州重离子加速器装置-冷却储存环(HIRFL-CSR)、在建的强流重离子加速器装置(HIAF)和在建的低温高密核物质测量谱仪的研制进展, 并讨论未来基于我国大科学装置开展核物质状态方程实验研究的机遇与挑战.
-
关键词:
- 核物质状态方程 /
- 重离子碰撞 /
- 兰州重离子加速器装置-冷却储存环(HIRFL-CSR) /
- 强流重离子加速器装置(HIAF)
Abstract: The equation of state (EoS) of nuclear matter is a description of the macroscopic properties of nuclear matter under different thermodynamic conditions or external fields, which is critical for understanding the theory of the strong interaction—quantum chromodynamics (QCD), the nature of nuclei, the dynamics of heavy-ion collisions (HICs), the internal structure of compact stars, the merger of binary neutron stars, and other physical phenomena. Heavy-ion collisions (HICs) are the only method in laboratories to create nuclear matter with extreme conditions such as high temperatures and high densities. HICs at different energy levels offer the possibility to quantitatively study the properties of nuclear matter under diverse thermodynamic conditions. This paper mainly presents the current research status of the EoS of nuclear matter and introduces the fundamental observables in HICs that are sensitive to the EoS, as well as the typical experiments and results used to explore the EoS. The progress in studying the EoS containing strangeness is also described and its possible research directions in the future are also discussed. The status and progress of worldwide heavy-ion accelerators and experimental spectrometers in the high-baryon density region are introduced, including China’s large-scale scientific facilities, i.e HIRFL-CSR and HIAF, as well as the CEE experiment. Additionally, the opportunities and challenges for experimental research on the EoS of nuclear matter in China are discussed.-
Key words:
- equation of state (EoS) /
- heavy-ion collisions /
- HIRFL-CSR /
- HIAF .
-

-
图 3 地面重离子碰撞实验和天文观测提取到
$ E_\text{sym}(\rho_0) $ (a)和$ L_\text{sym}(\rho_0) $ (b)的结果. 图(a)和图(b)均取自文献[24]Figure 3.
$ E_\text{sym}(\rho_0) $ (a) and$ L_\text{sym}(\rho_0) $ (b) extracted from terrestrial heavy-ion experiments and astrophysical observations respectively. Panel (a) and panel (b) both are taken from Ref. [24].图 10 KaoS实验测量
$ {\mathrm{K}}^+ $ 介子在Au+Au和Cu+Cu碰撞中产额比随碰撞能量的变化, 来自输运模型IQMD和RQMD的硬EoS和软EoS分别用短线和点线表示. 图片取自文献[50]Figure 10. Yield ratio of
$ {\mathrm{K}}^+ $ in Au+Au and Cu+Cu collisions as a function of collision energy measured by the KaoS experiment. The hard and soft EoS from the transport models IQMD and RQMD are represented by dashed and dotted lines, respectively. Figure taken from Ref. [50].图 11 FOPI实验测量0.4, 1.0和1.5 GeV/u的Au+Au碰撞中质子和氘核的椭圆流随快度的变化, 基于IQMD模型硬EoS和软EoS理论计算结果分别用虚线和实线表示. 图片取自文献[56]
Figure 11. Elliptic flow of proton and deuteron as a function of rapidity in Au+Au collisions at 0.4, 1.0, and 1.5 GeV/u mesured by the FOPI experiment, red dashed line and black line represent the IQMD predictions with hard EoS and soft EoS respectively. Figure taken from Ref. [56].
图 13 (a) 30 MeV/u的Ar+Au反应中, 轻带电粒子的约化中子丰度随实验室角度的变化关系, 曲线为理论模型计算结果; (b)轻核约化中子丰度小角度区的下降斜率(红色区域)与理论计算(空心圆圈)的比较. 图片取自文献[58]
Figure 13. (a) In 30 meV/u Ar+Au reactions,
$ Y_{{\mathrm{n, ex}}}/Y_{{\mathrm{p, CL}}} $ as a function of polar angle, curves are theoretical calculations; (b) comparison the slope of$ Y_{{\mathrm{n, ex}}}/Y_{{\mathrm{p, CL}}} $ in$ \theta_{{\mathrm{lab}}}<100^{\circ} $ from experiment (red band) and theoretical predictions (open circles). Figure taken from Ref. [58]图 15 不同的实验和理论给出的对称能参数
$ L_\text{sym}-J_\text{sym} $ 的限制, 黑色空心圈为PREX-II测量结果, 红色实线和虚线表示其他实验中提取的$ L_\text{sym} = (58.9\pm16 )$ MeV的中心值和误差. 图片更新自文献[63]Figure 15. Constraints on symmetry energy parameters
$ L_\text{sym}-J_\text{sym} $ , open circle presents the results of PREX-II experiment, solid and dashed horizontal lines represent the central value and error of$ L_\text{sym} = (58.9\pm16 )$ MeV, respectively. Figure was taken and updated from Ref. [63].图 18 400 MeV/u的Au+Au半中心碰撞(b < 7.5 fm)中ASY-EOS实验测量到的中子和带电粒子椭圆流的比值
$ v_2^{\mathrm{n}}/v_2^{{\mathrm{ch}}} $ 和横动量的关联(黑色方框), 三角和圆分别代表UrQMD在硬($ \gamma = 1.5 $ )和软($ \gamma = 0.5 $ )对称能时计算结果, 实线是对理论计算结果做线性延拓, 得到与实验数据符合得最好时$ \gamma = 0.75\pm0.1 $ . 图片取自文献[68]Figure 18. Elliptic flow ratio of neutron and charged particle as a function of transverse momentum, in semi-central Au+Au collisions (b < 7.5 fm) at 400 MeV/u measured by ASY-EoS experiment. Triangles and squares are UrQMD predictions with hard (
$ \gamma = 1.5 $ ) and soft ($ \gamma = 0.5 $ ) symmetry energy, solid line is the linear interpolation of predictions which can describe the data best, correspond to$ \gamma = 0.75\pm0.1 $ . Figure taken from Ref. [68]图 19 FOPI实验测量400 MeV/u的核核中心碰撞中
$ {\pi}^-/{\pi}^+ $ 产额比对碰撞系统N/Z的依赖(空心菱形)和IBUU04模型在x = 1.0 (软EoS)、0.5 (中等EoS)和0 (硬EoS)模拟结果比较, 图片取自文献[72]Figure 19.
$ {\pi}^-/{\pi}^+ $ yield ratio measured the FOPI experiment in central nucleus-nucleus collisions at 400 MeV/u as a function of N/Z ratio of the colliding systems (open diamonds), and compared simulation results from the IBUU04 model for x = 1.0 (soft EoS), 0.5 (medium EoS), and 0 (hard EoS). Figure taken from Ref. [72]图 20 HADES实验(方框)、FOPI实验(圆点)、Stream chamber(三角)和E895(五角星)测量到的约化π多重数与
$ \langle {A}_\text{part}\rangle $ 的关系. 图片取自文献[81]Figure 20. π multiplicity measured by HADES (squares), FOPI (filled circles), Stream chamber (triangles), and E895 experiment (star) as a function of
$ \langle {A}_\text{part} \rangle $ . Figure taken from Ref. [81]图 23 (a) SπRIT实验测量270 MeV/u时, 不同Sn+Sn碰撞系统
$ {\pi}^-/{\pi}^+ $ 产额比; (b)系统132Sn+124Sn和108Sn+112Sn系统双$ \pi^-/\pi^+ $ 产额比; 7个输运模型计算结果用不同颜色标记. 图片取自文献[88]Figure 23. (a)
$ \pi^-/\pi^+ $ yield ratio measured by the SπRIT experiment in Sn+Sn collisions with different N/Z ratio; (b) double${\pi}^-/{\pi}^+ $ yield ratio in 132Sn+124Sn and 108Sn+112Sn, results from 7 transport models are marked by bands with different color. Figure taken from Ref. [88]图 24 中子星质量(M)和半径(R)的关系, 其中绿色区域为核物质, 红色区域代表在核物质基础上再加入
$ {\Lambda}{\mathrm{N}} $ 相互作用后中子星的M-R关系, 其中考虑了两种都可以描述超核数据的YNN相互作用. 图片取自文献[96]Figure 24. The relationship between the mass (M) and radius (R) of a neutron star, where the green region represents pure nuclear matter, and the red region shows the M-R relationship of neutron stars after incorporating ΛN interactions on top of the nuclear matter, considering two types of YNN interactions that can both describe hyper-nuclear data. Figure taken from Ref. [96]
图 28 从能量为
$ \sqrt{s_{{\mathrm{NN}}}} = 2—5020 $ GeV重离子碰撞数据中提取到的化学冻出温度(T)和重子化学势($ \mu_{\mathrm{B}} $ ). 图片取自文献[108]Figure 28. Chemical freeze-out temperature (T) and baryon chemical potential (
$ \mu_{\mathrm{B}} $ ) extracted from HICs with colliding energy$ \sqrt{s_{{\mathrm{NN}}}} = 2-5020 $ GeV. Figure taken from Ref. [108]表 1 世界上重离子加速器与其典型实验, 基于文献[108]数据扩充
Table 1. Heavy-ion accelerator in the world and its typical Experiments, expanded based on data listed in Ref. [108]
Facility $ \sqrt{s_{{\mathrm{NN}}}} $ /GeVPeriod Experiments Bevalac 2.0—2.7 1975-1993 EOS/et al. SIS18 2.4—2.7 1990—now FOPI/Hades/et al. FRIB 1.9—2.1 >2025 AT-TPC $ ^* $ RIBF 1.9—2.1 1986—now SπRIT RAON 1.9—2.0 >2030 LAMPS HIRFL 2.0—2.4 2008—now CEE/ETE Nuclotron 2.0—3.5 2000—now BM@N JPARC-HI 2.0—6.2 >2030 DHS SIS100 2.7—5.0 >2029 CBM/Hades NICA 2.7—11.0 >2025 BM@N/MPD RHIC 3.0—200 2000—2025 STAR SPS 4.5—17.3 1981—now NA49/NA61/SHINE AGS 2.7—4.8 2022—now E895/et al. HIAF 2.2—3.5 >2027 CEE+/CHNS LHC 2760 2018—now ALICE LHC 72 >2027 LHCb/ALICE-FT -
[1] Wilson K G 1974 Phys. Rev. D 10 2445 doi: 10.1103/PhysRevD.10.2445 [2] Ishii N, Aoki S, Hatsuda T 2007 Phys. Rev. Lett. 99 022001 doi: 10.1103/PhysRevLett.99.022001 [3] Inoue T 2021 Few-Body Syst. 62 106 doi: 10.1007/s00601-021-01685-2 [4] Nemura H 2011 Few-Body Syst. 50 105 doi: 10.1007/s00601-011-0215-z [5] Pásztor A 2024 EPJ Web Conf. 296 01009 doi: 10.1051/epjconf/202429601009 [6] Weinberg S 1979 Physica A 96 327 doi: 10.1016/0378-4371(79)90223-1 [7] Weinberg S 1991 Nucl. Phys. B 363 3 doi: 10.1016/0550-3213(91)90231-L [8] Drischler C, Holt J W, Wellenhofer C 2021 Ann. Rev. Nucl. Part. Sci. 71 403 doi: 10.1146/annurev-nucl-102419-041903 [9] Machleidt R, Sammarruca F 2016 Phys. Scr. 91 083007 doi: 10.1088/0031-8949/91/8/083007 [10] Drischler C, Hebeler K, Schwenk A 2016 Phys. Rev. C 93 054314 doi: 10.1103/PhysRevC.93.054314 [11] Lee D 2009 Prog. Part. Nucl. Phys. 63 117 doi: 10.1016/j.ppnp.2008.12.001 [12] Elhatisari S, Bovermann L, Ma Y, et al. 2024 Nature 630 59 doi: 10.1038/s41586-024-07422-z [13] 马远卓, 吕炳楠, 李宁, 王倩 2024 原子核物理评论 41 172 doi: 10.11804/NuclPhysRev.41.2023CNPC77 Ma Y Z, Lv B N, Li N, Wang Q 2024 Nucl. Phys. Rev. 41 172 doi: 10.11804/NuclPhysRev.41.2023CNPC77 [14] Luo X, Shi S, Xu N, Zhang Y 2020 Particles 3 278 doi: 10.3390/particles3020022 [15] Borsanyi S, Fodor Z, Guenther J N, Kara R, Katz S D, Parotto P, Pasztor A, Ratti C, Szabo K K 2020 Phys. Rev. Lett. 125 052001 doi: 10.1103/PhysRevLett.125.052001 [16] Andronic A, Braun-Munzinger P, Redlich K, Stachel J 2018 Nature 561 321 doi: 10.1038/s41586-018-0491-6 [17] McLerran L, Pisarski R D 2007 Nucl. Phys. A 796 83 doi: 10.1016/j.nuclphysa.2007.08.013 [18] Weber F 2001 J. Phys. G 27 465 doi: 10.1088/0954-3899/27/3/326 [19] Demorest P, Pennucci T, Ransom S, Roberts M, Hessels J 2010 Nature 467 1081 doi: 10.1038/nature09466 [20] Romani R W, Kandel D, Filippenko A V, Brink T G, Zheng W 2022 Astrophys. J. Lett. 934 L17 doi: 10.3847/2041-8213/ac8007 [21] Miller M C, Lamb F K, Dittmann A J, Bogdanov S, Arzoumanian Z, Gendreau K C, Guillot S, Harding A K, Ho W C G, Lattimer J M, Ludlam R M, Mahmoodifar S, Morsink S M, Ray P S, Strohmayer T E, Wood K S, Enoto T, Foster R, Okajima T, Prigozhin G, Soong Y 2019 Astrophys. J. Lett. 887 L24 doi: 10.3847/2041-8213/ab50c5 [22] Miller M C, Lamb F K, Dittmann A J, Bogdanov S, Arzoumanian Z, Gendreau K C, Guillot S, Ho W C G, Lattimer J M, Loewenstein M, Morsink S M, Ray P S, Wolff M T, Baker C L, Cazeau T, Manthripragada S, Markwardt C B, Okajima T, Pollard S, Cognard I, Cromartie H T, Fonseca E, Guillemot L, Kerr M, Parthasarathy A, Pennucci T T, Ransom S, Stairs I 2021 Astrophys. J. Lett. 918 L28 doi: 10.3847/2041-8213/ac089b [23] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2017 Phys. Rev. Lett. 119 161101 doi: 10.1103/PhysRevLett.119.161101 [24] Li B A, Krastev P G, Wen D H, Zhang N B 2019 Eur. Phys. J. A 55 117 doi: 10.1140/epja/i2019-12780-8 [25] LIGO Scientific and Virgo Collaboration, Abbott B P, et al. 2018 Phys. Rev. Lett. 121 161101 doi: 10.1103/PhysRevLett.121.161101 [26] Alvarez-Castillo D E, Blaschke D B, Grunfeld A G, Pagura V P 2019 Phys. Rev. D 99 063010 doi: 10.1103/PhysRevD.99.063010 [27] Li B A, Cai B J, Xie W J, Zhang N B 2021 Universe 7 182 doi: 10.3390/universe7060182 [28] HADES Collaboration, Adamczewski-Musch J, et al. 2019 Nature Phys. 15 1040 doi: 10.1038/s41567-019-0583-8 [29] Fuchs C, Wolter H H 2006 Eur. Phys. J. A 30 5 doi: 10.1140/epja/i2005-10313-x [30] Garg U, Colò G 2018 Prog. Part. Nucl. Phys. 101 55 doi: 10.1016/j.ppnp.2018.03.001 [31] Margueron J, Hoffmann Casali R, Gulminelli F 2018 Phys. Rev. C 97 025805 doi: 10.1103/PhysRevC.97.025805 [32] Li B A, Cai B J, Chen L W, Xie W J, Xu J, Zhang N B 2022 Nuovo Cimento C 45 54 [33] Bleicher M, Zabrodin E, Spieles C, Bass S, Ernst C, Soff S, Bravina L, Belkacem M, Weber H, Stöcker H, Greiner W 1999 J. Phys. G 25 1859 doi: 10.1088/0954-3899/25/9/308 [34] Sorensen A, Agarwal K, Brown K W, Chajęcki Z, Danielewicz P, Drischler C, Gandolfi S, Holt J W, Kaminski M, Ko C M, Kumar R, Li B A, Lynch W G, McIntosh A B, Newton W G, Pratt S, Savchuk O, Stefaniak M, Tews I, Tsang M B, Vogt R, Wolter H, Zbroszczyk H, Abbasi N, Aichelin J, Andronic A, Bass S A, Becattini F, Blaschke D, Bleicher M, Blume C, Bratkovskaya E, Brown B A, Brown D A, Camaiani A, Casini G, Chatziioannou K, Chbihi A, Colonna M, Cozma M D, Dexheimer V, Dong X, Dore T, Du L, Dueñas J A, Elfner H, Florkowski W, Fujimoto Y, Furnstahl R J, Gade A, Galatyuk T, Gale C, Geurts F, Gramegna F, Grozdanov S, Hagel K, Harris S P, Haxton W, Heinz U, Heller M P, Hen O, Hergert H, Herrmann N, Huang H Z, Huang X G, Ikeno N, Inghirami G, Jankowski J, Jia J, Jiménez J C, Kapusta J, Kardan B, Karpenko I, Keane D, Kharzeev D, Kugler A, Le Fèvre A, Lee D, Liu H, Lisa M A, Llope W J, Lombardo I, Lorenz M, Marchi T, McLerran L, Mosel U, Motornenko A, Müller B, Napolitani P, Natowitz J B, Nazarewicz W, Noronha J, Noronha-Hostler J, Odyniec G, Papakonstantinou P, Paulínyová Z, Piekarewicz J, Pisarski R D, Plumberg C, Prakash M, Randrup J, Ratti C, Rau P, Reddy S, Schmidt H R, Russotto P, Ryblewski R, Schäfer A, Schenke B, Sen S, Senger P, Seto R, Shen C, Sherrill B, Singh M, Skokov V, Spaliński M, Steinheimer J, Stephanov M, Stroth J, Sturm C, Sun K J, Tang A, Torrieri G, Trautmann W, Verde G, Vovchenko V, Wada R, Wang F, Wang G, Werner K, Xu N, Xu Z, Yee H U, Yennello S, Yin Y 2024 Prog. Part. Nucl. Phys. 134 104080 doi: 10.1016/j.ppnp.2023.104080 [35] Voloshin S, Zhang Y 1996 Z. Phys. C 70 665 doi: 10.1007/s002880050141 [36] HADES Collaboration, Adamczewski-Musch J, et al. 2023 Eur. Phys. J. A 59 80 doi: 10.1140/epja/s10050-023-00936-6 [37] ALICE Collaboration, Aamodt K, et al. 2010 Phys. Rev. Lett. 105 252302 doi: 10.1103/PhysRevLett.105.252302 [38] Herrmann N, Wessels J P, Wienold T 1999 Ann. Rev. Nucl. Part. Sci. 49 581 doi: 10.1146/annurev.nucl.49.1.581 [39] Danielewicz P, Lacey R, Lynch W G 2002 Science 298 1592 doi: 10.1126/science.1078070 [40] Herrmann N 2022 EPJ Web Conf. 259 09001 doi: 10.1051/epjconf/202225909001 [41] MPD Collaboration, Abgaryan V, et al. 2022 Eur. Phys. J. A 58 140 doi: 10.1140/epja/s10050-022-00750-6 [42] Guo D, He X, Li P, Qin Z, Hu C, Wang B, Zhou Y, Zheng K, Zhang Y, Wei X, Yang H, Hu D, Shao M, Duan L, Yu Y, Sun Z, Wang Y, Li Q, Xiao Z 2024 Eur. Phys. J. A 60 36 doi: 10.1140/epja/s10050-024-01245-2 [43] Brown B A, Gade A, Stroberg S R, Escher J, Fossez K, Giuliani P, Hoffman C R, Nazarewicz W, Seng C Y, Sorensen A, Vassh N, Bazin D, Brown K W, Capri M A, Crawford H, Danielewic P, Drischler C, Garcia Ruiz R F, Godbey K, Grzywacz R, Hlophe L, Holt J W, Iwasaki H, Lee D, Lenzi S M, Liddick S, Lubna R, Macchiavelli A O, Martinez Pinedo G, McCoy A, Mercenne A, Minamisono K, Monteagudo B, Navratil P, Ringle R, Sargsyan G, Schatz H, Spieker M C, Volya A, Zegers R G, Zelevinsky V, Zhang X 2025 J. Phys. G 52 050501 [44] SπRIT Collaboration Shane R, et al. 2015 Nucl. Instrum. Meth. A 784 513 doi: 10.1016/j.nima.2015.01.026 [45] Hong B, Ahn D, Ahn J, Bae J, Bae Y, Bok J, Choi S, Do S, Heo C, Huh J, Hwang J, Jang Y, Kang B, Kim A, Kim B, Kim C, Kim E J, Kim G, Kim G, Kim H, Kim J, Kim J, Kim S, Kim Y, Kim Y, Kim Y, Kim Y, Kweon M, Lee C, Lee H, Lee H, Lee H, Lee J, Lee J, Lee J W, Lee J, Lee S, Lee S, Lim S, Moon D, Nam S, Park J, Park J, Seo J, Yang H 2023 Nucl. Instrum. Methods Phys. Res., Sect. B 541 260 doi: 10.1016/j.nimb.2023.05.030 [46] STAR Collaboration, Abdallah M S, et al. 2022 Phys. Lett. B 827 137003 doi: 10.1016/j.physletb.2022.137003 [47] Li B A 2002 Phys. Rev. Lett. 88 192701 doi: 10.1103/PhysRevLett.88.192701 [48] Chen L W, Ko C M, Li B A 2003 Nucl. Phys. A 729 809 doi: 10.1016/j.nuclphysa.2003.09.010 [49] Yong G C, Li B A, Xiao Z G, Lin Z W 2022 Phys. Rev. C 106 024902 doi: 10.1103/PhysRevC.106.024902 [50] Hartnack C, Oeschler H, Leifels Y, Bratkovskaya E L, Aichelin J 2012 Phys. Rep. 510 119 doi: 10.1016/j.physrep.2011.08.004 [51] Gustafsson H A, Gutbrod H H, Kolb B, Löhner H, Ludewigt B, Poskanzer A M, Renner T, Riedesel H, Ritter H G, Warwick A, Weik F, Wieman H 1984 Phys. Rev. Lett. 52 1590 doi: 10.1103/PhysRevLett.52.1590 [52] EOS Colllaboration, Partlan M D, et al. 1995 Phys. Rev. Lett. 75 2100 doi: 10.1103/PhysRevLett.75.2100 [53] E895 Collaboration, Liu H, et al. 2000 Phys. Rev. Lett. 84 5488 doi: 10.1103/PhysRevLett.84.5488 [54] E877 Collaboration, Barrette J, et al. 1997 Phys. Rev. C 56 3254 doi: 10.1103/PhysRevC.56.3254 [55] FOPI Collaboration, Gobbi A, et al. 1993 Nucl. Instrum. Meth. A 324 156 doi: 10.1016/0168-9002(93)90974-M [56] FOPI Collaboration, Reisdorf W, et al. 2012 Nucl. Phys. A 876 1 doi: 10.1016/j.nuclphysa.2011.12.006 [57] Xu H, Tsang M, Liu T, Liu X, Lynch W, Tan W, Verde G, VanderMolen A, Wagnera A, Xib H, Gelbke C, Beaulieu L, Davin B, Larochellec Y, Lefort T, de Souza R, Yanez R, Viola V, Charity R, Sobotka L 2000 Phys. Rev. Lett. 85 716 doi: 10.1103/PhysRevLett.85.716 [58] Zhang Y, Tian J, Cheng W, Guan F, Huang Y, Li H, Lü L, Wang R, Wang Y, Wu Q, Yi H, Zhang Z, Zhao Y, Duan L, Hu R, Huang M, Jin G, Jin S, Lu C, Ma J, Ma P, Wang J, Yang H, Yang Y, Zhang J, Zhang Y, Zhang Y, Ma C, Qiao C, Tsang M B, Xiao Z 2017 Phys. Rev. C 95 041602 [59] Roca-Maza X, Centelles M, Vinas X, Warda M 2011 Phys. Rev. Lett. 106 252501 doi: 10.1103/PhysRevLett.106.252501 [60] Zhang W 2023 Ph. D. Dissertation (New York: Stony Brook University [61] Donnelly T W, Dubach J, Sick I 1989 Nucl. Phys. A 503 589 doi: 10.1016/0375-9474(89)90432-6 [62] PREX Collaboration, Adhikari D, et al. 2021 Phys. Rev. Lett. 126 172502 doi: 10.1103/PhysRevLett.126.172502 [63] Reed B T, Fattoyev F J, Horowitz C J, Piekarewicz J 2021 Phys. Rev. Lett. 126 172503 doi: 10.1103/PhysRevLett.126.172503 [64] FOPI Collaboration Y Leifels, et al. 1993 Phys. Rev. Lett. 71 963 doi: 10.1103/PhysRevLett.71.963 [65] LAND Collaboration, Blaich T, et al. 1992 Nucl. Instrum. Meth. A 314 136 doi: 10.1016/0168-9002(92)90507-Z [66] Russotto P, Wu P, Zoric M, Chartier M, Leifels Y, Lemmon R, Li Q, Lukasik J, Pagano A, Pawlowski P, Trautmann W 2011 Phys. Lett. B 697 471 doi: 10.1016/j.physletb.2011.02.033 [67] Cozma M D, Leifels Y, Trautmann W, Li Q, Russotto P 2013 Phys. Rev. C 88 044912 doi: 10.1103/PhysRevC.88.044912 [68] Russotto P, Gannon S, Kupny S, Lasko P, Acosta L, Adamczyk M, Al-Ajlan A, Al-Garawi M, Al-Homaidhi S, Amorini F, Auditore L, Aumann T, Ayyad Y, Basrak Z, Benlliure J, Boisjoli M, Boretzky K, Brzychczyk J, Budzanowski A, Caesar C, Cardella G, Cammarata P, Chajecki Z, Chartier M, Chbihi A, Colonna M, Cozma M D, Czech B, De Filippo E, Di Toro M, Famiano M, Gašparić I, Grassi L, Guazzoni C, Guazzoni P, Heil M, Heilborn L, Introzzi R, Isobe T, Kezzar K, Kiš M, Krasznahorkay A, Kurz N, La Guidara E, Lanzalone G, Le Fèvre A, Leifels Y, Lemmon R C, Li Q F, Lombardo I, Lukasik J, Lynch W G, Marini P, Matthews Z, May L, Minniti T, Mostazo M, Pagano A, Pagano E V, Papa M, Pawlowski P, Pirrone S, Politi G, Porto F, Reviol W, Riccio F, Rizzo F, Rosato E, Rossi D, Santoro S, Sarantites D G, Simon H, Skwirczynska I, Sosin Z, Stuhl L, Trautmann W, Trifirò A, Trimarchi M, Tsang M B, Verde G, Veselsky M, Vigilante M, Wang Y, Wieloch A, Wigg P, Winkelbauer J, Wolter H H, Wu P, Yennello S, Zambon P, Zetta L, Zoric M 2016 Phys. Rev. C 94 034608 doi: 10.1103/PhysRevC.94.034608 [69] Gaitanos T, Di Toro M, Typel S, Baran V, Fuchs C, Greco V, Wolter H H 2004 Nucl. Phys. A 732 24 doi: 10.1016/j.nuclphysa.2003.12.001 [70] Li Q, Li Z, Soff S, Bleicher M, Stoecker H 2005 Phys. Rev. C 72 034613 doi: 10.1103/PhysRevC.72.034613 [71] FOPI Collaboration, Reisdorf W, et al. 2007 Nucl. Phys. A 781 459 doi: 10.1016/j.nuclphysa.2006.10.085 [72] Xiao Z, Li B A, Chen L W, Yong G C, Zhang M 2009 Phys. Rev. Lett. 102 062502 doi: 10.1103/PhysRevLett.102.062502 [73] Feng Z Q, Jin G M 2010 Phys. Lett. B 683 140 doi: 10.1016/j.physletb.2009.12.006 [74] Xie W J, Su J, Zhu L, Zhang F S 2013 Phys. Lett. B 718 1510 doi: 10.1016/j.physletb.2012.12.021 [75] Xu J, Chen L W, Tsang M B, Wolter H, Zhang Y X, Aichelin J, Colonna M, Cozma D, Danielewicz P, Feng Z Q, Le Fevre A, Gaitanos T, Hartnack C, Kim K, Kim Y, Ko C M, Li B A, Li Q F, Li Z X, Napolitani P, Ono A, Papa M, Song T, Su J, Tian J L, Wang N, Wang Y J, Weil J, Xie W J, Zhang F S, Zhang G Q 2016 Phys. Rev. C 93 044609 doi: 10.1103/PhysRevC.93.044609 [76] Xu J, Wolter H, Colonna M, Cozma M D, Danielewicz P, Ko C M, Ono A, Tsang M B, Zhang Y X, Cheng H G, Ikeno N, Kumar R, Su J, Zheng H, Zhang Z, Chen L W, Feng Z Q, Hartnack C, Le Fèvre A, Li B A, Nara Y, Ohnishi A, Zhang F S 2024 Phys. Rev. C 109 044609 doi: 10.1103/PhysRevC.109.044609 [77] E-0895 Collaboration, Klay J L, et al. 2003 Phys. Rev. C 68 054905 doi: 10.1103/PhysRevC.68.054905 [78] Wolf A, Appenheimer M, Averbeck R, Charbonnier Y, Diaz J, Doppenschmidt A, Hejny V, Hlavac S, Holzmann R, Kugler A, Lohner H, Marin A, Metag V, Novotny R, Ostendorf R, Pleskac R, Schubert A, Schutz Y, Simon R, Stratmann R, Stroher H, Tlusty P, Vogt P, Wagner V, Weiss J, Wilschut H, Wissmann F, Wolf M 1998 Phys. Rev. Lett. 80 5281 doi: 10.1103/PhysRevLett.80.5281 [79] Wagner A, Muntz C, Oeschler H, Sturm C T, Barth R, Cieslak M, Debowski M, Grosse E, Koczon P, Mang M, Miskowiec D, Schicker R, Schwab E, Senger P, Beckerle P, Brill D, Shin Y, Strobele H, Walus W, Kohlmeyer B, Puhlhofer F, Speer J, Volkel K 1998 Phys. Lett. B 420 20 doi: 10.1016/S0370-2693(97)01549-9 [80] HADES Collaboration, Agakishiev G, et al. 2009 Eur. Phys. J. A 41 243 doi: 10.1140/epja/i2009-10807-5 [81] HADES Collaboration, Adamczewski-Musch J, et al. 2020 Eur. Phys. J. A 56 259 doi: 10.1140/epja/s10050-020-00237-2 [82] Kubo T, Ishihara M, Inabe N, Kumagai H, Tanihata I, Yoshida K, Nakamura T, Okuno H, Shimoura S, Asahi K 1992 Nucl. Instrum. Methods Phys. Res., Sect. B 70 309 [83] Motobayashi T 2010 Nucl. Phys. A 834 707c doi: 10.1016/j.nuclphysa.2010.01.128 [84] Kurata-Nishimura M 2017 Proceedings of Science INPC2016 p218 [85] Barney J, Estee J, Lynch W, Isobe T, Jhang G, Kurata-Nishimura M, McIntosh A, Murakami T, Shane R, Tangwancharoen S, Tsang M, Cerizza G, Kaneko M, Lee J, Tsang C, Wang R, Anderson C, Baba H, Chajecki Z, Famiano M, Hodges-Showalter R, Hong B, Kobayashi T, Lasko P, Łukasik J, Nakatsuka N, Olsen R, Otsu H, Pawłowski P, Pelczar K, Powell W, Sakurai H, Santamaria C, Setiawan H, Taketani A, Winkelbauer J, Xiao Z, Yennello S, Yurkon J, Zhang Y 2021 Rev. Sci. Instrum. 92 063302 doi: 10.1063/5.0041191 [86] Lasko P, Adamczyk M, Brzychczyk J, Hirnyk P, Łukasik J, Pawłowski P, Pelczar K, Snoch A, Sochocka A, Sosin Z, Barney J, Cerizza G, Estee J, Isobe T, Jhang G, Kaneko M, Kurata-Nishimura M, Lynch W, Murakami T, Santamaria C, Tsang M, Zhang Y 2017 Nucl. Instrum. Meth. A 856 92 doi: 10.1016/j.nima.2017.03.006 [87] Barney J E 2019 Ph. D. Dissertation (East Lansing: Michigan State University [88] SπRIT & TEMP Collaboration, Jhang G, et al. 2021 Phys. Lett. B 813 136016 doi: 10.1016/j.physletb.2020.136016 [89] Yong G C 2021 Phys. Rev. C 104 014613 doi: 10.1103/PhysRevC.104.014613 [90] Glendenning N K 1982 Phys. Lett. B 114 392 doi: 10.1016/0370-2693(82)90078-8 [91] Millener D J, Dover C B, Gal A 1988 Phys. Rev. C 38 2700 doi: 10.1103/PhysRevC.38.2700 [92] Gal A, Hungerford E V, Millener D J 2016 Rev. Mod. Phys. 88 035004 doi: 10.1103/RevModPhys.88.035004 [93] Schaffner J, Mishustin I N 1996 Phys. Rev. C 53 1416 doi: 10.1103/PhysRevC.53.1416 [94] Schaffner-Bielich J 2010 Nucl. Phys. A 835 279 doi: 10.1016/j.nuclphysa.2010.01.203 [95] Yong G C 2023 Phys. Rev. D 108 L091507 doi: 10.1103/PhysRevD.108.L091507 [96] Lonardoni D, Lovato A, Gandolfi S, Pederiva F 2015 Phys. Rev. Lett. 114 092301 doi: 10.1103/PhysRevLett.114.092301 [97] Antoniadis J, Freire P C C, Wex N, Tauris T M, Lynch R S, van Kerkwijk M H, Kramer M, Bassa C, Dhillon V S, Driebe T, Hessels J W T, Kaspi V M, Kondratiev V I, Langer N, Marsh T R, McLaughlin M A, Pennucci T T, Ransom S M, Stairs I H, van Leeuwen J, Verbiest J P W, Whelan D G 2013 Science 340 6131 [98] Bombaci I 2017 JPS Conf. Proc. 17 101002 [99] Gerstung D, Kaiser N, Weise W 2020 Eur. Phys. J. A 56 175 doi: 10.1140/epja/s10050-020-00180-2 [100] Feng Z Q 2021 Eur. Phys. J. A 57 18 doi: 10.1140/epja/s10050-020-00305-7 [101] Ji Y 2024 EPJ Web Conf. 296 02004 doi: 10.1051/epjconf/202429602004 [102] STAR Collaboration, Aboona B, et al. 2023 Phys. Rev. Lett. 130 212301 doi: 10.1103/PhysRevLett.130.212301 [103] Oliinychenko D, Shen C, Koch V 2021 Phys. Rev. C 103 034913 doi: 10.1103/PhysRevC.103.034913 [104] Neidig T, Gallmeister K, Greiner C, Bleicher M, Vovchenko V 2022 Phys. Lett. B 827 136891 doi: 10.1016/j.physletb.2022.136891 [105] Sun K J, Wang R, Ko C M, Ma Y G, Shen C 2024 Nat. Commun. 15 1074 doi: 10.1038/s41467-024-45474-x [106] Coci G, Gläßel S, Kireyeu V, Aichelin J, Blume C, Bratkovskaya E, Kolesnikov V, Voronyuk V 2023 Phys. Rev. C 108 014902 doi: 10.1103/PhysRevC.108.014902 [107] Bruce R, Alemany Fernandez R, Argyropoulos T, Bartosik H, Bracco C, Cai R, D’ Andrea M, Frasca A, Hermes P, Jowett J, Mirarchi D, Redaelli S, Solfaroli M, Triantafyllou N, Wenninger J 2023 14th International Particle Accelerator Conference (IPAC 2023) Venice, Italy, May 7–12, 2023 pMOPL021 [108] Galatyuk T 2019 Nucl. Phys. A 982 163 doi: 10.1016/j.nuclphysa.2018.11.025 [109] Fu W J, Pawlowski J M, Rennecke F 2020 Phys. Rev. D 101 054032 doi: 10.1103/PhysRevD.101.054032 [110] Gunkel P J, Fischer C S 2021 Phys. Rev. D 104 054022 doi: 10.1103/PhysRevD.104.054022 [111] Hippert M, Grefa J, Manning T A, Noronha J, Noronha-Hostler J, Portillo Vazquez I, Ratti C, Rougemont R, Trujillo M 2024 Phys. Rev. D 110 094006 [112] Basar G 2024 Phys. Rev. C 110 015203 doi: 10.1103/PhysRevC.110.015203 [113] Odyniec G 2019 Proceedings of Science CORFU2018 p151 [114] Spiller P, Balss R, Bartolome P, Blaurock J, Blell U, Boine-Frankenheim O, Bozyk L, Chorowski M, Eisel T, Frey M, Giacomini T, Kaether F, Khodzhibagiyan H, Klammes S, Klingbeil H, Koenig H, Kornilov V, Kowina P, Lens D, Meier J, Ondreka D, Petzenhauser I, Plyusnin V, Pongrac I, Pyka N, Raginel V, Rottlaender P, Roux C, Schmidt J, Schwickert M, Sugita K, Szwangruber A, Szwangruber P, Trockel R, Waldt A, Welker H, Wilfert S, Winkler T, Winters D 2020 JINST 15 T12013 doi: 10.1088/1748-0221/15/12/T12013 [115] Friman B, Hohne C, Knoll J, Leupold S , Randrup J, Rapp R, Senger P 2011 The CBM Physics Book: Compressed Baryonic Matter in Laboratory Experiments (Berlin: Springer [116] Kapishin M 2019 Nucl. Phys. A 982 967 doi: 10.1016/j.nuclphysa.2018.07.014 [117] Sissakian A N, Kekelidze V D, Sorin A S 2009 Nucl. Phys. A 827 630C doi: 10.1016/j.nuclphysa.2009.05.138 [118] Ahn J K, Bak S I, Blumenfeld Y, et al. 2013 Few Body Syst. 54 197 doi: 10.1007/s00601-012-0359-5 [119] 夏佳文, 詹文龙, 魏宝文, 原有进, 赵红卫, 杨建成, 石健, 盛丽娜, 杨维青, 冒立军 2016 科学通报 61 467 Xia J W, Zhan W L, Wei B W, Yuan Y J, Zhao H W, Yant J C, Shi J, Sheng L N, Yang W Q, Mao L J 2016 Science Bulletin 61 467 [120] Yang J, Sun L, Yuan Y 2023 JACoW CYCLOTRONS2022 MOAI01 [121] Zhou X, Yang J 2022 AAPPS Bull. 32 35 doi: 10.1007/s43673-022-00064-1 [122] Saito T R, Dou W, Drozd V, et al. 2021 Nat. Rev. Phys. 3 803 doi: 10.1038/s42254-021-00371-w [123] Mroczek D, Yao N, Zine K, Noronha-Hostler J, Dexheimer V, Haber A, Most E R 2024 arXiv:2404.01658 [astro-ph.HE] [124] Huang M, Zhuang P 2023 Symmetry 15 541 doi: 10.3390/sym15020541 [125] Liang Z T, Wang X N 2005 Phys. Rev. Lett. 94 102301 [Erratum: Phys. Rev. Lett. 96 039901 (2006)] Liang Z T, Wang X N 2005 Phys. Rev. Lett. 94 102301 [Erratum: Phys. Rev. Lett. 96 039901 (2006)] [126] STAR Collaboration, Adamczyk L, et al. 2017 Nature 548 62 doi: 10.1038/nature23004 [127] STAR Collaboration, Abdallah M S, et al. 2023 Nature 614 244 doi: 10.1038/s41586-022-05557-5 [128] 梁作堂, 王群, 马余刚 2023 物理学报 72 070101 doi: 10.7498/aps.72.070101 Liang Z T, Wang Q, Ma Y G 2023 Acta Phys. Sin. 72 070101 doi: 10.7498/aps.72.070101 [129] 尹伊 2023 物理学报 72 111201 doi: 10.7498/aps.72.20222458 Yi Y 2023 Acta Phys. Sin. 72 111201 doi: 10.7498/aps.72.20222458 [130] 浦实, 黄旭光 2023 物理学报 72 071202 doi: 10.7498/aps.72.20230036 Pu S, Huang X G 2023 Acta Phys. Sin. 72 071202 doi: 10.7498/aps.72.20230036 [131] 江泽方, 吴祥宇, 余华清, 曹杉杉, 张本威 2023 物理学报 72 072504 doi: 10.7498/aps.72.20222391 Jiang F Z, Wu X Y, Yu Q H, Cao S S, Zhang B W 2023 Acta Phys. Sin. 72 072504 doi: 10.7498/aps.72.20222391 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: