-
激光技术在实现高精度目标测量方面发挥着至关重要的作用, 已成为提升测量精度的关键手段, 广泛应用于引力波探测[1–4]、生物成像[5,6]和天基传感[7,8]等领域. 然而, 测量系统的精度在很大程度上受限于激光源本身的噪声特性. 为获得低噪声光源, 通常采用主动反馈控制[9–12]或滤波腔[13,14]等噪声抑制手段. 这些方法在降低噪声方面已经取得了一定的成效, 但在某些频段内(如1—100 Hz的低频段和10 kHz—1 MHz的高频段)的噪声抑制效果仍然存在局限性. 因此, 发展高效的噪声抑制技术对提升精密测量的性能具有重要意义.
目前, 经过几十年的发展, 世界范围内已形成多种不同的方法用来抑制光场的强度噪声. 实验上已实现了注入锁定、光电反馈、模清洁器等技术对激光强度噪声进行抑制. 其中, 主动反馈降噪是抑制噪声的有效方法之一, 例如直流(direct current, DC)耦合与交流耦合(alternating current, AC)反馈系统, 通过传感器(探测器)和执行器(振幅调制器amplitude modulator, AM或声光调制器acousto-optic modulator, AOM)结合反馈控制环路降低光场的强度噪声[15–17], 其噪声抑制能力主要取决于反馈控制环路的增益[18]和传感器的灵敏度[19]. 然而在引力波探测等精密测量中, 只有有限的光功率用于降低低频噪声, 光功率的大小与传感器的灵敏度直接相关, 在这种情况下, 如何进一步降低光场的噪声, 正是本研究要解决的问题.
使用DC耦合[20]的功率探测方法, 可以允许光场的全频段通过, 包括直流和低频分量, 且信号保留完整性高. 2006年, Seifert等[10]通过在DC耦合控制环路中使用高功率、低噪声的光电探测器, 在10 Hz处相对强度噪声达到5×10–9 Hz–1/2, 在kHz处达到3.5×10–9 Hz–1/2. 2009年, Kwee等[11]采用4个低噪声光电二极管阵列串接的探测技术, 完成了低噪声、大电流探测器的设计(光电流189 mA), 对连续波Nd:YAG激光器1 Hz到1 kHz的强度噪声进行了有效抑制, 10 Hz处相对强度噪声首次低至2.4×10–9 Hz–1/2. 2017年, Junker等[12]采用同样的技术(光电流128.8 mA), 在100 Hz到1 kHz频带范围将噪声抑制到2.6×10–9 Hz–1/2. 2023年, 王在渊等[21]通过采用光电负反馈技术控制光纤放大器的泵浦电流并对关键器件进行温度控制, 在1 Hz处相对强度噪声达到5×10–6 Hz–1/2, 在1 mHz处达到6.8×10–4 Hz–1/2.
使用AC耦合[22]的功率探测方法, 可以在保持功率波动边带的同时, 降低光场载波的功率. 2008年, Kwee等[23]提出AC耦合技术, 由谐振腔反射端提取到仅仅3 mA的光电流即完成了7.2×10–10 Hz–1/2相对强度噪声抑制, 等价于传统探测器702 mA的抑噪效果. 2011年, Kwee等[24]同样利用AC耦合技术, 在反射光束中额外插入一个模式清洁器, 构成光学带通滤波反馈控制传感器, 探测光电流为23 mA时, 首次实现了1.1×10–10 Hz–1/2的相对功率噪声, 等效于光电流为32 A(探测功率为67 W)的传统抑噪技术. 2019年, Kaufer和Willke等[25]使用一个线宽为4 kHz的光学谐振腔, 在4—50 kHz频率范围内、光电流50 mA时, 噪声水平达到7×10–9 Hz–1/2.
随着以上高精度经典反馈控制系统的不断优化, 噪声的抑制水平达到了经典降噪的极限, 利用经典的手段无法突破. 而压缩态光场作为一种典型的非经典光场[26], 通过非线性过程, 可以抑制其中一个正交分量的噪声涨落, 在特定的正交分量上实现噪声的量子压缩. 因此, 通过将振幅压缩态光场引入经典的反馈控制系统, 有望进一步抑制经典反馈控制系统的强度噪声, 突破经典反馈控制系统降噪的极限. 近年来, 压缩光在多个高精度测量系统(如LIGO引力波探测器)中得到了应用, 验证了其在突破量子噪声极限方面的显著潜力[27–29].
在国际上, 1986年, Wu等[30]首次利用运转于阈值以下光学参量下转换过程, 使输出场噪声功率相对于真空涨落降低超过50%(–3 dB). 1998年, 德国康斯坦茨大学采用了由532 nm倍频Nd: YAG激光器泵浦的半单片简并MgO: LiNbO3光学参量放大器, 制备得到–6.2 dB的1064 nm压缩[31]. 2007年, Vahlbruch等[32]首次在1 Hz到3.2 kHz频段, 观察到–6.5 dB的压缩态光场. 到2016年9月, 德国马普所通过进一步降低光学损耗, 减小位相抖动, 产生了–15 dB@1064 nm的压缩态光场[33], 为国际上的最高指标. 2020年, Kleybolte等[34]在一种低温冷却微机械膜的压缩光位置传感装置中, 通过压缩光将传感精度提高了约4.8 dB. 2022年, Meylahn等[35]首次在地面引力波探测装置的完整检测带宽(1 Hz至10 kHz)内, 通过采用蝴蝶结式的光学参量腔产生了高达11.5 dB@1550 nm的压缩态光场. 在国内, 2017年, Yang等[36]在原有平衡零拍探测器的基础上减小跨阻, 改进电路不再将交直流分开, 使得探测器在20 Hz至20 kHz频段有较大的增益, 最终在分析频率15.2 kHz处直接探测到了–9.9 dB真空压缩态光场. 2019年, Zhang等[37]通过考虑压缩态产生过程中由腔失谐和相位不匹配引起的相移的补偿特性, 在5 MHz处将正交振幅噪声降低–12.3 dB@1550 nm.
本文提出了一种非经典光场辅助降噪的反馈控制系统, 将非经典光场与经典反馈控制系统相结合, 利用非经典光场的低噪声特性, 实现更深层次的强度噪声抑制. 在有无振幅压缩态光场注入的条件下, 理论上分别计算了该反馈控制系统外环与内环的强度噪声方差, 发现压缩光的注入对外环光场强度噪声的抑制效果显著优于内环. 通过分析内外环光场中各噪声因子与系统参数对噪声抑制效果的影响, 进一步得出上述现象的原因以及噪声抑制的最佳增益. 此外, 为了检验非经典手段在噪声抑制方面的物理极限, 在不同增益下深入探究了外环光场强度噪声方差与压缩度之间的内在关联. 该方法将压缩态光场与经典控制系统有效融合, 为当前精密测量和量子信息技术的发展[38]提供了新的解决方案.
-
光场的强度噪声是指光场功率的波动情况. 光场强度噪声通常用相对强度噪声(relative intensity noise, RIN)来定量表示[39]:
它定义为光功率的波动与平均光功率的比值. 其中,
$ \Delta P $ 为单位频带内的噪声功率谱密度,$ P $ 为激光器的平均功率, RIN可以通过功率谱密度(power spectral density, PSD)来描述, 其单位通常为1/Hz, 但常常以对数形式表示, 单位为dBc/Hz.散粒噪声极限(shot noise limit, SNL)的计算公式为[40]
其中
$ h = 6.626 \times {10^{ - 34}} $ J⋅s为普朗克常量;$ p $ 为进入探测器(PD)的光功率, 单位为$ W $ ;$ v = c/\lambda $ 为光场的频率, 单位为Hz;$ c = 3.0 \times {10^8}{\text{ m/s}} $ 为光速,$ \lambda $ 为光场的波长, 单位为m. -
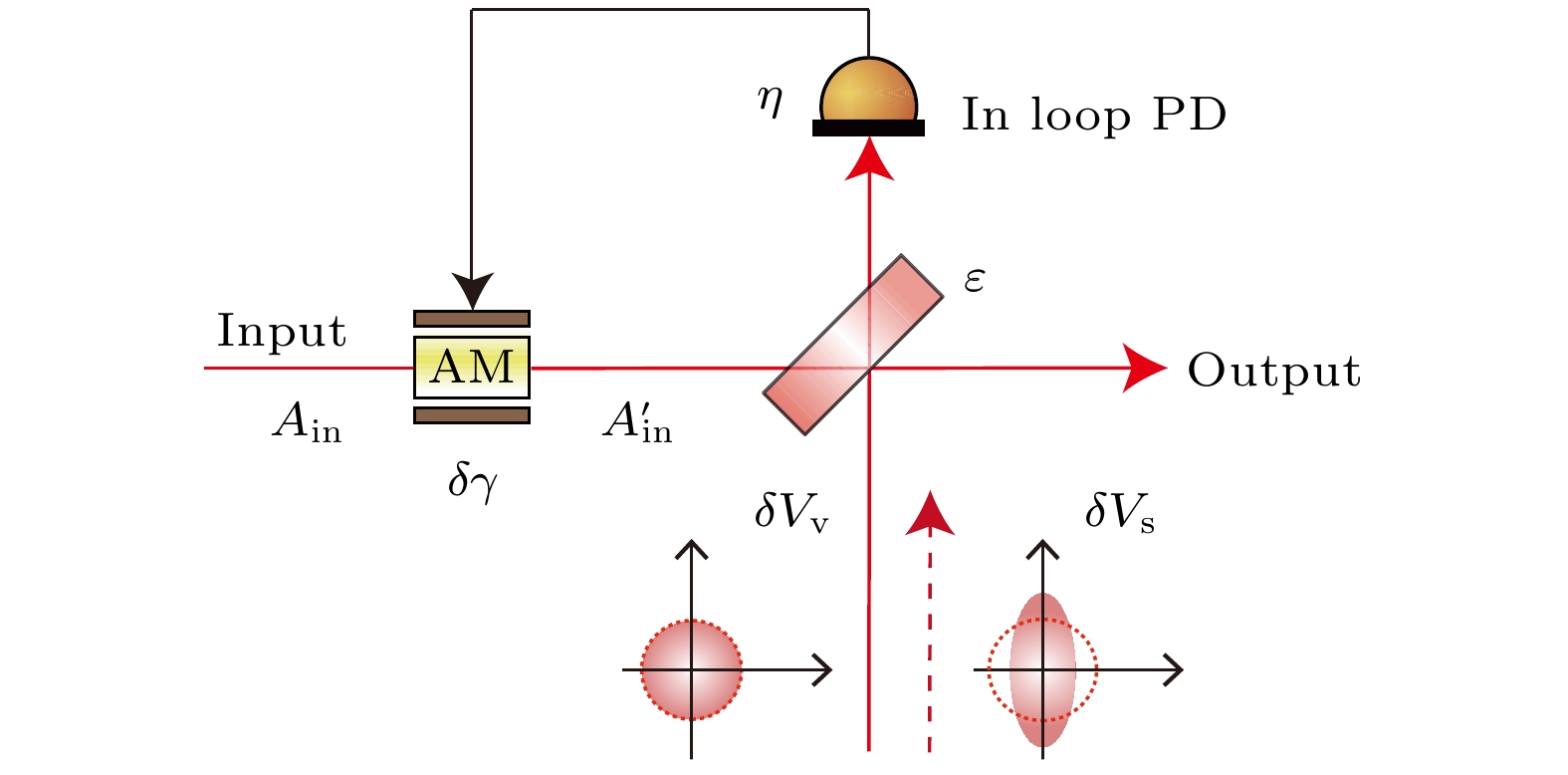
图1展示了反馈控制回路的原理图, 激光器输出的激光
$ {A_{{\text{in}}}} $ 经振幅调制后变为$ {A'_{{\text{in}}}} $ , 通过分束器$ \varepsilon $ 分为两束, 其中一束作为内环场, 用于反馈控制, 另一束作为输出场, 用于探测和应用.首先, 我们可以将输入光场写为线性形式[27]:
其中
$ {\hat A_{{\text{in}}}} $ 是光场湮灭算符;$ {\bar A_{{\text{in}}}} $ 是光场的经典平均值;$ \delta {\hat A_{{\text{in}}}} $ 是一个包含输入光场所有噪声的起伏算符, 其平均值为0. 激光通过振幅调制器(AM)后, 光场的湮灭算符表示为这里,
$ \delta \hat \gamma $ 是振幅调制器在激光场中添加的波动项, 不影响光场的平均值. 光场经过透射率为$ \varepsilon $ 的分束镜后分成两束. 反射光场入射到探测效率为$ \eta $ 的内环光电探测器上, 产生反馈电流, 透射的光束作为输出场(外环光场). 外环光场和内环光场的湮灭算符分别表示为其中
$ \delta \hat V $ 代表分束器所引入的真空起伏;$ \delta {\hat V_{\text{p}}} $ 代表内环光电探测器由于损耗所引入的真空噪声起伏. 内环反馈回路的平均值和起伏项可以表示为内环反馈回路中的光电流
$ {I_{{\text{in-loop}}}}(t) $ 可以根据内环的产生算符和湮灭算符表示为$ \sigma $ 是一个常数, 与探测器带宽有关. 当我们只保留一阶抖动项时, 内环电流的抖动由下式给出:其中
$ \delta {\hat X_{{\text{in}}}} $ ,$ \delta {\hat X_\gamma } $ ,$ \delta {\hat X_v} $ ,$ \delta {\hat X_{{v_{\text{p}}}}} $ 是分别与输入光场的噪声起伏$ \delta {\hat A_{{\text{in}}}} $ 、振幅调制器在光场中添加的波动项$ \delta \hat \gamma $ 、由分束器和非理想探测效率引入的真空噪声起伏$ \delta \hat V $ 和$ \delta {\hat V_{\text{p}}} $ 相对应的振幅噪声起伏, 分别表示为$ \delta {\hat X_{{\text{in}}}} = \delta {\hat A_{{\text{in}}}}(t) + \delta {\hat A^ + }_{{\text{in}}}(t) $ ,$ \delta {\hat X_\gamma } = \delta \hat \gamma (t) + \delta {\gamma ^ + }(t) $ ,$ \delta {\hat X_v} = \delta \hat V(t) + \delta {\hat V^ + }(t) $ ,$ \delta {\hat X_{{v_{\text{p}}}}} = \delta {\hat V_{\text{p}}}(t) + \delta {\hat V_{\text{p}}}^ + (t) $ . 反馈回路引入的小起伏项$ \delta \hat \gamma $ 可表示为反馈回路特征函数($ k(t) $ )和环路光电流的交流分量($ \delta I(t - \tau ) $ )的卷积:此式中的负号与负反馈有关. 振幅噪声波动的傅里叶变换[20,23]是
上述方程可化简为
其中回路增益参数
$ h(w) = 2\sigma k(w)\eta (1 - \varepsilon ){\bar A_{{\text{in}}}} $ ,$ k(w) $ 为反馈控制回路的特征函数[27–29].外环的波动项由下式给出:
根据方程
$ \delta {\hat X_\gamma }(w) $ , 外环的振幅噪声波动$ \delta {\hat X_{{\text{out-of-loop}}}} $ 可以表示为外环的正交振幅方差
$ {V_{{\text{out-of-loop}}}} = \langle {{{\left| {\delta {X_{{\text{out-of-loop}}}}} \right|}^2}} \rangle $ 表示为这里,
$ {V_{{\text{in}}}} $ ,$ {V_{\text{v}}} $ , 和$ {V_{\text{p}}} $ 分别代表输入场的噪声方差、分束镜引入的噪声方差和内环光电探测器引入的噪声方差.使用相同的方法, 内环正交振幅噪声方差可表示为
当
$ {V_{\text{p}}} = 1 $ 时, 外环和内环的正交振幅噪声方差分别表示为通过
$ \dfrac{{\partial {V_{{\text{out-of-loop}}}}(w)}}{{h(w)}} = 0 $ , 最小化$ {V_{{\text{out-of-loop}}}}(w) $ , 可以得到经典反馈回路的最佳增益:在最佳增益下, 获得经典反馈的最小外环噪声方差为
-
在最优增益下, 噪声的抑制水平达到了经典反馈降噪的极限, 无法利用经典的手段进一步降低光场的强度噪声. 而量子压缩态光场可以在满足海森伯不确定原理的条件下, 使某一个正交分量的噪声涨落突破量子噪声极限, 在经典反馈控制环路中引入振幅压缩态光场
$ {V_{\text{s}}} $ , 取代真空场$ {V_{\text{v}}} $ , 进一步降低光场的强度噪声.此时, 在分束器中注入压缩光
$ {V_{\text{s}}} $ , 取代(18)式与(19)式中的$ {V_{\text{v}}} $ , 外环与内环的正交振幅噪声方差分别表示为 -
反馈控制系统中, 依据实际情况, 取折射率
$ \varepsilon $ = 0.99, 光电探测效率$ \eta $ = 0.98, 输入场噪声项$ {V_{{\text{in}}}} = 1000 $ , 系统整体的效率为为了进一步降低光场的噪声, 注入–10 dB的压缩态光场
$ {V_{\text{s}}} $ , 经过系统整体的损耗后变为将外环噪声方差(18)式和(22)式、内环噪声方差(19)式和(23)式, 与经典反馈控制回路系统实际的参数相结合, 计算并绘制曲线, 如图2所示.
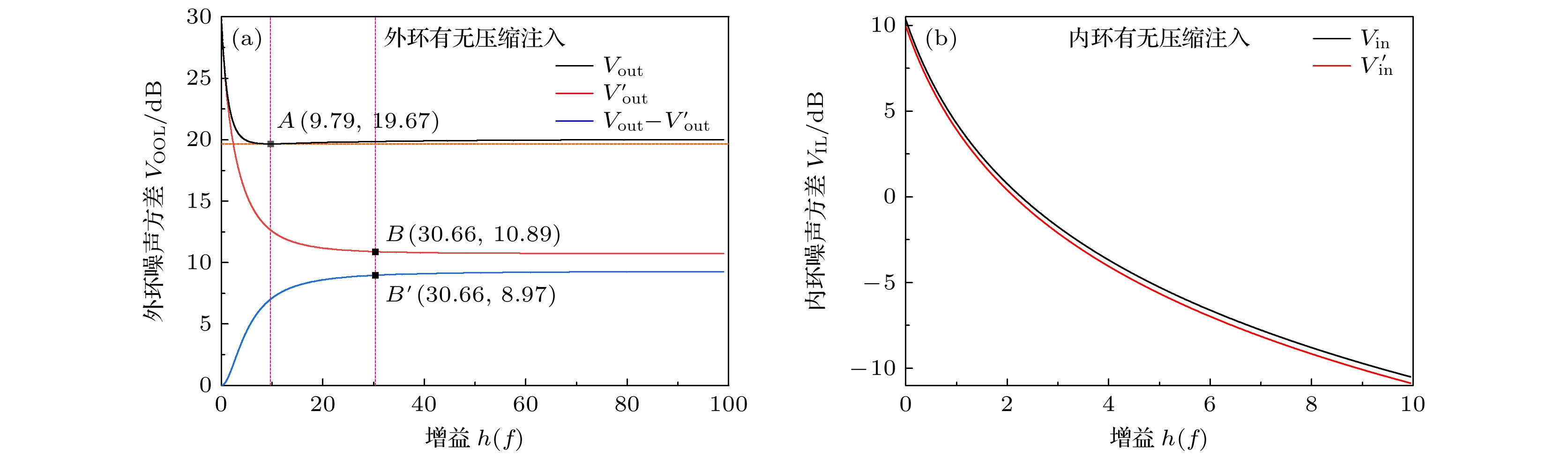
在图2(a)中, 黑色曲线为未注入压缩光时外环光场的强度噪声方差; 红色曲线为注入压缩光时外环光场的强度噪声方差; 蓝色曲线为无压缩光注入时与有压缩光注入时, 外环光场的强度噪声方差的差值. 在注入–10 dB的压缩态光场后, 经过系统损耗最终外环实际噪声应至少降低约8.97 dB. 通过黑色曲线可以清晰看出系统在增益为9.79时(点A), 噪声方差降低约10.29 dB, 此时为经典反馈控制系统的最佳增益, 此后黑色曲线略有回升, 表明降噪效果出现反跳现象. 通过红色曲线和蓝色曲线可以看到系统在增益为30.66时(点B和
$ B' $ ), 压缩态光场经系统损耗后8.97 dB的降噪效果已经完全显现, 系统整体降噪水平达到19.07 dB. 此外, 红色曲线从增益为0时显著下降至增益为83.04时, 噪声方差降低约19.21 dB, 表明通过不断加强增益的输出仍可在降噪效果完全显现后进一步抑制噪声. 通过整体曲线趋势, 可以发现压缩态光场的注入有助于外环光场突破经典反馈控制系统的降噪极限.图2(b)表示有无压缩光注入时内环光场的强度噪声方差. 黑色曲线表示未注入压缩光时内环光场的强度噪声方差; 红色曲线表示注入压缩光时内环光场的强度噪声方差. 相比于外环光场, 内环光场强度噪声方差曲线在注入压缩光后, 曲线较为接近, 变化不明显, 表明压缩态光场的注入对内环光场突破经典反馈控制系统的降噪极限影响不大.
-
根据外环正交振幅噪声方差(18)式与(22)式, 内环正交振幅噪声方差(19)式与(23)式, 我们发现外环与内环的正交振幅噪声方差主要包括三项: 输入场引入的噪声项
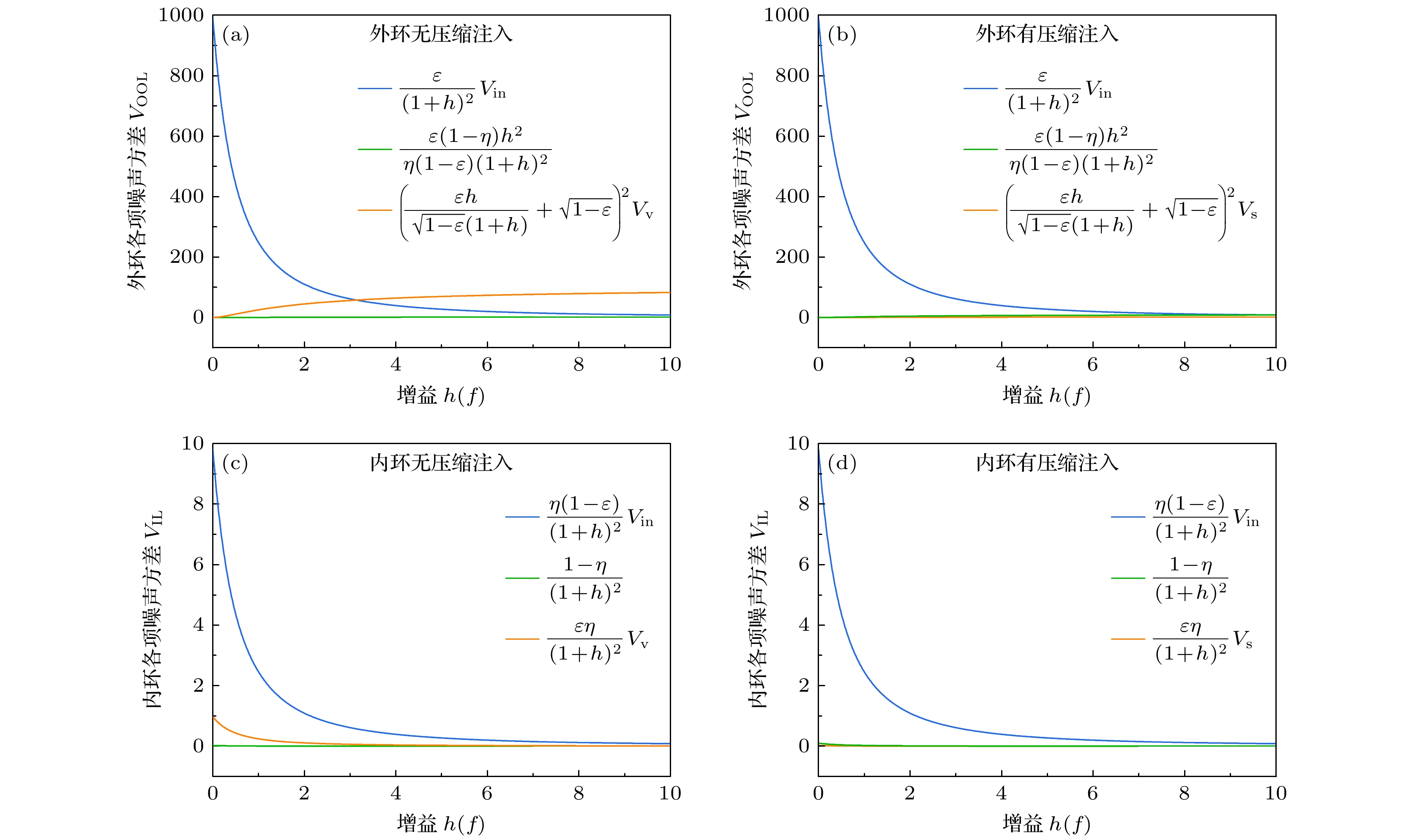
$ {V_{{\text{in}}}} $ 、内环光电探测器引入的噪声项$ {V_{\text{p}}} $ 和分束镜引入的噪声项$ {V_{\text{v}}} $ . 各个分量对振幅噪声抑制的影响如图3(a)—(d)所示.图3中, 在注入和未注入压缩光的情况下, 清晰地展现了内环光场与外环光场中各分量噪声方差的曲线差异.
对于外环光场, 在未注入压缩光时(见图3(a)), 随着增益的增加, 分束镜引入的真空噪声项
$ {\left( {\dfrac{{\varepsilon h}}{{\sqrt {1 - \varepsilon } \left( {1 + h} \right)}} + \sqrt {1 - \varepsilon } } \right)^2}{V_{\text{v}}} $ 永远高于输入场引入的噪声项$ \dfrac{\varepsilon }{{1 + {h^2}}}{V_{{\text{in}}}} $ 和内环光电探测器引入的噪声项$ \dfrac{{\varepsilon (1 - \eta ){h^2}}}{{\eta (1 - \varepsilon ){{\left( {1 + h} \right)}^2}}} $ . 因此, 外环光场的强度噪声方差水平主要受限于分束镜引入的真空噪声项$ {\left( {\dfrac{{\varepsilon h}}{{\sqrt {1 - \varepsilon } \left( {1 + h} \right)}} + \sqrt {1 - \varepsilon } } \right)^2}{V_{\text{v}}} $ (橙色曲线). 在注入压缩光的情况下(图3(b)), 即通过分束镜的真空通道注入–10 dB的压缩态光场时, 可以清晰地看到分束镜引入的噪声方差水平(橙色曲线)显著降低, 这表明压缩光的注入有助于突破经典反馈控制系统的降噪极限, 通过压缩光注入的优势, 进一步抑制光场的振幅噪声. 在注入压缩光的情况下, 随着反馈控制环路的增益逐渐增加, 外环光场的降噪水平将受到压缩态光场的振幅噪声的限制.对于内环光场, 在未注入压缩光时(见图3(c)), 分束镜引入的真空噪声项
$ \dfrac{{\varepsilon \eta }}{{{{\left( {1 + h} \right)}^2}}}{V_{\text{v}}} $ (橙色曲线)随着增益的少量增加而显著降低, 逐渐接近0噪声水准; 在注入压缩光的情况下(图3(d)), 即通过分束镜的真空通道注入–10 dB的压缩态光场时, 可以看到分束镜引入的噪声项$ \dfrac{{\varepsilon \eta }}{{{{\left( {1 + h} \right)}^2}}}{V_{\text{s}}} $ (橙色曲线)整体接近0噪声水准, 这表明压缩光的注入有助于进一步抑制噪声, 但是相比于外环光场, 内环光场在未注入压缩光的情况下, 少量的增益也可达到注入压缩光后的噪声抑制水平. 即使增益的增加可以提升降噪水平, 但对内环光路注入压缩光后, 噪声的抑制并不明显, 最终的降噪水平仍将受到压缩态光场的振幅噪声的限制.最后, 结合四幅图观察到, 注入压缩态光场的压缩度越大, 压缩光辅助降噪效果越明显. 在理想情况下(不考虑损耗), 经典反馈控制方案中注入–10 dB压缩光的降噪效果相当于探测光功率增加10倍. 通过利用压缩光辅助降噪的反馈控制系统, 能够在经典反馈控制系统的基础上进一步降低约10 dB的噪声, 验证了非经典手段在有限探测光功率下抑制噪声的能力.
-
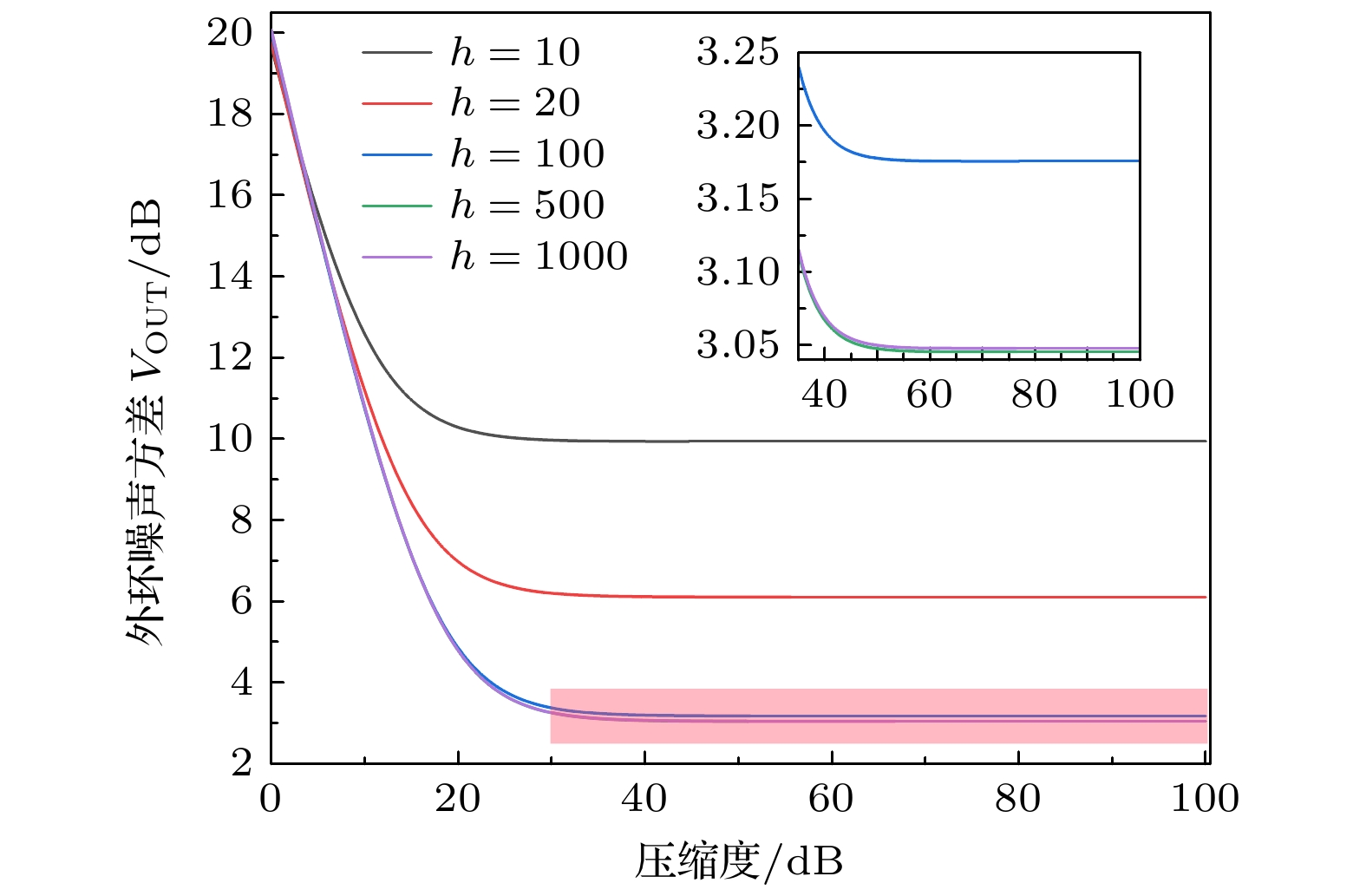
图4为该系统中不同增益下压缩度与外环噪声方差的关系, 揭示了系统降噪能力的物理极限. 显然, 增加系统反馈增益或提升压缩态光场的压缩度可以有效地抑制外环光场的强度噪声, 尤其在
$ h = 500 $ 时, 系统已接近最优增益, 噪声方差显著降低; 然而在$ h = 1000 $ 时, 由于经典反馈控制系统的抑噪能力减弱, 导致总的外环噪声方差略有上升, 但也趋于稳定. 最后, 图4中外环噪声方差的收敛趋势表明, 系统的降噪水平最终会受限于SNL. 这意味着, 尽管振幅压缩态光场的注入能够使强度噪声的抑制水平低于经典噪声极限, 实现对经典反馈控制系统噪声抑制瓶颈的突破, 但随着反馈控制系统增益和压缩态光场压缩度的进一步提升, 系统总噪声方差会在SNL附近收敛, 无法突破0 dB噪声水平.换句话说, 即使反馈增益趋于无限大和压缩态光场压缩度趋向理想极限时, 系统的降噪效果也只能无限接近SNL, 而无法真正超越, 达到理论最低噪声水平. 这表明, SNL是该反馈控制系统噪声抑制技术的绝对下限, 同时也反映了量子力学原理在精密测量中的根本约束条件.
-
本研究针对量子精密测量系统中激光光源噪声对测量精度的限制问题, 提出了一种量子压缩态光场与经典反馈控制系统相结合的方法. 通过理论模型, 分析了振幅压缩态光场对反馈控制系统噪声抑制的影响, 揭示了反馈回路增益与噪声抑制水平的关系. 理论分析结果表明, 经典反馈控制系统的输出噪声主要受输入场、光电探测器以及分束器三部分引入的噪声影响, 在经典反馈回路增益最优时, 噪声水平达到了经典噪声极限, 无法进一步降低. 引入–10 dB振幅压缩态光场后, 有效抑制了分束器引入的噪声, 进一步将外环光场的强度噪声降低了8.97 dB, 整体降噪水平达到19.07 dB, 接近SNL水平. 这意味着, 压缩态光场的引入使系统噪声抑制能力相当于将光电探测器的灵敏度提升9倍. 但压缩态光场辅助技术对内环光场的噪声抑制效果有限, 是因其主要噪声源来自输入场的噪声, 而分束器带来的影响较小. 尽管压缩态光场提高了外环光场的降噪性能, 但噪声抑制的水平仍受限于压缩度和散粒噪声极限的影响. 本文理论分析了压缩态光场与经典反馈控制技术结合的优势, 在不增加激光功率的情况下实现了显著降噪效果, 为引力波探测和量子通信等领域提供了理论支撑, 开辟了精密测量的新方向.
压缩增强的强度噪声抑制机理
Mechanism of suppressing noise intensity of squeezed state enhancement
-
摘要: 激光光源的噪声直接影响精密测量系统的精度和灵敏度, 特别是在引力波探测和生物成像等高精度应用中. 尽管经典反馈控制技术能有效地抑制强度噪声, 但其降噪水平受到经典噪声极限的限制. 本研究提出一种结合量子压缩光与经典反馈控制技术的新方法, 旨在进一步降低系统中的强度噪声, 突破经典反馈控制技术的抑噪瓶颈. 通过引入正交振幅压缩态光场, 在理论上建立了压缩光辅助的反馈控制系统, 理论分析了反馈增益和压缩度对噪声抑制的影响, 并与经典方案进行对比. 理论分析结果表明, 压缩光的引入显著地提高了噪声抑制水平, 接近散粒噪声极限, 从而大幅提升系统的灵敏度. 该方法为在不增加激光功率的情况下实现更低噪声水平提供了新的量子控制手段, 对精密测量技术的发展具有重要意义.Abstract: This research focuses on advanced noise suppression technologies for high-precision measurement systems, particularly addressing the limitations of classical noise reducing approaches. The noise level of laser sources is a crucial factor that directly affects the measurement sensitivity in applications such as gravitational wave detection and biomedical imaging. Classical feedback control technologies are effective but often encounter a bottleneck resulting from the classical noise suppression limits. To cope with these challenges, a novel method integrating quantum squeezed light with classical feedback control systems to reduce intensity noise is proposed in this work. By employing an amplitude-squeezed light field, a quantum-enhanced feedback control model is developed, thereby theoretically examining the influence of both the feedback loop gain and the degree of squeezing on the noise suppression performance. The results show that the injection of squeezed light significantly reduces the intensity noise, approaching the shot noise limit (SNL), thereby improving the system sensitivity beyond the classical noise reduction boundaries. Specifically, –10 dB squeezed state injection into the feedback system yields an additional noise suppression of approximately 8.97 dB, exceeding what is achievable using classical feedback alone. This demonstrates that the potential of the proposed method can enhance measurement precision close to the quantum noise limits without increasing the laser power. The analysis highlights the asymmetric noise suppression effects between the inner feedback loop and outer feedback loop. Although the outer loop benefits significantly from the squeezed light injection and achieves noise levels that are unattainable by classical feedback methods, the inner loop shows relatively minor improvements. This asymmetry is attributed to the inherent characteristics of quantum squeezing and the limitations of the feedback loop design. Further investigation into the individual noise components reveals that the primary contributors to the intensity noise include input noise, photodetector noise, and beam splitter-induced vacuum fluctuations. The injection of squeezed light effectively mitigates these vacuum fluctuations, which are typically a major noise source in high-precision laser systems. Theoretical research results show that the use of squeezed light in feedback control systems can effectively enhance noise suppression, equivalent to a nine fold increase in detected optical power, without the physical drawbacks of increasing laser power such as thermal noise. In conclusion, this study provides a theoretical validation of combining quantum squeezed states with classical feedback control to exceed classical noise suppression limits. The integration of a –10 dB squeezed state demonstrates a significant noise reduction, showing that this hybrid approach could revolutionize noise management in precision measurement applications. The results pave the way for further exploring quantum-enhanced control technologies in fields such as gravitational wave detection, quantum communication, and advanced optical sensing, providing a pathway for improving sensitivity and noise suppression without increasing additional power requirements.
-
Key words:
- precision measurement /
- squeezed state /
- noise suppression /
- feedback control .
-

-
-
[1] The LIGO Scientific Collaboration 2015 Classical Quantum Gravity 32 074001 doi: 10.1088/0264-9381/32/7/074001 [2] Acernese F, Agathos M, Agatsuma K, Aisa D, Allemandou N, Allocca A, Meidam J 2014 Classical Quantum Gravity 32 024001 doi: 10.1088/0264-9381/32/2/024001 [3] LIGO Scientific and Virgo Collaborations 2016 Phys. Rev. Lett. 116 061102 doi: 10.1103/PhysRevLett.116.061102 [4] LIGO Scientific and Virgo Collaborations 2017 Phys. Rev. Lett. 119 141101 doi: 10.1103/PhysRevLett.119.141101 [5] Taylor M A, Janousek J, Daria V, Knittel J, Hage B, Bachor H A, Bowen W P 2013 Nat. Photonics 7 229 doi: 10.1038/nphoton.2012.346 [6] Casacio C A, Madsen L S, Terrasson A, Waleed M, Barnscheidt K, Hage B, Bowen W P 2021 Nature 594 201 doi: 10.1038/s41586-021-03528-w [7] Brito R, Ghosh S, Barausse E, Berti E, Cardoso V, Dvorkin I, Klein A, Pani P 2017 Phys. Rev. D 96 064050 doi: 10.1103/PhysRevD.96.064050 [8] Armano M, Audley H, Baird J, Binetruy P, Born M, Bortoluzzi D, Zweifel P 2018 Phys. Rev. Lett. 120 061101 doi: 10.1103/PhysRevLett.120.061101 [9] Kaufer S, Kasprzack M, Frolov V, Willke B 2017 Classical Quantum Gravity 34 145001 doi: 10.1088/1361-6382/aa7119 [10] Seifert F, Kwee P, Heurs M, Willke B, Danzmann K 2006 Opt. Lett. 31 2000 doi: 10.1364/OL.31.002000 [11] Kwee P, Willke B, Danzmann K 2009 Opt. Lett. 34 2912 doi: 10.1364/OL.34.002912 [12] Junker J, Oppermann P, Willke B 2017 Opt. Lett. 42 755 doi: 10.1364/OL.42.000755 [13] 王俊萍, 张文慧, 李瑞鑫, 田龙, 王雅君, 郑耀辉 2020 物理学报 69 234204 doi: 10.7498/aps.69.20200890 Wang J P, Zhang W H, Li R X, Tian L, Wang Y J, Zheng Y H 2020 Acta Phys. Sin. 69 234204 doi: 10.7498/aps.69.20200890 [14] 王雅君, 王俊萍, 张文慧, 李瑞鑫, 田龙, 郑耀辉 2021 物理学报 70 204202 doi: 10.7498/aps.70.20210234 Wang Y J, Wang J P, Zhang W H, Li R X, Tian L, Zheng Y H 2021 Acta Phys. Sin. 70 204202 doi: 10.7498/aps.70.20210234 [15] Yamamoto Y, Haus H A 1986 Rev. Mod. Phys. 58 1001 doi: 10.1103/RevModPhys.58.1001 [16] Xiao M, Wu L A, Kimble H J 1987 Phys. Rev. Lett. 59 27 doi: 10.1364/josab.4.001465 [17] Zhao J, Guiraud G, Pierre C, Floissat F, Casanova A, Hreibi A, Chaibi W, Traynoer N, Boullet J, Santarelli G 2018 Appl. Phys. B 124 1 doi: 10.1007/s00340-018-6989-7 [18] Paschotta R, Fiedler K, Kürz P, Mlynek J 1994 Appl. Phys. B 58 117 doi: 10.1007/bf01082345 [19] Haus H A, Yamamoto Y. 1984 Phys. Rev. A 29 1268 doi: 10.1103/physreva.29.1261 [20] Zhang J, Ma H L, Xie C D, Peng K C 2003 Appl. Opt. 42 1068 doi: 10.1364/AO.42.001068 [21] 王在渊, 王洁浩, 李宇航, 柳强 2023 物理学报 72 054205 doi: 10.7498/aps.72.20222127 Wang Z Y, Wang J H, Li Y H, Liu Q 2023 Acta Phys. Sin. 72 054205 doi: 10.7498/aps.72.20222127 [22] 王雅君, 高丽, 张晓莉, 郑耀辉 2020 红外与激光工程 49 20201073 doi: 10.3788/IRLA20201073 Wang Y J, Gao L, Zhang X L, Zheng Y H 2020 Infrared Laser Eng. 49 20201073 doi: 10.3788/IRLA20201073 [23] Kwee P, Willke B, Danzmann K 2008 Opt. Lett. 33 1509 doi: 10.1364/OL.33.001509 [24] Kwee P, Willke B, Danzmann K 2011 Opt. Lett. 36 3563 doi: 10.1364/OL.36.003563 [25] Kaufer S, Willke B 2019 Opt. Lett. 44 1916 doi: 10.1364/OL.44.001916 [26] 姚德民, 郭光灿 1988 物理学报 37 463 doi: 10.7498/aps.37.463 Yao D M, Guo G C 1988 Acta Phys. Sin. 37 463 doi: 10.7498/aps.37.463 [27] Vahlbruch H, Wilken D, Mehmet M, Willke B 2018 Phys. Rev. Lett. 121 173601 doi: 10.1103/PhysRevLett.121.173601 [28] Eberle T, Steinlechner S, Bauchrowitz J, Händchen V, Vahlbruch H, Mehmet M, Müller-Ebhardt H, Schnabel R 2010 Phys. Rev. Lett. 104 251102 doi: 10.1103/PhysRevLett.104.251102 [29] Liu F, Zhou Y Y, Yu J, Guo J L, Wu Y, Xiao S X, Wei D, Zhang Y, Jia X J, Xiao M 2017 Appl. Phys. Lett. 110 021106 doi: 10.1063/1.4973895 [30] Wu L A, Kimble H J, Hall J L, Wu H F 1986 Phys. Rev. Lett. 57 2520 doi: 10.1103/PhysRevLett.57.2520 [31] Schneider K, Lang M, Mlynek J, Schiller S 1998 Opt. Express 2 59 doi: 10.1364/OE.2.000059 [32] Vahlbruch H, Chelkowski S, Danzmann K, Schnabel R 2007 New J. Phys. 9 371 doi: 10.1088/1367-2630/9/10/371 [33] Vahlbruch H, Mehmet M, Danzmann K, Schnabel R 2016 Phys. Rev. Lett. 117 110801 doi: 10.1103/PhysRevLett.117.110801 [34] Kleybolte L, Gewecke P, Sawadsky A, Korobko M, Schnabel R 2020 Phys. Rev. Lett. 125 213601 doi: 10.1103/PhysRevLett.125.213601 [35] Meylahn F, Willke B, Vahlbruch H 2022 Phys. Rev. Lett. 129 121103 doi: 10.1103/PhysRevLett.129.121103 [36] Yang W H, Jin X L, Yu X D, Zheng Y H, Peng K C 2017 Opt. Express 25 24262 doi: 10.1364/OE.25.024262 [37] Zhang W H, Wang J R, Zheng Y H, Wang Y J, Peng K C 2019 Appl. Phys. Lett. 115 171105 doi: 10.1063/1.5125632 [38] 潘建伟 2024 物理学报 73 010301 doi: 10.7498/aps.73.20231795 Pan J W 2024 Acta Phys. Sin 73 010301 doi: 10.7498/aps.73.20231795 [39] Clerk A A, Devoret M H, Girvin S M, Marquardt F, Schoelkopf R. J 2010 Rev. Mod. Phys. 82 1155 doi: 10.1103/RevModPhys.82.1155 [40] Aspelmeyer M, Kippenberg T J, Marquardt F 2014 Rev. Mod. Phys. 86 1391 doi: 10.1103/RevModPhys.86.1391 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: