量子密钥分发(quantum key distribution, QKD)^[1–3]以其建立在量子力学和信息论框架下的安全特性, 能够在通信双方之间分配安全密钥, 结合“一次一密”^[4]加密算法可以实现信息论意义下的安全保密通信. 量子密钥分发根据密钥信息编码方式可以分为离散变量量子密钥分发(discrete-variable QKD, DV-QKD)和连续变量量子密钥分发(continuous-variable QKD, CV-QKD), “墨子号”量子科学实验卫星验证了空间信道星地下行DV-QKD的可行性^[5], 在地面光纤QKD技术逐渐成熟^[6,7]和空间信道DV-QKD实验成功的背景下, 借鉴空间DV-QKD理论和实验发展路径, 依托经典激光通信链路、捕获跟踪瞄准系统等物理实现技术基础, 探索空间CV-QKD的可行性理论与实验研究, 是全天候、高稳定、高码率的空间量子保密通信发展方向.

CV-QKD从调制方式上可分为高斯调制和离散调制. 高斯调制CV-QKD (Gaussian modulation CV-QKD, GM CV-QKD)^[8]采用对称性相对较高的高斯分布, 利用高斯最优定理可证明较高的安全性, 每个脉冲可编码多比特信息, 但是调制过程相对复杂, 效率相对较低. 离散调制CV-QKD (discrete modulation CV-QKD, DM CV-QKD)^[9–15]将离散调制后处理纠错相对简单优势与连续调制安全性证明优势结合在一起, 能够容忍较强的过量 噪声, 采用类似于经典激光通信中的正交相移键控(quadrature phase shift keying, QPSK)调制方式, 与现有系统的兼容性更高, 近年来在理论和实验方面都得到越来越多的关注和研究^[16–20].

Vasylyev等^[21]在下行链路场景中分析了地球大气对卫星量子光学通信的影响, 发现大气折射、大气吸收和湍流引起的信号失真与天顶角有很大的相关性. Pirandola^[22]分析卫星量子通信在各种实际场景下的极限性能, 探讨其在远距离安全密钥分发和纠缠分发中的可行性及优势, 特别是展示了连续变量量子密钥分发协议在上下行链路中的实现潜力. Li等^[20]在自由空间信道下通过数值模拟, 证明离散调制连续变量量子密钥分发协议适用于卫星到地面的量子通信, 具备实现简便、抗噪性强和兼容性高的优势. 目前研究中大部分采用固定的圆形轨道进行星地几何建模, 采用固定距离和俯仰角参数进行协议可行性分析. 然而, 低轨卫星的空间DM CV-QKD面临星地链路动态时变、大气信道湍流、光束指向误差等实际环境因素的影响. 此外, 卫星平台的轨道选择、通信链路损耗的补偿、核心器件参数的优化都会影响空间信道DM CV-QKD的可行性理论.

本文研究实际空间信道环境下DM CV-QKD协议的可行性, 分析空间衍射和大气衰减、湍流信道退化模型对于空间信道DM CV-QKD协议的影响, 讨论卫星轨道高度、天顶角、接收器孔径、束腰尺寸和过量噪声等实际参数对空间DM CV-QKD的密钥生成率影响, 搭建星地量子密钥分发仿真平台分析空间信道DM CV-QKD协议的可行性, 并进一步研究DM CV-QKD协议幅度优化和后处理优化选择, 为后续空间信道DM CV-QKD的实验提供理论依据和参数选择.

本文第2节是DM CV-QKD协议、星地链路信道模型及渐近极限下DM CV-QKD密钥率的相关理论; 第3节基于墨子号卫星轨道, 仿真分析实际参数对空间DM CV-QKD密钥生成率的影响; 第4节对空间信道DM CV-QKD可行性分析研究进行总结.

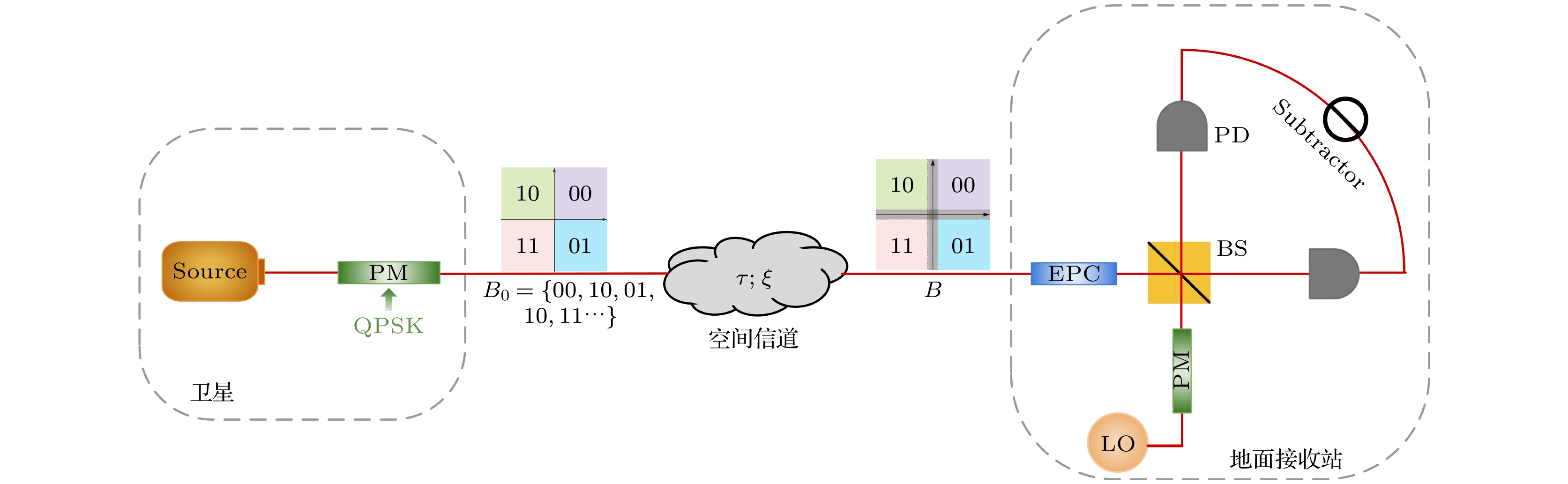
本工作基于QPSK调制的零差探测CV-QKD协议开展^[17], 在理想探测下使用严密的数值方法求解在渐近状态下针对集体攻击的密钥率, 协议的空间信道制备测量模型和QPSK星座图如图1所示.

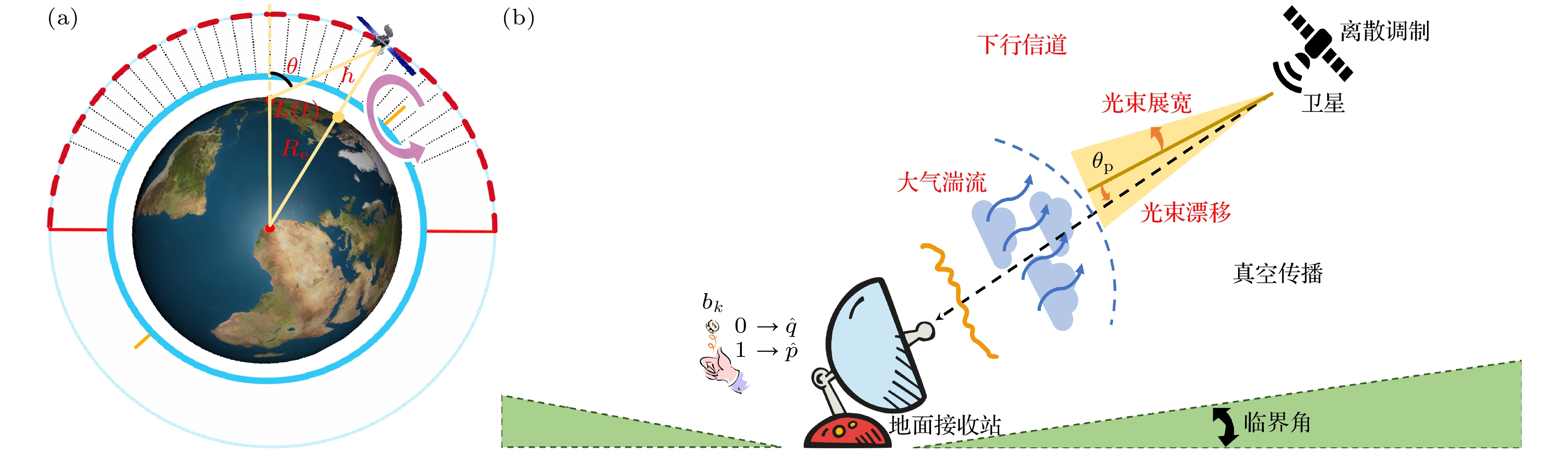
本文首先建立空间信道离散调制相干态信道传输退化模型. 通常把从海平面以上1000—1400 km高度内的气层作为地球大气层的厚度, 其中大气总质量的$ 98.2 {\text{%}} $集中在30 km以下. 在这个范围内, 大气衰减和湍流现象较为显著. 如图2(a)所示, 将卫星与地面站通信时间划分为N段, 时间间隔Δt = 1 s, 相干光的传播距离L(t). 相干光经过大气湍流发生衰减和偏移的过程如图2(b)所示. 可以得到:

其中地球半径$ {R_{\text{e}}} \simeq 6371\; {\text{km}} $, $ \theta(t) $是卫星与地面站的实时天顶角, $ h(t) $是卫星离地面实时高度.

地球大气的光学折射率与真空中的折射率不同, 折射率值随海拔、地理位置和气象条件变化而变化. 由于折射率的不同, 相干光在大气中发生折射现象. 相干光束在大气层中的传播距离变大, 但是当天顶角小于70°时, 光路长度伸长因子接近 于1^[21]. 假设本文分析的天顶角范围限制在70°以内, 可以忽略折射带来的路径影响. 本文对波长λ = 1550 nm, 下行链路弱湍流、能见度为20 km的中纬度夏季大气模型开展研究, 考虑空间衍射和大气衰减、湍流信道退化对于空间信道DM CV-QKD协议的影响.

在空间信道CV-QKD协议传输过程中, 相干光束初始束腰半径为$ w_{0} $, 经过距离L的传播后到达接收端, 受到空间衍射的影响, 接收端的光斑尺寸为

其中$ {Z_{\text{R}}} = {\text{π}}\omega _0^2{\lambda ^{ - 1}} $为瑞利距离, λ是相干光的波长, $ R_{0} $为曲率^[23]. 理论上聚焦光束可以减小接收口径有限带来的损耗, 但对光学系统的对准和跟踪精度提出了更高的要求, 在模型中采用准直光束($ R_{0} \approx +\infty $), 接收端光斑尺寸可简化为^[22]

接收端望远镜的孔径为a_R, 由于接收望远镜的孔径尺寸限制, 光束只有一部分能被望远镜接收, 因此空间衍射影响下的透过率为

气溶胶的吸收和瑞利散射会导致光的消失, 这取决于链路长度以及气溶胶分布模型^[21]. 大气衰减还很大程度上取决于天空条件和传输波长. 在天顶角小于70°时, 大气透射效率$ {\tau _{{\text{atm}}}} $可以表示为^[24]

其中$ {\tau _{{\text{zen}}}} $是$\theta=0° $的传输效率. 天顶传输效率$ {\tau _{{\text{zen}}}} $的估算采用广泛使用的大气透射率和辐射度网络应用程序计算器MODTRAN^[25]. 考虑波长λ = 1550 nm、能见度为20 km的中纬度夏季大气模型, 得到高度h = 50 km处的天顶传输效率$ {\tau _{{\text{zen}}}} = 0.90 $. 由于高度50 km以上的空气密度几乎为0, 大气影响可以忽略不计, $ {\tau _{{\text{zen}}}} = 0.90 $可以适用于此模型下的任何高度的卫星平台. 光束在传播中经历空间衍射和大气衰减后, 望远镜还会带来探测损耗$ {\tau _{{\text{eff}}}} \simeq 0.4 $等固定损耗^[26], 因此空间信道透过率可表示为

大气温度的随机变化会导致空气运动, 带来强度波动、光束漂移和光束展宽, 从而导致信道透射率的波动, 具有一定的统计特性. 在大气湍流的影响下, 卫星信号光束中心与接收平台中心瞬时偏转距离r的概率分布遵循Weibull分布^[24], 表示为

其中, 标准差$ {\sigma _{\text{r}}} = \sqrt {{{\left( {L{\theta _{\text{p}}}} \right)}^2} + \sigma _{{\text{turb}}}^{2}} $, 指向误差$ {\theta _{\text{p}}} $为光束中心与接收望远镜中心之间的夹角. 这里$ \sigma_{\text{turb}}^2 $是大气湍流产生的光束中心方差, 取决于湍流强度、传播距离和光束初始束腰半径. 在弱湍流的条件下光束偏差主要由卫星指向误差决定, 可以得到$ {\sigma _{\text{r}}} \simeq L{\theta _{\text{p}}} $ ^[27]. 透射效率$ {\tau _{{\text{end}}}} $与瞬时偏转距离r之间的近似解析关系可以表示为

其中S和γ分别是尺度参数和形状参数^[28].

星地间通信的噪声来源多样, 除了在传播信道中不可避免的固定噪声外^[24], 还有检测噪声^[17]、相位波动噪声^[29]等. 所有的噪声随机相互独立, 由于方差的可加性可以表示为

其中$ {\xi _{{\text{fix}}}} $是信号进行光纤耦合产生的; $ {\xi _{{\text{det}}}} $是检测设备的不完美导致的, 本质上不可避免; $ {\xi _{{\text{phase}}}} $是振荡器初始频率偏移以及大气闪烁引起的随机相位波动.

位于卫星平台的发送端采用相干光源随机生成4种等概率的相干光, 分别代表{00, 10, 11, 01}, 经过自由空间退化信道传输到达接收望远镜, 位于地面站的接收端等概率随机地使用正交基$\hat q $和$\hat p $进行测量, 反向调和后生成密钥. 在渐近极限下进行联合窃听时, 空间信道DM CV-QKD协议的密钥生成率$ {R^\infty } $可以表示为^[17]

其中$ {{\boldsymbol{\rho }}_{{\text{AB}}}} $是描述卫星和接收望远镜之间信息的状态, $ \displaystyle\sum\nolimits_{y \in \left\{ {\hat q, \hat p} \right\}} {D\left( {{\varsigma _y}\left( {{{\boldsymbol{\rho }}_{{\text{AB}}}}} \right)\parallel Z\left[ {{\varsigma _y}\left( {{{\boldsymbol{\rho }}_{{\text{AB}}}}} \right)} \right]} \right)} $是通过量子相对熵衡量窃听者对接收望远镜产生密钥的不确定度, $ \displaystyle\sum\nolimits_{y \in \left\{ {\hat q, \hat p} \right\}} {p_{{\text{pass}}}^y\delta _{{\text{EC}}}^y} $是卫星对接收望远镜产生密钥的经典信息.

在时间间隔Δt内, 光的传播距离L和星地之间的天顶角θ基本不变, 本文假设在时间间隔内信道的统计特性不变. 由于后选择的筛选概率p_pass和信息泄漏量$ {\delta _{{\text{EC}}}} $只涉及卫星和接收望远镜掌握的信息, $\displaystyle \sum\nolimits_{y \in \left\{ {\hat q, \hat p} \right\}} {p_{{\text{pass}}}^y\delta _{{\text{EC}}}^y} $可以根据定义 计算^[30]. 采用优化数值方法^[30,31]计算密钥率部分$ \displaystyle\sum\nolimits_{y \in \left\{ {\hat q, \hat p} \right\}} {D\left( {{\varsigma _y}\left( {{{\boldsymbol{\rho }}_{{\text{AB}}}}} \right)\parallel Z\left[ {{\varsigma _y}\left( {{{\boldsymbol{\rho }}_{{\text{AB}}}}} \right)} \right]} \right)} $:

其中x属于{00, 10, 11, 01}, $ {\left\langle {\hat q} \right\rangle _x} , {\left\langle {\hat p} \right\rangle _x} , {\left\langle {\hat n} \right\rangle _x} $和$ {\langle {\hat d} \rangle _x} $是接收望远镜测量x的算子期望值.

在空间信道中, 卫星轨道高度$h(t) $、天顶角$\theta \left( t \right) $、接收器孔径a_R和束腰尺寸${\omega _0} $这些变量决定空间衍射、大气衰减和大气湍流对信号的损耗. 通过信道透射效率$ {\tau _{{\text{end}}}} $和过量噪声$ {\xi _{{\text{tot}}}} $确定空间信道中算子$ {\left\langle {\hat q} \right\rangle _x} = \sqrt {2{\tau _{{\text{end}}}}} {R_{\text{e}}}\left( {{a_x}} \right) $, $ {\left\langle {\hat p} \right\rangle _x} = \sqrt {2{\tau _{{\text{end}}}}} {{\mathrm{Im}}} \left( {{a_x}} \right) $, $ {\left\langle {\hat n} \right\rangle _x} = {\tau _{{\text{end}}}}{\left| {{a_x}} \right|^2} + {{{\tau _{{\text{end}}}}{\xi _{{\text{tot}}}}}}/{{2}} $和$ {\langle {\hat d} \rangle _x} = {\tau _{{\text{end}}}}[ {{{\left( {{a_x}} \right)}^2} + {{\left( {a_x^*} \right)}^2}} ] $的期望值, 代入(11)式求解密钥率, $ {a_x} $为接收到的信号状态.

仿真中采用墨子号卫星轨道数据进行场景建模, 具体使用了墨子号2016年3月22日17时28分—17时35分(国际标准时间)的星历数据进行卫星轨道参数设定. 地面站可以选择兴隆、德令哈、丽江、南山地面站, 考虑卫星与地面站的通连时间和信道损耗, 本文选择丽江地面站开展分析.

卫星与地面站的相关参数, 即用于模拟墨子号-丽江站的参数和DM CV-QKD系统参数设置分别如表1和表2所列.

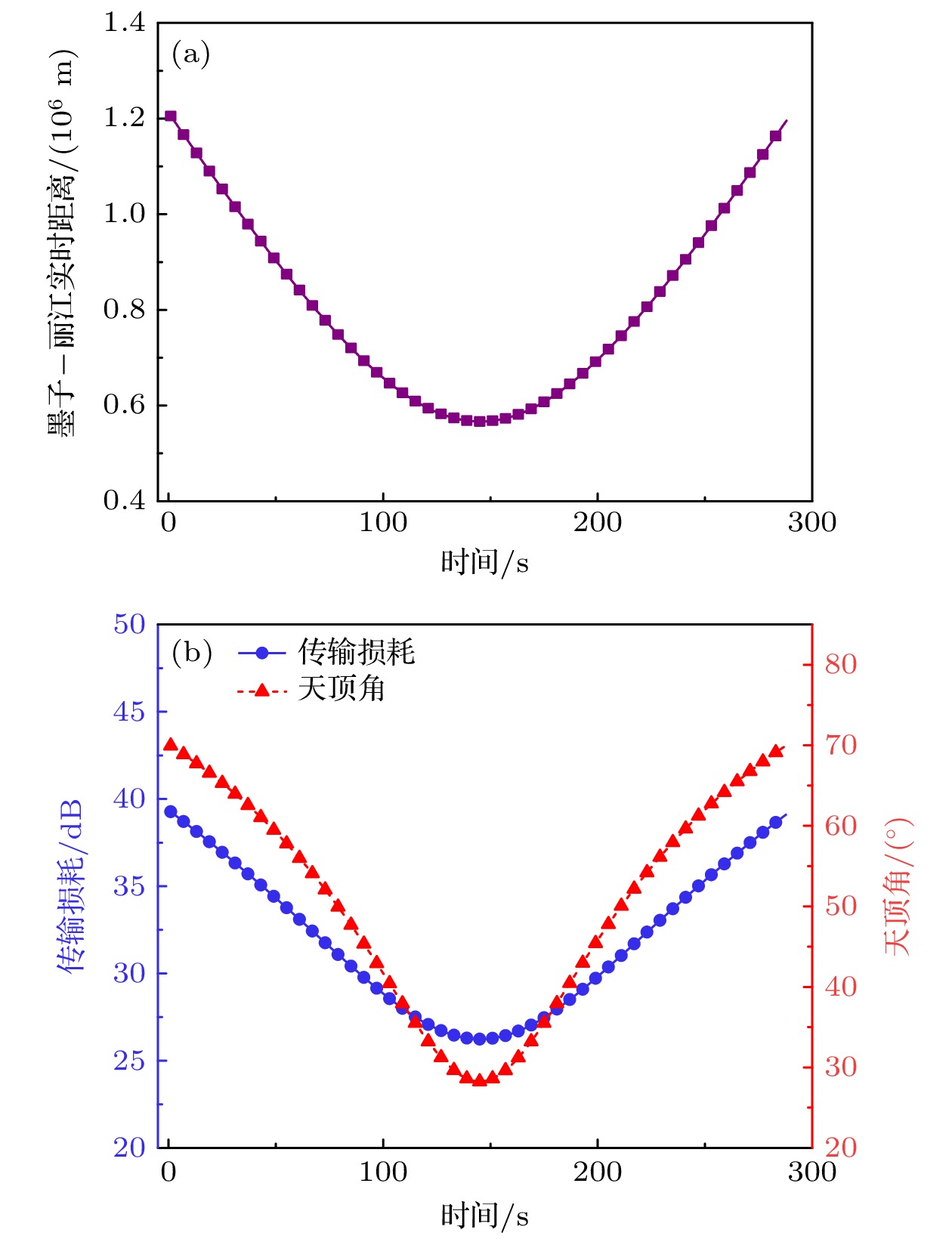
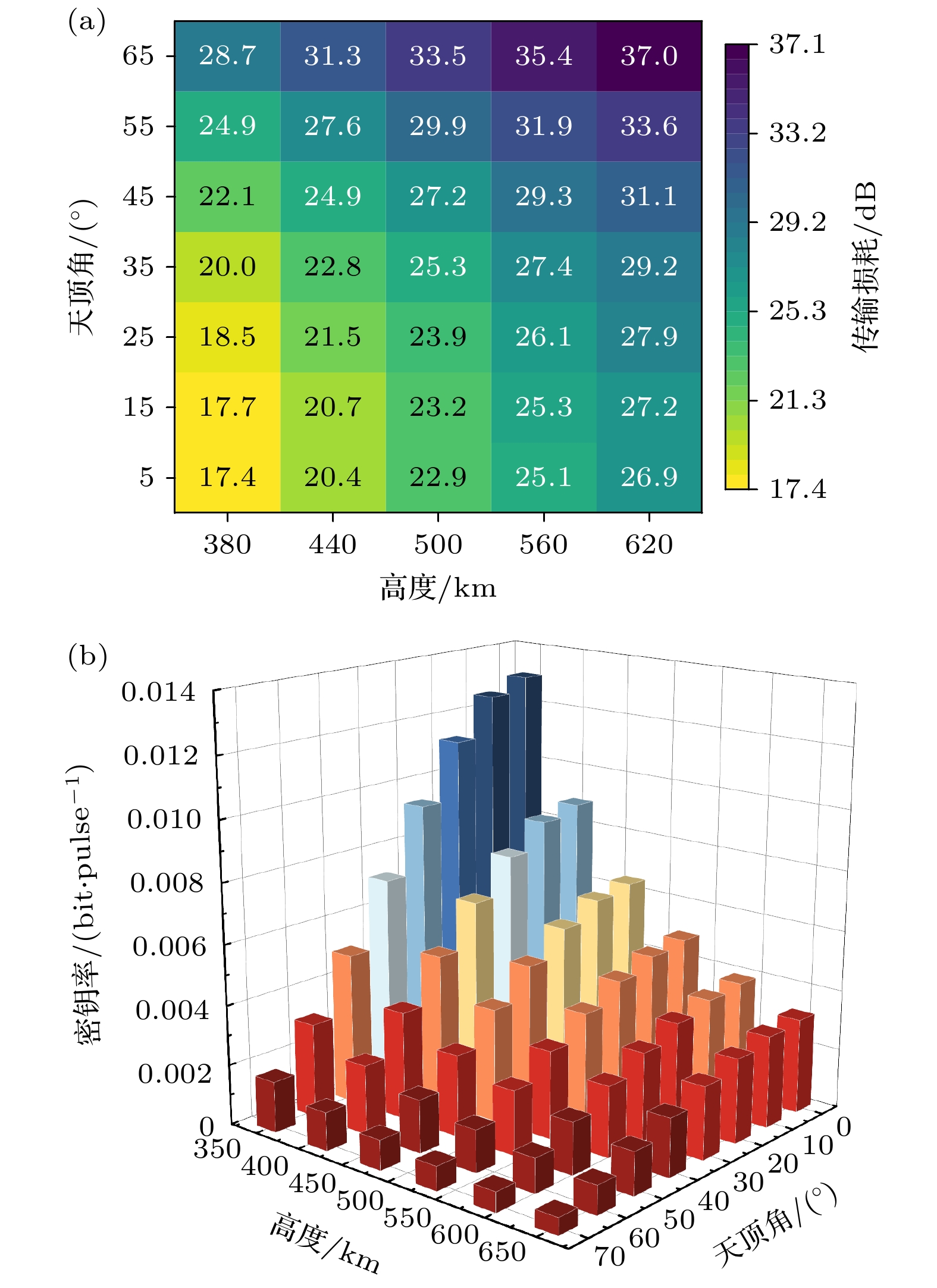
仿真得到在通信窗口内卫星与地面站的距 离、天顶角以及传输损耗与时间的关系如图3所示, 其中传输损耗是由传输效率$ {\tau _{{\text{end}}}} $取对数后计算得到. 从图3可以看到, 墨子号卫星与丽江站通信接入时间持续了大约288 s, 信道最高损耗约为39.3 dB, 距离约为1205.3 km, 天顶角约为69.9°. 最低损耗约为26.2 dB, 距离约为566.7 km, 天顶角约为28.3°.

链路的损耗与距离和天顶角有关, 在相同条件下, 距离越短, 天顶角越小, 传输损耗越小. 图4分析了轨道高度和天顶角对传输损耗以及密钥率生成的影响. 如图4(a)所示, 在下行链路中, 传输损耗随着天顶角和轨道高度的增加而增大. 在通信传输损耗的分析中, 当保持天顶角不变时, 传输损耗随轨道高度变化的影响相对较小; 而当轨道高度保持不变时, 天顶角的变化对传输损耗的影响则更为显著. 从图4(b)可以看到, 密钥率随着传输损耗的增大而减小, 即轨道高度和天顶角这两个参数同时影响着传输损耗和密钥率. 由于密钥量是持续时间和密钥率的乘积, 参数优化过程需要考虑通信接入时间与密钥率的平衡.

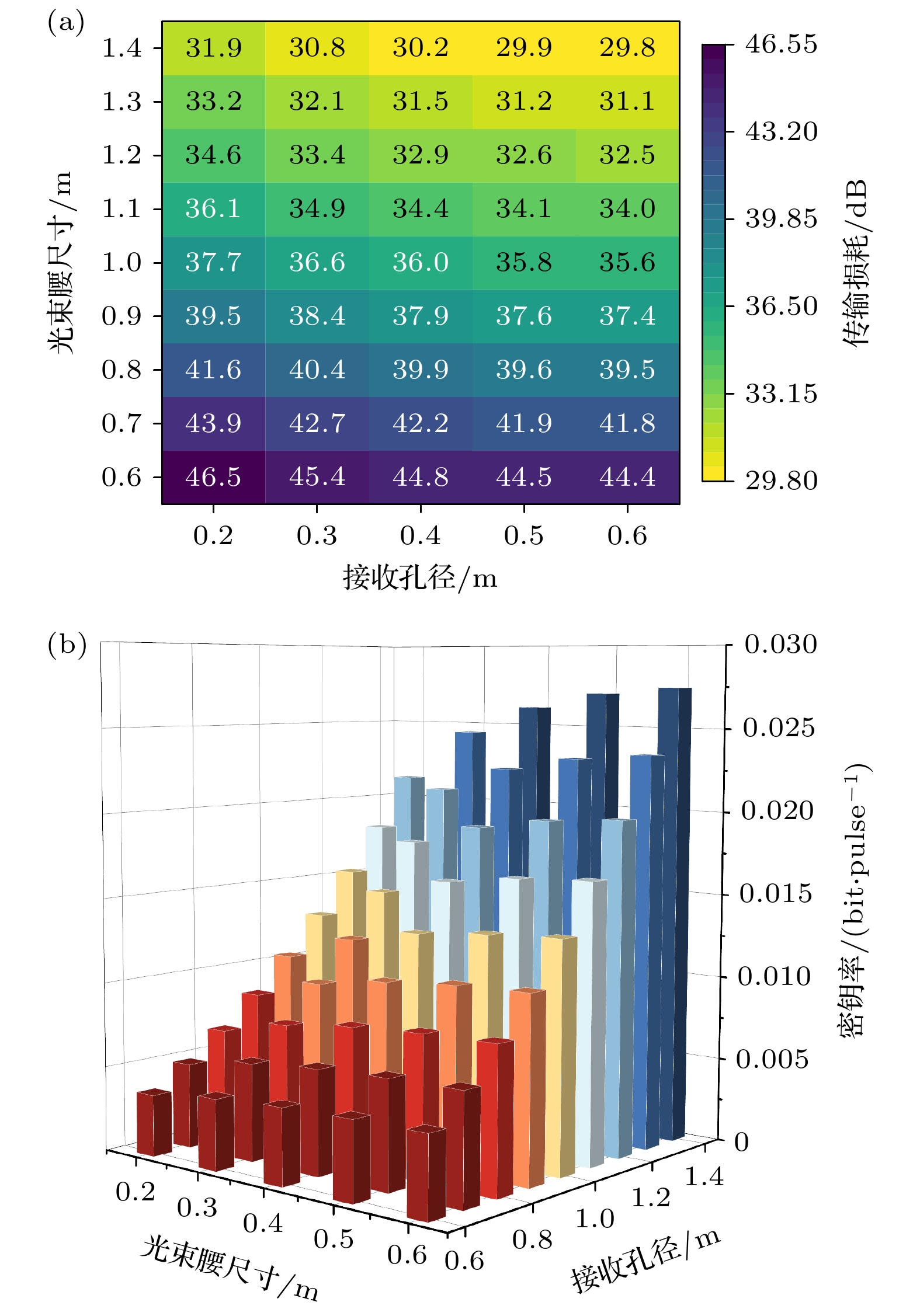
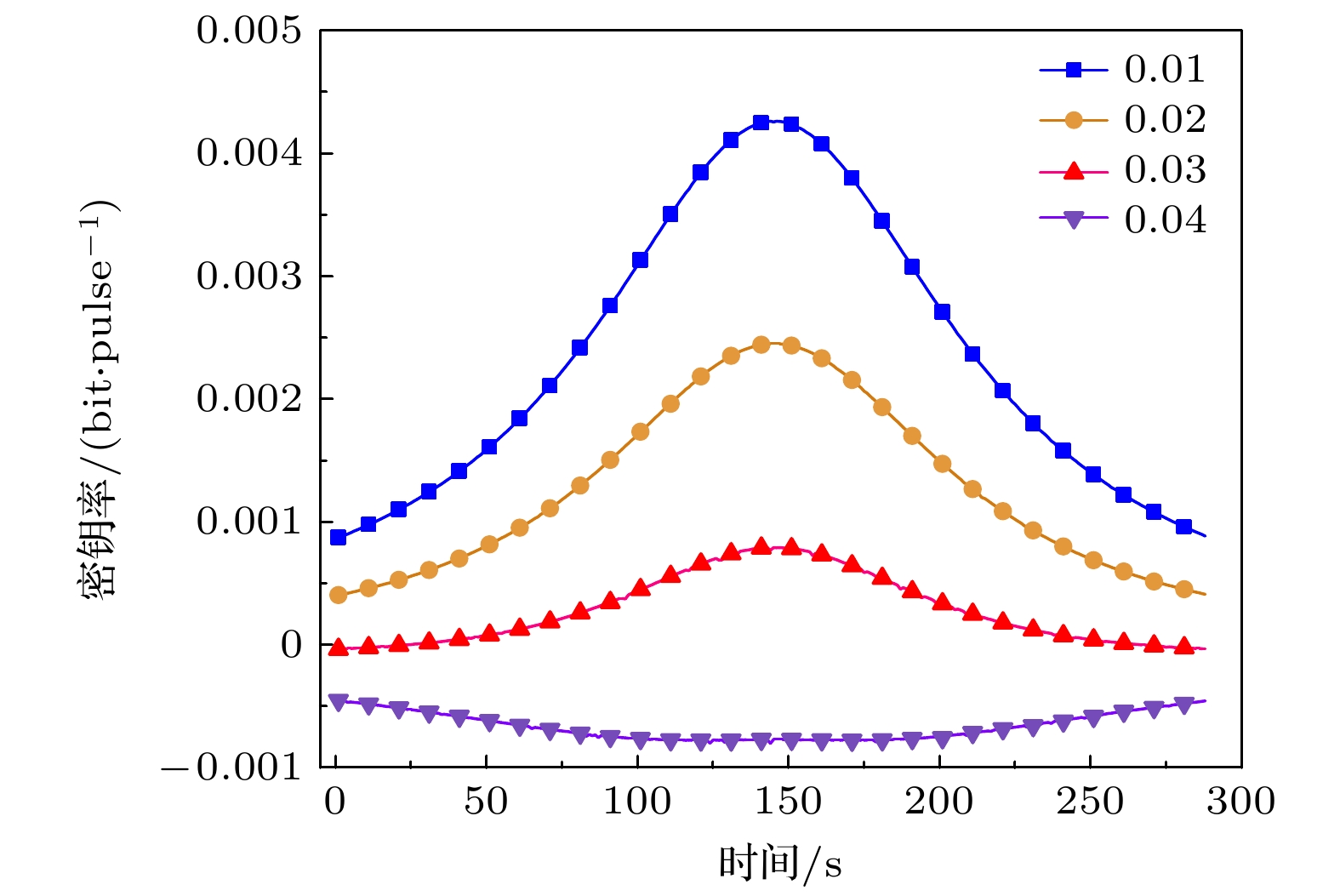
本文分析了卫星发射的光束腰尺寸和接收孔径对于协议性能的影响. 目前, 接收望远镜的孔径最大可达2.4 m^[32]. 为了探究两者对传输损耗的影响, 设置卫星高度为400 km, 天顶角为70°的情况下, 光束腰尺寸$w_{0} \in[0.2,0.6] $和接收孔径$ {a_{\text{R}}} \in \left[ {0.6, 1.4} \right] $对传输损耗和密钥率生成的影响如图5所示. 如图5(a)所示, 光束腰尺寸增大, 传输损耗逐渐减小, 尤其是在较小的接收孔径$(0.6,0.8) $范围内更加明显. 较小的光束腰尺寸会导致空间衍射影响更加突出, 空间衍射透过率$ {\tau _{\text{d}}} $变小, 带来更多的损耗. 接收孔径增大, 空间衍射透过率$ {\tau _{\text{d}}} $变大, 损耗逐渐减小. 这表明增大接收孔径可以减少损耗, 提高传输效率, 较低的损耗出现在接收孔径较大和光束腰尺寸较大的组合中. 从图5(b)可以看到, 密钥率随着传输损耗的增大而减小, 光束腰尺寸和接收孔径这两个参数同时影响着传输损耗和密钥率.

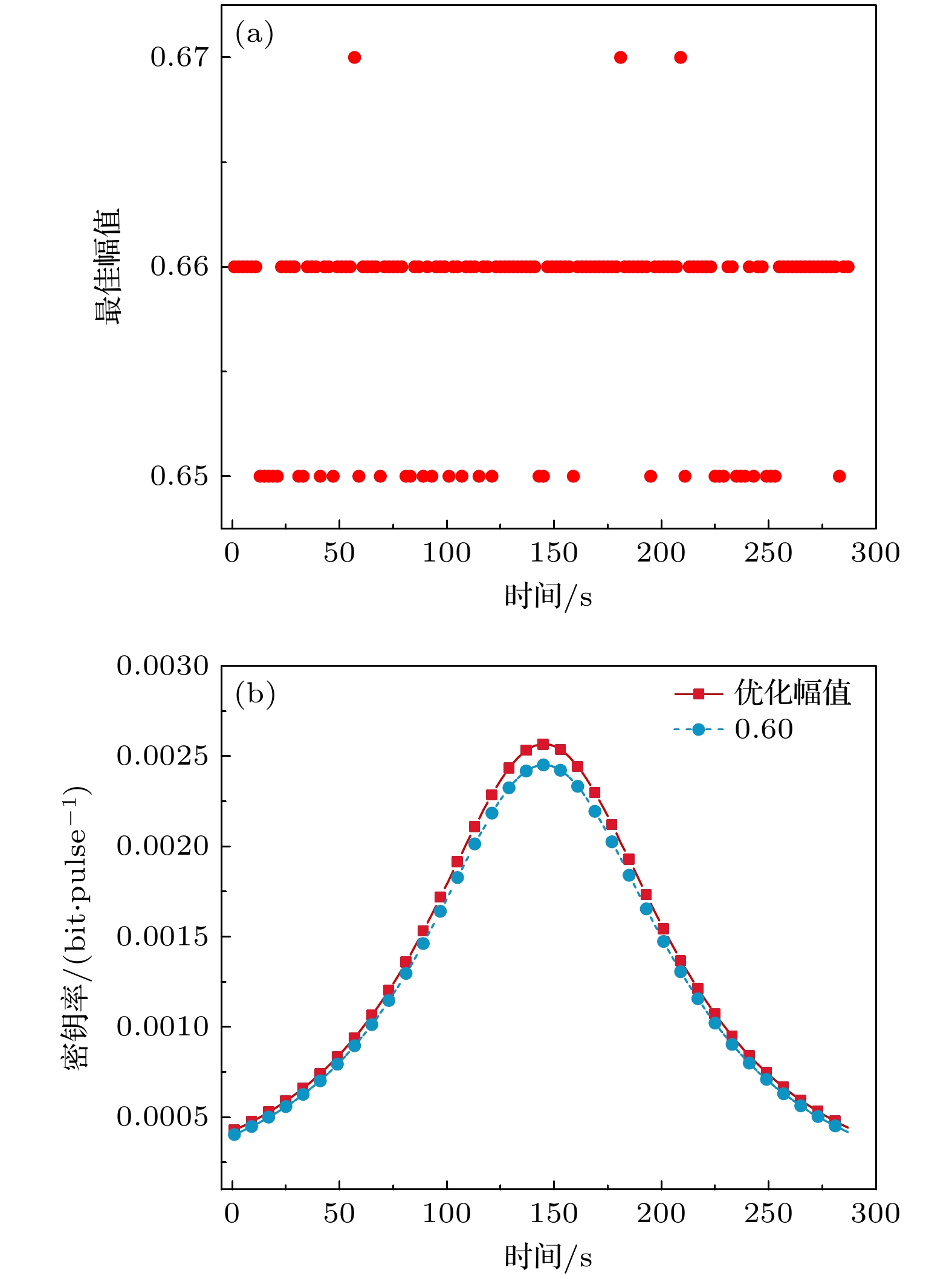
现实环境中不可避免的噪声因素会对量子信号产生破坏, 从而影响到密钥率的生成. 本文分析了过量噪声在实际动态轨道变化中对密钥率的 影响, 不同过量噪声下的协议密钥生成率如图6所示. 在墨子号-丽江站实时动态轨道中, 卫星与 地面站实时的距离$L $和天顶角θ不断变化, 影响着空间衍射、大气衰减和大气湍流变化, 进而影响 透射效率$ {\tau _{{\text{end}}}} $变化, 其中L, θ和$ {\tau _{{\text{end}}}} $变化成正相关. 在过量噪声固定时, 密钥率随着透射效率变化而 变化, 当透射效率最小时, 密钥率最大. 协议对0.01, 0.02和0.03的过量噪声具有较好的耐受性, 过量噪声超过0.03后空间信道DM CV-QKD协议不可行.

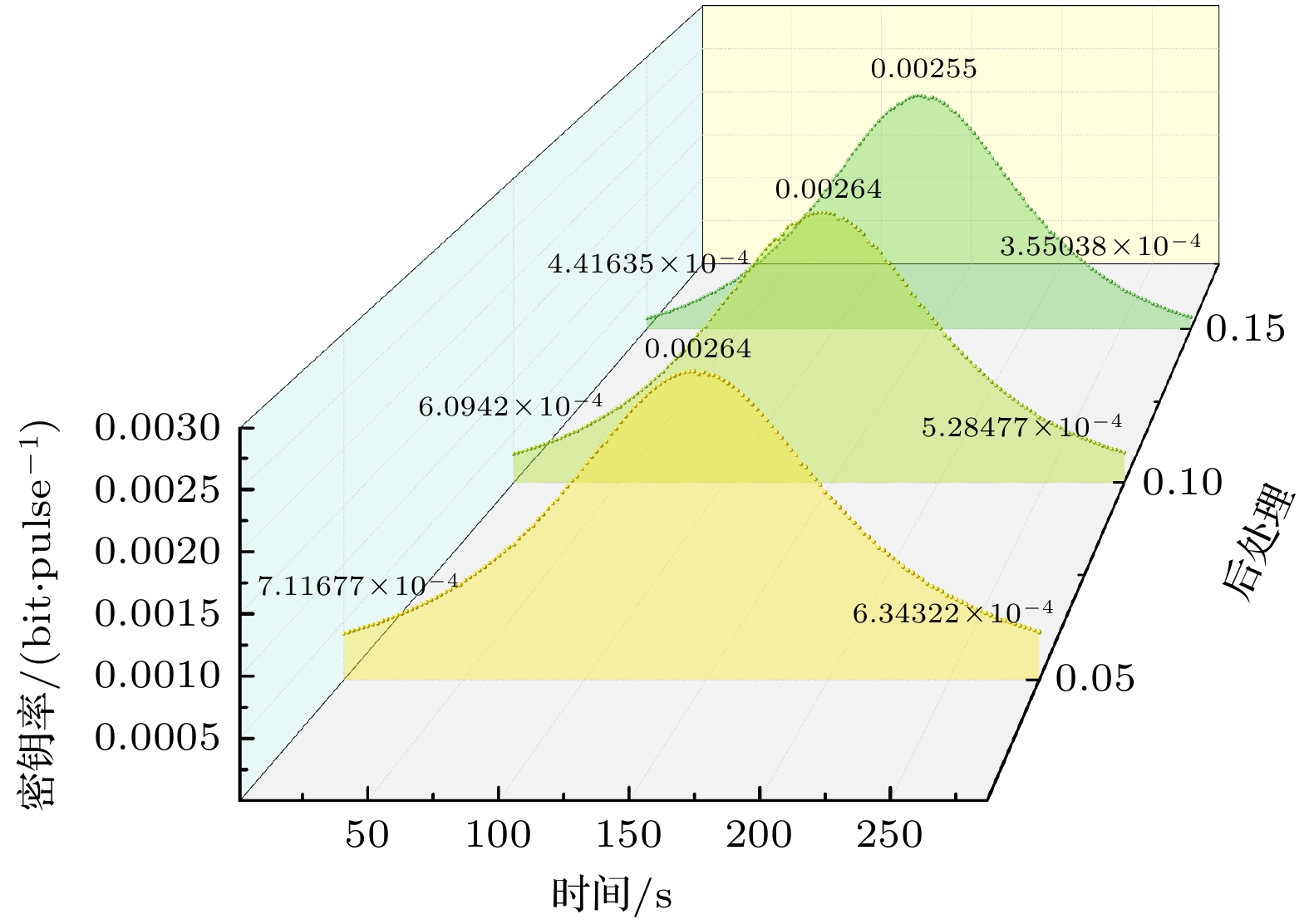
光量子调制幅度的改变, 密钥率也会发生变化. 较大的调制幅度会提高信号的识别概率, 从而在理论上提升密钥率, 但在实际应用中, 过大的调制幅度也会导致错误增多, 需要进行更多的纠错, 进而降低密钥率. 本文通过优化墨子号-丽江站实时轨道所对应的最佳幅值, 得到最佳幅值和优化后的密钥率如图7所示, 优化过程选取的过量噪声$ {\xi _{{\text{tot}}}} = 0.02 $, 后处理Δ = 0. 从图7(a)可得到, 在墨子号-丽江站实时动态轨道中, 最佳幅值集中在 0.66. 在最佳幅值下计算密钥率与预置调制幅度为0.6的密钥率进行比较, 从图7(b)可以看出密钥率有一定的提升. 通过后处理调整Δ进一步优化密钥率, 本文在过量噪声$ {\xi _{{\text{tot}}}} = 0.02 $和调制幅度α = 0.66的条件下, 分析不同后处理Δ对密钥的影响如图8所示.

从图8可以看出, 在每条曲线的峰值位置, 即传输损耗最小时, 光量子在传输过程中受到的影响较小, 后处理对密钥率的提升效果并不明显. 然而, 当传输损耗较大时, 尤其是在曲线的两端区域, 后处理的作用则显得尤为显著. 在实际空间实验中当空间环境变化较大或传输条件更为恶劣时, 可以通过调整后处理参数来优化密钥率, 以适应不同的传输状况.

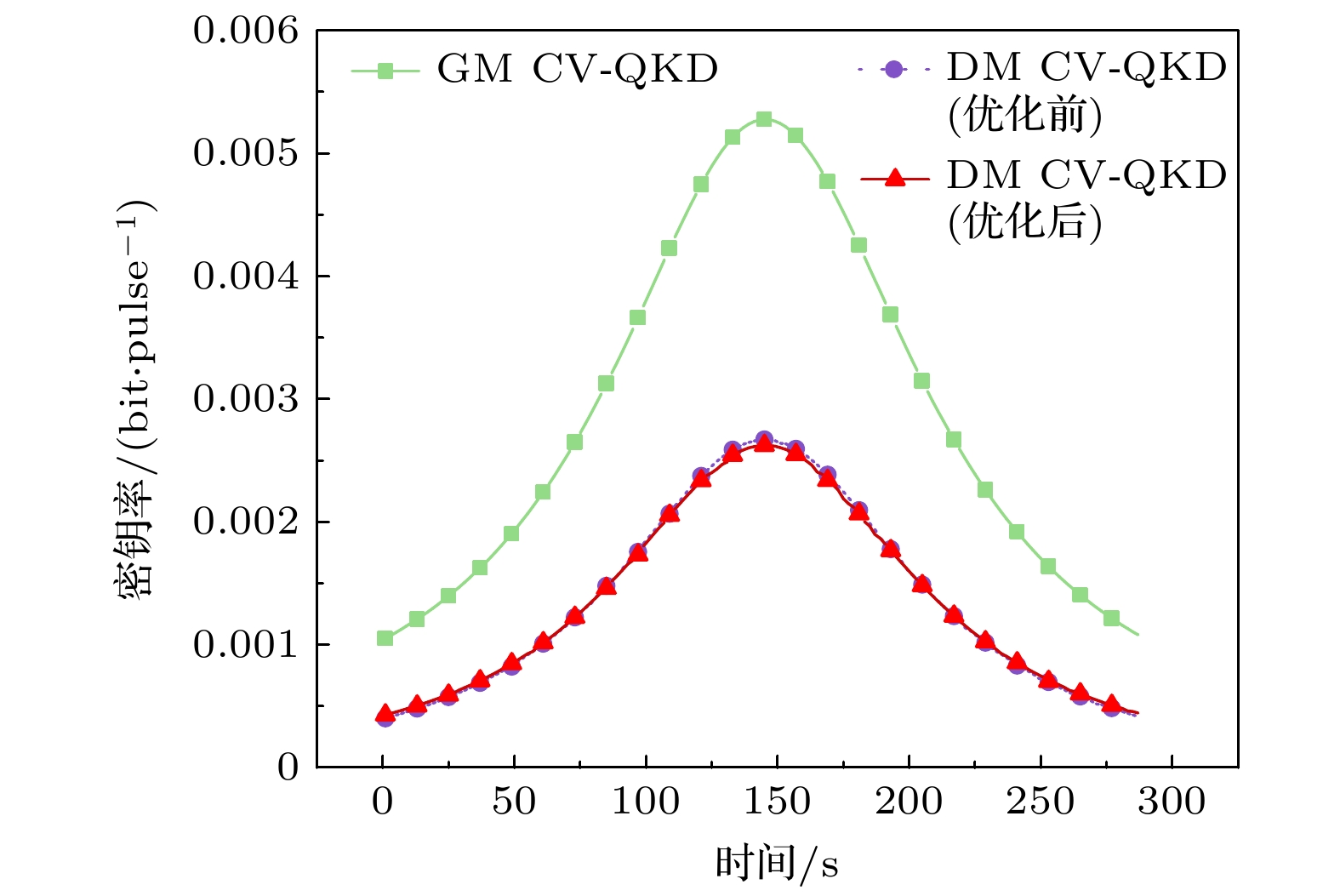
类比QKD在光纤信道中的结果分析对比, 本文比较了在墨子号-丽江站的相同轨道参数场景下, 空间GM CV-QKD与DM CV-QKD协议的性能. 其中GM CV-QKD采用的是在渐近极限时联合窃听下的GG02协议^[3], 部分仿真参数如表3所列, 协议对比效果如图9所示. 在墨子号-丽江站的轨道中, GM CV-QKD协议的密钥率明显优于DM CV-QKD协议, 即便通过幅值优化提升DM CV-QKD的密钥率, 其效果在GM CV-QKD的密钥率尺度上仍不显著. 高斯调制通过利用连续分布的信号空间, 实现了更高的信息熵, 从理论上提升了量子信道的容量和信息提取效率, 从而显著增强了量子密钥分发的性能. 而离散调制由于信号点的离散性, 其密钥率受到一定限制.

本文建立了星地轨道几何参数模型和大气信道退化模型, 分析了空间信道DM CV-QKD的可行性. 首先研究了卫星轨道高度、天顶角、接收器孔径、束腰尺寸和过量噪声对密钥生成率的影响, 考虑到轨道选择具有约束性, 可以通过增大接收孔径和束腰尺寸来提高密钥率. 其次是协议性能方面, 由于光量子在传输过程中受大气湍流影响, 其方差变大对后处理产生影响. 针对不同的大气环境, 在制备和后处理中, 找到最佳调制幅度和后处理值组合来提高密钥率. 文章对比分析了低轨卫星场景下空间信道渐近极限GM CV-QKD与DM CV-QKD的密钥生成率, 仿真结果表明在低轨卫星对地通信场景, 过量噪声$ {\xi _{{\text{tot}}}} = 0.02 $时, GM CV-QKD的密钥率性能优于DM CV-QKD. 但是考虑现有系统的兼容性和后处理的复杂程度, 离散调制的耦合性更高, 需要后处理计算量更少, 使其在现代通信系统中更具优势. 本文的参数选择优化方法可以为空间信道DM CV-QKD的实验研究提供理论支撑和参数选择.