高级搜索

计入枝晶运动生长的铸锭宏观偏析的研究

,  ,  , 

downloadPDF

上一篇

下一篇

张洋, 张士杰, 李云博, 李日. 计入枝晶运动生长的铸锭宏观偏析的研究[J]. 物理学报, 2025, 74(10): 108102-1. doi: 10.7498/aps.74.20241702
引用本文: 张洋, 张士杰, 李云博, 李日. 计入枝晶运动生长的铸锭宏观偏析的研究[J]. 物理学报, 2025, 74(10): 108102-1. doi: 10.7498/aps.74.20241702
shu
Yang ZHANG, Shijie ZHANG, Yunbo LI, Ri LI. Study of macroscopic segregation in ingot considering the movement and growth of equiaxial crystals[J]. Acta Physica Sinica, 2025, 74(10): 108102-1. doi: 10.7498/aps.74.20241702
Citation: Yang ZHANG, Shijie ZHANG, Yunbo LI, Ri LI. Study of macroscopic segregation in ingot considering the movement and growth of equiaxial crystals[J]. Acta Physica Sinica, 2025, 74(10): 108102-1. doi: 10.7498/aps.74.20241702
shu

计入枝晶运动生长的铸锭宏观偏析的研究

  • 河北工业大学材料科学与工程学院, 天津　300401

    • 作者简介: 张洋. E-mail: ZY504527442@163.com .
    通讯作者: E-mail: sdzllr@163.com.

  • 中图分类号: 81.10.Aj, 81.10.Mx, 47.11.Bc

Study of macroscopic segregation in ingot considering the movement and growth of equiaxial crystals

  • School of Materials Science and Engineering, Hebei University of Technology, Tianjin 300401, China

    • Corresponding author: E-mail: sdzllr@163.com.

  • MSC: 81.10.Aj, 81.10.Mx, 47.11.Bc

  • 摘要: 合金铸锭凝固过程中经常伴随着游离枝晶在运动的同时生长运动及相互碰撞等现象, 其对铸锭的温度场、流场、溶质场及微观组织等具有不可忽视的影响, 是研究铸锭凝固组织形成的关键问题之一. 元胞自动机-格子玻尔兹曼(CA-LB)耦合模型近年来在处理运动枝晶方面发展迅速, 该模型不仅可以很好地维持运动枝晶的形貌, 还可以合理地计算出枝晶间的相互碰撞. 本文改进了模拟游离枝晶运动生长的元胞自动机-格子玻尔兹曼模型, 采用交替方向隐式迭代法求解导热微分方程, 模拟参数不受稳定性条件限制. 分别验证了流场与固相和温度场耦合的准确性. 随后采用该模型分别模拟了Fe-0.34%C合金铸锭中等轴晶运动与否的凝固过程, 模拟结果表明, 等轴晶的运动会增大与临近枝晶的接触概率, 会使铸锭中的晶粒尺寸更加均匀; 枝晶的运动还会改变熔体中心部位的溶质分布, 特别是增大了顶部正偏析的大小以及范围; 等轴晶的运动会受到柱状晶的阻碍, 所以CET区域受枝晶运动的影响不大.
    Abstract: The solidification process of alloy ingot is often accompanied by the phenomena of free dendrites growing and colliding with each other while moving, which has a non-negligible influence on the temperature field, flow field, solute field and microstructure of the ingot, and it is one of the key issues in the study of ingot solidification organization formation. The cellular automata-lattice Boltzmann (CA-LB) coupling model has been developed rapidly in recent years in dealing with the moving dendrites, which can not only maintain the morphology of the moving dendrites well, but also calculate the mutual collisions between the dendrites reasonably. In this work, the cell-automata-lattice Boltzmann model for simulating the growth of free dendrites is improved. Alternating direction implicit iteration method is used to solve the differential heat conduction equation, and the simulation parameters are not limited by stability conditions in this method. In this research, the accuracy of the flow-solid coupling of the model is verified by taking the flow around a circular cylinder for example, and the temperature field of the model is well coupled under the natural convection condition. Finally, the solidification process of Fe-0.34%C alloy ingots with or without equiaxed grain movement is simulated using this model. The simulation results show that the movement of equiaxed grains increases the contact probability with the neighboring dendrites, which leads to a more uniform grain size in the ingot; the movement of dendrites also changes the solute distribution in the center of the melt, especially increasing the size and range of the hot-top segregation; the movement of equiaxed grains is impeded by the columnar crystals, and therefore the CET region is not much affected by the movement of dendrites.
  • 加载中

  • 图 1  圆柱绕流物理模型

    Figure 1.  Model of the flow around a cylinder.

    下载: 全尺寸图片 幻灯片

    图 2  圆柱绕流的结果　(a) Fs = 0.02; (b) Fs = 0.038; (c) Fs = 0.138; (d) Fs = 0.363

    Figure 2.  Result of the flow around a cylinder: (a) Fs = 0.02; (b) Fs = 0.038; (c) Fs = 0.138; (d) Fs = 0.363.

    下载: 全尺寸图片 幻灯片

    图 3  圆柱绕流结果对比

    Figure 3.  Comparison of results.

    下载: 全尺寸图片 幻灯片

    图 4  Rayleigh–Bénard自然对流模型示意图

    Figure 4.  Schematic of the Rayleigh-Bénard natural convection model.

    下载: 全尺寸图片 幻灯片

    图 5  不同Ra数下系统达到稳态时的等温线分布　(a) Ra = 2500; (b) Ra = 5000; (c) Ra = 10000; (d) Ra = 50000

    Figure 5.  Isothermal distribution of the system reaching steady state for different Ra numbers: (a) Ra = 2500; (b) Ra = 5000; (c) Ra = 10000; (d) Ra = 50000.

    下载: 全尺寸图片 幻灯片

    图 6  稳态Nu数随Ra数的变化规律

    Figure 6.  Variation rule of steady state Nu number with Ra number.

    下载: 全尺寸图片 幻灯片

    图 7  铸锭物理模型

    Figure 7.  Physical model of ingot.

    下载: 全尺寸图片 幻灯片

    图 8  不考虑等轴晶运动时铸锭的凝固过程　(a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s

    Figure 8.  Solidification process of ingot without considering the equiaxial crystal motion: (a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s.

    下载: 全尺寸图片 幻灯片

    图 9  考虑等轴晶运动的铸锭凝固过程　(a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s

    Figure 9.  Solidification process of ingot considering equiaxial crystal motion: (a) t = 2.0 s; (b) t = 4.5 s; (c) t = 4.6 s; (d) t = 4.8 s; (e) t = 5.2 s; (f) t = 5.6 s; (g) t = 6.0 s; (h) t = 7.0 s; (i) t = 10.0 s; (j) t = 18.0 s.

    下载: 全尺寸图片 幻灯片

    图 10  不同情况下铸锭完全凝固时的形貌　(a) 等轴晶运动; (b) 等轴晶不运动

    Figure 10.  Morphology of a fully solidified ingot in different cases: (a) Equiaxed grain motion; (b) equiaxed grain immobility.

    下载: 全尺寸图片 幻灯片

    图 11  不同情况下铸锭完全凝固的溶质分布　(a) 等轴晶运动; (b) 等轴晶不运动

    Figure 11.  Solute distribution in the fully solidified ingot for different cases: (a) Equiaxed grain motion; (b) equiaxed grain immobility.

    下载: 全尺寸图片 幻灯片

    图 12  等轴晶运动与否和实验结果的偏析程度对比

    Figure 12.  Comparison between the presence or absence of equiaxed crystal movement and the degree of segregation observed in experimental results.

    下载: 全尺寸图片 幻灯片

    表 1  不同位置的${C_{\text{e}}}$与${D_{\text{e}}}$的取值方法

    Table 1.  Methods of taking values of ${C_{\text{e}}}$ and ${D_{\text{e}}}$ at different locations.

    液相固相界面界面与固相之间界面与液相之间
    ${C_{\text{e}}}$${C_{\text{l}}}$${C_{\text{s}}}/k$${C_{\text{l}}}$${C_{\text{l}}}$${C_{\text{l}}}$
    ${D_{\text{e}}}$${D_{\text{l}}}$${D_{\text{s}}}$${D_{\text{l}}}$${D_{\text{s}}}$${D_{\text{l}}}$
    下载: 导出CSV

    表 2  模拟用到的参数

    Table 2.  Parameters used for simulation.

    Physical parameter Value
    Solidus temperature, ${T_{\text{m}}}/K$ 1811.15
    Liquidus temperature, ${T_0}/K$ 1723.15
    Liquidus slope, ${m_{\text{l}}}/({{\mathrm{K}} {\cdot} {{\text{%}} ^{-1}}})$ –80.45
    Interface kinetics coefficient, ${\mu _{\text{k}}}/({1{0^{ - 3}}\;{\mathrm{m}} {\cdot} {{\mathrm{s}}^{ - 1}} {\cdot} {\mathrm{K}}})$ 2
    Kinetic anisotropy strength, ${\delta _{\text{k}}}$ 0.3
    Thermodynamic anisotropy, ${\delta _{\text{t}}}$ 0.3
    Liquid Viscosity, $\nu /({1{0^{ - 3}}\;{\mathrm{kg}} {\cdot} {{\mathrm{m}}^{ - 1}} {\cdot} {{\mathrm{s}}^{ - 1}}})$ 3.6
    Diffusivity in liquid, ${D_{\text{l}}}/( {{{10}^{ - 8}}\;{{\text{m}}^2} {\cdot} {{\text{s}}^{ - 1}}} )$ 2
    Diffusivity in solid, ${D_{\text{s}}}/( {{{10}^{ - 9}}\;{{\text{m}}^2} {\cdot} {{\text{s}}^{ - 1}}} )$ 1
    Partition coefficient, $k$ 0.36
    Average Gibbs-Tomson
    coefficient, $ {\bar \varGamma /( {{{10}^{ - 7}}\;{\text{m}} {\cdot} {\text{K}}} )}$    		 1.9
    Specific heat capacity, ${C_{\text{p}}}/( {{\text{J}} {\cdot} {\text{k}}{{\text{g}}^{ - 1}} {\cdot} {{\text{K}}^{ - 1}}} )$ 455
    Convective heat transfer
    coefficient, $h/({\mathrm{W}} {\cdot} {{\mathrm{m}}^{ - 2}} {\cdot} {{\mathrm{K}}^{ - 1}})$    		 600
    Thermal conductivity, $\lambda /({\text{W}} {\cdot} {{\text{m}}^{ - 1}} {\cdot} {{\text{K}}^{ - 1}})$ 30
    Thermal expansion coefficient, $ {\beta _{\text{T}}}/( {{{10}^{ - 4}}\;{{\mathrm{K}}^{ - 1}}} ) $ 2
    Solutal expansion coefficient, $ {\beta _{\text{c}}}/( {{{10}^{ - 2}} \;{{\text{%}} ^{ - 1}}} ) $ 1.1
    Latent heat, $L/( {{{10}^3}\;{\text{J}} {\cdot} {\text{k}}{{\text{g}}^{ - 1}}} )$ 269.55
    Density, $\rho /( {{\text{kg}} {\cdot} {{\text{m}}^{ - 3}}} )$ 7001
    下载: 导出CSV

    表 3  不同位置的平均浓度以及偏析程度

    Table 3.  Average concentration and segregation of index (SI) at different locations.

    ⅠⅡⅢⅣⅤⅥⅦⅧⅨ
    运动0.2270.2570.2920.3090.3230.4410.2820.2890.351
    偏析/%–33.2–24.4–14.1–9.1–5.029.7–17.1–15.03.2%
    不运动0.2280.2780.2980.30.3410.3840.2780.2890.345
    偏析/%–32.9–18.2–12.4–11.80.312.9–18.2–15.01.5%
    下载: 导出CSV
  • [1] Qi X B, Chen Y, Kang X H, Li D Z, Gong T Z 2017 Sci Rep 7 45770 doi: 10.1038/srep45770
    [2] Rátkai L, Pusztai T, Gránásy L 2019 npj Comput. Mater. 5 113 doi: 10.1038/s41524-019-0250-8
    [3] 张士杰, 王颖明, 王琦, 李晨宇, 李日 2021 物理学报 70 238101 doi: 10.7498/aps.70.20211292 Zhang S J, Wang Y M, Wang Q, Li C Y, Li R 2021 Acta Phys. Sin. 70 238101 doi: 10.7498/aps.70.20211292
    [4] Sakane S, Takaki T, Ohno M, Shibuta Y, Aoki T 2020 Comput. Mater. Sci. 178 109639 doi: 10.1016/j.commatsci.2020.109639
    [5] Ren J K, Chen Y, Cao Y F, Sun M Y, Xu B, Li D Z 2020 J. Mater. Sci. Tech. 58 171 doi: 10.1016/j.jmst.2020.05.005
    [6] Yamanaka N, Sakane S, Takaki T 2021 Comput. Mater. Sci. 197 110658 doi: 10.1016/j.commatsci.2021.110658
    [7] Zhang S J, Zhu B F, Li Y B, Zhang Y, Li R 2024 Comput. Mater. Sci. 245 113308 doi: 10.1016/j.commatsci.2024.113308
    [8] Liu L, Pian S, Zhang Z, Bao Y C, Li R, Chen H J 2018 Comput. Mater. Sci. 146 9 doi: 10.1016/j.commatsci.2018.01.015
    [9] Wang Q, Wang Y M, Zhang S J, Guo B X, Li C Y, Li R 2021 Crystals 11 1056 doi: 10.3390/cryst11091056
    [10] Sakane S, Aoki T, Takaki T 2022 Comput. Mater. Sci. 211 111542 doi: 10.1016/j.commatsci.2022.111542
    [11] Meng S X, Zhang A, Guo Z P, Wang Q G 2020 Comput. Mater. Sci. 184 109784 doi: 10.1016/j.commatsci.2020.109784
    [12] Takaki T 2023 IOP Conf. Ser. Mater. Sci. Eng. 1274 012009 doi: 10.1088/1757-899X/1274/1/012009
    [13] Flemings M C, Mehrabian R, Nereo G E 1968 T. Metall. Soc. AIME 239 1449
    [14] Bennon W D, Incropera F P 1987 Int. J. Heat Mass Tran. 30 2161 doi: 10.1016/0017-9310(87)90094-9
    [15] Bennon W D, Incropera F P 1987 Int. J. Heat Mass Tran. 30 2171 doi: 10.1016/0017-9310(87)90095-0
    [16] Beckermann C, Viskanta R 1988 Physicochemical Hydrodynamics 10 195
    [17] Gu J P, Beckermann C 1999 Metall. Mater. Trans. A 30 1357 doi: 10.1007/s11661-999-0284-5
    [18] Wu M, Ludwig A, Kharicha A 2016 Appl. Math. Model. 41 102 doi: 10.1016/j.apm.2016.08.023
    [19] Zhang Z, Bao Y, Liu L, Pian S, Li R 2018 Metall. Mater. Trans. A 49 2750 doi: 10.1007/s11661-018-4609-0
    [20] Zhang S, Li Y, Zhang S, Zhu B, Li R 2025 Int. J. Therm. Sci. 211 109737 doi: 10.1016/j.ijthermalsci.2025.109737
    [21] Rappaz M, Thévoz P H 1987 Acta Metall. 35 2929 doi: 10.1016/0001-6160(87)90292-6
    [22] Zhu M F, Lee S Y, Hong C P 2004 Phys. Rev. E 69 061610 doi: 10.1103/PhysRevE.69.061610
    [23] Sun D K, Zhu M F, Pan S Y, Yang C R, Raabe D 2011 Comput. Math. Appl. 61 3585 doi: 10.1016/j.camwa.2010.11.001
    [24] Zhu M, Stefanescu D 2007 Acta Mater. 55 1741 doi: 10.1016/j.actamat.2006.10.037
    [25] Wen B, Zhang C, Tu Y, Wang C, Fang H 2014 J. Comput. Phys. 266 161 doi: 10.1016/j.jcp.2014.02.018
    [26] Mei R, Yu D, Shyy W, Luo L S 2002 Phys. Rev. E 65 041203 doi: 10.1103/PhysRevE.65.041203
    [27] Drummond J E, Tahir M I 1984 Int. J. Multiphase Flow 10 515 doi: 10.1016/0301-9322(84)90079-X
    [28] 张照 2020 硕士学位论文 (天津: 河北工业大学) Zhang Z 2020 M. S. Thesis (Tianjin: Hebei University of Technology
    [29] Shan X 1997 Phys. Rev. E 55 2780 doi: 10.1103/PhysRevE.55.2780
    [30] Clever R M, Busse F H 1974 J. Fluid Mech. 65 625 doi: 10.1017/S0022112074001571
    [31] Wu M, Könözsy L, Ludwig A, Schützenhöfer W, Tanzer R 2008 Steel Res. Int. 79 637 doi: 10.1002/srin.200806177
    [32] Luo S, Wang W, Zhu M 2018 Int. J. Heat Mass Tran. 116 940 doi: 10.1016/j.ijheatmasstransfer.2017.09.074
    [33] Ge H H, Li J, Guo Q T, Ren F L, Xia M X, Yao J H, Li J G 2021 Metall. Mater. Trans. B 52 2992 doi: 10.1007/s11663-021-02194-7
  • 加载中
图( 12) 表( 3)
计量
  • 文章访问数:  35
  • HTML全文浏览数:  35
  • PDF下载数:  0
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-09
  • 刊出日期:  2025-05-20

计入枝晶运动生长的铸锭宏观偏析的研究

    通讯作者: E-mail: sdzllr@163.com.
    作者简介: 张洋. E-mail: ZY504527442@163.com
  • 河北工业大学材料科学与工程学院, 天津　300401
  • 收稿日期:  2024-12-09

摘要: 合金铸锭凝固过程中经常伴随着游离枝晶在运动的同时生长运动及相互碰撞等现象, 其对铸锭的温度场、流场、溶质场及微观组织等具有不可忽视的影响, 是研究铸锭凝固组织形成的关键问题之一. 元胞自动机-格子玻尔兹曼(CA-LB)耦合模型近年来在处理运动枝晶方面发展迅速, 该模型不仅可以很好地维持运动枝晶的形貌, 还可以合理地计算出枝晶间的相互碰撞. 本文改进了模拟游离枝晶运动生长的元胞自动机-格子玻尔兹曼模型, 采用交替方向隐式迭代法求解导热微分方程, 模拟参数不受稳定性条件限制. 分别验证了流场与固相和温度场耦合的准确性. 随后采用该模型分别模拟了Fe-0.34%C合金铸锭中等轴晶运动与否的凝固过程, 模拟结果表明, 等轴晶的运动会增大与临近枝晶的接触概率, 会使铸锭中的晶粒尺寸更加均匀; 枝晶的运动还会改变熔体中心部位的溶质分布, 特别是增大了顶部正偏析的大小以及范围; 等轴晶的运动会受到柱状晶的阻碍, 所以CET区域受枝晶运动的影响不大.

English Abstract

    全文HTML

    1.   引　言

    • 铸锭的凝固过程对其最终质量有极其重要的影响, 在其冷却凝固进程中, 熔体内部存在着大量等轴晶粒的移动、碰撞或分离、下沉及堆集等运动行为, 这些游离枝晶沉降在铸锭底部形成了底部三角锥形负偏析, 同时游离枝晶的运动也对铸锭凝固过程的温度场、流场、溶质场、微观组织形貌等均有影响. 研究铸锭凝固过程中游离枝晶的运动对准确预测铸锭质量有重要的意义.

      当前模拟枝晶运动的主要方法是相场法(phase field, PF), 也有部分研究采用元胞自动机(cellular automata, CA)模型, 这两个模型在处理枝晶运动方面各有优劣. Qi等[1]提出了一种包含枝晶与熔体两相流动的相场模型, 并将其用于模拟铝基合金枝晶的运动生长以及碰撞行为, 结果初步说明了晶体沉降会影响溶质分布. Rátkai等[2]使用可重叠的多网格方案处理流体中运动粒子, 其中每个粒子都有一套独立的带有局部物理场的运动网格, 通过多小球下落与强制对流下的枝晶CET过程验证了模型在模拟凝固过程中的枝晶生长、运动和碰撞以及溶质扩散和熔体移动的可行性. Zhang等[3]同样使用多套网格的方法改进了基于CA与LBM (lattice Boltzmann methods)耦合的方法模拟枝晶生长的模型, 它不仅能很好地维持运动中枝晶的形貌, 而且能很好地模拟出枝晶间的碰撞行为. Sakane等[4]使用相场法加上多GPU并行计算模拟了铸锭中大量枝晶的运动过程. Ren等[5]基于矢量相场和两相流模型对凝固过程中多个枝晶的运动和生长进行了建模, 模型中采用两级时间步进方案、自适应网格细化和并行计算等方式提高计算速度, 使用该模型分别模拟了单个与多个Al-Cu合金的枝晶的沉降与生长. Yamanaka等[6]在Takaki的基础上引入双障碍势的多相场(multi phase field, MPF)并评估了其准确性, 并用来计算多枝晶沉降与半固态变形过程. Zhang等[7]在其原有研究的基础上开发了一种GPU加速的CA-LBM耦合的模型, 模拟了Al-Cu合金的CET过程中大量的枝晶下落堆叠过程.

      文献[8-11]采用这两种方法进行三维枝晶运动计算, 与二维模拟相比, 三维计算的计算量激增, 即便是使用大型计算机集群也只能模拟相当有限的计算尺度[12], 大计算域模拟方面的研究存在巨大挑战.

      宏观偏析数值模拟的研究在Flemings等[13]于20世纪60年代提出局部溶质再分配方程之后经过几十年的发展已经取得了较大进展. 20世纪80年代Bennon和Incropera[14]将固相、液相和糊状区统一为连续介质建立了连续介质模型, 在他们后续的研究[15]中模拟了NH4Cl-H2O 的凝固过程, 并首次预测了 A 型偏析. 20世纪80年代末Beckermann和Viskanta[16]将模拟区域划分为有限个体积单元, 用同一套守恒方程处理体积单元内的固相和液相, 建立了体积平均模型. 使用该模型模拟[17]的最终凝固组织中存在顶部正偏析以及A型偏析. 在此之后的21世纪多相模型迅速发展, Wu等[18]建立了液相、柱状晶、等轴晶、气相的四相体积平均模型, 模拟了 CET 过程并与 10.5 t铸件实验对比, 结果吻合良好.

      连续介质模型和体积平均模型均是在连续性方程的基础上建立起来的, 多相体积平均模型虽然考虑了不同的枝晶组织, 但没有计算枝晶生长过程中的具体形态. 若要更加真实地模拟出铸锭中的宏观偏析, 枝晶的组织形貌与运动都是不可忽略的重要因素. 以往关于铸锭微观组织凝固的研究论文中, 考虑铸锭凝固过程中游离枝晶运动的数量很少, 其中模拟了大量枝晶运动的论文[4]并未给出最终的完全凝固的计算结果, 也没有分析枝晶的运动是否会对铸锭中的偏析产生影响. 本文拟旨本课题组的研究基础上[3,7,19,20], 将游离枝晶的运动计入铸锭凝固过程中, 建立相应的数值模型, 模拟分析铸锭中微观组织的形成发展过程和宏观偏析的分布, 分析等轴晶运动对计算结果的影响.

    2.   模　型

    • 本文采用CA模型计算枝晶的生长以及捕获、LBM处理流场、显示有限差分法计算溶质分布、基于FDM的交替方向隐式(alternating direction implicit, ADI)方法处理温度场的演化. 分别采用具有伽利略不变性的动量交换法(Galilean-invariant momentum exchange GME)和硬球模型处理枝晶的运动和碰撞.

      • 2.1.   CA-LBM模型

    • CA中的溶质扩散模型自Rappaz和Thévoz[21]提出之后经多位学者改进, 本文采用Zhu等[22]于2004年改进的用于定量分析合金凝固过程的模型. 该模型考虑了温度、溶质浓度与界面曲率, 可以很好地模拟出枝晶微观组织的演化过程. 枝晶尖端的总过冷度由以下公式给出:

      其中ΔTT代表温度过冷，ml是液相线斜率, ${C_0}$是初始浓度, 界面曲率$ \bar K $由(3)式计算, $\varGamma $是Gibbs-Thomson系数可通过下式计算:

      其中${\delta _{\text{t}}}$为热力学各向异性系数, $\theta $和${\theta _0}$分别是固液界面法向和晶体择优取向与水平面之间的夹角.

      枝晶生长速度${V_{\text{g}}}$为

      其中${\mu _{\text{k}}}$是界面动力学系数, ${\delta _{\text{k}}}$代表动力学各向异性的大小.

      界面元胞的固相变化率可以由枝晶生长速度${V_{\text{g}}}$通过下式计算:

      其中${f_{\text{s}}}$是固相分数、$t$是时间、$\Delta a$是元胞尺寸、$G$是几何因子, 与邻近元胞状态相关, 可通过下式计算:

      式中${b_0}$是经验系数, 一般取$0.4$. $ {s}_{m}^{\mathrm{I}} $和$ {s}_{m}^{\mathrm{II}} $分别代表元胞最邻近与次临近的元胞状态:

      LBM采用单松弛时间的D2Q9模型处理流场的演化过程, 相应的格子玻尔兹曼方程如下:

      其中, $x$和$t$分别代表粒子的位置与时间; $\Delta t$代表时间步长; ${{\boldsymbol{e}}_i}$代表离散后的粒子速度, ${f_i}$为流场的粒子分布函数, ${\tau _f}$为流场的松弛时间, ${F_i}$为流场的外力项, 流场的平衡分布函数$f_{\text{i}}^{{\text{eq}}}$可通过下式计算获得

      其中${\omega _{\text{i}}}$是权重系数, $c$是格子声速, ${\boldsymbol{u}}$是流体宏观速度, 流场的松弛时间${\tau _{\mathrm{f}}}$与运动黏度$\nu $存在以下关系:

      流场中的外力项可通过下式计算:

      根据Boussinesq近似[23], 在小Mach数流动条件下除浮力项外流体的密度为常数, 在浮力部分密度表示为局部温度与浓度的线性函数:

      是粒子受到的合力$F$由下式计算:

      其中${\boldsymbol{g}}$为重力加速度; ${\rho _0}$, ${T_0}$, ${C_0}$分别是初始密度, 温度和浓度; ${\beta _{\text{T}}}$和${\beta _{\text{C}}}$分别为温度膨胀系数与溶质膨胀系数. 流体的密度$\rho $, 速度${\boldsymbol{u}}$由下式计算:

      • 2.2.   溶质场计算的数值格式

    • 大多数使用LBM计算枝晶溶质分布的研究都是假设固相不扩散来简化问题, 这种假设很大程度上影响了铸锭完全凝固后的溶质分布, 而显式有限差分法可以有效地同时处理固相、液相以及界面处的溶质扩散问题, 使计算的结果更加符合实际情况. 同时考虑固相扩散与液相扩散的对流方程[24]如下:

      其中${\boldsymbol{u}}$是速度矢量, ${f_{\text{s}}}$是单位元胞的固相率, $\nabla $是梯度算子, $k$为固相与液相间的平衡分配系数, $t$是时间, ${C_{\text{e}}}$与${D_{\text{e}}}$分别代表不同条件下等价处理的溶质组分与扩散系数, 具体处理见表1, 其中${C_{\text{l}}}$, ${C_{\text{s}}}$分别表示液相与固相中的溶质浓度, ${D_{\text{s}}}$和${D_{\text{l}}}$分别表示液相与固相中的溶质扩散系数.

      固液界面的溶质分配方法如下:

      对于每个固相率非零的界面元胞n, 在迭代N次后其溶质成分由下式计算:

      其中$N$代表该元胞转变为界面元胞后进行的迭代次数, 当一个元胞被捕获为界面元胞时, $N = 1$.

      • 2.3.   温度场计算的数值格式

    • 合金的溶质扩散系数Dl、运动黏度$\nu $以及热扩散率$\alpha $之间的差距很大, 往往会超过3个数量级, 常规方法无法同时满足溶质场、流场以及温度场这三场的稳定性条件. 本文采用ADI方法计算三场中稳定性条件最为苛刻的温度场, 该方法可以将二维问题转化为一维问题, 在每一迭代步中, 所求解的方程具有更为简单的结构.

      在每一次ADI方法的循环中都会分别经历一次X方向的隐式计算与Y方向上的隐式计算. (18)式为包含对流项的温度扩散方程, 其中${\boldsymbol{u}}$是速度矢量, $\nabla $和${\nabla ^2}$分别是梯度算子和拉普拉斯算子, 为了方便解释下文以二维不含对流项的导热微分方程(19)式为例加以说明:

      其中$\alpha $为热扩散率, 由热导率$\lambda $, 密度$\rho $和热容${C_{\text{p}}}$共同决定.

      通过时间导数向前差分, 空间导数中心差分将换热方程离散. 并拆分为X与Y两个方向迭代处理, 对于X方向来说:

      可以整理为以下形式:

      当j = 1时:

      综上, 当j = 1时, X方向的ADI算法可写为以下形式:

      以此类推可以得到经过一半时间步不同行数的温度分布.

      Y方向的导热微分方程如下:

      同样可以整理类似(21)式的格式:

      由于整个计算域上半个时间步的温度$T_{i, j}^{n + 0.5}$已经通过(23)式计算求得, 它们将被并入常数项数组$d$中.

      当i = 1时:

      整理后Y方向的ADI算法可写为以下形式:

      先对整个计算域的每一行都进行一次X方向的隐式计算, 此时经过了${{\Delta }}t/2$, 再根据求得的新的温度值对整个计算域的每一列进行Y方向的隐式计算, 至此完成了一次温度场ADI方法的计算.

      对流项采用迎风格式处理, 带有对流项的温度扩散方程同样可以在离散后整理成如(23)式和(27)式的形式, 由于系数矩阵是三对角矩阵, 使用追赶法很容易求出某一时刻同一行或列温度的值. 凝固过程中的潜热采用等效比热法处理, 此方法认为铸件凝固过程中的比热容由两部分组成, 一是铸件材料的真实比热容, 二是结晶潜热对相变过程比热容的贡献, 即

      式中, ${C_{\text{E}}}$是等效比热容, ${C_{\text{p}}}$是真实比热容, $L$是结晶潜热.

      • 2.4.   枝晶运动与碰撞的数值模型

    • 将在熔体中运动的枝晶看作刚体处理, 采用具有伽利略不变性的动量交换法[25]计算流体对其界面的作用力, 计算方法如下:

      其中下标$i$和$\bar i$表示粒子迁移的相反方向; f和b分别表示相邻的流体和边界点, ${\tilde f_i}\left( {{{\boldsymbol{x}}_{\text{f}}}, t} \right)$和${\tilde f_{\bar i}}\left( {{{\boldsymbol{x}}_{\text{b}}}, t} \right)$表示流体和边界节点碰撞后的分布函数, 使用曲线边界条件[26]处理. 边界速度$v$计算方法如下:

      其中${\boldsymbol{R}}$是枝晶质心的位置, ${v_\alpha }$和${\omega _\alpha }$分别为平动与转动速度. 考虑重力与浮力的影响, $\alpha $枝晶受到总的力${{\boldsymbol{F}}_\alpha }$和扭矩${{\boldsymbol{T}}_\alpha }$为

      其中$\varOmega $代表枝晶$\alpha $的边界; ${\rho _{\text{l}}}$和${\rho _{\text{s}}}$分别为液相与固相的密度, 固相质量计算表达式为$ M_{\alpha}= \displaystyle \sum\nolimits_{x \in \alpha} \rho_{{\mathrm{s}}} f_{{\mathrm{s}}}(\boldsymbol{x}) $.

      枝晶的速度与角速度为

      其中${I_\alpha }$为惯性张量.

      假定游离枝晶在熔体中的碰撞为完全弹性碰撞, 采用硬球模型处理碰撞步骤, 将枝晶看作刚性粒子并对其应用动量定理与动量矩定理:

      其中$m$为枝晶质量, ${v_0}$和$v$是碰撞前后的速度; ${\omega _0}$和$\omega $是碰撞前、后的角速度; ${\boldsymbol{S}}$为内力冲量.

      枝晶碰撞的瞬间, 由于两枝晶碰撞所受内力冲量相等, 根据冲量定理和冲量矩定理, 可以求得:

      其中${\omega _{10}}$, ${\omega _{20}}$和${\omega _1}$, ${\omega _2}$分别为枝晶1和2碰撞前与碰撞后的角速度; ${{\boldsymbol{v}}_{10}}$, ${{\boldsymbol{v}}_{20}}$和${{\boldsymbol{v}}_1}$, ${{\boldsymbol{v}}_2}$分别为枝晶1和2碰撞前与碰撞后的速度; ${{\boldsymbol{I}}_1}$, ${{\boldsymbol{I}}_2}$为枝晶1和2的转动惯量; ${{\boldsymbol{r}}_1}$和${{\boldsymbol{r}}_2}$分别为碰撞点与枝晶1和2质心的位置矢量. 引入恢复系数$e$便可求得两碰撞枝晶的平动与转动速度:

    3.   模型验证

    • 枝晶的生长运动以及相互碰撞模型已经在本课题组发表的论文[3]中进行验证, 枝晶生长过程中的溶质变化也已在文献[20]中进行检验, 单个枝晶在运动生长的过程中全域平均溶质与初始值的偏差在0.014%以内, 且随着枝晶的生长, 偏差还会逐渐减小, 本文使用的溶质模型满足守恒条件. 本节分别通过圆柱绕流与Rayleigh-Bénard对流检验本模型流固耦合与自然对流的准确性.

      • 3.1.   流固耦合的准确性验证

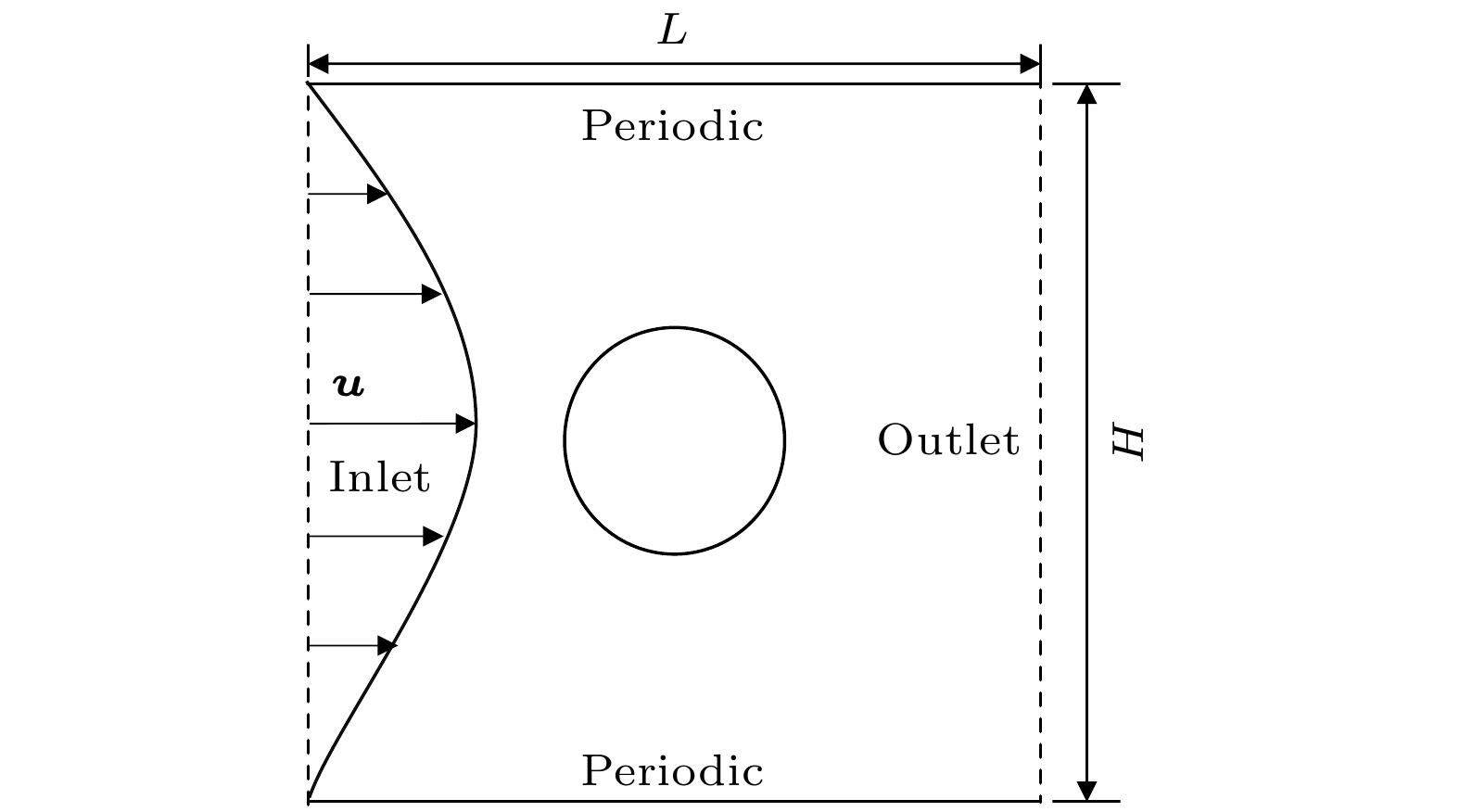
    • 在模拟铸锭凝固的过程中, 整个计算域的固相分数会随着时间的变化发生变化, 为了验证本模型计算流固耦合的准确性, 采用圆柱绕流作为准确性测试案例. 本节将计算域划分为100×100的均匀正方形网格, 流场的松弛时间$\tau = 0.6$. 算例的物理模型如图1所示, 计算区域上下边界为周期性边界条件, 流体与固体间的迁移过程采用反弹格式处理.

      圆柱绕流流固耦合问题中, 圆柱体被视为一个不发生形变的刚体, 而流体在驱动力$F$的作用下绕过圆柱体. 对如图1所示的绕流问题, Drummond和Tahir[27]采用解析方法得出了近似解:

      其中, ${U_{{\text{ave}}}}$代表整个计算域中流体的平均流速(m/s), Fs代表障碍物在计算区域中的体积分数, $\mu $代表黏度.

      为了方便分析和对比, 将(37)式以$ F/(8{\text{π}}\mu ) $为参考将流场的平均速度无量纲化可得

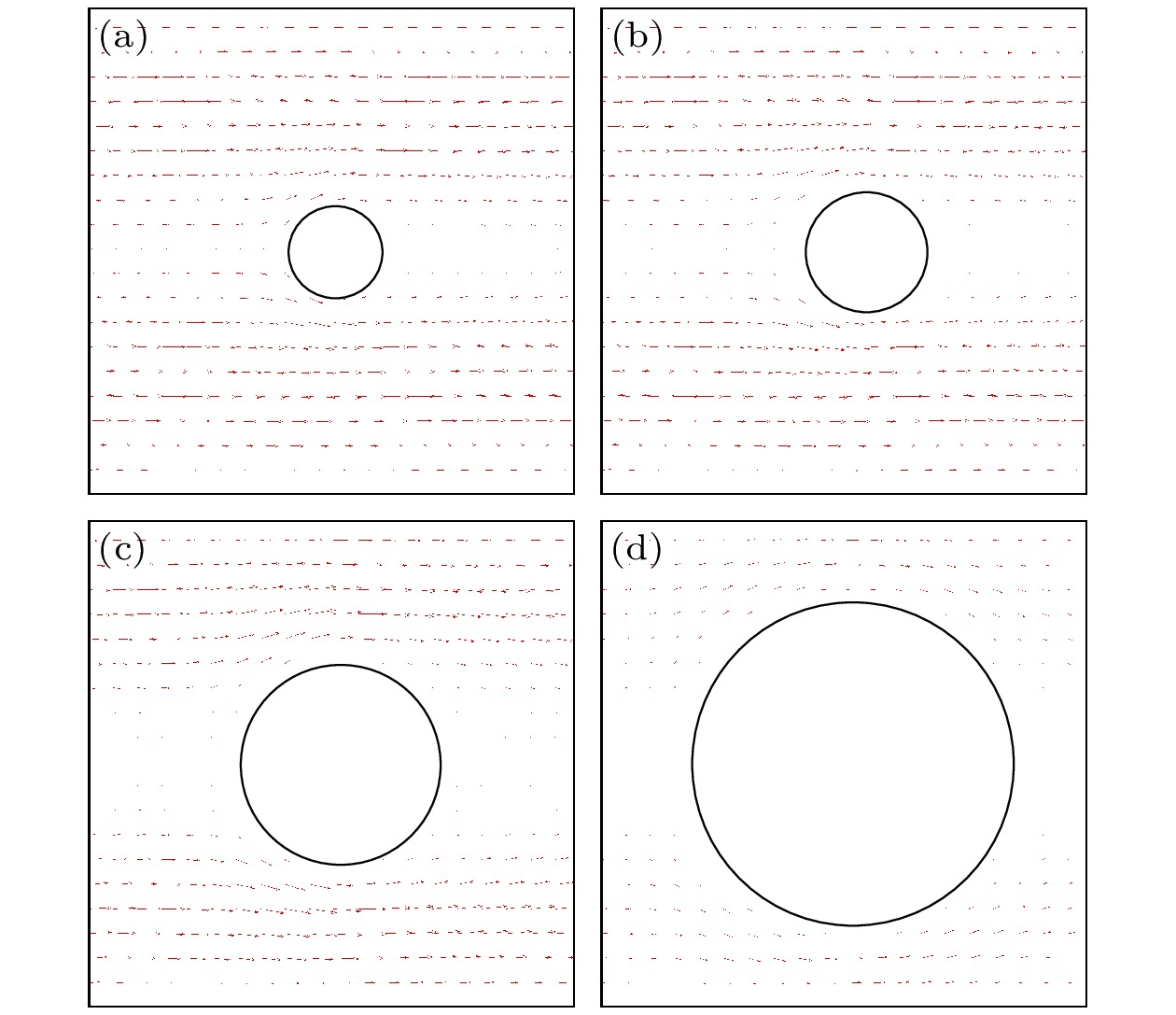
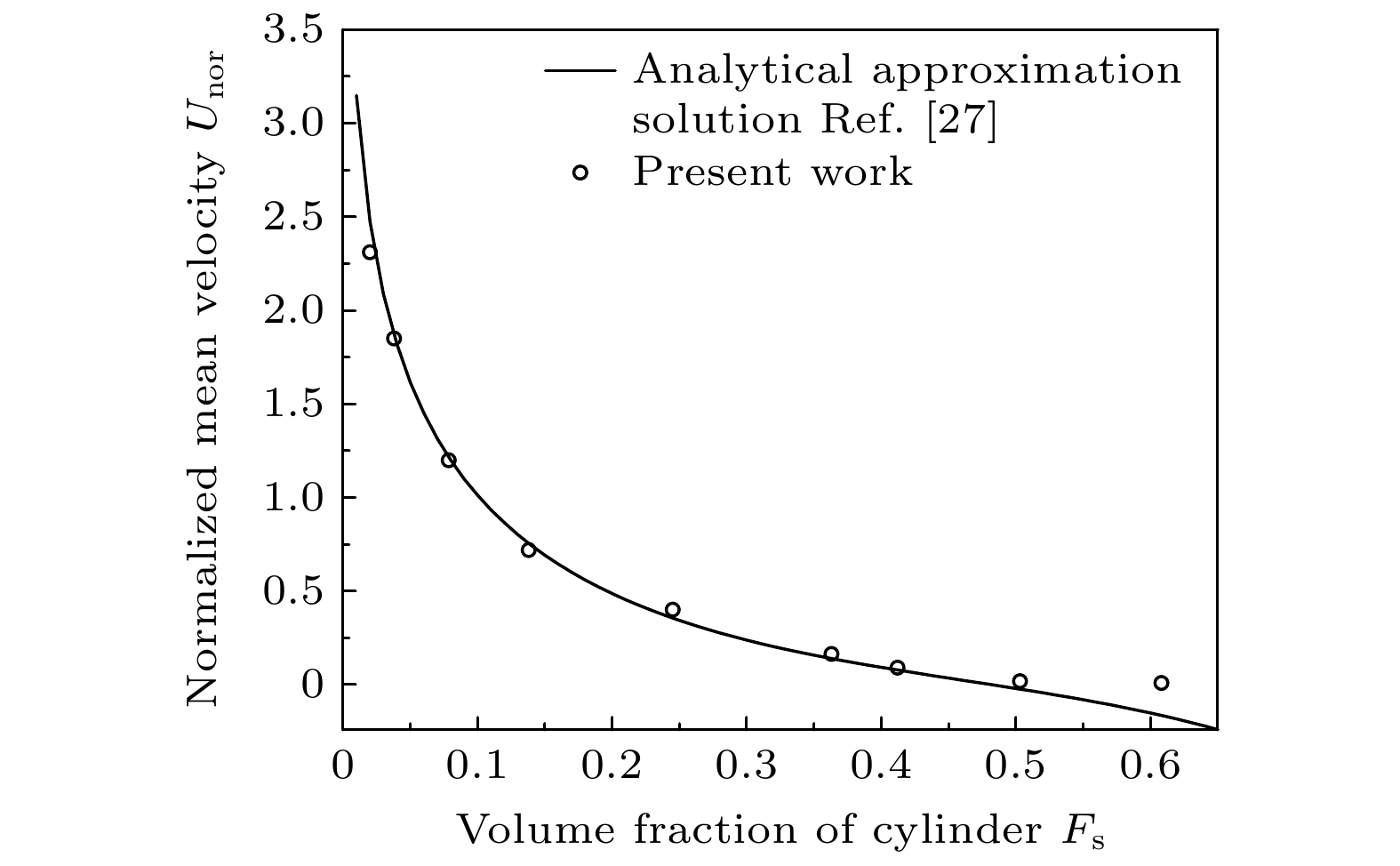
      其中, ${U_{{\text{nor}}}}$为无量纲的流场平均速度.

      为了更直观地展示固相分数对流场的影响, 图2采用红色箭头表示流场的分布情况, 箭头的长度代表流速的大小, 方向代表流体流动的方向. 当固相分数较小时流场流速较大; 反之, 当固相分数较大时流场流速较小. 这是由于流体在流动过程中受到了固体的阻碍, 固相体积分数越大, 流固边界就越长, 固体障碍物对流体的阻碍作用就越强. 因此, 在同样大的外力驱动下固相分数越高则平均流速就越低. 图3为本文所用模型与解析解之间的对比结果, 可以明显看出本次模拟计算得到的结果与解析近似解的结果吻合良好.

      • 3.2.   自然对流条件下温度场的准确性验证

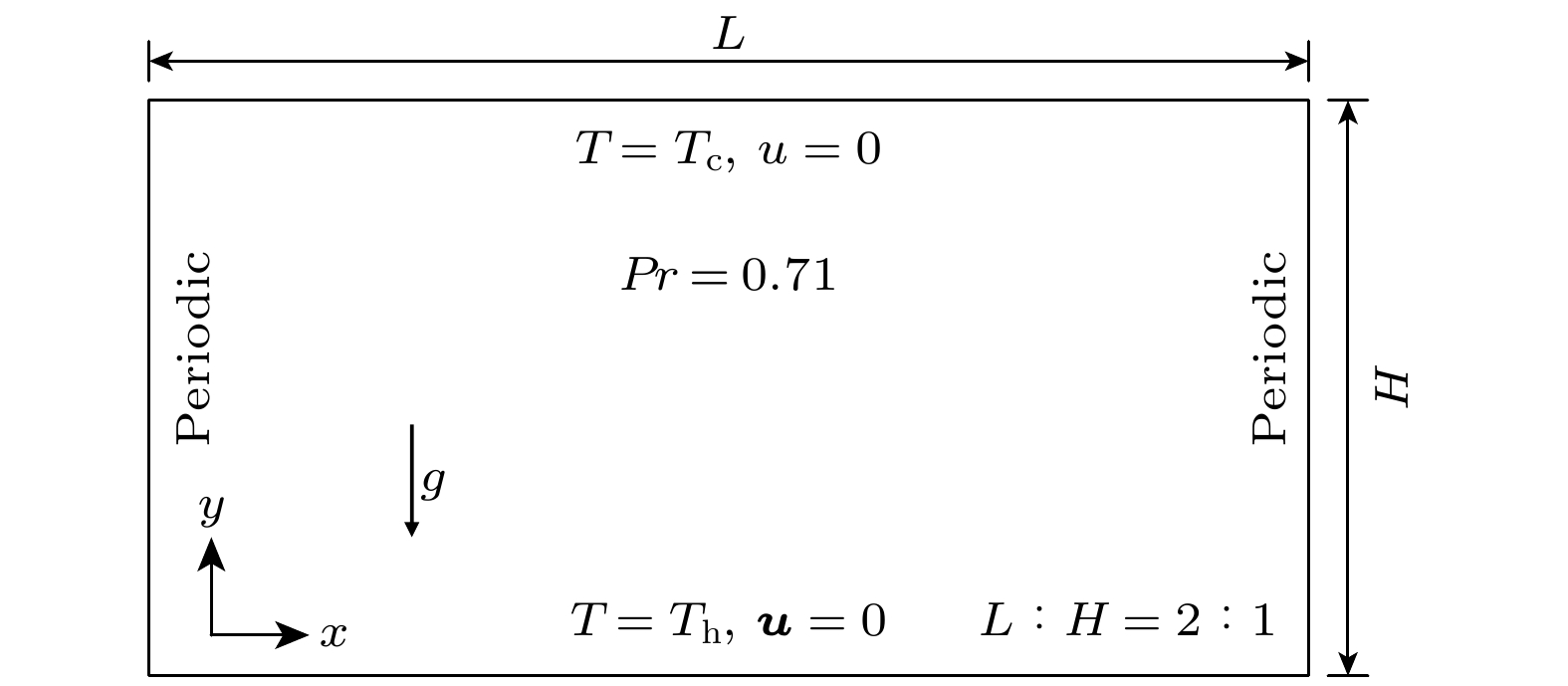
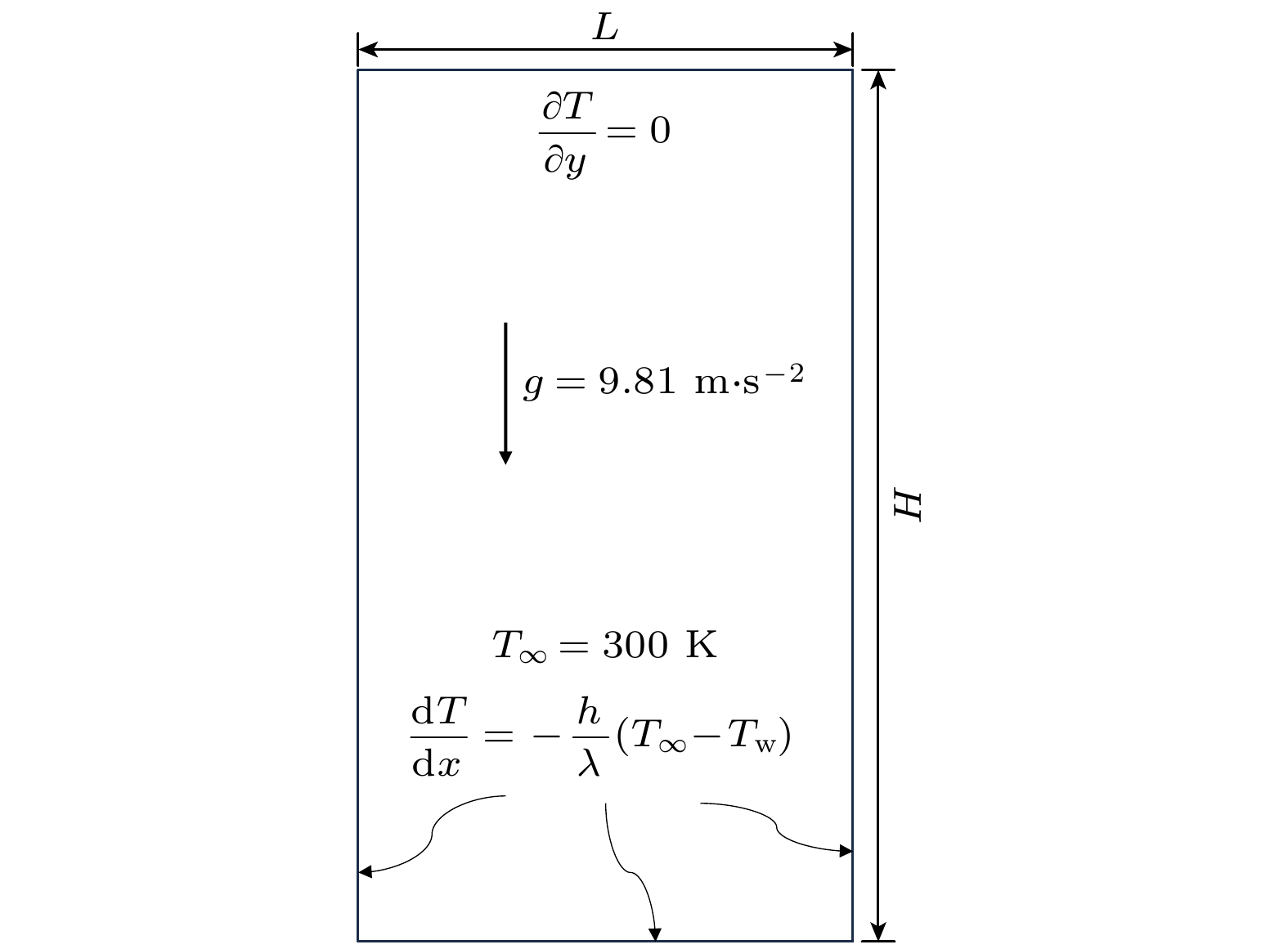
    • Rayleigh–Bénard对流经常作为不可压缩热LBM的验证案例. 相关的物理模型以及边界条件如图4所示. 流体置于长为 $L$高为$H$的矩形腔中, 其长高比$L/H = 2$矩形腔上下壁均为无滑移固壁边界, 上下温度恒定为${T_{\text{c}}}$和${T_{\text{h}}}$, 且${T_{\text{c}}} < {T_{\text{h}}}$. 在模拟过程中, 使用非平衡外推格式处理流场上下边界, 左右两边采用周期性边界条件.

      瑞利数$Ra$是表征流体运动强烈的一个无量纲参数, 根据线性稳定性的分析, 在Boussinesq假设的前提下, 当流体流动的$Ra$数大于临界值$R{a_{\text{c}}}$时, 流体的流动将丧失稳定性, 热量的传递机制将由导热转换成对流换热. 参数$Ra$为

      式中, g为重力加速度, ${\beta _{\text{T}}}$为热膨胀系数, $\alpha $为热扩散率, $\nu $为运动黏度.

      $Nu$数是表征换热快慢的一个重要参数, 可以作为检验程序正确性的标准, $Nu$数定义为

      式中, ${u_y}$为y方向的速度, H代表系统宽度, $\left\langle \cdot \right\rangle $ 代表整个区域的系统平均值.

      此算例中$Nu$随Ra的变化规律遵循以下经验公式[28]:

      在本模拟中, Prandtl数$Pr = \nu /\alpha $固定为0.71, 上壁面温度取无量纲值为${T_{\text{c}}} = 0$, 下壁面温度取无量纲值${T_{\text{h}}} = 1.0$. 为方便展示边界条件已在图中标出.

      温度场与压力场的初始条件如下:

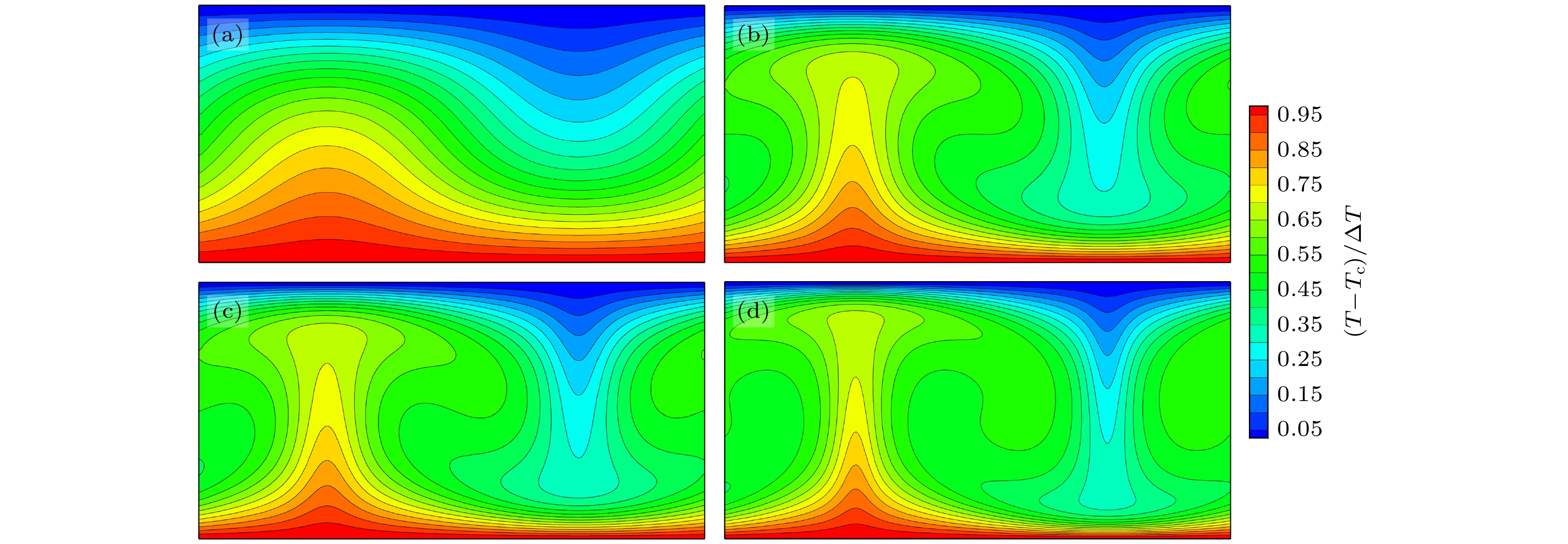
      当对流到达最终的稳定状态时, 典型的温度场如图5 所示, 可以观察到, 由于底部和顶部壁之间的温度梯度引起的流体密度之间的差异造成的对流现象. 在较小Rayleigh数Ra条件下等温线形状较为平缓, 靠近上下壁面的边界层较厚, 随着瑞利数的增大, 对流作用的效果逐渐增强, 等温线形状逐渐由平缓转为曲折, 结果与参考文献[29]相一致.

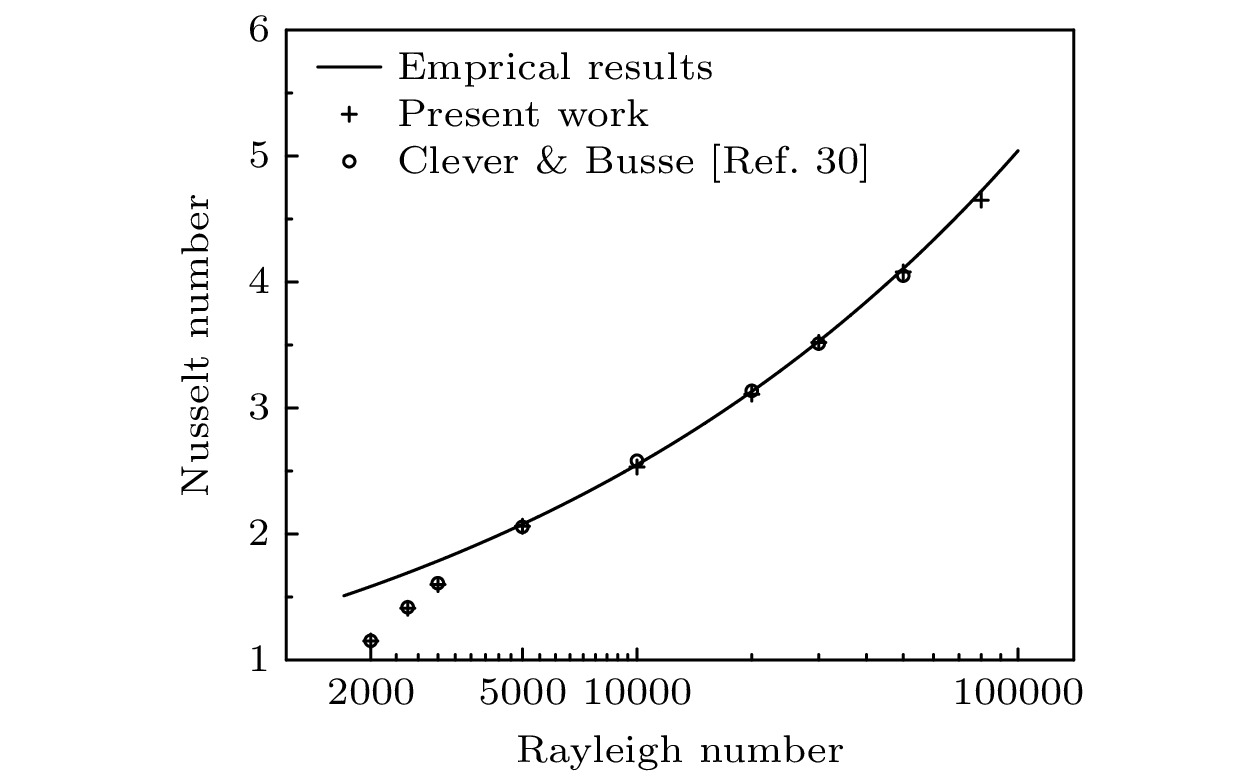
      图6给出了本文计算得到的$Nu$随$Ra$变化与经验式计算结果以及Clever和Busse[30]计算得到的结果对比. 可知, 本文模型的计算结果与经验式以及先前文献中的结果吻合良好.

    4.   结果与讨论:

    • 本文模拟用到的Fe-0.34%C合金的物理模型如图7所示, 计算区域为L × H = 10 mm × 20 mm, 铸件的顶部绝热, 其余部分采用对流换热边界条件, 内部的初始温度设定为1811.65 K, 环境温度恒定为300 K, 其余模拟参数由表2给出, 表中模拟参数源自文献[31, 32], 热力学参数源自相图软件Thermo-Calc.

      • 4.1.   不考虑等轴晶运动时的铸锭宏观偏析的计算分析

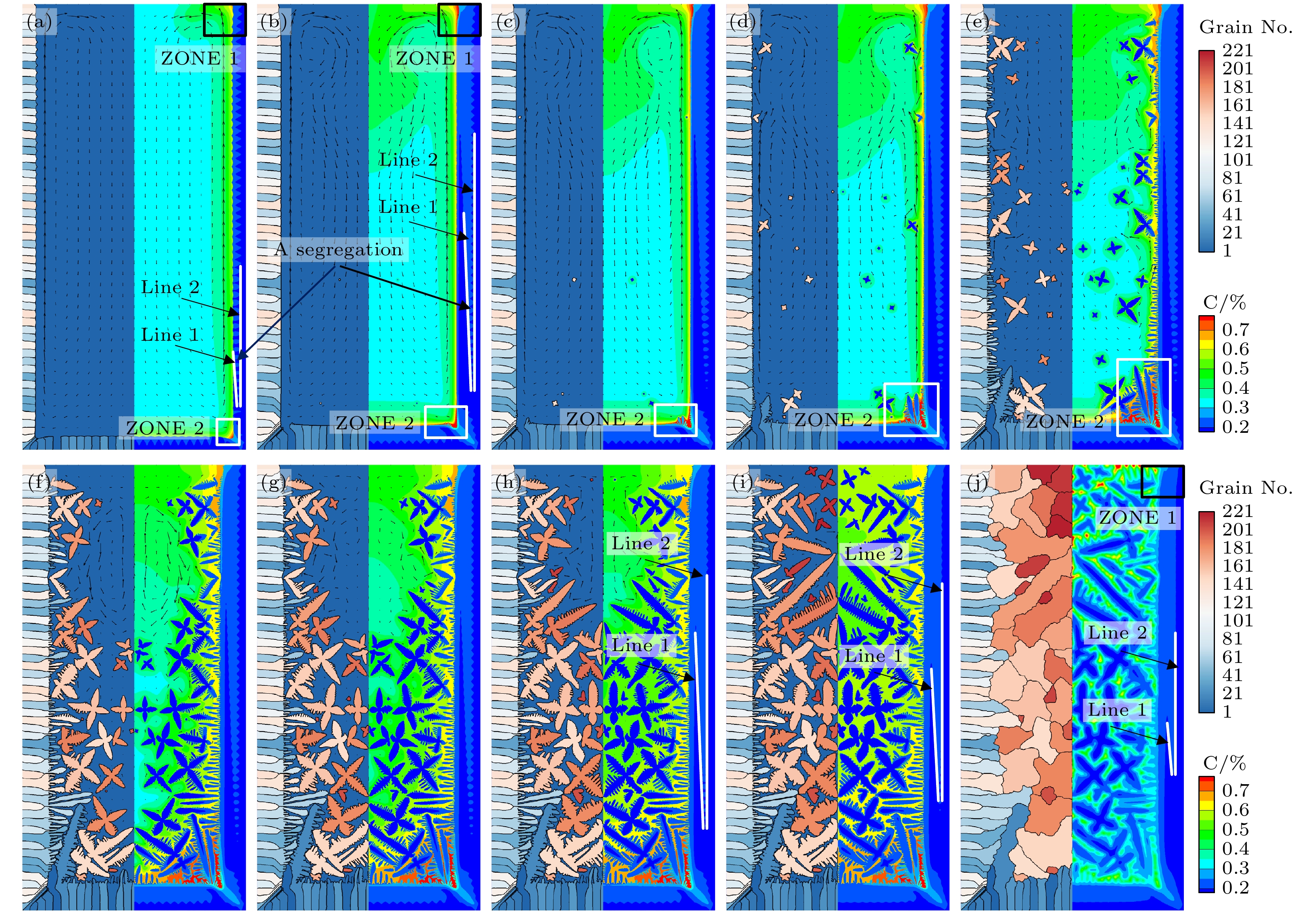
    • 图8为不考虑等轴晶运动时铸锭的凝固过程, 每张分图的左半边展示了特定时刻的晶体形貌, 右半边展示相同时刻的溶质分布, 图中箭头的长短代表流速的大小, 箭头越长流速越大, 箭头方向代表流体的流动方向.

      在凝固开始时, 在壁面处形核的晶粒在对流换热边界条件的作用下获得了足够的过冷度开始沿着散热的相反方向生长呈规则的柱状排列, 为柱状晶. 随着这些柱状晶的继续生长, 排出的溶质富集在固液界面处, 在几何形状的影响下铸锭左下以及右下方的拐角处很容易发生溶质富集, 图8(a)中区域ZONE2所示. 区域在图8(a)的区域ZONE1中也存在着一定程度的溶质富集, 不均匀分布的溶质引起的自然对流流线向上, 对流作用将溶质从铸锭底部带到铸锭上方, 几何形状限制了这些溶质继续向上运动并进一步促成了这块区域的溶质富集. 凝固前期柱状晶的生长主要受热过冷影响, 壁面处的柱状晶在向铸锭内部生长的过程中前沿的溶质会受到自然对流的影响. 固液界面处高浓度溶质受对流影响由底部向顶部运动的过程中会在固相的溶质分布上呈现出一条较高浓度的偏析带(图8(a), (b)中Line 1和Line 2所指示的区域), 与文献[19]中描述的偏析形成过程一致. 由于此区域在铸锭的左右两侧对称出现呈A型, 该类偏析被称为A型偏析. 在凝固的后期由于固相之间溶质会发生扩散偏析区域会逐渐减小, 如图8(h)—(j)中Line 1和Line 2之间区域所示. 如图8(a), (b)区域ZONE 1所示, 这里的固相前沿在对流引起的溶质富集作用下生长速度较慢, 随着凝固的持续进行铸锭顶部会出现一部分浓度凸起区域. 图8(j)为直到固相完全凝固, 区域1也保持着相对较高的溶质浓度.

      合金中的柱状晶在足够高的温度梯度下也总是稳定的. 在本节的模拟条件下, 铸锭的壁面部分直接暴露于冷却介质中, 在凝固前期如图8(a)—(d)所示, 铸锭边缘与熔体内部之间存在很高的温度梯度, 表面处的柱状晶近乎呈平面状向前推进. 对流与扩散改变了界面与熔体内部的温度梯度, 再加上自然对流带走了部分富集在前端的溶质从而减小了枝晶生长的阻力, 原本平面状向前推进的柱状晶以树枝状向前生长. 铸锭底部两角上的枝晶, 如图8(b)—(e)中区域ZONE 2所示, 在两边同时散热的条件下拥有比周围柱状晶大的生长驱动力, 当界面前沿的温度梯度发生变化时它们会最先以树枝状向熔体内部生长. 当柱状晶向前推进到一定程度时, 界面前沿出现了等轴晶(图8(e)), 当等轴晶数量增加且生长到一定尺度时, 柱状晶前沿停止推进(图8(f)), 此后则主要为铸锭内部的等轴晶的形核和生长过程, 直至凝固结束(图8(j)).

      • 4.2.   考虑等轴晶运动时铸锭宏观偏析的计算分析

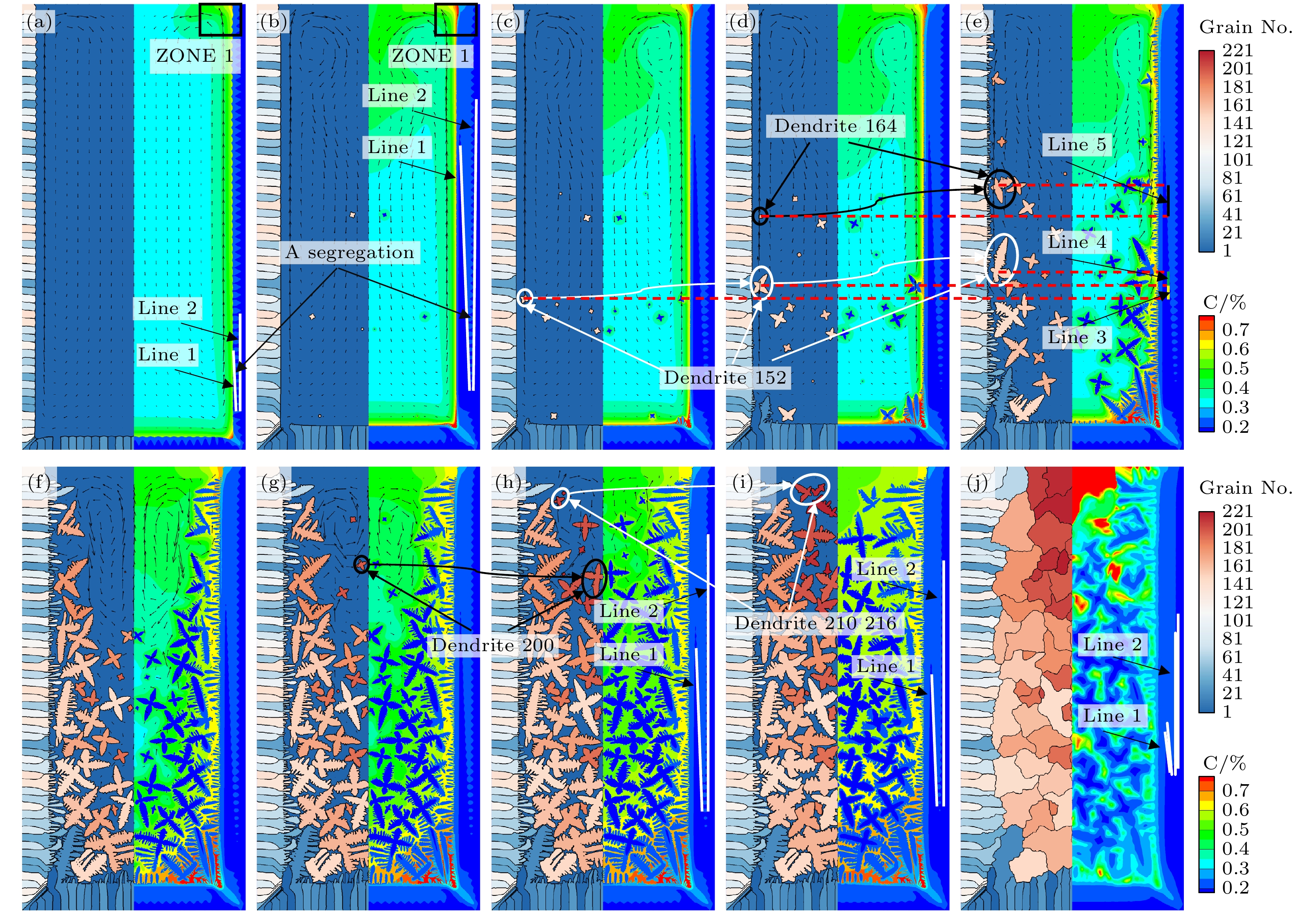
    • 计入等轴晶运动的铸锭凝固过程如图9所示, 其中A偏析的形成与演化过程、界面推进的方式以及图9(a), (b)区域ZONE 1标注的溶质浓度突出部分的形成原因皆与上节相同.

      图9(c)—(e)表示不同时刻下的铸锭形貌与溶质分布, 图9(e)右侧的竖直Line 3, 4和5表示了时间段下两个枝晶在竖直方向运动的距离, 其中Line 3和Line 4的长度分别表示白色区域枝晶从4.6—4.8 s与4.8—5.0 s的运动距离. Line 5的长度表示Dendrite 枝晶164从 4.8—5.0 s运动的距离, 靠近壁面的枝晶由于所处位置向上的浮力大于自身受到的重力会自下向上移动, 但随着时间的推移枝晶长大重力增大, Dendrite枝晶152上浮的距离明显低于同时刻的Dendrite枝晶164.

      自由枝晶的运动状态大多都可以通过流线的方向得出. 图9(g), (h)中Dendrite枝晶200受到流体力和重力的作用向下移动, 与下方的枝晶发生接触后运动停止. 图9(i)中的Dendrite枝晶210和Dendrite枝晶216在外力的作用下旋转碰撞, 最后与周围枝晶接触不再发生移动.

      • 4.3.   等轴晶的运动对铸锭微观组织和形貌的影响

      4.3.1.   形貌对比

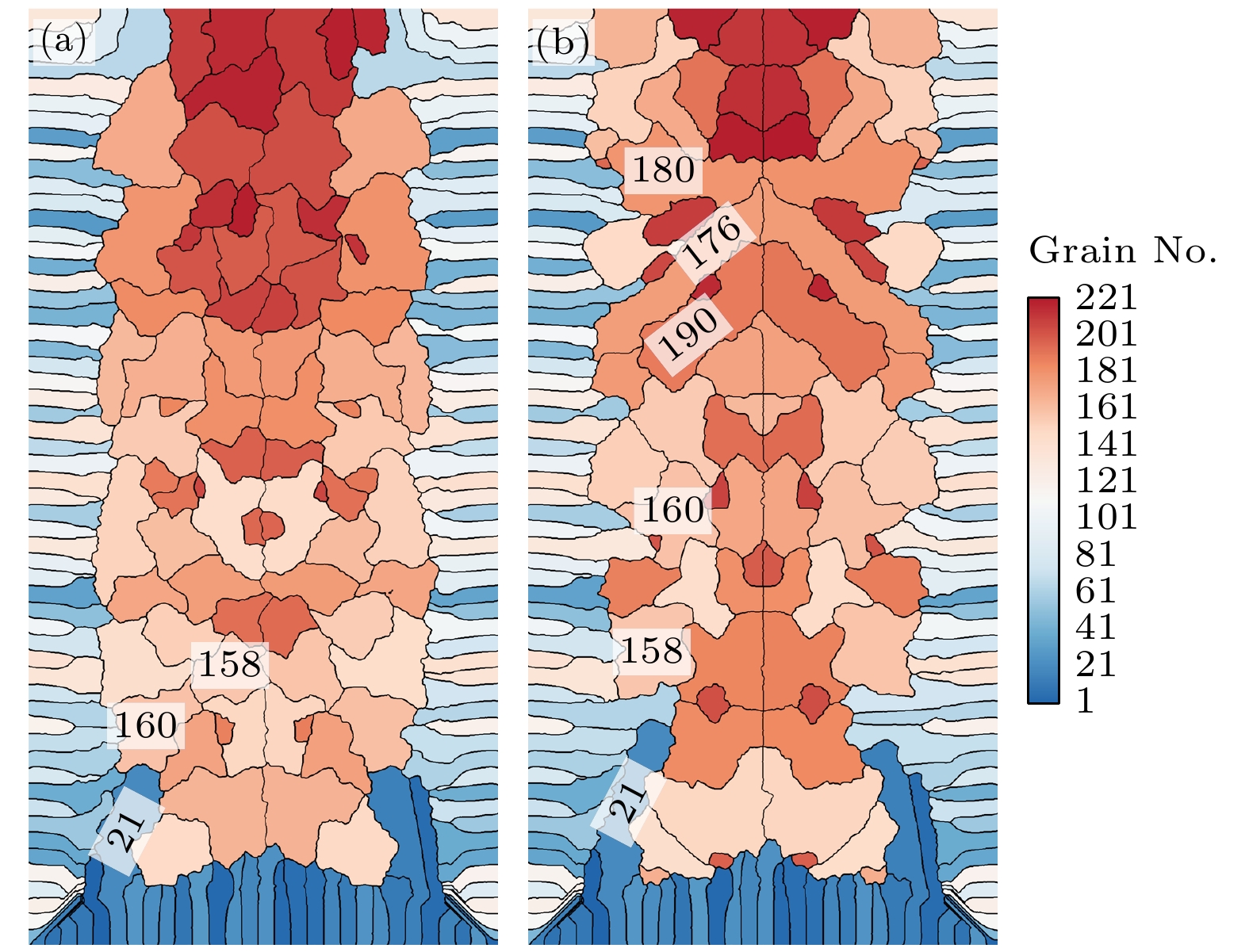
    • 由图10可以看出, 等轴晶运动与否对铸锭的微观组织形貌具有显著的影响. 本文的计算假设铸锭沿中轴线左右两侧对称形核, 可以明显看出无论运动与否在铸锭完全凝固之后大部分区域都保持了很高的对称性, 但是在计入枝晶运动的情况下, 凝固中期流场的演化变得复杂再加上枝晶之间的相互碰撞, 铸锭上方区域变得不再左右对称, 同时也不会长出特别的大的枝晶. 总体来看, 枝晶运动具有细化晶粒的作用. 如图10(b)中编号为180, 176以及190的枝晶以及它们对称方向的枝晶因为在生长过程中没有其余固相阻碍生长, 完全凝固后的晶粒尺寸会相对较大; 图10(a)中的晶粒大小相对平均, 等轴晶的运动会增大阻碍其他枝晶生长的概率. 例如两张图中的21号枝晶大小不同, 在等轴晶存在运动的情况下160号枝晶会阻碍21号枝晶的生长, 而在不运动的情况下21号枝晶是受到壁面处柱状晶的阻碍停止了生长.

      • 4.3.2.   偏析情况对比

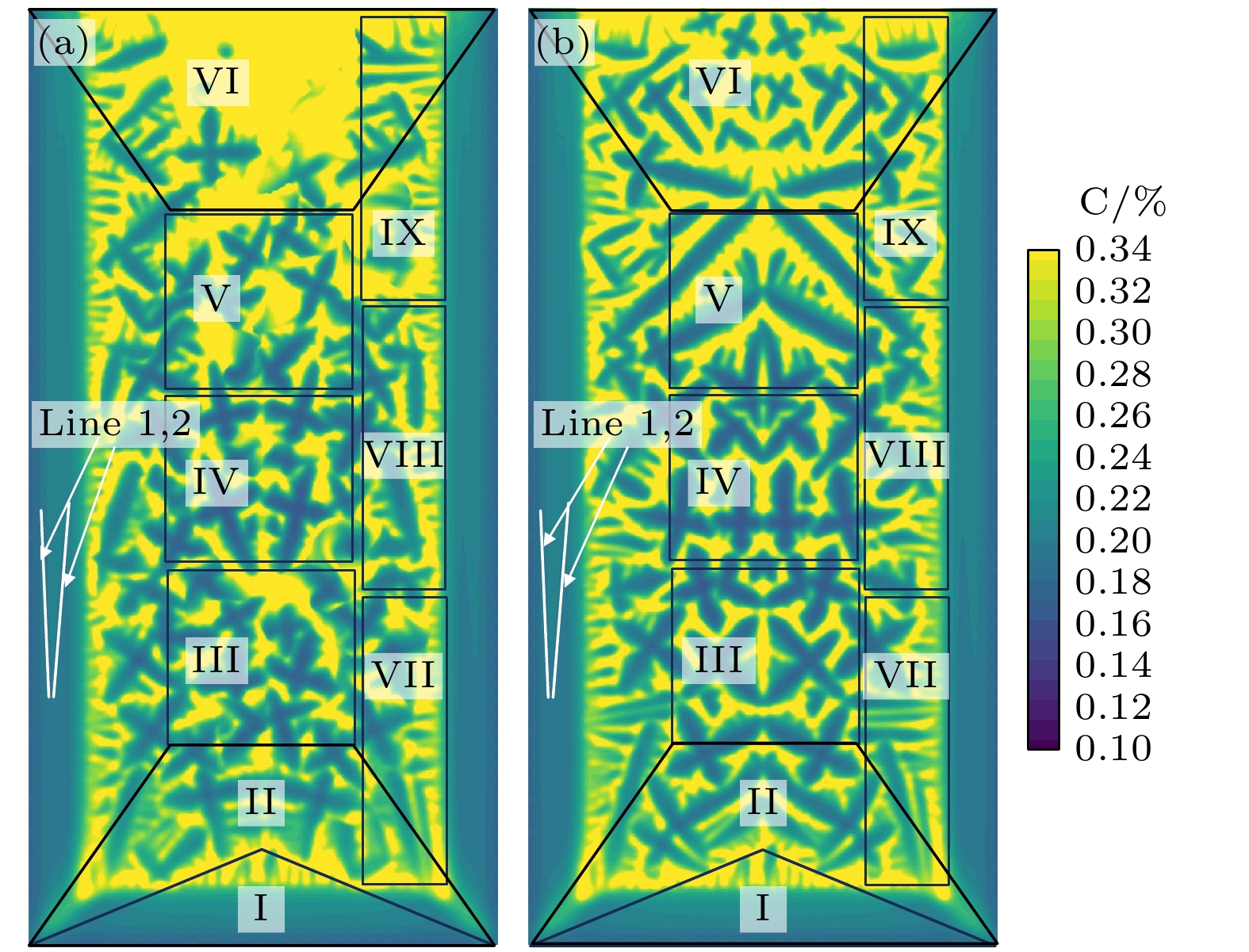
    • 图11(a), (b)分别为等轴晶运动与否的铸锭完全凝固下的溶质分布情况, 由色度标尺可知, 图中亮色区域是正偏析区域, 暗色区域是负偏析区域. 可以明显看出无论是否计入等轴晶运动, 图11中Line 1 和Line 2所划区域铸锭中的A偏析带没有明显区别, 而计入等轴晶运动之后铸锭的顶部正偏析要比不计入的情况大得多. 为了方便对比, 本文将整个计算域的中心部分沿y轴方向分为6块区域, 如图11(a), (b)中黑色线条框选的部分, 区域Ⅰ和Ⅱ分别是以铸锭底部为底, 高为铸锭总高10%和20%的等腰三角形与等腰梯形, 其中梯形的上底为铸锭总宽的20%, 带有等轴晶的负偏析主要产生于此; 区域 Ⅵ 与区域Ⅱ沿铸锭中心高度呈轴对称关系, 铸锭中的正偏析主要发生在此处. 竖直方向余下的60%区域被均分为3块正方形, 由下至上分别为区域Ⅲ, Ⅳ和Ⅴ, 它们主要被用于分析铸锭中心的偏析情况.

      铸锭中大部分区域是对称的, 铸锭CET区域的溶质只分析右半边, 因本文主要分析等轴晶运动对铸锭偏析的影响, 故分析该区域时选区尽量避开了只有柱状晶的范围. 将CET区域等高分为3份如图11 中区域Ⅶ, Ⅷ和Ⅸ所示.

      铸锭中不同位置的溶质平均浓度以及偏析情况如表3所示. 无论运动与否铸锭的底部负偏析以及顶部正偏析都被很好地模拟出来, 但就数值而言区域Ⅴ以下即整个铸锭的中下层区域, 等轴晶的运动并未对相应区域的平均溶质造成明显的影响.

      等轴晶的数量越多, 平均溶质越低. 在铸锭的上半区域等轴晶的运动对铸锭的宏观偏析造成了相当明显的影响. 主要原因在于区域Ⅴ和Ⅵ在凝固中期(t = 6—10 s)还存在大量的液相, 此时形核主要发生在区域Ⅵ中, 区域Ⅴ中的液相为枝晶的生长以及等轴晶的运动提供了条件; 在等轴晶运动的情况下, 区域Ⅵ中形核的枝晶会受重力下落至区域Ⅴ; 在等轴晶不发生运动的情况下, 图11(b)区域Ⅴ液相周围的柱状晶会迅速生长并占据区域Ⅴ. 所以图11(a)相较于图11(b)中区域Ⅴ的平均溶质浓度较低, 区域Ⅵ的平均溶质较高.

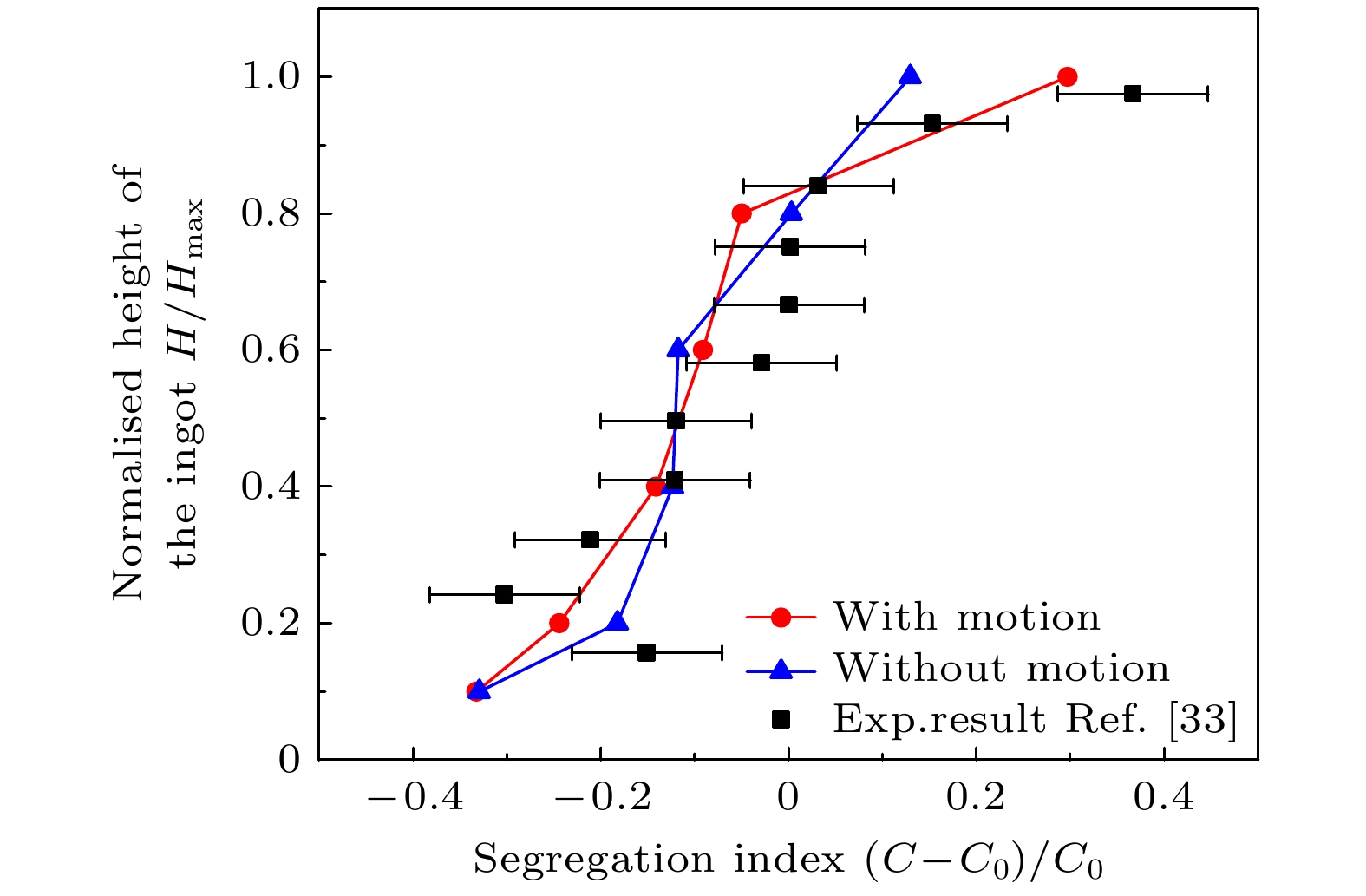
      为了更直观地说明等轴晶的运动对铸锭整体溶质分布造成的影响, 以下通过将尺度和偏析程度无量纲化与大型铸锭实验的结果进行定性分析对比. 图12展示了上文划分的Ⅰ, Ⅱ, Ⅲ, Ⅳ, Ⅴ和Ⅵ区域的无量纲平均溶质与实验结果[33]的对比, 无量纲化的处理方法已在图中变量名后方标出, 结果显示, 在计入等轴晶运动时存在等轴晶的铸锭底部区域Ⅱ负偏析的程度比不运动更高, 计入等轴晶运动的模拟数据中顶部正偏析的程度比不运动要大的多并且更符合实际情况. 铸锭中靠近壁面一侧的区域随着所处位置的升高而升高, Ⅶ, Ⅷ和区域的平均溶质浓度受等轴晶运动的影响较小, Ⅸ区域的溶质受到影响最大但也只相差1.7%, 造成这种现象的原因在于柱状晶的生长限制了等轴晶运动的范围.

    5.   结　论

    • 考虑到等轴晶运动对铸锭凝固过程有着重要影响, 建立了三场(流场、溶质场以及温度场)耦合且计入枝晶运动的模型, 并对Fe-0.34%C的合金铸锭的凝固过程进行了模拟, 说明了等轴晶的运动对铸锭的微观组织形貌以及顶部的平均溶质偏析程度具有显著的影响. 得到如下结论.

      1)等轴晶的运动会一定程度上增大铸锭中晶粒的均匀性. 相邻枝晶的生长会受到彼此的阻碍, 在等轴晶运动的过程中会增大其与周围枝晶接触的概率, 从而降低大尺寸晶粒出现的可能性.

      2)铸锭顶部的偏析程度在有无等轴晶运动的影响下会有接近30%的差异. 在模拟中无论是否存在等轴晶的运动, 铸锭顶部都会出现正偏析, 但偏析的大小会在很大程度上受到等轴晶运动的影响. 在铸锭顶端形核的等轴晶在重力作用下会运动到铸锭的中上层区域, 这些等轴晶的运动会增大铸锭顶部的正偏析的大小, 同时会影响到次顶部区域的偏析情况.

      3)铸锭中CET区域的偏析程度受到等轴晶运动的影响较小. 靠近壁面部分的等轴晶的运动会受到柱状晶生长的限制, 在这一区域的溶质受等轴晶影响的程度很小, 偏差最大的顶部尚未高于2%. 理论上铸锭底部的等轴晶的运动下沉会对底部负偏析产生影响, 也许是因为本文的模拟区域不够大使得游离枝晶数量不够多, 模拟结果中底部负偏析的程度低于实际铸锭中的负偏析. 这是将来扩大计算规模后进一步研究的内容.

    参考文献 (33)

目录

/

返回文章
返回