高级搜索

铁电异质结T-NbTe2/Ga2S3的接触性质及调控

,  , 

downloadPDF

上一篇

下一篇

孙智玄, 赵长松, 程芳. 铁电异质结T-NbTe2/Ga2S3的接触性质及调控[J]. 物理学报, 2025, 74(10): 107101-1. doi: 10.7498/aps.74.20241705
引用本文: 孙智玄, 赵长松, 程芳. 铁电异质结T-NbTe2/Ga2S3的接触性质及调控[J]. 物理学报, 2025, 74(10): 107101-1. doi: 10.7498/aps.74.20241705
shu
Zhixuan SUN, Changsong ZHAO, Fang CHENG. Control of contact properties in ferroelectric heterojunction T-NbTe2/Ga2S3[J]. Acta Physica Sinica, 2025, 74(10): 107101-1. doi: 10.7498/aps.74.20241705
Citation: Zhixuan SUN, Changsong ZHAO, Fang CHENG. Control of contact properties in ferroelectric heterojunction T-NbTe2/Ga2S3[J]. Acta Physica Sinica, 2025, 74(10): 107101-1. doi: 10.7498/aps.74.20241705
shu

铁电异质结T-NbTe2/Ga2S3的接触性质及调控

  • 长沙理工大学物理与电子科学学院, 长沙　410114

    • 作者简介: 孙智玄. E-mail: 1162537399@qq.com .
    通讯作者: E-mail: chengfang@csust.edu.cn.

  • 中图分类号: 71.15.Mb, 71.20.-b, 79.60.Jv, 73.40.Lq

Control of contact properties in ferroelectric heterojunction T-NbTe2/Ga2S3

  • School of Physics and Electronic Science, Changsha University of Science & Technology, Changsha 410114, China

    • Corresponding author: E-mail: chengfang@csust.edu.cn.

  • MSC: 71.15.Mb, 71.20.-b, 79.60.Jv, 73.40.Lq

  • 摘要: 单层的铁电半导体Ga2S3因具有卓越的延展性, 极高的载流子迁移率以及独特的面外非对称极化特性而备受关注. 利用铁电半导体Ga2S3面外非对称极化特性, 本研究构建了T-NbTe2/Ga2S3铁电异质结, 并选用了两个能量最稳定且Ga2S3极化强度方向不同的异质结PD1 ($ \boldsymbol P_{\downarrow}$)和PU2 ($\boldsymbol P_{\uparrow} $), 对其结构稳定性和电接触性质进行相关研究. 结果表明, 由于Ga2S3极化强度方向的不同, 本征态下的异质结PD1和PU2分别形成了N型肖特基接触和P型肖特基接触. 改变铁电半导体Ga2S3的极化特性, 能改变铁电异质结T-NbTe2/Ga2S3肖特基势垒的接触类型, 这为设计多功能的肖特基器件提供了一种实用的方法. 对于异质结PD1和PU2, 施加外加正电场或者双轴应变拉伸, 都能够有效地实现肖特基接触至欧姆接触的转变. 这些结果为高性能电接触界面的二维铁电纳米器件提供了理论参考.
    Abstract: A monolayer ferroelectric semiconductor, Ga2S3, has received extensive attention because of its outstanding ductility, extremely high carrier mobility and unique out-of-plane asymmetric polarization characteristics. In this work, T-NbTe2/Ga2S3 ferroelectric heterojunctions are constructed using out-of-plane asymmetric polarization characteristics of Ga2S3. The structural stability, preparation possibility and electrical contact properties for various ferroelectric heterojunction T-NbTe2/Ga2S3 ferroelectric heterojunctions with the different polarization directions of Ga2S3 are systematically studied by the first-principles calculations. It is found that heterojunctions T-NbTe2/Ga2S3 exhibit sensitive responses to out-of-plane asymmetric polarization characteristics of Ga2S3. The two heterojunctions with the most stable energy, PD1 ($ \boldsymbol P_{\downarrow}$) and PU2 ($ \boldsymbol P_{\uparrow} $), in the intrinsic state form N-type and P-type Schottky contact, respectively. The polarization characteristics of the ferroelectric semiconductor Ga2S3 are dependent on the contact type of the Schottky barrier in the ferroelectric heterojunction T-NbTe2/Ga2S3, which provides a practical approach for designing multifunctional Schottky devices. Specifically, the electrical contact depends on the external electric field. For the heterojunction, PD1 (and PU2), the contact can transition from Schottky contact to Ohmic contact at an electric field strength of +0.5 V/Å (+0.6 V/Å). Besides electric field, the contact properties of both heterojunctions PD1 and PU2 may also be tuned by an external biaxial strain. For the heterojunction, PD1, the contact can transition from Schottky contact to Ohmic contact at a biaxial strain tensile of 8%. And for the heterojunction, PU2, the contact can transition from P-type Schottky contact to N-type Schottky contact at a biaxial strain tensile of 2%, then from N-type Schottky contact to Ohmic contact at a strain tensile of 10%. These results provide a theoretical reference for designing two-dimensional ferroelectric nanodevices with high-performance electrical contact interfaces.
  • 加载中

  • 图 1  单层原子结构　(a) T-NbTe2, (b) Ga2S3 (极化向下)和(c) Ga2S3 (极化向下)的正视图和侧视图. 红色箭头表示极化方向. 单层(d) T-NbTe2和(e) Ga2S3能带结构

    Figure 1.  Top-view and side-view of single-layer atomic structures: (a) T-NbTe2; (b) Ga2S3 (polarized downward); (c) Ga2S3 (polarized upward). The red arrow indicates the polarization direction. Energy band structures of single layers: (d) T-NbTe2; (e) Ga2S3.

    下载: 全尺寸图片 幻灯片

    图 2  (a)异质结的6种堆垛方式, 阴影为两种最稳定的堆垛结构; (b)优化后各堆垛的结合能(柱状图)以及层间距(蓝色点); (c) PD1和PU2的电子定位函数

    Figure 2.  (a) The six stacking sequences of heterojunctions, with the shaded ones representing the two most stable stacking structures; (b) pptimized binding energy (presented as a bar chart) and interlayer spacing (blue dots) for each stacking sequence; (c) the electron localization function of PD1 and PU2.

    下载: 全尺寸图片 幻灯片

    图 3  300 K的(a) PD1和(b) PU2的AIMD模拟; (c) PD1和(d) PU2的声子谱

    Figure 3.  AIMD simulation of at 300 K (a) PD1 and (b) PU2; the phonon spectra of (c) PD1 and (d) PU2.

    下载: 全尺寸图片 幻灯片

    图 4  (a)异质结PD1和PU2的投影能带结构; (b)异质结PD1和PU2的空间电荷密度差. 插图中红色(蓝色)表示电子积累(消耗), 等值面设为0.0005 e/Å3

    Figure 4.  (a) Projected band structures of heterojunctions PD1 and PU2; (b) the spatial charge density difference for heterojunctions PD1 and PU2. In the illustration, the red (blue) represent electron accumulation (depletion), and the isosurface is set to 0.0005 e/Å3

    下载: 全尺寸图片 幻灯片

    图 5  (a) PD1和PU2的肖特基势垒高度随外加电场的变化曲线; (b) 异质结PD1在外加电场下的能带结构; (c) 异质结PU2在外加电场下的能带结构. 红色表示Ga2S3, 蓝绿色表示T-NbTe2

    Figure 5.  (a) Variation curves of the Schottky barrier height of PD1 and PU2 with the applied electric field; (b) band structure of the heterojunction PD1 under the applied electric field; (c) band structure of the heterojunction PU2 under the applied electric field. The red lines represent Ga2S3, and the cyan lines represent T-NbTe2.

    下载: 全尺寸图片 幻灯片

    图 6  (a)异质结PD1和PU2的肖特基势垒高度随双轴应变的变化曲线; (b)异质结PD1在应变下的能带结构; (c)异质结PU2在应变下的能带结构. 红色表示Ga2S3, 蓝绿色表示T-NbTe2

    Figure 6.  (a) Trend of SBH of heterojunction PD1 and PU2 with the biaxial strain; (b) band structure of the heterojunction PD1 under strains; (c) band structure of the heterojunction PU2 under strain. The red lines represent Ga2S3, and the cyan lines represent T-NbTe2.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Li Z H, Han J N, Cao S G, Zhang Z H 2023 Appl. Surf. Sci. 636 157766 doi: 10.1016/j.apsusc.2023.157766
    [2] Zheng Y, Gao J, Han C, Chen W 2021 Cell Rep. Phys. Sci. 2 100298 doi: 10.1016/j.xcrp.2020.100298
    [3] Chen S Y, Wang S, Wang C, Wang Z C, Liu Q 2022 Nano Today 42 101372 doi: 10.1016/j.nantod.2021.101372
    [4] Zheng S, Lu H C, Liu H, Liu D M, Robertson J 2019 Nanoscale 11 4811 doi: 10.1039/C8NR07812B
    [5] Chhowalla M, Jena D, Zhang H 2016 Nat. Rev. Mater. 1 16052 doi: 10.1038/natrevmats.2016.52
    [6] Allain A, Kang J, Banerjee K, Kis A 2015 Nat. Mater. 14 1195 doi: 10.1038/nmat4452
    [7] Nguyen H T, Obeid M M, Bafekry A, Idrees M, Vu T V, Phuc H V, Hieu N N, Hoa L T, Amin B, Nguyen C V 2020 Phys. Rev. B 102 075414 doi: 10.1103/PhysRevB.102.075414
    [8] Cao L M, Ang Y S, Wu Q Y, Ang L K 2019 Appl. Phys. Lett. 115 241601 doi: 10.1063/1.5130756
    [9] Zheng Y L, Tang X, Wang W L, Jin L, Li G Q 2021 Adv. Funct. Mater. 31 2008307 doi: 10.1002/adfm.202008307
    [10] Jastrzebskia C, Jastrzebskib D J, Kozaka V, Pietakb K, Wierzbicki M, Gebicki W 2019 Mater. Sci. Semicond. Process. 94 80 doi: 10.1016/j.mssp.2019.01.029
    [11] Dénoue K, Cheviré F, Calers C, Verger L, Coq D L, Calvez L 2020 J. Solid State Chem. 292 121743 doi: 10.1016/j.jssc.2020.121743
    [12] Zhang G T, Lu K J, Wang Y F, Wang H W, Chen Q 2022 Phys. Rev. B 105 235303 doi: 10.1103/PhysRevB.105.235303
    [13] Liu X H, Mao Y L 2024 Appl. Phys. Lett. 125 043102 doi: 10.1063/5.0220466
    [14] Khusayfan N M, Khanfar H K 2018 Results Phys. 10 332 doi: 10.1016/j.rinp.2018.06.018
    [15] Khusayfan N M, Qasrawi A F, Khanfar H K 2018 Results Phys. 8 1239 doi: 10.1016/j.rinp.2018.02.017
    [16] Shang X X, Zhang Y L, Li T, Zhang H N, Zou X F, Wageh S, Al-Ghamdi A A, Zhang H, Si S H, Li D W 2024 J. Materiomics 10 355 doi: 10.1016/j.jmat.2023.05.015
    [17] Dong J Z, Li C S, Yang J, Chen B B, Song H J, Chen J S, Peng W X 2016 Cryst. Res. Technol. 51 671 doi: 10.1002/crat.201600235
    [18] Suonan Z X, Wu H X, Mi S, Xu H, Xu H W, Zhang H Y, Pang F 2024 J. Cryst. Growth 648 127891 doi: 10.1016/j.jcrysgro.2024.127891
    [19] Behera S K, Ramamurthy P C 2024 New J. Chem 48 15493 doi: 10.1039/D4NJ03076A
    [20] Ataca C, Şahin H, Ciraci S 2012 J. Phys. Chem. C 116 8983 doi: 10.1021/jp212558p
    [21] Li H, ZhangY F, Liu F B, Lu J 2024 Nanoscale 16 18005 doi: 10.1039/D4NR02419B
    [22] Fang S B, Li Q H, Yang C, Wu B C, Liu S Q, Yang J, Ma J C, Yang Z M, Tang K C, Lu J 2023 Phys. Rev. Mater. 7 084412 doi: 10.1103/PhysRevMaterials.7.084412
    [23] Han J N, Cao S G, Li Z H, Zhang Z H 2023 J. Phys. D: Appl. Phys. 56 045002 doi: 10.1088/1361-6463/acab12
    [24] Xu Y H, Han J N, Li Z H, Zhang Z H 2023 J. Phys. D: Appl. Phys. 56 365504 doi: 10.1088/1361-6463/acd64f
    [25] Brandbyge M, Mozos J L, Ordejón P, Taylor J, Stokbro K 2002 Phys. Rev. B 65 165401 doi: 10.1103/PhysRevB.65.165401
    [26] Perdew J P, Burke K, Ernzerhof M 1996 Phys. Rev. Lett. 77 3865 doi: 10.1103/PhysRevLett.77.3865
    [27] Troullier N, Martins J L 1991 Phys. Rev. B 43 1993 doi: 10.1103/PhysRevB.43.1993
    [28] Soler J M, Artacho E, Gale J D, García A, Junquera J, Ordejón P, Sánchez-Portal D 2002 J. Phys. Condens Matter 14 2745 doi: 10.1088/0953-8984/14/11/302
    [29] Grimme S 2006 J. Comput. Chem. 27 1787 doi: 10.1002/jcc.20495
    [30] Xu Z, Luo W D, Guo S Y, Liu S Z 2024 ACS Appl. Mater. Interfaces 16 40123 doi: 10.1021/acsami.4c04617
    [31] Ramezani H R, Şaşıoğlu E, Hadipour H, Soleimani H T, Friedrich C, Blügel S, Mertig I 2024 Phys. Rev. B 109 125108 doi: 10.1103/PhysRevB.109.125108
    [32] Fu C F, Sun J Y, Luo Q Q, Li X X, Hu W, Yang J L 2018 Nano Lett. 18 6312 doi: 10.1021/acs.nanolett.8b02561
    [33] Hieu N N, Phuc H V, Kartamyshev A I, Vu T V 2022 Phys. Rev. B 105 075402 doi: 10.1103/PhysRevB.105.075402
    [34] Jin H, Wei T, Huang B 2024 Nano Lett. 24 10892
    [35] Xia J L, Gu Y X, Mai J, Hu T Y, Wang Q K, Xie C, Wu Y K, Wang X 2023 Heliyon 9 20619 doi: 10.1016/j.heliyon.2023.e20619
    [36] Sun N, Qi S M, Zhou B Z, Mi W B, Wang X C 2021 J. Alloys Compd. 875 160048 doi: 10.1016/j.jallcom.2021.160048
    [37] Tuckerman M, Berne B J, Martyna G J 1992 J. Chem. Phys. 97 1990 doi: 10.1063/1.463137
    [38] Zhao C S, Li Z H, Zhang Z H 2024 Appl. Surf. Sci. 672 160859 doi: 10.1016/j.apsusc.2024.160859
    [39] Wang Q H, Li H, Si L N, Dou Z L, Yan H J, Yang Y, Liu F B 2023 Mater. Today Commun. 35 105724
    [40] Zhang W X, Yin Y, He C 2020 Phys. Chem. Chem. Phys. 22 26231 doi: 10.1039/D0CP04474A
    [41] Li Z H, Han J N, Cao S G, Zhang Z H 2023 Appl. Surf. Sci. 614 156095 doi: 10.1016/j.apsusc.2022.156095
    [42] Nguyen C V, Idrees M, Phuc H V, Hieu N N, Binh N T, Amin B, Vu T V 2020 Phys. Rev. B 101 235419 doi: 10.1103/PhysRevB.101.235419
    [43] Vicario C, Monoszlai B, Hauri C P 2014 Phys. Rev. Lett. 112 213901 doi: 10.1103/PhysRevLett.112.213901
  • 加载中
图( 7)
计量
  • 文章访问数:  28
  • HTML全文浏览数:  28
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-10
  • 刊出日期:  2025-05-20

铁电异质结T-NbTe2/Ga2S3的接触性质及调控

    通讯作者: E-mail: chengfang@csust.edu.cn.
    作者简介: 孙智玄. E-mail: 1162537399@qq.com
  • 长沙理工大学物理与电子科学学院, 长沙　410114
  • 收稿日期:  2024-12-10

摘要: 单层的铁电半导体Ga2S3因具有卓越的延展性, 极高的载流子迁移率以及独特的面外非对称极化特性而备受关注. 利用铁电半导体Ga2S3面外非对称极化特性, 本研究构建了T-NbTe2/Ga2S3铁电异质结, 并选用了两个能量最稳定且Ga2S3极化强度方向不同的异质结PD1 ($ \boldsymbol P_{\downarrow}$)和PU2 ($\boldsymbol P_{\uparrow} $), 对其结构稳定性和电接触性质进行相关研究. 结果表明, 由于Ga2S3极化强度方向的不同, 本征态下的异质结PD1和PU2分别形成了N型肖特基接触和P型肖特基接触. 改变铁电半导体Ga2S3的极化特性, 能改变铁电异质结T-NbTe2/Ga2S3肖特基势垒的接触类型, 这为设计多功能的肖特基器件提供了一种实用的方法. 对于异质结PD1和PU2, 施加外加正电场或者双轴应变拉伸, 都能够有效地实现肖特基接触至欧姆接触的转变. 这些结果为高性能电接触界面的二维铁电纳米器件提供了理论参考.

English Abstract

    全文HTML

    1.   引　言

    • 由于接触势垒的不同, 金属性与半导体性材料构成的异质结接触通常被划分为两大类: 肖特基接触(SC)与欧姆接触(OC)[1,2]. 肖特基接触是一种整流型的金属-半导体接触[3], 这一过程会导致半导体能带结构弯曲, 并随之在界面处形成肖特基势垒[4]. 这个势垒的存在使得电流只能在一个方向上流动, 即从金属流向半导体(正向偏置)时容易通过, 而反向偏置时则很难通过. 欧姆接触是一种理想的金属-半导体接触, 它提供了一个低电阻的路径, 允许电流在金属和半导体之间自由流动. 在欧姆接触中, 金属与半导体之间的肖特基势垒高度(SBH)非常小, 接近于零, 这一特性为高速、低功耗电子设备的实现提供了有力保障. 因此, 若要达成高性能、低功耗电子器件的目标, 需要选用具备高载流子迁移率特性的通道材料, 同时确保金属-半导体界面的接触电阻足够低[5,6].

      目前已有多种调控方法来改变SBH, 而石墨烯与非对称极化半导体构成的异质结接触, 为异质结的调控提供了新的思路. 由于半导体原子终端的影响, 使得在非对称极化半导体形成的异质结在接触面上表现出固有的偶极, 如GR/Ga2SSe[7], GR/PtSSe[8], Gr/Ga2S3[9]. Ga2S3是一类具有自发极化的铁电半导体M2X3 (M = Ga, In; X = S, Se)家族的成员, 现已被实验合成[10–12]. 单层的Ga2S3展现出了卓越的延展性, 在施加了3%的应变条件下, 载流子的迁移率可高达1800 cm2·V–1·s–1 [13]. 目前基于铁电材料Ga2S3进行了一系列异质结的构造, 如Gr/Ga2S3[9], InSe/Ga2S3[14], Au/In4Se3/Ga2S3[15], 发现它们在纳米器件、光电器件以及场效应晶体管中有着诸多优势, 为设计具有高性能电接触界面的器件做出了理论参考. 1 T相NbTe2是一种少层2D过渡金属二硫族化合物(TMDs)材料, 可通过液相剥离(LPE)法[16]、湿球磨诱导分层法[17]、化学气相沉积法[18]等方法进行制备. Sushant与Ramamurthy[19]和Ataca等[20]分别研究了T-NbTe2的评估交换相关函数以及稳定性和金属性. T-NbTe2在一定的条件下可呈现超导性, 而且具有非线性吸收特性和优异的光学响应[16]. 目前基于T-NbTe2进行了一系列异质结的构造, 例如T-NbTe2/SnS2[21], T-NbTe2/$ \alpha $-In2S3[22]等, 发现其在场效应管和二极管等器件上有着非常广阔的应用前景.

      为了进一步探索铁电半导体Ga2S3面外非对称极化特性, 我们考虑了二维材料T-NbTe2与两种不同极化特性的铁电半导体Ga2S3组成的二维异质结[23,24], 对结构稳定性、以及外加电场或外加双轴应力对接触性质的调控进行深入研究. 通过结合能、AIMD模拟、声子谱等计算, 表明T-NbTe2与两种不同极化特性的铁电半导体Ga2S3 构成的异质结结构稳定, 在实验下具有制备的可能性. 通过改变Ga2S3的极化强度方向, 可以改变异质结的接触类型. 具体来说, 就是当模型由T-NbTe2/Ga2S3 (Ga2S3的面外极化强度方向向下)转变成T-NbTe2/Ga2S3 (Ga2S3的面外极化强度方向向上)时, 接触类型由N型肖特基接触转变成了P型肖特基接触, 实现了肖特基接触的转换, 为设计多功能的肖特基器件提供了一种实用的方法. 同时施加外电场和双轴应变, 都实现了肖特基接触至欧姆接触的转变, 为制作高性能电接触界面的二维铁电纳米器件提供了理论参考.

    2.   计算方法

    • 本文所有计算均使用Quantum Atomistix Toolkit软件包来进行[25], 采用基于密度泛函理论(DFT)的第一性原理方法进行模型几何形状的优化以及结构的稳定性等计算. 在求Kohn-Sham方程过程中, 交换关联势采用了广义梯度近似(GGA)中Perdew-Burke-Ernzerhof (PBE)泛函[26], 原子与价电子之间的相互作用采用Troullier-Martins模守恒赝势[27]. 选用DZP (Double ζ +Polarization)作为基函数组[28], 将价电子的波函数通过原子轨道的线性组合(LACO)进行展开. 综合计算效率、精度以及时间成本的考虑, 使用了14×14×1的Γ中心k点网格对第一布里渊区进行采样, 将能量截断半径设定为185 Ha, 几何模型优化收敛标准能量10–5 eV, 原子间的相互作用的收敛准则为10–2 eV/Å, 晶格内应力小于0.01 GPa. 为了消除模型与其“像”之间的相互作用, 我们在非周期z轴方向上设置了一个大于20 Å的真空层. 为了方便, 所有系统的费米能级都设置为0.0 eV. 计算中同时考虑界面偶极子矫正和Grimme的DFT-D3方法色散矫正[29]. 在几何模型结构优化后, 才会进行几何模型的稳定性评估、电子结构以及后续的计算工作.

    3.   结果与讨论

      3.1.   异质结结构模型与稳定性

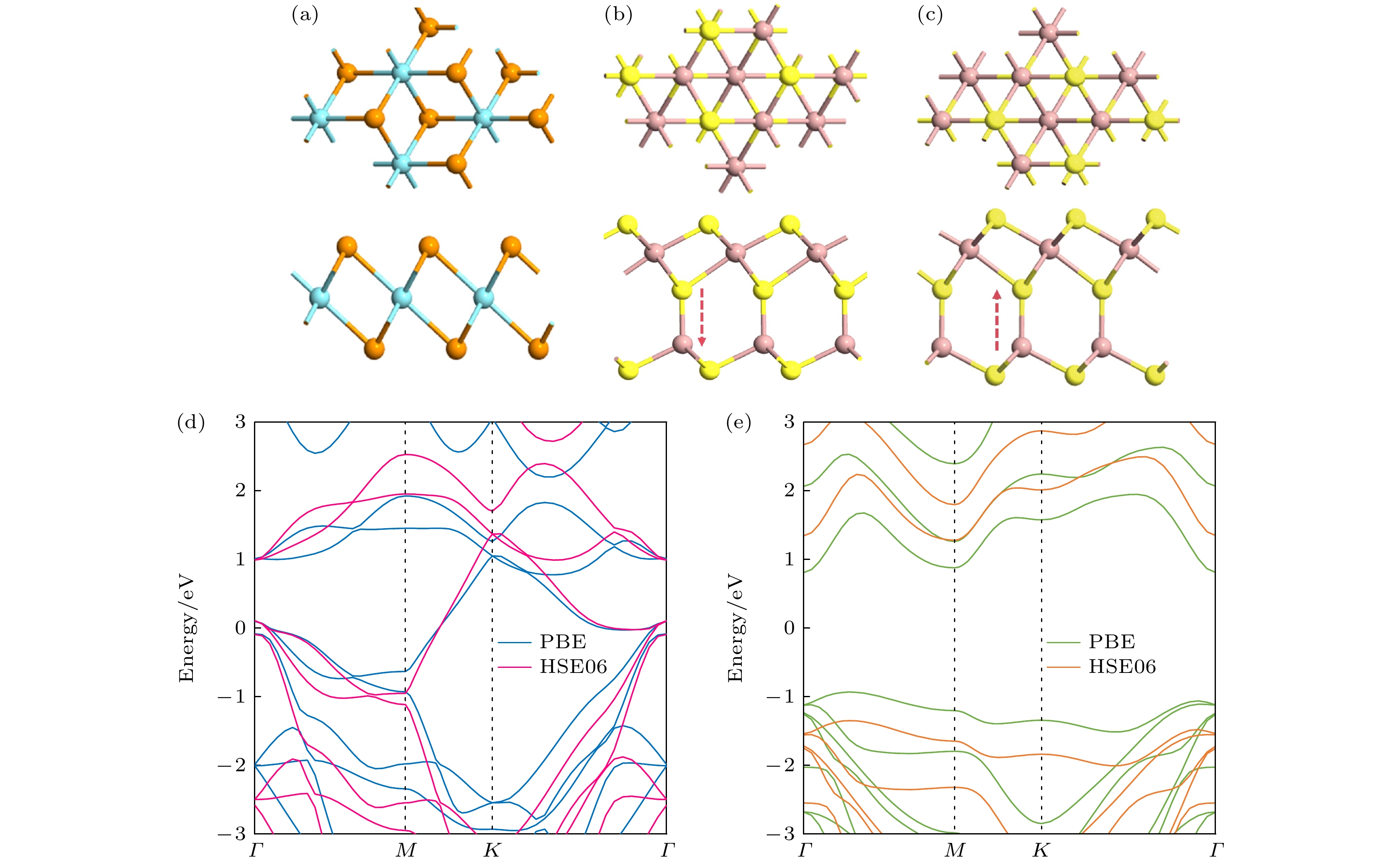
    • 为研究异质结的界面性质, 本研究首先对各单层材料的几何结构和电子性质进行了详细探讨. T-NbTe2属于P3m1空间群, Ga2S3的原子构型由堆叠的S-Ga-S-Ga-S原子层组成. 优化后的单层原子结构如图1(a)—(c)所示, T-NbTe2(Ga2S3)的晶格常数是3.653 Å (3.628 Å), T-NbTe2的功函数为4.767 eV (PBE)和5.099 eV (HSE06), Ga2S3的功函数为4.630 eV (PBE)和4.875 eV (HSE06), 这与前人研究结果非常接近[30–33]. 计算的能带结构图1(d), (e)所示, T-NbTe2是无磁金属, Ga2S3是带隙为1.743 eV (PBE), 2.628 eV (HSE06)的半导体, 结果与之前的研究都很接近[13,34].

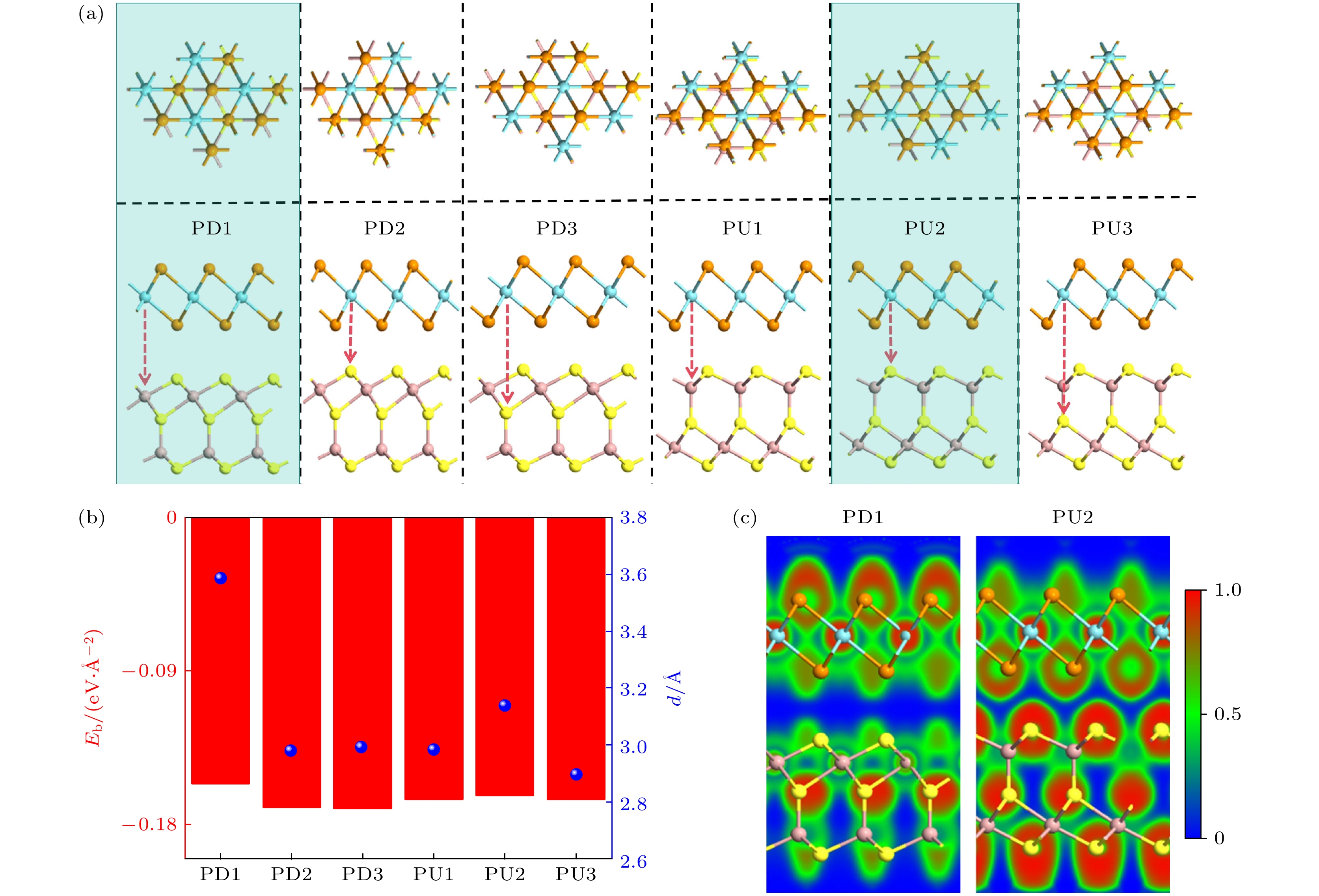
      对单层材料T-NbTe2与Ga2S3, 采用1×1的单胞来构建T-NbTe2/Ga2S3异质结. 晶格失配率定义为$ \sigma = ({\alpha _1} - {\alpha _2})/{\alpha _1} $, 式中$ {\alpha _1} $和$ {\alpha _2} $分别为T-NbTe2和Ga2S3的晶格常数. 计算得到异质结的晶格失配率约为0.684%, 这表明构成的异质结具有非常高的晶格匹配度, 可以确保理论模拟更接近实验情况. 由于单层Ga2S3面外非对称极化的特性, 使得上下两侧的S原子发生了分化, 从而在构建的异质结时出现了两种异质结: 一种$ \overrightarrow P $向下的T-NbTe2/Ga2S3异质结(命名为PD), 一种$ \overrightarrow P $向上的T-NbTe2/Ga2S3异质结(命名为PU). 在构建异质结时, 我们考虑了6种堆垛情况. 图2(a)给出了优化后的正视图和侧视图, 其中PD1—PD3堆垛为T-NbTe2中的Nb原子分别与Ga2S3层中最上层的S原子, 中间层的S原子以及上中层之间的Ga原子对齐. 用同样的对齐方式得到PU1—PU3堆垛结构. 结合能定义为

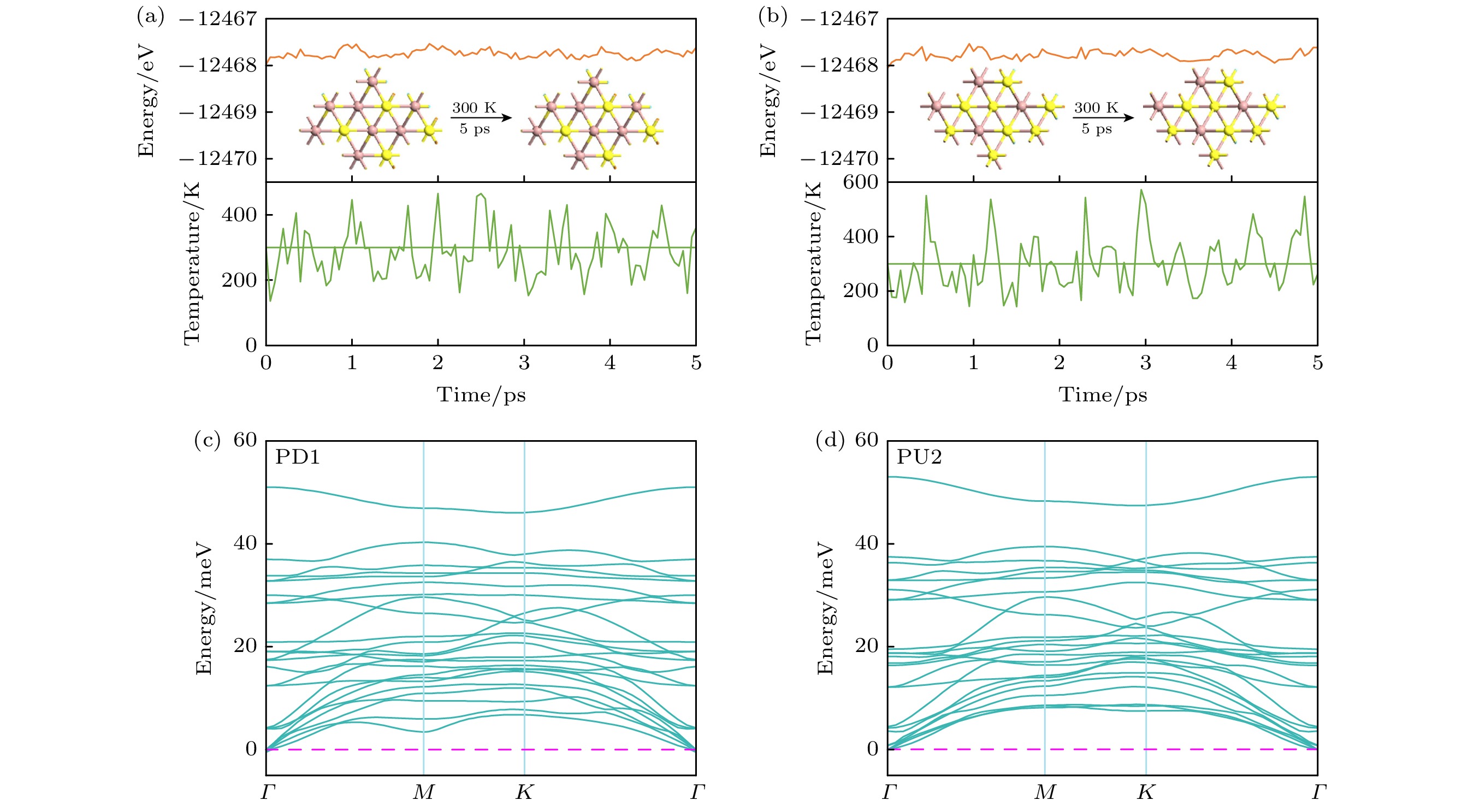
      其中$ {E_{{\text{vdWH}}}} $, $ {E_{{\text{NbT}}{{\text{e}}_{2}}}} $以及$ {E_{{\text{G}}{{\text{a}}_{2}}{{\text{S}}_{3}}}} $分别是异质结, T-NbTe2单层以及Ga2S3单层的总能量; A表示异质结界面的面积. 结合能计算结果如图2(b)所示, PD1堆垛和PU2堆垛异质结的结合能最低, 分别为–0.156 eV/Å, –0.163 eV/Å, 是最稳定的异质结. 它们的结合能比多数vdWHs要低, 如TaS2/MoSi2N4[35], Gr/WSeTe[36]等, 证实了异质结结构的稳定性. 为了可视化异质结的成键特征, 计算了6种异质结堆叠构型的电子定位函数, 发现6种结构相似. 因此, 这里只给出了A型和B型中结合能最低的堆叠构型, 即PD1和PU2作为代表, 如图2(c)所示, 可以明显看出电子局域化只存在于每一层中, 两层之间没有化学键, 只有较弱的范德瓦耳斯力发生键合.

      为了评估T-NbTe2/Ga2S3异质结的热力学稳定性, 选取了最稳定的异质结PD1和PU2, 使用了带有Nose Hoover热浴方案的NVT规范系综[37]. 在分子动力学模拟过程中, 热浴温度固定在300 K, 三个并发调温器模拟过程持续5 ps. 从图3(a)和图3(b)中的模拟结果可以看到, 整个模拟过程中总能量随时间的变化幅度很小, 而且结构中的原子没有偏离其平衡位置, 没有出现几何重构和断键现象[38], 因此表明PD1和PU2具有良好的热力学稳定性. 我们同时计算了PD1和PU2的声子谱, 如图3(c)和图3(d)所示, 发现异质结PD1和PU2的声子谱在布里渊区没有出现虚频, 证明了$\boldsymbol P_{\downarrow} $的T-NbTe2/Ga2S3异质结和$ \boldsymbol P_{\uparrow}$的T-NbTe2/Ga2S3异质结都具有好的动力学稳定性.

      • 3.2.   异质结电子结构以及电接触性质

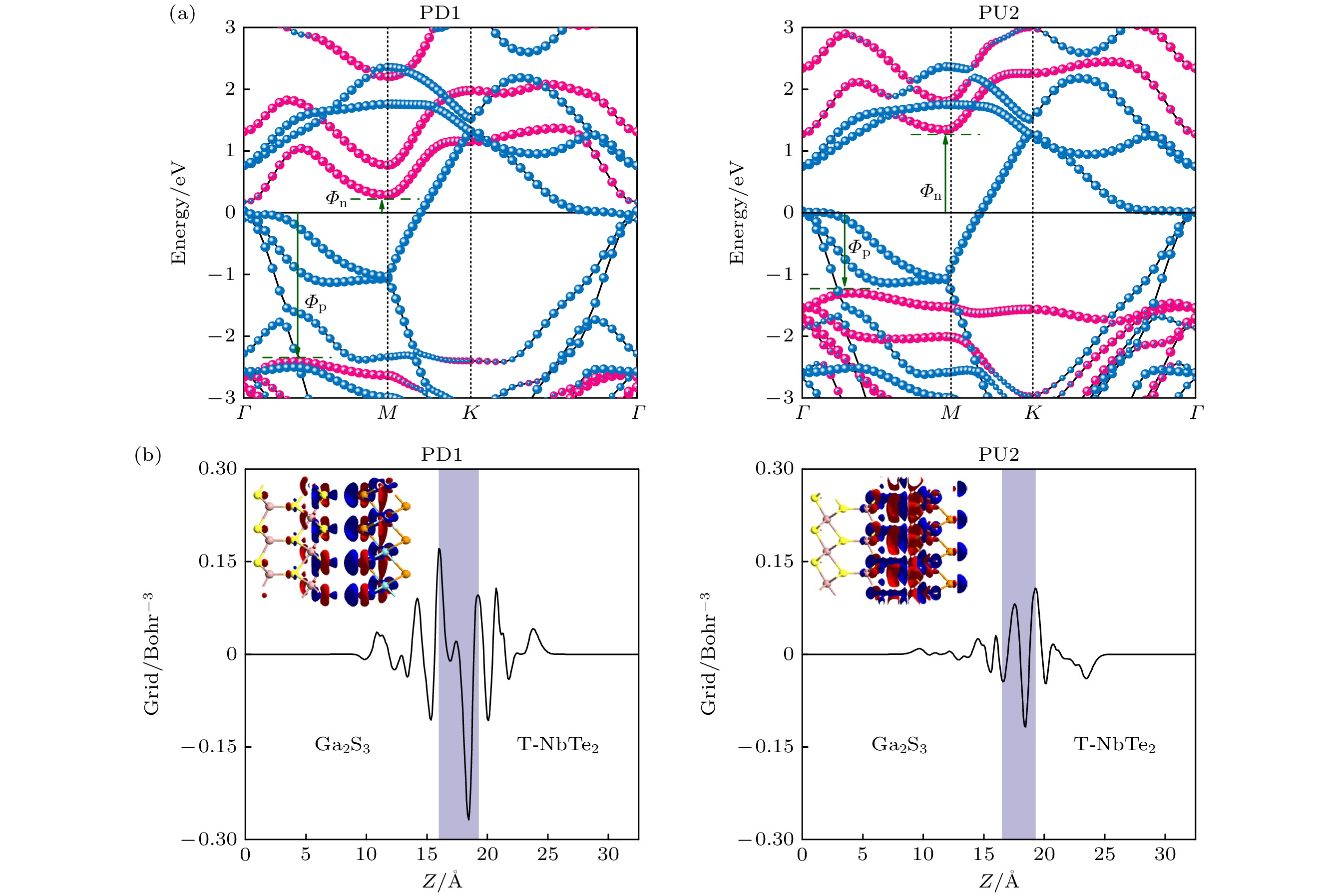
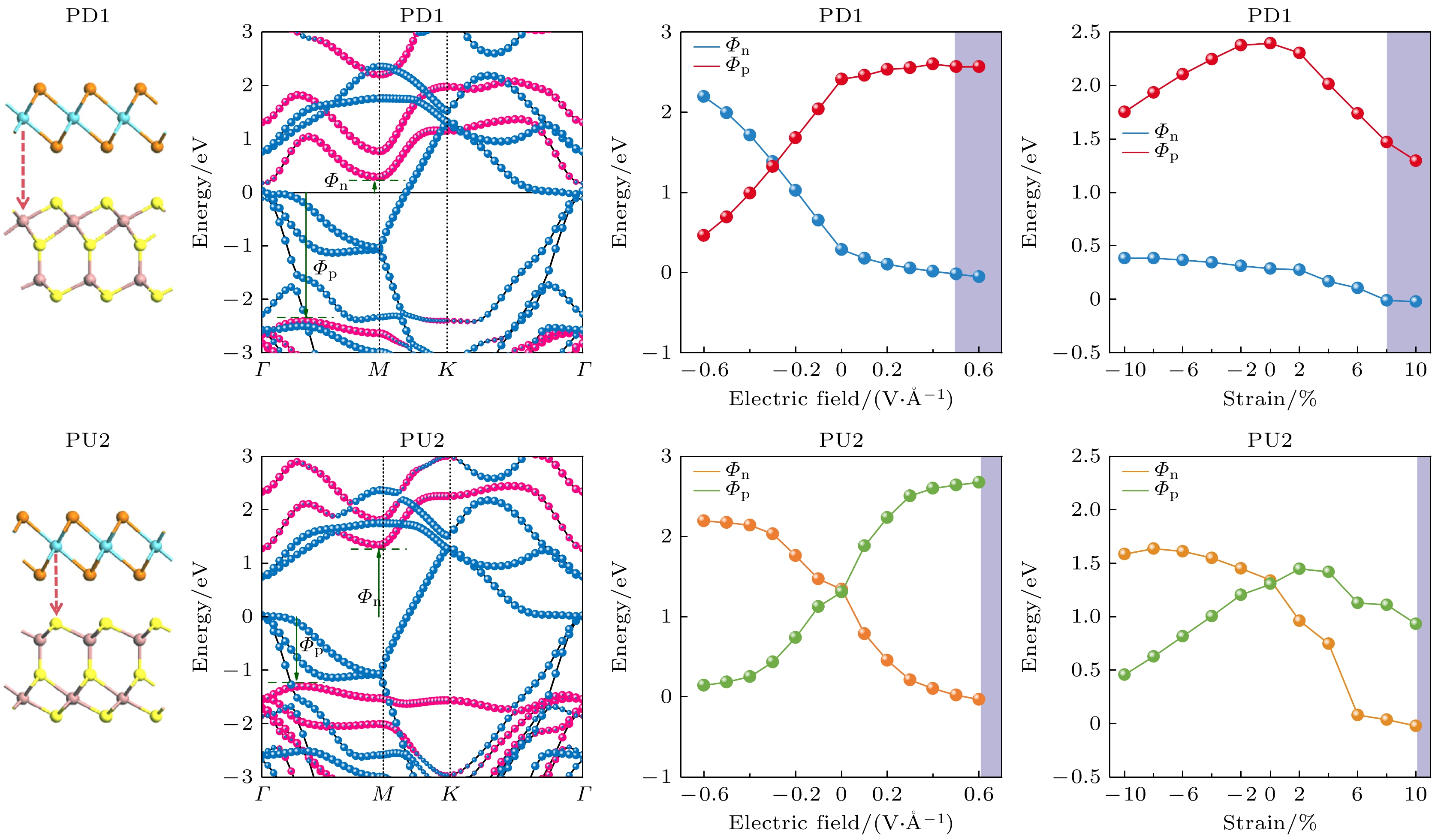
    • PD1和PU2的投影能带如图4(a)所示, T-NbTe2和Ga2S3的贡献分别为蓝色和红色. 金属与半导体之间的接触通常被划分为两大类: 肖特基接触(SC)与欧姆接触(OC). 这两种电接触主要取决于半导体能带边缘相对于费米能级($ {E_{\text{F}}} $)的位置. 由金属-半导体异质结的Schottky-Mott规则[39]:

      其中$ {E_{\text{C}}} $是半导体层的导带最低能量; $ {E_{\text{V}}} $是半导体层的价带最高能量; $ {E_{\text{F}}} $是费米能级. N型肖特基势垒高度$ {\varPhi _{\text{N}}} $小于P型肖特基势垒高度$ {\varPhi _{\text{P}}} $, 即$ {\varPhi _{\text{N}}} $<$ {\varPhi _{\text{P}}} $对应N型肖特基接触, 而$ {\varPhi _{\text{N}}} $>$ {\varPhi _{\text{P}}} $对应P型肖特基接触. 如果肖特基接触高度$ {\varPhi _{\text{N}}} $≤0或$ {\varPhi _{\text{P}}} $≤0, 则形成了N型或P型欧姆接触. 从图4(a)可以看出, 异质结PD1和PU2的T-NbTe2和Ga2S3层之间没有发生明显的轨道杂化, 且由于PD1和PU2是通过范德瓦耳斯力接触形成, 有效地避免了界面化学键. PD1和PU2的$ {\varPhi _{\text{N}}} $($ {\varPhi _{\text{P}}} $)分别为0.288 eV (1.543 eV)和1.344 eV (1.269 eV), 所以半导体极化方向不同的两种异质结PD1和PU2在界面处分别形成两种不同的肖特基接触——N型肖特基接触和P型肖特基接触. 异质结PD1的$ {\varPhi _{\text{N}}} $低于其他大多数金属半导体异质结, 如石墨烯/WSSe[40], 石墨烯/MoSi2N4[41]和石墨烯/PbI2[42]形成的$ {\varPhi _{\text{N}}} $= 0.350, 0.680和0.890 eV的N型肖特基接触, 表明PD1设计高性能电接触界面的二维铁电纳米器件更加有利. 此外由于PD1和PU2只是改变了异质结的接触界面, 就实现了肖特基的转换, 为设计多功能的肖特基器件提供了一种实用的方法.

      对比Ga2S3单层的能带结构(见图1), 发现Ga2S3的投影能带结构在PD1 (PU2)中有一定的下(上)移, 这是因为投影能带的移动受到电荷转移的影响, 而电荷转移由两个因素决定: 两种单层材料之间的费米能级差和最靠近界面的原子层之间的电负性差. 计算PD1和PU2的空间电荷密度差, 来观察PD1和PU2的电荷转移情况. 空间电荷密度差定义为

      其中$ {\rho _{{\text{T-NbT}}{{\text{e}}_{2}}{\text{/G}}{{\text{a}}_{2}}{{\text{S}}_{3}}}}(x,y,z)$, $ {\rho _{{\text{T-NbT}}{{\text{e}}_{2}}}}(x{, }y{, }z) $和$ {\rho _{{\text{G}}{{\text{a}}_{2}}{{\text{S}}_{3}}}}(x{, } y{, }z) $分别表示异质结, 孤立单层T-NbTe2和孤立单层Ga2S3在(x, y, z)的电荷密度. 空间电荷密度差随着z的变化图如图4(b)所示, 大于零表示获得电子, 小于零表示失去电子, 插图中红色(蓝色)表示电子累积(耗尽). 对于异质结PD1, 半导体Ga2S3层失去电子而T-NbTe2层得到电子, 电子由Ga2S3流向T-NbTe2层. 这是因为PD1的层间距更大(见图2), 电荷转移的方向由两个单层 之间的费米能级差主导, T-NbTe2层的费米能 级 (–5.010 eV)比半导体Ga2S3层的费米能级(–4.875 eV)低, 因此电子会从半导体Ga2S3层转移至T-NbTe2层, 异质结PD1的半导体Ga2S3层N型掺杂, 其投影能带结构向下移动. 而对于PU2来说, PU2的T-NbTe2层失电子而Ga2S3层得电子, 电子由T-NbTe2层流向Ga2S3层. 这是由于两个单层层间距较小, 原子S原子和Te原子更接近, 电荷转移的方向由原子层之间的电负性差主导. 同一主族元素从上到下, 电负性依次减小, T-NbTe2 (Ga2S3)层中离界面最近的原子层是Te(S)原子层, 所以S原子比Te原子有更强的电负性, 会导致电子从T-NbTe2层整体流向了Ga2S3层. 最终PU2的Ga2S3层为P型掺杂, 其投影能带结构向上移动. 电子转移导致两单层间形成内建电 场$ {E_{{\text{in}}}} $, PD1的Ga2S3层失电子而T-NbTe2层得电子, 所以在PD1中, 内建电场由Ga2S3层指向T-NbTe2层; 而在PU2中, PU2的T-NbTe2层失电子而Ga2S3层得电子, 内建电场由T-NbTe2层指向Ga2S3层.

      • 3.3.   异质结电接触性质的物理调控

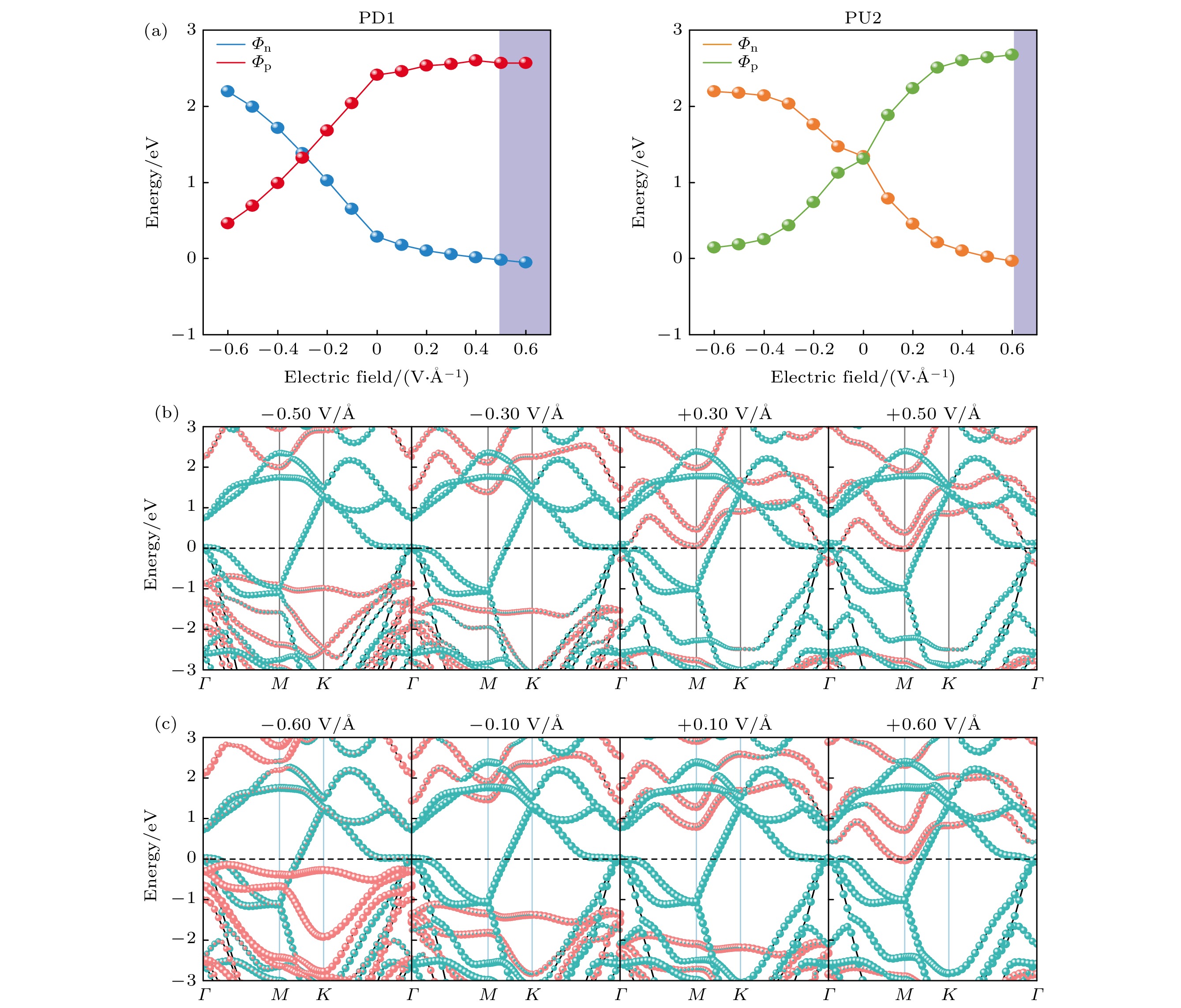
    • 在实验中制备高性能电子器件时, 使用脉冲交流场技术允许应用的最大外部电场高达0.6 V/Å[43]. 本研究以异质结PD1和PU2为例, 探讨外电场对铁电异质结电接触特性的影响. 定义从Ga2S3层指向T-NbTe2层的方向为电场正方向. 图5(a)是外电场对异质结PD1(PU2)的肖特基势垒高度(SBH)的调控. 对于异质结PD1, 如图5(a)和图5(b)所示, 施加负外电场时, $ {\varPhi _{\text{N}}} $随着电场强度的增大而增大, 而与之相反, $ {\varPhi _{\text{P}}} $随着电场强度的增大而减小. 当负的电场强度达到–0.3 V/Å时, 异质结PD1从N型肖特基接触转变成了P型肖特基接触; 施加正外电场时, $ {\varPhi _{\text{N}}} $随着电场强度的增大而减小, 而$ {\varPhi _{\text{P}}} $随着电场强度的增大而增大. 当正的电场强度增大到+0.5 V/Å时, 异质结PD1实现了N型肖特基接触到欧姆接触的转变. 对于异质结PU2, 如图5(a)—(c)所示, 施加负外电场时, $ {\varPhi _{\text{N}}} $随着电场强度的增大而增大, 而$ {\varPhi _{\text{P}}} $随着电场强度的增大而减小. 当负的电场强度增大到–0.6 V/Å时, 此时的$ {\varPhi _{\text{P}}} $仅为–0.143 eV, 非常靠近费米能级; 施加正外电场时, $ {\varPhi _{\text{N}}} $随着电场强度的增大而减小, 而$ {\varPhi _{\text{P}}} $随着电场强度的增大而增大. 当正的电场强度增大到+0.1 V/Å时, 异质结PU2从P型肖特基接触转变成了N型肖特基接触; 当正的电场强度增大到+0.6 V/Å时, 异质结PU2实现了从N型肖特基接触到N型欧姆接触转变. 对于PD1 (PU2), 只需要较小的电场强度–0.3 V/Å (+0.1 V/Å), 就可以实现N型肖特基接触和P型肖特基的互相转化, 为设计多功能的肖特基整流管开辟了可能性. 同时对于异质结PD1 (PU2), 当电场强度增大到+0.5 V/Å (+0.6 V/Å), 实现了肖特基接触到欧姆接触的转变. 因此, 对于铁电异质结来说, 外加电场能有效提高电流的传输能力, 为高性能电接触界面的二维铁电纳米器件提供了理论参考.

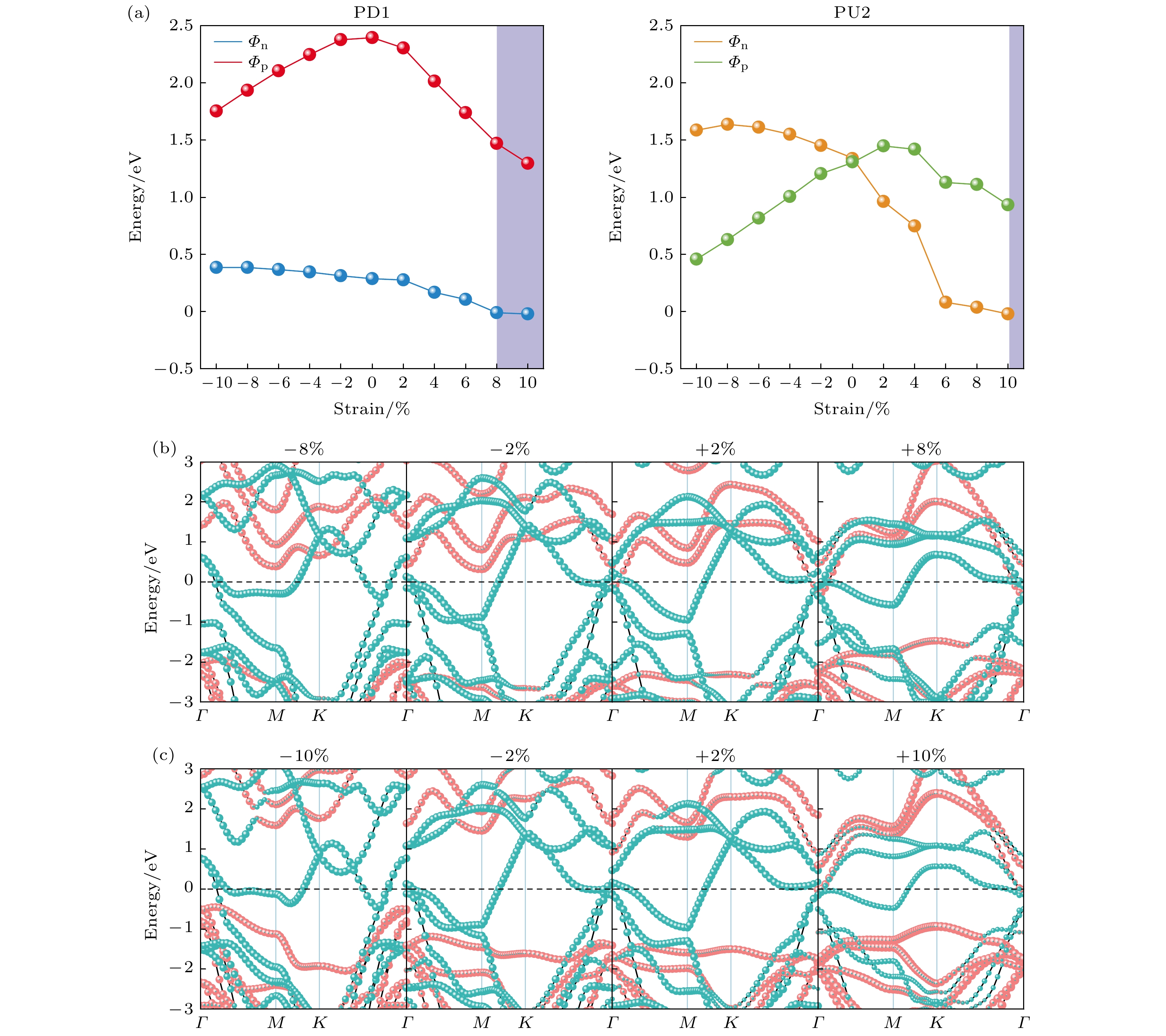
      除了外加电场之外, 平面双轴应变同样对肖特基势垒高度以及电接触性起着至关重要的作用. 双轴应变的应变系数$ \varepsilon = (a - {a_0})/{a_0} $, 其中$ {a_0} $和$ a $分别代表异质结在平衡状态和应变下的晶格常数. 两个轴向取相同的应变, 压缩应变对应于应变系数$ \varepsilon < 0 $, 拉伸应变对应于应变系数$ \varepsilon > 0 $. 本研究以异质结PD1和PU2为例, 探讨双轴应变对铁电异质结电接触特性的影响. 考虑到双轴应变对晶格影响较大, 应变范围只选取了–10%—10%. 异质结PD1(PU2)的SBH随双轴应变的变化关系如图6(a)所示. 对于异质结PD1, 如图6(a)和图6(b)所示, 压缩时, $ {\varPhi _{\text{N}}} $有所增加, $ {\varPhi _{\text{P}}} $持续减小; 拉伸时, $ {\varPhi _{\text{N}}} $和$ {\varPhi _{\text{P}}} $随着电场强度的增大持续减小, 当拉伸到+8%时, PD1实现了N型肖特基接触到欧姆接触的转变. 对于异质结PU2, 如图6(a)—(c)所示, 压缩时, $ {\varPhi _{\text{N}}} $持续增大, $ {\varPhi _{\text{P}}} $持续减小; 拉伸时, $ {\varPhi _{\text{N}}} $和$ {\varPhi _{\text{P}}} $随着电场强度的增大持续减小, 当拉伸到+2%时, PU2从P型肖特基接触转变成了N型肖特基接触; 当拉伸到+10%时, PU2实现了从N型肖特基接触到欧姆接触转变. 因此对于异质结PU2只需要2%的拉伸, 就可以实现P型肖特基接触至N型肖特基的转化, 为设计多功能肖特基整流管开辟了可能性. 同时对于异质结PD1 (PU2), 当拉伸增大8% (10%)时, 实现了肖特基接触到欧姆接触的转变. 因此, 对于铁电异质结来说, 双轴应变也能够有效地提高电流的传输能力, 为高性能电接触界面的二维铁电纳米器件提供了理论参考.

    4.   结　论

    • 本文构建了6个T-NbTe2/Ga2S3异质结, 通过计算6个异质结的结合能, 并根据Ga2S3的极化方向, 选取了最稳定的两个结构PD1和PU2进行研究. 通过对异质结PD1和PU2结合能、AIMD模拟以及声子谱的计算, 表明异质结PD1和PU2满足能量、热力学以及动力学稳定性, 证实其在实验下具有制备的可能性. 异质结PD1和PU2在本征态下分别形成了N型肖特基接触和P型肖特基接触. 改变异质结中铁电半导体Ga2S3极化方向, 改变了肖特基接触类型, 为设计多功能肖特基器件开辟了一条切实可行的路径. 对于异质结PD1 (PU2), 外加电场达到+0.5 V/Å (+0.6 V/Å), 或者双轴应变拉伸至8% (10%)时, 均可以实现肖特基接触到欧姆接触的转换, 这些发现为设计基于T-NbTe2/Ga2S3铁电异质结的高性能多功能器件做出了理论参考.

    参考文献 (43)

目录

/

返回文章
返回