自从Isidor Rabi于1939年发现核磁共振现象至今, 以核磁共振为基础的波谱和成像技术在材料、化学、生物等领域取得了广泛应用, 孕育了多个诺贝尔奖成果. 20世纪90年代, Lloyd^[1]和DiVincenzo^[2]先后提出将核自旋用于量子计算. 得益于核自旋的长相干时间以及强大的射频脉冲操控核自旋的能力, 核磁共振平台特别是液态核磁共振平台成为最早演示量子计算的先驱平台之一^[3–5]. 其中丰富的脉冲量子控制技术的发展^[6–8]也为其他新兴量子计算和量子模拟平台提供了宝贵的技术经验^[9–13]. 然而由于分子间磁偶极相互作用在分子的随机热运动(翻转和扩散)下的时间平均为零, 液态核自旋体系只能基于分子内的核自旋构建小规模的量子计算机或量子模拟器^[14–16]. 相比之下, 固态核自旋体系由于晶格的束缚, 热运动无法消除分子间的磁偶极相互作用, 这使得固态核自旋之 间能够建立长程的量子关联^[17]. 基于这一重要的特性, 固态核自旋体系在量子多体物理模拟、量子增强的精密测量方面展现出重要的潜力和研究价值^[18–27]. 近十多年来, 利用固态核自旋体系, 国际研究组相继发现和揭示了量子多体物理中多个 重要的现象和机制. 例如离散时间晶体^[21,26]、多 体局域化^[20]、信息输运和弥散^{[19,23,25,28–31]}、量子热化^[22,24]、非平衡动力学普适性^[25,27]等.

同大多数可扩展的量子体系一样, 固态核磁共振也一直追求更完备和更精密的控制能力. 当前在固态核磁共振中广泛应用的控制手段包括动力学解耦、魔角旋转、交叉极化、动态核极化等^[32–39]. 这些控制技术帮助固态核磁共振体系实现了更高的核自旋极化度、更灵活的动力学调控以及更高分辨率的谱线探测. 随着前沿量子技术的发展, 如何利用量子纠缠态、量子压缩态等重要的量子资源实现多个方向的量子优势成为了前沿量子技术中的关键科学问题^[40–42]. 作为有望实现这一科学目标的重要量子体系之一, 固态核磁共振领域需要发展更为强大的量子调控技术, 例如多体自旋纠缠/关联态的制备、量子多体哈密顿量的调控和层析、固态核自旋的超极化、固态核自旋压缩态的制备等. 令人期待的是, 伴随着量子调控能力的每一次突破, 会有更多的非平庸的量子多体物理现象和机理如雨后春笋般涌现出来. 这方面的前沿研究近几年逐渐成为国际热点.

本文围绕固态核磁共振量子控制及其应用这一主题, 系统介绍了固态核磁共振量子控制的研究对象和理论基础, 包括固态核磁共振研究的基本量子模型、体系中不同的相互作用及其哈密顿量、弛豫机制、射频脉冲控制原理以及一些重要的脉冲序列等. 此外, 重点介绍了近年来在固态核磁共振量子控制取得的前沿进展, 包括核自旋极化技术、弗洛凯哈密顿量调控技术、自旋多体量子态层析技术等. 最后, 结合一些重要的研究进展, 阐述了固态核磁共振量子控制技术在量子模拟领域中的应用.

宏观的核磁共振样品中包含了大量的电子和原子核. 原则上整个样品的系统演化由以下含时薛定谔方程描述:

式中整体哈密度量$ \hat{H}_{\rm full} $包含了所有电子、原子核以及电磁场之间的相互作用. 尽管(1)式是完备的, 但实际上无法研究这么复杂的动力学方程. 为了简化问题, 在核磁共振系统中, 只考虑核自旋部分, 而电子的影响则以平均的效应包含在核自旋哈密顿量里. 这便是所谓的自旋哈密顿量假设. 因此有:

自旋哈密顿量$ \hat{H}_{\mathrm{NMR}} $按来源可以分为外部和内部相互作用.

外部相互作用包括核自旋与静磁场、射频场等来自于样品以外的电磁场之间的相互作用. 当样品分子中核自旋的量子数不为0时, 在外加的静磁场$ {\boldsymbol{B}}_0 $(一般约定沿z方向)作用下, 原子核的自旋能级发生塞曼劈裂. 塞曼相互作用的哈密顿量为$ \hat{H}_{\rm Z}=-\displaystyle\sum\nolimits_j\hbar\gamma_jB_0\hat{I}_z^j $, 其中$ \gamma_j $为第j个核的旋磁比, $ \omega_0=-\gamma_jB_0 $表示塞曼劈裂的强度, 也称为拉莫尔频率. 在强度为几个特斯拉的静磁场中, 核自旋的拉莫尔频率处于射频波段. 一般在垂直于静磁场方向施加射频场对核自旋体系进行调控. 如果射频场的振荡频率$ \omega_{\rm rf} $接近某同位素原子核的拉莫尔频率, 即$ \omega_{\rm rf}\approx\omega_0 $, 那么射频辐照范围内属于该同位素的所有核自旋都将被共振激发. 因此, 固态核磁共振原则上无法对核自旋进行局域操控, 从而无法发展基于逻辑门的通用量子计算. 记集体自旋算符为$ \hat{O}_{\alpha}=\displaystyle\sum\nolimits_i\hat{I}_\alpha^i $($ \alpha=x, y, z $), 同种核自旋的射频场哈密顿量为^[6]

其中ϕ为射频脉冲的相位, $ \omega_{1} $正比于射频场的强度, 称为拉比频率. 在固态核磁共振谱仪中$ \omega_1 $可达到几百kHz的量级. 我们通常在绕z轴以$ \omega_{\rm rf} $旋转的旋转坐标系中考虑核自旋系统的演化. 旋转坐标系和实验室坐标系的量子态的变换规则为

射频场哈密顿量的变换规则为

于是有:

在实验中, 通过调节相位ϕ, 可以设置转轴方向, 我们一般设置相位为$ 0 $, $ \pi/2 $, π, $ 3\pi/2 $, 分别对应于$ \hat{x} $, $ \hat{y} $, $ -\hat{x} $, $ -\hat{y} $方向. 通过改变脉冲宽度$ t_{{\mathrm{w}}} $, 可以改变旋转的角度, 称为章动角, 我们常用的是$ \pi/2 $或者π章动角度的脉冲. 在射频脉冲作用完成后, 核自旋会继续在静磁场下作拉莫尔进动, 在横向的探测线圈内产生自由感应衰减(free induction decay, FID)信号, 信号强度反映了横向磁化矢量的大小. 对FID作傅里叶变换得到的频谱可以反映内部相互作用信息.

除静磁场和射频场外, 样品内部的相互作用同样会对核自旋的状态产生影响. 这些内部相互作用一般被称为局域场, 其通常来源于如下几类机制: 核自旋周围电子对核产生的化学屏蔽作用、核自旋之间的偶极相互作用, 以及高自旋样品中的电四极矩相互作用. 通常情况下, 外加静磁场$ {\boldsymbol{B}}_{0} $远大于样品内部产生的局域场. 考虑久期近似^[43–45]后, 大多数和塞曼相互作用不对易的内部相互作用对自旋态的长时累积影响可以忽略不计, 而只保留和塞曼相互作用对易的哈密顿量成分. 这些保留的相互作用一般包括同塞曼场平行的纵向分量, 其会改变核自旋的共振频率; 此外还包括同核偶极相互作用中的自旋交换(flip-flop)相互作用, 其可以将塞曼相互作用下简并的自旋能级混合. 局域场$ {\boldsymbol{B}}_{\text{loc}} $与核自旋$ \hat{{\boldsymbol{I}}} $相互作用的哈密顿量可以统一表示为如下形式:

将局域场$ {\boldsymbol{B}}_{\rm loc} $表示为张量的形式:

其中$ {\boldsymbol{A}}_{\rm loc} $表示耦合张量, $ {\boldsymbol{J}} $表示局域场$ {\boldsymbol{B}}_{\rm loc} $的最终来源, 例如化学屏蔽作用中的外加静磁场$ {\boldsymbol{B}}_0 $, 偶极相互作用中的其他核自旋等. 接下来分别具体阐述固态核磁共振中重要的相互作用机理.

在样品内, 各个核感受到的周围电子云环境是有差别的. 外加静磁场诱导的核周围电子分布的改变及其运动会产生局域磁场, 对核自旋起到一定的屏蔽作用. 这个屏蔽场会改变核的共振频率, 称为化学位移^[46,47]. 化学位移由电子的抗磁性和顺磁性共同贡献. 在固体中, 其具有各向异性. 在实验室坐标系下外磁场$ {\boldsymbol{B}}_0=(0, 0, B_0) $. 描述核自旋$ \hat{{\boldsymbol{I}}}= (\hat{I}_x, \hat{I}_y, \hat{I}_z $)的化学位移的哈密顿量可以写为

其中$ {\boldsymbol{\sigma}} $表示化学位移张量, 其一般形式为

因为核周围的电子分布不是球对称的, 该张量依赖于外磁场$ {\boldsymbol{B}}_{0} $中分子的取向. 理论上可以选择某一方向的坐标系, 使得屏蔽张量对角化, 我们将这一坐标系称为主轴坐标系, 此时屏蔽张量写为

对角化后的3个对角元被称为屏蔽张量的3个主值分量. 主轴坐标系的取向由核自旋周围的电子云结构决定, 相对于分子结构是固定的. 可以将屏蔽张量描绘为一个固定在分子内的椭球体, 以其原子核为中心. 椭球体的长轴与张量的主轴(一般约定为$ z^{\rm PAF} $轴)重合, 椭球体各主轴的长度与该主轴相关的张量主值分量成比例. 如果分子取向发生变化, 那么实验室坐标系下屏蔽张量的取向也会发生变化. 一般情况下x和y方向不对称, 但如果分子围绕某个轴线快速旋转, 其旋转平均的结果使得其z方向主轴往往与旋转轴重合, 而x和y方向则变为互相对称, 于是这种情况下有$ \sigma_{xx}^{\rm PAF}=\sigma_{yy}^{\rm PAF}\neq \sigma_{zz}^{\rm PAF} $. 由于屏蔽场的强度一般远小于外部静磁场, 因此在久期近似下只有外磁场$ {B{\boldsymbol{}}}_0 $方向的分量$ \sigma_{zz} $起作用, 化学位移的哈密顿量可以写为$ \hat{H}_{\rm CS}\approx -\gamma\hbar \hat{I}_{z}\sigma_{zz}B_{0} $. 不同核自旋的化学环境不同, 导致其对应的$ \sigma_{zz} $也不同, 因此样品中所有核自旋的化学位移哈密顿量写为

其中i为自旋指标.

每个核自旋具有的磁矩之间会通过空间产生相互作用, 我们把这种相互作用叫做偶极-偶极相互作用. 偶极相互作用是固态核自旋1/2体系中的主要相互作用. 在经典图像中, 相距为r的两个磁偶极子$ {\boldsymbol{\mu}}_{1} $和$ {\boldsymbol{\mu}}_{2} $的相互作用能量为

其中$ {\boldsymbol{r}} $为点近似下两个磁偶极子之间的相对位矢. 量子力学中, 核自旋的磁矩算符可以写为$ \hat{\mu}=\gamma\hbar \hat{I} $, 代入经典相互作用能量的表达式中得到自旋$ \hat{{\boldsymbol{I}}} $和$ \hat{{\boldsymbol{S}}} $的偶极相互作用哈密顿量为

其中, $ \mu_0 $是真空磁导率, $ \gamma_{I} $和$ \gamma_{S} $是两自旋的旋磁比. 在球坐标下展开整理得到:

其中,

式中, $ \hat{I}_{+}\hat{S}_{+} $, $ \hat{I}_{-}\hat{S}_{-} $表示升降算符, 如前所述, 在强磁场下考虑久期近似, 可以只保留上述6项中与塞曼相互作用$ \hat{H}_{\rm Z}=-\hbar\gamma_{I} B_{0}\hat{I}_{z}-\hbar\gamma_{S} B_{0}\hat{S}_{z} $对易的项. 对于$ \hat{{\boldsymbol{I}}} $和$ \hat{{\boldsymbol{S}}} $属于同一种核自旋的情形, 二者的塞曼能级劈裂相匹配($ \gamma_{I} B_{0}=\gamma_{S} B_{0} $), 因此同核偶极相互作用的久期项不仅包含$ \hat{A} $项代表的平行于静磁场的成分, 也包含$ \hat{B} $项代表的flip-flop项, 因为该项不改变塞曼能量. 同核偶极哈密顿量的久期形式为

而对于异核耦合的情形, 两个自旋的拉莫尔频率相差很远, 因此flip-flop项无法保持塞曼能量守恒. 故异核偶极相互作用的久期项仅由$ \hat{A} $项贡献, 形式为

在液态样品中, 分子的无规则快速翻转和扩散运动导致任意两个核自旋的相对位矢对全空间进行取向平均, 使得偶极相互作用在时间平均意义上为零($ \overline{{3 \cos ^2 \theta-1}}=0 $). 而在固体中, 分子运动受到很大的限制, 因此偶极相互作用得以保留而具有显著作用. 固态样品包含大量的核自旋, 我们更多是利用同核(如$ ^1{\rm H} $核, $ ^{19}{\rm F} $核)耦合网络去研究一些量子多体物理问题. 由于涉及到多个同类核自旋的相互作用, 我们用携带不同上标的算符$ \hat{I}^{i}_{x/y/z} $来表示不同的核自旋, 其中i为自旋指标. 整个样品的同核偶极相互作用哈密顿量为

其中耦合系数:

不同样品可能具有不同的晶体结构和核自旋排布, 因此其偶极耦合网络也各有不同. 这里介绍两种在固态核磁共振量子控制中常用的样品: 金刚烷和氟磷灰石, 分别对应于三维和一维耦合网络. 金刚烷的分子式为$ {\rm C}_{10}{\rm H}_{16} $, 其化学结构如图1(a)所示. 在室温下, 其为面心立方结构, 所有分子的$ ^1{\rm H} $核自旋构成了三维偶极耦合网络(同核耦合导致的共振线展宽为12.5 kHz左右). 热运动导致接近球形的金刚烷分子在其晶格位置上作无规律翻滚运动(关联时间$ 10^{-11} $ s ^[48]), 使得分子内偶极相互作用在时间平均的意义下为零, 而仅保留分子间偶极相互作用. 基于该样品, 国际上开展了固态核自旋量子寄存器的退相干以及退相干导致的局域化现象研究^{[17,19,29,49–54]}; 近年来, 利用该样品哈密顿量开展了量子多体系统的算符增长和混沌动力学^[23,55,56], 以及随机相互作用自旋模型的非平衡动力学中普适性的量子模拟研究^[27].

氟磷灰石样品为六方晶格结构(分子式$ {\rm Ca_5(PO_4)_3 F} $), 其$ ^{19}{\rm F} $核自旋($ I=1/2 $)沿晶格c主轴排布, 形成很多条一维链(图1(b)). 每个$ ^{19}{\rm F} $周围有3个$ ^{31}{\rm P} $核自旋, 而Ca和O的主要同位素不具有核自旋. 最近邻核自旋间的最大耦合强度为: $ J_{\rm FF}= -5.21 $ kHz, $ J_{\rm PP}=0.191 $ kHz, $ J_{\rm FP}=0.97 $ kHz. 当外磁场平行于晶格c主轴方向时, $ ^{19}{\rm F} $核自旋链之间的相互作用比同链上的相互作用弱40倍左右, 因此可以很好地近似成一个准一维自旋模型^[57–59]. 该样品曾被用来研究量子线上的自旋输运问题^[28,30,60]; 近年来, 基于该样品开展了量子多体系统的热化动力学的量子模拟研究^{[20,22,24,25]}.

核自旋$ I>1/2 $的核具有电四极矩$ eQ $, 其中e是质子电荷. 电四极矩作为一类非线性相互作用, 在一些前沿研究中可以用来抑制核自旋之间的角动量交换^[61], 以及产生自旋压缩^[62]、自振荡时间晶体^[63]等重要的物理现象. 核电四极矩与核自旋所处的化学环境无关. 核电四极矩会与核所处位置的电场梯度发生相互作用, 形式为

其中$ \hat{V} $为二阶无迹张量($ V_{xx}+V_{yy}+V_{zz}=0 $), 表示核自旋所处位置的电场梯度. 特别地, 如果核自旋位点具有立方对称性, 则有$ V_{xx}=V_{yy}=V_{zz}=0 $, 不具有电场梯度. 这时通过引入应力造成晶格扭曲, 可以引入电四极矩相互作用. 在电场梯度张量的主轴坐标系$ (x^{\rm PAF}, y^{\rm PAF}, z^{\rm PAF}) $下, $ \hat{V} $的非对角元为零, 这时电四极矩相互作用哈密顿量可以写为^[44]

可定义电四极矩耦合常数:

如果$ \omega_{\rm Q} $远小于磁塞曼相互作用强度$ \omega_0=\gamma B_0 $, 则可以对电四极矩相互作用进行久期近似, 其主要效应是对塞曼能级进行修正. 久期近似下的电四极矩相互作用哈密顿量为

其中, θ和ϕ为$ \hat{z} $方向外磁场在电场梯度主轴坐标系中的方位角. 具体来说, θ表示外磁场和$ V_{zz} $主轴的夹角, ϕ表示外磁场在V_xx-V_yy主轴平面上的投影与$ V_{xx} $主轴的夹角.

弛豫是系统通过和环境热库的相互作用, 恢复到热平衡态的过程. 根据系统范围选取的不同, 环境热库的作用可由电子、晶格或系统以外的核自旋贡献. 描述弛豫过程需要用到开放量子系统理论. 系统和环境耦合的普遍形式为$ \displaystyle\sum\nolimits_\alpha h_\alpha\hat{S}_\alpha(t)\hat{B}_\alpha(t) $, 其中$ \hat{S}_\alpha $, $ \hat{B}_\alpha $分别为系统算符和环境算符, $ h_\alpha $表示耦合强度. 在最基础的弛豫理论中, 通常假设系统与环境之间的耦合足够弱, 以及环境的动力学远快于系统的演化, 这两个假设分别称为弱耦合近似和马尔可夫近似. 在满足上述假设的情况下, 开放量子系统的演化可以由Redfield方程或者Lindblad方程描述^[64]. 该基础弛豫理论可以描述液态核自旋体系中的弛豫过程^[65]. 但是, 在固态核自旋体系中, 某些开放量子系统的动力学过程可能不符合上述假设. 例如, 在交叉极化过程中, 丰核自旋热库和系统自旋的耦合与系统内部耦合的强度相当. 这时, 需要发展更完善的理论手段来解决固态核自旋体系中的开放系统动力学问题. 近年来, 已经有理论提出利用环境算符$ \hat{B}_\alpha(t) $的所有时序关联信息可以完备构建系统的开放动力学演化方程^[66–68]. 并且, 已经有实验工作原理性演示了可以提取任意阶时序关联的方案^[67–70].

固态核自旋系综的量子态由密度矩阵描述. 由于环境热库带来的弛豫效应, 在施加操控之前, 系统的初始量子态一般为晶格温度T下的热平衡态. 通常情况下, 塞曼场相互作用远大于样品内部局域场相互作用. 考虑同核情形, 热平衡态的密度矩阵可以写为

其中, $ \omega_0 $为塞曼劈裂强度, $ \hat{O}_z= \displaystyle\sum\nolimits_{j} \hat{I}_{z}^{j} $为集体自旋算符, $ \beta=1/(k_{\rm B}T) $为倒逆自旋温度($ k_{\rm B} $为玻尔兹曼常数). 我们采用$ {O}(x) $表示和x同一量级的项, 室温下$ \epsilon=-\beta\hbar\omega_0 $在$ 10^{-5} $量级, 所以该态为高度混态.

系统极化度与量子效应息息相关, 体系极化度太低, 体系将无法产生量子纠缠^[71]. 因此在核磁共振体系中, 提高核自旋体系的极化度对量子信息应用具有重要意义. 如果单纯依靠核自旋的热平衡带来的极化, 提高核自旋极化度需要进一步增强磁场或者降低样品温度, 但都非常困难且提升有限. 故另一个更好的思路是通过极化转移, 即通过相互作用将极化从某一类自旋转移到另一类自旋上. 目前主要的极化转移手段是交叉极化(cross polarization, CP)技术和动态核极化(dynamic nuclear polarization, DNP)技术.

交叉极化技术已广泛应用于固态核磁共振, 这种方法通过射频脉冲控制手段将有着较高旋磁比的丰核(如$ {}^1\mathrm{H} $)上的极化转移到较低旋磁比的稀核(如$ {}^{13}\mathrm{C} $和$ {}^{15}\mathrm{N} $)上, 进而提高稀核的灵敏度, 提升倍数上限为二者旋磁比之比. 目前, Hartmann-Hahn交叉极化(HHCP)^[37,72–75]是固态核磁共振中最常用的交叉极化方案, 其他方案还有偶极序交叉极化(dipolar-order CP, DOCP)^[76,77]以及绝热退磁交叉极化(adiabatic demagnetization CP, ADCP)^[38,78,79]等. 接下来分别介绍.

HHCP的脉冲序列如图2(a)所示. 首先丰核自旋I在静磁场$ B_0 $中极化, 然后被$ -y $方向的90°脉冲打到$ -x $方向; 接着通过连续作用的射频场照射, 丰核自旋极化被锁定在x轴方向. 此时, 稀核自旋S同样被自旋锁定, I和S的自旋都处在双旋转框架中. 当照射它们的射频场满足能量匹配条件: $ \omega_{1 I}=\omega_{1 S} $, 即Hartmann-Hahn匹配条件时, 丰核与稀核间就会发生极化转移^[37]. 在过去的几十年中, 研究人员提出了许多谱学方法来拓宽匹配条件以提高CP效率^[80–85].

DOCP的脉冲序列如图2(b)所示. 丰核自 旋I通过绝热退磁过程, 由塞曼序态转变为偶极 序态, 再将射频脉冲应用于稀核自旋S, 使旋转坐标系中S自旋与偶极序态之间发生热接触来达到极化转移的目的. 由于不存在HHCP中的匹配 条件, DOCP对射频不均匀性不那么敏感, 然而局域偶极序高度依赖于自旋系统和实验条件: 例如当样品旋转时, 局部偶极序很难保持, 极化转移就 很难发生.

ADCP的脉冲序列如图2(c)所示. 在丰核自旋I绝热退磁的过程中, 同时对稀核自旋施S加恒定的射频脉冲, 两者发生热接触而进行极化转移. 理论分析表明, ADCP利用绝热通道可以有效地实现了从丰核自旋到稀核自旋的极化转移, 此外, 在丰核自旋退磁后产生的偶极序态也可以转化为稀核自旋(即AD/DO-CP, 如图2(d)所示), 从而进一步增强稀核信号灵敏度^[38].

交叉极化是利用核与核之间的极化转移来提升极化度, 而相比于核自旋, 电子自旋更容易极化. 1953年, Overhauser^[86]提出通过使材料中未成对电子的电子顺磁共振跃迁饱和, 电子的玻尔兹曼极化可以转移到相邻的核上, 从而显著增大了核的极化度. 这种技术被称为动态核极化^[39,87,88].

传统的动态核极化实验通常在低温下进行(<100 K). 为了实现有效的电子-核极化转移, 需要在样品中添加自由基充当极化剂. 基本原理是通过强磁场和低温实现自由基电子较高的热极化度, 然后利用电子-核相互作用实现极化转移. 为了驱动极化转移过程, 需要施加处在电子拉莫尔频率(140 GHz, 5 T)附近的高功率微波. 得益于高频高功率微波源以及各种用作极化剂的自由基和双自由基的发展, DNP如今可以在18.8 T的磁场下实现. 极化转移有如下4种主要机制: Overhauser效应、固态效应、交叉效应以及热混合效应. 理论上对核磁共振信号的增强倍数的上限为$ \gamma_{\rm e}/\gamma_{\rm n} $, 其中$ \gamma_{\rm e} $是电子的旋磁比, $ \gamma_{\rm n} $是核的旋磁比. 对于$ ^1{\rm H} $而言, 增强倍数大约为660, 而对于¹³C而言, 增强倍数可以达到2600. 因此, 相比于交叉极化技术, 动态核极化方法具有很大的优越性.

此外, 动态核极化还可以通过光泵浦^[89–93]、手性诱导自旋选择^[94]等手段来实现. 动态核极化技术原则上可以实现接近100%的核自旋极化度.

通过给样品施加共振频率附近的周期性射频脉冲序列, 可以将自旋哈密顿量在一定范围内进行改造, 已经有工作给出了固态核磁共振系统的自旋哈密顿量可达集^[95]. 本节将介绍其基本理论思想, 即平均哈密顿量理论(average Hamiltonian theory)^[96]以及计算平均哈密顿量的技巧, 也就是翻转坐标系(toggling frame)^[44].

在一般的周期性驱动(弗洛凯)调控过程中, 旋转坐标系中总的哈密顿量$ \hat{H}(t) = \hat{H}_{\mathrm{s}} + \hat{H}_{\mathrm{rf}}(t) $, 其中$ \hat{H}_{\mathrm{rf}}(t) = h_x(t) \hat{O}_x + h_y(t) \hat{O}_y $为由射频脉冲引起的周期性哈密顿量, 满足$ h_x(t) = h_x(t+T) $和$ h_y(t) = h_y(t+T) $. 如果我们只在驱动周期T的整数倍时刻对系统进行观测, 则系统的演化动力学由$ \hat{H}_{\rm F}+ \delta \hat{H}(t) $描述. 其中$ \hat{H}_{\rm F} $是一个不含时的有效哈密顿量, 称为平均哈密顿量或者弗洛凯哈密顿量; $ \delta \hat{H}(t) $刻画了系统动力学中无法由弗洛凯哈密顿量描述的部分, 它的强度随驱动频率$ 1/T $的增大而呈指数级减小: $ \|\delta \hat{H}(t)\|<\exp [-{O}(1/T)] $^[97,98], 其中$ \|\cdots\| $表示矩阵的范数. $ \hat{H}_{\mathrm{F}} $可通过计算弗洛凯-马格努斯(Floquet-Magnus)展开而获得^[96–100], 前几项的表达式为^[96,99,100] (采用自然单位制$ \hbar=1 $):

由于弗洛凯-马格努斯展开的高阶项面临收敛性问题, 存在最佳截断阶数$ n_* $, 使得$ \|\delta \hat{H}(t)\| $最小^[97,98], 这样$ \hat{H}_{\mathrm{F}}\equiv \displaystyle\sum\nolimits_{n=0}^{n_*} \hat{H}_{\mathrm{F}}^{(n)} $.

为了较高保真度地实现目标哈密顿量, 通常需要在脉冲序列设计中考虑如下几点: 1)$ \hat{H}^{(0)}_{\mathrm{F}}=\hat{H}_{\rm tar} $, 即零阶项实现所需的目标哈密顿量; 2)通过设置脉冲的对称性, 让$ \hat{H}(t)=\hat{H}(T-t) $, 可以实现奇数阶项$ \hat{H}_{\rm F}^{(1, 3, 5, \cdots)}=0 $; 3)让脉冲序列形成一个闭环, 即脉冲的演化算符的乘积$ \hat{P}_{n_{\rm p}}\cdots\hat{P}_2\hat{P}_1 = \hat{\mathbb{1}} $, 其中$ n_{\rm p} $为一个周期的脉冲个数. 这样不仅可以降低脉冲翻转角误差带来的不利影响, 也有利于下文介绍的在翻转坐标系中的计算.

当射频功率足够高, 脉冲宽度可以忽略不计时, 脉冲施加期间的演化算符就是一个旋转操作$ \hat{P}_k=\exp (-{\mathrm{i}} \theta_k {\boldsymbol{n}}_k \cdot \hat{{\boldsymbol{I}}}) $, 其中$ \hat{{\boldsymbol{I}}} $为自旋算符, $ {\boldsymbol{n}}_k $为单位矢量, 表示脉冲在旋转坐标系中的施加方向. 这时在翻转坐标系中考虑系统的演化更为方便^[44]. 从实验室坐标系到旋转坐标系是进行了一次相互作用绘景变换; 而从旋转坐标系到翻转坐标系, 实际上是再进行一次含时的相互作用绘景变换. 变换算符为

即一系列离散旋转操作的乘积. 翻转坐标系下的系统哈密顿量变为$ \hat{H}_{\rm tog}(t)=\hat{U}_{\rm rf}^{\dagger}(t)\hat{H}_{\rm s}\hat{U}_{\rm rf}(t) $. 演化算符满足:

翻转坐标系和旋转坐标系的态的联系为$ \hat{\rho}_{\rm tog}= \hat{U}_{\rm rf}^{\dagger}(t)\hat{\rho} \hat{U}_{\rm rf}(t) $. 利用弗洛凯-马格努斯展开, 翻转坐标系中一个脉冲序列周期的演化算符可以写为$ \hat{U}_{\rm tog}(T)={\rm e}^{-{\rm i}\bar{H}_{\rm tog}T} $, 其平均哈密顿量$ \hat{H}^{\rm tog}_{\rm F}=\bar{H}^{(0)}_{\rm tog}+ \bar{H}_{\rm tog}^{(1)}+\bar{H}_{\rm tog}^{(2)}+\cdots $, 则有:

如果脉冲序列满足闭环特征, 即$ \hat{U}_{\rm rf}(T)= \hat{P}_{n_{\rm p}}\cdots \hat{P}_2\hat{P}_1 = \hat{\mathbb{1}} $, 则在整数倍周期时刻, 翻转坐标系和旋转坐标系重合, 两个参考系中的平均哈密顿量和密度矩阵均等价, 有$ \hat{H}_{\rm F}(nT)=\hat{H}^{\rm tog}_{\rm F}(nT) $, $ \hat{\rho}_{\rm tog}(nT)= \hat{\rho}(nT) $, $ n=0, \ 1, \ 2, \ 3, \cdots $.

脉冲调控的目标是使平均哈密顿量尽可能接近目标哈密顿量, 即$ \hat{H}_{\rm F}\approx\hat{H}_{\rm tar} $. 因此, 必须要考虑哈密顿量在脉冲的作用(全局旋转)下如何变化. 首先, 考虑最一般的旋转-欧拉角$ ZYZ $转动(对于特殊的转动仅需考虑其中特殊的转角即可): $ \hat{R}(\alpha, \beta, \gamma)={\rm e}^{-{\rm i}\hat{O}_z\alpha}{\rm e}^{-{\rm i}\hat{O}_y\beta}{\rm e}^{-{\rm i}\hat{O}_z\gamma} $. 其中($ \alpha, \beta, \gamma $)为3个转角, $ \hat{O}_{n}=\displaystyle\sum\nolimits_i\hat{I}_n^i $为集体自旋角动量算符($ n= x, y, z $). 首先考虑自旋算符在转动下如何变化, 由Baker-Campbell-Hausdorff (BCH)公式:

可以得到:

这里以同核偶极耦合为例, 由3个自旋算符 的变化规则可以得到偶极哈密顿量(19)$ \hat{H}_{\rm D}^{(z)}= \displaystyle\sum\limits_{i<j} J_{ij}(2\hat{I}^i_z\hat{I}^j_z-\hat{I}^i_x\hat{I}^j_x-\hat{I}^i_y\hat{I}^j_y) $在转动下的变换规则:

下面给出两个代表性脉冲序列的设计思路以及可以实现的平均哈密顿量.

1) 8脉冲序列: 核心思路是将脉冲序列设计为^[95]

其中$ P_i\bar{P}_i= \hat{\mathbb{1}} $. 为了阐释该脉冲序列的设计原理, 我们以实现目标哈密顿量$ \hat{H}_{\rm tar}=C\displaystyle\sum\nolimits_{ij} J_{ij} [\hat{I}^i_z\hat{I}^j_y+ \hat{I}^i_y\hat{I}^j_z] $(C为缩放因子)为例. 首先考虑等间隔的脉冲序列, 即$ \tau_1=\tau_2=\tau_3=\tau_4=\tau $. 在这一情况下需要设定脉冲角度$ \{\beta_i, \gamma_i\} $, 使得这些角度满足:

求解方程得到$ \beta_1=\beta_2=\beta_3=\beta_4=\beta_m\approx 54.74^{\circ} $(这个角度在固态核磁共振中被称为“魔角”), $ \gamma_1= \gamma_3 = \dfrac{\pi}{4},\; \gamma_2 = \gamma_4 = \dfrac{3\pi}{4} $. 这里验算可得, 弗洛凯-马格努斯展开的零阶项为$ \hat{H}^{(0)}_{\rm F}=\displaystyle\frac{1}{3}\sum_{ij}J_{ij}[\hat{I}^i_z\hat{I}^j_y+\hat{I}^i_y\hat{I}^j_z] $, 即实现了我们的目标哈密顿量, 满足了哈密顿量调控的要求1). 为了实现要求2), 即消除弗洛凯-马格努斯展开的奇数阶项$ \hat{H}^{(1, 3, 5\cdots)} $, 只需将该8脉冲序列按对称性扩充为16脉冲序列.

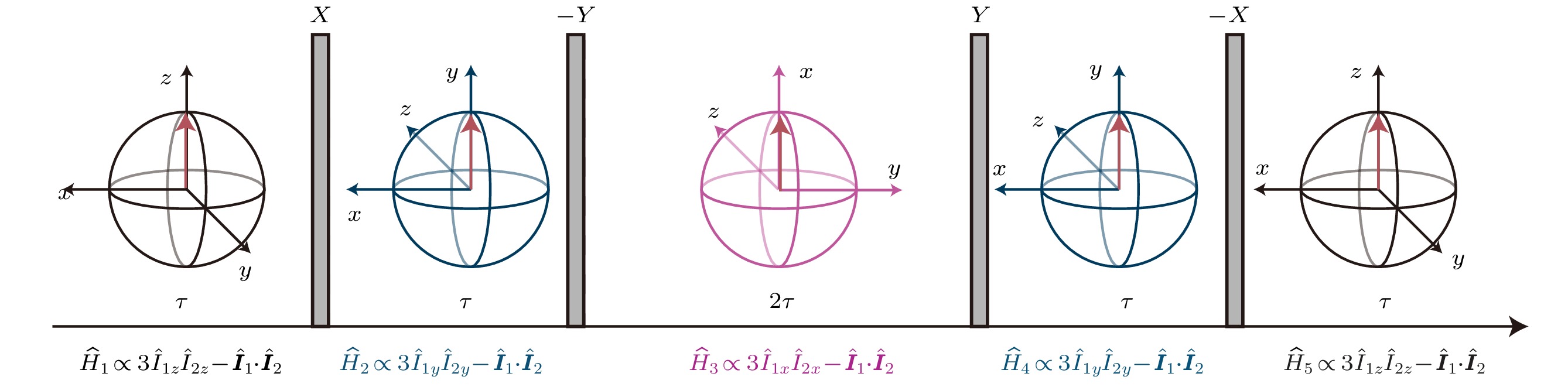
综上所述, 该8脉冲序列的核心是通过设计不同的脉冲角度实现不同的目标哈密顿量$ \hat{H}^{(0)}= C\hat{H}_{\rm tar} $, 表1给出不同的目标哈密顿量$ \hat{H}_{\rm tar} $所需的脉冲角度, 以及对应的缩放因子C.

2) 16脉冲序列: 这里作为另一个例子, 介绍一个由Suter等^{[20,22–25,101]}提出的由16个脉冲组成的序列如图3所示:

其中$ \hat{R}_\alpha = {\rm e}^{-{\rm i}\hat{O}_\alpha \tfrac{\pi}{2}}, \tau_{\alpha} = \tau(1 + \xi_{\alpha}) $ ($ \alpha=x, y, z $). 通过4.1节中介绍的方法给出体系等效的演化算符:

其中$ \hat{H}_{\rm D}^{(\alpha)}=\displaystyle\sum\nolimits_{i<j} J_{ij}(3\hat{I}^i_\alpha\hat{I}^j_\alpha-{\boldsymbol{\hat{I}}}^i\cdot{\boldsymbol{\hat{I}}}^j) $($ \alpha=x, y, z $)为不同方向的偶极哈密顿量. 可计算弗洛凯-马格努斯展开的零阶项为

即, 通过调节脉冲间隔$ \{\tau_\alpha\} $可以实现不同构型的目标哈密顿量(满足$ \xi_x+\xi_y+\xi_z=0 $).

由于系统和环境之间相互作用导致的弛豫效应, 量子系统会发生退相干, 如何抑制量子系统的退相干是量子控制的重要目标之一. 动力学解耦(dynamical decoupling, DD)是保持量子相干性的最有效的实验手段之一, 特别是在仅具有对系统的操控能力的情况下^{[33,52,102–105]}. 动力学解耦的核心思路是利用平均哈密顿量理论构造系统-环境耦合演化的时间反演. Hahn echo^[106]是最早也是最简单的DD序列, 也称自旋回波. 其脉冲序列如下:

其中, $ (\pi/2)_{x} $, $ (\pi)_{y} $分别表示沿x方向的$ \pi/2 $脉冲、沿y方向的π脉冲; τ为回波时间, 期间不施加脉冲, 让核自旋自由演化. 在翻转坐标系下, 该序列π脉冲的作用使得第1个间隔τ的等效磁场方向与第2个τ的等效磁场方向相反, 因此可以将不含时的类似于化学位移的项(如静磁场不均匀性)带来的演化抵消. 对于含时的环境(如异核偶极耦合等), 可以将回波时间缩短, 这样单个π脉冲扩充为一系列短间隔的π脉冲, 称为CPMG (Carr-Purcell-Meiboom-Gill)序列^[107,108]. 研究人员进一步发展出误差更小, 适用性更广的DD序列, 如PDD (Periodic DD)^[102], CDD (Concatenated DD)^[105,109], Uhrig DD (UDD)^[110]等. 动力学解耦方法反过来也可以用于研究环境的噪声谱^[52].

对于同核偶极相互作用, π脉冲无法有效对其解耦, 因此需要另外一些不同的脉冲序列. 例如Magic echo序列, 它由两个不同方向的$ {\pi}/{2} $脉冲和连续的沿x方向的脉冲组成^[111], 序列如图4所示. 根据平均哈密顿量理论, 该序列实现一个负的偶极哈密顿量$ -\dfrac{1}{2}\hat{H}_{\rm D}^{(z)} $, 因此可以用两倍的时间抵消正的偶极哈密顿量$ H_{\rm D}^{(z)} $带来的演化.

另一个经典的同核解耦序列为WAHUHA序列^[112], 如图5所示. 在实验室系下哈密顿量一直保持不变, 而在翻转坐标系下哈密顿量被脉冲序列调控, 为时间依赖的分段函数. 根据$ H_{\rm D}^{(x)}+H_{\rm D}^{(y)}+ H_{\rm D}^{(z)}=0 $的性质, 可以得到该序列平均哈密顿量零阶项为零, 消除了同核偶极耦合.

在固态体系中, 经典同核解耦序列还有Cory 48 ^[113]. 在实际实验中, 脉冲存在一定宽度, 会使得实际调控得到的平均哈密顿量零阶项相比于理论值出现偏差. 实验中可以通过调整脉冲之间的间隔对误差进行修正. 除了这种较为粗糙的修正方法, 研究人员利用深度强化学习方法设计出了对角度偏差、脉宽等误差有很好鲁棒性的解耦序列^[114].

魔角旋转技术是固态核磁共振中常用的提高谱图分辨率的技术, 其是让样品沿一固定轴高速旋转(数千Hz至超过100 kHz), 在时间平均的意义上(部分)去除化学位移各向异性、偶极-偶极相互作用、电四极矩相互作用等^[115].

以偶极-偶极相互作用为例, 两核自旋间的偶极耦合系数有一依赖于空间取向的因子$ (3\cos^2{\theta}- 1) $, 其中θ为两自旋连线和静磁场方向的夹角(如图6所示). 这一因子的转动平均为

其中γ为两自旋连线与旋转轴的夹角, β为转轴与静磁场的夹角. 显然只需令$ \beta=54.74^{\circ} $(魔角)即可满足$ 3\cos^2{\beta}-1=0 $, 从而消除偶极相互作用.

魔角旋转技术不仅可以用于消除某些相互作用, 也可以结合射频脉冲序列恢复一些相互作用的影响, 丰富体系哈密顿量的调控手段. 不同于静态情形, 在魔角旋转的情况下, 相互作用系数$ C_{ij} $会随时间发生改变:

其中$ d_{ij} = \Big(\dfrac{\mu_{0}}{4\pi}\Big) \dfrac{\gamma_{i}\gamma_{j}\hbar^2}{r_{ij}^{3}} $, $ \omega_{\rm R} $为魔角旋转速率(单位: Hz). 一个简单的魔角旋转条件下的偶极恢复(dipolar recovery at the magic angle, DRAMA)序列^[44]如图7所示, 其在每一个魔角旋转周期$ \tau_{\rm R}=1/\omega_{\rm R} $施加了两个相位相反的90°脉冲. 该序列实现的平均哈密顿量为

由于多体相互作用的存在, 固态核自旋体系中存在信息弥散(information scrambling)过程——量子信息在幺正演化下由局域弥散到整体的行为^{[11,116–118]}. 在信息弥散的过程中, 固态核自旋之间的量子关联建立起来, 形成多体关联态. 下面介绍固态核自旋体系的多体关联态的一般层析方法.

量子态信息的提取在量子计算与量子信息中是至关重要的, 这一过程通常也被称为量子态层析. 量子态层析的基本目标是将量子态在某一基底下展开: $ \hat{\rho}=\displaystyle\sum\nolimits_k C_k \left| {k} \right\rangle \left\langle {k} \right| $. 通过实验测量和数学分析(例如求解线性方程组)可以得到$ \{C_k\} $的信息, 从而实现量子态的层析.

如今, 得益于控制手段以及实验手段的不断进步, 诸如超导、离子阱、液态核磁共振等实验体系已经能实现小尺度量子比特系统的完全层析^{[6,16,119–121]}. 借助单比特量子态层析的过程, 可以理解量子态层析的一般原理和思路. 单比特密度矩阵表示为

其中$ \hat{\sigma}_k $是泡利矩阵, $ k=x, y, z $. 泡利矩阵具有正交性质$ \text{Tr}(\hat{\sigma}_k\hat{\sigma}_l)=2\delta_{kl} $, 因此只要测量体系自旋角动量3个分量即可得到$ \{C_k\} $:

由于固态核磁共振平台无法实现局域自旋算符的观测, 因而无法实现多体量子态的完全层析. 退而求其次, 存在部分层析的方法. 可以将量子态的不同组分按照其对全局旋转操作的响应的不同进行区分, 如按照不可约球张量算符(irreducible spherical tensor operators, ISTOs)或者多量子相干(multiple quantum coherences, MQC)进行分类^[122,123]. 这种方式虽然存在简并性而无法完全区分所有组分, 但是同时具有完备性, 即任意一个量子态都可以被ISTOs或者MQC展开.

固态核自旋系综量子态的密度矩阵可表示为一系列相互正交的自旋算符的叠加. 对于三维全局转动群中的任意旋转操作:

可以写出一组由ISTOs构成的完备正交基$ \{\hat{T}_{l, m}^{(\cdots)}\} $, 让系统的密度矩阵按该正交基进行分解^[122,123]:

记括号$ (i, j, \cdots) $中涉及的自旋指标数目为K, 表明该ISTOs属于K体自旋算符. $ l=0, \ 1, \ 2, \ \cdots, \ K $, 表示ISTOs的秩; $ m=-l, -l+1, \cdots, l $, 表示ISTOs的阶. 前两阶ISTOs的形式如下:

构造高阶ISTOs的规则和角动量本征态的合成规则一样, 即计算Clebsch-Gordan系数:

ISTOs对全局转动的响应为

式中, $ D_{m^{\prime}, m}^{l}(\alpha, \beta, \gamma)={\rm e}^{-{\rm i}m^{\prime}\alpha}d_{m^{\prime}, m}^{l}(\beta){\rm e}^{-{\rm i}m\gamma} $表示Wigner-D矩阵. $ d_{m^{\prime}, m}^{l}(\beta)=\left\langle {lm^{\prime}} \right|\exp(-{\rm i}\beta \hat{J}_y)\left| {lm} \right\rangle $是角动量量子数为l的$ \hat{y} $方向转动算符的矩阵元, 其中$ \hat{J}_y $是角动量量子数为l的$ \hat{y} $方向角动量算符. 可以看到, ISTOs对欧拉角$ (\alpha, \ \beta, \ \gamma) $的响应函数形式只依赖于其秩l和阶m, 除此之外的指标在全局转动下为简并指标. 因此, 全局转动只能按秩l和阶m对ISTOs进行区分, 无法实现ISTOs的完全层析.

相比于施加任意三维转动对算符进行分类的方式, 更简单的情形是将算符按照其对单轴转动$ {\rm exp}\bigg({-{\rm i}\phi\displaystyle\sum\nolimits_j\hat{S}_j^z}\bigg) $的响应进行分类, 称为多量子相干^[124–129]. 在前面给出的ISTOs形式中, m指标相同的ISTOs属于同一阶量子相干. 因此, 多量子相干的简并度比ISTOs更高, 相应地, 提取它们所耗费的实验资源也更少. 属于同一阶的多量子相干对$ \hat{z} $方向的全局旋转具有统一的响应:

m阶ISTOs的幅度模平方之和等于m阶量子相干的强度:

量子相干强度还有更直观的计算方式. 如果把密度矩阵$ \hat{\rho} $在集体自旋算符$ \hat{O}_z=\displaystyle\sum\nolimits_{j}\hat{I}_{z}^{j} $的本征基下表示, 则每一个矩阵元都分别归属于某一阶量子相干, 矩阵元所联系的两个本征态的本征值之差就是阶数m. 例如, 矩阵元$ \hat{\mathbb{1}} ^1\hat{I}_+^2\hat{I}_-^3\hat{I}_z^4 $的相干阶是0, 而$ \hat{\mathbb{1}}^1\hat{I}_+^2\hat{I}_-^3\hat{I}_+^4 $的相干阶是1. 因此, m阶量子相干的强度也可以表示为对矩阵元的求和:

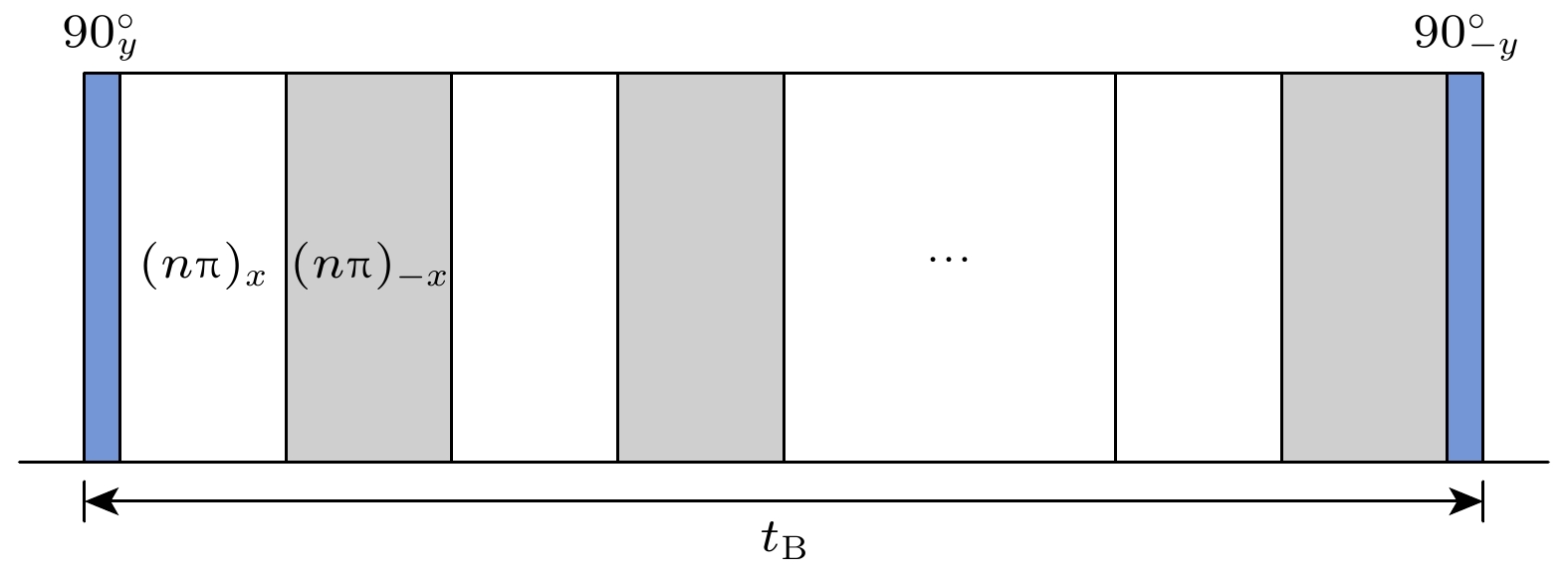
对于厄米算符有$ I_m^{(z)}= I_{-m}^{(z)} $.

测量各阶量子相干强度的实验框架在核磁共振发展历史的早期阶段就已经被发明^[128,129]. 如图8所示, 首先让初态$ \hat{\rho}_\alpha\propto \hat{\mathbb{1}} +\epsilon\hat{O}_\alpha $($ \alpha=x, y, z $)进行持续时间为t的正向演化$ \hat{U}_t $; 然后施加旋转操作$ {\rm e}^{-{\rm i}\hat{O}_z\phi} $进行相位编码, 其中ϕ是旋转角; 而后给量子态施加反向演化$ \hat{U}_t^\dagger $; 最后观测集体自旋$ \langle\hat{O}_\alpha\rangle $:

根据方程(49)中多量子相干对单轴旋转操作的响应, $ F(\phi, t) $可以分解为算符$ \hat{O}_\alpha(t)=\hat{U}_t\hat{O}_\alpha\hat{U}_t^\dagger $中多量子相干强度的叠加:

对$ F(\phi) $进行离散傅里叶变换就可以提取出$ \{I_m^{(z)}\} $. 类似地, 也可以定义并测量$ \{I_m^{(x)}\} $, $ \{I_m^{(y)}\} $. 多量子相干是自旋-自旋量子关联的体现, 因为m阶量子相干只可能由K体($ K\geqslant|m| $)的自旋积算符贡献.

得益于固态核自旋长的相干时间和灵活的哈密顿量调控技术, 固态核磁共振体系为操控和观测量子多体系统提供了良好的实验平台. 量子多体系统的非平衡动力学是近年来的热点问题, 通过量子淬火操作, 固态核磁共振体系可以对远离平衡的量子多体动力学进行实验模拟研究. 在非平衡多体动力学的研究中, 一个基本问题是孤立量子多体系统在幺正演化下是否会热化？研究人员已经发现某些特殊的量子态或者哈密顿量违背本征态热化假设, 如多体局域化^[130]、多体疤痕态^[131]等. 通过调控固态核自旋系统的哈密顿量, Álvarez等^[19,29,54]和Wei等^[20]分别对三维和一维偶极耦合自旋系统的局域化现象开展了实验研究. Wei等^[22,24]还研究了一维偶极耦合核自旋链的预热化. 此外, 近年来在非平衡动力学相变中时间晶体备受关注, 而固态核磁共振体系是实现离散时间晶体的一个有趣候选者. Rovny等^[21]在周期性哈密顿量驱动的偶极耦合自旋系统中观测到了离散时间晶体的特征. Stasiuk和Cappellaro^[26]通过调控驱动哈密顿量来设计结晶度, 最终观测到预热化离散时间晶体.

另一个基本问题是, 在非平衡多体动力学中是否存在一些简单和普适的规律？此前针对普适性的研究大多集中在平衡态附近的低能物理, 而关于远离平衡的动力学的普适性的研究相对较少. Peng等^[25]研究了一维核自旋链在不同哈密顿量下的输运动力学行为, 它们分别属于不同的普适类; 本课题组实验模拟了一类随机相互作用自旋模型, 揭示了其退极化动力学中的普适性行为^[27]. 此外, Sánchez等^[23,55]针对Loschmidt echo的动力学行为在固态核磁共振系统开展了系列研究工作.

人类对微观世界的认知和控制一直以来都是两个相辅相成、相互促进的发展历程. 对微观物态和动力学的控制建立在对体系基本参数和性质的认知上; 而更完备、更精确的控制能力则驱使我们进一步窥探到更深层次的物理规律. 固态核自旋作为一类重要的凝聚态和量子多体物理系统, 其中蕴含了丰富的量子物理现象和机制等待研究人员的发掘, 而基于固态核磁共振的量子控制技术必然会在这类探索过程中起到不可替代的作用. 笔者以本文为契机, 向相关领域的科研工作者分享了固态核磁共振量子控制领域的基本原理和前沿进展. 借助本文的介绍和阐述, 一方面期望引导更多的科研工作者投身这一前沿研究领域; 另一方面, 也希望固态核磁共振技术中一些重要的量子控制理念和方法论能够为其他量子实验系统提供宝贵的经验和启发.