扫描隧道显微镜(scanning tunneling microscope, STM)自20世纪80年代初发明以来, 一直是纳米科学领域的重要探测工具, 其核心原理是基于金属针尖与样品之间的电子隧穿效应来探测样品表面的原子结构^[1,2]. STM的独特之处在于其原子级分辨率, 这使得它能够在样品表面精确成像^[3]. 当STM探针尖端与金属衬底之间的间隙减小到纳米甚至亚纳米尺度时, 针尖和衬底表面的等离激元会被激发, 产生局部的电磁场增强效应, 从而导致发光现象, 这种技术称为STM诱导发光(STM induced luminescence, STML), 为研究分子特性包括分子构型和光谱特性, 提供了新的研究路径^[4-7]. 这种由STM针尖和金属衬底两个紧邻的金属纳米结构构成的纳米间隙称为STM纳米腔, 最早由Stroscio和Eigler^[8]于1991年提出, 它的出现实现了在纳米尺度下的原子控制和组装. 而STM皮米腔这一概念最早由Benz等^[9]提出, 是纳米腔的一种特殊形式, 电场局域在一个立方纳米量级及更小的空间体积上^[10], 使得光与物质的相互作用更强, 从而在基于拉曼散射的纳米甚至亚纳米光学成像领域展现出巨大的应用潜力^[11,12].

超辐射是量子发射体自发辐射的一种叠加效应, 因此也被称作量子发射体的集体自发辐射^[13]. 在超辐射研究中, STM腔因能够精确操控分子和有较高的局域场增强而具有其独特的优势. 2019年Luo等^[14]报道了基于STM纳米腔中水平放置的酞菁锌(ZnPc)分子链的电驱动光子超辐射, 他们构筑了包含2—12个酞菁染料分子的有序分子链结构, 研究了这些分子链体系的发光特性, 为染料分子材料在STM纳米腔中的超辐射研究开辟了新的路径. 但在他们的实验中酞菁染料分子水平放置在STM纳米腔中, 分子不可避免地会随着探针的移动而晃动和旋转, 可能会对实验结果产生影响. Chikkaraddy等^[15]应用分子笼组装技术将分子束缚, 使得分子可以竖直固定在STM纳米腔中, 并发现竖直放置的分子与光场的相互作用效率显著增强, 可以实现单分子与纳米腔的较强的耦合效应. 作为特殊的STM纳米腔, STM皮米腔中竖直放置的分子必然也与腔等离激元场有较强的耦合, 此外等离激元效应也会影响分子或团簇的辐射行为. 根据调研, 目前尚无理论研究STM纳米腔和皮米腔中分子团簇构形对分子团簇辐射过程的影响. 本文分别在STM纳米腔和皮米腔中计算了不同构形的分子团簇在光激发下的辐射光谱及其相关规律. 根据研究结果提出了改变分子团簇超辐射效率的方法.

本文中第2节给出了研究的理论和模型, 即分子动力学的量子主方程和计算远场辐射光谱的公式. 第3节系统地研究了STM纳米腔和皮米腔中不同构形的分子团簇的远场辐射效应及激发波长对辐射光谱的影响. 第4节对我们的工作进行总结和展望.

由于亚甲基蓝(methylene blue, MB)分子具有显著的光吸收和荧光发射特性, 实验上在可见光区域可以观测到明显的吸收峰^[16], 且可以通过分子笼组装技术竖直放置在腔内^[15], 本文以亚甲基蓝分子作为研究对象, 其相应的性质可以推广到类似的染料分子体系. STM纳米腔和皮米腔在相同激光照射下的共振特性存在差异, 而与分子的共振特性是增强辐射的一个主要原因, 这样需要首先通过调节两种腔的结构参数, 使其在某一特定波长处达到共振状态, 这里设其均与单个亚甲基蓝分子的吸收峰660 nm共振. 这一调整不仅有助于消除因共振频率差异带来的干扰, 而且能够更清晰地揭示辐射现象及其在不同腔结构中的表现.

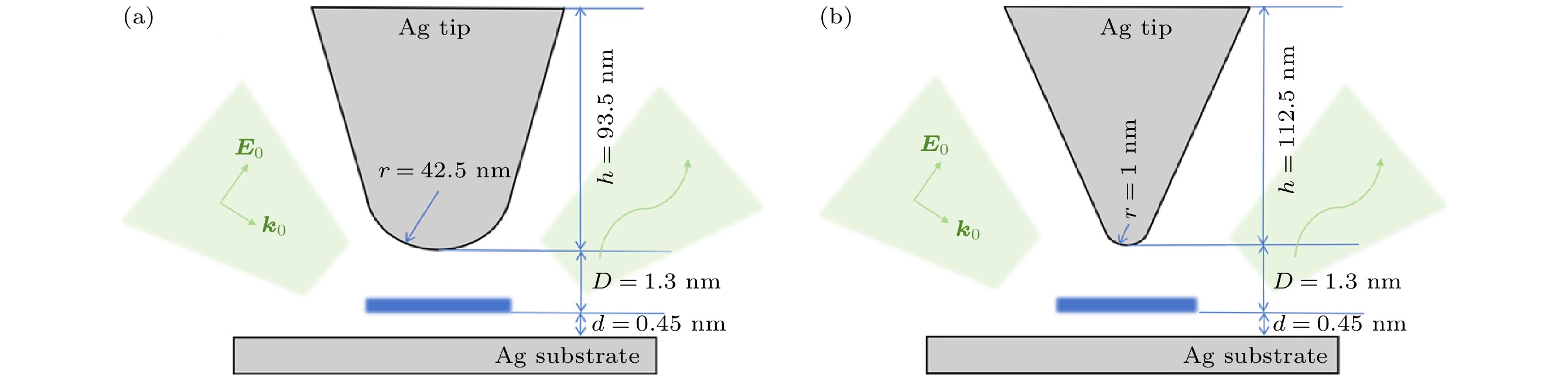
图1为本文构建的STM纳米腔和皮米腔的模型及相应的结构参数. 模型均由一个锥形针尖和衬底组成, 其中针尖由一个倒立圆锥体和曲率半径为r的球体相结合构成. 按照已报道的实验装置, 针尖和衬底的材料通常选银或金等贵金属, 本文选取银作为研究材料, 使用Johnson-Christy提供的实验中测量的银介电参数^[17]. 同时, 腔均受到与衬底法线呈55°角的平面波激发(偏振为$ \boldsymbol{{E}} _{0} $、传播为$ \boldsymbol{{k}} _{0} $), 并根据STM相关实验在腔的另一侧收集辐射信号.

在实验上研究STM腔中单分子或分子团簇的发光现象时, 电磁场与腔体系之间的相互作用通常是弱耦合的^[14,18,19], 这意味着电磁场的变化对系统量子态的影响相对较小. 因此, 可以将电磁场视为一个外部的经典场, 而不需要考虑其量子性质. 对于分子本身, 我们仍应用量子力学理论来进行描述. 采用密度矩阵理论, 设$ \hat{\rho } $为体系的约化密度矩阵算符. 在半经典近似下, 根据宏观量子电动力学理论^[20,21], 结合分子的激发和耗散过程, 其有效量子主方程为

其中,

式中, $ \hat{H}_{\text{mol}} $是由频率为$ \omega_s $的N个分子组成的聚集体的哈密顿量, $ \hat{\sigma } _{s}^{22} $是投影算符, 表示第s个分子处于激发态. 这里设所有的分子全同, 其跃迁频率为$ \omega_s= \omega_e $. $ \hat{H}_{\text{ext}} $是分子与外场相互作用的哈密顿量, $ \hat{\sigma } _{s}^{21} $和$ \hat{\sigma } _{s}^{12} $是第s个分子的跃迁算符, 其中基态和激发态由上标1, 2标记, 耦合系数为$ \hbar \nu _{s} = -\boldsymbol{{d}} _{s}\cdot \boldsymbol{{E}}\left (\boldsymbol{{r}} _{s}, \omega _{{\mathrm{l}}} \right ) $, $ \boldsymbol{{d}} _{s} $是分子的偶极矩, $ \boldsymbol{{E}}\left (\boldsymbol{{r}} _{s}, \omega _{{\mathrm{l}}} \right ) $是经典处理的分子位置$ \boldsymbol{{r}} _{s} $处的表面等离激元增强场, $ \omega _{{\mathrm{l}}} $是外场激发的频率. $ \hat{H}_{\text{pla}} $是表面等离激元与分子激发态的相互作用有效哈密顿量, 描述了表面等离激元导致的分子激发能降低, 即兰姆位移$ \varOmega _{ss} \left ( s= s' \right ) $ 和分子间的相干耦合$ \varOmega _{ss'} \left ( s\ne s' \right ) $. $ D_{\text{plas} }\left [ \hat{\rho } \right ] $是耗散项, 描述了Purcell增强的分子衰变$ \varGamma _{ss} \left ( s= s' \right ) $ 和分子间的耗散耦合$ \varGamma _{ss'} \left ( s\ne s' \right ) $.

分子间的相干耦合$ \varOmega _{ss'} $和耗散耦合$ \varGamma _{ss'} $表达式分别为

其中$ \varepsilon _{0} $是真空介电常数, c是光速, $ \boldsymbol{{d}}_{s} $为分子跃迁偶极矩, $ \overleftrightarrow{G}\left ( \boldsymbol{{r}}_{s}, \boldsymbol{{r}} _{s'};\omega _{{\mathrm{e}}} \right ) $是并矢格林张量, $ {\mathrm{Re}}\overleftrightarrow{G} ( \boldsymbol{{r}} _{s}, \boldsymbol{{r}} _{s'};\omega _{{\mathrm{e}}} ) $表示其实部, $ \text{Im} \overleftrightarrow{G}\left ( \boldsymbol{{r}} _{s}, \boldsymbol{{r}} _{s'};\omega _{{\mathrm{e}}} \right ) $表示其虚部.

位置$ \boldsymbol{{r}} $处的远场辐射强度为^[22,23]

其中,

(9)式和(10)式分别为在位置$ \boldsymbol{{r}} $处的传播因子和跃迁算符$ \left \langle \hat{\sigma } _{s'}^{21} \hat{\sigma } _{s}^{12} \right \rangle $的期望值.

为了阐明分子聚集体或团簇远场辐射的集体性质, 我们将总辐射$ I\left ( t \right ) $分为单个分子的贡献$ I_{\text{ind}} \approx \text{Re} { \displaystyle\sum\nolimits_{s}^{N}} K_{ss} \left \langle \hat{\sigma } _{s}^{21} \hat{\sigma } _{s}^{12} \right \rangle (t) $和分子间的贡献$ I_{\text{int}} \approx \text{Re} { \displaystyle\sum\nolimits_{s\ne s'}^{N}} K_{ss'} \left \langle \hat{\sigma } _{s'}^{21} \hat{\sigma } _{s}^{12} \right \rangle (t) $两部分, 它们分别由矩阵I的对角项和非对角项确定.

为了模拟尽可能多的分子, 在密度矩阵理论框架下采用平均场方法^[24]求解量子主方程, 任意算符$ \hat{O} $的期望值$ \langle \hat{O} \rangle = \text{Tr} \{ \hat{\rho }\hat{O} \} $的动力学方程为$ \partial _{t} \langle \hat{O} \rangle = \text{Tr} \{ \partial _{t} \hat{\rho }\hat{O} \} $, 在这里将方程进行合理的截断, 得到一系列阶层方程, 包括一阶均值方程, 如激发态布居数$ \left \langle \hat{\sigma } _{s}^{22} \right \rangle $和分子相干性$ \left \langle \hat{\sigma } _{s}^{12} \right \rangle $, 以及二阶方程, 如分子关联$ \left \langle \hat{\sigma } _{s}^{21} \hat{\sigma } _{s'}^{12} \right \rangle $, $ \left \langle \hat{\sigma } _{s}^{22} \hat{\sigma } _{s'}^{22} \right \rangle $, $ \left \langle \hat{\sigma } _{s}^{22} \hat{\sigma } _{s'}^{12} \right \rangle $, $ \left \langle \hat{\sigma } _{s}^{12} \hat{\sigma } _{s'}^{12} \right \rangle $.

为了说明分子聚集体的集体动力学的过程, 需引入集体自旋算符$ \hat{J} $:

和集体自旋矢量$ \boldsymbol{{A}} $:

其中$ \langle \hat{J}_i \rangle $是集体期望值, $ \boldsymbol{{e}}_i $是笛卡尔坐标系的单位矢量. 对于纯量子态的分子来说, 集体自旋矢量是一个以原点为中心、半径为$ {N}/{2} $的布洛赫球面. 对于完全处于基态或处于激发态的分子, 集体自旋矢量分别指向布洛赫球的南极和北极, 对于混合态或纠缠态的分子, 它指向球体内部的位置.

我们将考虑3种常见的不同分子团簇构形: 环状构形、二维平面构形和一维链状构形^[25]. 将这3种构形的分子团簇分别放置在已调节至660 nm共振状态的STM纳米腔和皮米腔中. 由于分子团簇的超辐射脉冲对分子数量N有很强的依赖性, 随着N的增加, 超辐射脉冲会变得更明显^[26], 同时考虑到模拟10个以上分子需要耗费较多的计算资源, 这里选择由9个全同亚甲基蓝分子组成不同构形的分子团簇.

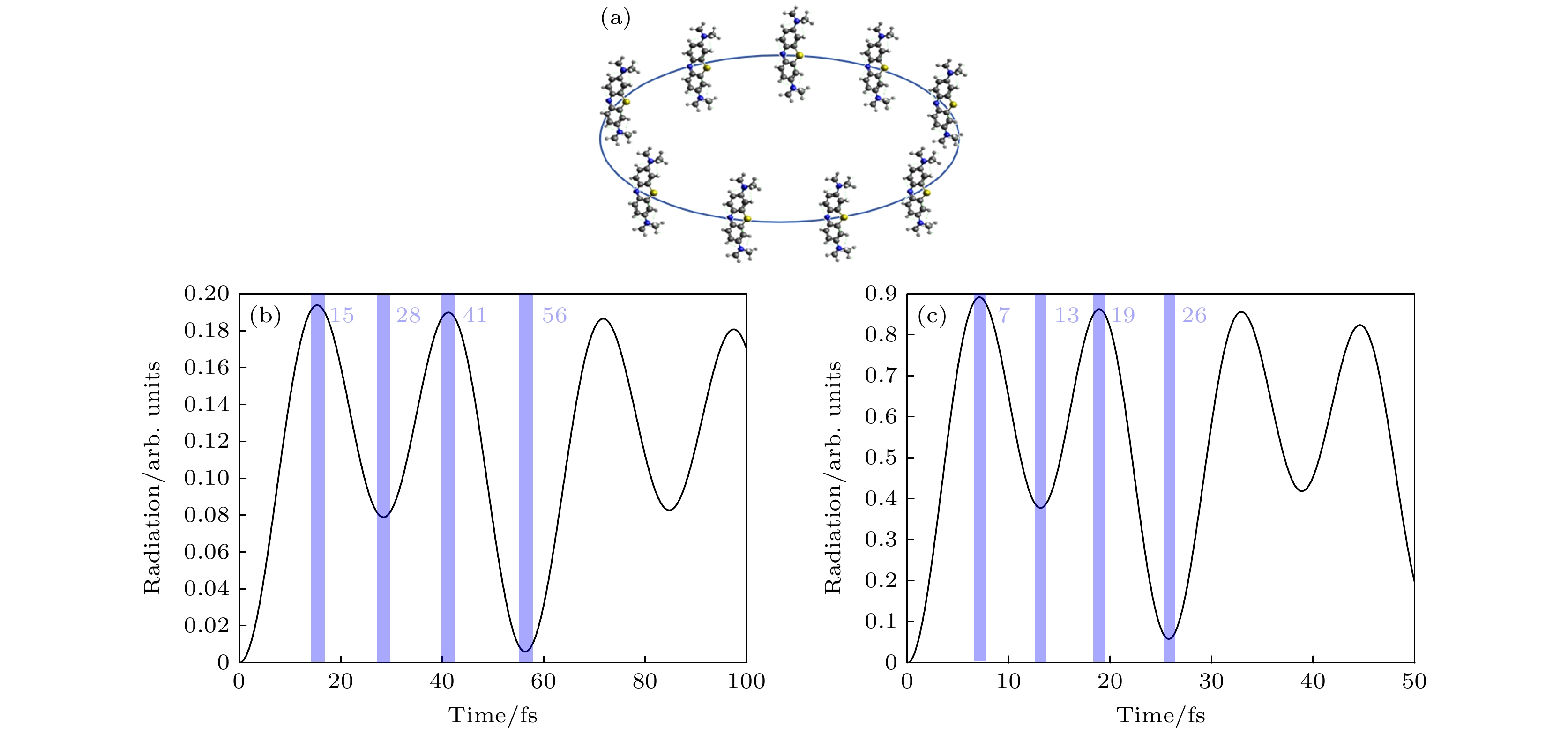
本工作根据文献[25]设计了由9个全同亚甲基蓝分子组成的半径为2 nm的环状构形分子团簇, 如图2(a)所示, 并将其分别置于调节后的STM纳米腔和STM皮米腔中, 设圆心均处于腔的中心位置. 在强度为I_ext = 10³ μW/μm²的连续激光激发下, STM纳米腔和皮米腔中的辐射光谱图如图2(b), (c)所示. 通过对比, 发现两种结构中分子团簇的总辐射均呈现出复杂的振荡行为, 说明在不同的激发时刻分子团簇所处的激发程度是不同的. 超辐射往往在系统具有较高激发程度时更易发生且表现更为显著. 为探究强激光作用下分子团簇的超辐射脉冲行为, 需要选择合适的激发时间, 从而保证团簇中尽可能多的分子能够达到接近其完全激发状态.

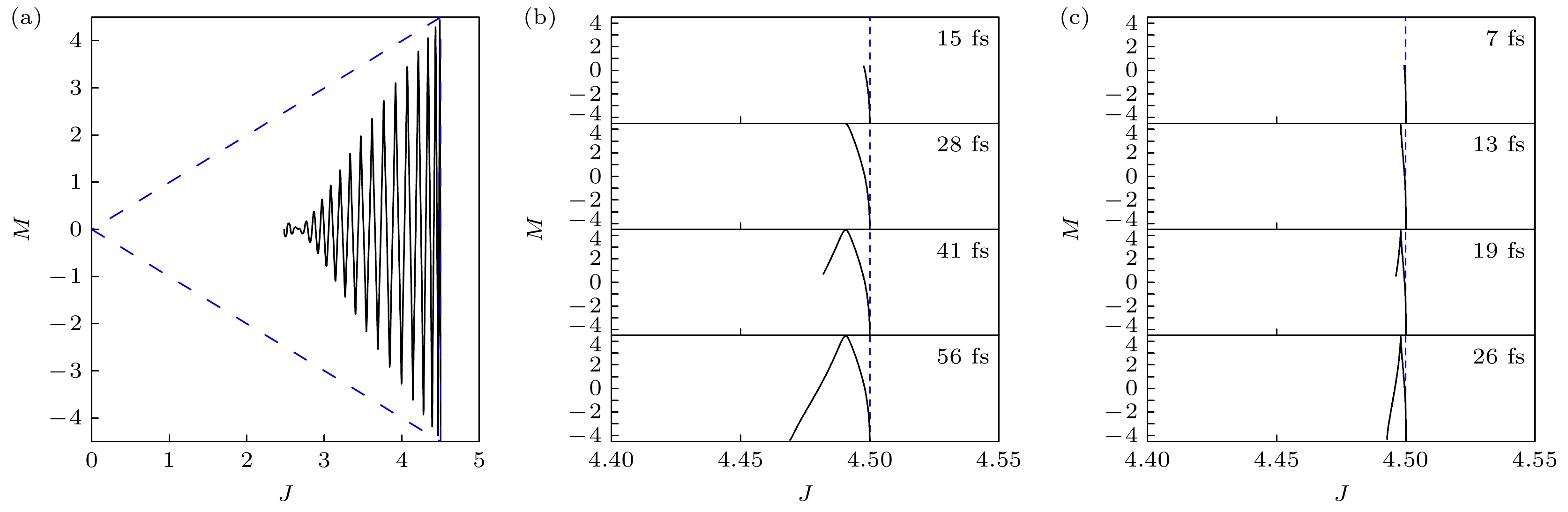
为了更精确地阐释分子团簇的激发过程, 引入了Dicke态理论来描述其动力学行为. 在Dicke态的框架下, 量子数J表征着Dicke态的总角动量, 而M则描绘了该角动量在特定方向上的投影, 这两个量子数分别表示Dicke态的对称性和激发程度. 其中$ J\leqslant {N}/{2} $, $ -J< M< J $. 所有可能的Dicke态共同构成了一个三角形的空间结构, 如图3(a)中蓝色虚线所示. 这个三角形的顶点象征着纯量子态, 如所有分子均处于激发态$ \left ( M= J \right ) $或基态$ \left ( M=-J \right ) $, 三角形的边界点和内部的点则代表混合态, 这些态的M值介于$ -J $和J之间, 反映了系统部分激发的状态, 即分子既有处于激发态的部分, 又有处于基态的部分, 且二者比例因态而异. 在Dicke三角形空间中的动力学演化可以通过其位置的变化来追踪. 例如, 当STM纳米腔中的分子团簇被外场激发时, 它从基态沿右边界向上移动, 随后通过辐射衰减过程返回到略高于基态的位置, 然后重复同样的过程直至$ M\approx 0 $的Dicke态. 这一演化过程揭示了分子团簇在不同量子态之间的转换和相互作用. 若在连续激光激发过程中某一时刻的Dicke态在三角形空间中十分接近$ M=J $这一顶点, 表明此刻更多的分子趋向于达到完全激发的状态, 从而为研究超辐射现象提供有利条件.

为此, 选择图2(b), (c)中连续激发过程中辐射的前两个波峰和波谷对应的时刻停止激发, 可以观察到图3(b), (c)中的现象. 发现无论是在STM纳米腔还是皮米腔条件下, 均在连续辐射的第1个波谷时刻, 分子团簇的激发程度达到最优状态. 因此, 我们确定该时间点作为触发超辐射脉冲的理想激发时长. 具体而言, 在STM纳米腔中, 选取28 fs的激发时长, 而在STM皮米腔中, 则选取13 fs的激发时长.

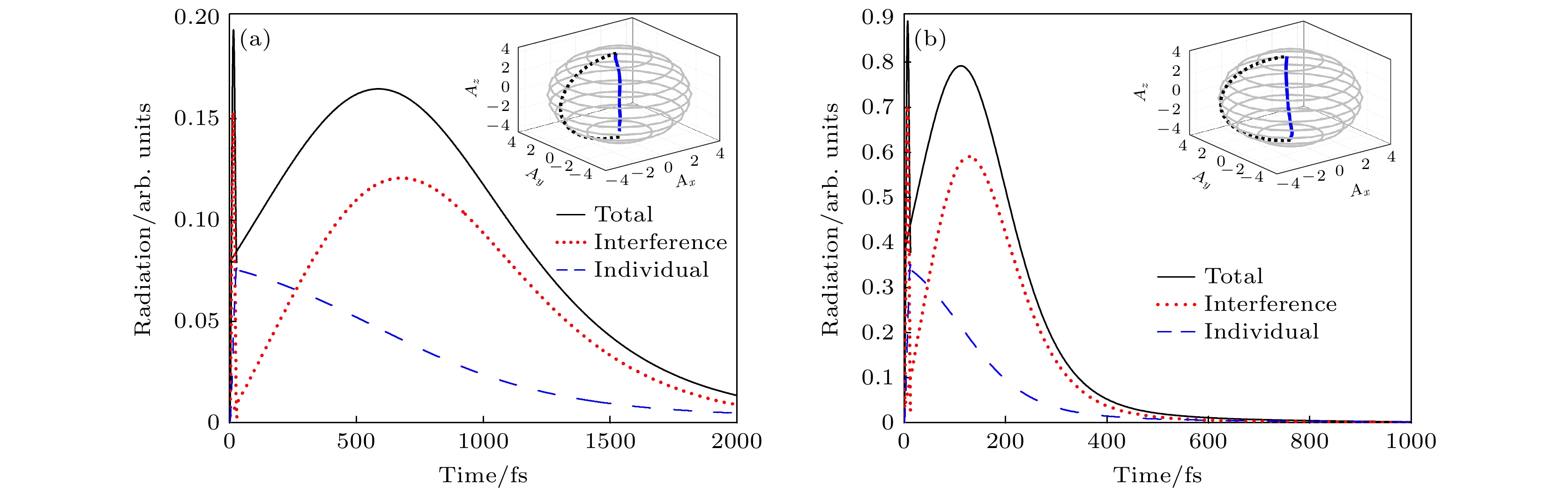
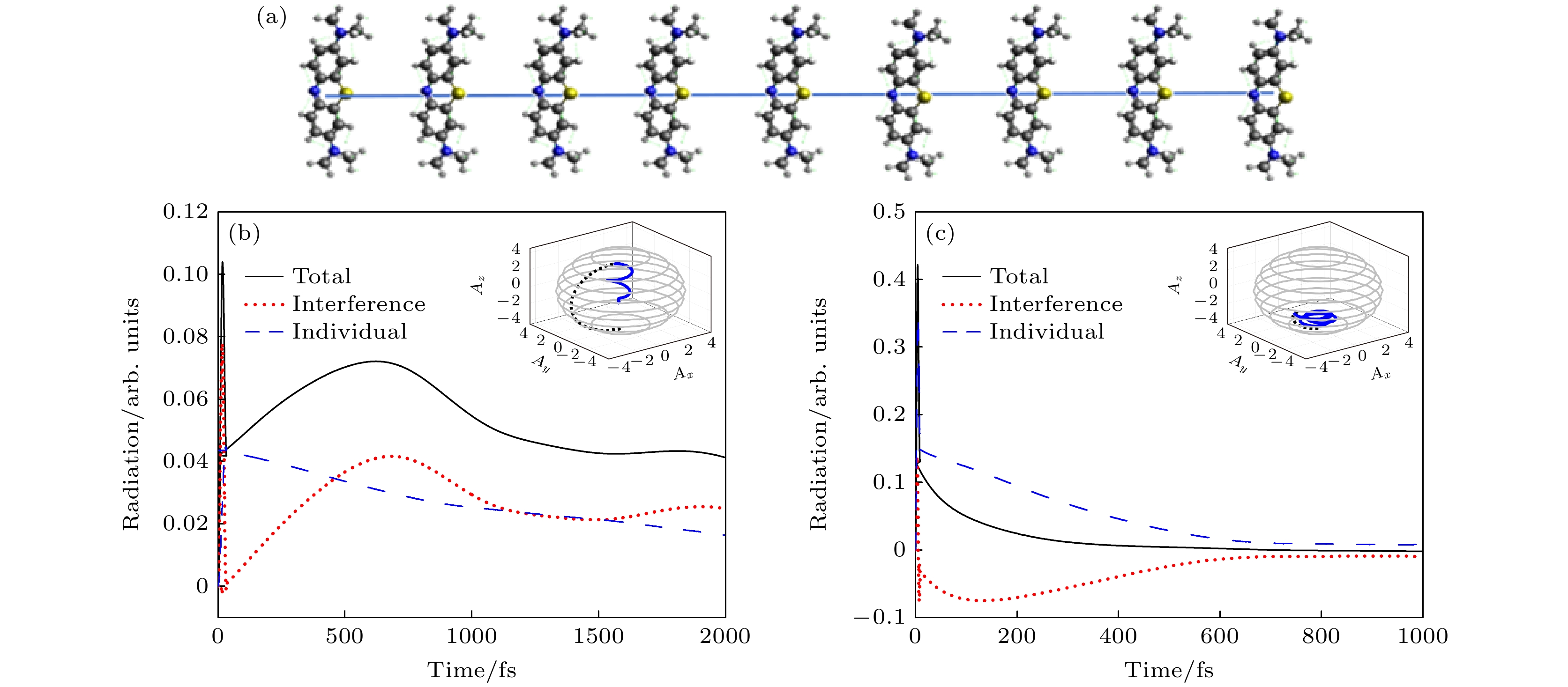
基于上面的分析, 采用28 fs和13 fs的激光脉冲分别驱动STM纳米腔和皮米腔中的分子, 图4(a), (b)给出了相应的辐射谱及分子团簇的动力学特性. 在图4(a)中, 我们发现在STM纳米腔中, 当激发停止后, 辐射谱中出现了明显的总辐射曲线 峰值. 该峰值的中心位置大约在606 fs, 宽度约为750 fs. 这一峰值的强度显著高于单个分子的辐射强度, 并且与分子间干涉曲线显示出显著的正相关性. 由于这种快速的辐射增强和随后的衰减符合超辐射的典型特征, 所以认为这是产生了超辐射现 象^[26]. 图4(a)中插图蓝线显示了分子的集体自旋矢量从北极几乎垂直拉伸到南极, 进一步证明了分子团簇经历了一个非常快速的跃迁过程. 这种快速跃迁现象再一次证实了超辐射行为的存在. 相比之下, STM皮米腔中的分子团簇展现出更为集中且强烈的超辐射行为, 其辐射谱中的峰值中心约在125 fs, 宽度约为150 fs. 这种在辐射强度和时间尺度上的差异与腔体中等离激元散射格林张量z分量的虚部有关. 在STM纳米腔中, 这个虚部较小, 意味着分子间的耗散耦合较弱, 导致能量损失较小, 相干长度增大. 同时导致单个分子的激发能级较低, 从而使得整体脉冲的强度较弱. 此外, STM皮米腔的超辐射行为更为显著, 这与其更小的尺寸和更强的局域场增强效应有关. 分子间的距离1.3 nm与STM皮米腔的针尖尖端半径1 nm相近, 导致分子间相互作用更强, 从而在激发后能更快地达到相干态, 产生更强烈的超辐射脉冲.

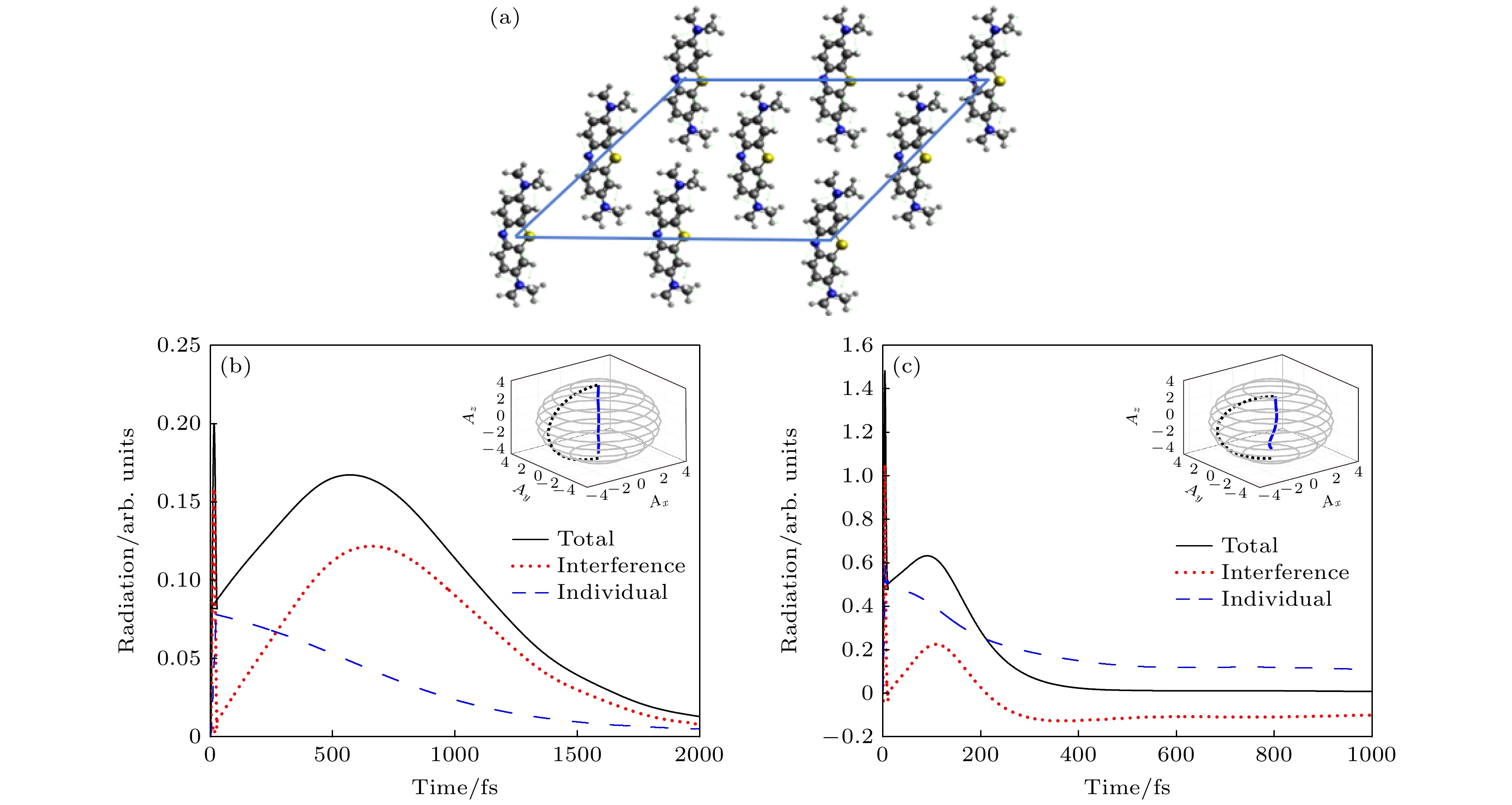
本文还根据文献[25]设计了如图5(a)所示的二维平面状构形的分子团簇, 设中心分子位于不同腔的中心且分子间彼此相距1.3 nm. 同样根据之前的分析选取连续辐射的第一个波谷时刻为该构形下的激发时长, 但由于分子构形的改变, STM纳米腔和皮米腔第一个波谷分别出现在28 fs和11 fs. 结果显示, 在这两种腔结构下都观察到了超辐射现象. 同样在STM纳米腔中, 超辐射的脉冲强度相对较低, 持续时间较长, 而STM皮米腔内, 超辐射则表现为脉冲短而强度高的特性. 这是因为环状构形和二维平面构形都是较为紧凑的平面结构, 因此观察到的现象及产生原因都比较类似. 虽然二维平面和环状构形分子团簇同时具有轴对称和中心对称性, 但环状分子团簇还具有多个旋转对称性, 所以二维平面构形的排列对称性低于环状构形, 这导致二维平面构形在空间分布上的能量分布模式不如环状构形均匀, 从而使得分子间的相互作用效率有所下降. 因此, 在这种构形下, 超辐射的强度有所减弱, 特别是在STM皮米腔中, 这一现象更为显著.

最后根据文献[25], 设计由9个分子以1.3 nm的步长沿腔径向排列构成的一维链状构形, 并将径向排列的第1个分子置于腔中心处, 如图6(a)所示. 用33 fs的激光脉冲驱动STM纳米腔, 9 fs的激光脉冲驱动STM皮米腔中的分子. 图6(b), (c)辐射谱显示停止激发后在STM纳米腔中出现了轻微的超辐射, 而在STM皮米腔中没有出现先增大后减小的峰, 图6(c)插图显示分子团簇也没有从北极到南极的快速衰减的动力学行为, 所以我们认定STM皮米腔中没有产生超辐射. 这是因为当9个分子以一维链状排列时, 不同分子所经历的激发参数有所不同. 在较大的STM纳米腔中, 整个分子团簇都位于腔内, 使得分子之间仍保持一定的相干性, 但相对于二维平面和环状构形分子团簇, 一维链状构形的分子团簇只具有轴对称性, 因此其强度有所减弱. 在STM皮米腔中, 由于腔体尺寸的限制, 一维链状排列的分子无法全部被有效激发, 这限制了分子间的相互作用, 从而阻碍了超辐射现象的发生.

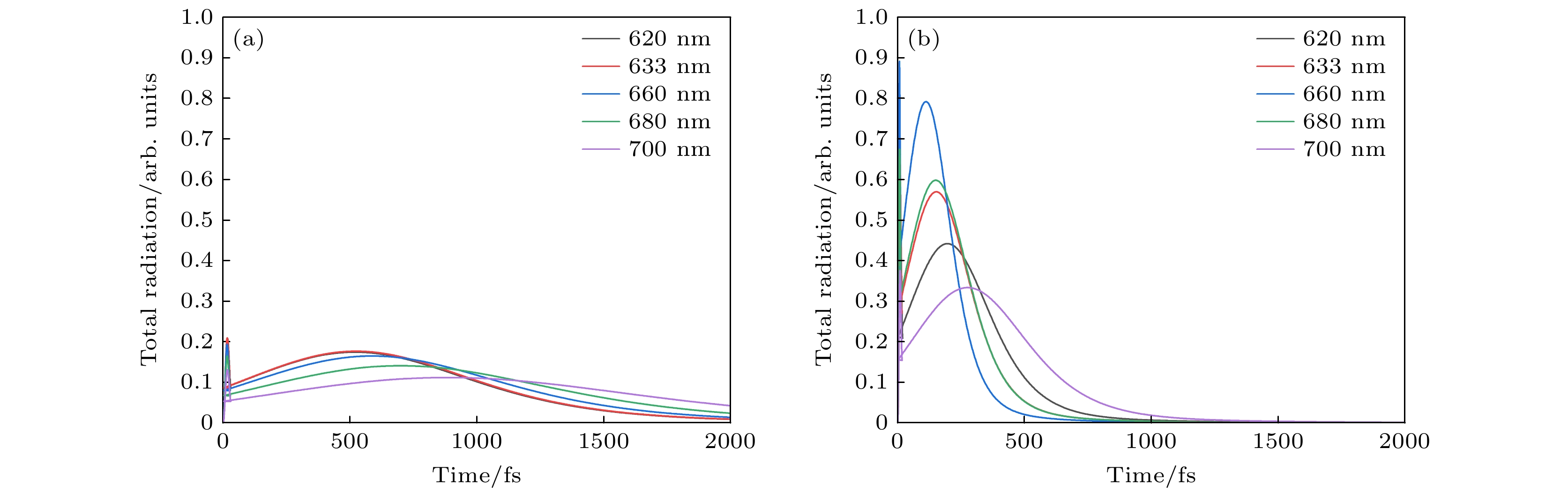
在上文研究中, 我们设腔中的等离激元与单个亚甲基蓝分子共振, 但当多个全同亚甲基蓝分子形成团簇时, 其共振能级会发生变化. 根据Kasha理论, 分子团簇可分为J型和H型. 对于J型分子团簇, 吸收峰较单体发生红移, 而H型分子团簇的吸收峰则较单体发生蓝移^[27,28]. 为了更全面地了解外场对腔中分子团簇辐射的影响, 以环状构形为例探讨了在固定外场激光强度I_ext = 10³ μW/μm²下, 激发波长对辐射光谱的影响, 如图7所示. 结果表明, 在所有不同的激发波长条件下, 都观察到了辐射强度先增强后减弱的现象, 这表明超辐射现象在STM腔中普遍存在. 当激发波长逐渐接近单分子的共振波长(即660 nm)时, 发现STM纳米腔中的分子团簇所表现出的超辐射强度及宽度的变化相对较小, 而STM皮米腔中超辐射现象则显得更为短暂且强烈, 出现时间更早. 随着激发波长远离660 nm, STM纳米腔中的分子团簇所表现出的超辐射强度略有减弱, 出现时间延后, 而STM皮米腔中超辐射强度显著降低, 出现时间也延后, 但持续时间延长. 这些结果表明相对于单个亚甲基蓝分子, 我们所使用的9个全同亚甲基蓝分子团簇的吸收峰变化不大, 验证了我们设定腔内等离激元效应与单个亚甲基蓝分子共振的合理性. 此外还揭示了分子团簇在不同尺度的腔中的行为差异, 具体来说, 在微小尺度的结构中, 入射光对分子的激发和相干性的影响更大, 因而对超辐射效应的影响也更加显著和敏感.

基于宏观量子电动力学与开放量子系统理论结合提出的半经典理论, 本文探讨了环状、二维平面和一维链状3种不同构形的亚甲基蓝分子团簇在STM纳米腔和皮米腔中的辐射特性. 发现对于同一个腔来说, 分子团簇在腔中的排列对称性越高, 越容易形成明显的超辐射脉冲, 这是因为其对光场的捕获能力更强, 这使得团簇中的各分子更容易处于相同的激发状态. 这种影响在STM皮米腔中会更加显著, 因为皮米腔具有更高的空间分辨率和更强的局域场增强效应, 这有助于放大由分子团簇结构引起的微小差异. 另外, 对于放在不同尺寸腔中的同种分子团簇, 在能够产生超辐射的情况下, STM纳米腔中的超辐射强度普遍低于STM皮米腔, 而持续时间普遍长于STM皮米腔, 这一现象表明, 腔体的尺寸和结构对分子团簇的辐射特性有着直接的影响. 因此, 我们可以通过增大STM针尖的尖端半径或降低分子团簇在腔中的排列对称性, 使得耗散耦合降低, 将超辐射脉冲的时间尺度拉长到皮秒量级. 未来的研究将进一步探索更多分子团簇构形及其在不同腔体环境中的超辐射特性, 以期获得更加全面的认识和应用前景.