高级搜索

事件顺序重建对康普顿相机成像分辨的影响

,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

王春杰, 关清帝, 姜文刚, 余青江, 解峰, 余功硕, 梁建峰, 李雪松, 徐江. 事件顺序重建对康普顿相机成像分辨的影响[J]. 物理学报, 2025, 74(10): 100701-1. doi: 10.7498/aps.74.20241723
引用本文: 王春杰, 关清帝, 姜文刚, 余青江, 解峰, 余功硕, 梁建峰, 李雪松, 徐江. 事件顺序重建对康普顿相机成像分辨的影响[J]. 物理学报, 2025, 74(10): 100701-1. doi: 10.7498/aps.74.20241723
shu
Chunjie WANG, Qingdi GUAN, Wengang JIANG, Qingjiang YU, Feng XIE, Gongshuo YU, Jianfeng LIANG, Xuesong LI, Jiang XU. Influence of event sequence reconstruction on imaging resolution of Compton camera[J]. Acta Physica Sinica, 2025, 74(10): 100701-1. doi: 10.7498/aps.74.20241723
Citation: Chunjie WANG, Qingdi GUAN, Wengang JIANG, Qingjiang YU, Feng XIE, Gongshuo YU, Jianfeng LIANG, Xuesong LI, Jiang XU. Influence of event sequence reconstruction on imaging resolution of Compton camera[J]. Acta Physica Sinica, 2025, 74(10): 100701-1. doi: 10.7498/aps.74.20241723
shu

事件顺序重建对康普顿相机成像分辨的影响

  • 西北核技术研究所, 西安　710024

    • 通讯作者: E-mail: wangchunjie@nint.ac.cn.; 

  • 中图分类号: 07.85.Nc, 07.85.-m, 52.70.La, 85.60.Gz

Influence of event sequence reconstruction on imaging resolution of Compton camera

  • Northwest Institute of Nuclear Technology, Xi’an 710024, China

    • Corresponding author: E-mail: wangchunjie@nint.ac.cn.; 

  • MSC: 07.85.Nc, 07.85.-m, 52.70.La, 85.60.Gz

  • 摘要: 康普顿相机用于γ射线成像具有装置轻便、探测效率高和成像能区广的优点. 然而, 由于探测系统难以分辨康普顿散射事件和散射光子吸收事件, 造成图像重建错误. 使用GEANT4蒙特卡罗程序构建了基于三维位置灵敏碲锌镉探测器的康普顿相机模型, 模拟探测远场137Cs点源特征γ射线并逐个事件地记录探测器中发生相互作用的位置和沉积的能量. 使用反投影图像重建算法对有效康普顿散射事件的康普顿散射角进行重建并对放射源成像, 研究了事件顺序重建对成像分辨的影响. 结果表明, 错误排序事件对成像分辨的影响主要在偏离源点位置30°以内的区域, 源点位置附近产生的错误重建像点在26°附近形成环状分布. 使用基于沉积能量大小的康普顿边缘测试和简单比较法对事件进行排序, 正确排序事件的比例提升至82%, 源点位置的像点分布密度提升了47%, 成像分辨得到了提升.
    Abstract: The Compton camera for γ-ray imaging has the advantages of light weight, high detection efficiency, and wide imaging energy range. However, it is difficult for the detection system to distinguish between the Compton scattering event and scattering photon absorption event, which results in erroneous image reconstruction. In this work, a simulation model of Compton camera based on a three-dimensional position-sensitive CdZnTe detector is constructed using GEANT4 program. The detection of characteristic γ-ray from a far-field 137Cs point-like source is simulated. The location of the interaction and energy deposition in the detector are recorded by means of event-by-event. The Compton scattering angles of effective Compton scattering events and imaging of the radioactive source are reconstructed using a simple back-projection algorithm which is an image reconstruction algorithm suitable for real-time imaging scenes. The influences of event sequence reconstruction on the imaging resolution and its improvement are investigated. The results show that the influence of incorrect sequence events on imaging resolution is mainly in the area within 30° deviation from the source position, resulting in a decrease in the density of the image points distributed at the source position. Incorrectly reconstructed image points are generated near the source position and form a ring at 26°. The percentage of correctly sequenced events increases to 82% by using Compton edge test and simple comparison method based on the deposited energy for sequencing events. The density of image points distributed at the source location is improved by 47%, and the incorrect reconstruction of the image point distribution near the source location is greatly suppressed, resulting in an improved imaging resolution. The research results provide support for designing Compton camera and optimizing image reconstruction.
  • 加载中

  • 图 1  康普顿散射及γ射线入射方向重建示意图

    Figure 1.  Schematic of Compton scattering and γ-ray incidence direction reconstruction.

    下载: 全尺寸图片 幻灯片

    图 2  简单反投影图像重建算法示意图

    Figure 2.  Schematic of the simple back-projection image reconstruction algorithm.

    下载: 全尺寸图片 幻灯片

    图 3  3D-CZT晶体及测量原理示意图

    Figure 3.  Schematic of 3D-CZT and measurement principle.

    下载: 全尺寸图片 幻灯片

    图 4  正确排序事件的散射光子能量与康普顿散射角的分布

    Figure 4.  Distribution of scattering photon energy and Compton scattering angles for correctly sequenced events.

    下载: 全尺寸图片 幻灯片

    图 5  正确排序事件和混乱排序事件的散射光子能量分布

    Figure 5.  Scattering photon energy distribution for correct and scrambled sequence events.

    下载: 全尺寸图片 幻灯片

    图 6  正确排序事件和错误排序事件的反投影康普顿圆锥示意图

    Figure 6.  Schematic of the back-projection Compton cone for correct and incorrect sequence events.

    下载: 全尺寸图片 幻灯片

    图 7  错误排序事件的反投影康普顿散射角与正确重建所需康普顿散射角的差异分布

    Figure 7.  Distribution of the difference between the back- projection Compton scattering angle of incorrect sequence events and the Compton scattering angle required for correct reconstruction.

    下载: 全尺寸图片 幻灯片

    图 8  $\theta $和${\theta _{{\text{geo}}}}$差异分布　(a) 正确排序事件; (b)混乱排序事件. ${\theta _{{\text{ARM}}}}$分布　(c) 正确排序事件; (d) 混乱排序事件

    Figure 8.  Distribution of the difference between $\theta $ and ${\theta _{{\text{geo}}}}$: (a) Correct sequence events; (b) scrambled sequence events. Distribution of ${\theta _{{\text{ARM}}}}$: (c) Correct sequence events; (d) scrambled sequence events.

    下载: 全尺寸图片 幻灯片

    图 9  综合排序后的分布　(a) $\theta $和${\theta _{{\text{geo}}}}$差异; (b) ${\theta _{{\text{ARM}}}}$分布

    Figure 9.  Distribution after sequence reconstruction: (a) Difference between $\theta $ and ${\theta _{{\text{geo}}}}$; (b) distribution of ${\theta _{{\text{ARM}}}}$.

    下载: 全尺寸图片 幻灯片

    图 10  137Cs点源图像重建结果　(a) 事件正确排序; (b) 混乱排序; (c) 使用康普顿边缘测试和简单比较法排序

    Figure 10.  137Cs point source image reconstruction: (a) Correct sequence; (b) scrambled sequence; (c) sequencing using Compton edge test and simple comparison.

    下载: 全尺寸图片 幻灯片
  • [1] Todd R W, Nightingale J M, Everett D B 1974 Nature 251 132 doi: 10.1038/251132a0
    [2] Gal O, Gmar M, Ivanov O P, Lainé F, Lamadie F, Le Goaller C, Mahé C, Manach E, Stepanov V E 2006 Nucl. Instrum. Methods Phys. Res. A 563 233 doi: 10.1016/j.nima.2006.01.119
    [3] 孙世峰 2020 物理学报 69 198701 doi: 10.7498/aps.69.20200674 Sun S F 2020 Acta Phys. Sin. 69 198701 doi: 10.7498/aps.69.20200674
    [4] 杨靖, 谭放, 吴玉迟, 谷渝秋 2016 核电子学与探测技术 36 966 doi: 10.3969/j.issn.0258-0934.2016.09.020 Yang J, Tan F, Wu Y C, Gu Y Q 2016 Nucl. Electron. Detect. Technol. 36 966 doi: 10.3969/j.issn.0258-0934.2016.09.020
    [5] Strong A 1996 Space Sci. Rev. 76 205 doi: 10.1007/BF00197840
    [6] Kamae T, Hanada N, Enomoto R 1988 IEEE Trans. Nucl. Sci. 35 352 doi: 10.1109/23.12741
    [7] Mihailescu L, Vetter K, Burks M, Hull E, Craig W 2007 Nucl. Instrum. Methods Phys. Res. A 570 89 doi: 10.1016/j.nima.2006.09.111
    [8] He Z, Li W, Knoll G, Wehe D, Berry J, Stahle C 1999 Nucl. Instrum. Methods Phys. Res. A 422 173 doi: 10.1016/S0168-9002(98)00950-4
    [9] Du Y, He Z, Knoll G, Wehe D, Li W 2001 Nucl. Instrum. Methods Phys. Res. A 457 203 doi: 10.1016/S0168-9002(00)00669-0
    [10] Lehner C E, He Z, Zhang F 2004 IEEE Trans. Nucl. Sci. 51 1618 doi: 10.1109/TNS.2004.832573
    [11] Wahl C G, Kaye W, Wang W, Zhang F, Jaworski J, Boucher Y A, King A, He Z 2014 IEEE Nuclear Science Symposium and Medical Imaging Conference (NSS/MIC) Seattle, USA, November 8–15, 2014 p1
    [12] 宋张勇, 于得洋, 蔡晓红 2019 物理学报 68 118701 doi: 10.7498/aps.68.20182245 Song Z Y, Yu D Y, Cai X H 2019 Acta Phys. Sin. 68 118701 doi: 10.7498/aps.68.20182245
    [13] 王薇, 李传龙, 吴建华, 李兴隆 2019 原子能科学技术 53 2471 doi: 10.7538/yzk.2018.youxian.0905 Wang W, Li C L, Wu J H, Li X L 2019 Atomic Energy Sci. Tech. 53 2471 doi: 10.7538/yzk.2018.youxian.0905
    [14] Song Z Y, Zhang B Z, Yu D Y 2021 Nucl. Phys. Rev. 38 215 doi: 10.11804/NuclPhysRev.38.2020066
    [15] Shy D, He Z 2020 Nucl. Instrum. Methods Phys. Res. A 954 161443 doi: 10.1016/j.nima.2018.10.121
    [16] Xiaofeng G, Qingpei X, Dongfeng T, Yi W, Fanhua H, Yingzeng Z, Chengsheng C, Na L 2017 Appl. Radiat. Isot. 124 93 doi: 10.1016/j.apradiso.2017.03.019
    [17] Liu Y L, Fu J Q, Li Y L, Li Y J, Ma X M, Zhang L 2018 Nucl. Sci. Tech. 29 1 doi: 10.1007/s41365-017-0340-6
    [18] 张峰, 闫镔, 汪先超, 江桦, 魏星 2013 物理学报 62 168702 doi: 10.7498/aps.62.168702 Zhang F, Yan B, Wang X C, Jiang H, Wei X 2013 Acta Phys. Sin. 62 168702 doi: 10.7498/aps.62.168702
    [19] Agostinelli S, Allison J, Amako K 2003 Nucl. Instrum. Methods Phys. Res. A 506 250 doi: 10.1016/S0168-9002(03)01368-8
    [20] Tian F, Geng C R, Yao Z Y, Wu R Y, Xu J F, Cai F, Tang X B 2022 Phys. Med. 96 140 doi: 10.1016/j.ejmp.2022.03.005
    [21] Xu D, He Z, Lehner C E, Zhang F 2004 Hard X-Ray and Gamma-Ray Detector Physics VI Denver, USA, October 21, 2004 p144
  • 加载中
图( 10)
计量
  • 文章访问数:  31
  • HTML全文浏览数:  31
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-13
  • 刊出日期:  2025-05-20

事件顺序重建对康普顿相机成像分辨的影响

  • 收稿日期:  2024-12-13

摘要: 康普顿相机用于γ射线成像具有装置轻便、探测效率高和成像能区广的优点. 然而, 由于探测系统难以分辨康普顿散射事件和散射光子吸收事件, 造成图像重建错误. 使用GEANT4蒙特卡罗程序构建了基于三维位置灵敏碲锌镉探测器的康普顿相机模型, 模拟探测远场137Cs点源特征γ射线并逐个事件地记录探测器中发生相互作用的位置和沉积的能量. 使用反投影图像重建算法对有效康普顿散射事件的康普顿散射角进行重建并对放射源成像, 研究了事件顺序重建对成像分辨的影响. 结果表明, 错误排序事件对成像分辨的影响主要在偏离源点位置30°以内的区域, 源点位置附近产生的错误重建像点在26°附近形成环状分布. 使用基于沉积能量大小的康普顿边缘测试和简单比较法对事件进行排序, 正确排序事件的比例提升至82%, 源点位置的像点分布密度提升了47%, 成像分辨得到了提升.

English Abstract

    全文HTML

    1.   引　言

    • 康普顿相机是一种利用康普顿散射原理对γ射线进行成像的装置, 相比于传统的机械准直型γ成像装置, 康普顿相机具有独特的优势[1–3]. 例如, 康普顿相机不使用笨重且复杂的机械准直或编码孔系统, 结构相对简单, 成像探测效率高; 康普顿相机对各个方向入射的γ射线不作部分屏蔽, 成像视野宽广; 康普顿相机对不同能量γ射线的成像效率取决于γ射线在探测材料中的康普顿散射截面大小, 由于百keV—十几MeV能量的γ射线在探测材料中的康普顿散射截面较大, 因此康普顿相机对该能区的γ射线成像效率较高, 这个能区覆盖了大部分常见的γ射线能量[4]. 总体而言, 康普顿相机具有结构轻便、成像效率高、成像视野宽和成像能量范围广等优点, 在核医学、辐射环境监测和天体物理研究等领域具有重要的潜在应用价值.

      早期的康普顿相机通常是双层探测器结构, 即由两块平行放置的位置灵敏探测器构成. 两个探测器分别为散射探测器和吸收探测器, 通过获取γ射线分别在两层探测器中沉积的能量和位置, 根据康普顿散射原理, 重建入射光子的方向[5–7]. 基于双层探测器结构的康普顿相机需要在分离的探测器中做康普顿散射事件的符合测量, 成像视野较小, 探测效率较低. 近年来, 一种基于“一体式”三维位置灵敏碲锌镉(three-dimensional position-sensitive CdZnTe, 3D-CZT)探测器的康普顿相机被提出[8], 该型康普顿相机仅使用一个探测器同时获取反冲电子和散射光子的沉积能量和位置信息. 3D-CZT康普顿相机对γ射线的入射方向没有限制, 成像视野约为4π; “一体式”的结构使得探测器具有较大的灵敏体积, 成像效率较高. He等[9–11]对3D-CZT康普顿相机开展了大量的研究, 开发的康普顿成像系统对137Cs点源的成像效率高于2%, 实时成像的角分辨率好于30°.

      康普顿相机使用符合测量的方法获取康普顿散射事件的信息, 并重建入射光子的径迹. 测量数据存在误差, 导致重建结果出现误差. 文献[12–14]讨论了成像误差的来源, 主要有能量测量误差、位置测量误差和散射光子能量的多普勒展宽误差等. 此外, 由于散射光子在探测器中以光速传播, 发生康普顿散射到散射光子被吸收的时间间隔极短(< 1 ns), 现有的探测系统难以分辨事件发生的顺序, 可能导致事件排序错误, 从而造成图像重建错误, 使得本底增大、信噪比降低、成像分辨变差. 目前, 国内外针对事件顺序重建对康普顿相机成像分辨的影响仅有少量的研究. Shy等[15]使用能量比较法(first-is-largest, FIL)和最小平方差法(minimum squared difference, MSD)相结合的方法对较高能量(> 1 MeV) γ射线的康普顿散射事件进行排序, 使得事件顺序正确率提高约20%, 提升了成像分辨; Guo等[16]使用理论计算的方法, 预先获取不同事件类型排序的能量集中分布范围, 从而实现低计数条件下的事件顺序甄别, 获得了更好的成像分辨.

      本文使用GEANT4蒙特卡罗程序构建了基于3D-CZT的康普顿相机模型, 模拟获取混乱顺序的康普顿散射事件数据, 分析了事件顺序重建对康普顿相机成像分辨的影响. 模拟结果可以为成像数据的筛选和重建算法的优化提供参考.

    2.   成像原理和成像算法

      2.1.   成像原理

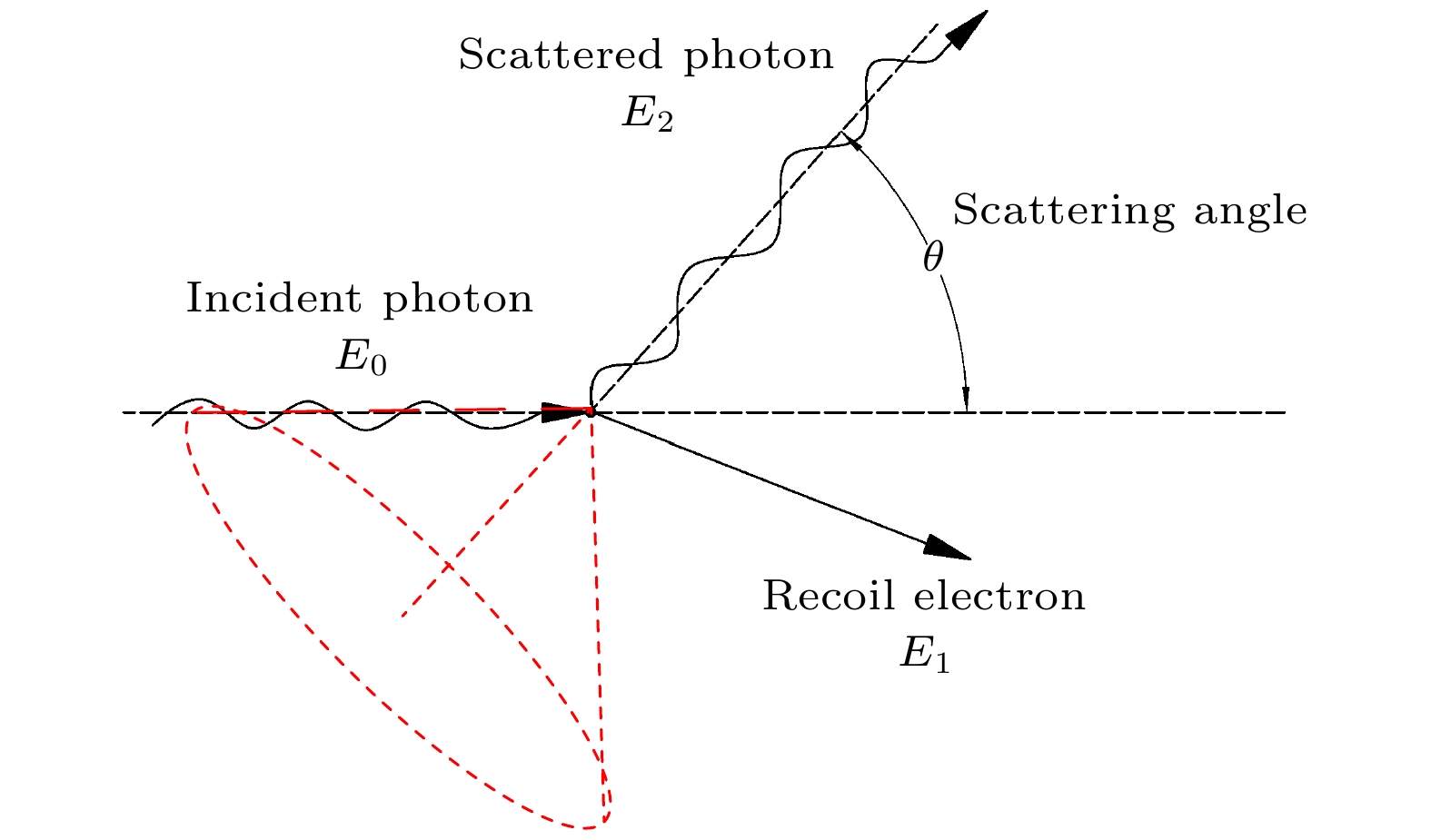
    • 康普顿相机基于γ射线与物质发生康普顿散射相互作用的原理对γ射线源进行成像. 能量为${E_0}$的γ射线在探测器中发生康普顿散射相互作用生成反冲电子和散射光子, 反冲电子沉积能量${E_1}$, 散射光子进一步被探测器吸收并沉积能量${E_2}$, 相互作用过程中能量守恒和动量守恒, 康普顿散射角$\theta $可以通过沉积的能量计算得到:

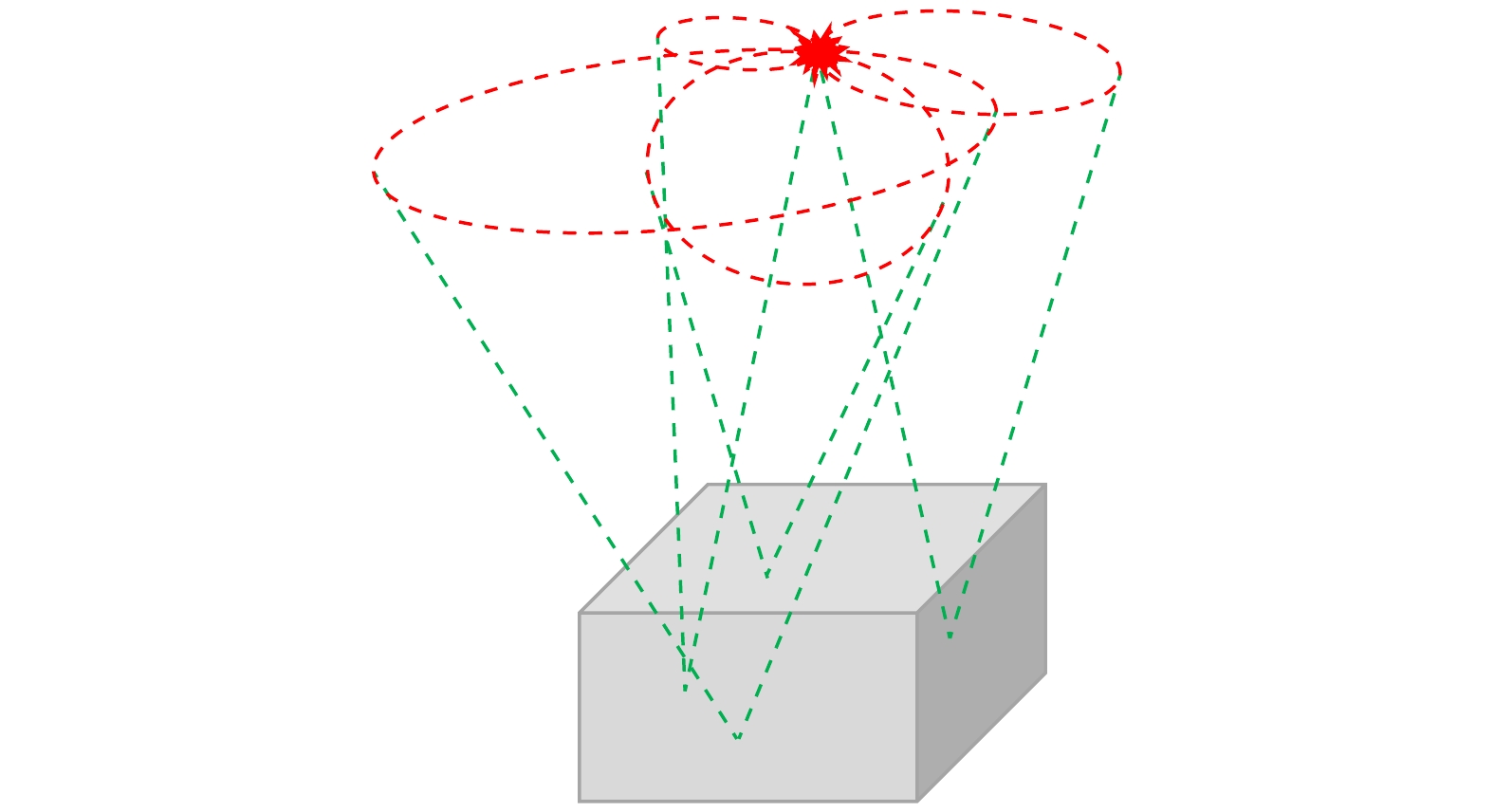
      其中, ${m_{\text{e}}}$为电子的静止质量, $c$为真空中的光速. 根据康普顿散射过程的几何关系可以得到, γ射线的入射方向位于以发生康普顿散射的位置为顶点, 以散射事件和吸收事件发生位置的连线为轴线, 以康普顿散射角$\theta $为半角的圆锥面上, 如图1所示. 一组康普顿散射事件仅能得到一个这样的圆锥面, γ射线的入射方向无法唯一确定. 通过测量大量的康普顿散射事件, 获取大量的圆锥面, 从而获得放射源在空间的分布.

      • 2.2.   成像算法

    • 为了获取放射源在空间的分布, 需要使用合适的图像重建算法对采集到的数据进行处理. 简单反投影图像重建算法(simple back-projection, SBP)具有运算速度快的特点, 是一种适用于实时成像场景的图像重建算法[17,18]. 反投影法图像重建算法利用康普顿散射的基本规律, 直接反演出图像,图像为每组康普顿散射事件的康普顿圆锥在空间上简单叠加. 理论上, 圆锥面重叠的位置就是放射源所在的位置, 如图2所示. 由于探测器测量的数据存在一定的误差, 使得大量反演的康普顿圆锥面不总是相交于实际源点所在的位置, 圆锥面在空间的叠加量是一个分布, 那么放射源在某处空间出现的概率与圆锥面在该处分布的权重值一致.

    3.   康普顿相机模型构建

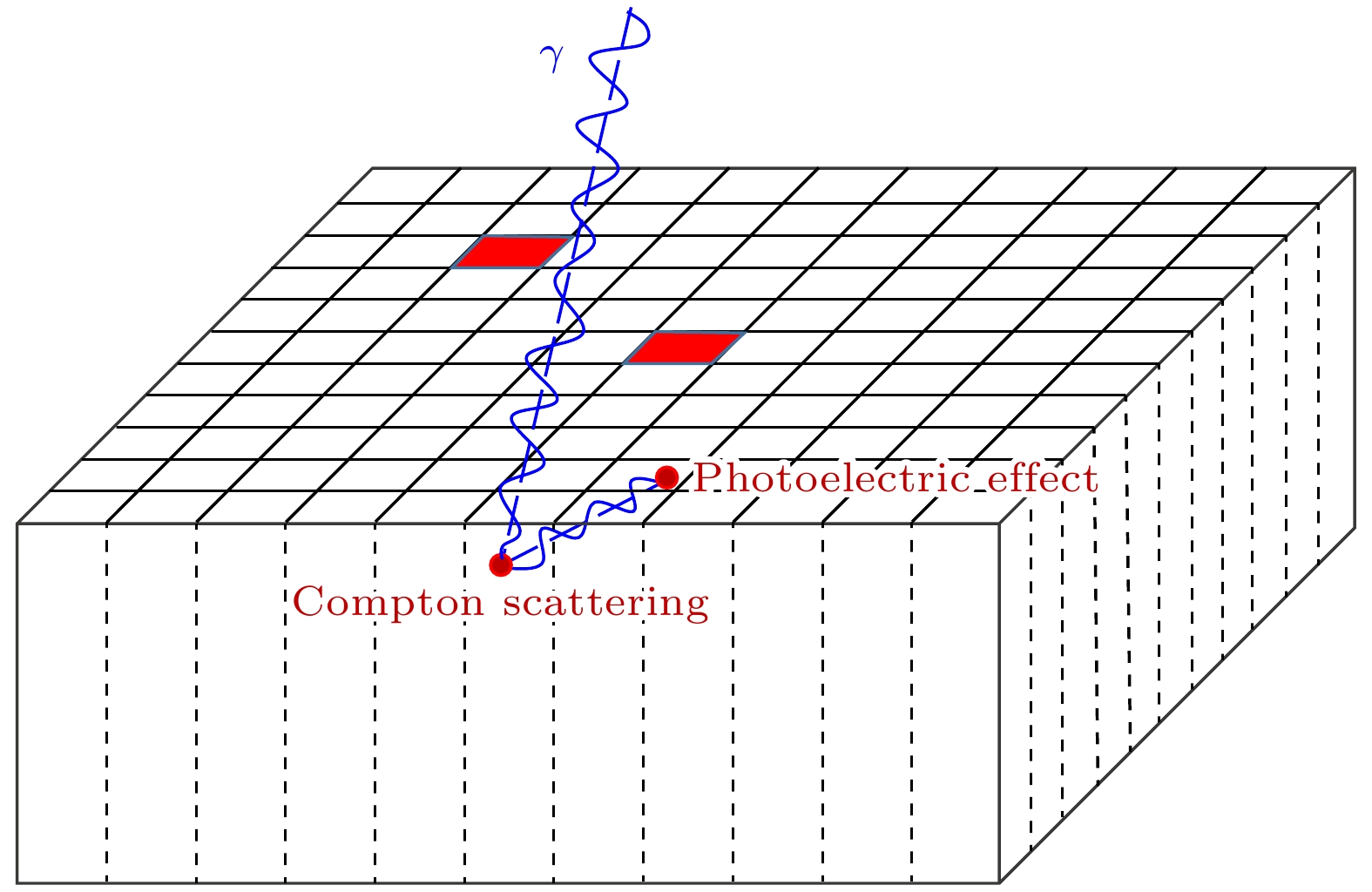
    • 使用基于蒙特卡罗方法的粒子输运程序GEANT4[19]对康普顿相机探测模型进行构建. 参考Kromek公司生产的基于3D-CZT探测器的康普顿相机参数构建探测晶体模型, 其晶体尺寸为22 mm×22 mm×15 mm, 被分割成11×11的探测单元阵列[20]. 康普顿相机的探测晶体及测量模型如图3所示. 探测晶体的材料为碲锌镉, 被分割为121个尺寸为2 mm×2 mm×15 mm的探测单元阵列, 每个探测单元可以独立获取γ射线在其中沉积的能量. 整块晶体由1 mm厚的铝壳包裹. 由于康普顿相机的大部分应用场景是较远距离的放射源测量, 因此这里模拟远场成像的情况. 使用标准的137Cs点源作为放射源, 将放射源置于距离探测器中心1 m处. 由康普顿相机的成像原理可知, 需要探测器能够同时获取γ射线发生相互作用的位置和沉积能量. 探测晶体对γ射线的康普顿散射过程作位置灵敏测量. 一组可用于成像的有效康普顿散射事件包括入射光子散射和散射光子吸收两部分, 入射的γ光子在一个探测单元中发生康普顿散射并沉积部分能量, 散射光子进入另一个探测单元被吸收沉积全部能量. 相互作用事件发生的位置通过产生沉积信号的探测单元坐标获取, 沉积的能量通过同一个探测单元获取. 模拟探测γ射线并逐个事件地记录探测器中发生相互作用的位置和沉积的能量. 为了模拟事件顺序这一单一误差源项对成像分辨的影响, 模拟时不考虑位置测量和能量测量引入的误差.

    4.   事件顺序对成像的影响及其在图像重建中的改进方法

      4.1.   事件顺序对成像角分辨的影响

    • 模拟探测获得了大量的数据, 根据相邻事件沉积能量的关系, 筛选出发生康普顿散射相互作用且能量完全沉积在探测器中的真符合事件. 由于同时发生3次或3次以上相互作用的事件占比较少, 这里仅选择发生两次相互作用的事件. 筛选获得了80000个有效康普顿事件. 在实际的探测过程中, 每组事件的两次相互作用时间远小于探测器的时间分辨, 顺序是混乱的, 记为混乱排序事件; 其中, 一部分事件的顺序是正确的, 记为正确排序事件; 一部分事件的顺序是错误的, 即反冲电子沉积事件被错误判断为散射光子沉积事件, 记为错误排序事件. 模拟计算分别获取事件混乱排序、正确排序和错误排序情况的数据.

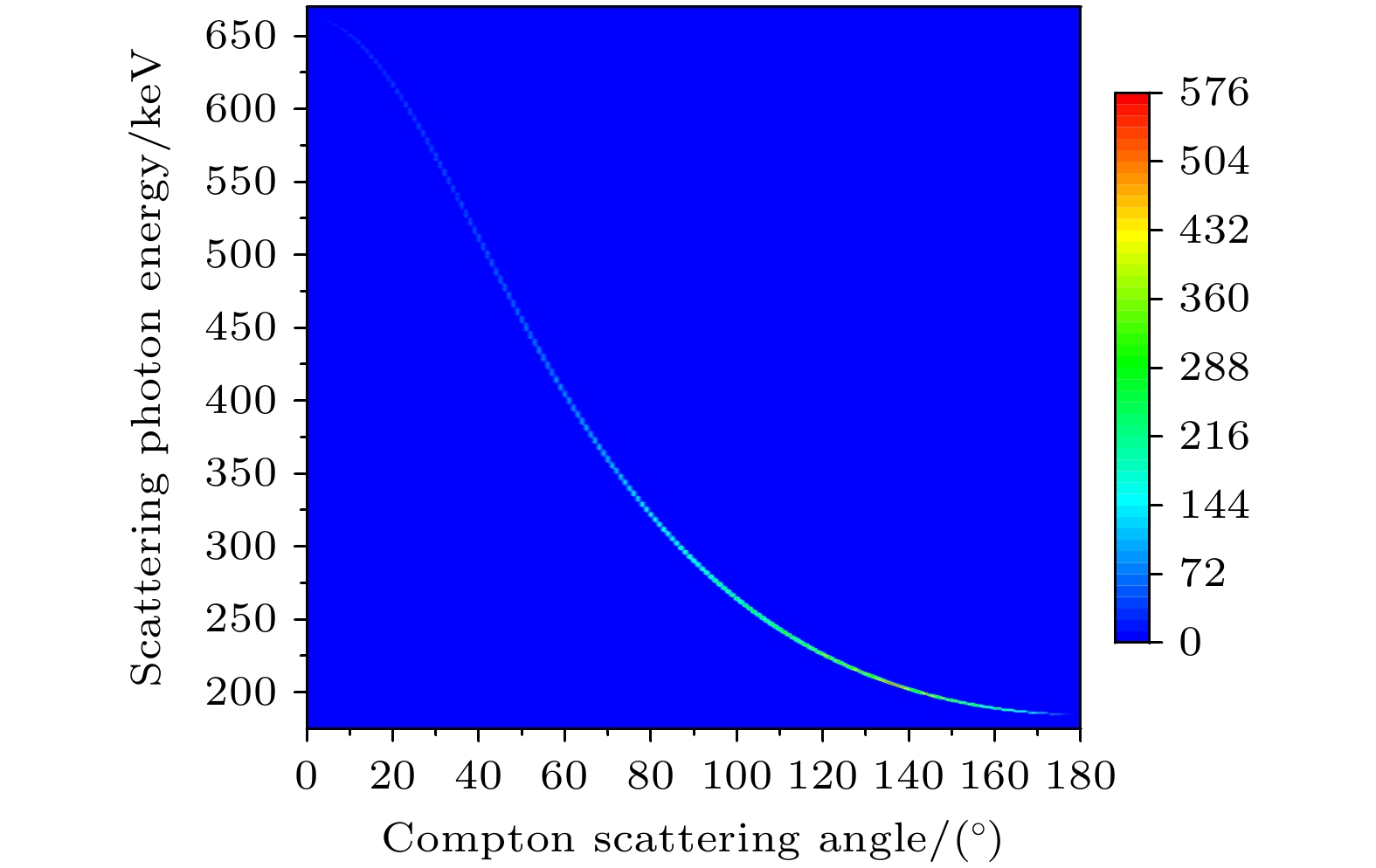
      正确排序事件的散射光子能量与康普顿散射角的分布如图4所示. 可以看出, 低能散射光子较多, 发生大角度散射的情况占优. 这是由于较高能量的散射光子发生光电效应沉积全部能量的概率较低; 另一方面, 探测晶体的尺寸有限, 较高能量的散射光子容易逃逸出晶体.

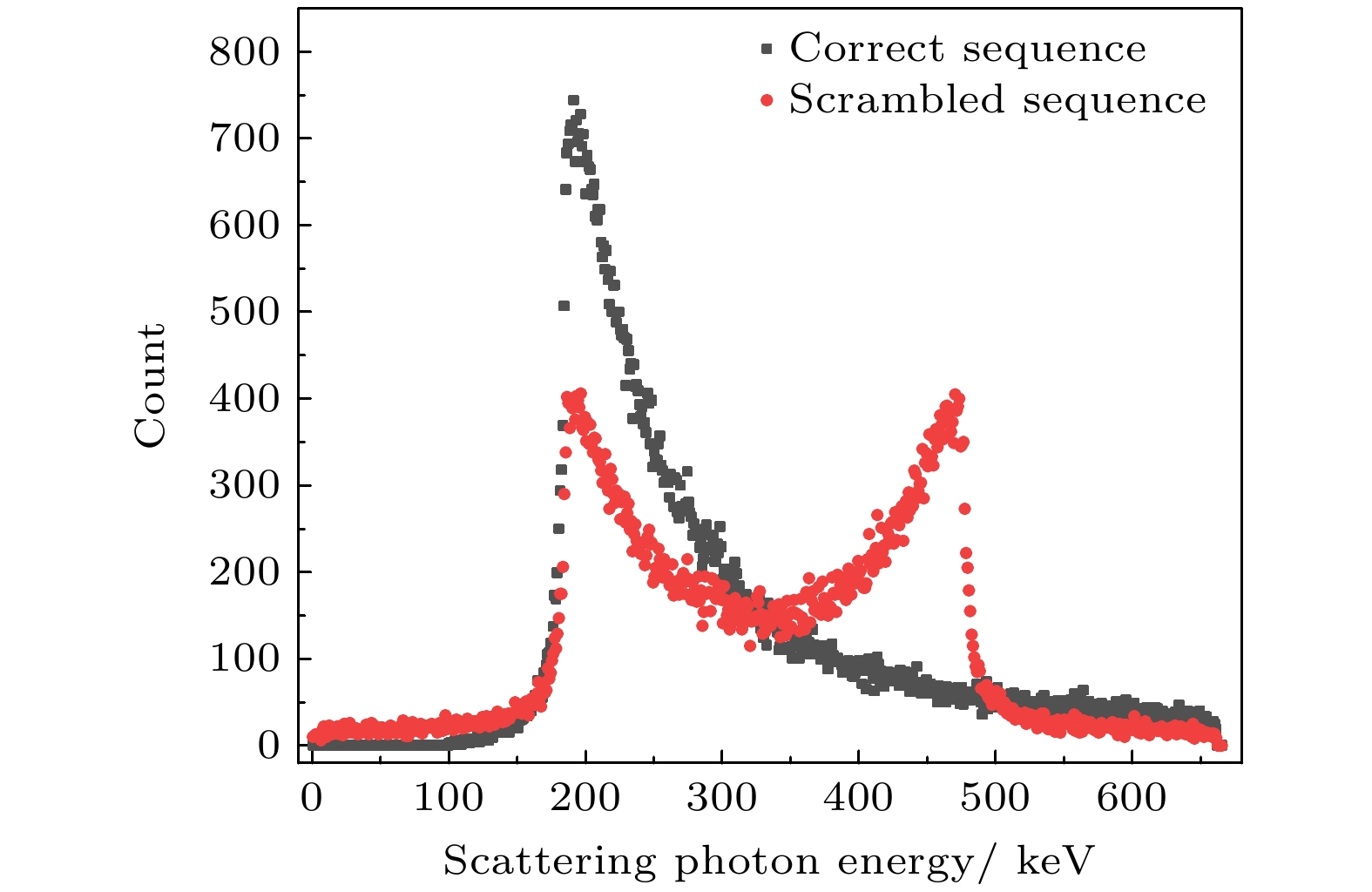
      正确排序事件和混乱排序事件的散射光子能量分布如图5所示. 可以看出, 事件混乱排序时, 低能端的散射光子数量分布减少, 但分布趋势变化不大; 在散射光子能量为470 keV附近, 分布差异明显, 对应的康普顿散射角为47°, 这主要是由错误排序事件贡献的, 这里的分布差异是图像重建误差的主要来源.

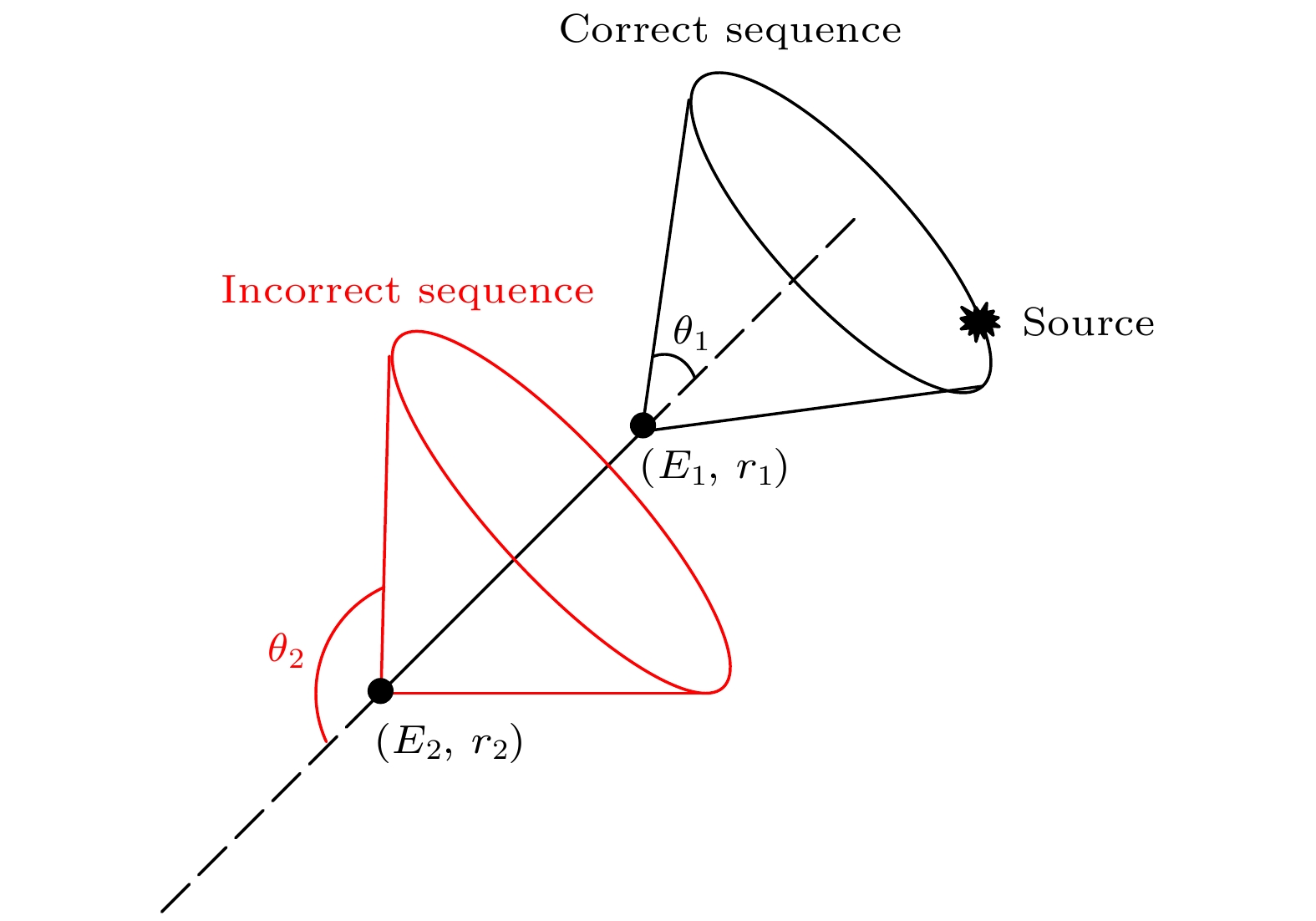
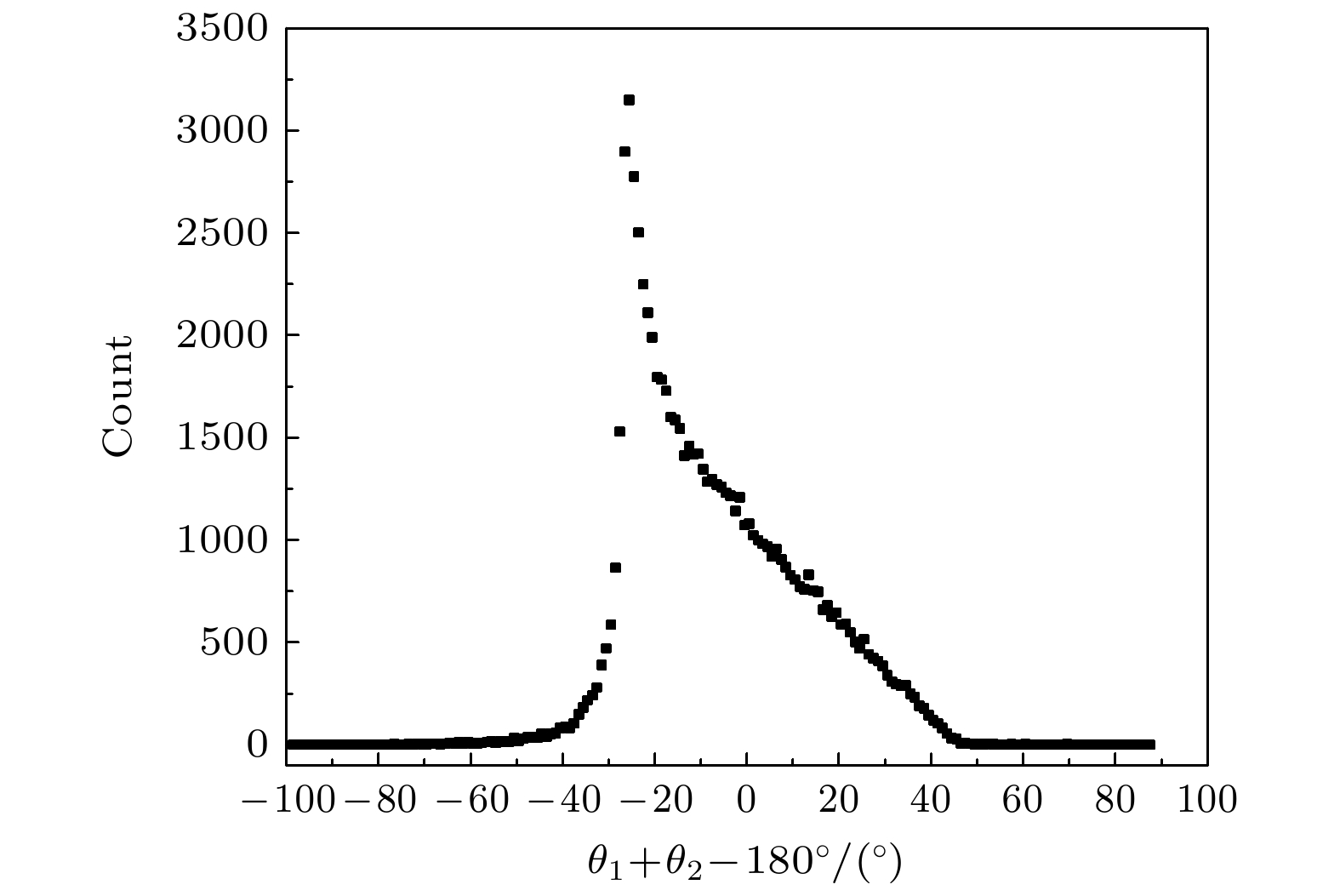
      正确排序事件和错误排序事件重建的反投影康普顿圆锥如图6所示. 事件错误排序时, 两次相互作用发生的顺序对调, 重建获得错误的反投影康普顿圆锥, 圆锥的轴线不变, 顶点由发生康普顿散射的位置${r_1}$变化为散射光子沉积的位置$ {r_2} $. 根据几何关系可以看出, 当事件错误排序时的康普顿散射角${\theta _2}$与正确排序时的康普顿散射角${\theta _1}$之和为180°(即${\theta _1}$+${\theta _2}$–180° = 0)时, 在远场近似的情况下, 两个康普顿圆锥重叠, γ射线的入射方向依然能够得到正确重建.

      错误排序事件的反投影康普顿散射角与正确重建所需康普顿散射角的差异(即${\theta _1}$+${\theta _2}$–180°)分布如图7所示. 可以看出, 错误排序事件的反投影康普顿散射角与正确重建所需康普顿散射角的差异主要分布于–40°—+40°区域, 0°附近区域的分布相对较少, 表明利用错误排序事件能够正确重建入射γ射线方向的概率较低. 错误排序事件的反投影康普顿散射角与正确重建所需康普顿散射角偏差较大, 错误排序事件会导致γ射线入射方向重建出现较大的误差.

      康普顿相机的成像质量可以用测量角分辨(angle resolution measurement, ARM)来评估. γ射线入射方向重建所用的康普顿散射角$\theta $和真实的康普顿散射角${\theta _{{\text{geo}}}}$之间的偏差定义为

      其中, $\theta $由康普顿散射过程中散射点和吸收点沉积的能量计算得到((1a)式和(1b)式); ${\theta _{{\text{geo}}}}$根据放射源、散射点和吸收点的位置计算得到, 即

      其中, $ {{\boldsymbol{r}}_{0}} $, $ {{\boldsymbol{r}}_{1}} $和$ {{\boldsymbol{r}}_{2}} $分别为放射源、散射点和吸收点的位置.

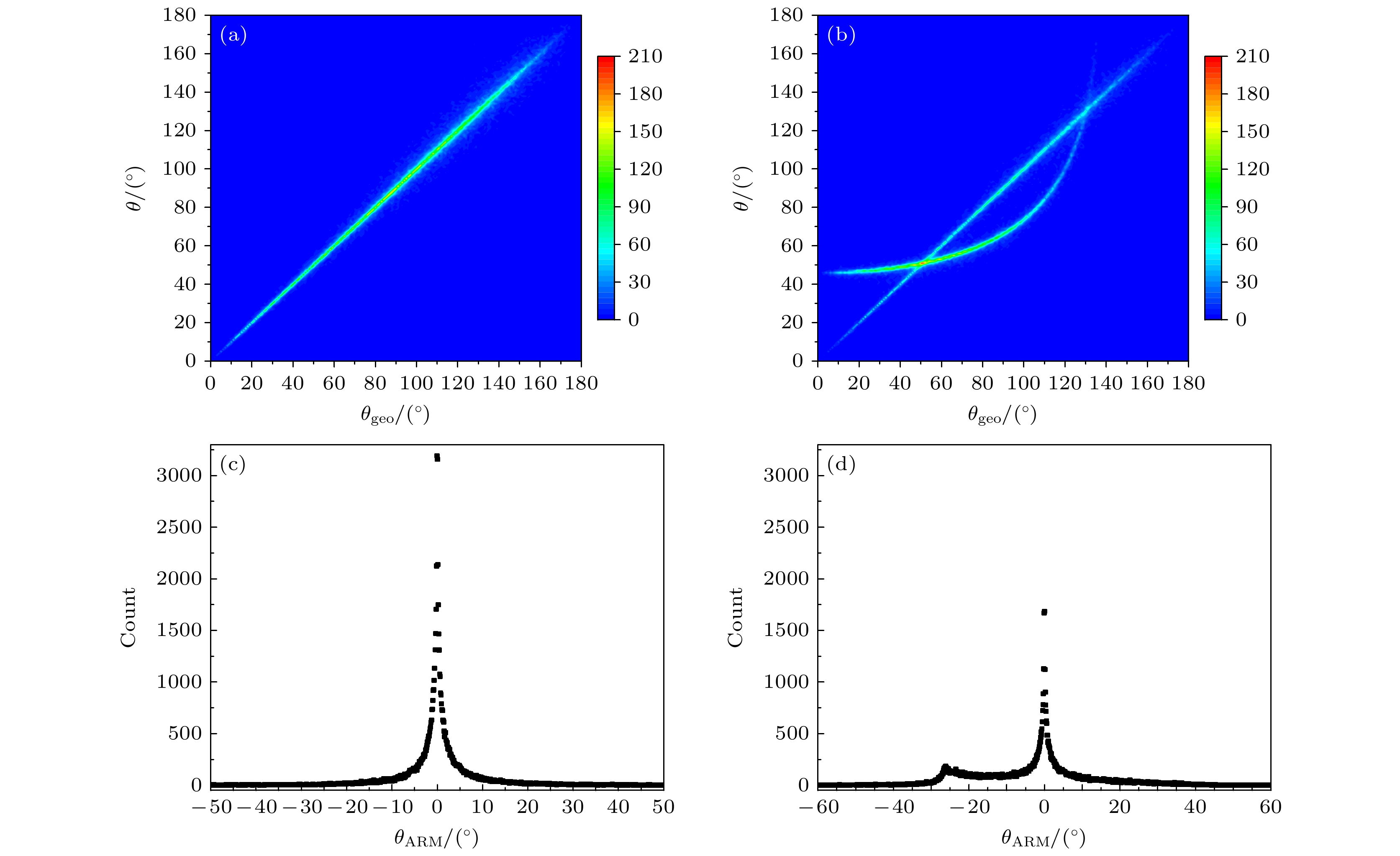
      对正确排序事件和混乱排序事件的$\theta $和${\theta _{{\text{geo}}}}$的差异进行统计, 结果分别如图8(a), (b)所示, 相应的${\theta _{{\text{ARM}}}}$分布分别如图8(c), (d)所示. 事件正确排序时, $\theta $和${\theta _{{\text{geo}}}}$的分布基本呈线性相关, 展宽较小, 表明每组事件的$\theta $和${\theta _{{\text{geo}}}}$相差不大; 相应的${\theta _{{\text{ARM}}}}$以0°为中心大致呈高斯分布, 半高宽(full with at half maximum, FWHM)表征的成像角分辨为2.1°. 成像误差主要是由康普顿散射过程中多普勒效应导致的能量展宽贡献的, 多普勒效应导致的误差与探测材料本身相关, 是一个内禀误差, 无法被消除. 事件混乱排序时, $\theta $和${\theta _{{\text{geo}}}}$的差异呈现两种分布, 一种分布依然呈线性, 是由正确排序事件贡献的; 一种分布呈非线性, 是由错误排序事件贡献的. 由方程(1a)和(1b)可以看出, 事件错误排序时的$\theta $与正确排序时的$\theta $呈非线性, 而事件错误排序时的${\theta _{{\text{geo}}}}$为正确排序时的补角(图6), 依然呈线性, 因此事件错误排序时的$\theta $和${\theta _{{\text{geo}}}}$的差异分布呈非线性. 相比于正确排序事件的${\theta _{{\text{ARM}}}}$, 混乱排序事件的${\theta _{{\text{ARM}}}}$在0°附近大致呈高斯分布, 与前者一致; 不同的是, 0°附近的分布量减少, 峰的底部展宽, 尤其是在–30°—–10°区域, 展宽较大, 在${\theta _{{\text{ARM}}}}$ = –26°处出现一个峰, 这些因事件错误排序引入的分布差异将导致图像重建产生误差.

      • 4.2.   事件顺序重建方法

    • 在实际测量中, 同一条γ射线在探测器中沉积产生的事件被认为是同时的, 因此无法通过时间信息对事件进行排序, 可以用于排序的信息有事件数量、每个事件发生的位置和沉积的能量. 康普顿散射动力学为事件排序提供了一定的指导. 由康普顿散射公式((1b)式)可知, 能量为${E_0}$的γ射线发生康普顿散射沉积的能量随着散射角的增大而增大, 最小值为0, 对应的散射角为0°; 沉积的能量有一个最大值, 该能量被称为康普顿边缘, 对应的散射角为180°. 沉积能量的最大值$ {E_{{\text{edge}}}} $为

      可以看出, 发生康普顿散射沉积的能量不可能高于$ {E_{{\text{edge}}}} $, 若两次事件沉积的能量中有一个能量高于$ {E_{{\text{edge}}}} $, 那么高于$ {E_{{\text{edge}}}} $的能量沉积必定属于散射光子沉积事件, 这种排序方法被称为康普顿边缘测试. 对于能量为662 keV的入射γ射线, 康普顿边缘为478 keV. 在混乱排序事件中, 康普顿散射沉积能量高于478 keV的事件比例约为5%, 康普顿边缘测试方法使得正确排序事件的比例提高为55%, 该方法对事件排序正确率的提升有限.

      当散射事件和吸收事件沉积的能量均小于康普顿边缘时, 通过比较沉积能量的大小对事件进行排序, 这种排序方法被称为简单比较法. “一体式”探测器的体积较小, 散射光子能量较高时, 容易从探测器中逃逸, 高能散射光子完全沉积在探测器中的比例较低[21]. 入射γ射线能量为662 keV时, 散射光子能量在低能区域的分布占优(图5), 散射光子的能量小于${E_0}$/2的比例为74%. 使用简单比较法排序, 直接比较两次相互作用沉积能量的大小, 选择沉积能量较高的事件作为散射事件, 能量较低的事件作为吸收事件.

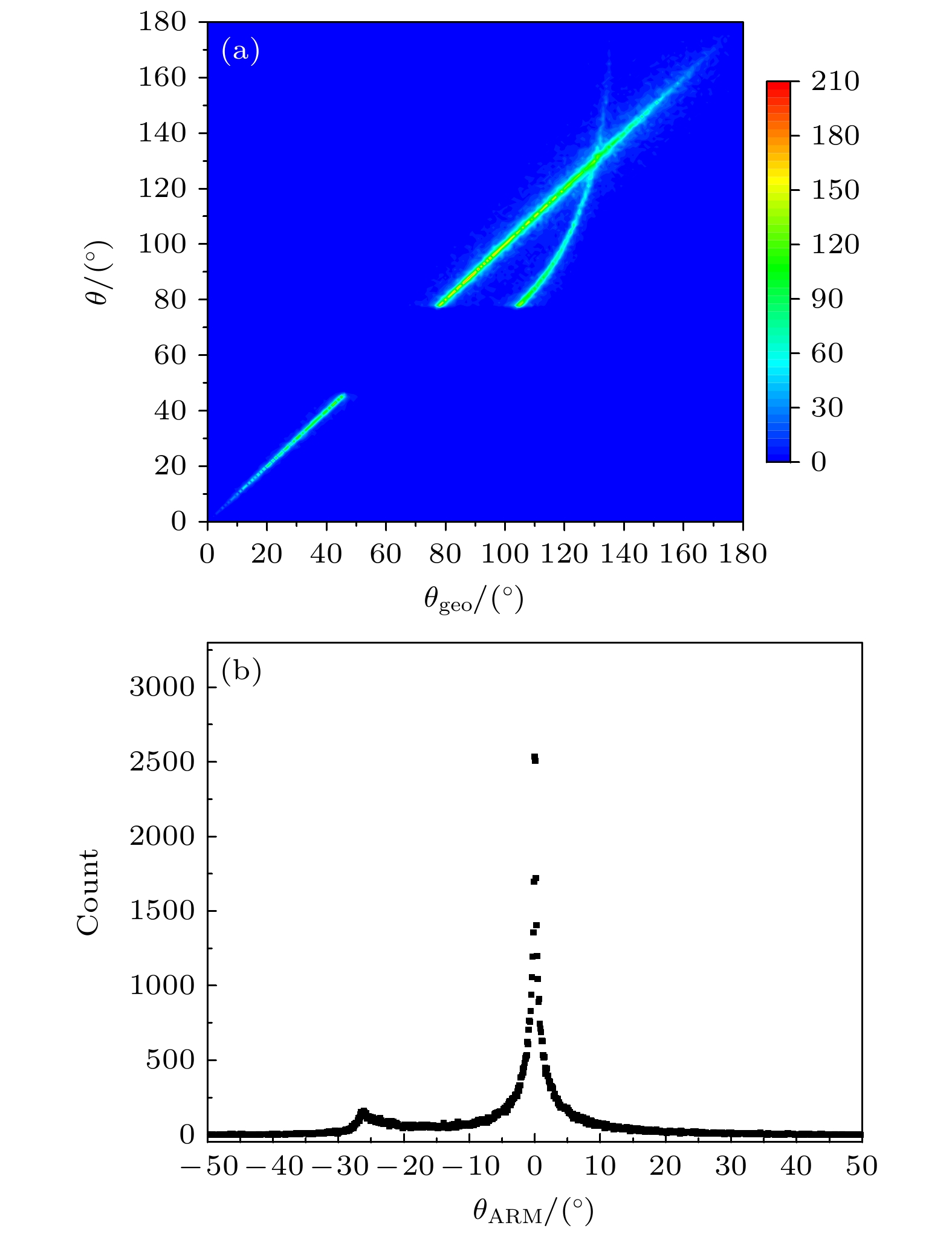
      综合使用康普顿边缘测试和简单比较法对事件进行排序, 排序后$\theta $和${\theta _{{\text{geo}}}}$的分布以及${\theta _{{\text{ARM}}}}$的分布如图9所示. 相比于混乱排序事件的$\theta $和${\theta _{{\text{geo}}}}$分布, 综合排序后的$\theta $和${\theta _{{\text{geo}}}}$分布呈线性相关的比例明显增大, 相应地, 正确排序事件的比例增大. 排序后的康普顿散射角在45°—77°区间出现缺失, 这是由于排序时, 只有沉积能量在(${E_0}- {E_{{\text{edge}}}})- {E_0}/2$和$ {E_{{\text{edge}}}} - {E_0}$区间的事件被判断为散射光子吸收事件, 当实际散射光子的能量在${E_0}/2- {E_{{\text{edge}}}} $区间时, 不被判断为散射光子, 导致事件排序错误, 散射光子的能量在${E_0}/2- {E_{{\text{edge}}}} $区间是缺失的, 对应的康普顿散射角为45°—77°.

      排序后的${\theta _{{\text{ARM}}}}$分布与排序前的${\theta _{{\text{ARM}}}}$分布(图8(d))相似, 不同的是${\theta _{{\text{ARM}}}}$= 0°附近的分布量增多, 展宽减小, ${\theta _{{\text{ARM}}}}$= –26°处的峰高度降低. 综合使用两种方法对事件进行排序, 使得正确排 序事件的比例提高为82%, 正确排序事件比例的提高意味着图像重建时因事件错误排序引入的误差降低.

      • 4.3.   图像重建

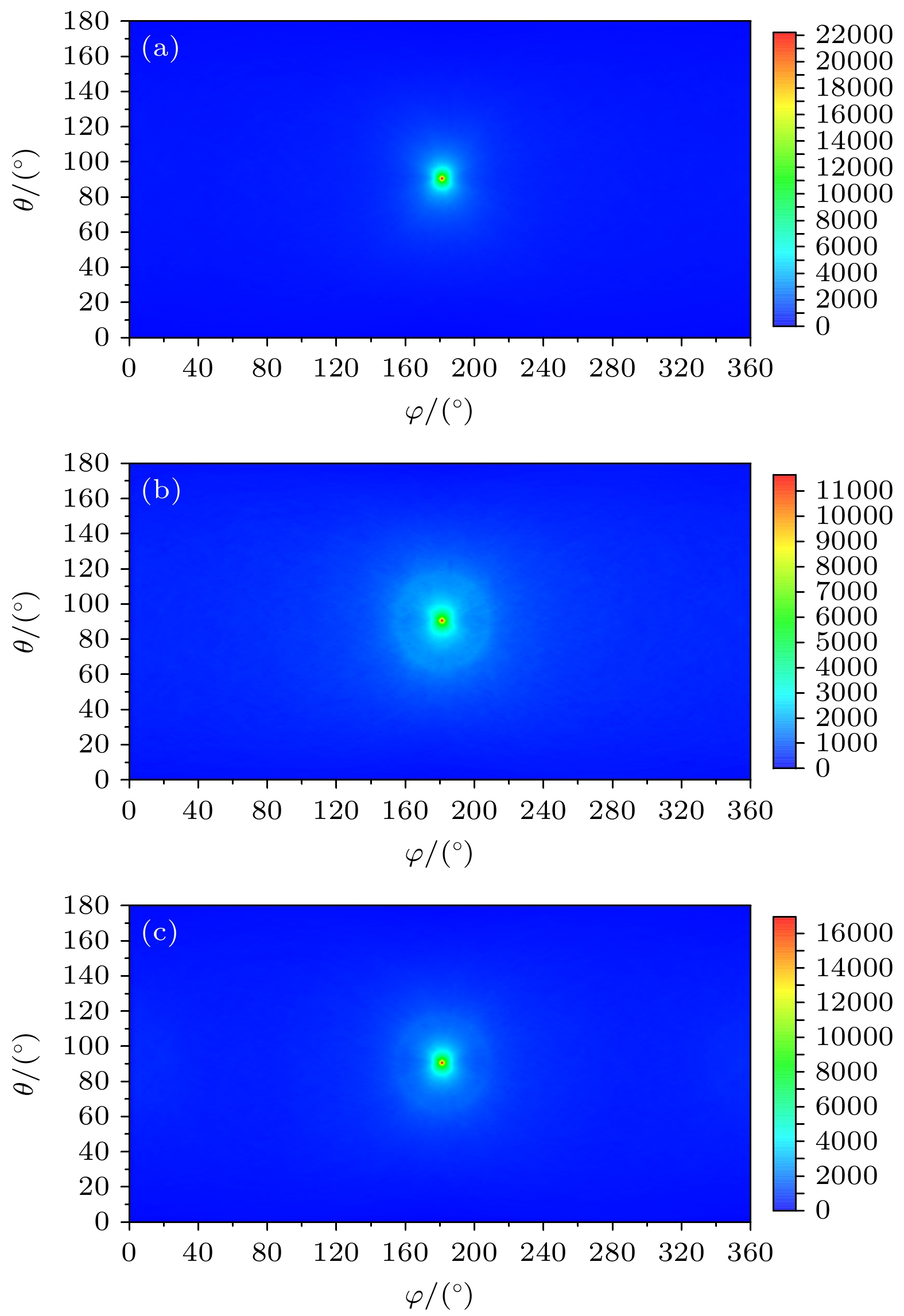
    • 在图像重建过程中, 反投影圆锥的顶点随机地分布于探测器中, 对于大多数的γ射线成像应用场景, 探测器的尺寸远小于放射源与探测器的距离, 因此可以忽略反投影圆锥的顶点分布差异, 认为所有的顶点均位于探测器中心, 这种图像重建模型简化被称为远场近似(far-field approximation). 由于反投影圆锥都是从同一个顶点引出, 这些反投影圆锥的交点仅提供了放射源所在位置的方向信息. 事实上, 即使不做远场近似, 图像重建也难以获得放射源的距离信息[15]. 远场近似图像重建适合使用球坐标系, 以探测器中心为坐标系中心, 重建的反投影圆锥参数为极角θ和方位角φ, 成像空间为4π全空间.

      在事件正确排序、混乱排序和使用康普顿边缘测试与简单比较法排序的情况下对137Cs点源进行图像重建, 结果如图10所示. 在事件正确排序时, 重建图像以(θ, φ)=(90°, 180°)为中心大致呈高斯分布, 中心点的分布密度最高, 表明放射源位于中心点位置, 成像角分辨为2°, 图像重建结果与实际情况相符. 在事件混乱排序时, 图像重建仍然获得了正确的放射源位置信息, 但放射源位置的像点分布密度减小为事件正确排序时的一半; 放射源位置附近30°以内区域的像点分布密度增大, 尤其是在偏离放射源位置约26°的区域, 像点分布密度较高, 形成一个圆环, 这是由于错误排序事件的康普顿散射角与正确重建所需的康普顿散射角的差异大部分在30°以内, 且在26°位置分布最多, 图像重建结果与${\theta _{{\text{ARM}}}}$的分布(图7)一致. 在使用康普顿边缘测试和简单比较法对事件进行排序后, 图像重建获得了正确的放射源位置信息, 放射源位置的像点分布密度比事件混乱排序时提高了47%, 放射源位置以外区域的像点分布密度有所减小, 环状分布明显减弱, 表明使用康普顿边缘测试和简单比较法对事件进行排序能够大幅提升图像重建质量, 但由于该排序方法无法完全消除错误排序事件, 使得错误排序事件对图像的正确重建仍然存在一定的影响.

    5.   结　论

    • 本文使用GEANT4蒙特卡罗程序构建了基于3D-CZT探测器的康普顿相机模型, 使用简单反投影图像重建算法对远场137Cs点源进行了重建, 研究了事件顺序重建对成像分辨的影响. 错误排序事件重建的γ射线入射方向与实际方向的角度差异主要在–30°—–10°之间, 峰值在–26°; 不对事件进行排序时, 放射源位置的像点分布密度减小为事件正确排序时的一半, 偏离放射源位置26°的区域形成一个圆环. 使用基于沉积能量大小的康普顿边缘测试和简单比较法对事件进行排序, 事件正确排序的比例提升至82%. 重建图像上放射源位置的像点分布密度提高了47%, 非放射源位置区域的像点分布密度明显降低, 排序后的重建图像分辨率得到了大幅提升. 康普顿边缘测试和简单比较法能够减少因事件错误排序对图像重建产生的干扰, 但无法完全消除, 需要进一步发展更加完备的方法对事件进行排序.

    参考文献 (21)

目录

/

返回文章
返回