高级搜索

基于强场层析成像方案的异核分子结构成像

,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

吴文卓, 王世军, 王艳兰, 赖炫扬, 全威, 柳晓军. 基于强场层析成像方案的异核分子结构成像[J]. 物理学报, 2025, 74(9): 093201-1. doi: 10.7498/aps.74.20241792
引用本文: 吴文卓, 王世军, 王艳兰, 赖炫扬, 全威, 柳晓军. 基于强场层析成像方案的异核分子结构成像[J]. 物理学报, 2025, 74(9): 093201-1. doi: 10.7498/aps.74.20241792
shu
Wenzhuo WU, Shijun WANG, Yanlan WANG, Xuanyang LAI, Wei QUAN, Xiaojun LIU. Imaging of heteronuclear molecular structures based on strong-field tomographic scheme[J]. Acta Physica Sinica, 2025, 74(9): 093201-1. doi: 10.7498/aps.74.20241792
Citation: Wenzhuo WU, Shijun WANG, Yanlan WANG, Xuanyang LAI, Wei QUAN, Xiaojun LIU. Imaging of heteronuclear molecular structures based on strong-field tomographic scheme[J]. Acta Physica Sinica, 2025, 74(9): 093201-1. doi: 10.7498/aps.74.20241792
shu

基于强场层析成像方案的异核分子结构成像

  • 1.

    中国科学院精密测量科学与技术创新研究院, 武汉　430071

  • 2.

    中国科学院大学物理科学学院, 北京　100049

    • 作者简介: 吴文卓: 957904443@qq.com .
    通讯作者: E-mail: xylai@wipm.ac.cn.;  E-mail: xjliu@wipm.ac.cn.

  • 中图分类号: 32.80.-t, 33.60.+q, 33.90.+h

Imaging of heteronuclear molecular structures based on strong-field tomographic scheme

  • 1.

    Innovation Academy for Precision Measurement Science and Technology, Chinese Academy of Sciences, Wuhan 430071, China

  • 2.

    School of Physical Sciences, University of Chinese Academy of Sciences, Beijing 100049, China

    • Corresponding authors: E-mail: xylai@wipm.ac.cn.;  E-mail: xjliu@wipm.ac.cn

  • MSC: 32.80.-t, 33.60.+q, 33.90.+h

  • 摘要: 强场层析成像通过强场驱动的电子再散射实现取向分子的结构成像, 其优势在于无需预先计算不同原子的散射截面. 强场层析成像已成功应用于同核双原子分子结构的提取, 但对于更为普遍的异核分子体系, 其电子散射截面更为复杂, 该成像方案的适用性仍需进一步研究. 本文以异核双原子分子为例, 基于强场层析成像方案开展分子结构成像研究. 通过求解含时薛定谔方程, 获得光电子产量随分子轴取向角的变化, 并发展了一种异核分子散射截面随取向角变化的拟合方法. 通过拟合, 成功提取了分子核间距信息, 拟合结果与预设的分子核间距相一致. 研究结果表明, 强场层析成像方案同样适用于异核分子结构信息的提取, 为复杂分子体系的结构研究提供了新的可能性.
    Abstract: The study of atomic and molecular structure imaging is of great significance in revealing the microscopic nature of matter and promoting the frontier development of materials science and life science. The rapid development of femtosecond laser technology provides a new method for detecting atomic and molecular structures on an ultrafast time scale, such as strong-field tomography scheme. Strong-field tomography uses strong-field driven electron rescattering to detect the structure of oriented molecules. The advantage of this scheme is that it does not require priori knowledge of atomic differential cross-sections. Using the strong-field tomography scheme, the structural extraction of homonuclear diatomic molecules can be realized successfully. However, it is currently unclear whether this imaging scheme is applicable to the heteronuclear molecular system with more complex cross section of the electron. In this work, heteronuclear diatomic molecules are taken for example and the strong-field tomography scheme is used to study the imaging of the molecular structure. By solving the time-dependent Schrödinger equation, the variation of the photoelectron yield with the orientation angle of the molecular axis is obtained. Next, a fitting method for the variation of the photoelectron yields of the heteronuclear molecules with the orientation angle is presented, and then the fitted value of the internuclear separation is obtained. It is found that the fitting result is comparable to the real molecular internuclear separation, indicating that the strong-field tomography scheme is also suitable for the extraction of heteronuclear molecular structural information.
  • 加载中

  • 图 1  (a)—(c)通过TDSE计算得到的不同取向角下异核双原子分子的二维光电子动量分布, 其中分子取向角θL分别为(a) 0°, (b) 60°和(c) 90°, 左下角展示分子取向的示意图; (b)和(c)中两个白色箭头指向以z轴为对称轴的二维动量谱上下出现明显不对称的区域; (d)—(f)为提取出来的沿激光极化方向(z轴)的光电子能谱, 其中红色框区域代表高阶阈上电离谱平台结构的截止位置, 10Up

    Figure 1.  (a)–(c) Two-dimensional photoelectron momentum distributions of heteronuclear diatomic molecules at different orientation angles calculated with TDSE. The molecular orientation angles are (a) 0°, (b) 60°, and (c) 90°. The lower left corner shows a schematic diagram of the molecular orientation. The white arrows in panel (b) and (c) point to the regions of apparent asymmetry of the spectra along the z axis. (d)–(f) The extracted photoelectron spectra along the laser polarization direction (z axis). The red box areas denote the cutoff region of the high-order above-threshold ionization platform structure, 10Up.

    下载: 全尺寸图片 幻灯片

    图 2  (a)不同分子轴取向角下电子再散射过程的示意图, Δ代表散射前后电子的动量变化量; (b)截止位置附近(9.83 Up—10.17 Up)的光电子产率随分子取向角的变化(黑色散点), 其中红色曲线是利用(7)式拟合的结果

    Figure 2.  (a) Diagram of electron rescattering at different molecular orientation angles, Δ represents the change of the electron momentum before and after the scattering; (b) the variation of the photoelectron yields at the cutoff region (9.83 Up–10.12 Up) with the orientation angle (black dots), where the red curve is the fitting result using Eq. (7).

    下载: 全尺寸图片 幻灯片

    图 3  核间距Rf = 2.068 a.u.的同核双原子分子, 在高阶阈上电离谱截止位置区域的光电子产率随分子轴取向角的变化(黑色散点), 其中红色曲线是利用公式$ {\left|{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\right[(p - k){R}_{{\mathrm{f}}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}{\theta }_{{\mathrm{L}}}\left]\right|}^{2} $进行最优拟合的结果, 使用的激光参数与图1的激光参数相同

    Figure 3.  For a homonuclear diatomic molecule with internuclear distance Rf = 2.068 a.u., the variation of the photoelectron yields at the cutoff region with the orientation angle (black dots). The red curve is the best fitting result according to the formula $ {\left|{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\right[(p-k){R}_{{\mathrm{f}}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}{\theta }_{{\mathrm{L}}}\left]\right|}^{2} $. The laser parameters are the same as those used in Fig. 1.

    下载: 全尺寸图片 幻灯片

    图 4  采用强场层析成像方案, 针对不同核间距R0的异核双原子分子, 拟合出的核间距, 其中红色的点代表拟合值, 其对应的误差来源于曲线拟合过程中的误差

    Figure 4.  Internuclear distance of heteronuclear diatomic molecules with different internuclear separation R0 obtained with strong-field tomography method. The red dots represent the fitted values, and the errors are obtained from the fitting errors of the corresponding curves.

    下载: 全尺寸图片 幻灯片
  • [1] Corkum P B 1993 Phys. Rev. Lett. 71 1994 doi: 10.1103/PhysRevLett.71.1994
    [2] Schafer K J, Yang B, DiMauro L F, Kulander K C 1993 Phys. Rev. Lett. 70 1599 doi: 10.1103/PhysRevLett.70.1599
    [3] Becker W, Grasbon F, Kopold R, Milošević D B, Paulus G G, Walther H 2002 Adv. At. Mol. Opt. Phys. 48 35 doi: 10.1016/S1049-250X(02)80006-4
    [4] Paulus G G, Nicklich W, Xu H, Lambropoulos P, Walther H 1994 Phys. Rev. Lett. 72 2851 doi: 10.1103/PhysRevLett.72.2851
    [5] Zuo T, Bandrauk A, Corkum P B 1996 Chem. Phys. Lett. 259 313 doi: 10.1016/0009-2614(96)00786-5
    [6] Blaga C I, Xu J L, DiChiara A D, Sistrunk E, Zhang K K, Agostini P, Miller T A, DiMauro L F, Lin C D 2012 Nature 483 194 doi: 10.1038/nature10820
    [7] Meckel M, Comtois D, Zeidler D, Staudte A, Pavičić D, Bandulet H C, Pépin H, Kieffer J C, Dörner R, Villeneuve D M, Corkum P B 2008 Science 320 1478 doi: 10.1126/science.1157980
    [8] Xu J, Blaga C I, Zhang K, Lai Y H, Lin C D, Miller T A, Agostini P, DiMauro L F 2014 Nat. Commun. 5 4635 doi: 10.1038/ncomms5635
    [9] Pullen M G, Wolter B, Le A T, Baudisch M, Sclafani M, Pires H, Schröter C D, Ullrich J, Moshammer R, Pfeifer T, Lin C D, Biegert J 2016 Nat. Commun. 7 11922 doi: 10.1038/ncomms11922
    [10] Sanchez A, Amini K, Wang S J, Steinle T, Belsa B, Danek J, Le A T, Liu X, Moshammer R, Pfeifer T, Richter M, Ullrich J, Gräfe S, Lin C D, Biegertet J 2021 Nat. Commun. 12 1520 doi: 10.1038/s41467-021-21855-4
    [11] Rajak D, Beauvarlet S, Kneller O, Comby A, Cireasa R, Descamps D, Fabre B, Gorfinkiel J D, Higuet J, Petit S, Rozen S, Ruf H, Thiré N, Blanchet V, Dudovich N, Pons B, Mairesse Y 2024 Phys. Rev. X 14 011015 doi: 10.1103/PhysRevX.14.011015
    [12] Yang Y Z, Hu X Q, Wu L, Wang Z P, Li X K, Zhou S P, Wang Z Z, Guo F M, He L H, Luo S Z, Zhang D D, Wang J G, Chen X J, Wu Y, Wang C C, Ding D J 2024 Phys. Rev. Lett. 133 113203 doi: 10.1103/PhysRevLett.133.113203
    [13] Sun R P, Lai X Y, Yu S G, Wang Y L, Xu S P, Quan W, Liu X J 2019 Phys. Rev. Lett. 122 193202 doi: 10.1103/PhysRevLett.122.193202
    [14] Busuladžić M, Gazibegović-Busuladžić A, Milošević D B, Becker W 2008 Phys. Rev. Lett. 100 203003 doi: 10.1103/PhysRevLett.100.203003
    [15] Busuladžić M, Gazibegović-Busuladžić A, Milošević D B, Becker W 2008 Phys. Rev. A 78 033412 doi: 10.1103/PhysRevA.78.033412
    [16] Feit M D, Fleck J A, Steiger A 1982 J. Comput. Phys. 47 412 doi: 10.1016/0021-9991(82)90091-2
    [17] Chelkowski S, Foisy C, Bandrauk A D 1998 Phys. Rev. A 57 1176 doi: 10.1103/PhysRevA.57.1176
    [18] Tong X M, Watahiki S, Hino K, Toshima N 2007 Phys. Rev. Lett. 99 093001 doi: 10.1103/PhysRevLett.99.093001
    [19] Huismans Y, Rouzée A, Gijsbertsen A, Jungmann J H, Smolkowska A S, Logman P S W M, Lépine F, Cauchy C, Zamith S, Marchenko T, Bakker J M, Berden G, Redlich B, Meer A F G, Muller H G, Vermin W, Schafer K J, Spanner M, Ivanov, M Y, Smirnova O, Bauer D, Popruzhenko S V, Vrakking M J J 2011 Science 331 61 doi: 10.1126/science.1198450
    [20] Porat G, Alon G, Rozen S, Pedatzur O, Krüger M, Azoury D, Natan A, Orenstein G, Bruner B D, Vrakking M J J, Dudovich N 2018 Nat. Commun. 9 2805 doi: 10.1038/s41467-018-05185-6
  • 加载中
图( 4)
计量
  • 文章访问数:  33
  • HTML全文浏览数:  33
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-12-30
  • 刊出日期:  2025-05-05

基于强场层析成像方案的异核分子结构成像

    通讯作者: E-mail: xylai@wipm.ac.cn.; 
    通讯作者: E-mail: xjliu@wipm.ac.cn.
    作者简介: 吴文卓: 957904443@qq.com
  • 1. 中国科学院精密测量科学与技术创新研究院, 武汉　430071
  • 2. 中国科学院大学物理科学学院, 北京　100049
  • 收稿日期:  2024-12-30

摘要: 强场层析成像通过强场驱动的电子再散射实现取向分子的结构成像, 其优势在于无需预先计算不同原子的散射截面. 强场层析成像已成功应用于同核双原子分子结构的提取, 但对于更为普遍的异核分子体系, 其电子散射截面更为复杂, 该成像方案的适用性仍需进一步研究. 本文以异核双原子分子为例, 基于强场层析成像方案开展分子结构成像研究. 通过求解含时薛定谔方程, 获得光电子产量随分子轴取向角的变化, 并发展了一种异核分子散射截面随取向角变化的拟合方法. 通过拟合, 成功提取了分子核间距信息, 拟合结果与预设的分子核间距相一致. 研究结果表明, 强场层析成像方案同样适用于异核分子结构信息的提取, 为复杂分子体系的结构研究提供了新的可能性.

English Abstract

    全文HTML

    1.   引　言

    • 开展原子分子结构成像研究对于揭示物质微观本质、推动材料科学和生命科学前沿发展具有重要的意义. 飞秒激光技术的快速发展, 为在超快的时间尺度探测原子分子结构提供了新方法. 在飞秒激光场的驱动下, 原子分子内部的电子会通过隧穿的方式发生电离, 并在激光场的驱动下加速运动; 当激光电场反向时, 部分电离电子会返回原子实, 与原子实发生弹性碰撞后从激光场中获得更多的能量[1,2]. 相应地, 在光电子谱上形成一个典型的平台结构, 并在高能区域出现一个显著的截止, 这种非线性现象被称为高阶阈上电离[3,4]. 再散射过程中, 电子从隧穿到返回时间在亚周期量级, 其返回能量在几十到几百个电子伏特左右, 相应的德布罗意波长在亚埃的量级, 因此, 利用激光诱导的电子再散射可以在飞秒时间和亚埃的空间尺度同时实现原子分子结构成像. 目前, 利用激光诱导电子衍射的方案, 研究者们已经成功实现了分子结构以及超快动力学过程的探测[5–11]. 最近, 研究者们发展了椭圆激光诱导电子衍射技术, 提取了氮分子离子与电子散射的弹性微分截面, 并基于此获取了分子离子的结构信息[12].

      在之前的工作中, 我们基于激光诱导的电子再散射过程, 提出了一种新的分子结构成像方案, 即强场层析成像方案[13]. 在这个方案中, 采用准直分子与强激光场相互作用, 获得不同分子轴取向角下高阶阈上电离谱; 接着, 选定某个背向散射光电子的能量, 得到其电离强度随取向角的变化关系; 最后, 利用再散射电子与分子内多核发生作用形成的双中心干涉[14,15], 借助数值拟合的方法, 提取分子核间距的信息. 这种通过探测特定电子动量大小和方向、旋转分子轴取向的分子结构成像方法, 被称为强场层析成像方法. 与其他的激光诱导电子衍射方案相比, 强场层析成像方案固定电子散射动量的大小和方向, 因此分子内每个原子的散射截面大小不随取向角发生变化, 在拟合过程中可以简化为常数处理, 从而无需事先精确计算不同原子的散射截面, 简化了拟合过程. 利用强场层析成像方案, 以氮气分子为例开展研究[13], 实验上成功地提取了氮气分子核间距信息. 然而, 对于同核分子体系(如氮气分子), 由于其电子散射截面随分子轴取向角的变化可以进一步简化, 在实际拟合过程中并未考虑每个原子的散射截面的大小. 但是, 对于更为普遍的异核分子体系, 原子的散射截面的大小则会影响电子散射截面随分子轴取向角的变化, 因此在拟合过程中必须考虑每个原子的散射截面. 在这种情况下, 强场层析成像方案在异核分子体系中的适用性仍需进一步研究.

      本工作基于强场层析成像方案, 针对异核分子核间距信息的提取开展研究. 以异核双原子分子为例, 采用求解含时薛定谔方程方法, 计算不同分子取向下的高阶阈上电离谱, 提取能谱截止位置附近的光电子产率, 获得其随取向角的变化关系; 接着发展了一种异核分子散射截面随取向角变化的拟合方法, 通过拟合提取出分子核间距的大小, 发现得到的结果与真实的分子核间距大小相当. 此外, 我们还改变了分子的核间距, 采用相同方法提取分子核间距, 结果与设定值一致. 研究结果表明, 强场层析成像方案同样适用于异核分子结构信息的提取.

    2.   理论方法

    • 本工作采用求解二维含时薛定谔方程(TDSE)方法获得异核分子的光电子动量谱. 在单电子近似和长度规范下, 该方程表示为

      这里, 分子库仑势采用二维模型:

      式中$ r=\sqrt{{x}^{2}+{z}^{2}}$, ${\theta }_{{\mathrm{L}}} $是分子轴与激光偏振方向的夹角, $ R $代表分子核间距, $ {s}_{{\mathrm{c}}1} $和$ {s}_{{\mathrm{c}}2} $分别为两原子的软化参数. $ E\left(t\right) $为线偏振的激光电场:

      式中$ {E}_{0} $是激光电场峰值大小, $ f\left(t\right) $代表激光的包络, $ \omega $是激光的中心频率. 在本工作中, 采用虚时演化法获得分子的基态波函数, 然后使用分裂算符法求解波函数的演化[16]. 为了获得二维光电子动量谱, 采用 “两盒子” 算法[17,18], 将波函数在空间上拆分为内部$ (0 -{r}_{{\mathrm{c}}}) $和外部$ ({r}_{{\mathrm{c}}}-{r}_{{\mathrm{m}}{\mathrm{a}}{\mathrm{x}}}) $两部分:

      式中, 吸收函数$ {F}_{{\mathrm{a}}}=1/\left[1+{{\mathrm{e}}}^{-({r-{r}_{{\mathrm{c}}}})/{\eta }}\right] $, $ \eta $和$ {r}_{{\mathrm{c}}} $是其中两个参数. 当$ r > {r}_{{\mathrm{c}}} $后, 库仑场对电离电子的影响可以忽略. 因此, 内部波函数$ {\varPsi }_{{\mathrm{i}}{\mathrm{n}}} $在哈密顿量作用下严格演化, 而外部波函数$ {\varPsi }_{{\mathrm{o}}{\mathrm{u}}{\mathrm{t}}} $只在激光场作用下演化. 在实际计算过程中, 时间每向前演化一步, 根据(3)式获得外部波函数$ {\varPsi }_{{\mathrm{o}}{\mathrm{u}}{\mathrm{t}}}\left(t\right) $, 然后将$ {\varPsi }_{{\mathrm{o}}{\mathrm{u}}{\mathrm{t}}}\left(t\right) $转换至动量空间:

      接着, $ {\varPsi }_{{\mathrm{o}}{\mathrm{u}}{\mathrm{t}}} $从时间t开始解析地演化:

      式中$ \stackrel{-}{C}\left(\boldsymbol{p}, t\right)={{\mathrm{e}}}^{-{\mathrm{i}}{\int }_{t}^{\infty }{\frac{1}{2}\left[\boldsymbol{p}+\boldsymbol{A}\left(t\right)\right]}^{2}{\mathrm{d}}\tau }C\left(\boldsymbol{p}, t\right) $, $ \boldsymbol{A}\left(t\right) $表示激光场矢势. 最后, 我们把不同时刻获得的系数相干叠加, 得到光电子的动量分布:

      其中, $ E={\boldsymbol{p}}^{2}/2 $ 代表光电子能量, $ \theta $代表发射角. 本工作使用的线偏振激光电场峰值$ {E}_{0}=0.0925\;{\mathrm{a}}. {\mathrm{u}}. $, $ f\left(t\right) $为${{\mathrm{s}}{\mathrm{i}}{\mathrm{n}}}^{2} $包络, 共有6个光学周期, 激光波长为800 nm. 异核双原子分子的软化势分别为$ {s}_{{\mathrm{c}}1}= 3 $和${s}_{{\mathrm{c}}2}=4.33 $. 当$ R=2.5\;{\mathrm{a}}. {\mathrm{u}}. $时, 对应的分子电离势$ {I}_{{\mathrm{p}}}=0.609\;{\mathrm{a}}. {\mathrm{u}}. $ (3)式中吸收函数的两个参数为$ \eta = 8 $和$ {r}_{{\mathrm{c}}} =120\;{\rm a.u.}$

    3.   结果与讨论

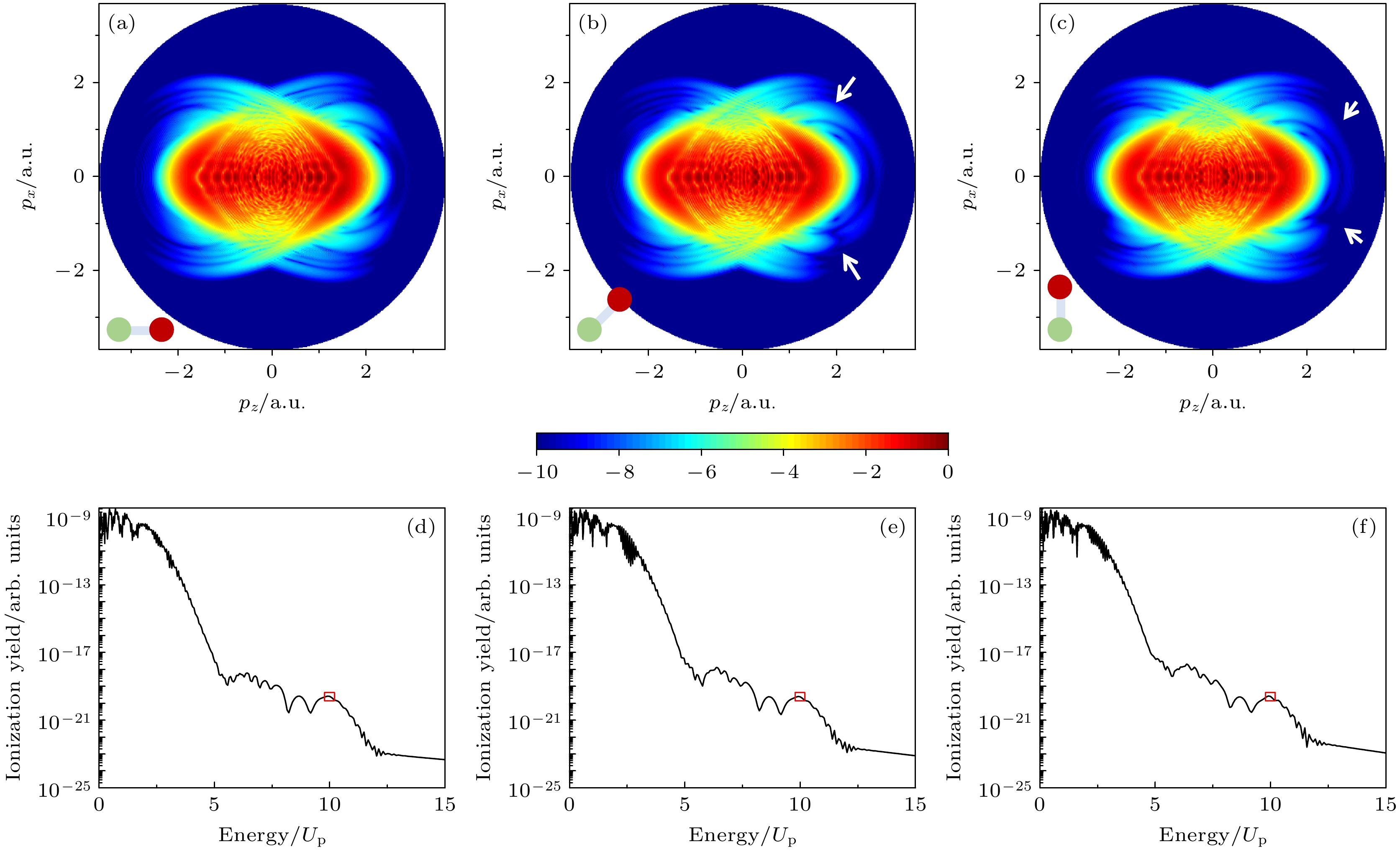
    • 图1(a)—(c)分别展示了取向角θL分别为0°, 60°和90°时异核双原子分子的二维光电子动量分布. 在低能区域, 可观察到清晰的干涉结构, 比如, 光电子全息图[19,20]. 在高能区域, 我们看到一系列环状的结构, 这些结构对应于高阶阈上电离. 另外, 当取向角为0°时, 光电子动量谱分布相对激光极化方向(z轴)呈现上下对称性. 这是因为在该取向角下, 分子轴沿着z轴方向, 分子体系相对z轴具有上下对称性. 然而, 随着取向角的增大, 分子体系相对于激光极化方向(z轴)变成上下非对称的. 通过仔细分析可以发现, 在高能区域表现出明显的上下非对称特征(见图中两箭头指向区域). 本工作利用再散射电子形成的高阶阈上电离进行分子结构成像. 由于高阶阈上电离强度通常远小于直接电离电子的强度, 为了更清楚展示高阶阈上电离谱的结构, 图1(d)—(f)分别展示了沿激光极化方向(z轴)的光电子能谱. 另外, 由于异核分子的左右不对称, 导致两边的高阶阈上电离谱强度出现不同, 为此我们选择右边的高阶阈上电离谱为例, 开展研究. 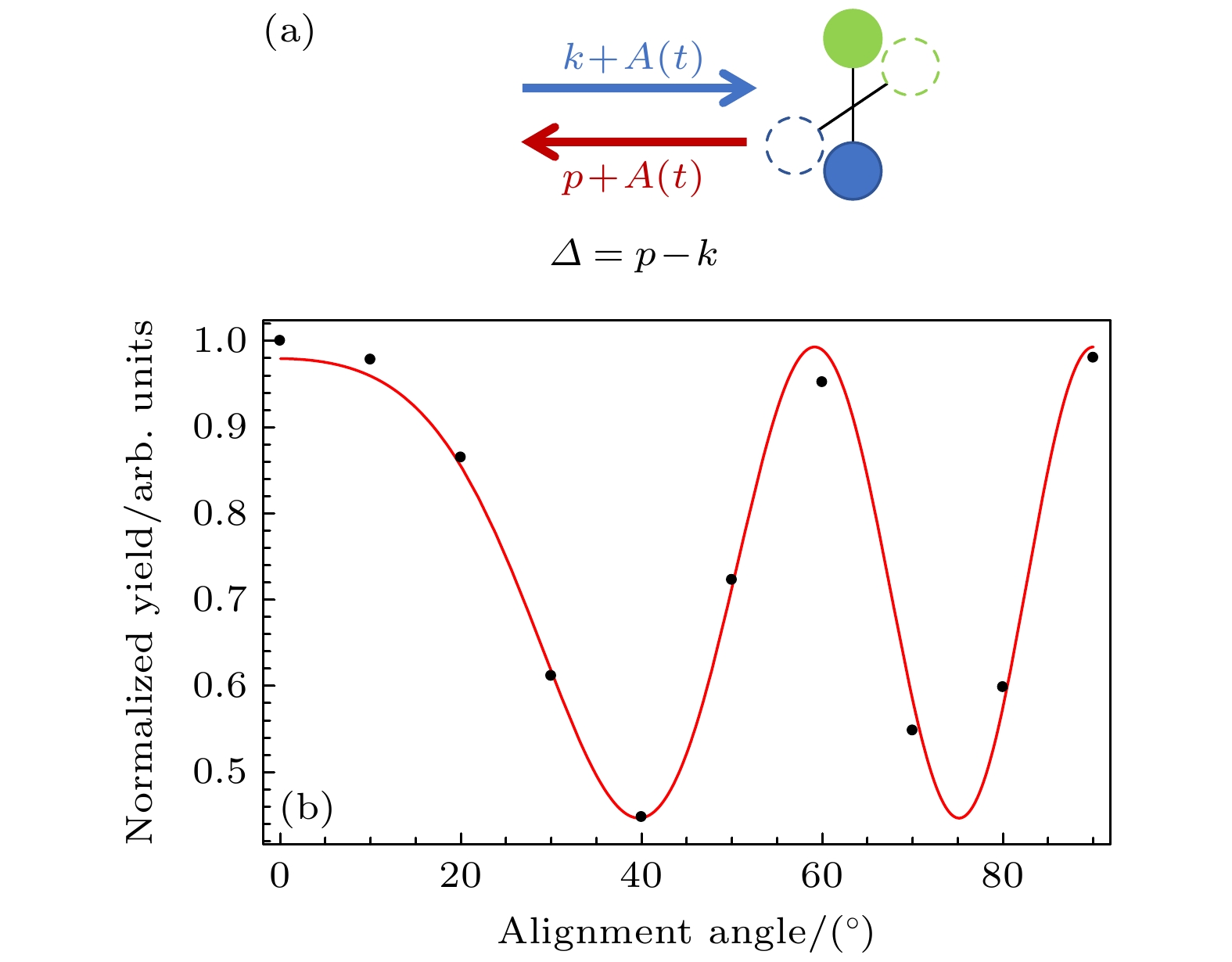此时, 我们可以看到清晰的高阶阈上电离形成的平台结构, 以及显著的截止, 其截止位置均在10Up附近$ ({U}_{{\mathrm{p}}}={{E}_{0}}^{2}/4{\omega }^{2}) $, 这和传统半经典模型预测的结果相一致[1,2].

      接下来通过分析光电子产率随取向角的变化提取分子结构信息. 根据三步模型[1,2], 高阶阈上电离包含长轨道和短轨道的贡献. 而在截止位置区域, 长短轨道合并为一条轨道. 为了简化分子结构提取过程, 选择高阶阈上电离谱截止位置区域的光电子进行分子结构成像. 由于本文关注的是电子再散射截面随分子轴取向角的变化, 但随着分子轴取向角的变化, 分子的隧穿电离率亦随之改变, 导致光电子的产生随取向角的变化不仅受到了再散射截面的影响, 同时还叠加了隧穿电离率变化所带来的效应. 为了消除隧穿电离率变化带来的影响, 采取归一化处理策略, 即在每个取向角下, 对光电子产率相对于总产率进行归一化处理, 而这总产率指的是所有光电子产量. 在实际计算过程中, 首先通过对二维光电子动量谱进行积分, 以求得光电子的总产量; 随后, 将各个取向角下的光电子产率除以这一总产量, 实现了归一化处理, 从而使光电子强度随取向角的变化主要反映电子再散射截面的差异. 图2(b)所示为归一化后截止位置区域的光电子产量随分子轴取向角的变化. 从图2(b)可以看到明显的振荡结构. 现有理论分析表明[6], 再散射电子与包含多核分子的散射截面可以近似为$ M\left(\theta_{\mathrm{L}}\right)\propto\left|A_{\mathrm{L}}\mathrm{e}^{-\mathrm{i}\varDelta\cdot\boldsymbol{R}/2}+A_{\mathrm{R}}\mathrm{e}^{\mathrm{i}\varDelta\cdot\boldsymbol{R}/2}\right|^2 $, 其中AL和AR分别代表两个原子的散射因子, $ \varDelta =\left[\boldsymbol{p}+\boldsymbol{A}\left(t\right)\right]- \left[\boldsymbol{k}+\boldsymbol{A}\left(t\right)\right]=\boldsymbol{p}-\boldsymbol{k} $代表电子散射的动量变化量, p是光电子的动量, k是电子再散射前的正则动量(见图2(a)). 本文利用背向散射电子进行成像, p和k均沿着激光极化方向, 那么再散射截面公式可进一步简化成:

      在强场层析成像方案中, 保持光电子动量大小和方向不变, 那么再散射电子的动量也不随分子取向发生变化, 因此每个原子的散射因子可分别近似看成一个常数, 从而简化拟合过程. 利用(7)式对图2(b)进行拟合, 就可以得到核间距的大小.

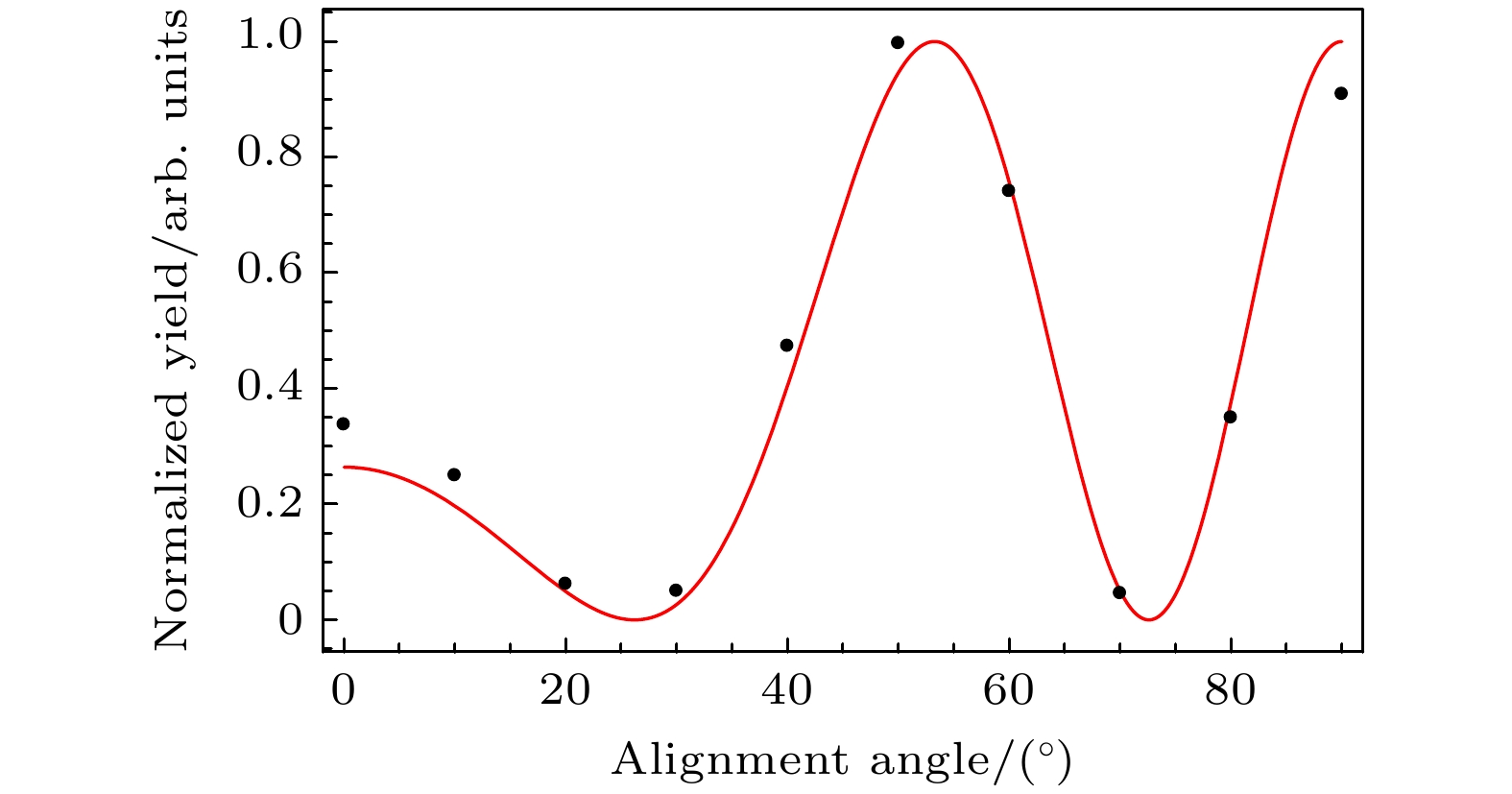
      但是, 在实际拟合过程中, 根据(7)式, 我们只能得到指数项中$ (p-k)R $的大小. 为了确定核间距R, 还必须知道电子再散射前的正则动量k的大小. 根据强场近似理论, 正则动量k的大小主要由激光场决定[3]. 为了获取k的大小, 在本工作中, 选择一个已知核间距的分子体系作为参考, 采用同样的激光参数与该体系相互作用, 以获取k的大小. 为了简单起见, 选择了同核双原子分子(软化参数$ {s}_{{\mathrm{c}}}=4.33 $), 并采用求解含时薛定谔方程方法, 得到高阶阈上电离谱, 提取截止位置区域的光电子产率, 获得其随分子轴取向角的变化, 如图3所示. 由于是同核分子, 那么其散射截面公式可以进一步简化为$ M\left({\theta }_{{\mathrm{L}}}\right)\propto {|{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}[(p-k){R}_{{\mathrm{f}}}{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}{\theta }_{{\mathrm{L}}}\left]\right|}^{2} $. 利用这个公式对数值计算结果进行最优拟合(见图3), 结合已知的核间距大小, 得到了该激光参数下对应的k 值大小.

      借助参考分子确定了k值大小后, 利用(7)式对图2(b)的数值计算结果进行拟合. 在给定核间距的初始猜测范围后, 我们就可以实现快速拟合. 从图2(b)可以看到, 拟合曲线与数值结果定性相一致, 表明(7)式能够很好地描述实验数据. 通过拟合提取出异核分子的核间距大小约为2.42 a.u., 此结果与设定值R0 = 2.5 a.u.相当. 这表明基于强场层析成像方案的拟合方法在提取异核分子核间距方面具有较高的准确性. 因此, 本工作成功利用强场层析成像技术提取了异核分子的核间距, 验证了该方法的有效性. 值得一提的是, 利用该方法也可以获得原子的散射因子相对大小. 通过数值拟合, 发现散射因子比值AR/AL大约为0.2. 未来, 将模拟三维的分子体系, 然后与真实的原子的散射截面作比较, 进一步验证我们的成像方案. 此外, 为了判断所选择的截止能量区域大小是否对成像结果有影响, 我们也改变了所选择的截止能量区域大小, 然后采用同样的成像方案进行拟合, 得到的核间距大小与之前结果几乎相同.

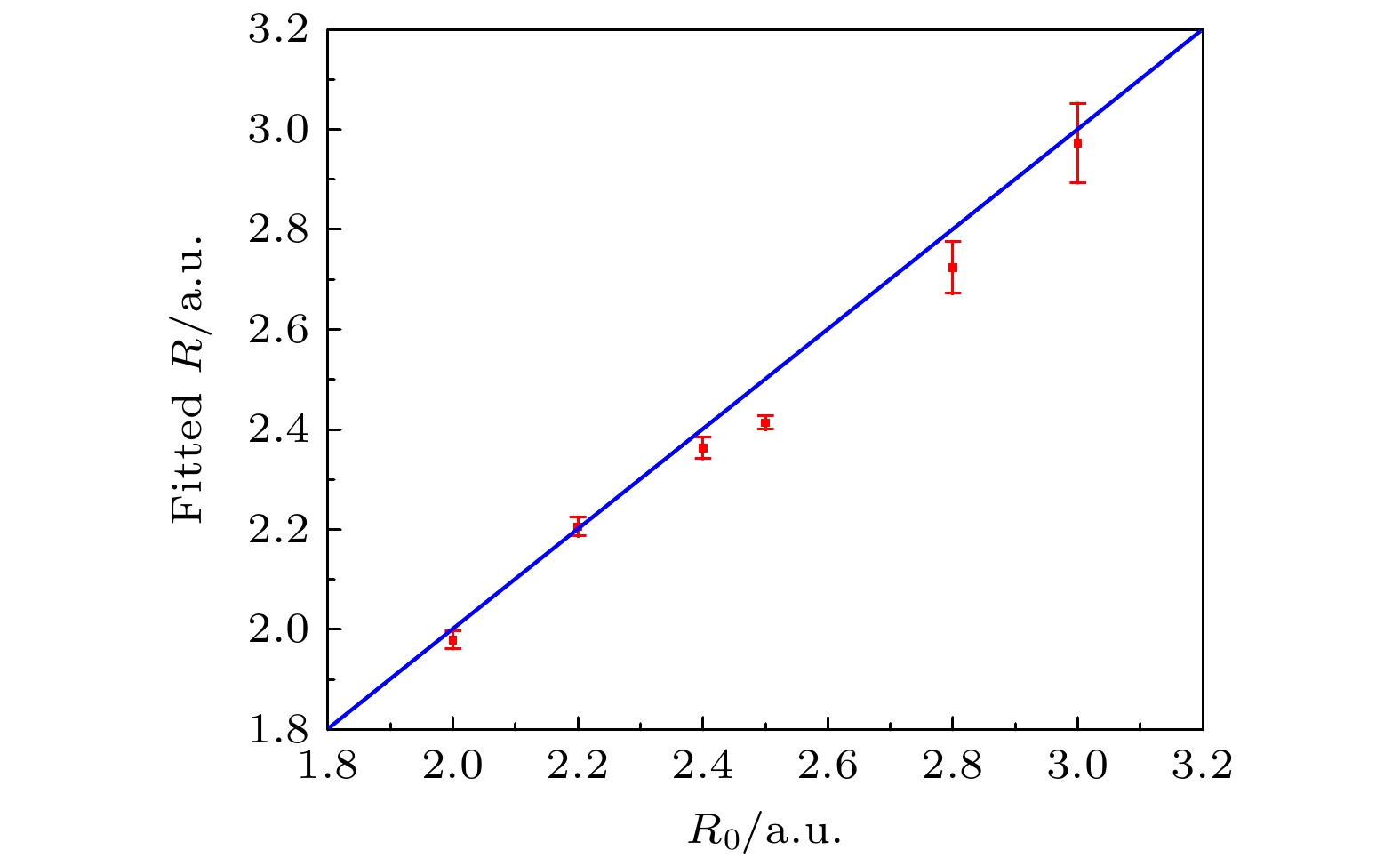
      最后, 为了进一步验证该方案的有效性, 将该方法应用于多种不同核间距R0的异核分子体系中. 利用图3参考分子的结果, 对每种异核分子的核间距进行拟合, 结果如图4所示. 图4所示为拟合结果与设定值之间的对比, 横坐标代表设定的核间距R0, 纵坐标代表拟合得到的核间距R. 结果表明, 在不同核间距的情况下, 拟合值与设定值基本一致, 验证了该方案的可靠性和普适性. 然而, 需要注意的是, 从图4可以看出, 拟合结果与真实值之间仍存在一定的偏差. 这可能是由于我们对正则动量k的处理存在简化. 在(7)式中, 假设k值主要由激光场决定, 但在实际过程中, k值还可能受到其他因素(如库仑场)的影响, 从而导致拟合结果出现偏差.

    4.   结　论

    • 基于强场层析成像方案, 开展了异核双原子分子核间距信息提取的理论研究. 采用求解含时薛定谔方程的方法, 获得了高阶阈上电离谱截止位置区域的光电子产率随分子取向角的变化. 利用强场层析成像方案中原子散射截面不随取向角变化的特性, 发展了一种适用于异核分子的截面随取向角变化的拟合方法. 通过拟合, 成功提取了异核双原子分子的核间距大小, 发现其与理论设定的核间距相当, 验证了该方案在提取异核分子结构信息方面的有效性. 结果表明, 强场层析成像方案不仅适用于原子体系, 还可以推广应用于异核分子的结构信息提取.

      值得注意的是, 在本工作中假设分子是完美取向. 但是, 在真实的物理体系中分子并非完美取向. 计算发现, 考虑分子取向度后, 图2中截止位置区域的光电子产量随分子轴取向角的变化, 其对比度会减小. 为了利用我们的成像方案从中提取分子结构信息, (7)式也必须考虑分子取向度的影响. 目前初步模拟发现, 即使考虑分子的非完美取向, 本文方案同样可以准确提取分子核间距信息. 此外, 在我们的成像方案中, 分子体系还是简单的模型体系, 其中分子库仑势中各个原子电荷数相同, 仅调整两个核上的软核参数(见(2)式). 其原因是, 根据(7)式, 分子结构成像还依赖提前确定电子再散射前的正则动量k的大小. 在本工作中, 选择同核双原子分子作为参考, 获取正则动量k. 因此, 为了利用该k值, 构建异核分子的库仑势时, 各个原子仍保留相同的电荷数. 未来, 将针对具体的异核分子体系, 解决正则动量k获取的难题, 以期将我们的方案推广到更为实际的异核分子体系中.

    参考文献 (20)

目录

/

返回文章
返回