-
1956年, Brown和Twiss[1]利用光场的二阶关联特性并通过计算两路探测器所记录光强信息的二阶自相关函数获得了星体的角直径, 开启了基于光场高阶关联特性获取目标信息的新篇章. 1963年, Glauber[2]建立了光场的相干性理论, 阐述了光场一阶、二阶以及更高阶关联特性的差异, 为关联成像技术的诞生奠定了理论基础. 目前, 关联成像技术主要分为自相关和互相关两类探测系统, 前者以HBT(Hanbury Brown-Twiss)为代表性架构[1,3], 后者以鬼成像(ghost imaging, GI)为代表性架构[4–6]. 经过近年来的持续性深入研究, 关联成像技术已经在遥感探测[7,8]、三维成像[9,10]、显微成像[11,12]以及医学成像[13,14]等方向取得了较为显著的研究进展.
与GI技术直接获取目标的实空间像不同, HBT技术往往只能获取目标的傅里叶变换频谱信息, 需要通过相位恢复算法重建目标的实空间像, 对频谱信息的质量有较高的要求[15,16]. 然而, 该技术在运动目标成像[17,18]、散射介质成像[19]和X射线成像[20,21]具有更好的优势. 在实际过程中, 为了获取高质量的目标频谱信息, 关联成像技术往往需要大量的随机测量次数才能保证较高信噪比, 同时, 傅里叶变换频谱图像的频率带宽和成像分辨率通常也与探测器的像素规模相关[22]. 目前, 为了减少高质量目标频谱信息获取所需的测量次数, 许多相关的数据处理方法和重建算法也相应地被提出, 比如: 基于探测信号的空域分割法[23]、基于压缩感知和基于深度学习的频谱信息重建算法[24,25]. 然而, 上述方法虽然能够提升目标频谱信息的信噪比, 但是图像重建所需的时间通常比较长且不能提升系统的成像分辨率. 近年来, 基于实空间像探测的傅里叶叠层成像技术证明了提升系统成像分辨率的可行性, 其核心是基于傅里叶变换的频移特性以及不同频谱图像信息之间存在部分重叠区域的特点, 通过频谱叠层和频率扩展可以获取待测目标更高空间分辨率的图像信息[26,27]. 对于基于HBT架构的目标频谱信息获取方法, 面阵探测器上采样点的移动将会导致目标频谱信息的移动, 这一特性与傅里叶叠层成像技术类似. 因此, 本文借鉴于傅里叶叠层成像的思想, 将频谱叠层方法引入基于HBT架构的目标频谱信息获取过程, 提出了一种基于多点并行关联重建和频谱叠层的处理方法, 试图在较低测量次数下获取高质量目标频谱信息并实现超分辨成像. 本文对该方法进行了相关的理论分析, 详细介绍了其图像重建过程, 并搭建了相应的实验系统对该方法的有效性进行了实验验证.
-
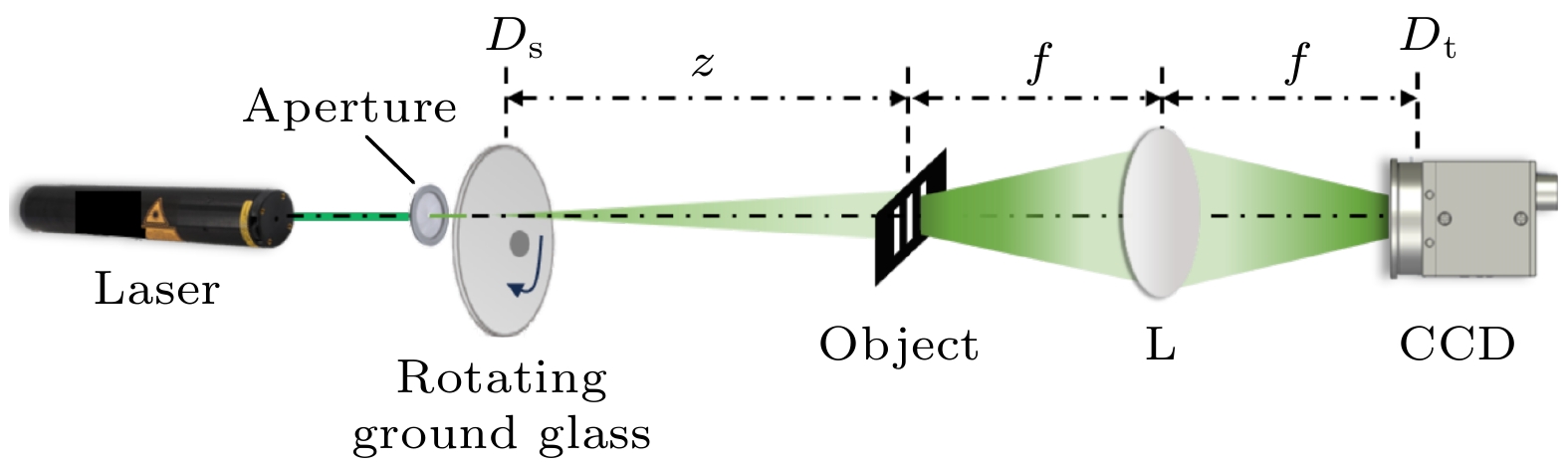
图1所示为基于自相关和频谱叠层的超分辨成像装置结构图, 激光穿过直径为D的光阑照射于旋转毛玻璃(rotating ground glass)上形成赝热光源, 经过自由传播一段距离z后到达待测物体, 物体的透射信息经过一个f-f光学系统后由面阵探测器(charge-coupled device, CCD)进行探测与记录.
根据光场的高阶相干性和关联成像理论[2–5], 二阶关联函数
$ \Delta {G^{(2, 2)}}({x_{\text{t}}}, x_{\text{t}}') $ 可以表示为其中,
$ {G^{(1, 1)}}({x_1}, {x_2}) $ 表示毛玻璃平面处光场的一阶关联函数;${h_{\text{t}}}({x_1}, {x_{\text{t}}})$ 表示毛玻璃平面到CCD平面的脉冲响应函数;$h_{\text{t}}^{{*}}({x_1}, {x_{\text{t}}})$ 表示该脉冲响应函数的复共轭. 假设激光发出的光束经旋转毛玻璃调制后产生的赝热光源是均匀且完全非相干的, 可得其中,
${I_0}$ 为常数,$ \delta (x) $ 为狄拉克$\delta $ 函数. 对于图1所示的光学系统, 若透镜L的有效通光孔径足够大且满足旁轴近似的条件下, 则毛玻璃平面${D_{\text{s}}}$ 到CCD平面${D_{\text{t}}}$ 之间的脉冲响应函数可以表示为其中,
$ t(x) $ 为待测物体的透过率分布, 将(2)式和(3)式代入(1)式中, 则二阶关联函数为若照射在毛玻璃平面上的激光光斑大小足 够大且CCD的横向尺寸大小为R, 则(4)式可以化简为
其中,
$\widetilde F\left[ {f(x)} \right]$ 表示对$f(x)$ 进行傅里叶变换,${\text{rect}}({x}/{R}) = \left\{ \begin{aligned}& 1,~~ \left| x \right| \leqslant {R}/{2}, \\& 0,~~ {\text{else}}, \end{aligned} \right.$ ,$ \odot $ 表示哈达玛积. 从(5)式可以看出, 对于图1所示的光学系统, 关联运算的结果为物体透过率函数模平方的傅里叶变换. 对于以往的数据处理方法, 通常选取$ x_{\text{t}}' =0$ 位置所对应的关联运算结果作为待测物体的信息提取结果, 即$ \Delta {G^{(2, 2)}}({x_{\text{t}}}, x_{\text{t}}' = 0) $ . 然而, 由于实际过程中CCD横向尺寸大小往往是有限的, 我们只能获得待测物体傅里叶谱的局部信息, 其对应的频谱带宽为$B = {{{{2\pi }}R}}/({{\lambda f}})$ , 从而限制了系统的成像分辨率. 值得注意的是, 对于(5)式, 当$ x_{\text{t}}' $ 取不同值时, 其对应的目标频谱图将以$ \Delta \omega = \dfrac{{2{\text{π}}}}{{\lambda f}}x_{\text{t}}' $ 进行平移, 随着$ x_{\text{t}}' $ 偏离光轴距离的增加将会获得待测物体更高的频率信息, 从而拓展目标信息的频谱带宽, 并且当$ x_{\text{t}}' $ 从CCD的中心位置平移到边缘时, 其频谱信息将增大1倍, 这将意味着在CCD横向尺寸相同的情况下能够实现2倍的超分辨成像(即理论空间分辨率为${{0.61\lambda f}}/{R}$ ). 此外, 由于平移后的频谱之间存在相同的部分, 将不同平移量的频谱图进行对齐叠加可以提升图像重建的信噪比, 从而有利于降低图像重建所需的采样数, 这一点在文献[23,28]中得到了类似的验证. -
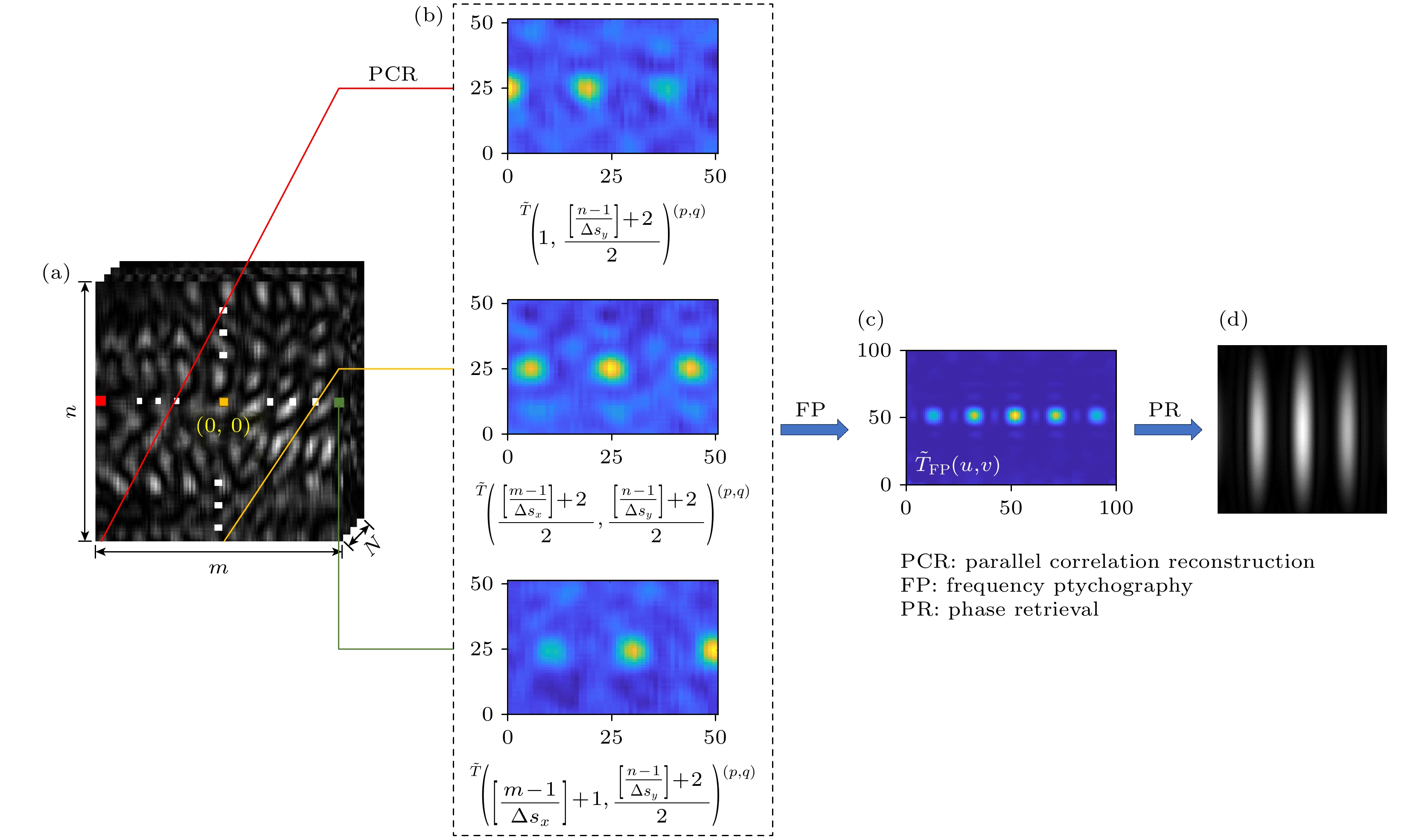
为了获取目标的超分辨图像信息, 图2给出了基于多点并行关联重建和频谱叠层处理实现超分辨重构的基本框架, 主要分为多点并行关联重建、频谱叠层处理和基于相位恢复算法的实空间图像重建3个步骤. 其中, 多点并行关联重建主要是基于(5)式的物理机制获取不同探测点
$ x_{\text{t}}' $ 处所对应的目标傅里叶频谱图像, 频谱叠层处理则是将多点并行关联重建获得的具有频移特性的频谱图进行对齐处理, 而基于相位恢复算法的实空间图像重建对应于从频谱叠层处理得到的拓展频谱图中利用相位恢复算法获取目标的空间图像. -
如图2(a)所示, 设CCD的像素规模为m×n (m, n取奇数), 基于图1所示的光学系统, CCD采集并记录了N张待测物体的散斑图信息. 其对应的第k张散斑图记为
$ {I^k}(p, q), k = 1, 2, \cdots , N $ , 其中, p和q分别代表CCD所记录散斑图的横向和纵向像素位置. 以CCD中心像素点为零点建立x-y直角坐标系, 从零点出发分别以$\Delta {s_x}$ 和$\Delta {s_y}$ 为步 长遍历整个CCD面, 则CCD面上对应的取点 位置为:此时i和j的取值范围为:
$i = 1, 2, \cdots , [ {( {m - 1} )} {/ } {\Delta {s_x}} ] + 1{\text{; }}j = 1, 2, \cdots , [ {{{( {n - 1} )} {/ } {\Delta {s_y}}}} ] + 1$ ,$\left[ \cdot \right]$ 表示取整操作. 在实际测量过程中, 考虑到光源辐照的非均匀性, 该因素往往对频谱叠层处理的结果影响较大, 采取以下的二阶关联运算公式进行图像重建, 即:将所有i和j的取值代入(6)式, 可以获得
$\{ [ ( {m - 1} ) / {\Delta {s_x}} ] +1 \} \times \{ {[ {{{( {n - 1} )} {/ } {\Delta {s_y}}}} ] + 1} \}$ 张关联重构结果, 即为多点并行关联重建结果. 图2(b)所示为CCD上的3个像素点位置$ (p, q) $ 分别取$ \Big( - \dfrac{{[ {( {m - 1} )/\Delta {s_x}} ]}}{2}\Delta {s_x}, 0\Big), (0, 0), {\text{ }}\Big(\dfrac{{[ {( {m - 1} )/\Delta {s_x}} ]}}{2}\Delta {s_x}, 0\Big)$ 时所对应的关联重构结果, 即为$ {\tilde T_{ \left(1, \frac{{[ {( {n - 1} )/\Delta {s_y}} ] + 2}}{2}\right)}}, {\text{ }}{\tilde T_{\left(\frac{{[ {( {m - 1} )/\Delta {s_x}} ] + 2}}{2}, \frac{{[ {( {n - 1} )/\Delta {s_y}} ] + 2}}{2}\right)}} $ 和$ {\tilde T_{ \left([ {( {m - 1} )/\Delta {s_x}} ] + 1, \frac{{[ {( {n - 1} )/\Delta {s_y}} ] + 2}}{2}\right)}} $ . -
正如图2(b)所示, 随着CCD上所取的
$ {I^k}(p, q) $ 位置不同, 其重建的频谱图将发生平移, 可以将所获得的$(\left[ {{{\left( {m - 1} \right)} {/ } {\Delta {s_x}}}} \right] + 1) \times (\left[ {{{\left( {n - 1} \right)} {/ } {\Delta {s_y}}}} \right] + 1)$ 张频谱图进行叠层处理, 从而获得一张具有更高带宽的频谱图. 频谱叠层处理的具体可分为两步: 第1步, 针对基于(6)式所重建的每一张m×n像素的关联重建结果$ {\tilde T_{(i, j)}}\left( {p, q} \right) $ , 以$ {\tilde T_{\left(\frac{{[{{{( {m - 1} )} {/ } {\Delta {s_x}}}} ] + 2}}{2}, \frac{{[ {{{( {n - 1} )} {/ } {\Delta {s_y}}}} ] + 2}}{2}\right)}} (p, q) $ 作为基准图像, 在基准图像中, 目标频谱的零频位于该图像中心, 将$ (\left[ {{{\left( {m - 1} \right)} {/ } {\Delta {s_x}}}} \right] + 1) \times ([ ( n - 1 ) {/ } {\Delta {s_y}} ] + 1) $ 张频谱图按照计算出的平移量$ \Delta \omega = \dfrac{{2{\text{π}}}}{{\lambda f}}x_{\text{t}}' $ 与基准图像进行对齐, 使不同频谱图中的同一频率位置重合, 然后分别赋值于一个$ (2 m - 1) \times (2 n - 1) $ 的新矩阵中, 其对应的图像记为$ \tilde T_{{\text{FP}}}^{(i, j)}\left( {u, v} \right) $ ,$ u, v $ 为对齐后新矩阵的坐标索引; 第2步, 将上述$ (\left[\left(m-1\right)/\Delta s_x\right]+1)\times([(n-1)/\Delta s_y] +1) $ 张图像对齐叠加后的频谱图$ \tilde T_{{\text{FP}}}^{(i, j)}\left( {u, v} \right) $ 按照以下方式进行处理, 即:其中,
${\text{ceil}}\left( \cdot \right)$ 表示向上取整操作,$ \gamma \left( {u, v} \right) $ 为不同像素位置的重叠次数.(7)式所示的叠层操作实际上可以看作是在中心频谱图
$ \tilde{T}_{\left(\frac{\left[\left(m-1\right)/\Delta s_x\right]+2}{2},\frac{\left[\left(n-1\right)/\Delta s_y\right]+2}{2}\right)}(p,q) $ 上进行多次平均和频谱扩展, 有利于提升频谱信噪比和成像分辨率. 同时, 可以看出:$ {\tilde T_{{\text{FP}}}} $ 的最大带宽为$(2 m - 1) \times (2 n - 1)$ , 与$ \tilde{T}_{\left(\frac{\left[\left(m-1\right)/\Delta s_x\right]+2}{2},\frac{\left[\left(n-1\right)/\Delta s_y\right]+2}{2}\right)}(p,q) $ 相比, 其频谱拓展了1倍, 这将意味着可以实现2倍的超分辨成像.此外, 类似于傅里叶叠层成像[26,27], 相邻两张关联重构结果的重叠程度可以用重叠率来表示, 即:
$ \eta = \dfrac{{(m - \Delta {s_x}) \times (n - \Delta {s_y})}}{{mn}} \times 100{\text{%}} $ , 表示了重叠区域面积占CCD面积的百分比. 一般来说, 较高的重叠率可以提高频谱叠层结果的信噪比, 有利于相位恢复算法的实空间图像重建. -
对于所获得频谱图, 可以利用相位恢复算法获取其对应的实空间图像信息. 对于上文所述的并行关联重建结果和频谱叠层结果, 本文将采用差分映射(difference map, DM)相位恢复算法[15,29]重构实空间图像, 其重建模型可以表示为
其中,
${g_n}$ 是第$n$ 次迭代时的实空间预测图像,$ {P_{\text{F}}} $ 和$ {P_{\text{O}}} $ 分别代表频域投影操作和空域投影操作. -
为了验证基于自相关和频谱叠层的超分辨成像方法的有效性, 搭建如图1所示的光路系统进行实验验证. 所设置的参数如下: 激光器的输出波长λ = 532 nm, 光阑的通光孔径D = 3 mm, 赝热光源面与待测物体之间的距离z = 400 mm, 透镜焦距f = 200 mm, 透镜的有效通光孔径L = 50.8 mm, CCD的像素大小为6.9 μm × 6.9 μm. 实验所用的待测物体为三缝, 缝宽为a = 200 μm, 中心距d = 800 μm, 缝高h = 1600 μm, 其对应的傅里叶频谱见图3所示. 对于所采用的DM相位恢复算法, 根据自相关关联函数的特性, 由于关联函数不包含物体的相位信息, 因此在重建时利用物体相位分布, 设定为某一个常数且成像区间受到物体尺寸大小限制等相关先验信息, 这样有利于待测物体实空间像的精确重构.
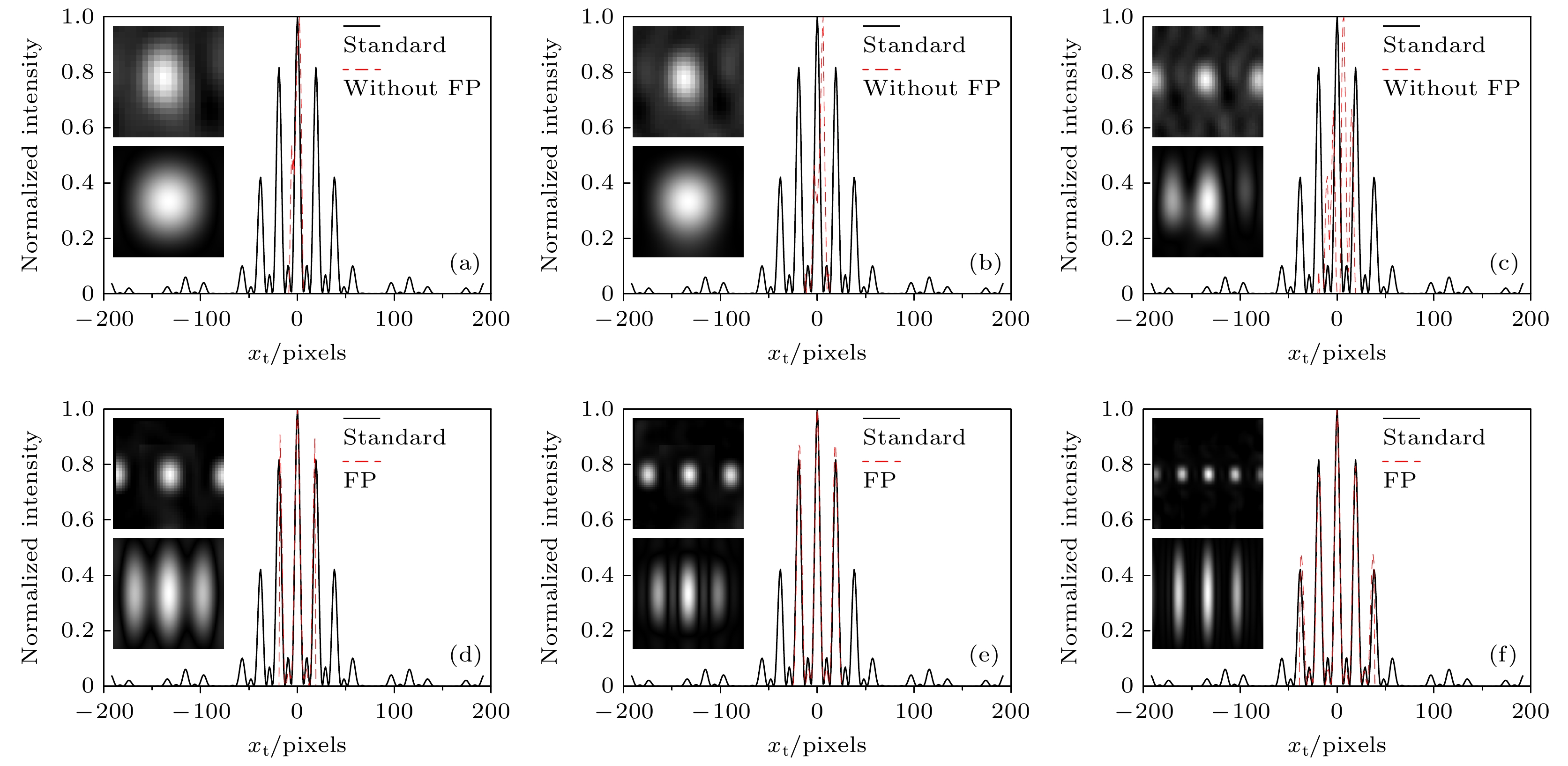
当测量次数N = 500时, 图4给出了基于自相关和频谱叠层的超分辨成像实验验证结果. 在不采用频谱叠层处理的情况下, 图4(a)—(c)展示了CCD像素规模大小分别为19×19, 25×25, 39×39像素下的成像结果(即
$ \Delta {G^{(2, 2)}}({x_{\text{t}}}, x_{\text{t}}' = 0) $ ). 其中图4(a)左上方依次对应于关联重构获取的目标频谱图和基于DM相位恢复算法重建的实空间图像, 其对应的关联重构频谱图与物体傅里叶变换频谱的横截面见图中的红色虚线和黑色实线. 可以看出, 随着探测器像素规模的增大, 通过关联重构得到的目标频谱带宽增大, 其对应的空间分辨率也将得到提升. 然而, 在测量次数较少时, 其重建的频谱图和恢复的实空间图像均不佳(图4(c)). 当采用多点并行关联重建和频谱叠层处理时, 相邻两个像素点的距离为5个像素, 对应于相邻两张频谱图的重叠率分别为$\eta {\text{ = 54}}{\text{%}} , {\text{64{\text{%}} , 76{\text{%}} }}$ , 此时与图4(a)—(c)所对应的重建结果见图4(d)—(f). 可以清晰地看出, 采用多点并行关联重建和频谱叠层处理后, 所重构的目标频谱图的信噪比不但得到大幅提升(图4(c), (d)), 而且其频谱带宽拓展到了原来频谱图的2倍, 因此在使用相同的CCD像素规模条件下实现了2倍的超分辨成像, 该实验结果与上述的理论分析结果相符合. 另外, 为保证目标频谱信息测量的准确性, 要求CCD必须能不失真地记录目标频谱信息. 对于图3所示的三缝物体, 根据(5)式和光栅方程, 三缝物体的次极大条纹宽度为$ {{\lambda f}}/({{{3}d}}) $ . 为了能够准确地记录该级次的频谱信息(如图4曲线部分所示), 结合奈奎斯特采样定理, 则要求CCD的横向像素不大于$ \Delta x = {{\lambda f}}/({{6 d}}) = $ 22.2 μm (对应为3个像素左右). 因此, 在实际工程中, 对于图1所示的系统, 在CCD像素规模相同的情况下, 可以通过选择合适的CCD像元大小或者透镜焦距f获得最佳的成像分辨率.为了测试所提方法在较低的测量次数下仍然能够得到高质量的成像结果, 图5所示为CCD像素规模大小为25×25、测量次数N = 50, 100, 200, 500下所重建的频谱图和实空间图像. 此时多点并行关联重建时所选择的两个测量点的间距仍然为5个像素, 所对应的相邻两张频谱图的重叠率为
$ \eta = 64{\text{%}} $ . 为了定量评价图像重建质量的好坏, 使用均方误差函数(MSE)计算重建结果与参考图像之间的差异, 即其中,
$O({x_i}, {y_j})$ 表示参考图像,${O_{{\text{rec}}}}({x_i}, {y_j})$ 表示相位恢复重建图像,${N_{{\text{pix}}}}$ 为图像的总像素数. 实验验证时, 参考图像选用图5最右侧一列测量次数为9000次时所对应的重建结果. 可以看出, 当测量次数N < 200时, 频谱图低频区域对比度较高, 但在频谱图的高频边缘区域有一些较为明显的噪声, 从而导致基于相位恢复算法重建的实空间图像有一定的失真. 这是因为在做多点并行关联重建和叠层处理时, 最外围的高频边缘区域参与系综平均的次数越少且高频信号自身也较弱, 因此其重建的频谱图信噪比较低. 此外, 从MSE值也可看出, 当测量次数N ≥ 200时, 所重建的实空间图像质量与参考结果基本相当, 从而验证了该方法在较低测量次数下仍然可以获取高质量的超分辨图像信息. 此外, 值得说明的是, 为了保证目标频谱和图像重构的质量, 通常要求辐照于待测目标区域内的光强分布经过N次测量叠加后是均匀的, 从而改善光源的非均匀性和散斑噪声对成像质量的影响. -
针对现有HBT系统获取目标频谱图像信息存在测量次数多、成像分辨率受限于探测器像素规模的问题, 结合HBT的关联特性和频谱叠层方法, 本文提出了一种基于多点并行关联重建和频谱叠层处理提升HBT系统信噪比和空间分辨率的方法. 理论和实验证明, 随着探测器像素规模的增大, 关联重构得到的目标频谱带宽增大, 其对应的空间分辨率也将得到提升; 同时为了保证较好的成像结果, 频谱叠层处理过程中相邻两张频谱图的重叠率要求保证在50%以上. 总体来说, 与无频谱叠层处理的成像结果相比, 所提方法不但可以减少获取高质量目标频谱图像信息所需的测量次数, 而且在相同探测器像素规模的条件下可以实现频谱信息的扩展, 得到2倍的超分辨率成像, 该方法对于动目标成像和显微成像具有重要的借鉴意义.
基于自相关与频谱叠层的超分辨成像
Super-resolution imaging based on auto-correlation and frequency ptychography
-
摘要: 基于HBT(Hanbury Brown-Twiss)的二阶自相关技术在非相干源照明和近场探测的条件下可以获得目标的傅里叶频谱信息, 然而获取高质量的频谱图像所需的测量次数较多, 且成像分辨率受到探测器的像素规模的限制. 为了解决上述问题, 本文结合多点并行关联重建算法和叠层成像的思想, 提出了一种基于自相关和频谱叠层的超分辨成像方法. 通过多点并行关联重建算法获取目标的不同频率信息, 在此基础上, 利用傅里叶变换的移频特性和叠层成像的思想实现频谱信息的扩展, 进而采用相位恢复算法重建目标的实空间图像. 理论分析和实验结果表明, 该方法在相同探测器像素规模的条件下可以实现2倍的超分辨率成像, 同时可以降低高质量频谱图像重建所需的测量次数. 该方法对于超分辨显微成像和高分辨运动目标成像具有重要的借鉴意义.Abstract:
The second-order auto-correlation technology based on Hanbury Brown-Twiss (HBT) can obtain the Fourier spectrum information of a target even under the conditions of incoherent source illumination and near-field detection, which has better advantages in the fields of moving-target imaging, imaging in scattering medium, and X-ray imaging. However, a great number of measurements are required and the imaging resolution is also restricted by the pixel scale of the detector for high-quality Fourier spectrum image for HBT. At present, many relevant data processing methods and reconstruction algorithms can reduce the number of measurements required for the acquisition of high-quality spectral information, but the time of image reconstruction required by these methods is usually long and cannot improve the imaging resolution of the system. In recent years, Fourier ptychography based on real-space image detection has proven that higher-resolution imaging can be obtained through spectral ptychography and frequency extension. In this paper, by combining the idea of Fourier ptychography with HBT, a processing method based on multi-point parallel correlation reconstruction and spectral ptychography is proposed, which attempts to obtain high-quality spectral information of the target and achieve super-resolution imaging with few measurements. The proof-of-principle schematic of super-resolution imaging method based on autocorrelation and spectral ptychography is obtained. The corresponding super-resolution reconstruction framework is displayed, which mainly consists of three steps: multi-point parallel correlation reconstruction, spectral ptychography, and real-space image reconstruction based on phase-retrieval algorithm. Firstly, based on the physical mechanism, Fourier spectrum images of the target at different detection points are obtained through multi-point parallel correlation reconstruction. Secondly, according to the idea of spectrum ptychography, the frequency shifted spectrum obtained by multi-point parallel correlation reconstruction is aligned to form an extended spectrum. Finally, the target’s real-space image is reconstructed by phase-retrieval algorithm. The super-resolution imaging method based on auto-correlation and spectral ptychography is experimentally verified by using the setup. At the number of measurements N = 500, the experimental results are obtained on different pixel scales of the detector. The results indicate that the imaging resolution increases with the pixel scale of the detector increasing. However, when the number of measurements is small, both the Fourier spectrum and the real-space image obtained by single point detection are poor. When the multi-point parallel correlation reconstruction and spectral ptychography are adopted, the signal-to-noise ratio of the reconstructed Fourier spectrum can be significantly improved, and its spectral bandwidth can be expanded to twice that of the original spectrum at the same parameters. In addition, the experiments also show that for a 50×50 spectral image, even with 200 measurements (i.e. a sampling rate of 8%), high-quality super-resolution imaging can still be obtained. All in all, the proposed method provides important insights into super-resolution microscopy imaging and high-resolution imaging of moving target. -
Key words:
- super-resolution imaging /
- auto-correlation /
- frequency ptychography /
- phase-retrieval algorithm .
-

-
图 2 基于多点并行关联重建和频谱叠层处理实现超分辨重建的基本框架 (a) CCD记录的图片; (b)多点并行关联重建结果; (c)频域叠层结果; (d)基于相位恢复算法的实空间图像重建结果
Figure 2. The framework of super-resolution image reconstruction based on multiple-point parallel correlation reconstruction and frequency ptychography: (a) The recorded images recorded by CCD; (b) the results of multi-point parallel correlation algorithm; (c) the results of frequency ptychography; (d) the image in the spatial domain reconstructed by phase-retrieval algorithm.
图 4 基于自相关和频谱叠层的超分辨成像实验验证结果(N = 500) (a)—(c)CCD像素规模大小分别为19×19, 25×25, 39×39像素不采用频谱叠层处理下的成像结果; (d)—(f)采用多点并行关联重建和频谱叠层处理后对应的成像结果, 左上角依次为关联重构的频谱图和相位恢复算法重建的实空间图像, 黑色实线为待测物体傅里叶变换频谱横截面, 红色虚线为关联重构频谱图的横截面
Figure 4. Experimental demonstration results of super-resolution imaging via autocorrelation and frequency ptychography (N = 500): (a)–(c) The imaging results without frequency ptychography when the pixel sizes of the CCD are 19×19, 25×25, and 39×39 pixels, respectively; (d)–(f) the corresponding results with multiple-point parallel correlation reconstruction and frequency ptychography. The upper left corner shows the frequency spectrums obtained by correlation reconstruction and the images in spatial domain reconstructed by phase-retrieval algorithm. The black solid line represents the cross-section of the testing object’s Fourier-transform spectrum, and the red dashed line represents the cross-section of the frequency spectrums obtained by correlation reconstruction.
图 5 不同测量次数下基于自相关和频谱叠层的成像结果(CCD像素规模大小为25×25像素) (a)多点并行关联重建和频谱叠层处理后的目标频谱图; (b)基于相位恢复算法重建的实空间图像
Figure 5. Imaging results based on autocorrelation and frequency ptychography in different measurements (with 25×25 pixels for the CCD): (a) The target’s frequency spectrum with multiple-point parallel correlation reconstruction and frequency ptychography; (b) the images in the spatial domain reconstructed by phase-retrieval algorithm.
-
[1] Brown R H, Twiss R Q 1956 Nature 177 27 doi: 10.1038/177027a0 [2] Glauber R J 1963 Phys. Rev. 130 2529 doi: 10.1103/PhysRev.130.2529 [3] Zhang M H, Wei Q, Shen X, Liu Y F, Liu H L, Bai Y F, Han S S 2007 Phys. Lett. A 366 569 doi: 10.1016/j.physleta.2007.04.021 [4] Gatti A, Bache M, Magatti D, Brambilla E, Ferri F, Lugiato L A 2006 J. Mod. Opt. 53 739 doi: 10.1080/09500340500147240 [5] Shapiro J H, Boyd R W 2012 Quantum Inf. Process. 11 949 doi: 10.1007/s11128-011-0356-5 [6] Shih Y H 2024 Chin. Opt. Lett. 22 060011 doi: 10.3788/COL202422.060011 [7] Zhao C Q, Gong W L, Chen M L, Li E R, Wang H, Xu W D, Han S S 2012 Appl. Phys. Lett. 101 141123 doi: 10.1063/1.4757874 [8] Erkmen B I. 2012 J. Opt. Soc. Am. A 29 782 doi: 10.1364/JOSAA.29.000782 [9] Gong W L, Zhao C Q, Yu H, Chen M L, Xu W D, Han S S 2016 Sci. Rep. 6 26133 doi: 10.1038/srep26133 [10] Stellinga D, Phillips D B, Mekhail S P, Selyem A, Turtaev S, Čižmár T, Padgett M J 2021 Science 374 1395 doi: 10.1126/science.abl3771 [11] Sun Z, Tuitje F, Spielmann C 2019 Opt. Express 27 33652 doi: 10.1364/OE.27.033652 [12] Peng J Z, Yao M H, Huang Z B, Zhong J G 2021 APL Photonics 6 046102 doi: 10.1063/5.0042779 [13] Wu D X, Luo J W, Huang G Q, Feng Y H, Feng X H, Zhang R S, Shen Y C, Li Z H 2021 Nat. Commun. 12 4712 doi: 10.1038/s41467-021-24990-0 [14] Ota S, Horisaki R, Kawamura Y, et al. 2018 Science 360 1246 doi: 10.1126/science.aan0096 [15] Elser V 2003 J. Opt. Soc. Am. A 20 40 doi: 10.1364/JOSAA.20.000040 [16] Ying G R, Wei Q, Shen X, Han S S 2008 Opt. Commun. 281 5130 doi: 10.1016/j.optcom.2008.07.026 [17] Zhang C, Gong W L, Han S S 2013 Appl. Phys. Lett. 102 021111 doi: 10.1063/1.4788727 [18] Bo Z W, Gong W L, Han S S 2016 Chin. Opt. Lett. 14 070301 doi: 10.3788/COL201614.070301 [19] Katz O, Small E, Silberberg Y 2012 Nat. Photonics 6 549 doi: 10.1038/nphoton.2012.150 [20] Cheng J, Han S S 2004 Phys. Rev. Lett. 92 093903 doi: 10.1103/PhysRevLett.92.093903 [21] Yu H, Lu R H, Han S S, Xie H L, Du G H, Xiao T Q, Zhu D M 2016 Phys. Rev. Lett. 117 113901 doi: 10.1103/PhysRevLett.117.113901 [22] 林洁, 程静 2010 光学学报 30 2912 doi: 10.3788/AOS20103010.2912 Lin J, Cheng J 2010 Acta Opt. Sin. 30 2912 doi: 10.3788/AOS20103010.2912 [23] Lei Z, Wang C F, Zhang D W, Wang L X, Gong W L 2017 IEEE Photonics J. 9 1 [24] Wang H, Han S S 2012 Europhys. Lett. 98 24003 doi: 10.1209/0295-5075/98/24003 [25] Zhu R G, Yu H, Tan Z J, Lu R H, Han S S, Huang Z F, Wang J 2020 Opt. Express 28 17556 doi: 10.1364/OE.395000 [26] Zheng G A, Horstmeyer R, Yang C H 2013 Nat. Photonics 7 739 doi: 10.1038/nphoton.2013.187 [27] 孙佳嵩, 张玉珍, 陈钱, 左超 2016 光学学报 36 1011005 doi: 10.3788/AOS201636.1011005 Sun J S, Zhang Y Z, Chen Q, Zuo C 2016 Acta Opt. Sin. 36 1011005 doi: 10.3788/AOS201636.1011005 [28] Liu H L, Cheng J, Han S S 2007 J. Appl. Phys. 102 103102 doi: 10.1063/1.2812597 [29] Loh N T D, Eisebitt S, Flewett S, Elser V 2010 Phys. Rev. E 82 061128 doi: 10.1103/PhysRevE.82.061128 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: