-
外加电场控制液滴行为广泛存在于科学技术领域, 例如电喷涂、喷墨印刷以及微流体控制等[1-3]. 最早O’Konski和Thacher[4]对理想介质(电导率为零)液滴进行了理论分析, 通过最小化液滴的表面能与静电势能, 推导出预测液滴形变的理论公式, 该公式表明液滴总是呈现扁长型形变(与电场方向平行). 随后, Taylor[5]对漏电介质液滴(有限电导率)研究发现, 在电场作用下自由电荷会在液滴表面积聚, 从而产生切向应力导致液滴发生形变, 并给出了经典的漏电介质理论, 预测了漏电介质液滴的扁长型和扁平型(与电场方向垂直)两种形变模式. 由于理论分析受限于液滴的小形变, 近年来数值方法也被用于研究电液滴控制问题. 然而, 数值研究该问题的一大难点在于如何准确捕捉相界面的变化. 为了获取相界面变化的详细信息, 研究者发展了几类不同的模型或方法, 例如边界积分法[6]、流体体积法[7]、界面跟踪法[8]、水平集法[9]和相场法[10]. 在上述方法中, 相场法是通过扩散界面方程自动捕捉相界面的拓扑变化, 由于无需额外处理相界面, 相场方法在实际问题研究中得到了广泛应用[11]. Lin等[10]首先利用相场模型研究了理想介质液滴和漏电介质液滴的流动问题. 随后, 相场模型也被应用于研究电场作用下液滴的破裂、聚合以及气泡上升等现象 [12]. 上述工作所采用的相场模型均为四阶的Cahn-Hilliard (C-H)方程[13], 但C-H方程求解的数值色散较大, 因此Liu等[14-16]采用二阶Allen-Cahn (A-C)方程来捕捉相界面, 并发现A-C方程在预测液滴小形变时与理论解一致[5,17], 在大形变时与数值解和实验数据相符合[10,18], 这为研究电液滴控制提供了新的数值手段.
在实际应用中, 液滴通过添加表面活性剂的方式来实现形变、破裂和聚合等行为[19–20]. 表面活性剂依据其在体相中的溶解行为分为两类: 可溶性表面活性剂和不可溶表面活性剂, 其中可溶性表面活性剂在体相中溶解(浓度非零)并可形成胶束、分散体或单分子溶解状态, 而不溶性表面活性剂在体相中溶解度极低(浓度近乎零), 主要在界面形成单分子膜[21]. 含表面活性剂的液滴由于受到毛细力和马兰戈尼应力作用, 液滴的界面动态行为会发生显著改变[22]. 由于该过程涉及复杂多物理场耦合, 传统的数值方法存在计算过程复杂、计算效率低以及处理复杂边界困难等问题, 因此难以准确高效地模拟该问题. 介观格子Boltzmann (lattice Boltzmann, LB)方法凭借其算法的简单性、并行性以及边界处理能力在复杂多相流体输运问题研究中得到了成功应用[23]. 其中, 基于相场理论的LB模型由于无需显示地标记界面以及可以自然地处理界面复杂的拓扑变化, 十分适合用于研究含表面活性剂液滴复杂的动力学行为. 最早, van der Sman和van der Graaf [24]提出了一种含有可溶性表面活性剂的相场LB模型, 该模型利用三组LB分布函数求解两类C-H型方程和不可压Navier-Stokes (N-S)方程, 其中化学势由表面活性剂和相场的自由能泛函最小化导出. 通过选择合理的自由能泛函, 该模型能够表现出真实的Langmuir吸附等温线. 随后, Liu和Zhang[21]以及van der Sman和Meinders[25]将该模型[24]推广到体相区表面活性剂浓度不同的多相体系, 并通过采用更广义的自由能泛函, 使模型可以准确恢复Langmuir和Frumkin吸附等温线. 然而这些模型仍只适用于低密度比和低表面活性剂浓度的多相系统. 最近, Shi等[26]发展了一类改进的相场LB模型, 该模型通过忽略化学势中的扰动项以及选择合理的表面张力形式, 能够准确捕捉含表面活性剂液滴流动问题中液滴的界面行为[26]. 在此基础上, Zong等[27]提出了一种改进的相场LB模型, 该模型通过利用修正的化学势和合理的表面张力形式, 可以解决含表面活性剂的多相体系中大密度问题.
近年来, 通过施加电场和表面活性剂来实现对液滴的操控引起广泛关注. 在理论和实验研究方面, Ha和Yang[28]利用Taylor理论并结合实验探讨了不溶性表面活性剂对匀强电场作用下液滴形变和稳定性的影响, 然而理论和实验结果只在液滴发生小形变时表现一致. 随后, Nganguia等[29]利用球体模型研究了匀强电场作用下含不溶性表面活性剂液滴的大形变问题, 发现液滴的平衡形状取决于介电系数比、电导系数比、表面活性剂的覆盖率(surfactant coverage)和弹性系数. 最近, Painuly等[30]通过实验分析了电毛细数等参数对电场中含表面活性剂液滴聚合的影响, 实验结果表明: 电场中含表面活性剂液滴存在聚合、部分聚合以及不聚合三种状态, 并得到了液滴从聚合状态转化为部分聚合状态的临界电毛细数. 在数值研究方面, Teigen和Munkejord[31]使用水平集方法研究了不溶性 表面活性剂对电场中液滴形变的影响, 结果表明: 表面活性剂对液滴形变的影响很大程度上取决于两种流体之间的介电系数比和电导系数比. 随后, Sorgentone等[32]基于边界积分法, 发展了一种研究匀强电场作用下含不溶性表面活性剂液滴动 力学行为的高精度数值方法, 研究发现, 当形变因子小于0.2时, 不溶性表面活性剂的浓度分布与Nganguia等[29]的解析解以及Ha和Yang[33]的实验数据一致. 近期, Li等[34]通过分子动力学模拟, 研究了表面活性剂对电场中液滴形变和破裂的影响, 研究表明增加表面活性剂会促进液滴的形变和破裂. 需要指出的是, 目前关于电场中含表面活性剂液滴的动力学行为研究, 大部分针对的是不溶性表面活性剂[28−29,31-33], 对可溶性表面活性剂液滴在匀强电场作用下的动力学行为尚缺乏系统研究.
本文基于Zong等[27]和Liu等[14]的模型, 利用相场LB方法系统研究匀强电场作用下含可溶性表面活性剂液滴的动力学行为. 首先通过研究静态液滴表面活性剂浓度分布和漏电介质液滴在电场中的形变两个基准问题验证方法的可靠性, 并在此基础上, 深入研究电毛细数
$ Ca_{\mathrm{E}} $ 和体相区表面活性剂浓度$ \psi_{\mathrm{b}} $ 对单液滴形变、破裂及双液滴聚合的影响. -
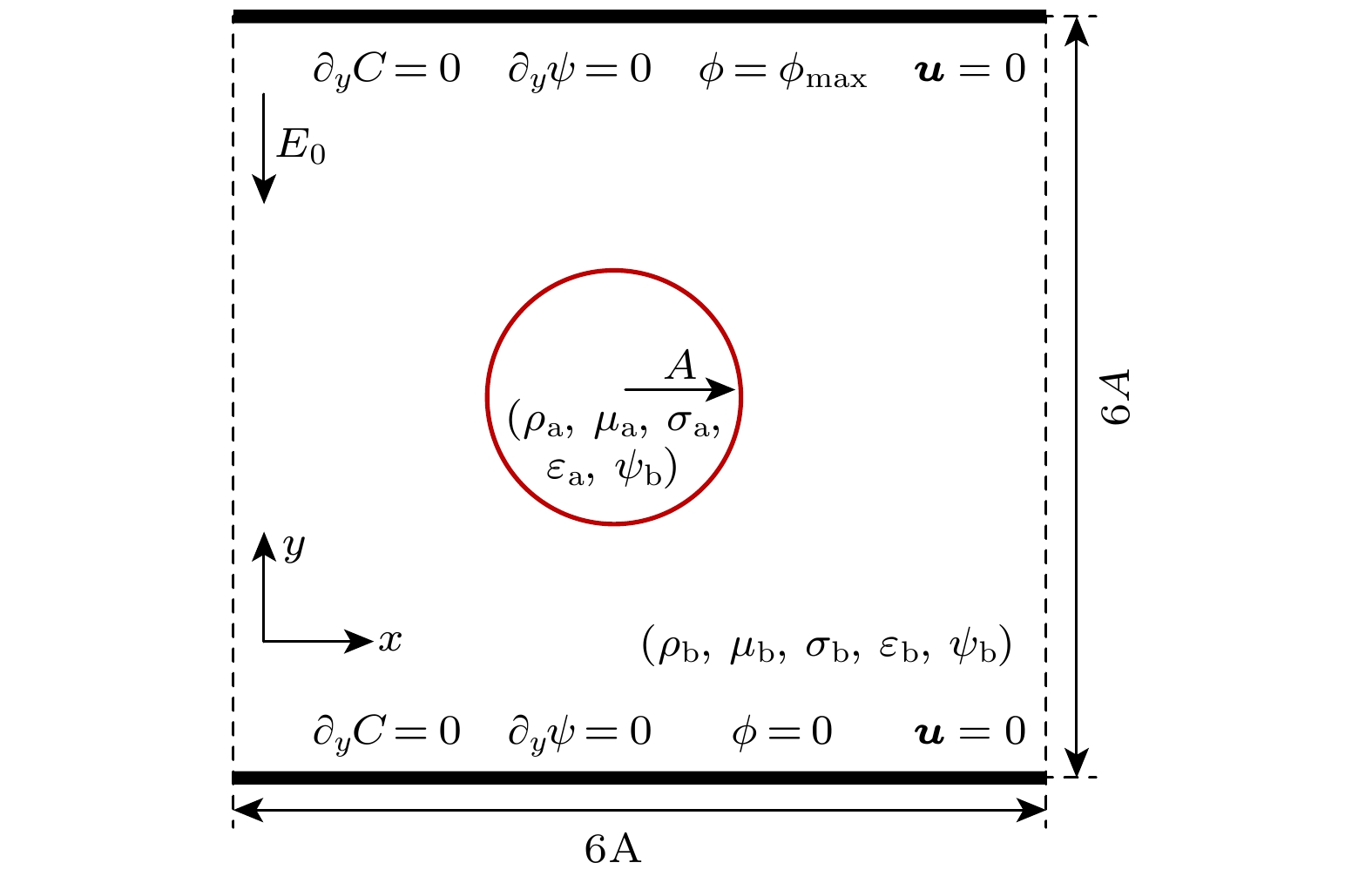
本文主要考虑含可溶性表面活性剂液滴在电场作用下的动力学行为, 物理工况如图1所示, 区域上下边界设置电极板, 中心悬浮着半径为A的漏电介质液滴, 液滴周围则被另一种电介质流体填充, 可溶性表面活性剂存在于整个区域. 该问题涉及相场、表面活性剂浓度场、电场和流场的相互耦合, 具体的控制方程如下.
首先, 相场采用A-C方程刻画相界面变化[35]:
其中C为相场序参数,
$ C = -1 $ 表示连续相流体,$ C = 1 $ 表示分散相液滴, u表示流体速度,$ M_{{\mathrm{c}}} $ 表示相场迁移率, W表示液滴界面厚度.其次, 浓度场采用如下形式的对流扩散方程描述浓度分布[27]:
其中ψ表示表面活性剂浓度,
$ M_{\psi} $ 表示表面活性剂浓度迁移率,$ \mu_{\psi} $ 表示表面活性剂的化学势, 其表达式为式中
$ k_{\mathrm{B}}T = 4 \beta Pi $ ,$ B = 4 \beta / E_x $ ,$ k_{\mathrm{B}} $ 是Boltzmann常数, T是温度,$ Pi $ 和$ E_x $ 是用来初始化表面活性剂浓度分布的两个无量纲参数[36], β是自由参数.然后对于电场, 本文研究对象是漏电介质液滴, 电场的弛豫时间远小于流场的弛豫时间, 因此可以采用Laplace方程刻画电势分布[8,14]:
其中σ表示电导系数, E表示电场强度, 利用电场强度和电势的关系(
$ {\boldsymbol{E}} = - \nabla \phi $ ), 可以将控制方程转化成以下形式:最后, 对于流场, 本文假设研究对象为不可压缩两相流, 其可以由不可压缩N-S方程来描述[8,10,27]:
其中ρ表示流体的密度, p表示压强, μ表示动力学黏性,
$ {{\boldsymbol{F}}_{\rm{E}}} $ 表示电场力.$ {{\boldsymbol{F}}_{\rm{S}}} $ 表示表面张力[27], 其形式如下:其中
$ \mu_{\mathrm{C}} $ 表示相场的化学势, 根据Yun等[37]的工作, 本文采用如下化学势:其中
$ \kappa = 3 \gamma_0 W / 8 $ ,$ \beta = 3 \gamma_0 / 4 W $ ,$ \alpha = \sqrt{9 \kappa / 32 \beta} $ , κ为自由参数, W表示界面厚度,$ \gamma_0 $ 表示初始表面张力系数. 表面张力系数γ与$ \gamma_0 $ 的关系由Langmuir状态方程给出[3]:其中
$ \beta_{\mathrm{s }}$ 是弹性系数, 它决定了γ相对于ψ的变化强度, 根据(10)式可知, 随着ψ的增加, γ逐渐减小, 但相关实验表明[38], 当γ减小到一定程度后, ψ的增大将不会引起γ的变化. 为了保证Langmuir方程的有效性, 本文研究的表面活性剂浓度都满足$ \gamma \left( \psi \right) \geqslant 0.5 \gamma_0 $ . 另外, 电场力的表达式为[14]其中ε为介电系数,
$ \rho_{\mathrm{e}} = \nabla \cdot \left( \varepsilon {\boldsymbol{E}} \right) $ 为单位体积电荷密度. (11)式右边第一项是极化应力, 作用于液滴界面的法线方向; 第二项是库仑力, 是由电荷和电场相互作用产生的沿电场方向的电应力; 第三项是电限制力, 由于本文考虑的是不可压流体, 该项可以省略, 故电场力的表达式可简化为对于上下边界, 相场和表面活性浓度场采用Neumann边界条件, 电场采用Dirichlet边界条件, 流场采用无滑移条件; 对于左右边界, 本文均使用周期边界条件.
-
对上述控制方程, 用以下LB模型进行求解[27]:
其中x表示粒子的空间位置;
$ {\boldsymbol{c}}_i $ 表示粒子的离散速度; t表示当前时刻,$ {\text{δ}} t $ 表示离散时间步长;$ f_i $ ,$ r_i $ ,$ h_i $ ,$ g_i $ 分别表示相场、表面活性剂浓度场、电场和流场的粒子分布函数;$ \tau_{\mathrm{f}} $ ,$ \tau_{\mathrm{r}} $ ,$ \tau_{\mathrm{h }}$ ,$ \tau_{\mathrm{g}} $ 为对应四个场的松弛时间, 表达式如下:其中
$ c_{\mathrm{s}} $ 是格子声速, 在本文采用的模型中,$ c_{\mathrm{s}} $ 与格子速度c的关系为$ c_{\mathrm{s}}^2 = c^2 / 3 $ .$ f_i^{{\mathrm{eq}}} $ ,$ r_i^{{\mathrm{eq}}} $ ,$ h_i^{{\mathrm{eq}}} $ ,$ g_i^{{\mathrm{eq}}} $ 分别表示四个场的平衡态分布函数, 表达式如下:这里
$ s_i (\boldsymbol{u}) = \omega_i \big[ {\boldsymbol c}_i \cdot {\boldsymbol u}/c_{\rm s}^2 + ( {\boldsymbol c}_i \cdot {\boldsymbol u} )^2 / 2 c_{\rm s}^4 - {\boldsymbol u} \cdot {\boldsymbol u}/2 c_{\rm s}^2 \big] $ .$ F_i $ ,$ R_i $ ,$ G_i $ 表示源项, 表达式如下:其中,
$ {\boldsymbol{F}} = {{\boldsymbol{F}}_{\rm{S}}} + {{\boldsymbol{F}}_{\rm{E}}} $ . 最后, 四个场的宏观量通过以下格式计算:需要注意的是, 上述LB模型中涉及密度ρ、动力学黏性μ、电导系数σ和介电系数ε的计算, 这里给出它们的计算方式:
其中χ可以表示
$ \rho, \mu, \sigma, \varepsilon $ 中任一物理量,$ \chi_{{\mathrm{a, b}}} $ 表示液滴内部或外部相应的物理量. 除此之外, 上述过程还涉及时间偏导数、梯度算子和拉普拉斯算子的计算, 本文采用如下的计算格式:由于本文研究的是二维问题, 故针对相场、浓度场和流场使用D2Q9格子模型, 电场使用D2Q5格子模型. 下面详细介绍这两个模型[39]. 首先, D2Q9格子模型中粒子有9个离散速度, 其形式如下:
其中
$ c = {\text{δ}} x / {\text{δ}} t $ ,$ {\text{δ}} x $ 代表离散时间步长, 为了方便起见, 本文设定$ {\text{δ}} x = {\text{δ}} t = 1 $ . 除此之外, 模型中的9个离散速度还对应9个权系数, 其值设置如下:类似地, D2Q5格子模型的离散速度和对应的权系数如下:
除此之外, 本文使用半反弹格式处理相场、表面活性剂浓度场和流场的上下边界, 反-反弹格式处理电场的上下边界, 左右边界使用周期格式[40].
-
在开展匀强电场下含表面活性剂液滴的动力学行为研究前, 本文首先通过两个基准算例对该模型进行数值验证, 包括静态液滴表面活性剂浓度分布和漏电介质液滴在电场中的形变.
-
本节主要通过模拟静态液滴表面活性剂浓度分布基准问题来验证模型(13a), (13b), (13c)的准确性. 数值模拟参数设置为
$ A = 47 $ ,$ W = 0.1 A $ ,$ Pi = 1.35 $ ,$ E_x = 0.5 $ ,$ \gamma_0 = 0.001 $ ,$ \beta_{\mathrm{s}} = 0.5 $ ,$ \rho_a = \rho_b = 1 $ ,$ \mu_a = \mu_b = 0.1 $ ,$ M_{\mathrm{C}} = 0.01 $ ,$ M_{\psi} = 0.01 $ , 液滴质心位置为$ (x_{\mathrm{c}}, y_{\mathrm{c}}) = (3 A, 3 A) $ . 相场序参数采用以下函数进行初始化:表面活性剂浓度的初始化函数为
其中
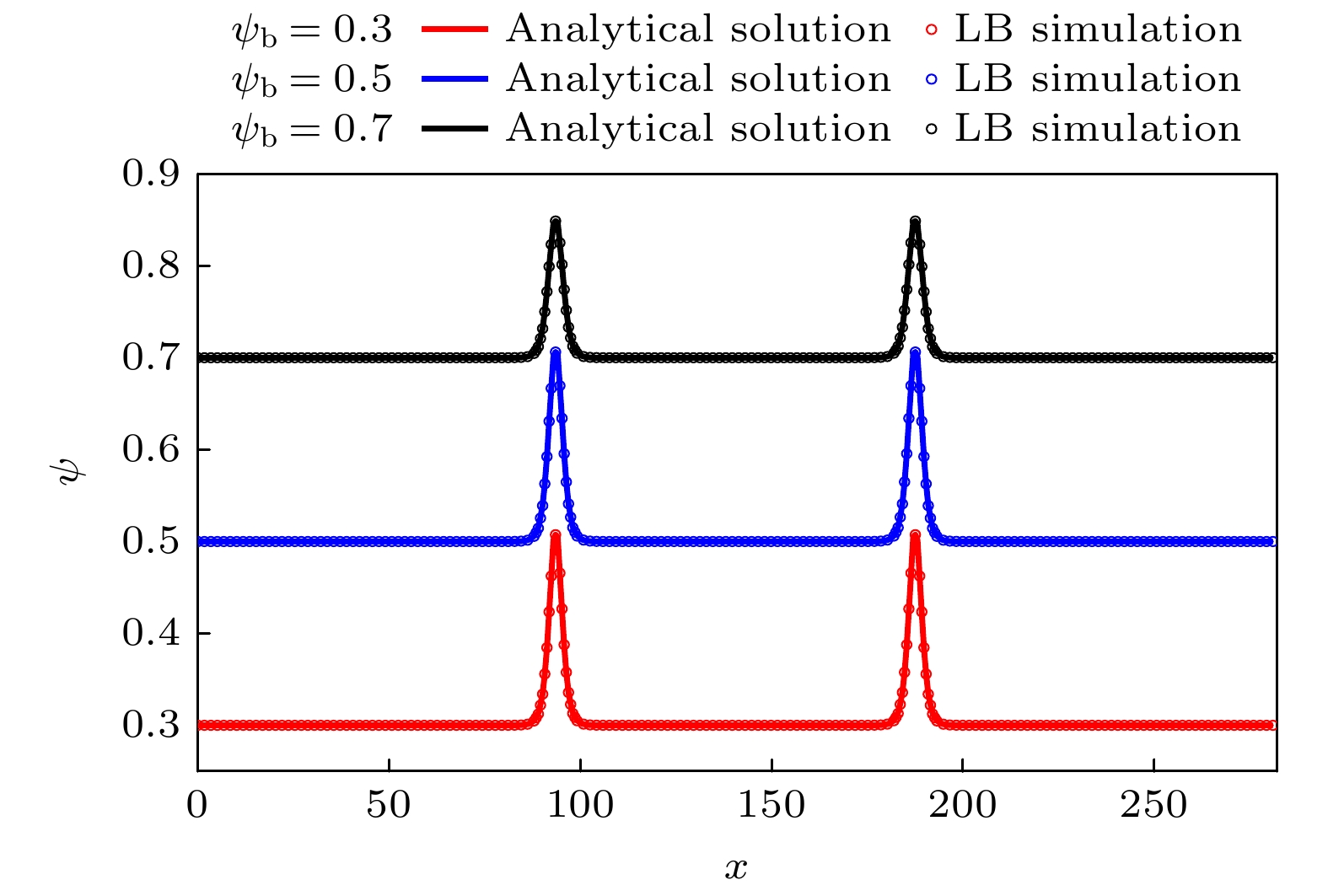
$ \psi_{\mathrm{b}} $ 表示体相区表面活性剂浓度,$ \psi_{\mathrm{c}} $ 的形式如下:图2展示了
$ \psi_{\mathrm{b }}= $ 0.3, 0.5, 0.7时表面活性剂浓度ψ的分布. 可以看出, 相场LB方法的数值结果(圆圈)与解析解((27)式, 实线)符合较好, 表明该模型能够准确刻画液滴的表面活性剂浓度分布. -
本节进一步通过模拟漏电介质液滴在电场中的形变问题来验证模型(13a), (13c), (13d)的准确性. 根据Taylor[5]提出的漏电介质理论, 液滴形变程度可以用形变因子
$ D = (L - H)/(L + H) $ 表征, 其中L代表平行于电场方向液滴两端的距离, H 代表垂直电场方向液滴两端的距离. 当液滴形变较小时, 形变因子D与电毛细数$ Ca_{\mathrm{E}}\;( = \varepsilon_{\mathrm{b}} E_0^2 A / \gamma_0) $ 、电导系数比$ R\;( = \sigma_{\mathrm{a}} / \sigma_{\mathrm{b}}) $ 、介电系数比$ S\;( = \varepsilon_{\mathrm{a}} / \varepsilon_{\mathrm{b}}) $ 和黏性系数比$ N\;( = \mu_{\mathrm{a }}/ \mu_{\mathrm{b}}) $ 的关系为$ f_{\mathrm{T}} = R^2 + 1 - 2 S + 3 \left( 3 N + 2 \right) \left( R - S \right) / 5 \left( N + 1 \right) $ . Feng[17]基于Taylor的理论提出了预测匀强电场下二维漏电介质液滴形变程度的一阶近似公式:其中
$ f_{\mathrm{F}} = R^2 + R + 1 - 3 S $ . 根据(29)式和(30)式可知, 当$ D < 0 $ 时, 液滴最终形变为扁平型;$ D > 0 $ 时液滴最终形变为扁长型. 此外, Taylor[5]和Feng[17]的理论还表明R与S的相对大小会影响流场涡的方向. 当$ R > S $ 时, 流线方向为从液滴赤道横截面指向两极; 当$ R < S $ 时, 流线方向为从液滴两极指向赤道横截面.图3展示了
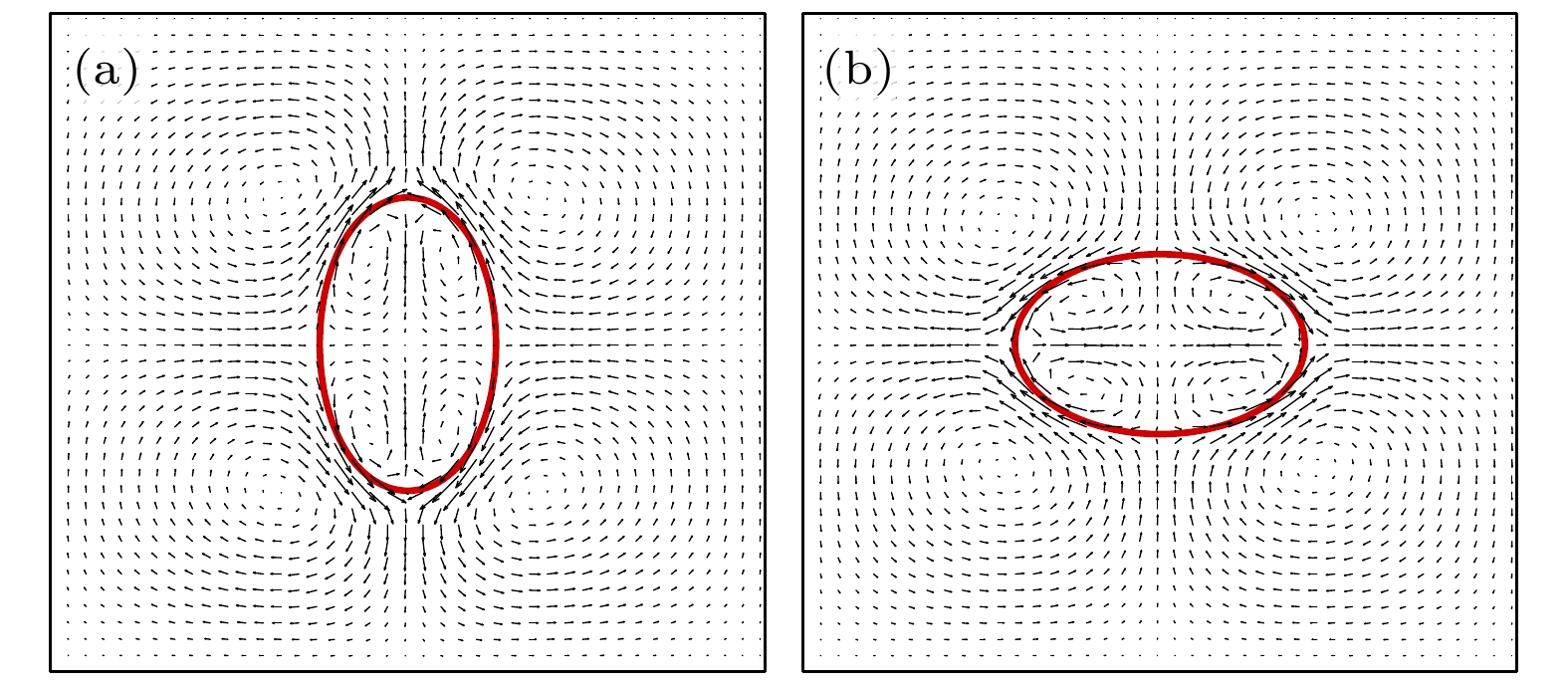
$ Ca_{\mathrm{E}} = 1 $ ,$ (S, R) = (3.5, 4.75) $ 以及$ (S, R) = (3.5, 1.75) $ 两种情形下的液滴形变模式, 即扁长型形变(见图3(a))和扁平型形变(见图3(b))(其中$ u_{{\mathrm{max}}} = \max \|{\boldsymbol{u}}\| $ ), 两种液滴周围流线的方向与上述理论一致. 更进一步, 比较了不同参数下本文结果D与理论解(29)式和(30)式以及已有数值结果[10,14,18]的差异. 从 表1可以看出, 当液滴形变较小时 ($ \left| D \right| < 0.02 $ ), 数值解和理论解几乎一致; 当液滴形变较大时($ \left| D \right| > 0.2 $ ), 理论解存在局限性, 本文的结果与已有数值结果符合更好. 这些结果也表明, 本文的模型可以准确模拟漏电介质液滴在电场中的形变过程. -
本节主要探究在匀强电场作用下可溶性表面活性剂对单液滴形变、破裂以及双液滴聚合的影响.
-
在下文的数值模拟中,
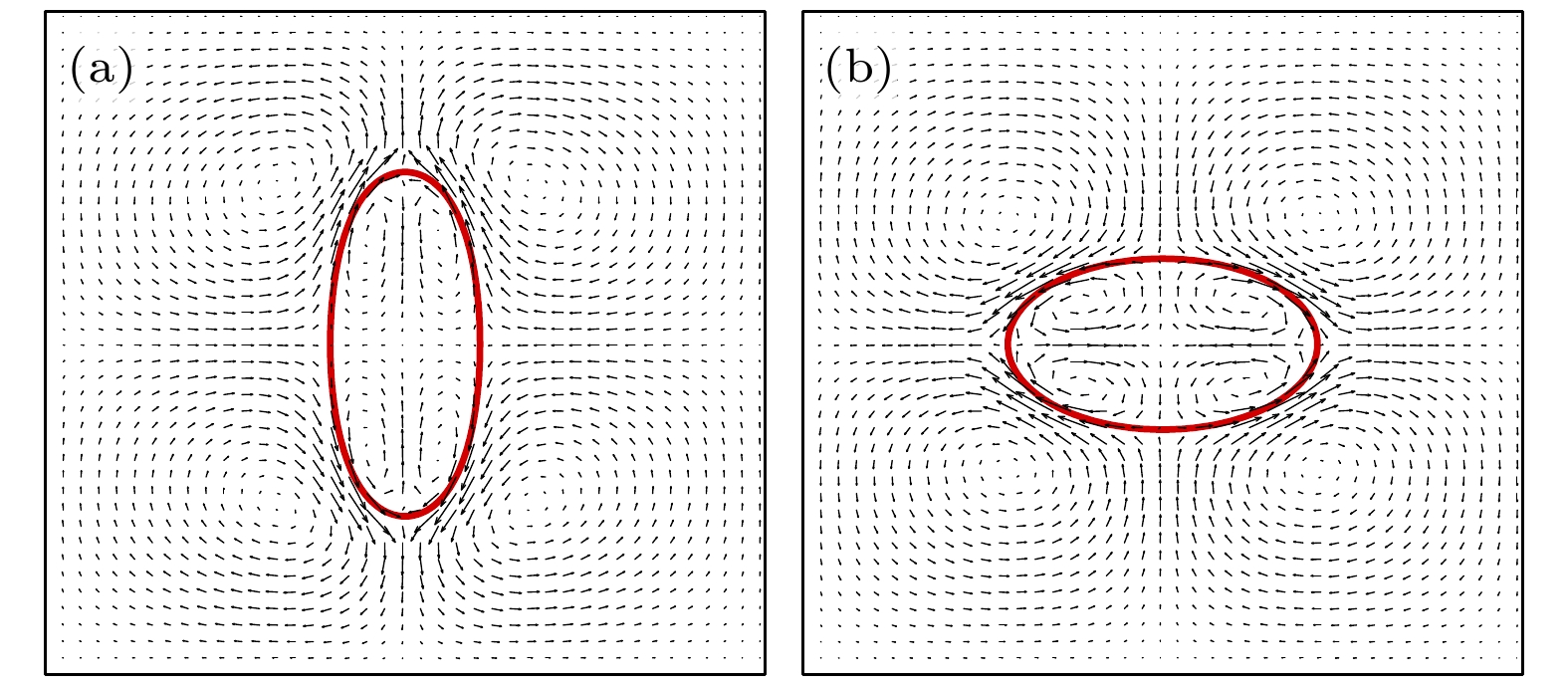
$ Ca_{\mathrm{E}} = 1 $ ,$ \psi_{\mathrm{b}} = 0.5 $ ,$ M_{\mathrm{C}} = 0.1 $ ,$ M_{\psi} = 0.1 $ ,$ \psi_{\mathrm{b}} = 0.1 $ ,$ E_0 = 0.1 $ , 其余参数则与4.1.1节中的参数保持一致. 如图4所示, 分别展示了$ (S, R) = (3.5, 4.75) $ 和$ (S, R) = (3.5,1.75) $ 时液滴的稳定形态以及周围的流线方向. 通过比较图3和图4可知, 表面活性剂只改变了液滴的形变程度, 并没有改变液滴周围的流线方向.此外, 探究了干净液滴与含表面活性剂液滴的形变因子D随电毛细数
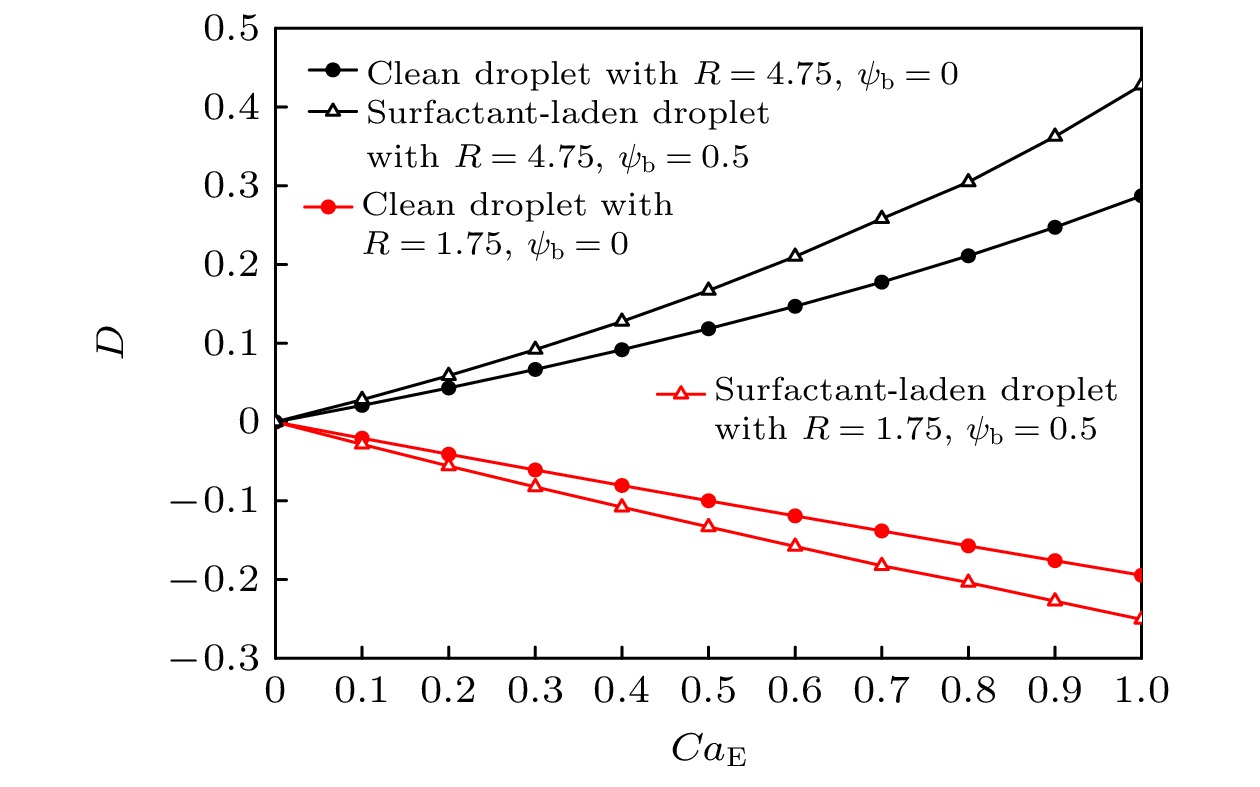
$ Ca_{\mathrm{E}} $ 的变化曲线(见图5), 图中红色曲线代表液滴形变为扁平型($ R = 1.75 $ ), 黑色曲线代表液滴形变为扁长型($ R = 4.75 $ ), 圆形代表干净液滴, 三角形代表含表面活性剂液滴. 从图中可以看出, 与干净液滴的形变相比, 表面活性剂对液滴的形变起促进作用, 并且随着$ Ca_{\mathrm{E}} $ 的增大, 液滴的形变程度逐渐增大. 事实上从(10)式可知, 表面活性剂浓度的增加会导致表面张力减小, 进而抑制液滴形变的作用力减小, 因此添加表面活性剂可以促进液滴形变.本文进一步研究了液滴形变因子D随体相区表面活性剂浓度
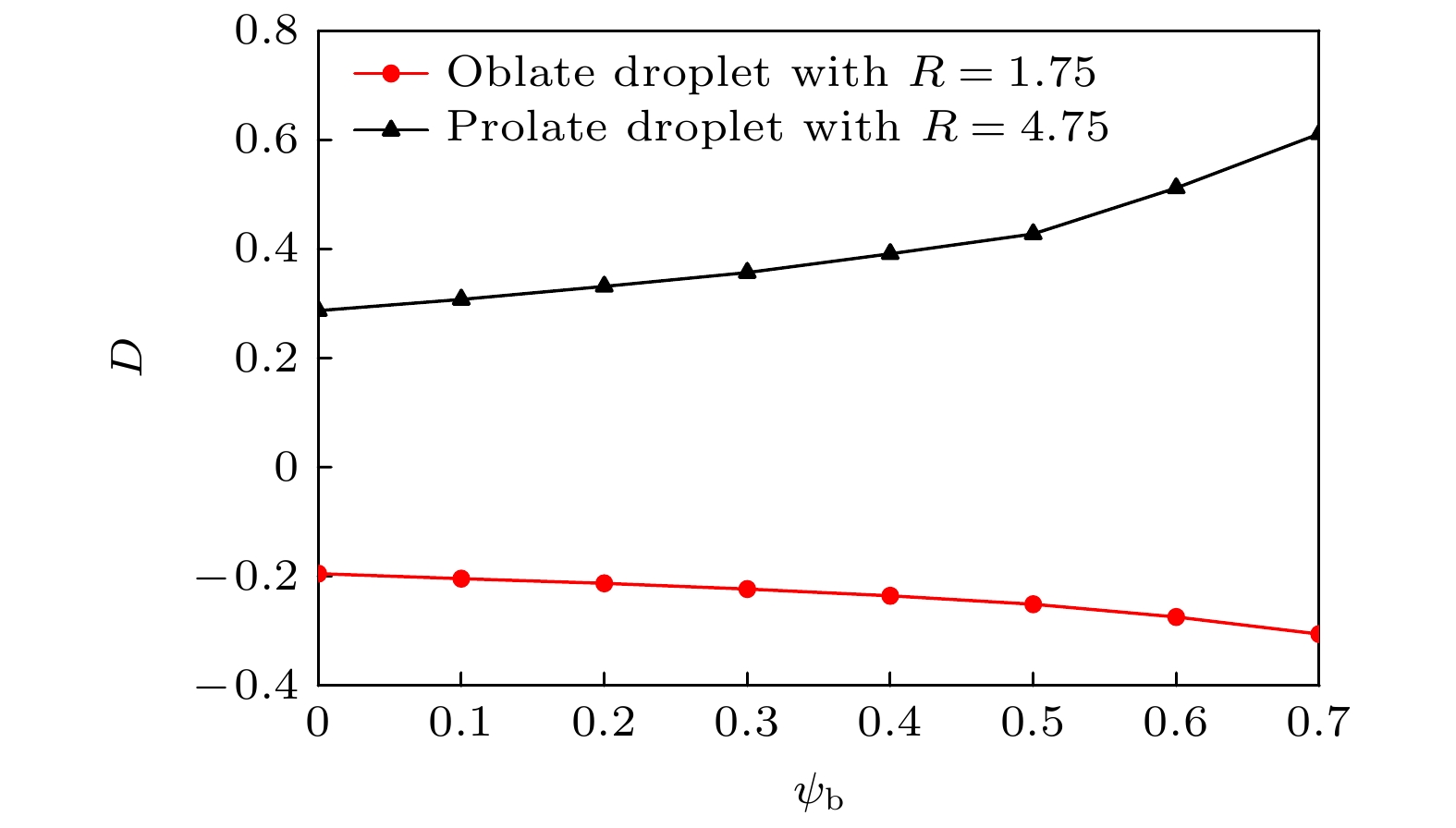
$ \psi_{\mathrm{b}} $ 的变化, 如图6所示, 红色曲线代表扁平型液滴($ R = 1.75 $ ), 黑色曲线代表扁长型液滴($ R = 4.75 $ ). 在设置的阈值内, 液滴无论是扁长型还是扁平型, 都可以得到表面活性剂的浓度越大, 液滴形变越强的结论.最后, 发现在
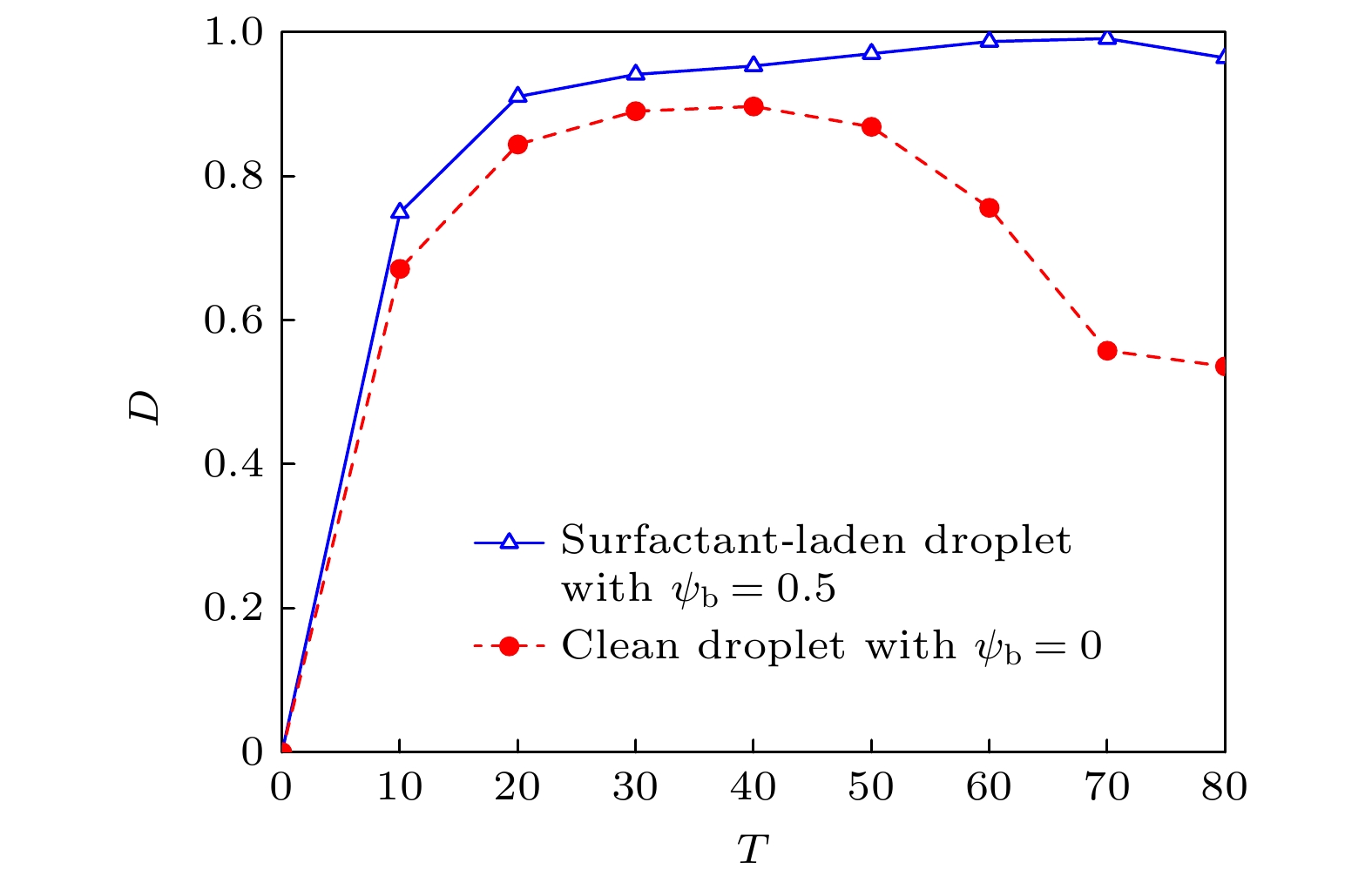
$ Ca_{{\mathrm{E}}} = 0.9,R = 7.5,S = 1.37, \gamma_0 = 0.01, L_x = 6 A, Ly = 36 A, T = 1000{\text{δ}} t $ 的情况下(见图7), 干净液滴会在电场力的作用下先拉长到极限长度($ D = 0.89686 $ ), 随后在表面张力的作用下回缩, 而含表面活性剂液滴则延长了极限长度($ D = 0.99107 $ )的到达时间, 同时减缓了回缩程度, 这是因为在液滴形变过程中表面活性剂降低了其表面张力. -
在4.2.1节研究液滴形变的基础上, 继续研究了液滴形变后破裂的现象. 这里设置
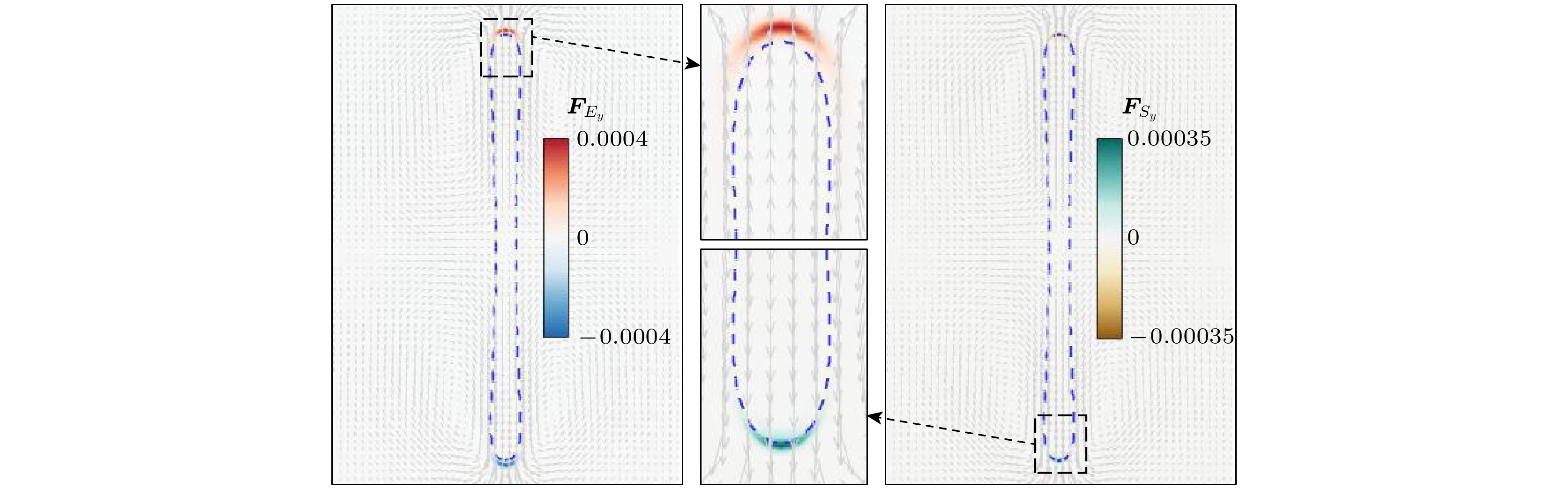
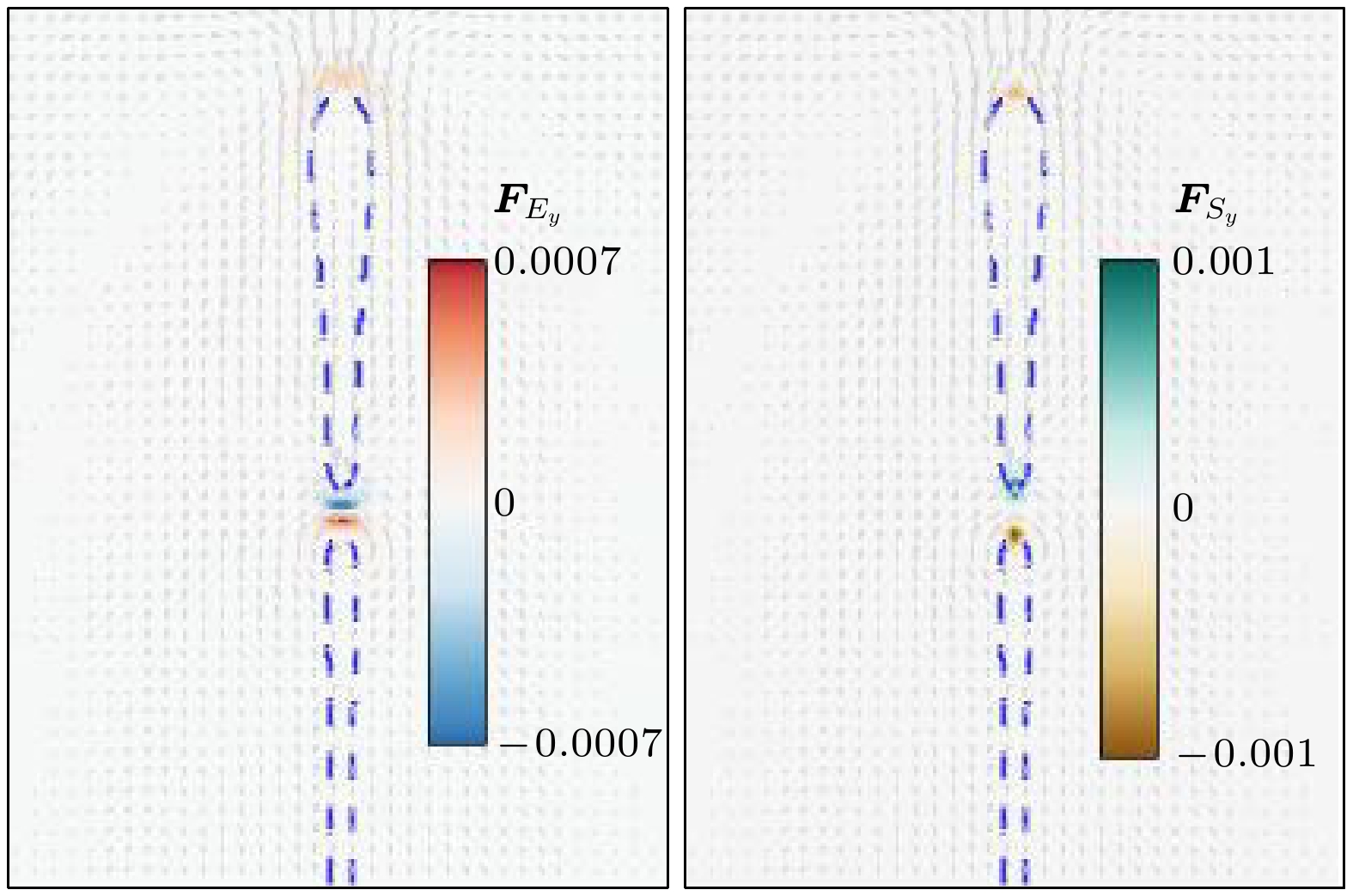
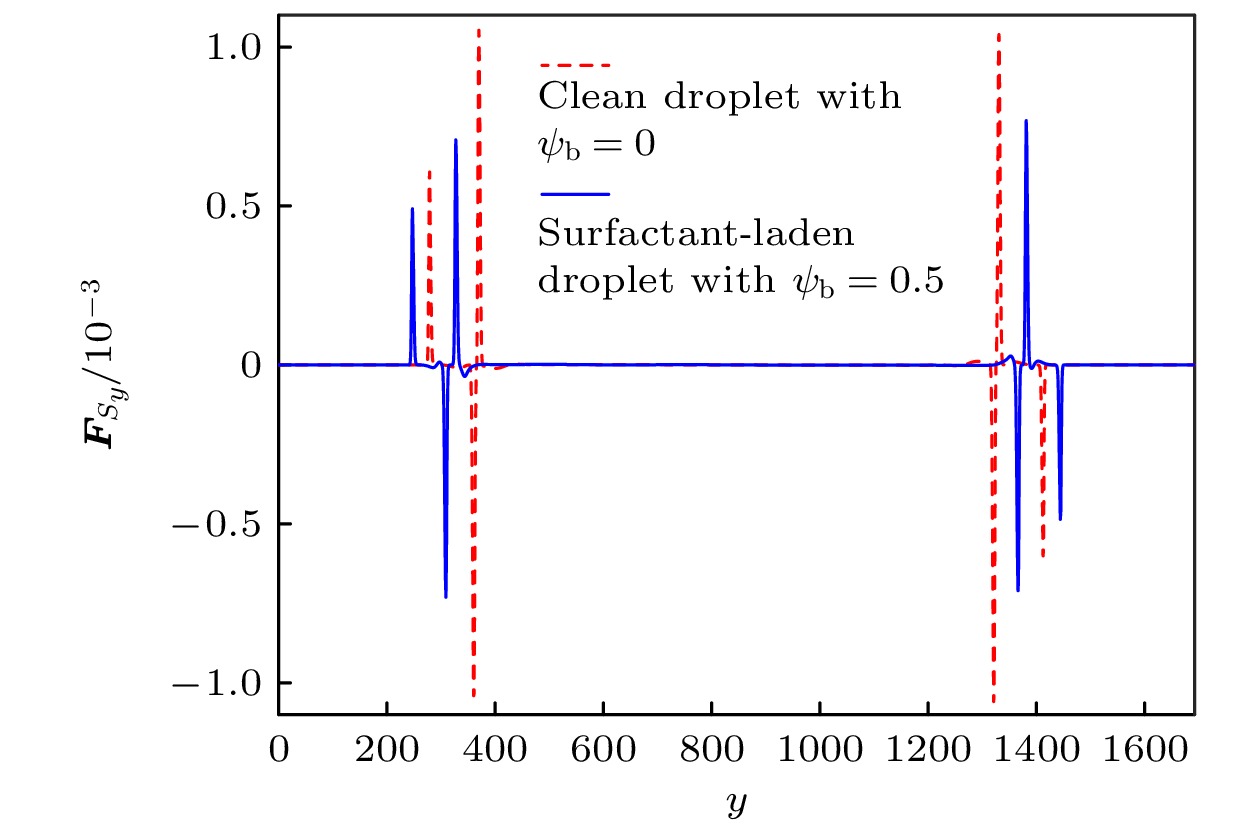
$ Ca_{{\mathrm{E}}} = 1.2 $ ,$ R = 15 $ ,$ S = 1.37 $ ,$ \gamma_0 = 0.01 $ ,$ L_x = 6 A $ ,$ Ly = 36 A $ ,$ T = 1000{\text{δ}} t $ , 其余参数与4.2.1节保持一致. 图8展示了干净液滴($ \psi_{\mathrm{b}} = 0$ )(见图8(a))与含表面活性剂液滴($ \psi_{\mathrm{b}}= 0.5 $ )(见图8(b))的细丝状破裂过程. 可以发现, 含表面活性剂的液滴更容易发生破裂, 这是因为在液滴形变过程中, 电场力促使液滴形变而表面张力抑制液滴形变(如图9所示, 其中$ {\boldsymbol{F}}_{{\rm{E}}y} $ 和$ {\boldsymbol{F}}_{{\rm{s}}y} $ 分别为沿电场方向电场力和表面张力), 而表面活性剂的存在减弱了表面张力的作用, 因此含表面活性剂液滴优先发生破裂. 除此之外, 还能观察到干净液滴破裂后, 主液滴产生了回缩现象, 这是由于液滴破裂后电场力继续促使液滴形变, 可能发生二次聚合, 而表面张力则促使液滴回缩, 维持液滴的破裂状态. 如图10所示, 由于此时表面张力的作用大于电场力, 液滴没有产生二次聚合, 但由于干净液滴受表面张力作用更大(如图11所示), 主液滴产生了明显的回缩.此外还研究了在
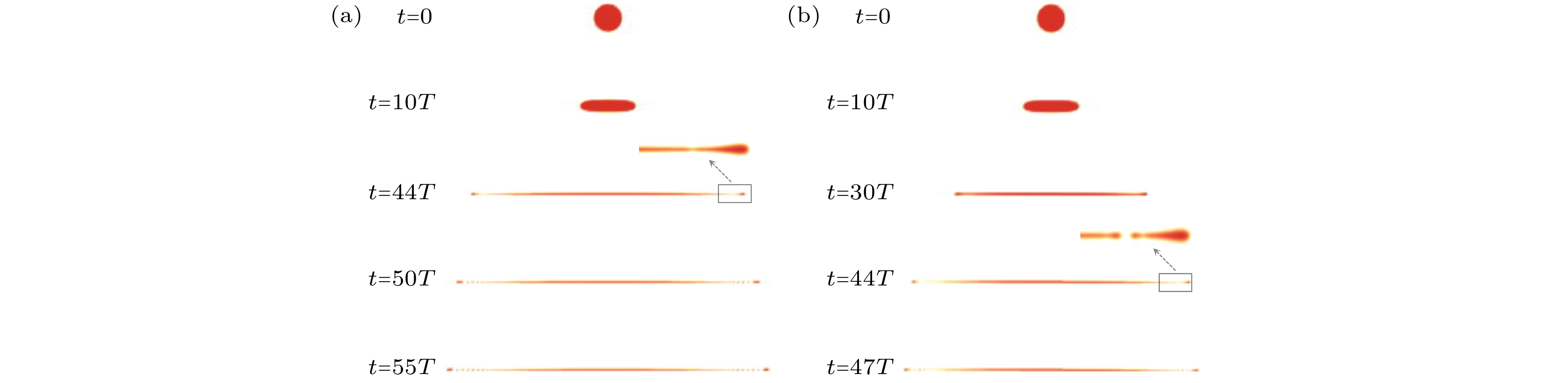
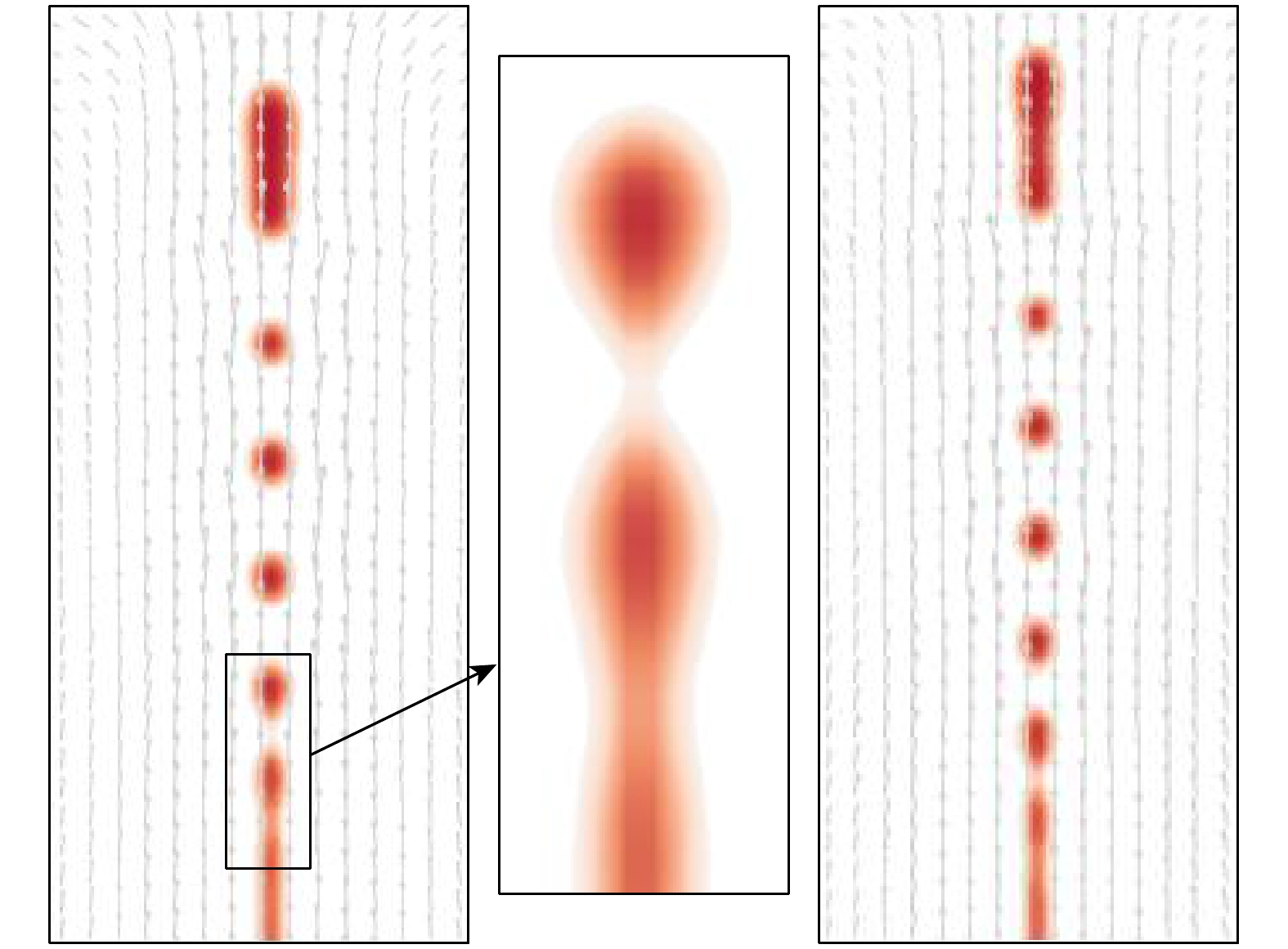
$ Ca_{{\mathrm{E}}} = 3.0, R = 25, \gamma_0 = 0.001 $ 时, 干净液滴和含表面活性剂液滴的窄颈状破裂过程(如图12所示), 其余参数与上述一致. 依旧可以发现含表面活性剂的液滴优先发生破裂, 与此同时, 在液滴的末端形成了一些细小的子液滴, 并且随着时间的推移, 子液滴的数量也在增多. 图13展示了两种液滴破裂6T后的状态, 发现干净液 滴末端只分裂出4个子液滴, 而含表面活性剂液滴末端已经分裂出5个子液滴, 这是由于在子液滴 的形成过程中表面张力起抑制作用, 而表面活性 剂的存在导致表面张力减小, 从而促进了子液滴的形成. -
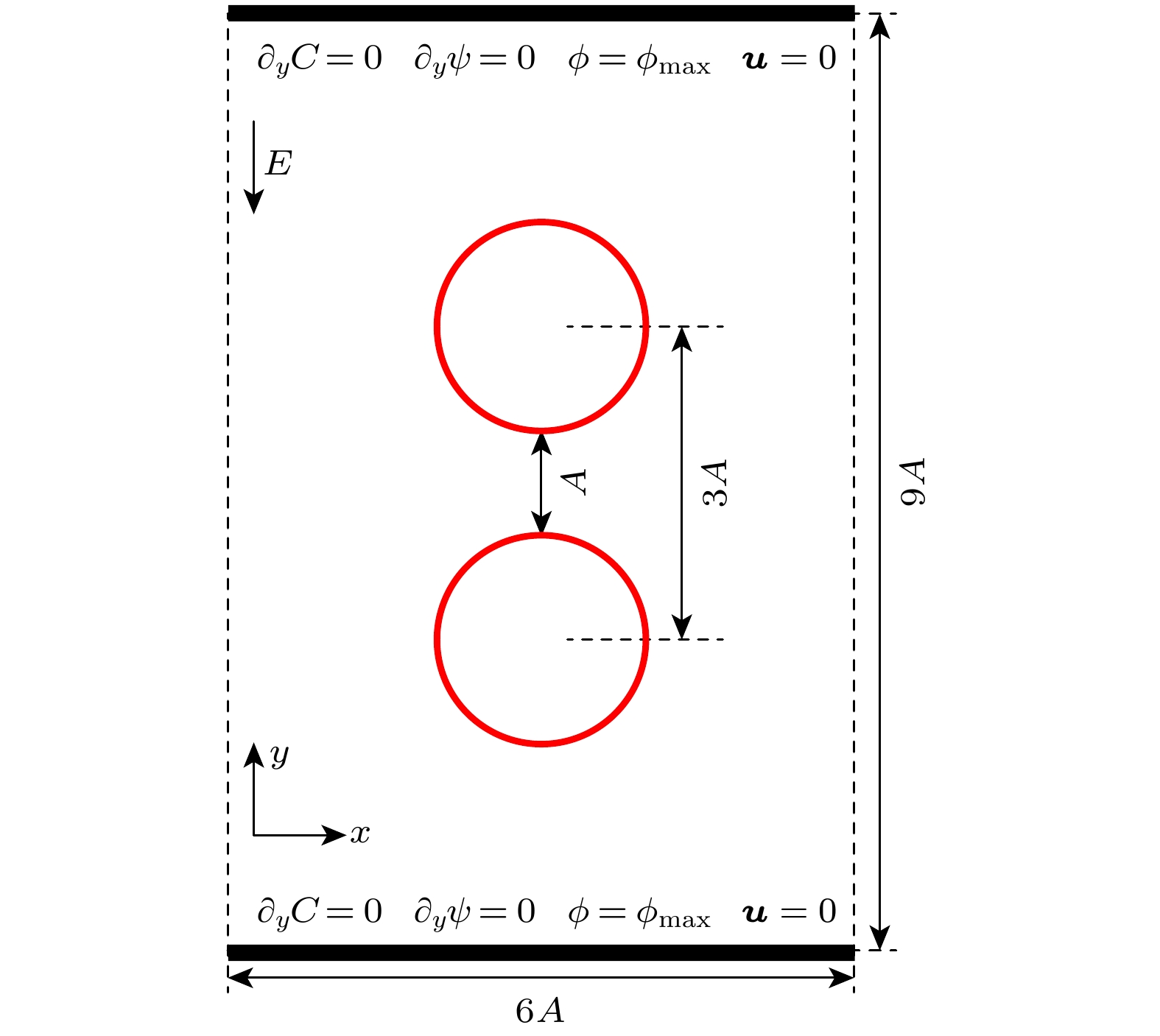
4.2.2节研究了可溶性表面活性剂对电场作用下单液滴破裂的影响, 本节继续研究表面活性剂对双液滴聚合的影响. 图14展示的是本节所研究问题的物理工况示意图,
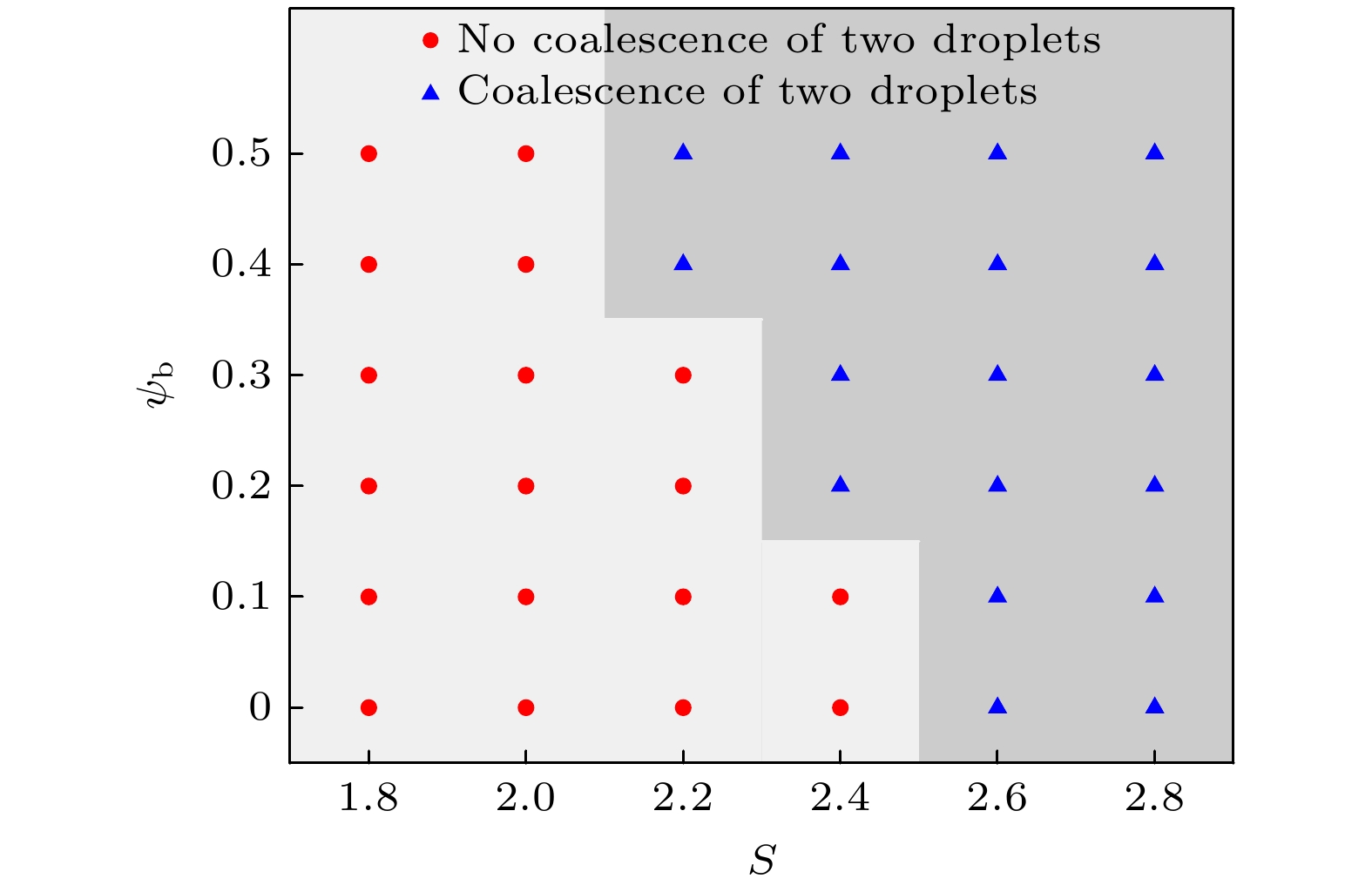
$ A = 40 $ ,$ L_x = 6 A $ ,$ L_y = 9 A $ , 上方液滴质心位置为$ \left( x_{{\mathrm{c}}1}, y_{{\mathrm{c}}1}\right) = \left( 3 A, 6 A\right) $ , 下方液滴质心位置为$ \left( x_{{\mathrm{c}}2}, y_{{\mathrm{c}}2}\right) = \left( 3 A, 3 A\right) $ ,$ \gamma_0 = 0.02 $ ,$ Ca_{\mathrm{E}} = 0.5 $ ,$ R = 5.0 $ ,$ \sigma_{\mathrm{b}} = 1/6 $ , 其余参数见4.2.2节. 本节首先研究介电系数比S、体相区表面活性剂浓度$ \psi_{\mathrm{b}} $ 对双液滴聚合的影响, 如图15所示, 红色圆形代表两液滴不聚合, 蓝色三角形代表两液滴聚合. 从图中可以发现, 当$ S \leqslant 2.0 $ 时, 两液滴不聚合, 这是因为此时两液滴之间的电驱动流体相互作用(排斥)占主导作用; 当$ S \geqslant 2.6 $ 时, 由于两液滴的电相互作用(吸引)占主导作用, 液滴会发生聚合, 这些现象与前人理论一致[41]; 当$ S = 2.2 $ 和$ S=2.4 $ 时发现, 两液滴在低表面活性剂浓度时不发生聚合(如图16(a)), 而在高表面活性剂浓度时发生聚合(如图16(b)), 这是因为低浓度时液滴的形变量较小, 无法使液滴发生接触聚合, 而高浓度则能够诱导液滴发生较大形变, 进而接触聚合.如图17所示, 本文还研究了
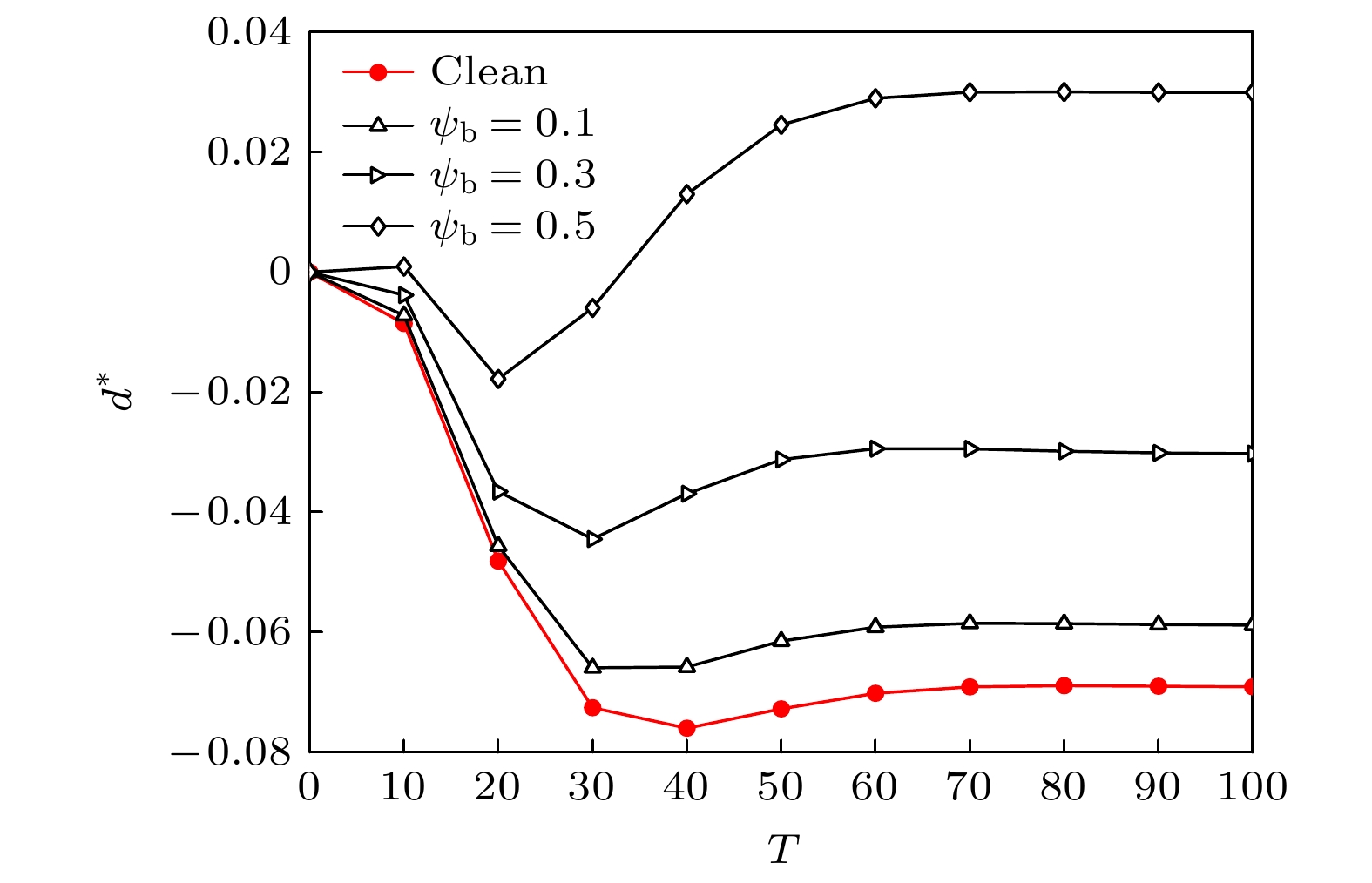
$ S = 2.0 $ 时, 两液滴质心距离随时间的变化规律, 其中$ d^* = (d - d_0) / d_0 $ 表示归一化的两液滴质心距离, d表示两液滴质心距离,$ d_0 = 3 A $ 表示初始两液滴质心距离. 图中圆形红色曲线代表干净液滴, 黑色曲线代表含不同表面活性剂浓度的液滴. 从图中可以看出, 两液滴运动均会先靠近后远离, 但高表面活性剂浓度的液滴($ \psi_{\mathrm{b}} = 0.5 $ )质心距离超过初始位置$ d_0 $ , 这说明表面活性剂对两液滴的吸引起阻碍作用. 结合图15, 可以得出表面活性剂在两液滴运动过程中, 既对两液滴的吸引聚合起阻碍作用, 又对两液滴的形变聚合起促进作用. 在$ S = 2.2 $ 和$S= 2.4 $ 两组参数下, 表面活性剂对形变聚合的促进作用占主导地位, 因此在高浓度情形下, 液滴发生聚合现象.最后研究了当
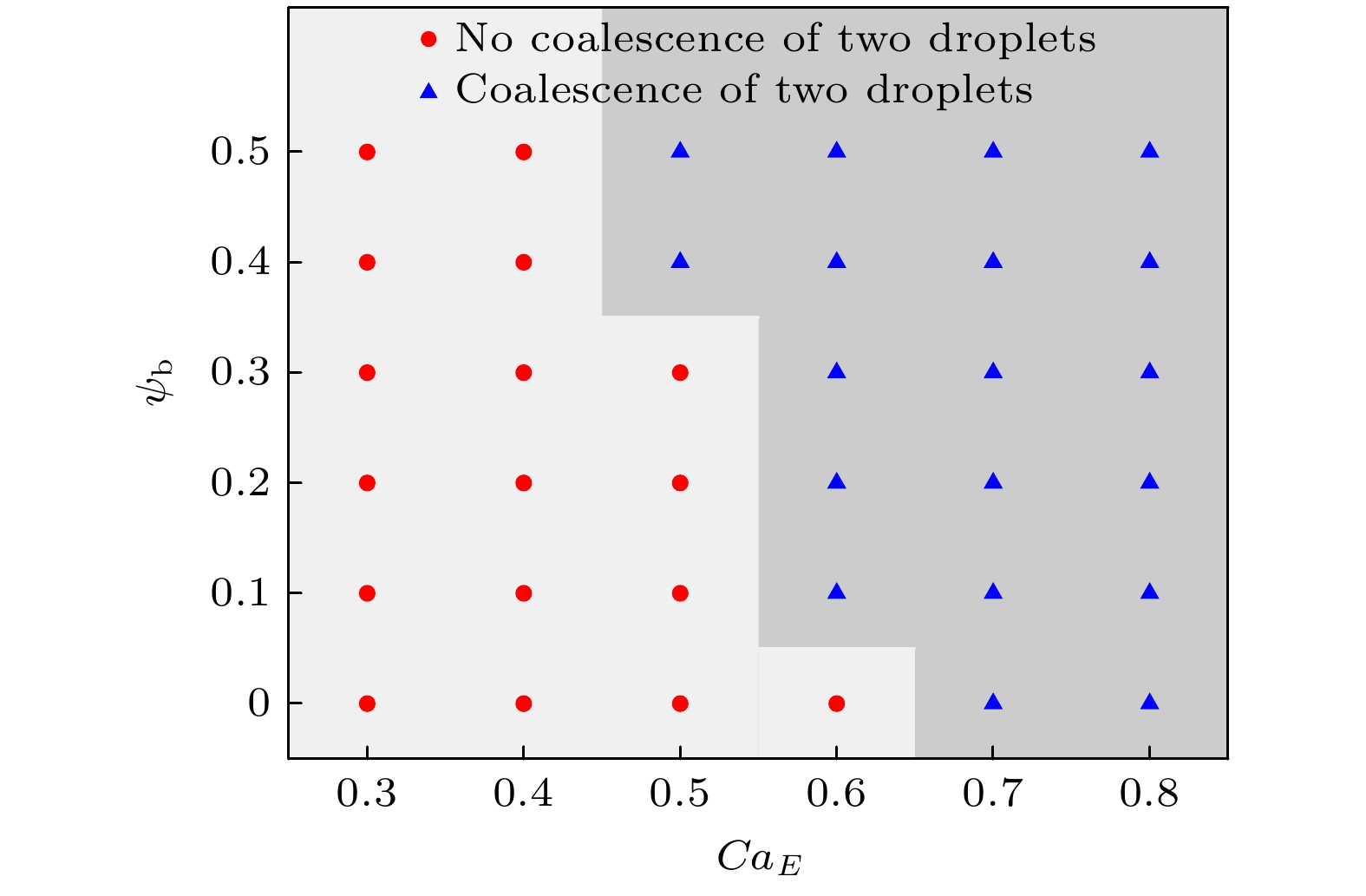
$ S = 2.2 $ 时, 体相区表面活性剂浓度$ \psi_{\mathrm{b}} $ 和电毛细数$ Ca_{\mathrm{E }}$ 对两液滴聚合的影响. 如图18所示, 红色实心圆代表液滴不聚合, 蓝色实心三角形代表液滴聚合. 当$ Ca_{\mathrm{E}} \leqslant 0.4 $ 时, 液滴形变较小, 两液滴不发生聚合; 当$ Ca_{\mathrm{E}} \geqslant 0.7 $ 时, 液滴形变较大, 故发生聚合; 当$ Ca_{\mathrm{E}} = 0.5 $ 和$ Ca_{\mathrm{E}} =0.6 $ 时, 干净液滴形变无法使其接触聚合, 但表面活 性剂浓度的增大促进了两液滴的形变聚合. 另外, 由于$ Ca_{\mathrm{E}} $ 的增大能促进液滴形变, 所以$ Ca_{\mathrm{E}} = 0.6 $ 的液滴比$ Ca_{\mathrm{E}} = 0.5 $ 的液滴先发生聚合. -
本文利用基于相场理论的格子Boltzmann方法研究了匀强电场下含可溶性表面活性剂液滴的动力学行为. 首先通过模拟静态液滴表面活性剂浓度分布以及漏电介质液滴在电场中形变两个基准问题验证了模型的可靠性, 并在此基础上深入地研究了电毛细数
$ Ca_{\mathrm{E}} $ 、体相区表面活性剂浓度$ \psi_{\mathrm{b}} $ 等参数对液滴形变、破裂以及聚合过程的影响. 主要结论如下.1)对于形变行为, 单液滴存在扁长型和扁平型两种形变模式, 电毛细数
$ Ca_{\mathrm{E}} $ 和体相区表面活性剂浓度$ \psi_{\mathrm{b}} $ 越高, 液滴的形变程度越大.2)对于破裂行为, 单液滴存在细丝状和窄颈状两种破裂模式, 表面活性剂能促进两种模式下的破裂, 并且可以降低细丝状破裂后主液滴的回缩程度以及增加窄颈状破裂后液滴末端生成子液滴的数量.
3)对于聚合行为, 双液滴存在形变聚合和吸引聚合两种过程, 电毛细数
$ Ca_{\mathrm{E}} $ 越高, 液滴越容易聚合, 而表面活性剂不仅会促进液滴的形变聚合还会抑制液滴的吸引聚合, 但促进作用占主导, 因此体相区表面活性剂浓度$ \psi_{\mathrm{b }}$ 越高, 液滴越容易聚合.综上所述, 本文研究了电毛细数
$ Ca_{\mathrm{E}} $ 与体相区表面活性剂浓度$ \psi_{\mathrm{b}} $ 对含可溶性表面活性剂的漏电介质液滴在电场作用下的形变、破裂及聚合的影响, 相关结果对非常规石油开采、污水处理以及研发新型电聚结脱水器具有重要的理论指导和应用价值.
匀强电场作用下含表面活性剂的液滴动力学行为
Dynamic behaviors of surfactant-containing droplets under a uniform electric field
-
摘要: 利用基于相场理论的格子Boltzmann方法研究了匀强电场作用下含可溶性表面活性剂液滴的动力学行为. 首先通过模拟静态液滴表面活性剂浓度分布和漏电介质液滴在电场作用下形变两个基准问题验证了方法的可靠性. 其次, 本文重点研究了含表面活性剂液滴在电场作用下的形变、破裂和聚合行为. 研究发现, 对于形变行为, 单液滴存在扁长型和扁平型两种形变模式, 表面活性剂浓度越高, 液滴形变越大; 对于破裂行为, 单液滴存在细丝状和窄颈状两种破裂模式, 含表面活性剂的液滴更容易发生破裂行为; 对于聚合行为, 双液滴存在形变聚合和吸引聚合两种过程, 表面活性剂促进其形变聚合, 但抑制其吸引聚合.
-
关键词:
- 格子Boltzmann方法 /
- 可溶性表面活性剂 /
- 漏电介质液滴
Abstract: This paper adopts the phase-field based lattice Boltzmann (LB) method to study the dynamic behaviors of soluble surfactant-laden droplets in a uniform electric field. First, two benchmark problems including the surfactant concentration distribution on a static droplet and the deformation of a leaky dielectric droplet in an electric field, are used to validate the reliability of the LB method. Then, we investigate the deformation, breakup, and coalescence behaviors of surfactant-laden droplets in an electric field. The obtained results are shown below. 1) Regarding deformation, the single droplet exhibits two distinct deformation modes: Prolate and oblate shapes. A higher electric capillary number and a higher concentration of bulk surfactants both promote greater droplet deformation. 2) Regarding breakup, a single droplet exhibits two distinct breakup modes: filamentous breakup and conical jetting breakup. Droplets containing surfactants are more like to break up. Specifically, surfactants reduce the retraction degree of the main droplet after filamentous breakup, while increasing the number of satellite droplets formed at the ends of the main droplet after jetting breakup. 3) Regarding coalescence, the double droplets exhibit two distinct processes: deformation coalescence and attractive coalescence. A higher electric capillary number facilitates droplet coalescence. Surfactants promote the deformation coalescence while retarding attractive coalescence, but the promotional effect dominates. Consequently, a higher concentration of bulk surfactants will enhance the tendency of droplet coalescence.-
Key words:
- lattice Boltzmann method /
- soluble surfactant /
- leaky dielectric droplet .
-

-
图 3 干净液滴 (a) 扁长型
$ [(S, R) = (3.5, 4.75)] $ ,$ u_{{\mathrm{max}}} = $ $ 0.00020 $ ; (b) 扁平型$ [(S, R) = (3.5, 1.75)] $ ,$ u_{{\mathrm{max}}} = 0.00043 $ Figure 3. Clean droplet: (a) Prolate droplet
$ [(S, R) = (3.5, $ $ 4.75)] $ ,$ u_{{\mathrm{max}}} = 0.00020 $ ; (b) oblate droplet$ [(S, R) = (3.5, $ $ 1.75)] $ ,$ u_{{\mathrm{max}}} = 0.00043 $ .图 4 含表面活性剂液滴 (a) 扁长型
$ [(S, R) = (3.5, 4.75)] $ ,$ u_{{\mathrm{max}}} = 0.00016 $ ; (b) 扁平型$ [(S, R) = (3.5, 1.75)] $ ,$ u_{{\mathrm{max}}} = $ 0.00034Figure 4. Surfactant-laden droplet: (a) Prolate droplet
$ [(S, R) = $ $ (3.5, 4.75)] $ ,$ u_{{\mathrm{max}}} = 0.00016 $ ; (b) oblate droplet$ [(S, R) = $ $ (3.5, 1.75)] $ ,$ u_{{\mathrm{max}}} = 0.00034 $ .图 16 当
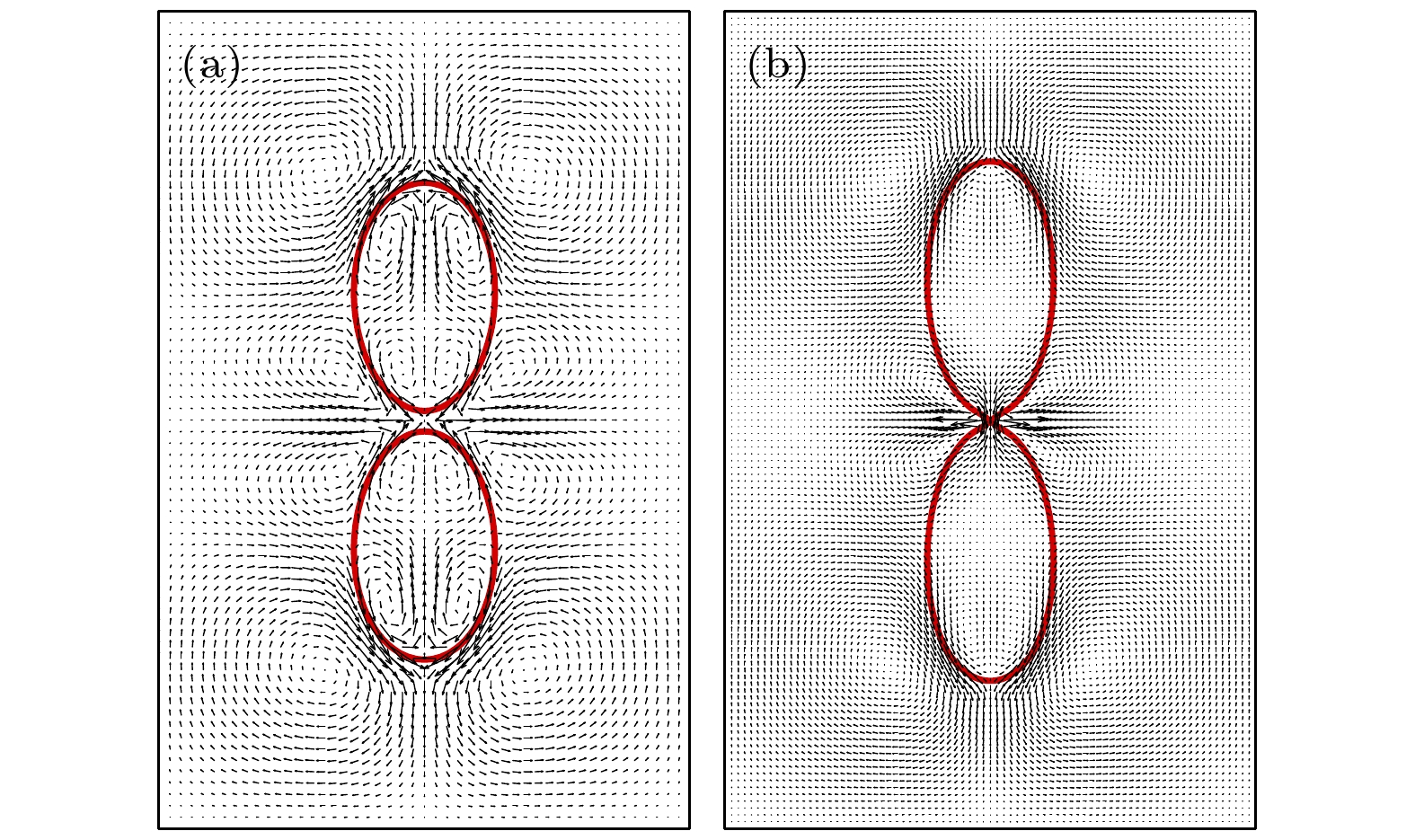
$ S = 2.2 $ ,$ t = 30 T $ 时, 两液滴状态 (a) 干净液滴不聚合状态,$ u_{{\mathrm{max}}} = 0.00086 $ ; (b) 含表面活性剂液滴聚合状态($ \psi_{\mathrm{b}} = 0.5 $ ),$ u_{{\mathrm{max}}} = 0.00274 $ Figure 16. The states of the two droplets under
$ S = 2.2 $ and$ t = 30 T $ : (a) Two clean droplets without coalescence,$ u_{{\mathrm{max}}} = 0.00086 $ ; (b) the coalescence of two surfactant-laden droplets ($ \psi_{\mathrm{b}} = 0.5 $ ),$ u_{{\mathrm{max}}} = 0.00274 $ .表 1 漏电介质液滴形变因子的数值解和理论解对比
Table 1. A comparison between the numerical results and analytical solution of the deformation factor of leaky dielectric droplet.
$ R $ $ S $ $ Ca_{\mathrm{E}} $ 形变因子 $ D $ 本文结果 Taylor[5] Feng[17] Liu等[14] 其他数值结果 5 5 0.2 0.03543 0.03670 0.02960 0.03524 0.04080[10] 5 60 0.2 –0.25758 –0.40520 –0.27590 –0.25708 –0.25980[10] 1 2 0.2 –0.04826 –0.04380 –0.05000 –0.04751 –0.02377[10] 50 2 0.2 0.10733 0.10690 0.06520 0.10756 0.09931[10] 1.75 3.5 0.1 –0.02065 –0.02230 –0.02070 –0.02232 –0.02198[18] 3.25 3.5 0.1 0.00888 0.00850 0.00800 0.00833 0.00879[18] 4.75 3.5 0.1 0.02102 0.00228 0.01800 0.01953 0.02088[18] -
[1] Salipante P F, Vlahovska P M 2010 Phys. Fluids 22 112110 doi: 10.1063/1.3507919 [2] Stone H A, Stroock A D, Ajdari A 2004 Annu. Rev. Fluid Mech. 36 381 doi: 10.1146/annurev.fluid.36.050802.122124 [3] Manikantan H, Squires T M 2020 J. Fluid Mech. 892 1 [4] O’konski C T, Thacher H C 1953 J. Phys. Chem. 57 955 doi: 10.1021/j150510a024 [5] Taylor G 1966 Proc. R. Soc. Lond. A 291 159 doi: 10.1098/rspa.1966.0086 [6] Sherwood J D 1988 J. Fluid Mech. 188 133 doi: 10.1017/S0022112088000667 [7] Tomar G, Gerlach D, Biswas G, Alleborn N, Sharma A, Durst F, Welch S W J, Delgado A 2007 J. Comput. Phys. 227 1267 doi: 10.1016/j.jcp.2007.09.003 [8] Hua J S, Lim L K, Wang C H 2008 Phys. Fluids 20 113302 doi: 10.1063/1.3021065 [9] Teigen K E, Munkejord S T 2009 IEEE Trans. Dielectr. Electr. Insul. 16 475 doi: 10.1109/TDEI.2009.4815181 [10] Lin Y, Skjetne P, Carlson A 2012 Int. J. Multiphase Flow 45 1 doi: 10.1016/j.ijmultiphaseflow.2012.04.002 [11] Fakhari A, Bolster D 2017 J. Comput. Phys. 334 620 doi: 10.1016/j.jcp.2017.01.025 [12] Yang Q, Li B Q, Ding Y 2013 Int. J. Multiphase Flow 57 1 doi: 10.1016/j.ijmultiphaseflow.2013.06.006 [13] Novick-Cohen A 2008 Handbook of Differential Equations: Evolutionary Equations (Vol. 4) (Amsterdam: North-Holland) p201 [14] Liu X, Chai Z H, Shi B C 2019 Phys. Fluids 31 092103 doi: 10.1063/1.5119891 [15] Liu X, Chai Z H, Shi B C 2021 Commun. Comput. Phys. 30 1346 doi: 10.4208/cicp.OA-2021-0025 [16] Liu X, Chai Z H, Shi B C, Yuan X L 2024 Physica D 468 134294 doi: 10.1016/j.physd.2024.134294 [17] Feng J Q 2002 J. Colloid Interface Sci. 246 112 doi: 10.1006/jcis.2001.8037 [18] Cui Y T, Wang N N, Liu H H 2019 Phys. Fluids 31 022105 doi: 10.1063/1.5080210 [19] Baret J C 2012 Lab Chip 12 422 doi: 10.1039/C1LC20582J [20] Anna S L 2016 Annu. Rev. Fluid Mech. 48 285 doi: 10.1146/annurev-fluid-122414-034425 [21] Liu H H, Zhang Y H 2010 J. Comput. Phys. 229 9166 doi: 10.1016/j.jcp.2010.08.031 [22] Ceniceros H D 2003 Phys. Fluids 15 245 doi: 10.1063/1.1528940 [23] Wooding R A, Morel–Seytoux H J 1976 Annu. Rev. Fluid Mech. 8 233 doi: 10.1146/annurev.fl.08.010176.001313 [24] van der Sman R G M, van der Graaf S 2006 Rheol. Acta 46 3 doi: 10.1007/s00397-005-0081-z [25] van der Sman R G M, Meinders M B J 2016 Comput. Phys. Commun. 199 12 doi: 10.1016/j.cpc.2015.10.002 [26] Shi Y, Tang G H, Cheng L H, Shuang H Q 2019 Comput. Fluids 179 508 doi: 10.1016/j.compfluid.2018.11.018 [27] Zong Y J, Zhang C H, Liang H, Wang L, Xu J R 2020 Phys. Fluids 32 122105 doi: 10.1063/5.0028554 [28] Ha J W, Yang S M 1995 J. Colloid Interface Sci. 175 369 doi: 10.1006/jcis.1995.1468 [29] Nganguia H, Young Y N, Vlahovska P M, Blawzdziewicz J, Zhang J, Lin H 2013 Phys. Fluids 25 092106 doi: 10.1063/1.4821205 [30] Painuly R, Kumar S, Anand V 2024 Colloids Surf., A 697 134389 doi: 10.1016/j.colsurfa.2024.134389 [31] Teigen K E, Munkejord S T 2010 Phys. Fluids 22 112104 doi: 10.1063/1.3504271 [32] Sorgentone C, Tornberg A, Vlahovska P M 2019 J. Comput. Phys. 389 111 doi: 10.1016/j.jcp.2019.03.041 [33] Ha J W, Yang S M 1998 J. Colloid Interface Sci. 206 195 doi: 10.1006/jcis.1998.5676 [34] Li N, Pang Y, Sun Z, Li W, Sun Y, Sun X, Liu Y, Li B, Wang Z, Zeng H 2024 Fuel 358 130328 doi: 10.1016/j.fuel.2023.130328 [35] Wang H L, Chai Z H, Shi B C, Liang H 2016 Phys. Rev. E 94 033304 doi: 10.1103/PhysRevE.94.033304 [36] Soligo G, Roccon A, Soldati A 2019 J. Comput. Phys. 376 1292 doi: 10.1016/j.jcp.2018.10.021 [37] Yun A, Li Y, Kim J 2014 Appl. Math. Comput. 229 422 [38] Chang C H, Franses E I 1995 Colloids Surf., A 100 1 doi: 10.1016/0927-7757(94)03061-4 [39] Qian Y H, D’Humières D, Lallemand P 1992 EPL 17 479 doi: 10.1209/0295-5075/17/6/001 [40] Guo Z L, Shu C 2013 Lattice Boltzmann Method and Its Application in Engineering (Vol. 3) (Singapore: World Scientific) pp35–59 [41] Dong Q, Sau A 2018 Phys. Rev. Fluids 3 073701 doi: 10.1103/PhysRevFluids.3.073701 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: