量子导引的理论根源可追溯至Einstein, Podolsky和Rosen (简称为EPR)于1935年发表的里程碑式论文^[1]. 在该文中, 虽未直接提及“导引”一词, 但其对量子力学非定域性的探讨为后续理论发展奠定了基础. 随后, Schrödinger^[2]在深入分析EPR论文的过程中, 首次引入了“导引”(steering)这一概念. 在此基础上, Wiseman等^[3]对量子导引进行了精确的数学描述和严格的理论界定, 给出了量子导引是描述对一个粒子的本地测量能够非局域地影响另一个粒子状态的能力, 从而为其在量子信息科学领域的应用提供了理论框架. 相较于量子纠缠^[4,5]和贝尔非局域性^[6], 量子导引展现出独特的非对称性, 即Alice对Bob的导引能力与Bob对Alice的能力并不总是相等^[7–9]. 这种独特的特性使得量子导引成为量子信息领域的研究热点, 并成为完成一些量子信息任务不可或缺的资源, 例如单边设备无关(1sDI)量子密钥分发^[10,11]、量子隐形传态^[12,13]和量子秘密共享^[14–17]. 在多组份量子导引中, 量子导引能力在参与者之间的分配受到单配性关系的严格限制. 具体而言, 某一方的量子态无法同时被多个其他参与者导引. 以三组份量子系统为例, 如果A可以导引B, 那么B就不能同时被C导引^[18,19]. 这种特性被称为量子导引的单配性关系, 它在量子密码协议中起到了关键作用, 确保了协议的安全性和可靠性.

量子资源交换是构建量子网络和实现高效量子通信的关键技术之一^[20,21]. 其可以在不同的量子节点之间共享和分配量子资源, 使得量子网络能够更灵活地支持各种量子信息处理任务. 与纠缠交换^[22–25]不同, 量子导引交换依托于其独特的不对称性, 能够在两个独立的光学模式之间建立单向或双向不对称的量子导引, 这对于构建非对称量子网络具有至关重要的意义^[26]. 2016年, 山西大学苏晓龙研究小组^[27]基于前馈技术, 通过单通道和双通道两个方案实现了两组份导引交换; 随后, 该小组于2017年, 实现了对称和不对称模数的多组份纠缠态之间的导引交换^[28]并在实验上进行了验证^[29]. 2024年, 华东师范大学荆杰泰研究小组等^[30]提出了无需测量的两组份全光导引交换方法, 这一方法避免了光电和电光转换的步骤. 全光导引交换技术克服了传统方案中贝尔态测量的限制, 大大扩展了量子导引交换在构建宽带量子网络中的应用范围, 不仅推动了量子通信技术的发展, 也为未来量子网络的构建提供了新的可能性.

本文提出了基于三组份与两组份纠缠态的全光学量子导引交换方案, 通过低噪声、高带宽的四波混频过程实现了无需检测的全光贝尔态测量. 方案一利用四波混频过程联合线性分束器制备三组份纠缠态, 方案二利用四波混频过程联合非线性分束器(四波混频过程)制备三组份纠缠态. 通过调节线性分束器的透射率和四波混频过程的增益, 来操控交换后的不对称导引, 对非对称量子信息处理具有重要的意义.

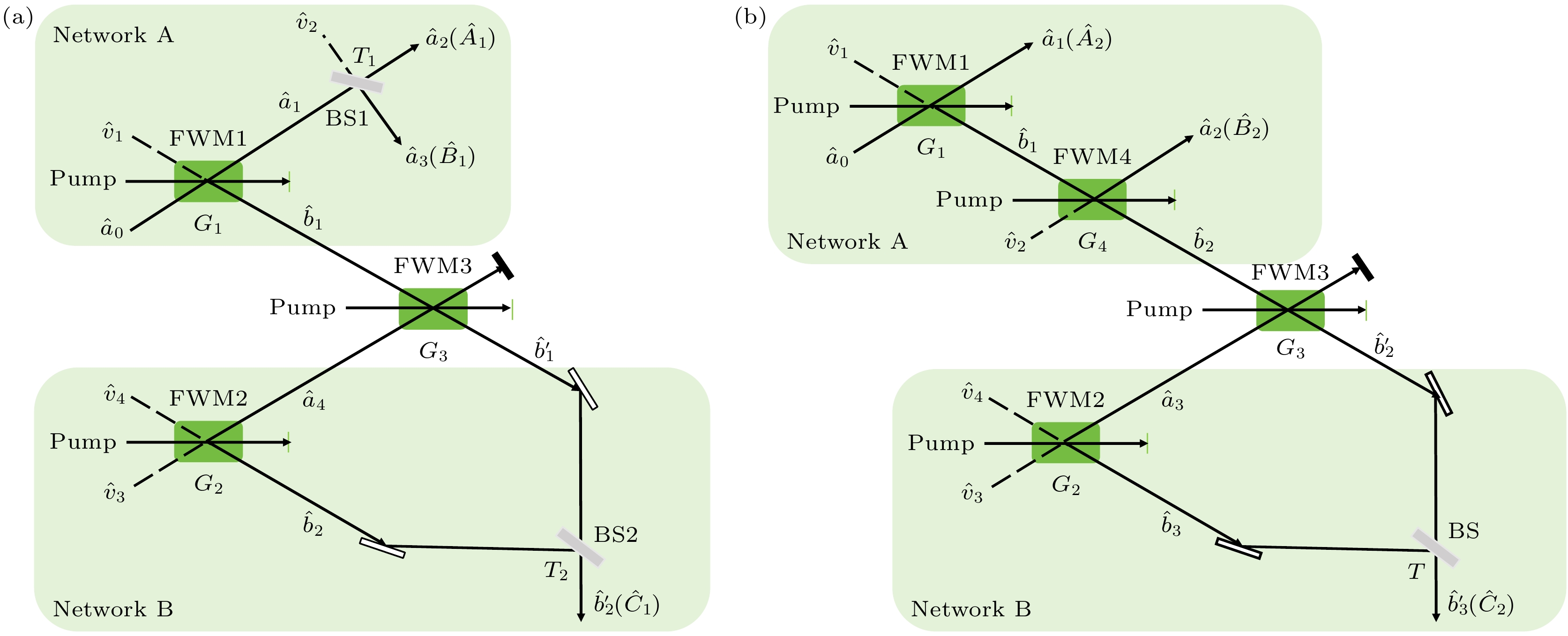
图1是基于四波混频过程产生三组份全光量子导引交换方案示意图, 图1(a)中网络A (Network A)的初始三组份纠缠态是由四波混频腔FWM1联合一个线性分束器BS1产生的, 图1(b)的初始三组份纠缠态是由四波混频腔FWM1联合一个非线性分束器(四波混频腔FWM4)产生.

如图1(a)所示, 由四波混频腔FWM1联合线性分束器产生的三组份纠缠态和由一个四波混频腔FWM2产生的两组份纠缠态的导引交换方案中, 三束泵浦光分别注入到3个四波混频腔中, ${G_1}, {G_2}$和${G_3}$分别是3个四波混频过程的强度增益. 种子光${\hat a_0}$和真空模式${\hat v_1}$注入四波混频腔FWM1中, 产生一对纠缠光束$ ( {{{\hat a}_1}, {{\hat b}_1}} ) $, $ {\hat a_1} \;= \;\sqrt {{G_1}} {\hat a_0} \;+ \sqrt {{G_1} - 1} \hat v_1^\dagger , \; {\hat b_1} = \sqrt {{G_1} - 1} \hat a_0^\dagger + \sqrt {{G_1}} {\hat v_1} $, 将产生的模$ {\hat a_1} $与真空模式${\hat v_2}$在透射率为$ {T_1} $的线性分束器BS1处耦合, 产生三组份纠缠态$ ( {{{\hat b}_1}, {{\hat a}_2}, {{\hat a}_3}} ) $, 3个模式分别表示为

真空光模${\hat v_3}$和${\hat v_4}$注入四波混频腔FWM2, 产生纠缠光束$ ( {{{\hat a}_4}, {{\hat b}_2}} ) $, $ {\hat a_4} = \sqrt {{G_2}} {\hat v_3} + \sqrt {{G_2} - 1} \hat v_4^\dagger , {\hat b_2} = \sqrt {{G_2} - 1} \hat v_3^\dagger + \sqrt {{G_2}} {\hat v_4} $. 模式${\hat b_1}$与$ {\hat a_4} $注入四波混频腔FWM3中, FWM3作为一个低噪声的参量放大器^[31,32], 将输出的模式$ {\hat b'_1} = \sqrt {{G_3}} {\hat b_1} + \sqrt {{G_3} - 1} \hat a_4^\dagger $与四波混频过程FWM2输出的$ {\hat b_2} $在线性分束器BS2耦合, 最终输出模式$ {\hat b'_2} $. 调节线性分束器BS2的透射率$ {T_2} = {1}/{{{G_3}}} $, 模式$ {\hat b'_2} $的表达式为

在此过程中, 四波混频腔FWM3, 以低噪声的参量放大方式, 将${\hat b_1}$和$ {\hat a_4} $的信息都传输给了$ {\hat b'_2} $, 成功实现了无需检测的全光贝尔态测量.

图1(b)是利用非线性分束器产生三组份纠缠态和利用四波混频产生两组份纠缠态的导引交换方案, 4束泵浦光分别注入到4个四波混频腔, $ {G_1}, {G_2}, {G_3} $和${G_4}$分别是4个四波混频过程的强度增益. 种子光${\hat a_0}$和真空模式${\hat v_1}$注入四波混频腔FWM1, 产生纠缠光束$ ( {{{\hat a}_1}, {{\hat b}_1}} ) $, 其中模式$ {\hat a_1} \;= \;\sqrt {{G_1}} {\hat a_0} \;+ \sqrt {{G_1} - 1} \hat v_1^\dagger $, $ {\hat b_1} = \sqrt {{G_1} - 1} \hat a_0^\dagger + \sqrt {{G_1}} {\hat v_1} $. 将模式${\hat b_1}$和真空模式${\hat v_2}$注入非线性分束器FWM4, 产生三组份纠缠态$ ( {{{\hat a}_1}, {{\hat a}_2}, {{\hat b}_2}} ) $, 3个模式分别表示为

真空光模${\hat v_3}$和${\hat v_4}$注入四波混频腔FWM2产生的两组份纠缠态$ ( {{{\hat a}_3}, {{\hat b}_3}} ) $为$ {\hat a_3} = \sqrt {{G_2}} {\hat v_3} + \sqrt {{G_2} - 1} \hat v_4^\dagger , {\hat b_3} = \sqrt {{G_2} - 1} \hat v_3^\dagger + \sqrt {{G_2}} {\hat v_4} $, 四波混频腔FWM3作为低噪声的参量放大器, 将模式${\hat b_2}$和$ {\hat a_3} $耦合, 这两个模式的信息通过模$ {\hat b'_2} = \sqrt {{G_3}} {\hat b_2} + \sqrt {{G_3} - 1} \hat a_3^\dagger $与四波混频过程FWM2产生的$ {\hat b_3} $在线性分束器BS上耦合, 最终输出模式$ {\hat b'_3} $. 调节线性分束器BS的透射率$ T = {1}/{{{G_3}}} $, 模式$ {\hat b'_3} $的表达式为

与方案一类似, 四波混频腔FWM3, 以低噪声参量放大的方式, 将${\hat b_2}$和$ {\hat a_3} $的信息都传输给了$ {\hat b'_3} $, 从而实现了全光贝尔态测量.

在执行全光交换操作后, 从协方差矩阵出发研究各个输出模式之间的量子导引关系. 对于由$ \left( {{n_{\text{A}}} + {m_{\text{B}}}} \right) $个模式组成的两组份高斯态, 其协方差矩阵可写为

其中矩阵元${\sigma _{ij}} = {{\langle {{{\hat \xi }_i}{{\hat \xi }_j} + {{\hat \xi }_j}{{\hat \xi }_i}} \rangle } {/ } {2 - }}\langle {{{\hat \xi }_i}} \rangle \langle {{{\hat \xi }_j}} \rangle $, $ \hat{\xi}\equiv(\hat{x}_1^{\mathrm{A}}, \hat{p}_1^{\mathrm{A}},\cdots,\hat{x}_n^{\mathrm{A}},\hat{p}_n^{\mathrm{A}},\hat{x}_1^{\mathrm{B}},\hat{p}_1^{\mathrm{B}},\cdots,\hat{x}_m^{\mathrm{B}},\hat{p}_m^{\mathrm{B}}) $是模式的正交振幅和正交位相分量, 子矩阵${\boldsymbol{A}}$和${\boldsymbol{B}}$是两个子系统的协方差矩阵, C是两个系统的交叉矩阵, 子系统A对B的导引能力可以量化为^[33]

其中, $ {\bar v_j^{\boldsymbol {AB/A}}}\left(j=1,2,\cdots,m_{\mathrm{B}}\right) $是$ \overline{\boldsymbol{\sigma}}_{\boldsymbol{AB/A}}=\boldsymbol{B}\;- \boldsymbol{C}^{\text{T}}\boldsymbol{A}^{-1}\boldsymbol{C} $的辛本征值, 可以从协方差矩阵$ \boldsymbol{\sigma}_{\mathrm{AB}} $的子矩阵A的舒尔补码得到. 当$ {\mathcal{G}^{{\text{A}} \to {\text{B}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) > 0 $时, 表示子系统A可以导引B. 子系统B对A的导引能力$ {\mathcal{G}^{{\text{B}} \to {\text{A}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) $可以通过交换两者位置实现. 当$ {\mathcal{G}^{{\text{A}} \to {\text{B}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) > 0 $且$ {\mathcal{G}^{{\text{B}} \to {\text{A}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) > 0 $, 意味着两个系统间存在双向导引; 在此基础上, 如果$ {\mathcal{G}^{{\text{A}} \to {\text{B}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) \ne {\mathcal{G}^{{\text{B}} \to {\text{A}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) $, 则意味着两个系统间存在双向不对称导引. 当$ {\mathcal{G}^{{\text{A}} \to {\text{B}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) > 0 $, $ {\mathcal{G}^{{\text{B}} \to {\text{A}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) = 0 $时, 意味着两个系统间只存在子系统A对B的单向导引; 当$ {\mathcal{G}^{{\text{A}} \to {\text{B}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) = 0 $, $ {\mathcal{G}^{{\text{B}} \to {\text{A}}}}\left( {{{\boldsymbol{\sigma }} _{{\text{AB}}}}} \right) > 0 $时, 意味着两个系统间只存在子系统B对A的单向导引. 依据上述判据, 在可行性实验参数下, 对交换后的量子导引特性进行数值分析.

在两个全光导引交换方案中, 通过交换操作, 分别得到了属于两个独立网络的三组份输出态. 设置方案一中的四波混频过程FWM3的增益${G_3} = 8 \gg 1$, 确保输出的$ {\hat b'_1} $可以看作是经典光场^[34]; 同样, 设置方案二中的四波混频过程FWM3的增益${G_3} = 8 \gg 1$.

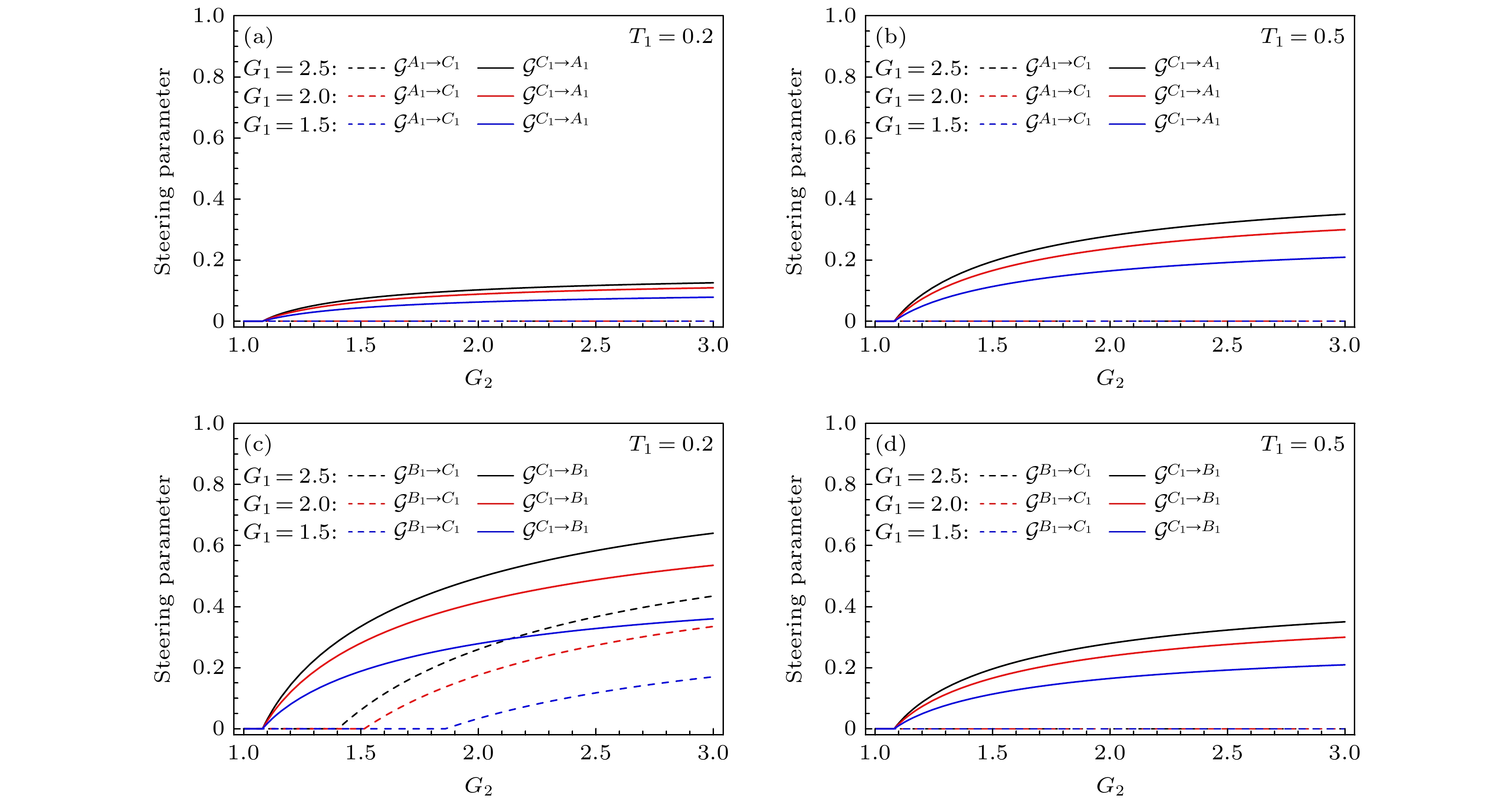
基于线性分束器产生的三组份纠缠态与两组份纠缠态交换, 对输出模式${\hat A_1}, {\hat B_1}$和${\hat C_1}$之间的导引特性进行分析. 图2是在不同增益$ {G_1} $下, 任意两模之间的量子导引对四波混频过程FWM2的增益$ {G_2} $的依赖关系. 从图2的4张关系图可以看出, 经过一定的阈值($ {G_2} > 1.08 $)条件后, 任意两模之间的量子导引能力随着增益$ {G_2} $的增大而增大.

接下来分析线性分束器BS1的透射率${T_1}$对两模间导引能力的影响, 在${T_1} = 0.2$时, 如图2(a)所示, 无论增益$ {G_1} $取值多少, 模${\hat A_1}$和${\hat C_1}$之间只有单向导引$ {\mathcal{G}^{{C_1} \to {A_1}}} $; 如图2(c)所示, 模${\hat B_1}$和${\hat C_1}$之间的导引能力随着增益$ {G_2} $的增大, 由${\hat C_1} \to {\hat B_1}$的单向导引变为双向不对称导引. 在${T_1} = 0.5$时, 如图2(b)及图2(d)所示, 模${\hat A_1}$和${\hat C_1}$以及模${\hat B_1}$和${\hat C_1}$之间只有单向导引$ {\mathcal{G}^{{C_1} \to {A_1}}} $和$ {\mathcal{G}^{{C_1} \to {B_1}}} $. 双模之间导引的不对称性, 主要源于双模量子态的不对称性, 其中模${\hat C_1}$包含了四波混频过程FWM3处理后的信息.

最后, 分析增益$ {G_1} $对两模间导引能力的影响, 如图2中4幅图所示, 随着$ {G_1} $的增大, 两模间导引能力也随之增强. 在图2(c)中, 增益$ {G_1} $取不同的值时, 增益$ {G_1} $越大, 产生双向导引$ {\mathcal{G}^{{C_1} \leftrightarrow {B_1}}} $所需要的增益$ {G_2} $值越小. 从图2可以看出, 通过全光量子导引交换的操作, 两个没有直接相互作用的网络A和网络B成功产生了导引.

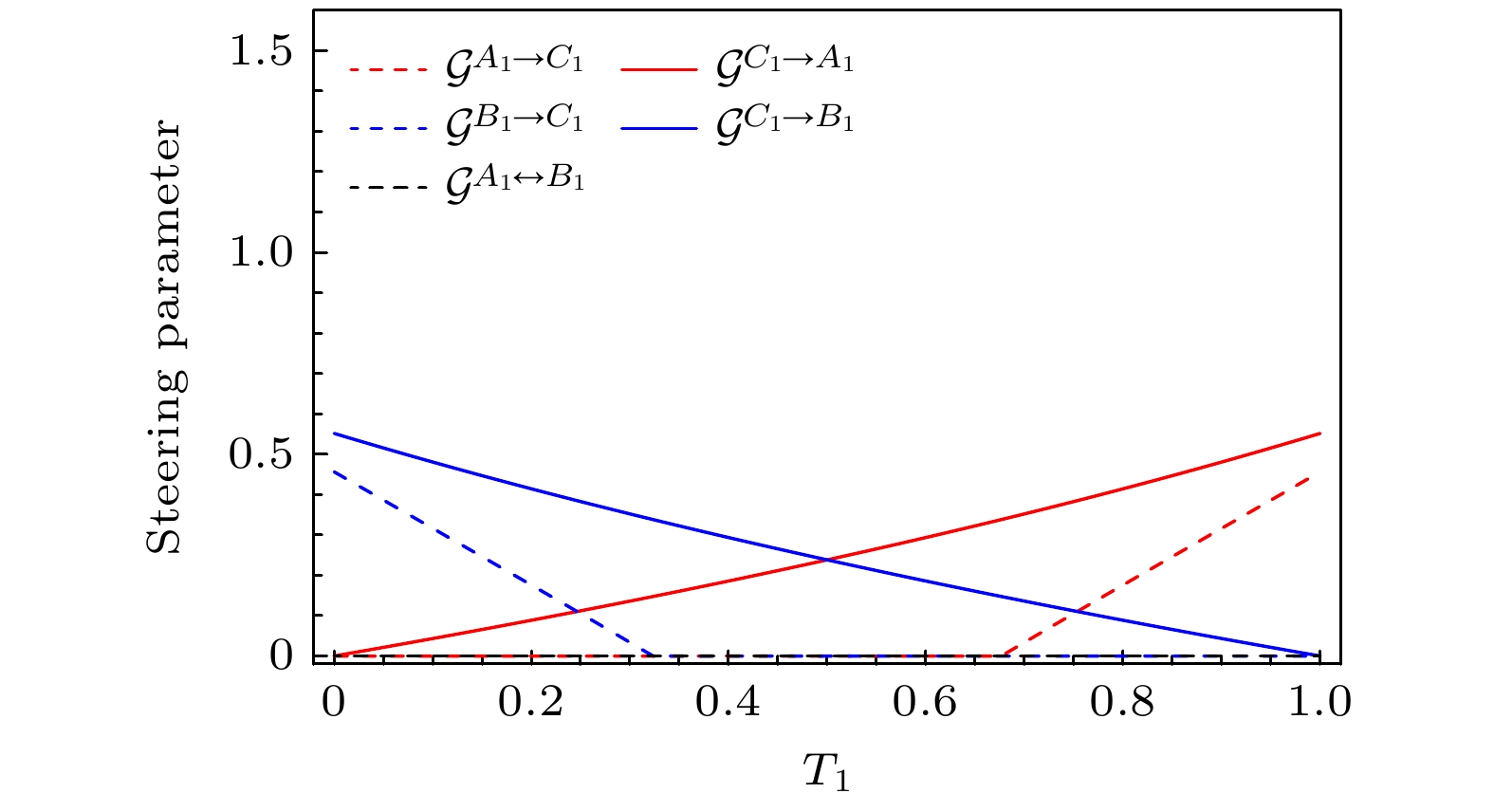
设两个四波混频过程的强度增益${G_1} = {G_2} = 2$, 接下来分析输出模式${\hat A_1}, {\hat B_1}$和${\hat C_1}$之间的导引特性随线性分束器BS1的透射率${T_1}$的变化. 图3表明了方案一中任意两模间的导引随透射率${T_1}$的变化关系. 从图3可以看出, 网络A中的模$ {\hat A_1} $与${\hat B_1}$之间没有导引, 网络B中的模${\hat C_1}$可以确定性地导引模$ {\hat A_1} $和${\hat B_1}$, 而反方向的导引$ {\hat A_1} \to {\hat C_1} $只存在于${T_1} > 0.68$, 模${\hat B_1} \to {\hat C_1}$的导引只存在于${T_1} < 0.32$. 因此, 当${T_1} < 0.68$时, 可以实现${\hat C_1}$对$ {\hat A_1} $的单向导引, 当${T_1} > 0.32$时, 可以实现${\hat C_1}$对${\hat B_1}$的单向导引.

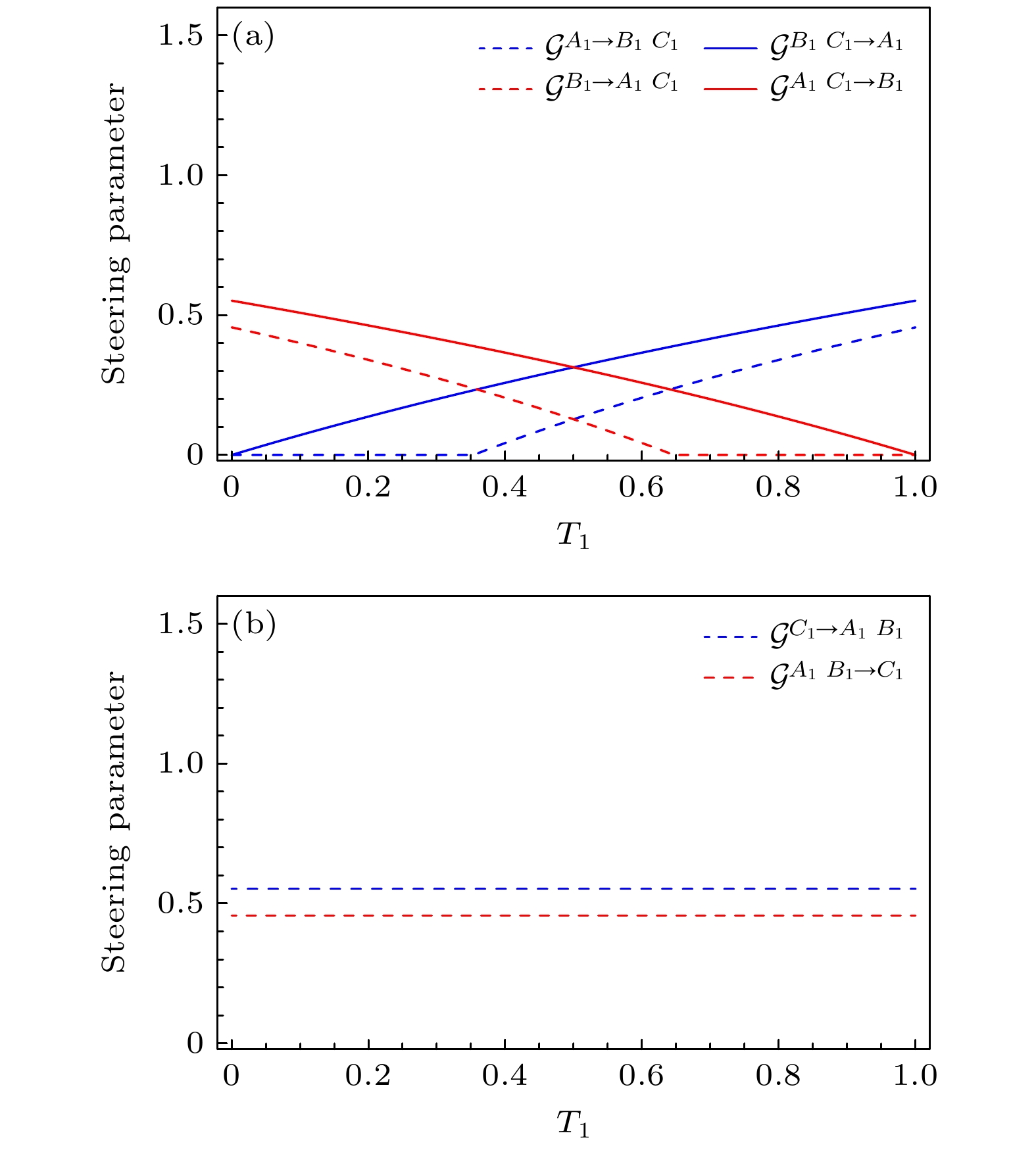
图4是一个模式与另外两个模式之间的导 引关系随透射率${T_1}$的变化. 图4(a)是模式$ {\hat A_1} $和 ${\hat B_1}$分别作为导引方和被导引方的导引关系. 图4(b)是模式$ {\hat C_1} $作为导引方和被导引方的导引关系. 在图4(a)中, 当${T_1} < 0.35$时, 存在组合$( {{{\hat B}_1}{{\hat C}_1}} )$对 模$ {\hat A_1} $的单向导引, 当${T_1} > 0.35$时, 单向导引变为双向不对称导引; 当${T_1} < 0.65$时, 组合$( {{{\hat A}_1}{{\hat C}_1}} )$ 对${\hat B_1}$存在双向不对称导引, 当${T_1} > 0.65$时, 存在组合$( {{{\hat A}_1}{{\hat C}_1}} )$对${\hat B_1}$的单向导引. 在图4(b)中, 在整个范围内, 组合$( {{{\hat A}_1}{{\hat B}_1}} )$与模$ {\hat C_1} $存在双向不对称 导引.

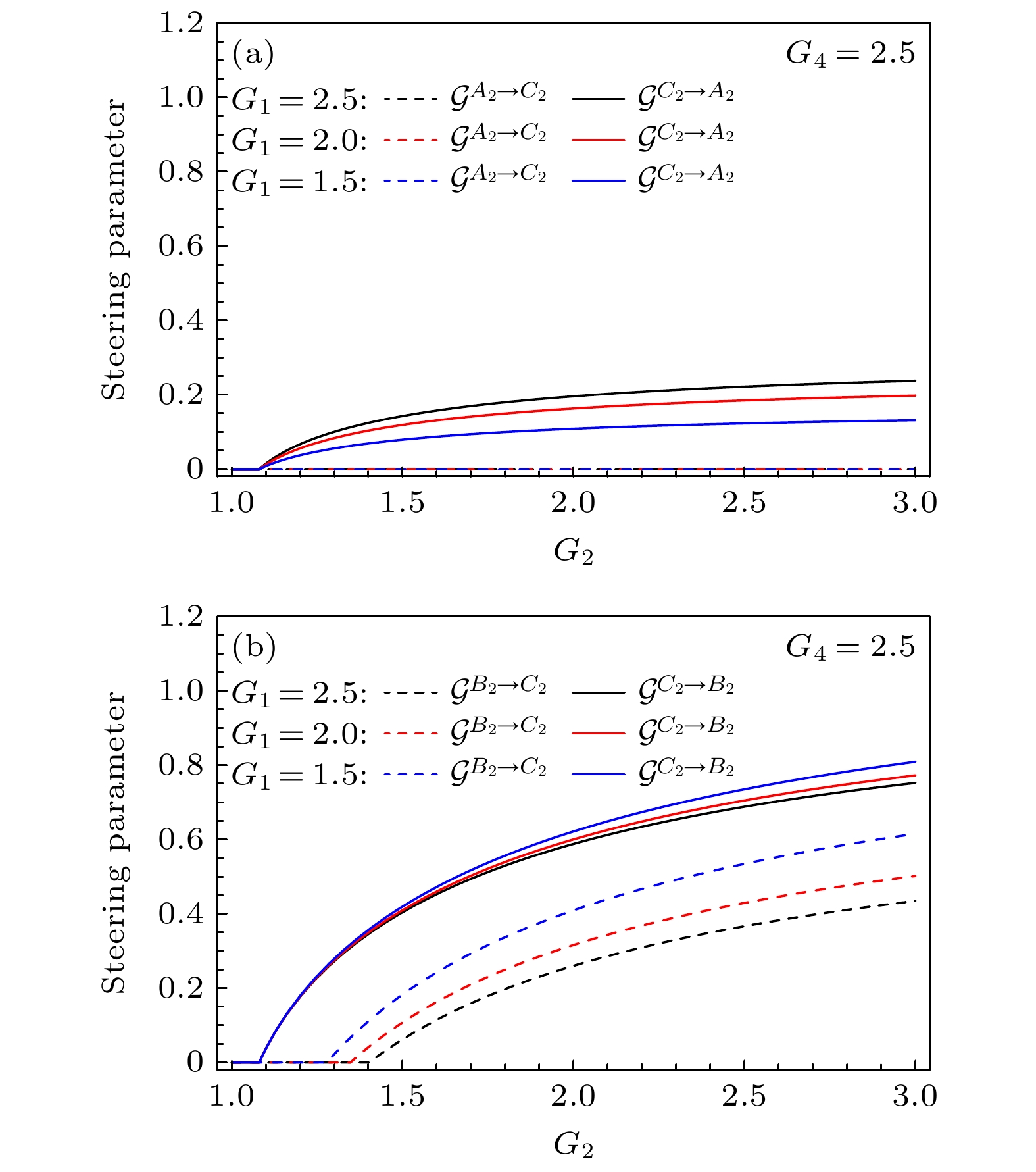
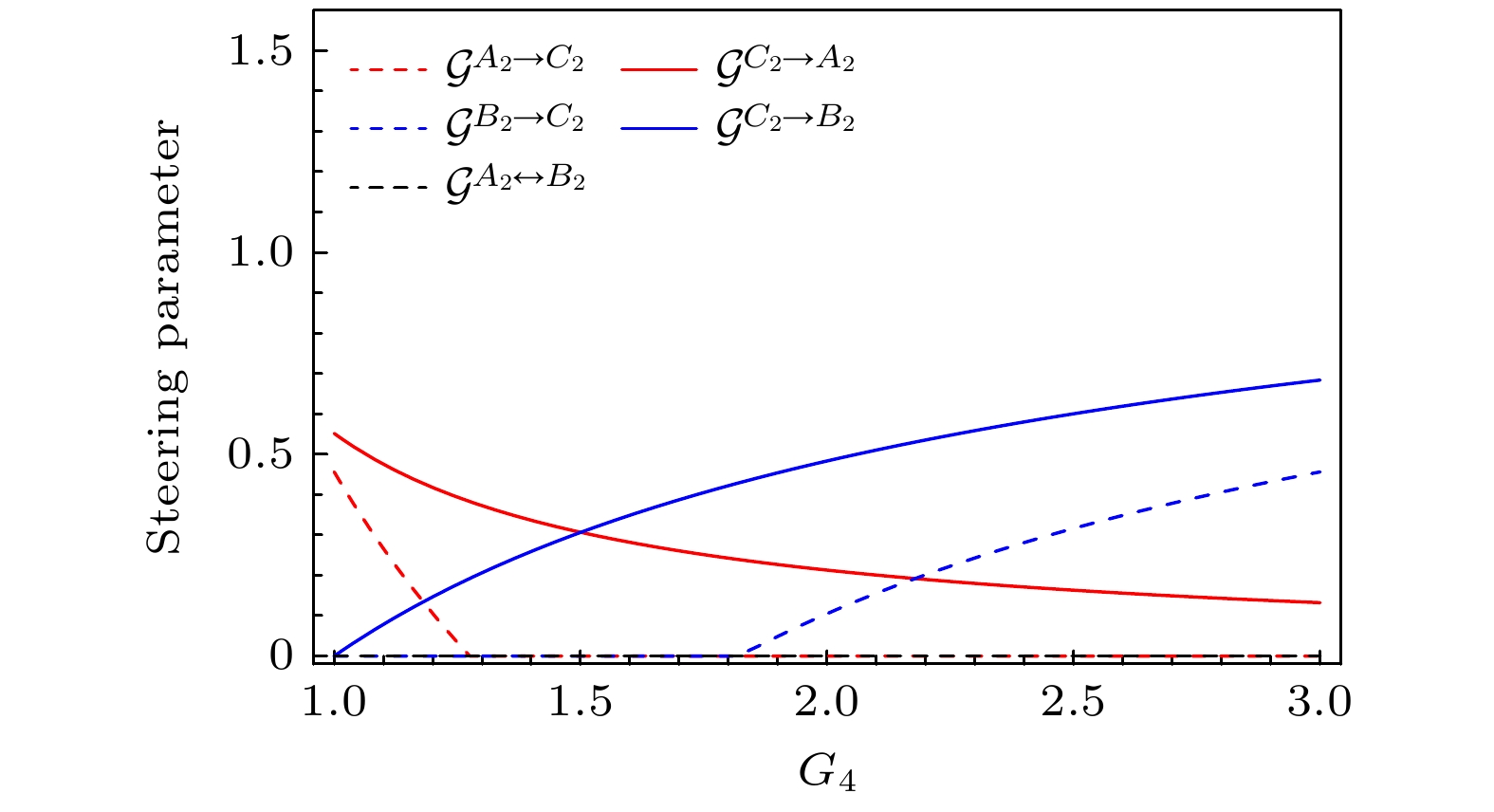
基于非线性分束器产生的三组份纠缠态与两组份纠缠态交换, 对输出模式${\hat A_2}, {\hat B_2}$和${\hat C_2}$之间的导引特性进行分析. 图5是${G_4} = 2.5$时, 在不同的增益$ {G_1} $下, 任意两模之间的量子导引随增益$ {G_2} $的变化关系. 与方案一相同, 从图5可以看出, 当增益$ {G_2} $大于阈值1.08时, 任意两模之间的量子导引随着增益$ {G_2} $的增大而增大. 接下来分析增益$ {G_1} $对两模间导引能力的影响, 从图5(a)可以看出, 模${\hat A_2}$和${\hat C_2}$间的导引随着$ {G_1} $的增大, 导引能力也随之增大. 从图5(b)可以看出: 模${\hat B_2}$和${\hat C_2}$之间的导引随着$ {G_1} $值的增大, 导引能力降低; 而增益$ {G_1} $越小, 实现双向导引$ {\mathcal{G}^{{C_2} \leftrightarrow {B_2}}} $所需要的增益$ {G_2} $值越小. 因此, 在给定的$ {G_2} $取值范围内, 增益$ {G_1} $越大, 单向导引范围越大.

图6是当${G_1} = {G_2} = 2$时, 方案二中任意两模之间的量子导引随四波混频过程FWM4的增益${G_4}$的变化. 与方案一相同, 网络A中的模式$ {\hat A_2} $与${\hat B_2}$之间没有导引; 网络B中的模${\hat C_2}$可以确定性地导引模$ {\hat A_2} $和${\hat B_2}$, 而$ {\hat A_2} $对${\hat C_2}$的导引只存在于$1.0 < {G_4} < 1.27$, 模${\hat B_2}$对${\hat C_2}$的导引只存在于${G_4} > 1.83$. 从图6可以看出, 通过调节四波混频过程FWM4的增益值${G_4}$, 可以实现$ {\hat A_2} $与$ {\hat C_2} $、${\hat B_2}$与$ {\hat C_2} $之间单向、双向导引的自由操控. 如图6中的红色虚线和红色实线所示, 模${\hat A_2} \to {\hat C_2}$及${\hat C_2} \to {\hat A_2}$的导引能力随着${G_4}$值的增大而降低; 如图6中的蓝色虚线和蓝色实线所示, 模${\hat B_2} \to {\hat C_2}$及${\hat C_2} \to {\hat B_2}$之间的导引能力随着${G_4}$值的增大而提高. 这是因为增大四波混频过程FWM4的增益${G_4}$, 增强了模${\hat B_2}$和${\hat C_2}$的量子关联性, 但在四波混频过程FWM4引入的真空噪声, 削弱了模${\hat A_2}$和${\hat C_2}$之间的量子关联性.

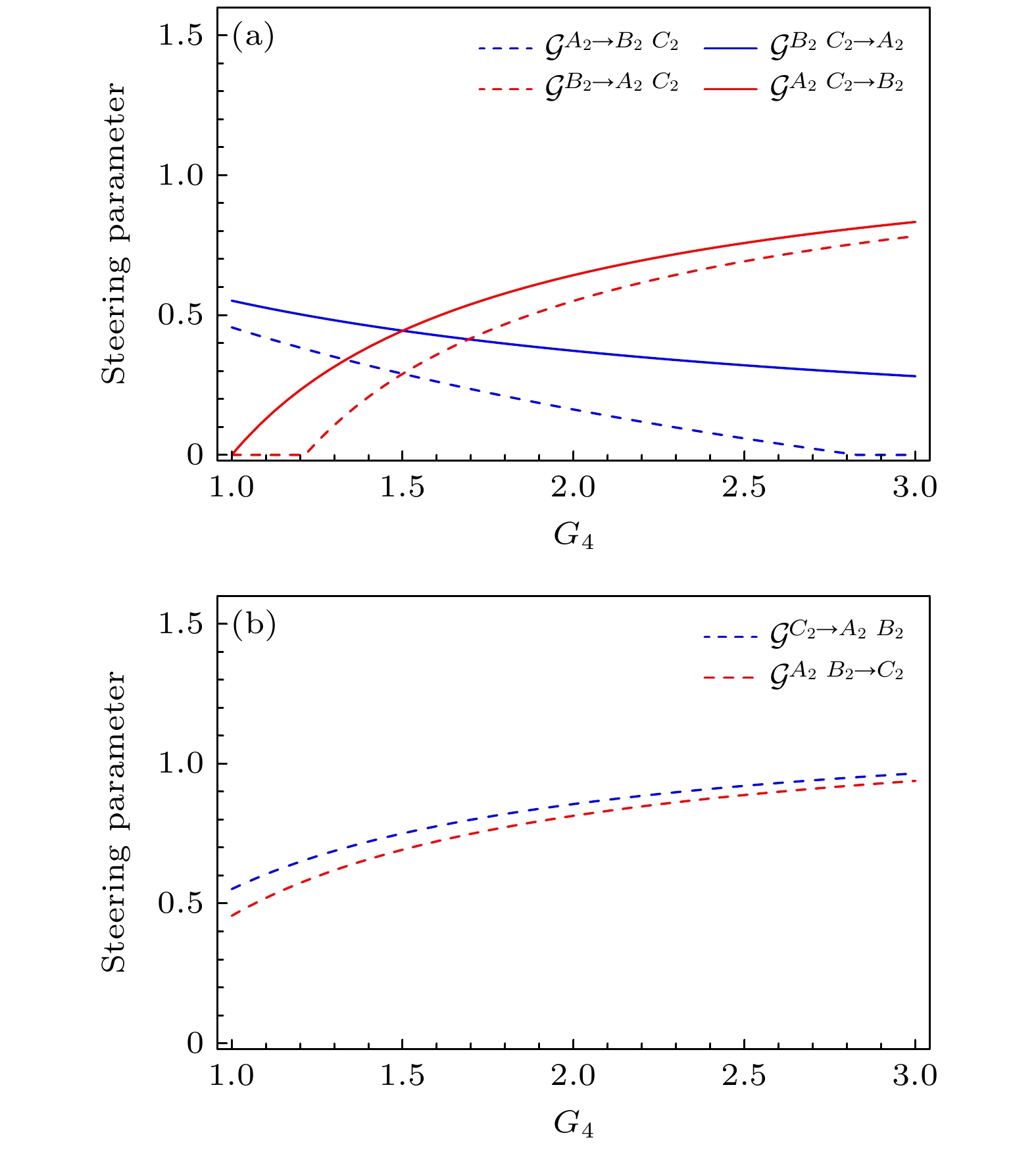
图7是一个模式与另外两个模式组合之间的导引随增益${G_4}$的变化. 在图7(a)中, 当${G_4} < 1.2$时, 存在单向导引$ {\mathcal{G}^{{A_2}{C_2} \to {B_2}}} $; 当${G_4} > 2.8$时, 存在单向导引$ {\mathcal{G}^{{B_2}{C_2} \to {A_2}}} $, 在其余区域存在双向不对称导引. 可以看出, 通过对增益${G_4}$的调节, 可以调节不同组合间的导引情况. 在图7(b)中, 在整个范围内, 组合$( {{{\hat A}_2}{{\hat B}_2}} )$与模$ {\hat C_2} $存在双向不对称导引, 且导引随着增益${G_4}$的增大而增大.

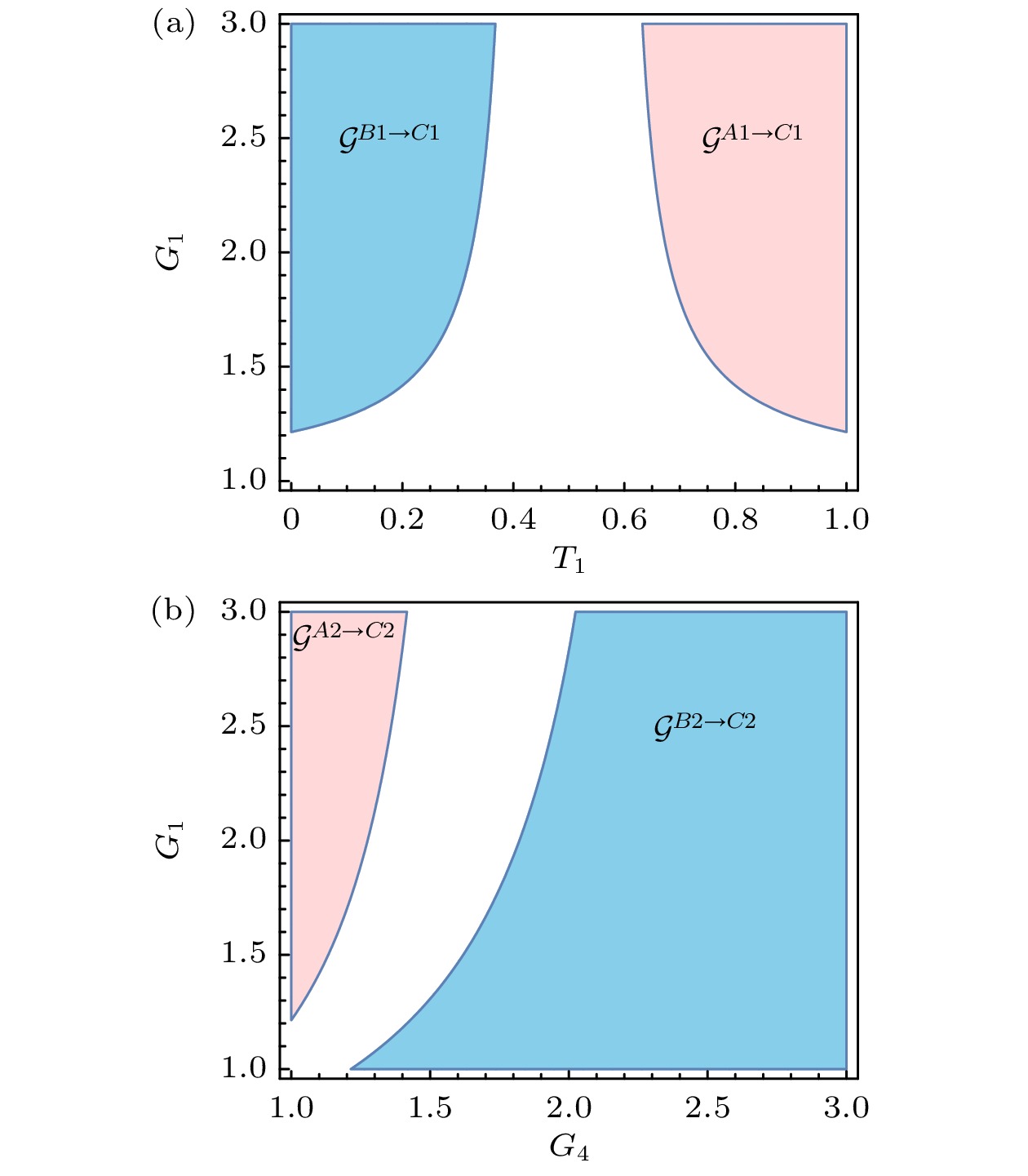
分析三组份输出态中, 网络A的两个模式分别对网络B中模式的导引. 图8(a)表示的是方案一的导引单配性关系, 导引$ {\mathcal{G}^{{A_1} \to {C_1}}} $和$ {\mathcal{G}^{{B_1} \to {C_1}}} $随四波混频过程FWM1的增益${G_1}$和线性分束器BS1透射率${T_1}$的变化. 当$1.0 < {G_1} < 1.2$时, 无论透射率${T_1}$为何值, 导引$ {\mathcal{G}^{{A_1} \to {C_1}}} = {\mathcal{G}^{{B_1} \to {C_1}}} = 0 $. 图8(b)表示的是方案二的导引单配性关系, 导引$ {\mathcal{G}^{{A_2} \to {C_2}}} $和$ {\mathcal{G}^{{B_2} \to {C_2}}} $随四波混频过程FWM1和FWM4的增益${G_1}$和${G_4}$的变化. 当$1.0 < {G_1} < 1.2$时, 选取合适的${G_4}$值, 就可以实现导引$ {\mathcal{G}^{{B_2} \to {C_2}}} $. 由此可以看出, 方案二与方案一相比, 可以更加灵活地操控量子导引的单配性关系. 这也充分说明, 方案二中的非线性分束器(四波混频过程FWM4)不仅可以将四波混频腔FWM1产生的导引分配, 还可以产生更丰富的导引.

本文基于一个三组份纠缠态与两组份纠缠态, 利用四波混频低噪声放大的特点, 实现了无需测量的全光学量子导引交换, 无论三组份纠缠态是由四波混频过程联合线性分束器或非线性分束器产生, 在导引交换操作后, 原本独立的无直接相互作用的两个纠缠态产生了量子导引. 通过对交换后导引特性的分析, 这两个方案都表现出丰富的多组份导引类型, 分别对线性分束器BS1的透射率和四波混频过程增益的调节, 都可以实现单向导引和双向不对称导引. 四波混频过程联合非线性分束器产生三组份纠缠态的方案, 不仅显著提升了导引能力, 还可以在更大的范围内灵活操控量子导引的单配性关系. 这种多组份全光学量子导引交换方法为单向量子通信和量子信息处理提供了新的可能性, 使得量子资源的利用更加高效和可控.