首页
登录
注册
下载:
-
介质阻挡放电(dielectric barrier discharge, DBD)被认为是产生低温等离子体经济、广泛、可靠的方法之一[1–3]. 它被广泛应用于表面处理[4]、臭氧生成[5,6]、催化[7,8]、生物医学[9,10]和材料沉积[11]等各种技术领域. 一般来说, DBD在空间中可以表现出3种模式: 大量随机分布的放电细丝形成的丝状放电模式, 具有时空分布规律的微放电组成的斑图模式, 均匀或弥散模式[12,13]. 在一定的条件下, 使用氦气或氖气作为工作气体, 比较容易实现均匀或弥散放电[14–16]. 当工作气体为氩气或混合气体时, 最常见的是丝状放电模式[17,18]. 在合适的条件下, 电极间的微放电通道会自组织形成具有精细和有序的宏观结构的斑图[19,20]. 在过去20年里, DBD系统中形成的斑图引起了广泛的关注[21]. 电压幅值[22]、驱动频率[23]、间隙宽度[24]、气体含量[25]、气体压力[26]等实验条件都会对斑图的结构产生影响. 此外, 如果放电区域存在边界, 边界附近区域的电场会被扭曲, 使边界附近的电场和壁电荷分布与边界内部区域的分布不同, 进而影响自组织斑图的形成与演化规律[27–29]. 通过改变实验条件, 研究者们观察到许多空间规则稳定的斑图, 包括方形斑图[30,31]、蜂窝六边形斑图[32]、条纹斑图[33]、同心环斑图[34]和超晶格斑图[35]. 实验发现, 空间规则的斑图在 时间上也呈现规律性的发展过程[36,37]. Pan等[38]发现了具有暗放电的蜂窝-Kagome六边形超晶格斑图, 其时空结构是由3个子晶格交错叠加而成, 每半个电压周期内有3个电流脉冲, 其中每一个电流脉冲对应一套子晶格. Li等[39]发现了一个由5种子晶格构成的三维斑图, 每半个电压周期内有3个电流脉冲, 部分电流脉冲中包含2个子晶格放电, 斑图的时空结构是子晶格交错叠加的结果. 这说明斑图的演化过程具有多样性, 其演化过程的不同与形成机理有关, 因此, 通过对演化过程的分析可以对其机理进行深入研究.
本文设计了一种特殊的组合气隙, 在利用正六边形和方形组成的双边界条件下观察到一系列新斑图. 利用增强电荷耦合设备(ICCD)拍摄短曝光时间的照片研究了方形点阵斑图的时间演化行为, 利用发射光谱, 对方形点阵斑图的等离子体参数进行了诊断. 该斑图丰富了DBD中斑图的多样性, 相关研究对其他实验系统中斑图的研究提供理论参考.
-
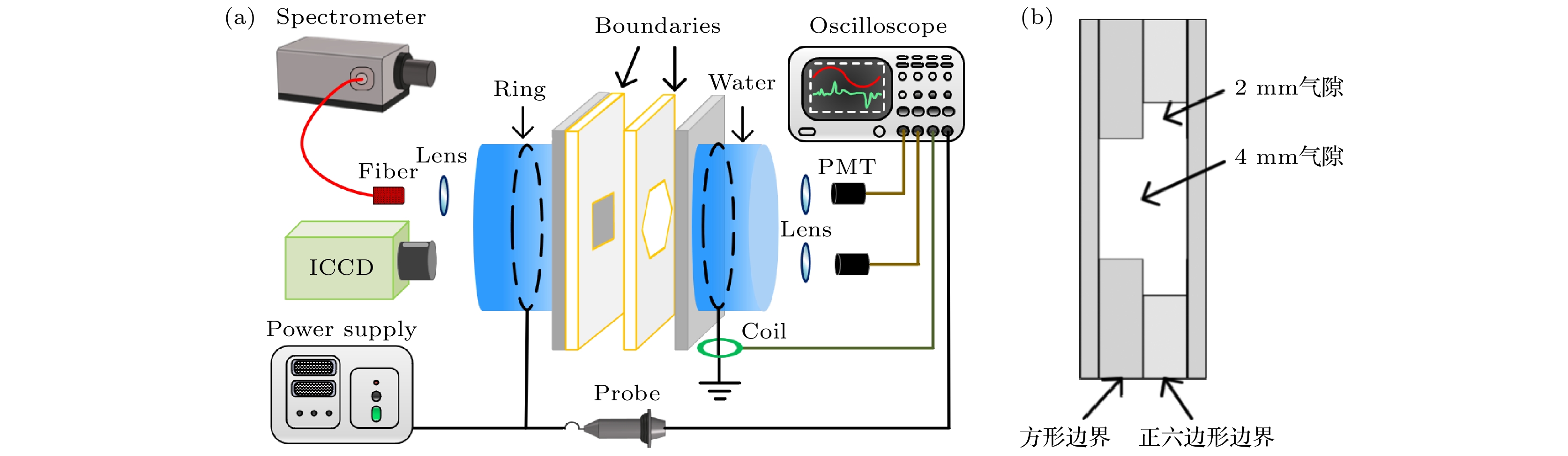
实验装置示意图如图1(a)所示. 两个内径为80 mm的圆柱形容器相对放置, 两端分别用1 mm厚的石英玻璃板密封并作为DBD的电介质层. 在容器内注满水, 将两个铜环分别浸入水中, 形成了DBD的水电极. 其中一个铜环与正弦交流电源(南京苏曼 CTP-2000 K)相连, 另一个铜环接地. 将两个厚度分别为2 mm的方形孔洞(边长为20 mm)和正六边形孔洞(边长为20 mm)的石英玻璃框架贴紧固定在两个水电极中间并压紧. 介质层与石英玻璃框架的排列方式如图1(a)所示, 实验时, 两个石英玻璃框架贴紧并被固定在两个石英介质中间并压紧, 如图1(b)侧视图所示. 即图中四边形区域内的气隙距离是4 mm, 四边形边界与六边形边界所包围的区域的气隙距离为2 mm. 整个装置被放置在装有混合气体(氩气75%, 空气25%, 气压20 kPa)的真空室中. 外加电压由高压探头(Tektronix P6015A)测量, 放电电流由电流探头(Tektronix TCPA 300)测量. 放电的发光信号通过石英透镜后由光电倍增管(PMT) (ET 9130/100B)测量. 外加电压、放电电流以及发光信号的波形均通过示波器(Tektronix DPO4104)记录和显示. 放电图片由数码相机(Canon EOS 5D)和增强型电荷耦合设备(ICCD)(Andor DH334T)拍摄. 利用自制的触发器将激励DBD的正弦信号转换为与之同步的晶体管逻辑(transistor-transistor logic, TTL)信号, 用于触发ICCD和示波器. 由于放电时刻相对于激励电压存在一定抖动, 为了实现ICCD快门和放电的精确同步, 将TTL和放电发光信号同时输入示波器, 通过调节ICCD的延迟时间在示波器上可以获得ICCD相对于放电的曝光时刻. 放电的发光信号经透镜汇聚后, 通过光纤(PI LG- 455-020-1)传入光谱仪(PI ACTON SP2750), 采集放电的发射光谱.
-
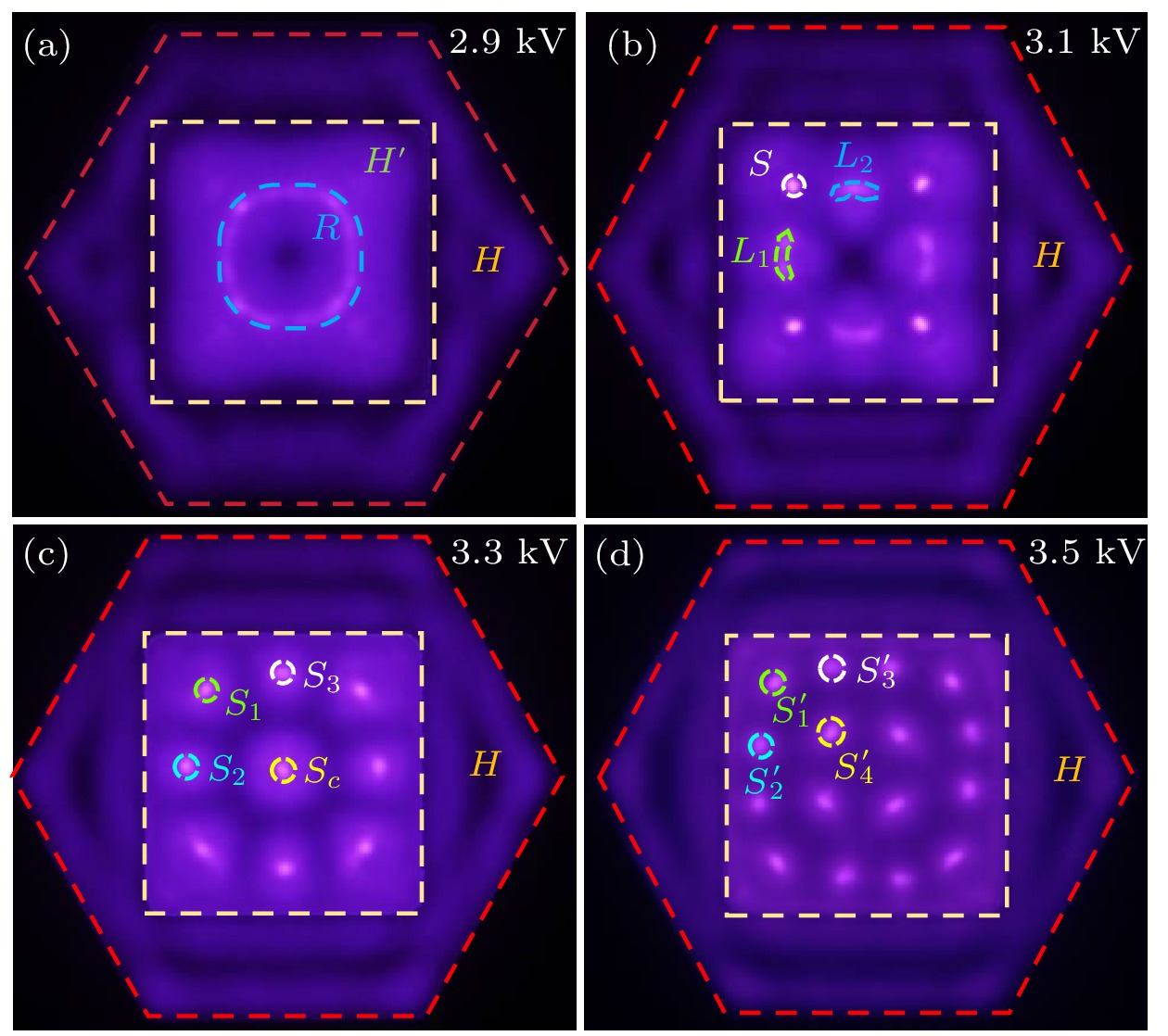
图2(a)—(d)所示为随外加电压变化的放电斑图. 当外加电压峰值Va为2.9 kV时, 形成了一个单环斑图, 如图2(a)所示, 其中2 mm气隙处即正六边形边界至方形边界包围的区域中出现的光晕用H表示, 4 mm气隙的方形边界内出现的环形区域内部用R表示, 环外光晕用H'表示. 当Va增至3.1 kV时, 环型区域分裂为如图2(b)所示的正方形点线结构, 称其为方形点线斑图. 靠近方形边界的顶点附近的发光点用S表示, 靠近纵向边界线的发光线用L1表示, 靠近横向边界线的发光线用L2表示. 随着Va进一步增至3.3 kV, 方形点线斑图中的发光线变为发光点, 同时正中心区域出现一个发光点, 称此斑图为方形点阵斑图, 如图2(c)所示, 方形点阵斑图中方形边界中顶点附近的点用S1表示, 靠近纵向的边界的点用S2表示, 靠近横向边界的点用S3表示, 位于方形边界中心位置的点用Sc表示. 当Va继续升高到3.5 kV时, 方形点阵斑图中S2, S3与Sc分裂形成回形点阵斑图, 如图2(d)所示, 此时回形点阵斑图中方形边界顶点附近的点用
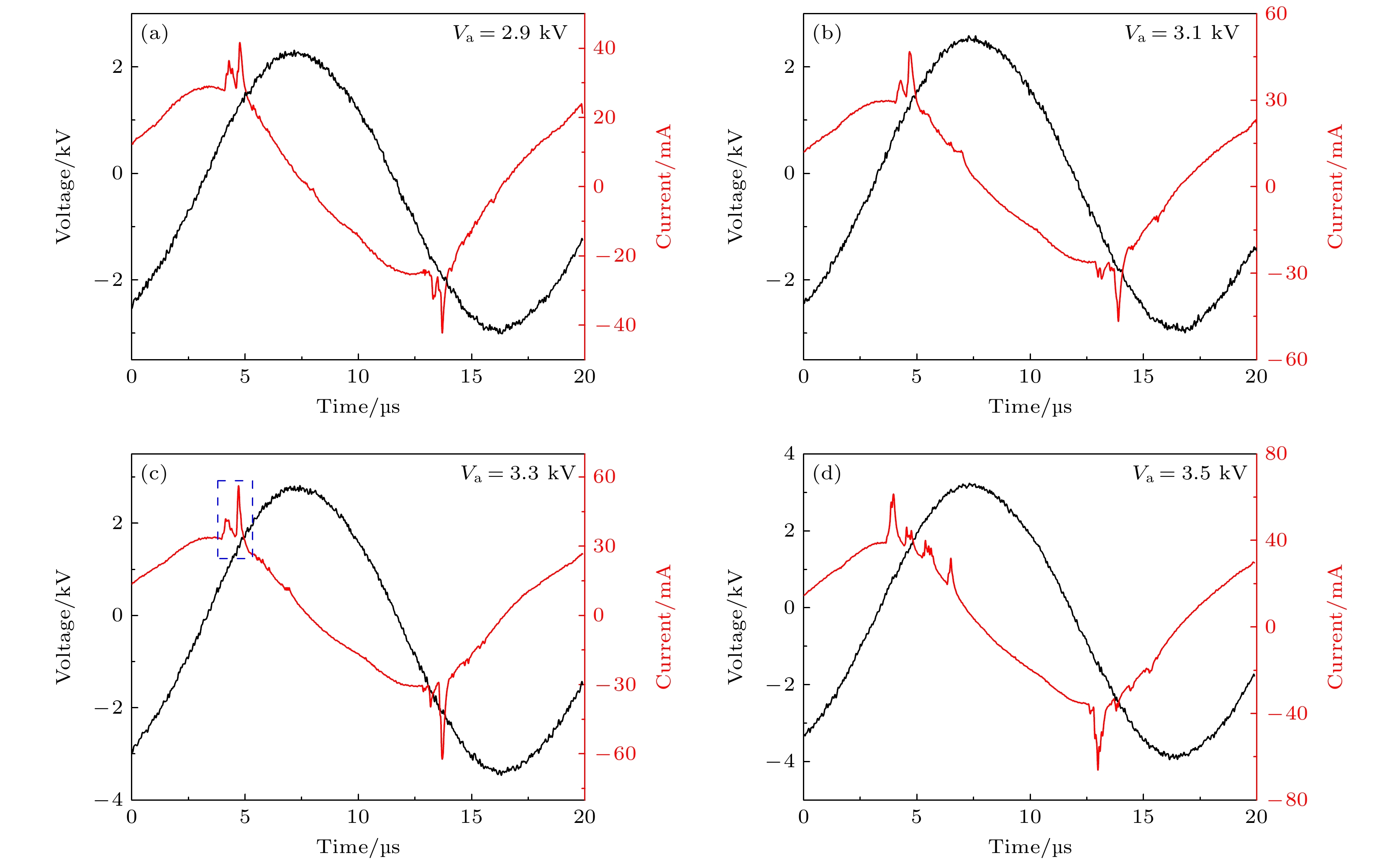
$ S_{1}' $ 表示, 靠近纵向边界的点用$ S_{2}' $ 表示, 靠近横向边界的点用$ S_{3}' $ 表示, 回形中心的点用$ S_{4}' $ 表示.图3(a)—(d)为图2(a)—(d)对应的放电的外加电压和放电电流的波形图. 通过分析发现, 在单环斑图、方形点线斑图和方形点阵斑图中, 每半个电压周期始终存在两个电流脉冲, 并且都是第1个电流脉冲强度小, 第2个电流脉冲强度大. 而对于回形点阵斑图来说, 每半个电压周期具有4个不同的电流脉冲, 其中第1个电流脉冲的幅值最大.
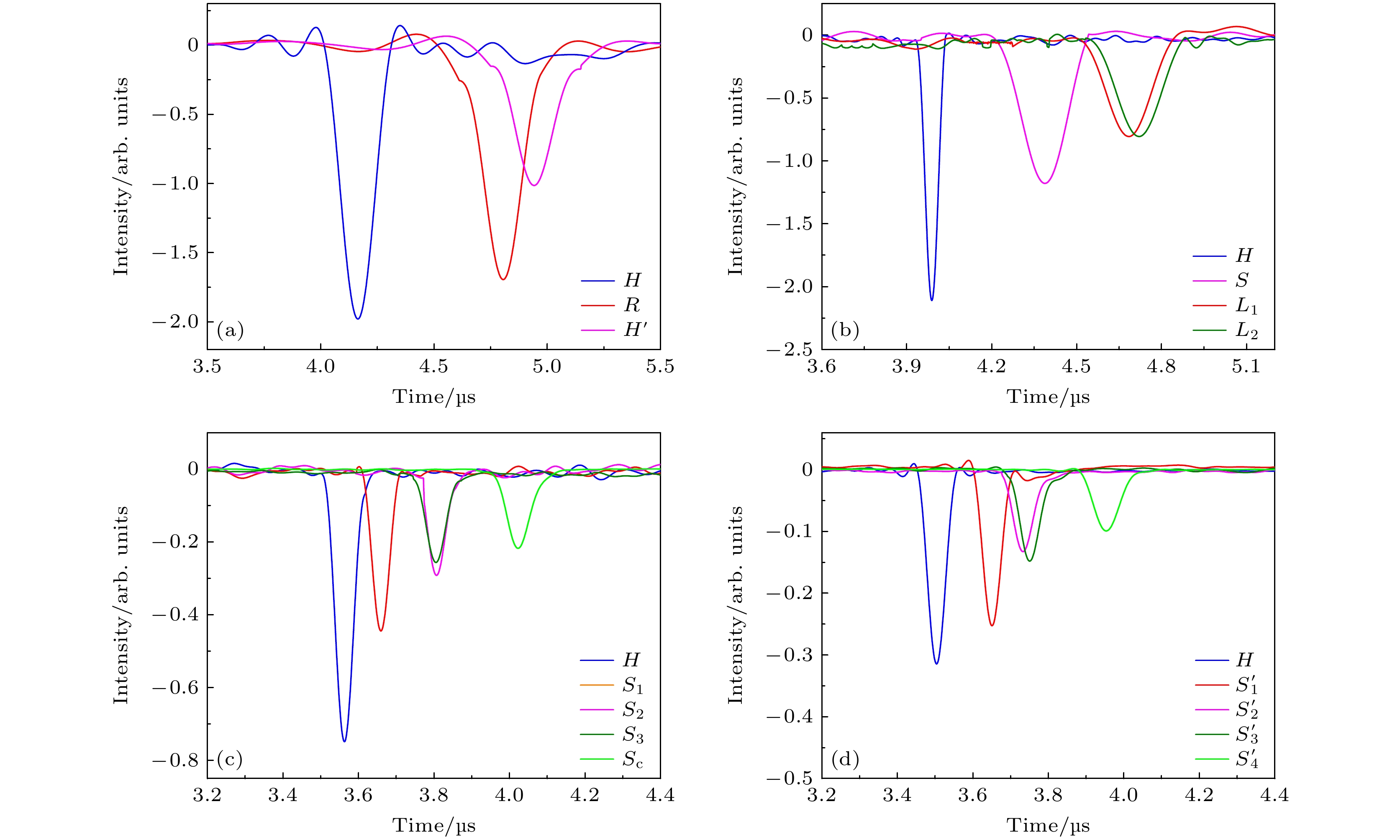
为了研究构成斑图的各个发光点的放电时间行为, 图2中H区域整体变化较小, 选择了整体研究, 其余部分根据斑图的对称性选择了斑图的1/4进行研究. 利用高灵敏度的光电倍增管精确 地测量了图2中4种斑图所标示不同位置的放电细丝的光学特性, 如图4所示. 结果表明4种斑图中都是正六边形边界至方形边界包围的区域(H)处首先放电. 对于单环斑图, 在4 mm气隙内的环形(R)紧接着开始放电, 后产生电晕(H'), 如图4(a)所示. 对于方形点线斑图, 4 mm气隙内先是靠近方形边界的4个顶点附近的发光点(S)先放电, 之后是靠近边界线的发光线(L1与L2)放电, 如图4(b)所示. 对于方形点阵斑图, 4 mm气隙内先是靠近方形边界的4个顶点附近的发光点(S1)先放电, 之后是靠近边界线的发光点(S2与S3)放电, 最后是正中心区域的发光点(Sc)放电, 如图4(c)所示. 对于回形点阵斑图来说, 4 mm气隙内靠近方形边界的4个顶点附近的发光点(
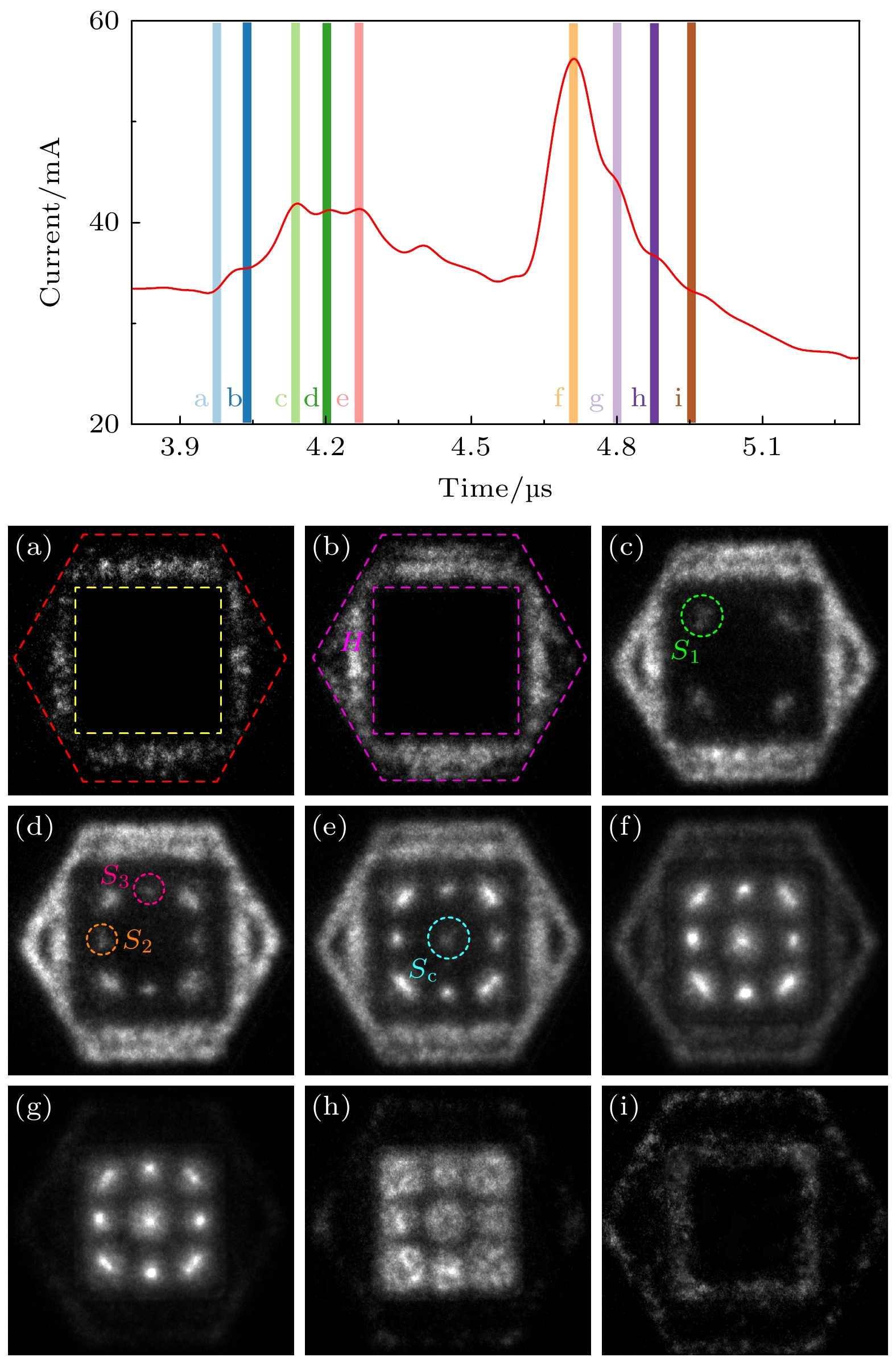
$ S_{1}' $ )先放电, 之后是靠近边界线的发光点($ S_{2}' $ 与$ S_{3}' $ )放电, 最后是回形中心的发光点($ S_{4}' $ )放电. 在4 mm气隙中可以很明显观察到越靠近边界的放电丝放电时间越早, 即对应的放电呈现一个由外向内的整体发展趋势.为了更清楚地研究放电斑图整体的时间演化行为, 利用ICCD相机拍摄了方形点阵斑图短曝光时间的照片. 图5上方的波形图为图3(c)中蓝色线框包围的电流脉冲的局部放大图. 图5下方为放电期间拍摄的单次放电图像(曝光时间texp = 20 ns), 其中图5(a)—(i)的拍摄时刻分别对应图5上方波形图上a—i时刻. 从图5可以发现, 放电最早出现在2 mm气隙区域内(a时刻). 随着放电电流的增大, 放电逐渐填满整个2 mm气隙区域(b时刻). 随后, 在方形边界顶点附近区域S1的位置处出现放电丝(c时刻). 紧接着放电丝出现在S2与S3处(d时刻), 最后放电丝出现在Sc位置(e时刻). 在电流最大值时刻(f时刻), 可以清楚地观察到完整的方形点阵斑图. 随后, 放电开始逐渐减弱, 首先是正六边形边界区域的放电开始减弱(g时刻). 之后正方形边界区域的放电开始整体减弱(h时刻). 在i时刻, 两个边界边缘附近仍有放电, 之后随着电流的减小, 放电逐渐消失. 上述过程中可以发现方形点阵斑图是沿径向方向从外到内逐渐形成的, 这和前面利用光电倍增管测量各个位置的发光信号测量的结果是一致的, 即肉眼看到的方形点阵斑图的形貌, 其实是图5所示演化过程中这些不同位置的点在时间上的叠加.
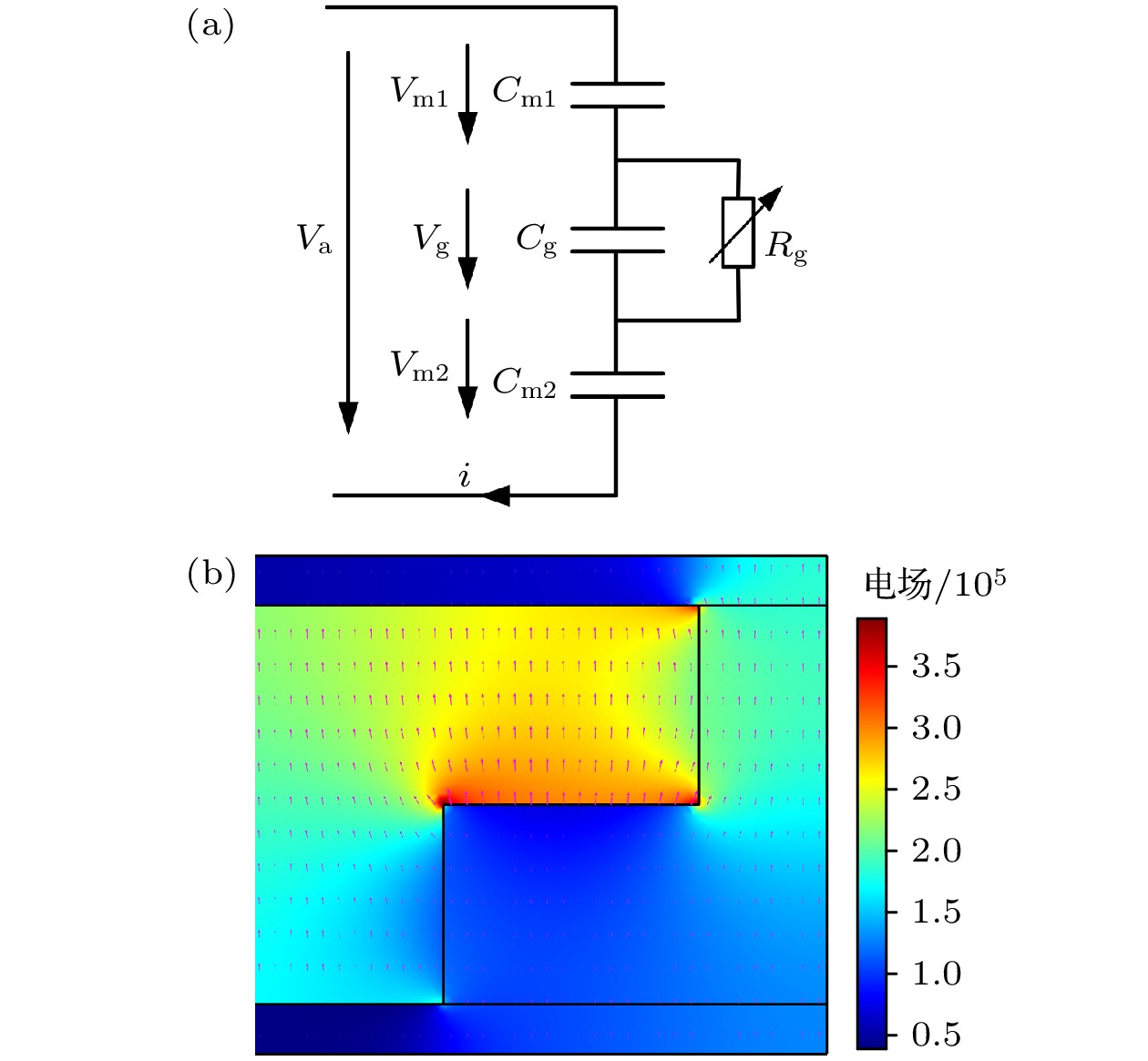
当外加电压相同时, 不同气隙内的电场是不同的. 通过等效电路可以计算出不同气隙的击穿电压进而得到它们的击穿电场[40]. 图6(a)为该介质 阻挡放电的等效电路. 首次击穿之前, 气隙的等效电容Cg和阻挡介质的等效电容Cm1, Cm2呈串联关系, 它们对外加电压Va(t)分压. 气隙电压Vg(t)的升高完全依赖于Va(t)的升高, 只有当Va(t)达到一定数值, 使得Vg(t)达到气隙的静态击穿电压Vb0, 气隙击穿才有可能发生. Vb0可由(1)式计算获得. 实验中不同气隙的阻挡介质厚度不同, 因此不同的Cg对应不同的Cm1, Cm2. Cm1, Cm2可由平板电容公式计算得到. Cm为阻挡介质等效电容之和, 通过(2)式计算获得. 击穿电场E可由(3)式得到:
根据(1)—(3)式计算得到2 mm气隙处电场为480 kV/m, 高于4 mm气隙处的电场330 kV/m, 根据气体放电理论, 电场强度大处先放电, 因此正六边形边界区域内(H)首先放电, 这也与图6(b)中静电场仿真结果相吻合, 从图6(b)可以看出, 2 mm气隙处的电场要强于4 mm气隙处的电场. 在后续过程中, 随着外加电压的持续升高, 放电发展到2 mm气隙与4 mm气隙的过渡区域, 如图6(b)所示, 靠近边界处的电场是最强的, 两个边界交汇处即四边形的顶点位置的电场会强于周围其他区域的电场. 因此, 边界的顶角附近位置(S1)会更早的产生放电细丝. 气体放电受多种因素影响, 如电场均匀性、电极形状、气体性质等因素影响气体击穿阈值. 当外加电场强度超过气体击穿阈值时, 气体被击穿, 形成微放电, 并且由于电源极性的转换, 微放电会反复出现在相同位置, 形成微放电通道. 微放电通道形成的同时将会产生正负电荷粒子以及具有激发态的粒子. 在外加电场的作用下, 这些粒子会向正负电极运动, 并最终沉积在介质板上形成壁电荷. 大量壁电荷沉积在介质表面上后会形成一个新的电场, 称为壁电荷场. 壁电荷场与外加电场的方向相反, 因此壁电荷场会熄灭该位置的放电, 同时壁电荷场还会抑制放电通道周围的放电. S1处产生放电细丝后会在该位置形成一个壁电荷场, 该壁电荷场会抑制放电丝周围的放电, 因此 后续放电会在该壁电荷场抑制最弱的位置出现. 由于S2与S3 的位置靠近边界, 并且受到S1处壁电荷场抑制最弱, 因此位于S2与S3处的放电细丝会在S1处放电细丝产生后出现. 后续的放电会受到3个壁电荷场的共同作用, 而Sc是整个边界的几何中心, 受到周围壁电荷场的抑制最弱, 因此, 会在Sc位置产生放电细丝. 这就是放电为何沿径向由外向内产生的原因.
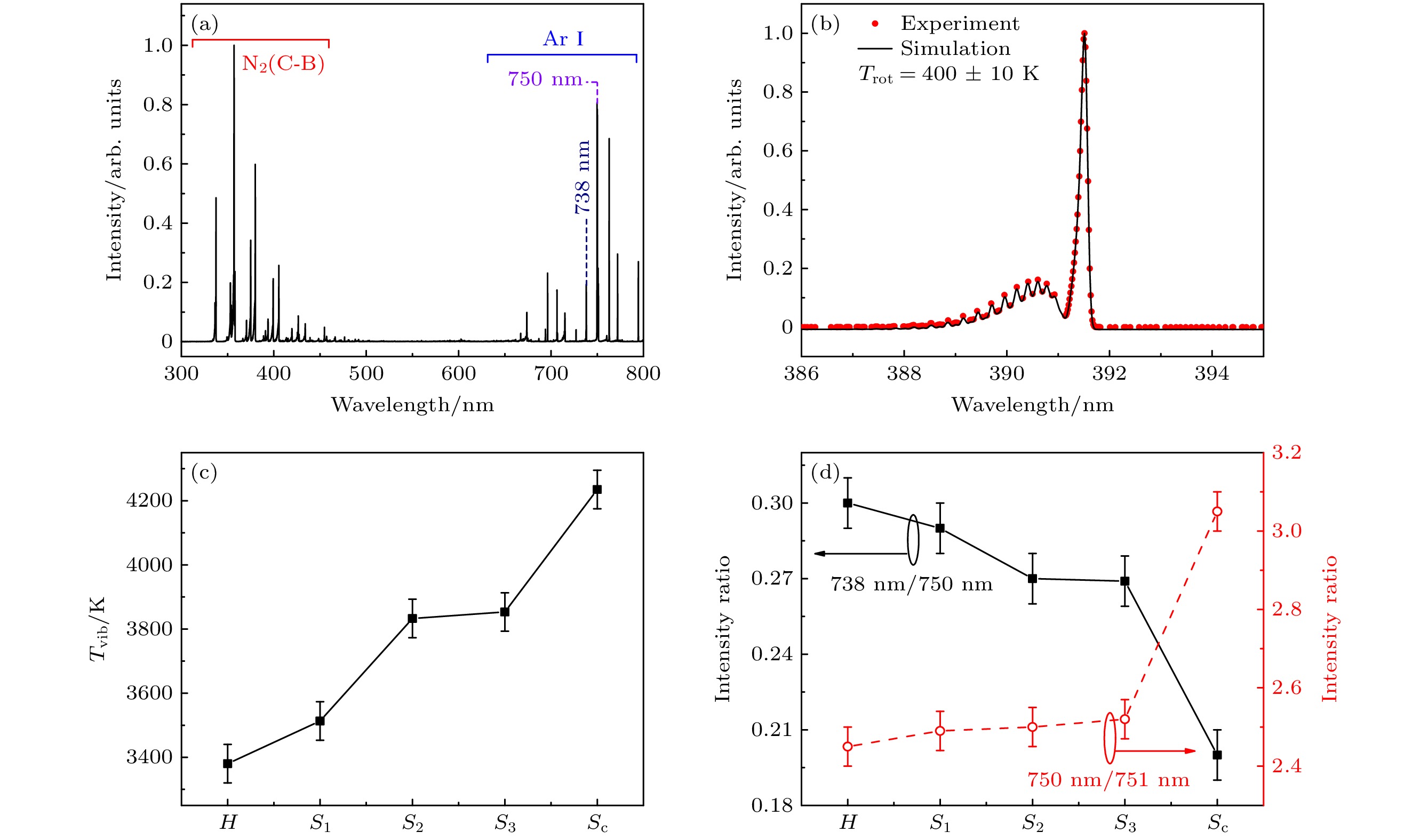
图7(a)显示了方形点阵斑图在300—800 nm范围内的发射光谱. 从谱线的分布可以观察到许多分子谱带和原子谱线, 典型的谱线包括N2的第二正带系N2 (C3∏u→B3∏g)、氮分子离子谱线
$ {\text{N}}_{2}^{+} $ (B-X)和Ar I(4p→4s)的发射谱线, 本文利用上述谱线估算了各个微放电通道的等离子体参数. 利用391.4 nm的氮分子离子谱线$ {\text{N}}_{2}^{+} $ (B-X)进行拟合计算了分子转动温度, 如图7(b)所示, 非平衡等离子体的气体温度(Tg)近似等于其分子转动温度(Trot)[41], 实验发现各个微放电通道的分子转动温度基本相同, 约为(400±10) K; 利用N2 (C3∏u→B3∏g)氮分子谱线进行玻尔兹曼拟合[42], 计算了分子振动温度如图7(c)所示, 可以看到, 沿径向方向从外到内分子振动温度逐渐升高. 根据碰撞-辐射模型, 谱线738 nm/750 nm和750 nm/751 nm的强度比分别可用于表征电子密度(ne)和电子温度(Te)[43]. 图7(d)所示为方形点阵斑图各个位置的ne和Te的变化趋势, 从图7(d)可以看出, ne 沿着径向方向从外到内逐渐减小, Te沿着径向方向从外到内逐渐增大. -
利用一个由正六边形和方形组成的组合边界, 在55 kHz的交流电源激励下产生了多个复杂斑图, 重点研究了最具代表性的方形点阵斑图. 结果表明方形点阵斑图在每半个电压周期内呈现两个强度不同的电流脉冲, 构成方形点阵斑图的各个放电细丝其实是放电沿径向从外向内逐渐击穿的过程. 利用ICCD拍摄了方形点阵斑图的时间演化过程, 并从理论上分析了其形成机理, 发现其形成过程是外加电场和壁电荷场共同作用的结果. 通过对方形点阵斑图的等离子体参数诊断结果表明, 气体转动温度为(400 ± 10) K, 分子振动温度与电子温度沿着径向方向从外到内逐渐增大, 电子密度沿着径向方向从外到内逐渐减小. 这些结果丰富DBD斑图的时空结构, 促进对介质阻挡放电中斑图放电特性的研究.
双气隙下介质阻挡放电斑图的放电特性与参数诊断
Discharge characteristics and parameter diagnosis of dielectric barrier discharge patterns in double-gap configuration
-
摘要: 斑图放电是介质阻挡放电的重要模式之一, 在众多领域具有广泛的应用前景. 本工作在氩气/空气混合气体介质阻挡放电系统中, 采用正六边形和方形组成的双气隙边界, 通过改变实验参数, 获得了多个全新的复杂斑图. 利用光学与电学手段研究了其放电特性及其时间相关性. 结果表明放电斑图在每半个电压周期内均有多次放电并在时间上具有相关性. 利用增强型电荷耦合设备拍摄了方形点阵斑图时间分辨的放电图像, 发现半个电压周期内的多次放电其实是斑图在径向上从外向内逐渐点亮的过程, 理论分析了该斑图的形成机理. 采集了方形点阵斑图的发射光谱, 通过线比法和玻尔兹曼拟合法探究了方形点阵斑图的电子密度、电子温度、分子振动温度、分子转动温度的变化. 结果显示电子密度沿着径向方向从外到内逐渐减小, 电子温度与分子振动温度沿着径向方向从外到内逐渐增加, 分子转动温度几乎不变.Abstract: Pattern discharge is a common mode in dielectric barrier discharge (DBD) and has broad application prospects in various industrial fields, such as material surface treatment, environmental monitoring, and biomedical applications. In this work, a mixed gas of 75% argon and 25% air is used to generate a pattern discharge. A double-gap boundary composed of hexagonal configuration and square configuration is employed, and the gas pressure is fixed at 20 kPa. By varying the applied voltage amplitude, single-ring pattern, square-point-line pattern, square lattice pattern, and annular-lattice pattern are obtained for the first time. The discharge characteristics and their temporal correlation are studied using both optical method and electrical method. The results show that the discharge patterns exhibit multiple discharges in each half of the voltage cycle, and these discharges are temporally correlated with each other. Time-resolved discharge images of the square lattice pattern are captured using an enhanced charge-coupled device (ICCD). The experimental results reveal that multiple discharges in a half-voltage cycle correspond to the ignition process of the pattern in the radial direction from the outside to the inside. The morphology of the square lattice pattern observed by the naked eye is actually the result of the temporal superposition of luminescence from points at different positions in the evolution process. The formation mechanism of this pattern is analyzed through electric field simulations and theoretical calculations. Plasma parameters are diagnosed by collecting the emission spectrum of the square dot-lattice pattern. The results show that the electron density gradually decreases radially from the outer region to the inner region, while the electron temperature and molecular vibrational temperature increase radially from the outer region to the inner region, and the molecular rotational temperature remains almost unchanged. The temporal evolution of the square lattice pattern is shown in the following figures, where the current waveform marks the timing of each frame of ICCD imaging for the complete square lattice pattern.
-
Key words:
- discharge barrier discharge /
- pattern discharge /
- spatio-temporal evolution .
-
-
图 1 (a)实验装置示意图; (b)气隙结构侧视图
Figure 1. (a) Schematic diagram of the experimental setup; (b) side view of the gap structure.
图 2 不同电压下斑图照片, 曝光时间为0.1 s
Figure 2. Patterned discharges under different applied voltages with an exposure time of 0.1 s.
图 3 不同斑图对应的电压与放电电流的波形图
Figure 3. Waveforms of applied voltage and discharge current for different patterns.
图 5 方形点阵斑图的时间演化, 上方的电流波形中标示了各幅图对应的ICCD拍摄时刻, 曝光时间为20 ns (单次拍摄)
Figure 5. Temporal evolution of the square lattice pattern. The current waveform shows the ICCD shooting time of each picture, and the exposure time is 20 ns (single shot).
图 6 (a) 介质阻挡放电等效电路图; (b) 外加电场仿真结果
Figure 6. (a) Equivalent circuit diagram of dielectric barrier discharge; (b) simulation results of applied electric field.
图 7 (a) 300—800 nm放电的发射光谱; (b)
$ {\text{N}}_{2}^{+} $ (B-X)转动谱带拟合结果; (c)方形点阵斑图不同位置处的Tvib; (d)方形点阵斑图不同位置处的Te和neFigure 7. (a) 300–800 nm optical emission spectrum from the discharge; (b) fitting result of rotational bands of the
$ {\text{N}}_{2}^{+} $ (B-X); (c) Tvib at different positions in the square lattice pattern; (d) Te and ne at different positions in square lattice pattern. -
[1] Zhang J, Tang W W, Wang Y H, Wang D Z 2023 Plasma Sources Sci. Technol. 32 055005 doi: 10.1088/1361-6595/accca8 [2] Li J Y, Zhou D S, Rebrov E, Tang X, Kim M 2024 J. Phys. D: Appl. Phys. 57 395201 doi: 10.1088/1361-6463/ad58ee [3] Fang J L, Zhang Y R, Lu C Z, Gu L L, Xu S F, Guo Y, Shi J J 2024 Chin. Phys. B 33 015201 doi: 10.1088/1674-1056/ad0118 [4] Guan H L, Chen X R, Jiang T, Du H, Paramane A, Zhou H 2020 Chin. Phys. B 29 075204 doi: 10.1088/1674-1056/ab8a3f [5] Li X C, Liu R J, Li X N, Gao K, Wu J C, Gong D D, Jia P Y 2019 Phys. Plasmas 26 023510 doi: 10.1063/1.5063328 [6] Remy A, Geyter N D, Reniers F 2023 Plasma Process. Polym. 20 2200201 doi: 10.1002/ppap.202200201 [7] Hosseini H 2023 RSC Adv. 13 28211 doi: 10.1039/D3RA05580A [8] Li Y W, Yuan H, Zhou X F, Liang J P, Liu Y Y, Chang D L, Yang, D Z 2022 Catalysts 12 203 doi: 10.3390/catal12020203 [9] Song H, Dang Y M, Ki S H, Park S, Ha J H 2024 LWT 207 116637 doi: 10.1016/j.lwt.2024.116637 [10] Domonkos M, Tichá P, Trejbal J, Demo P 2021 Appl. Sci. 11 4809 doi: 10.3390/app11114809 [11] Massines F, Sarra-Bournet C, Fanelli F, Naudé N, Gherardi N 2012 Plasma Process. Polym. 9 1041 doi: 10.1002/ppap.201200029 [12] Akishev Y, Alekseeva T, Karalnik V, Petryakov A 2022 Plasma Sources Sci. Technol. 31 084001 doi: 10.1088/1361-6595/ac8075 [13] Tschiersch R, Nemschokmichal S, Bogaczyk M, Meichsner J 2017 J. Phys. D: Appl. Phys. 50 415206 doi: 10.1088/1361-6463/aa8519 [14] 刘凯, 方泽, 戴栋 2023 物理学报 72 135201 doi: 10.7498/aps.72.20230385 Liu K, Fang Z, Dai D 2023 Acta Phys. Sin. 72 135201 doi: 10.7498/aps.72.20230385 [15] Ran J X, Zhang X X, Zhang Y, et al. 2023 Plasma Sci. Technol. 25 055403 doi: 10.1088/2058-6272/acaa93 [16] Lu X P, Fang Z, Dai D, Shao T, Liu F, Zhang C, Liu D W, Nie L L, Jiang C Q 2023 High Volt. 8 1132 doi: 10.1049/hve2.12382 [17] Brandenburg R 2018 Plasma Sources Sci. Technol. 26 053001 [18] Wang Y Y, Yan H J, Li T, Bai X D, Wang X, Song J, Zhang Q Z 2023 AIP Adv. 13 085327 doi: 10.1063/5.0155171 [19] 万海容, 郝艳捧, 房强, 苏恒炜, 阳林, 李立浧 2020 物理学报 69 145203 doi: 10.7498/aps.69.20200473 Wang H R, Hao Y P, Fang Q, Su H W, Yang L, Li L C 2020 Acta Phys. Sin. 69 145203 doi: 10.7498/aps.69.20200473 [20] Wu K Y, Wu J C, Jia B Y, Ren C H, Kang P C, Jia P Y, Li X C 2020 Phys. Plasmas 27 082308 doi: 10.1063/5.0002697 [21] Ouyang J T, Li B, He F, Dai D 2018 Plasma Sci. Technol 20 103002 doi: 10.1088/2058-6272/aad325 [22] Hao Y P, Han Y Y, Huang Z M, Yang L, Dai D, Li L C 2018 Phys. Plasmas 25 013516 doi: 10.1063/1.5021128 [23] Li X C, Liu R, Jia P Y, Wu K Y, Ren C H, Yin Z Q 2018 Phys. Plasmas 25 013512 doi: 10.1063/1.4998615 [24] Li Z Y, Jin S H, Xian Y B, Nie L L, Liu D W, Lu X P 2021 Plasma Sources Sci. Technol. 30 065026 doi: 10.1088/1361-6595/ac02b1 [25] Zhang Y H, Ning W J, Dai D, Wang Q 2019 Plasma Sources Sci. Technol. 28 075003 doi: 10.1088/1361-6595/ab2520 [26] Zhang J H, Pan Y Y, Feng J Y, He Y N, Chu J H, Dong L F 2023 Plasma Sci. Technol. 25 025406 doi: 10.1088/2058-6272/ac9027 [27] Duan X X, Ouyang J T, Zhao X F, He F 2009 Phys. Rev. E 80 016202 doi: 10.1103/PhysRevE.80.016202 [28] Wang X, Yan H J, Wang Y Y, Yu S Q, Li T, Song J 2023 J. Phys. D: Appl. Phys. 56 105201 doi: 10.1088/1361-6463/acb8c6 [29] Mokrov M S, Raizer Y P 2018 Plasma Sources Sci. Technol 27 065008 doi: 10.1088/1361-6595/aac9fc [30] Hao F, Dong L F, Du T, et al. 2018 Phys. Plasmas 25 033510 doi: 10.1063/1.5001897 [31] Han R, Dong L F, Huang J Y, Sun H Y, Liu B B, Mi Y L 2019 Chin. Phys. B 28 075204 doi: 10.1088/1674-1056/28/7/075204 [32] Sun H Y, Dong L F, Liu F C, Mi Y L, Han R, Huang J Y, Liu B B, Hao F, Pan Y Y 2018 Phys. Plasmas 25 113507 doi: 10.1063/1.5042306 [33] Wei L Y, Dong L F, Fan W L, et al. 2018 Sci. Rep. 8 3835 doi: 10.1038/s41598-018-21855-3 [34] Feng J Y, Dong L F, Wei L Y, Fan W L, Li C X, Pan Y Y 2016 Phys. Plasmas 23 093502 doi: 10.1063/1.4962176 [35] Pan Y Y, Li Y H, Dou Y Y, Fu G S, Dong L F 2022 Phys. Plasmas 29 053502 doi: 10.1063/5.0082128 [36] Liu F C, Liu Y N, Liu Q, et al. 2022 Plasma Sources Sci. Technol 31 025015 doi: 10.1088/1361-6595/ac4dde [37] Li C X, Dong L F, Feng J Y, Huang Y P 2019 Phys. Plasmas 26 023505 doi: 10.1063/1.5066222 [38] Pan Y Y, Feng J Y, Li C X, Dong L F 2022 Plasma Sci. Technol. 24 115401 doi: 10.1088/2058-6272/ac7c62 [39] Li Y H, Pan Y Y, Tian M, Wang Y, He Y N, Zhang J H, Chu J H, Dong L F 2023 Phys. Plasmas 30 033502 doi: 10.1063/5.0129483 [40] Liu S H, Neiger M 2003 J. Phys. D: Appl. Phys. 36 3144 doi: 10.1088/0022-3727/36/24/009 [41] Bruggeman P J, Sadeghi N, Schram D C, Linss V 2014 Plasma Sources Sci. Technol. 23 023001 doi: 10.1088/0963-0252/23/2/023001 [42] Yang F X, Mu Z X, Zhang J L 2016 Plasma Sci. Technol. 18 79 doi: 10.1088/1009-0630/18/1/14 [43] Zhu X M, Pu Y K 2008 Plasma Sources Sci. Technol. 17 024002 doi: 10.1088/0963-0252/17/2/024002 -
图( 7)
计量
- 文章访问数: 84
- HTML全文浏览数: 84
- PDF下载数: 3
- 施引文献: 0