-
自整数量子霍尔效应被观测到以来[1], 关于拓扑物态的研究取得了蓬勃发展, 成为了凝聚态物理的重要研究方向之一. 近年来, 根据体系的维度与对称性等特征, 基于拓扑能带论和拓扑量子场论等理论研究方法, 物理学家们预言了一系列拓扑物态. 例如无需对称性保护的量子反常霍尔态[2-9]、时间反演对称保护的量子自旋霍尔态[10-12]、粒子-空穴对称性保护的拓扑超导态[13,14]等. 实验上, 在凝聚态材料和人工系统中都已成功制备和观测到了多种拓扑态[14-26]. 这些相关理论与实验结果催生了拓扑电子器件的研究和发展.
在拓扑绝缘态的能隙中存在着普通绝缘态中不具有的无能隙边缘态[27,28]. 与传统量子态不同, 这是一种宏观量子态. 它受体系的拓扑序保护, 且对于无序、杂质等不敏感. 理论上, 基于其制备的功能器件不依赖于样品细节, 并且对不同的环境均能表现出鲁棒特性, 这使得宏观调控拓扑量子器件成为可能. 与此同时, 由于拓扑态往往能够锁定载流子的额外自由度, 因此相应量子器件的功能将与这些自由度捆绑, 并超出拓扑态电荷特性的预期. 然而, 拓扑绝缘体材料的边缘态均出现在绝缘体的边界, 其空间分布受到拓扑态材料形状的限制, 因此并不利于实验调控. 这一特性极大限制了拓扑绝缘态量子器件的实际应用. 随着对拓扑物态的理解逐渐加深, 人们发现拓扑边缘态起源于其两侧物质拓扑性质的转变. 具体来说, 可以将真空视作拓扑平庸态, 那么拓扑边缘态就束缚在拓扑非平庸态(拓扑绝缘体)与拓扑平庸态(真空)形成的界面上(如图1所示). 基于这一思路, 两种不同的拓扑态的界面上也能够束缚拓扑非平庸态, 而不依赖于真实的样品边界. 通过恰当的设计, 这些拓扑界面态将主导体系的输运. 参与输运的拓扑界面态不仅具有拓扑边缘态的所有性质, 而且由于输运不再局限在样品边界, 将极大地开拓器件功能设计的思路. 下面结合我们近些年来的工作, 以陈绝缘体与轴子绝缘体为例, 通过设计拓扑界面, 实现对拓扑界面态输运通道的调控, 并构筑具有特定功能的拓扑态集成器件.
-
首先以陈绝缘体为例, 系统性地分析无序陈绝缘体中的拓扑界面态及其输运特性[29]. 基于这些输运特性, 进一步给出基于无序陈绝缘体拓扑界面态的量子器件设计方案.
-
陈绝缘体的拓扑非平庸态为量子反常霍尔态, 其拓扑特性不依赖对称性, 而仅受拓扑不变量——陈数的保护. 其中陈数可以表示为占据态的贝里曲率
$ \varOmega({\boldsymbol{k}}) $ 在第一布里渊区的积分, 表示为$ C_{xy}= \displaystyle \int_{{\mathrm{BZ}}}\varOmega({\boldsymbol{k}}){\mathrm{d}}k_x{\mathrm{d}}k_y $ [30-32]. 当体系具有时间反演对称性时, 贝里曲率满足$ \varOmega({\boldsymbol{-k}})=-\varOmega({\boldsymbol{k}}) $ . 这意味着, 在具有时间反演对称性的系统中, 陈数总是等于零. 因此, 非零陈数要求破缺样品的时间反演对称性[6]. 虽然磁场是破缺时间反演对称性的有效手段, 但是陈绝缘体原则上并不依赖于外磁场. 1988 年, Haldane[33]提出了不需要外磁场的陈绝缘体模型. 2013年, 薛其坤及其团队[22]在Cr掺杂的拓扑绝缘体薄膜中, 才首次实现了零磁场下的量子化霍尔电导. 这一实验结果证实了陈绝缘体中无耗散的边缘态的存在, 为进一步研究陈绝缘体的可调控输运特性提供了实验基础.尽管陈绝缘体摆脱了对外磁场的依赖, 但是它的量子化输运带隙非常小, 且无耗散边缘态主要集中在样品的边界, 这限制了陈绝缘体在量子器件中的应用. 因此如何摆脱这些限制成为了理论以及实验研究中的重要问题之一. 考虑到陈绝缘体的边缘态可以理解为两种不同陈数界面的拓扑界面态 (图1(b)). 当陈数发生跳变时, 在跳变界面处会束缚具有手性的界面态, 这类手性界面态的出现是基于界面拓扑特性的必然结果[28]. 由此, 可以通过在实空间样品中构造不同的陈数界面以实现无耗散通道的空间分布的调控.
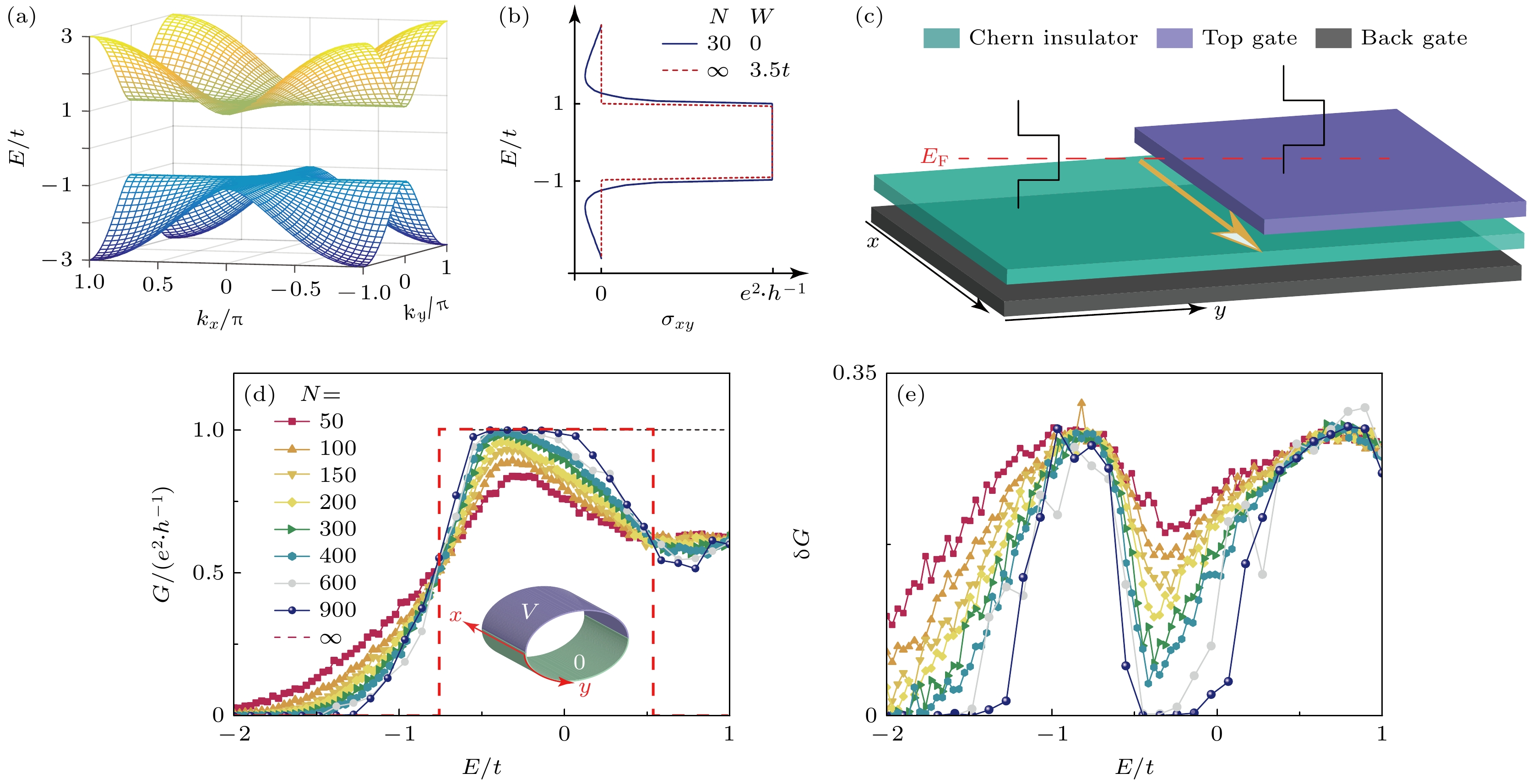
为了拓展这一图像, 给出陈数随费米能级的演化. 如图2(a)和图2(b)所示, 计算发现, 在热力学极限下, 干净以及无序陈绝缘体的陈数表现出了截然不同的分布特性[29]. 对于干净体系, 所有的体态均表现出拓展特性, 而非零的贝里曲率依赖于波函数的拓展特性. 原则上, 每部分体态均会贡献贝里曲率以及陈数. 考虑到整个导带贡献的总的陈数为整数, 即
$ C_{xy} = 1 $ . 因此当费米面偏离带隙时, 费米面以下体态的贡献将会偏离$ C_{xy} = 1 $ . 这将使得陈数不再表现出量子化. 具体来说, 随着费米面的提高或降低, 这种偏离将被逐步放大并使得陈数最终趋于零. 但是对于无序陈绝缘体, 由于其哈密顿量属于幺正类, 基于普适的安德森相变理论, 该体系所有的拓展态均集中于离散的临界能量点内. 而临界点之间的所有态在热力学极限下均为局域态[34,35]. 由于局域态对陈数的贡献为0, 因此陈数只有在 费米能穿过那些离散的临界点(拓展态)时才会发生改变. 这引出了如图2(b)虚线所示的陈数跳变特性. 这种无序陈绝缘体的陈数跳变特性对于构造完美的陈数跳变界面是十分重要的.下面以Qi-Wu-Zhang模型为基础[4], 在理论上详细分析陈绝缘体拓扑界面的性质. 该模型作为陈绝缘体的典例, 能够完整准确地展示出无序陈绝缘体中陈数跳变对应的拓扑界面态的输运特性. 为了分析图2(c) 所示的界面, 考虑如下哈密顿量:
其中,
$ c_i^\dagger $ ($ c_i $ )是i位置处的产生(湮灭)算符;$ {\boldsymbol{\sigma}}_{x/y/z} $ 是泡利矩阵;$ {\boldsymbol{\sigma}}_0 $ 是2 × 2的单位矩阵; t为跃迁能;$ v = 0.5 t $ 和$ m=t $ 分别为费米速度与质量项;$ W_i $ 为安德森无序, 均匀分布在$ -W/2 $ —$ W/2 $ 之间, W 为无序强度;$ V_i $ 为门电压调制带来的势能, 它能够调控空间不同区域的费米能, 从而产生具有完整拓扑特性的拓扑界面(图2(c))[29].为了研究这一模型的输运性质, 本文采用如下数值方法: i)为了表征其二端口输运性质, 采用Landauer-Büttiker公式, 即
其中
$ T_{j, i} $ 表示从第i个端口散射到第j个端口的几率; ii)为了表征输运电流的空间特性, 利用非平衡格林函数方法计算其局域电流. l与r端口间电导为$ G_{lr}=\dfrac{e^2}{h} $ Tr$ [\varGamma_lG^r\varGamma_rG^a] $ , 其中推迟/超前格林函数$ G^{r/a} = \Big[E_{\mathrm{F}}\pm {\mathrm{i}}0^+ - H - \displaystyle\sum\nolimits_l\varSigma_l \Big]^{-1} $ , 线宽函数$ \varGamma_l=l[\varSigma_l-\varSigma_l^\dagger] $ ($ \varSigma_l $ 为l端口处的自能). 局域电流由$ {\boldsymbol{J}}_{i\rightarrow j}=\dfrac{2 e^2 V}{h}{\mathrm{Im}} [H_{i, j}(G^r\varGamma_lG^a)_{j, i}]$ 给出. 其中$ H_{i, j} $ 为i格点与j格点的耦合矩阵元. i格点的电流可表示为$ {\boldsymbol{J}}_i=[{\boldsymbol{J}}_{i\rightarrow i+\hat{x}}+{\boldsymbol{J}}_{i\rightarrow i+\hat{y}}] $ .为了消除已有边缘态对结果的影响, 考虑如图2(d)中插图所示的周期性边界条件[29]. 当电势能
$ V_i = 0 $ 时, 体系不存在沿着x方向的边缘导电通道. 原则上来说, 只有当完美的陈数界面出现时, 才能得到无耗散的手性界面通道, 且这些通道会表现出量子化的输运特性. 当引入电势后, 沿x方向的二端口电导G随能量E的变化见图2(d), (e)[29]. 样品尺寸较小的时候, 量子化仅仅出现在相对较小的能量范围内. 量子化区域表现出趋于零的电导涨落, 这表明此时的界面态输运是无耗散的. 随着样品尺寸的增加, 这一量子化区域的范围显著增加. 基于电导的标度特性, 我们预期在热力学极限下(N 趋向于无穷大时), 图像趋于图2(d) 中虚线的结果. 除离散的临界点外, 电导G 要么趋于$ G= e^2/h $ , 要么趋于$ G = 0 $ . 它们分别对应于陈数差$ \Delta C_{xy} = 1 $ 和$ \Delta C_{xy} = 0 $ 的拓扑界面. 这些结果表明, 由于无序的影响, 陈数随能量的变化的确表现出跳变特性. 当二端口电导趋于$ G=e^2/h $ , 此时在界面处存在一个完美的手征导电通道[29]. -
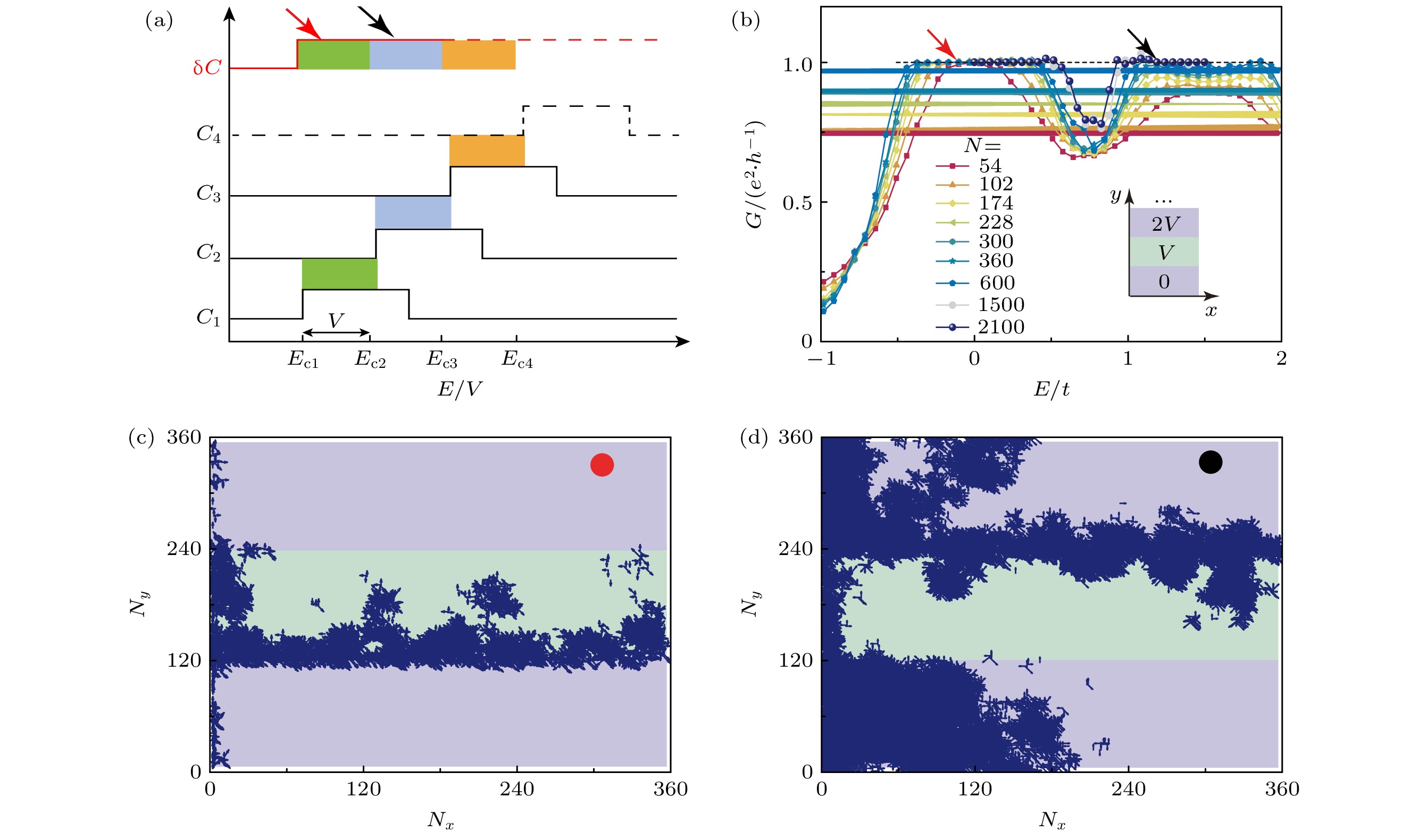
2.1节已经证明了无序陈绝缘体中可以存在跳变的陈数差界面以及相应的界面态引起的量子化输运. 下面进一步论证, 通过合理地设计空间电势分布, 能够实现远超陈绝缘体迁移率带隙的量子化输运能量窗口. 如图3(a)所示, 由于无序陈绝缘体的陈数的跳变特性, 除少数离散的临界点外, 样品的陈数差能量窗口可以通过增加界面的数量来调控. 通过合适的空间电势分布, 这些非平庸陈数差界面会覆盖一个连续的能量区间(少数离散临界点可忽略). 基于2.1节的分析, 这些能量窗口都会给出量子化的输运结果. 如图3(b)所示, 对比只有一个界面的情况(图2(d)), 量子化输运的能量区间几乎扩大了一倍. 通过继续堆叠这些拓扑界面, 可以极大地拓宽量子化输运对应的能量窗口. 除此之外, 对于不同的能量位置, 对应的量子化电导来自不同拓扑界面的界面态, 这可以通过图3(c)和图3(d)中局域电流的分布来确认.
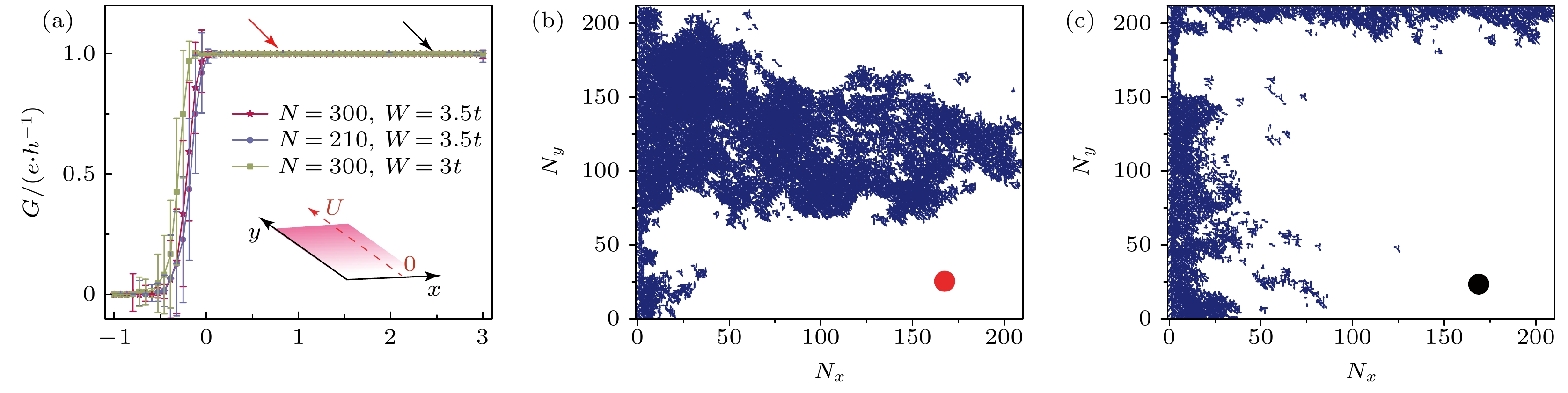
除上述调控特性外, 对拓扑态局域化特性的调控近些年也受到关注. 基于拓扑界面态, 可以进一步通过合理的设计, 实现对输运通道局域化特性的有效调控[36]. 如图4(a)所示, 将阶梯势转化为线性势, 该体系依然展现出完美的量子化输运特性[29]. 这种量子化输运同样源于带有非平庸陈数的拓扑界面, 相较于阶梯势, 线性势给出的拓扑界面表现出更大的有效界面宽度. 这一特性可以通过比较如图4(a)中不同能量位置的局域电流分布加以确定. 如图4(b)所示, 样品中有更多的格点参与到该能量位置所对应的量子化输运通道中, 这与图4(c)基于阶梯势的局域电流分布具有明显不同的局域特性. 图4(b)相较于图4(c), 非平庸空间传输通道更倾向于表现出拓展特性. 这意味着通过改变电势的分布特性, 可以进一步实现拓扑界面态宽度以及对应量子化输运电流空间分布的有效调控. 最近已有相关实验报道与我们提出的这种具有拓展特性的局域电流分布相符合[37–39].
因此, 电压调控的无序陈绝缘体中的拓扑界面具有两个显著特性: i)更宽的量子化输运能量窗口; ii)空间可调的传输通道. 这些特性能够极大地提高我们对量子化输运以及输运通道空间分布的调控能力. 需要强调的是, 这些特性源于安德森转变的普适特性[40,41], 故而并不依赖于模型细节. 因此, 本文的结果在广泛的陈绝缘体体系中都适用. 基于这些特性, 下面阐述如何通过恰当的设计实现基于无序陈绝缘体的量子器件.
-
参考传统逻辑电路, 主要由两部分构成: i)基本逻辑器件; ii)连接器件的导线. 基于2.2节的结果, 下面以无序Qi-Wu-Zhang模型为例, 给出基于拓扑界面态的量子集成器件的设计方案[42].
首先, 为了实现集成电路中的可调“导线”功能, 对无序陈绝缘体样品做如下设计. 假设有一块陈绝缘体样品, 如图5(a)所示, 首先将样品划分为若干区域[42]. 这些区域均可以由外接的门电压控制其电位. 类似于印刷电路板, 这些区域与一系列外部器件相连. 控制方格的电压取
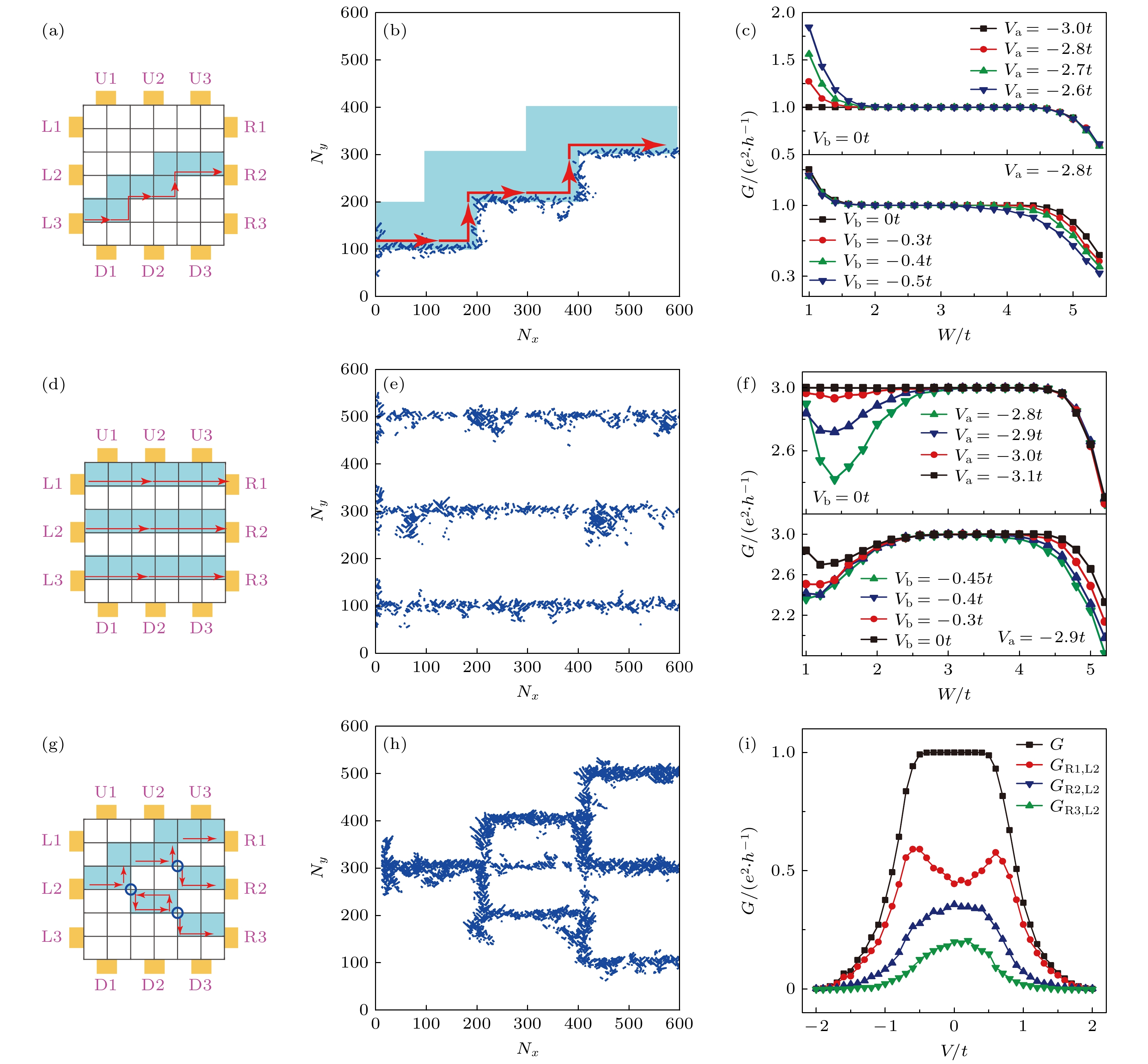
$ V_{\mathrm{a}} = 2.8 t $ 和$ V_{\mathrm{b}} = 0 $ 两个标准值, 分别对应陈数$ C = 0 $ 与$ C = 1 $ , 在示意图中分别标记为白色与蓝色. 电压引起的电势能可以十分有效地调控体系的费米能量. 通过合理设计$ V_{\mathrm{a}} $ 和$ V_{\mathrm{b}} $ , 能够实现对无序陈绝缘体中拓扑界面输运特性的调控. 以不导通为例: 当所有方格区域的电压均为$ V_{\mathrm{a}} = 2.8 t $ 时, 样品内部不导通. 虽然费米能位于体能带内, 但是由于无序效应的存在, 此时样品内部整体表现为安德森绝缘体, 内部各个部分陈数差为零. 因此样品内部不存在导通的通道. 相反地, 如果不同方格区域的电位存在差异, 此时在样品中可以存在陈数不同的区域, 在这些区域边界原则上将出现手征界面态, 构成无耗散的输运通道[5,29]. 这些通道能够承担传统电路中的导线输运电子的功能.相比于传统导线中固定的连接方式, 基于无序陈绝缘体的“导线”具有更好的可调自由性. 在传统集成电路中, 一旦样品被制备, 它们的连接方式将是唯一固定的. 但是, 基于无序陈绝缘体的“导线”可以通过调控拓扑界面实现导线连接模式的转变. 下面结合三种情况阐述基于无序陈绝缘体的“导线”的功能性、可调性以及鲁棒性[42], 分别为: i) 样品中存在单通道(图5(a)—(c)); ii)样品中存在多通道(图5(d)—(f)); iii)样品中存在单通道对多通道(图5(g)—(i)).
功能性 如图5(b), 图5(e), 图5(h)所示, 这三种情况均存在电输运通道, 通道出现在蓝色与白色区域的交界面, 表明这些拓扑界面态能够行使“导线”的基本功能.
可调性 如图5(b)和图5(e)所示, 通过控制不同区域的门电压, 可以实现对通道数量和形状的调控. 这一过程对样品的物理特性不会造成不可逆的影响, 因此它们彼此之间可以相互转化. 进一步, 通过调控电压可以实现传统电路中的多导线分流过程. 当样品中存在单通道对多通道传输时, 图5(i) 进一步表明, 每个“导线”中的电流(电导)大小可以通过偏压
$ V_{\mathrm{b}} $ 调控. 这些“导线”的关系与在实际电路中的导线是十分类似的. 此外, 若能够在本系统中实现向图5(b)中具有拓展特性的输运通道的转变, 也可以在保持总电导不变的前提下, 实现单端口通道和多端口通道之间的转化. 总而言之, 人们可以操纵不同的通道表现出不同的性质, 来满足复杂电路的设计需求. 这一思路极大地提高了拓扑绝缘体的绝缘体态在器件设计中的利用率.鲁棒性 它们都表现出非平庸的量子化电导平台
$ G=ne^2/h $ (图5(c), 图5(f)和图5(i)). 此外, 基于图5(b), 图5(e)和图5(h)中的局域电流分布, 可以给出如图5(a), 图5(d)和图5(g)中的空间电流分布及其流向(由红色箭头标注). 从示意图不难发现, 所有蓝色区域下边界的电流都是自L指向R的, 而图5(g)中蓝色区域上边界的电流是从R指向L的, 说明这些电输运通道是手性的. 这与我们给出的拓扑界面态的物理图像一致. 考虑到实际制造工艺的影响, 实际样品的无序强度与门电压$ V_{\mathrm{a}} $ 和$ V_{\mathrm{b}} $ 难免会与标准值有偏差. 我们进一步验证了在不同无序强度与门电压下样品的量子化输运特性的鲁棒性. 如图5(c)和图5(f)所示, 当$ V_{\mathrm{a}} $ 和$ V_{\mathrm{b }}$ 偏离标准值$ V_{\mathrm{a}} = 2.8 t $ 达到10%时, 相应的结果依然成立. 这表明相应器件的功能具有非常强的稳定性.整体来说, 基于拓扑界面的“导线”, 其输运性质对于空间分布是鲁棒的. 这些“导线”的形状、数量等可通过外部调控, 具有更好的调控自由性. 需要强调的是, 这种量子化输运特性只对无序的陈绝缘体体系适用. 对于干净样品, 电导不能保证非平庸量子化. 因此这是无序陈绝缘体独特的输运效应.
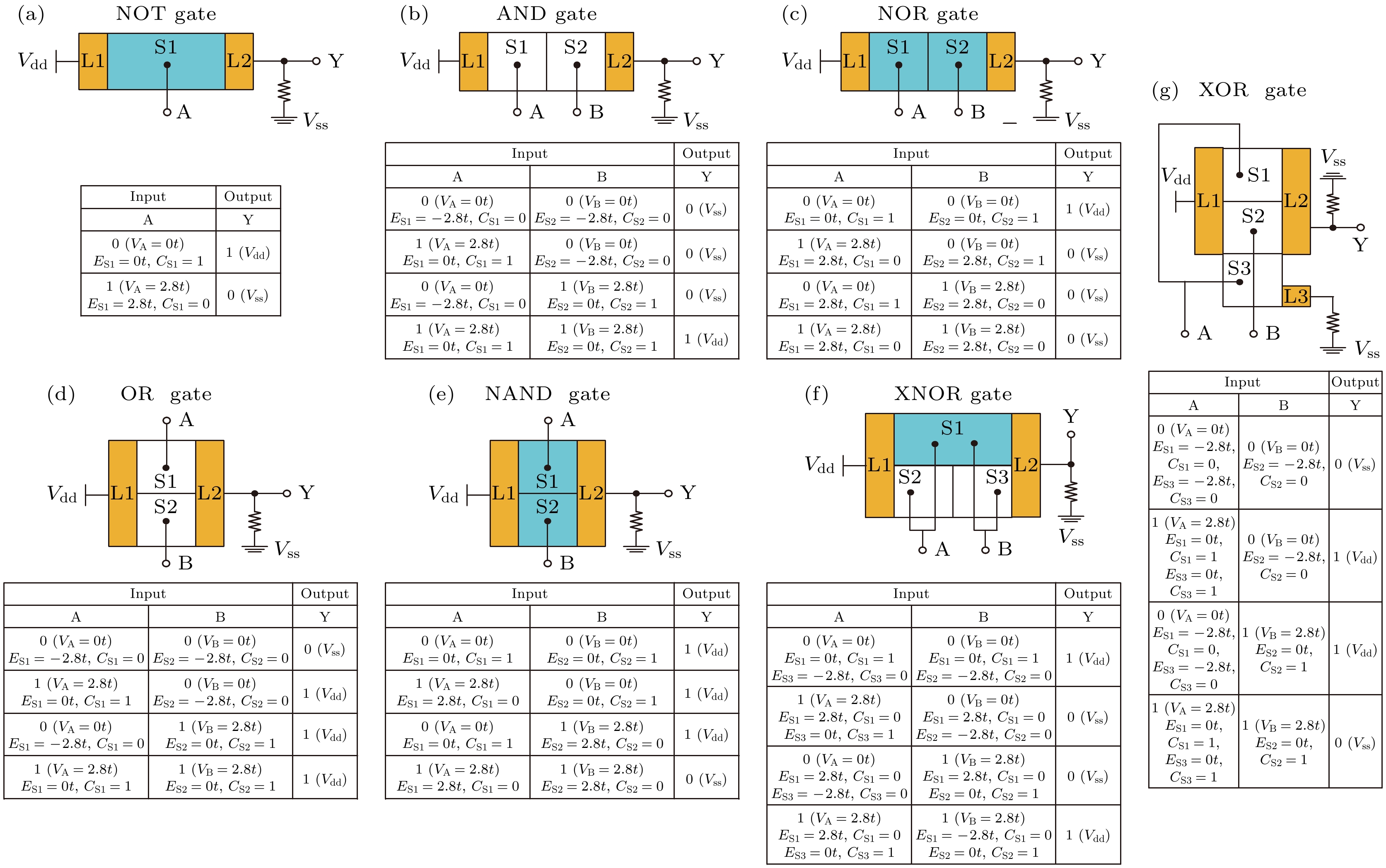
在集成电路中, 除导线外, 用于逻辑计算的基本逻辑门也具有十分重要的作用. 图6展示了基于拓扑界面态所提出的全部7种基本的门电路及其真值表[42]. 定义 A, B两个端口分别可以输入电压信号
$ V_{\mathrm{A}} $ 和$ V_{\mathrm{B}} $ ,$ V_{{\mathrm{dd}}} $ 和$ V_{{\mathrm{ss}}} $ 分别为工作电压与电源电压. 器件中蓝色区域的初始费米能设为$ E_{\mathrm{F}} = 0 $ , 代表陈数为1的陈绝缘体态; 白色区域的初始费米能设为$ E_{\mathrm{F}}=-2.8 t $ , 代表陈数为0的安德森绝缘体态. 设定$ V_{{\mathrm{A/B}}}=V_{{\mathrm{dd}}} = 2.8 t $ 时为高电位, 逻辑值为1;$ V_{{\mathrm{A/B}}}=V_{{\mathrm{ss}}} = 0 $ 时为低电位, 逻辑值为0. 它们的工作原理如下: 以图6(f)同或门(XNOR gate)的构造与真值表为例, 当$ V_{\mathrm{A}}= V_{\mathrm{B}} = 0 t\;(2.8 t) $ 时, A和B的逻辑值均为0(1), 此时$ {\mathrm{S}}_1 $ 区域的费米能级$ E_{{\mathrm{S}}1} = 0 t\;(2. 8 t) $ , 陈数$ C_{{\mathrm{S}}1} = 1 (0) $ ; 而白色区域$ E_{{\mathrm{S}}2}= E_{{\mathrm{S}}3}=-2.8 t(0) $ , 陈数$ C_{{\mathrm{S}}2}= C_{{\mathrm{S}}3} = 0(1) $ . 此时存在输运通道, Y端口输出值为$ V_{{\mathrm{dd}}} = 2.8 t $ , 是高电位, 逻辑值为1. 以此类推, 通过设计实现与传统逻辑电路中一致的输入输出特性. 总的来说, 我们给出了基于拓扑界面态的所有7种逻辑门器件的设计方案.基于我们的设计思路, 最近有多个实验组已经在实验上实现了多种基于陈绝缘体的分流器, 并有望制备出拓扑逻辑门器件[43-45]. 我们预期, 在实现所有基本的逻辑门后, 结合我们给出的基于拓扑界面的“导线”, 有望实现基于拓扑绝缘体的量子器件以及量子电路. 相比于传统逻辑器件, 基于无序陈绝缘体的拓扑器件具有三大特点: i)源于拓扑保护的鲁棒性; ii)源于拓扑界面态手征特性的低功耗性; iii)更高的调控自由性. 这将开辟出有别于传统逻辑电路的量子电路设计思想以及应用前景.
-
事实上, 拓扑界面态的出现只依赖于界面两侧的整数陈数差值. 除了基于陈绝缘体的、两侧为
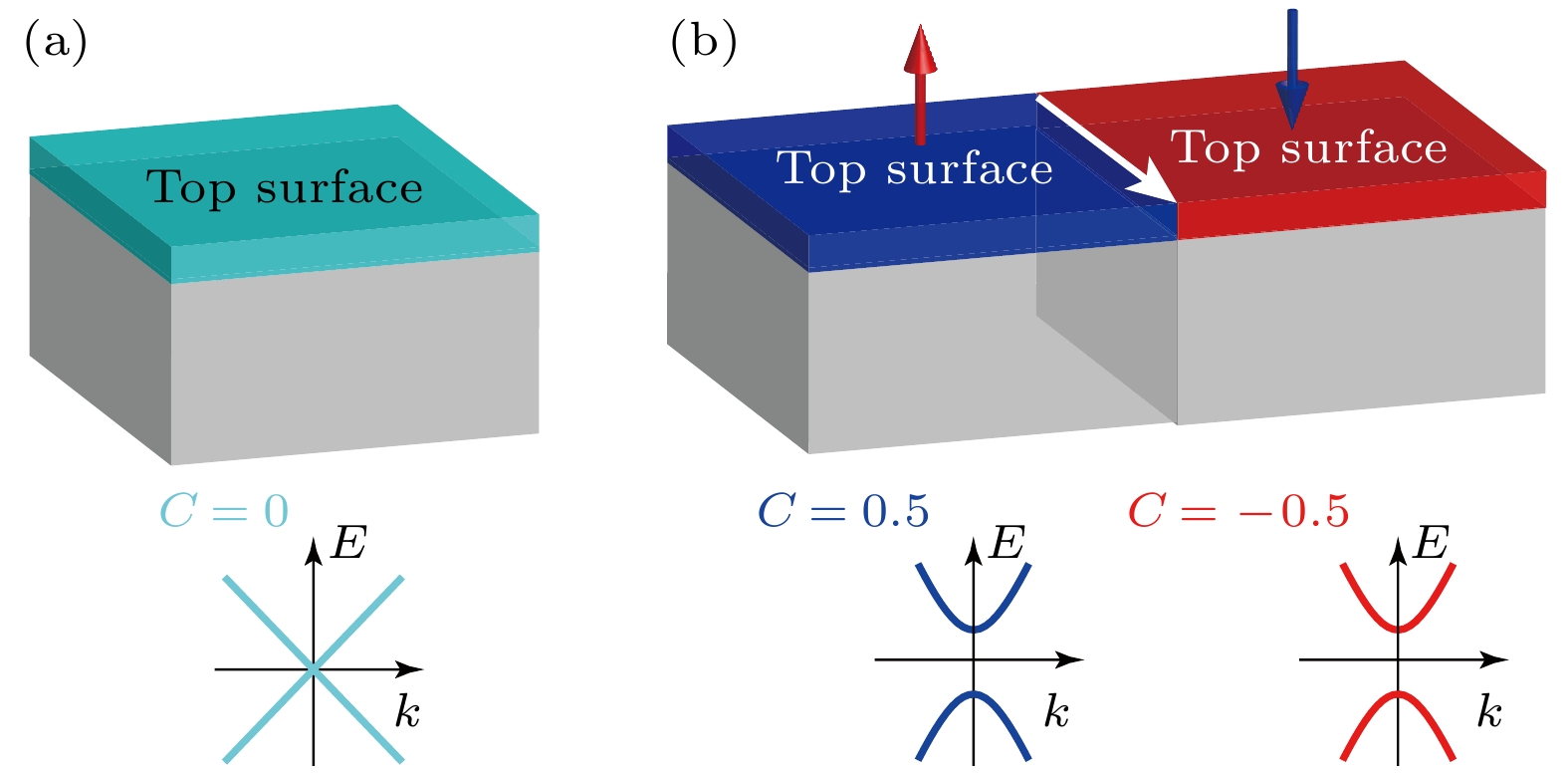
$ \Delta C=(1-0) $ 的陈数差模式之外, 还有一类基于半整数陈数差的反铁磁质量畴壁模式. 如图7(a)所示, 对于三维拓扑绝缘体, 它具有单个狄拉克锥表面态, 满足$ H_{{\mathrm{top}}}=k_x\sigma_x+k_y\sigma_y $ . 并且这些表面不表现出任何的陈数特征. 但是, 当考虑表面具有磁性掺杂等特性后, 这些受时间反演对称保护的表面态将被打开带隙, 即$ H_{{\mathrm{top}}}(M)=M\sigma_z+ k_x\sigma_x+ k_y\sigma_y $ . 这个体系的陈数满足$ C={\mathrm{sgn}}(M)/2 $ . 这暗含着一类新的拓扑界面模式. 如图7(b) 所示, 当两块样品的表面表现出相反的磁化M, 它们的界面也将给出整数陈数差值$ \Delta C = 0.5-(-0.5) = 1 $ . 若上下表面的磁化结构不同, 将会给出丰富的拓扑界面结构, 并且这类结构的输运性质会表现出表面/层依赖特性. -
实验上, MnBi2Te4 由于独特的磁结构[46-50]而具有不同的表面态磁化特性. 具体来说, MnBi2Te4层内为铁磁耦合, 层间为反铁磁耦合. 因此, 不同层数的样品会表现出不同的拓扑特性. 对于奇数层样品, 其上下表面具有相同的磁化以及陈数, 这使得它的基态表现出量子反常霍尔相. 而偶数层样品上下表面表现出相反的磁化, 具有相反的陈数, 其基态为轴子绝缘体相[46,51]. 目前, 人们已经在MnBi2Te4中陆续观测到了陈绝缘体、轴子绝缘体等一系列新奇的量子现象.
2021年, Gao等[52]证实了MnBi2Te4中存在层霍尔效应, 这一效应源于层锁定的贝里曲率. 通过改变电场, 实验上能够调控MnBi2Te4 的层自由度, 这就使得构建基于空间自由度的电子学器件成为可能. 但是, 他们提出的层霍尔效应无法利用拓扑材料低能耗的特性, 并且难以用于设计相关的量子器件[52,53]. 事实上, 基于MnBi2Te4的反铁磁畴壁及其界面处束缚的拓扑界面态, 不仅保持了贝里曲率的层依赖特性, 而且有望表现出无耗散输运特性. 这种模式下, 上下表面界面态的传输方向相反, 并且这些通道在空间上被绝缘的体态隔离. 为了实现对层输运的调控, 实验室需要实现对MnBi2Te4磁化特性的精确调控. Guo等[54]进一步论证了磁力显微镜调控样品磁化畴壁的可行性. 基于这些结果, 人们可以利用轴子绝缘体表面态设计可调层电子学量子器件. 下面将详细介绍基于MnBi2Te4的
$ C = 0.5 $ 和$ C=-0.5 $ 的陈数差界面及其独特的层自由度依赖输运特性. -
反铁磁的MnBi2Te4哈密顿量可以通过一个三维拓扑绝缘体加上反向平行的层磁化构造[50,55], 其形式为
$ H=H_0+H_{{\mathrm{mag}}} $ , 其中$ H_0 $ 是一个四能带的拓扑绝缘体的哈密顿量[56,57], 表达式为$ H_0= \displaystyle\sum\nolimits_{i = 1}^4 d_i({\boldsymbol{k}}){\boldsymbol{\varGamma}}_i $ , 其中$ d_1({\boldsymbol{k}})=A_1 k_x $ ,$ d_2({\boldsymbol{k}})=A_1 k_y $ ,$ d_3({\boldsymbol{k}})=A_2 k_z $ ,$ d_4({\boldsymbol{k}})=M_0-B_1 k_z^2-B_2(k_x^2+k_y^2) $ , 而$ {\boldsymbol{\varGamma}}_i $ 为狄拉克矩阵,$ {\boldsymbol{\varGamma}}_i=s_i\otimes{\sigma_1} $ , 其中$ i = 1, 2, 3 $ ,$ {\boldsymbol{\varGamma}}_4=s_0\otimes{\sigma_3} $ .$ H_{{\mathrm{mag}}}=M(z)s_3\otimes{\sigma_0} $ , 使能级发生塞曼劈裂,$ M(z)=\pm{M_z}=\pm 0.05 $ 为每层沿着z方向的磁化项.与谷电子学的发展类似[58-68], 层电子学也需要提出新的基于空间分辨的输运算法[69]. 基于局域电流的表达式
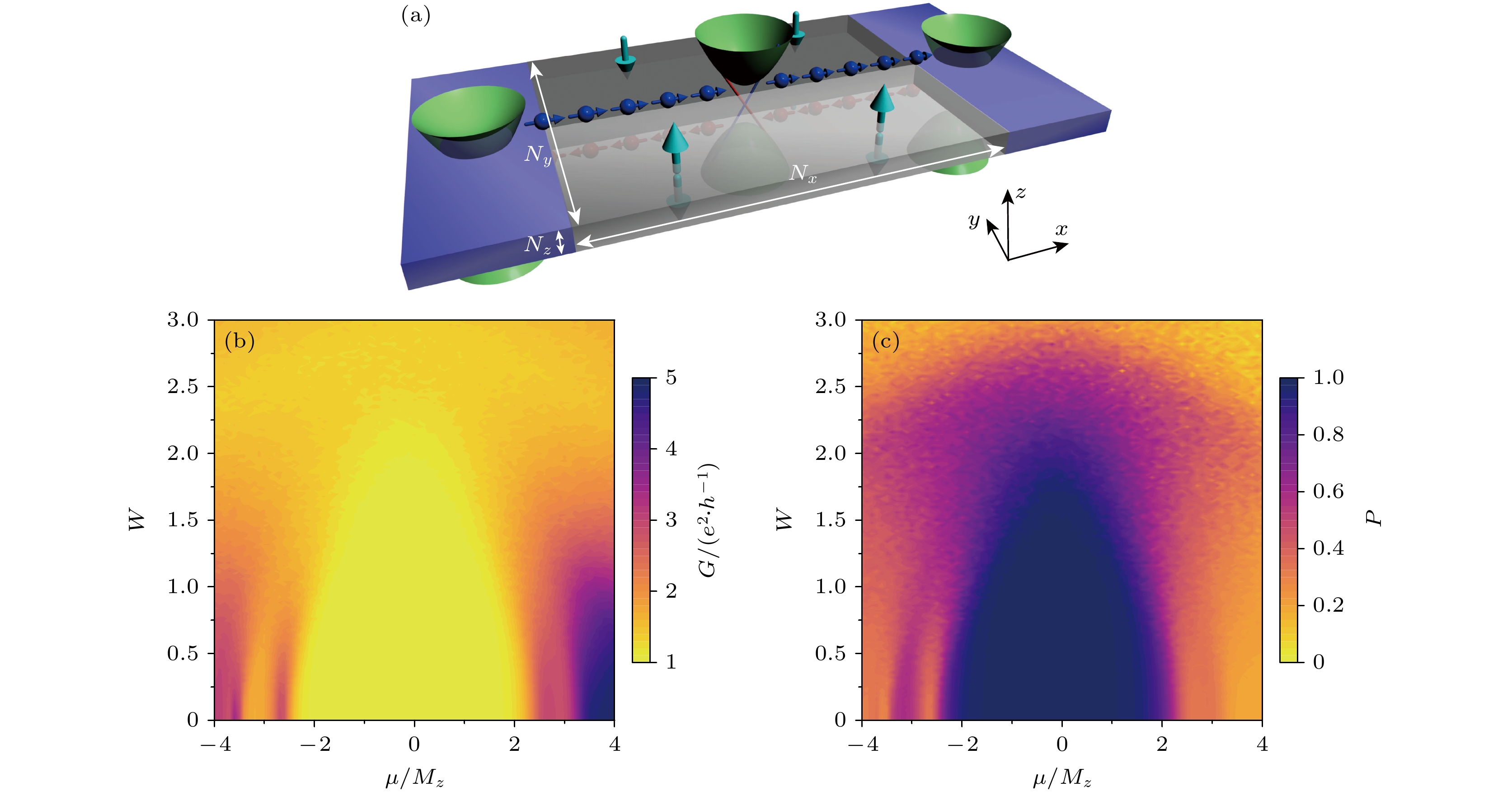
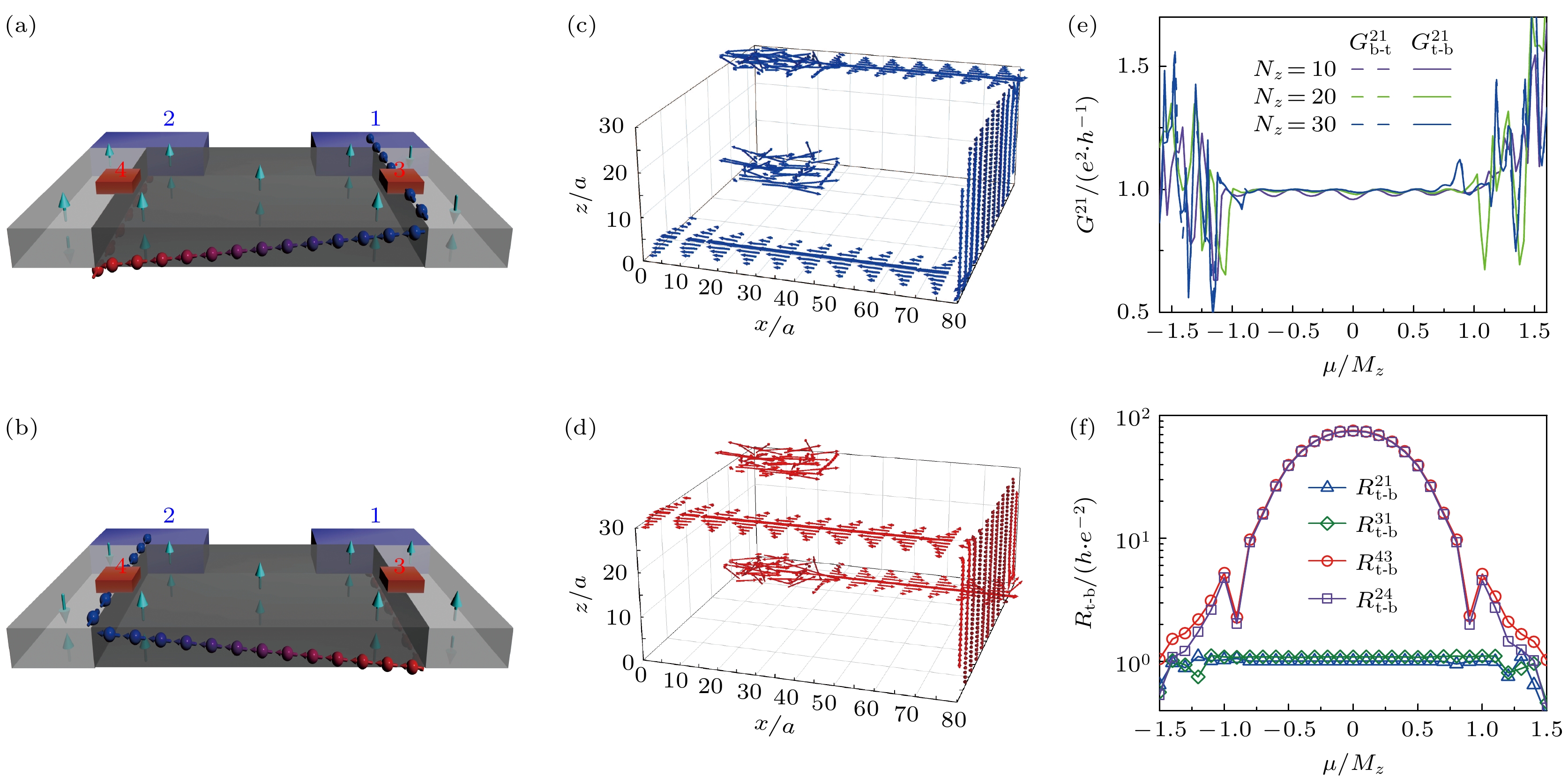
$ J_{i\to{j}}=\dfrac{e^2 V}{h}{\mathrm{ImTr}}[t_{ij}(G^r\varGamma_{\alpha}G^a)_{ji}] $ ,上层电流为$ J_{\mathrm{t}}=\dfrac{e^2 V}{h}T_{\mathrm{t}}= \displaystyle\sum\limits_{i_z > N_z/2}J_{i, i+\delta_x} $ , 下层电流为$ J_{\mathrm{b}}=\dfrac{e^2 V}{h}T_{\mathrm{b}}= \displaystyle\sum\limits_{i_z\leqslant {N_z/2}}J_{i, i+\delta_x} $ . 至此, 就可以得到总电导(透射率)$ G={e^2}T/{h}= {e^2}(T_{\mathrm{t}}+T_{\mathrm{b}})/{h} $ , 以及层极化率$ P= {(T_{\mathrm{t}}-T_{\mathrm{b}})}/{(T_{\mathrm{t}}+T_{\mathrm{b}})} $ . 下面详细论述基于该体系的层输运特性以及相关的层电子学器件构造, 包括层过滤器、层阀和层转换器. 它们分别具有独特的层调控特性.层过滤器 层过滤器作为层电子学最基础的器件, 主要作用是产生层极化电流. 如图8(a)所示, 层过滤器主要由反铁磁MnBi2Te4中的一个畴壁构成[69]. 由于反铁磁磁化, 能隙在轴子绝缘体的狄拉克表面态处打开, 在上表面或下表面产生了半量子化的陈数[70,71]. 当两个不同的反铁磁序毗邻, 就会在界面形成异质结构, 并形成界面态[72]. 由于体态呈现出绝缘态, 畴壁处的手性界面态与层自由度紧密联系, 即从左向右的电流只会发生在上表面(图8(a)中蓝色箭头), 而相反方向的电流只会存在于下表面(图8(a)中红色箭头), 这就促使了层极化电流的产生. 实验中, 反铁磁MnBi2Te4中的畴壁已经可以通过比较简单的方法实现[73], 且反铁磁序可以通过
$ E\cdot{B} $ 项来改变方向[52], 这就意味着通过外接门电压可以控制畴壁的产生与变化.不同表面的畴壁的非平庸陈数差还保证了层过滤器的鲁棒性. 因此对于无序以及畴壁形状的变化均不敏感. 如图8(b)所示, 对层过滤器的无序计算表明, 在一个较大的无序强度下, 即
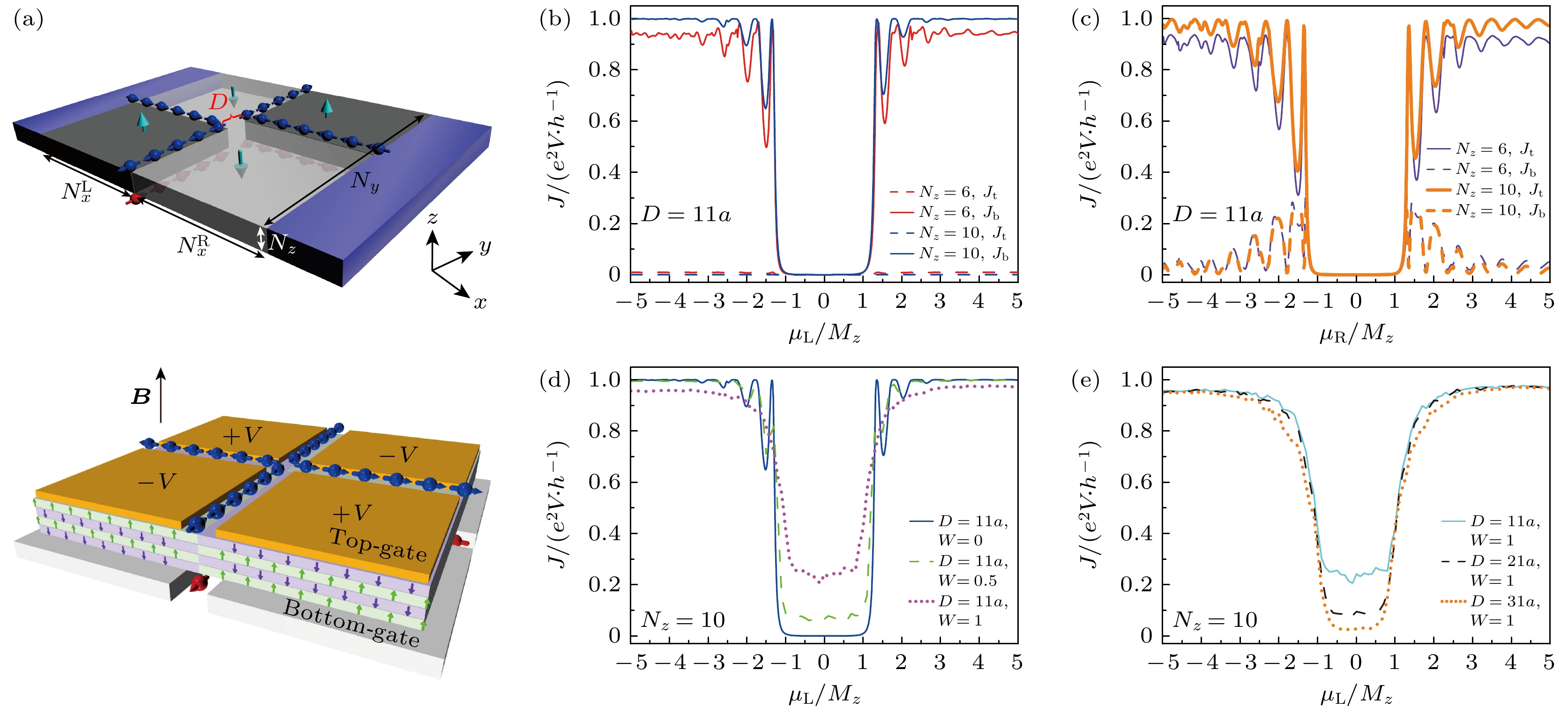
$ W < 1.5 t $ , 二端口电导能够在较大范围的费米能级下保持量子化$ e^2/h $ , 并且如图8(c)所示完美地保持完全的层极化率($ P = 1 $ ). 而当畴壁发生形变时, 无论是弯曲还是畴壁变为有限宽度, 对于层过滤器的影响都不大. 这些结果与拓扑界面的理论预期是一致的.层阀 层阀的功能是“开”“关”层极化电流, 其设计思路为连接上下层的层过滤器(图9(a))[69],
$ \mu_{\mathrm{L}} $ ($ \mu_{\mathrm{R}} $ )为上层过滤器(下层过滤器)的化学势. 通过调节化学势, 可以看到电流为零的情况, 此时层阀就处于“关闭”状态. 工作原理是此时上下层过滤器的畴壁手性相反, 同时阻断了上下层电流的输运. 当单独调节$ \mu_{\mathrm{L}} $ ($ \mu_{\mathrm{R}} $ )至表面态, 层阀就处于“打开”的状态, 产生对应的导通层极化电流(图9(b)), 调节$ \mu_{\mathrm{L}} $ ,$ J_{\mathrm{t}} $ 保持为0, 而$ J_{\mathrm{b}} $ 开始产生直至在$ 1.0 e^2 V/h $ 附近呈现出量子化. 图9(c)与图9(e)的结果显示, 随着距离D 的增大, 层阀的开关比会提高, 层阀可以通过设计实现高开关比, 达到比较优异的性能. 且对于一定的无序强度, 层阀表现出鲁棒性(见图9(d)), 这是因为层阀的性能同时受到层自由度的空间保护及畴壁的拓扑性保护. 其良好的性能即使相较于许多现有的新型量子器件, 也能展现出显著的优势[60,74].层转换器 层转换器的功能类似于转换逻辑器件中存储的二进制比特. 在自旋电子学与谷电子学中, 实验上通常较难实现对于电子内禀自旋的精准调控. 相较之下, 层转换器的构造更为简单, 并且可以表现出无耗散的性能. 考虑到反铁磁的轴子绝缘体能够转变成为铁磁的陈绝缘体相, 这为无耗散转换层自由度的层转换器提供了思路. 如图10(a), (b)所示, 层转换器由两层相反反铁磁序的轴子绝缘体包着的陈绝缘体构成, 在实验上可以由控制垂直MnBi2Te4的外磁场来实现[69]. 在这个结构中, 一个表面的层电流通过穿越层间的手性边缘模式, 穿过陈绝缘体的边缘态, 到达另一个表面, 颜色的变化体现了模式的变化. 图10(c), (d)中上下层电流的方向是相反的, 表明这个结构能够实现上层下层电子的转换. 图10(e)中, 层转换器端口1与端口2间的电导也表现出了良好的量子化. 图10(f)则展示出了与端口1有关的电阻, 由于手性模的存在, 也保持着量子化.
-
本文对过去几年拓扑界面态的输运特性及其应用的相关研究做了简要回顾. 拓扑界面态克服了拓扑边缘态对于样品形状的依赖, 具有很强的鲁棒性以及可调控特性. 我们发现基于陈数的非平庸拓扑界面态, 可以极大地提高对于陈绝缘体量子化输运在能量以及实空间的调控. 应用这些输运特性, 我们提出通过构造和调控拓扑界面态, 可以实现集成电路中的线路结构以及7种基本逻辑门器件. 在此基础上, 拓扑界面结合额外自由度则大大拓宽了量子器件的设计思路. 结合MnBi2Te4体系独特的层依赖贝里曲率特性, 还提出了多类无耗散的层输运器件, 包括层过滤器、层阀以及层转换器. 这些基本的逻辑以及输运器件, 为后续设计基于量子特性的存储和逻辑计算结构提供了理论基础, 并为实现低功耗大型集成电路开辟了新的设计思路. 接下来有望提出越来越多的性质奇特、性能优异稳定的拓扑量子器件理论设计.
相关研究仍有很多问题亟待解决. 例如近年来, 人们在陈绝缘体器件中发现拓扑界面态在量子极限情况下仍然存在耗散, 且无法判断在集成电路中耗散发生的具体位置[75]; 层电子学器件设计依赖于轴子绝缘体中的磁畴, 虽然相关的磁畴已经在实验上实现, 但是利用电磁学的方法对磁畴的精确调控还十分困难. 尽管如此, 这些新型的拓扑界面态量子器件依然展现出了优异的特性与应用前景. 相关研究的不断发展将会加深人们对基于拓扑界面构建的量子器件设计的理解, 并有望在实验上取得更大突破.
感谢北京大学谢心澄教授、孙庆丰教授对本综述总结工作中的指导; 感谢香港科技大学刘军伟副教授、苏州大学陈垂针教授、复旦大学吴宜家青年研究员、西北大学成淑光教授、北京大学宫明博士后、四川师范大学王孜博副教授、苏州大学吴冰兰博士、安徽大学肖瑞春副教授提供的合作; 感谢复旦大学李海龙副教授、复旦大学闫青博士后、苏州大学刘宏芳博士、复旦大学张志帆博士后、复旦大学李傲龙、复旦大学陈澄等的深入讨论以及他们在本综述中的贡献.
拓扑界面态器件设计理论进展
Research progress of topological interface device design theory
-
摘要: 随着对拓扑态体系理解的深入, 大家普遍认为非平庸的拓扑态直接关联于某些独特的拓扑界面. 基于这一思路, 通过构建不同的拓扑界面, 能够实现对不同自由度输运的调控. 目前, 拓扑界面态已经在多类拓扑体系中被实现, 并且在相关领域引起了广泛关注. 拓扑界面态主要表现出两个基本特点: (i)它是受拓扑保护的; (ii)由于两侧体系的不同又会展现出独特的输运性质. 特别地, 不同特性的拓扑界面态在空间自由度体系中会表现出新奇的拓扑输运特性. 这些输运特性是构建新型拓扑器件的重要理论基础. 结合我们近年的理论工作以及相关进展, 本综述介绍了基于拓扑界面态的可编程集成电路以及层电子学器件的最新进展与未来展望.Abstract: With the development of the topological theory, it is believed that topological states originate from topologically protected interfaces in condensed matter systems. Significantly, by adjusting the topological interfaces, one can manipulate the transport properties of a sample, thereby possessing distinct features. This paper briefly reviews recent progresses about topological interfaces and their potential applications in quantum devices. In the first part, we expound the fundamental ideas about topological interfaces in disordered Chern insulators. Based on their transport properties, the designs of programmable circuits and logical gates are also clarified. These designs significantly improve the utilization of sample compared with topological surface devices. The second part focuses on the topological interfaces in three-dimensional systems, which exhibits the layertronics of the interfaces. We present axion insulator MnBi2Te4 as a typical example, and the realization of the basic layertronics devices is proposed. Finally, this work summarizes the advantages of topological interface devices and proposes some potential breakthroughs to be achieved in this field.
-
Key words:
- topological insulator /
- quantum anomalous Hall effect /
- disorder effect /
- axion insulator .
-

-
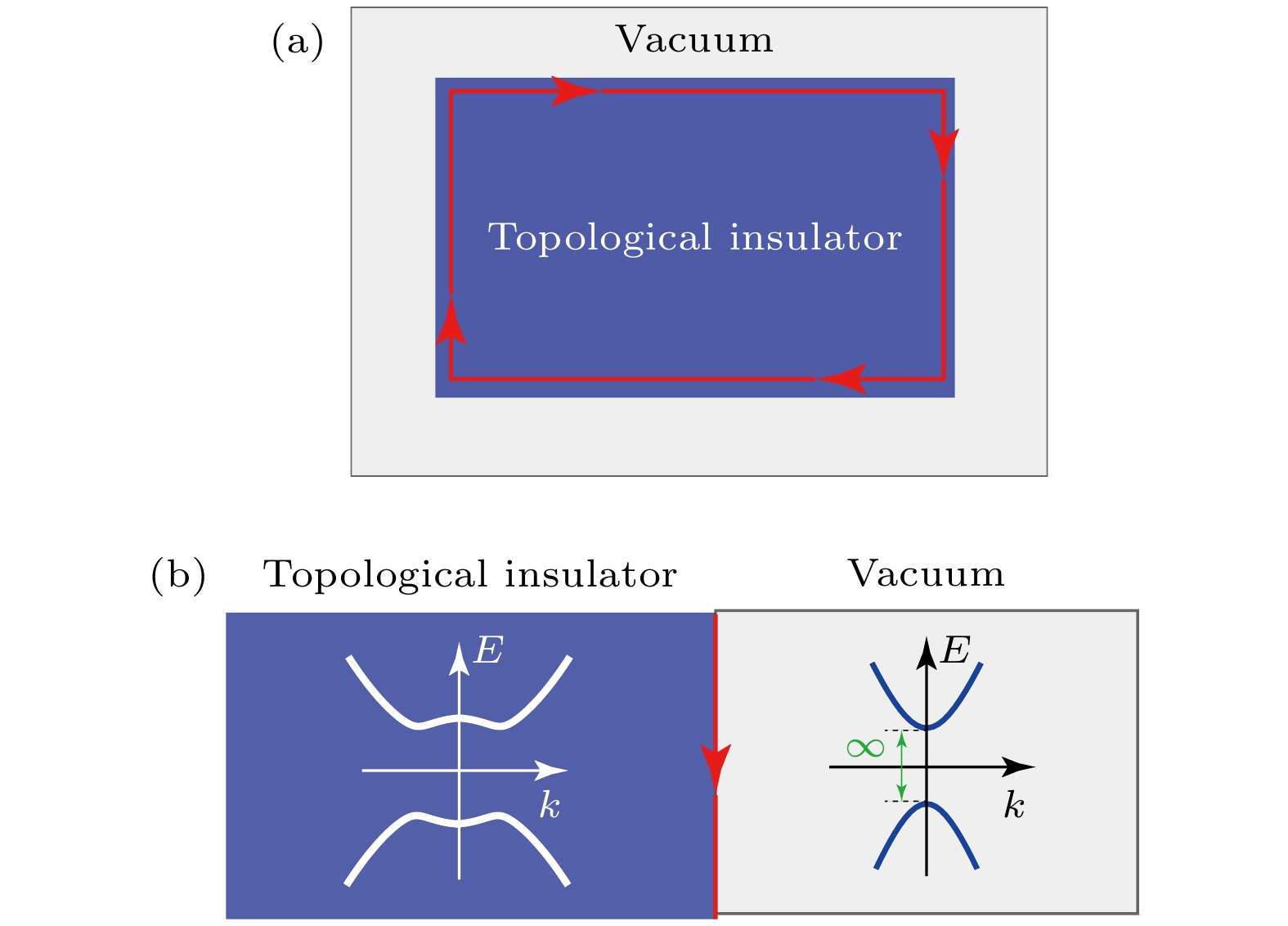
图 1 (a) 陈绝缘体及其边缘态分布. 灰色部分表示真空, 蓝色部分表示陈绝缘体样品, 红色箭头表示陈绝缘体的边缘态. (b) 边缘态的形成可以简化为由拓扑平庸与非平庸界面形成的束缚态. 其中真空可以简化为具有带隙无穷大的普通绝缘体
Figure 1. (a) Schematic of Chern insulator and the edge state. The grey region represents the vacuum, the blue region represents the Chern insulator, and the red arrow shows the edge state. (b) The edge state can be viewed as a bound state located at the interface of topological trivial state and non-trivial state. The vacuum can be viewed as normal insulator with infinite energy gap.
图 2 (a)体能带图[29]; (b)干净(实线)与无序(虚线)样品的陈数
$ C_{xy} $ 随费米能级的演化, 其中霍尔电导率$ \sigma_{xy}=C_{xy}e^2/h $ [29]; (c)具有电压势阶梯的样品示意图, 其中电压势可以通过外接门电压调控[29]; (d), (e)特定无序下样品的二端口电导G以及对应的电导涨落δG随费米能的分布[29]Figure 2. (a) Bulk energy band diagram[29]; (b) Chern number in clean sample (solid line) and disordered sample (dashed line)[29]; (c) schematic of the sample with electrical potential ladder. The voltage potential is under the control of external gate voltage[29]; (d), (e) the conductances and the distribution of corresponding fluctuations versus Fermi energy for different sample sizes and disorder strengthes[29].
图 3 (a)具有两个拓扑界面的二端口电导随费米能的变化. 插图为实空间电势引起的两个拓扑界面的示意图[29]. (b) 陈数界面示意图, 这里考虑三个陈数界面. 每部分的陈数标记为
$ C_i $ , 其中$ i = 1, 2, 3\cdots $ . 定义$ {\text{δ}}C=C_{i}-C_{i+1} $ , 染色区域标记非平庸量子化输运区域, 不同颜色标记它们来源于对应的i和$ i+1 $ 拓扑界面[29]. (c), (d)分别对应图(a)中红色和蓝色箭头能量位置的局域电流[29]Figure 3. (a) The two-terminal conductance versus Fermi energy. The inset shows two topological interfaces caused by the voltage potential in real space[29]. (b) Schematic plots of Chern number distribution. We consider three interfaces, with the corresponding Chern number
$ C_i $ marked in the figure. Here,$ i = 1, 2, 3\cdots $ . We define$ {\text{δ}} C=C_{i}-C_{i+1} $ . Colored regions represent the non-trivial transport energy regions[29]. (c), (d) Correspond the local current density marked by red or blue arrow in panel (a)[29].图 4 (a)线性势
$ V=U_y/N_y $ 下的电导随费米能的变化, 其中样品尺寸$ N_x=N_y=N $ [29]; (b), (c) 局域电流分布, 分别对应于图(a)中对应颜色箭头标示的能量位置[29]Figure 4. (a) Conductance versus Fermi energy under linear voltage potential
$V=U_y/N_y $ , and the size of sample$ N_x=N_y=N $ [29]; (b), (c) distribution of local current, which are labeled by arrows with the same color in panel (a)[29].图 5 样品中电输运通道不同时, 不同标准电压下电导与无序强度的关系[42] (a)—(c) 单通道; (d)—(f) 多通道; (g)—(i) 单通道对多通道
Figure 5. Relationship between conductance and disorder strength at different standard voltages with different transmission channels in the sample[42]: (a)–(c) Single-channel; (d)–(f) multi-channel; (g)–(i) single-terminal to multi-terminal.
图 9 (a)层阀示意图[69]; (b), (c) 输运电流随上下层过滤器化学势的变化[69]; (d)不同无序强度下输运电流随上层过滤器化学势的变化[69]; (e)不同距离(图(a)中D)输运电流随上层过滤器化学势的变化[69]
Figure 9. (a) Schematic of a layer valve[69]; (b), (c) transmission current J versus the chemical potential of top layer filter and bottom layer filter[69]; (d) transmission current versus the chemical potential of top layer filter for different disorder[69]; (e) transmission current versus the chemical potential of top layer filter for different distance (D in panel (a))[69]
图 10 (a), (b)层转换器示意图, 箭头表示输运方向, 不同颜色表示不同模式[69]; (c), (d)分别描绘了图(a)和(b)的局域电流分布[69]; (e)两种层转换器中端口1与端口2间电导随化学式的变化[69]; (f)上层-下层转换器的局域电阻随化学式的变化[69]
Figure 10. (a), (b) Schematic of layer reversers, the arrows show the direction of transmission, while different colors represents opposite mode[69]; (c), (d) distributions of local current in panels (a) and (b)[69]; (e) conductance between terminals 1 and 2 versus chemical potential in two kinds of reversers[69]; (f) local resistances of the top-bottom reverse versus chemical potential[69].
-
[1] Klitzing K, Dorda G, Pepper M 1980 Phys. Rev. Lett. 45 494 doi: 10.1103/PhysRevLett.45.494 [2] Yu R, Zhang W, Zhang H J, Zhang S C, Dai X, Fang Z 2010 Science 329 61 doi: 10.1126/science.1187485 [3] Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2008 Phys. Rev. Lett. 101 146802 doi: 10.1103/PhysRevLett.101.146802 [4] Qi X L, Wu Y S, Zhang S C 2006 Phys. Rev. B 74 085308 doi: 10.1103/PhysRevB.74.085308 [5] Qi X L, Hughs T L, Zhang S C 2008 Phys. Rev. B 78 159901 doi: 10.1103/PhysRevB.78.159901 [6] Nomura K, Nagaosa N 2011 Phys. Rev. Lett. 106 166802 doi: 10.1103/PhysRevLett.106.166802 [7] Yoshimi R, Yasuda K, Tsukazaki A, Takahashi K S, Nagaosa N, Kawasaki M, Tokura Y 2015 Nat. Commun. 6 8530 doi: 10.1038/ncomms9530 [8] Gao Y, Zhang Y Y, Sun J T, Zhang L, Zhang S, Du S 2020 Nano Res. 13 1571 doi: 10.1007/s12274-020-2772-2 [9] Dutta O, Przysirzna A, Zakrzewski J 2015 Sci. Rep. 5 11060 doi: 10.1038/srep11060 [10] Kane C L, Mele E J 2005 Phys. Rev. L 95 226801 doi: 10.1103/PhysRevLett.95.226801 [11] Kane C L, Mele E J 2005 Phys. Rev. L 95 146802 doi: 10.1103/PhysRevLett.95.146802 [12] Bernevig B A, Hughes T L, Zhang S C 2006 Science 314 1757 doi: 10.1126/science.1133734 [13] Read N, Green D 2000 Phys. Rev. B 61 10267 doi: 10.1103/PhysRevB.61.10267 [14] Kitaev A Y 2001 Phys. Usp. 44 131 doi: 10.1070/1063-7869/44/10S/S29 [15] König M, Wiedmann S, Brüne C, Roth A, Buhmann H, Molenkamp L W, Qi X L, Zhang S C 2007 Science 318 766 doi: 10.1126/science.1148047 [16] Hsieh D, Qian D, Wray L, Xia Y Q, Hor Y S, Cava R J, Hasan M Z 2008 Nature 452 970 doi: 10.1038/nature06843 [17] Xu Y, Miotkowski I, Liu C, Tian J, Nam H, Alidoust N, Hu J, Shih C K, Hasan M Z, Chen Y P 2014 Nat. Phys. 10 956 doi: 10.1038/nphys3140 [18] Yoshimi R, Tsukazaki A, Kozuka Y, Falson J, Takahashi K S, Checkelsky J G, Nagaosa N, Kawasaki M, Tokura Y 2015 Nat. Commun. 6 6627 doi: 10.1038/ncomms7627 [19] Zou W, Wang W, Kou X, Lang M, Fan Y, Choi E S, Fedorov A V, Wang K, He L, Xu Y, Wang K L 2017 Appl. Phys. Lett 110 212401 doi: 10.1063/1.4983684 [20] Koirala N, Brahlek M, Salehi M, Wu L, Dai J, Waugh J, Nummy T, Han M G, Moon J, Zhu Y, Dessau D, Wu W, Armitage N P, Oh S 2015 Nano Lett. 15 8245 doi: 10.1021/acs.nanolett.5b03770 [21] Moon J, Koirala N, Salehi M, Zhang W, Wu W, Oh S 2018 Nano Lett. 18 820 doi: 10.1021/acs.nanolett.7b04033 [22] Chang C Z, Zhang J, Feng X, Shen J, Zhang Z, Guo M, Li K, Ou Y, Wei P, Wang L L, Ji Z Q, Feng Y, Ji S, Chen X, Jia J, Dai X, Fang Z, Zhang S C, He K, Wang Y, Lu L, Ma X C, Xue Q K 2013 Science 340 167 doi: 10.1126/science.1234414 [23] Fang Y, Feng X, Ou Y, Wang J, Liu C, Zhang L, Zhao D, Jiang G, Zhang S C, He K, Ma X, Xue Q K 2015 Phys. Rev. Lett. 115 126801 doi: 10.1103/PhysRevLett.115.126801 [24] Chang C Z, Zhao W, Kim D Y, Zhang H, Assaf B A, Heiman D, Zhang S C, Liu C, Chan M H W, Moodera J S 2015 Nat. Mater. 14 473 doi: 10.1038/nmat4204 [25] Checkelsky J G, Yoshimi R, Tsukazaki A, Takahashi K S, Kozuka Y, Falson J, Kawasaki M, Tokura Y 2014 Nat. Phys. 10 731 doi: 10.1038/nphys3053 [26] Kou X, Guo S T, Fan Y, Pan L, Lang M, Jiang Y, Shao Q, Nie T, Murata K, Tang J, Wang Y, He L, Lee T K, Lee W L, Wang K L 2014 Phys. Rev. Lett. 113 137201 doi: 10.1103/PhysRevLett.113.137201 [27] Hasan M Z, Kane C L 2010 Rev. Mod. Phys. 82 3045 doi: 10.1103/RevModPhys.82.3045 [28] Qi X L, Zhang S C 2011 Rev. Mod. Phys. 83 1057 doi: 10.1103/RevModPhys.83.1057 [29] Zhang Z Q, Chen C Z, Wu Y J, Jiang H, Liu J W, Sun Q F, Xie X C 2021 Phys. Rev. B 103 075434 doi: 10.1103/PhysRevB.103.075434 [30] Thouless D J, Kohmoto M, Nightingale M P, Nijs M D 1982 Phys. Rev. Lett. 49 405 doi: 10.1103/PhysRevLett.49.405 [31] Simons B 1983 Phys. Rev. Lett. 51 2167 doi: 10.1103/PhysRevLett.51.2167 [32] Niu Q, Thouless D J, Wu Y S 1985 Phys. Rev. B 31 3372 doi: 10.1103/PhysRevB.31.3372 [33] Haldane F D M 1988 Phys. Rev. Lett. 61 2015 doi: 10.1103/PhysRevLett.61.2015 [34] Onoda M, Avishai Y, Nagaosa N 2007 Phys. Rev. Lett. 98 076802 doi: 10.1103/PhysRevLett.98.076802 [35] Onada M, Nagaosa N 2003 Phys. Rev. Lett. 90 206601 doi: 10.1103/PhysRevLett.90.206601 [36] Wang W, Wang X, Ma G 2022 Nature 608 50 doi: 10.1038/s41586-022-04929-1 [37] Douçot B, Kovrizhin D, Moessner R 2024 Proc. Natl. Acad. Sci. U.S.A. 121 39 doi: 10.1073/pnas.2410703121 [38] Rosen I T, Anderson M P, Rodenbach L K, Tai L, Zhang P, Wang K L, Kastner M A, Goldhaber-Gordon D 2022 Phys. Rev. Lett. 129 246602 doi: 10.1103/PhysRevLett.129.246602 [39] Ferguson G M, Xiao R, Richardella A R, Low D, Samarth N, Nowack K C 2023 Nat. Mater. 22 1100 doi: 10.1038/s41563-023-01622-0 [40] Beenakker C W J 1997 Rev. Mod. Phys. 69 731 doi: 10.1103/RevModPhys.69.731 [41] Evers F, Mirlin A D 2008 Rev. Mod. Phys. 80 1355 doi: 10.1103/RevModPhys.80.1355 [42] Wu B L, Wang Z B, Zhang Z Q, Jiang H 2021 Phys. Rev. B 104 195416 doi: 10.1103/PhysRevB.104.195416 [43] Zhao Y F, Zhang R X, Cai J Q, Zhou D Y, Zhou L J, Yan Z J, Chan M H W, Xu X D, Chang C Z 2023 Nat. Commun. 14 770 doi: 10.1038/s41467-023-36488-y [44] Remeo F, Bartolomeo A D 2023 Nat. Commun. 14 3709 doi: 10.1038/s41467-023-39503-4 [45] Ovchinnikov D, Cai J Q, Lin Z, Fei Z Y, Liu Z Y, Cui Y T, Cobden D H, Chu J H, Chang C Z, Xiao D, Yan J Q, Xu X D 2022 Nat. Commun. 13 5967 doi: 10.1038/s41467-022-33645-7 [46] Li J, Li Y, Du S, Wang Z, Gu B L, Zhang S C, He K, Duan W, Xu Y 2019 Sci. Adv. 5 eaaw5685 doi: 10.1126/sciadv.aaw5685 [47] Rienks E D L, Wimmer S, Sanchez-Barriga J, Caha O, Mandal P S, Ruzicka J, Ney A, Steiner H, Volobuev V V, Groiss H, Albu M, Kothleitner G, Mickalicka J, Khan S A, Minar J, Ebert H, Bauer G, Freyse F, Varykhalov A, Rader O, Springholz G 2019 Nature 576 423 doi: 10.1038/s41586-019-1826-7 [48] Gong Y, Guo J W, Li J H, et al. 2019 Chin. Phys. Lett. 36 076801 doi: 10.1088/0256-307X/36/7/076801 [49] Otrokov M M, Klimovskikh I I, Bentmann H, et al. 2019 Nature 576 416 doi: 10.1038/s41586-019-1840-9 [50] Zhang D, Shi M, Zhu T, Xing D, Zhang H, Wang J 2019 Phys. Rev. Lett. 122 206401 doi: 10.1103/PhysRevLett.122.206401 [51] Otrokov M M, Rusinov I P, Blanco-Ray M, Hoffmann M, Vyazovskaya A Y, Eremeev S V, Ernst A, Echenique P M, Arnau A, Chulkov E V 2019 Phys. Rev. Lett. 122 107202 doi: 10.1103/PhysRevLett.122.107202 [52] Gao A, Liu Y F, Hu C, Qiu J X, Tzschaschel C, Ghosh B, Ho S C, Bérubé D, Chen R, Sun H, Zhang Z, Zhang X Y, Wang Y X, Wang N, Huang Z, Felser C, Agarwal A, Ding T, Tien H J, Akey A, Gardener J, Singh B, Watanabe K, Taniguchi T, Burch K S, Bell D C, Zhou B B, Gao W, Lu H Z, Bansil A, Lin H, Chang T R, Fu L, Ma Q, Ni N, Xu S Y 2021 Nature 595 521 doi: 10.1038/s41586-021-03679-w [53] Liu C, Wang Y, Li H, Wu Y, Li Y, Li J, He K, Xu Y, Zhang J, Wang Y 2020 Nat. Mater. 19 522 doi: 10.1038/s41563-019-0573-3 [54] Guo J F, Wang H, Wang X Y, Gu S Z, Mi S, Zhu S Y, Hu J W, Pang F, Ji W, Gao H J, Xia T L, Cheng Z H 2022 J. Phys. Chem. C 126 32 doi: 10.1021/acs.jpcc.2c02223 [55] Li H L, Jiang H, Chen C Z, Xie X C 2021 Phys. Rev. Lett. 126 156601 doi: 10.1103/PhysRevLett.126.156601 [56] Zhang H, Liu C X, Qi X L, Dai X, Fang Z, Zhang S C 2009 Nat. Phys. 5 438 doi: 10.1038/nphys1270 [57] Liu C X, Qi X L, Zhang H, Dai X, Fang Z, Zhang S C 2010 Phys. Rev. B 82 045122 doi: 10.1103/PhysRevB.82.045122 [58] Rycerz A, Tworzydlo J, Beenakker C W J 2007 Nat. Phys. 3 172 doi: 10.1038/nphys547 [59] Xiao D, Yao W, Niu Q 2007 Phys. Rev. Lett. 99 236809 doi: 10.1103/PhysRevLett.99.236809 [60] Akhmerov A R, Bardarson J H, Rycerz A, Beenakker C W J 2008 Phys. Rev. B 77 205416 doi: 10.1103/PhysRevB.77.205416 [61] Jung J, Zhang F, Qiao Z, MacDonald A H 2011 Phys. Rev. B 84 075418 doi: 10.1103/PhysRevB.84.075418 [62] Qiao Z, Jung J, Niu Q, MacDonald A H 2011 Nano Lett. 11 3453 doi: 10.1021/nl201941f [63] Zhang F, Jung J, Fiete G A, Niu Q, MacDonald A H 2011 Phys. Rev. Lett. 106 156801 doi: 10.1103/PhysRevLett.106.156801 [64] Gunlycke D, White C T 2011 Phys. Rev. Lett. 106 136806 doi: 10.1103/PhysRevLett.106.136806 [65] Cai T, Yang S A, Li X, Zhang F, Shi J, Yao W, Niu Q 2013 Phys. Rev. B 88 115140 doi: 10.1103/PhysRevB.88.115140 [66] Pan H, Li X, Zhang F, Yang S A 2015 Phys. Rev. B 92 041404 doi: 10.1103/PhysRevB.92.041404 [67] Cheng S G, Zhou J, Jiang H, Sun Q F 2016 New J. Phys. 18 103024 doi: 10.1088/1367-2630/18/10/103024 [68] Lee J, Mak K F, Shan J 2016 Nat. Nanotechnol. 11 421 doi: 10.1038/nnano.2015.337 [69] Li S, Gong M, Cheng S G, Jiang H, Xie X C 2023 Natl. Sci. Rev. 10 nwad262 doi: 10.1093/nsr/nwac262 [70] Chu R L, Shi J, Shen S Q 2011 Phys. Rev. B 84 085312 doi: 10.1103/PhysRevB.84.085312 [71] Vernava N, Vanderbilt D 2018 Phys. Rev. B 98 245117 doi: 10.1103/PhysRevB.98.245117 [72] Zhou H M, Li H L, Xu D H, Chen C Z, Sun Q F, Xie X C 2022 Phys. Rev. Lett. 129 096601 doi: 10.1103/PhysRevLett.129.096601 [73] Sass P M, Ge W, Yan J, Obeysekera D, Yang J J, Wu W 2020 Nano Lett. 20 2609 doi: 10.1021/acs.nanolett.0c00114 [74] Averkiev N S, Golub L E 1999 Phys. Rev. B 60 15582 doi: 10.1103/PhysRevB.60.15582 [75] Li H L, Jiang H, Sun Q F, Xie X C 2024 Sci. Bull. 69 1221 doi: 10.1016/j.scib.2024.03.024 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: