高级搜索

融合节点动态传播特征与局域结构的复杂网络传播关键节点识别

,  , 

downloadPDF

上一篇

下一篇

侯诗雨, 刘影, 唐明. 融合节点动态传播特征与局域结构的复杂网络传播关键节点识别[J]. 物理学报, 2025, 74(10): 108901-1. doi: 10.7498/aps.74.20250179
引用本文: 侯诗雨, 刘影, 唐明. 融合节点动态传播特征与局域结构的复杂网络传播关键节点识别[J]. 物理学报, 2025, 74(10): 108901-1. doi: 10.7498/aps.74.20250179
shu
Shiyu HOU, Ying LIU, Ming TANG. Identification of key spreaders in complex network by integrating dynamic characteristics and local structure of nodes[J]. Acta Physica Sinica, 2025, 74(10): 108901-1. doi: 10.7498/aps.74.20250179
Citation: Shiyu HOU, Ying LIU, Ming TANG. Identification of key spreaders in complex network by integrating dynamic characteristics and local structure of nodes[J]. Acta Physica Sinica, 2025, 74(10): 108901-1. doi: 10.7498/aps.74.20250179
shu

融合节点动态传播特征与局域结构的复杂网络传播关键节点识别

  • 1.

    西南石油大学计算机与软件学院, 成都　610500

  • 2.

    华东师范大学物理与电子科学学院, 上海　200241

  • 3.

    华东师范大学, 上海多维信息处理重点实验室, 上海　200241

    • 通讯作者: E-mail: shinningliu@163.com; 

  • 中图分类号: 89.75.-k, 89.75.Fb, 89.20.Ff, 87.23.Ge

Identification of key spreaders in complex network by integrating dynamic characteristics and local structure of nodes

  • 1.

    School of Computer Science and Software Engineering, Southwest Petroleum University, Chengdu 610500, China

  • 2.

    School of Physics and Electronic Science, East China Normal University, Shanghai 200241, China

  • 3.

    Shanghai Key Laboratory of Multidimensional Information Processing, East China Normal University, Shanghai 200241, China

    • Corresponding author: E-mail: shinningliu@163.com; 

  • MSC: 89.75.-k, 89.75.Fb, 89.20.Ff, 87.23.Ge

  • 摘要: 识别复杂网络中的传播关键节点在加速信息扩散、抑制病毒或谣言的传播等应用中至关重要. 现有识别网络传播中关键节点的方法各有局限: 复杂网络中心性方法仅从局域或者全局拓扑结构预测节点影响力; 传统机器学习和深度学习方法不适用于图结构数据; 已有基于图神经网络的方法忽视了传播过程自身的动力学特性. 鉴于此, 本文提出一种融合传播过程动力学特征与节点局域结构的传播动态图神经网络(propagation dynamics graph neural network, PDGNN), 用于识别复杂网络传播中的关键节点. 通过结合易感-感染-恢复传播模型, 提取节点传播过程中的动态感染特征, 构建高维特征向量并设计优化的损失函数, 以实现对复杂网络传播关键节点的准确识别. 在2个合成网络和7个真实网络上的实验结果表明, PDGNN在复杂网络传播关键节点识别准确性上优于经典的中心性方法、基于传统机器学习和深度学习的方法以及现有的基于图神经网络的方法.
    Abstract: Identifying the most influential nodes in the spreading process in complex networks is crucial in many applications, such as accelerating the diffusion of information and suppressing the spread of viruses or rumors. Existing methods of identifying influential spreaders have their limitations. Specifically speaking, classical network centrality methods rely solely on local or global topology to predict node influence; traditional machine learning and deep learning methods are not suitable for graph-structured data; existing graph neural network-based methods neglect the dynamic characteristics of the propagation process itself. Researchers have pointed out that the spreading influence of nodes not only depends on their structural location, but is also significantly influenced by the dynamics of the spreading process itself. In this work, we propose a propagation dynamics graph neural network (PDGNN) that integrates the dynamic features of the propagation process and the structural features of nodes to identify influential nodes. Specifically speaking, based on the susceptible-infected-recovered (SIR) propagation model, the dynamic infection features and potential infection capacity of nodes are extracted from the epidemic spreading process. Then a high-dimensional feature vector of each node consisting of the embedding and degree of its local transmission tree, as well as its dynamics-sensitive centrality is constructed and used as the input to the graph neural network. To deal with the problem of imbalanced numbers between critical nodes and non-critical nodes in training the model and optimizing the output, an optimized loss function is designed, which combines focal loss with mean squared error. Experimental results in two synthetic networks and seven real-world networks show that the PDGNN outperforms classical centrality methods, traditional machine learning and deep learning-based methods, and existing graph neural network-based methods in identifying influential nodes in the spreading process in complex networks. The performance of PDGNN is robust when the infection rate and the size of the training set change. In a wide range of infection rates, the proposed PDGNN can accurately identify influential spreaders. Despite the fact that the training set accounts for 30% of the total dataset, the PDGNN has the smallest inaccuracy in all nine studied networks.
  • 加载中

  • 图 1  PDGNN框架, 以11个节点和11条边组成的网络G作为示例　(a)计算图G中每个节点的三个特征, 作为每个节点的特征向量, 进而得到G的特征矩阵X; (b)将特征矩阵X和图的邻接矩阵A作为模型的输入; (c)使用包含两层SAGEConv的图神经网络模型进行训练, 计算损失函数, 根据损失函数值对模型参数进行优化, 使用训练好的模型进行分类, 输出测试集中每个节点的分类概率和预测类别

    Figure 1.  Framework of PDGNN. A network G consisting of 11 nodes and 11 edges is used as an example: (a) Three features of each node in graph G are calculated and uesd as the feature vectors of each node, which form feature matrix X of graph G; (b) the feature matrix X and adjacency matrix A of the graph are used as the inputs of the model; (c) the graph neural network model with two layers of SAGEConv is trained and the loss function is calculated. Based on the loss function, the model’s parameters are optimized. By using the trained model, the classification probabilities and predicted class of each node in the test set are output.

    下载: 全尺寸图片 幻灯片

    图 2  感染节点的局部传播树　(a)网络的局域结构, 红色节点为初始I态节点, 蓝色节点为S态节点. (b)—(d)三步SIR传播中, 局部传播树的生成过程. 图中深橙、浅橙和黄色节点分别表示第一步、第二步、第三步传播被感染的节点. 最终生成的局部传播树由图(d)中红、深橙、浅橙和黄色节点及它们之间的连边共同构成. 虚线表示局部传播树与其余节点之间的连接, 连接的数目定义为局部传播树的度

    Figure 2.  Local transmission tree for the infected node: (a) Local structure of the network. The red node is in I state and blue nodes are in S state initially. (b)–(d) The generation of local transmission tree in a three-step SIR propagation. The dark orange, light orange and yellow nodes in the graph are nodes infected in the first, second and third steps of transmission respectively. The generated local transmission tree in panel (d) consists of the red, dark orange, light orange and yellow nodes and the connecting edges between them. The dashed lines indicate the connections between the local transmission tree and the remaining nodes, and the number of connections is defined as the degree of the local transmission tree.

    下载: 全尺寸图片 幻灯片

    图 3  7个方法在9个网络上的不精确函数曲线　(a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2

    Figure 3.  The imprecision function curves for seven methods in nine networks: (a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2.

    下载: 全尺寸图片 幻灯片

    图 4  7个方法在9个网络上得到的节点重要性排序与真实传播影响力排序之间的肯德尔相关系数. 实际传播能力排序在前p 的节点被用于计算　(a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2

    Figure 4.  Kendall’s τ correlation between nodes’ importance and their real spreading influence under seven methods in nine networks. The top ranked p nodes with the highest spreading influence are taken into calculation: (a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2.

    下载: 全尺寸图片 幻灯片

    图 5  不同感染速率下PDGNN模型的不精确函数值. α表示传播阈值$ \beta_{\mathrm{c}} $的倍数, $ p=5{\text{%}} $, 训练集比例$ r=60{\text{%}} $　(a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2

    Figure 5.  Imprecisions of PDGNN under different infection rates $ \beta=\alpha\beta_{\mathrm{c}} $. Other parameters are set as $ p=5{\text{%}} $, the training set fraction $ r=60{\text{%}} $ and recovery rate $ \mu=1 $: (a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2.

    下载: 全尺寸图片 幻灯片

    图 6  不同训练集比例下PDGNN模型的不精确函数值. 其中$ p=5{\text{%}} $, 感染速率$ \beta=1. 8\beta_{\mathrm{c }}$　(a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2

    Figure 6.  Imprecision of the PDGNN model under different training fractions. Other parameters are set as $ p=5{\text{%}} $, infection rate $ \beta=1. 8\beta_{\mathrm{c}} $ and recovery rate $ \mu=1 $: (a) Musae_chameleon; (b) Router; (c) Blogs; (d) Jazz; (e) Celegans; (f) Ca-netscience; (g) CollegeMsg; (h) SCF1; (i) SCF2.

    下载: 全尺寸图片 幻灯片

    表 1  9个网络的统计特性. $ \left|N\right| $为网络中节点数, $ \left|E\right| $为网络中边数, $ \langle k \rangle $为网络的平均度, $ k_{{\mathrm{max}}} $为网络的最大度, c为网络的平均聚类系数, $ \beta_{\mathrm{c}} $为SIR传播过程的爆发阈值

    Table 1.  Statistical features of nine networks. $ \left|N\right| $ and $ \left|E\right| $ are the number of nodes and edges in the network respectively, $ \langle k \rangle $ is the average degree, $ k_{{\mathrm{max}}} $ is the maximum degree, c is the average clustering coefficient, and $ \beta_{\mathrm{c}} $ is the epidemic threshold in SIR spreading.

    网络 $ \left|N\right| $ $ \left|E\right| $ $ \langle k \rangle $ $ k_{{\mathrm{max}}} $ c $ \beta_{\mathrm{c}} $
    Musae_chameleon 2277 31371 27. 555 732 0. 481 0. 036
    Router 5022 6258 2. 492 106 0. 012 0. 401
    Blogs 3982 6803 3. 417 189 0. 284 0. 293
    Jazz 198 2742 27. 69 78 0. 242 0. 036
    Celegans 295 2244 15. 214 116 0. 189 0. 066
    Ca-netscience 379 914 4. 823 34 0. 741 0. 207
    CollegeMsg 1893 13835 14. 62 255 0. 109 0. 068
    SCF1 1000 2991 5. 982 99 0. 032 0. 167
    SCF2 2000 8997 8. 997 43 0. 009 0. 111
    下载: 导出CSV

    表 2  4个方法在9个网络上的分类性能. 在所有的结果中, 粗体表示最好的结果

    Table 2.  Classification performance of the four methods in nine networks. Among all the results, we emphasize the best one in bold.

    Networks SVM CGNN RF PDGNN
    Recall PR_AUC Recall PR_AUC Recall PR_AUC Recall PR_AUC
    Musae_chameleon 0 3603 0.3603 0 0.378 0 0.2667 0.9524 0.3991
    Router 0.4048 0.7776 0.3864 0.603 0.4762 0.7714 1 0.8761
    Blogs 0.5897 0.8095 0.4651 0.6582 0.3333 0.7134 1 0.9089
    Jazz 0 1 0 0.1843 0.5 1 1 1
    Celegans 0.6 0.75 0 0 0.2 0.3333 1 0.8889
    Ca-netscience 0.1667 0.7452 0 0.1607 0 0.6389 1 1
    CollegeMsg 0.1579 0.5673 0.125 0.2968 0.0526 0.6965 1 0.6431
    SCF1 0.2 0.5741 0.6 0.7783 0.2 0.4792 1 0.9709
    SCF2 0.4091 0.8158 0.2268 0.7653 0.1818 0.8002 1 0.8837
    下载: 导出CSV
  • [1] 汪小帆, 李翔, 陈关荣 2012 网络科学导论 (北京: 高等教育出版社)第7—14页 Wang X F, Li X, Chen G R 2012 Network Science: An Introduction (Beijing: Higher Education Press) pp7–14
    [2] Nielsen B F, Simonsen L, Sneppen K 2021 Phys. Rev. Lett. 126 118301 doi: 10.1103/PhysRevLett.126.118301
    [3] Song K, Park H, Lee J, Kim A, Jung J 2023 Sci. Rep. 13 11469 doi: 10.1038/s41598-023-38314-3
    [4] Kitsak M, Gallos L K, Havlin S, Liljeros F, Muchnik L, Stanley H E, Makse H A 2010 Nat. Phys. 6 888 doi: 10.1038/nphys1746
    [5] Kim S, Jiang J Y, Han J, Wang W 2023 Proceedings of the International AAAI Conference on Web and Social Media Limassol, Cyprus, June 5–8 2023, pp482–493
    [6] Lü L, Chen D, Ren X L, Zhang Q M, Zhang Y C, Zhou T 2016 Phys. Rep. 650 1 doi: 10.1016/j.physrep.2016.06.007
    [7] Pei S, Morone F, Makse H A 2018 Complex Spreading Phenomena in Social Systems: Influence and Contagion in Real-World Social Networks (Berlin: Springer) pp125–148
    [8] Liu J, Li X, Dong J 2021 Sci. China Tech. Sci. 64 451 doi: 10.1007/s11431-020-1683-2
    [9] Fan T, Lü L, Shi D, Zhou T 2021 Commun. Phys. 4 272 doi: 10.1038/s42005-021-00781-3
    [10] Liu Y, Zeng Q, Pan L, Tang M 2023 IEEE Trans. Netw. Sci. Eng. 10 2201 doi: 10.1109/TNSE.2023.3243560
    [11] Zhao G, Jia P, Huang C, Zhou A, Fang Y 2020 IEEE Access 8 65462 doi: 10.1109/ACCESS.2020.2984286
    [12] Asgharian Rezaei A, Munoz J, Jalili M, Khayyam H 2023 Expert Syst. Appl. 214 119086 doi: 10.1016/j.eswa.2022.119086
    [13] Yu E Y, Wang Y P, Fu Y, Chen D B, Xie M 2020 Knowledge-Based Syst. 198 105893 doi: 10.1016/j.knosys.2020.105893
    [14] Ou Y, Guo Q, Xing J L, Liu J G 2022 Expert. Syst. Appl. 203 117515 doi: 10.1016/j.eswa.2022.117515
    [15] Ahmad W, Wang B, Chen S 2024 Appl. Intell. 54 3260 doi: 10.1007/s10489-024-05336-x
    [16] Zhao G, Jia P, Zhou A, Zhang B 2020 Neurocomputing 414 18 doi: 10.1016/j.neucom.2020.07.028
    [17] Rashid Y, Bhat J I 2024 Knowledge-Based Syst. 283 111163 doi: 10.1016/j.knosys.2023.111163
    [18] Xiong Y, Hu Z, Su C, Cai S M, Zhou T 2024 Appl. Soft Comput. 163 111895 doi: 10.1016/j.asoc.2024.111895
    [19] Munikoti S, Das L, Natarajan B 2021 In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics Melbourne, Australia, October 17–20 2021, pp3245–3251
    [20] Xhonneux L P, Qu M, Tang J 2020 Proceedings of the 37th International Conference on Machine Learning Virtual Event, July 13–18 2020, pp10432–10441
    [21] Pastor-Satorras R, Vespignani A 2001 Phys. Rev. Lett. 86 3200 doi: 10.1103/PhysRevLett.86.3200
    [22] Wang W, Tang M, Zhang H F, Gao H, Do Y, Liu Z H 2014 Phys. Rev. E 90 042803 doi: 10.1103/PhysRevE.90.042803
    [23] 李江, 刘影, 王伟, 周涛 2024 物理学报 73 048901 doi: 10.7498/aps.73.20231416 Li J, Liu Y, Wang W, Zhou T 2024 Acta Phys. Sin. 73 048901 doi: 10.7498/aps.73.20231416
    [24] Šikić M, Lančić A, Antulov-Fantulin N, Štefančić H 2013 Eur. Phys. J. B 86 1 doi: 10.1140/epjb/e2012-30793-6
    [25] Lawyer G 2015 Sci. Rep. 5 8665 doi: 10.1038/srep08665
    [26] Liu Y, Tang M, Zhou T, Do Y 2016 Phys. A 452 289 doi: 10.1016/j.physa.2016.02.028
    [27] Narayanan A, Chandramohan M, Venkatesan R, Chen L H, Liu Y, Jaiswal S 2017 arXiv: 1707.05005 [cs.LG]
    [28] Liu J G, Lin J H, Guo Q, Zhou T 2016 Sci. Rep. 6 21380 doi: 10.1038/srep21380
    [29] Wu Y, Hu Y, Yin S, Cai B, Tang X, Li X 2024 Knowledge-Based Syst. 301 112235 doi: 10.1016/j.knosys.2024.112235
    [30] Lin T Y, Goyal P, Girshick R, He K, Dollár P 2017 Proceedings of the IEEE International Conference on Computer Vision Venice, Italy, October 22–29 2017, pp2980–2988
    [31] Rozemberczki B, Allen C, Sarkar R 2021 J. Complex Netw. 9 cnab014 doi: 10.1093/comnet/cnab014
    [32] Spring N, Mahajan R, Wetherall D, Anderson T 2004 IEEE/ACM Trans. Netw. 12 2 doi: 10.1109/TNET.2003.822655
    [33] Adamic L A, Glance N 2005 Proceedings of the 3rd International Workshop on Link Discovery Chicago Illinois, USA, August 21–25 2005, pp36–43
    [34] Gleiser P M, Danon L 2003 Adv. Complex. Syst. 6 565 doi: 10.1142/S0219525903001067
    [35] Watts D J, Strogatz S H 1998 Nature 393 440 doi: 10.1038/30918
    [36] Rossi R, Ahmed N 2015 Proceedings of the 29th AAAI Conference on Artificial Intelligence Austin, Texas, USA, January 25–30 2015, pp4292–4293
    [37] Panzarasa P, Opsahl T, Carley K M 2009 J. Am. Soc. Inf. Sci. Technol. 60 911 doi: 10.1002/asi.21015
    [38] Castellano C, Pastor-Satorras R 2010 Phys. Rev. Lett. 105 218701 doi: 10.1103/PhysRevLett.105.218701
    [39] 李睿琪, 王伟, 舒盼盼, 杨慧, 潘黎明, 崔爱香, 唐明 2016 复杂系统与复杂性科学 13 1 doi: 10.13306/j.1672-3813.2016.01.001 Li R Q, Wang W, Shu P P, Yang H, Pan L M, Cui A X, Tang M 2016 Complex Syst. Complex Sci. 13 1 doi: 10.13306/j.1672-3813.2016.01.001
    [40] Morone F, Makse H A 2015 Nature 524 65 doi: 10.1038/nature14604
  • 加载中
图( 6) 表( 2)
计量
  • 文章访问数:  37
  • HTML全文浏览数:  37
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-02-14
  • 刊出日期:  2025-05-20

融合节点动态传播特征与局域结构的复杂网络传播关键节点识别

    通讯作者: E-mail: shinningliu@163.com; 
  • 1. 西南石油大学计算机与软件学院, 成都　610500
  • 2. 华东师范大学物理与电子科学学院, 上海　200241
  • 3. 华东师范大学, 上海多维信息处理重点实验室, 上海　200241
  • 收稿日期:  2025-02-14

摘要: 识别复杂网络中的传播关键节点在加速信息扩散、抑制病毒或谣言的传播等应用中至关重要. 现有识别网络传播中关键节点的方法各有局限: 复杂网络中心性方法仅从局域或者全局拓扑结构预测节点影响力; 传统机器学习和深度学习方法不适用于图结构数据; 已有基于图神经网络的方法忽视了传播过程自身的动力学特性. 鉴于此, 本文提出一种融合传播过程动力学特征与节点局域结构的传播动态图神经网络(propagation dynamics graph neural network, PDGNN), 用于识别复杂网络传播中的关键节点. 通过结合易感-感染-恢复传播模型, 提取节点传播过程中的动态感染特征, 构建高维特征向量并设计优化的损失函数, 以实现对复杂网络传播关键节点的准确识别. 在2个合成网络和7个真实网络上的实验结果表明, PDGNN在复杂网络传播关键节点识别准确性上优于经典的中心性方法、基于传统机器学习和深度学习的方法以及现有的基于图神经网络的方法.

English Abstract

    全文HTML

    1.   引　言

    • 复杂网络由大量节点和边组成, 具有非规则、非均匀分布特性, 可用于表示交通、社交、生物等真实系统[1], 为理解和分析复杂系统提供了理论框架. 复杂网络的关键节点指对网络的结构和功能起决定性作用的节点或节点集, 例如: 1)新冠肺炎疫情期间, 少数个体作为超级传播者在短时间内将病毒通过人际接触网络传给了大量人群[2,3]; 2)网络中最有效的“传播者”是优化利用现有资源和确保信息高效传递的关键[4,5]; 3)恐怖分子组织间的秘密通信依靠核心成员, 识别并移除这些关键人物能极大破坏其通信网络. 上述例子表明, 疾病或信息的迅速传播依赖于网络中的关键节点, 识别这些关键节点对抑制或促进传播过程至关重要. 由于复杂网络结构的多样性, 如何准确识别复杂网络传播中的关键节点仍是一个极具挑战的任务. 研究人员提出各种方法来识别复杂网络传播中的关键节点, 主要分为基于中心性的方法, 基于传统机器学习和深度学习的方法以及基于图神经网络的方法.

      节点中心性通常用于区分网络中节点的结构重要性, 例如度中心性、特征向量中心性、介数中心性、k核指数、紧密度中心性等. 具有较高中心性的节点被认为在网络中具有较大的传播影响力. 基于网络的中心性, 研究人员提出了许多算法来识别复杂网络传播中的关键节点[4,6–10]. 然而, 单一的中心性指标难以准确预测复杂网络中节点的传播影响力. 研究者转向基于机器学习和深度学习的方法, 挖掘节点特征与节点传播影响力之间的复杂关系. 例如, 研究人员提出机器学习框架, 通过支持向量机、随机森林等机器学习算法学习节点传播影响力与多个中心性特征之间的关系[11]. 在使用机器学习模型的基础上, 研究人员结合聚类采样方法从大规模网络中选取一小部分作为训练节点, 在保持模型精度的同时提高了训练效率[12]. 基于局部子图的模型如RCNN[13]及其改进算法M-RCNN[14]将关键节点识别问题转化为回归问题, 学习节点结合了中心性特征的邻域结构与传播影响力之间的映射关系. LCNN[15]使用卷积神经网络和结合了多尺度度量与局部邻接矩阵的特征来识别关键节点, 平衡了特征提取的丰富性与运行效率. 由于传统的机器学习和深度学习方法无法处理图结构数据, 上述方法忽略了节点间的连接关系.

      图神经网络通过捕获图中节点和边之间的复杂关系, 实现了高效的节点表示学习和图结构信息的利用, 进一步推动了复杂网络传播关键节点识别的研究. InfGCN[16]和OlapGN[17]利用图神经网络进行全局嵌入学习, 通过多层图卷积网络识别关键节点. AGNN[18]结合自编码器与图神经网络, 全面捕捉图的拓扑特性. 图鲁棒贝叶斯归纳学习器(bayesian inductive learner for graph robustness, BILGR)[19]系统考虑网络中边或节点的不确定性, 在不确定网络上实现关键节点识别, 同时降低了计算复杂度. 受基于扩散的图方法的启发, 研究人员提出了连续图神经网络CGNN[20], 用常微分方程建模节点表示的连续动态, 突破了离散动态的图神经网络的局限, 为关键节点识别提供了新的模型选择. 这些方法在提高关键节点识别的精度上取得了显著成效.

      尽管基于图神经网络的模型在传播关键节点识别任务中具有较好的性能, 现有模型仍仅依赖静态网络结构特征, 忽略了传播过程本身的动力学特性. 实际上, 节点的传播影响力不仅与其在网络中的结构特性相关, 还受到传播动力学的显著影响[4,10,21–23]. 如果传播参数变化, 节点的传播影响力排名会发生显著变化[24]. 为了弥补这一缺陷, 本文提出一种基于节点传播动态特征的传播动态图神经网络PDGNN. 与现有仅依赖于网络静态结构特征的方法不同, PDGNN充分融合传播过程中节点传播影响力的动态特征与局域结构信息. 利用图神经网络的深度特征学习功能, 模型能够捕捉节点在网络中的传播影响力, 实现复杂网络传播关键节点的准确识别. 在2个合成网络和7个真实网络上, 将提出的PDGNN与基于中心性的方法、基于机器学习和深度学习的方法以及基于图神经网络的方法进行了关键节点识别性能的比较. 实验结果表明, 本文提出的方法能够更为准确地识别网络传播中的关键节点. 本文的主要贡献如下.

      1) 设计了一种图神经网络模型以准确识别复杂网络上的传播关键节点. 将传播动力学引入特征工程, 生成节点的潜在表示. 利用图神经网络的深度特征学习功能, 模型能够全面地学习节点特征和传播影响力之间的复杂非线性关系, 提高传播关键节点识别准确性.

      2) 为优化模型性能, 引入新的损失函数FocalMSE, 该损失函数解决了类别不均衡问题, 并通过输出的分类概率精确量化了同一类别下节点间的传播影响力差异.

      3) 在合成网络和真实网络上进行了大规模的实验来评估提出模型的性能. 结果表明, PDGNN模型能够更为有效地识别关键节点.

      文章剩余部分组织如下: 第2节系统阐述本文提出的模型; 第3节描述实验设计, 展示在真实网络上的实验结果并进行了分析; 最后, 第4节对工作进行总结.

    2.   模　型

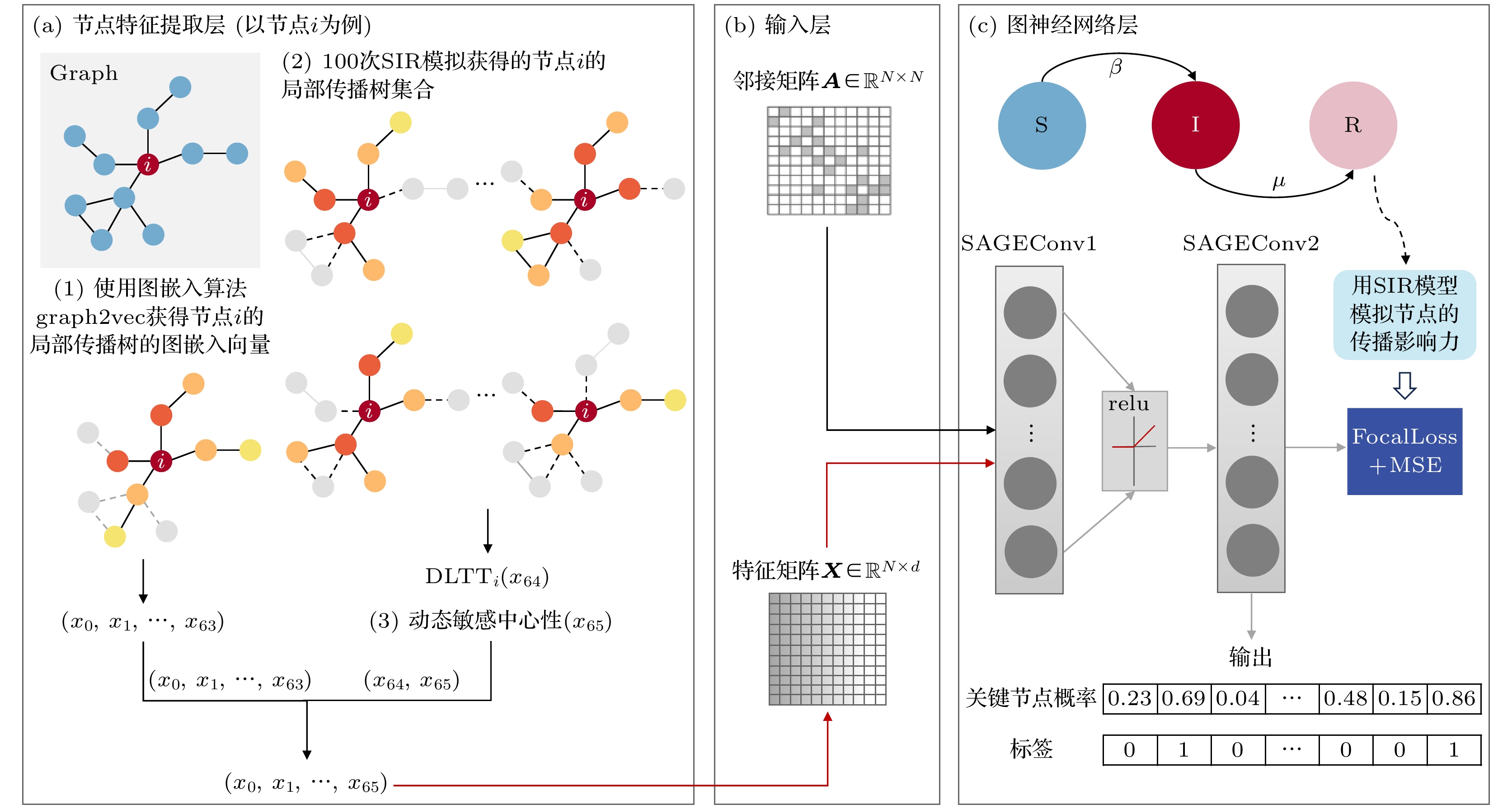
    • 提出传播动态图神经网络模型PDGNN, 将关键节点识别问题转化为分类任务, 利用图神经网络有效识别复杂网络传播中的关键节点. 该模型的框架如图1所示, 包括: (a)节点特征提取层, (b)输入层和(c)图神经网络层. 节点特征提取层提取节点的三个传播特征, 输入层接收初始特征矩阵$ {\boldsymbol{X}}\in{\mathbb{R}^{N\times{d}}} $和网络的邻接矩阵$ {\boldsymbol{A}}\in{\mathbb{R}^{N\times{N}}} $, 其中N为网络总节点数, d为特征向量维度. 图神经网络层对节点特征进行逐层更新, 最终输出节点的分类概率和类别.

      首先, 使用经典的易感-感染-恢复(susceptible-infected-recovered, SIR)传播模型模拟节点的实际传播影响力以获取标签, 并将传播影响力排在前5%的节点标注为关键节点. 提取节点基于传播动力学的三个特征向量, 将邻接矩阵和特征矩阵作为图神经网络模型的输入. 考虑到关键节点在网络中占比极小导致的关键节点和非关键节点间类别不均衡问题, 以及同一类别节点之间传播影响力存在差异却无法精确衡量的问题, 我们设计了损失函数FocalMSE. 通过学习节点特征与标签之间的映射关系, PDGNN能够实现节点的准确分类, 并输出相应的分类概率.

      • 2.1.   节点标签

    • 采用SIR模型来模拟网络中节点的传播影响力, 生成节点标签, 为关键节点的识别提供训练数据. SIR模型是一种经典的传播动力学模型, 用于描述个体在感染疾病后具备永久免疫力的传播过程. SIR模型中每个节点可处于以下三种状态之一: 易感态(susceptible, S)、感染态(infected, I) 和恢复态(recovered, R). 在每个时间步, 易感态个体被相邻的感染态个体以感染率β感染, 变成感染态. 感染态个体以恢复率μ恢复, 变为恢复态. 恢复态的个体不会传播疾病, 也不再被感染. 当网络中不存在感染态个体时, 网络达到稳态, 不再有流行病的传播.

      为模拟网络中节点i的传播影响力, 初始时将节点i的状态设置为感染态, 网络中其余节点的状态设置为易感态. 随后进行SIR传播. 在网络达到稳态后, 记录下此刻处于恢复态节点的比例, 表示整个传播过程中曾经被感染过的节点占比. 鉴于SIR传播的随机性, 以节点i作为初始感染节点进行1000次独立的SIR传播, 将节点i的传播影响力$ M_i $定义为1000次传播达到稳态时恢复态节点比例的平均值. 计算图G中每个节点的传播影响力$ M_i $之后, 传播影响力排名前5%的节点被视为关键节点, 标记为1, 其余节点标记为0.

      • 2.2.   节点特征

    • 节点特征描述网络中节点的属性和关系, 有效的特征选择能够显著提高模型的精度与泛化能力. 传统的识别关键节点的方法多依赖静态结构特征, 忽略了网络上的传播动力学特性, 限制了传播关键节点识别的效果. 为更准确地识别关键节点, 模型需要在特征构造时充分考虑传播动力学因素. 通过在特征构造中融入节点传播过程, 模型能够更全面地捕捉节点的影响力, 提升识别的准确性. 本文定义了三个特征作为图神经网络的输入: 局部传播树的嵌入向量、局部传播树的度和动态敏感中心性. 局部传播树的嵌入向量通过图嵌入得到, 主要捕捉局部传播树的拓扑结构信息, 是一种高维的表示; 局部传播树的度直接反映节点的局部连接强度, 衡量节点的初期扩散潜力, 是一个结构指标; 动态敏感中心性量化了节点将疾病传播给有限时间步内可达节点的总概率.

      • 2.2.1.   局部传播树的嵌入

    • 为捕获节点在传播时的动态特征, 本文定义局部传播树(local transmission tree, LTT). 局部传播树是指以一个节点为传播源形成的包含传播路径和被感染节点的前期传播簇. 具体来说, 通过SIR模型模拟以一个节点作为初始感染节点时的疾病传播过程, 记录下传播过程中形成的包含新增感染节点和传播路径的动态传播树. 已有研究表明, 三步传播即可提供充足的信息来预测节点的传播影响力, 而超过三步的传播对最终传播范围和深度的预测贡献较为有限[25,26]. 本实验中局部传播树的传播步数设为3. 图2展示了以红色节点作为初始I态节点进行SIR传播时, 每一个时间步节点的受感染情况. 在三个时间步后, 记录下此时网络中的I态节点和R态节点及其之间的连边, 获得以节点i为传播源的局部传播树.

      使用图嵌入算法对局部传播树进行处理, 以便将节点的传播动态特征和局部结构信息转化为图神经网络可处理的输入形式. 图嵌入算法将图中的节点和边转化为多维向量表示, 捕捉了节点之间的连接关系. 与传统的静态特征方法相比, 局部传播树的嵌入不仅能够更好地表征节点在传播时的影响力, 还能捕捉到其在传播过程中的动态特性. 使用图嵌入算法graph2vec[27]对局部传播树进行图嵌入, 得到局部传播树的嵌入向量. 由于每一次SIR传播模拟可能会产生不同的局部传播树, 因此将每个节点作为初始传播源进行100次SIR传播模拟, 将模拟所得局部传播树集合中出现频率最高的局部传播树进行图嵌入. 在本文中, graph2vec为每一个局部传播树LTT学习一个δ维的嵌入表示$ \phi({\mathrm{LTT}}) $, 主要流程如下:

      1)定义训练轮数和学习率、期望的图嵌入向量维度δ和学习嵌入时要考虑的子图的最大深度D.

      2)获得网络G中所有节点的局部传播树, 记为$ \mathbb{LTT} $.

      3)通过Weisfeiler-Lehman (WL)核实现从LTT中提取子图信息. 具体来说, 在训练的每一轮, 获取$ \mathbb{LTT} $里每个LTT中节点i周围以该节点为根, 深度为d的子图$ sg_i^{(d)} $ (深度d从0取到D). 将每个节点的度作为初始特征, 每轮迭代时将节点特征与邻居特征组合, 并通过哈希函数生成新特征. 达到预设训练轮数时结束特征更新. 输出一组特征哈希值, 表示$ \mathbb{LTT} $里所有子图的集合.

      4)最小化图-子图共现概率的损失函数:

      其中, ϕ表示$ \mathbb{LTT} $里所有LTT的嵌入表示, $ Pr(sg_i^{(d)}\mid{\phi({\mathrm{LTT}})}) $表示图LTT-子图$ sg_i^{(d)} $的共现概率. 通过最小化(1)式来学习LTT的嵌入表示, 有效捕捉图的结构信息. $ Pr(sg_i^{(d)}\mid{\phi({\mathrm{LTT}})}) $定义为

      (2)式计算了给定图LTT的情况下出现子图$ sg_i^{(d)} $的条件概率. 这里$ sg^{(d)} $和$ \phi({\mathrm{LTT}}) $分别是子图和LTT的表示向量, $ \mathbb{V} $是$ \mathbb{LTT} $中所有子图哈希值.

      5)使用梯度下降更新嵌入表示ϕ, 即

      其中α是学习率.

      在实验中, 训练轮数设定为10轮, 学习率设置为0.025, δ取64, D设为2. 通过graph2vec得到的图嵌入向量不仅包含图的局部子图信息, 还融合了全局拓扑信息. 这种嵌入方式能够有效比较不同节点的局部传播树的相似性, 识别传播影响力相似的节点. 同时, 嵌入向量显著降低了数据维度, 在去除冗余信息的基础上保留了节点在传播过程中的关键特征, 提升了模型训练的效率和性能.

      • 2.2.2.   局部传播树的度

    • 局部传播树的度(degree of local transmission tree, DLTT)是指局部传播树中所有节点与树外节点之间连边的数量. 如图2(d)所示, 红色节点的局部传播树的度为图中黑色虚线的数量. 局部传播树的度越高, 意味着节点具备更强的扩散潜力, 能够通过较短的传播路径感染更多的剩余节点.

      局部传播树的度有助于模型识别出传播过程中影响范围大的关键节点, 更精确地捕捉不同节点在网络感染动态过程中的影响力. 本文将节点作为初始传播源进行100次SIR传播获得的局部传播树的平均度作为节点的局部传播树的度. 具体的计算过程如算法1所示.

      Algorithm 1 计算节点v的局部传播树的度

      输入: 图G, 节点v和以节点v作为初始感染节点进行100次SIR模拟获得的局部传播树集合trees;

      1: $ {\mathrm{degree}}_{{\mathrm{list}}} \gets [\; ] $;

      2: for LTT in trees do

      3: 　　$ {\mathrm{degree}} \gets 0 $;

      4: 　　for each node $ u \in {\mathrm{LTT}} $ do

      5: 　　　　for each node $ w \in G.\; {\mathrm{neighbors}}(u) $ do

      6: 　　　　　if $ w \notin {\mathrm{LTT}} $ then

      7: 　　　　　　$ {\mathrm{degree}} \gets {\mathrm{degree}} + 1 $;

      8: 　　　　　end if

      9: 　　　　end for

      10:　　end for

      11:　　Add $ {\mathrm{degree}} $ to $ {\mathrm{degree_{list}}} $;

      12: end for

      13: $ {\mathrm{DLTT}} \gets \dfrac1 {100}{\sum {\mathrm{degree}}_{{\mathrm{list}}}} $;

      输出: 节点v的局部传播树的度DLTT

      • 2.2.3.   动态敏感中心性

    • 动态敏感(dynamics-sensitive, DS)中心性[28]是一种结合节点动态传播特性与静态网络结构的中心性指标, 用于量化节点在传播过程中的影响力. 相比于静态中心性指标, 动态敏感中心性能够描述节点在传播过程中的影响力. 具体来说, 动态敏感中心性衡量了节点在时间步t内对网络中其他节点感染概率的累计贡献. 节点i的动态敏感中心性定义为

      其中β是传播率, A是网络的邻接矩阵, $ A^k_{j, i} $表示从节点j到节点i长度为k的路径数, n是网络中的总节点数, t是考虑的传播步数.

      (4)式计算了在t步内, 所有其他节点j通过不同长度的路径传播到节点i的概率之和. 动态敏感中心性量化节点在给定时间步内的传播影响力. 已有研究表明, 三步传播能够捕捉足够的信息以表征节点的传播影响力, 因此在本研究中时间步长t设置为3. 通过计算节点在最多三步内的传播贡献, 动态敏感中心性能够捕捉到广泛的节点和路径. 通过累加不同步数下的传播概率, 动态敏感中心性反映了节点在整个网络传播中的综合影响力. 计算节点动态敏感中心性的过程见算法2.

      Algorithm 2 计算动态敏感中心性

      输入: 图G, 传播步数t;

      1: 获得图G的邻接矩阵A和总节点数n;

      2: $ P \gets [\beta A, \beta A^2, \cdots, \beta A^t]; $

      3: for node $ i = 1 $ to n do

      4: $ {\mathrm{DS}}[i] \gets \sum_{k=1}^{t} \sum_{j=1}^{n} P_k[j, i]; $

      5: end for

      输出: 每个节点的动态敏感中心性值DS

      • 2.3.   损失函数

    • 损失函数通过量化模型预测值与真实值之间的差距, 指导模型在训练过程中不断优化参数, 以最小化这种差距. 选择合适的损失函数对于确保模型在特定任务上的性能至关重要. 在已有使用图神经网络分类模型进行关键节点识别的工作中[16,29], 损失函数的设计未充分考虑类别不平衡问题(关键节点数量远少于普通节点), 导致模型偏向于多数类, 影响少数类(关键节点) 的识别效果. 本文设计复合损失函数FocalMSE, 在解决类别不平衡的同时兼顾对传播影响力的细化建模. 其定义如下:

      其中, Focal Loss用于解决类别不均衡问题, MSE用于对传播影响力的细化建模, 两项结合使得模型能够同时处理类别不平衡问题并优化关键节点的影响力预测. Focal Loss (FL)[30]通过调整样本权重来使模型更加关注少数类样本, 从而提高其对少数类样本的识别能力, 并减少对多数类样本的关注. 公式如下:

      其中$ \alpha_{t} $是类别平衡因子, 用于调节不同类别之间的损失权重, $ p_{t} $是模型对正确类别的预测概率, γ是焦点调节因子, 用于控制模型对易分类和难分类样本的关注程度. $ (1-p_{t})^{\gamma} $用于降低非关键节点的权重, 使模型更加注重关键节点. 在本实验中, 设置$ \gamma=2 $以增强对关键节点的关注. 同时, $ \alpha_{t} $被设置为每个类别的样本数量的倒数, 并进行了归一化处理, 使得所有类别的权重和为1.

      均方误差(mean squared error, MSE)是一种常用的回归损失函数, 用于衡量模型预测值与真实值之间的差异, 定义为

      在本实验中, $ y_{i} $表示第i个样本的传播影响力, $ \hat{y}_{i} $表示模型认为第i个样本属于关键节点的预测概率, $ n=2 $. 引入MSE主要是为了在提升模型分类性能的同时提供更细粒度的信息. 具体来说, 预测概率$ \hat{y}_{i} $代表模型对该节点属于关键节点的置信度, 反映了节点的重要程度. 最小化$ y_i $和$ \hat{y}_{i} $之间的差异将使得节点的预测概率与节点的传播影响力靠近, 可在准确分类的基础上精确量化节点的重要性.

    3.   实　验

    • 为评估所提出模型的关键节点识别性能, 在2个合成网络和7个真实网络上进行了大规模模拟实验. 实验结果表明, PDGNN在网络传播关键节点识别准确性上优于经典的中心性方法、基于机器学习和深度学习的方法以及现有图神经网络的方法.

      • 3.1.   数据集

    • 本实验使用的9个数据集包括2个合成网络和由7个真实数据集构建的无向无权网络. 这9个网络包括: 1) Musae_chameleon[31]: 维基百科特定主题页面互引网络, 节点表示文章, 边表示它们之间的相互链接; 2) Router[32]: 路由器级别的互联网, 节点代表路由器, 边表示这些路由器通过光纤或其他方式直接相连并交换数据包; 3) Blogs[33]: 在2004年美国大选的背景下, 博客之间的首页超链接网络; 4) Jazz[34]: 爵士音乐家之间的合作网络; 5) Celegans[35]: 秀丽隐杆线虫的神经元网络, 其中节点代表神经元, 边代表神经元之间的突触接触; 6) Ca-netscience[36]: 科学家合作网络, 记录了网络科学领域中科学家的合作关系; 7) CollegeMsg[37]: 加利福尼亚大学欧文分校的一个在线社交网络, 边$ (u, v) $表示用户u向用户v发送了一条私人消息(或反之); 8) SCFN1和SCFN2: 合成的无标度网络. 表1列出了这9个网络的一些统计性质.

      流行病传播的临界阈值$ \beta_{{\mathrm{c}}} $为引发广泛传播的最小传播率[38], 是网络传播动力学的重要参数. 根据平均场理论[39], 网络的流行病阈值$ \beta_{{\mathrm{c}}} $计算为

      其中$ \langle k \rangle $表示网络中所有节点的度数的平均值. 通过预实验发现, 1.8倍阈值能够较好地平衡传播规模和关键节点的区分度. 因此, 在获取节点的标签和特征时将感染速率β设置为$ \beta = 1. 8\beta_{{\mathrm{c}}} $, 使绝大多数节点作为初始感染节点时, 疾病能够在整个网络中扩散开来, 从而可以度量初始感染节点的传播影响力, 同时避免阈值附近传播信号过于局部化. 为简单起见, 在实验中将恢复速率μ设置为1.

      • 3.2.   对比方法

    • 为了与本文提出的PDGNN模型比较, 选择了两种基于中心性的方法、两种分别基于传统机器学习和深度学习以及一种基于图神经网络的传播关键节点识别方法作为比较的基准方法.

      集体影响(collective influence, CI)中心性[40]. 集体影响中心性是一种基于节点局部拓扑特性的中心性指标, 通过构造以节点为中心, 半径为l的局部球结构, 结合节点度数和球内邻居节点的度数来计算节点的中心性值. 集体影响中心性计算为

      其中$ k_i $表示节点i的度数, $ \partial{{\mathrm{Ball}}(i, l)} $表示以节点i为中心, 半径为l的球面上节点的集合(即与节点i距离为l的节点集合), $ k_j $是球面上节点的度.

      特征向量中心性(eigenvector centrality, EC). 特征向量中心性的思想是: 节点的重要性不仅取决于自身的连接数目, 还与其邻居节点的重要性直接相关. 特征向量中心性定义为以下特征向量问题的解:

      其中A是网络的邻接矩阵, λ是特征值, x是λ对应的特征向量. 矩阵A的最大特征值对应的特征向量为节点的特征向量中心性.

      支持向量机(support vector machine, SVM). SVM是一种基于最大间隔原则的监督学习算法, 旨在寻找能够最好区分不同类别数据的最优超平面. 对比实验中, 模型的输入为与PDGNN相同的特征矩阵, 使用与PDGNN相同的标签学习节点特征与标签之间的复杂非线性关系. 使用与PDGNN相同的数据集划分比例, 最终输出节点是否为关键节点的分类结果和分类概率.

      随机森林(random forest, RF). 随机森林是一种基于决策树集成的非参数监督学习方法, 通过随机选择特征和样本子集, 训练出一组决策树, 并通过投票(分类任务)策略对节点的重要性进行预测. 对比实验中, 模型的输入为与PDGNN相同的特征矩阵, 使用与PDGNN相同的标签学习特征与标签之间的复杂非线性关系. 使用与PDGNN相同的数据集划分比例, 最终输出节点是否为关键节点的分类结果和分类概率.

      LCNN[15]. LCNN使用节点的一跳邻接结构来生成邻接矩阵. 从度中心性和H指数中心性中各衍生出三个不同尺度的特征, 为每个节点构建2个通道集, 即基于度的局部组和基于H指数的局部组, 作为模型的输入. 经过卷积层和全局平均池化层后, LCNN使用前馈神经网络进行回归预测节点的影响力.

      RCNN[13]. RCNN为每个节点构建其领域局部子图和特征矩阵Bu. 特征矩阵Bu由邻接矩阵Au转换而来, 定义如下:

      其中$ K_{u_{i}} $为原网络中节点$ u_{i} $的度. 经过2个卷积层和2个池化层, RCNN最终通过一个全连接层输出节点的影响力预测值.

      CGNN[20]. CGNN是一种图神经网络模型, 将节点表示的更新过程视为时间上的连续演化过程. 对比实验中, 模型的输入为与PDGNN相同的特征矩阵和邻接矩阵, 使用与PDGNN相同的标签学习节点特征与标签之间的复杂非线性关系, 并充分利用图的拓扑结构来增强学习效果. 使用与PDGNN相同的数据集划分比例, 最终输出节点是否为关键节点的分类结果和分类概率.

      • 3.3.   评估指标

    • 为了评估PDGNN和对比方法识别关键节点的准确性, 使用不精确函数[4]、肯德尔相关系数、召回率和PR_AUC作为评估指标.

      不精确函数用于评估模型识别关键节点的不精确性, 定义为

      其中p是计算节点的比例$ (0\leqslant p\leqslant1) $; $ M(p) $表示规模为N的网络中, 预测结果排序在前p的节点的平均传播影响力; $ M_{{\mathrm{eff}}}(p) $表示实际传播影响力排序在前p的节点的平均传播影响力. $ \varepsilon(p) $量化了实际关键节点与预测的关键节点间平均传播影响力的接近程度, $ \varepsilon(p) $越小说明关键节点识别越准确.

      肯德尔相关系数用于度量2个排序序列的相关性. 在识别关键节点任务时, 用来衡量预测的节点重要性序列与实际重要性序列之间的一致性. 肯德尔相关系数定义为

      其中X和Y是长度均为n的2个列表, C和D分别表示2个列表之间一致对和不一致对的个数. 如果$ X_{i}>X_{j} $, $ Y_{i}>Y_{j} $或$ X_{i}<X_{j} $, $ Y_{i}<Y_{j} $, 则$ (X_{i}, Y_{i}) $和$ (X_{j}, Y_{j}) $是一致对; 如果$ X_{i}>X_{j} $, $ Y_{i}<Y_{j} $或$ X_{i}<X_{j} $, $ Y_{i}>Y_{j} $, 则$ (X_{i}, Y_{i}) $和$ (X_{j}, Y_{j}) $是不一致对; 若$ X_{i}=X_{j} $或$ Y_{i}=Y_{j} $, 则$ (X_{i}, Y_{i}) $和$ (X_{j}, Y_{j}) $既不是一致对也不是不一致对. τ越大表明预测的节点重要性序列与实际重要性序列越一致. 肯德尔相关系数专注于排序的一致性, 能够评估模型在关键节点排序上的细粒度表现.

      召回率表示有多少实际的关键节点被正确识别为关键节点, 它衡量的是模型识别出所有关键节点的能力. 召回率的计算公式如下:

      其中, TP是真正例个数, FN是假负例个数. 在关键节点识别任务中, TP表示被模型正确识别为关键节点的实际关键节点, 而FN则表示实际关键节点中被模型错误地识别为非关键节点的部分. 较高的Recall值意味着该模型能够有效捕获大多数关键节点, 从而减少遗漏风险.

      PR_AUC是一种专为类别不均衡数据集设计的指标, 旨在衡量模型在正负样本比例严重失衡情况下的性能表现. PR-AUC关注正类样本的预测质量, 适用于关键节点识别这种正类稀少但对正类的精准识别尤为重要的场景. PR-AUC的定义基于PR曲线, 通过连接不同阈值下的(recall, precision)点形成的曲线计算其包围的面积. 曲线越接近理想状态(精确率和召回率同时较高), 其面积越大, 说明模型在尽量避免漏报(高召回率) 的同时减少了误报(高精确率). 精确率的计算公式如下: $ {\mathrm{Precision}} = \dfrac{{\mathrm{TP}}}{{\mathrm{TP}}+{\mathrm{FP}}} $, 其中FP是假正例个数, 表示非关键节点被模型错误地识别为关键节点的数量. 在关键节点识别任务中, 严重的类别不均衡使得传统评估指标如准确率易受“多数类”节点的干扰, 高准确率可能无法反映模型的实际效果. 例如, 直接预测所有节点为非关键节点就能获得较高的准确率, 但这种预测无意义. 由于PR-AUC关注关键节点的识别效果, 能够避免数据不平衡导致的评估偏差, 适合在数据集类别不均衡的情况下反映模型性能.

      • 3.4.   实现细节

    • PDGNN基于GraphSAGE聚合机制, 使用PyTorch Geometric中的SAGEConv层更新节点表示, 捕捉网络中的拓扑结构信息和节点特征之间的关系. 使用均值聚合来更新每个节点的特征, 聚合公式如下:

      其中$ {\boldsymbol{x}}_{i} $是节点i的初始特征向量, $ {\boldsymbol{x}}_{i}' $是经过聚合后的节点特征向量, $ {\boldsymbol{W}}_{1} $和$ {\boldsymbol{W}}_{2} $是可学习的权重矩阵, 用于对节点自身的特征和邻居节点的特征进行线性变换. $ N(i) $表示节点i的邻居节点集合, $ {\mathrm{mean}}_{j\in{N(i)}}x_{j} $表示对所有邻居节点的特征进行平均. 对于每个中心节点i, 它的邻居节点特征的平均值为

      其中$ \left|N(i)\right| $是中心节点i的邻居节点数量. 通过聚合邻居节点的特征来更新当前节点的表示, 使得每个节点的表示不仅考虑了节点自身的特性, 还考虑了它在网络中的位置及其与其他节点的交互. 这种均值聚合可以充分利用所有邻居的特征并对其进行平滑处理, 在我们的任务中被证明是有效的.

      本文的模型主要包含2个SAGEConv层来对节点特征进行更新. 第一层接收输入特征的维度为66维, 并通过计算后输出128维的中间表示. 为了防止过拟合, 在前向传播过程中对输入特征进行了dropout处理. 经过第一层的聚合操作后, 应用了ReLU激活函数, 引入非线性变换以增强模型的表达能力. 第二层接收128维的中间表示, 并最终输出节点的分类结果. 每个SAGEConv层都设置了L2归一化, 确保输出特征的范数保持一致, 有助于提高模型的稳定性和泛化能力. 训练模型时, 使用训练集节点的标签y和传播影响力M用于监督学习. 在验证和测试阶段, 模型根据节点最终的表示向量进行分类, 输出分类概率. 模型的训练使用了Adam优化器, 学习率设置为0.01, 权重衰减系数设置为0.001, 训练的轮数设定为200. 为了防止模型过拟合, 在训练过程中引入了早停机制, 设置早停机制中的patience值为20, 最小训练轮数为10. 将数据集按照60%, 20%和20% 的比例划分为训练集、验证集和测试集. 训练集用于模型的参数更新, 验证集用于监控模型的泛化能力并决定是否触发早停, 测试集则用于最终模型性能的评估. 在训练过程中, 每当验证集上的性能达到新高时, 会自动保存当前的最佳模型. 训练结束后, 使用保存的最佳模型对测试集进行分类, 并输出每个节点的分类概率. 分类概率通过Sigmoid函数计算.

      • 3.5.   实验结果

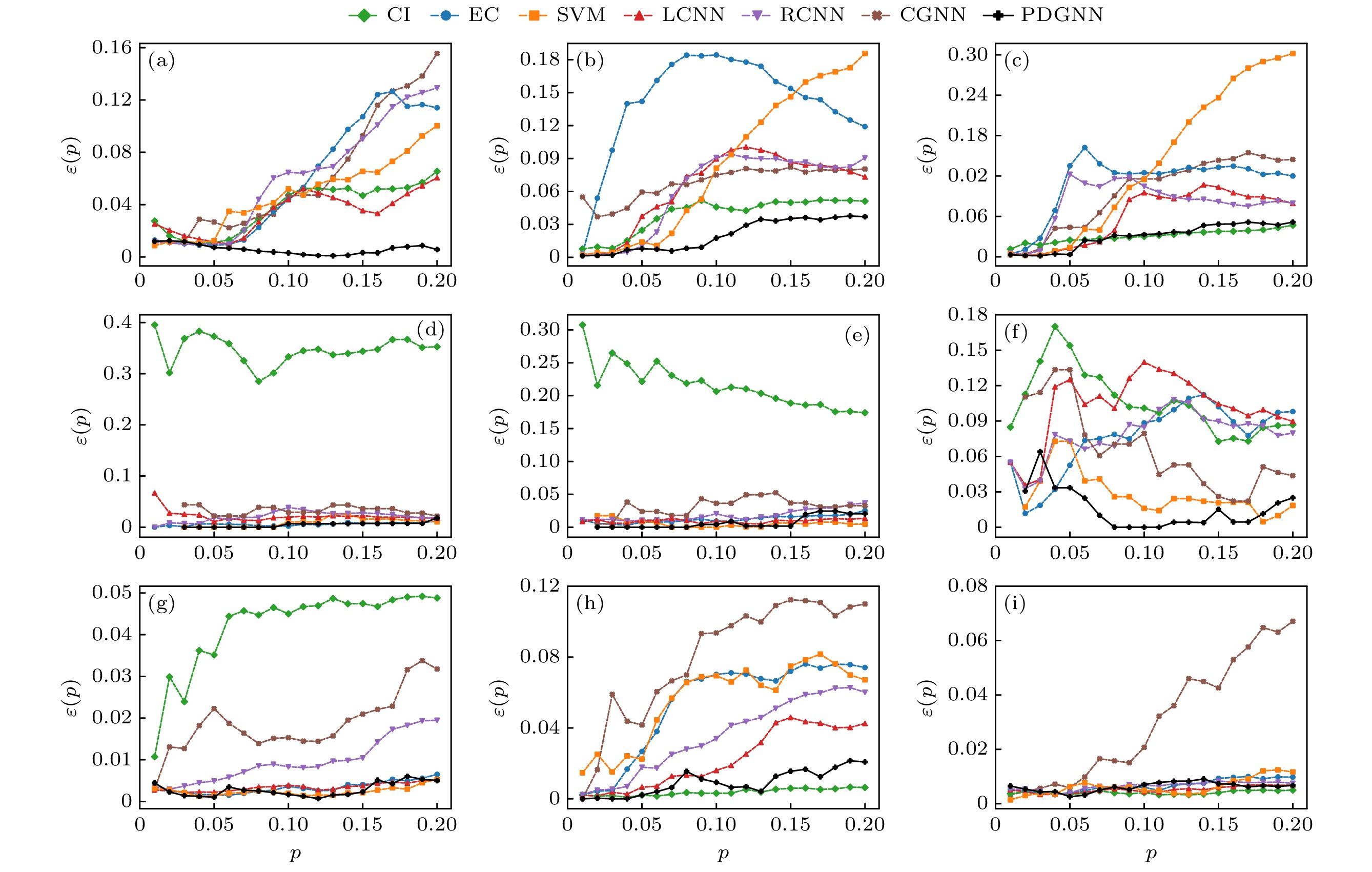
    • 本节展示了提出的模型在不同网络上的关键节点识别性能, 并与对比方法进行了比较. 在本实验中, 为了确保评估的公正性和可靠性, 对于机器学习、深度学习和图神经网络方法, 仅使用测试集的数据进行实验结果的比较. 图3展示了7个方法在9个网络上的不精确函数.

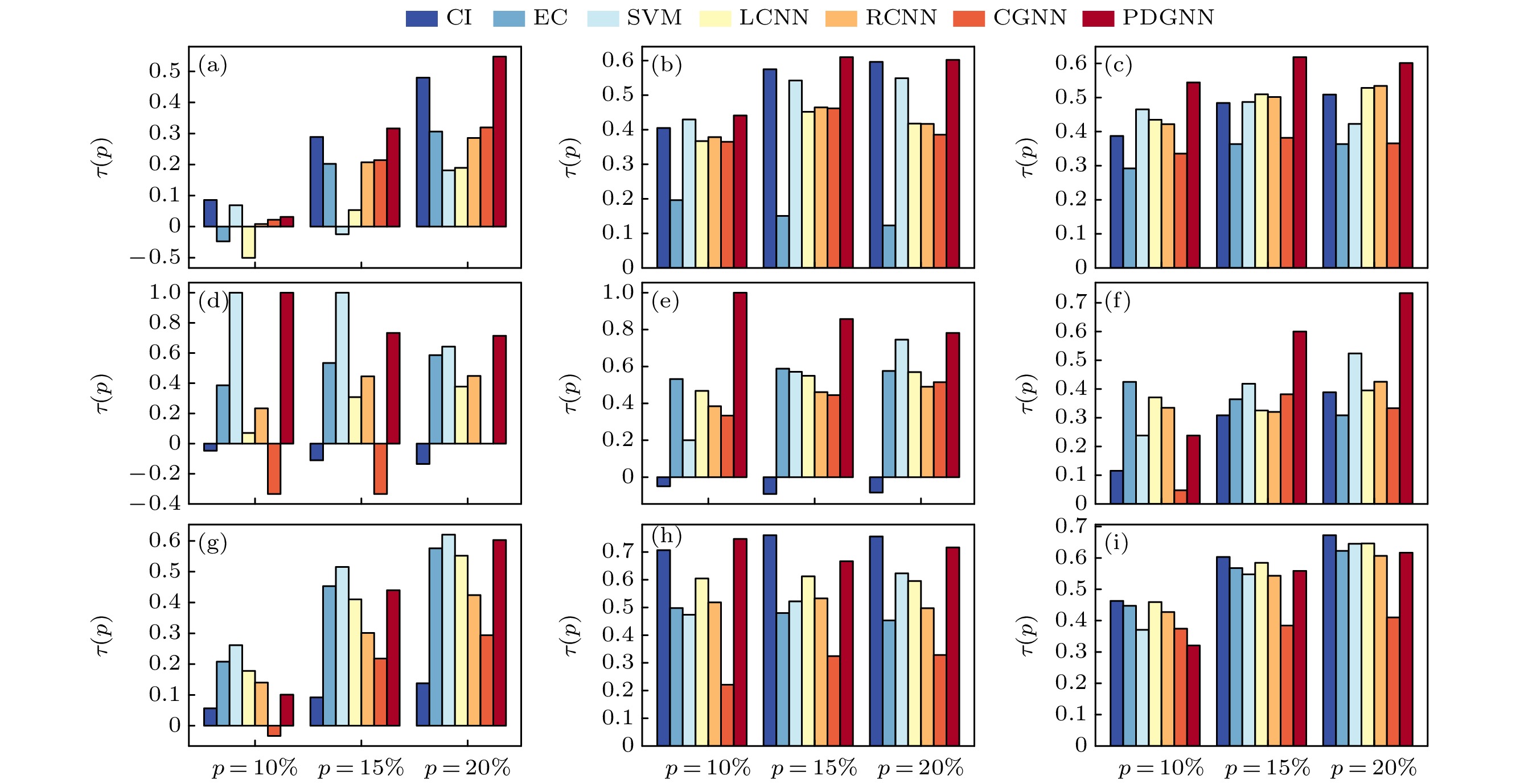
      PDGNN的不精确函数值在全部网络中均低于0.065, 表明PDGNN能准确识别关键节点. 在Musae_chameleon, Router, Jazz和Ca-netscience数据集上, PDGNN优于其他对比方法, 说明其能够准确预测网络中的关键节点. 在Blogs数据集中, PDGNN与CI为最佳方法. 在Celegans数据集中, PDGNN在$ p=8{\text{%}} $之前表现最优, 之后的不精确函数值也保持较低. 在CollegeMsg数据集中, PDGNN与SVM为最佳方法. 在SCF1数据集中, PDGNN的表现略差于CI, 但其不精确函数值显著低于其他方法. 在SCF2数据集中, PDGNN的表现与除CGNN外的其他方法相当, 其不精 确函数值保持在较低的数值范围. 由于PDGNN考虑了节点的动态传播特征、邻域结构和全局拓 扑结构, 更符合复杂网络中的传播过程, 因此可 以更准确地识别出大多数网络中的关键节点. 值 得注意的是, 由于SVM, CGNN和PDGNN的测 试集占比为数据集的20%, 因此在小规模数据集Jazz, Celegans和Ca-netscience上, p = 3%, 2%和2%时分别对应测试集中的第一个关键节点.

      接下来, 考虑不同关键节点识别算法的预测排名与节点实际传播影响力排名的相关性. 图4展示了在9个网络上, 不同方法生成的节点重要性排序与节点传播影响力排序之间的肯德尔相关系数. τ越大, 表明节点重要性排序算法预测的排序与节点实际传播影响力排序之间的相关性越高. p表示考虑的节点比例. 当$ p=5{\text{%}} $, $ p=10{\text{%}} $和$ p=15{\text{%}} $时, PDGNN在Router, Blogs和Celegans数据集上均具有最高的肯德尔相关系数, 说明由PDGNN获得的重要性排序与传播影响力排序较为一致. 此外, 在Musae_chameleon, Jazz, Ca-netscience和SCF1数据集上, PDGNN同样获得了较高的肯德尔相关系数值, 进一步验证了其在不同网络下的关键节点识别能力.

      接下来, 使用分类评估指标Recall和PR_AUC来评估所提出的模型与其他三种分类方法在关键节点识别任务中的性能. 由表2可知, 本文的方法PDGNN在8个数据集上的Recall值和PR_AUC分数均高于其他方法. 在CollegeMsg数据集中, PDGNN的PR_AUC值略低于随机森林算法, 位居第二. 值得注意的是, 小规模数据集Jazz, Ca-netscience和Celegans中测试集的关键节点数量很少, 如果模型没有将少数几个关键节点识别出来, Recall值将为0. 由于本文的方法设计了优化的损失函数, 有效提升了关键节点的识别能力, 在小规模数据集上也取得了令人满意的分类结果.

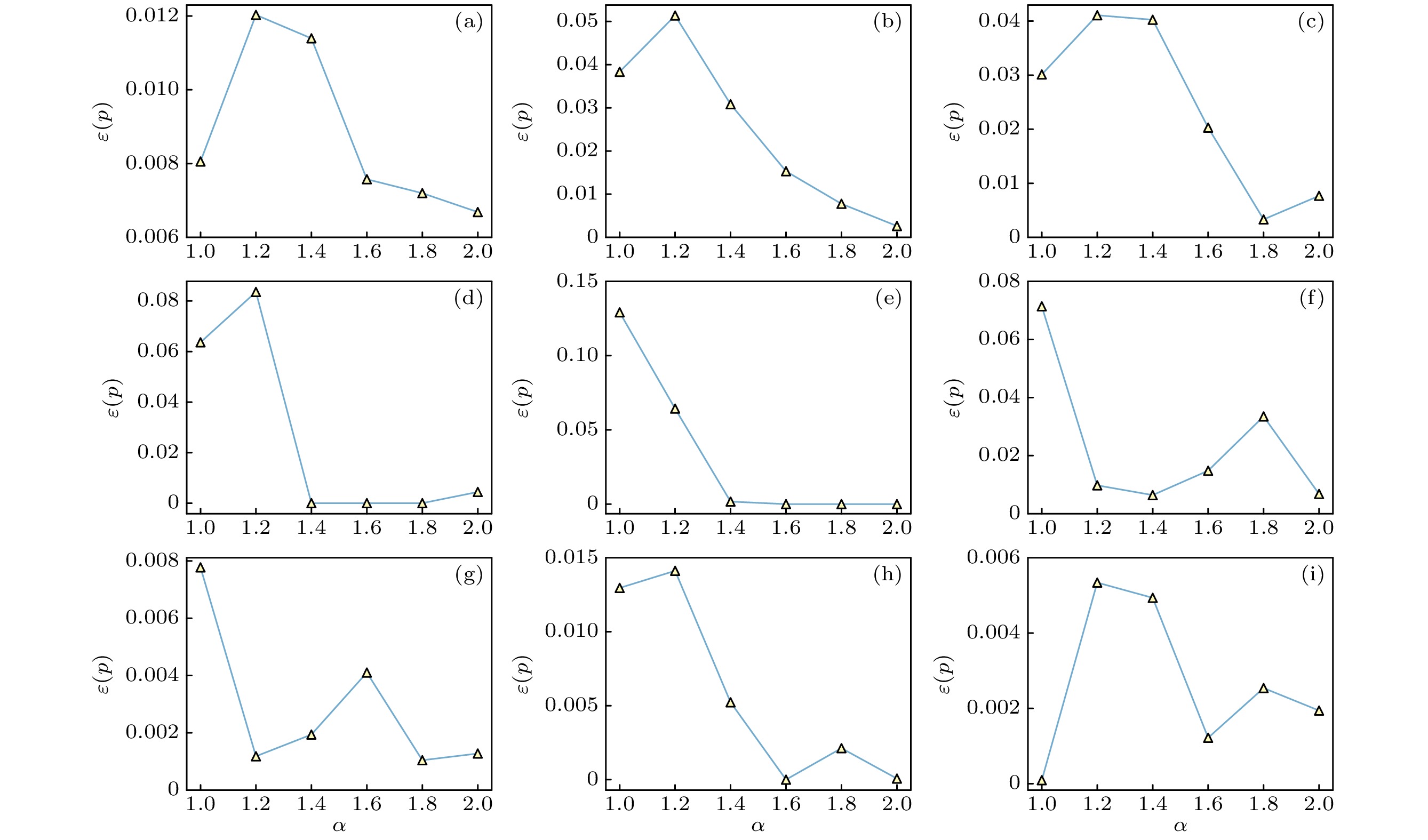
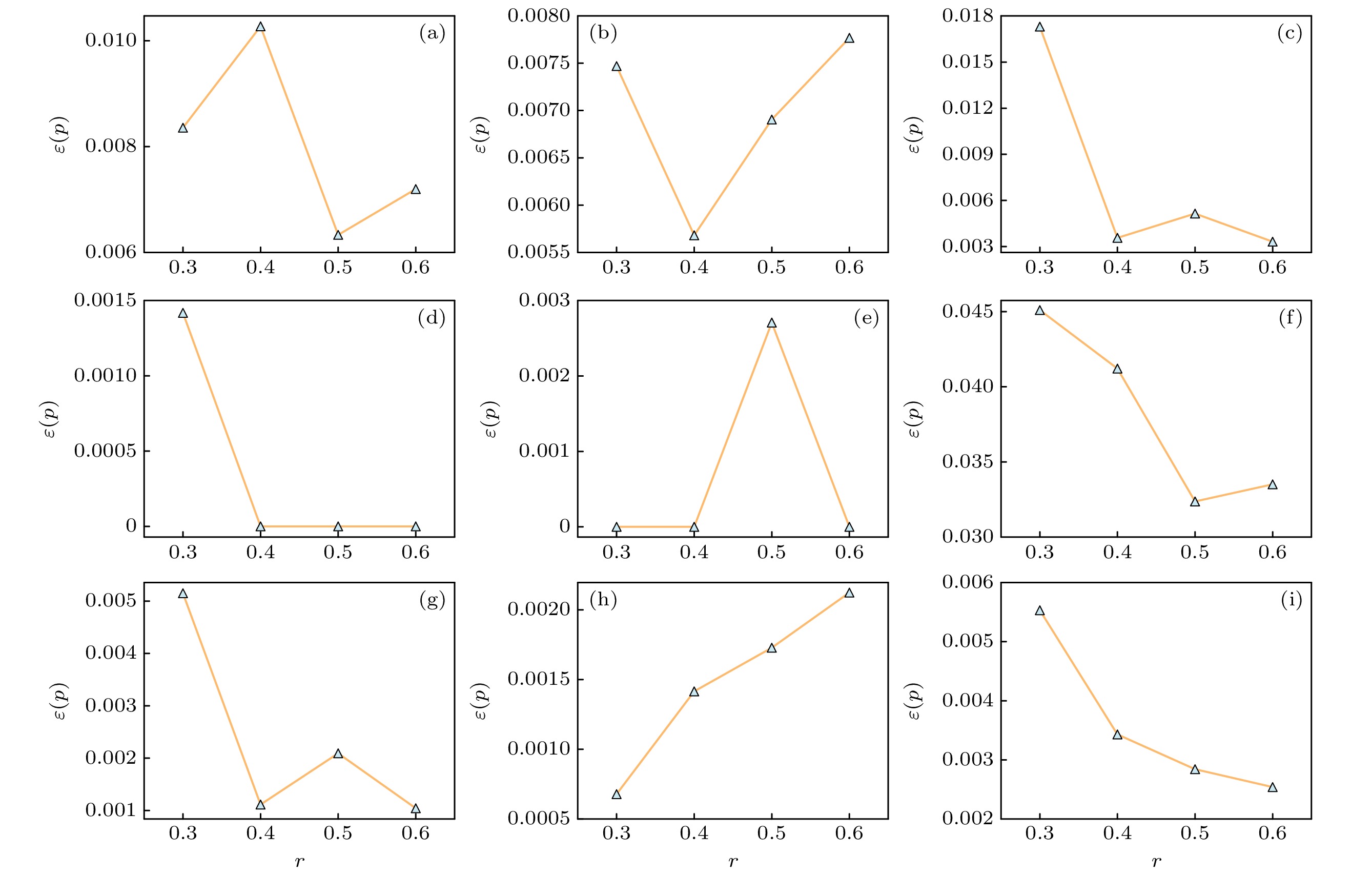
      为验证提出的模型在不同感染速率β和训练集比例r下传播关键节点识别的性能, 设置多组感染速率和训练集比例进行实验. 图5展示了在感染速率变化时, PDGNN方法的不精确函数值, 其中$ p=5{\text{%}} $. 由图5可知, PDGNN在不同感染速率下不精确函数值均较低. 感染速率较小时, 一些节点可能无法使得感染在整个网络中爆发, 且节点间的传播影响力差异可能不明显. 当感染速率增大后, 节点间传播影响力的差异更加显著, 使得模型能够更有效捕捉网络中的关键节点. 图6展示了在模型的训练集占比变化时, PDGNN方法的不精确函数值, 其中$ p=5{\text{%}} $. 由图6可知, 在大多数数据集上, 随着训练集占比的增加, 不精确函数曲线呈降低趋势. 当训练集占比较小时, 训练模型的数据量较少. 随着训练集数据量的增大, 模型能够更充分捕捉到关键节点的特性, 表现出更好的关键节点识别性能. 然而, 即使训练集仅占网络节点数的30%, PDGNN仍具有较低的不精确函数值, 表明该模型在训练集数据量较小的情况下具有良好的关键节点识别性能.

    4.   结　论

    • 识别复杂网络传播中的关键节点是网络科学研究的热点问题. 以往基于复杂网络中心性的方法主要基于网络结构来识别关键节点, 而采用机器学习、深度学习和图神经网络的方法也主要利用节点的结构特征作为模型的输入. 考虑到节点在传播过程中的动力学特性和节点的局域结构, 本研究提出了一个图神经网络模型PDGNN. 该模型将传播动力学过程纳入模型设计, 充分融合传播过程中的动态特征与网络局域结构信息, 有效提高了复杂网络传播中的关键节点识别准确性.

      大量模拟实验表明, 相比于2个经典中心性方法、2个基于机器学习的方法和3个基于深度学习的方法, PDGNN在绝大多数情况下优于对比方法. 值得注意的是, 图神经网络作为一种深度学习方法, 需要更多的计算资源来完成特征工程、模型训练和预测过程. 实验结果表明, PDGNN在合成网络和真实网络中几乎均取得了更高的预测准确性. 这种性能提升源于图神经网络能够有效考虑网络的拓扑结构, 捕获复杂网络中的非线性关系. 因此, 尽管计算时间有所增加, PDGNN在准确性上的提升足以弥补这一不足, 在需要高精度预测的场景中具有应用价值. 同时, 该模型在节点特征学习、类别不均衡处理和鲁棒性方面的优越性, 为未来在复杂网络中进行传播关键节点识别提供了新的思路.

    参考文献 (40)

目录

/

返回文章
返回