首页
登录
注册
-
在现代材料加工和半导体制造领域, 容性耦合等离子体(CCP)源由于其腔室结构简单, 能够产生大面积均匀等离子体等优势, 被广泛应用于薄膜表面改性和微电子刻蚀等领域[1–3]. 随着工业制造精度和效率要求的不断提高, 传统的单频放电模式因鞘层电压与离子能量之间存在强耦合关系, 难以同时满足高刻蚀速率与低损伤的工艺要求. 而双频技术通过分离电子加热(高频主导)与离子加速(由低频调制)过程, 显著提升了工艺的灵活性[4–6]与可控性, 受到了学界和工业界的广泛关注.
Goto等[7,8]论证了在双频激励系统中, 可通过选择合适的激发频率, 实现对离子密度和离子轰击能量的独立控制. Tsai等[9]运用双频电容式射频放电, 实现了对SiO2的高选择性等离子体刻蚀, 并且通过PIC/MCC (particle-in-cell/Monte Carlo collision)模拟, 发现等离子体密度与射频源频率的平方成正比关系. Sharma 等[10]通过模拟研究了双频电容放电中波的发射现象, 当高频频率与低频频率的比值为16时, 观察到较高频率在较低频率上叠加了16次, 高频与低频的重叠显著, 且在鞘层边缘附近发现波现象. Kim等[11]研究低频对放电参数的影响时发现, 在较短的间隙距离下, 等离子体密度会随低频的增大而显著增大.
Yang等[12]通过建立二维流体模型, 深入研究了射频驱动频率对CCP放电的影响, 发现平均电子密度随频率的增大而增大. Sharma 等[13]使用PIC/MCC研究了固定电压下射频频率对电子密度的影响, 发现等离子体密度在一定驱动频率范围内保持稳定, 之后随频率的增大而上升. Yin 等[14]通过实验探究不同频率下的容性耦合氩等离子体的放电特性, 发现在较低的驱动频率下, 电子能量概率分布函数(EEPF)呈现典型的单麦克斯韦分布, 而随着驱动频率的增大, EEPF形状逐渐演变为Druyvesteyn分布, 这一现象揭示了频率变化对电子能量分布的重要影响. 而后又探究了在单频甚高频容性耦合氩/甲烷等离子体中, 激发频率对EEPF分布的影响, 发现EEPF呈Druyvesteyn分布[15].
近年来, 磁化CCP成为研究热点[16–19]. 在CCP源中施加外部磁场, 会对垂直于磁力线方向的输 运机制产生极大的影响, 引发一系列复杂的磁 化效应, 进而导致功率耗散和电子加热机制发生转 变[20,21]. 此外, 外部磁场能够有效约束电子的定向移动, 增强电离效率, 从而提升等离子体密度[17,22]. Liu等[23]研究发现, 在更高频率(>60 MHz)下, 等离子体密度分布由驻波效应等电磁效应决定. Yin 等[24]通过数值模拟, 研究了在自身磁场影响下, 频率对容性耦合氩等离子体放电特性的影响, 结果表明电子密度随频率的增大呈线性上升, 且EEPF中高能电子的布局数随频率的增大而增多.
目前, 由于甲烷放电过程较为复杂, 双频等离子体的研究主要集中在氩等离子体体系, 而对于氩/甲烷等离子体合成碳膜的内在机理尚未得到足够关注. 低频电源通过调制鞘层动力学和离子能量分布[25], 在优化等离子体均匀性、控制离子轰击能量等方面具有独特优势. 因此, 本文通过在双频磁化条件下, 分析低频频率对容性耦合氩/甲烷等离子体放电特性的影响, 期望为实验制备碳膜研究提供有实际应用价值的参考.
-
PIC/MCC模拟[26–29]方法是一种基于跟踪大量带电粒子的微观运动来研究等离子体的宏观行为的模拟方法, 通过引入“宏粒子”的概念来代表大量的真实粒子[29]. 本文采用具有外磁场的一维空间-三维速度(1D3V)的显式格式[30]的PIC/MCC程序, 模拟了双频磁化容性耦合氩/甲烷等离子体中低频频率对等离子体放电的影响.
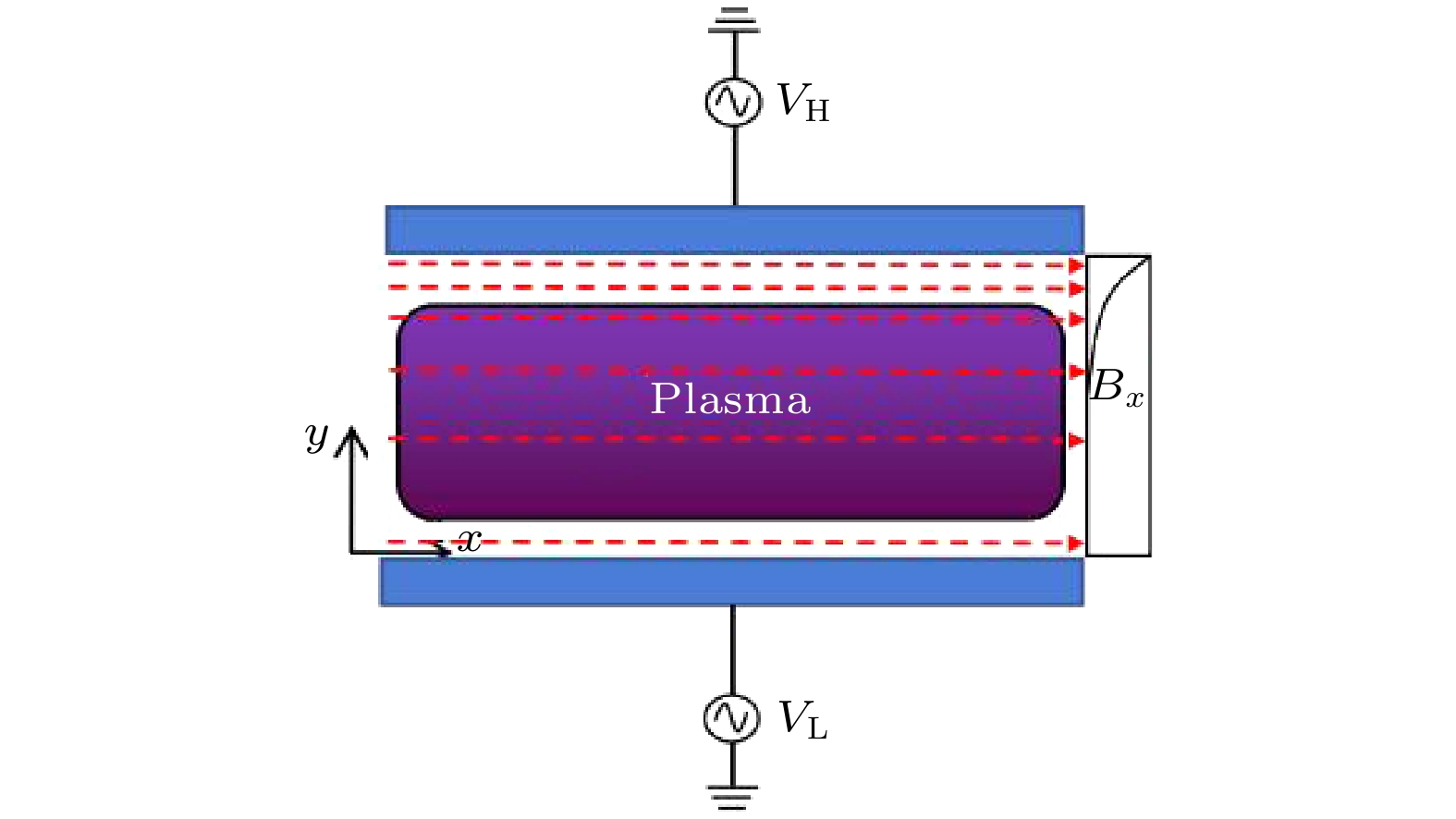
在模拟中, 电子与氩气及甲烷气体的碰撞类型如表1所示. 这些截面数据均来自LXCat数据库中[31]. 模拟装置图如图1所示, 放电发生在两个平行对称的极板之间, 两极板间距为3.2 cm, 气压固定为30 mTorr (1 Torr = 1.33×102 Pa), 上下两个极板分别连接一个高频电压源(100 MHz)和一个低频电压源(20 MHz), 电压源波形为
其中
$ {V_{\text{L}}} = 100\; {\text{V}}—{V_{\text{H}}} = 50\; {\text{V}} $ 之间. 模拟中, 固定气体比例为Ar∶CH4 = 0.85∶0.15, 设置初始电子密度为1×1015 m–3, 时间步长为4×10–11 s, 因为两个极板材质均为合金, 故设其二次电子系数设为0.1. 程序运行10000个射频周期后达到稳态.如图1所示, 外加的磁场沿x轴方向平行于电极, 磁场强度沿y轴方向向下极板衰减, 衰减长度为
$ l $ , 分布函数为$ {B_0} $ 为最大磁场强度, 固定为20 G (1 G = 10–4 T),$ l = 0.5 $ cm[32]. -
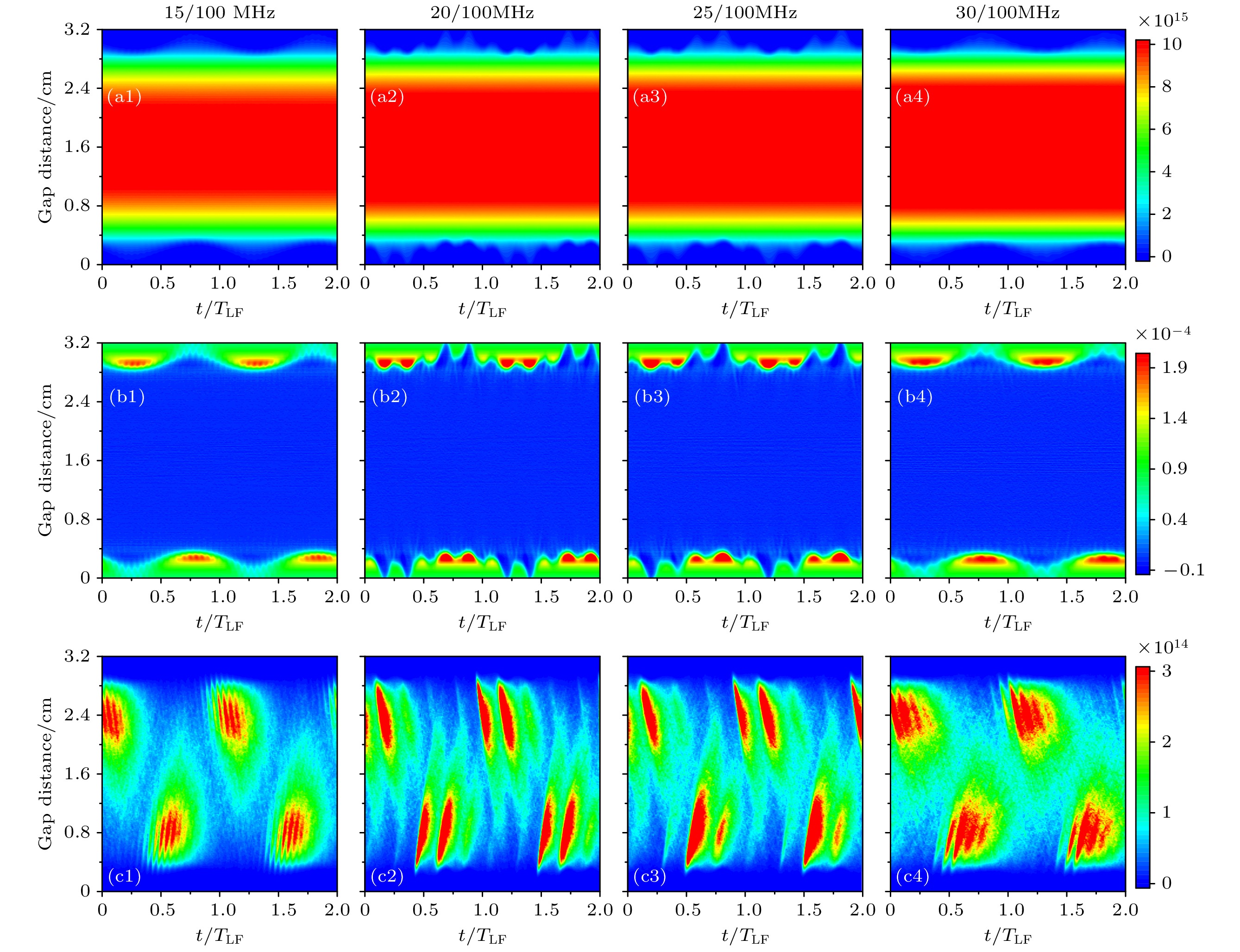
图2(a)模拟了固定高频频率为100 MHz, 磁场强度为20 G, 电子密度随低频频率变化的时空分布图. 电子密度在两个放电极板的中央区域最大, 随着低频频率的增大, 电子密度逐渐增大, 且高电子密度的区域范围也增大. 这是因为当增大频率时, 电子更容易从外部电场中获得能量, 电子与中性粒子的碰撞过程加剧, 从而增大电离. 在极板附近由于存在鞘层电场, 电子密度急剧下降, 同时发现当高频频率与低频频率之间存在整数倍时, 高频与低频重叠显著. 鞘层振荡更明显且有规律性, 如双频频率为20 MHz/100 MHz时, 鞘层振荡在一个周期内会有5个峰, 这与Sharma 等[10]的发现相似. 在整数倍频率关系下, 高频电场的振荡周期与低频电场周期存在着固定的联系, 使得电场在某些时刻增强某些时刻减弱. 这种周期性的电场强度变化直接作用于鞘层区域, 导致鞘层电场的强度和分布随时间发生更为复杂的振荡. 在整数倍频率关系下, 电子在复合电场中的这种独特运动模式, 使得其与离子的相互作用方式也发生了显著变化. 一方面, 电子与离子的碰撞频率受高频振荡和低频驱动的双重影响, 碰撞过程中的能量交换更为复杂; 另一方面, 电子在复合电场下的运动轨迹改变, 导致其与离子在空间中的分布关系发生变化. 图2(b)模拟了固定高频频率为100 MHz, 磁场强度为20 G, 电荷密度(离子密度-电子密度)随低频频率变化的时空分布图. 电荷密度在鞘层扩张最大处出现最大值. 鞘层电场的存在会减少等离子体中电子向极板的运动, 加速带正电的离子向极板运动, 因此等离子体中电子密度大于正离子的密度, 从而在等离子体中出现了电荷密度为负的情况. 从粒子的产生机制来看, 由于电子质量小, 在电场加速下更容易获得较高能量, 因此电子引发的电离过程相对更容易发生, 从而产生大量的电子. 而正离子由于质量较大, 运动速度较慢, 在一定程度上限制了其产生速率, 导致电子的产生速率可能会高于正离子. 从粒子的损失机制来看, 在Ar/CH4等离子体中, 可能会发生一系列复杂的复合反应, 但由于电子运动得快, 使得电子与正离子之间的复合概率相对较低. 因此在一定时间内, 电子的损失较少, 从而维持电子密度大于正离子密度的状态. 另一方面, 电子还可能会与一些中性粒子或分子发生反应形成负离子. 但由于甲烷含量较少, 电子与中性粒子或分子发生附着反应的概率较低, 电子的这种损失机制不显著, 电子密度就不容易因此降低, 从而大于正离子密度. 随低频频率的增大, 鞘层附近的电荷密度也逐渐增大. 图2(c)模拟了高频频率为100 MHz, 磁场强度为20 G, 高能电子(>30 eV)密度[24]随低频频率变化的时空分布图. 由于鞘层电场的增强, 电子被加速, 会在鞘层形成一束高能电子射向等离子体内部. 低频频率增大, 高能电子的密度也随之增大.
-
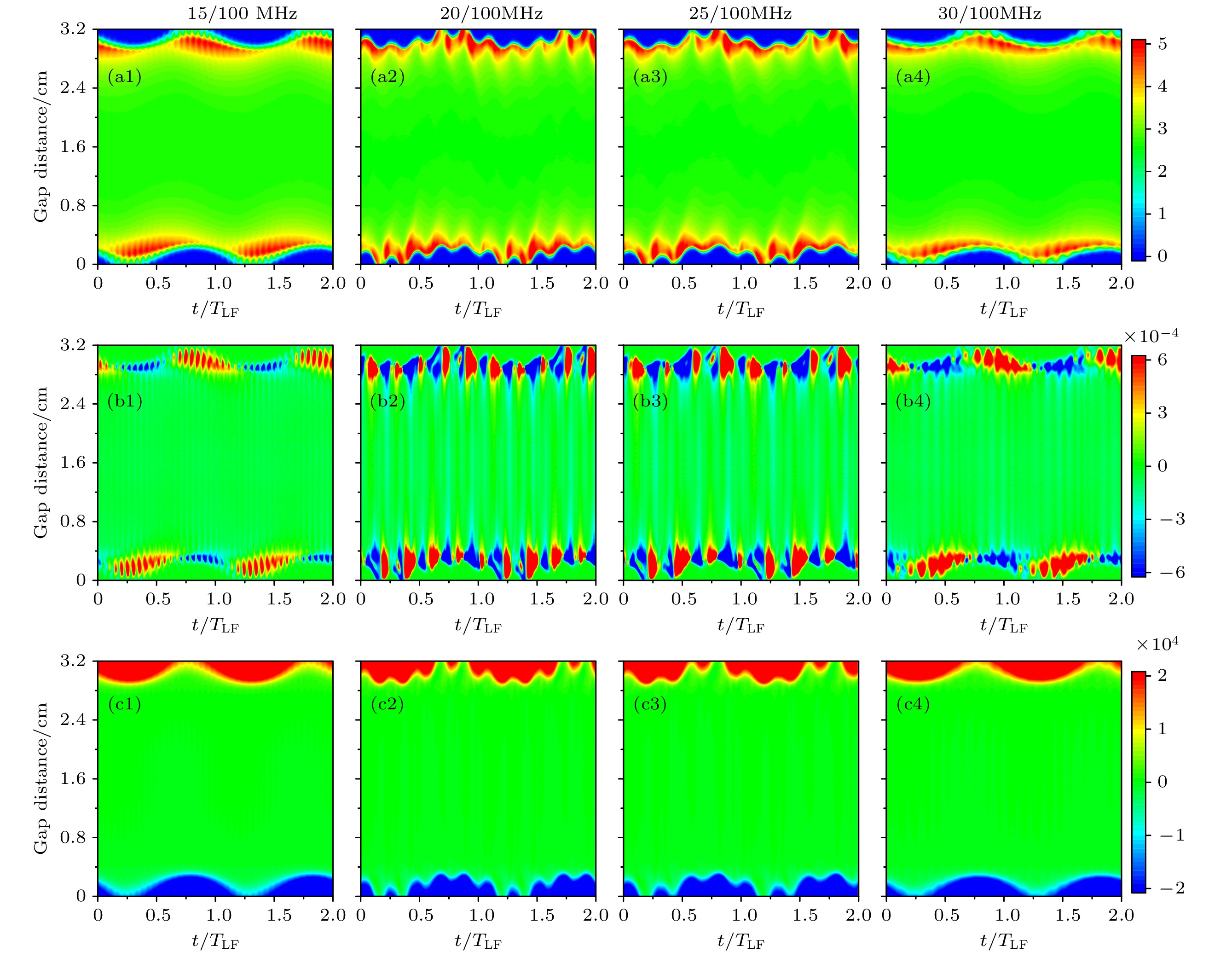
图3(a)模拟了固定高频频率为100 MHz, 磁场强度为20 G, 电子温度随低频频率变化的时空分布图. 鞘层边界的电子和电场发生耦合, 电子被场加速, 就会获得很高的能量, 从而温度增大. 图中可以明显地看出电子温度主要在鞘层扩张阶段最高, 这是由于在鞘层扩张阶段, 鞘层电场增强, 使更多的电子被鞘层加热或反弹. 在鞘层区域, 由于鞘层电场会减少电子向极板的运动, 电子的能量比在等离子体区域的低, 因此电子温度是最低的. 当高频频率与低频频率之间存在整数倍时, 即图3(a2), (a3), 电子温度随低频频率的变化没有明显变化, 有可能是高频电源的作用. 从图3(a1), (a4)可以看出, 电子温度随低频频率的增大而减小. 一方面, 低频频率增大会加剧电子和离子的碰撞频率, 电子会更频繁地将能量传递给离子, 从而导致电子温度降低. 另一方面, 当低频频率增大时, 鞘层运动周期缩短. 电子在鞘层电场中的加速时间缩短, 使得电子从鞘层电场中获得的能量减小, 导致电子温度降低. 图3(b)模拟了固定高频频率为100 MHz, 磁场强度为20 G, 电子加热率随低频频率变化的时空分布图. 从图3(b)可以看出, 电子主要在鞘层附近被加热, 在鞘层扩张时, 电场增强, 电子在电场的作用下迅速获得能量, 电子加热率快速上升, 同时鞘层附近电子密度降低, 等离子体内的低能电子回流到鞘层, 鞘层会再次加热电子, 另一方面, 在鞘层扩张过程中, 电子与其他粒子的碰撞频率增大, 进一步促进电子加热. 因此在鞘层扩张阶段, 电子加热率显著提高. 在鞘层塌缩阶段, 原本维持鞘层的电场会迅速减弱, 电子在电场中获得能量的能力下降, 电子加热率降低. 随着低频频率的增大, 电子加热率逐渐增大. 图3(c)模拟了固定高频频率为100 MHz, 磁场强度为20 G, 电场随低频频率变化的时空分布图. 当低频频率增大时, 电场强度的大小没有明显的变化. 但由于电子质量较小, 能更快地响应电场的变化, 电子分布的快速变化进一步影响空间电荷分布, 进而使得鞘层电场在时间和空间上的振荡增强.
-
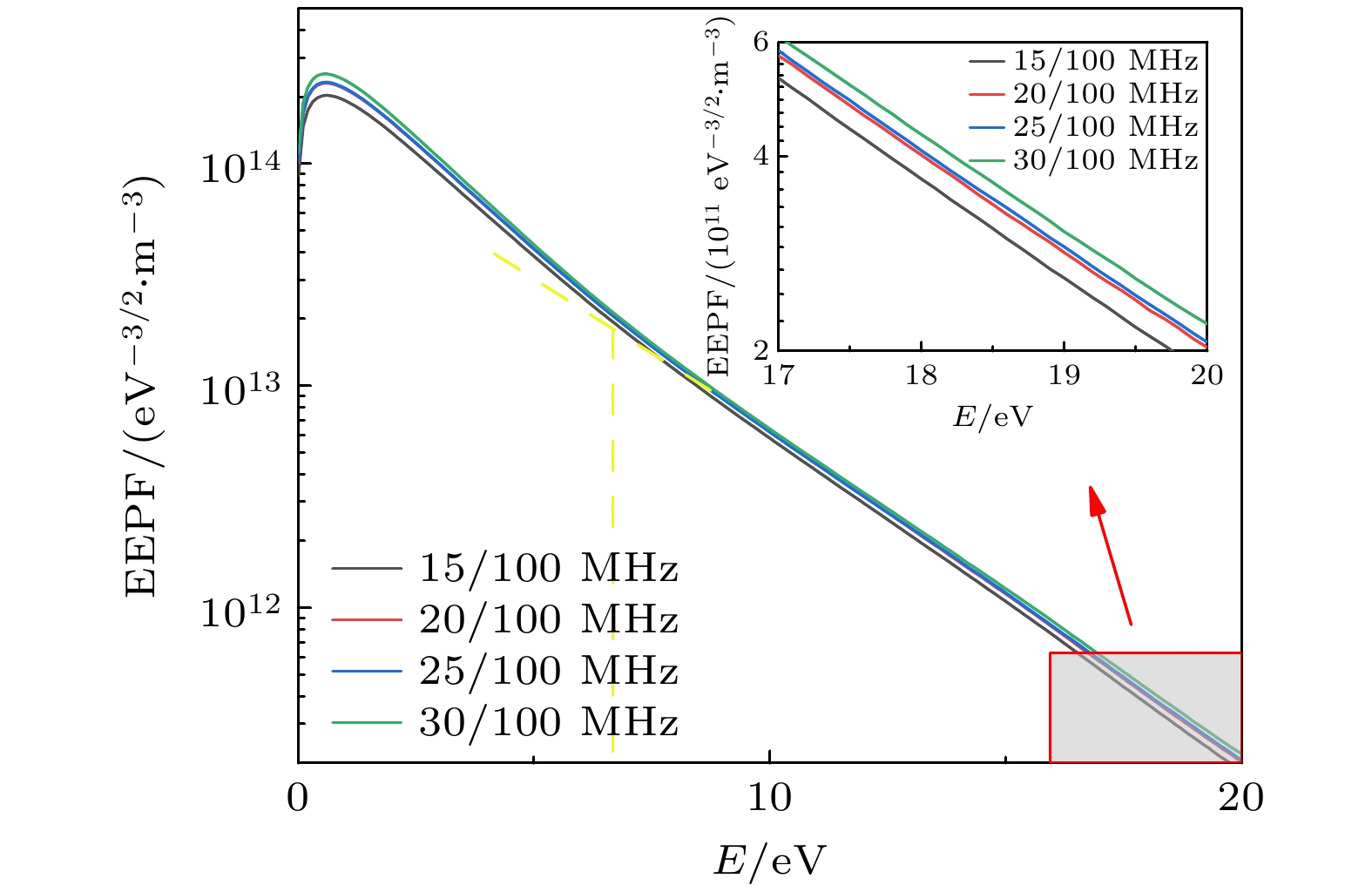
图4为固定高频频率为100 MHz, 磁场强度为20 G, 电子能量概率分布函数(EEPF)随低频频率变化的模拟结果图. EEPF呈现双麦克斯韦分布, 低能电子布局数和高能电子布局数均随低频频率的增大而增多. 随着低频频率升高, 电子与离子碰撞频繁, 能量更容易被离子吸收或散射, 导致低能电子的能量进一步降低, 从而使低能电子的布局数增大. 同时, 高能电子自身能量降低, 导致高能电子布局数在整体分布中明显减少.
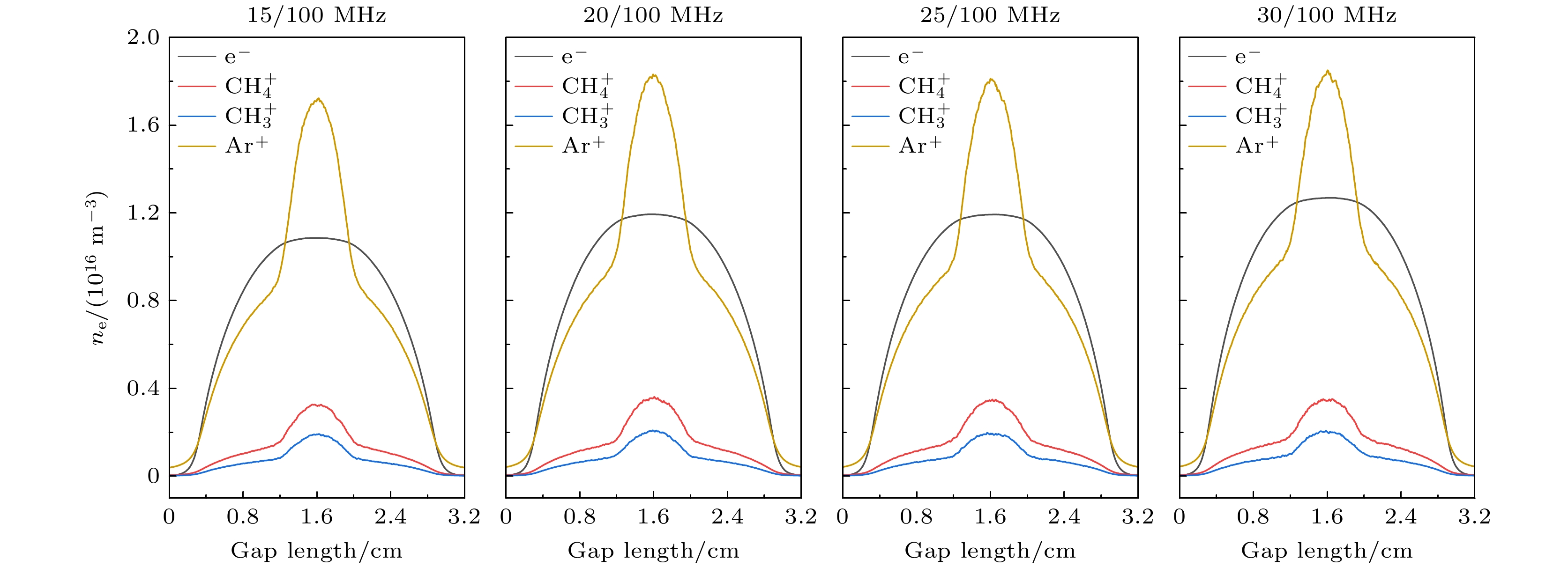
图5为高频频率100 MHz, 磁场强度20 G, 电子、
$ {\text{CH}}_{4}^{+} $ 、$ {\text{CH}}_{3}^{+} $ 、Ar+的离子密度随低频频率变化的分布图. 可以看出随低频频率的增大, 电子和Ar+的密度均呈增大趋势, 因为氩离子在鞘层运动变化时更容易引起电离.$ {\text{CH}}_{4}^{+} $ ,$ {\text{CH}}_{3}^{+} $ 的离子密度均没有明显的变化. 这可能是因为这些离子的产生过程与其他反应达到了动态平衡. 随着低频频率变化, 虽然会引发等离子体参数的一系列改变, 但这些竞争反应的平衡关系并未被打破. 此外,$ {\text{CH}}_{4}^{+} $ ,$ {\text{CH}}_{3}^{+} $ 在等离子体中的扩散系数和复合速率可能受低频频率变化影响较小. -
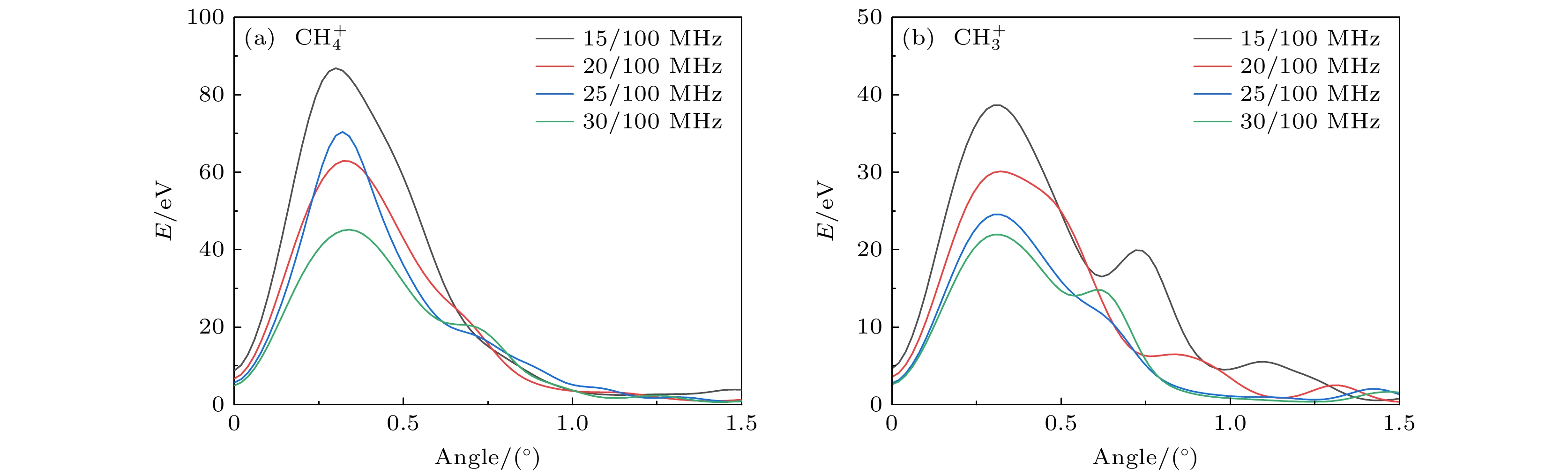
图6为固定高频频率为100 MHz, 磁场强度为20 G, 到达极板的
$ {\text{CH}}_{4}^{+} $ ,$ {\text{CH}}_{3}^{+} $ 粒子的角度与能量随低频频率变化的分布图. 从图6(a)可以看出, 到达极板的$ {\text{CH}}_{4}^{+} $ 粒子的能量平均值的峰值出现在0.32°左右, 且总体上呈下降趋势, 从86 eV下降到45 eV. 图6(b)显示到达极板的$ {\text{CH}}_{3}^{+} $ 粒子的能量平均值的峰值也出现在0.32°左右, 且随着低频频率的增大, 到达极板的$ {\text{CH}}_{3}^{+} $ 粒子的能量平均值的峰值逐渐下降, 从38 eV 减小到21 eV. 由图6可知, 频率组合差值相差较大时(15/100 MHz), 含碳基团的离子浓度相对较高, 由于双频放电过程中, 对于频率差值较大的组合, 其耦合效应较小, 能够较好地进行独立控制, 这对工艺优化具有重要的指导意义. -
本文在双频双极容性耦合氩/甲烷等离子体放电体系中, 固定高频频率为100 MHz, 磁场强度为20 G, Ar∶CH4 = 0.85∶0.15, 通过一维PIC/MCC模拟研究了低频频率对双频磁化容性耦合氩/甲烷等离子体放电特性的影响. 模拟结果表明当高频频率与低频频率存在整数倍时, 高频与低频之间会发生叠加, 且有规律性. 随着低频频率的增大, 电子与中性气体分子碰撞更频繁, 更容易发生电离, 产生更多的离子和电子, 电子密度增大, 同时也促进了电荷密度的增大. 此外, 碰撞频率增大, 电子将更多的能量传递给离子, 电子温度降低. 在鞘层扩张时, 电场增强, 电子在电场的作用下迅速获得能量, 电子加热率快速上升, 同时鞘层附近电子密度降低, 等离子体内的低能电子回流到鞘层, 鞘层会再次加热电子, 电子加热率显著提高. 且随着低频频率的增大, 电子加热率逐渐增大. 电场没有明显的变化. EEPF呈双麦克斯韦分布, 随低频频率的增大, 低能电子布局数和高能电子的布局数均增多. 分析了低频频率的增大对各种离子的密度的影响, 发现电子和Ar+密度均呈增大趋势,
$ {\text{CH}}_{4}^{+} $ ,$ {\text{CH}}_{3}^{+} $ 的离子密度均没有明显的变化. 以及发现到达极板的$ {\text{CH}}_{4}^{+} $ ,$ {\text{CH}}_{3}^{+} $ 粒子的能量的平均值随低频频率的增大总体上呈下降趋势.在双频磁化的Ar/CH4等离子体体系中, 离子能量的可控性可有效优化含碳薄膜结构与性能. 通过放电参数调控离子入射到基底的角度, 能够使得含碳原子沿着特定的方向沉积, 从而实现含碳膜的定向生长. 这对制备具有特定取向的石墨烯薄膜、碳纳米管阵列等具有重要意义. 同时离子入射角度的调控有助于改善碳膜与基底的结合力. 本研究发现, 离子的角度在0.32°左右时, 离子平均能量达到峰值, 且在低频频率为15 MHz时该峰值最为显著.
本文的研究为基于甲烷的碳薄膜制备工艺提供了理论参考依据, 但由于一维PIC模型只能讨论沿着两极板间放电方向的特性, 难以准确模拟实际制备薄膜中薄膜自身二维结构的特性. 因此, 一维的模拟方法仅仅是为讨论甲烷放电特性做铺垫, 为后续的进一步建立二维模型打基础, 以期获取优化含碳膜制备的关键参数.
双频磁化容性耦合氩/甲烷等离子体放电特性
Discharge characteristics of dual-frequency magnetized capacitively coupled Ar/CH4 plasma
-
摘要: 近年来, 双频容性耦合等离子体放电技术在先进材料加工领域展现出显著优势. 本文通过一维粒子模拟/蒙特卡罗碰撞(PIC/MCC)模拟方法, 引入外加磁场, 研究了在双频(20/100 MHz)双极容性耦合等离子体放电中, 低频频率对双频容性耦合氩/甲烷等离子体放电特性的影响. 模拟结果表明, 在高频频率为低频频率的整数倍时, 高频与低频叠加显著, 鞘层振荡更明显. 随着低频频率的增大, 电子密度、电荷密度、高能电子密度以及电子加热率都随之增大, 其中电子密度随低频频率增大达14%. 鞘层附近的电子温度随低频频率的增大出现下降趋势, 大约下降12%. 电子能量概率分布(EEPF)表现为双麦克斯韦分布, 且当低频频率增大时, 低能电子和高能电子的布居数都增多, 同时讨论了低频频率的增大对各种离子的密度的影响, 以及到达极板处的$ {\text{CH}}_{4}^{+} $, $ {\text{CH}}_{3}^{+} $粒子的角度与能量的变化分布.
-
关键词:
- 容性耦合等离子体放电 /
- Ar/CH4等离子体 /
- 粒子模拟/蒙特卡罗碰撞
Abstract:In recent years, dual-frequency capacitively coupled plasma discharge technology has demonstrated remarkable advantages in the fields of material processing. In this paper, a one-dimensional PIC/MCC (particle-in-cell/Monte Carlocollision) simulation method is used to discuss the influence of low frequency on the discharge characteristics of capacitively coupled argon/methane plasma driven by dual-frequency (20/100 MHz) dipole, with an external magnetic field added. The simulation results show that when the high frequency is an integer multiple of the low frequency, the superposition of high and low frequencies is significant, and the sheath oscillation is more obvious. As low frequency increases, the electron density, charge density, high-energy electron density and electron heating rate all increase. Specifically, as low frequency increase, the electron density increases to 14%, the electron temperature near the sheath decreases by about 12%, the electron energy probability distribution (EEPF) shows a double Maxwellian distribution, the populations of both low-energy electrons and high-energy electrons increase, and at the same time, the densities of various ions and the angle and energy distributions of ${\text{CH}}_{4}^{+} $ and ${\text{CH}}_{3}^{+} $ particles reaching the electrode plates are influenced. In the Ar/CH4 plasma driven by dual-frequency, with external magnetic field added, the controlling of ion energy can effectively optimize the structure and performance of carbon-containing films. By regulating discharge parameters to control the incident angle of the ions on the substrate, carbon-containing atoms can be deposited in a specific direction, thereby achieving the directional growth of carbon-containing films. This is significant for the preparation of graphene films, carbon nanotube arrays, etc. Meanwhile, the regulation of the incident angle of ions is helpful to improve the binding force between the carbon film and the substrate. It is found in this study that when the incident angle of the ions is around 0.32, the average energy of the ions reaches its peak. This peak is most significant at a low frequency of 15 MHz. The results in this paper provide a theoretical reference for preparing carbon films. -
-
图 2 固定磁场强度为20 G, Ar∶CH4 = 0.85∶0.15时, (a)电子密度; (b)电荷密度; (c)高能电子密度随低频频率变化的时空分布图
Figure 2. Spatiotemporal distribution diagram of the (a) electron density, (b) charge density, (c) high-energy electron density with low frequency at a fixed magnetic field strength of 20 G and Ar∶CH4 = 0.85∶0.15.
图 3 固定磁场强度为20 G, Ar∶CH4 = 0.85∶0.15, (a)电子温度 (eV), (b)电子加热率, (c)电场(V/m)随低频频率变化的时空分布图
Figure 3. Spatiotemporal distribution diagram of the (a) electron temperature (eV); (b) electron heating rate; (c) electric field (V/m) with low frequency at a fixed magnetic field strength of 20 G and Ar∶CH4 = 0.85∶0.15.
图 4 固定磁场强度为20 G, Ar∶CH4 = 0.85∶0.15, 电子能量概率分布函数随低频频率变化的分布图
Figure 4. Distribution of the electric energy probability function with low frequency at a fixed magnetic field strength of 20 G and Ar∶CH4 = 0.85∶0.15.
图 5 固定磁场强度为20 G, Ar∶CH4 = 0.85∶0.15, 电子、CH4+、CH3+、Ar+的离子密度随低频频率变化的分布图
Figure 5. The ion density distributions of electron、CH4+, CH3+, Ar+ with low frequency at a fixed magnetic field strength of 20 G and Ar∶CH4 = 0.85∶0.15.
图 6 固定磁场强度为20 G, Ar∶CH4 = 0.85∶0.15, 到达极板处的
$ {\text{CH}}_{4}^{+} $ ,$ {\text{CH}}_{3}^{+} $ 粒子在每个速度方向与轴向的夹角处能量的平均值随低频频率变化的分布图Figure 6. Distribution of the average value of the energy of
$ {\text{CH}}_{4}^{+} $ and$ {\text{CH}}_{3}^{+} $ particles arriving at the pole plate at the angle between each velocity direction and the axial direction with low frequency at a fixed magnetic field strength of 20 G and Ar∶CH4 = 0.85∶0.15.表 1 碰撞反应类型
Table 1. Collision reaction type in the simulation.
序号 反应式 碰撞类型 阈值/eV 1 $ {{\text{e}}^{{ - }}}{\text{ + Ar}} \to {{\text{e}}^{{ - }}}{\text{ + Ar}} $ 弹性碰撞 0 2 $ {{\text{e}}^{{ - }}}{\text{ + Ar}} \to {{\text{e}}^{{ - }}}{\text{ + Ar}} $ 激发碰撞 11.5 3 $ {{\text{e}}^{{ - }}}{\text{ + Ar}} \to 2{{\text{e}}^{{ - }}}{\text{ + A}}{{\text{r}}^{+}} $ 电离碰撞 15.80 4 $ {\text{A}}{{\text{r}}^{+}}{\text{ + Ar}} \to {\text{A}}{{\text{r}}^{+}}{\text{ + Ar}} $ 弹性碰撞 0.00 5 $ {\text{A}}{{\text{r}}^{+}}{\text{ + Ar}} \to {\text{Ar + A}}{{\text{r}}^ + } $ 电荷交换 0.00 6 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} $ 弹性碰撞 0 7 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_{4}}\left( {{{\text{V}}_{2}}} \right) $ 激发碰撞 0.162 8 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_{4}}\left( {{{\text{V}}_{1}}} \right) $ 激发碰撞 0.362 9 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_{3}}{\text{ + H}} $ 激发碰撞 7.5 10 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_{2}}{+}{{\text{H}}_2} $ 激发碰撞 9.1 11 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + C + 2}}{{\text{H}}_2} $ 激发碰撞 15.5 12 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {{\text{e}}^{{ - }}}{\text{ + CH + }}{{\text{H}}_{2}}{\text{ + H}} $ 激发碰撞 15.5 13 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {2}{{\text{e}}^{{ - }}}{\text{ + CH}}_4^ + $ 电离碰撞 12.63 14 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {2}{{\text{e}}^{{ - }}}{\text{ + H + CH}}_3^ + $ 电离碰撞 12.63 15 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to {2}{{\text{e}}^{{ - }}}{+}{{\text{H}}_{2}}{\text{ + CH}}_2^ + $ 电离碰撞 16.2 16 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to 2{{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_{3}}{+}{{\text{H}}^ + } $ 电离碰撞 21.1 17 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to 2{{\text{e}}^{{ - }}}{\text{ + 2}}{{\text{H}}_{2}}{+}{{\text{C}}^ + } $ 电离碰撞 22 18 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to 2{{\text{e}}^{{ - }}}{\text{ + H + }}{{\text{H}}_{2}}{\text{ + C}}{{\text{H}}^ + } $ 电离碰撞 22.2 19 $ {{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_4} \to 2{{\text{e}}^{{ - }}}{\text{ + C}}{{\text{H}}_{2}}{+}{{\text{H}}_2^ +} $ 电离碰撞 22.3 
下载: 导出CSV
-
[1] Li Y M, Mann D, Rolandi M, Kim W 2004 Nano Lett. 4 317 doi: 10.1021/nl035097c [2] Donnelly V M, Kornblit A 2013 J. Vac. Sci. Technol. A. 31 050825 doi: 10.1116/1.4819316 [3] Jung C O, Chi K K, Hwang B G, Moon J T, Lee M Y, Lee J G 1999 Thin Solid Films 341 112 doi: 10.1016/S0040-6090(98)01522-3 [4] Schulze J, Gans T, O'Connell D, Czarnetzki U, Ellingboe A R, Turner M M 2007 J. Phys. D: Appl. Phys. 40 7008 doi: 10.1088/0022-3727/40/22/022 [5] Boyle P C, Ellingboe A R, Turner M M 2004 J. Phys. D: Appl. Phys. 37 697 doi: 10.1088/0022-3727/37/5/008 [6] Robiche J , Boyle P C , Turner M M, Ellingboe A R 2003 J. Phys. D: Appl. Phys. 36 1810 [7] Goto H H, Löwe H D, Ohmi T 1992 J. Vac. Sci. Technol. A. 10 3048 doi: 10.1116/1.577863 [8] Goto H H, Löwe H D, Ohmi T 1993 IEEE Trans. Semicond. Manuf. 6 58 doi: 10.1109/66.210658 [9] Tsai W, Mueller G, Lindquist R, Frazier B, Vahedi V 1996 J. Vac. Sci. Technol. B 14 3276 doi: 10.1116/1.588820 [10] Sharma S, Turner M M 2014 J. Phys. D: Appl. Phys. 47 285201 doi: 10.1088/0022-3727/47/28/285201 [11] Kim H C, Lee J K, Shon J W 2003 Phys. Plasmas 10 4545 doi: 10.1063/1.1621000 [12] Yang S, Zhang W, Shen J F, Liu H, Tang C J, Xu Y H, Cheng J, Shao J R, Xiong J, Wang X Q, Liu H F, Huang J, Zhang X, Lan H, Li Y C 2024 AIP Adv. 14 065104 doi: 10.1063/5.0202071 [13] Sharma S, Sirse N, Turner M M, Ellingboe A R 2018 Phys. Plasmas 25 063501 doi: 10.1063/1.5031221 [14] Yin G Q, Gao S S, Liu Z H, Yuan Q H 2022 Phys. Lett. A 426 127910 doi: 10.1016/j.physleta.2021.127910 [15] 高闪闪2022 硕士学位论文(兰州: 西北师范大学) Gao S S 2022 M. S. Thesis (Lanzhou: Northwest Normal University [16] Yang S L, Zhang Y, Wang H Y, Cui J W, Jiang W 2017 Plasma Processes Polym. 14 1700087 doi: 10.1002/ppap.201700087 [17] Yang S L, Chang L, Zhang Y, Jiang W 2018 Plasma Sources Sci. Technol. 27 035008 doi: 10.1088/1361-6595/aab47e [18] Yan M H, Wu H H, Wu H, Peng Y L, Yang S L 2024 J. Vac. Sci. Technol. A 42 053007 doi: 10.1116/6.0003692 [19] Sharma S, Patil S, Sengupta S, Sen A, Khrabrov A, Kaganovich I 2022 Phys. Plasmas 29 063501 doi: 10.1063/5.0094409 [20] Sun J Y, Wen H, Zhang Q Z, Schulze J, Liu Y X, Wang Y N 2022 Plasma Sources Sci. Technol. 31 085012 doi: 10.1088/1361-6595/ac882d [21] Zheng B C, Wang K L, Grotjohn T, Schuelke T, Fan Q H 2019 Plasma Sources Sci. Technol. 28 09LT03 doi: 10.1088/1361-6595/ab419d [22] Yang S L, Zhang Y, Wang H Y, Wang S, Jiang W 2017 Phys. Plasmas 24 033504 doi: 10.1063/1.4977806 [23] Liu Y X, Liang Y S, Wen D Q, Bi Z H, Wang Y N 2015 Plasma Sources Sci. Technol. 24 025013 doi: 10.1088/0963-0252/24/2/025013 [24] Yin G Q, Jiang Y B, Yuan Q H 2024 Mod. Phys. Lett. B 38 2450269 [25] Wang J-C, Tian P, Kenney J, Rauf S, Korolov I, Schulze J 2021 Plasma Sources Sci. Technol. 30 075031 doi: 10.1088/1361-6595/ac0da4 [26] Birdsall C K 1991 IEEE Trans. Plasma Sci. 19 65 doi: 10.1109/27.106800 [27] Vahedi V, Surendra M 1995 Comput. Phys. Commun. 87 179 doi: 10.1016/0010-4655(94)00171-W [28] Verboncoeur J P 2001 J. Comput. Phys. 174 421 doi: 10.1006/jcph.2001.6923 [29] 沈向前, 谢泉, 肖清泉, 陈茜, 丰云 2012 物理学报 61 165101 doi: 10.7498/aps.61.165101 Shen X Q, Xie Q, Xiao Q Q, Chen Q, Feng Y 2012 Acta Phys. Sin. 61 165101 doi: 10.7498/aps.61.165101 [30] 金晓林, 杨中海 2006 物理学报 55 5930 doi: 10.3321/j.issn:1000-3290.2006.11.058 Jin X L, Yang Z H 2006 Acta Phys. Sin. 55 5930 doi: 10.3321/j.issn:1000-3290.2006.11.058 [31] Song M Y, Yoon J S, Cho H, Itikawa Y, Karwasz G P, Kokoouline V, Nakamura Y, Tennyson J 2015 J. Phys. Chem. Ref. Data. 44 023101 doi: 10.1063/1.4918630 [32] Sun J Y, Zhang Q Z, Liu J R, Song Y H, Wang Y N 2020 Plasma Sources Sci. Technol. 29 114002 doi: 10.1088/1361-6595/abad55 -
图( 6) 表( 1)
计量
- 文章访问数: 23
- HTML全文浏览数: 23
- PDF下载数: 1
- 施引文献: 0