首页
登录
注册
-
边界层从层流到湍流的转捩是多因素耦合的复杂过程, 是空气动力学领域的重要研究方向[1]. 在实际应用中, 边界层转捩后湍流状态下的热流与摩阻比层流高3—5倍, 因此转捩是飞行器气动设计需要考虑的重要因素, 也是制约先进飞行器发展最具挑战性的基础科学难题之一[2].
一般情况下, 自然转捩是由边界层模态失稳主导发生的. 在高速领域, 若流动中温度不足以改变气体比热容, 气体仍满足理想气体状态方程, 则称之为量热完全气体(CPG), 该状态下二维边界层通常以Mack模态失稳主导转捩. 当高马赫数下边界层内温度足够高时, 表面气体将发生一系列热化学反应过程, 显著改变边界层内的流动特征, 从而影响模态失稳过程. 根据热化学反应过程是否处于平衡[3,4], 流动可分为热化学冻结(TCF)、热化学平衡(TCE)、热化学非平衡(TCNE)和化学非平衡(CNE).
对于考虑热化学反应过程的流动, 流向不稳定性依然是Mack模态占据主导, 相关研究早在20世纪90年代就已开展. Malik[5]较早地开展了考虑高温真实气体效应的流动稳定性研究, 发现热化学平衡会使第二模态更不稳定, 但对第一模态具有稳定作用; Stuckert和Reed[6]针对化学非平衡流动的研究也得到相同的结论. 此外, 还有研究对比了热化学非平衡和化学非平衡流动, 结果表明振动非平衡对第二模态具有稳定作用[7,8]. 对于更高频的不稳定模态, Chen等[9]在马赫数20的钝锥热化学非平衡流动中发现明显的第三模态, 但其增长率仍未超过第二模态. 相同气体模型下, 赵洲源等[10]利用LPSE研究了尖楔流动中壁温的影响, 壁温越低, 相同频率扰动沿流向发展延迟, 但下游最大N值增大. 另外, 由于高温非平衡流动模拟需要采用合适的模型表征各组分物理化学特性[11], 学者探索了不同热力学模型[12,13]、扩散模型[14-16]、输运模型[12,17-21]、化学反应模型[22-24]和壁面催化效应[25]对边界层稳定性的影响, 这里不再展开.
飞行器在高速飞行状态下面临着恶劣的气动力、热环境, 对热防护系统设计和材料性能提出了更高的要求, 而现有超高温材料的最高耐受温度不超过3000 K[26]. 为降低热防护系统的设计难度, 提升航程, 许多研究人员采用主/被动手段对边界层转捩进行控制. 多孔材料可用于飞行器外表面来吸收高频声波和抑制第二模态, 可作为一种有效的被动转捩控制手段[27]. 在量热完全气体状态下, 针对孔隙效应如何影响边界层失稳的研究较为丰富. Fedorov与Malmuth[28]和Zhao等[29]分别推导了体现孔隙效应的有效导纳模型, 并且后者的模型考虑了高阶衍射模态. Fedorov与Malmuth [28]通过考虑孔隙效应的线性稳定性(LST)方法, 探究了壁面圆孔对平板边界层稳定性的影响, 结果显示多孔效应使第二模态增长率减小, 但对第一模态有轻微促进作用, Wartemann等[30]和Xu等[31]的研究得到了相同的结论. Wang与Zhong[32]结合实验和数值探究了局部多孔涂层对高速边界层的作用机理, 发现其控制效果与边界层内快、慢模态的同步过程紧密相关; 若多孔涂层设置在同步点下游可以明显抑制第二模态, 在上游则促进模态增长. Rasheed等[33]和Lukashevich等[34]的实验结果与该结论一致. 郭启龙等[35]通过直接数值模拟(DNS)研究毫米级微槽对第二模态扰动的影响, 发现微槽能在一个宽带频率范围内抑制第二模态, 其抑制效果随开槽率增大而增强. 刘勇等[36]针对同尺寸量级的微槽进一步研究, 结果表明微槽设置在最大增长率区间或快/慢模态同步中心附近时, 对第二模态扰动抑制最为显著. Gui等[37]的风洞实验结果也表明多孔涂层可以抑制第二模态, 而且多孔壁的模态非线性作用比光滑壁弱得多; 同时, 还发现考虑规则圆孔效应的LST计算所得不稳定模态增长率与实验符合较好. Liu等[38]探究了多孔耦合微吹吸对马赫数6边界层稳定性影响, 当吹吸点位于主导模态同步点上游时, 发现有助于多孔结构抑制高频扰动; 若吹吸点位于第二模态主导区域, 多孔结构则会过早激发低频不稳定模态.
以上孔隙效应对边界层流动失稳的影响研究是基于量热完全气体模型, 对于微孔隙结构在高温化学非平衡流动中的应用研究, 目前还比较少, Wang和Zhong[39]在研究量热完全气体和热化学非平衡流动的差异时, 初步开展了该问题的数值模拟研究, 发现量热完全气体状态下由壁面吹吸激发的边界层扰动波会被规则的多孔涂层显著抑制. 随后, Wang[40]等进一步对比了马赫数10的平板壁面压力脉动幅值, 发现对于主导的第二模态扰动(频率300和400 kHz), 热化学非平衡效应可以增强多孔涂层的抑制效果, 但研究并未对比TCNE假设下多孔壁的LST和DNS结果. Ken等[41]在考虑热化学非平衡效应LST中加入Fedorov的多孔导纳模型. 通过DNS发现在CPG和TCNE假设下, 二者的无量纲壁面压力脉动沿流向分布较为一致, 这是由于TCNE对微孔腔内不稳定扰动衰减的影响较小. 该研究还对比了TCNE工况同一频率下多孔壁的LST和DNS结果, 证明若多孔涂层区域足够长, 在LST中使用壁面导纳模型可以很好地预测DNS中扰动增长的趋势. 然而, 该工作还未对高温气体模型下微孔隙效应对不同频率扰动、N值的影响做进一步研究.
总体而言, 考虑化学非平衡与表面孔隙效应的共同作用对边界层失稳的认识还不够深入, 其影响机制还不够明确, 对两种效应下的边界层失稳研究有待进一步开展. 本文建立了能体现高温化学非平衡效应和微孔隙效应的线性稳定性理论, 探索了化学非平衡、微孔隙以及二者共存时高速边界层的失稳机制, 同时还考察了马赫数和微孔几何拓扑对稳定性的影响.
-
本文针对多孔表面与高温化学非平衡气体共存的边界层流动稳定性问题, 建立同时考虑高温化学非平衡气体效应和多孔边界效应的流动稳定性分析方法. 首先是推导高温化学非平衡的流动控制方程和线性稳定性方程, 然后在稳定性方程的壁面边界条件上增加多孔导纳模型, 建立考虑以上两种效应的流动稳定性分析方法.
-
针对高温化学非平衡流动问题, 构造二维N-S方程组, 其守恒型表达形式如下[25]
(1)式—(4)式分别为质量守恒方程、动量守恒方程、总能量守恒方程和组分守恒方程. 其中, ρ, ui, p, T和Ys分别为密度、速度、压力、温度和组分质量分数, H为总比焓, E为总比能; λ, Ds, hs,
$ \dot \omega_{s} $ 分别为热传导系数、组分扩散系数、组分比焓和组分质量生成率;$ \tau_{ij} $ 是黏性切应力张量; 下标i或j表示速度分量, 下标s表示组分数.研究中使用空气5组分模型(对应N2, O2, N, O, NO, 即ns = 5)模拟反应流动, 来流气体组分为O2和N2, 质量分数分别为22%和78%. 单一组分的热力学参数(如比热、比焓)采用Chemkin拟合式[13]进行计算; 黏性系数、热传导系数和质量扩散系数则分别采用Blottner拟合式[18]、Eucken经验式[42]和基于Schmidt数的双极性扩散近似模型[43]进行计算. 空气混合物的输运系数则采用Wilke混合律[44]进行计算.
-
本研究采用考虑化学非平衡效应的LST程序对反应流动进行分析, 对于量热完全气体流动则采用传统的LST方法[45]进行分析. 在此主要给出基于化学非平衡效应的线性稳定性理论框架[25]. 在稳定性理论中, 物理量
${\boldsymbol q} $ 可以表示为基本量$ {{\boldsymbol q}_0} $ 和扰动量$ {\boldsymbol q}' $ , 其中$ {\boldsymbol q} = {\left[ {\rho , u, v, w, T, {Y_s}} \right]^{\text{T}}}, s = 1, 2, 3, 4 $ ; u表示流向速度; v表示法向速度; w表示展向速度. 由于基本量和扰动量均满足方程(1)—方程(4), 代入方程中相减可得到扰动量满足的方程组:式中, 矩阵F, A, B, C, D和V的大小由量热完全气体模型的5×5增加到化学非平衡气体模型的9×9(多了组分项), 矩阵中系数只与基本流有关. N表示非线性项, 在线性稳定性分析中忽略此项. 假设流动满足局部平行条件, 扰动方程的解可表示为
其中
$ \hat q(y) $ 表示扰动形函数, 是法向高度y的函数. 在空间模式中,$ \omega $ 是实数, 表示波的频率;$ \alpha $ ,$ \beta $ 至少有一个是复数, 其实部分别表示流向、展向波数, 虚部代表增长率, 对二维波有$ \beta = 0 $ . 将(6)式代入方程(5)中, 忽略高阶项和非线性项, 推导得到线性稳定性方程, 一阶微分方程形式如下:其中系数矩阵A0大小由量热完全气体模型的8×8增加到化学非平衡气体模型的16×16,
$ \hat {\boldsymbol{\varPhi}} $ 是16个扰动量构成的向量. 针对方程(7), 采用Malik两点四阶紧致差分方法进行求解, 得到失稳模态的特征值. -
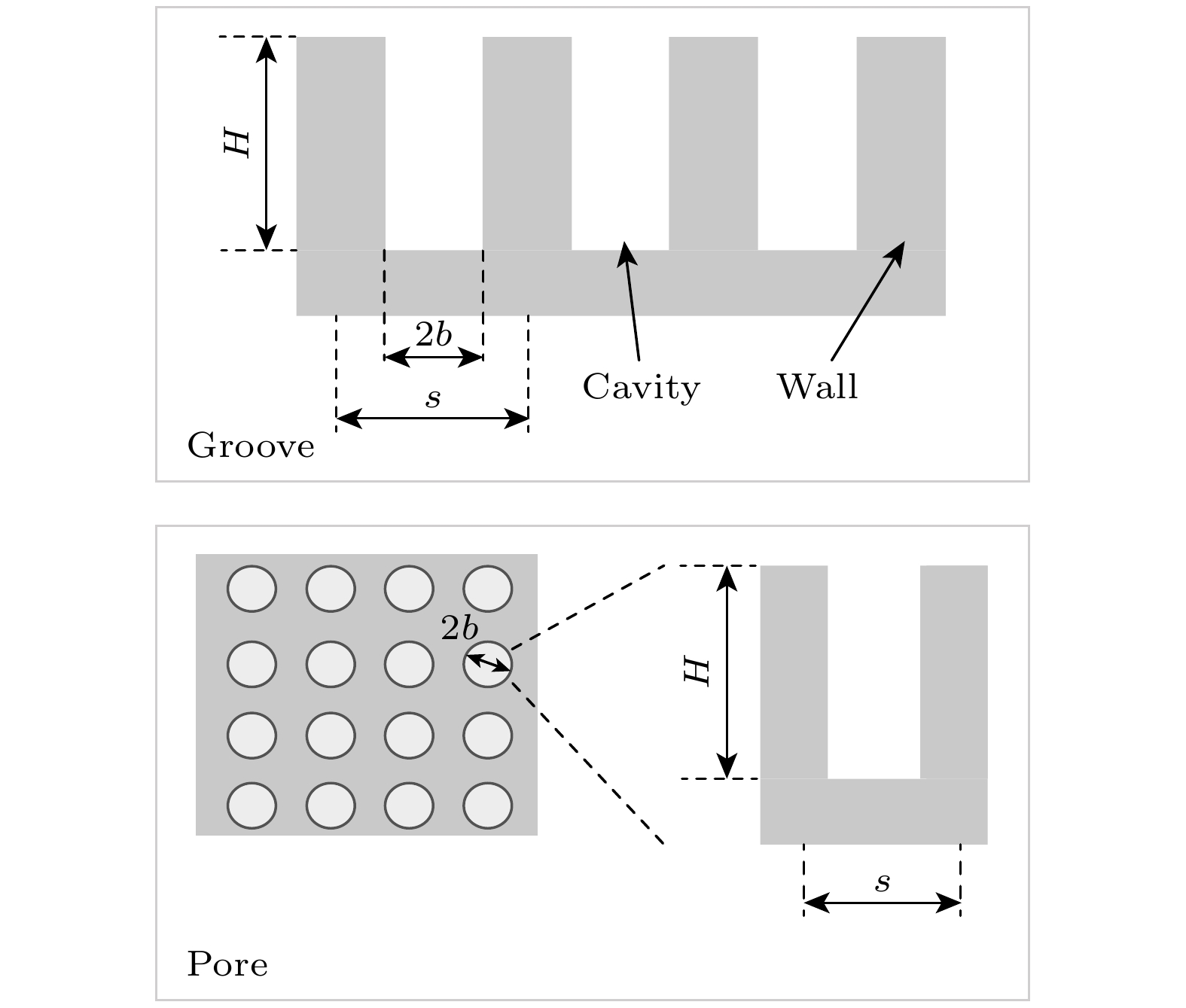
多孔壁面的孔壁会对边界层内扰动波存在干扰, 壁面扰动不再为零. 一般地, 规则多孔壁需要考虑的关键参数包括半宽/半径b、孔深H、周期宽度s、孔隙率n (孔隙表面积/开孔区域总表面积). 图1给出周期分布的微槽和圆孔简单构型示意图, 展向满足无限长假设.
当孔周期s远小于边界层厚度时, 孔壁对边界层基本流场影响可忽略[46,47], 因此只在稳定性方程中考虑多孔效应. 同时, 考虑高温化学非平衡效应的多组分气体边界, 假设各组分气体质量分数法向梯度为零(即非催化壁), 多孔壁面上高温化学非平衡流动边界条件表示为
其中A, B分别为声导纳、热导纳, 但热导纳的影响一般很小[48], 后续研究主要考虑导纳A的影响. 将Mack模态不稳定波简化为垂直入射, 假设周期宽度s远小于入射波长λacs, 则有效导纳可表示为
式中,
$ {\rho _{\text{w}}} $ 和$ {c_{\text{w}}} $ 分别为壁面密度和声速. 当满足s远小于入射波长λacs时, 高阶衍射模态无法辐射到远场[29], 主要考虑镜面反射,$ {R_0} $ 为反射系数. 对于二维波, 具体表达式如下:式中, r阶反射波的垂直和平行动量分别为
$ k_y^{\left( r \right)} = \sqrt {k_0^2 - (k_x^{(r)})^2} $ ,$ k_x^{\left( r \right)} = {k_x} + 2\pi r/s $ . 波数$ {k_0} = \omega /{c_{\text{w}}} $ ; 有效密度$ \tilde \rho $ 和波数$ {k_{\text{c}}} $ 都是与频率$ \omega $ 有关的复参数, 具体定义为对于规则圆孔:
其中, 黏性波数
$ {k_{\text{v}}} = \sqrt {{\mathrm{j}}\omega {\rho _{\text{w}}}/\mu } $ 和热波数$ {k_{\text{t}}} = \sqrt {{\text{j}}\omega {\rho _{\text{w}}}{C_{\text{p}}}/\kappa } $ ,$ \mu $ ,$ {C_{\text{p}}} $ 和$ \kappa $ 分别为黏性系数、定压比热和热传导系数;$ {{\text{J}}_0}\left( \cdot \right) $ ,$ {{\text{J}}_1}\left( \cdot \right) $ 和$ {{\text{J}}_{2}}\left( \cdot \right) $ 分别为第一类Bessel函数的零阶、一阶和二阶形式.对于二维微槽:
-
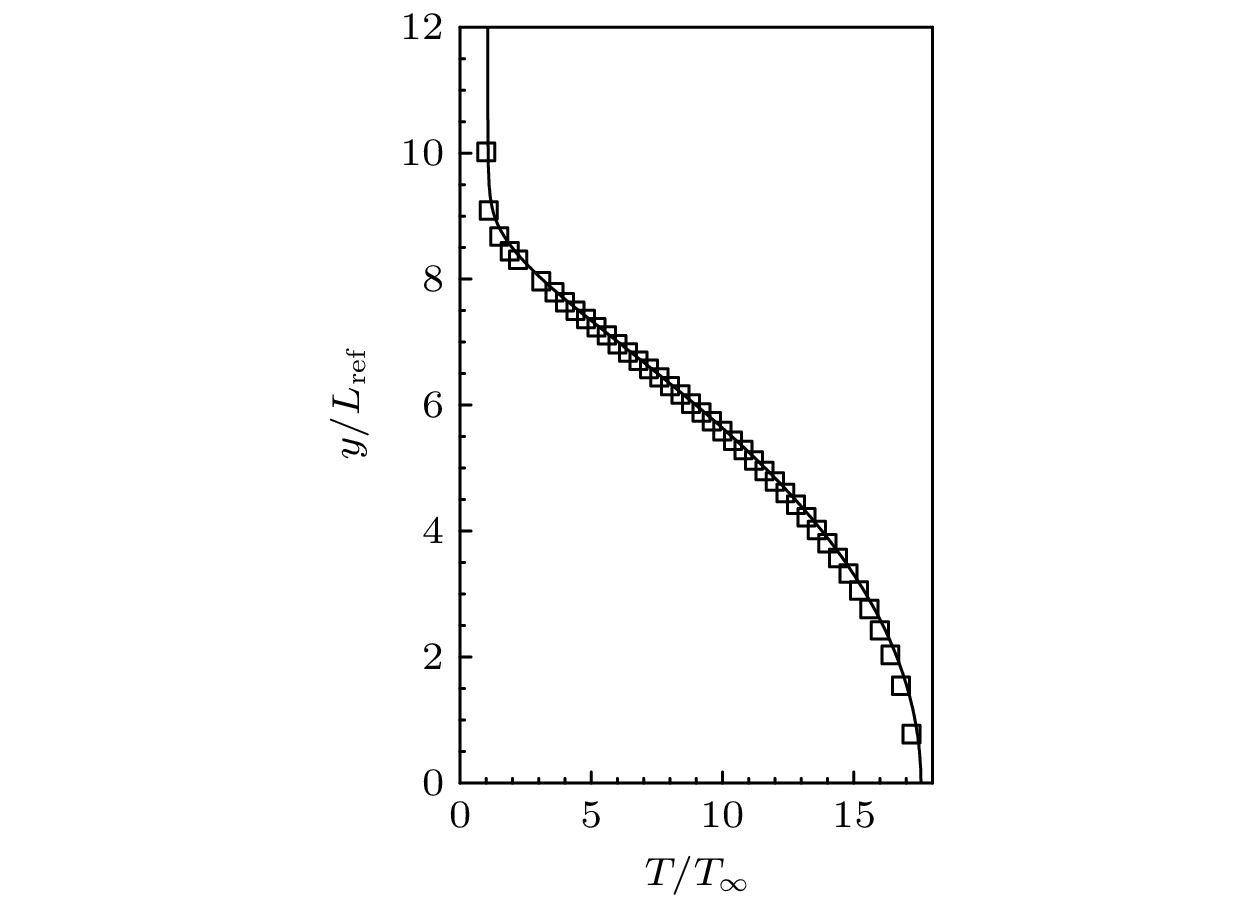
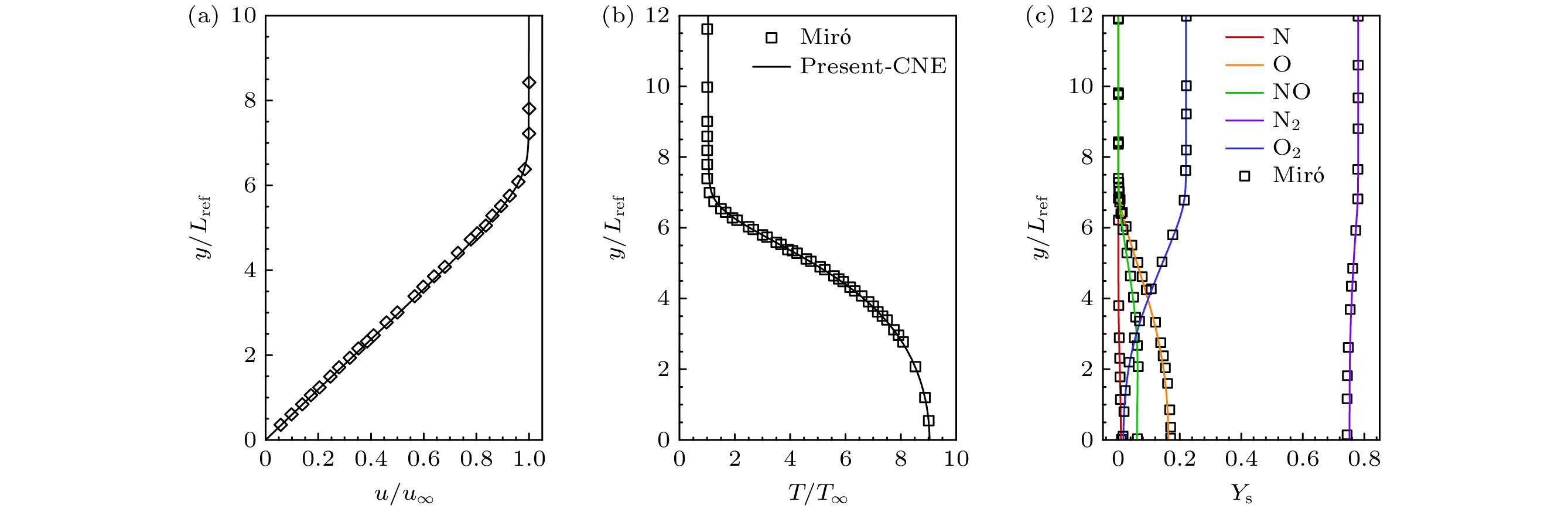
研究中基本流场的计算均依托国家数值风洞工程CFD软件NNW-HyFLOW进行, 流场求解过程采用2阶迎风插值的AUSMPW+格式以及Minmod限制器计算空间对流通量, 黏性项则采用中心格式计算, 并通过LUSGS隐式时间推进方法进行迭代. 首先验证该软件模拟的可靠性, 分别对量热完全气体(CPG)模型和化学非平衡(CNE)气体模型进行校验. 针对前者, 选取的验证算例为Kline[50]的绝热平板边界层: 来流马赫数Ma = 10, 来流温度T∞ = 350 K, 雷诺数Re = 6.0×106 m–1, 与文献对比验证结果见图2. 对于后者, 验证算例为Miró[51]的化学非平衡绝热平板边界层: 来流马赫数和单位雷诺数与Kline的设置一致, 来流温度T∞ = 600 K, 与文献对比验证结果见图3. 从图2和图3的对比结果来看, 研究中采用HyFLOW模拟基本流场是可行的. 无特别说明, 文中无量纲参考长度均为Lref = 1 mm.
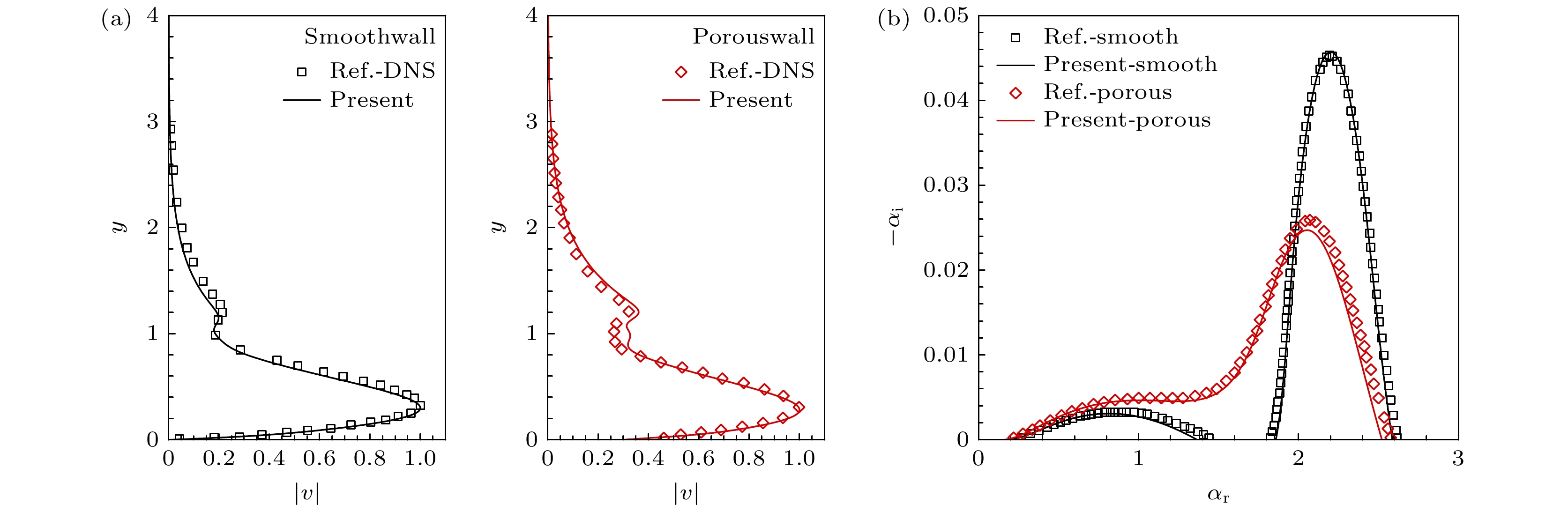
下面验证考虑多孔效应的稳定性分析方法有效性, 在此给出量热完全气体模型下多孔壁面稳定性分析算例: 雷诺数Re = 1.0×107 m–1, 来流温度T∞ = 216.65 K, 壁面为绝热壁; 多孔壁上圆孔参数分别为: n = 0.25, h = 2 mm, b = 0.09375 mm. 图4给出光滑/多孔壁下Mack模态的形状函数和增长率与Wartemann等[30]和Luedeke等[48]结果的对比, 对应流向位置的绝热壁温为Tw = 1522.44 K, 二者结果的一致性验证了本文LST程序分析多孔效应的可靠性.
-
本文选取高度H = 25 km的大气参数, 分别用量热完全气体(CPG)和化学非平衡(CNE)气体模型进行计算, 基本流计算壁面条件为绝热壁, 具体参数如表1所列, ρ∞和U∞为来流密度和来流速度.
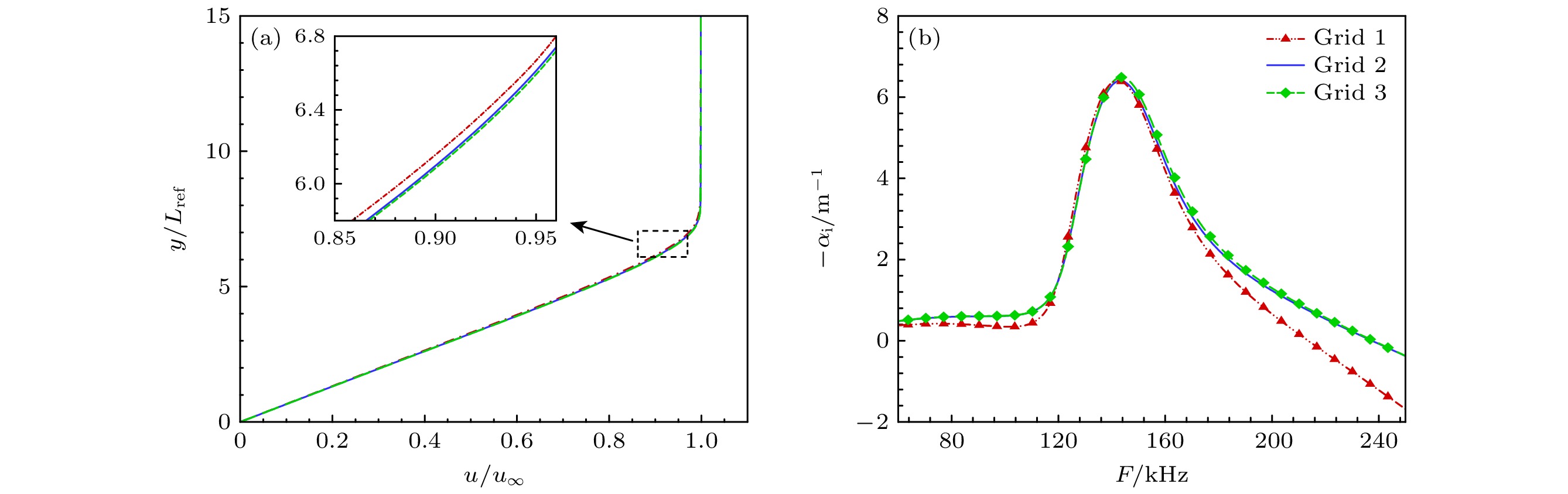
首先对计算网格做无关性验证, 对比三套不同网格, 分别是Grid1: 301×401, Grid2: 501×701, Grid3: 651×1051, 第一层高度均不超过0.001 mm. 计算工况为表1中Ma = 10参数. 图5给出了有效计算域中部位置x/Lref = 450的流向速度和模态增长率分布. 可以看出Grid1的流向速度和增长率分布与Grid2和Grid3存在一定差异, 综合考虑计算精度和时间成本, 后续采用Grid2网格进行计算.
-
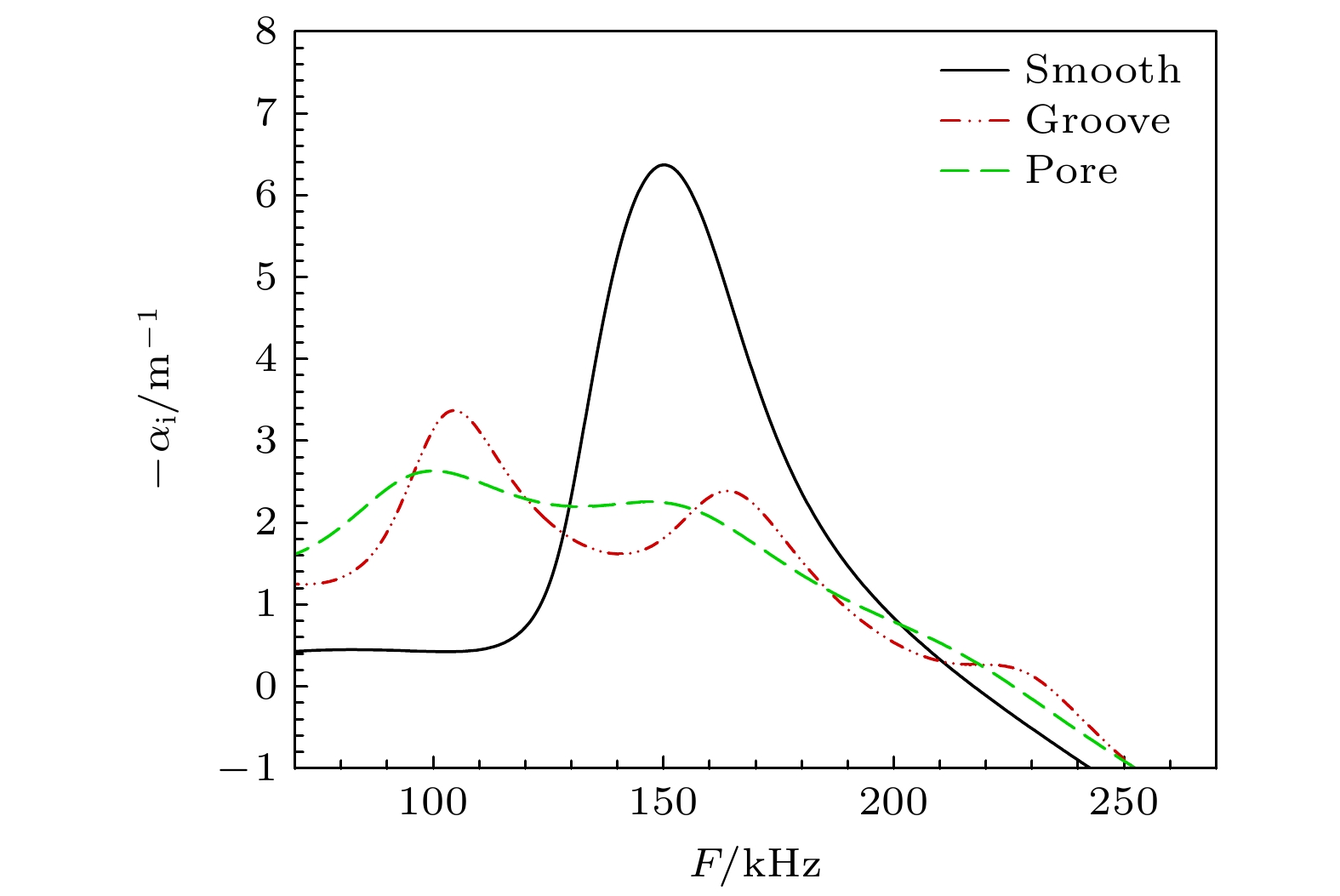
利用多孔壁面的吸声特性, 研究孔隙效应对Mack模态的影响. 首先, 基于2.3节中给出的两种多孔模型, 探究不同壁面孔隙模型的影响差异, 选定的关键参数分别为半宽(或半径)b = 0.945 mm、孔深H = 6.752 mm、孔隙率n = 0.66. 以量热完全气体假设下Ma10工况为例, 图6给出两种多孔模型计算的x/Lref = 400位置增长率对比. 可以看出, 虽然这两种多孔模型的增长率分布差异较大, 但两者均能明显地抑制不稳定模态.
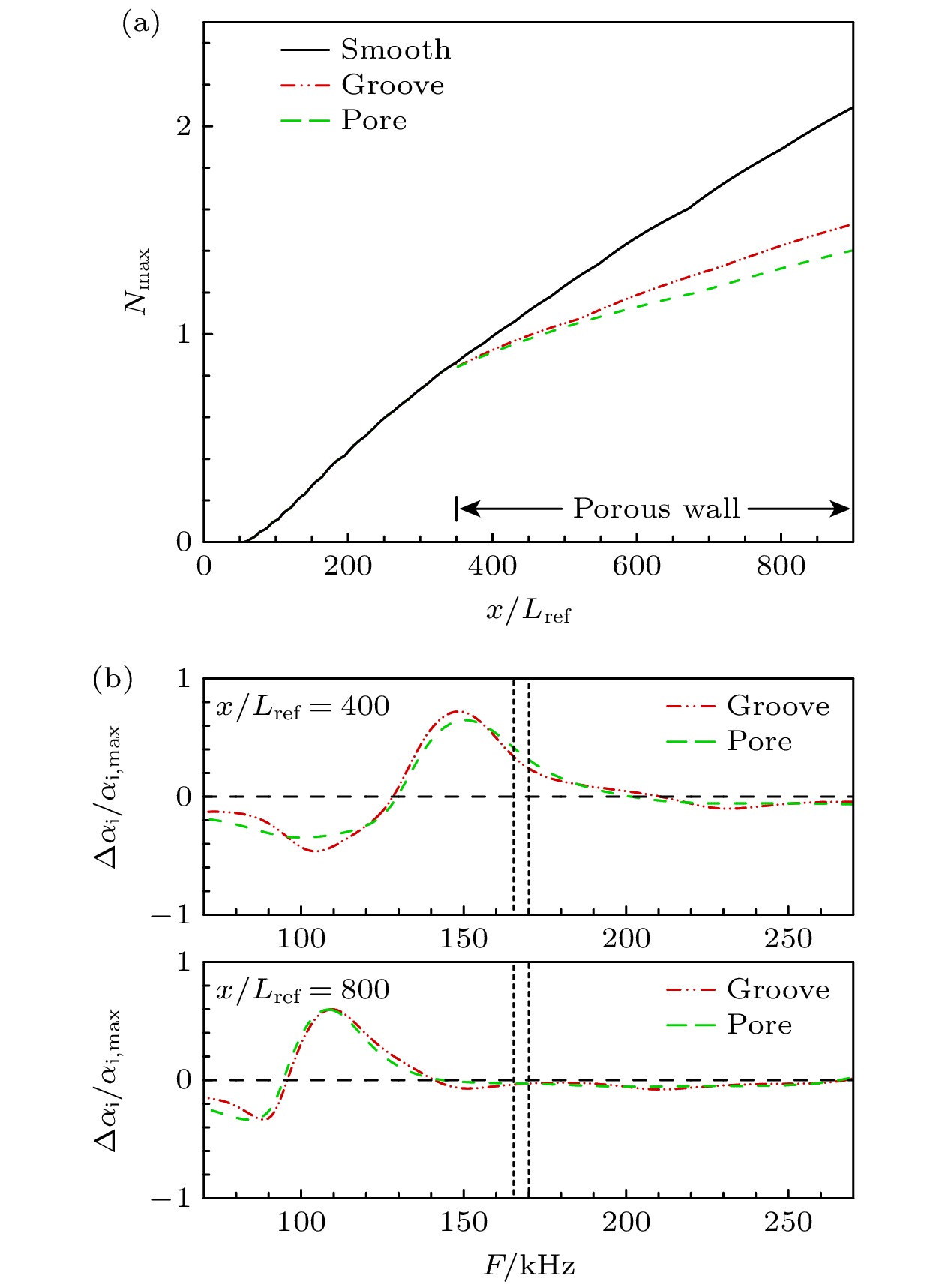
为进一步分析其差异, 图7给出基于微槽和圆孔模型计算的N值曲线和模态增长率相对变化率
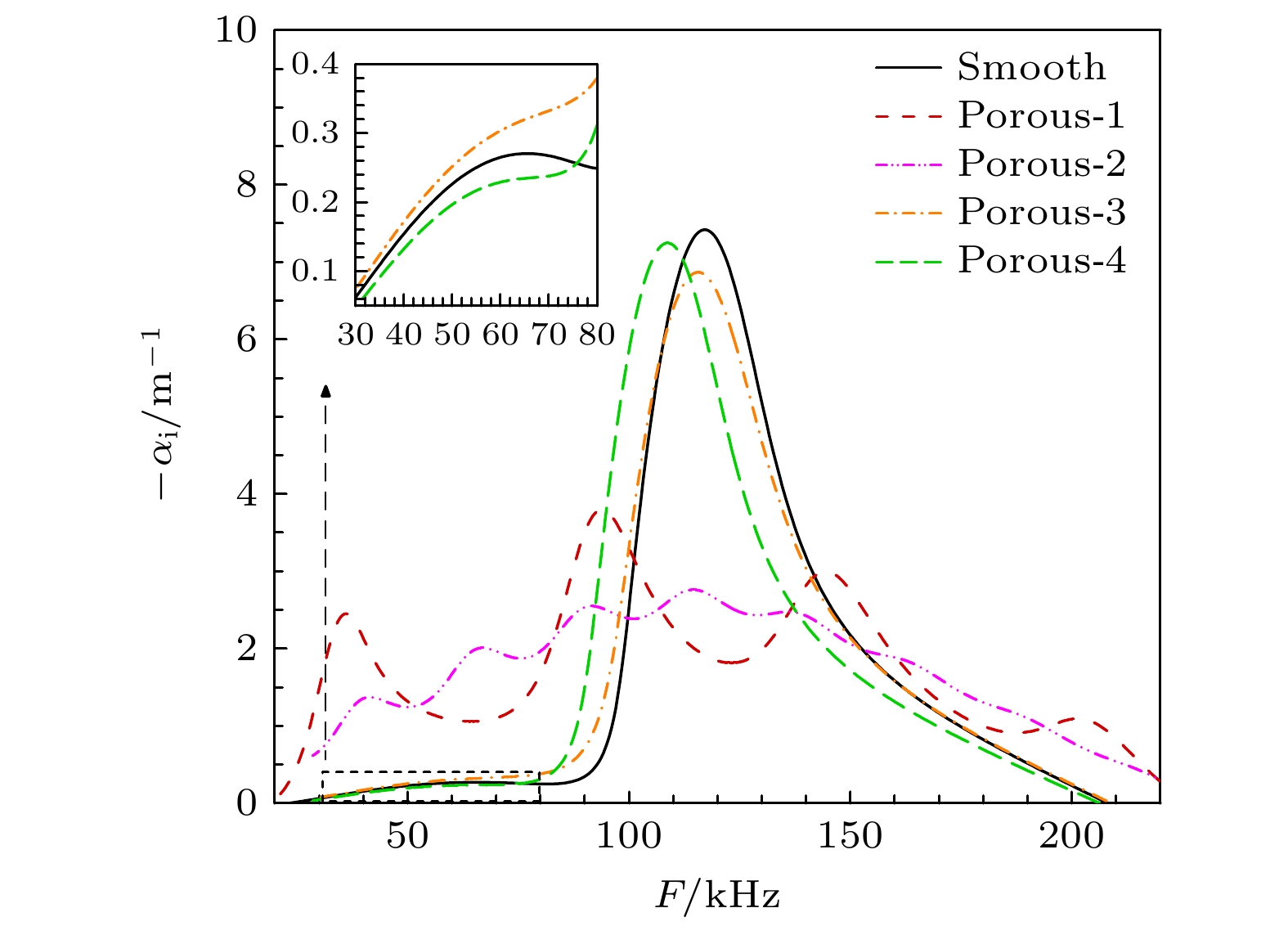
$ {\left( {\left( { - {\alpha _{ {\text{i,smooth}}}} + {\alpha _{{\text{i,porous}}}}} \right)/{\alpha _{{\text{i,max}}}}} \right)_{{\text{groove/pore}}}} $ 曲线. 与光滑壁相比, 可以看出规则圆孔和微槽对边界层失稳的抑制效果明显, 平板出口的最大N值均明显减小. 虽然图6中显示规则圆孔和微槽的增长率有所差别, 但其相对变化率的趋势表明不同形状孔隙具有相似的声学特性. 另外, 圆孔对应的最大N值略小于微槽, 这是由于多孔壁下最大N值对应的主导频率增加(位于图7(b)中虚线频率范围), 在该主导频率下平板靠前部分有Δαnom, pore＞Δαnom, groove; 而从x/Lref = 400位置的变化率曲线峰值来看, 微槽对最不稳定模态的抑制效果更好一点. 总体而言, 两者抑制能力的差异相对不大, 后续分析中选用微槽孔隙模型.为探究不同微槽截面参数下微孔隙效应对Mack第一、第二模态的影响, 选取不同文献的微槽截面参数, 如表2所列. 利用考虑微孔隙效应的LST计算量热完全气体假设下Ma10工况不同壁面参数的模态增长率随频率的变化, 如图8所示. 可以看出Porous-1—3均对第二模态有明显的抑制作用, 但同时也会使第一模态有所增强; Porous-4对第一模态起抑制作用, 第二模态最大增长率基本不变, 但其对应的频率向低频移动. 对比前三种型面参数的影响, 可以看出Porous-1对频率范围在F = 113.7—145.6 kHz的第二模态抑制作用更强, 但会使得第二模态由单峰变为明显的多峰. 由于在高马赫条件下, 第二模态一般为主导模态, 因此, 选用Porous-1的参数进一步分析.
-
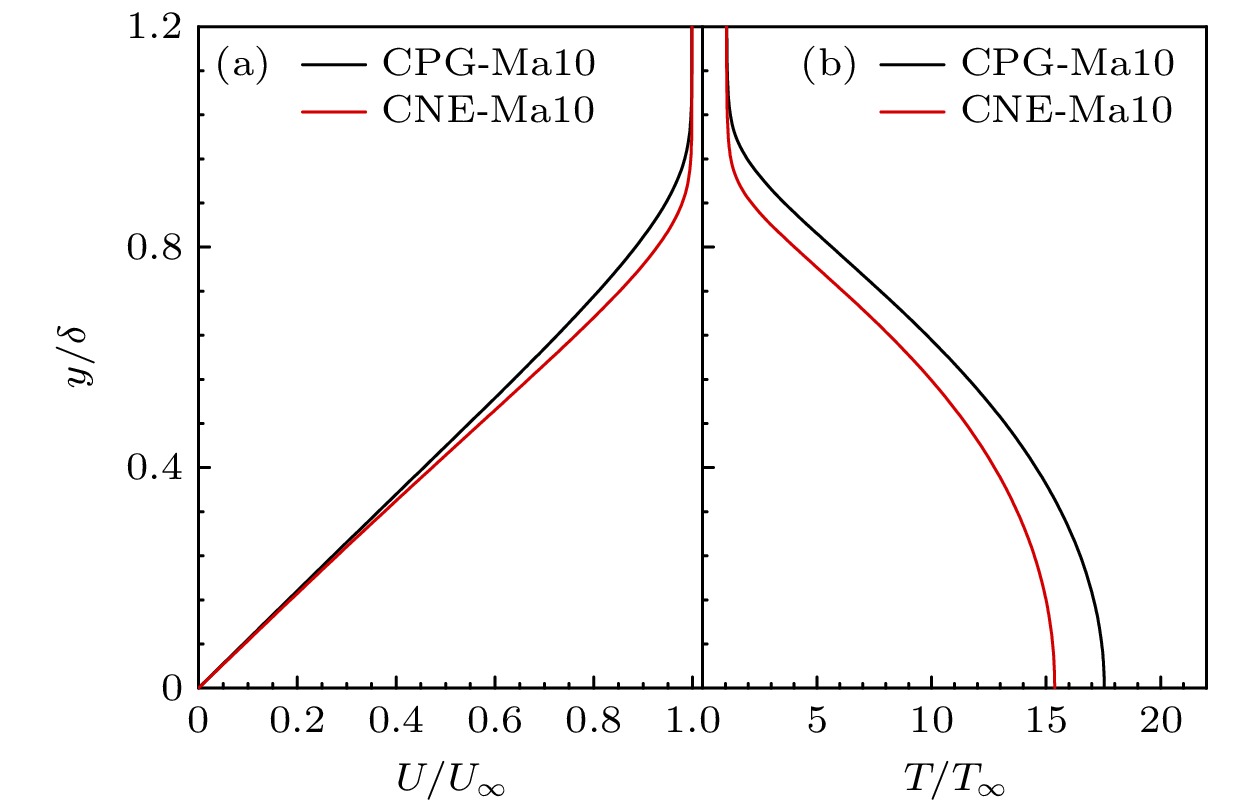
化学非平衡效应会影响基本流剖面特征, 进而影响边界层失稳特性. 首先, 以Ma10工况中流向位置x/Lref = 600为例, 图9对比了不同气体模型的速度、温度剖面, 图中采用量热完全气体下该位置边界层厚度8.64 mm(对应99.5%边界层外缘速度)作为无量纲化长度. 由速度剖面可以看出, 考虑化学非平衡效应时, 边界层厚度减小. 从温度的法向分布可知, 化学非平衡流动由于存在化学反应吸收热量, 其壁面温度明显低于量热完全气体, 在Ma10工况下两者壁温相差481 K. 由此可知, 为准确模拟流动, 在高马赫条件下考虑高温气体效应是十分必要的.
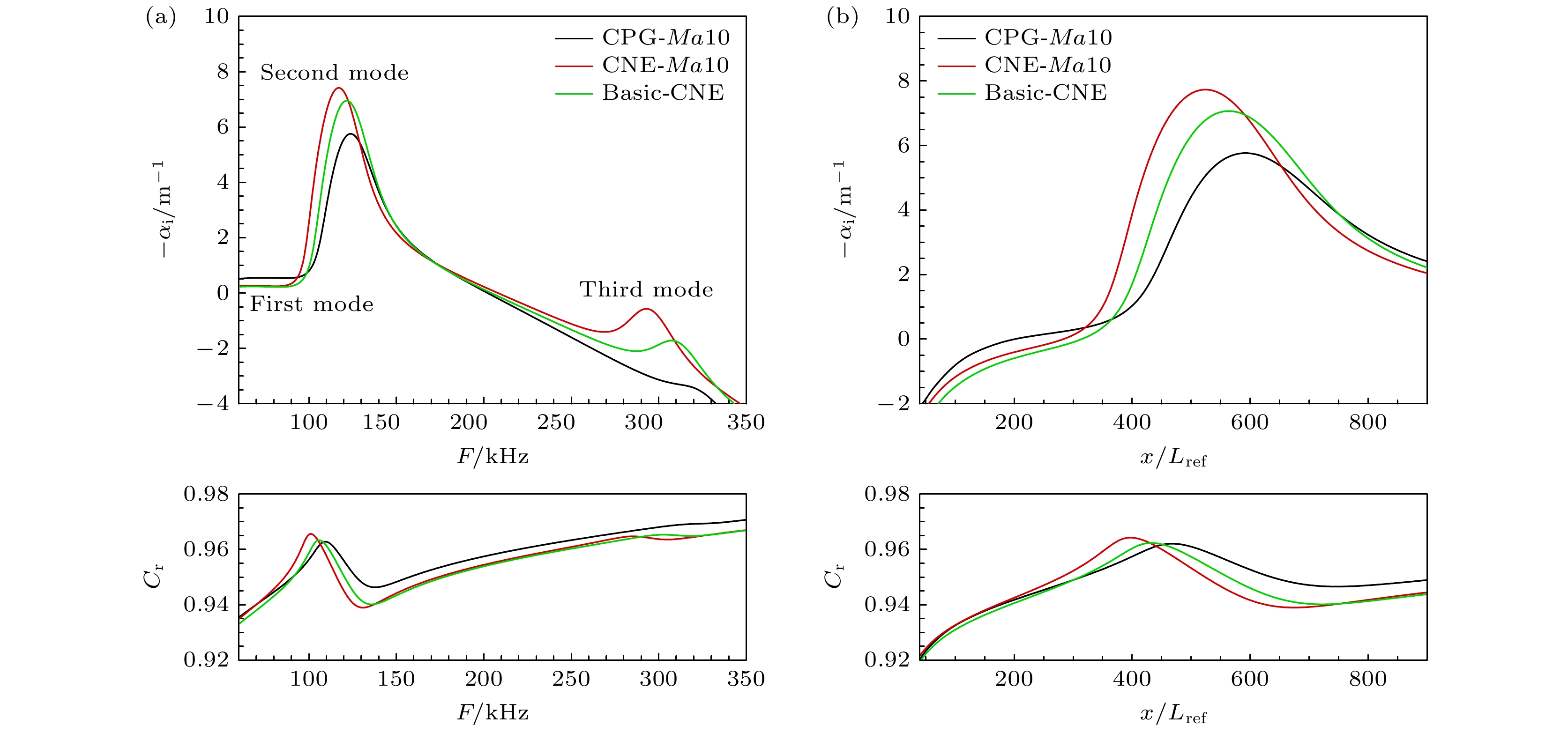
通过上述分析可知, 化学反应的存在显著地改变基本流剖面, 边界层内的扰动发展也必然改变, 分别利用量热完全气体和考虑化学非平衡的线性稳定性(LST)程序计算边界层内的扰动特性. 首先, 基于Ma10工况研究化学非平衡效应的影响, 图10(a)给出不同气体模型在流向位置x/Lref = 600处模态增长率随频率的变化和对应相速度变化, 其中频率
$ F=\omega_{\text{r}}\dfrac{u_{\text{e}}}{2\pi}L_{\text{ref}}^{-1} $ , 相速度Cr = ωr/αr, αr和ωr分别为流向波数实部和圆频率实部.图10(a)分别展示了量热完全气体(CPG)、化学非平衡(CNE)和仅基本流考虑化学非平衡(Basic-CNE)的结果. 从图10(a)可以看出, 考虑化学非平衡效应时第一模态被抑制、第二模态被促进、第三模态被激发, 第二、第三模态最大增长率对应的频率降低, 且其模态相速度峰值向低频移动. 此外, 仅在基本流考虑化学非平衡效应而稳定性方程里不考虑时, 第二模态计算结果比较接近于CNE, 但介于CPG和CNE之间. 对比上述三种情况, 第一模态被抑制的主要原因是化学非平衡效应对基本流的影响. 图10(b)给出不同气体模型下频率F = 124 kHz的扰动增长率沿流向的变化及其对应的相速度. 对于流动中的同频率扰动, 化学非平衡效应使得第二模态增长率及模态相速度更快达到峰值.
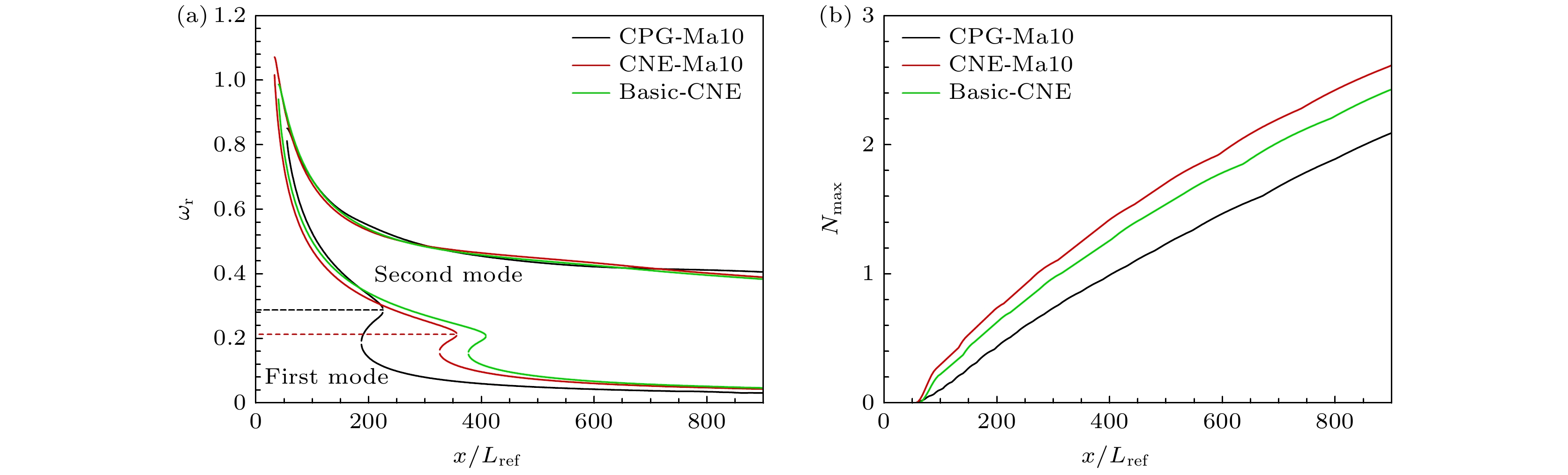
为更直观地讨论化学非平衡效应对模态稳定性的影响, 图11(a)给出不同气体模型下第一模态和第二模态中性曲线分布. 在平板靠前区域, 化学非平衡效应使不稳定的第二模态向高频区域延伸, 高频扰动更早被激发. 第二模态中性曲线下支也表明其不稳定频率稍向低频移动, 整体上第二模态的不稳定频率范围增大. 针对第一模态, 化学非平衡效应起到抑制作用, 其不稳定频率范围减小. 但仅在基本流中考虑化学非平衡效应的计算结果并不像第二模态那样介于CPG与CNE之间, 而是比CNE的中性曲线还要更靠下游, 说明基本流中的化学非平衡效应对第一模态是抑制的, 但扰动稳定性方程中的化学非平衡效应是促进的, 前者的抑制作用大于后者的促进作用. 图11(b)对比了三者的N值包络线, 可以看出基本流和稳定性方程中的化学非平衡效应均会使最大N值增加, 促进边界层失稳.
总体来说, 高温化学非平衡效应对模态稳定性的影响主要是通过对基本流的影响, 但该效应对稳定性方程的影响从科学研究角度也不容忽视, 在工程应用兼顾效率时可以有所取舍.
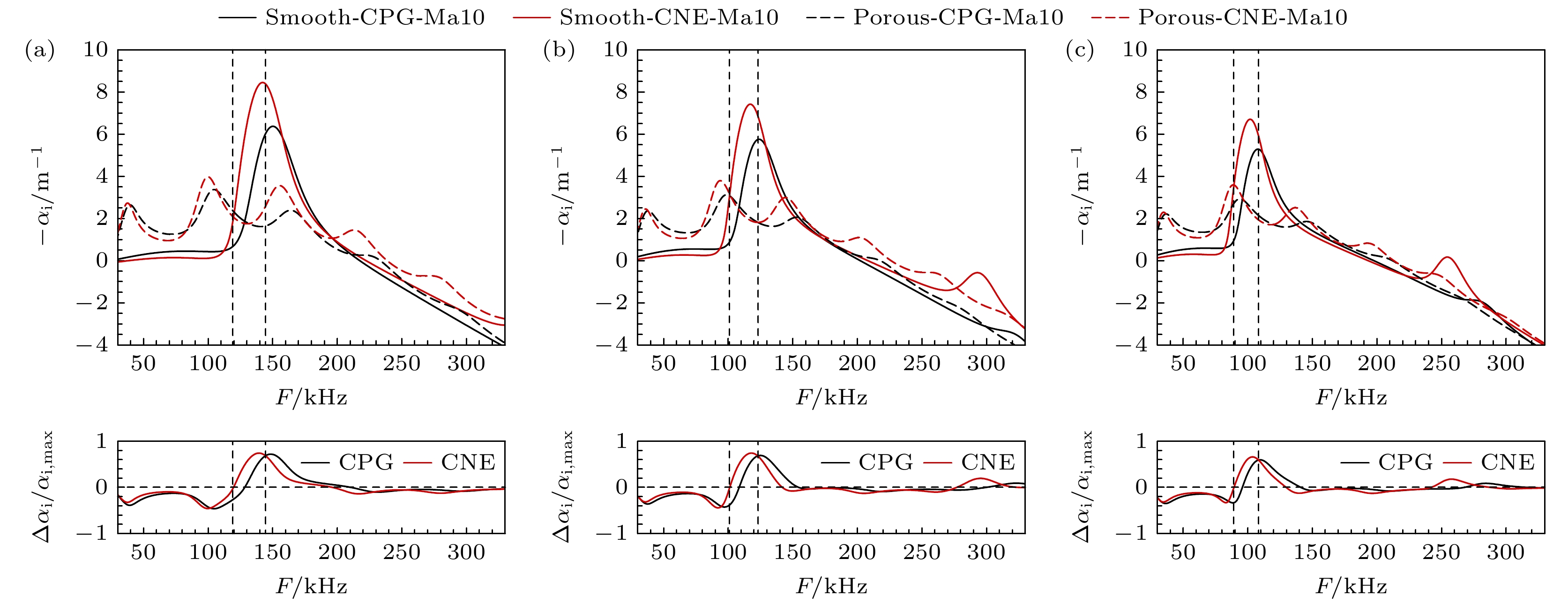
对于考虑化学非平衡和微孔隙效应共存的研究, 选取马赫10工况对比相同壁面参数下不同气体模型的模态增长率, 图12给出位置x/Lref = 400, 600和800的增长率及相对变化率(
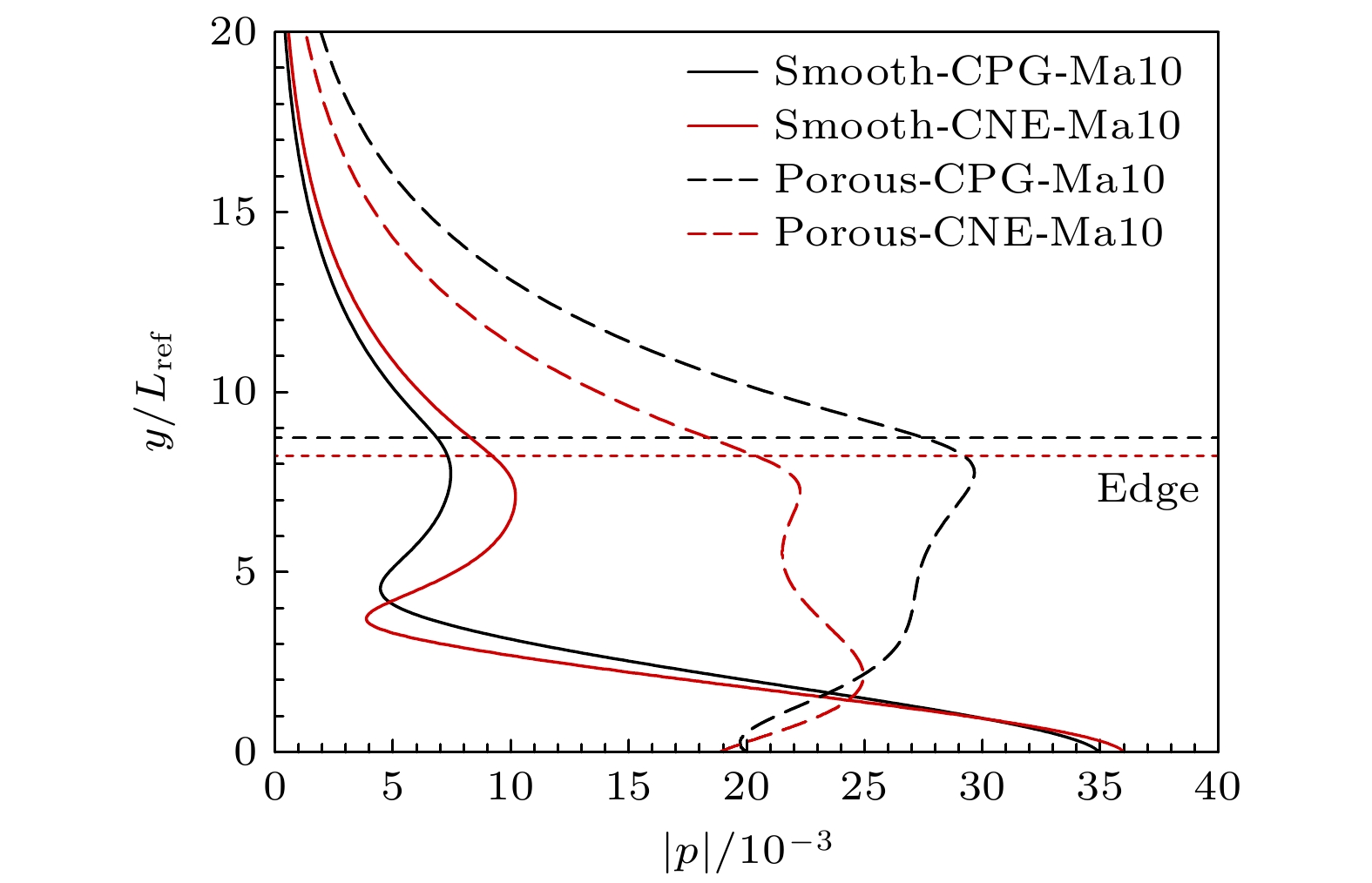
$ ( - {\alpha _{ {\text{i,smooth}}}} + {\alpha _{ {\text{i,porous}}}} )/{\alpha _{ {\text{i,max}}}} $ )对比. 从图12(a)可以看出不同气体模型下多孔壁均使第一模态更不稳定, 但第二模态被明显抑制; 对比相对变化率曲线, 在第二模态频率范围内, CNE工况多孔壁的抑制效果随频率增加先大于CPG工况、后小于CPG工况, 说明化学非平衡效应降低了孔隙效应起抑制作用的模态频率范围. 这种现象造成在局部低频范围内(两条虚线之间)化学非平衡效应会增强微孔隙效应的抑制作用, 在其他大部分频率范围(第二条虚线右侧区域)则表现为减弱. 此外, 从相对变化率的峰值来看, 化学非平衡效应的影响不明显. 通过对比不同位置结果, 不稳定模态的主导频率随流向位置增加而减小, 图12(b)和图12(c)中增长率相对变化趋势与图12(a)相同, Δαnom, CNE＞Δαnom, CPG对应频率范围也随流向位置增加而减小.为分析微孔隙效应对扰动形状的影响, 取频率F = 124 kHz对应的特征解, 其对应的压力特征函数幅值分布如图13所示, 图中黑色和红色横虚线分别表示CPG工况和CNE工况在流向位置x/Lref = 600的边界层外缘. 从图13可以看出, CNE工况和CPG工况的形状函数基本一致, 但在微孔隙效应影响下, 近壁区的扰动幅值显著减小, 且压力的扰动峰值对应的法向位置由近壁区变成靠近边界层外缘的区域.
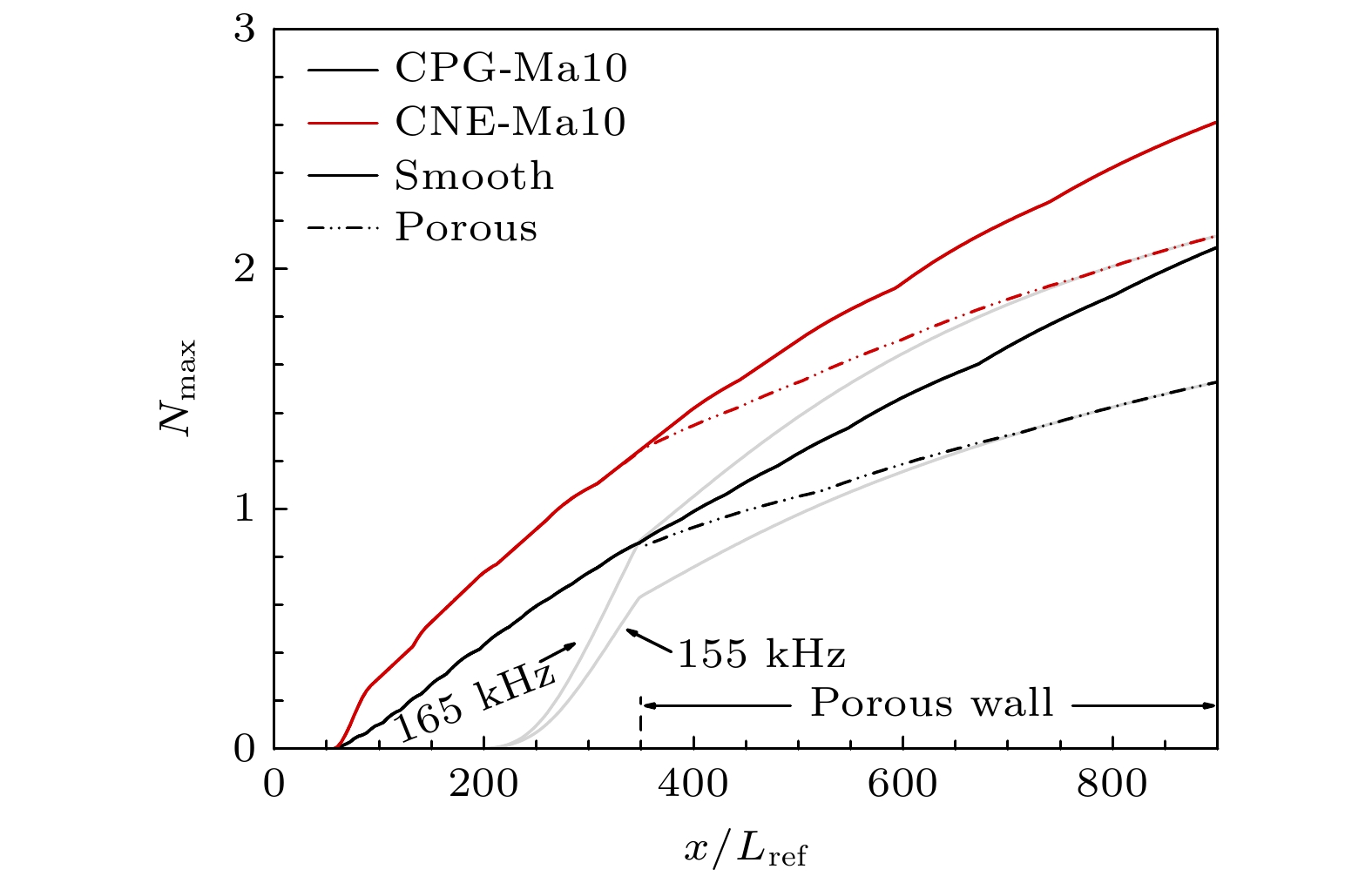
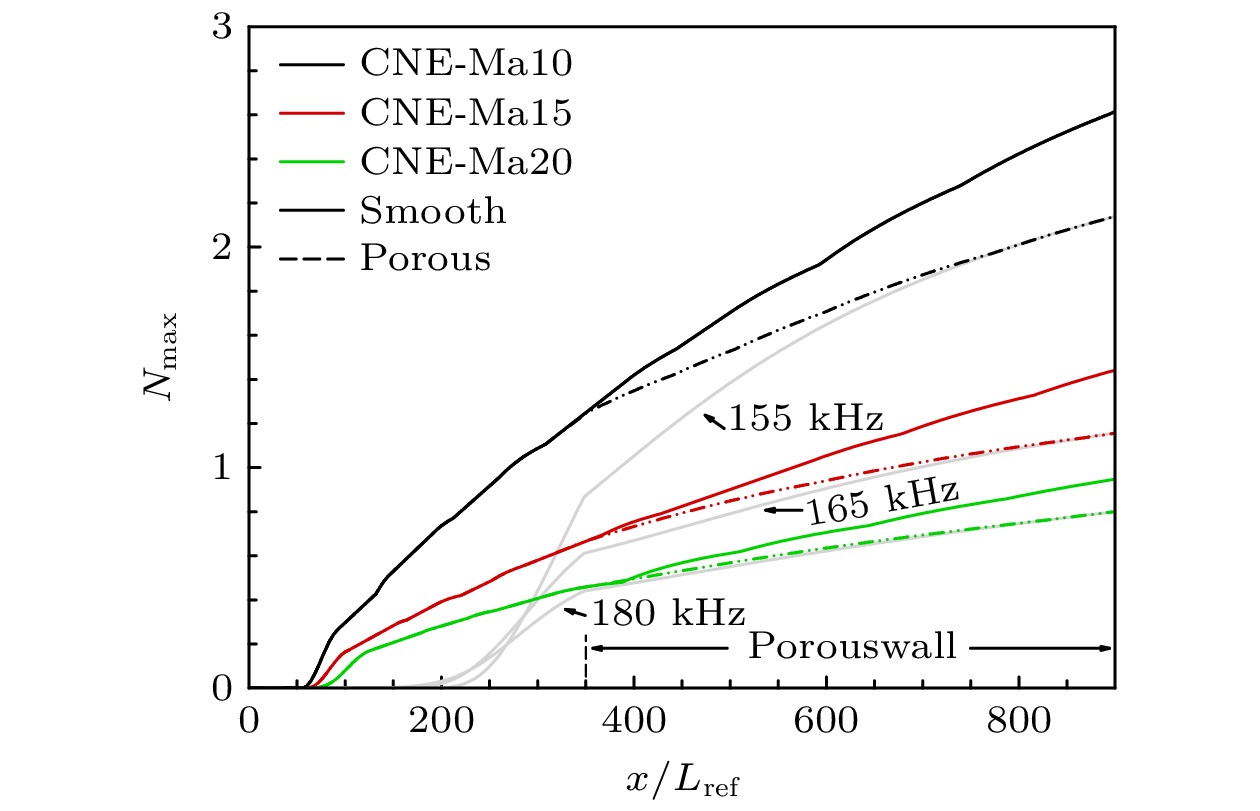
根据现有研究[32], 在平板前缘设置多孔壁会激发不稳定模态, 使N值增大. 因此, 为考察微孔隙的抑制作用, 在流向位置x/Lref = 350处开始设置多孔壁, 进一步给出两种气体模型下光滑和多孔壁的N值曲线对比, 如图14所示. 不同气体模型下微孔隙效应均能使最大N值减小, 其中CPG工况减小26.83%, CNE工况减小18.22%, 两者的差异主要是多孔壁下最大N值对应的频率增大, 分别为155 kHz和165 kHz, 根据图12可知对应频率下有Δαnom, CNE＜Δαnom, CPG. 由此说明两种气体模型下孔隙效应均有明显的延迟失稳效果, 但化学非平衡效应对孔隙的延迟效果有所削弱, 这与Wang[40]的结论相反. 原因在于Wang的工作仅考察了300, 400 kHz的单频结果, 无法代替评估宽频范围的整体效果. 此外, 对比红色点划线和黑色实线, 可以发现同时考虑化学非平衡和孔隙效应的N值比都不考虑的结果大, 说明化学非平衡效应对模态的促进作用比孔隙效应的抑制作用强, 导致整体上两种效应共存时是促进失稳.
-
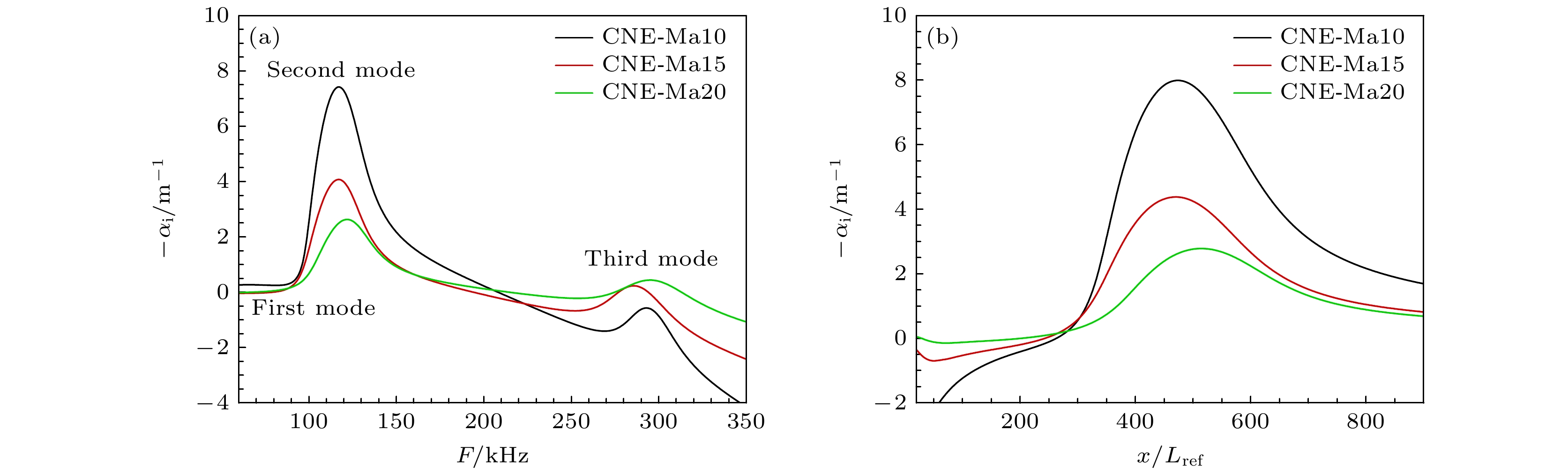
在量热完全气体流动中, 马赫数增大将导致边界层更稳定、转捩位置推迟[1]. 下面考察马赫数10, 15和20工况, 分析化学非平衡流动中马赫数对不稳定模态的影响. 首先比较光滑壁条件下不同马赫数的化学非平衡流动稳定性, 图15(a)中展示了不同马赫数在流向位置x/Lref = 600的增长率对比. 从图15(a)可以看出, 随马赫数增加, 第一、第二模态的扰动均被抑制, 增长率峰值减小, 其对应的频率影响不大. 另外, 马赫数增加使第三模态扰动被激发, 并逐渐趋于不稳定, 但第二模态依旧占主导地位. 进一步地, 给出第二模态F = 130 kHz的扰动增长率沿流向的变化, 如图15(b)所示. 随马赫数增加, 模态增长率峰值减小, 但到达最不稳定增长率的位置相近, 这意味着马赫数影响模态增长率的变化快慢.
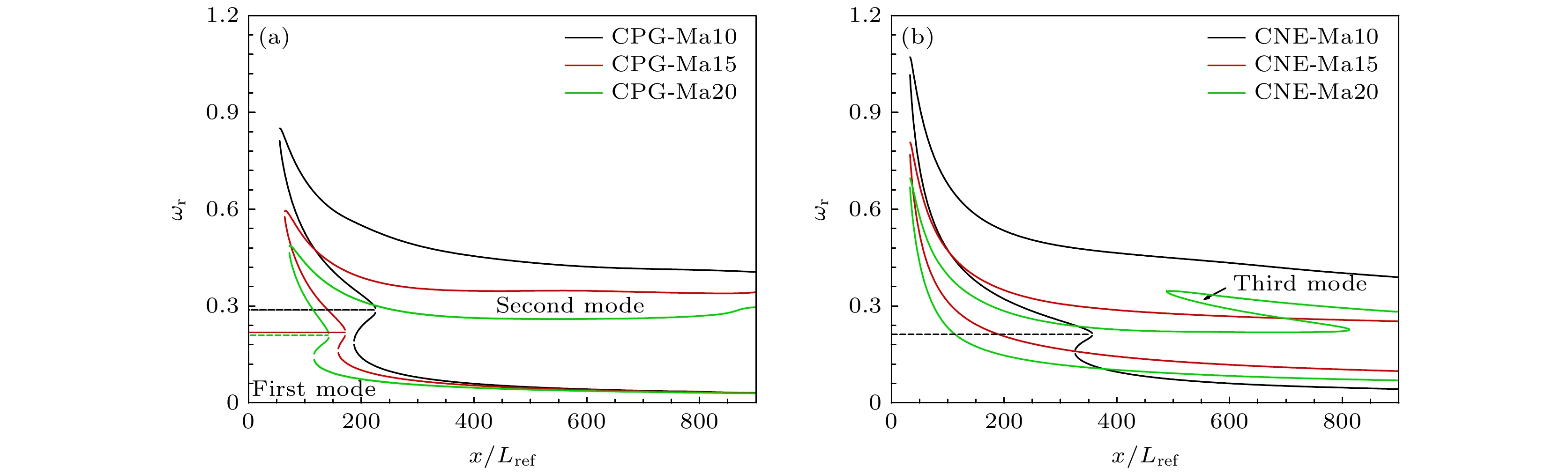
同样地, 图16给出不同马赫数下的边界层中性曲线, 图16(b)为化学非平衡气体模型的计算结果, 并在图16(a)给出量热完全气体模型的计算结果作为对比. 由图16(a)可以看出, 随着马赫数增加, 边界层第一模态和第二模态的不稳定频率向低频移动, 而低频扰动开始失稳的流向位置向上游移动, 同时第一模态和第二模态在下游相连, 相连的频率范围不存在中性点. 对于化学非平衡气体模型, 马赫数的影响规律相对复杂. 图16(b)中Ma10边界层存在不稳定的第一模态和第二模态, 且二者不稳定区域在下游相连; Ma15边界层仅存在不稳定的第二模态, 第一模态变得稳定; Ma20边界层除了存在不稳定的第二模态, 还出现不稳定的第三模态, 并在下游与第二模态相连.
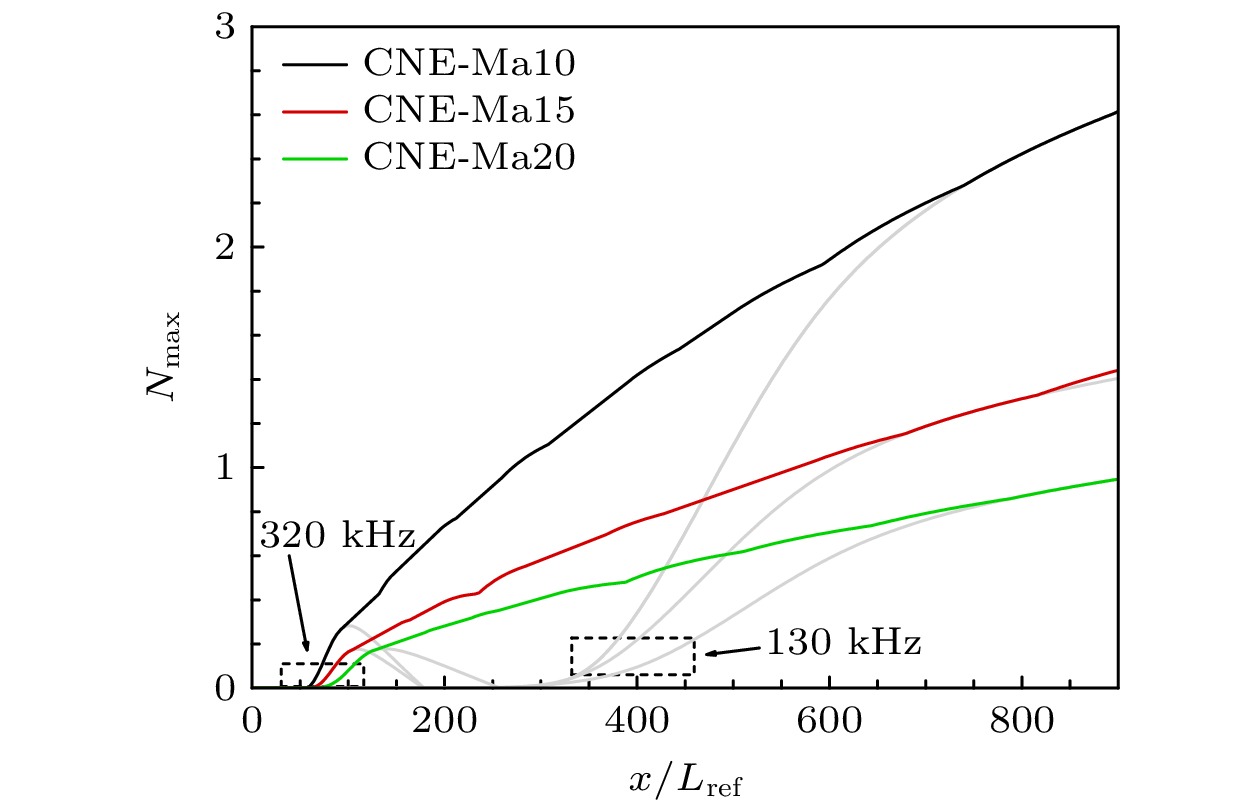
图17给出不同马赫数下的N值包络, 同时给出模态频率130 kHz对应的单频N值曲线. 可以看出, 随着马赫数增大, N值减小, 但最大N值对应的模态频率相近, 说明马赫数对化学非平衡边界层的失稳具有抑制作用.
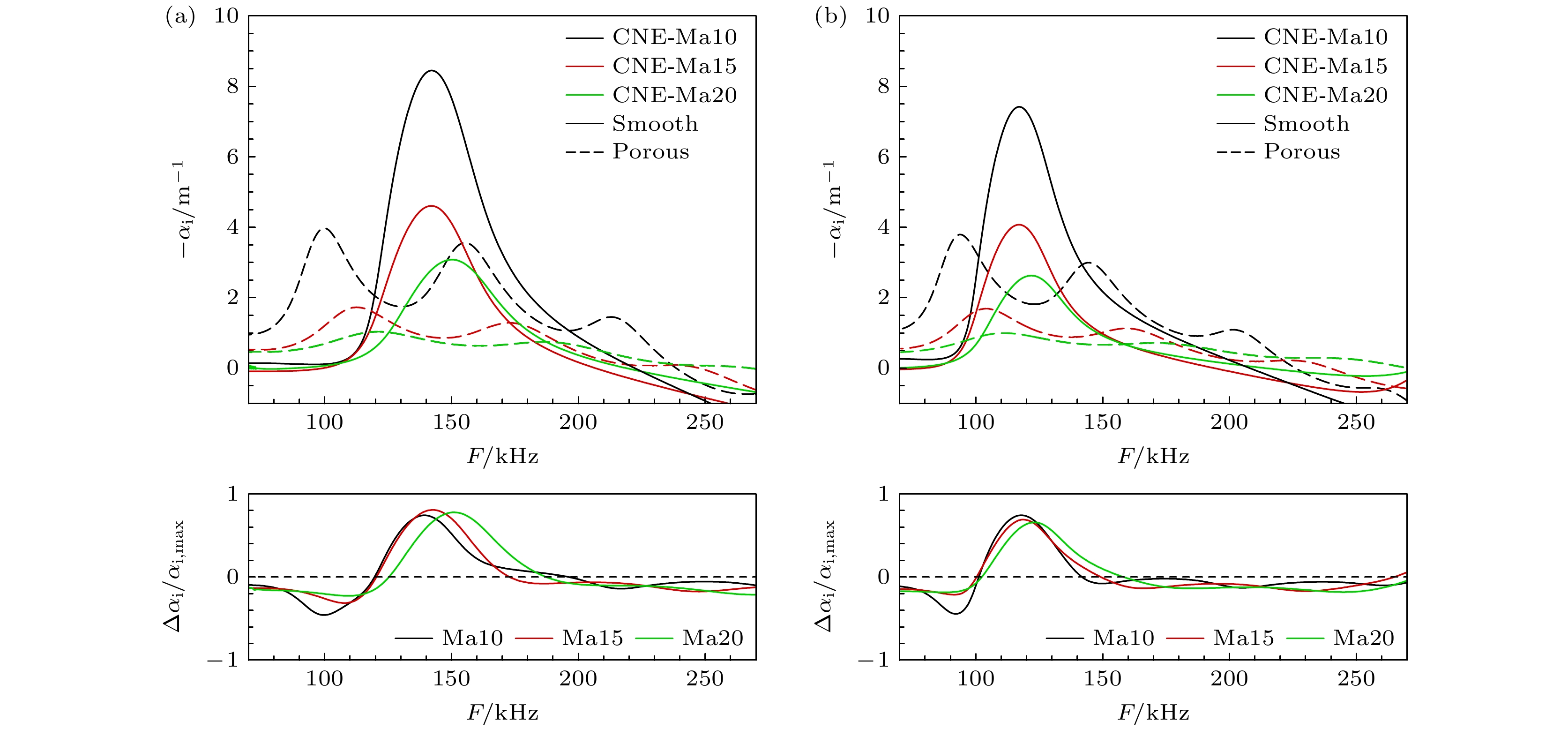
下面分析多孔壁条件下马赫数对化学非平衡边界层稳定性的影响, 图18给出了不同马赫数工况在流向位置x/Lref = 400和600处的模态增 长率及其相对变化率, 并与光滑壁进行对比. 根据 图18(a)可以看出, 马赫数增大同样可以抑制多孔壁边界层第一模态和第二模态. 对比光滑壁, 孔隙效应对边界层模态的影响能力随马赫数增大而有所减弱, 从x/Lref = 400位置来看: 马赫数越大, 孔隙效应对第一模态的激发效果越弱, 但对第二模态的抑制效果基本不变, 多孔壁抑制效果最显著对应的频率基本与最大不稳定增长率对应的频率相近. 下游x/Lref = 600位置也呈现相同的趋势.
图19给出化学非平衡流动在光滑和多孔壁的N值包络线. 从图19可以看出, 不同马赫数下多孔壁均能有效减小N值, 但最大N值对应的主导频率随马赫数增加而增加. 表3列出了不同马赫数下两种气体模型在出口x/Lref = 900位置的N值相对变化率(ΔN/Nmax, smooth), 分析孔隙效应对不同工况下边界层失稳的整体抑制作用. 在所研究的马赫数范围内, CPG工况的相对减小量大于CNE工况, 说明不同马赫数下化学非平衡效应均对多孔壁的抑制效果有所削弱.
-
在高马赫数条件下高温化学非平衡与表面微孔隙效应二者共存, 本文建立了同时考虑化学非平衡效应和微孔隙效应的线性稳定性分析方法LST, 研究了飞行工况(H = 25 km)下化学非平衡效应、孔隙效应、马赫数等对高焓边界层流动失稳的影响. 主要结论如下:
1) 化学非平衡效应能够促进第二模态、抑制第一模态、激发第三模态, 但第二模态总体上始终占据主导地位, 因此促进边界层失稳. 虽然化学非平衡效应对第一模态的整体效果为抑制, 但是稳定性方程中的化学非平衡效应则表现为促进, 其对第一模态的抑制作用主要来源于对基本流的改变. 因此从科学研究角度来看, 对稳定性方程考虑化学非平衡效应的影响也是不容忽视的.
2) 当化学非平衡流动进一步考虑微孔隙效应时, 微孔隙效应能促进第一模态、抑制第二模态, 整体上是抑制失稳的, 微孔隙效应的作用效果与 化学非平衡效应大致相反, 前者对第二模态的抑制作用弱于后者的促进作用, 导致整体上两种效应 共存时相比量热完全气体模型下光滑壁条件是 促进失稳的. 相比量热完全气体模型的孔隙效应, 由于化学非平衡效应降低了孔隙效应抑制第二模态对应的频率范围, 造成孔隙效应的抑制失稳能力在局部低频范围内增强, 但在其他第二模态失稳区域内则是减弱的, 导致孔隙效应对N值的降低量有所减小.
3) 在化学非平衡流动中, 随马赫数增加, 第一、第二模态均被抑制, 第三模态被激发并逐渐不稳定, 增长率峰值对应频率相近, 这导致最大N值减小, 但主导频率相近. 若考虑微孔隙效应, 马赫数增加则会减弱多孔壁对第一模态的激发作用, 对第二模态抑制效果影响不大. 在考察的马赫数范围(10—20)内, 微孔隙效应仍能有效地抑制失稳, 但与不考虑微孔隙效应的量热完全气体工况相比, 两种效应共存时呈现的效果是促进.
本文得到中国空气动力研究与发展中心计算空气动力研究所NNW-HyFLOW团队的大力支持, 以及空天飞行空气动力科学与技术全国重点实验室张彬、李晓虎、巩耕等的帮助, 在此表示感谢.
高温化学非平衡与表面微孔隙效应对边界层稳定性影响
Influence of high-temperature chemical non-equilibrium and surface micropore effect on boundary layer stability
-
摘要: 层流-湍流的转捩问题是飞行器设计研制面临的重要气动难题. 当飞行马赫数较高时, 飞行器表面同时存在高温气体热化学反应与微孔隙效应, 此时边界层失稳问题更加复杂, 其机理认识尚不清楚. 本文建立了同时考虑高温化学非平衡效应和表面微孔隙效应的线性稳定性分析方法, 并针对高空H = 25 km、马赫数10, 15和20的飞行工况, 对比分析了化学非平衡效应、微孔隙效应以及两种效应共存时对流动稳定性的影响. 研究发现, 化学非平衡效应能够促进边界层模态失稳, 微孔隙效应能够抑制第二模态失稳, 前者作用强于后者, 导致两者共存时整体上促进第二模态失稳. 化学非平衡效应能够降低孔隙效应抑制第二模态对应的频率范围, 造成在局部低频范围内化学非平衡效应可以增强微孔隙效应的抑制效果, 而在高频范围内减弱其抑制效果, 导致孔隙效应N值降低量整体上减小. 此外, 两种效应共存时马赫数变化对微孔隙效应抑制第二模态的能力影响不大.Abstract: The transition from laminar to turbulent flow is one of the main aerodynamic challenges in aircraft design and development. When the flight Mach number is sufficiently high, the aircraft surface experiences micropore effects and high-temperature gas thermochemical reactions. At present, boundary layer instability has become a more complex problem, and its mechanism is still unclear. In this study, a linear stability analysis method is developed which takes into consideration high-temperature chemical non-equilibrium process and surface micropore effect. For flight conditions at high altitude (H = 25 km) with Mach numbers 10, 15, and 20, the effects of micropore effects, chemical non-equilibrium effects, and their joint effect on flow stability are contrasted and investigated. The results show that the chemical non-equilibrium effect can contribute to the boundary layer's mode instability, while the micropore effect can restrain the second mode instability. The coexistence of the two often contributes to the instability of the second mode, because the former is heavier than the latter. The chemical non-equilibrium effect can reduce the frequency range corresponding to the second mode of pore effect inhibition, which results in the chemical non-equilibrium effect enhancing the inhibition effect of the micropore effect in the local low-frequency range and weakening its inhibition effect in the high-frequency range. This, in turn, causes a decrease in the corresponding N value variation by pore effect. Furthermore, when both effects are present, the micropore effect’s capacity to inhibit the second mode is not significantly affected by change in Mach number.
-
Key words:
- boundary layer /
- stability /
- chemical non-equilibrium /
- micropore effect .
-
-
图 2 CPG工况流向x/Lref = 600处温度剖面对比
Figure 2. Temperature profile comparison under CPG circumstance at x/Lref = 600.
图 3 CNE工况流向x/Lref = 600处基本流对比 (a)流向速度; (b)温度; (c)组分浓度
Figure 3. Baisc flow profiles at x/Lref = 600 under CNE circumstance: (a) Streamwise velocity; (b) temperature; (c) species concentration.
图 4 稳定性分析结果与文献对比 (a)特征函数; (b)模态增长率
Figure 4. Comparison of literature and present results: (a) Eigenfunction; (b) growth rate.
图 5 网格无关性验证 (a)流向速度; (b)模态增长率
Figure 5. Verification of grid independence: (a) Streamwise velocity; (b) growth rate.
图 6 CPG下Ma10工况在位置x/Lref = 400模态增长率对比
Figure 6. Comparison of growth rate at position x/Lref = 400 for Ma10 condition under CPG.
图 7 微槽和圆孔的对比 (a) N值曲线; (b) 模态增长率变化率
Figure 7. Comparison of results between microgrooves and micropores: (a) N-value curves; (b) relative change of growth rate.
图 8 不同截面参数下在位置x/Lref = 600的模态增长率变化
Figure 8. Changes in growth rate under different cross-sectional parameters at x/Lref = 600.
图 9 Ma10工况不同气体模型边界层基本流剖面 (a)速度; (b)温度
Figure 9. Basic flow profiles of boundary layer for different gas models under Ma10 condition: (a) Streamwise velocity; (b) temperature.
图 10 Ma10工况不同气体模型模态增长率和相速度对比 (a) x/Lref = 600; (b)沿流向F = 124 kHz
Figure 10. Comparison of growth rate and phase velocity of different gas models under Ma10: (a) x/Lref = 600; (b) modal frequency F = 124 kHz along the streamwise direction.
图 11 Ma10工况不同气体模型对比 (a)中性曲线; (b)N值包络
Figure 11. Comparison of different gas models under Ma10: (a) Neutral curves; (b) N-value envelope.
图 12 不同气体模型光滑和多孔壁增长率及其相对变化率对比 (a) x/Lref = 400; (b) x/Lref = 600; (c) x/Lref = 800
Figure 12. Comparing the growth rates of smooth and porous walls and their relative change for different gas models: (a) x/Lref = 400; (b) x/Lref = 600; (c) x/Lref = 800.
图 13 光滑和多孔壁在x/Lref = 600处压力特征函数对比
Figure 13. Comparison of the pressure eigenfunctions for smooth and porous walls at x/Lref = 600.
图 14 不同气体模型光滑与多孔壁的N值包络线对比
Figure 14. Comparison of N-value envelope for smooth and porous walls of different gas models.
图 15 CNE工况不同马赫数的模态增长率对比 (a) x/Lref = 600; (b) 沿流向F = 130 kHz
Figure 15. Comparison of growth rates at different Mach numbers under CNE condition: (a) x/Lref = 600; (b) modal frequency F = 130 kHz along the streamwise direction
图 16 不同马赫数中性曲线对比 (a) CPG; (b) CNE
Figure 16. Comparison of neutral curves at different Mach numbers: (a) CPG; (b) CNE.
图 17 CNE工况不同马赫数N值包络对比
Figure 17. Comparison of N-value envelopes at different Mach numbers under CNE condition.
图 18 不同马赫数光滑和多孔壁增长率及相对变化率对比 (a) x/Lref = 400; (b) x/Lref = 600
Figure 18. Comparison of growth rates and relative change of smooth and porous walls at different Mach numbers: (a) x/Lref = 400; (b) x/Lref = 600.
图 19 不同马赫数下光滑与多孔壁的N值包络
Figure 19. N-value envelopes of smooth and porous walls at different Mach numbers.
表 1 不同马赫数对应来流参数
Table 1. Flow characteristics for various Mach numbers.
Ma T∞/K ρ∞/(kg·m–3) U∞/(m·s–1) Re/m–1 10 221.55 0.040085 2983.6 8.26×106 15 221.55 0.040085 4475.4 1.24×107 20 221.55 0.040085 5967.2 1.65×107 
下载: 导出CSV
表 3 不同马赫数下x/Lref = 900位置的N值相对变化率
Table 3. Relative change of N-values at x/Lref = 900 under different Mach numbers.
Ma (ΔN/Nmax, smooth) CPG (ΔN/Nmax, smooth) CNE 10 26.8% 18.2% 15 22.1% 19.8% 20 27.2% 15.5%
下载: 导出CSV
-
[1] 陈坚强, 涂国华, 张毅锋, 徐国亮, 袁先旭, 陈诚 2017 空气动力学报 35 311 Chen J Q, Tu G H, Zhang Y F, Xu G L, Yuan X X, Chen C 2017 Acta Aerodyn. Sin. 35 311 [2] Currie J G, Dickason A M 1988 Report of the Defense Science Board Task Force on the National Aerospace Plane (NASP) Report No. AD-A201 124 [3] Candler G V 2019 Annu. Rev. Fluid Mech 51 379 doi: 10.1146/annurev-fluid-010518-040258 [4] Bitter N P 2015 Ph. D. Dissertation (Pasadena: California Institute of Technology [5] Malik M R 1991 Phys. Fluids 3 803 doi: 10.1063/1.858012 [6] Stuckert G, Reed H L 1994 AIAA J. 32 1384 doi: 10.2514/3.12206 [7] Hudson M L, Chokani N, Candler G V 1997 AIAA J. 35 958 doi: 10.2514/2.204 [8] Franko K, Maccormack R, Lele S 2010 40th Fluid Dynamics Conference and Exhibit Chicago, June 28–July 1, 2010 p4601 [9] Chen X L, Wang L, Fu S 2021 Phys. Fluids 33 034132 doi: 10.1063/5.0045184 [10] 赵洲源, 陈贤亮, 王亮, 符松 2023 气体物理 8 35 doi: 10.19527/j.cnki.2096-1642.1023 Zhao Z Y, Chen X L, Wang L, Fu S 2023 Phys. Gases 8 35 doi: 10.19527/j.cnki.2096-1642.1023 [11] 李晨辉, 万兵兵, 涂国华, 胡伟波, 陈坚强, 蒋崇文 2024 空气动力学报 42 12 doi: 10.7638/kqdlxxb-2024.0002 Li C H, Wan B B, Tu G H, Hu W B, Chen J Q, Jiang C W 2024 Acta Aerodyn. Sin. 42 12 doi: 10.7638/kqdlxxb-2024.0002 [12] Fernando M M, Beyak E S, Pinna F, Reed H L, Brussels B 2019 Phys. Fluids 31 044101 doi: 10.1063/1.5084235 [13] Mcbride B J, Zehe M J, Sanford G 2002 NASA Glenn Coefficients for Calculating Thermodynamic Properties of Individual Species (National Aeronautics and Space Administration Glenn Research Center) Report No. NASA/TP-2002-211556 [14] Magin T, Degrez G 2005 J. Comput. Phys. 198 424 doi: 10.1016/j.jcp.2004.01.012 [15] Yos J M 1963 Transport Properties of Nitrogen, Hydrogen, Oxygen and Air to 30000 K (Research & Advanced Development Division Avco Corporation Technical Memorandum) Report No. AD-435 053 [16] Ramshaw J D 1993 J. Non-Equilibrium Thermodyn. 18 12 doi: 10.1515/jnet.1993.18.2.121 [17] Chapman S, Cowling T G 1952 Math. Gaz. 38 323 doi: 10.2307/3609795 [18] Blottner F G, Johnson M, Ellis M 1971 Chemically Reacting Viscous Flow Program for Multi-component Gas Mixtures Report No. SC-RR-70-754 [19] Brokaw R S 1965 J. Chem. Phys. 42 1140 doi: 10.1063/1.1696093 [20] Gupta R N, Yos J M, Thompson R A 1990 A Review of Reaction Rates and Thermodynamic and Transport Properties for the 11-species Air Model for Chemical and Thermal Nonequilibrium Calculations to 30000 K (National Aeronautics and Space Administration Langley Research Center) Report No. NASA-TM-101528 [21] 万兵兵, 韩宇峰, 樊宇, 罗纪生 2017 航空动力学报 32 188 doi: 10.13224/j.cnki.jasp.2017.01.025 Wan B B, Han Y F, Fan Y, Luo J S 2017 J. Aerosp. Power 32 188 doi: 10.13224/j.cnki.jasp.2017.01.025 [22] Park C, Jaffe R L, Partridge H 2001 J. Thermophys. Heat Transfer 15 76 doi: 10.2514/2.6582 [23] Park C 1985 AIAA 23rd Aerospace Sciences Meeting, Reno, Nevada, January 14–17, 1985 p85–0247 [24] PARK C 1993 J. Thermophys. Heat Transfer 7 385 doi: 10.2514/3.431 [25] Li C H, Wan B B, Chen J Q, Tu G H, Hu W B, Jiang C W 2024 Int. J. Heat Mass Transfer 233 126018 doi: 10.1016/j.ijheatmasstransfer.2024.126018 [26] Al-Jothery H K M, Albarody T M B, Yusoff P S M, Abdullah M A, Hussein A R 2020 IOP Conference Series: Materials Science and Engineering 863 012003 doi: 10.1088/1757-899X/863/1/012003 [27] Malmuth N, Fedorov A, Shalaev V, Cole J, Khokhlov A, Hites M, Williams D 1998 2nd AIAA Theoretical Fluid Mechanics Meeting, Albuquerque, New Mexico, June 15–18, 1998 p2695 [28] Fedorov A, Malmuth N, Rasheed A, Hornung H G 2001 AIAA J. 39 605 doi: 10.2514/2.1382 [29] Zhao R, Liu T, Wen C Y, Zhu J, Cheng L 2018 AIAA J. 56 2942 doi: 10.2514/1.J057272 [30] Wartemann V, Heinrich L, Sandham N D 2009 16th AIAA/DLR/DGLR International Space Planes and Hypersonic Systems and Technologies Conference, Bremen, Germany, October 19–22, 2009 AIAA 2009-7202 [31] Xu J K, Liu J X, Mughal S, Yu P X, Bai J Q 2020 Phys. Fluids 32 044105 doi: 10.1063/5.0001914 [32] Wang X Q, Zhong X L 2012 Phys. Fluids 24 034105 doi: 10.1063/1.3694808 [33] Rasheed A, Hornung H G, Fedorov A, Malmuth N D 2002 AIAA J. 40 481 doi: 10.2514/2.1671 [34] Lukashevich S V, Morozov S O, Shiplyuk A N 2016 J. Appl. Mech. Tech. Phys. 57 873 doi: 10.1134/S002189441605014X [35] 郭启龙, 涂国华, 陈坚强, 袁先旭, 万兵兵 2020 航空动力学报 35 135 doi: 10.13224/j.cnki.jasp.2020.01.016 Guo Q L, Tu G H, Chen J Q, Yuan X X, Wan B B 2020 J. Aerosp. Power 35 135 doi: 10.13224/j.cnki.jasp.2020.01.016 [36] 刘勇, 涂国华, 向星皓, 李晓虎, 郭启龙, 万兵兵 2022 物理学报 71 1947011 doi: 10.7498/aps.71.20220851 Liu Y, Tu G H, Xiang X H, Li X H, Guo Q L, Wan B B 2022 Acta Phys. Sin. 71 194701 doi: 10.7498/aps.71.20220851 [37] Gui Y T, Wang W Z, Zhao R, Zhao J Q, Wu J 2022 AIAA J. 60 4453 doi: 10.2514/1.J060930 [38] Liu X, Zhao R, Wen C Y, Yuan W 2024 Acta Mech. 235 1109 doi: 10.1007/s00707-023-03788-9 [39] Wang X W, Zhong X L 2013 51st AIAA Aerospace Sciences Meeting including the New Horizons Forum and Aerospace Exposition Grapevine, Texas, January 7–10, 2013 p827 [40] Wang X W 2018 AIAA Aerospace Sciences Meeting Kissimmee, Florida, January 8–12, 2018 p2088 [41] Ken C K U, Hao J, Zhao R, Wen C Y 2023 Aerosp. Sci. Technol. 141 108520 doi: 10.1016/j.ast.2023.108520 [42] Walter G V, Charles H K, Teichmann T 1966 Phys. Today 19 95 doi: 10.1063/1.3047788 [43] Bird R B, Stewart W E, Lightfoot E N 2002 Appl. Mech. Rev. 55 R1 doi: 10.1115/1.1424298 [44] Wilke C R 1950 J. Chem. Phys. 18 517 doi: 10.1063/1.1747673 [45] Wan B B, Su C H, Chen J Q 2020 AIAA J. 58 4047 doi: 10.2514/1.J058816 [46] Zhao R, Wen C Y, Tian X D, Long T H, Yuan W 2018 Int. J. Heat Mass Transfer 121 986 doi: 10.1016/j.ijheatmasstransfer.2018.01.054 [47] Brès G A, Inkman M, Colonius T, Fedorov A 2013 J. Fluid Mech 726 312 doi: 10.1017/jfm.2013.206 [48] Luedeke H, Sandham N D, Wartemann V 2012 AIAA J. 50 1281 doi: 10.2514/1.J051355 [49] 赵瑞, 张新昕, 魏昊功, 温志涌 2021 中国专利 CN110135062B [2021-10-29]] Zhao R, Zhang X X, Wei H G, Wen C Y 2021 China Patent CN110135062B [2021-10-29] [50] Kline H L, Chang C L, Li F 2018 Fluid Dynamics Conference Atlanta, Georgia, June 25–29, 2018 p3699 [51] Miró M Fernando, Pinna F, Beyak E S, Barbante P, Reed H L 2018 AIAA Aerospace Sciences Meeting Kissimmee, Florida, January 8–12, 2018 p1824 [52] 赵瑞, 严昊, 席柯, 温志涌 2020 航空科学技术 31 104 Zhao R, Yan H, Xi K, Wen C Y 2020 Aeronaut. Sci. Technol. 31 104 -
计量
- 文章访问数: 42
- HTML全文浏览数: 42
- PDF下载数: 0
- 施引文献: 0