-
量子传感是指利用量子系统、量子性质或量子现象对物理量进行高灵敏度测量, 在基础科学研究和实际应用领域均展现出巨大的潜力[1–8]. 近年来, 相互作用量子系统被视为开发精密传感技术的前沿平台[9–16], 涵盖了固态核自旋、玻色-爱因斯坦凝聚、氮-空位中心、里德伯原子和离子 等系统. 在这些相互作用系统中, 探针系统间的 相互作用作为一种关键的量子资源, 能够显著提升测量精度和其他传感性能指标, 如实现超越海 森伯极限的灵敏度[17–19]、增强对热噪声的鲁棒 性[13]、实现临界增强测量[16,20,21]以及抑制快速热 化[11,22,23]. 此外, 探针系统间的相互作用能够驱动动力学过程产生量子纠缠态, 这一过程对初始态是否纠缠并无依赖性. 因此, 通过调控探针系统间的相互作用来实现量子关联, 可显著降低实验上制备纠缠探针态的技术门槛[14,24].
然而, 当前基于相互作用的量子传感研究主要集中于单一物理量的测量[13–19,22,25–27], 忽略了许多现实条件下的应用. 事实上, 许多实际传感应用本质上是需要多物理量测量的, 例如在测量电场、磁场或引力场中, 获取不同方向的分量信息. 目前, 基于非相互作用系统的矢量场测量已在理论和实验上得到了广泛研究[28–37]. 这类传统传感器通常仅使用单一自旋种类, 在进动频率处形成一个单一共振峰[26,38,39], 因此只能测得磁场的大小, 而无法获得磁场的三个独立分量. 目前最常见的解决方案是引入已知的参考场, 将其与未知场进行矢量叠加, 从而间接估算未知场的三个分量[33–36]. 然而, 这种方法的测量精度严重依赖于外部线圈产生偏置场的校准精度. 此外, 引入外部参考场不可避免地会产生磁场干扰, 产生技术噪声, 从而限制了矢量场量子传感的极限精度[30,32]. 相比之下, 基于相互作用系统的量子传感与矢量场测量的结合具有显著优势. 我们的研究表明, 这种结合可以消除对外部参考场的依赖, 从而避免技术噪声和校准误差. 这一跨学科结合为发展应用物理和基础物理中的精密测量提供了新的可能性, 例如量子成像[40,41]、传感器网络[42]、导航[43–45]、矢量场检测[33–36,46], 以及对自旋-引力耦合和超轻暗物质轴子的搜索[47–49]. 尽管这些特性极具吸引力, 但迄今为止利用相互作用资源实现多物理量传感的实验仍然缺乏.
本文提出了一种基于强相互作用核自旋系统的矢量磁场测量方法, 在超低场核磁共振平台上成功实现了高精度矢量磁场测量. 当核自旋之间的相互作用强度显著大于其拉莫尔频率时, 强相互作用自旋能够同时对多维磁场的各个分量灵敏响应. 此外, 使用原子磁力计实现对核自旋信号的高灵敏非侵入式探测, 观察到核自旋之间的强相互作用可以将其量子相干时间延长至秒量级, 从而实现测量精度的提升. 通过实验验证, 证明了基于相互作用的矢量场测量的可行性, 成功实现对磁场各分量的精确测量, 测量精度达到10–11 T, 方向分辨率为0.2 rad, 这为超低场条件下的绝对磁场计量[50]提供了一种新的技术途径. 与传统的测量方法相比, 基于相互作用的量子传感器在多物理量方面展现出独特的优势. 该方法摆脱了传统技术中施加偏置场作为参考磁场的依赖[33–36], 从而有效避免了之前因参考场引入的校准误差和技术噪声. 更进一步, 将本文方法与现有实验技术相结合[44,51–53], 测量精度有望超越现有的传感器多个数量级. 此外, 本文工作可推广应用于其他相互作用系统, 开发出一类全新的多参数量子传感器[33–36,40,42,46–49,54].
-
本文以强相互作用核自旋系统为实验平台, 重点研究对未知磁场三个独立分量的高精度测量方法. 与现有的基于非相互作用自旋的研究[33–36,45,46]不同, 我们采用了一类至少包含两种不同核自旋的分子系统, 这些自旋通过标量自旋-自旋耦合相互作用. 当这些核自旋置于未知磁场
$ {\boldsymbol{B}}(\theta, \phi) $ 中时, 其动力学行为可由以下哈密顿量描述:其中
$ \gamma_j $ 表示第j个自旋的旋磁比(此处设定$ \hbar = 1 $ ),$ {\boldsymbol{I}}_j = (\hat{I}_{jx}, \hat{I}_{jy}, \hat{I}_{jz}) $ 为第j个自旋的自旋角动量算符,$ {\boldsymbol{I}}_i {\cdot} {\boldsymbol{I}}_j $ 表示强度为$ J_{ij} $ 的标量自旋-自旋耦合. 如图1(a)所示, 未知磁场$ {\boldsymbol{B}}(\theta, \phi) = (B \sin \theta \cos \phi, B \sin \theta \sin \phi, B \cos \theta) $ 可通过极角θ、方位角ϕ和强度B三个参数进行完整描述, 这些参数正是本实验测量的目标物理量.本文提出的基于相互作用的量子传感方案包括三个关键阶段: 探针态制备、基于强相互作用自旋进行编码、以及探针态的读出, 如图1(b)所示. 在探针态制备阶段, 核自旋首先在永磁体中被极化, 随后转移至编码区域. 在转移过程中施加一个引导场, 转移结束后引导场在10 μs内关闭, 自旋系统仍保持在高场本征态. 在高温近似下, 核自旋的初始探针态为[55]
其中
$ \varepsilon_j = \gamma_jB_{\mathrm{p}}/k_ {\rm{B}} T \sim 10^{-6} $ ,$ k_ {\rm{B}} $ 是玻尔兹曼常数, T是温度,$ B_{\mathrm{p}} $ 为极化磁场;$ {\hat{\boldsymbol{k}}}_{\mathrm{g}} $ 是沿引导场方向的单位矢量, 例如,$ {\hat{\boldsymbol{k}}}_{\mathrm{g }}= (0, 0, 1) $ 对应于z方向的引导场. 因此, 初始状态可以通过引导磁场方向$ {\hat{\boldsymbol{k}}}_{\mathrm{g }}$ 进行控制. 在编码阶段, 利用强相互作用自旋的量子动力学来编码未知参数:其中,
$ \rho(\theta, \phi, B, t) $ 是核自旋随时间变化的密度 矩阵. 随后, 原子磁力计作为探测器, 测量磁化强度随时间的演化$ {\rm{Tr}} [\rho(\theta, \phi, B, t) {\hat{\boldsymbol{O}}}_z] $ [55–58]. 其中,$ {\hat{\boldsymbol{O}}}_z = \displaystyle\sum\nolimits_j \gamma_j {\hat{I}}_{jz} $ 表示z方向磁化强度. 测量的时域信号可以通过傅里叶变换得到频谱. 由此, 哈密顿量$ {\cal{H}}(\theta, \phi, B) $ 中的磁场信息$ {\boldsymbol{B}}(\theta, \phi) $ 可以被编码到相互作用自旋的频谱特征中, 每条谱线对应于哈密顿量$ {\cal{H}}(\theta, \phi, B) $ 中相关本征态$ | \varPsi_i \rangle $ 与$ | \varPsi_j \rangle $ 之间的跃迁, 其谱线强度与$ \langle \varPsi_i |\rho_0 |\varPsi_j \rangle \langle \varPsi_j |{\hat{\boldsymbol{O}}}_z | \varPsi_i \rangle $ 的乘积成正比(具体形式参见(10)式和(11)式). -
磁场强度B可直接通过强相互作用自旋系统的谱线位置确定. 为阐明这一测量机制, 下面以具有星型拓扑结构的分子为例进行说明: 该结构由一个中心核自旋与
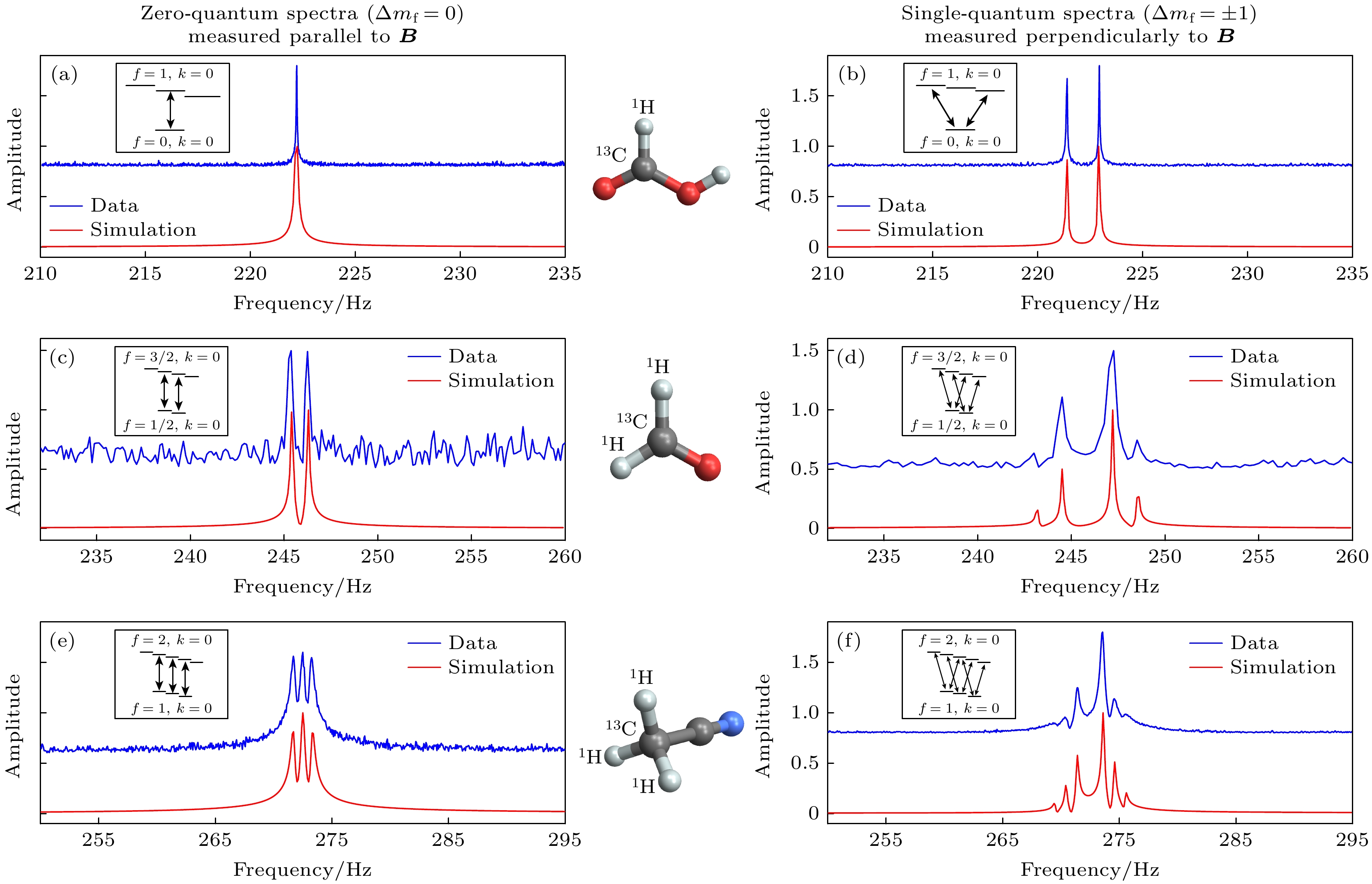
$ n-1 $ 个等效自旋相互耦合而成, 例如13CHn分子. 当未知磁场强度远小于标量自旋-自旋耦合(即满足$ \gamma_{\mathrm{H}} B, \gamma_{\mathrm{C}} B \ll |J| $ )时, 13CHn分子中的核自旋之间会形成强耦合. 在这种情况下, 好量子数是总自旋角动量$ F = F_{\mathrm{C}}+F_{\mathrm{H }}$ 及其对应的磁量子数$ m_{\mathrm{F}} $ , 其中$ m_{\mathrm{F}} $ 的取值范围为$ -F\leqslant m_{\mathrm{F}} \leqslant F $ . 这里,$ F_{\mathrm{C}} = \pm 1/2 $ 为13C的总自旋角动量,$ F_{\mathrm{H}} = n/2-k $ 表示13H的总自旋角动量. 对于偶数n,$ k = 0, 1, \cdots, n/2 $ ; 对于奇数n,$ k = 0, 1, \cdots, (n- 1)/2 $ . 13CHn分子的本征态表示为$ |{Fm_{\mathrm{F}};k}\rangle $ [59,60], 为零场哈密顿量$ {\cal{H}} = \displaystyle\sum\nolimits_{j>i}^n {{ J_{ij}}} {\boldsymbol{I}}_i \cdot {\boldsymbol{I}}_j $ 的本征态. 图2展示了13CH, 13CH2, 13CH3的能级结构.在实验中, 当测量方向平行于未知磁场时, 量子跃迁遵循以下选择定则(称为零量子跃迁):
$ \Delta F = 0, \pm 1 $ ,$ \Delta m_{\mathrm{F}} = 0 $ . 由于在13CHn中质子是等价的, 还有一个额外的选择定则$ \Delta k = 0 $ [59]. 因此, 实验上可观测到以$ {1}/{2}J(1+n-2 k) $ 为中心的$ n-2 k $ 个共振谱线, 其频率为其中
$ \nu_{F, m_{\mathrm{F}};k}^{F', m'_{\mathrm{f}};k'} $ 表示本征态$ |{Fm_{\mathrm{F}};k}\rangle $ 和$ |{F'm'_{\mathrm{f}};k'}\rangle $ 之间的跃迁频率. 相邻的零量子跃迁频率为当测量方向垂直于未知磁场时, 允许跃迁的选择定则为(称为零量子跃迁):
$ \Delta F = 0, \pm 1 $ ,$ \Delta m_{\mathrm{F}} = l \pm 1 $ (即单量子跃迁), 且$ \Delta k = 0 $ . 因此, 实验上可观测到以$ J(1+n-2 k)/2 $ 为中心的$ n-2k $ 个共振谱线, 其频率为离中心频率最近的两条跃迁线相较于其他的跃迁线具有最高信噪比, 其频率之差为
以
$ n = 1 $ 且$ k = 0 $ 的甲酸分子为例, 当测量方向垂直于外部磁场时, 甲酸在中心频率附近产生两条共振峰, 并且其频率之差为$ \varDelta = (\gamma_{\mathrm{C}}+\gamma_{\mathrm{H}})B $ , 磁场强度即可通过$ B = \varDelta/(\gamma_{\mathrm{C}}+\gamma_{\mathrm{H}}) $ 来确定. 磁场测量的理论精度极限可由Cramr-Rao lower Bound (CRLB)理论来确定, 其表达式为这里
$ g = \gamma_{\mathrm{C}}+\gamma_{\mathrm{H}} $ , SNR代表谱线的信噪比,$ f_{\mathrm{BW}} $ 为测力计带宽, C为衰减因子[61]. 根据该理论模型, 较长的相干时间能够有效降低频谱的线宽, 从而提升信噪比(SNR), 最终实现更高精度的磁场测量. 需要指出的是, 这些讨论仅考虑了13CHn分子的一阶塞曼效应. 高阶塞曼效应在测量磁场强度时会引入系统误差, 参见文献[47,60]. -
磁场方向可以通过强相互作用自旋系统的谱线振幅分布确定. 磁场B的方向用极角θ和方位角ϕ描述, 如图1(a)所示. 在未知磁场B的作用下, 每个分子内自旋量子态的演化产生振荡的磁化矢量, 由87Rb原子磁力计检测. 实验中的可观测量为z方向的总磁化强度, 表示为
因此, 以频率
$ \nu_{F, m_{\mathrm{F}};k}^{F', m_{\mathrm{F}}';k'} $ 演化的信号分量可以写为其中, 振幅
$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'}(\rho_0, \theta, \phi) $ 和相位Φ由下式定义:其中自旋算符
$ {\hat{\boldsymbol{O}}}_l \equiv \displaystyle\sum\nolimits_j \gamma_j \hat{I}_{jl} $ ($ l = x, y, z $ ),$ {\mathrm{e}}^{-t/\tau_{ {\rm{coh}}}} $ 表示退相干效应的影响. 振幅$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'}(\rho_0, \theta, \phi) $ 可以通过观测到的NMR谱确定.为了得到振幅
$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'}(\rho_0, \theta, \phi) $ 与未知参数θ和ϕ之间的明确关系, 引入一个正交坐标系, 该坐标系仅由θ和ϕ定义. 在这样的坐标系中(见图1(a)的插图), 量子轴($ {\boldsymbol{z}}' $ )沿磁场方向, 即因此, 实验室坐标系中的自旋算符可以通过以下公式转换:
其中
$ {\hat{\boldsymbol{O}}} = ({\hat{\boldsymbol{O}}}_x, {\hat{\boldsymbol{O}}}_y, {\hat{\boldsymbol{O}}}_z)^{{\mathrm{T}}} $ ,$ {\hat{\boldsymbol{O}}}' = ({\hat{\boldsymbol{O}}}'_{x'}, {\hat{\boldsymbol{O}}}'_{y'}, {\hat{\boldsymbol{O}}}'_{z'})^{{\mathrm{T}}} $ , 而$ {\cal{P}}(\theta, \phi) $ 是一个$ 3\times3 $ 的变换矩阵:进一步, 实验室坐标系中元素
$ \langle {F'm_{\mathrm{F}}';k}| {\hat{\boldsymbol{O}}}_l\times |{Fm_{\mathrm{F}};k}\rangle $ 可以在新定义的坐标系中表示为此外,
$ \langle {F'm_{\mathrm{F}}';k}| {\hat{\boldsymbol{O}}}'|{Fm_{\mathrm{F}};k}\rangle $ 与磁场的方向($ \theta, \phi $ )无关, 因此在超低场条件下不需要知道磁场B的任何信息就可进行计算. 关于计算$ \langle {F'm_{\mathrm{F}}';k}| {\hat{\boldsymbol{O}}}' |{Fm_{\mathrm{F}};k}\rangle $ 的详细方法可以参见文献[62]. 例如, 对于典型的13CH分子, 可以得到基于(14)式和(15)式,
$ \langle {F'm_{\mathrm{F}}';k}| {\hat{\boldsymbol{O}}}_z|{Fm_{\mathrm{F}};k}\rangle $ 可以仅用参数θ和ϕ表示, 即其中单位矢量
$ \hat{{\boldsymbol{z}}} = (0, 0, 1) $ . 对于密度矩阵${\boldsymbol{ \rho}}_0 $ ,$ \langle Fm_{\mathrm{F}}; k|{\boldsymbol{\rho}}_0 |{F'm_{\mathrm{F}}';k'}\rangle $ 有类似的结果:根据(11)式和(15)—(17)式, 振幅
$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'} (\rho_0, \theta, \phi) $ 最终可以用两个未知参数θ和ϕ表示, 即可以观察到,
$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'}(\rho_0, \theta, \phi) $ 可以分为两部分: 一部分与θ, ϕ相关, 即$ {\cal{P}}(\theta, \phi) $ ; 另一部分与θ, ϕ无关, 例如$ \langle {F'm_{\mathrm{F}}';k}| {\hat{\boldsymbol{O}}}'|{Fm_{\mathrm{F}};k}\rangle $ . 这一结果揭示了多个未知参数与$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'}(\rho_0, \theta, \phi) $ 之间的关系, 而振幅$ {\cal{R}}_{Fm_{\mathrm{F}};k}^ {F'm_{\mathrm{F}}';k'}(\rho_0, \theta, \phi) $ 可以通过NMR谱实验直接测得. -
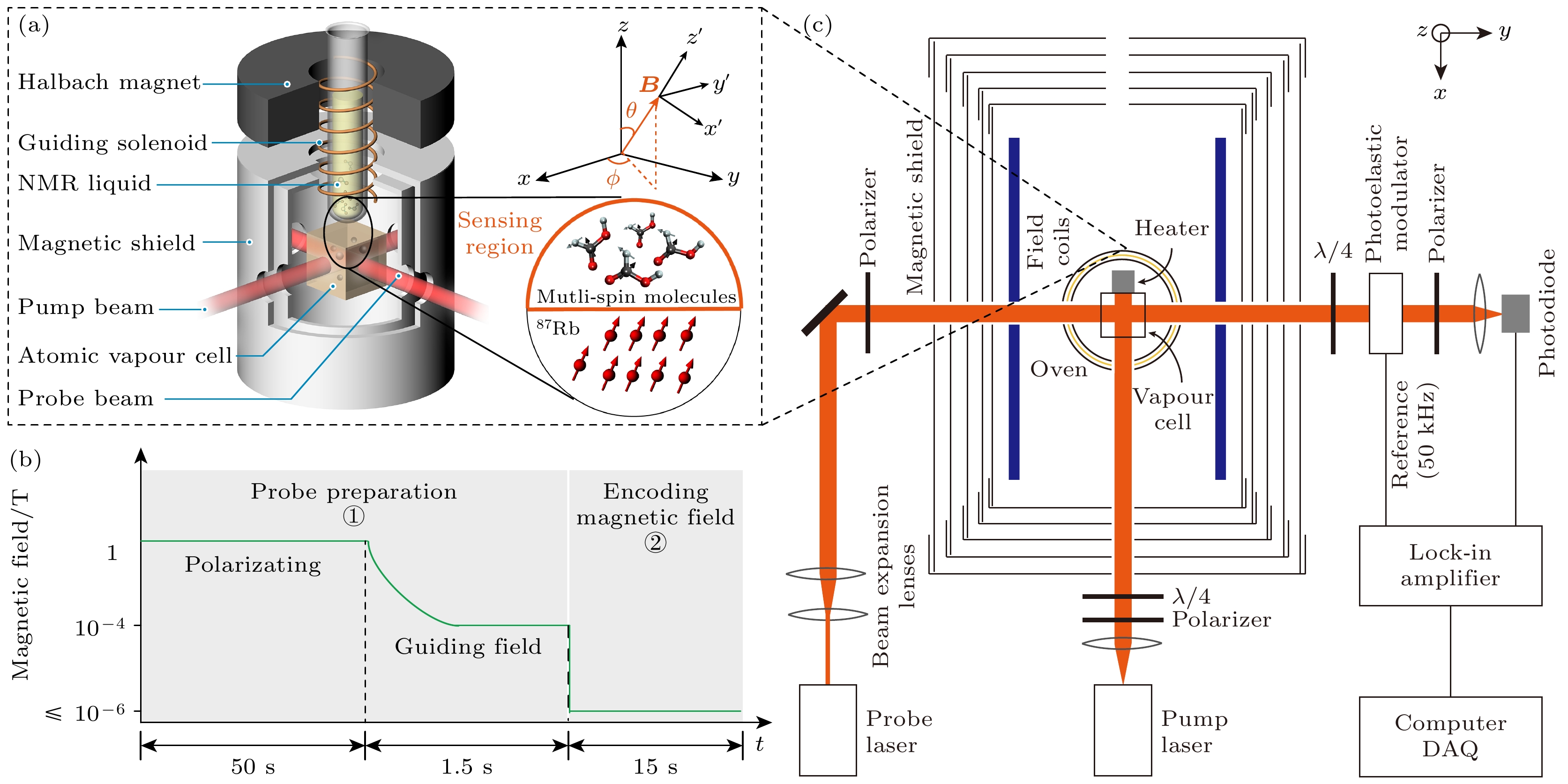
基于相互作用的量子传感实验装置如图1(a)所示. 在实验开始前需对样品进行去氧处理, 因为样品中的氧气分子具有顺磁性, 含有未成对电子自旋, 会在热运动过程中引入强烈的局域磁场波动, 从而降低自旋相干时间, 影响磁场测量的精度[63]. 去氧的具体操作步骤如下: 取约300 μL的NMR样品, 采用冷冻-抽气-解冻循环法进行去氧处理; 重复5次该循环以确保样品中溶解氧的完全去除, 最后使用火焰密封技术将去氧后的样品真空封装于标准的5mm NMR试管中. 矢量磁场测量实验主要包括NMR样品的极化、编码与读出3个过程. 首先使用
$ B_{\mathrm{p}} \approx 1.3\; {\rm{T}} $ 的Halbach磁体对去氧后的NMR样品进行热极化, 极化时间持续约50 s, 样品最终极化度约$ 10^{-6} $ . 极化后的样品通过气动的方式输送至距离极化区域30 cm的编码和读出区域, 且该区域被5层坡莫合金磁屏蔽包围. 在气动输送过程中, 使用一个引导螺线管和一套相互正交的亥姆霍兹线圈来生成沿某一轴(x, y或z)的引导场, 该引导场的大小$ B_{\mathrm{g}}\approx 10^{-4}\; {\rm{T}} $ , 满足$ B_{\mathrm{g}} \gg J /(\gamma_{\mathrm{H}}-\gamma_{\mathrm{C}}) $ , 以实现极化核自旋向编码区域的绝热转移. 当样品输送到编码区后, 引导磁场在10 μs内被迅速关闭, 初始自旋态制备为$ \rho_0 $ , 如(2)式所示. 随后, 样品中的核自旋在未知磁场的作用下演化, 其振荡磁化信号通过87Rb原子磁力计读出[55–57,59]. 原子磁力计的核心为一个包含足量87Rb同位素的原子气体室, 位于样品下方1 mm处, 以最大程度读出NMR样品信号. 该气体室通过纯铜双绞加热丝加热至180 ℃, 以产生足量的碱金属Rb原子蒸气(约$ 10^{14} $ cm–3). 如图1(c)所示, 使用一束与87Rb原子$ {\rm{D}}1 $ 线共振的5 mW圆偏振激光沿x方向对Rb原子进行极化, 并使用一束沿y方向传播的与Rb原子$ {\rm{D}}2 $ 线失谐100 GHz的3 mW线偏振激光作为探测光, 利用磁致旋光效应读出Rb原子y方向的自旋分量大小, 以测定出z方向磁场大小. 为抑制低频噪声的影响, 使用光弹调制器调制探测光的偏振(见图1(b)), 并通过锁相放大器解调探测信号. 最终, 87Rb原子磁力计沿z轴的灵敏度优化至约$ 20\; {\rm{fT}} \cdot {\rm{Hz}}^{-1/2} $ . -
实验中, 测量强相互作用核自旋系统在磁场B作用下的跃迁谱线至关重要, 这些谱线直接编码了外磁场的信息. 我们观察到, 核自旋间的强相互作用可延长量子相干时间, 最长可达十几秒, 从而提高测量精度. 本文的实验中采用了3种不同的液体样品: 甲酸(H13COOH)、甲醛(13CH2O)和乙腈(13CH3CN), 这些样品均来自Sigma-Aldrich. 甲酸的核自旋相干时间为
$ \tau_{ {\rm{coh}}}\approx 10.4 $ s, 标量自旋-自旋耦合强度为$ J\approx 222.2 $ Hz, 甲醛的$ \tau_{ {\rm{coh}}}\approx 0.8 $ s,$ J\approx 163.9 $ Hz, 乙腈的$ \tau_{ {\rm{coh}}}\approx 4.7 $ s,$ J\approx 136.25 $ Hz.测量了13CHn分子的不同量子跃迁. 当测量方向与未知磁场B平行时(即
$ \theta = 0 $ ), 允许跃迁的选择定则是$ \varDelta = 0, \pm 1 $ ,$ \Delta m_{\mathrm{F}} = 0 $ . 例如, 甲酸会在222.2 Hz处产生一个单一的共振峰(图2(a)). 另一方面, 当沿着与磁场B垂直的轴测量时(即$ \theta = \pi/2 $ ), 允许跃迁的选择定则是$ \varDelta = 0, \pm 1 $ ,$ \Delta m_{\mathrm{F}} = \pm 1 $ . 这种情况下, 甲酸在222.2 Hz处产生两条共振峰(图2(b)), 其之间的分裂为$ (\gamma_{\mathrm{H}}+\gamma_{\mathrm{C}})B $ . 这里, 碳自旋的旋磁比为$ \gamma_{\mathrm{C}}\approx 10.7077 $ MHz/T, 氢自旋的旋磁比为$ \gamma_{\mathrm{H}} \approx 42.5775 $ MHz/T. 其他13CHn分子的谱线表现出类似的分裂模式, 如图2(c)—(f)所示. 详细的理论分析在2.2节的(4)—(7)式. 值得注意的是, 图2(e)和图2(f)展示的 14N-13C-乙腈分子, 由于14N核的四极弛豫效应, 表现出一种“自解偶”现象[64], 因此与甲基中的13C和 1H并无可观测的J耦合相互作用. 此外, 当测量方向既不平行也不垂直于磁场时, 零量子跃迁与单量子跃迁可以同时发生. 这意味着, 磁场的方向信息可以通过分析测得的13CHn分子的谱线来提取. 类似的现象在多电子原子的光谱学中已有研究[65,66], 而我们的工作在NMR谱学中实现了实验验证. -
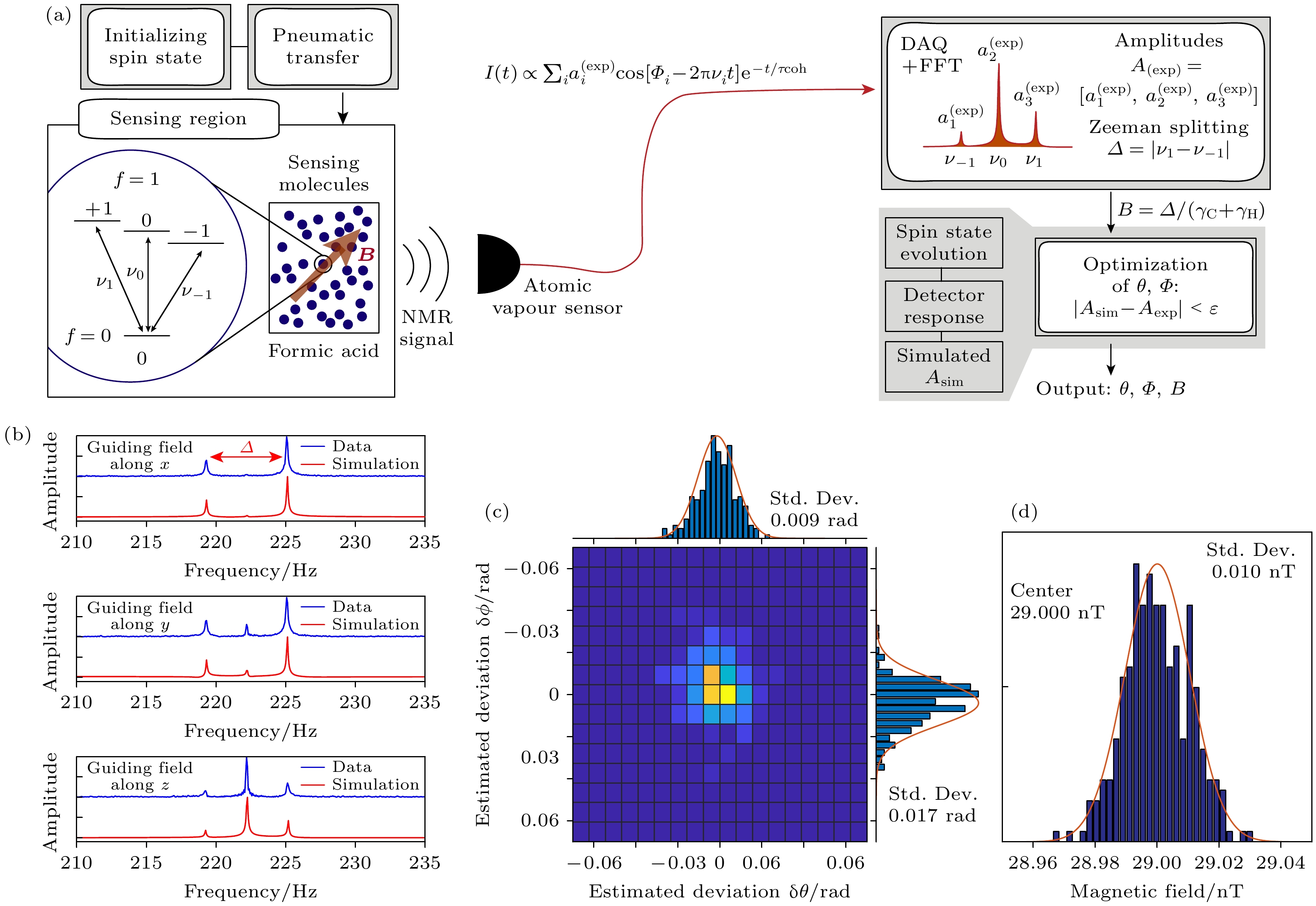
为了验证基于强相互作用核自旋的矢量磁场测量原理, 选择甲酸分子(即一个两自旋相互作用系统)作为实验体系. 如图3(a)所示, 在单次测量中, 频率为
$ \nu_{0} $ 的零量子谱线和频率为$ \nu_{\pm 1} $ 的单量子谱线的振幅被同时记录, 通过以下归化形式表示:磁场引起的塞曼分裂为
因此, 可以通过
$ B = \varDelta/(\gamma_{{\mathrm{C}}}+\gamma_{{\mathrm{H}}}) $ 提前确定测量的磁场强度(任意13CHn分子的分裂Δ在2.2节的(4)—(7)式中展示). 此外, 使用2.3节中的模 型来计算NMR谱线的振幅, 当θ和ϕ给定时, 这些振幅标记为$ {\boldsymbol{A}}_{ {\rm{sim}}}(\theta, \phi) = [ {{a}}_1^{( {\rm{sim}})}(\nu_{-1}),{{a}}_2^{( {\rm{sim}})}(\nu_0), {{a}}_3^{( {\rm{sim}})}(\nu_1)] $ . 反过来, 通过最小化范数$ |{\boldsymbol{A}}_{ {\rm{sim}}}(\theta, \phi)- {\boldsymbol{A}}_{{\rm{exp}}}| $ 可以获得参数θ和ϕ. 然而在满足某些对称条件时, 多对$ (\theta, \phi) $ 可能会导致相同的谱线. 为了消除这种歧义, 我们通过依次控制引导场沿x, y和z方向来测量核自旋谱和三组$ {\boldsymbol{A}}_{{\rm{exp}}} $ [55]. 相应的NMR谱线如图3(b)所示. 通过找到同时与三个初始状态下测量的$ {\boldsymbol{A}}_{{\rm{exp}}} $ 最佳匹配的模拟$ {\boldsymbol{A}}_{ {\rm{sim}}}(\theta, \phi) $ , 可以明确确定θ和ϕ. 最终确定的磁场为$ \theta \approx 1.289 $ rad,$ \phi \approx 0.047 $ rad,$ B\approx 1.0788 \times 10^{-7} $ T. 模拟谱线(红线)与实验谱线高度符合.为了评估本文方法的测量精度, 首先模拟了 频谱振幅变化对θ和ϕ测量偏差的影响. 假设谱 振幅变化量
$ \{ {\text{δ}}{{a}}_1^{( {\rm{exp}})}, {\text{δ}} {{a}}_2^{( {\rm{exp}})}, {\text{δ}} {{a}}_3^{( {\rm{exp}})}\} $ 服从高斯噪声$ \sim {\cal{N}}(0, \sigma ^2) $ , 主要来源于实验中探测光束的光子散粒噪声. 图3(c)展示了在$ \sigma = 0.01 $ (对应于当前 实验的信噪比100)下θ和ϕ的联合统计分布. θ和ϕ值的不确定性(标准差)分别估计为$ \sigma_{\theta}\approx 0.009 $ rad和$ \sigma_{\phi}\approx0.017 $ rad, 如图3(c)直方图所示. 通过提高核自旋的初始极化和$ \text{NMR} $ 探测灵敏度, 可以进一步减小σ, 从而实现更高的磁场方向分辨率. 接下来, 通过重复300次实验测量来量化磁场强度的测量精度. 如图3(d)所示, 从直方图轮廓拟合, 提取出的频率Δ的不确定度约为$ 0.3\; \text{mHz} $ , 相应的磁场强度的统计标准差为$ 10^{-11}\; {\rm{T}} $ . -
尽管现有的多种量子传感器已展示了测量三维磁场的能力[33–37,45,46,67], 但他们主要是基于自旋进动的非相互作用探针系统, 本质上仍属于标量传感器. 在这些传感器中, 获取磁场方向信息需要额外引入外部偏置场或调制场[33–36], 其精度受到外部施加场校准误差的限制. 例如, 最常用的用于校准场线圈参数的磁力计是磁通门磁力计, 其精度仅在
$ 10^{-9}\; {\rm{T}} $ 量级. 标量原子磁力计也可以用于校准场线圈, 其误差为$ 10^{-10} $ —$ 10^{-9}\; {\rm{T}} $ [68]. 此外, 外部施加的偏置场本身会引入特定的技术磁场噪声, 如$ 1/f $ 噪声和热漂移, 这些通常在$ 10^{-11}\; {\rm{T}} $ 量级. 这些校准误差和技术噪声已成为基于非相互作用自旋系统传感器的主要性能瓶颈, 阻碍了其达到量子力学允许的极限精度. 与现有技术不同, 本文的研究利用强自旋相互作用作为量子传感的参考, 突破了传统矢量传感器的性能限制. 随着进一步的优化, 该方法有望将精度提高到现有传感器所能达到的五个数量级以上. 本研究为超低场条件下的绝对磁场计量[50]开辟了新途径.通过多种实验上可行的技术手段, 有望进一步提升测量精度. 首先, 原子磁力计的读出灵敏度可提高至少一个数量级. 例如, 最近在文献[56]中展示的磁梯度计应用于检测核自旋信号, 可将测量精度提高约10倍. 其次, 提高强相互作用自旋系统的核自旋极化度是最具潜力的改进方向之一. 目前实验中使用的热平衡态自旋极化度较低(约
$ 10^{-6} $ ). 而通过仲氢诱导极化(PHIP)[51,52,69]、动态核极化(DNP)[53]和光泵浦[44]等技术可制备出极化度接近1的超极化态, 使测量精度提升至少5个数量级. 将PHIP技术应用于超低场核磁共振已被证明能大幅提高自旋极化度, 这意味着实现基于PHIP的量子传感器具有极大的发展潜力, 其理论磁场测量精度可达$ 10^{-16} $ T. 结合最近在超低场NMR[57–59,70]中量子控制技术的发展[55,71], 可以在每个分子中创建核自旋的NOON态, 从而显著增强测量灵敏度[72].尽管本方案是在强相互作用核自旋系统中实现的, 但其核心原理同样适用于其他强相互作用自旋系统, 为新型量子传感器的设计提供了新的思路. 未来可在理论和实验层面对基于相互作用的量子传感展开更深入的研究, 特别是在涉及电子-核[73–75]或电子-电子[76,77]相互作用的自旋系统中, 进一步拓展其在光谱学、磁力测量、成像、导航以及生物磁感应机制等领域的应用潜力. 例如, 当前的技术可以应用于研究电子-电子自旋系统对磁场方向依赖性, 如磁性蛋白质中的自由基对, 这与长期未解的生物磁感应机制密切相关[76,77]. 因此, 本文提出的基于相互作用的量子传感有望为研究开辟一个充满希望的新领域.
基于强相互作用核自旋系统的量子传感
Quantum sensing based on strongly interacting nuclear spin systems
-
摘要: 相互作用量子系统在精密测量领域正受到广泛的关注, 尤其是量子关联态的实现以及相互作用系统的动力学研究, 为量子资源提供了全新的研究方向, 推动了基于相互作用系统的传感技术的深入探索. 然而, 现有研究主要局限于单一物理量的测量, 如何利用相互作用系统实现多物理量的精密测量仍亟待实验验证. 本研究基于超低场条件下强相互作用核自旋系统, 并结合高灵敏的原子磁力计实现信号读出, 成功实现了三维矢量磁场的精密测量, 测量精度达到10–11 T, 方向分辨率高达0.2 rad. 有效克服了传统方法中因外部参考场引入的校准误差和技术噪声的限制. 通过实验上的优化, 基于相互作用的传感器在测量精度上实现了5个数量级的提升, 为开发超高精度的新型量子传感器开辟了全新的技术路径.Abstract: Quantum sensing utilizes the quantum resources of well-controlled quantum systems to measure small signals with high sensitivity, and has great potential in both fundamental science and concrete applications. Interacting quantum systems have attracted increasing interest in the field of precise measurements, owing to their potential to generate quantum-correlated states and exhibit rich many-body dynamics. These features provide a novel avenue for exploiting quantum resources in sensing applications. Although previous studies have shown that using such systems can improve sensitivity, they mainly focused on measuring individual physical quantities. In experiment, the challenge of using interacting quantum systems to achieve high-precision measurements of multiple physical parameters simultaneously has not been explored to a large extent. In this study, we demonstrate a first realisation of interaction-based multiparameter sensing by using strongly interacting nuclear spins under ultra-low magnetic field conditions. We find that, as the interaction strength among nuclear spins becomes significantly larger than their Larmor frequencies, a different regime emerges where the strongly interacting spins can be simultaneously sensitive to all components of a multidimensional field, such as a three-dimensional magnetic field. Moreover, we observe that the strong interactions between nuclear spins can increase their quantum coherence times to as long as several seconds, thereby improving measurement precision. Our sensor successfully achieves precision measurement of three-dimensional vector magnetic fields with a field sensitivity reaching the order of 10–11 T and an angular resolution as high as 0.2 rad. Importantly, this approach eliminates the need for external reference fields, thereby avoiding calibration errors and technical noise commonly encountered in traditional magnetometry. Experimentally optimized protocol further enhances the sensitivity of the interacting spin-based sensor by up to five orders of magnitude compared with non-interacting or classical schemes. These results demonstrate the enormous potential of interacting spin systems as a powerful platform for high-precision multi-parameter quantum sensing. The techniques developed here pave the way for a new generation of quantum sensors that use intrinsic spin interactions to exceed the traditional sensitivity limits, presenting a promising route toward ultra-sensitive, calibration-free magnetometry in complex environments.
-
Key words:
- nuclear magnetic resonance /
- quantum sensing /
- quantum metrology /
- nuclear spin interactions .
-

-
图 1 基于相互作用系统的量子传感实验示意图 (a)实验装置示意图; (b)多参数传感的基本过程, 包括探针态制备、未知磁场编码以及探针态的读出; (c) 87Rb原子磁力计示意图
Figure 1. Experimental schematic of interaction-based quantum sensing: (a) Diagram of the experimental setup; (b) basic procedure of quantum sensing, including probe state preparation, encoding unknown magnetic field, and probe readout; (c) diagram of the 87Rb atomic magnetometer.
图 2 在不同方向磁场下测量的13CHn分子谱学 (a), (b) 13C-甲酸; (c), (d) 13C-甲醛; (e), (f) 13C-乙腈. 分裂模式与插图中显示的跃迁高度匹配
Figure 2. Spectra of 13CHn molecules measured at various orientations of the magnetic field: (a), (b) 13C-Formic aci; (c), (d) 13C-formaldehyde; (e), (f) 13C-acetonitrile. The splitting patterns match well the transitions shown in the inset.
图 3 使用甲酸分子进行磁场测量 (a)测量矢量磁场的实验过程; (b)重构矢量磁场的实例; (c)当谱振幅受高斯噪声
$ \sim {\cal{N}}(0, \sigma^2) $ 影响时, θ和ϕ的测量精度; (d)进行300次重复测量磁场强度的直方图Figure 3. Magnetic field measurement with formic acid molecules: (a) The procedure of determining a magnetic field vector; (b) as one example of reconstructing the magnetic field vector; (c) measured precision of θ, ϕ when spectral amplitude suffers from Gaussian noise
$ \sim {\cal{N}}(0, \sigma ^2) $ ; (d) histograms of magnetic field strength obtained from 300 repeated measurements. -
[1] Giovannetti V, Lloyd S, Maccone L 2011 Nat. Photonics 5 222 doi: 10.1038/nphoton.2011.35 [2] Degen C L, Reinhard F, Cappellaro P 2017 Rev. Mod. Phys. 89 035002 doi: 10.1103/RevModPhys.89.035002 [3] Pezze L, Smerzi A, Oberthaler M K, Schmied R, Treutlein P 2018 Rev. Mod. Phys. 90 035005 doi: 10.1103/RevModPhys.90.035005 [4] Braun D, Adesso G, Benatti F, Floreanini R, Marzolino U, Mitchell M W, Pirandola S 2018 Rev. Mod. Phys. 90 035006 doi: 10.1103/RevModPhys.90.035006 [5] Aasi J, Abadie J, Abbott B, et al. 2013 Nat. Photonics 7 613 doi: 10.1038/nphoton.2013.177 [6] Budker D, Romalis M 2007 Nat. Phys. 3 227 doi: 10.1038/nphys566 [7] Safronova M, Budker D, DeMille D, Kimball D F J, Derevianko A, Clark C W 2018 Rev. Mod. Phys. 90 025008 doi: 10.1103/RevModPhys.90.025008 [8] 彭世杰, 刘颖, 马文超, 石发展, 杜江峰 2018 物理学报 67 167601 doi: 10.7498/aps.67.20181084 Peng S J, Liu Y, Ma W C, Shi F Z, Du J F 2018 Acta Phys. Sin. 67 167601 doi: 10.7498/aps.67.20181084 [9] Álvarez G A, Suter D, Kaiser R 2015 Science 349 846 doi: 10.1126/science.1261160 [10] Lucchesi L, Chiofalo M L 2019 Phys. Rev. Lett. 123 060406 doi: 10.1103/PhysRevLett.123.060406 [11] Kong J, Jiménez-Martínez R, Troullinou C, Lucivero V G, Tóth G, Mitchell M W 2020 Nat. Commun. 11 1 doi: 10.1038/s41467-019-13993-7 [12] Peyronel T, Firstenberg O, Liang Q Y, Hofferberth S, Gorshkov A V, Pohl T, Lukin M D, Vuletić V 2012 Nature 488 57 doi: 10.1038/nature11361 [13] Dooley S, Hanks M, Nakayama S, Munro W J, Nemoto K 2018 NPJ Quant. Inf. 4 1 doi: 10.1038/s41534-017-0051-1 [14] Nolan S P, Szigeti S S, Haine S A 2017 Phys. Rev. Lett. 119 193601 doi: 10.1103/PhysRevLett.119.193601 [15] Zhou H, Choi J, Choi S, et al. 2020 Phys. Rev. X 10 031003 [16] Frérot I, Roscilde T 2018 Phys. Rev. Lett. 121 020402 doi: 10.1103/PhysRevLett.121.020402 [17] Roy S, Braunstein S L 2008 Phys. Rev. Lett. 100 220501 doi: 10.1103/PhysRevLett.100.220501 [18] Napolitano M, Koschorreck M, Dubost B, Behbood N, Sewell R, Mitchell M W 2011 Nature 471 486 doi: 10.1038/nature09778 [19] Boixo S, Flammia S T, Caves C M, Geremia J M 2007 Phys. Rev. Lett. 98 090401 doi: 10.1103/PhysRevLett.98.090401 [20] Chu Y, Zhang S, Yu B, Cai J 2021 Phys. Rev. Lett. 126 010502 doi: 10.1103/PhysRevLett.126.010502 [21] Rams M M, Sierant P, Dutta O, Horodecki P, Zakrzewski J 2018 Phys. Rev. X 8 021022 [22] Rovny J, Blum R L, Barrett S E 2018 Phys. Rev. Lett. 120 180603 doi: 10.1103/PhysRevLett.120.180603 [23] Kominis I, Kornack T, Allred J, Romalis M V 2003 Nature 422 596 doi: 10.1038/nature01484 [24] Boixo S, Datta A, Davis M J, Flammia S T, Shaji A, Caves C M 2008 Phys. Rev. Lett. 101 040403 doi: 10.1103/PhysRevLett.101.040403 [25] 李辉, 江敏, 朱振南, 徐文杰, 徐翔, 彭新华 2019 物理学报 68 160701 doi: 10.7498/aps.68.20190868 Li H, Jiang M, Zhu Z N, Xu W J, Xu M X, Peng X H 2019 Acta Phys. Sin. 68 160701 doi: 10.7498/aps.68.20190868 [26] 张语珊, 许廷发 2016 地球物理学进展 31 2346 doi: 10.6038/pg20160564 Zhang Y S, Xu T F 2016 Prog. Geophys 31 2346 doi: 10.6038/pg20160564 [27] Wang X, Zhu M, Xiao K, Guo J, Wang L 2019 J. Magn. Reson. 307 106580 doi: 10.1016/j.jmr.2019.106580 [28] Szczykulska M, Baumgratz T, Datta A 2016 Adv. Phys.: X 1 621 [29] Vidrighin M D, Donati G, Genoni M G, et al. 2014 Nat. Commun. 5 1 [30] Hou Z, Tang J F, Chen H, Yuan H, Xiang G Y, Li C F, Guo G C 2021 Sci. Adv. 7 eabd2986 [31] Roccia E, Cimini V, Sbroscia M, et al. 2018 Optica 5 1171 doi: 10.1364/OPTICA.5.001171 [32] Hou Z, Zhang Z, Xiang G Y, Li C F, Guo G C, Chen H, Liu L, Yuan H 2020 Phys. Rev. Lett. 125 020501 doi: 10.1103/PhysRevLett.125.020501 [33] Seltzer S, Romalis M 2004 Appl. Phys. Lett. 85 4804 doi: 10.1063/1.1814434 [34] Patton B, Zhivun E, Hovde D, Budker D 2014 Phys. Rev. Lett. 113 013001 doi: 10.1103/PhysRevLett.113.013001 [35] Thiele T, Lin Y, Brown M O, Regal C A 2018 Phys. Rev. Lett. 121 153202 doi: 10.1103/PhysRevLett.121.153202 [36] Li R, Quan W, Fan W, Xing L, Wang Z, Zhai Y, Fang J 2017 Chin. Phys. B 26 120702 doi: 10.1088/1674-1056/26/12/120702 [37] Liu J, Yuan H 2017 Phys. Rev. A 96 042114 doi: 10.1103/PhysRevA.96.042114 [38] Legchenko A, Baltassat J M, Beauce A, Bernard J 2002 J. Appl. Geophys. 50 21 doi: 10.1016/S0926-9851(02)00128-3 [39] Gross S, Barmet C, Dietrich B E, Brunner D O, Schmid T, Pruessmann K P 2016 Nat. Commun. 7 1 [40] Genovese M 2016 J. Optics 18 073002 doi: 10.1088/2040-8978/18/7/073002 [41] 王宁, 金贻荣, 邓辉, 吴玉林, 郑国林, 李绍, 田野, 任育峰, 陈莺飞, 郑东宁 2012 物理学报 61 213302 doi: 10.7498/aps.61.213302 Wang N, Jin Y R, Deng H, Wu Y L, Zheng G L, Li S, Ye T, Ren Y F, Chen Y F, Zheng D N 2012 Acta Phys. Sin. 61 213302 doi: 10.7498/aps.61.213302 [42] Komar P, Kessler E M, Bishof M, Jiang L, Sørensen A S, Ye J, Lukin M D 2014 Nat. Phys. 10 582 doi: 10.1038/nphys3000 [43] Donley E A 2010 IEEE Sensors Waikoloa, HI, USA, November 01–04, 2010 p17–22 [44] Walker T G, Happer W 1997 Rev. Mod. Phys. 69 629 doi: 10.1103/RevModPhys.69.629 [45] Kornack T, Ghosh R, Romalis M 2005 Phys. Rev. Lett. 95 230801 doi: 10.1103/PhysRevLett.95.230801 [46] Hurwitz L, Nelson J 1960 J. Geophys. Res. 65 1759 doi: 10.1029/JZ065i006p01759 [47] Wu T, Blanchard J W, Kimball D F J, Jiang M, Budker D 2018 Phys. Rev. Lett. 121 023202 doi: 10.1103/PhysRevLett.121.023202 [48] Garcon A, Blanchard J W, Centers G P, et al. 2019 Sci. Adv. 5 eaax4539 doi: 10.1126/sciadv.aax4539 [49] Jiang M, Su H, Garcon A, Peng X, Budker D 2021 arXiv: 2102.01448 [50] Farooq M, Chupp T, Grange J, et al. 2020 Phys. Rev. Lett. 124 223001 doi: 10.1103/PhysRevLett.124.223001 [51] Adams R W, Aguilar J A, Atkinson K D, et al. 2009 Science 323 1708 doi: 10.1126/science.1168877 [52] Theis T, Ganssle P, Kervern G, Knappe S, Kitching J, Ledbetter M, Budker D, Pines A 2011 Nat. Phys. 7 571 doi: 10.1038/nphys1986 [53] Maly T, Debelouchina G T, Bajaj V S, et al. 2008 J. Chem. Phys. 128 02B611 [54] Spagnolo N, Aparo L, Vitelli C, Crespi A, Ramponi R, Osellame R, Mataloni P, Sciarrino F 2012 Sci. Rep. 2 1 [55] Jiang M, Wu T, Blanchard J W, Feng G, Peng X, Budker D 2018 Sci. Adv. 4 eaar6327 [56] Jiang M, Frutos R P, Wu T, Blanchard J W, Peng X, Budker D 2019 Phys. Rev. Appl. 11 024005 doi: 10.1103/PhysRevApplied.11.024005 [57] Tayler M C, Theis T, Sjolander T F, Blanchard J W, Kentner A, Pustelny S, Pines A, Budker D 2017 Rev. Sci. Instrum. 88 091101 doi: 10.1063/1.5003347 [58] Jiang M, Xu W, Li Q, Wu Z, Suter D, Peng X 2020 Adv. Quantum Technol. 3 2000078 doi: 10.1002/qute.202000078 [59] Ledbetter M, Theis T, Blanchard J, et al. 2011 Phys. Rev. Lett. 107 107601 doi: 10.1103/PhysRevLett.107.107601 [60] Appelt S, Häsing F, Sieling U, Gordji-Nejad A, Glöggler S, Blümich B 2010 Phys. Rev. A 81 023420 doi: 10.1103/PhysRevA.81.023420 [61] Gemmel C, Heil W, Karpuk S, et al. 2010 Eur. Phys. J. D 57 303 doi: 10.1140/epjd/e2010-00044-5 [62] Sjolander T F, Tayler M C, King J P, Budker D, Pines A 2016 J. Phys. Chem. A 120 4343 doi: 10.1021/acs.jpca.6b04017 [63] Alcicek S, Put P, Kubrak A, Alcicek F C, Barskiy D, Gloeggler S, Dybas J, Pustelny S 2023 Commun. Chem. 6 165 doi: 10.1038/s42004-023-00965-8 [64] Picazo-Frutos R, Sheberstov K F, Blanchard J W, et al. 2024 Nat. Commun. 15 4487 doi: 10.1038/s41467-024-48390-2 [65] Zeeman P 1897 Nature 55 347 [66] Condon E U, Condon E, Shortley G 1935 The Theory of Atomic Spectra (Cambridge: Cambridge University Press) pp378–380 [67] Hou Z, Jin Y, Chen H, Tang J F, Huang C J, Yuan H, Xiang G Y, Li C F, Guo G C 2021 Phys. Rev. Lett. 126 070503 doi: 10.1103/PhysRevLett.126.070503 [68] Bao G, Wickenbrock A, Rochester S, Zhang W, Budker D 2018 Phys. Rev. Lett. 120 033202 doi: 10.1103/PhysRevLett.120.033202 [69] 王忻昌, 江文龙, 黄程达, 孙惠军, 曹晓宇, 田中群, 陈忠 2020 光谱学与光谱分析 40 665 Xin-Chang Wang C D H H J S X Y C Z Q T Wen-Long Jiang, Chen Z 2020 Spectrosc. Spectral Anal. 40 665 [70] Jiang M, Bian J, Li Q, Wu Z, Su H, Xu M, Wang Y, Wang X, Peng X 2021 Fundamental Research 1 68 doi: 10.1016/j.fmre.2020.12.007 [71] Jiang M, Bian J, Liu X, Wang H, Ji Y, Zhang B, Peng X, Du J 2018 Phys. Rev. A 97 062118 doi: 10.1103/PhysRevA.97.062118 [72] Jones J A, Karlen S D, Fitzsimons J, Ardavan A, Benjamin S C, Briggs G A D, Morton J J 2009 Science 324 1166 doi: 10.1126/science.1170730 [73] Bermudez A, Jelezko F, Plenio M B, Retzker A 2011 Phys. Rev. Lett. 107 150503 doi: 10.1103/PhysRevLett.107.150503 [74] Zhao N, Hu J L, Ho S W, Wan J T, Liu R 2011 Nat. Nanotechnol. 6 242 doi: 10.1038/nnano.2011.22 [75] Schweiger A, Jeschke G 2001 Principles of Pulse Electron Paramagnetic Resonance (Oxford: Oxford University Press on Demand) pp29–32 [76] Xiao D W, Hu W H, Cai Y, Zhao N 2020 Phys. Rev. Lett. 124 128101 doi: 10.1103/PhysRevLett.124.128101 [77] Qin S, Yin H, Yang C, et al. 2016 Nat. Mater. 15 217 doi: 10.1038/nmat4484 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: