首页
登录
注册
-
高能量密度物理(high energy density physics, HEDP)致力于研究能量密度≥1011 J/m3 (对应等效压强≥1 Mbar (1 bar=105 Pa))条件下的极端物质状态, 作为实验室天体物理与惯性约束聚变领域的核心科学问题[1], 已成为国际前沿科技竞争的重点方向. 其中, 靶核心区物质状态诊断面临等离子体极端环境(高温高压高密度)与屏蔽效应的双重挑战: 现有的可见光诊断技术受限于等离子体外层区域探测范围, 谱线易被连续谱掩盖, 且受等离子体不透明度影响, 难以获取靶核心区域的有效物理信息[2]. 相较之下, X射线诊断技术凭借其强穿透性(可穿透高电离度物质)和特征线携载的温度、密度、离化度等关键参数信息, 已成为诊断HEDP的重要路径之一[3–6]. 晶体谱仪作为X射线诊断的核心工具, 依托晶体周期结构与X射线波长的布拉格衍射匹配, 通过分光实现高分辨率的光谱测量[7]. 当前主要采用平面晶体与曲面晶体两种构型, 其中曲面晶体谱仪(如含柱面晶体von Hamos谱仪、球面晶体FSSR谱仪、掠入射KB成像系统)因兼具高亮度和高谱分辨优势占据主流地位, 并已与高性能探测器协同工作实现对高空间和高谱分辨的同步获取[8].
然而, 晶体谱仪仍面临着谱分辨与探测效率的固有矛盾: 高谱分辨要求导致可用波长范围窄化, 通常限制可覆盖的波长范围, 同时, 衍射过程引起的X射线强度损耗(2—3个数量级)显著地抑制了其在低驱动源条件下的应用性能[9,10]. 尽管激光器可产生高强度X射线源(亮度提升显著), 但其庞大体积与高昂成本限制了普及应用[11,12]. 因此, 亟须发展低驱动源条件下的X射线收集与传输效率优化方案, 重点提升弱光源环境下的信噪比与测量数据可靠性, 为极端条件下的物质研究提供普适性诊断技术.
毛细管X射线透镜是一种适用于实验室光源和同步辐射光源的调控器件[13–15], 其原理是基于X射线全反射. 作为全反射类型的调控器件之一, 其灵活的设计, 可满足不同实验所需的调控要求, 可用于聚焦, 发散和准直等[16,17]. 目前毛细管X射线光学相关的透镜已经被用于X射线成像[18–20]、X射线荧光分析[21–25]、X射线吸收精细结构等领域[26,27]. 从20世纪90年代开始, 研究员们就开展了毛细管X射线光学的研究, 对于新型设计的毛细管, 最常用的是用光线追迹法进行数值模拟[28–30]; 这种方式可以直观准确地研究X射线在毛细管中的传输过程, 对实际拉制工艺有着指导性的作用.
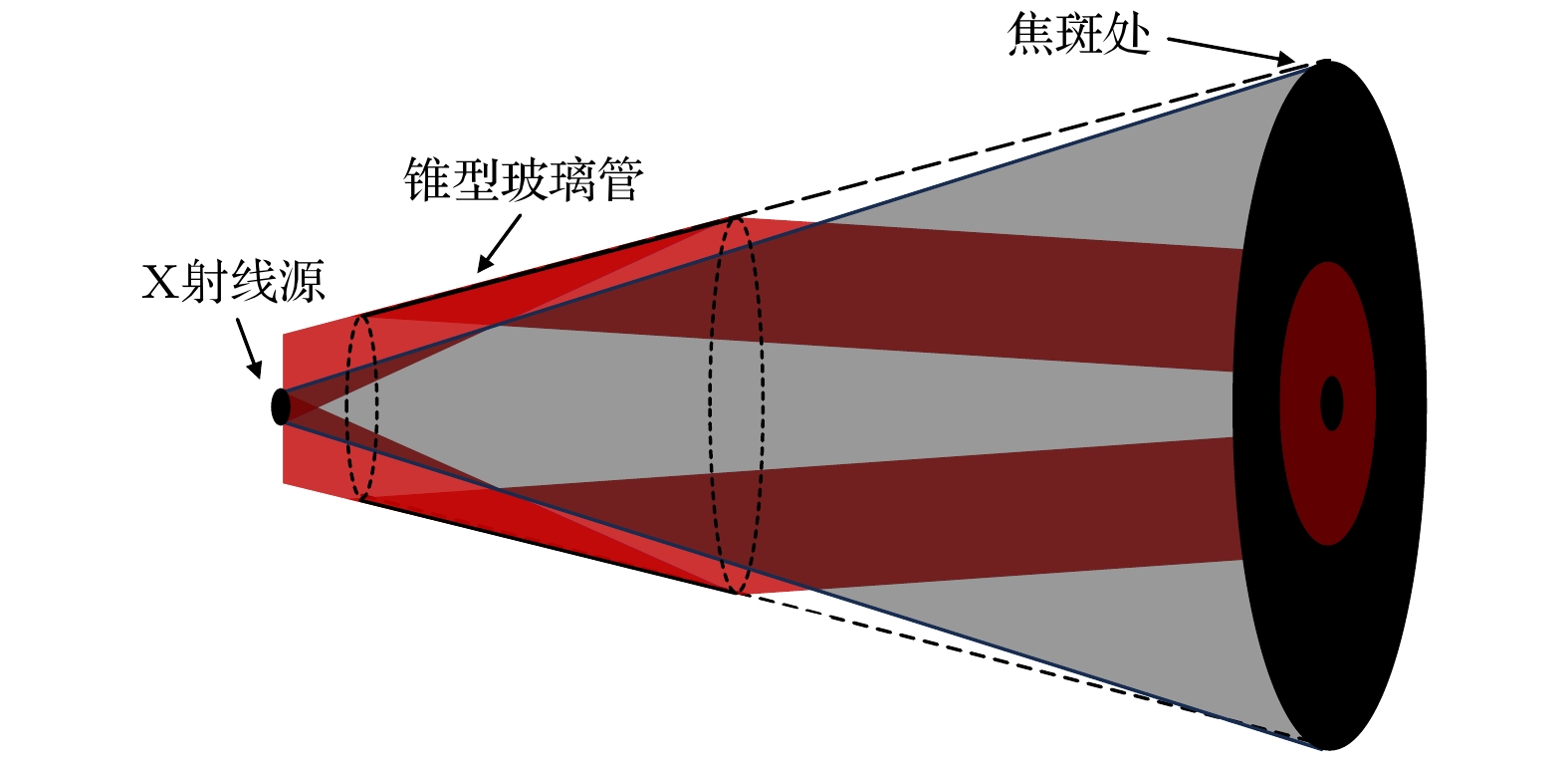
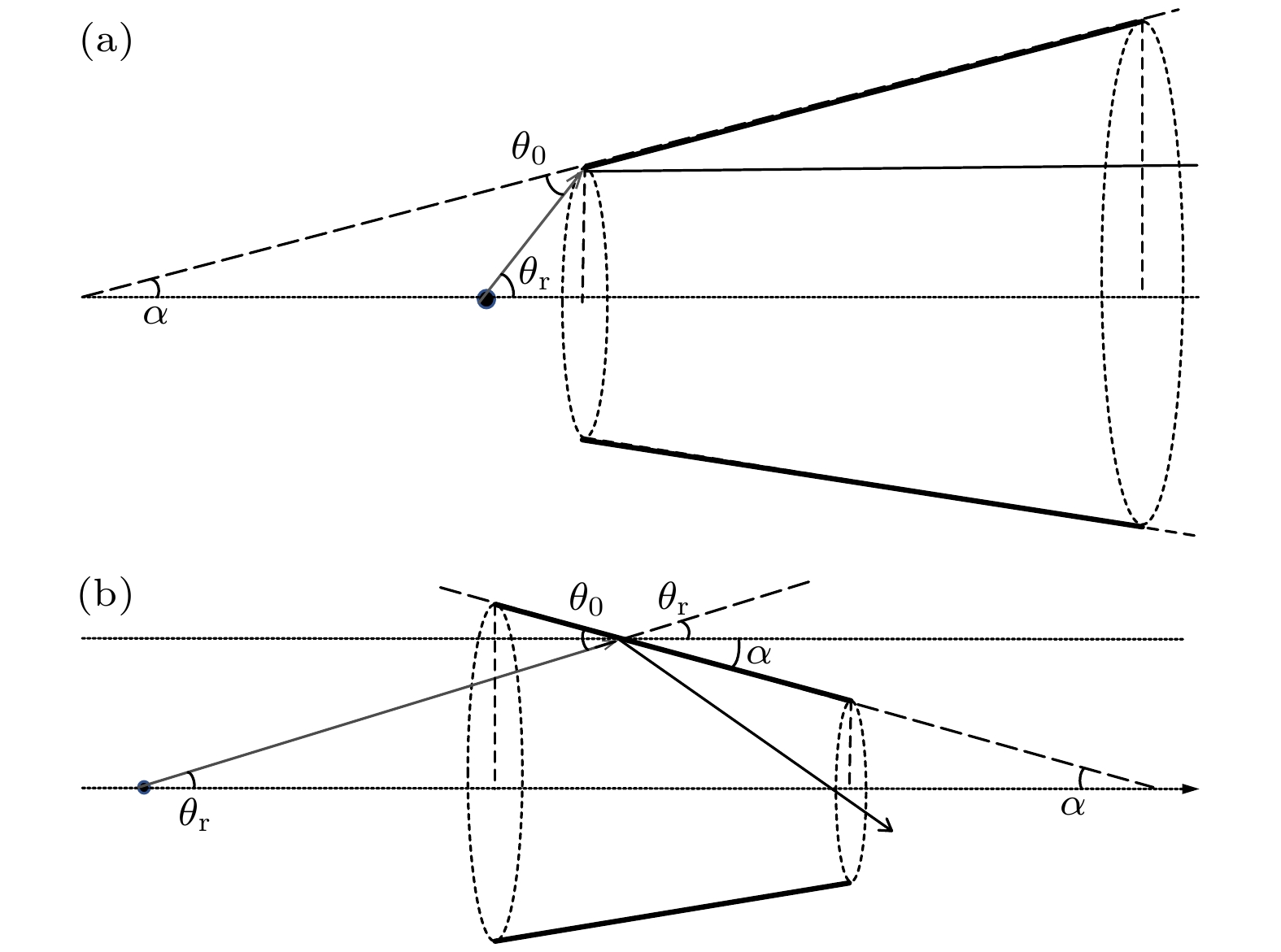
毛细管X射线透镜主要分为多毛细管透镜和单毛细管透镜; 其中多毛细管根据调控作用可分为多毛细管聚焦透镜和多毛细管平行束透镜[31]; 另外单毛细管可以根据反射面的曲面类型不同分为: 锥型单毛细管[32]、抛物面型单毛细管[33]、椭球型单毛细管[34]. 这些不同类型的毛细管透镜系统根据自身的特性可应用在不同的实验条件, 例如椭球型单毛细管由于其高传输效率和具有压缩光源尺寸的特性, 被用于同步辐射光源中调控X射线以获得纳米级焦斑[35]; 后续也有研究人员对其进行改进设计, 提出了大口径的椭球型玻璃管, 并对其传输性能进行了数值模拟[36]. 由于口径变大, 我们在本文称之为玻璃管. 在单毛细管中, 椭球型单毛细管一般用来聚焦和压缩光源[37], 抛物面型单毛细管一般用于准直X射线以获得低发散度的光束[38], 这两种都是进行单次全反射, 所以传输效率较高(80%左右). 而锥型单毛细管是用其出口端口径较小的优势来获得小焦斑, 由于进行了多次全反射[39], 所以一般传输效率低于20%. 此前研究人员也提出创新型的拉制工艺以极大减小其出口端口径[40], 可获得7.5 μm的出口内径. 本研究基于锥型单毛细管提出一种新型设计和使用方式, 将锥型单毛细管的口径增大, 并将其逆向使用. 这种设计目的之一是为了利用圆锥面的斜面优势, 利用全反射原理对X射线进行调控; 众所周知, X射线发生全反射, 须满足全反射临界角的条件, 即掠入射角小于全反射临界角[41]. 圆锥面逆向使用的优势在于入射光线斜率和圆锥面切线斜率是正向关系, 并非反向关系; 具体原理如图1所示, 其中图1(a)是逆向使用, 此时掠入射角
$ \theta $ 等于入射角$ {\theta }_{{\mathrm{r}}} $ 减去圆锥切面斜率$ a $ ; 而正向的使用如图1(b)所示, 此时掠入射角$ \theta $ 等于入射角$ {\theta }_{{\mathrm{r}}} $ 加上圆锥切面斜率$ a $ . 可以看出逆向使用可以使掠入射角更小, 更容易满足全反射临界角条件.本研究主要目的是为了解决类似于多分幅聚焦成像型(FSSR)谱仪[7,42]中大尺寸光源的光源利用率过低的问题. 在此系统中, 弯晶所接收的光线, 是直接由半径为0.5 mm左右的靶点照射的, 为了方便后续玻璃管传输性能的描述, 这里称之为直通光. 由于弯晶的传输效率很低, 仅用直通光的情况下, 无法满足实验所需的焦斑处的功率密度. 为了解决这一问题, 本研究提出了一种新型设计的大口径锥型玻璃管X射线透镜(LCGTXL), 具体光路传输图可参照图2. 经过透镜反射的光线传输情况为标红部分, 直通光为淡灰色部分, 图中表明透镜在不遮挡原本直通光的情况下, 对其他发散光线进行调控, 以增大光源利用率和焦斑处的功率密度增益, 这里焦斑处匹配了多分幅FSSR谱仪中的弯晶位置. 另外, 这种设计可以根据需求设计匹配不同增强部分(图2中环形光斑可调可控). 本研究为这种新型设计建立了数学模型, 并基于光线追迹法进行了数值模拟.
-
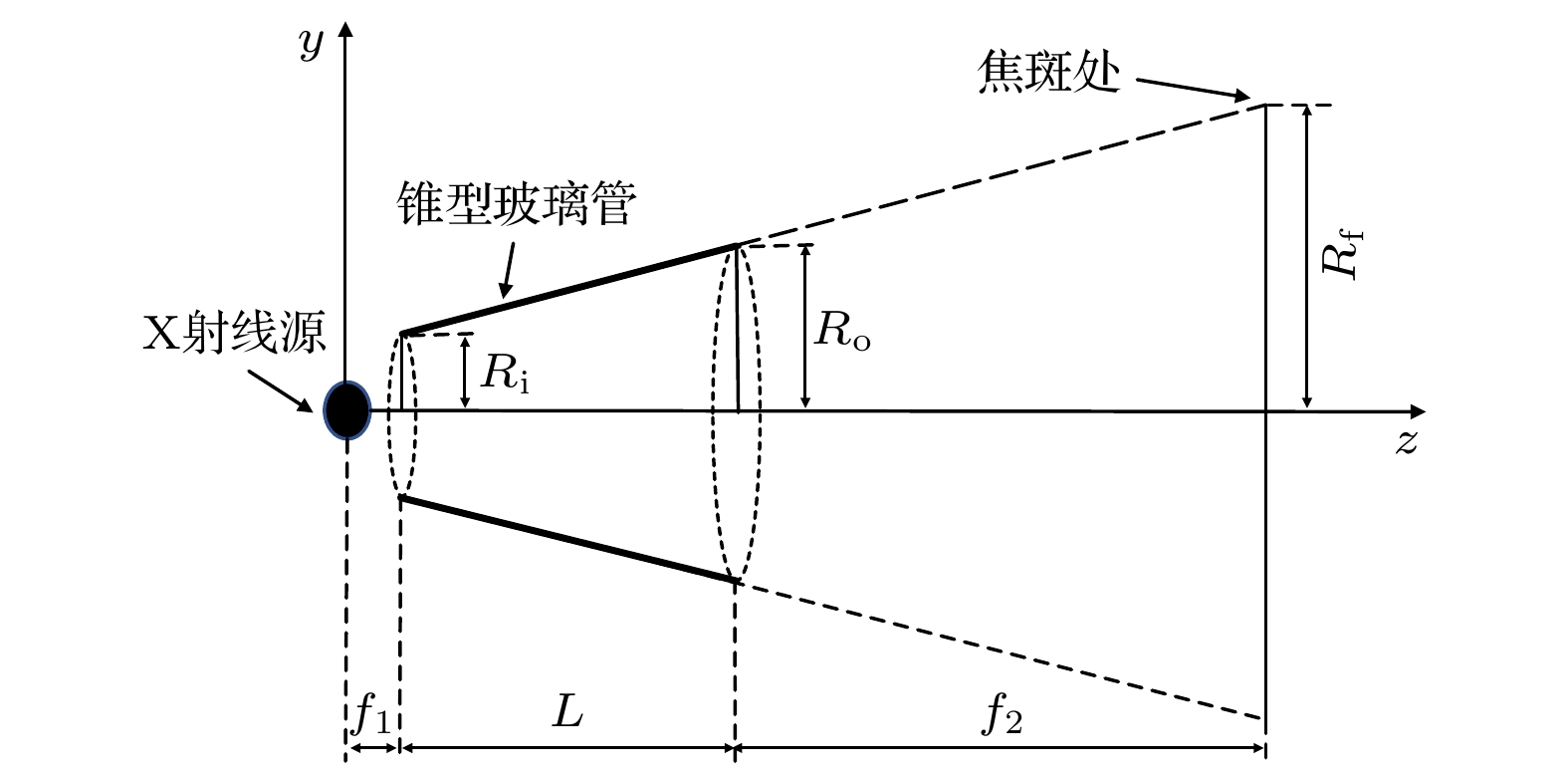
在理论设计过程中, 为了更好地说明相关参数的设计过程, 本文给出LCGTXL的数学模型设计图3. 作为毛细管X射线光学调控系统, LCGTXL可以归属于单毛细管的一种, 在本研究当中充当调控X射线以最大化光源利用率的作用. 在LCGTXL数学模型中, 以X射线光源作为空间直角坐标系的原点, 以LCGTXL的中心轴为Z轴建立坐标系, 因此, LCGTXL的内表面符合数学方程:
其中:
$ a = ({{R}_{0}-{R}_{\text{i}}})/{L},\; b={R}_{\text{i}} $ ,$ L $ 是LCGTXL的轴向长度,$ {f}_{1} $ 是X射线光源点到玻璃管入口端的距离,$ {R}_{{\mathrm{i}}} $ 和$ {R}_{0} $ 分别为LCGTXL的入口端半径和出口端半径. 另外,$ {f}_{2} $ 是玻璃管出口端到设备焦斑处的距离,$ {R}_{{\mathrm{f}}} $ 是焦斑面的半径.在具体设计参数的过程中, 根据接收面焦斑的大小和距离进行设计. 在光源和接收面的距离固定,
$ {R}_{{\mathrm{f}}} $ 也为定值时, 为了不影响原本直通光的传播, 本文所设计的锥面斜率$ a $ 符合参数设计公式: -
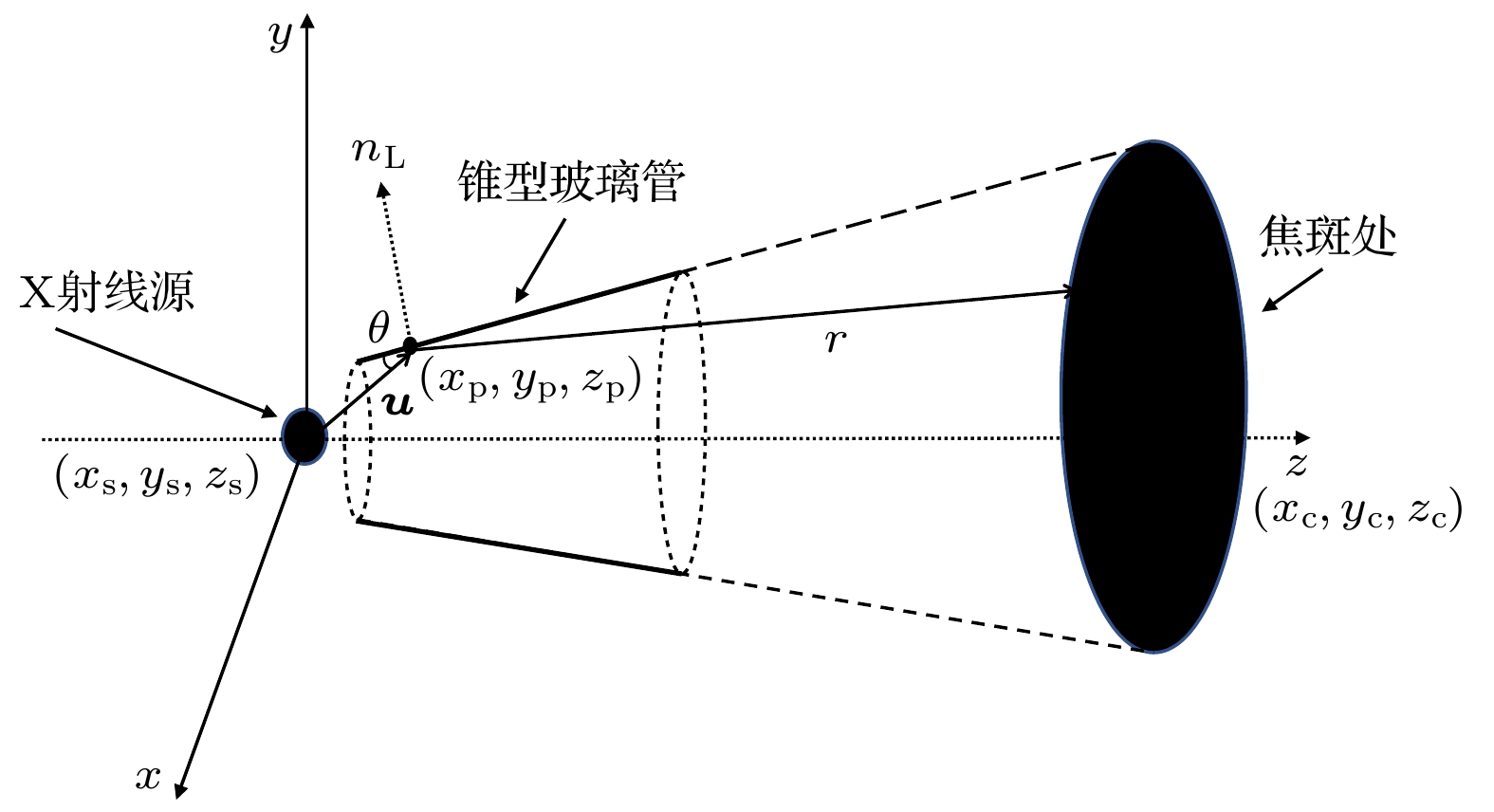
模拟X射线在玻璃管内传输是基于光线追迹原理, 如图4所示, 在X射线源平面中随机取一点
$ ({x}_{{\mathrm{s}}}, {y}_{{\mathrm{s}}}, {z}_{{\mathrm{s}}}) $ 作为入射光线起点, 并在透镜入口平面随机取一点$ ({x}_{\rm{p}}, {y}_{\rm{p}}, {z}_{\rm{p}}) $ , 可得入射光线的方向向量式中,
$ {d}_{{\mathrm{i}}}=\sqrt{{\left({x}_{{\mathrm{p}}}-{x}_{{\mathrm{s}}}\right)}^{2}+{\left({y}_{{\mathrm{p}}}-{y}_{{\mathrm{s}}}\right)}^{2}+{\left({z}_{{\mathrm{p}}}-{z}_{{\mathrm{s}}}\right)}^{2}} $ .由(1)式可得LCGTXL的内反射面的外法线矢量
式中,
$ {m}_{x}=2 x;{m}_{y}=2 y;{m}_{z}=2{a}^{2}{f}_{1}-2 ab-2{a}^{2}{{z}}$ .对于玻璃管的内表面而言, 实际拉制的内反射面与设计值之间存在偏差, 我们把这种偏差称为面型误差, 面型误差通常有两种表征方式: 斜率误差和外形误差. 在本研究中, 为了更符合实际光路传播, 在模拟中引入斜率误差, 在计算中以平均斜率误差
$ \varphi $ 来表征面型误差. 引入斜率误差$ \varphi $ 后内反射面的法向量表示为$ {\boldsymbol{n}}' $ , 具体可由下列公式转换计算:入射光线与反射面的外法线夹角即掠入射角
$ \theta $ 为在X射线发生全反射的过程中, 当掠入射角
$ \theta $ 大于全反射临界角$ {\theta }_{{\mathrm{c}}} $ 时, 反射率会迅速降低, 本研究在模拟过程中引入反射率R公式[43]:其中
$ h={\left(\dfrac{\theta }{{\theta }_{{\mathrm{c}}}}\right)}^{2}+{\bigg\{{\bigg[{\left(\dfrac{\theta }{{\theta }_{{\mathrm{c}}}}\right)}^{2}-1 \bigg]}^{2} + {\left(\dfrac{\beta }{\delta }\right)}^{2} \bigg\}}^{{1/2}} $ , 式中实部$ \delta $ 表示介质的散射特性, 虚部$ \beta $ 表示介 质的吸收特性, 用来描述X射线在介质中的吸收情况.上述所述的反射率
$ R $ 为完美光滑表面的条件, 在实际的玻璃管表面反射时, 表面的粗糙度在埃量级, 表面的粗糙度会使得X射线的反射率降低, 反射率的衰减系数为$ \Delta R $ , 因此在本文研究中, 为了更贴合实际过程, 我们对反射率R进行修正, 修正后的反射率$ {R}_{{\mathrm{e}}{\mathrm{n}}{\mathrm{d}}} $ 可由下列公式计算[44,45]:其中
$ {\theta }_{{\mathrm{c}}}=\sqrt{2\delta }\approx 0.02\sqrt{{\rho }_{{\mathrm{M}}}}/E $ .$ {\theta }_{{\mathrm{c}}} $ 为X射线的全反射临界角;$ {\rho }_{{\mathrm{M}}} $ 为光滑反射面介质的密度;$ E $ 为入射X射线的能量;$ \lambda $ 为掠入射X射线的波长;$ \sigma $ 为粗糙度标准差.入射向量
$ \boldsymbol{u} $ 经过玻璃管反射后得到的反射向量$ {\boldsymbol{r}}' $ 可以表示为本研究设计的LCGTXL属于单次全反射类型, 不再计算后续反射的向量计算. 另外, 本研究主要研究软X射线在真空中的传输情况, 所以不再考虑空气衰减系数. 通过记录每根射线的模拟过程, 可以表征接近实际LCGTXL的X射线调控性能.
-
光线追迹法是一种模拟射线传输的数学计算方法. 本研究基于光线追迹法用MATLAB软件模拟了X射线在LCGTXL中的传输过程, 目的是为了解决多分幅FSSR谱仪中光源利用率低的问题. 根据此系统中的参数, 本研究设计了如表1所列的几何参数, 并设计以均匀的圆形X射线光源进行模拟. 在模拟过程中, 本研究发现将玻璃管反射表面进行镀膜处理以增大全反射临界角能更好地适配此系统. 如表2所列, 以原本不加透镜的光源利用率作为对比, 加玻璃管后光源利用率和焦斑处的平均增益能提高至1.6倍左右; 对玻璃管进行镀金属铱处理, 光源利用率和焦斑处的平均增益能提高至3.1倍左右. 这是因为随着全反射临界角的提高, 会有更多符合条件的X射线光线进行反射. 另外, 为了更贴合实际传输过程, 本研究引入反射率
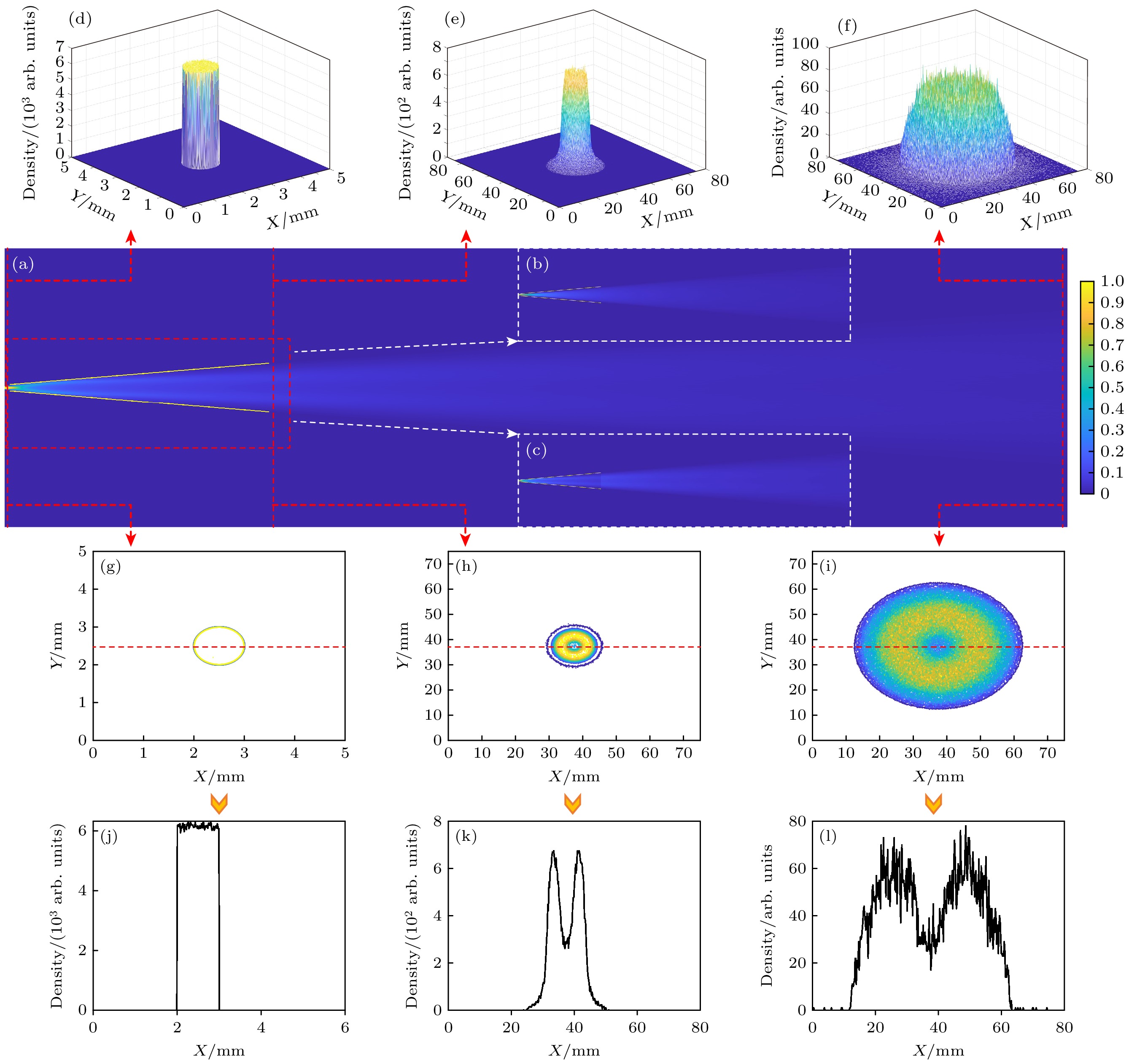
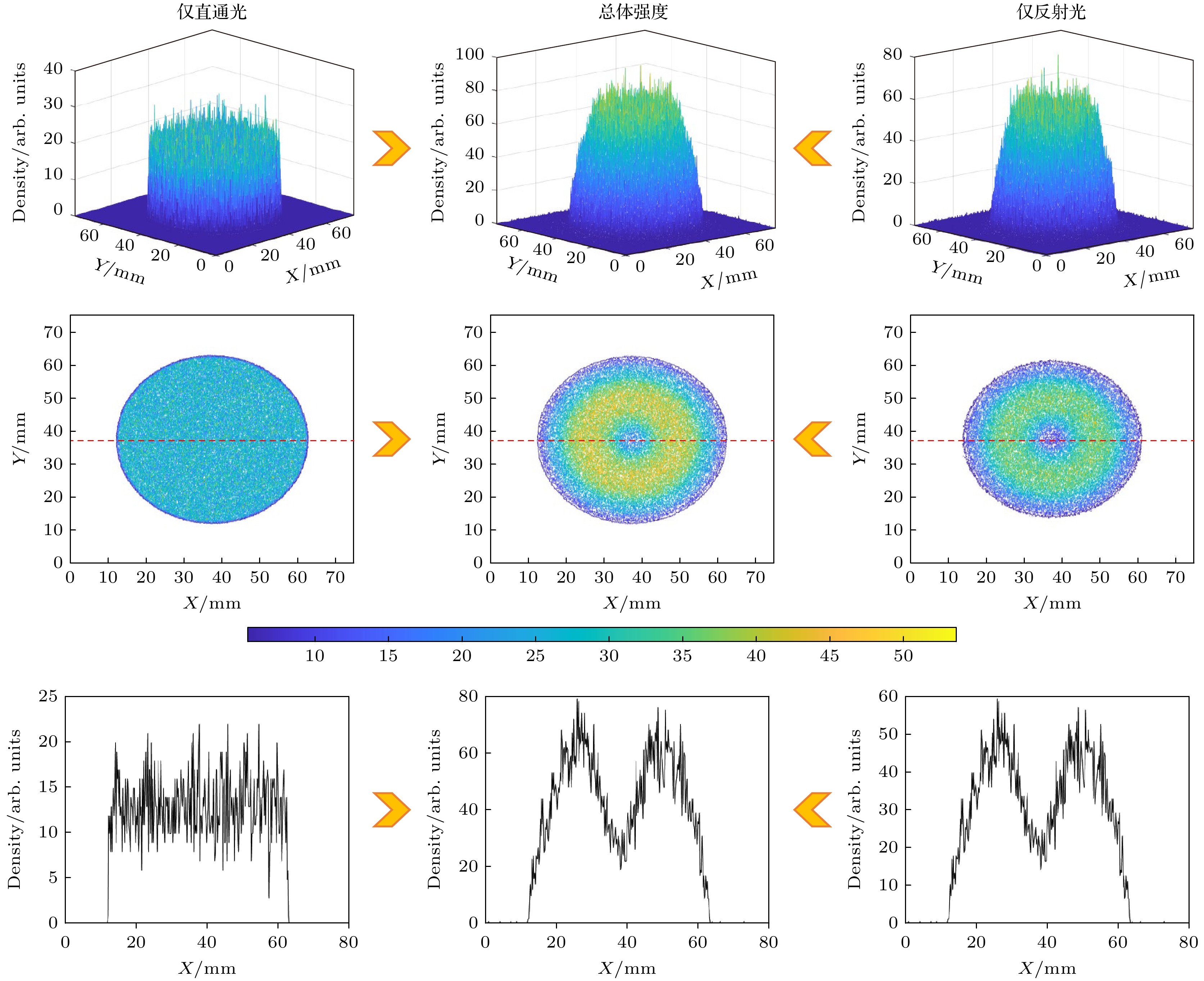
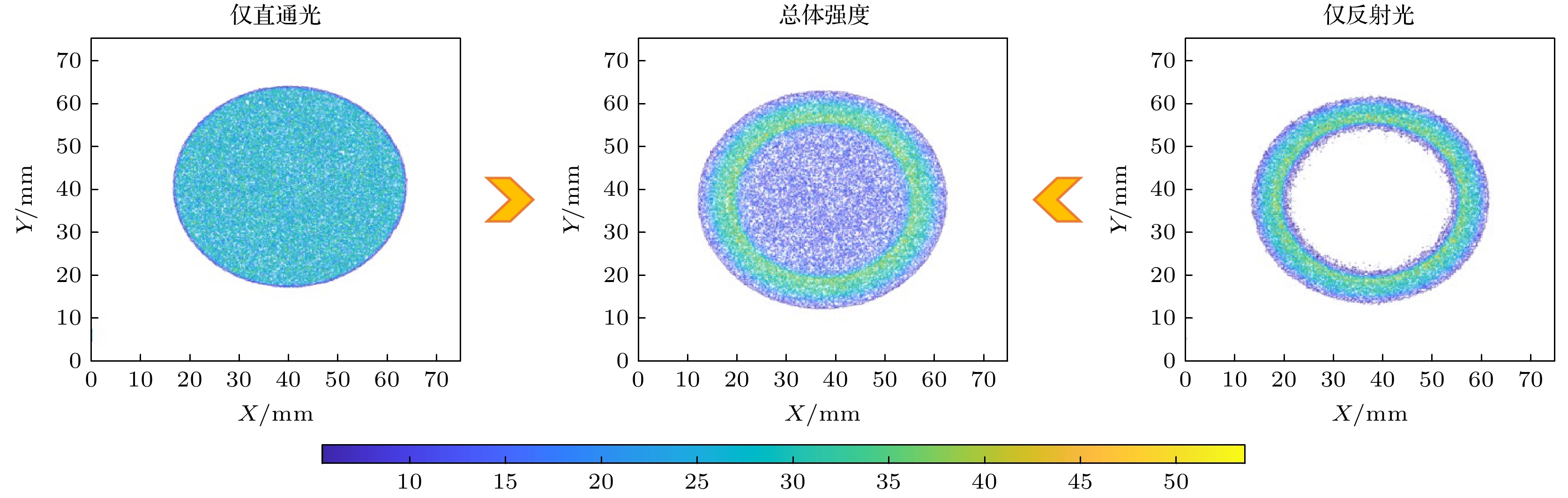
$ R $ 、表面粗糙度$ \sigma $ 、玻璃管反射表面的斜率误差$ \alpha $ 等参数. 图5是整个镀膜LCGTXL模拟过程中X射线可视化的示意图, 其中, 图5(a)是传输过程的剖面图, 管内只显示了反射光线的传输如图5(c)所示, 为了更好地与直通光比较, 本研究也给出了直通光的传输路径如图5(b)所示. 图5(a)中的3根红色虚线标注位置代表虚拟成像探测器的放置位置. 在此模拟过程中, X射线源的焦斑大小设置为1 mm, 能量设置为1.5 keV, 这符合多分幅FSSR谱仪中的光源参数. 另外, 模拟过程的镀膜处理为金属铱, 一般该材料镀膜的表面粗糙度为埃量级$ \sigma < 5\;{\text{Å}}$ , 由于拉制工艺所带来的反射表面的斜率误差$ \alpha $ 一般在几十微弧度左右. 为了更加贴切地反映真实的X射线传输情况, 本研究模拟过程设置PBCL的表面粗糙度$ \sigma $ 设置为5 Å, 斜率误差$ \alpha $ 设置为20 μrad. 图5(d)、图5(e)、图5(f)分别对应图5(a)中虚线位置的X射线焦斑的三维强度分布, 与其对应的焦斑的二维强度分布分别为图5(g)、图5(h)、图5(i). 相应地, 焦斑的二维强度分布沿中心轴即红色虚线位置的强度分布曲线分别为图5(j)、图5(k)、图5(l). 可以表明: 经过LCGTXL的调控后, 获得的焦斑明显获得了环形光束的增强, 一定程度上提高了多分幅FSSR谱仪中的光源利用率.为了更好地对比原本只用直通光获得的焦斑和经过LCGTXL的调控后的焦斑, 本研究给出了如图6的对比图. 由图6可以表明, 经过LCGTXL的调控, 在焦斑处可以获得整体增强的增益和部分环形的特别增强增益. 这是根据系统尺寸所设计的, 尽量使整体都获得一定的增益. 另外, 如图7所示, 如果玻璃管不进行镀膜处理, 因为全反射临界角过小, 导致光线反射角度小, 从而只能获得部分的环形增益, 并不会获得整体增益. 这种特殊环形的增强, 在多分幅FSSR谱仪中可以增强部分能谱的亮度, 这对于提高能谱分辨率有潜在的作用. 环形增强的宽度也可以根据需求来改变设计参数而调整.
-
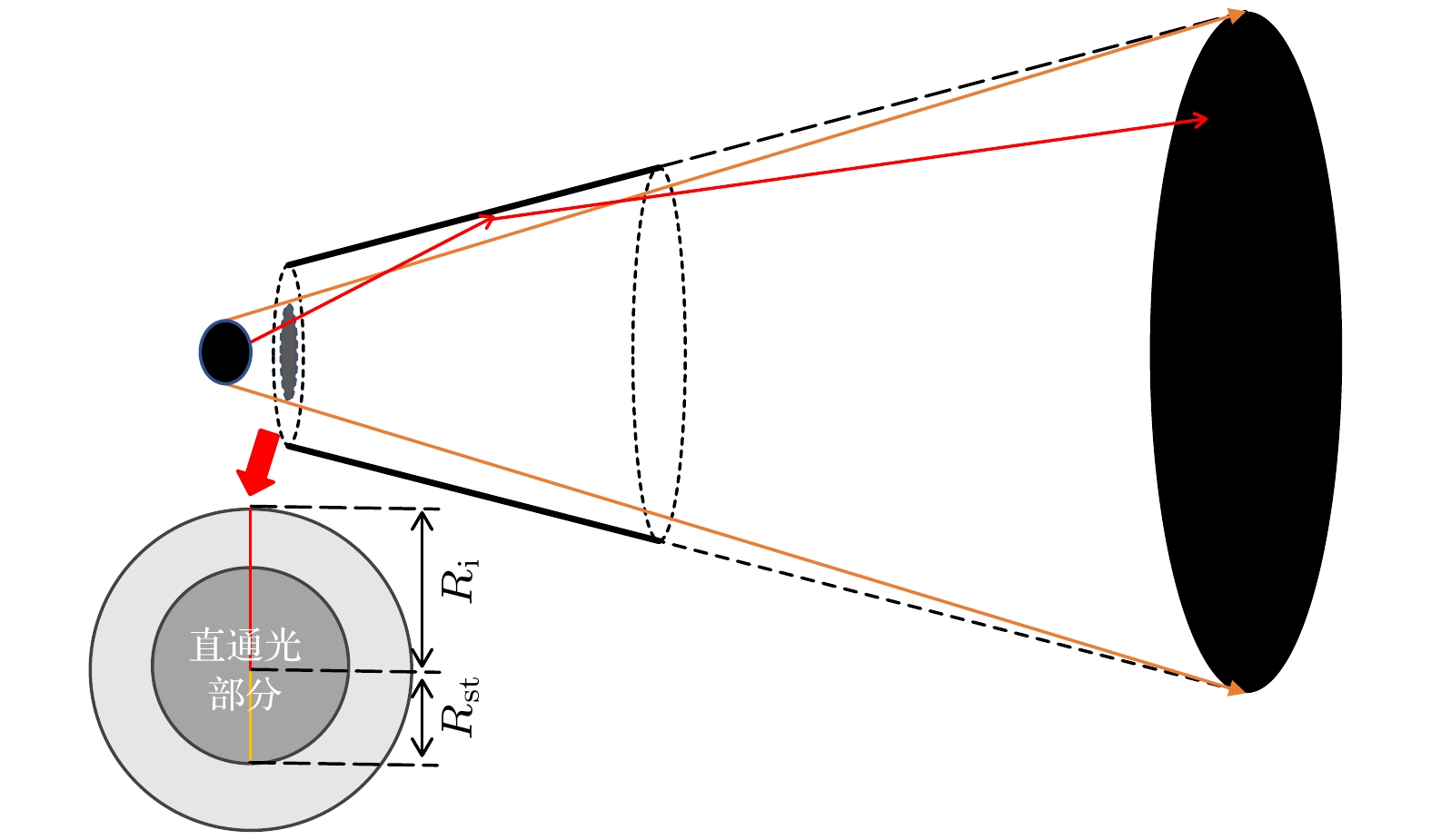
在毛细管X射线光学中, 对于单毛细管的光源利用率一般用立体接收角计算, 这是因为单毛细管一般会用光束遮挡器来挡住直通光的影响, 用立体接收角直接计算光源利用率比较方便快捷. 但在本研究中, 直通光不能遮挡, 用立体接收角计算光源利用率不再合适, 因此在本研究中, 我们通过记录经过反射和直接通过的光子数, 然后用反射光子数与直接通过光子数的比值来表征此系统中的光源利用率. 如果按照以往立体接收角方式来计算光源利用率, 根据本研究系统的基本参数, 如图8 所示, 根据算式
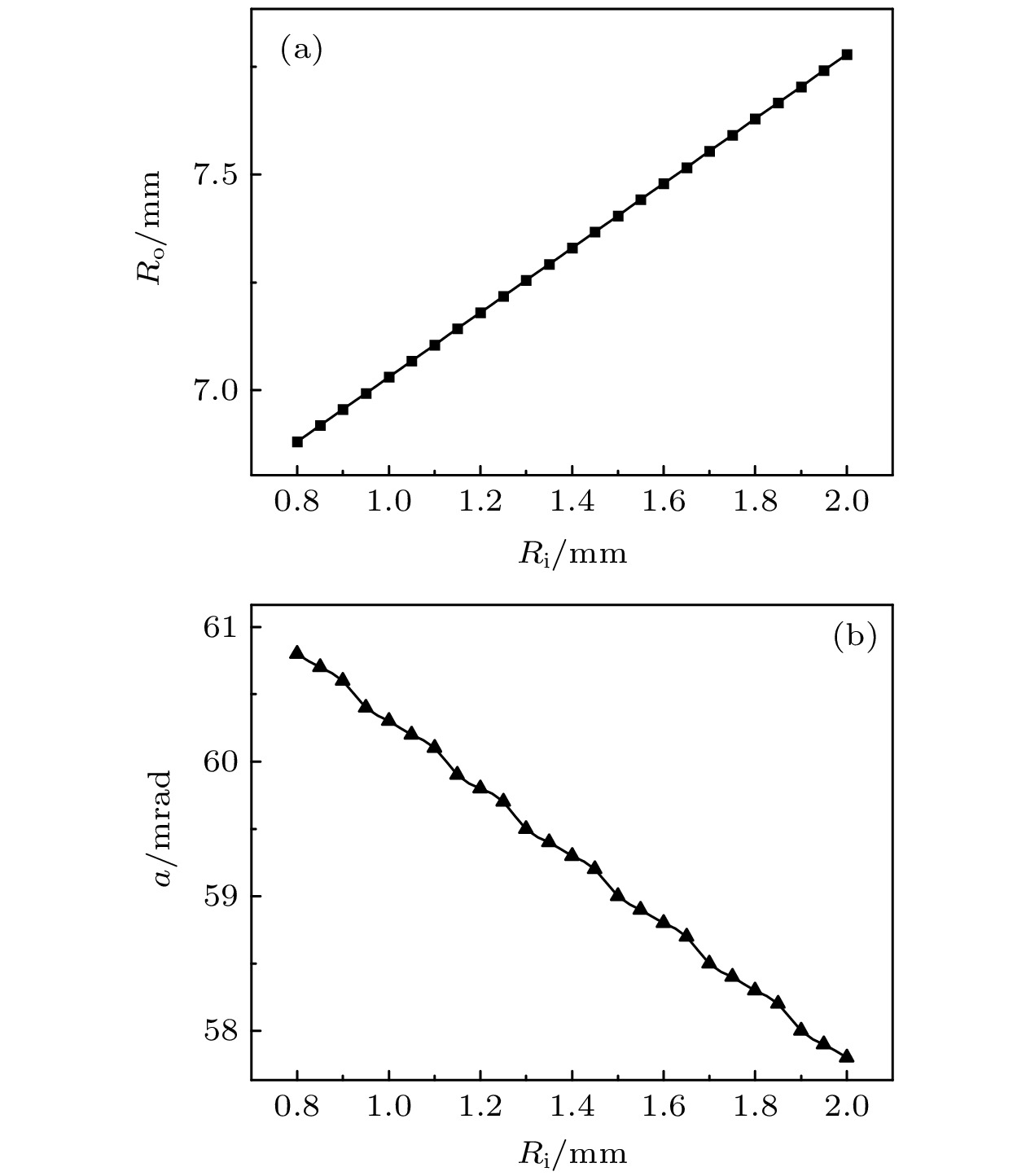
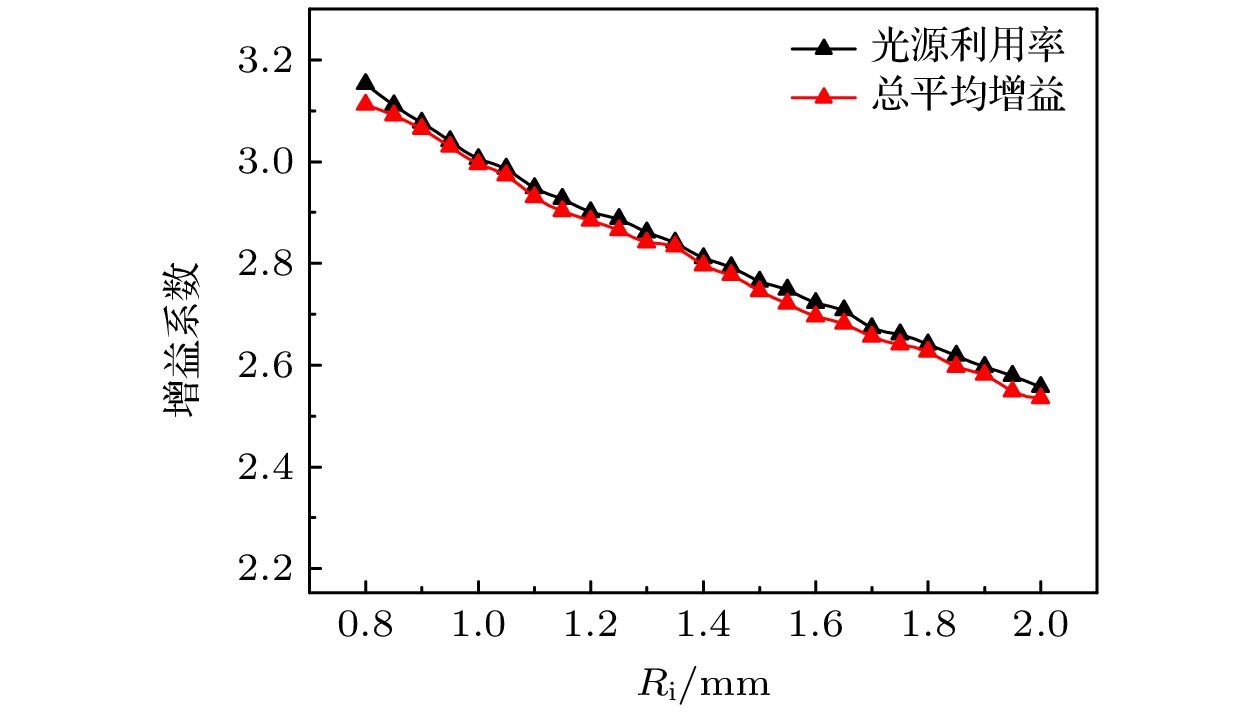
$ {R}_{{\mathrm{i}}}^{2}/ {R}_{{\mathrm{st}}}^{2} $ 计算出的光源利用率应 当为直通光的1.6倍左右, 而不是镀铱之后的3.1倍左右. 之所以出现这种差异, 是因为部分不满足直通光条件的光线能满足反射条件, 如图8红色光线所示.既然传统计算光源利用率的方式不可行, 本文针对入口大小不同进行数值模拟, 以找到最适合的入口半径. 为了不影响直通光的传输, 在增大入口半径时, 出口半径和反射面的斜率也会改变, 具体变化关系可以参考(2)式, 图9也表示了具体的线性关系. 图10展示了光源利用率和总平均增益随着入口半径的变化关系, 增益系数是与原本直通光的功率密度相比, 模拟结果表明, 光源利用率和总平均增益并不会因为入口半径的增大而增大, 反而是一种反比关系. 这是因为如图9(b)所示, 入口半径的增大导致反射面斜率的降低, 间接增大了入射光线和反射面的夹角, 从而使反射率降低, 最终导致光源利用率和总平均增益的下降.
-
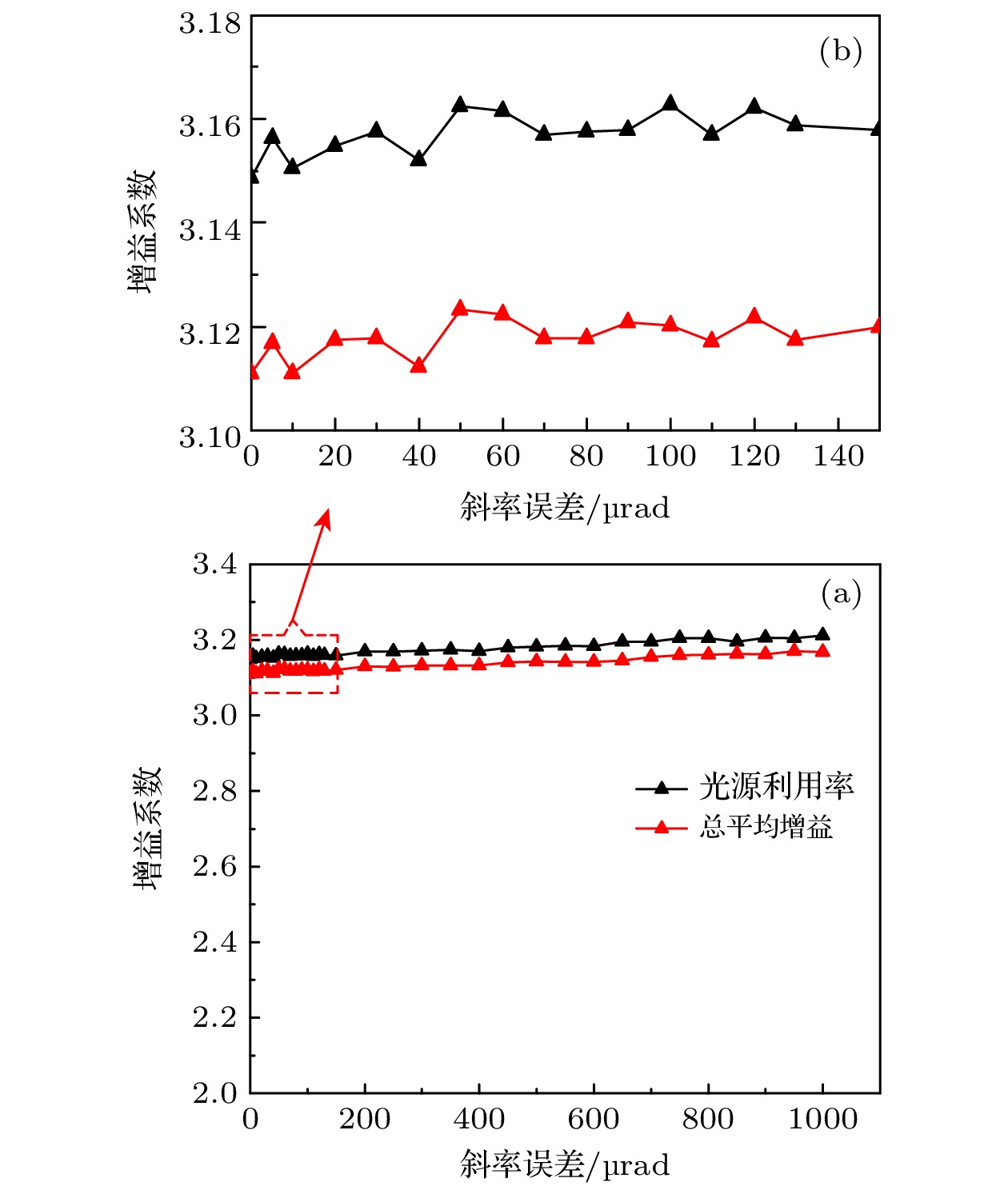
在毛细管拉制过程中, 因为拉制工艺导致反射表面不会严格符合理论设计的曲面, 存在一定的偏差, 为了更贴近实际传输过程, 本文研究了斜率误差
$ \alpha $ 对LCGTXL传输性能的影响. 目前毛细管的拉制一般需要进行多次拉制, 以找到斜率误差较低的情况, 一般斜率误差控制在$ 60\;{\text{μ}}{\mathrm{r}}{\mathrm{a}}{\mathrm{d}} $ 以下才算合格. 图11(a)可以表明本研究所设计的LCGTXL传输性能并不会受到斜率误差的影响, 这也为后续的实际制作提供了便捷. 图11(b)显示了斜率误差在$ 150\;{\text{μ}}{\mathrm{r}}{\mathrm{a}}{\mathrm{d}} $ 以内更细节的传输性能影响, 小范围波动是因为每次模拟计算中的误差, 均在可接受范围内. -
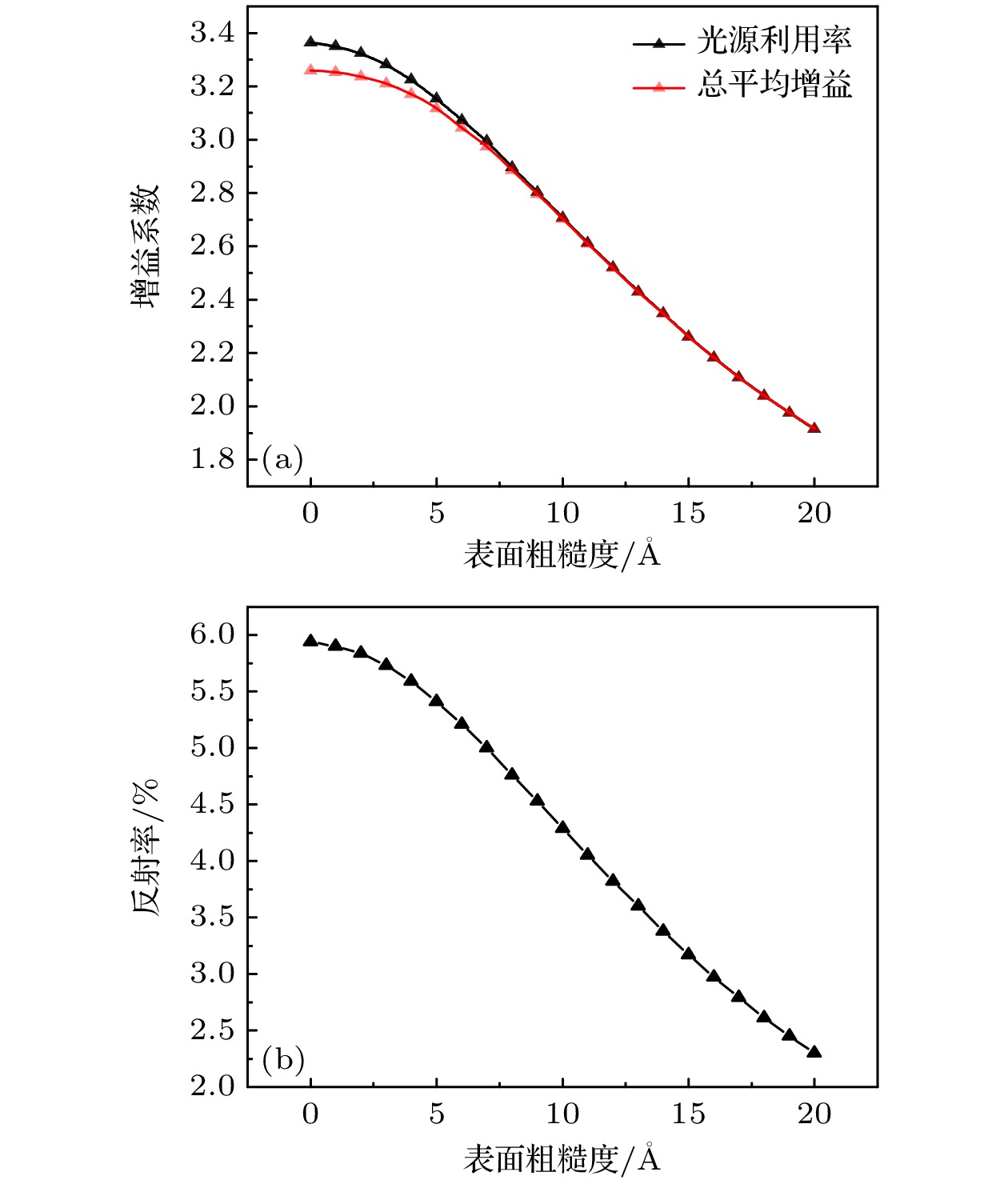
LCGTXL的制作材料为硅酸盐玻璃, 表面粗糙度一般
$ < 5\;{\text{Å}} $ . 不同制作材料或者镀膜材料的表面粗糙度都有所区别, 也是影响反射效率的主要参数之一. 为了更好地分析LCGTXL的传输性能, 本研究引入了表面粗糙度的影响, 并对不同表面粗糙度进行了LCGTXL的数值模拟. 如图12(a)所示表面粗糙度在$ 5\;{\text{Å}}$ 之内, 对LCGTXL的反射率性能影响不大, 但随着表面粗糙度的逐渐增大, 光源利用率和总平均增益迅速下降. 这是因为随着表面粗糙度的增大, 光线的反射率迅速下降, 反射率性能可以参考图12(b); 反射率之所以在6%以下, 主要是因为大部分入射光线与管壁的夹角过大, 导致有效反射的光线较少; 本研究统计的反射率, 是有效反射光线与打到管壁光线数量的比值. -
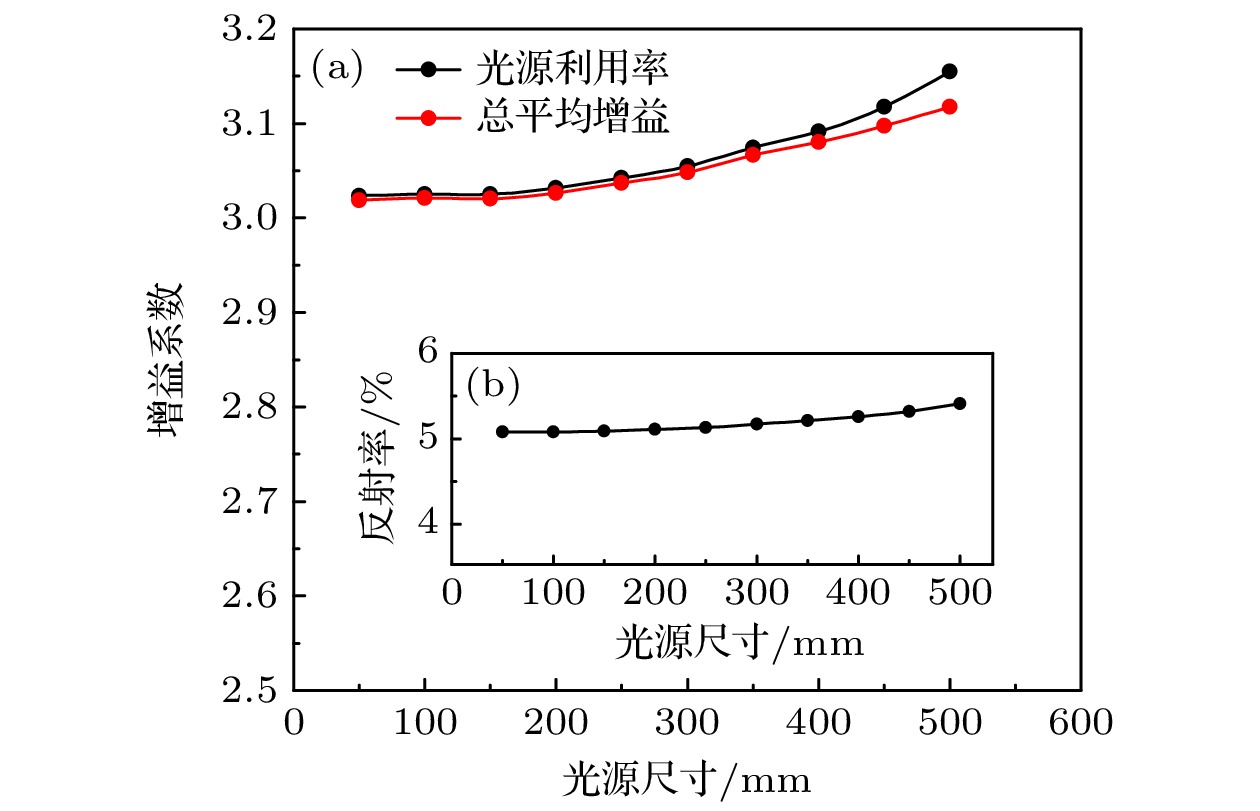
为探究LCGTXL的传输性能是否受光源尺寸的影响, 本研究通过限制光源生成范围进行数值模拟, 结果如图13(a)所示, 新型设计的LCGTXL的传输性能受光源尺寸影响较小, 随着光源尺寸的增大, 光源利用率和总平均增益逐渐增大, 但波动范围很小. 如图13(b), 结果显示光源尺寸的增大, 反而对传输效率有一点正反馈, 这是因为光斑尺寸的增大, 导致能满足反射条件的光线略微增多. 所以新型设计的LCGTXL更适用于大尺寸光源. 反观大尺寸光源对于直通光的利用率是偏低的, 这也进一步印证了LCGTXL的优势.
-
为解决多分幅FSSR谱仪中X射线光源利用率过低的问题, 本文基于锥型单毛细管, 提出一种LCGTXL的新型设计并改变其使用方式, 使光源利用率提高至原来的3.1倍左右. 由于这种设计方式可以根据实验需求改变环形增强的宽度和位置, 拥有可根据具体实验需求设计不同效果的优势. 另外, 本研究建立了LCGTXL的数学模型, 编写了基于光线追迹法的LCGTXL数值仿真程序, 并对LCGTXL的传输性能影响因数进行了多方面的研究, 结果显示LCGTXL的传输性能对面型误差要求较低, 并且适用各种不同尺寸的实验室光源. 该仿真程序可以直观演示X射线在LCGTXL的传输过程, 为LCGTXL的优化设计提供了便捷和理论指导. 最后, 本研究提出的LCGTXL的新型设计方式也为实验室大焦斑光源的使用提供了新的调控思路. 在X射线光谱分析、X射线透射成像等领域都有其应用前景.
大口径锥型玻璃管X射线透镜的设计与模拟
Design and simulation of X-ray lens with large diameter conical glass tube
-
摘要: 高能量密度物理实验诊断中, 采用晶体谱仪等X射线分光元件可实现靶物质中心区温度和密度等参数的高谱线分辨要求, 通过优化靶点光源到探测器间的光输运效率, 可极大地提升在低光源发射度下实验诊断精度. 本文介绍了一种大口径锥型玻璃管的X光传输部件, 构建了对应的数学模型, 基于光线追迹法, 用MATLAB软件对其X射线的传输图像进行了数值模拟. 结果显示: 新设计的大口径锥型玻璃管传输部件对面型误差要求较低, 其焦斑范围可控; 可以有效提升光源的利用率, 其平均增益约为3.1. 另外, 本文还介绍了该大口径锥型玻璃管传输部件系统性的性能模拟和分析结果, 为实验室高能量密度物理研究中的低发射度X射线诊断技术升级提供了新的思路和参考.Abstract: In high-energy density physics (HEDP) experiments, accurate diagnostics of physical parameters such as electron temperature, plasma density, and ionization state are essential for understanding matter behavior under extreme conditions. In these cases, X-ray spectroscopic technique, especially those using crystal spectrometers, is widely used to achieve high spectral resolution. However, a common challenge in such experiments lies in the inherent low brightness and poor spatial coherence of laboratory-based X-ray sources, which limit photon throughput, thus the diagnostic accuracy. Therefore, improving the X-ray optical transmission efficiency between the source and the detector is a key step to improve the performance of the whole system. Capillary X-ray optics, which function based on the principle of total internal reflection within hollow glass structures, provides a promising avenue for beam shaping, collimation, and focusing in the soft-to-hard X-ray range. These optical devices are usually divided into polycapillary type and monocapillary type. While polycapillary optics are composed of numerous micro-channels and used primarily for collimating or focusing divergent X-rays, monocapillary lenses—consisting of single curved channels—provide more precise beam control and are particularly suitable for customized X-ray pathways. Depending on the curvature of the inner reflective surface, monocapillaries are classified into conical, parabolic, and ellipsoidal geometries. In this study, we propose and analyze a novel design of a large-caliber conical glass tube, specifically tailored to address the issue of low light utilization in multi-channel focusing spectrographs with spatial resolution (FSSR). The proposed conical glass tube is made of a single large-diameter capillary structure, simplifying alignment requirements and reducing the surface manufacturing precision typically required by complex aspheric lenses. Its geometric configuration enables X-rays from extended or weak sources to be redirected and controlled to convergef, thereby improving photon collection without significantly altering beam divergence. To quantify the performance of this optical system, we develop a detailed mathematical ray-tracing model and implement it in MATLAB. The model combines physical parameters such as capillary inner diameter, taper angle, reflection loss, and source-detector geometry. Numerical simulations show that compared with traditional flat or slit based systems, the new conical design improves source utilization efficiency by 3.1 times. Furthermore, the lens exhibits a ring-shaped enhancement region in the output intensity profile, which can be regulated by adjusting the capillary geometry and source positioning. This feature enables the spatial customization of the beam profile, thereby facilitating optimized coupling with downstream spectroscopic components or imaging systems. In conclusion, the proposed large-aperture conical monocapillary X-ray lens provides a practical and efficient solution for enhancing X-ray optical transport in low-brightness source environments. Its simple construction, tunable focusing characteristics, and compatibility with diverse X-ray source types make it a compelling candidate for integration into a high-resolution X-ray diagnostic system, particularly in HEDP and laboratory-scale X-ray spectroscopy. This work not only introduces a novel optical approach but also provides a robust theoretical and simulation framework for guiding future experimental design and application of capillary-based X-ray optics.
-
-
图 1 锥型玻璃管使用对比图 (a)锥管逆向使用的光路图; (b)锥管正向使用的光路图
Figure 1. Comparison of conical glass tube usage: (a) Light path with reverse use of the tube; (b) light path with forward use of the tube.
图 5 LCGTXL X射线传输的可视化 (a) X射线传输的整体剖面图; (b)直通光的部分传输图; (c)反射光的部分传输图; (d)—(f)在图(a)中红色虚线的三维强度分布图; (g)—(i)在图(a)中红色虚线的二维分布; (j)—(l)分别沿着图(g)—(i)中的红色虚线的强度分布
Figure 5. Visualization of X-ray transmission in LCGTXL: (a) Overall profile of X-ray transmission; (b) partial transmission diagram of straight light; (c) partial transmission diagram of reflected light; (d)–(f) three-dimensional intensity distribution of the red dotted line in Figure (a); (g)–(i) two-dimensional distribution of the red dotted line in Figure (a); (j)–(l) intensity distribution along red dotted lines in Figure(g)–(i), respectively.
图 9 斜率
$ a $ 和出口半径$ {R}_{{\mathrm{o}}} $ 随入口半径$ {R}_{{\mathrm{i}}} $ 的变化关系Figure 9. Relationship between slope
$ a $ and outlet radius$ {R}_{{\mathrm{o}}} $ with inlet radius$ {R}_{{\mathrm{i}}} $ .
图 10 LCGTXL传输性能与入口半径的关系
Figure 10. Relationship between LCGTXL transmission performance and inlet radius.
图 11 LCGTXL传输性能与斜率误差的关系
Figure 11. Relationship between LCGTXL transmission performance and slope error.
图 12 LCGTXL传输性能与表面粗糙度的关系 (a)光源利用率和总平均增益随表面粗糙度的变化关系; (b)表面粗糙度对反射率的影响
Figure 12. Relationship between LCGTXL transmission performance and surface roughness: (a) Variation of source utilization and total average gain with surface roughness; (b) effect of surface roughness on reflectivity.
图 13 LCGTXL传输性能与光源尺寸的关系 (a)光源尺寸对光源利用率和总平均增益的影响; (b) 光源尺寸对反射率的影响
Figure 13. Relationship between LCGTXL transmission performance and source size: (a) Effect of source size on source utilization and total average gain; (b) effect of source size on reflectivity.
表 1 LCGTXL中的几何仿真参数
Table 1. Geometric simulation parameters in LCGTXL.
参数 $ {f}_{1} $ $ L $ $ {f}_{2} $ $ {R}_{{\mathrm{i}}} $ $ {R}_{{\mathrm{o}}} $ $ {R}_{{\mathrm{f}}} $ 单位/mm 2 100 298 0.8 6.88 25 
下载: 导出CSV
表 2 不同条件下的传输性能
Table 2. Transmission performance under different conditions.
种类 X射线能量/keV 光源利用率 增益 不加透镜 1.50 1.000 1.000 玻璃管 1.50 1.588 1.599 镀铱玻璃管 1.50 3.155 3.118
下载: 导出CSV
-
[1] Reverdin C, Thais F, Loisel G, Bougeard M 2010 Rev. Sci. Instrum. 81 10E327 doi: 10.1063/1.3491285 [2] Varentsov D, Ternovoi V Y, Kulish M, Fernengel D, Fertman A, Hug A, Menzel J, Ni P, Nikolaev D N, Shilkin N, Turtikov V, Udrea S, Fortov V E, Golubev A A, Gryaznov V K, Hoffmann D H H, Kim V, Lomonosov I V, Mintsev V, Sharkov By, Shutov A, Spiller P, Tahir N A, Wahl H 2007 Nucl. Instrum. Methods Phys. Res. , Sect. A 577 262 doi: 10.1016/j.nima.2007.02.060 [3] Ryazantsev S N, Skobelev I Y, Filippov E D, Martynenko A S, Mishchenko M D, Krůs M, Renner O, Pikuz S A 2021 Matter Radiat. Extremes 6 014402 doi: 10.1063/5.0019496 [4] Glenzer S H, Landen O L, Neumayer P, Lee R W, Widmann K, Pollaine S W, Wallace R J, Gregori G, Höll A, Bornath T, Thiele R, Schwarz V, Kraeft W D, Redmer R 2007 Phys. Rev. Lett. 98 065002 doi: 10.1103/PhysRevLett.98.065002 [5] Regan S P, Falk K, Gregori G, Radha P B, Hu S X, Boehly T R, Crowley B J B, Glenzer S H, Landen O L, Gericke D O, Döppner T, Meyerhofer D D, Murphy C D, Sangster T C, Vorberger J 2012 Phys. Rev. Lett. 109 265003 doi: 10.1103/PhysRevLett.109.265003 [6] Vinko S M, Ciricosta O, Cho B I, Engelhorn K, Chung H K, Brown C R D, Burian T, Chalupský J, Falcone R W, Graves C, Hájková V, Higginbotham A, Juha L, Krzywinski J, Lee H J, Messerschmidt M, Murphy C D, Ping Y, Scherz A, Schlotter W, Toleikis S, Turner J J, Vysin L, Wang T, Wu B, Zastrau U, Zhu D, Lee R W, Heimann P A, Nagler B, Wark J S 2012 Nature 482 59 doi: 10.1038/nature10746 [7] Yi S Z, Du H Y, Si H X, Zhou Z X, Jiang L, Wang Z S, Cheng R 2023 Nucl. Instrum. Methods Phys. Res. , Sect. A 1057 168722 doi: 10.1016/j.nima.2023.168722 [8] Yi Q, Meng S J, Ye F, Lu J, Yan X S, Yang R H, Jiang S Q, Ning J M, Zhou L, Chen F X, Yang J L, Xu Z P, Li Z H 2023 AIP Adv. 13 035216 doi: 10.1063/5.0143584 [9] Renner O, Šmíd M, Batani D, Antonelli L 2016 Plasma Phys. Controlled Fusion 58 75007 doi: 10.1088/0741-3335/58/7/075007 [10] Eftekhari-Zadeh E, Loetzsch R, Manganelli L, Blümcke M S, Tauschwitz A, Uschmann I, Pukhov A, Rosmej O, Spielmann C, Kartashov D 2023 Phys. Scr. 98 115615 doi: 10.1088/1402-4896/acff8c [11] Hurricane O A, Herrmann M C 2017 Annu. Rev. Nucl. Part. Sci. 67 213 doi: 10.1146/annurev-nucl-101916-123227 [12] Zhao Y, Yang J M, Zhang J Y, Liu J S, Yuan X, Jin F T 2009 Rev. Sci. Instrum. 80 043505 doi: 10.1063/1.3116483 [13] Kumakhov M A, Komarov F F 1990 Phys. Rep. 191 289 doi: 10.1016/0370-1573(90)90135-O [14] Balaic D X, Nugent K A, Barnea Z, Garrett R, Wilkins W 1995 J. Synchrotron Radiat. 2 296 doi: 10.1107/S0909049595010831 [15] Yokomae S, Motoyama H, Mimura H 2018 Precis. Eng. 53 248 doi: 10.1016/j.precisioneng.2018.04.010 [16] MacDonald C A 2010 X-Ray Opt. Instrum. 2010 867049 [17] Gibson W M, Kumakhov M 1993 Proc. SPIE. 172 [18] Bilderback D H, Hoffman S A, Thiel D J 1994 Science 263 201 doi: 10.1126/science.8284671 [19] Sowa K M, Jany B R, Korecki P 2018 Optica 5 577 doi: 10.1364/OPTICA.5.000577 [20] Korecki P, Sowa K M, Jany B R, Krok F 2016 Phys. Rev. Lett. 116 233902 doi: 10.1103/PhysRevLett.116.233902 [21] Szwedowski-Rammert V, Baumann J, Schlesiger C, Waldschläger U, Gross A, Kanngießer B, Mantouvalou I 2019 J. Anal. At. Spectrom. 34 922 doi: 10.1039/C8JA00427G [22] Matsuyama T, Tanaka Y, Taniguchi N, Oh J S, Tsuji K 2024 J. Anal. At. Spectrom. 39 76 doi: 10.1039/D3JA00168G [23] Matsuyama T, Tanaka Y, Mori Y, Tsuji K 2023 Talanta 265 124808 doi: 10.1016/j.talanta.2023.124808 [24] Peng S, Liu Z G, Sun T X, Ma Y Z, Ding X L 2014 Anal. Chem. 86 362 doi: 10.1021/ac403188k [25] Fittschen U E A, Falkenberg G 2011 Spectrochim. Acta, Part B 66 567 doi: 10.1016/j.sab.2011.06.006 [26] Wallen S L, Pfund D M, Fulton J L, Yonker C R, Newville M, Ma Y 1996 Rev. Sci. Instrum. 67 2843 doi: 10.1063/1.1147115 [27] Alexandre B J, Gomes M G, Real S 2015 Mater. Struct. 48 2869 doi: 10.1617/s11527-014-0364-x [28] Lin X Y, Li Y D, Sun T X, Pan Q L 2010 Chin. Phys. B 19 070205 [29] Liu A D, Lin Y Z 2004 Math. Comput. Simul. 66 577 doi: 10.1016/j.matcom.2004.05.001 [30] Peng S Q, Liu Z G, Sun T X, Wang K, Yi L T, Yang K, Chen M, Wang J B 2015 Nucl. Instrum. Methods Phys. Res., Sect. A 795 186 doi: 10.1016/j.nima.2015.05.051 [31] Sun T X, Ding X L 2015 Rev. Anal. Chem. 34 45 [32] Stern E A, Kalman Z, Lewis A, Lieberman K 1988 Appl. Opt. 27 5135 doi: 10.1364/AO.27.005135 [33] Wen H, Zhou M, Wu Y M, Yuan T Y, Liu Z G 2022 Appl. Opt. 61 3656 doi: 10.1364/AO.450639 [34] Motoyama H, Sato T, Iwasaki A, Takei Y, Kume T, Egawa S, Hiraguri K, Hashizume H, Yamanouchi K, Mimura H 2016 Rev. Sci. Instrum. 87 051803 doi: 10.1063/1.4950735 [35] Koch R J, Jozwiak C, Bostwick A, Stripe B, Cordier M, Hussain Z, Yun W, Rotenberg E 2018 J. Synchrotron Radiat. 31 50 doi: 10.1080/08940886.2018.1483660 [36] 邵尚坤, 袁天语, 李惠泉, 孙学鹏, 华陆, 刘志国, 孙天希 2022 北京师范大学学报(自然科学版) 58 681 Shao S K, Yuan T Y, Li H Q, Sun X P, Hua L, Liu Z G, Sun T X 2022 J. Beijing Norm. Univ. (Nat. Sci.) 58 681 [37] Jiang B W, Liu Z G, Sun X P, Sun T X, Deng B, Li F Z, Yi L T, Yuan M N, Zhu Y, Zhang F S, Xiao T Q, Wang J, Tai R Z 2017 Opt. Commun. 398 91 doi: 10.1016/j.optcom.2017.04.035 [38] Balaic D X, Barnea Z, Nugent K A, Garrett R F, Varghese J N, Wilkins S W 1996 J. Synchrotron Radiat. 3 289 doi: 10.1107/S0909049596009351 [39] Wang Y B, Li Y L, Shao S K, Zhang X Y, Li Y F, Sun X P, Tao F, Deng B, Sun T X 2020 Opt. Commun. 464 125544 doi: 10.1016/j.optcom.2020.125544 [40] Wang X Y, Li Y D, Luo H, Ye L, Zhou M, Duan J Y, Lin X Y 2019 Nucl. Instrum. Methods Phys. Res., Sect. A 947 162762 doi: 10.1016/j.nima.2019.162762 [41] Sun X P, Zhang X Y, Zhu Y, Wang Y B, Shang H Z, Zhang F S, Liu Z G, Sun T X 2018 Nucl. Instrum. Methods Phys. Res. , Sect. A 888 13 doi: 10.1016/j.nima.2018.01.033 [42] Zhou Z X, Cheng R, Du H Y, Yi S Z, Fu F, Wang G D, Shi L L, Wang Z, Jin X J, Chen Y H, Zhang Y S, Chen L W, Yang J, Su M G 2024 J. Anal. At. Spectrom. 39 31 [43] 孙天希 2022 光学学报 42 1134002 doi: 10.3788/AOS202242.1134002 Sun T X 2022 Acta Opt. Sin. 42 1134002 doi: 10.3788/AOS202242.1134002 [44] Shao S K, Li H Q, Yuan T Y, Zhang X Y, Hua L, Sun X P, Liu Z G, Sun T X 2022 Front. Phys. 10 816981 doi: 10.3389/fphy.2022.816981 [45] Zymierska D 1996 Acta. Phys. Pol. A 89 347 doi: 10.12693/APhysPolA.89.347 -
计量
- 文章访问数: 21
- HTML全文浏览数: 21
- PDF下载数: 1
- 施引文献: 0