高级搜索

自旋-轨道耦合玻色气体中集体激发动力学

,  ,  ,  , 

downloadPDF

上一篇

下一篇

郑鸿燕, 原梓洲, 渠晓旭, 胥文雨, 陈小龙. 自旋-轨道耦合玻色气体中集体激发动力学[J]. 物理学报, 2025, 74(14): 147101-1. doi: 10.7498/aps.74.20250411
引用本文: 郑鸿燕, 原梓洲, 渠晓旭, 胥文雨, 陈小龙. 自旋-轨道耦合玻色气体中集体激发动力学[J]. 物理学报, 2025, 74(14): 147101-1. doi: 10.7498/aps.74.20250411
shu
Hongyan ZHENG, Zizhou YUAN, Xiaoxu QU, Wenyu XU, Xiaolong CHEN. Collective excitation dynamics in spin-orbit coupled Bose gases[J]. Acta Physica Sinica, 2025, 74(14): 147101-1. doi: 10.7498/aps.74.20250411
Citation: Hongyan ZHENG, Zizhou YUAN, Xiaoxu QU, Wenyu XU, Xiaolong CHEN. Collective excitation dynamics in spin-orbit coupled Bose gases[J]. Acta Physica Sinica, 2025, 74(14): 147101-1. doi: 10.7498/aps.74.20250411
shu

自旋-轨道耦合玻色气体中集体激发动力学

  • 1.

    浙江理工大学物理学系, 杭州　310018

  • 2.

    浙江理工大学, 全省量子物态与光场调控重点实验室, 杭州　310018

    • 通讯作者: E-mail: xiaolongchen@zstu.edu.cn

  • 中图分类号: 71.70.Ej, 73.22.Lp, 67.85.-d

Collective excitation dynamics in spin-orbit coupled Bose gases

  • 1.

    Department of Physics, Zhejiang Sci-Tech University, Hangzhou 310018, China

  • 2.

    Zhejiang Key Laboratory of Quantum State Control and Optical Field Manipulation, Zhejiang Sci-Tech University, Hangzhou 310018, China

    • Corresponding author: E-mail: xiaolongchen@zstu.edu.cn

  • MSC: 71.70.Ej, 73.22.Lp, 67.85.-d

  • 摘要: 基于数值求解定态与含时Gross-Pitaevskii方程, 本文研究了一维拉曼型自旋-轨道耦合玻色气体中的静态特性与低能集体激发动力学性质. 分析了凝聚体动量、自旋极化率和基态能量来分类三种基态物相(条纹相、平面波相和零动量相)以及对应的相变. 在此基础上, 通过设计不同的微扰激发方式, 重点研究了四种典型的低能集体激发模式(偶极、呼吸、自旋-偶极和自旋-呼吸模式)的频率特性和动力学行为. 结果发现, 四种模式频率随拉比频率增加呈现非单调变化行为且不同物相中的集体激发模式表现出显著差异, 尤其是自旋相关的两种模式在条纹相中呈现自旋自由度相关的独特振荡行为. 这些发现将为理解自旋-轨道耦合玻色气体中新奇物相的量子多体动力学提供重要参考和理论依据.
    Abstract: The ground-state properties and collective excitations in a weakly interacting Bose gas with Raman-type spin-orbit coupling in one dimension are systematically investigated by numerically solving static and time-dependent Gross-Pitaevskii equations in this work. Our analysis focuses on three different quantum phases, i.e., stripe phase, plane-wave phase, and zero-momentum phase, which are characterized by key static properties including condensate momentum, spin polarization, and ground-state energy. The dynamic behaviors of total-density collective modes, i.e., the dipole mode that drives harmonic oscillations of the atomic cloud's center of mass and the breathing mode that is responsible for periodic expansion and contraction of density profile, are all explored using time-dependent simulations. Mode frequencies exhibit non-monotonic dependence on Rabi frequency in the three phases, and are significantly suppressed at the transition point between the plane-wave and the zero-momentum phases. Additionally, the spin-dependent collective excitations, particularly the spin-dipole and spin-breathing modes, are studied, which are governed by the time-dependent spin density distribution $(\delta n(x, t) \equiv n_\uparrow(x, t)-n_\downarrow(x, t)\,)$ as shown in the following figure. The results indicate that two spin oscillation modes exist only in the stripe phase and the zero-momentum phase, with the latter exhibiting substantially higher frequencies. Notably, mode frequencies decrease monotonically with the increase of Rabi frequency in the stripe phase, whereas they rise linearly in the zero-momentum phase. The spin-dipole mode induces rigid, out-of-phase oscillations of the two spin components, while the spin-breathing mode modulates the spin density distribution periodically. These findings offer fundamental theoretical insights into the dynamic behaviors of spin-orbit-coupled quantum gases, particularly regarding spin-related collective excitations, and provide valuable guidance for future cold-atom experiments.
  • 加载中

  • 图 1  拉曼型自旋-轨道耦合玻色气体三种基态物相 ST, PW 以及 ZM 中 (a)凝聚体动量$ P_x $; (b) 自旋极化率$ \langle\sigma_z\rangle $; (c)能量E, 随拉比频率Ω的变化行为. (a)中插图表示各物相中典型密度分布, 其中蓝色实线、红色虚线分别表示自旋向上和自旋向下组分的密度分布. (c)中插图为帮助判断相变类型的能量关于拉比频率的导数$ {\mathrm{d}}E/{\mathrm{d}}\varOmega $. 图中竖划线和竖点线分别表示本文理论框架确定的ST-PW和PW-ZM相变点处拉比频率$ 2.08 E_{\rm{r}} $和$ 3.95 E_{\rm{r}} $.

    Figure 1.  (a) The condensate momentum $ P_x $, (b) the spin polarization $ \langle\sigma_z\rangle $, and (c) the energy E in the ST, PW, and ZM phases, as functions of the Rabi frequency Ω in the Raman-type spin-orbit coupled Bose gases. The insets in (a) denote the typical density distribution in respective phases, where the density distributions of the spin-up and spin-down components are indicated by the blue-solid and red-dashed lines, respectively. The insets in (c) denote the derivative of the energy with respect to the Rabi frequency $ {\mathrm{d}}E/{\mathrm{d}}\varOmega $ to determine the type of phase transitions. The vertical dashed and dotted lines indicate the critical Rabi frequencies of the ST-PW and PW-ZM phase transitions, respectively, determined by our numerical calculations.

    下载: 全尺寸图片 幻灯片

    图 2  条纹相中偶极、呼吸、自旋-偶极以及自旋-呼吸四种模式对应观测量的含时演化行为

    Figure 2.  Time-dependent observables of the dipole, breathing, spin-dipole, and spin-breathing modes in the stripe phase.

    下载: 全尺寸图片 幻灯片

    图 3  偶极、呼吸、自旋-偶极及自旋-呼吸四种集体激发模式频率$ \omega_{{\mathrm{d, b, sd, sb}}} $与拉比频率Ω的关系

    Figure 3.  Collective excitation frequencies $ \omega_{{\mathrm{d, b, sd, sb}}} $ of the dipole mode, breathing mode, spin-dipole mode, and spin-breathing mode, as functions of the Rabi frequency Ω.

    下载: 全尺寸图片 幻灯片

    图 4  偶极模式(第一行)和呼吸模式(第二行)中的典型密度动力学特征　(a), (c) $ \varOmega=1.0 E_{\mathrm{r}} $处的条纹相; (b), (d) $ \varOmega=3.0 E_{\mathrm{r}} $处的平面波相. 其中, 三种颜色线分别表示$ 0, \;T/4,\; T/2 $三个时间点的密度分布

    Figure 4.  Typical density evolution of dipole-mode (top panel) and breathing-mode (bottom panel) oscillations: (a), (c) Stripe phase at $ \varOmega=1.0 E_{\mathrm{r}} $; (b), (d) plane-wave phase at $ \varOmega=3.0 E_{\mathrm{r}} $. Here, three colorful lines indicate the density distributions at $ 0 $, $ T/4 $, and $ T/2 $ of one full period T.

    下载: 全尺寸图片 幻灯片

    图 5  $ \varOmega=1.0 E_r $处条纹相中自旋-偶极振荡动力学, 不同颜色曲线分别表示不同自旋分量的密度分布

    Figure 5.  Oscillating behavior of the spin-dipole mode in the stripe phase at $ \varOmega=1.0 E_r $. Here, the colorful lines indicate the spin-up and spin-down density distributions.

    下载: 全尺寸图片 幻灯片

    图 6  $ \varOmega=1.0 E_{\mathrm{r}} $处条纹相中自旋-呼吸振荡动力学, 不同颜色曲线分别表示不同自旋分量的密度分布

    Figure 6.  Oscillating behavior of the spin-breathing mode in the ST phase at $ \varOmega=1.0 E_{\mathrm{r}} $. Here, the colorful lines indicate the spin-up and spin-down density distributions.

    下载: 全尺寸图片 幻灯片

    图 7  自旋-偶极模式(第一行)和自旋-呼吸模式(第二行)中自旋密度分布$ {\text{δ}} n(x, t)\equiv n_\uparrow(x, t)-n_\downarrow(x, t) $的t-x平面等高图　(a), (c) $ \varOmega=1.0 E_{\mathrm{r}} $处的条纹相; (b), (d) $ \varOmega=5.0 E_{\mathrm{r}} $处的零动量相. (a)—(d)中色条表示范围分别为: [–15, 15], [–0.1, 0.1], [–10, 15], [–0.14, 0]

    Figure 7.  Contour plots of time-dependent spin density $ {\text{δ}} n(x, t)\equiv n_\uparrow(x, t)-n_\downarrow(x, t) $ of spin-dipole mode (top panel) and spin-breathing mode (bottom panel) in the t-x plane: (a), (c) Stripe phase at $ \varOmega=1.0 E_{\mathrm{r}} $; (b), (d) zero-momentum phase at $ \varOmega=5.0 E_{\mathrm{r}} $. Color scales: (a) –15 to 15; (b) –0.1 to 0.1; (c) –10 to 15; (d) –0.14 to 0.

    下载: 全尺寸图片 幻灯片

    表 1  四种集体激发模式(偶极, 呼吸, 自旋-偶极, 自旋-呼吸)所对应的激发方式以及观测量. 其中, x0和α均为小量以使得系统被微弱地扰动

    Table 1.  Exciting approaches and observables for four collective excitation modes, including dipole mode, breathing mode, spin-dipole mode, and spin-breathing mode. Here, x0 and α are both small enough to perturb the systems slightly.

    集体激发模式 $ V_1(x) $ 物理观测量
    偶极模式 $ \dfrac{1}{2} m\omega_x^{2} (x-x_0)^2 $ $ \left\langle x\right\rangle $
    呼吸模式 $ \dfrac{1}{2} m(1+\alpha )^2\omega_x^{2} x^2 $ $ \left\langle x^2\right\rangle $
    自旋-偶极模式 $ \dfrac{1}{2} m\omega_x^{2} (x-\sigma_{z}x_0)^2 $ $ \left\langle\sigma_{z}x \right\rangle $
    自旋-呼吸模式 $ \dfrac{1}{2} m(1+\sigma_{z} \alpha )^2\omega_x^{2} x^2 $ $ \left\langle\sigma_{z}x^2\right\rangle $
    下载: 导出CSV
  • [1] Bloch I, Dalibard J, Zwerger W 2008 Rev. Mod. Phys. 80 885 doi: 10.1103/RevModPhys.80.885
    [2] Dalibard J, Gerbier F, Juzeliūnas G, Öhberg P 2011 Rev. Mod. Phys. 83 1523 doi: 10.1103/RevModPhys.83.1523
    [3] Goldman N, Juzeliūnas G, Öhberg P, Spielman I B 2014 Rep. Prog. Phys. 77 126401 doi: 10.1088/0034-4885/77/12/126401
    [4] Lin Y J, Jiménez-García K, Spielman I B 2011 Nature 471 83 doi: 10.1038/nature09887
    [5] Wang P, Yu Z Q, Fu Z, Miao J, Huang L, Chai S, Zhai H, Zhang J 2012 Phys. Rev. Lett. 109 095301 doi: 10.1103/PhysRevLett.109.095301
    [6] Cheuk L W, Sommer A T, Hadzibabic Z, Yefsah T, Bakr W S, Zwierlein M W 2012 Phys. Rev. Lett. 109 095302 doi: 10.1103/PhysRevLett.109.095302
    [7] Wu Z, Zhang L, Sun W, Xu X T, Wang B Z, Ji S C, Deng Y, Chen S, Liu X J, Pan J W 2016 Science 354 83 doi: 10.1126/science.aaf6689
    [8] Huang L, Meng Z, Wang P, Peng P, Zhang S L, Chen L, Li D, Zhou Q, Zhang J 2016 Nat. Phys. 12 540 doi: 10.1038/nphys3672
    [9] Chen H R, Lin K Y, Chen P K, Chiu N C, Wang J B, Chen C A, Huang P, Yip S K, Kawaguchi Y, Lin Y J 2018 Phys. Rev. Lett. 121 113204 doi: 10.1103/PhysRevLett.121.113204
    [10] Zhang D, Gao T, Zou P, Kong L, Li R, Shen X, Chen X L, Peng S G, Zhan M, Pu H, Jiang K 2019 Phys. Rev. Lett. 122 110402 doi: 10.1103/PhysRevLett.122.110402
    [11] Wang Z Y, Cheng X C, Wang B Z, Zhang J Y, Lu Y H, Yi C R, Niu S, Deng Y, Liu X J, Chen S, Pan J W 2021 Science 372 271
    [12] Galitski V, Spielman I B 2013 Nature 494 49
    [13] Zhai H 2015 Rep. Prog. Phys. 78 026001 doi: 10.1088/0034-4885/78/2/026001
    [14] Wang C, Gao C, Jian C M, Zhai H 2010 Phys. Rev. Lett. 105 160403 doi: 10.1103/PhysRevLett.105.160403
    [15] Ho T L, Zhang S 2011 Phys. Rev. Lett. 107 150403 doi: 10.1103/PhysRevLett.107.150403
    [16] Li Y, Pitaevskii L P, Stringari S 2012 Phys. Rev. Lett. 108 225301 doi: 10.1103/PhysRevLett.108.225301
    [17] Hu H, Ramachandhran B, Pu H, Liu X J 2012 Phys. Rev. Lett. 108 010402 doi: 10.1103/PhysRevLett.108.010402
    [18] Gong M, Tewari S, Zhang C 2011 Phys. Rev. Lett. 107 195303 doi: 10.1103/PhysRevLett.107.195303
    [19] Hu H, Jiang L, Liu X J, Pu H 2011 Phys. Rev. Lett. 107 195304 doi: 10.1103/PhysRevLett.107.195304
    [20] Yu Z Q, Zhai H 2011 Phys. Rev. Lett. 107 195305 doi: 10.1103/PhysRevLett.107.195305
    [21] Zhang J Y, Ji S C, Chen Z, Zhang L, Du Z D, Yan B, Pan G S, Zhao B, Deng Y J, Zhai H, Chen S, Pan J W 2012 Phys. Rev. Lett. 109 115301 doi: 10.1103/PhysRevLett.109.115301
    [22] Khamehchi M A, Zhang Y, Hamner C, Busch T, Engels P 2014 Phys. Rev. A 90 063624 doi: 10.1103/PhysRevA.90.063624
    [23] Ji S C, Zhang J Y, Zhang L, Du Z D, Zheng W, Deng Y J, Zhai H, Chen S, Pan J W 2014 Nat. Phys. 10 314 doi: 10.1038/nphys2905
    [24] Ji S C, Zhang L, Xu X T, Wu Z, Deng Y, Chen S, Pan J W 2015 Phys. Rev. Lett. 114 105301 doi: 10.1103/PhysRevLett.114.105301
    [25] Zhu Q, Zhang C, Wu B 2012 EPL 100 50003 doi: 10.1209/0295-5075/100/50003
    [26] Zhang Y C, Yu Z Q, Ng T K, Zhang S, Pitaevskii L, Stringari S 2016 Phys. Rev. A 94 033635 doi: 10.1103/PhysRevA.94.033635
    [27] Yu Z Q 2017 Phys. Rev. A 95 033618 doi: 10.1103/PhysRevA.95.033618
    [28] Chen X L, Wang J, Li Y, Liu X J, Hu H 2018 Phys. Rev. A 98 013614 doi: 10.1103/PhysRevA.98.013614
    [29] Chen X L, Liu X J, Hu H 2022 Phys. Rev. A 106 023302 doi: 10.1103/PhysRevA.106.023302
    [30] Meng Z, Huang L, Peng P, Li D, Chen L, Xu Y, Zhang C, Wang P, Zhang J 2016 Phys. Rev. Lett. 117 235304 doi: 10.1103/PhysRevLett.117.235304
    [31] Sun W, Yi C R, Wang B Z, Zhang W W, Sanders B C, Xu X T, Wang Z Y, Schmiedmayer J, Deng Y, Liu X J, Chen S, Pan J W 2018 Phys. Rev. Lett. 121 250403 doi: 10.1103/PhysRevLett.121.250403
    [32] Zhang J Y, Yi C R, Zhang L, Jiao R H, Shi K Y, Yuan H, Zhang W, Liu X J, Chen S, Pan J W 2023 Phys. Rev. Lett. 130 043201 doi: 10.1103/PhysRevLett.130.043201
    [33] Martone G I, Li Y, Pitaevskii L P, Stringari S 2012 Phys. Rev. A 86 063621 doi: 10.1103/PhysRevA.86.063621
    [34] Zheng W, Yu Z Q, Cui X, Zhai H 2013 J. Phys. B: At. Mol. Opt. Phys. 46 134007 doi: 10.1088/0953-4075/46/13/134007
    [35] Chen X L, Liu X J, Hu H 2017 Phys. Rev. A 96 013625 doi: 10.1103/PhysRevA.96.013625
    [36] Chen L, Pu H, Yu Z Q, Zhang Y 2017 Phys. Rev. A 95 033616 doi: 10.1103/PhysRevA.95.033616
    [37] Rajat, Roy A, Gautam S 2022 Phys. Rev. A 106 013304 doi: 10.1103/PhysRevA.106.013304
    [38] Liang J C, Zhang A X, Xue J K 2024 Phys. Rev. A 109 053307 doi: 10.1103/PhysRevA.109.053307
    [39] Li J R, Lee J, Huang W, Burchesky S, Shteynas B, Top F Ç, Jamison A O, Ketterle W 2017 Nature 543 91 doi: 10.1038/nature21431
    [40] Léonard J, Morales A, Zupancic P, Esslinger T, Donner T 2017 Nature 543 87 doi: 10.1038/nature21067
    [41] Geier K T, Martone G I, Hauke P, Stringari S 2021 Phys. Rev. Lett. 127 115301 doi: 10.1103/PhysRevLett.127.115301
    [42] Geier K T, Martone G I, Hauke P, Ketterle W, Stringari S 2023 Phys. Rev. Lett. 130 156001 doi: 10.1103/PhysRevLett.130.156001
    [43] Li Y, Martone G I, Stringari S 2012 EPL 99 56008 doi: 10.1209/0295-5075/99/56008
    [44] Sartori A, Marino J, Stringari S, Recati A 2015 New J. Phys. 17 093036 doi: 10.1088/1367-2630/17/9/093036
    [45] Bienaimé T, Fava E, Colzi G, Mordini C, Serafini S, Qu C, Stringari S, Lamporesi G, Ferrari G 2016 Phys. Rev. A 94 063652 doi: 10.1103/PhysRevA.94.063652
    [46] Fava E, Bienaimé T, Mordini C, Colzi G, Qu C, Stringari S, Lamporesi G, Ferrari G 2018 Phys. Rev. Lett. 120 170401 doi: 10.1103/PhysRevLett.120.170401
    [47] Dalfovo F, Giorgini S, Pitaevskii L P, Stringari S 1999 Rev. Mod. Phys. 71 463 doi: 10.1103/RevModPhys.71.463
    [48] Menotti C, Stringari S 2002 Phys. Rev. A 66 043610 doi: 10.1103/PhysRevA.66.043610
    [49] Pitaevskii L, Stringari S 2016 Bose-Einstein Condensation and Superfluidity (Oxford: Oxford University Press) p406
  • 加载中
图( 7) 表( 1)
计量
  • 文章访问数:  18
  • HTML全文浏览数:  18
  • PDF下载数:  1
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-03-30
  • 刊出日期:  2025-07-20

自旋-轨道耦合玻色气体中集体激发动力学

    通讯作者: E-mail: xiaolongchen@zstu.edu.cn
  • 1. 浙江理工大学物理学系, 杭州　310018
  • 2. 浙江理工大学, 全省量子物态与光场调控重点实验室, 杭州　310018
  • 收稿日期:  2025-03-30

摘要: 基于数值求解定态与含时Gross-Pitaevskii方程, 本文研究了一维拉曼型自旋-轨道耦合玻色气体中的静态特性与低能集体激发动力学性质. 分析了凝聚体动量、自旋极化率和基态能量来分类三种基态物相(条纹相、平面波相和零动量相)以及对应的相变. 在此基础上, 通过设计不同的微扰激发方式, 重点研究了四种典型的低能集体激发模式(偶极、呼吸、自旋-偶极和自旋-呼吸模式)的频率特性和动力学行为. 结果发现, 四种模式频率随拉比频率增加呈现非单调变化行为且不同物相中的集体激发模式表现出显著差异, 尤其是自旋相关的两种模式在条纹相中呈现自旋自由度相关的独特振荡行为. 这些发现将为理解自旋-轨道耦合玻色气体中新奇物相的量子多体动力学提供重要参考和理论依据.

English Abstract

    全文HTML

    1.   引　言

    • 自旋-轨道耦合(spin-orbit coupling, SOC)是指粒子的自旋与其运动之间的耦合相互作用, 普遍存在于半导体及各类新颖量子材料中, 并在多个物理领域备受关注. 而超冷原子气体由于具有高纯净性以及高自由度的精准调控[1], 已成为人工合成规范场和模拟SOC的重要平台[2,3]. 在冷原子实验中, 实验物理学家利用拉曼激光精密调控原子-光相互作用, 相继在超冷玻色与费米气体中实现了一维拉曼型SOC[4–6], 二维不同类型SOC[7–10]和三维SOC[11]. 这些突破性实验进展极大推动了SOC在量子多体物理中非平庸量子效应和新奇物理现象的研究热潮[12,13], 包括但不限于体系中新奇玻色与费米量子物相[14–20]、激发谱与集体激发性质[21–24]、超流性质[25–29]、拓扑能带性质[30–32]等研究方向.

      对于拉曼型自旋-轨道耦合量子气体, SOC能显著改变单粒子色散关系, 因此可通过调节拉曼耦合强度(即拉比频率)依次诱导产生条纹相、平面波相和零动量相等多种新颖基态物相[33,34]. 特别是, SOC显著改变体系中平面波相的激发谱, 使其呈现类似液氦中的roton-maxon结构[33–35]. 随着拉比频率减小, roton能隙软化趋向于零, 系统将呈现平面波相到条纹相的一阶相变, 并伴随着基态能量、密度等不连续的常见一阶相变现象[16,33,35]. 而在另一边随着拉比频率增大, 系统等效质量[33,34]、磁化率[16]趋于发散, 且伴随着各向异性声速被极大地抑制[24,33,35]. 在临界拉比频率处, 体系基态发生平面波相到零动量相的二阶相变, 体系激发谱呈现二次型色散关系[33–35], 将完全抑制临界速度或声速到零值[27,34]. 这些关于低能激发谱roton-maxon结构和各向异性声速等新奇特性已在冷原子实验中得到验证[21–24]. 截至目前, 关于拉曼型自旋-轨道耦合玻色气体的研究十分广泛并已取得了大量进展, 但大多数实验或理论研究都关注在体系的静态特性或平庸物相, 如平面波和零动量相. 在此双组分玻色气体体系, 实验与理论关注的激发特性研究多聚焦于低能激发谱和集体激发动力学行为[21,22,36–38]. 这些研究多采用Bogoliubov理论直接求解激发谱能量, 并多关注于与整体密度关联的单一模式(如偶极模式或呼吸模式)频率. 针对新奇物相尤其是条纹相[39–42]以及与自旋自由度紧密相关的集体激发动力学行为(如自旋-偶极振荡模式[43–46]、自旋-呼吸振荡模式)的研究十分缺乏.

      关于自旋-轨道耦合玻色气体的研究已经非常广泛, 包括与本文相关的集体激发模式研究. 本文描述的不同模式频率随拉比频率的非单调性依赖行为并非首次, 已在之前的相关理论和实验文献(如文献[21-22,38-40,43]) 中发现. 但这些研究多采用与本文不同的方法, 如Bogoliubov理论直接求解激发谱能量, 并多聚焦于与整体密度关联的单一模式(如偶极模式)频率, 缺少本文关注的对于不同物相尤其是条纹相, 以及对于与自旋自由度相关的集体激发模式独特振荡行为的刻画.

      基于上述背景, 本文在简单回顾一维自旋-轨道耦合弱相互作用玻色气体的典型静态特征后, 着重研究三种基态物相中几种典型低能集体激发模式的频率和动力学行为. 通过数值求解静态Gross-Pitaevskii (GP)方程(见第2节), 首先计算拉比频率调控的凝聚体动量、自旋极化率、能量等物理量分类三种基态物相以及界定两个相变处的典型特征(见第3节). 紧接着, 重点考虑四种常见的低能集体激发模式以及动力学行为, 包括整体密度相关的偶极、呼吸或单极模式, 以及与自旋自由度相关的自旋-偶极和自旋-呼吸模式. 利用不同的激发方式分别激发对应的振荡模式, 并通过求解含时GP方程得到含时波函数和构建对应观测量. 通过分析观测量与各自旋分量密度分布随时间的变化, 展示三种基态物相中所关注的集体激发模式频率以及动力学行为(见第4节). 最后, 第5节做简短的总结.

    2.   理论模型

    • 本文考虑具有拉曼型自旋-轨道耦合的一维弱相互作用玻色气体, 可由两组分的哈密顿量描述, 即$ \hat{H}=\hat{H}_{0}+\hat{H}_{{\rm{int}}} $. 其中, 单粒子哈密顿量$ \hat{H}_{0} $和相互作用哈密顿量$ \hat{H}_{{\rm{int}}} $分别为[4,16,34]

      其中, $ g_{\sigma=\sigma'} $和$ g_{\sigma\neq\sigma'} $分别为等效的一维种内和种间相互作用强度. 本文将考虑相同种内相互作用强度的情况, 即 $ g_{\uparrow\uparrow}=g_{\downarrow\downarrow}\equiv g $. 其中, 包含自旋-轨道耦合的单粒子哈密顿量具体形式为

      式中$ \hat{P}_x=-{\mathrm{i}}\hbar\nabla_x $为x方向上的正则动量算子, 其通过$ \propto \hat{P}_x\hat{\sigma}_{z} $项与自旋自由度耦合形成自旋-轨道耦合项. Ω, δ和$ \hat{\sigma}_{x, z} $分别为拉比频率、拉曼激光失谐和泡利算符. 激光的反冲动量$ {\boldsymbol{k}}_{\rm{r}} $沿x方向, 对应的反冲能量可写成$ E_{\rm{r}}=\dfrac{\hbar^2 k_{\rm{r}}^2}{2 m} $.

      在平均场近似下, 可以把玻色场算符$ \hat{\varPsi}_{\sigma} $表示为经典场$ \psi_\sigma $, 再通过海森伯运动方程得到描述含谐振势$ V_0(x)={1}/{2}m\omega^{2} x^{2} $的一维自旋-轨道耦合玻色气体的Gross-Pitaevskii (GP)方程, 即($ \sigma\neq\bar{\sigma} $):

      其中, $ {\cal{L}}_{\sigma=\uparrow, \downarrow}\equiv\dfrac{\left(P_x\mp k_{\rm{r}} \right)^2}{2 m}+V_0(x) $. 考虑分离变量$ \psi_\sigma(x, t)=\psi_\sigma(x) {\mathrm{e}}^{-{\mathrm{i}}\mu t/\hbar} $, 上述含时方程将变为静态方程, 可用于观察体系的波函数、密度、能量等静态特征. 在此基础上, 利用含时GP方程(2)研究体系中不同集体激发模式的动力学行为和性质. 需要注意的是, 低维系统中量子涨落效应较强, GP方程可能会存在可用性和有效性等问题, 需要谨慎地考虑适用范围. 在本文的计算中, 已通过对比三维实验测量和理论计算结果, 如临界拉比频率、凝聚体动量等物理量, 认为本文中的低维GP方程能够定性地甚至定量地描述此自旋-轨道耦合玻色气体.

      先简单介绍一下自旋-轨道耦合玻色气体中的三种典型物相以及相关性质. 之前的研究发现[34], 自旋-轨道耦合能显著地改变体系单粒子能谱结构, 即在一定小拉比频率范围内单粒子色散呈现出简并的双最小值结构. 因此, 系统基态波函数可以表示为两个或多个简并态的叠加, 从而破坏空间平移对称性形成具有空间周期性调制密度分布的条纹相(stripe phase, ST). 本文仅考虑两个简并单粒子基态的等权叠加构成的条纹相. 随着拉比频率逐渐增大, 相互作用促使体系发生自发对称破缺, 系统倾向于选择双简并态中的单一动量态, 形成具有非零值动量的平面波相(plane-wave phase, PW). 而当拉比频率继续增加, 系统单粒子能谱将从简并双最小值结构变成原点单最小值结构, 即单粒子色散在零动量处呈现全局能量极小点. 此时, 系统或原子倾向于凝聚到动量空间原点, 表现为零动量相(zero-momentum phase, ZM). 此时, 基态波函数由两个自旋分量的等权叠加构成, 且两个分量均具有零值动量. 采取两种平面波叠加的变分波函数形式以及应用变分方法[16], 可以得到三种物相的相变点. 例如, ST-PW相变的临界拉比频率为$ \varOmega_{{\mathrm{c}}1}=2\left[(2 E_{{\rm{r}}}+ G_{1})(2 E_{{\rm{r}}}-2 G_{2})\dfrac{2 G_{2}}{G_{1}+2 G_{2}}\right]^{1/2} $以及PW-ZM相变的临界拉比频率为$ \varOmega_{{\mathrm{c}}2}=4 E_{{\rm{r}}}-4 G_{2} $, 其中, $ G_{1}=(g+ g_{\uparrow\downarrow})\bar{n}/4 $和$ G_{2}=(g-g_{\uparrow\downarrow})\bar{n}/4 $为基于密度$ \bar{n} $定义的相互作用能量常数.

      在具体的数值计算中, 选取零值激光失谐$ \delta=0 $以及相互作用常数$ g_{\uparrow\downarrow}=0.7 g $以增大新奇的条纹相空间. 在这组参数下, 基态中三个典型物相都存在, 利用上述变分法确定的ST-PW相变和PW-ZM相变的临界拉比频率分别为$ \varOmega_{{\mathrm{c}}1}=2.08 E_{\rm{r}} $和$ \varOmega_{{\mathrm{c}}2}=3.88 E_{\rm{r}} $. 本文使用反冲动量$ k_{\rm{r}} $和反冲能量$ E_{\rm{r}} $作为后文计算的凝聚体动量$ P_x $, 拉比频率Ω, 基态能量E对应的单位. 而在其他物理量的计算中, 使用常用的谐振子本征频率$ \omega_x $, 时间$ 1/\omega_x $, 长度$ l\equiv\sqrt{\hbar/m\omega_x} $作为单位.

    3.   静态特性: 凝聚体动量、自旋极化率及基态能量

    • 通过求解静态GP方程(2), 首先研究一定拉比频率Ω范围内自旋-轨道耦合玻色气体在谐振势中的典型基态及其部分静态特性. 具体来说, 利用算符劈裂近似和虚时演化方法数值求解此方程, 得到系统在特定Ω处的基态波函数以及密度分布.

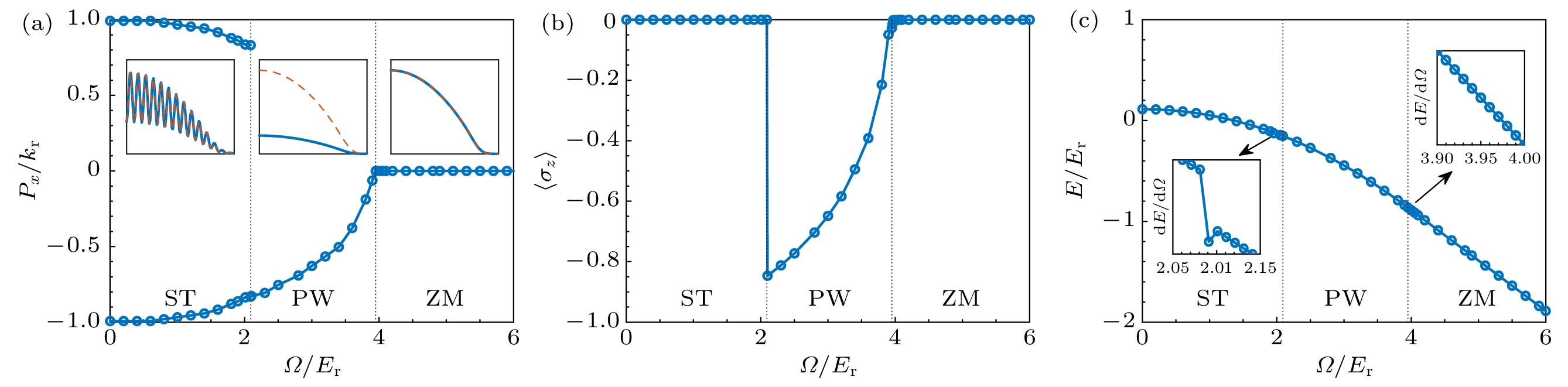
      图1(a)通过傅里叶变换分析基态凝聚体波函数, 画出了基态凝聚体动量$ P_x $随Ω的变化行为. 在选取的Ω范围内, 发现三种典型的基态物相, 分别为: 1)具有两种不同动量$ \pm P_x $平面波叠加的ST相, 表现为周期性调制的密度分布(见左插图)且$ |P_x| $随Ω增大而缓慢减小; 2)具有单一凝聚体动量的PW相, 表现为不同比例的自旋分量密度(见中插图)且其动量$ |P_x| $随Ω增大而单调递减直至零; 3)凝聚体动量$ P_x=0 $的ZM相, 表现为相同比例的自旋分量密度(见右插图).

      图1(b)中进一步计算了三个物相中的凝聚体自旋极化率$ \langle\sigma_z\rangle\equiv\dfrac{\langle\psi| \sigma_z|\psi\rangle}{\langle\psi|\psi\rangle} $, 此处已定义自旋量$ \left| \psi \right\rangle =[\psi_\uparrow(x), \psi_\downarrow(x)]^{\mathrm{T}} $. 可以看到, 对于ST和ZM相, 体系凝聚体的两自旋分量密度分布完全相同, 自旋极化率为零, 表现为“非磁性的”物相. 与此形成鲜明对比, PW相的两个自旋分量密度是不对等的, 自旋极化率为非零且随Ω增大而单调递减直至零, 表现为“磁性的”物相.

      此外, 图1(c)还画出凝聚体基态能量E关于拉比频率Ω的变化, 呈现出随着Ω的增加而单调平缓下降的趋势. 通过计算能量关于拉比频率的导数$ \dfrac{{\mathrm{d}}E}{{\mathrm{d}}\varOmega} $, 可以看到在ST-PW相变点处导数不连续(见左插图), 揭示此处为一阶相变. 而对于PW-ZM相变点处, 一阶导数为平滑连续的(见右插图), 意味着其二阶相变的特性, 这也与此相变点处发散的磁化率特征相对应[16]. 对于一阶ST-PW相变, 通过数值方法计算上述静态特性确定的相变点为$ 2.08 E_{\rm{r}} $(图中竖虚线), 与通过变分法确定的相变点$ \varOmega_{{\mathrm{c}}1} $重合[16]. 而对于二阶PW-ZM相变, 难以通过能量或密度区分相变点. 上述数值方法确定的相变点为$ 3.95 E_{\rm{r}} $(图中竖点线), 与变分法确定的相变点$ \varOmega_{{\mathrm{c}}2} $还有微小的差距, 但不影响本文对三种物相基本性质的研究结论.

    4.   低能集体激发动力学

    • 低能集体激发或元激发是研究量子多体系统激发态特性和动力学行为的重要内容. 实验上常通过外加微弱的扰动激发体系从基态到激发态并测量响应来定量研究系统的物理特性[21,22]. 本文通过微扰改变外部束缚势阱来激发四种常见低能集体激发振荡模式, 并通过数值求解含时GP方程(2)来研究系统在不同激发下的动力学行为.

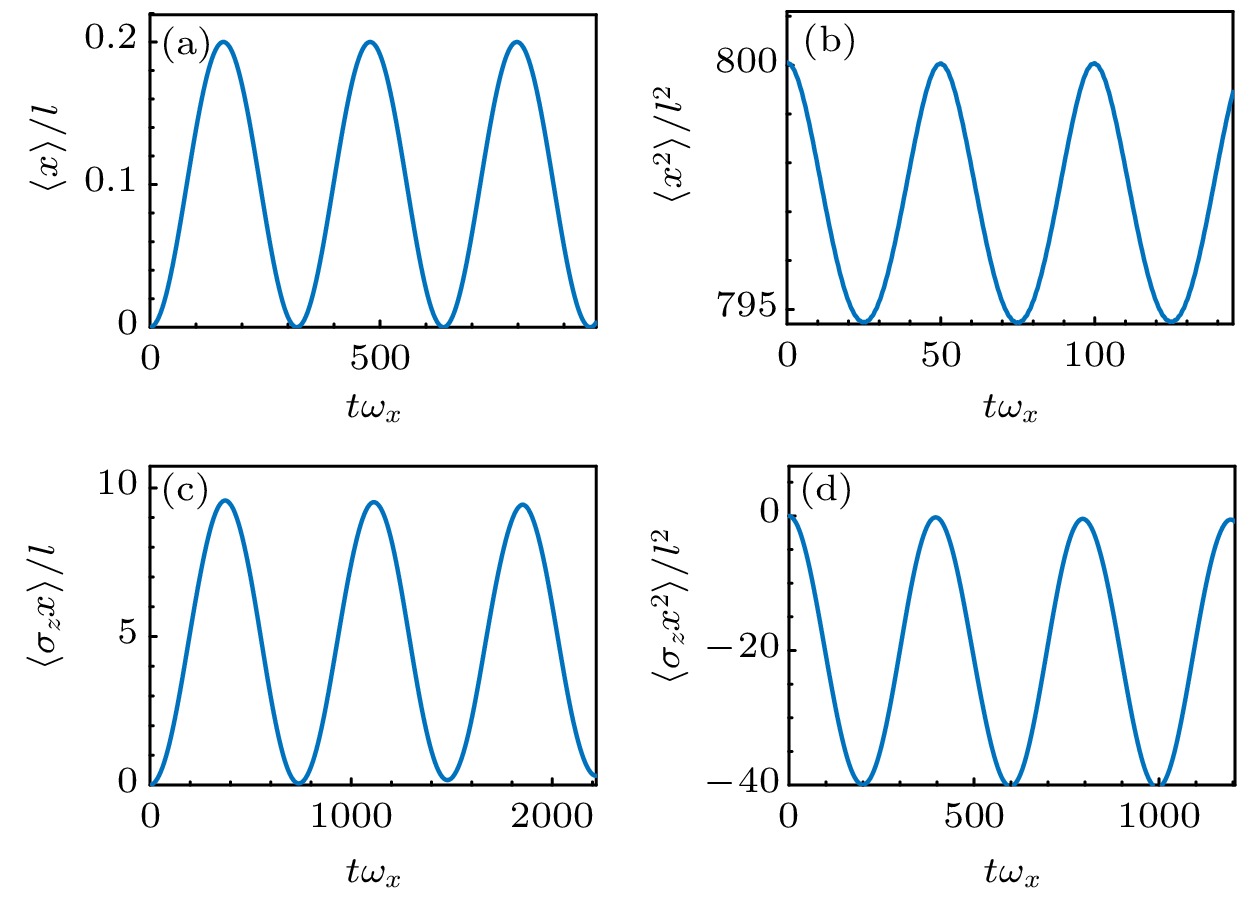
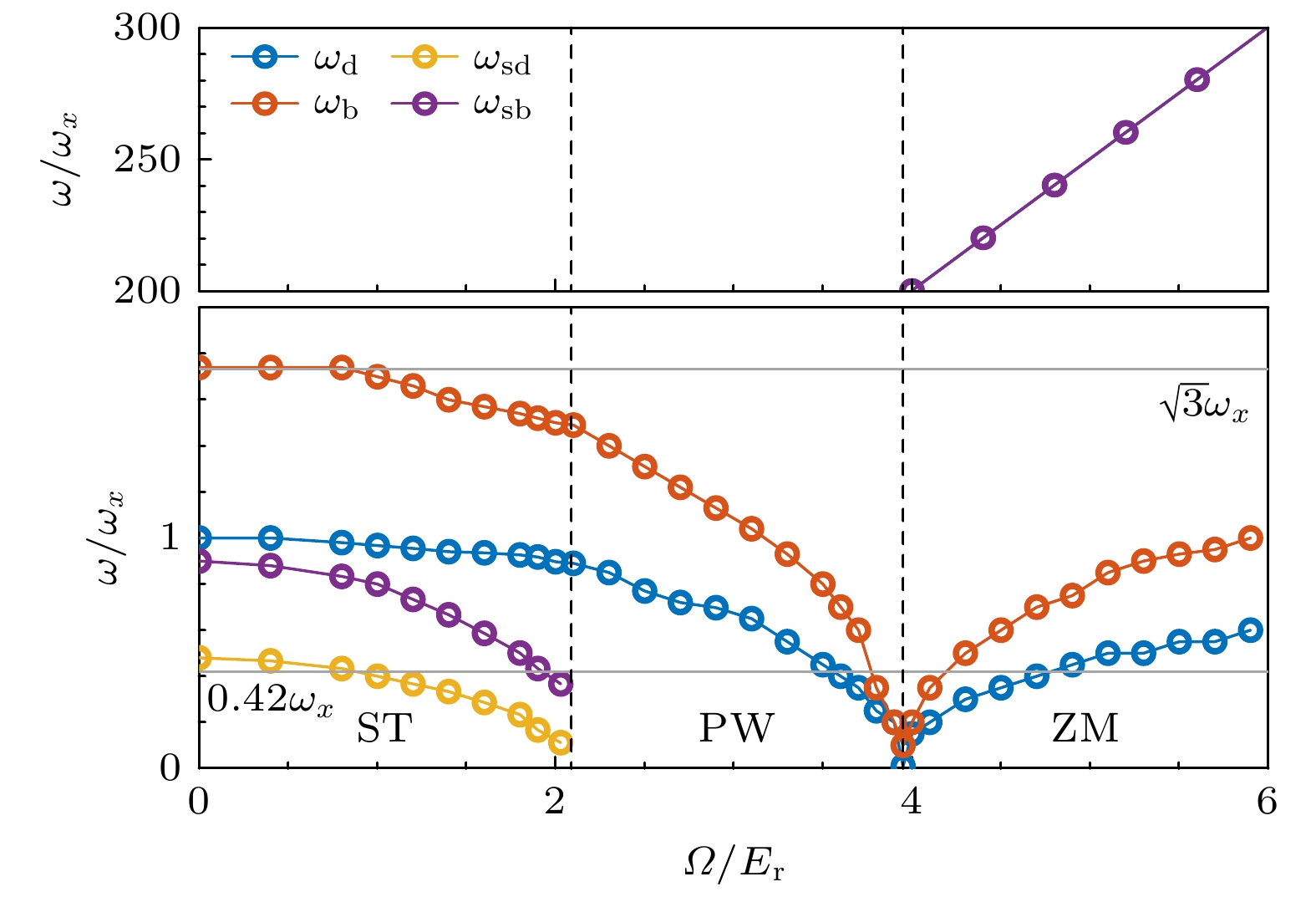
      具体来说, 通过突然改变外势$ V_0(x) $为不同形式的$ V_1(x) $激发体系对应的集体激发模式, 重点关注偶极(dipole, d)、呼吸或单极(breathing or monopole, b)、自旋-偶极(spin-dipole, sd)和自旋-呼吸(spin-breathing, sb)几种重要模式的振荡动力学行为. 如表1所列, 通过四种不同形式$ V_1(x) $分别激发特定的集体振荡模式, 并通过计算对应的物理观测量含时演化行为来确定对应集体振荡模式的动力学行为以及振荡频率. 以偶极模式为例, 通过将未扰动谐振势$ V_0(x) $中心偏移微小位移$ x_0 $, 即$ V_1(x)=\dfrac{1}{2} m\omega_x^{2} (x-x_0)^2 $, 求解含时GP方程得到波函数或密度分布的实时演化图像. 进一步以此含时波函数构建观测量原子云质心位移的含时振荡变化, 即$ \langle x(t)\rangle\equiv \dfrac{\langle\psi(x, t)| x|\psi(x, t)\rangle}{\langle\psi(x, t)|\psi(x, t)\rangle} $, 便可通过傅里叶变换分析出存在其中的偶极振荡模式频率$ \omega_{\rm{d}} $. 类似地, 可以计算并分析相应算符$ {\cal{O}}=x^2, \sigma_{z} x, \sigma_{z} x^2 $的含时观测量$ \langle \mathcal{O}(t) \rangle \equiv \dfrac{\langle\psi(x, t)| {\cal{O}}|\psi(x, t)\rangle}{\langle\psi(x, t)|\psi(x, t)\rangle} $来求得其中的偶极振荡、自旋-偶极振荡和自旋-呼吸振荡模式频率. 如图2所示, 以ST相为例, 通过微扰系统并观测对应观测量, 即$ \langle x\rangle $, $ \langle x^2\rangle $, $ \langle\sigma_{z}x\rangle $, $ \langle\sigma_{z}x^2\rangle $的含时演化行为, 可以通过其中简谐振荡行为得到四种关注的集体激发模式频率. 其中, 自旋-偶极模式的含时观测量$ \langle\sigma_{z}x\rangle $为不同自旋组分密度分布的质心坐标的差值随时间的变化, 自旋-呼吸模式的含时观测量$ \langle\sigma_{z}x^2\rangle $为不同自旋组分原子云大小的差值随时间的变化. 需要注意的是, 这里均采用极其微小的扰动或激发幅度来激发不同振荡模式, 即表1中$ x_0 $和α的取值均为微小量, 目的在于不破坏系统稳定性的前提下使得激发模式简谐振荡的时间相对较长.

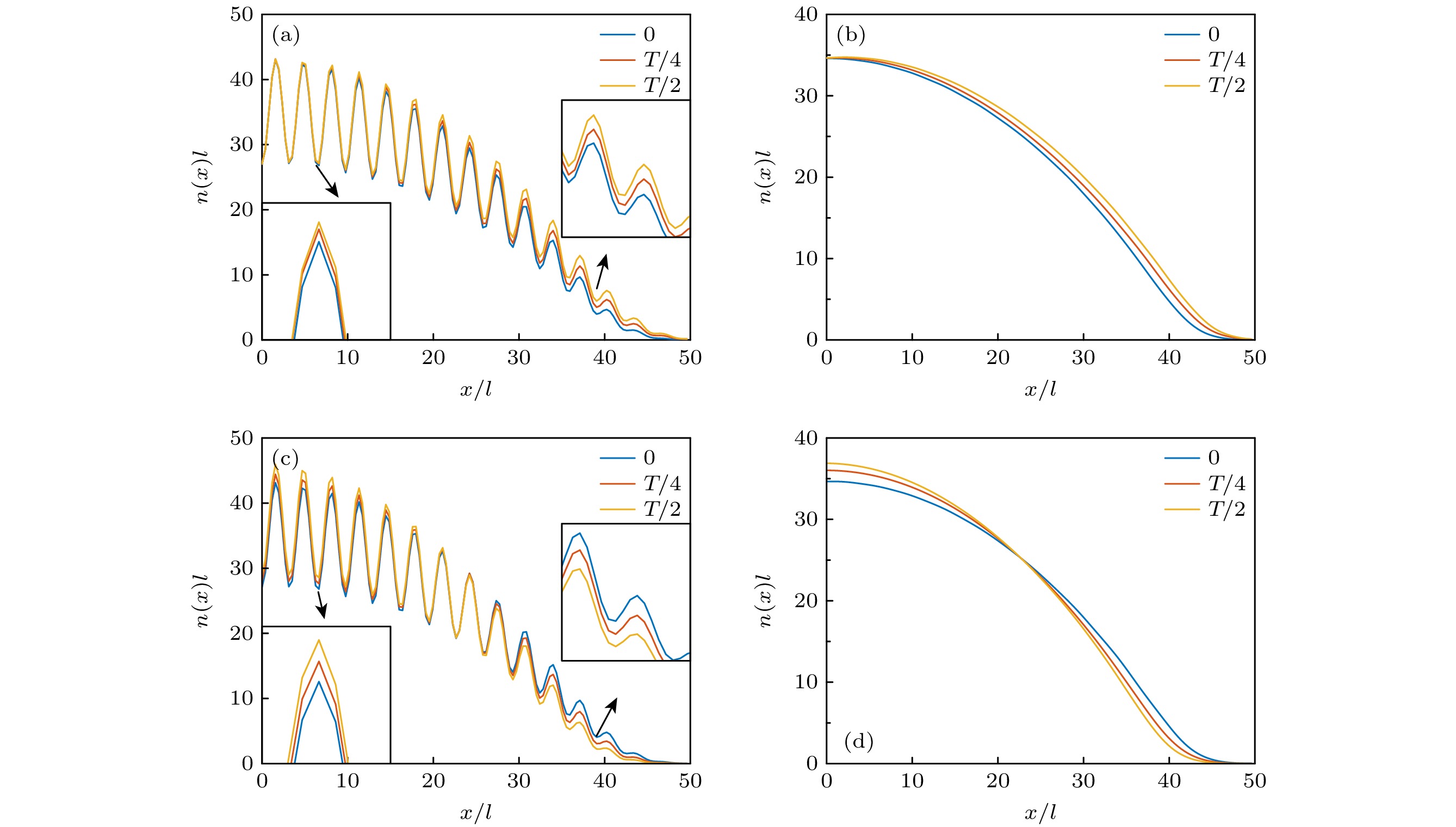
      通过上述动力学分析方式, 在一定的拉比频率范围内将三种不同物相对应的几种集体模式频率提取出来并画于图3中, 其中分别以蓝色、红色、黄色和紫色圈线表示偶极、呼吸、自旋-偶极和自旋-呼吸模式频率结果. 在ST相中, 分别观察到四种激发模式频率随Ω增加而缓慢地减小的行为. 在零拉比频率($ \varOmega\to0 $)极限下, 偶极模式和呼吸模式频率能分别回到一维弱相互作用玻色气体的解析结果$ \omega_{{\mathrm{d}}}=\omega_{x} $[47]和$ \omega_{{\mathrm{b}}}=\sqrt{3} \omega_{x} $[48], 但自旋-偶极模式频率$ \omega_{{\mathrm{sd}}}\approx0.48\omega_{x} $与求和规则得到的解析结果$ \omega_{{\mathrm{sd}}}^{\rm{analytic}}=\sqrt{\dfrac{g-g_{12}}{g+g_{12}}}\omega_{x}\approx 0.42\omega_{x} $[49]存在微小的差异. 在极化的PW相中, 自旋极化率偏离于0, 两组分密度占比相差较大, 与自旋相关的模式难以被激发出来或被观测得到, 均淹没在更显著的整体密度相关的偶极模式和呼吸模式振荡行为之中. 偶极和呼吸模式频率均随Ω增加而平滑减小并在PW-ZM相变点显著地变成零. 这是因为在PW-ZM相变点处, 长波极限下单粒子能谱基于准动量的二阶导数趋于零, 换言之, 体系的等效质量趋于发散[33,34], 这将极大地抑制系统的振荡行为, 从而使得集体激发模式频率趋于零值. 同时, 相变点处的超流密度分数[26,28,29]、声速[24,33,35]等与体系超流特性紧密关联的物理量也被完全抑制到零值. 在ZM相中, 随着Ω变大, 偶极和呼吸模式频率从零单调递增. 同时, 自旋-偶极和自旋-呼吸两种模式频率完全相同并比前两种模频平均高两个数量级, 且呈现一个类似线性的Ω依赖行为.

      在刻画完体系整体的不同集体激发模式频率与拉比频率的关系图后, 进一步关注不同模式具体的振荡动力学行为. 如图4所示, 首先在ST和PW两种物相中研究常见的偶极和呼吸模式动力学行为(ZM相中两种模式的结果与PW的结果类似), 分析一个完整周期内的三个关键时间节点的整体密度分布. 两种模式都可通过对系统施加整体扰动(如谐振势质心偏移和频率改变)而激发, 并观察其整体密度动力学. 对于偶极模式, 系统表现为整体原子云质心在x方向上的运动行为. 因此可在图4(a)和图4(b)中看到一个周期内不同时刻原子云整体的左右偏移, 且在半个周期时(黄色线)偏移量相对于初始时刻的密度分布(蓝色线)变化最大. 而对于呼吸模式, 系统在图4(c)和图4(d)中表现为密度表面的改变, 原子云的峰部和尾部的密度分布呈现上下偏移, 呈现类似一种类似“呼吸”过程的周期性变化趋势.

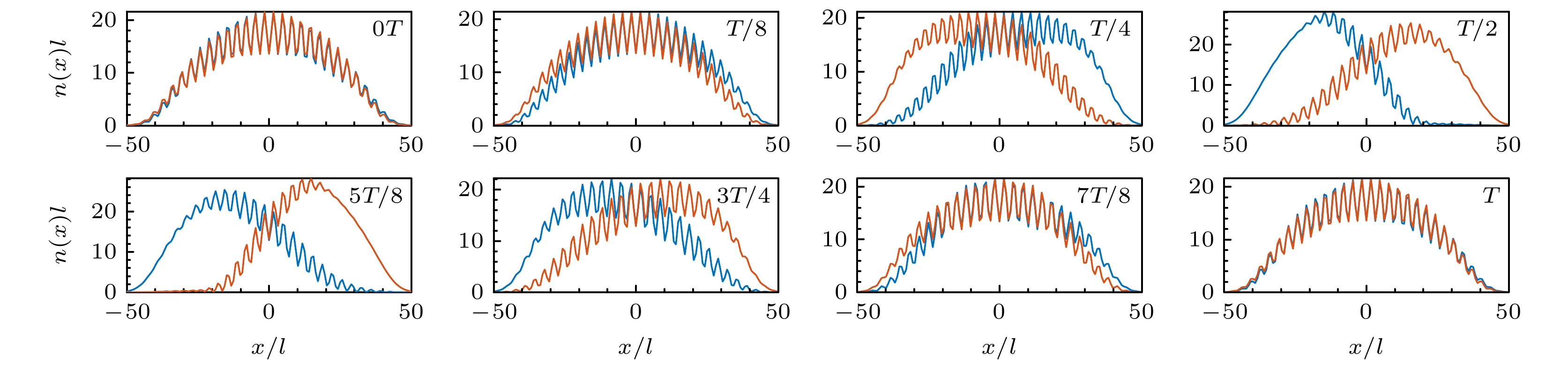
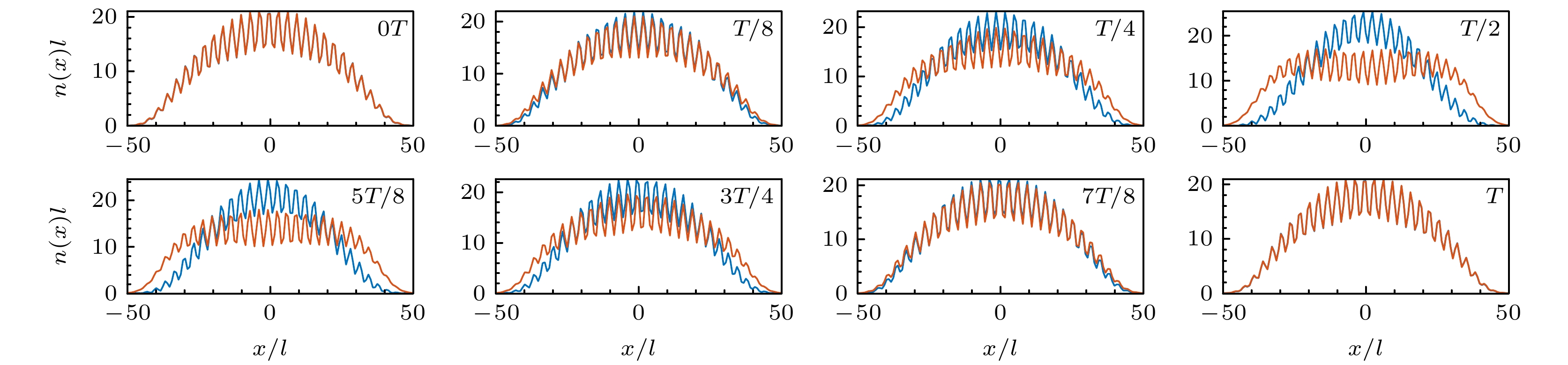
      相比常见的偶极和呼吸模式, 本文重点关注与自旋自由度密切相关的自旋-偶极和自旋-呼吸模式, 尤其是在新奇的ST相中的独特动力学表现. 这两种模式可以通过引入自旋相关的外部势场来激发, 从而使得两个自旋分量分别经历不同的外部势场作用. 在超冷原子实验中, 可通过施加一个短暂的梯度磁场使得两个自旋态的势阱中心发生微小相对位移诱导激发自旋-偶极振荡, 并进一步通过吸收成像技术记录并分析相应观测量随时间的变化得到模式振荡频率[43,44]. 图5和图6选取了一个完整振荡周期中8个不同时刻($ 0,\; \dfrac{T}{8}, \;\dfrac{T}{4}, \;\dfrac{T}{2},\; \dfrac{5 T}{8},\; \dfrac{3 T}{4},\; \dfrac{7 T}{8},\; T $)分别观察$ \varOmega = 1.0 E_r $处 ST相的两种振荡模式中不同自旋分量的密度动 力学行为. 两种激发模式下的两个组分密度均表 现出相对运动的趋势, 但它们的运动方式存在显 著差异. 作为最简单的集体激发模式之一, 自旋- 偶极振荡的典型特征是两个组分原子云围绕平衡点以相反的相位做刚性运动. 可以针对不同组分 原子云的束缚谐振势施加不同的质心偏移, 即$ V_1(x)=\dfrac{1}{2}m\omega_x^{2}(x- \sigma_{z}x_0)^2 $(见表1), 来诱导两组分密度的相对运动. 从图5可以看到, 两组分密度在前半个周期内开始沿x方向相向运动并在半周期处密度差异最为显著, 紧接着两组分密度趋于重叠, 直至整个周期处回到差异最小的状态. 自旋-呼吸模式通常表现为自旋密度分布随时间发生周期性的膨胀和收缩. 类似地, 可以通过引入自旋相关的束缚谐振势频率, 即表1中的$ V_1(x)=\dfrac{1}{2} m(1+ \sigma_{z}\alpha)^2\omega_x^{2} x^2 $, 来诱导自旋密度分布的变化. 在图6中, 不同自旋分量密度呈现膨胀和收缩的相对变化趋势, 两者相对运动的差异在半周期处达到最大并在整周期时恢复到最小. 两种集体激发模式中相对运动趋势的变化可以通过研究$ \langle\sigma_{z}x\rangle $和$ \langle\sigma_{z}x^2\rangle $随时间的变化关系得出, 并定量求出各自振荡模式频率, 见图2(c)和图2(d).

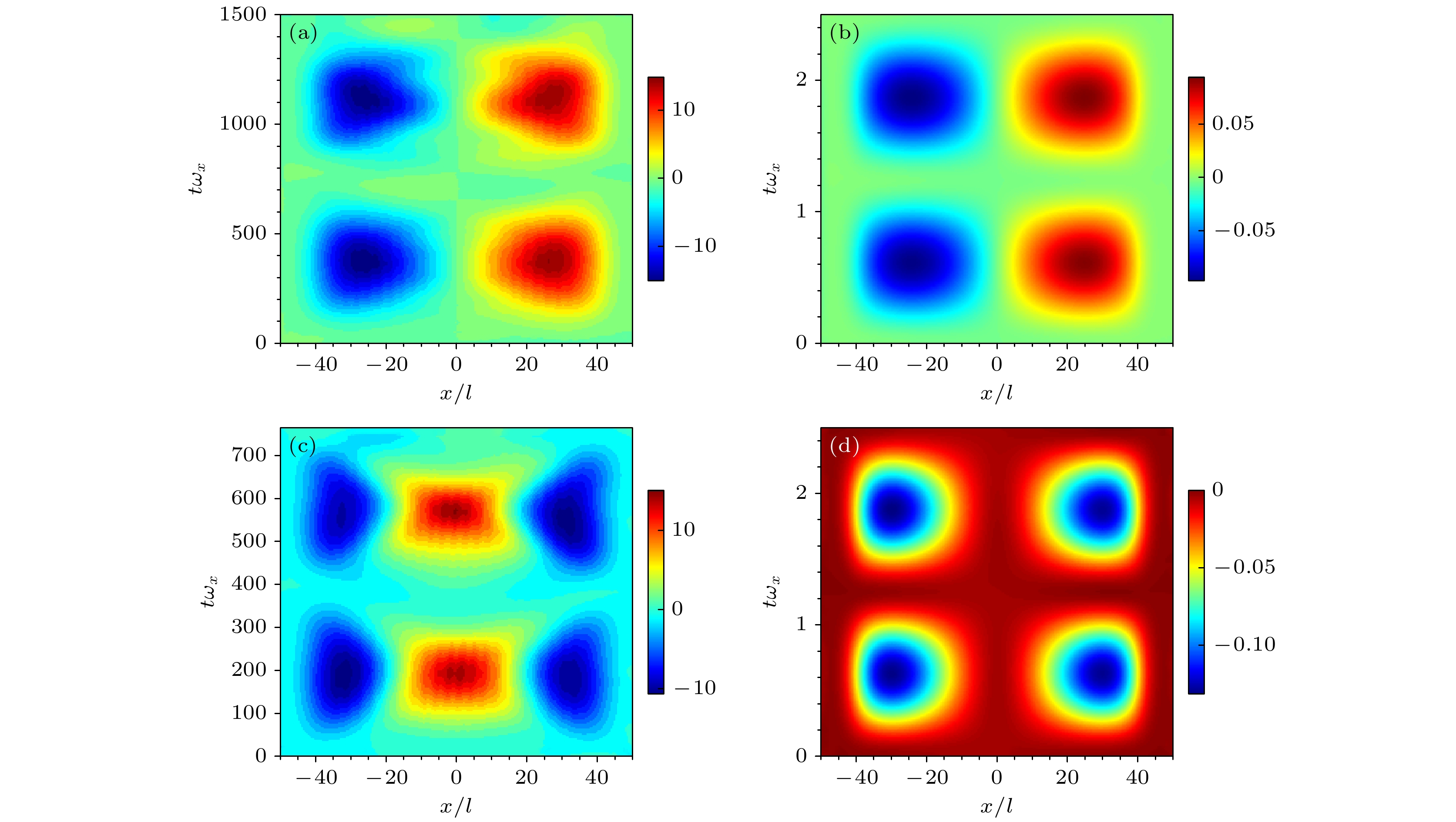
      为了更清晰地展示自旋-偶极模式和自旋-呼吸模式中与自旋自由度相关的特征, 图7展示了自旋密度分布$ {\text{δ}} n(x, t)\equiv n_{\uparrow}(x, t)-n_{\downarrow}(x, t) $在时间t和位移x平面的等高图. 此处选取了$ \varOmega=1.0 E_{\mathrm{r}} $处的条纹相(图7(a), 图7(c))和$ \varOmega=5.0 E_{\mathrm{r }}$处的零动量相(图7(b), 图7(d)). 对于自旋-偶极模式, 两种物相中自旋密度分布$ {\text{δ}}n(x, t) $的行为相似, 仅展现的振荡周期不一致. 如图图7(a)和图7(b)中红色和蓝色区域所示, 不同自旋分量密度进行相对运动导致密度分布两端出现高低交替的差异, 因而自旋密度分布会在两端处呈现异号分布的特征并随时间变化周期性呈现. 而对于自旋-呼吸模式, 两种物相中自旋密度分布$ {\text{δ}} n(x, t) $的行为表现不同. 在条纹相中, 不同自旋分量密度在中心处和尾部有着不同的交替行为, 因此自旋密度分布的中间和两端区域呈现不同符号且关于$ x=0 $展现对称的结构, 见图7(c)和图6. 而在零动量相中, 不同自旋分量密度在膨胀和收缩过程中仅两端附近出现差异, 因此其自旋密度分布只在两端处表现为非零值且关于时间呈现周期性变化. 值得注意的是, 在零动量相中自旋-偶极模式与自旋-呼吸模式的自旋密度分布行为不同, 但两种模式的激发频率一致且远大于条纹相中的振荡频率. 综上, 两种自旋模式振荡在不同物相中均表现为两组分密度分布的相对运动(相对平移、相对膨胀和压缩), 或表现为自旋密度分布的周期性改变. 它们在不同物相中表现的相对运动趋势是类似的, 只不过因不同物相密度差异性(如条纹相中周期性调制的密度分布以及零动量相中的平滑密度分布)导致其自旋密度分布可能出现不一致的周期性变化.

    5.   结　论

    • 通过数值求解定态和含时Gross-Pitaevskii方程, 本文系统地研究了一维拉曼型自旋-轨道耦合玻色气体的静态特性以及几种常见的低能集体激发模式频率和动力学行为. 通过计算基态凝聚体动量成分、自旋极化率以及基态能量, 揭示了体系在拉比频率调控下的三种基态物相及其相变性质. 静态分析表明, 条纹相中存在两种不同动量平面波的等权叠加, 与零动量相一样为非磁性相, 而平面波相为磁性相, 具有单独非零值动量. 设计了四种不同微扰方式激发并进一步探究这四种典型低能集体激发模式的振荡频率和密度演化特征. 其中, 偶极和呼吸模式频率呈现关于拉比频率的非单调性行为, 并在平面波相到零动量相的相变处被完全抑制. 而自旋-偶极与自旋-呼吸模式频率在不同物相中均呈现出明显的区别. 本文进一步剖析了这些模式中自旋分量密度分布的运动趋势, 从而更为清晰地揭示了这四种激发模式内部的动力学行为特征, 尤其是自旋相关模式在条纹相中独特的相对运动行为.

    参考文献 (49)

目录

/

返回文章
返回