多铁性材料作为兼具铁电、铁磁等两种及以上“铁”性序的新型量子功能材料, 因其独特的磁电耦合特性, 在低功耗存储、自旋电子学及量子信息器件等领域展现出广阔前景. 近年来, 其在斯格明子拓扑结构、光学二极管效应等前沿方向的研究突破, 进一步拓展了多功能量子器件的开发路径^[1–7].

作为近年来备受瞩目的多铁性材料, 极性磁体区别于晶格相变主导的第一类多铁材料(如BiFeO₃)和自旋序驱动的第二类多铁材料(如TbMnO₃)^[8–10], 极性磁体具有以下核心特征^[1,11,12]: 首先, 极性磁体在整个温区保持极性空间群对称性, 展现出本征极性结构, 赋予其稳定热释电与压电响应, 但因缺乏电场可控的极化翻转能力, 本质上属于热释电体而非典型铁电体^[13,14]. 其次, 作为新型磁电耦合体系, 极性磁体在自旋诱导电极化与多级磁电响应方面展现出突破性特征^[15,16]. 其自旋-晶格关联机制诱发的本征电极化强度可达μC/cm²量级(如Fe₂Mo₃O₈与Co₂Mo₃O₈分别达到0.36 μC/cm²和0.12 μC/cm²的自发极化), 该数值不仅超越传统第二类多铁材料两至三个数量级, 甚至接近第一类位移型铁电体的极化强度水平^[13,17]. 最后, 极性磁体呈现出线性与非线性磁电耦合共存现象—在强磁场作用下, 磁化强度呈现多阶段平台式跃迁(如Ni₃TeO₆和Fe₂Mo₃O₈的H//c方向磁化曲线), 同时电极化发生可逆翻转, 这种磁-电参量的量子协同演化揭示了交换伸缩机制与自旋重取向的深层关联^[15,18]. 通常情况, 总的铁电极化可以表达为^[19]

其中P_C表示晶格诱导的铁电极化, P_S表示自旋诱导的自发极化, H是外加磁场强度, α和β分别表示一阶和二阶磁电耦合系数^[20]. 另外, 此类材料还蕴含手性声子-磁振子耦合(如Fe₂Mo₃O₈的近室温磁圆二色性)及铁环序等新物性, 在非易失存储与量子传感领域潜力显著^[11,21–24].

Co₂Mo₃O₈作为M₂Mo₃O₈ (M = 3d过渡金属)家族的代表性极性磁体, 展现出独特的量子多铁性. 其基态下的对称性破缺诱导了较大的自发极化和显著的非线性磁电耦合效应^[17,25]. 实验研究揭示, 该材料在强磁场(H > 27 T)下会经历两次连续的磁电转变, 暗示磁场诱导自旋重取向导致出现的磁化跳变与电极化的同步翻转, 对应体系由二阶非线性磁电相进入了线性磁电主导的磁电态. 这种非线性-线性响应模式的转换机制可能源于以下效应: 1)在六方晶系P6₃mc对称框架下, Co²⁺的$ t_2^{\text{g}} $ 轨道简并消除与MoO₆极性位移协同作用, 形成了独特的层间极化梯度. 在磁场作用下会通过交换伸缩机制与自旋-轨道耦合产生强关联, 导致磁电耦合的二次方依赖性^[26]. 2)材料中的电偶极矩${{\boldsymbol{\mu}} }_{\text{e}} $和磁偶极矩${{\boldsymbol{\mu}} }_{\text{m}} $在基态呈现非共线排列, 其相互作用能可表述为$ {E}_{\text{ME}}={A}_{1}({{\boldsymbol{\mu}} }_{\text{e}}\cdot {{\boldsymbol{\mu}} }_{\text{m}})+{A}_{2}({{\boldsymbol{\mu}} }_{\text{e}}\cdot {{\boldsymbol{\mu}} }_{\text{m}})\text{²} $. 当 外加磁场突破临界值H > 27 T时, A₂项主导的非线性贡献被抑制, A₁线性关系逐渐显现, 这与太赫兹光谱观测到的三阶光学磁电效应高度吻合^[26].

本研究基于中子散射揭示的磁矩不对称分布^[17], 采用半经典分子场唯象理论, 构建Co₂Mo₃O₈双子格反铁磁模型. 通过引入差异化的子格分子场耦合系数λ_t和λ_o, 建立了自发极化强度与温度的理论关联模型, 并推导出磁化率、比热以及自发极化等热力学参数的温度依赖关系. 结合磁矩与磁化率耦合分析, 获得体系中一阶线性磁电耦合系数α和二阶非线性磁电耦合系数β, 结果显示Co₂Mo₃O₈比同构的Fe₂Mo₃O₈和Mn₂Mo₃O₈拥有更加明显的二阶磁电耦合效应, 和更稳定的反铁磁交换作用. 基于以上结果表明Co₂Mo₃O₈体系中自旋诱导的铁电极化和二阶磁电耦合效应来源于两个不同Co²⁺格子的反铁磁交换收缩机制, 而两个磁格子的磁矩不对称分布, 由于两个不同Co²⁺格子的p-d杂化机制诱导较弱的线性一阶磁电耦合效应, 暗示亚铁磁态的Mn₂Mo₃O₈拥有较强的一阶线性磁电耦合效应^[20]. 总之, 本研究建立的磁电耦合唯象模型, 深化了对极性磁体本征关联机制的理解, 为新型磁电功能材料的理性设计提供理论基础.

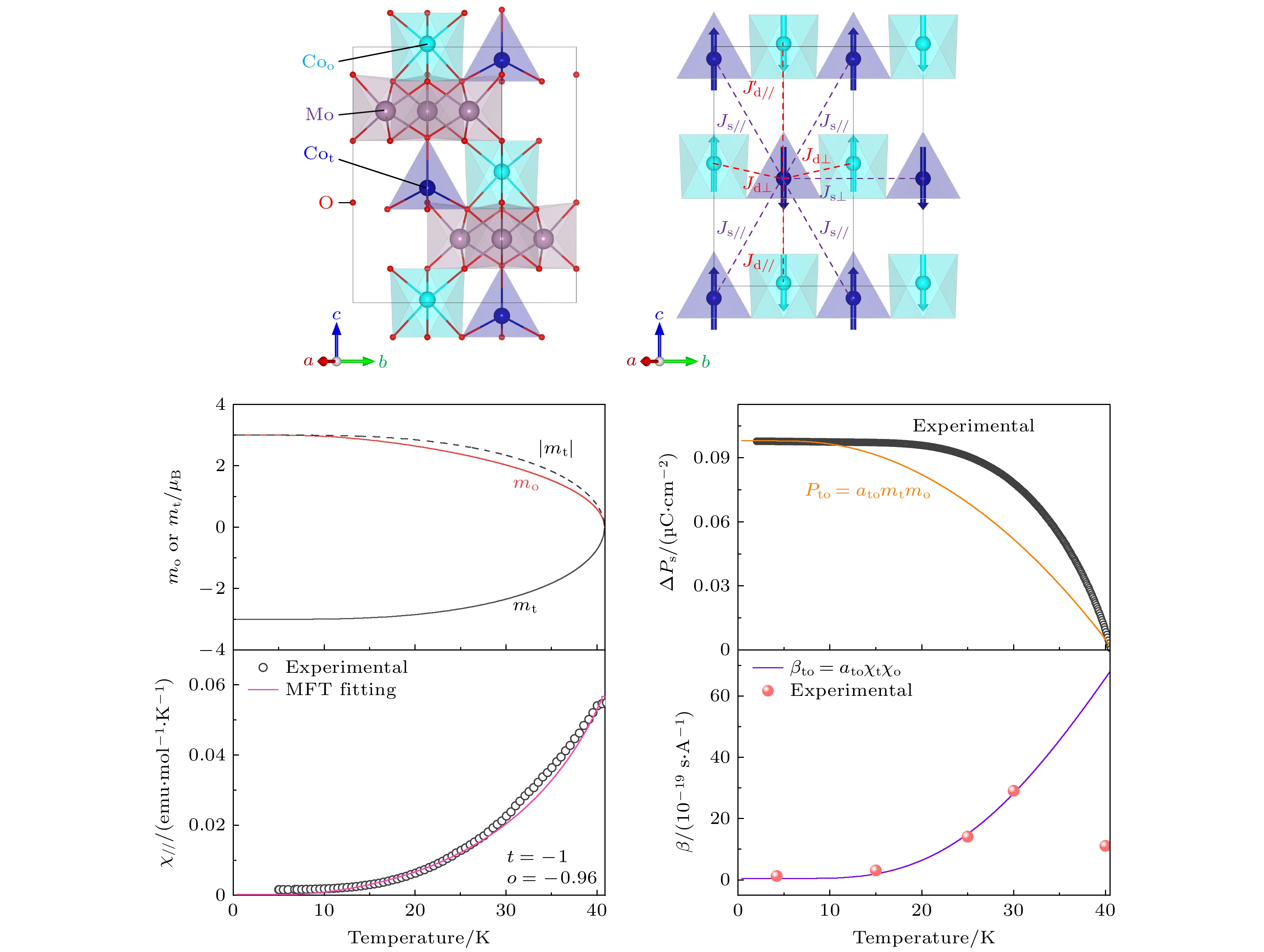
基于材料晶体结构与自旋排列特征的优化表达, 本研究体系Co₂Mo₃O₈具有极性六角晶格结构(空间群P6₃mc), 如图1(a)所示. 通过中子衍 射分析证实, 其晶胞中存在两类钴离子配位环 境: 占据氧八面体位的$ {\mathrm{Co}}_{\text{o}}^{2 + } $ (磁矩3.35 μ_B)与氧四面体位的$ {\mathrm{Co}}_{\text{t}}^{{{2 + }}} $(磁矩3.44 μ_B), 其中钼离子因氧八面体三聚化导致的d⁰电子构型呈现非磁性^[27,28], Co_o和Co_t分别形成两套独立的反铁磁亚晶格网络, 如图1(b)所示, 其自旋排列呈现共线反铁磁序特征. 理论计算表明, 此类共线自旋序通过交换伸缩机制诱导产生本征铁电极化, 其微观物理图像可归结为自旋-晶格耦合作用引起的Co—O键长周期性调制, 从而导致正负电荷中心分离, 验证了交换相互作用与电极化间的强关联性^[28].

对子晶格O(Co_o)与子晶格T(Co_t), 电场调控交换作用的哈密顿量可构建为

其中E为沿c轴施加的电场强度, $ {a_{ij}} $表示自旋S_i和S_j之间的交换作用常数. 当施加沿c轴方向磁场H (//c)时, 自旋磁矩满足$ \Delta {S_i}\sim{\chi _i}H $的线性响应关系, 其中χ_i表示在i格点上的磁化率. 由此, 交换作用项H_ex可表示为

分别对电场E和磁场H微分, 得自旋诱导的铁电极化和磁电耦合系数分别为

其中α_ex和β_ex分别为一阶线性磁电耦合系数和二阶非线性磁电耦合系数. 从对称性分析的角度来说, 对于Co₂Mo₃O₈中子散射中观测到的沿c轴的反铁磁序, 其磁点群通常被认为是6'mm'. 这意味着线性磁电耦合张量$ {\alpha _{cc}} = 0 $, 即沿磁化c轴方向施加电场E_c或磁场H_c没有线性磁电耦合, 即E_c不能诱导M_c方向的磁矩变化, H_c也不能诱导P_c方向的电极化^[29].

根据分子场近似^[30,31], 结合Co₂Mo₃O₈体系的自旋排列, 在自旋交换作用体系中构建两套子格子的自发磁矩, 其关联的分子场参数分别对应h_t与h_o, 表示CoO₄四面体位和CoO₆八面体位的局域分子场强度,

式中, h_i (i = t, o) 表示不同配位场中Co²⁺离子的有效分子场强度. 这里值得强调的是h_t和h_o并不相等. 例如分子场强度h_t, 除了来源于最近邻的m_o之外, 还和次近邻的m_t有关系, 因为磁矩m_t和m_o存在差异, 因此有必要引入一个差异化因子. 其中m_i (i = t, o)表示不同配位场中Co²⁺离子的磁矩(单位: μ_B); λ_s和λ_d分别为同配位场和异配位场的分子场耦合系数; $ \lambda = 2{k_{\text{B}}}/\left( {{N_{\text{A}}}{g^2}\mu _{\text{B}}^2} \right) $表示归一化参数, k_B是玻尔兹曼常数, N_A是阿伏伽德罗常数, g是朗德g因子$ (g = {\text{ }}2) $, μ_B是玻尔磁子; H是外加磁场强度; J与温度的维度相同; t和o是没有维度的两个自由系数, 这里引入t和o参数是考虑到四面体和八面体配位中的磁矩大小存在差异. 体系磁矩满足统计分布, 每摩尔体系的磁矩$ {m_i}(T) $以及磁化率与布里渊函数的关系为

其中$ {B_S}(y) $和$ {B'_S}(y) $分别为布里渊函数和其对y的一阶导数. 对于Co₂Mo₃O₈来说, 其自旋量子数S = 3/2 (高自旋态), 且磁相变温度T_N = 40.5 K (与J成正比关系) ^[17]. 考虑到对称矩阵

的特征值为

则体系的相变温度为

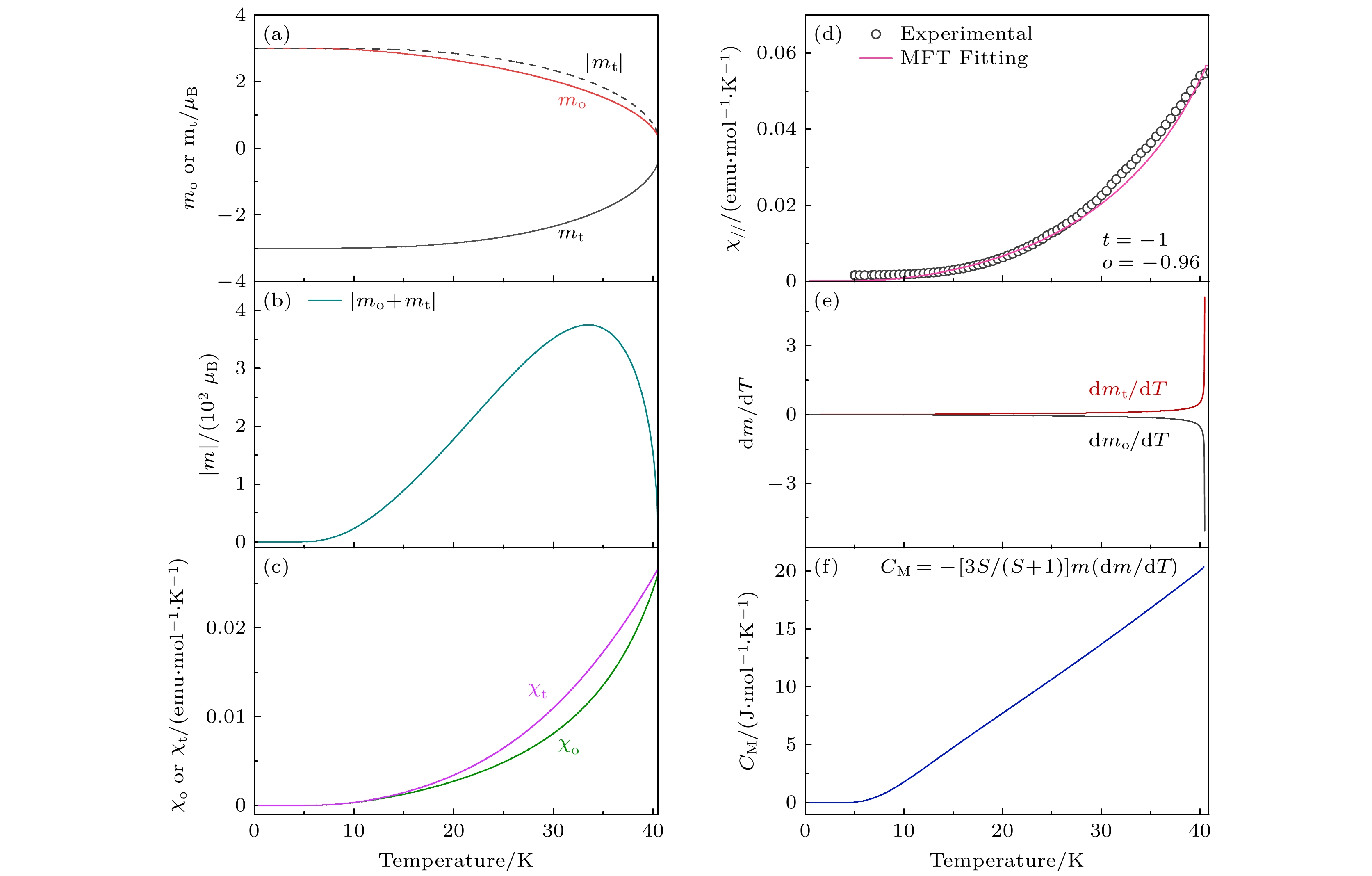
最后, 通过调节参数t和o的数值大小对χ(T )曲线进行拟合, 确定t和o大小分别取–1和–0.96拟合的曲线比较接近实验上观测的结果, 如图2(d)所示. 另外, 通过之前的中子散射实验可知四面体中Co_t和八面体中Co_o的磁矩大小分别为: 3.44 μ_B和3.35 μ_B, 两者的比值也非常接近t和o的取值. 总之, 可以看出t和o的取值, 在微观本质上和两个不同磁格子的磁矩大小是有关联的, 暗示了交换作用能的差异.

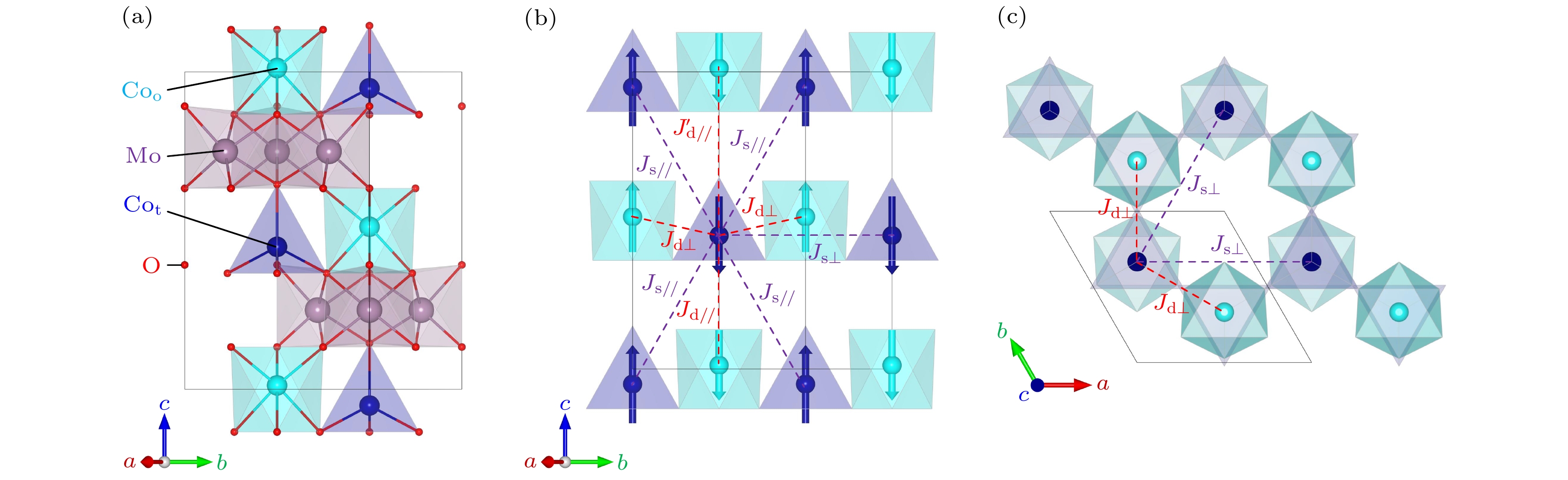
图2(a)展示了氧四面体(Co_t)和氧八面体(Co_o)两种不同晶格位点中Co²⁺离子的磁矩随温度演化关系. 实验观测到两类钴离子的磁矩温度依赖性存在显著差异, 该现象与同家族极性磁体Fe₂Mo₃O₈和Mn₂Mo₃O₈的报道结果具有相似性^[20,27,31]. 这种差异的物理机制可归因于: 1)不同晶体场环境对轨道磁矩的调制效应—氧四面体与八面体场产生的晶体场劈裂导致轨道磁矩差异^[11]; 2)自旋磁矩本征差异, 实验测得Co_t和Co_o的自旋磁矩分别为3.35 μ_B和3.44 μ_B^[17]. 基于分子场理论分析, 两类位点的磁矩差异源于其不同的分子场系数λ_i (i = t, o), 这对应着差异化的交换作用常数J_ij (i, j = t, o). 当体系进入长程反铁磁有序相(T < T_N)时, 反平行排列的$ {\text{Co}}_{\text{t}}^{2 + } $与$ {\text{Co}}_{\text{o}}^{2 + } $离子的磁矩$ m_i^{2 + }(T) $ 随温度变化呈现非对称演化, 导致局域净磁矩的产生, 如图2(b)所示. 然而, 在单磁胞尺度下, 相邻Co_t-Co_o离子对的净磁矩呈反平行排列, 使得体系在基态下表现为反铁磁性, 这与Fe₂Mo₃O₈基态下的特征一致^[31].

另外, 图2(c)展示了$ {\text{Co}}_{\text{t}}^{2 + } $与$ {\text{Co}}_{\text{o}}^{2 + } $离子在反铁磁相变温度T < T_N下的磁化率随温度的变化, 包含以下几点特性. 首先, 由于磁矩$ m_i^{2 + }(i = {\text{t}}, {\text{o}}) $的不同, 会引起两个不同子格子中的反铁磁排列的磁化率展现出不同的热动性质. 当然, 引起这一差异的原因可能包含最近邻、次近邻及其他次次近邻磁性离子间的交换作用常数J_ij (i, j = t, o)的不同. 其次, 对之前实验报道的顺磁态磁化率曲线进行居里-外斯拟合:

其中外斯温度$ {\theta _{\text{p}}} = - 70.9{\text{ K}} $, 居里常数C = 8.446^[17]. 根据分子场近似, 在T = T_N时, 体系的外斯温度和居里常数分别为

可得理论近似中的外斯温度和居里常数分别为: $ {\theta _{\text{p}}} = - 40{\text{ K}} $和C = 15, 与实验结果存在较大的差异. 这是因为在分子场理论中, 仅考虑最近邻及次近邻交换作用, 忽略高阶交换项及超交换作用, 而这些交换作用项在强失措体系中较为常见, 例如第二类多铁材料以及量子自旋液体^[32,33], 因此引起与实验结果上的差异. 但是这也并不影响我们基于自旋离子间的交换相互作用分析Co₂Mo₃O₈体系中的多铁性和磁电耦合效应等.

在Co₂Mo₃O₈体系中, 三维长程反铁磁序的形成会引发显著的热力学响应, 具体表现为比热容在相变温度处呈现典型的λ型反常峰. 该特征峰对应着体系磁自由能的突变过程, 图2(f)展示了磁比热容在反铁磁相变温度以下随温度演化的理论结果. 基于分子场理论框架, 该体系的磁比热容温度依赖性可定量描述为以下表达式:

其中S为3/2(Co²⁺处于高自旋态); $ {\text{d}}{m_i}/{\text{d}}T\,(i = {\text{t}}, {\text{o}}) $表示磁矩对温度的一阶导数, 如图2(e)所示. 值得注意的是, 图2(f)观测到的磁比热反常峰与Tang等^[17]报道的Co₂Mo₃O₈体系磁比热随温度的三次方$ (\sim{T^3}) $依赖关系存在显著差异. 具体而言, 分子场理论将磁性离子间的相互作用简化为等效平均场, 仅考虑近邻交换作用, 而忽略了长程关联和动态涨落效应. 这种简化导致理论预测的磁比热呈现近似线性温度依赖, 与实验观测的$ {T^3} $行为偏离. 分子场理论作为半经典唯象模型, 其主要适用于三维自旋序的体系, 且在高温顺磁自旋关联微弱的区域, 和实验的吻合度高, 而在临界区域和低温区域, 由于自旋涨落和自旋波激发等效应, 使理论和实验存在明显的偏差. 另外, 反铁磁相变温度T_N附近的强关联效应, 体系内短程自旋关联显著增强, 形成准二维或三维磁子激发, 其色散关系对磁比热的贡献呈现$ {T^3} $德拜模型特征^[34].

尽管存在上述理论-实验差异, 分子场理论仍能有效揭示Co²⁺离子在不同晶体场位的磁矩分布及交换作用. 这种磁相互作用为进一步分析自旋-晶格耦合诱导的铁电极化以及磁电耦合效应提供了理论框架.

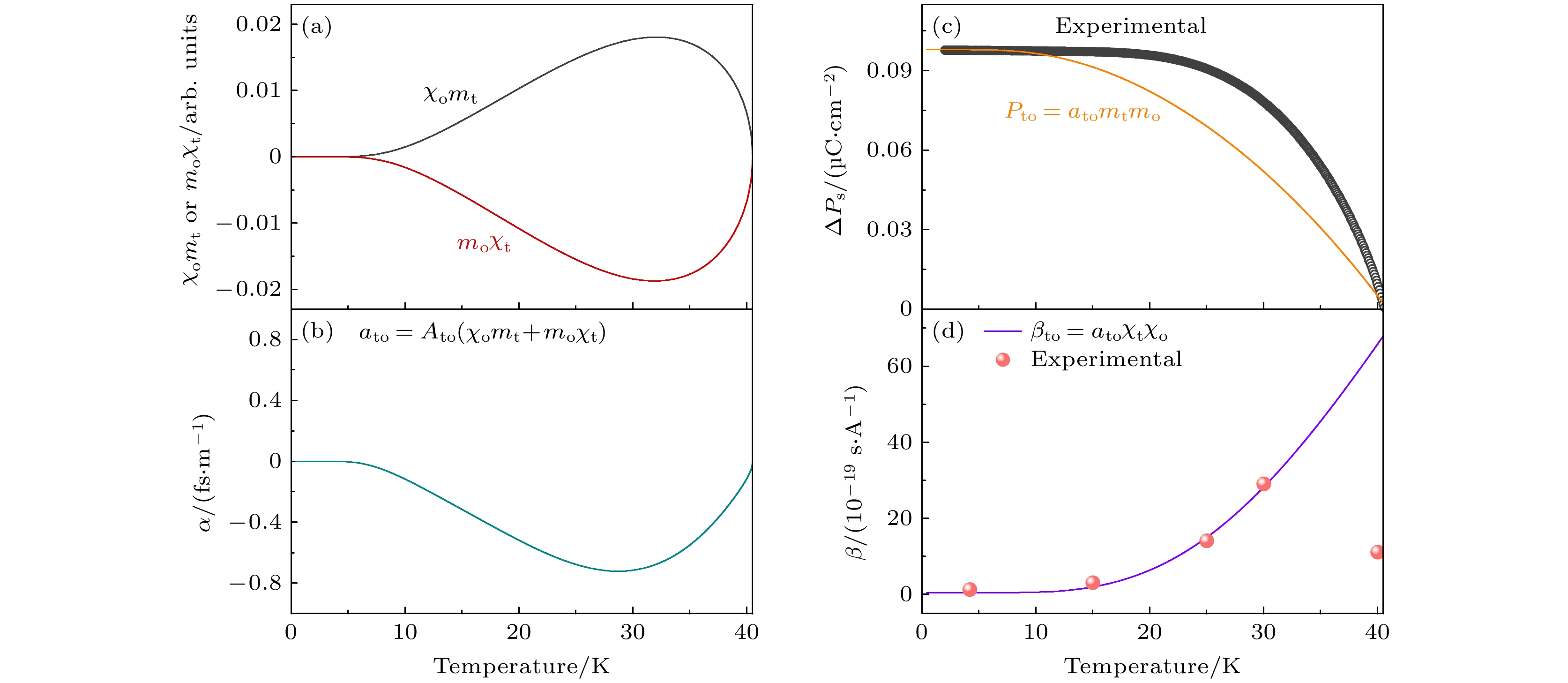
根据方程(1)可知, 对极性磁体M₂Mo₃O₈ (M为3d过渡金属)体系的铁电极化可包含3个独立分量: 1)晶格诱导极化P_C, 源于材料本身的极性晶体结构(空间群P6₃cm); 2)长程反铁磁序通过线性自旋关联的交换收缩效应诱发的自发极化P_S, 具体计算如方程(4)所示; 3)外磁场通过磁电耦合效应诱导的$ \Delta P\sim \alpha H + \beta {H^2} $, 其中一阶系数α和二阶系数β分别可由方程(5)和方程(6)求得. 值得注意的是, 中子散射实验表明Co₂Mo₃O₈的基态磁点群为6'mm', 由对称性分析该体系的一阶线性磁电耦合系数α是不存在的. 但是, 图3(a)和图3(b)的实验数据显示α大小约为0.01 ps/m, 这较常规磁电材料(通常为几个ps/m)低2—3个数量级. 此现象可能与基态自旋序的净磁矩相关, 例如在Mn₂Mo₃O₈的亚铁磁基态中观察到的线性磁电耦合效应^[20]. 对于基态下的Co₂Mo₃O₈, 分子场理论揭示了t和o参数的微小差异, 可能导致自旋排列偏离理想反铁磁构型, 进而产生等效线性磁电响应, 该发现为调控磁电耦合效应提供了新的视角.

由近邻磁性离子间的交换收缩机制, 诱导铁电极化大小可由方程(4)给出, 图3(c)分别展示了实验上和理论上自旋诱导的铁电极化随着温度的变化. 其中, 实验上测到的铁电极化与数值拟合得到的结果存在明显的差异. 产生这种差异的原因可能在于Co₂Mo₃O₈基态下的长程反铁磁序在T_N~40.5 K附近就已形成, 而T_N以下体系的磁化率随温度变化较弱. 这暗示了体系的磁性在温度的扰动下, 不会发生明显的变化, 只在T_N处体系的交换作用能发生显著的变化, 对应铁电极化的跳变, 温度再降低, 体系的交换作用能并没有发生变化. 然而, 在平均场近似下, Co₂Mo₃O₈的磁矩会随着外界温度的改变而发生变化, 导致交换作用能的变化, 从而铁电极化会受到温度明显的扰动, 于是和实验上产生明显的区别, 与之前报道的Fe₂Mo₃O₈类似^[31].

最后, 图3(d)展示了Co₂Mo₃O₈基态下的二阶耦合系数β随温度的变化. 可以看出, 实验和理论中的二阶耦合系数随温度的变化关系, 在低温条件下符合得很好, 满足${\beta _{{\text{ex}}}} = {a_{ij}}{\chi _i}{\chi _j}$的关系, 即与两个不同子格子的磁化率关联. 但是, 在温度接近T_N时, 实验中的二阶耦合系数显著减小, 理论上体系在T_N处的二阶耦合系数应达到最大值. 产生差异的主要原因可能是体系在T_N时的热扰动较为明显, 对高阶磁电耦合效应的影响较为明显, 因此耦合系数较弱.

总之, 平均场近似更加直观地展示Co₂Mo₃O₈基态下的线性磁电耦合效应和高阶的磁电耦合效应, 以及自旋诱导的铁电极化, 为进一步揭示极性磁体中的多铁性和磁电耦合效应提供了基础.

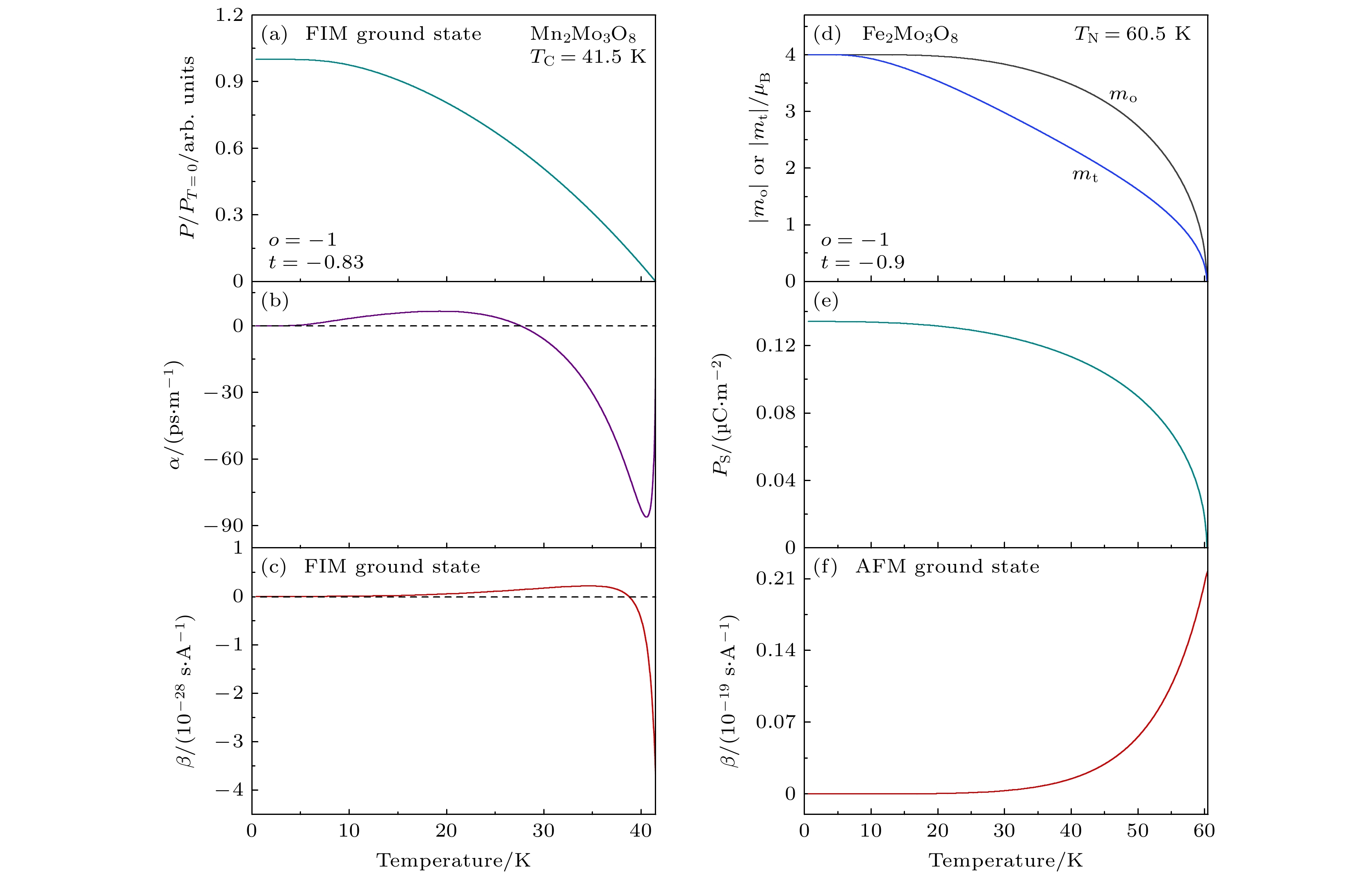
与Co₂Mo₃O₈类似, 对于M₂Mo₃O₈家族中的其他化合物Mn₂Mo₃O₈和Fe₂Mo₃O₈, 分别取不同的分子场系数^[20,31], 得到不同自旋序诱导的自发极化、一阶线性磁电耦合系数和二阶非线性磁电耦合系数, 如图4(a)—(f)所示. 其中, 图4(a)—(c)展示Mn₂Mo₃O₈的亚铁磁自旋序诱导的自发极化、线性磁电耦合系数和二阶非线性磁电耦合系数, 与之前Kurumaji等^[20]报道的结果类似, 表明我们所建立模型的可靠性. 不同于反铁磁序的Co₂Mo₃O₈以及Fe₂Mo₃O₈, Mn₂Mo₃O₈的一阶耦合系数比较大, 但其二阶耦合系数却是非常小. 对基态下反铁磁的Co₂Mo₃O₈和Fe₂Mo₃O₈, 其线性磁电耦合效应理论上是不存在的. 关于这一实验和理论上的差异, 主要是本文采用的计算模拟方法是基于唯象的分子场近似, 其中分子场理论是一个非常基础和常用的理论工具, 其将一个复杂的多体相互作用问题简化为一个单体在平均场(或等效场)中的问题. 对于反铁磁体, 这意味着每个磁性子晶格感受到的场是由其他子晶格的序参量(磁化强度)产生的平均场. 但是由于分子场理论中只考虑最近邻和次近邻的作用, 从而展现出较弱的一阶耦合效应, 但是它们的二阶耦合效应却是比较明显的, 且Co₂Mo₃O₈的二阶耦合系数明显更大. 这也表明Co₂Mo₃O₈磁性离子间的交换作用能可能比Fe₂Mo₃O₈的更大, 因此在外界能量的扰动下更加稳定, 与之前实验中报道的Co₂Mo₃O₈的多重磁矩和铁电极化转变的结果相对应^[25].

另外, 对于本文Co₂Mo₃O₈体系来说, 由上面提到的参数t和o分别为–1和–0.96可知, 体系中参数$ \lambda = 2{k_{\text{B}}}/{N_{\text{A}}}{g^2}\mu _{\text{B}}^2 $为归一化系数, 则对Co²⁺的高自旋态自旋量子数S = 3/2, 得J = 8.182 K, 进而得到氧四面体格子间的分子场系数为λ_t = Jλ_t = –8.182 K, 氧八面体格子的分子场系数为λ_o = Jλ_o = –7.854 K. 对于Mn₂Mo₃O₈体系, 由Kurumaji等^[20]报道可知, 相变温度T_N = 41.5 K, 且Mn²⁺的高自旋态S = 5/2, 可得J = 3.717 K. 同理可得氧四面体和氧八面体的分子场系数为λ_t = –3.048 K, λ_o = –3.717 K. 最后, 对于Fe₂Mo₃O₈体系, 由Solovyev等^[31]报道可知, 对于Fe²⁺-Fe²⁺配置的电子结构, 通用取$ \lambda = 2{k_{\text{B}}}/{N_{\text{A}}}{g^2}\mu _{\text{B}}^2 $为归一化系数, 则其氧四面体和氧八面体的分子场系数为λ_t = –9.84 K, λ_o = –10.26 K^[31].

分子场近似展示的结果表明Co₂Mo₃O₈体系中的自旋交换作用与同一家族体系中的其他材料之间存在明显的差异, 具体表现在: 首先, 对于基态下反铁磁的Co₂Mo₃O₈体系, 两个不同配位中的钴离子的磁矩大小与Fe₂Mo₃O₈相比, 差别较小. 两个最近邻反铁磁排列的钴离子之间有更大的交换作用能, 体系的磁电态更加的稳定. 其次, 与Mn₂Mo₃O₈不同, Co₂Mo₃O₈体系不同子格子间的反铁磁序使体系不存在一阶线性磁电耦合效应, 但是却拥有非常明显的抛物线行为的二阶非线性磁电耦合效应. 这种不可逆的磁电二极管(magnetoelectric diode)效应, 暗示了体系可能存在更广泛的潜在应用价值, 为磁电二极管(magnetoelectric diode)器件的发展了提供了坚实的实验基础^[35,36].

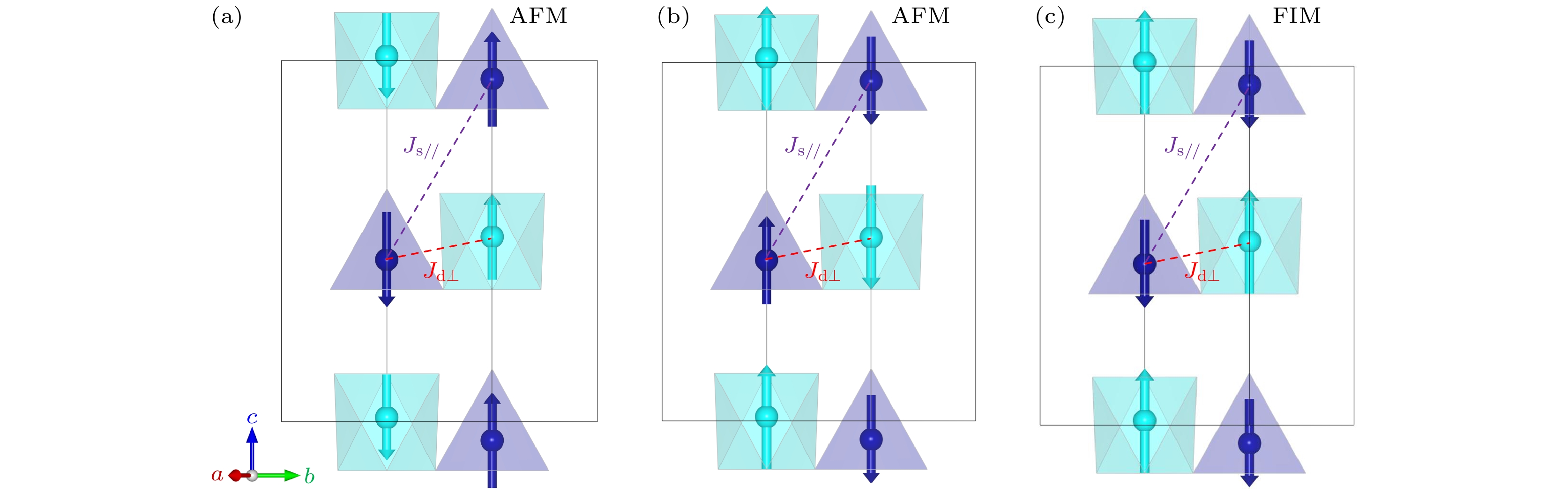
极性磁体M₂Mo₃O₈体系中纵向自旋序诱导的自发极化机制及其磁电耦合效应的理解, 需从系统的自旋排列框架出发. 以Co₂Mo₃O₈为例, 其基态自旋排列表现为两套反平行排列的Co²⁺离子亚晶格, 如图5(a)所示. 值得注意的是, 与Fe₂Mo₃O₈体系不同, 如图5(b)所示, 处于不同配位环境中的Co²⁺离子磁矩差异较小. 因此, 对于反平行排列的Co₂Mo₃O₈, 由海森伯模型, 两反铁磁自旋序之间的交换作用能为

当考虑沿着自旋方向施加一磁场, 则交换作用能为

可得, 当${S_i}{\chi _j}$和${\chi _i}{S_j}$相等时, 体系的能量最低, 即Co₂Mo₃O₈的两个不同子格子上的磁矩大小接近, 且呈现反铁磁态. 体系的能量相对于其他Fe₂Mo₃O₈和Mn₂Mo₃O₈来说, 能量更低, 系统更加稳定, 且对应的二阶非线性磁电耦合系数更强. 当沿着自旋方向施加磁场时, 由于Co²⁺离子间的交换作用能发生变化, 如(19)式, 从而诱导磁性离子的位移发生变化, 诱导铁电极化. 而且由于$ {J_{ij}}({S_i}{\chi _j}H\; - {S_j}{\chi _i}H) $相的存在, 而且S_i和S_j的磁矩大小不同, 因此p-d杂化机制也可能对磁电耦合效应有贡献. Mn₂Mo₃O₈由于基态下呈现亚铁磁态, 如图5(c)所示, 则允许出现较大的线性磁电耦合效应.

总之, 本文基于分子场近似的唯象理论, 分析了极性反铁磁体Co₂Mo₃O₈基态下的自发极化和磁电耦合效应, 指出了Co₂Mo₃O₈与Fe₂Mo₃O₈以及Mn₂Mo₃O₈磁结构的不同, 从而引起它们分子场系数的差异, 对应自旋之间交换作用能的差异, 最终影响不同体系之间的一阶和二阶磁电耦合系数的差异. 为人们进一步研究极性磁体磁电耦合效应的调控等提供了理论和实验基础^[28,37].

本文通过分子场近似方法, 构建了Co₂Mo₃O₈体系的两套不同的反铁磁子格子, 得出了体系的自发磁矩、自旋诱导的铁电极化、一阶线性磁电耦合系数以及二阶非线性磁电耦合系数随温度的变化关系. 结果显示Co₂Mo₃O₈的二阶磁电耦合系数要明显比同构的Fe₂Mo₃O₈以及Mn₂Mo₃O₈要大, 这主要是因为Co₂Mo₃O₈的两个不同子格子间的反铁磁交换作用能量更低, 体系所处的状态更加稳定. 另外, Co₂Mo₃O₈体系中自旋诱导的铁电极化和二阶磁电耦合效应来源于两个不同Co²⁺格子的反铁磁交换收缩机制, 而两个磁格子的磁矩不对称分布. 另外, 两个不同Co²⁺格子磁矩的差异也可能通过p-d杂化机制诱导磁电耦合效应. 总之, 本文通过分子场理论, 模拟并讨论了Co₂Mo₃O₈体系的多铁性和磁电耦合效应, 为磁电耦合材料的进一步发展提供了坚实的理论和实验基础^[38].