-
高超声速飞行器周围的流场温度可达20000 K以上, 流场气体各组分之间互相碰撞发生振动激发、解离、电离等一系列复杂动力学和化学反应过程, 对飞行器的受力和热性能均产生重要影响[1–4]. 高温环境下, 气体组分的诸多弛豫过程、化学反应的相互耦合使得整个流体处于强烈的热化学非平衡状态, 为动力学建模带来巨大挑战. 其中, 能量的振动自由度会显著影响分子相互作用及其产生的物理性质, 在非弹性碰撞传能、解离和交换等反应过程中起主要作用[5–7]. 因此, 开展高温非平衡流场气体的态-态碰撞传能研究十分必要, 其研究结果对于高温流场的诊断以及推动飞行器技术领域不断进步具有重要意义.
由于地面实验的操作困难和成本问题, 动力学模拟在高温气体动力学研究领域起着至关重要的作用. 其中, 态-态方法(state-to-state method, STS)基于原子、分子层面研究各组分气体不同能态间的碰撞、反应规律, 克服了传统模型经验性假设的局限性, 已经被广泛应用于等离子体、大气燃烧和非平衡气体数值模拟研究中[8,9]. 态-态模型中, 求解各组分气体能级数密度的方程组需要列出所有振-转能级跃迁和解离/交换反应过程的速率系数, 因此该模型的准确性强烈依赖于态-态反应速率系数的准确性和完善性. 近年来, 国内外学者一直致力于通过先进的光谱技术和量子力学模拟[10–13], 以更高的精度揭示高温非平衡气体碰撞的振动传能机制, 尤其是地球大气层的主要成分氮、氧体系的态-态碰撞过程[14–17]. 相比同种分子气体之间的碰撞(例如N2-N2, O2-O2), N2-O2的基本碰撞过程要复杂很多, 包含以下6种主要的振动激发和解离反应通道(∆v > 0):
1)非弹性振动-平动(VT)跃迁: 包含N2分子的振动退激发(VTN)和O2分子的振动退激发(VTO)两种情形:
2)非弹性振动-振动(VV)跃迁: 包含振动能量从N2分子传递到O2分子(VVN)和振动能量从O2分子传递到N2分子(VVO)两种情形:
3)单个O2解离反应:
4)单个N2解离反应:
5)产生一个NO分子的交换-解离反应:
6)双解离反应:
这里v和w分别为N2和O2的初始振动量子数, 标注上标符号的(如v', w')表示碰撞后产物分子的振动能级. 在非弹性碰撞VV/VT过程中, 如(1)式—(4)式所示, ∆v表示碰撞前后分子跃迁的振动量子数, ∆v = 1时一般称作单量子跃迁(single-quantum transition), ∆v = 2, 3时一般称作多量子跃迁(multi-quantum transition).
根据N2O2体系的电子基态从头算势能面[18]可知, N2分子约有9181个振-转态(vmax = 54), O2分子约有2950个振-转态(wmax = 36), 因此N2(v, j )-O2(w, n)碰撞需要考虑约3 × 108个不同的态-态过程, 采用动力学模拟逐一计算是难以实现的. 以往的研究结果大多局限于两个相同激发态(v = w)或一个基态与一个激发态组合(v = 0或w = 0)的碰撞过程[19–22], 关于一般形式(v ≠ w ≠ 0)碰撞过程中振动激发和解离反应传能机制的研究较为匮乏. 以VV跃迁为例, 较早的量子计算[23]和半经典计算[24]聚焦于(1, 0|0, 1)和(0, v|1, v – 1)这两个单量子跃迁过程; 近期的研究中也仅讨论了相同的跃迁过程或给出更高温度范围8000—20000 K的结果[21,25,20].
随着人工智能的快速发展, 机器学习技术已被用于高温气体碰撞传能研究工作中. 基于准经典轨迹方法(quasi-classical trajectory, QCT)获得的有限数据集, 通过训练神经网络预测模型(neural network model, NN)来填补未计算区域的数据空白, 保证精确度的同时, 可以大大提高传统动力学方法的计算效率. 例如, Koner等[26]利用NN模型预测了N(4S) + NO(2Π) → N2
$({\rm X}^1\Sigma^+_{\rm g}) $ + O(3P)过程的态-态交换反应截面, 相关系数R值可达到0.99; Chen等[27]利用高斯过程回归模型有效预测了CO(v) + CO(v)碰撞的振动非弹性VV跃迁截面. Hong等[28]采用NN模型获得了N2(v) + H2(0) → N2(v – Δv) + H2(0)(Δv = 1, 2, 3)过程完整的VT速率系数数据集; Gu等[29]和Huang等[30]以及Guo等[31]采用训练的NN模型分别预测了N2 + N、O2 + N体系的指定态碰撞解离截面[29,30]和N2(v1) + N2(v2)体系的非弹性VV/VT反应截面[31], 相关系数R值均达到0.99. 相比于原子-分子碰撞体系, NN模型在分子-分子碰撞体系中的应用还相对较少. 这是因为, 不同初始振动能级参与的态-态碰撞过程中, 非弹性VV/VT跃迁和解离/交换反应的传能机制及相互之间的耦合作用可能是不同的. 因此, 不同反应过程的NN预测模型构建可能依赖于不同的动力学输入特征和训练数据集, 这需要系统地研究每个反应通道的贡献以及动力学参量随不同能量自由度的演变趋势.本文采用QCT计算与NN模型相结合的方法, 系统地研究N2-O2碰撞的非弹性振动-振动VV跃迁、振动-平动VT跃迁和各种解离反应过程. 结构如下: 第2节介绍了QCT计算细节和神经网络模型; 第3节依次讨论了非弹性VV/VT反应截面和反应速率系数、各个解离通道的反应截面以及预测指定态碰撞总解离截面的神经网络模型; 第4节进行总结.
-
准经典轨迹方法(QCT)[32,33]是在Born-Oppenheimer近似条件下, 采用量子力学方法描述分子的初末振-转状态, 利用经典力学方法处理分子的碰撞轨迹, 通过求解哈密顿运动方程得到势能面上各原子核的运动轨迹, 根据大量轨迹模拟的统计分析结果, 计算得到反应体系的一系列动力学信息. 本文的所有轨迹计算均采用VENUS96化学反应动力学程序[34]完成. 每条轨迹的初始化空间相位角和分子核间距由Monte-Carlo近似统计平均方法随机采样确定, 碰撞参数b采用表达式b = ξ1/2bmax采样确定, 其中ξ为0—1之间的随机数, bmax为最大碰撞参数. 运行批量轨迹进行收敛性测试发现, 将bmax设置为6 Å足以对所有反应过程进行有效研究. 产物分子的振动能级使用Einstein-Brillouin-Keller(EBK)半经典近似[35]确定, 结果四舍五入为整数. 初始平动能量为Et的态-态碰撞过程中, 反应事件i发生的概率由以下公式进行计算:
其中反应事件i∈{VTN, VTO, VVN, VVO, O2单解离, N2单解离, 交换解离, 双解离}; Ni指反应事件i发生的轨迹数; Ntotal指模拟运行的总轨迹数. 反应事件i的散射截面σ表示为
由于蒙特卡罗抽样导致反应截面的统计误差表示为
在平动温度T下的反应速率系数表示为
其中kB为玻尔兹曼常数, μ为体系的约化质量, T是与相对平动能Et对应的平动温度(单位为K). 在所有的QCT计算中, 两个初始转动能级设置为基态, 即: N2(v, j = 0) + O2(w, m = 0). 分子质心之间的初始和最终距离都设置为15 Å. 为了保证能量和角动量守恒, 经过一系列试验, 时间步长设定为0.05 fs. 反应截面对应的初始平动能范围为0.2—10 eV, 反应速率系数对应的初始平动温度范围为5000—30000 K. 每次模拟运行105条轨迹, 累计运行约108条轨迹.
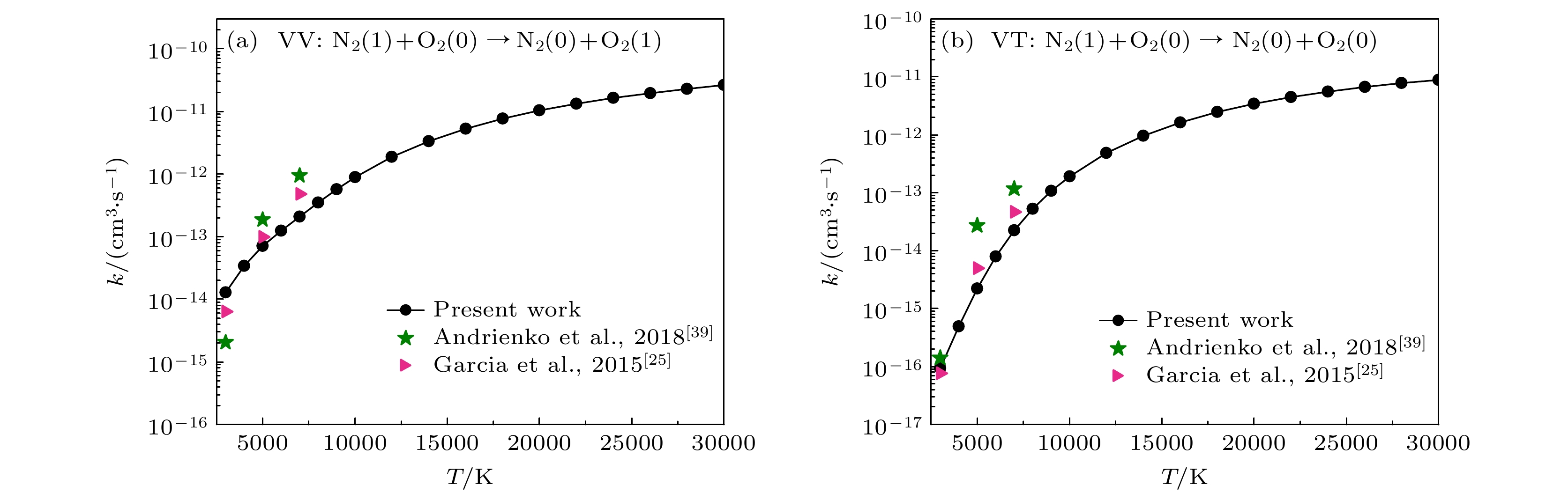
本文的研究采用Truhlar等构建的高精度N2-O2电子基态从头算势能面[18](potential energy surface, PES). 该PES是基于多组态完全活性空间二阶微扰理论、增强相关一致极化三重zeta基组计算以及外部相关性修正获得能量数据点, 然后采用置换不变多项式拟合多体相互作用得到的. 除了非弹性碰撞过程, 该PES还可以描述N2-O2碰撞过程中所有可能的解离和重组通道, 多次被用于研究高能振-转能量传递和碰撞诱导解离过程[19,36–38,14]. 为了验证该PES的准确性, 首先计算了VT过程(1, 0) → (0, 0)和VV过程(1, 0) → (0, 1)的速率系数结果与先前的研究[25,39]进行对比, 如图1所示. 由图1可以发现, 在3000 K以上的温度范围内VV和VT跃迁结果都与先前的理论结果符合较好, 尤其是与Garcia等[25]采用半经典方法在经验势能面上获得的结果(紫色符号)基本一致. 以上结果一方面表明采用的PES能够准确地描述高温区域的长程和短程相互作用, 可用于高温碰撞传能过程的研究; 另一方面也验证了本文动力学计算的可靠性.
-
神经网络是机器学习中一种常见的运算模型, 通过模拟人脑神经网络, 由大量的神经元节点(隐藏层)相互连接而成, 可以准确学习输入层和输出层之间的复杂相关关系. 基于QCT计算的解离截面数据集, 我们采用反向传播神经网络[40](back propagation, BP)对N2-O2碰撞体系的解离过程进行了有效预测, 模型包含1个输入层、1个输出层和4个隐藏层. 态-态碰撞诱导的解离过程由5个输入特征进行描述: 1)相对平动能Et; 2)初始振动态v和w; 3)初始态的振-转能量Eint1和Eint2. 输出层是指定振动态的总解离截面σ, 隐藏层神经元数量为(40, 10, 4, 4). 训练之前, 输入层和输出层需要先进行归一化转换:
其中a和b设置为–1和1, x和xrescaled分别为输入变量和归一化变量, xmax和xmin分别是变量的最大值和最小值. 选取正切sigmod函数
$ {\text{sig}}\left( x \right) =\left( 1 + {{\text{e}}^{ - x}} \right)^{ - 1} $ 作为激活函数. 选取均方误差(mean squared error, MSE)作为损失函数:其中n为样本数,
$ Y $ 为QCT值,$ Y_i' $ 为NN预测值. 使用Levenberg-Marquardt算法来优化权重和偏差矩阵的值[41]. 为保证训练结果的准确性和效率, 设置均方误差为10–6, 最大迭代次数为103. 训练之前, 需要准备一系列QCT数据作为神经网络的训练集(80%)和测试集(20%). 为了保证数据集具有代表性和覆盖性, 分别对两批初始振动量子数组合进行了QCT计算, 如表1所列. 不考虑重复的情况下, 两批次共包含90个N2(v) + O2(w)碰撞过程, 约占指定态组合过程总数的8.06%左右(vmax = 35, wmax = 30). 经过计算, 获得的数据集由1104个{Et, v, w, Eint1, Eint2, σ}数据点组成. -
N2(v)和O2(w)的振动-转动能级分布和解离能阈值不同, 振动跃迁过程的性质理论上也会有所不同. 因此, 对于任意初始振-转态组合的N2(v) + O2(w)碰撞, 应分别讨论N2分子和O2分子的振动能量传递过程, 包含VVN, VVO, VTN和VTO, 如(1)式—(4)式所示.
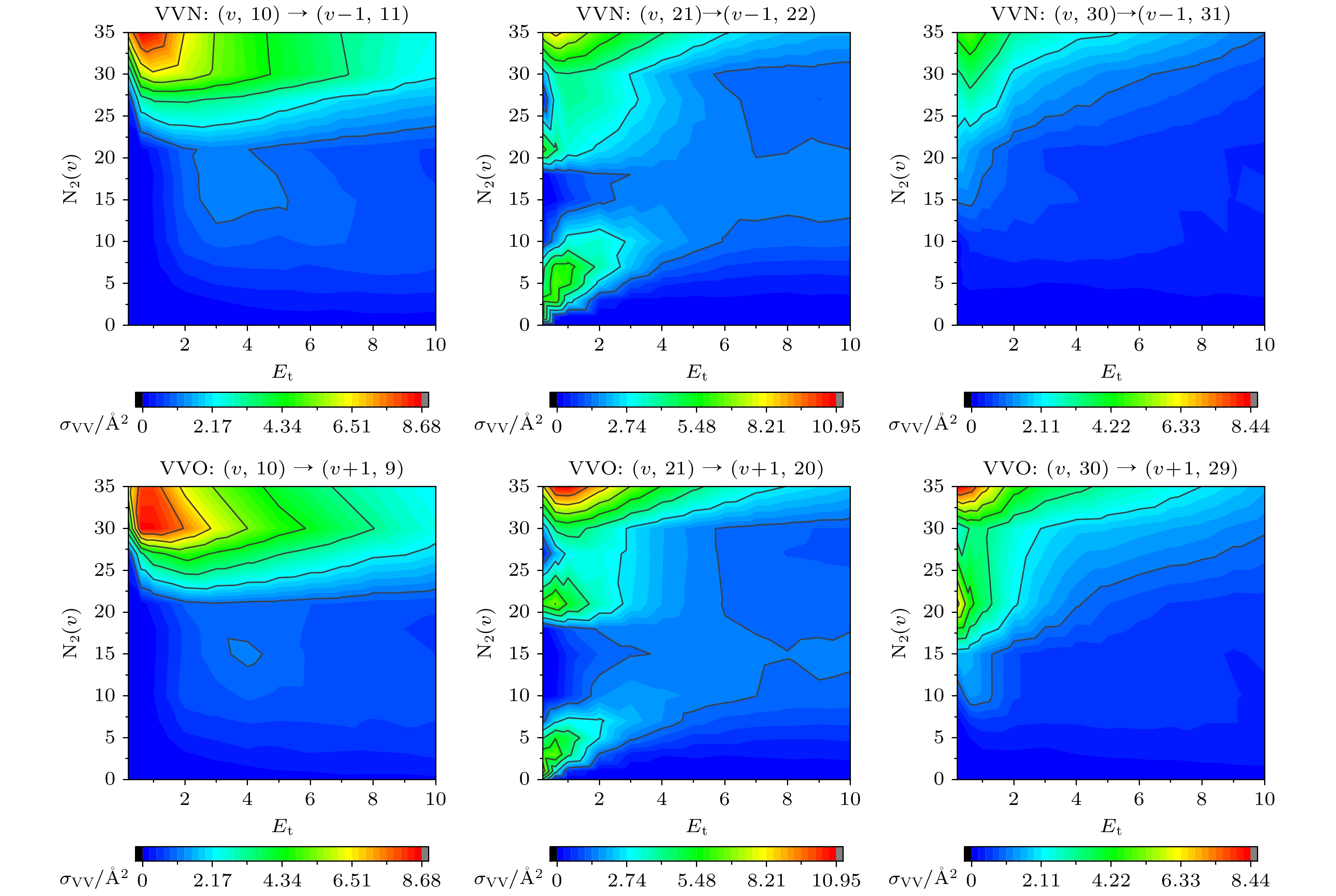
图2给出了N2(v) + O2(10), N2(v) + O2(21)和N2(v) + O2(30)过程中VVN和VVO单量子跃迁截面随初始能级(v)和初始平动能(Et)的等值线图. 为了更加直观地对比VVN和VVO的贡献大小, 同一组碰撞过程的截面等值线图采用相同的刻度尺. 由图2可以发现, 三个碰撞过程中VVN和VVO反应截面随平动能量和初始能级的变化趋势都非常相似, VVO的贡献略大一些. N2(v) + O2(10)碰撞中, 指定平动能量下VVN和VVO跃迁截面都随着碰撞伙伴初始振动态(v)的增加而不断增加, 然后趋于稳定. 对于给定N2(v), 随着平动能量的增加, VVN和VVO跃迁截面均有先增加后下降的趋势. N2(v) + O2(21)和N2(v) + O2(30)碰撞中, VV截面对于伙伴分子的初始振动态(v) 有复杂的依赖性, 尤其是低能碰撞区域. 例如在 N2(v) + O2(21)碰撞中的低能碰撞区域(Et < 1 eV), VVN和VVO均在v = 5和v = 20附近取得两个极大值, 在v = 15和v = 30附近取得两个极小值.
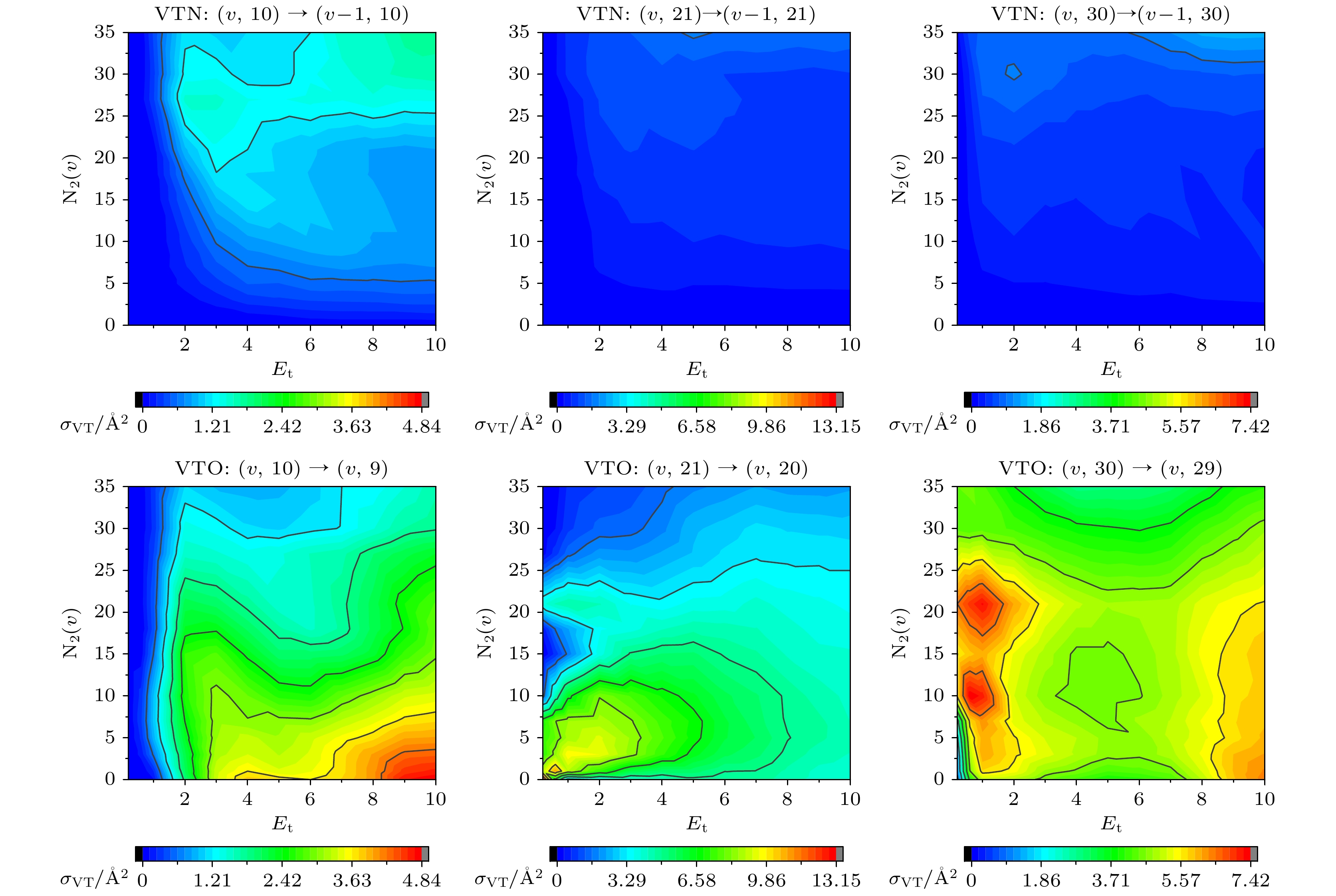
图3给出了N2(v) + O2(10), N2(v) + O2(21)和N2(v) + O2(30)过程中VTN和VTO单量子跃迁截面随初始能级(v)和初始平动能(Et)的等值线图. 为了更加直观地对比VTN和VTO的贡献大小, 同一组碰撞过程的截面等值线图采用相同的刻度尺. 三个碰撞过程中VTO的贡献都远大于VTN的贡献, N2(v) + O2(21)和N2(v) + O2(30)过程中VTN的贡献基本可以忽略不计. 这是因为O2在相邻振动能级之间的能量间距比N2小, 从而更快发生振动激发. 与VVO跃迁相比, VTO跃迁对平动能的敏感性更高: 随着平动能的增加, VTO(w = 10)逐渐增加, VTO(w = 21)逐渐减小, VTO(w = 30)先减小然后增加. 初始振动态处于低激发态的O2与低能态N2 (0 v 20)碰撞时, VVO截面值明显小于VTO; 与高能态N2 (20 < v 35)碰撞时VVO反应截面明显大于VTO跃迁. 然而, 处于高激发态的O2(30)与N2 (0 < v 30)碰撞时, 在整个平动能量范围内(0 < Et 10 eV), VTO跃迁的贡献显著大于VVO跃迁. 这一现象是由于两个分子的解离能量阈值和能级分布不同, 不同激发态之间的碰撞过程中VV跃迁事件可能会受到不同反应通道的抑制, 例如交换、解离通道或者具有更小能量差的非对称多量子共振过程.
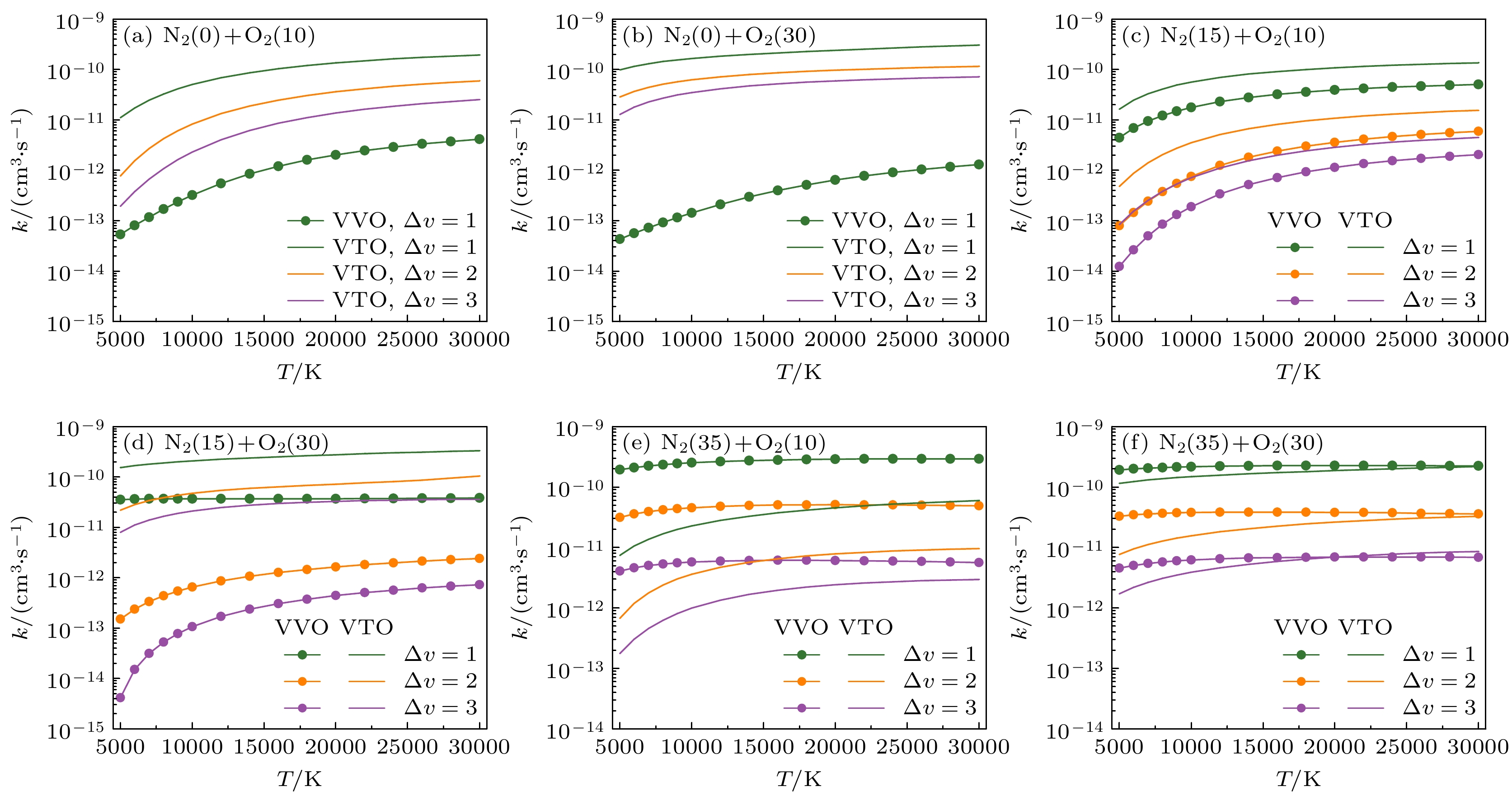
从VV和VT截面的等值线图发现, O2与不同N2(v)分子碰撞过程中, 单量子VV和VT跃迁的贡献是不同的. 图4显示了6组N2 + O2碰撞中单量子、多量子VVO和VTO反应速率系数在5000—30000 K范围内的温度依赖性. 对于振动激发态O2(w = 10, 30), 分别考虑三组碰撞伙伴: (a), (b)振动基态N2分子(v = 0); (c), (d)中间的振动激发态N2分子(v = 15); (e), (f)高振动激发态N2分子(v = 35). 随着温度的增加, O2(w)-N2(v = 0)和O2(w)-N2(v = 15)碰撞中单量子和多量子VVO和VTO都逐渐增加; O2(w)-N2(v = 35)碰撞中, VTO速率系数逐渐增大, VVO跃迁受温度变化影响不大. 这是因为解离反应通道通常会消耗高能态分子, 一定程度上会抑制高能态VV跃迁事件[36,42]. 与基态分子N2(v = 0)碰撞时, 单量子和多量子VTO通道的贡献远远大于VVO, 随着N2能级的增大, VTO速率系数逐渐减小, VVO速率系数逐渐增大. 如图4(f), 在两个高激发态碰撞中单量子和多量子VVO和VTO速率系数结果都比较接近, 尤其是在高温20000 K以上. 总的来说, 对于指定N2(v)分子, 伙伴O2(w)的振动能级越高, 振动能量传递效率越高, 反之亦然成立. 不同于先前研究的N2-N2体系[31], 由于异种分子的能级结构不同, N2-O2碰撞过程中VV和VT跃迁随振-转能级的演变趋势比较复杂, 不能表述为与初始振动能级间距相关.
为了便于在动力学建模中的调用, VV和VT速率系数可以拟合为Arrhenius形式:
其中A, n, B为拟合参数; 平动温度T的范围为5000—30000 K. 部分过程的拟合参数见附录中表A1, 均方误差(MSE)最小数量级为10–27.
-
N2-O2碰撞过程中发生的解离反应包括: O2单解离、N2单解离、生成一个NO分子的交换解离和双解离反应, 如(5)式—(8)式所示, 总解离截面由以下公式计算获得
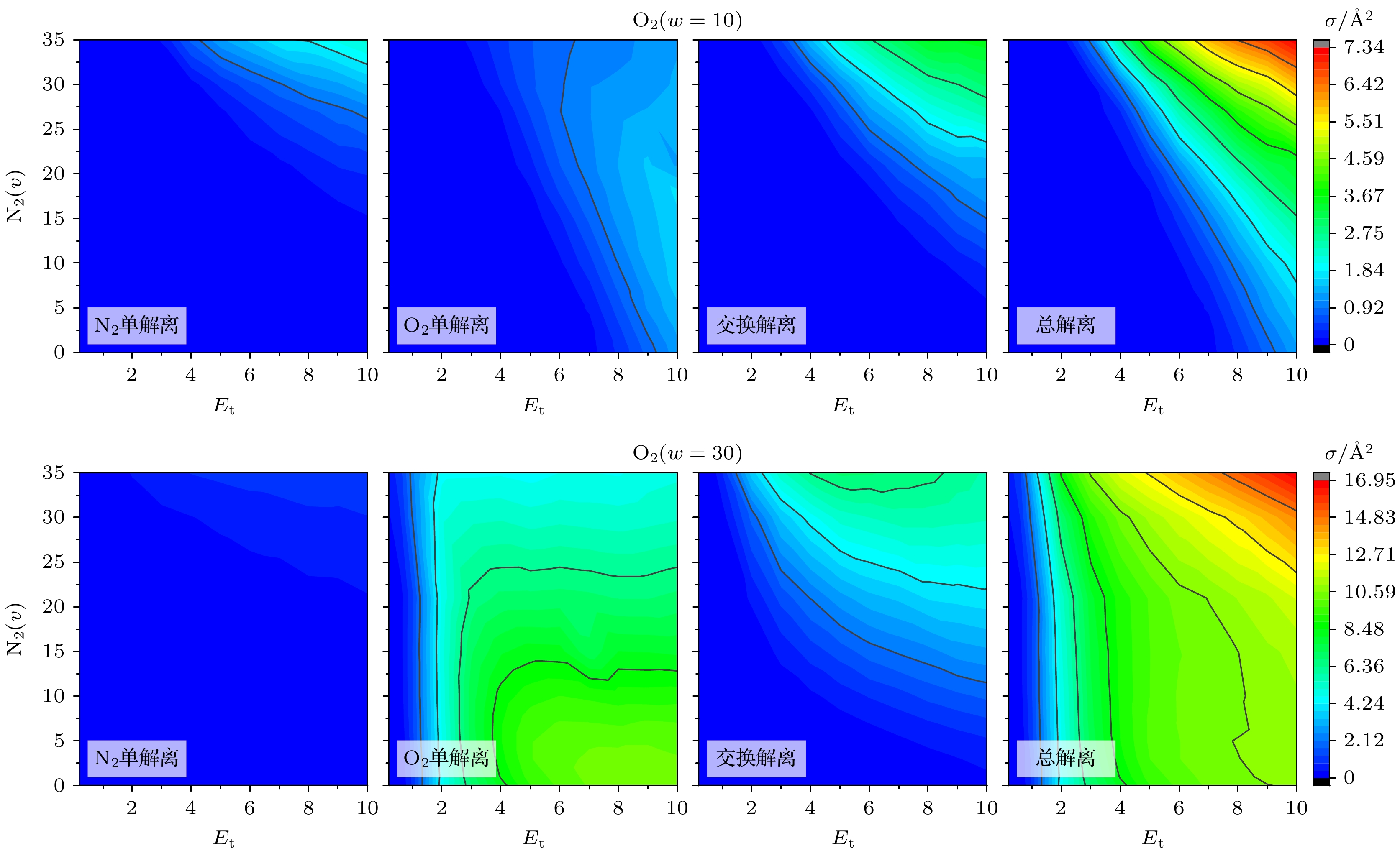
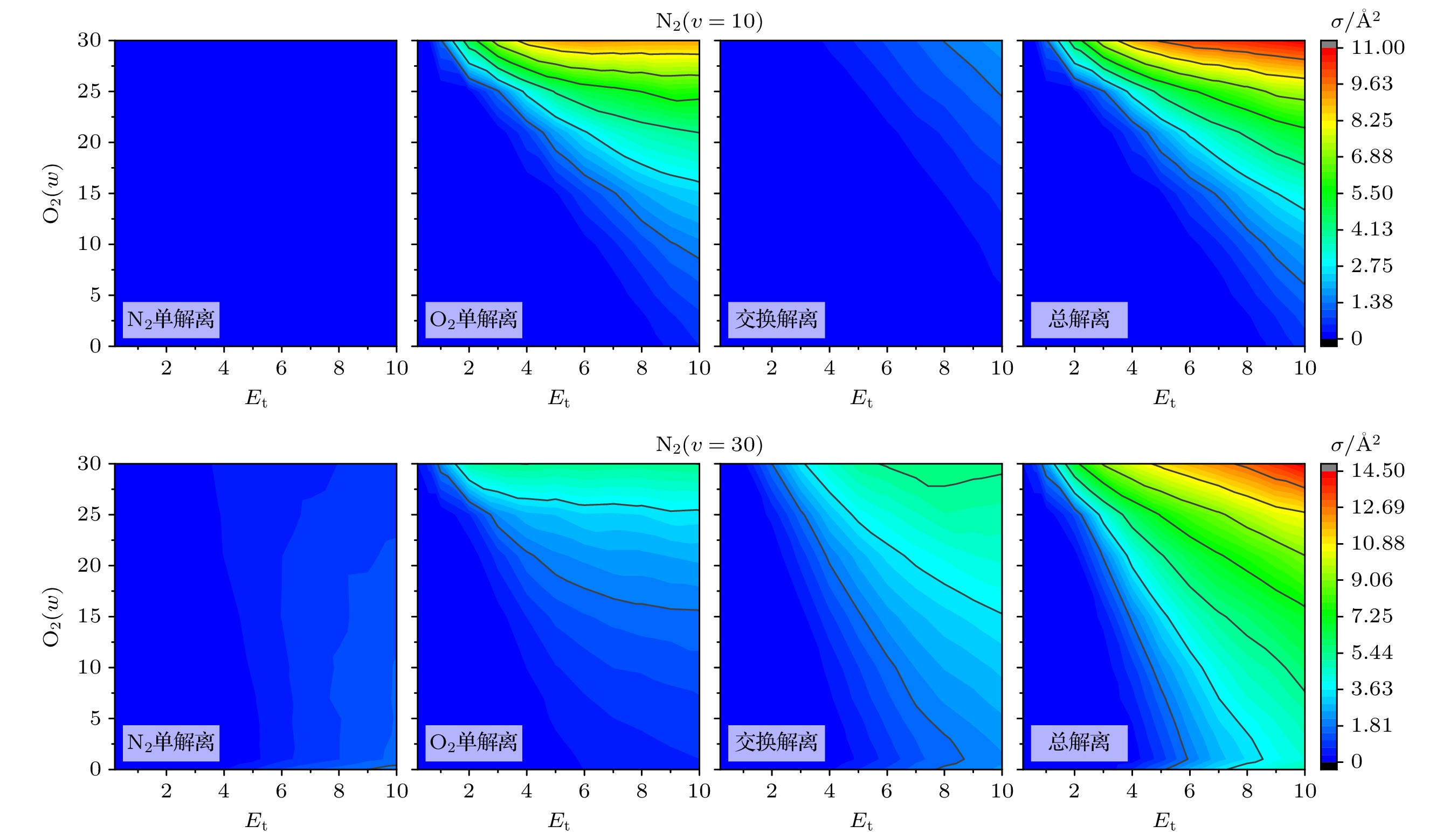
图5和图6分别展示了各个解离通道的反应截面随初始平动能(Et)和N2初始能级(v)、O2初始能级(w)的等值线图. 双解离通道因截面数值较小未在图中单独列出, 其贡献被包含在总解离截面中. 为了更加直观地观测到每个解离通道在总解离截面中的贡献, 同一组碰撞过程的截面等值线图采用相同的刻度尺. 由于O2分子的解离能小于N2分子(5.21 eV vs. 9.90 eV), 在所有碰撞中O2单解离通道的贡献明显大于N2单解离通道. 图5中, 随着N2振动能级(v)的增加, O2单解离截面的变化较小; 图6中, 随着O2振动能级(w)的增加, O2单解离截面增大. 这说明, N2-O2碰撞中的O2单解离截面主要由O2初始振动能级决定, 受伙伴分子N2振动能级变化的影响较小. 此外, 单解离和交换解离反应所需的平动能量阈值都会随着初始振动能级的增大而减小, 解离反应截面会随着平动能的增大而逐渐增大, 然后趋于稳定. 随着两个振动能级和平动能量的增加, 当总能量达到交换解离和双解离反应的能量阈值之后, 单解离事件一定程度上会受到抑制, 其贡献可能小于交换解离通道. 总的来说, 不论单个解离通道的贡献如何变化, 总的解离反应截面始终随着振动能级和平动能量的增加而不断增加, 直至趋于稳定.
-
研究发现, 随着平动能和初始振动能级的变化, 单解离和交换解离通道可能会受到促进或 抑制, 总解离截面始终保持单调增加. 基于这种单调性质和QCT计算获得的总解离截面数据集, 我们构建了NN-totaldiss神经网络模型, 可以直接预测N2-O2指定态碰撞诱导的总解离反应截面. 解离事件的发生依赖于总能量是否达到所需的 解离能阈值, 因此选取以下动力学参量作为描述指定态解离过程的输入特征: 初始平动能量Et、两个分子的初始振-转能量(Eint1, Eint2)以及初始振动能级(v, w).
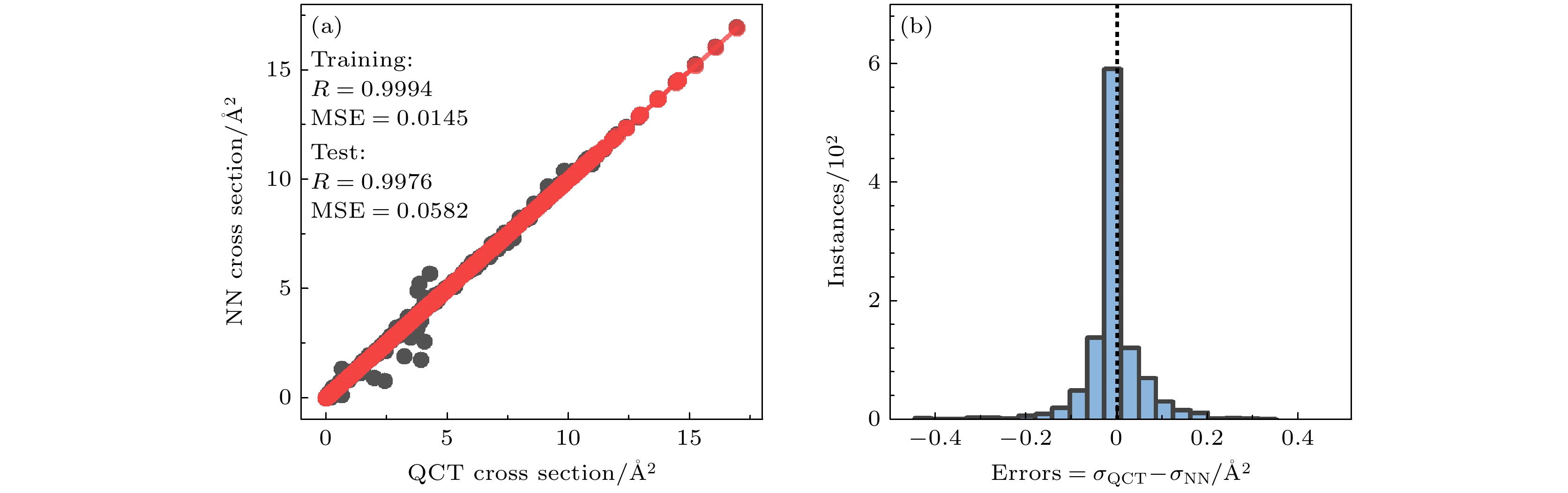
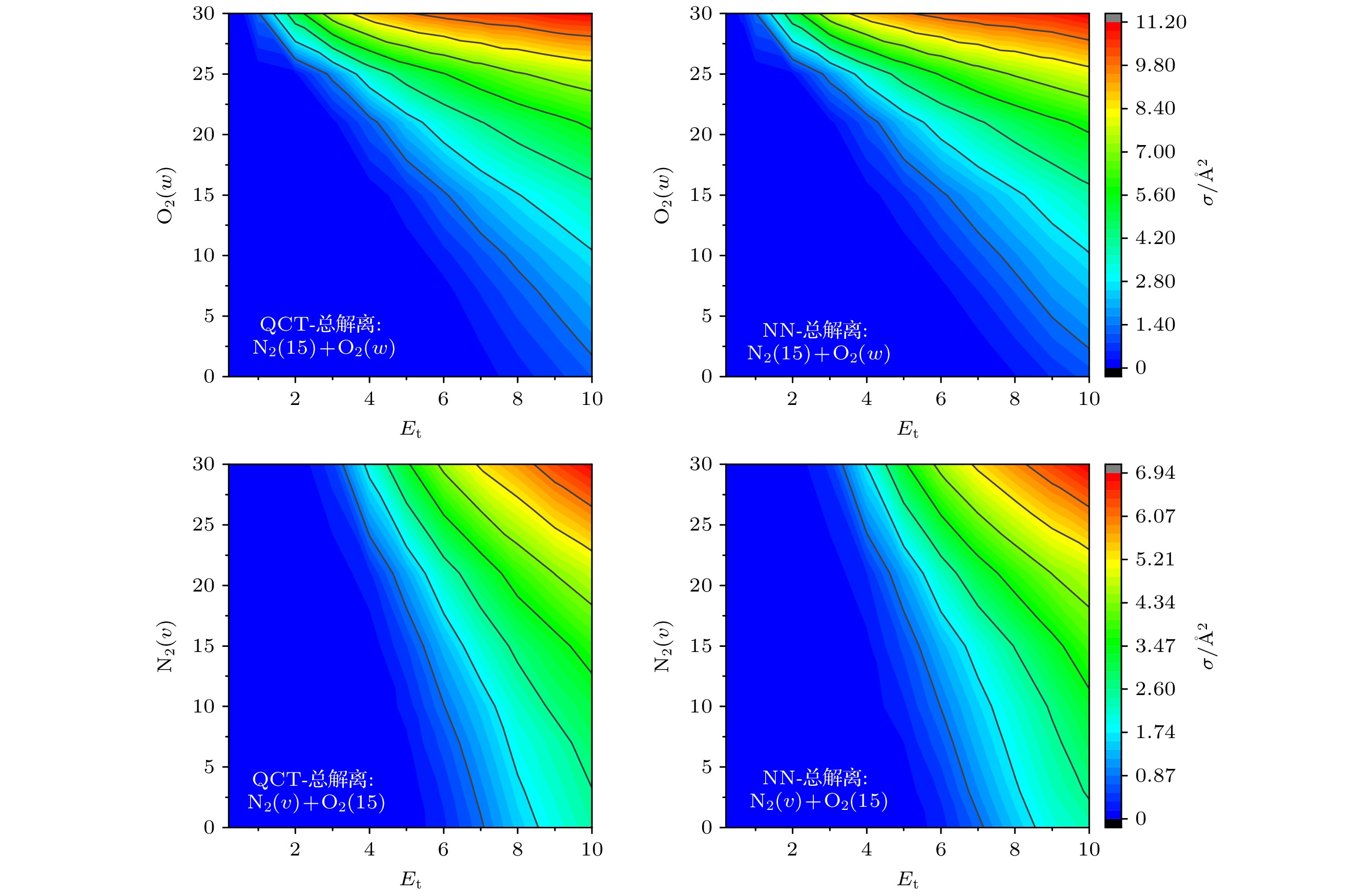
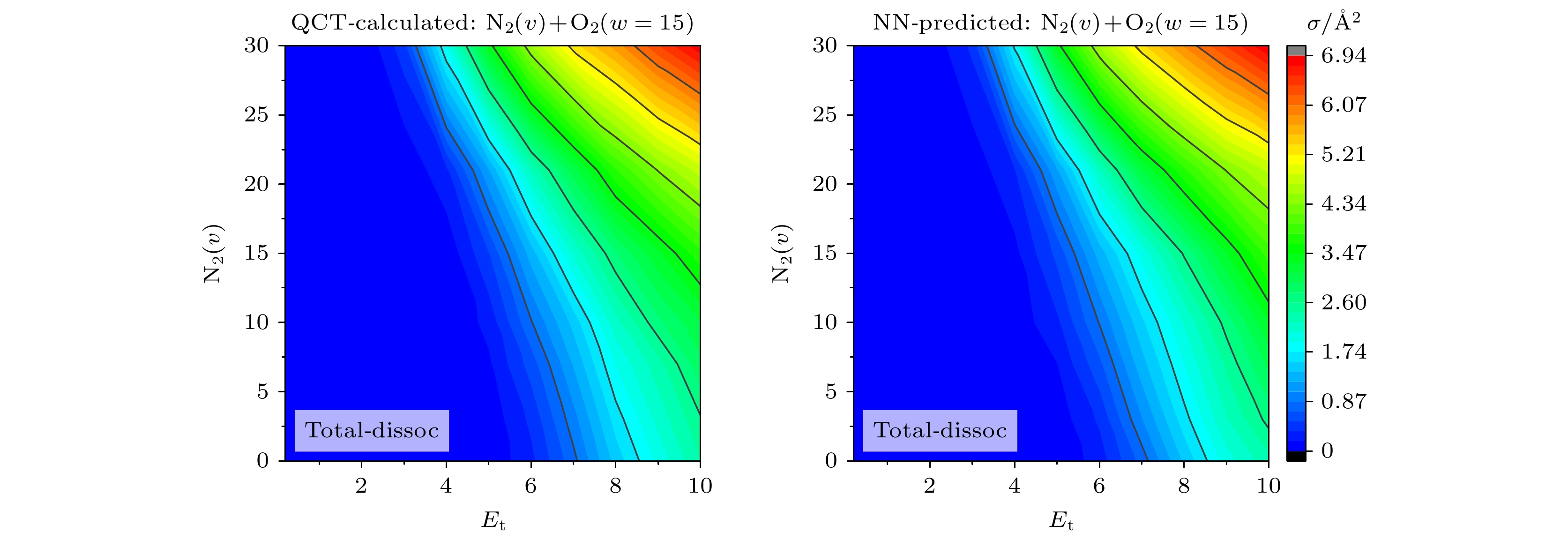
如图7所示, NN-totaldiss模型训练集和测试集的相关系数R值均达到了0.99, MSE值约为0.0145和0.0582, 绝大多数预测值和QCT计算值的相对误差都在0.2 Å2内, 表明了NN-totaldiss模型的可靠性和准确性. 图8给出了利用NN-totaldiss模型预测的总解离截面随初始平动能量(Et)和O2初始量子数(w)、N2初始量子数(v)变化的等值线图. 由图8可以发现, 随着平动能和两个初始量子数的变化, NN-totaldiss模型的预测值与QCT结果在数值和趋势上都符合非常好. 这说明NN-totaldiss模型准确再现了总解离截面随着平动能和N2, O2初始量子数变化的演变趋势. 由于模拟轨迹的数量限制和蒙特卡罗方法引起的采样误差, 在预测某些数值接近于0的截面时可能存在一些数值误差. 总体而言, NN-totaldiss模型可用于预测N2-O2体系态-态碰撞的总解离截面.
为了便于在动力学建模中调用, 获得的总解离截面数据按以下解析表达式[43]进行拟合:
其中a, b, c为拟合参数; 初始平动能Et范围为0.2—10 eV. 部分过程的拟合参数见附录中表A2, 均方根误差(RMSE)最小数量级为10–4.
-
本文采用准经典轨迹计算和神经网络模型相结合的方式对N2-O2态-态碰撞传能过程进行了详细的动力学研究. 首先采用QCT计算了90个不同初始振动态组合的N2(v) + O2(w)碰撞过程, 系统地讨论了非弹性VV/VT跃迁、N2/O2单解离、交换解离和双解离通道的贡献主次和反应截面变化趋势, 并在5000—30000 K温度范围内讨论了单量子和多量子VV/VT反应速率系数的温度依赖性. 研究发现: 1)两个分子发生近共振VV跃迁时退激发的概率相差较小, O2发生VT跃迁的概率要明显大于N2; 2) O2单解离通道是解离反应的主要通道, N2-O2交换解离通道其次, N2单解离和双解离的贡献相对较小; 3)随着振动能量和平动能量的增加, 总解离截面呈单调增加趋势. 基于QCT计算的总解离截面数据集, 训练了性能良好的NN-totaldiss模型(相关系数R ≈ 0.99), 可以准确地预测指定态N2(v) + O2(w)碰撞诱导的总解离截面. 相比传统的QCT计算, 神经网络模型的结合使得计算成本降低了约91.94%. 这一研究, 不仅为其他分子-分子体系的碰撞传能过程研究提供了新思路, 也为非热平衡动力学模型的合理优化提供了参考.
-
基于神经网络和动力学模拟方法研究高温N2-O2态-态碰撞振动激发和解离过程
Vibrational excitation and dissociation processes in high-temperature N2-O2 state-to-state collisions based on neural network and dynamic simulation
-
摘要: 散射截面和反应速率系数是阐明分子气体态-态碰撞传能机制的重要参数, 也是进行非平衡气体动力学建模的重要依据. 本文采用动力学模拟中的准经典轨迹方法(QCT)计算了90个不同初始振动态组合的N2(v) + O2(w)碰撞过程, 详细讨论了各个振动激发、解离反应通道的贡献和演变趋势. 研究发现: O2和N2在振动-振动能量交换(VV)通道的贡献比较接近, 振动-平动跃迁(VT)通道主要以O2为主; 总解离截面主要来自O2单解离通道, 交换解离其次, N2单解离和双解离通道的贡献相对较小. 基于QCT数据集, 训练了性能良好的神经网络模型(相关系数R值达到0.99), 可用于预测N2 + O2态-态碰撞的总解离截面. 和仅采用动力学模拟方法相比, 计算成本降低了约91.94%. 在5000—30000 K高温范围内, 给出了VV/VT速率系数的解析表达式.Abstract: The scattering cross-sections and reaction rate coefficients are crucial parameters for elucidating the energy transfer mechanism of state-to-state collisions between molecular gases and also serve as a fundamental basis for modeling the non-equilibrium flow field. However, the database of kinetic processes related to nitrogen shock flows is still being developed. In this work, a detailed kinetic study of the N2 + O2 collision is carried out by combining the quasi-classical trajectory method (QCT) and neural network model (NN). Firstly, QCT is used to calculate 90 N2(v) + O2(w) processes with various initial vibrational states (v,w), and the contributions of all vibrational excitation and dissociation reaction channels are discussed. The following conclusions are drawn: 1) The contributions of the vibration-vibration (VV) energy exchange channel of O2 and N2 are similar, while the vibration-translational (VT) transition mainly occurs on O2; 2) The total dissociation cross-section primarily results from the O2 single-dissociation channel, followed by the exchange-dissociation channel, with relatively minor contributions from the N2 single- and double-dissociation channels. Then, based on the QCT dataset, a high-performance NN model (R-value of 0.99) is trained to predict the total dissociation cross-section caused by N2(v) + O2(w) collisions. Compared with the method that only uses QCT, the method that jointly uses OCT and NN model can achieve an approximately 91.94% reduction in computational cost. Finally, to facilitate use in kinetic modeling, Arrhenius-type fits for the VV/VT rate coefficients are provided over the temperature range of 5000–30000 K, and an exponential form related to the translational energy Et is used to fit the total dissociation cross-section.
-

-
图 1 VV过程(1, 0) → (0, 1) (a) 和VT过程(1, 0) → (0, 0) (b)的速率系数作为平动温度的函数: 我们的计算结果(黑色实线)与已报道的理论数据[25,39]对比
Figure 1. Rate coefficients for the VV process (1, 0) → (0, 1) (a) and VT process (1, 0) → (0, 0) (b) as a function of translational temperature: comparison between our calculated results (in solid black line) and reported theoretical data[25,39].
图 2 N2(v) + O2(10), N2(v) + O2(21)和N2(v) + O2(30)过程中VVN和VVO单量子跃迁截面随初始能级(v)和初始平动能(Et)的等值线图
Figure 2. Contour map of VVN and VVO single-quantum transition cross sections with the initial energy level (v) and initial translational energy (Et) of N2(v) + O2(10), N2(v) + O2(21) and N2(v) + O2(30) processes.
图 3 N2(v) + O2(10), N2(v) + O2(21)和N2(v) + O2(30)过程中VTN和VTO单量子跃迁截面随N2初始能级(v)和初始平动能(Et)的等值线图
Figure 3. Contour map of VTN and VTO single-quantum transition cross sections with the initial energy level (v) and initial translational energy (Et) of N2(v) + O2(10), N2(v) + O2(21) and N2(v) + O2(30) processes.
表 1 QCT数据集包含的N2(v) + O2(w)碰撞过程
Table 1. N2(v) + O2(w) collision processes contained in the QCT dataset.
Group N2(v) O2(w) Et (eV) 1 {0, 5, 10, 21, 30} {0, 1, 3, 7, 10, 15, 21, 25, 30} {0.2, 0.6, 1, 2,
3, 4, 5, 6, 7, 8, 9, 10}2 {0, 1, 3, 7, 10, 15, 21, 25, 30, 35} {0, 5, 10, 21, 30} 表 A1 VV/VT反应速率系数(单位: k/(cm3·s–1))的Arrhenius拟合参数表(A, n, B). MSE是均方误差(单位: k/(cm3·s–1)), 温度范围为5000—30000 K
Table A1. Arrhenius fitting parameters (A, n, B) for VV/VT reaction rate coefficient (unit: k/(cm3·s–1)). MSE is the mean square error (unit: k/(cm3·s–1)), and the temperature range is 5000–30000 K.
N2(v) + O2(w) → N2(v') + O2(w') A n B MSE (0, 10) → (1, 9) 4.10 × 10–10 –2.91 × 10–1 4.81 × 104 4.27 × 10–26 (0, 10) → (0, 9) 2.44 × 10–10 4.28 × 10–2 2.01 × 104 7.67 × 10–22 (0, 10) → (0, 8) 3.33 × 10–10 –6.70 × 10–2 3.10 × 104 3.04 × 10–23 (0, 10) → (0, 7) 3.95 × 10–10 –1.39 × 10–1 3.96 × 104 2.66 × 10–24 (0, 21) → (1, 20) 4.24 × 10–10 –4.58 × 10–1 –4.53 × 103 4.21 × 10–23 (0, 21) → (0, 20) 3.50 × 10–10 2.04 × 10–1 2.78 × 103 7.96 × 10–21 (0, 21) → (0, 19) 2.51 × 10–10 –3.01 × 10–2 1.94 × 104 2.32 × 10–22 (0, 21) → (0, 18) 2.87 × 10–10 –7.43 × 10–2 2.46 × 104 5.62 × 10–23 (0, 30) → (1, 29) 3.01 × 10–10 –3.75 × 10–1 4.79 × 104 6.99 × 10–27 (0, 30) → (0, 29) 1.39 × 10–10 9.46 × 10–2 7.06 × 103 6.44 × 10–21 (0, 30) → (0, 28) 1.49 × 10–10 2.78 × 10–3 9.00 × 103 9.18 × 10–22 (0, 30) → (0, 27) 1.74 × 10–10 –5.01 × 10–2 1.14 × 104 2.99 × 10–22 (15, 10) → (16, 9) 2.31 × 10–10 –9.11 × 10–2 1.73 × 104 8.85 × 10–23 (15, 10) → (17, 8) 3.46 × 10–10 –2.77 × 10–1 3.64 × 104 2.77 × 10–25 (15, 10) → (18, 7) 3.94 × 10–10 –3.69 × 10–1 4.36 × 104 1.97 × 10–26 (15, 10) → (15, 9) 1.97 × 10–10 5.51 × 10–3 1.30 × 104 8.14 × 10–22 (15, 10) → (15, 8) 2.78 × 10–10 –1.96 × 10–1 2.58 × 104 4.40 × 10–24 (15, 10) → (15, 7) 3.17 × 10–10 –3.04 × 10–1 3.38 × 104 2.16 × 10–25 (15, 21) → (16, 20) 1.79 × 10–10 –2.61 × 10–2 1.56 × 104 2.42 × 10–22 (15, 21) → (17, 19) 2.69 × 10–10 –3.02 × 10–1 2.64 × 104 5.21 × 10–25 (15, 21) → (18, 18) 3.12 × 10–10 –3.82 × 10–1 3.60 × 104 3.42 × 10–26 (15, 21) → (15, 20) 1.96 × 10–10 7.64 × 10–2 1.35 × 104 2.82 × 10–21 (15, 21) → (15, 19) 2.46 × 10–10 –1.03 × 10–1 2.19 × 104 3.80 × 10–23 (15, 21) → (15, 18) 2.07 × 10–10 –1.88 × 10–1 2.49 × 104 3.33 × 10–24 (15, 30) → (16, 29) 9.24 × 10–11 –8.39 × 10–2 1.39 × 103 3.39 × 10–22 (15, 30) → (17, 28) 2.05 × 10–10 –3.47 × 10–1 2.70 × 104 1.23 × 10–25 (15, 30) → (18, 27) 3.20 × 10–10 –4.66 × 10–1 3.90 × 104 4.67 × 10–27 (15, 30) → (15, 29) 1.17 × 10–10 1.13 × 10–1 4.53 × 103 1.04 × 10–20 (15, 30) → (15, 28) 1.57 × 10–10 –1.67 × 10–2 1.10 × 104 5.05 × 10–22 (15, 30) → (15, 27) 5.12 × 10–10 –2.19 × 10–1 1.17 × 104 1.06 × 10–22 (35, 10) → (36, 9) 5.68 × 10–10 –5.32 × 10–2 3.17 × 103 1.51 × 10–20 (35, 10) → (37, 8) 1.30 × 10–9 –2.97 × 10–1 6.01 × 103 4.83 × 10–22 (35, 10) → (38, 7) 4.10 × 10–10 –3.94 × 10–1 6.35 × 103 7.64 × 10–24 (35, 10) → (35, 9) 2.01 × 10–10 –6.83 × 10–2 1.58 × 104 1.33 × 10–22 (35, 10) → (35, 8) 1.98 × 10–10 –2.33 × 10–1 1.85 × 104 3.73 × 10–24 (35, 10) → (35, 7) 1.88 × 10–10 –3.31 × 10–1 2.17 × 104 3.19 × 10–25 (35, 21) → (36, 20) 1.79 × 10–10 –2.60 × 10–2 1.56 × 104 2.42 × 10–22 (35, 21) → (37, 19) 2.69 × 10–10 –3.02 × 10–1 2.64 × 104 5.21 × 10–25 (35, 21) → (38, 18) 3.12 × 10–10 –3.82 × 10–1 3.60 × 104 3.4 × 10–26 (35, 21) → (35, 20) 1.96 × 10–10 7.64 × 10–2 1.35 × 104 2.82 × 10–21 (35, 21) → (35, 19) 2.46 × 10–10 –1.03 × 10–1 2.19 × 104 3.80 × 10–23 (35, 21) → (35, 18) 2.07 × 10–10 –1.88 × 10–1 2.49 × 104 3.33 × 10–24 (35, 30) → (36, 29) 5.99 × 10–10 –8.87 × 10–2 1.96 × 103 1.15 × 10–20 (35, 30) → (37, 28) 4.54 × 10–10 –2.35 × 10–1 3.14 × 103 3.48 × 10–22 (35, 30) → (38, 27) 9.69 × 10–11 –2.38 × 10–1 5.53 × 103 9.00 × 10–24 (35, 30) → (35, 29) 6.49 × 10–11 1.25 × 10–1 3.21 × 103 5.24 × 10–21 (35, 30) → (35, 28) 1.25 × 10–10 –9.18 × 10–2 1.26 × 104 6.00 × 10–23 (35, 30) → (35, 27) 1.61 × 10–10 –2.35 × 10–1 1.59 × 104 3.84 × 10–24 表 A2 总解离截面(单位: Å2)的拟合参数表(a, b, c). 初始平动能Et范围为0.2—10 eV, RMSE是均方根误差(单位: Å2)
Table A2. Fitting parameters (a, b, c) of total dissociation cross-section (unit: Å2). The range of initial translational energy Et is 0.2–10 eV, and RMSE is root mean square error (unit: Å2).
N2(v) O2(w) a b c RMSE 0 1 1.98 × 101 –1.02 × 102 9.03 × 100 1.82 × 10–4 0 3 1.13 × 101 –5.82 × 101 5.11 × 100 3.54 × 10–4 0 5 8.29 × 100 –4.30 × 101 3.87 × 100 2.95 × 10–3 0 7 6.43 × 100 –3.35 × 101 3.14 × 100 8.48 × 10–3 0 10 –2.46 × 102 3.52 × 101 –9.70 × 10–1 5.70 × 10–3 0 15 –9.18 × 101 1.06 × 101 2.57 × 10–1 8.02 × 10–3 0 21 –2.04 × 101 2.24 × 10–1 8.60 × 10–1 3.37 × 10–2 0 25 –5.67 × 100 –1.11 × 100 1.01 × 100 6.37 × 10–2 0 30 –6.06 × 10–1 –5.62 × 10–1 1.10 × 100 1.30 × 10–1 1 21 –2.03 × 101 3.57 × 10–1 8.50 × 10–1 2.33 × 10–2 1 30 –7.54 × 10–1 –4.60 × 10–1 1.09 × 100 1.58 × 10–1 3 15 –7.75 × 101 8.74 × 100 3.16 × 10–1 1.44 × 10–2 3 21 –2.10 × 101 1.02 × 100 7.94 × 10–1 4.72 × 10–2 3 30 –8.40 × 10–1 –3.81 × 10–1 1.09 × 100 1.73 × 10–1 5 30 –8.07 × 10–1 –3.74 × 10–1 1.09 × 100 1.94 × 10–1 5 0 8.27 × 100 –4.28 × 101 3.65 × 100 6.98 × 10–3 5 1 8.21 × 100 –4.25 × 101 3.75 × 100 3.78 × 10–3 5 3 7.21 × 100 –3.75 × 101 3.44 × 100 6.53 × 10–3 5 7 –3.96 × 102 6.61 × 101 –2.62 × 100 1.60 × 10–3 5 10 –2.83 × 102 4.83 × 101 –1.81 × 100 5.40 × 10–3 5 15 –7.95 × 101 9.94 × 100 2.43 × 10–1 2.80 × 10–2 5 21 –1.95 × 101 8.26 × 10–1 8.08 × 10–1 3.42 × 10–2 5 25 –6.46 × 100 –4.60 × 10–1 9.66 × 10–1 6.22 × 10–2 7 15 –6.79 × 101 8.41 × 100 2.93 × 10–1 2.57 × 10–2 7 21 –1.85 × 101 6.82 × 10–1 8.22 × 10–1 3.75 × 10–2 7 30 –7.52 × 101 –3.87 × 10–1 1.09 × 100 2.02 × 10–1 10 15 –6.21 × 101 7.99 × 100 3.14 × 10–1 3.16 × 10–2 10 21 –1.75 × 101 7.87 × 10–1 8.16 × 10–1 4.21 × 10–2 10 30 –6.64 × 10–1 –4.20 × 10–1 1.09 × 100 2.00 × 10–1 15 0 3.92 × 100 –2.04 × 101 2.03 × 100 1.68 × 10–2 15 3 3.21 × 100 –1.68 × 101 1.83 × 100 4.68 × 10–2 15 7 –1.97 × 102 3.56 × 101 –1.29 × 100 2.32 × 10–2 15 10 –1.12 × 102 1.78 × 101 –2.20 × 10–1 3.96 × 10–2 15 15 –4.74 × 101 5.30 × 100 5.20 × 10–1 3.20 × 10–2 15 21 –1.20 × 101 –4.00 × 10–1 9.19 × 10–1 5.88 × 10–2 15 25 –5.0 × 100 –5.65 × 10–1 9.88 × 10–1 3.51 × 10–2 15 30 –6.92 × 10–1 –3.97 × 10–1 1.09 × 100 1.50 × 10–1 18 21 –1.16 × 101 –2.55 × 10–1 9.34 × 10–1 5.33 × 10–2 21 15 –3.44 × 101 4.04 × 100 6.22 × 10–1 4.97 × 10–2 21 0 –7.70 × 101 5.01 × 100 5.89 × 10–1 1.06 × 10–2 21 1 –7.61 × 101 5.57 × 100 5.54 × 10–1 7.48 × 10–3 21 3 –8.50 × 101 9.82 × 100 2.65 × 10–1 1.68 × 10–2 21 7 –6.54 × 101 7.75 × 100 3.69 × 10–1 2.71 × 10–2 21 10 –4.66 × 101 4.61 × 100 5.73 × 10–1 1.65 × 10–2 21 18 –1.81 × 101 8.87 × 10–1 8.42 × 10–1 6.70 × 10–2 21 21 –1.09 × 101 8.07 × 10–2 9.19 × 10–1 5.56 × 10–2 21 25 –3.91 × 100 –8.38 × 10–1 1.04 × 100 6.94 × 10–2 21 27 –2.07 × 100 –7.80 × 10–1 1.07 × 100 6.97 × 10–2 21 30 –4.61 × 10–1 –5.58 × 10–1 1.12 × 100 1.79 × 10–1 27 21 –6.79 × 100 –4.70 × 10–1 1.02 × 100 8.37 × 10–2 30 15 –9.22 × 100 –3.68 × 10–1 9.65 × 10–1 1.25 × 10–1 30 21 –4.34 × 100 –9.02 × 10–1 1.08 × 100 1.40 × 10–1 30 30 1.01 × 10–1 –8.90 × 10–1 1.23 × 100 3.85 × 10–1 35 21 –2.49 × 100 –8.65 × 10–1 1.13 × 100 1.79 × 10–1 35 5 –1.15 × 101 5.75 × 10–1 8.62 × 10–1 5.73 × 10–2 35 10 –8.09 × 100 –4.55 × 10–2 9.44 × 10–1 7.15 × 10–2 35 30 1.06 × 10–1 –8.47 × 10–1 1.29 × 100 5.14 × 10–1 -
[1] 王庆洋, 丛堃林, 刘丽丽, 陆宏志, 徐胜金 2017 气体物理 2 46 doi: 10.19527/j.cnki.2096-1642.2017.04.005 Wang Q Y, Cong K L, Liu L L, Lu H Z, Xu S J 2017 Phys. Gases 2 46 doi: 10.19527/j.cnki.2096-1642.2017.04.005 [2] 吕达仁, 陈泽宇, 郭霞, 田文寿 2009 力学进展 39 674 doi: 10.6052/1000-0992-2009-6-J2009-039 Lu D R, Chen Z Y, Guo X, Tian W S 2009 Adv. Mech. 39 674 doi: 10.6052/1000-0992-2009-6-J2009-039 [3] 董维中, 丁明松, 高铁锁, 江涛 2013 空气动力学学报 31 692 Dong W Z, DIing M S, Gao T S, Jiang T 2013 Acta Aerodyn. Sin. 31 692 [4] 国义军, 曾磊, 张昊元, 代光月, 王安龄, 邱波, 周述光, 刘骁 2017 空气动力学学报 35 496 doi: 10.7638/kqdlxxb-2016.0114 Guo Y J, Zeng L, Zhang H Y, Dai G Y, Wang A L, Qiu B, Zhou S G, Liu X 2017 Acta Aerodyn. Sin. 35 496 doi: 10.7638/kqdlxxb-2016.0114 [5] Cacciatore M 1996 Mol. Phys. Hypersonic Flows 482 21 [6] Pavlov A V 2011 Geomag. Aeron. 51 143 doi: 10.1134/S0016793211020149 [7] Treanor C E 1965 J. Chem. Phys. 43 532 doi: 10.1063/1.1696777 [8] Nagnibeda E, Papina K, Kunova O 2018 AIP Conf. Proc. 1 060012 doi: 10.1063/1.5034673 [9] Laux C O, Pierrot L, Gessman R J 2012 Chem. Phys. 398 46 doi: 10.1016/j.chemphys.2011.10.028 [10] Zhao X, Xu X, Xu H 2024 J. Chem. Phys. 161 231101 doi: 10.1063/5.0241219 [11] Hong Q, Bartolomei M, Pirani F, Sun Q, Coletti C 2025 J. Chem. Phys. 162 114308 doi: 10.1063/5.0255380 [12] Feng D, Song Y, Wang Z, Yang L, Zhang Z, Yang Y 2025 J. Chem. Phys. 162 114107 doi: 10.1063/5.0250359 [13] He D, Liu T, Li R, Hong Q, Li F, Sun Q, Si T, Luo X 2024 J. Chem. Phys. 161 244302 doi: 10.1063/5.0239906 [14] Andrienko D, Boyd I D 2017 55th AIAA Aerospace Sciences Meeting Grapevine Texas, January 9-13, 2017 p2017-0659 [15] Kurnosov A K, Napartovich A P, Shnyrev S L, Cacciatore M 2010 Plasma Sources Sci. Technol. 19 045015 doi: 10.1088/0963-0252/19/4/045015 [16] Esposito F, Garcia E, Laganà A 2017 Plasma Sources Sci. Technol. 26 045005 doi: 10.1088/1361-6595/aa5d27 [17] Lino Da Silva M, Loureiro J, Guerra V 2012 Chem. Phys. Lett. 531 28 doi: 10.1016/j.cplett.2012.01.074 [18] Varga Z, Meana-Pañeda R, Song G, Paukku Y, Truhlar D G 2016 J. Chem. Phys. 144 024310 doi: 10.1063/1.4939008 [19] Garcia E, Verdasco J E, Laganà A 2020 J. Phys. Chem. A 124 6445 doi: 10.1021/acs.jpca.0c04937 [20] Andrienko D A, Boyd I D 2018 J. Chem. Phys. 148 084309 doi: 10.1063/1.5007069 [21] Garcia E, Pirani F, Laganà A, Martí C 2017 Phys. Chem. Chem. Phys. 19 11206 doi: 10.1039/C7CP01340J [22] Garcia E, Laganà A, Pirani F, Bartolomei M, Cacciatore M, Kurnosov A 2016 J. Phys. Chem. A 120 5208 doi: 10.1021/acs.jpca.6b00962 [23] Billing G D, Jolicard G 1982 Chem. Phys. 65 323 doi: 10.1016/0301-0104(82)85208-7 [24] Billing G D 1994 Chem. Phys. 179 463 doi: 10.1016/0301-0104(94)87022-5 [25] Garcia E, Kurnosov A, Laganà A, Pirani F, Bartolomei M, Cacciatore M 2016 J. Phys. Chem. B 120 1476 doi: 10.1021/acs.jpcb.5b06423 [26] Koner D, Unke O T, Boe K, Bemish R J, Meuwly M 2019 J. Chem. Phys. 150 211101 doi: 10.1063/1.5097385 [27] Chen J, Li J, Bowman J M, Guo H 2020 J. Chem. Phys. 153 054310 doi: 10.1063/5.0015101 [28] Hong Q, Storchi L, Bartolomei M, Pirani F, Sun Q, Coletti C 2023 Eur. Phys. J. D 77 128 doi: 10.1140/epjd/s10053-023-00688-4 [29] Gu K M, Zhang H, Cheng X L 2023 J. Chem. Phys. 158 244302 doi: 10.1063/5.0151331 [30] Huang X, Gu K M, Guo C M, Cheng X L 2023 Phys. Chem. Chem. Phys. 25 29475 doi: 10.1039/D3CP04044E [31] Guo C M, Zhang H, Cheng X L 2024 J. Phys. Chem. A 128 5435 doi: 10.1021/acs.jpca.4c00590 [32] Bernstein R B, Bederson B 1980 Phys. Today 33 79 doi: 10.1063/1.2913913 [33] Fernández-Ramos A, Miller J A, Klippenstein S J, Truhlar D G 2006 Chem. Rev. 106 4518 doi: 10.1021/cr050205w [34] Hu X, Hase W L, Pirraglia T 1991 J. Comput. Chem. 12 1014 doi: 10.1002/jcc.540120814 [35] Gutzwiller M C 1990 Chaos in Classical and Quantum Mechanics (Berlin: Springer [36] Chaudhry R S, Bender J D, Valentini P, Schwartzentruber T E, Candler G V 2016 46th AIAA Thermophysics Conference Washington, June 13–17, 2016 p4319 [37] Mankodi T K, Bhandarkar U V, Myong R S 2020 Phys. Fluids 32 036102 doi: 10.1063/1.5141148 [38] Andrienko D, Boyd I D 2017 47th AIAA Thermophysics Conference Denver, Colorado, June 5–9, 2017 p3163 [39] Andrienko D, Boyd I D 2018 J. Thermophys. Heat Transfer 32 904 doi: 10.2514/1.T4968 [40] Rumelhart D E, Hintont G E, Williams R J 1986 Nature 323 533 doi: 10.1038/323533a0 [41] Moré J J 1978 Numerical Analysis (Berlin, Heidelberg: Springer-Verlag) p105 [42] Chaudhry R S, Candler G V 2019 AIAA Scitech Forum San Diego, California, January 7–11, 2019 p2019-0789 [43] Mankodi T K, Bhandarkar U V, Puranik B P 2018 J. Chem. Phys. 148 144305 doi: 10.1063/1.5020125 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: