高级搜索

锂离子动力电池电化学建模进展及降阶方法研究

,  ,  ,  , 

downloadPDF

上一篇

下一篇

张艳岗, 董泽庆, 郑利锋, 王凯, 梁君飞. 锂离子动力电池电化学建模进展及降阶方法研究[J]. 物理学报, 2025, 74(14): 148803-1. doi: 10.7498/aps.74.20250591
引用本文: 张艳岗, 董泽庆, 郑利锋, 王凯, 梁君飞. 锂离子动力电池电化学建模进展及降阶方法研究[J]. 物理学报, 2025, 74(14): 148803-1. doi: 10.7498/aps.74.20250591
shu
Yangang ZHANG, Zeqing DONG, Lifeng ZHENG, Kai WANG, Junfei LIANG. Research on electrochemical modeling and order reduction methods for lithium-ion power batteries[J]. Acta Physica Sinica, 2025, 74(14): 148803-1. doi: 10.7498/aps.74.20250591
Citation: Yangang ZHANG, Zeqing DONG, Lifeng ZHENG, Kai WANG, Junfei LIANG. Research on electrochemical modeling and order reduction methods for lithium-ion power batteries[J]. Acta Physica Sinica, 2025, 74(14): 148803-1. doi: 10.7498/aps.74.20250591
shu

锂离子动力电池电化学建模进展及降阶方法研究

  • 中北大学能源与动力工程学院, 太原　030051

    • 作者简介: 张艳岗.E-mail: 20102507@nuc.edu.cn .
    通讯作者: E-mail: junfeiliang@buaa.edu.cn.

  • 中图分类号: 88.85.Hj, 82.47.Aa, 82.80.Fk, 95.75.-z

Research on electrochemical modeling and order reduction methods for lithium-ion power batteries

  • College of Energy and Power Engineering, North China University, Taiyuan 030051, China

    • Corresponding author: E-mail: junfeiliang@buaa.edu.cn.

  • MSC: 88.85.Hj, 82.47.Aa, 82.80.Fk, 95.75.-z

  • 摘要: 动力电池作为新能源汽车的核心动力装置, 其精准建模对于动力电池的运行状态估计、全生命周期故障诊断、多工况安全管控等具有重要意义. 以P2D(pseudo-two-dimensions)模型为代表的电化学模型作为能从微观尺度表征电池内部电化学反应过程的机理模型, 其对于动力电池的老化、生热行为的准确描述是电池单体容量衰减、内阻增大、受热不均以及电池模组性能不一致评价的重要依据. 本文梳理了目前锂离子动力电池电化学建模的最新研究进展, 剖析了电化学模型与等效电路模型、老化模型、热模型的耦合方法及应用现状, 重点针对电化学模型的参数繁多且辨识困难的问题, 对比分析了单粒子模型、带液相单粒子模型、电化学平均值模型、固液相重构模型、一维电化学模型等动力电池电化学模型降阶方法的优势与不足, 指出了电化学模型降阶表征的关键难点, 并对电化学模型降阶重构方法的研究趋势进行了展望, 以期为动力电池电化学模型的降阶重构研究指明方向.
    Abstract: As the core power unit of new energy vehicles, the accurate modeling of power batteries is of great significance for evaluating their operating status, diagnosing faults throughout their lifecycle, and ensuring safety control under multiple operating conditions. The electrochemical model represented by the P2D model serves as a mechanistic model that can characterize the internal electrochemical reaction process of batteries on a microscale. Its accurate description of the aging and heating behavior of power batteries is an important basis for evaluating the capacity degradation, increase in internal resistance, uneven heating, and inconsistent performance of battery modules. The paper summarizes the latest advances in electrochemical modeling of lithium-ion power batteries, analyzes the coupling methods and application status of electrochemical models with equivalent circuit models, aging models, and thermal models, and focuses on the problem of numerous parameters and difficult identification of electrochemical models. In this paper, the advantages and disadvantages of the single particle model, single particle model with electrolyte, electrochemical mean model, solid-liquid phase reconstruction model, one-dimensional electrochemical model and other methods are compared with each other and analyzed for reducing the order of power battery electrochemical models, the key difficulties in characterizing electrochemical model order reduction are pointed out, and the research trends of electrochemical model reduction order reconstruction methods are prospected, in order to provide direction for the research on electrochemical model reduction order reconstruction of power batteries.
  • 加载中

  • 图 1  等效电路模型　(a) 1阶RC模型; (b) 2阶RC模型

    Figure 1.  Equivalent-circuit model: (a) 1st order RC model; (b) 2nd order RC model.

    下载: 全尺寸图片 幻灯片

    图 2  P2D模型结构示意图

    Figure 2.  P2D model structure diagram.

    下载: 全尺寸图片 幻灯片

    图 3  电化学-热模型耦合关系图[8]

    Figure 3.  Electrochemical thermal model coupling relationship diagram[8].

    下载: 全尺寸图片 幻灯片

    图 4  P2D电化学析锂模型[15]

    Figure 4.  P2D electrochemical Li precipitation model[15].

    下载: 全尺寸图片 幻灯片

    图 5  不同倍率恒流放电精度对比[43]　(a) 1 C放电; (b) 2 C放电; (c) 3 C放电; (d) 4 C放电

    Figure 5.  Comparison of constant current discharge accuracy at different ratios[43]: (a) 1 C discharge; (b) 2 C discharge; (c) 3 C discharge; (d) 4 C discharge.

    下载: 全尺寸图片 幻灯片

    图 6  动态工况下模型输出电压对比[43]　(a) FUDS工况; (b) US06工况

    Figure 6.  Comparison of model output voltage under dynamic operating conditions[43]: (a) FUDS working condition; (b) US06 working condition.

    下载: 全尺寸图片 幻灯片

    图 7  三种模型在放电倍率为1 C和3 C时的放电曲线[63]

    Figure 7.  Discharge curves of three models at discharge rates of 1 C and 3 C[63].

    下载: 全尺寸图片 幻灯片

    图 8  各参数之间的关联关系图

    Figure 8.  Coupling relationship diagram between various parameters.

    下载: 全尺寸图片 幻灯片

    图 B1  P2D 模型

    Figure B1.  P2D model

    下载: 全尺寸图片 幻灯片

    图 B2  SPM模型

    Figure B2.  SPM model

    下载: 全尺寸图片 幻灯片

    图 B3  SPMe模型

    Figure B3.  SPMe model

    下载: 全尺寸图片 幻灯片

    图 B4  电化学平均值模型[47,48]

    Figure B4.  Electrochemical average value model[47,48]

    下载: 全尺寸图片 幻灯片

    图 B5  LSP2D模型[53.54,61–63]

    Figure B5.  LSP2D model[53.54,61–63]

    下载: 全尺寸图片 幻灯片

    图 B6  一维模型[68]

    Figure B6.  One-dimensional model[68]

    下载: 全尺寸图片 幻灯片

    表 1  P2D模型控制方程及边界条件

    Table 1.  P2D model control equations and boundary conditions.

    状态 控制方程 边界条件
    固相锂离子浓度 $ \dfrac{{\partial {c_{\text{s}}}}}{{\partial t}} = \dfrac{1}{{{r^2}}}\dfrac{\partial }{{\partial r}}\left( {{r^2}{D_{\text{s}}}\dfrac{{\partial {c_{\text{s}}}}}{{\partial r}}} \right) $ $ {D_{\text{s}}}\dfrac{{\partial {c_{\text{s}}}}}{{\partial r}}{\Big|_{r = 0}} = 0,\;\; {D_{\text{s}}}\dfrac{{\partial {c_{\text{s}}}}}{{\partial r}}{\Big|_{r = {R_{\text{s}}}}} = - \dfrac{j}{F} $
    液相锂离子浓度 $ \varepsilon \dfrac{{\partial {c_{\text{l}}}}}{{\partial t}} = \dfrac{\partial }{{\partial x}}\left( {{D_{\text{l}}}\dfrac{{\partial {c_{\text{l}}}}}{{\partial x}}} \right) + \left( {1 - {t^ + }} \right)\dfrac{{\nabla {i_{\text{l}}}}}{F} $ $ {D_{\text{l}}}\dfrac{{\partial {c_{\text{l}}}}}{{\partial x}}{\Big|_{x = 0}} = {D_{\text{l}}}\dfrac{{\partial {c_{\text{l}}}}}{{\partial x}}{\Big|_{x = L}} = 0 $
    固相电势 $ {i_{\text{s}}} + {\sigma _{\text{s}}}\nabla {\phi _{\text{s}}} = 0 $ $ {i_{\text{s}}}{|_{x = 0}} = {i_{\text{s}}}{|_{x = L}} = I $
    液相电势 $ {i_{\text{l}}} = - {\sigma _{\text{l}}}\nabla {\phi _{\text{l}}} + \dfrac{{2 RT{\sigma _{\text{l}}}}}{F}\left( {1 + \dfrac{{\partial \ln f}}{{\partial \ln {c_{\text{l}}}}}} \right)\left( {1 - {t^ + }} \right)\nabla \ln {c_{\text{l}}} $ $ {\sigma _{\text{l}}}\dfrac{{\partial {\phi _{\text{l}}}}}{{\partial x}}{\Big|_{x = 0}} = {\sigma _{\text{l}}}\dfrac{{\partial {\phi _{\text{l}}}}}{{\partial x}}{\Big|_{x = L}} = 0 $
    下载: 导出CSV

    表 2  电化学模型降阶重构方法对比

    Table 2.  Comparison of simplified methods for electrochemical models.

    模型
    名称    		 降阶电化学模型图 降阶条件 优势 不足 适用电池 相关文献
    P2D
    模型    		 见附录B
    图B1    		 常使用的电化学模型, 在该模型基础上降阶电化学模型 模型精确度高 参数辨识困难, 计算复杂, 适用性差 具有很强的通用性, 基本适用于所有锂离子电池 [9,13,
    15,20]
    SPM
    模型    		 见附录B
    图B2    		 假设 1: 固相锂离子浓度沿电极厚度方向上均匀分布;
    假设 2: 交换电流密度i0(x, t)用其均值代替;
    假设 3: 固-液相界面的反应电流密度 j(x, t)沿电极厚度方向均匀分布;
    假设 4: 电池内部液相浓度和电势均为不随时间改变的定值    		 模型求解简单, 在低倍率情况下效果较好 高倍率和动态工况下误差会变大 低极化特性的正极材料(LiFePO4)/石墨体系的锂离子电池 [30,31]
    SPMe
    模型    		 见附录B
    图B3    		 假设 1: 固相锂离子浓度沿电极厚度方向上均匀分布;
    假设 2: 交换电流密度i0(x, t)用其均值代替;
    假设 3: 固-液相界面的反应电流密度 j(x, t)沿电极厚度方向均匀分布    		 模型精度较SPM模型而言更高 电流变化剧烈的动态工况下, 误差会大 三元锂离子电池、磷酸铁锂离子电池等液态电解质锂离子电池 [41,43,44]
    电化学
    平均值
    模型    		 见附录B
    图B4(a)    		 假设 1: 电解液中锂离子浓度恒定不变;
    假设 2: 在正、负电极中, 分别用锂离子反应电流密度的平均值取代锂离子反应电流密度沿电极厚度方向的值    		 计算简单, 低倍率下精度高 无法精确描述电池在高倍率充放电和变电流密度等动态工况下的变化, 会使模型精度下降 正极为LiCoO2, 负极为MCMB2528电解质溶质为LiPF6, 溶剂为EC和DEC混合物的锂离子电池 [47]
    见附录B
    图B4(b)    		 假设 1: 反应电流密度用均值代替;
    假设 2: 正极固相扩散过程用2阶抛物线近似, 负极固相扩散过程用3阶Padé近似;
    假设3: 液相扩散过程用体积平均法近似    		 精度随着Padé近似的阶数增长 近似阶数增大, 其所需的变量也会相应增加, 计算难度增大 正负极为LiyMn2O4/LixC6的锂离子电池单元 [46,48]
    LSP2D
    模型    		 见附录B
    图B5(a)    		 假设 1: 用反应电流密度的平均值取代锂离子反应电流密度沿电极厚度方向的值;
    假设 2: 用2参数抛物线近似描述固相扩散过程;
    假设 3: 用3参数抛物线近似描述液相扩散过程    		 降阶重构了参数间的耦合关系, 精度较SPM而言更高 当外界工作条件变化剧烈时, 实际的固液相锂离子浓度变化偏离抛物线变化情况严重, 精度会下降 磷酸铁锂离子电池 [63]
    见附录B
    图B5(b)    		 假设 1: 液相锂离子浓度恒定;
    假设 2: 固相扩散过程用3参数近似模型    		 该模型简单的运算使得参数辨识更加容易 液相变化精度不足 18650三元锂
    离子电池    		 [53,54]
    见附录B
    图B5(c)    		 假设 1: 忽略电极内部反应不均匀分布效应, 反应电流密度用工作电流密度近似;
    假设 2: 电极用单个颗粒近似, 固相浓度分布服从三参数抛物线分布, 液相浓度分布服从二参数抛物线近似;
    假设 3: 两电极反应极化程度相同, 固相扩散过程相同;
    假设 4: 电池内部温度对模型参数的影响忽略不计    		 整体精度表现较好, 还可以建立电池内部与外电路电流密度的关系 仅在截止电压部分有较大误差 正极为LiCoO2负极为石墨的锂离子电池 [61,62]
    一维
    模型    		 见附录B
    图B6    		 假设 1: 参数恒定;
    假设 2: 固相液相交界面处的锂离子反应电流密度j与液相锂离子浓度cl解耦, 并认为 cl 恒定    		 维度更低涉及的状态量更少, 模型求解更简单 对于高放电电流密度或快速充放电等复杂工况, 一维模型无法准确反应电池内部动态相应, 精度下降 正极为LiCoO2, 负极为MCMB2528的锂离子电池 [68]
    下载: 导出CSV

    表 3  部分关键电化学参数的辨识方法

    Table 3.  Calculation methods for some key electrochemical parameters.

    参数类型参数名称测试方法测试设备测算方法
    动力学参数固相扩散系数恒流间歇滴定充放电测试仪测得
    液相扩散系数恒流间歇滴定充放电测试仪计算
    液相电导率四电极测量电导率仪测得
    固相电导率恒流间歇滴定充放电测试仪计算
    反应速率常数阻抗谱测试电化学工作站测得
    反应电流密度扫描伏安法电化学工作站计算
    交换电流密度扫描伏安法电化学工作站计算
    固相电流密度扫描伏安法电化学工作站计算
    液相电流密度扫描伏安法电化学工作站计算
    浓度场参数固相浓度恒流间歇滴定充放电测试仪计算
    固相表面浓度恒流间歇滴定充放电测试仪计算
    液相浓度扫描伏安法电化学工作站计算
    液相体积分数NMR测试法NMR波谱仪计算
    电相关参数过电势差值法电化学工作站计算
    液相电势微电极技术测量电化学工作站计算
    固相电势三电极体系法电化学工作站测得
    开路电压电压表直接测量法电压表测得
    下载: 导出CSV

    表 A1  不同模型的参数及其物理含义和来源

    Table A1.  Parameters of different models and their physical meanings and sources.

    模型名称 参数 物理含义 来源 对模型准确性影响
    SPM+SPMe 平均固相锂离子浓度 用平均值描述整体的固相锂离子浓度, 忽略了固相在不同电极位置处的浓度差异. [33]
    [34,43]    		 在高倍率下忽略固相锂离子浓度的动态变化会进一步造成过电位的偏差.
    平均交换电流密度 用平均值描述整体的交换电流密度, 忽略了其在不同电极位置处的差异性. 在高倍率下实际交换电流密度严重偏离平均值, 导致极化电压预测偏差.
    SPM+SPMe+电化学平均值模型 平均反应电流密度 用平均值描述整体的反应电流密度, 忽略了其在不同电极位置处的差异性. [43,33]
    [34,47]    		 在高倍率情况下会导致局部过电位的变化被忽略, 进而影响模型输出电压.
    SPM+电化学平均值模型 平均液相锂离子浓度 用平均值描述整体的液相锂离子浓度, 忽略了其动态变化. [43,47] 在高倍率情况下, 电解液浓度梯度变化显著, 平均化会低估浓差极化, 进而影响输出电压.
    LSP2D 体积平均浓度 描述固相锂离子浓度的体积平均值, 体现在微观颗粒层面. [51,52] 直接影响模型在稳态下的容量预测, 会导致SOC估计偏差.
    表面浓度 描述固相颗粒表面的锂离子浓度. 会影响交换电流密度和极化电压的计算进而影响输出端电压.
    体积平均浓度通量 描述固相锂离子浓度相对于系统中位置的平均变化. 和浓度梯度密切相关, 会导致扩散极化现象的预测偏差.
    下载: 导出CSV
  • [1] Li C L, Cui N X, Wang C Y, Zhang C H 2021 J. Power Sources 497 229900 doi: 10.1016/j.jpowsour.2021.229900
    [2] 武龙星, 庞辉, 晋佳敏, 耿院飞, 刘凯 2022 电工技术学报 37 1703 doi: 10.19595/j.cnki.1000-6753.tces.211030 Wu L X, Pang H, Jin J M, Geng Y F, Liu K 2022 Trans. China Electrotech. Soc. 37 1703 doi: 10.19595/j.cnki.1000-6753.tces.211030
    [3] 方儒卿, 张娜, 李哲 2021 清华大学学报(自然科学版) 61 1055 doi: 10.16511/j.cnki.qhdxxb.2021.22.032 Fang R Q, Zhang N, Li Z 2021 J. Tsinghua Univ. (Sci. & Tech. ) 61 1055 doi: 10.16511/j.cnki.qhdxxb.2021.22.032
    [4] 冯毅 2008 博士学位论文(北京: 中国科学院大学) Feng Y 2008 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences
    [5] Nie P B, Zhang S W, Ran A H, Yang C H, Chen S X, Li Z L, Zhang X, Deng W W, Liu T, Kang F Y 2021 Appl. Therm. Eng. 184 116258 doi: 10.1016/j.applthermaleng.2020.116258
    [6] Mama M, Solai E, Capurso T, Danlos A, Khelladi S 2025 Energy Convers. Manag. 325 119223 doi: 10.1016/j.enconman.2024.119223
    [7] Jian L, Liang H 2023 6th International Conference on Electronics and Electrical Engineering Technology Nanjing, China, December 1, 2023 p88
    [8] 熊瑞, 马骁, 陈泽宇, 孙逢春 2021 机械工程学报 57 179 doi: 10.3901/JME.2021.02.179 Xiong R, Ma X, Chen Z Y, Sun F C 2021 J. Mech. Eng. 57 179 doi: 10.3901/JME.2021.02.179
    [9] 熊瑞, 张凯旋, 李海龙 2024 机械工程学报 61 268 doi: 10.3901/JME.2025.02.268 Xiong R, Zhang K X, Li H L 2024 J. Mech. Eng. 61 268 doi: 10.3901/JME.2025.02.268
    [10] 陈少辉, 熊凯 2019 计量与测试技术 46 27 doi: 10.15988/j.cnki.1004-6941.2019.6.009 Chen S H, Xiong K 2019 Metrol. Meas. Tech. 46 27 doi: 10.15988/j.cnki.1004-6941.2019.6.009
    [11] Guo Z Q, Xiong Q, Zhang C, Zhu L Y, Ji S C 2021 Power System and Green Energy Conference Shanghai, China, August 20–22, 2021 p660
    [12] Atalay S, Sheikh M, Mariani A, Melra Y, Bower E, Widanage W D 2020 J. Power Sources 478 229026 doi: 10.1016/j.jpowsour.2020.229026
    [13] 张宇飞 2022 硕士学位论文(重庆: 重庆大学) Zhang Y F 2022 M. S. Thesis (Chongqing: Chongqing University
    [14] Petzl M, Danzer M A 2014 J. Power Sources 254 80 doi: 10.1016/j.jpowsour.2013.12.060
    [15] 梁峰伟, 夏煜华, 张玉龙, 赵树朋, 杨世春, 刘新华 2022 稀有金属 46 1235 doi: 10.13373/j.cnki.cjrm.XY21030007 Liang W F, Xia Y H, Zhang Y L, Zhao S P, Yang S C, Liu X H 2022 Chin. J. Ra. Met. 46 1235 doi: 10.13373/j.cnki.cjrm.XY21030007
    [16] 张成 2024 硕士学位论文(西安: 西安工业大学) Zhang C 2024 M. S. Thesis (Xian: Xian Technological University
    [17] 左东旭, 李培超 2024 电化学 30 13 doi: 10.61558/2993-074X.3468 Zuo D X, Li P C 2024 J. Electrochem. 30 13 doi: 10.61558/2993-074X.3468
    [18] Verma M K S, Basu S, Patil R S, Hariharan K S, Adiga S P, Kolake S M, Oh D, Song T, Sung Y 2020 IEEE Trans. Veh. Technol. 69 2563 doi: 10.1109/TVT.2020.2966266
    [19] Chen G W, Liu Z T, Su H Y, Zhang Q L 2019 Proceedings of the 38th Chinese Control Conference Guangzhou, Peoples R China, July 27–30, 2019 p697
    [20] Nicodemo N, Di Rienzo R, Lagnoni M, Bertei A, Baronti F 2024 J. Energy Storage 99 113257 doi: 10.1016/j.est.2024.113257
    [21] Zhang X, Lu J L, Yuan S F, Yang J, Zhou X 2017 J. Power Sources 345 21 doi: 10.1016/j.jpowsour.2017.01.126
    [22] Cai C X, Gong Y, Fotouhi A, Auger D J 2024 J. Energy Storage 99 113142 doi: 10.1016/j.est.2024.113142
    [23] Bala S, Popov B N, White R E 1998 J. Power Sources 75 56 doi: 10.1016/S0378-7753(98)00092-5
    [24] Huang L, Yao C 2016 Chin. J. Chem. Phys. 29 623 doi: 10.1063/1674-0068/29/cjcp1604063
    [25] Xu S C, Wang Y H, Shao J Y, Li J F, Yu Q Q 2022 Appl. Therm. Eng. 217 119282 doi: 10.1016/j.applthermaleng.2022.119282
    [26] Liu L H, Zhu J G, Zheng L F 2020 IEEE Access 8 211738 doi: 10.1109/ACCESS.2020.3039783
    [27] Gou F, Couto L D, Mulder G, Trad K, Hu G D, Capron O, Haghverdi K 2024 J. Energy Storage 101 113850 doi: 10.1016/j.est.2024.113850
    [28] Wang J R, Meng J H, Peng Q, Liu T Q, Peng J C 2024 J. Energy Storage 87 111473 doi: 10.1016/j.est.2024.111473
    [29] Sun X D, Xu N X, Chen Q, Yang J F, Zhu J G, Xu J, Zheng L F 2023 IEEE Trans. Transp. Electrif. 9 2453 doi: 10.1109/TTE.2022.3206452
    [30] 蔡雪, 张彩萍, 张琳静, 张维戈, 高乐 2021 机械工程学报 57 64 doi: 10.3901/JME.2021.14.064 Cai X, Zhang C P, Zhang L J, Zhang W G, Gao L 2021 J. Mech. Eng. 57 64 doi: 10.3901/JME.2021.14.064
    [31] 赵冬梅, 裴建楠, 刘崇茹, 徐辰宇, 宋晨铭 2024 中国电机工程学报 44 3916 doi: 10.13334/j.0258-8013.pcsee.230238 Zhao D M, Pei J N, Liu C R, Xu C Y, Song C M 2024 Proc. Chin. Soc. Electr. Eng. 44 3916 doi: 10.13334/j.0258-8013.pcsee.230238
    [32] 庞辉 2017 物理学报 66 238801 doi: 10.7498/aps.66.238801 Pang H 2017 Acta Phys. Sin. 66 238801 doi: 10.7498/aps.66.238801
    [33] Di Domenico D, Stefanopoulou A, Fiengo G 2010 J. Dyn. Syst. Meas. Contr. 132 061302 doi: 10.1115/1.4002475
    [34] Prada E, Di Domenico D, Creff Y, Bernard J, Sauvant Moynot V, Huet F 2012 J. Electrochem. Soc. 159 A1508 doi: 10.1149/2.064209jes
    [35] Moura S J, Argomedo F B, Klein R, Mirtabatabaei A, Krstic M 2017 IEEE Trans. Control Syst. Technol. 25 453 doi: 10.1109/TCST.2016.2571663
    [36] Li W H, Fan Y, Ringbeck F, Jost D, Han X B, Ouyang M G, Sauer D U 2020 J. Power Sources 476 228534 doi: 10.1016/j.jpowsour.2020.228534
    [37] 任立超 2022 硕士学位论文(武汉: 武汉理工大学) Ren L C 2022 M. S. Thesis (Wuhan: Wuhan University of Technology
    [38] Wang J G, Meng J H, Peng Q, Liu T Q, Zeng X Y, Chen G, Li Y 2023 Batteries 9 180 doi: 10.3390/batteries9030180
    [39] Desouza A K, Plett G L, Trimboli M S 2024 American Control Conference Toronto, Canada, July 10-12, 2024 p1449
    [40] Zhou J P, Xing B, Wang C Y 2020 International Conference on Energy Environment and Bioengineering Xi’an, China, August 7–9, 2020 p04001
    [41] 谢奕展, 程夕明 2022 机械工程学报 58 37 doi: 10.3901/JME.2022.22.037 Xie Y Z, Cheng X M 2022 J. Mech. Eng. 58 37 doi: 10.3901/JME.2022.22.037
    [42] Xie Y Z, Wang S H, Wang Z P, Cheng X M 2024 Chin. Phys. B 33 651 doi: 10.1088/1674-1056/ad1f52
    [43] 徐乐, 邓忠伟, 谢翌, 胡晓松 2022 机械工程学报 58 304 doi: 10.3901/JME.2022.22.304 Xu L, Deng Z W, Xie Y, Hu X S 2022 J. Mech. Eng. 58 304 doi: 10.3901/JME.2022.22.304
    [44] 谢奕展, 程夕明 2022 物理学报 71 048201 doi: 10.7498/aps.71.20211619 Xie Y Z, Cheng X M 2022 Acta Phys. Sin. 71 048201 doi: 10.7498/aps.71.20211619
    [45] Tang X P, Zou C F, Yao K, Lu J Y, Xia Y X, Gao F R 2019 Appl. Energy 254 113591 doi: 10.1016/j.apenergy.2019.113591
    [46] Kumar V S 2013 J. Power Sources 222 426 doi: 10.1016/j.jpowsour.2012.09.013
    [47] 应振华 2015 硕士学位论文(长春: 吉林大学) Ying Z H 2015 M. S. Thesis (Changchun: Jilin University
    [48] Wu L X, Liu K, Pang H 2021 Electrochim. Acta 368 137604 doi: 10.1016/j.electacta.2020.137604
    [49] 熊瑞, 李幸港 2025 机械工程学报 1 Xiong R, Li X G 2025 J. Mech. Eng. 1
    [50] 王位 2017 硕士学位论文(镇江: 江苏大学) Wang W 2017 M. S. Thesis (Zhenjiang: Jiangsu University
    [51] Subramanian V R, Ritter J A, White R E 2001 J. Electrochem. Soc. 148 E444 doi: 10.1149/1.1409397
    [52] Subramanian V R, Diwakar V D, Tapriyal D 2005 J. Electrochem. Soc. 152 A2002 doi: 10.1149/1.2032427
    [53] Klein R, Chaturvedi N A, Christensen J, Ahmed J, Findeisen R, Kojic A 2013 IEEE Trans. Control Syst. Technol. 21 289 doi: 10.1109/TCST.2011.2178604
    [54] Rahman M A, Anwar S, Izadian A 2016 J. Power Sources 307 86 doi: 10.1016/j.jpowsour.2015.12.083
    [55] Luo W L, Lyu C, Wang L X, Zhang L Q 2013 Microelectron. Reliab. 53 797 doi: 10.1016/j.microrel.2012.11.002
    [56] Han X B, Ouyang M G, Lu L G, Li J Q 2015 J. Power Sources 278 802 doi: 10.1016/j.jpowsour.2014.12.101
    [57] Han X B, Ouyang M G, Lu L G, Li J Q 2015 J. Power Sources 278 814 doi: 10.1016/j.jpowsour.2014.08.089
    [58] Deng Z W, Yang L, Deng H, Cai Y S, Li D D 2018 Energy 142 838 doi: 10.1016/j.energy.2017.10.097
    [59] 李旭昊, 周宇, 王冰川 2020 储能科学与技术 9 1991 doi: 10.19799/j.cnki.2095-4239.2020.0198 Li X H, Zhou Y, Wang B C 2020 Energy Stor. Sci. Technol. 9 1991 doi: 10.19799/j.cnki.2095-4239.2020.0198
    [60] Wang D F, Huang H Q, Tang Z H, Zhang Q, Yang B W, Zhang B 2020 Electrochim. Acta 362 137118 doi: 10.1016/j.electacta.2020.137118
    [61] Li J F, Wang L X, Lyu C, Liu E H, Xing Y J, Pecht M 2018 Electrochim. Acta 275 50 doi: 10.1016/j.electacta.2018.04.098
    [62] Fu Y J, Jun W, Mei W L, Jun F L, Jun Y S 2025 J. Energy Storage 112 115495 doi: 10.1016/j.est.2025.115495
    [63] 刘征宇, 杨昆, 魏自红, 姚利阳 2019 物理学报 68 098801 doi: 10.7498/aps.68.20190159 Liu Z Y, Yang K, Wei Z H, Yao L Y 2019 Acta Phys. Sin. 68 098801 doi: 10.7498/aps.68.20190159
    [64] Kandler A S, Christopher D R, Wang C Y 2007 Energy Convers. Manag. 48 2565 doi: 10.1016/j.enconman.2007.03.015
    [65] 陆浩然, 邹梦珍, 李哲 2024 机械工程学报 60 193 doi: 10.3901/JME.2024.20.193 Lu H R, Zou M Z, Li Z 2024 J. Mechan. Eng. 60 193 doi: 10.3901/JME.2024.20.193
    [66] Ma Y, Li X, Li G Y, Hu Y F, Bai Q W 2019 IEEE Acc. 7 156136 doi: 10.1109/ACCESS.2019.2949357
    [67] Sangiri J B, Sardar A, Ghosh S, Maiti S, Chakraborty C 2022 Electr. Eng. 104 3733 doi: 10.1007/s00202-022-01575-8
    [68] 李光远, 马彦 2018 吉林大学学报(信息科学版) 36 260 doi: 10.19292/j.cnki.jdxxp.2018.03.006 Li G Y, Ma Y 2018 J. Jilin Univ. (Inf. Sci. ) 36 260 doi: 10.19292/j.cnki.jdxxp.2018.03.006
    [69] 梁新成, 张志冬, 黄国钧 2023 西南大学学报(自然科学版) 45 214 doi: 10.13718/j.cnki.xdzk.2023.03.018 Liang X C, Zhang Z D, Huang G J 2023 J. Southwest Univ (Nat. Sci. ) 45 214 doi: 10.13718/j.cnki.xdzk.2023.03.018
    [70] 李涛, 程夕明, 胡晨华 2021 物理学报 70 138801 doi: 10.7498/aps.70.20201894 Li T, Cheng X M, Hu C H 2021 Acta Phys. Sin. 70 138801 doi: 10.7498/aps.70.20201894
    [71] Kong X R, Wetton B, Gopaluni B 2019 12th International-Federation-of-Automatic-Control Symposium on Dynamics and Control of Process Systems including Biosystems Florianopolis, Brazil, April 23–26, 2019 p946
    [72] 李皓天, 张玉龙, 赵树朋, 高山汀, 周玉宏, 刘江铎, 刘志豪 2021 科学技术创新 16 183 doi: 10.3969/j.issn.1673-1328.2021.26.080 Li H T, Zhang Y L, Zhao S P, Gao S T, Zhou Y H, Liu J D, Liu Z H 2021 Sci. Technol. Innov. 16 183 doi: 10.3969/j.issn.1673-1328.2021.26.080
    [73] Xu L, Lin X, Xie Y, Hu X S 2022 Energy Storage Mater. 45 952
    [74] 张毕 2022 硕士学位论文 (哈尔滨: 哈尔滨工业大学) Zhang B 2022 M. S. Thesis (Harbin: Harbin Institute of Technology
  • 加载中
图( 14) 表( 4)
计量
  • 文章访问数:  31
  • HTML全文浏览数:  31
  • PDF下载数:  6
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-05-01
  • 刊出日期:  2025-07-20

锂离子动力电池电化学建模进展及降阶方法研究

    通讯作者: E-mail: junfeiliang@buaa.edu.cn.
    作者简介: 张艳岗.E-mail: 20102507@nuc.edu.cn
  • 中北大学能源与动力工程学院, 太原　030051
  • 收稿日期:  2025-05-01

摘要: 动力电池作为新能源汽车的核心动力装置, 其精准建模对于动力电池的运行状态估计、全生命周期故障诊断、多工况安全管控等具有重要意义. 以P2D(pseudo-two-dimensions)模型为代表的电化学模型作为能从微观尺度表征电池内部电化学反应过程的机理模型, 其对于动力电池的老化、生热行为的准确描述是电池单体容量衰减、内阻增大、受热不均以及电池模组性能不一致评价的重要依据. 本文梳理了目前锂离子动力电池电化学建模的最新研究进展, 剖析了电化学模型与等效电路模型、老化模型、热模型的耦合方法及应用现状, 重点针对电化学模型的参数繁多且辨识困难的问题, 对比分析了单粒子模型、带液相单粒子模型、电化学平均值模型、固液相重构模型、一维电化学模型等动力电池电化学模型降阶方法的优势与不足, 指出了电化学模型降阶表征的关键难点, 并对电化学模型降阶重构方法的研究趋势进行了展望, 以期为动力电池电化学模型的降阶重构研究指明方向.

English Abstract

    全文HTML

    1.   引　言

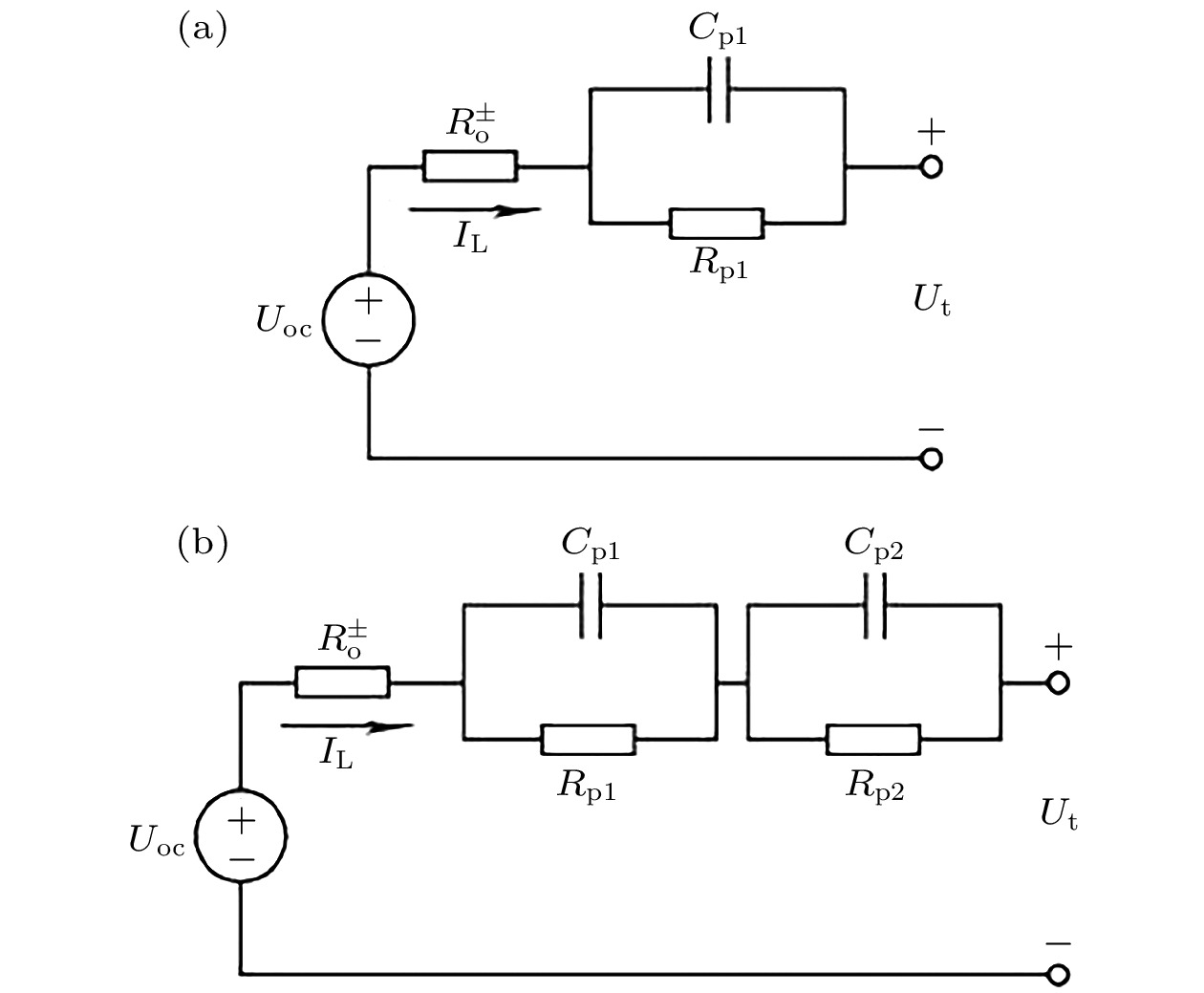
    • 动力电池作为新能源汽车的核心动力装置, 其精准建模对于动力电池的运行状态估计、全生命周期故障诊断、多工况安全管控等具有重要意义. 目前常用的锂离子电池模型主要有等效电路模型、电化学模型和数据驱动模型, 其中等效电路模型如图1所示, 采用电阻、电容、电源等元器件来描述电池特性, 结构简单、控制参数少、计算规模小是等效电路模型的主要优势, 但对实验数据的依赖、无法有效表征电池内部电化学反应过程等不足, 限制了其在动力电池老化行为表征以及全生命周期下的故障诊断; 数据驱动模型同样忽略了电池内部的电化学反应过程, 通过对大量电池运行数据进 行训练学习来构建模型, 具有参数辨识方便、模型自适应更新能力强的优势, 但缺乏对电池理化属性和老化生热行为的机理解释, 而且对特定、有限训练集的依赖导致其始终无法满足多工况、全气候下的动力电池管理应用需求; 相比于上述两类电池模型, 电化学模型能够详细描述电池内部的电化学反应、离子扩散、电极表面反应等过程, 可以为电池寿命估计及容量衰减提供更准确的预测, 但是当前电化学模型的参数繁多且获取困难, 复杂的模型参数辨识和庞大的计算规模限制了其在全生命周期下的模型自适应演化.

      因此, 以P2D (pseudo-two-dimensions)模型为代表的电化学模型作为从微观尺度表征电池内部电化学反应过程的机理模型, 对于老化生热行为的准确描述是电池单体容量衰减、内阻增大、受热不均以及电池模组性能不一致评价的重要依据. 学者们对动力电池的电化学建模方法、电化学模型与其他领域模型的耦合方法, 以及电化学模型的降阶重构方法等开展了大量工作, 为缓解电化学模型的参数辨识难度、计算复杂度和模型表征精度之间的矛盾做出了很多贡献.

    2.   锂离子动力电池电化学建模及其应用研究

      2.1.   锂离子动力电池电化学建模方法

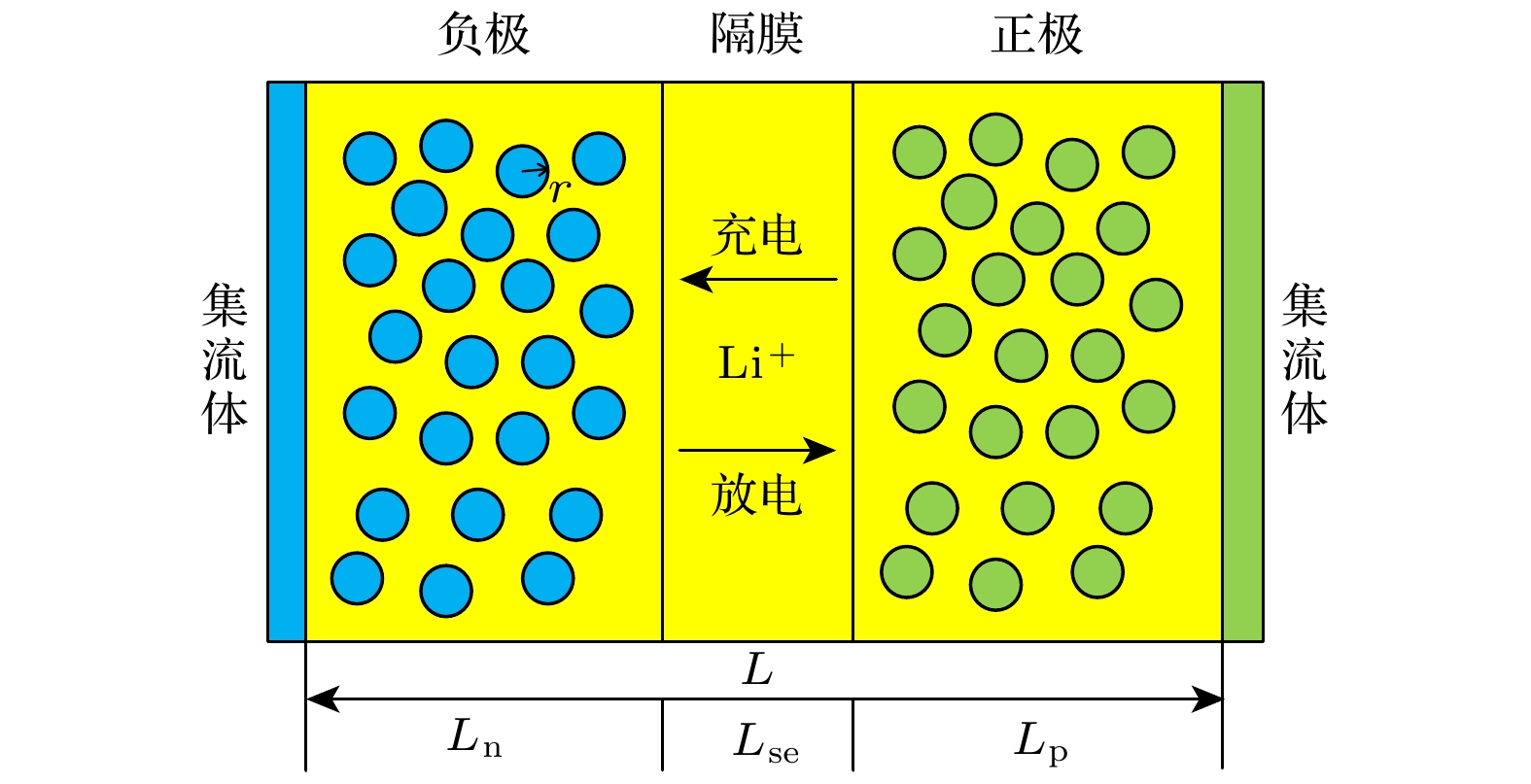
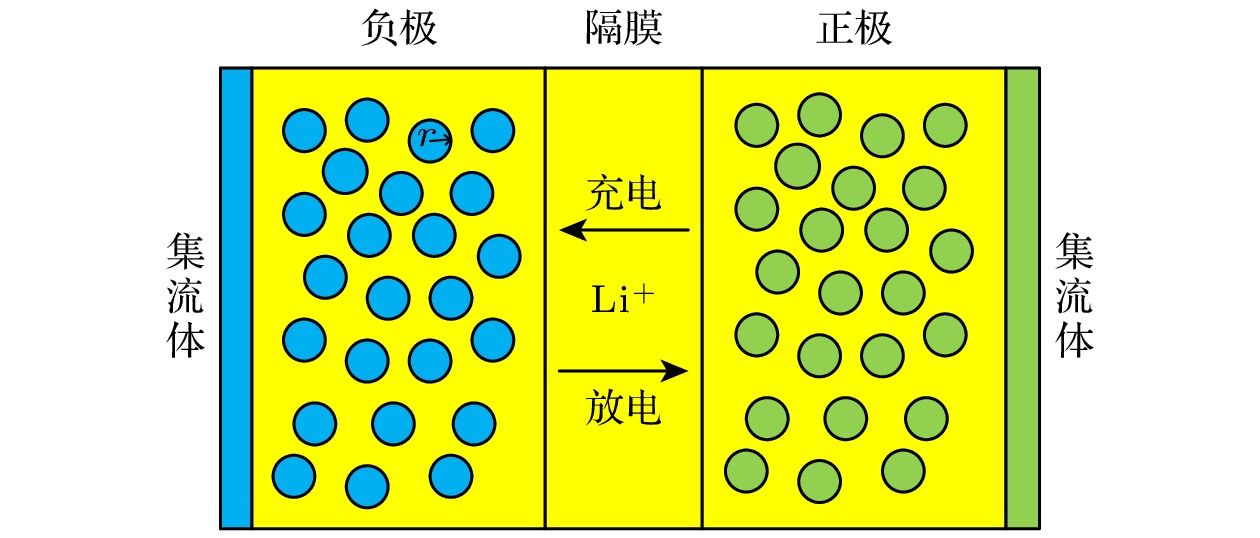
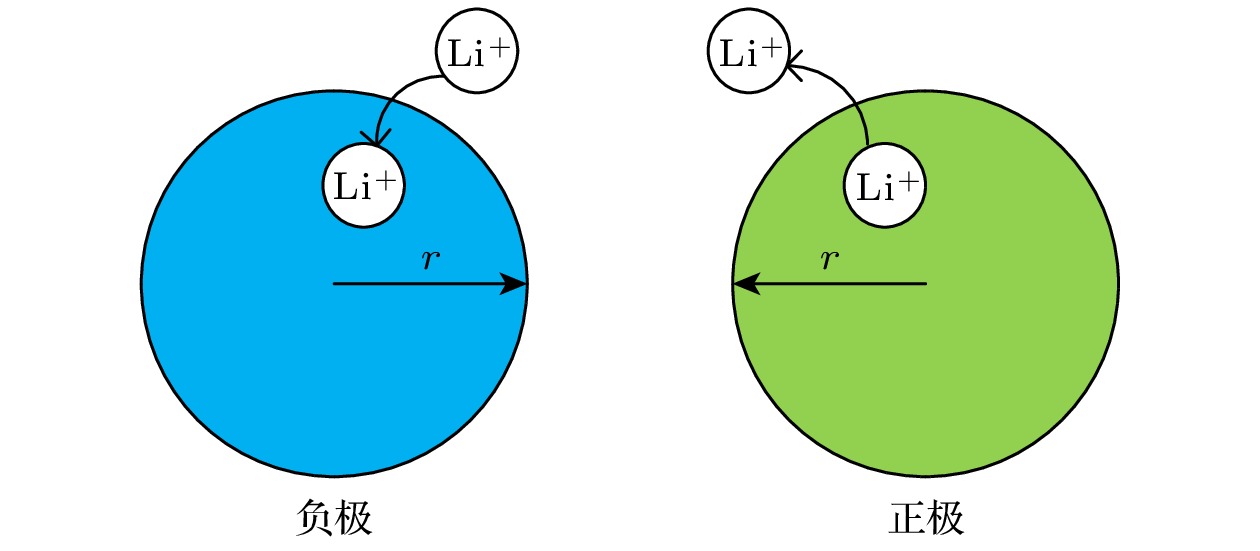
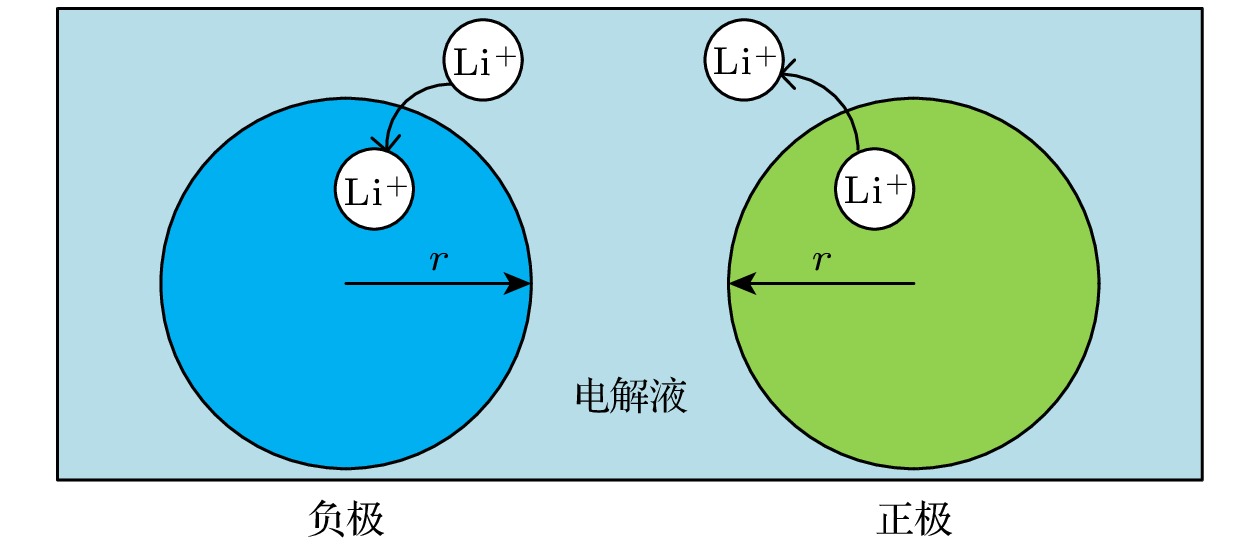
    • 如图2所示, P2D模型基于浓溶液理论和多孔电极理论构建而成, 主要由多孔正负极、隔膜和集流体组成, 模型假设了正负极活性材料为大小均匀且分布规律的球形颗粒[1], Lp, Ln分别为正负极的厚度, Lse为隔膜厚度, 正负极和隔膜区域内都充满电解液[2], 模型采用一个Butler-Volmer方程和4个偏微分方程来描述固、液相锂离子的扩散过程和固液相之间的电势分布, 其中锂离子在活性颗粒内部的浓度变化由Fick第二定律定义, 在液相中的迁移过程由Nernst-Volmer方程描述, 固液相电势变化基于电荷守恒定义, 表1为模型的控制方程和边界条件.

      Butler-Volmer方程描述的固液相之间界面反应速率如(1)式所示:

      式中, j为反应电流密度, ${i_0}$为交换电流密度, $\alpha $为传递常数, 下标a和c分别代表阳极和阴极, $\eta $为过电势. 交换电流密度${i_0}$为

      式中${k_0}$为反应速率常数, ${c_{{\text{s, max}}}}$为固相最大锂离子浓度, ${c_{{\text{s, surf}}}}$为颗粒表面锂离子浓度.

      鉴于P2D电化学模型能准确表征电池内部锂离子浓度场、电势分布以及电化学反应动力学特性[3], 冯毅[4]基于P2D模型系统研究了电极/电解质界面处的电流密度空间分布规律及荷电状态演变规律, 重点讨论了活性材料组分对电流密度及SOC状态分布的影响. 电化学模型通过揭示微观电化学反应机理, 可以进一步耦合电池老化、颗粒嵌入/嵌出应力和微观产热等多物理场模型来精细描述电池的老化、生热行为.

      • 2.2.   锂离子动力电池电化学-热耦合建模

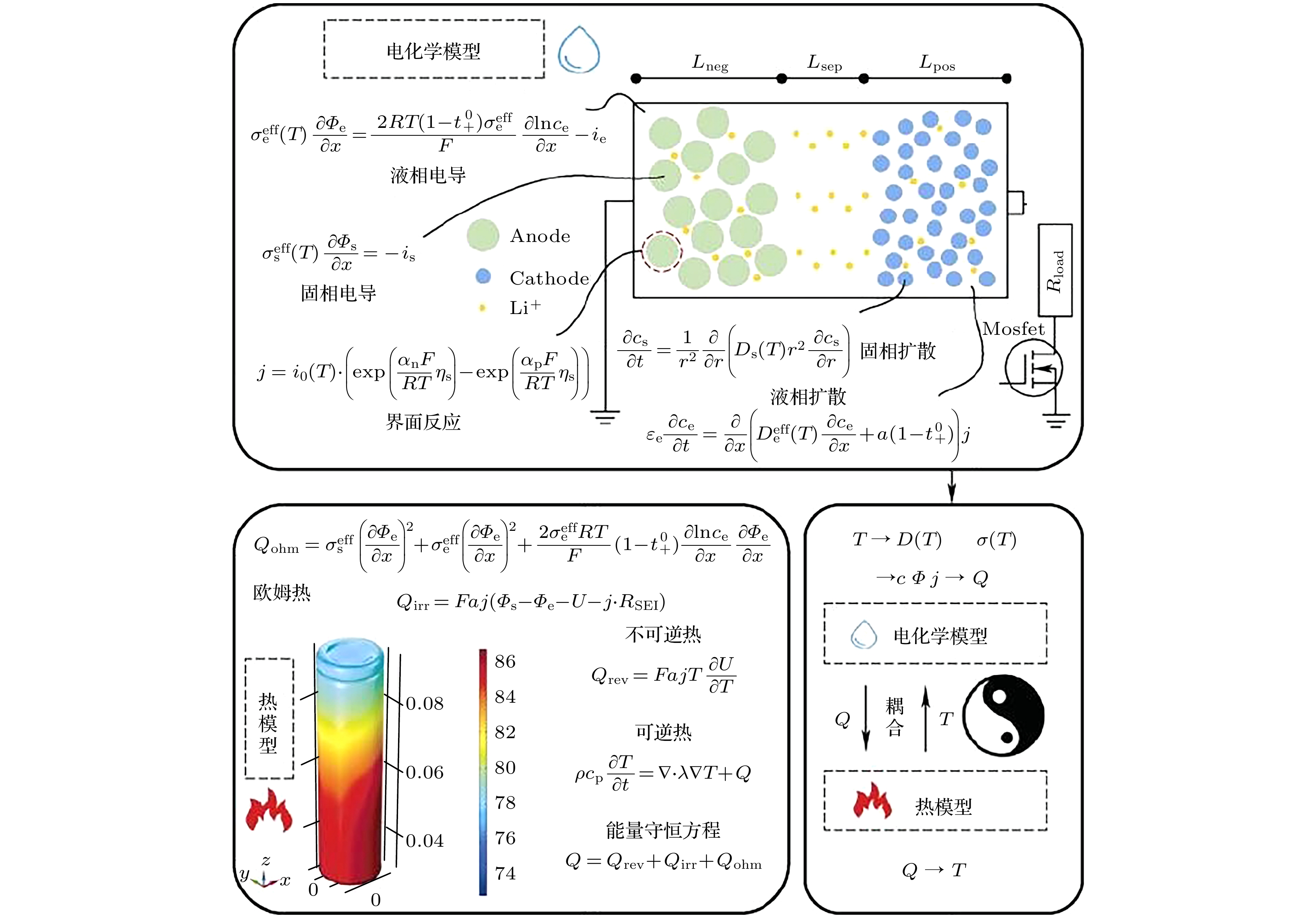
    • 电化学模型与热模型的耦合关系如图3所示, 热模型中的产热与电化学模型中锂离子浓度、电势、电流密度有关, 这些变量在电化学模型中又与扩散和迁移等受温度密切相关的参数有关. 产热作为热模型的输入量, 温度T作为热模型的输出量影响电化学模型中的参数, 从而实现电化学-热模型的耦合.

      锂离子电池的充放电性能和使用寿命很容易受到环境温度的影响, 严重的还会引起热失控、过热爆炸等安全风险[5], 因此常常通过电化学-热耦合模型来表征动力电池的生热传热过程[6], 同时还利用电化学-热耦合模型实现温度对电化学参数的有效修正. Jian等[7]提出并验证了Bernardi产热模型和电化学模型的耦合方法; Nie等[5]通过模拟热量的产生和电池损耗特性验证了所提电化学-热耦合模型的准确性和适用性; 熊瑞等[8]利用改进的P2D模型与热模型耦合得到低温极速加热模型, 为提高锂离子动力电池低温性能提供了新的思路, 该团队进一步提出一种融合宏观、介观和微观三尺度的电化学-热耦合模型[9], 为表征锂离子浓度梯度所引起的电池容量损失过程提供了可视化手段; 陈少辉和熊凯[10]将电化学热耦合模型由单体尺度推广至模组尺度, 基于动力电池组电化学-热耦合模型描述了电池组在充放电过程中的一致性问题和热传递行为; Guo等[11]将电化学-热耦合模型拓展至与力学模型的耦合领域, 精确分析动力电池微观生热放热过程的同时, 清晰表征了锂离子扩散应力导致的电极结构形变问题. 电化学-热耦合模型作为动力电池的基础耦合模型, 对于动力电池运行要素的描述具有重要价值, 电化学-热耦合模型与老化、力学、电学模型的耦合拓展将是未来一段时间内动力电池运行状态表征的主要研究方向.

      • 2.3.   锂离子动力电池电化学-老化耦合建模

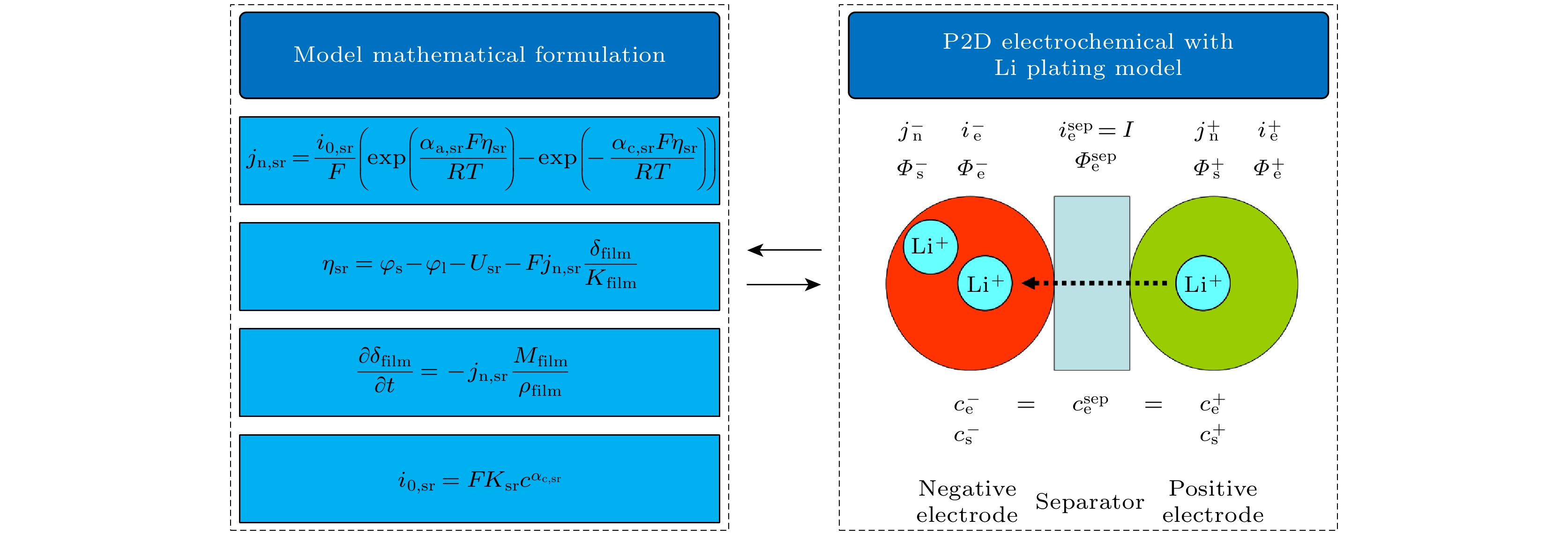
    • 电化学模型由于能够详细刻画动力电池内部的物理化学反应过程, 常作为老化行为描述的基础模型. Atalay等[12]基于P2D模型提出一种表征SEI膜和锂镀膜老化机制的老化模型, 可有效预测多种工况场景下的动力电池老化程度, 尤其能够捕捉到线性和非线性容量衰减的过程; 张宇飞[13]通过研究负极SEI膜生长机制构建了电池容量衰减的表征模型, 并提出一种分步恒流充电策略, 在提高充电效率的同时较大程度的避免了SEI膜的生长. 负极表面析锂是低温环境或大电流充电工况下诱发动力电池性能衰退的关键原因之一[14], 基于P2D模型构建的析锂模型如图4所示, 析锂副反应通过Bulter-Volmer方程来定量表征, 将副反应产生的电压代入电化学模型的过电势表达中来描述副反应产生的表面过电势; 梁峰伟等[15]基于上述析锂模型, 提出了电解质中添加抑制剂的化学层面析锂抑制和控制充电过程的物理层面析锂抑 制两种方案, 为解决低温快充析理难题提供了有效途径. 热效应是影响电池老化行为的关键要素, 过高或过低的环境温度都会加剧动力电池的老化 过程. 张成[16]通过在电化学-热耦合模型中引入SEI膜副反应分析了动力电池的老化过程和老化规律; 左东旭和李培超[17]基于电化学-热-力耦合模型分析, 指出充放电倍率和循环次数的增加不仅会使SEI膜增厚还会使电池热稳定性降低. 因此, 借助析锂模型能够深入解析引发电池老化的副反应, 进而制定针对性策略, 以有效应对电池老化所产生的影响.

      • 2.4.   锂离子动力电池电化学-等效电路模型耦合

    • 动力电池的荷电状态(state of charge, SOC)、健康状态(state of health, SOH)和功率状态(state of power, SOP)等状态估计一般基于ECM或P2D模型进行, 其中电化学模型的预测准确度较高[18]. Chen等[19]使用一种基于Backsteeping技术的偏微分方程观测器, 用于电池SOC的预测; Nicodemo等[20]分析了P2D模型参数与ECM模型参数之间的关联关系, 采用机器学习算法实现了ECM模型和P2D模型的参数联合估计, 有效改善了动力电池内部状态的估计效率和精度; Zhang等[21]基于一种改进的P2D模型, 根据等效电路模型和电化学模型传递函数的相似性, 提出了一种考虑电化学特性的锂离子电池等效电路模型参数辨识方法, 这两项研究工作均描述了ECM模型参数与P2D模型参数之间的关系. Cai等[22]结合等效电路模型求解速度及电化学模型精度的优势, 提出一种兼顾两模型优点的混合模型预测电池SOC, 并在预测过程中通过Fisher信息矩阵增强带遗忘因子的递推最小二乘法, 用于优化参数辨识过程, 最后在多种动态工况下验证了此模型预测SOC的准确性和有效性.

      综上所述, 以P2D模型为代表的电化学模型, 通过与其他物理场的耦合应用不仅能精确描述动力电池的运行状态, 更能清晰表征电池单体生热、老化等影响电池容量的现象, 对于电池状态估计、寿命预测、风险评估都有着重要的作用. 但电化学模型同时受限于偏微分方程组数值求解过程中的高计算复杂度, 以及固-液界面多相反应参数体系的非线性辨识难题, 使该模型在面向实际电池管理系统时面临可扩展性不足与工程适用性受限的双重挑战. 因此, 如何在满足工程表征精度的前提下实现电化学模型的降阶重构是目前电化学模型走向工程实践的关键难题.

    3.   动力电池电化学模型降阶及应用现状

    • 模型控制参数众多、参数辨识困难和计算规模庞大等局限性问题, 是限制电化学模型广泛工程应用的关键所在. 针对模型复杂度与计算效率之间的矛盾, 众多学者通过变量解耦、内部物理化学过程等效重构以及电化学降维等方法来实现电化学模型的降阶处理及应用. 目前提出的动力电池电化学模型降阶方法主要有单粒子电极模型、带液相单粒子电极模型、电化学平均值模型、固液相重构的P2D模型、一维电化学模型等, 下面分别综述其研究与应用现状.

      • 3.1.   基于单粒子电极模型的降阶研究

    • 基于物理假设的降阶P2D模型体系中, 单粒子模型(single particle model, SPM)作为最具代表性的理论模型, 最早可追溯到Bala等[23]在研究镍氢电池体系的创新性工作, 该模型的核心思想是采用几何简化的方法, 将电池正负两极活性物质的多孔电极结构抽象为理想化的球形颗粒近似表征, 并且, 该模型目前已经在电池内部锂离子浓度的实时监测中得到应用[24]; 相较P2D模型而言, SPM模型涉及的参数变化更少, 计算复杂度显著降低, 在锂离子电池动态行为仿真及控制策略优化领域展现出更高的工程适用性, 例如在多物理场耦合领域, Xu等[25]将研究中建立的二维热模型与SPM模型耦合, 用于快速预测电池热行为, 同时为满足预测精度的需求, 分出多个温度域, 通过激发响应分析方法和多组粒子群优化算法获得各个温度域的最佳参数集, 最后用自适应扩展的卡尔曼滤波算法进行温度估计和参数校正, 得到集精度与速度优势为一体的电池热行为预测结果.

      SPM模型能更高效地实现锂离子电池的状态估计[26,27], Wang等[28]针对SPM模型参数动态变化引发的SOC估计精度不足的问题, 利用双尺度双粒子滤波器调整参数得到精度更高的SOC; Sun等[29]根据SPM模型参数在宽温范围内的温度依赖性, 提出一种考虑温度效应的SOP预测方法, 显著增强了SPM模型的鲁棒性及SOP估计的准确性; 蔡雪等[30]针对等效电路模型在锂电池峰值功率预测中, 存在的因参数辨识精度不足而导致模型易陷入局部最优解以及计算效率低下的问题, 提出基于电化学机理的参数边界确定方法, 明确了等效电路模型中等效电路元件和电化学内部机理的映射关系, 并在动态工况下进行了验证, 通过比较各等效电路模型的鲁棒性, 发现带有非线性元件或方程的等效电路模型的电压仿真精度均有不同程度的提升, SOP估计效果也得到提升, 但是由于SPM只在低倍率情况下精度较高的特性, 基于SPM的参数边界确定方法在高倍率情况下各参数的精度均有不足. 同时SPM模型还为电化学模型与其他模型的联合应用提供了便捷, 赵冬梅等[31]结合等效电路模型求解速度以及电化学模型精度的优势, 提出一种兼顾两模型优点的混合模型, 从SPM模型出发推导出等值电路的拓扑形态以及SPM模型中各参数和等效电路元件之间的对应关系, 并通过实验验证了该模型的精度, 但是在高倍率情况下误差会变大, 原因在于SPM模型将液相动力学相关参数进行恒定值参数化处理, 在高倍率工况下运行时, 该降阶条件引发的缺陷更为显著; 庞辉[32]为验证电化学模型中液相动力学的重要性, 构建了一个只考虑液相动力学的降阶电化学模型, 并在多工况下验证了模型的准确性. 因此, 带液相单粒子电极模型的出现拓展了SPM模型的应用范围.

      • 3.2.   基于带液相单粒子电极模型的降阶研究

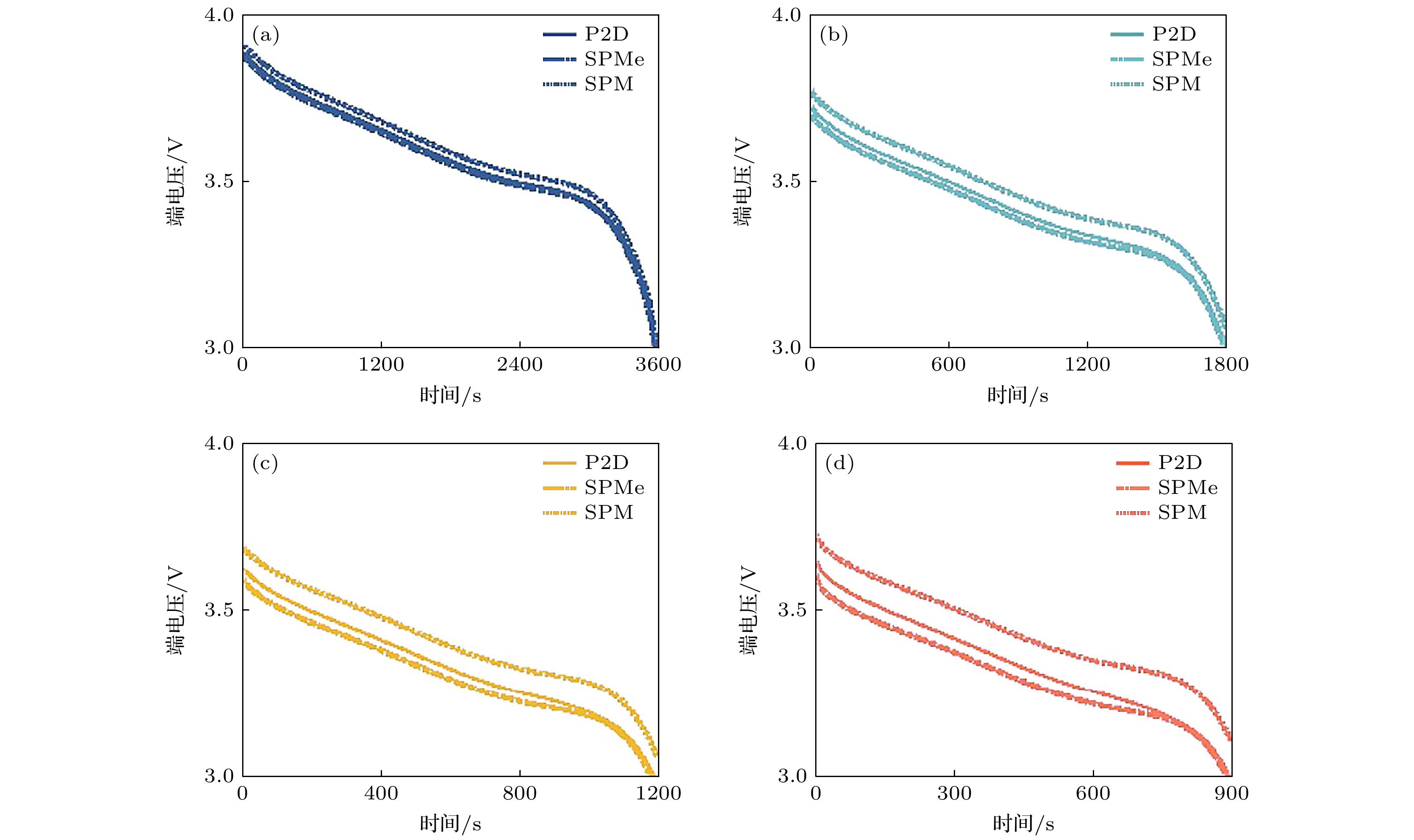
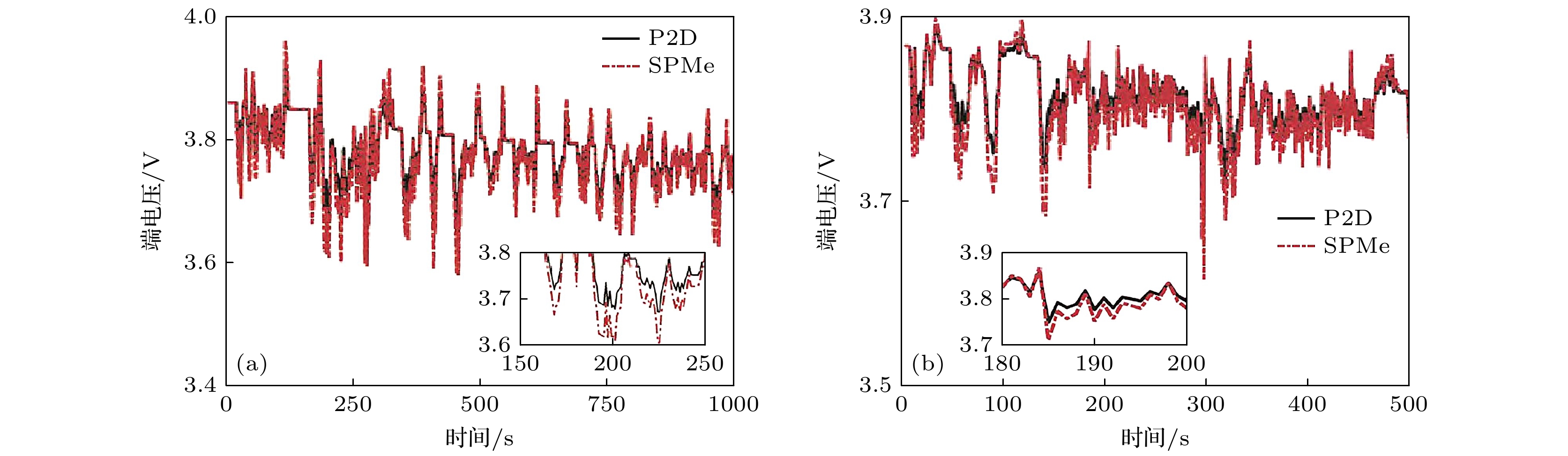
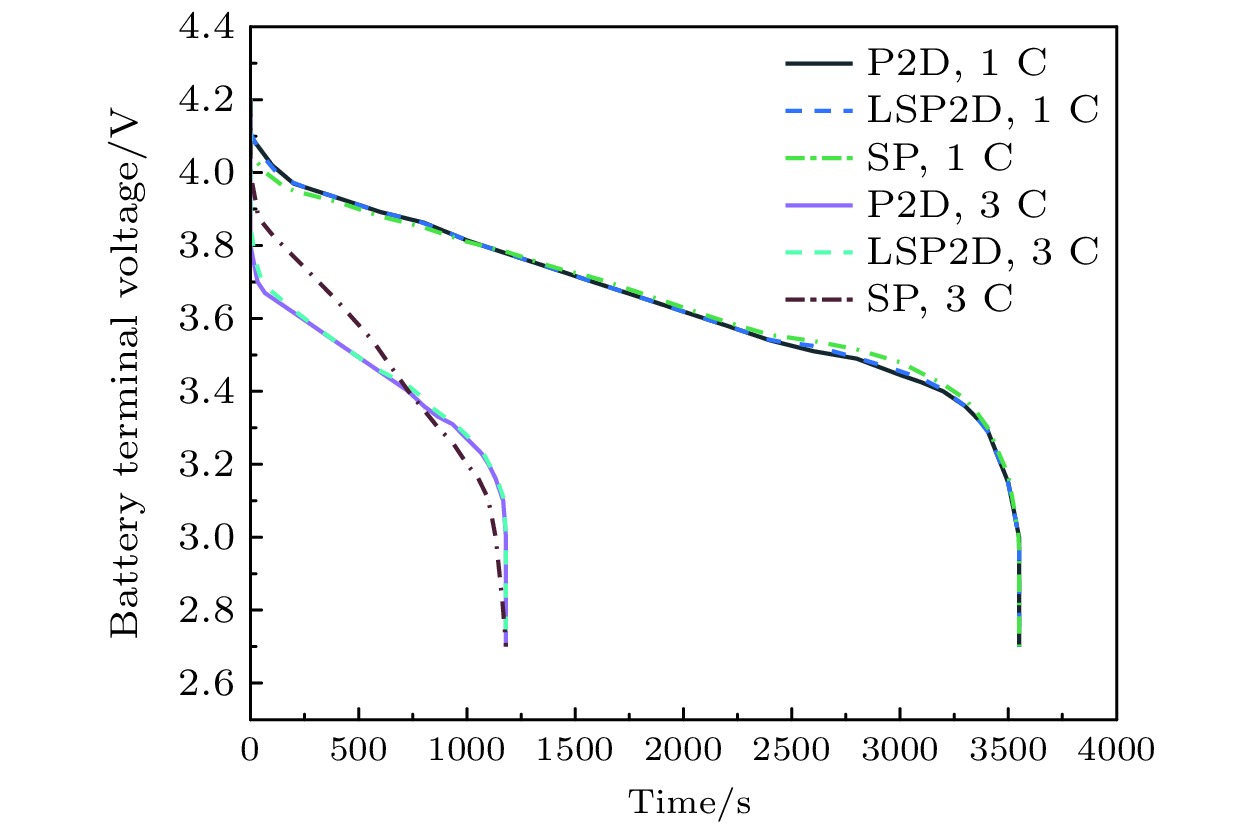
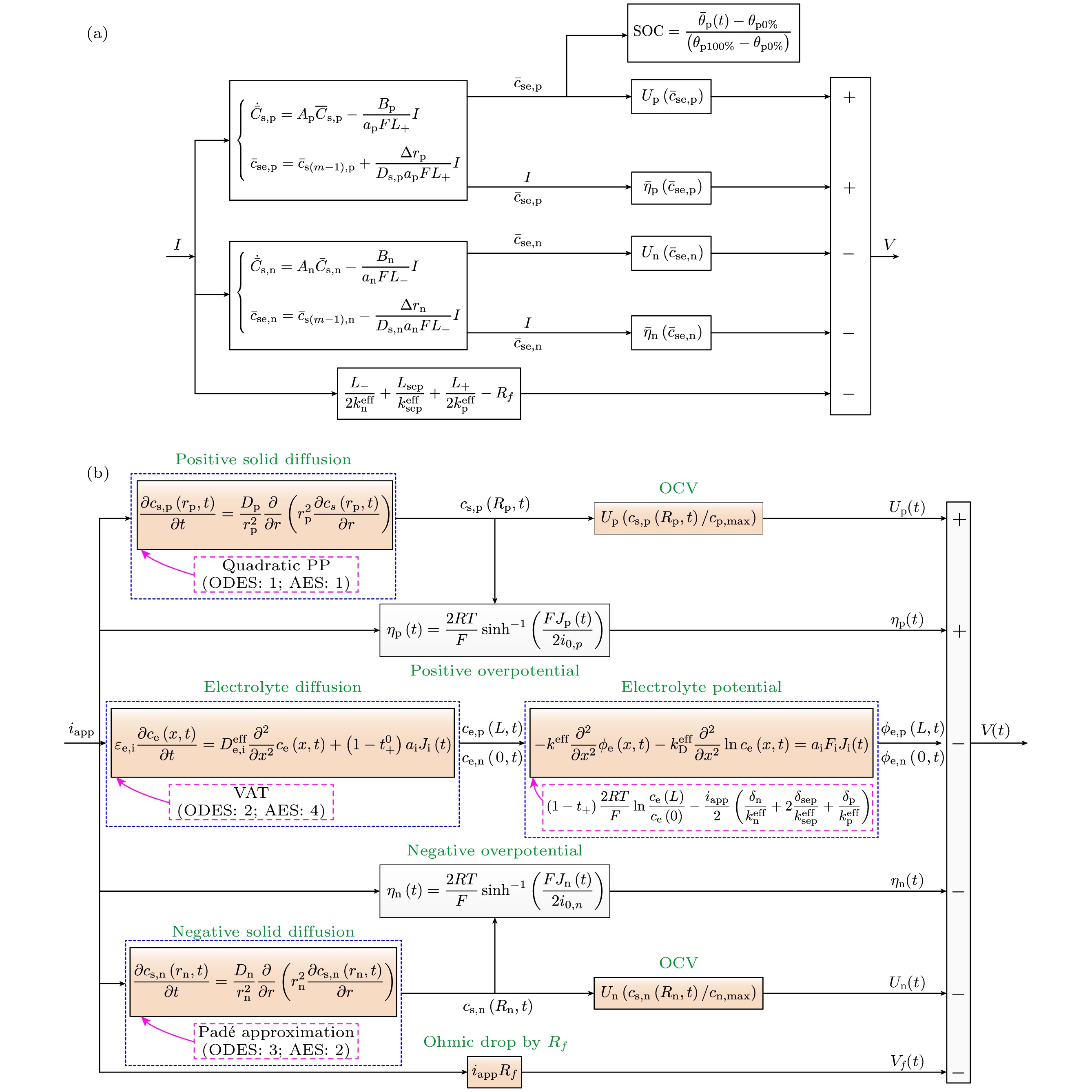
    • 针对单粒子模型(SPM)在液相动力学表征方面的局限性, 大量研究结果表明, 通过引入液相浓度、电势等液相传输动力学特性参数补偿SPM模型[33,34], 可有效拓展其精度以及预测范围, 研究中引入液相动力学方程后的SPM模型被称为带液相的单粒子模型(single particle model with electrolyte, SPMe); Moura等[35]提出了一种在SPMe模型的基础上利用锂的动态特性估计电池内部状态的方法; 为拓宽电池内部状态的估计范围, Li等[36]提出一种基于SPMe模型, 利用卡尔曼滤波算法估计电池SOC的方法, 并且该方法还能估计电池的内部参数状态, 通过对比发现在电池状态不确定性和参数不确定性的条件下该方法仍能准确地估计电池内部状态. 为对比SPMe模型与其他模型的电池内部状态估计能力, 任立超[37]在对电池SOC的估计研究中, 利用SPMe模型对电池SOC进行估算, 较等效电路模型而言SOC估计效果更优; Wang等[38]提出了一种在SPMe模型中基于粒子过滤器估算电池SOC的方法, 其中通过粒子群优化算法识别高敏感度参数, 在多个工况下与等效电路模型相比, SPMe模型不仅能够更高效地表征电池的电化学性能, 而且SOC的估算精度也较高; Desouza等[39]为准确估计包括SOC, SOH, SOP在内的电池内部状态, 提出一种互联的Sigma-point卡尔曼滤波器应用于SPMe模型中, 使部分电化学参数的可观测性得到提高, 进而改善电池内部状态估计效果. 但是SPMe模型是在P2D模型的基础上降阶得到的, 所以该模型较P2D模型而言仍会存在偏差; Zhou等[40]进一步对比分析了P2D模型、SPM模型和SPMe模型的特点, 并指出了各个模型的优势与不足. 为了进一步了解SPMe模型和P2D模型之间误差产生的原因, 谢奕展和程夕明[41]从模型的液相、固相以及动力学参数角度出发对SPMe模型进行误差分析, 指出反应电流密度是模型端电压误差产生的根源, 并提出一系列降低SPMe误差的措施; Xie等[42]针对锂离子电池在车载应用中将面临的温度变化做了进一步研究, 利用一种包括固液相锂离子传质方程降阶和改进瞬态极化电压降公式在内的电化学模型降阶方法, 建立了一个能够适应实时计算和温度变化的热耦合SPMe模型, 并通过对比验证了该模型在动态工况下的效果. 基于SPMe模型的优异性能, 有大量研究人员对SPMe模型和其他物理场的耦合特性做过研究, 徐乐等[43]基于锂离子电池电化学-热耦合理论框架, 系统分析了传统P2D模型在实际应用中的技术瓶颈, 指出该模型存在的一系列缺陷, 针对其缺陷研究团队从计算效率、参数敏感度以及预测精度这3个层面对常见的3种电化学模型进行系统的对比评估, 如图5所示, 发现恒流放电工况下SPMe模型的精度在各放电倍率下始终高于SPM模型, 图6对比了美国联邦城市行驶工况(the Federal Urban Driving Schedule, FUDS)和针对高速的联邦补充工况(United States Environmental Protection Agency US06, US06)下P2D模型和SPMe模型的端电压响应, 根据动态工况中两模型的对比发现电流变化缓慢时SPMe模型仍有较高精度, 但是电流剧烈变化时, SPMe模型误差显著增大, 因此SPMe模型还很难真正落实在工程应用中. 产生的原因在于该模型中部分参数与电极位置脱耦, 使该模型在遇到剧烈变化的工况时, 无法描述电池内部真实的变化.

      对液相的重视会导致模型计算效率降低, 谢奕展和程夕明[44]为减少SPMe模型中液相锂离子浓度的求解规模, 假设模型中电化学反应仅发生在电解质与集电极界面, 并提出一种有限离散卷积方法求解不同工况下的液相扩散过程.

      • 3.3.   基于电化学平均值模型的降阶方法

    • Di Domenico等[33]在微观与宏观耦合的电池模型基础上, 提出了另一类参数与x解耦所得到的降阶电化学模型——电化学平均值模型; Tang等[45]开发了一种预测电池老化轨迹的新方法, 采用机器算法预测电池老化过程中容量衰减和内阻变化, 提出了可行的寿命延长策略; Kumar[46]提出了液相锂离子扩散过程的体积平均近似方法, 应振华[47]基于P2D模型推导出电化学平均值模型的状态方程, 并对比分析了该模型假设条件的有效性. 但是只研究了在低放电电流密度条件下的情况, 根据其假设条件能推断出, 电池工作于高放电电流密度和动态工况下时, 电池内部参数变化幅度增大, 该模型涉及的参数误差会逐渐增大, 相对的模型精度损失也会增大. 结合电化学平均值模型中的近似条件, Wu等[48]利用Padé近似方法进一步模拟了电池的固相扩散过程, 以达到降阶重构电化学模型的目的; Padé近似作为一种在频域角度降阶重构电化学模型的方法, 熊瑞和李幸港[49]利用该方法同时降阶重构了固液相扩散过程, 并在锂离子电池的析锂评估中验证了该方法的有效性. 同时王位[50]基于平均电化学场理论模型, 构建了融合卡尔曼滤波架构的SOC估计系统, 通过实验表明, 该模型在大电流放电阶段和车载BMS显示中有明显误差. 该电化学模型存在的误差, 其本质源于模型降阶重构过程中忽略了部分电化学参数与电极位置间的耦合关系. 针对此类降阶重构方法而导致的一系列问题, 有学者通过降阶参数间的耦合关系重构电化学模型.

      • 3.4.   P2D模型的固液相重构降阶及应用

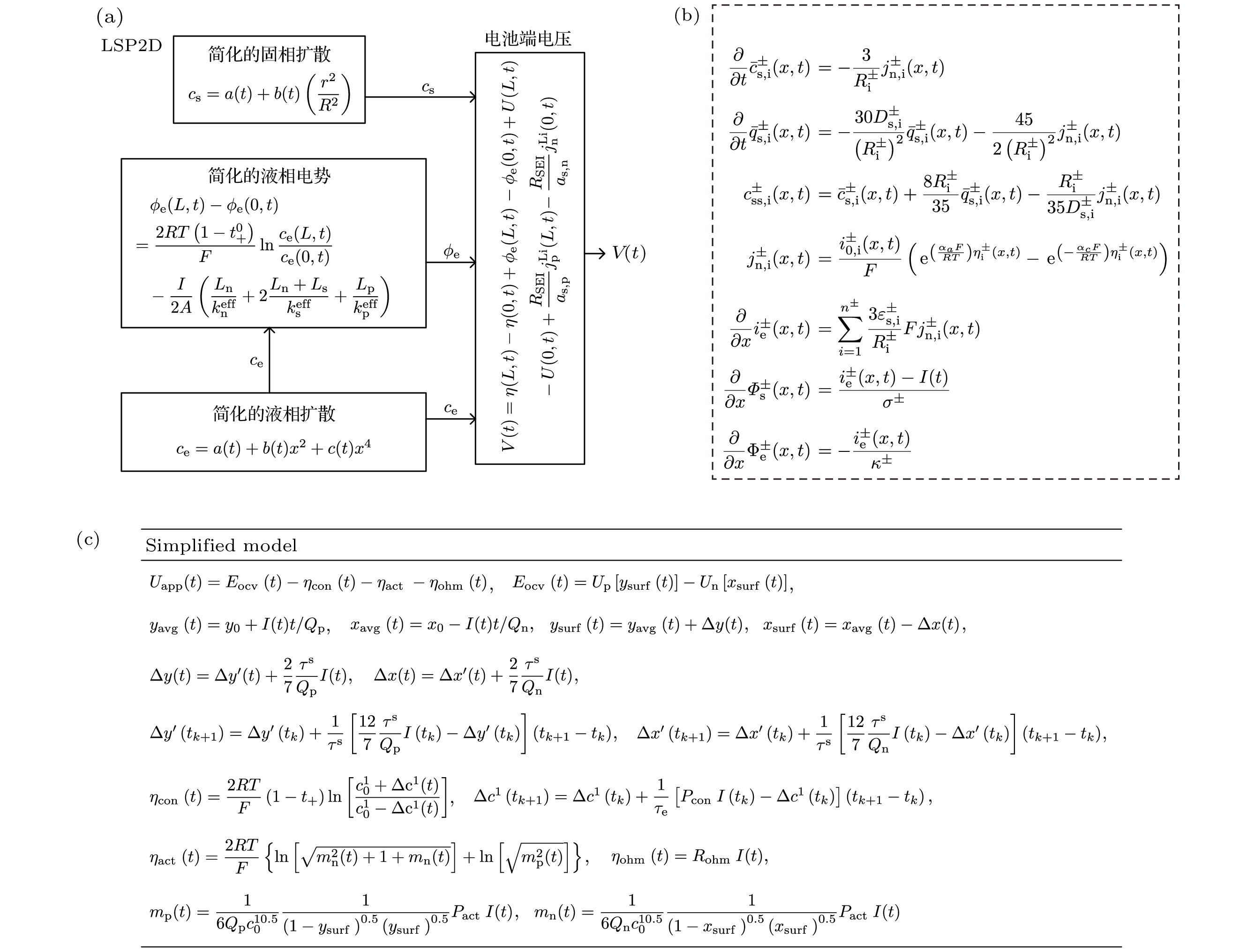
    • P2D模型存在参数间耦合复杂、模型求解困难的缺陷, 因此有学者通过降阶P2D方程的计算式重构电化学模型, 例如包含液相简化的P2D模型(liquid simplified pseudo-two-dimensions, LSP2D). 该模型通过构建固液相扩散动力学的近似处理机制, 降阶重构了电化学模型参数和电极位置x间的耦合关系, 创新性地将原始P2D模型中非线性偏微分控制方程体系重构为具有等效特性的常微分方程体系. Subramanian等[51]对固相扩散过程进行了近似求解, 基于2阶、4阶、6阶多项式分别开发了2阶2参数、4阶3参数、6阶4参数近似模型, 并在不同反应电流密度的情况下对比了近似模型与精确模型间的参数变化情况, 结果表明近似模型的精度随阶数的增加而增大, 但是此方法仅仅只是解决了简单的恒定扩散系数的情况, 对于电池内部动态变化的情况而言还需要继续探索; 根据上述情况, Subramanian等[52]基于变化的扩散系数做出了进一步研究, 对于固相扩散, 开发了与时间相关的扩散系数近似解, 研究中引入了体积平均浓度、表面浓度和体积浓度通量这3个参数, 并对不同阶近似模型进行无量纲分析, 在多种测试函数的对比下, 得到高阶近似模型普遍表现较好的结果; Klein等[53]为降阶重构电化学模型, 使用上述方法将固相扩散过程用三参数近似处理, Rahman等[54]根据此降阶重构方法, 提出一种基于粒子群优化算法辨识模型参数, 并在多种不同充放电情况下验证了该方法的有效性. 大量学者对液相浓度分布[55,56]和不均匀电流分布[57]进行了基于多项式近似的处理, 最终得到以多项式近似为基础的这一类的重构模型[58].

      李旭昊等[59]利用这种抛物线近似方法同时重构了固液相扩散方程, 将得到的重构电化学模型与热模型耦合, 并通过在不同工况下的对比验证了该模型的精度; Wang等[60]利用浓缩的质量热模型和该电化学模型耦合, 建立两模型参数间的联系, 使该模型中的电化学参数能根据热模型做出相应的更新, 并在不同工况下验证了此类电化学-热耦合模型的精度; Li等[61]利用抛物线近似重构固液相扩散方程, 并基于最小二乘拟合法辨识模型参数, 在模型对比研究中发现, 该方法下除截止电压阶段外, 整体模型精确度较高, Fu等[62]还将此方法应用到钠离子电池电化学模型的降阶重构中也取得较好的效果; 刘征宇等[63]也用类似的抛物线近似重构了固液相扩散方程, 研究中将端电压表达式中的非线性偏微分控制方程体系重构为具有等效特性的常微分方程体系, 并通过模型曲线对比分析如图7所示, 得到多项式近似的方法相比于单粒子模型而言在高倍率情况下精度较优, 但是相对于精确模型而言, LSP2D模型的液相锂离子浓度曲线并不与其完全符合, 误差相对较大, 是因为当外界工作条件变化剧烈时, 实际的固液相锂离子浓度变化偏离抛物线变化严重. 以上所有方法均是减少或消除参数间的耦合关系进而达到降阶重构电化学模型的目的, 还有部分学者研究了因为模型维度而导致的电化学参数状态量过多的问题.

      • 3.5.   基于一维电化学模型的降阶方法研究

    • 一维电化学模型是电化学模型维度降阶的直接构想, 该模型的优势在于与其他物理场模型的耦合. Kandler等[64]针对P2D模型的维度降阶电化学模型, 构建出一维电化学模型, 该模型通过降维解决了P2D模型状态量过多的问题; 陆浩然等[65]基于一维电化学模型构建了电化学-热耦合模型, 深入分析了不同变量对电池电化学特性的作用机制, 并通过产热分解法量化了各部件的产热贡献; Ma等[66]基于降阶的一维模型与热模型耦合, 开发了一种具有自适应特性的SOC观测器, 在电池SOC预测中展现出良好的应用效果. 为进一步提高一维电化学-热耦合模型的实用价值, Sangiri等[67]在一维电化学-热耦合模型的构建过程中纳入了质量守恒、电子传导、电荷平衡和能量平衡等关键物理规律, 使该模型在宽温区间内仍能高效的估计电池SOC; 李光远和马彦[68]为解决P2D模型在数值计算方面存在的核心缺陷——较高的计算资源需求和复杂的求解过程, 搭建了一种优化的一维电化学模型建模方法, 模型中运用了Laplace变换实现时域到频域的属性转换, 创新性地将电极材料固相中的锂离子径向扩散过程转换为无量纲导纳表达形式, 为进一步提高计算效率, 使用Padé近似对频域方程进行降阶近似处理, 经实验验证, 改进后的模型在低放电电流密度下有较高准确性, 但随着放电电流密度的提升, 该模型精度较实际相比偏差呈现增大的趋势, 在整个趋势下, 放电电流密度越大, 模型精度将会越差; 梁新成等[69]从P2D模型出发推导出一维电化学模型, 并利用部分参数的精度反应一维电化学模型的精度, 结果表明当放电电流密度增大时模型精度变差. 是因为随着放电电流密度的增大, 液相锂离子浓度的扩散也会加快, 对该参数耦合关系的忽略是造成一维模型在高放电电流密度情况下误差较大的主要原因.

    4.   动力电池电化学模型降阶策略研究

    • 表2综合对比了目前的电化学模型降阶重构方法. SPM模型将固相锂离子浓度、交换电流密度、反应电流密度、液相锂离子浓度和电势均看作是定值, 在高倍率工况下的模型表征精度较差; 而SPMe模型在SPM模型的基础上考虑了液相动力学的作用, 高倍率情况下模型表征精度有所增大, 但其计算复杂度相比SPM模型而言也会有所加剧. 电化学平均值模型中将液相锂离子浓度和反应电流密度用一定值代替, 无法精确描述电池在高倍率充放电及变电流密度等工况下的变化, 导致模型精度的不足. LSP2D模型是将描述固液相扩散过程的控制方程用抛物线函数近似表达, 相对SPM模型而言, 该模型的液相锂离子浓度仍是变化的, 因此在高倍率工况下LSP2D模型的精度相对SPM模型而言较好, 但是在工作条件剧烈变化时, 实际的参数变化趋势严重偏离抛物线趋势, 导致模型误差较大. 一维电化学模型将液相锂离子浓度看作是一个定值, 当放电电流密度增大时, 实际的液相锂离子浓度变化严重偏离这一定值, 该模型在高放电电流密度下的误差主要来源于此.

      目前研究中降阶电化学模型中除SPMe模型外均对液相锂离子浓度的变化做降阶处理, 其中LSP2D模型只是缓解了液相锂离子浓度与其他参数间的耦合关系, 而其他降阶模型均是将液相锂离子浓度与模型中参数解耦, 在高倍率工况下SPMe模型的精度大于LSP2D模型大于其他降阶模型, 因此进一步验证了描述液相动力学过程的控制参数对于电化学模型的表征精度具有重要意义. 此外, 除LSP2D模型外其他降阶模型均忽略了反应电流密度与模型中参数的耦合关系, 而反应电流密度与电池核心参数(端电压)高度耦合, 忽略该参数的变化对于电化学机理模型的精度影响较大.

      综上所述, 目前提出的电化学模型降阶方法主要集中在模型降维和模型参数等效缩减等方面, 而厘清电化学模型表征参数之间的耦合关系、明确关键电化学参数的测算方法是动力电池电化学模型降阶分析的必要前提. 李涛等[70]针对P2D模型在实际工程应用中所面临的参数难测或不可测问题, 以及因参数间复杂的耦合关系而导致的P2D模型求解耗时的问题, 指出需要通过降阶处理才能使 电化学模型成功应用于实际中; Kong等[71]针对电化学模型复杂性提出了一系列降阶策略, 并论证了各个降阶策略在效率和精度方面的可行性; 李皓天等[72]指出参数量大、参数耦合复杂是电化学模型不能满足在线仿真计算的实时性和高效性要求的主要原因. 此外模型降阶重构过程中大量参数的简化处理不可避免地会引入近似误差, 如何甄别并合理简化对系统输出响应敏感度低的参数, 是亟待深入解决的关键问题, Xu等[73]针对P2D模型参数辨识困难的问题, 通过全局参数敏感度分析得到了一系列高敏感度参数, 研究结果表明基于高敏感度参数的降阶重构电化学模型在减少计算的前提下仍能保持较高精度; 张毕[74]利用参数敏感度分析去缩减模型参数辨识的工作量, 并且提出一种通过观察参数曲线离散程度来判断参数敏感度的方法, 为动力电池电化学模型参数敏感性分析提供新的途径.

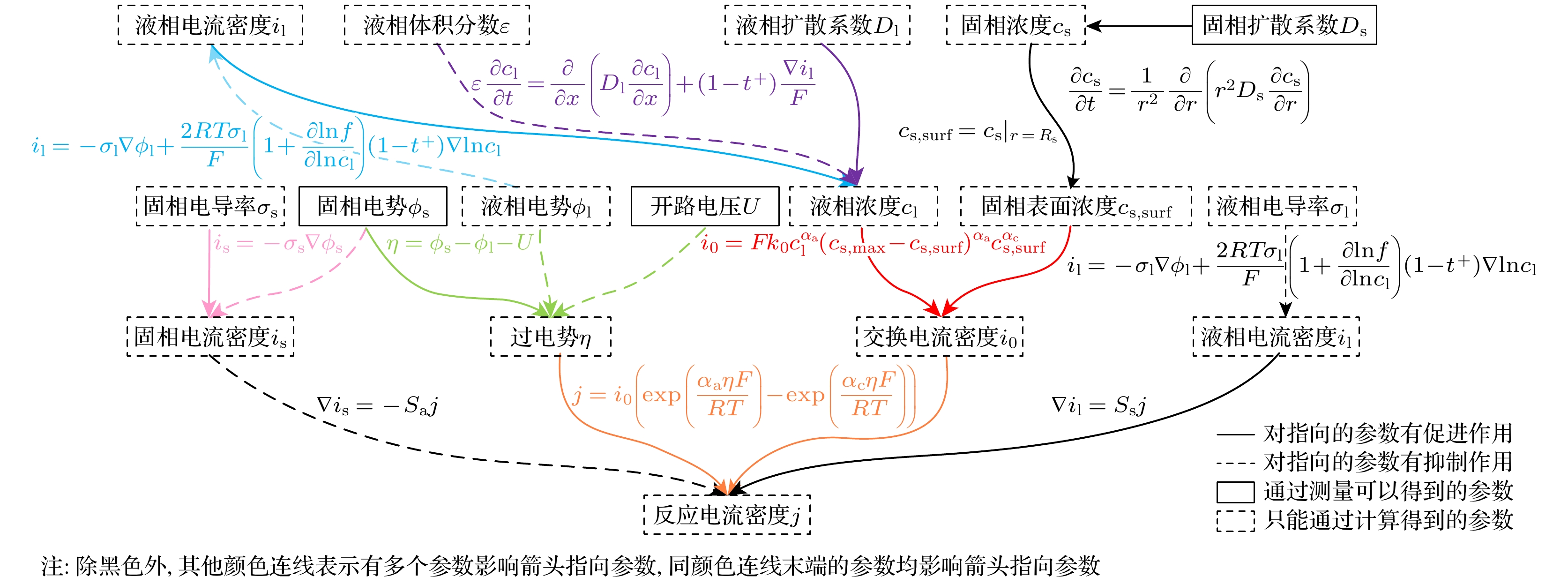
      鉴于电化学模型降维和模型参数等效缩减对于模型参数关联性的需求, 本文结合P2D模型的控制方程和边界条件以及电化学反应过程参数映射关系, 建立了图8所示的电化学模型表征参数关联关系图谱, 梳理了交换电流密度、过电势、反应电流密度、固相电流密度、液相电流密度、固相表面浓度、液相浓度、液相电势、开路电压、固相电势、液相体积分数、固相扩散系数之间关联关系和影响机制, 并进一步结合目前文献研究成果分析了关键电化学参数的测算过程(如表3所示)以及各电化学模型中独有的参数及其物理意义(如附录A中表A1所示). 分析结果表明极少数电化学模型参数可以通过测试得到, 而且此类参数不仅需要电化学工作站等昂贵的测试设备和专业技术人员操作, 大量电化学模型参数则需要通过复杂的运算才能辨识, 因此简化电化学参数的辨识过程, 对电化学模型降阶重构而言同样具有重要价值. 电化学模型各参数间存在的复杂非线性耦合关系, 显著制约了电化学模型在实际工况中的应用, 构建高效的降阶重构电化学模型, 对于推进电化学模型在电池管理系统中的实时状态估计有重要意义.

    5.   电化学模型降阶重构研究趋势

    • 以P2D模型为代表的电化学模型作为能从微观尺度表征电池内部电化学反应过程的机理模型, 其对于动力电池的老化、生热行为的准确描述是电池单体容量衰减、内阻增大、受热不均以及电池模组性能不一致评价的重要依据. 电化学模型的有效降阶一方面能够显著提升电化学模型的仿真效率和工程适用性, 另一方面可以有效降低电化学模型与其他物理场之间的耦合难度, 为动力电池运行状态的实时准确刻画和动态管控优化提供有力支撑. 因此, 开展高效的电化学模型降阶重构研究是动力电池应用领域不可回避的重要技术需求.

      1)重点研究面向多物理场耦合表征应用的电化学模型降阶重构方法, 有效拓展电化学机理模型的应用领域.

      尽管现有电化学模型降阶方法通过简化多孔电极内的粒子数目、孔隙率等微观结构参数显著提升了多物理场耦合计算效率, 但其对电极微观结构形变过程的表征缺失导致了电化学控制方程与温度场及力学场的跨尺度耦合机制存在理论缺陷. 这种多尺度关联性的弱化使得模型在预测电池热失控及寿命衰减机制等行为时存在明显缺陷. 针对多物理场耦合建模问题, 需通过系统整合热膨胀系数、应力应变方程等关键物理场参数与电化学本构方程间的跨尺度耦合机制. 模型降阶过程中需重点研究基于多项式近似展开的时域维度模型重构策略, 尤其对具有显著场间耦合特性的电化学敏感参数进行多项式近似重构, 可有效提升降阶后电化学机理模型的预测精度.

      2)加强探索基于大数据驱动的电化学模型降阶重构方法, 着力解决高倍率工况下动力电池运行状态的快速高精刻画问题.

      目前提出的电化学模型降阶方法在低倍率工况下的应用优势已得到充分证明, 但高倍率工况下的预测精度劣化问题成为制约电化学模型走向工程应用的关键瓶颈. 动力电池老化、生热行为所导致的电池单体容量衰减、内阻增大、受热不均及电池模组性能不一致的问题多发生于高倍率放电工况. 因此, 研究面向高倍率工况应用的动力电池电化学模型降阶重构方法, 对于充分描述多工况下动力电池的老化行为具有重要意义. 借助数据驱动方法和机器学习算法不依赖于模型预定义和预假设的优势, 通过在电化学模型降阶重构过程中融合数据驱动模型, 以充分发挥数据驱动方法在高维非线性条件下的时效性优势, 为最终解决高倍率工况下动力电池运行状态的快速高精刻画问题提供有效途径.

      3)研究面向车载运行状态实时快速仿真的电化学模型降阶重构方法, 建立兼具状态表征精度和仿真计算效率的降阶重构电化学模型.

      电化学模型在表征动力电池微观电化学机理反应过程和描述动力电池运行状态方面的高精度优势已得到论证, 目前提出的降阶重构方法多基于实验室数据进行验证, 忽略了车载运行工况下电化学模型状态实时更新能力差的问题, 上述问题导致电化学降阶模型在车载复杂工况下的工程化应用仍存在显著性局限. 因此, 受电化学模型降阶过程中假设条件的限制, 多数降阶重构模型目前仅适用于实验室环境下的准静态分析, 难以准确表征动力电池在实车运行中所面临的动态参数变化、宽域温度梯度及复杂老化机制等特征参量. 如何揭示车载实测参数与电化学模型敏感参数映射机制, 如何利用多项式近似等时域重构方法降阶电化学参数间的耦合关系, 进而构建面向车载运行状态实时快速仿真的电化学模型降阶重构框架, 通过嵌入自适应观测算法实现高精度电池状态参数估计(如荷电状态、健康状态、功率状态等), 进而优化电池管理系统的多目标协同控制策略, 有效解决传统电化学降阶重构模型在状态表征精度和仿真计算效率之间的矛盾.

      综上所述, 电化学模型作为当前能够从微观层面表征动力电池机理反应的基础模型, 能通过耦合其他物理场模型来精确描述动力电池的运行状态和运行变化过程, 但其庞大的计算规模与复杂的参数辨识过程严重限制了该模型在工程实践中的应用. 开展高效的电化学模型降阶重构研究是动力电池应用领域不可回避的重要技术需求, 重点研究面向多物理场耦合表征应用的电化学模型降阶重构方法、基于大数据驱动的电化学模型降阶重构方法、面向车载运行状态实时快速仿真的电化学模型降阶重构等方法, 突破高倍率工况下动力电池运行状态的快速高精刻画的关键技术, 建立兼具状态表征精度和仿真计算效率的电化学模型降阶重构方法体系, 解决目前车载动力电池的运行状态表征和故障诊断难题, 为未来动力电池系统数字孪生和云端智能管控提供模型和方法基础.

    附录A.   　

    • 不同模型参数及其物理含义和来源见表A1.

    附录B.   降阶电化学模型图
    参考文献 (74)

目录

/

返回文章
返回