高级搜索

mHz—MHz频段低噪声高增益平衡光电探测器实验研究

,  ,  ,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

卢波, 史少平, 高丽, 王璇, 林艺松, 田龙, 李卫, 王雅君, 郑耀辉. mHz—MHz频段低噪声高增益平衡光电探测器实验研究[J]. 物理学报, 2025, 74(18): 189501-1. doi: 10.7498/aps.74.20250640
引用本文: 卢波, 史少平, 高丽, 王璇, 林艺松, 田龙, 李卫, 王雅君, 郑耀辉. mHz—MHz频段低噪声高增益平衡光电探测器实验研究[J]. 物理学报, 2025, 74(18): 189501-1. doi: 10.7498/aps.74.20250640
shu
Bo LU, Shaoping SHI, Li GAO, Xuan WANG, Yisong LIN, Long TIAN, Wei LI, Yajun WANG, Yaohui ZHENG. Experimental research on low-noise and high-gain balanced detectors in mHz−MHz band[J]. Acta Physica Sinica, 2025, 74(18): 189501-1. doi: 10.7498/aps.74.20250640
Citation: Bo LU, Shaoping SHI, Li GAO, Xuan WANG, Yisong LIN, Long TIAN, Wei LI, Yajun WANG, Yaohui ZHENG. Experimental research on low-noise and high-gain balanced detectors in mHz−MHz band[J]. Acta Physica Sinica, 2025, 74(18): 189501-1. doi: 10.7498/aps.74.20250640
shu

mHz—MHz频段低噪声高增益平衡光电探测器实验研究

  • 1.

    山西大学光电研究所, 光量子技术与器件全国重点实验室, 太原　030006

  • 2.

    山西大学, 极端光学协同创新中心, 太原　030006

  • 3.

    山西大学物理电子工程学院, 太原　030006

    • 作者简介: 卢波: lubo202207@163.com .
    通讯作者: E-mail: ssp4208@sxu.edu.cn.; 

  • 中图分类号: 95.55.Ym, 85.60.Gz, 42.50.Lc, 42.60.–v

Experimental research on low-noise and high-gain balanced detectors in mHz−MHz band

  • 1.

    State Key Laboratory of Quantum Optics Technologies and Devices, Institute of Opto-Electronics, Shanxi University, Taiyuan 030006, China

  • 2.

    Collaborative Innovation Center of Extreme Optics, Shanxi University, Taiyuan 030006, China

  • 3.

    College of Physics and Electronic Engineering, Shanxi University, Taiyuan 030006, China

    • Corresponding author: E-mail: ssp4208@sxu.edu.cn.; 

  • MSC: 95.55.Ym, 85.60.Gz, 42.50.Lc, 42.60.–v

  • 摘要: 平衡光电探测器作为一种检测量子态噪声起伏通用技术的核心关键器件, 其性能参数在近直流的宽频带范围内(mHz—MHz)常受限于电子学噪声与电学增益的相互制约. 针对1 mHz—1 Hz极低频段, 为满足未来量子增强引力波探测计划中对量子压缩光源探测和评估等方面的需求, 本研究基于一种可调节阻抗匹配网络与两级差分放大的设计架构, 使用差分微调电路与可调偏置电压协同补偿方案, 优化光电二极管的非线性响应补偿机制, 在分析频段500 Hz处实现共模抑制比>75 dB. 实验结果表明, 在小于1 Hz的频段内, 探测器的电子学噪声优于3.5 × 10–5 V/Hz1/2, 满足空间引力波探测计划对于激光强度噪声的要求(1 × 10–4 V/Hz1/2); 同时当入射的本底探测光功率为4 mW时, 本平衡光电探测器可实现增益20 dB@1 mHz—1 MHz, 满足高指标压缩光源的高效探测需求, 为下一代空间引力波探测以及极低频段压缩态光场的探测提供了关键器件的解决方案.
    Abstract: Balanced detector is a fundamental component for the accurately measuring quantum state fluctuations, especially quantum noise, which is crucial for future quantum-enhanced interferometric gravitational wave detectors utilizing squeezed light. By using a transimpedance amplifier (TIA) model core for balanced detection, a detailed theoretical and practical analysis is conducted on the electronic factors that affect the performance of the detector in the target ultra-low-frequency range. The TIA stage is meticulously designed using a high-performance integrated operational amplifier characterized by low offset voltage drift. In order to ensure the critical gain stability for ultra-low-frequency operation, this design adopts low temperature-drift metal foil resistors. Subsequent voltage amplification is achieved using a noninverting amplifier configuration to attain the necessary high electrical gain, while strictly managing overall electronic noise. By recognizing the criticality of common-mode noise rejection for quantum noise measurements, the photodiode (PD) nonlinear response compensation mechanism is analyzed and optimized. This is achieved through the innovative implementation of a differential fine-tuning circuit (DFTC) coupled with an adjustable bias voltage (ABV) compensation scheme. Experimental validation confirms the effectiveness of the optimized design. The compensation scheme utilizing DFTC and ABV successfully achieves a high common mode rejection ratio (CMRR) exceeding 75 dB@500 Hz. Crucially, the detector achieves an electronic noise spectral density of 3.5 × 10–5 V/Hz1/2 within the 1 mHz–1 Hz band, exceeding the requirements for laser intensity noise (1 × 10–4 V/Hz1/2) in space-based gravitational wave detection. Furthermore, the detector demonstrates high gain capability and bandwidth: with an incident detection light power of 4 mW, the balanced detector achieves a gain of 20 dB maintained in a wide frequency range from 1 mHz to 1 MHz. This work presents the design, detailed analysis, and experimental realization of optimized balanced detectors specifically tailored for high-sensitivity measurements in the millihertz gravitational wave frequency band. The achieved low electronic noise base below 1 Hz and high CMRR meet the key requirements for future space-based gravitational wave detectors to detect squeezed states of light. This optimized balanced detector provides important components and technical support for the next-generation space-based gravitational wave detection and millihertz squeezed light characterization.
  • 加载中

  • 图 1  基于TIA的平衡光电探测器示意图(OPA1/2, 运算放大器1/2; PD, 光电二极管; Vbias, 偏置电压; VAC, 交流电压信号; VDC, 直流电压信号)

    Figure 1.  Schematic diagram of the balanced detector based on TIA. OPA1/2, operational amplifier 1/2; PD, photodiode; Vbias, bias voltage; VAC, AC voltage signal; VDC, DC voltage signal.

    下载: 全尺寸图片 幻灯片

    图 2  光电二极管和TIA的等效电路模型

    Figure 2.  Noise response model of photodiode and TIA.

    下载: 全尺寸图片 幻灯片

    图 3  平衡光电探测器电路原理图(FER, 磁珠; RP, 滑动变阻器)

    Figure 3.  Circuit layout of balanced detector. FER, ferrite bead; RP, variable resistor.

    下载: 全尺寸图片 幻灯片

    图 4  基于LTspice软件的电路仿真图　(a) 时域参数扫描分析图; (b) 频域参数扫描分析图

    Figure 4.  Electronic circuit simulation based on LTspice software: (a) Time domain parameter scan analysis results; (b) frequency domain parameter scan analysis results.

    下载: 全尺寸图片 幻灯片

    图 5  平衡光电探测器性能测试评估装置图(ISO, 光学隔离器; HWP, 半波片; PBS, 偏振分束器; EOAM, 电光振幅调制器; SG, 信号发生器; BHD, 平衡光电探测器; SA, 频谱分析仪; OSC, 示波器; Meter, 高精度数字万用表)

    Figure 5.  Balanced detector performance test and evaluation device. ISO, isolator; HWP, half-wave plate; PBS, polarization beam splitter; EOAM, electro-optic amplitude modulator; SG, signal generator; BHD, balanced homodyne detector; SA, spectrum analyzer; OSC, oscilloscope; Meter, high-precision digital multimeter.

    下载: 全尺寸图片 幻灯片

    图 6  平衡光电探测器CMRR测试图

    Figure 6.  CMRR of the balanced detector.

    下载: 全尺寸图片 幻灯片

    图 7  平衡光电探测器线性度测试噪声谱表征　(a) 1 kHz—1.5 MHz频段性能的测量结果; (b) 1 mHz—1 Hz频段性能的测量结果

    Figure 7.  Balanced detector linearity test noise spectral characterization: (a) Measured noise spectra from 1 kHz to 1.5 MHz; (b) noise power spectrum from 1 Hz downwards to 1 mHz.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Abbott R, Abbott T D, Abraham S, Acernese F, Ackley K, Adams A, Adams C, Adhikari R X, Adya V B, Affeldt C 2020 Phys. Rev. Lett. 125 101102 doi: 10.1103/PhysRevLett.125.101102
    [2] Vitale S 2021 Science 372 eabc7397 doi: 10.1126/science.abc7397
    [3] Abbott T D, Abraham S, Acernese F, et al. 2020 Astrophys. J. Lett. 896 L44 doi: 10.3847/2041-8213/ab960f
    [4] 李庆回, 李卫, 孙瑜, 王雅君, 田龙, 陈力荣, 张鹏飞, 郑耀辉 2022 物理学报 71 164203 doi: 10.7498/aps.71.20220552 Li Q H, Li W, Sun Y, Wang Y J, Tian L, Chen L R, Zhang P F, Zheng Y H 2022 Acta Phys. Sin. 71 164203 doi: 10.7498/aps.71.20220552
    [5] 王在渊, 王洁浩, 李宇航, 柳强 2023 物理学报 72 054205 doi: 10.7498/aps.72.20222127 Wang Z Y, Wang J H, Li Y H, Liu Q 2023 Acta Phys. Sin. 72 054205 doi: 10.7498/aps.72.20222127
    [6] Jia W X, Xu V, Kuns K, et al. 2024 Science 385 1318 doi: 10.1126/science.ado8069
    [7] McCuller L, Whittle C, Ganapathy D, Komori K, Tse K, Fernandez-Galiana A, Barsotti L, Fritschel P, MacInnis M, Matichard F, Mason K, Mavalvala N, Mittleman R, Yu H C, Zucker M E, Evans M 2020 Phys. Rev. Lett. 124 171102 doi: 10.1103/PhysRevLett.124.171102
    [8] Aasi J, Abadie J, Abbott B P, Abbott R, et al. 2013 Nat. Photonics 7 613 doi: 10.1038/nphoton.2013.177
    [9] Acernese F, Agathos M, Aiello L, et al. 2019 Phys. Rev. Lett. 123 231108 doi: 10.1103/PhysRevLett.123.231108
    [10] Mikhail K, Ma Y Q, Chen Y B, Schnabel R 2019 Light: Sci. Appl. 8 118 doi: 10.1038/s41377-019-0230-2
    [11] Harry G M, LIGO Scientific Collaboration 2010 Classical Quantum Gravity 27 084006 doi: 10.1088/0264-9381/27/8/084006
    [12] Matichard F, Lantz B, Mittleman R, et al. 2015 Classical Quantum Gravity 32 185003 doi: 10.1088/0264-9381/32/18/185003
    [13] Thorne K S, Winstein C J 1999 Phys. Rev. D 60 082001 doi: 10.1103/PhysRevD.60.082001
    [14] Acernese F, Agathos M, Agatsuma K, et al. 2014 Classical Quantum Gravity 32 024001 doi: 10.1088/0264-9381/32/2/024001
    [15] Luo J, Chen L S, Duan H Z, Gong Y G, Hu S C, Ji J H, Liu Q, Mei J W, Milyukov V, Sazhin M, Shao C G, Toth V T, Tu H B, Wang Y M, Wang Y, Yeh H C, Zhan M S, Zhang Y H, Zharov V, Zhou Z B 2016 Classical Quantum Gravity 33 035010 doi: 10.1088/0264-9381/33/3/035010
    [16] Jennrich O 2009 Classical Quantum Gravity 26 153001 doi: 10.1088/0264-9381/26/15/153001
    [17] Luo Z R, Wang Y, Wu Y L, Hu W R, Jin G 2021 Prog. Theor. Exp. Phys. 2021 05A108 doi: 10.1093/ptep/ptaa083
    [18] Luo Z R, Guo Z K, Jin G, Wu Y L, Hu W R 2020 Results Phys. 16 102918 doi: 10.1016/j.rinp.2019.102918
    [19] 罗子人, 白姗, 边星, 陈葛瑞, 董鹏, 董玉辉, 高伟, 龚雪飞, 贺建武, 李洪银, 李向前, 李玉琼, 刘河山, 邵明学, 宋同消, 孙保三, 唐文林, 徐鹏, 徐生年, 杨然, 靳刚 2013 力学进展 43 415 doi: 10.6052/1000-0992-13-044 Luo Z R, Bai S, Bian X, Chen G R, Dong P, Dong Y H, Gao W, Gong X F, He J W, Li H Y, Li X Q, Li Y Q, Liu H S, Shao M X, Song T X, Sun B S, Tang W L, Xu P, Xu S N, Yang R, Jin G 2013 Adv. Mech. 43 415 doi: 10.6052/1000-0992-13-044
    [20] Badaracco F, Rossi C D, Fiori I, Harms J, Miyo K, Paoletti F, Tanaka T, Washimi T, Yokozawa T 2021 Phys. Rev. D 104 042006 doi: 10.1103/PhysRevD.104.042006
    [21] Stefszky M S, Mow-Lowry C M, Chua S S Y, Shaddock D A, Buchler B C, Vahlbruch H, Khalaidovski A, Schnabel R, Lam P K, McClelland D E 2012 Classical Quantum Gravity 29 145015 doi: 10.1088/0264-9381/29/14/145015
    [22] 尚鑫, 李番, 马正磊, 黄天时, 党昊, 李卫, 尹王保, 田龙, 陈力荣, 郑耀辉 2025 物理学报 74 059501 doi: 10.7498/aps.74.20241635 Shang X, LI F, Ma Z L, Huang T S, Dang H, LI W, Yin W B, Tian L, Cheng L R, Zheng Y H 2025 Acta Phys. Sin. 74 059501 doi: 10.7498/aps.74.20241635
    [23] McKenzie K, Gray M B, Lam P K, McClelland D E 2007 Appl. Opt. 46 3389 doi: 10.1364/AO.46.003389
    [24] Schnabel R, Mavalvala N, McClelland D E, Lam P K 2010 Nat. Commun. 1 122 doi: 10.1038/ncomms1121
    [25] Vahlbruch H, Chelkowski S, Danzmann K, Schnabel R 2007 New J. Phys. 9 371 doi: 10.1088/1367-2630/9/10/371
    [26] Wu M C, Schmittberger B L, Brewer N R, Speirs R W, Jones K M, Lett P D 2019 Opt. Express 27 4769 doi: 10.1364/OE.27.004769
    [27] Meylahn F, Willke B, Vahlbruch H 2022 Phys. Rev. Lett. 129 121103 doi: 10.1103/PhysRevLett.129.121103
    [28] Gao L, Zheng L A., Lu B, Shi S P, Tian L, Zheng Y H 2024 Light: Sci. Appl. 13 294 doi: 10.1038/s41377-024-01606-y
    [29] Yang W H, Jin X L, Yu X D, Zheng Y H, Peng K C 2017 Opt. Express 25 24262 doi: 10.1364/OE.25.024262
    [30] 王炜杰, 李番, 李健博, 鞠明健, 郑立昂, 田宇航, 尹王保, 田龙, 郑耀辉 2022 红外与激光工程 51 20220300 doi: 10.3788/IRLA20220300 Wang W J, Li F, Li J B, Ju M J, Zheng L A, Tian Y H, Yin W B, Tian L, Zheng Y H 2022 Infrared Laser Eng. 51 20220300 doi: 10.3788/IRLA20220300
    [31] Wu Y M, Tian L, Yao W X, Shi S P, Liu X, Lu B, Wang Y J, Zheng Y H 2024 Appl. Phys. Lett. 124 114002 doi: 10.1063/5.0191643
    [32] Shi S P, Tian L, Wang Y J, Zheng Y H, Xie C D, Peng K C 2020 Phys. Rev. Lett. 125 070502 doi: 10.1103/PhysRevLett.125.070502
    [33] 史少平, 武奕淼, 刘璇, 田龙, 郑耀辉 2024 量子光学学报 30 040102 doi: 10.3788/JQO20243004.0102 Shi S P, Wu Y M, Liu X, Tian L, Zheng Y H 2024 J. Quantum Opt. 30 040102 doi: 10.3788/JQO20243004.0102
    [34] 王鼎康, 武晋泽, 宋志刚, 李晋红 2024 量子光学学报 30 041001 doi: 10.3788/JQO20243004.1001 Wang D K, Wu J Z, Song Z G, Li J H 2024 J. Quantum Opt. 30 041001 doi: 10.3788/JQO20243004.1001
    [35] Graeme J 1996 Photodiode amplifiers: op amp solutions (New York: McGraw-Hill) pp87–92
    [36] Lu Q, Shen Q, Cao Y, Liao S K, Peng C Z 2019 IEEE Trans. Nucl. Sci. 66 1048 doi: 10.1109/TNS.2018.2885364
    [37] AD797: Ultralow Distortion, Ultralow Noise Op Amp Data Sheet (Rev. K) https://www.analog.com/media/en/technical-documentation/data-sheets/AD797.pdf [2025-5-12]
    [38] AD8671/AD8672/AD8674: Precision, Very Low Noise, Low Input Bias Current Operational Amplifiers Data Sheet (Rev. F) https://www.analog.com/media/en/technical-documentation/data-sheets/AD8671_8672_8674.pdf [2025-5-12]
    [39] Jin X L, Su J, Zheng Y H, Chen C Y, Wang W Z, Peng K C 2015 Opt. Express 23 23859 doi: 10.1364/OE.23.023859
    [40] 李番, 王嘉伟, 高子超, 李健博, 安炳南, 李瑞鑫, 白禹, 尹王保, 田龙, 郑耀辉 2022 物理学报 71 209501 doi: 10.7498/aps.71.20220841 Li F, Wang J W, Gao Z C, Li J B, An B N, Li R X, Bai Y, Yin W B, Tian L, Zheng Y H 2022 Acta Phys. Sin. 71 209501 doi: 10.7498/aps.71.20220841
  • 加载中
图( 8)
计量
  • 文章访问数:  31
  • HTML全文浏览数:  31
  • PDF下载数:  2
  • 施引文献:  0
出版历程
  • 收稿日期:  2025-05-15
  • 刊出日期:  2025-09-20

mHz—MHz频段低噪声高增益平衡光电探测器实验研究

    通讯作者: E-mail: ssp4208@sxu.edu.cn.; 
    作者简介: 卢波: lubo202207@163.com
  • 1. 山西大学光电研究所, 光量子技术与器件全国重点实验室, 太原　030006
  • 2. 山西大学, 极端光学协同创新中心, 太原　030006
  • 3. 山西大学物理电子工程学院, 太原　030006
  • 收稿日期:  2025-05-15

摘要: 平衡光电探测器作为一种检测量子态噪声起伏通用技术的核心关键器件, 其性能参数在近直流的宽频带范围内(mHz—MHz)常受限于电子学噪声与电学增益的相互制约. 针对1 mHz—1 Hz极低频段, 为满足未来量子增强引力波探测计划中对量子压缩光源探测和评估等方面的需求, 本研究基于一种可调节阻抗匹配网络与两级差分放大的设计架构, 使用差分微调电路与可调偏置电压协同补偿方案, 优化光电二极管的非线性响应补偿机制, 在分析频段500 Hz处实现共模抑制比>75 dB. 实验结果表明, 在小于1 Hz的频段内, 探测器的电子学噪声优于3.5 × 10–5 V/Hz1/2, 满足空间引力波探测计划对于激光强度噪声的要求(1 × 10–4 V/Hz1/2); 同时当入射的本底探测光功率为4 mW时, 本平衡光电探测器可实现增益20 dB@1 mHz—1 MHz, 满足高指标压缩光源的高效探测需求, 为下一代空间引力波探测以及极低频段压缩态光场的探测提供了关键器件的解决方案.

English Abstract

    全文HTML

    1.   引　言

    • 自2015年美国激光干涉引力波天文台(LIGO)实现双黑洞并合释放引力波信号GW150914的直接探测以来, 基于激光干涉原理的精密测量技术已成为探索时空涟漪与极端天体物理事件的核心手段[1–3]. 随着环境噪声和技术噪声[4,5]的不断抑制, 限制干涉仪灵敏度提升的瓶颈已从经典技术噪声转向光场的量子涨落—即标准量子极限. 通过将压缩态光场注入干涉仪暗端口的方法[6,7], 可以实现突破标准量子极限的探测灵敏度[8–10]. 然而, 地基引力波探测器受限于地表机械振动、环境以及干涉臂长等因素[11–14]限制, 使得更低频段引力波信号的探测灵敏度显著受限. 相较而言, 空间引力波天文台通过构建百万公里级激光干涉链路[15–18], 可将引力波探测频段拓展至0.1 mHz—1 Hz[19], 对该频段丰富的引力波事件的探索研究有望揭开更多的宇宙奥秘[20]. 因此, 对应频段的量子噪声测量与评估成为引力波等微弱信号探测的关键技术挑战.

      随着量子压缩态光场制备和探测技术的不断研究发展, 可探测的压缩频谱已经拓展至赫兹甚至亚赫兹量级. 2012年Stefszky等[21]分析研究了低频段压缩光源的限制因素, 其噪声主要来源于光场波束抖动、电子器件热噪声[22]、本底探测光噪声耦合[23]及寄生干扰[24,25]等, 最终在10 Hz处测得压缩度达10 dB; 在2019年Wu等[26]利用铷原子系综为介质的四波混频过程并测量了低于10 Hz处的强度差压缩态光场; 2022年, Meylahn等[27]对比分析了1550 nm波段不同腔型结构光学参量腔在制备低频段压缩态光场过程中的优势, 并实现了分析频率0.5 Hz处压缩态光场的噪声探测. 2024年, 本课题组[28]利用多重噪声抑制技术, 首次将量子压缩频段拓展至毫赫兹量级, 其中低噪声高增益的平衡光电探测技术是实现压缩频段拓展的重要环节之一.

      在低频段压缩态光场实际测量中, 平衡光电探测器的电子学本底噪声与增益的相互制约是测量量子噪声需要解决的首要难题. 为了实现对该频段量子噪声的高效表征, 要求平衡光电探测器具备超高的稳定性与噪声抑制能力, 且探测器电子学噪声需达到空间引力波探测需求(1 × 10–4 V/Hz1/2). 通常, 平衡光电探测器的电子学噪声(如热噪声、1/f噪声)与增益漂移会掩盖散粒噪声的真实特征. 例如, 传统平衡探测器在亚音频段的共模抑制比(CMRR)通常因电路阻抗失配而急剧下降, 导致本应相消的经典技术噪声与量子噪声发生耦合, 最终影响压缩态光场的测量结果[29]. 2022年, 王炜杰等[30]研制了极低频段低噪声平衡光电探测器, 其电子学噪声谱密度在空间引力波频段在3.6 × 10–5 V/Hz1/2以下. 目前尚未有相应频段的商用平衡光电探测器能够满足需求, 因此开发一种针对低频段优化的高灵敏度高共模抑制比的平衡光电探测器, 不仅可以从实验上验证低频压缩光场的量子特性, 又能为未来空间引力波探测、量子精密测量、量子通信等方面[31–33]提供关键器件支撑.

      针对上述技术难题, 本研究主要阐述平衡光电探测器的设计架构及方法, 并基于理论建模, 通过使用跨阻运算放大器(TIA)结构的噪声分析模型, 优化光电转换路径、阻抗匹配和引入相应的补偿模块, 实现对电子学噪声的优化, 同时提高对共模信号的抑制能力. 本研究分析了两个光电二极管之间的不等效电容与电阻对CMRR的影响, 为解决因元件参数不一致导致的两路输出信号相位失真问题, 通过使用差分微调电路(DFTC)与可调偏置电压(ABV)协同补偿方案, 在光电流自减式的探测器的架构中, 解决了两个光电二极管间的电容/电阻匹配问题, 成功地消除因等效参数偏差引发的信号相位差. 进一步通过在运算放大器跨阻运放端口引入可调电容, 并基于LTspice软件仿真电路模拟, 分析该电容对频域响应特性的影响, 通过调整容值大小来优化整体电路, 在不增加补偿环路稳定时间的情况下可以提高系统的稳定性. 通过上述低噪声高增益的电路设计, 最终实现了在1 mHz—1 Hz频段电子学噪声谱密度在3.5 × 10–5 V/Hz1/2以下; 同时当入射的本底探测光功率为4 mW时, 本平衡光电探测器可实现增益20 dB@1 mHz—1 MHz. 实验验证了补偿策略的有效性, 以及电路的长时工作稳定性.

    2.   平衡光电探测器的设计原理

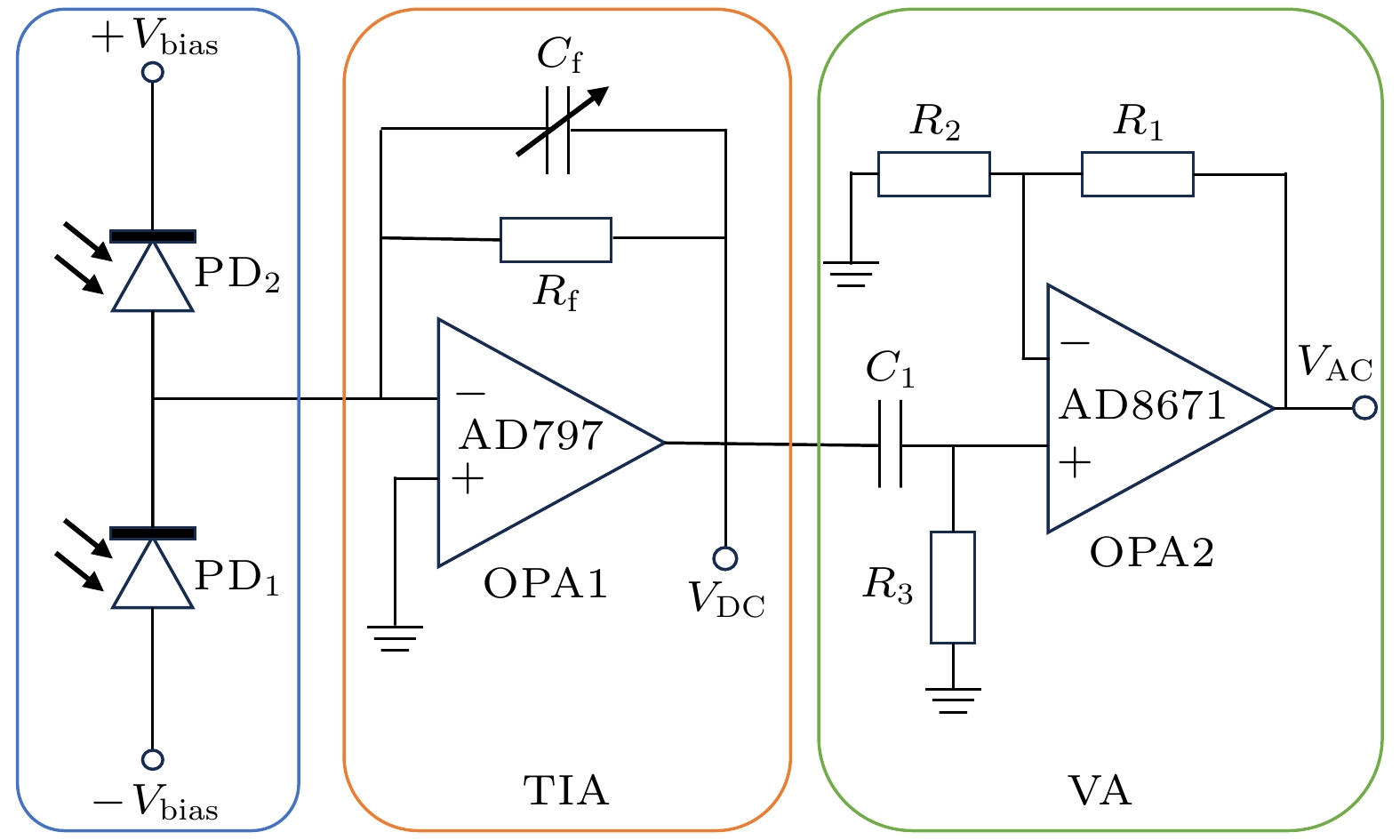
    • 平衡光电探测器的主要结构如图1所示, 其核心由三个模块构成: 第一部分是使用两个光电二极管采用串联构成的差分检测单元, 用来实现两路光强信号向光电流的转换及差值输出; 第二部分使用跨阻放大器(TIA), 将电流信号转化为电压信号; 第三部分使用同相电压放大器(VA)进行对信号的二次增益放大. 该平衡探测器的性能受多种因素的影响, 其中包括噪声水平、增益及光电二极管不匹配等. 本研究通过构建TIA噪声分析模型、优化二级放大电路, 以及使用差分微调电路(DFTC)并结合可调偏置电压(ABV)的方案, 提高对共模信号的抑制能力同时也实现了对微弱光信号的探测.

      • 2.1.   TIA噪声分析

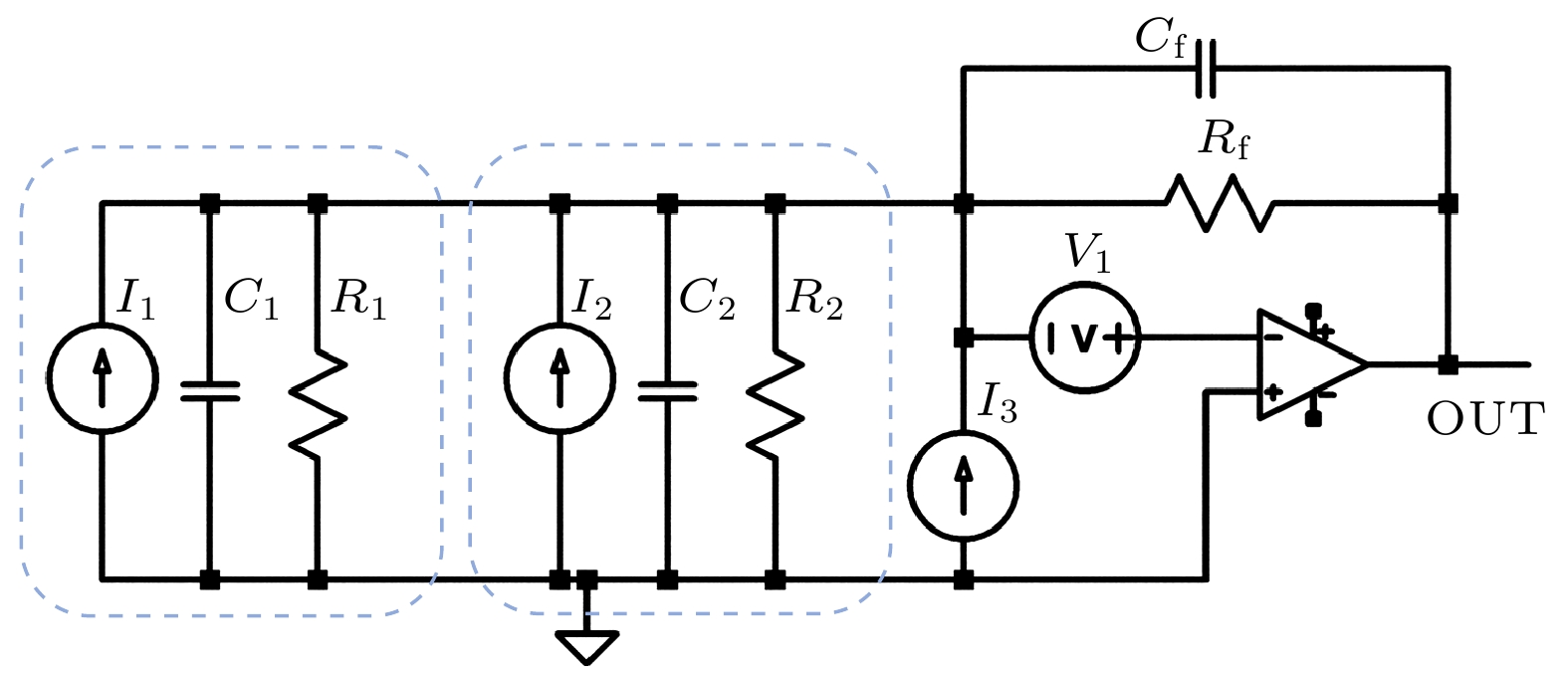
    • TIA作为电路的核心模块, 其参数配置将直接影响探测器的整体性能. 图2所示是光电二极管与跨阻放大器的等效电路模型, 其中关键元件包括: 等效电压源$ {V_1} $、等效电流源$ {I_3} $、非线性结电容$ {C_{1/2}} $及反馈电阻${R_{\text{f}}}$等. 其中两个虚线方框为两个光电二极管的等效模型[34], 可以等效为一个电流源${I_{1/2}}$, 一个结电容$ {C_{1/2}} $和一个结电阻${R_{1/2}}$. 值得注意的是, 给光电二极管施加不同的反向偏压, 会对其结电容有微小的改变, 该效应将在第2.2节详细分析. 结电阻${R_{1/2}}$大小通常高于MΩ量级, 因此对于和其串联的电阻在等效输入阻抗中可忽略不计. 其TIA等效输入电压噪声密度可以表述为[35]

      其中${e_{{\text{noi}}}}$是电流噪声的等效电压噪声密度, ${e_{{\mathrm{nor}}}}$代表运算放大器反馈电阻热噪声的等效电压噪声密度, $ {e_{{\text{noe}}}} $是运算放大器自身的电压噪声密度.

      (1)式第一项${e_{{\text{noi}}}}$为探测器电流噪声的等效电压噪声密度, 主要由光电二极管与跨阻放大器(${i_{{\text{opa}}}}$)的电流噪声分量共同决定, 其数学表达式如下:

      其中${i_{{\text{diode}}}}$为光电二极管电流噪声密度, ${i_{{\text{opa}}}}$为跨阻放大器的输入电流噪声密度. ${i_{{\text{diode}}}}$由三部分构成: 结电阻所产生热(约翰逊)噪声的等效电流密度${i_{\text{J}}}$、暗电流噪声密度${i_{\text{D}}}$以及光电流的散粒噪声密度${i_{\text{L}}}$, 其表达式如下:

      其中${k_{\text{B}}}$为玻尔兹曼常数; T为热力学温度; R为二极管结电阻大小; q为基本电荷; ${i_{\text{d}}}$为光电二极管的暗电流大小, 其与温度呈现正相关关系; ${i_{\text{l}}}$为光照射到光电二极管时所产生的电流, 其总的二极管电流噪声可以表示为${i_{{\text{diode}}}} = \sqrt {i_{\text{J}}^{2} + i_{\text{D}}^{2} + i_{\text{L}}^{2}} $, 电流将通过反馈电阻${R_{\text{f}}}$在输出端转换为电压噪声, 其电流噪声的等效电压噪声密度可表示为

      实验中我们采用了低温度漂移的InGaAs光电二极管(Fermionics FD 300W), 结合低噪声跨阻放大器AD797构建运放电路. 在T = 25 ℃时, FD 300W的暗电流仅为1 nA; AD797运放芯片在1 kHz处输入电流噪声密度为2 pA/Hz1/2. 选取低暗电流噪声的光电二极管和低输入电流噪声的运算放大器可有效降低由于电流噪声带来的影响.

      (1)式中第二项${e_{{\text{nor}}}}$为反馈电阻${R_{\text{f}}}$热噪声导致的TIA等效输入电压噪声密度, 其可表述为

      (7)式表明, 热噪声与电阻值呈正相关. 在实际电路中, 为了抑制热噪声的影响, 我们采用温漂系数为0.2 ppm/℃(1 ppm = 10–6), ${R_{\text{f}}}$= 10 kΩ的金属箔电阻. 在T = 25 ℃时, 计算得到反馈电阻的电压等效噪声密度为12.8 nV/Hz1/2.

      (1)式中第三项${e_{{\text{noe}}}}$是由于运算放大器输入电压噪声导致的TIA等效电压噪声密度, 其表示为[36]

      其中

      这里${e_{\text{n}}}$为运放的输入电压噪声密度, ${f_{{ - 3\text{ dB}}}}$为TIA电路的–3 dB带宽, ${C_{\text{i}}}$为输入电容, ${C_{\text{f}}}$为反馈电容, G为增益带宽乘积其性能由芯片参数决定.

      综合(1)式—(9)式可知, 跨阻放大器(TIA)总的等效电压噪声密度表达式为

      由上述理论公式可知, TIA噪声由输入电流、电压以及电阻热噪声构成, 其主要与反馈电阻及运算放大器选择有关. 为了平衡增益与热噪声的抑制, 选择使用低温度漂移${R_{\text{f}}}$为10 kΩ的金属箔电阻; 同时采用低温度漂移和低输入噪声运算放大器, 使用AD797芯片[37], 其失调电压漂移为0.2 μV/℃, 在0.1—10 Hz处的电压输入噪声为${v_{{\text{p-p}}}}$= 50 nV; 对于同相放大电压放大器的选择, 选择使用AD8671芯片[38], 其失调电压漂移为0.3 μV/℃, 在0.1—10 Hz频段的电压输入噪声为${v_{{\text{p-p}}}}$= 77 nV. 选择在低频处具有低输入电压噪声芯片可有效地降低在低频处的输入噪声, 且低温漂特性可有效抑制温度环境噪声耦合, 最大程度的提高抗温度干扰能力.

      • 2.2.   共模抑制比模型

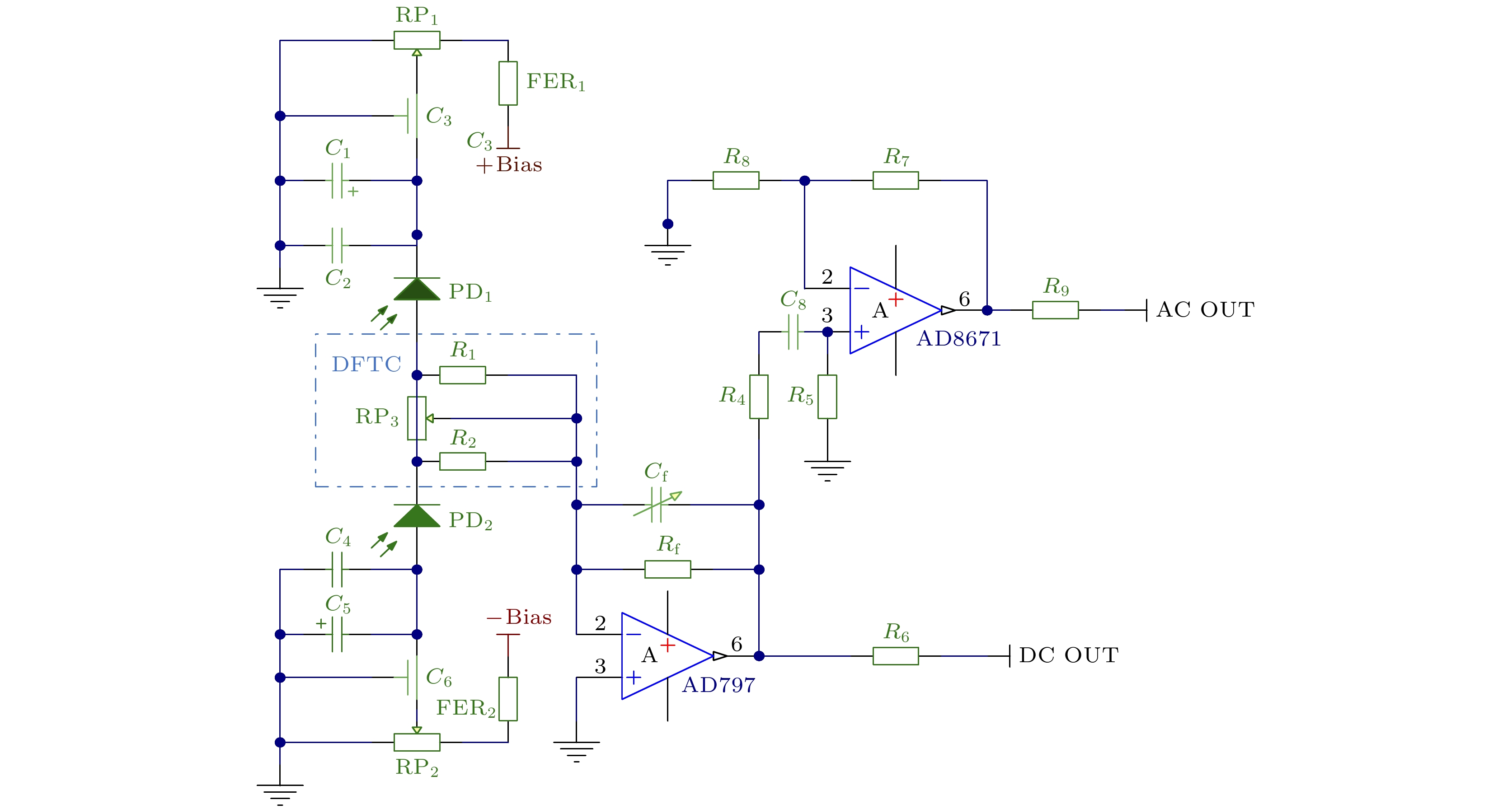
    • 现有平衡光电探测器主要采用两种电子设计架构: 可变增益设计与光电流自减设计[21]. 在可变增益设计中, 光电流经跨阻转换后通过独立放大模块进行信号处理, 采用差分减法器实现双路信号比对. 该设计架构核心优势在于可以进行增益范围的动态调节, 有效地补偿光功率波动及探测器响应非线性差异. 但是由于放大器增益环节的引入, 此结构会在低频处引入较大的暗噪声, 不利于低频段的实验测量. 光电流自减设计方案则在运算放大器前引入光学自减模块, 即在光电转换阶段直接实现光电流差值运算, 规避了电子增益调节环节. 然而, 该设计架构受限于光电二极管与电子元件的匹配精度, 导致对共模信号的抑制能力减弱. 为了解决每个光电二极管及每个电子元器件的微小差异, 在此基础上提出使用DFTC与AVB模块, 来补偿不同元器件及两个光电二极管的差异, 优化元件匹配精度, 进一步提高对共模信号的抑制能力. 光电流自减方案中, 平衡探测器的共模抑制比依赖于两个光电二极管之间的光电流相位, 而输出光电流信号的相位主要由等效电容来决定, 串联电阻对其影响很小, 因此可以通过改变其等效电容来改变光电流之间的相位, 来弥补不同光电二极管之间的差异, 从而提高共模抑制比.

      调节光电二极管反向偏置电压大小来补偿结电容差异[39]:

      其中${\varepsilon _0}$为真空介电常数, $\varepsilon $为材料的介电常数, A为扩散结面积, d是耗尽层宽度, ρ为材料的阻值, μ是在温度300 K时的载流子迁移率, Vin为光电二极管的内置电压, V为偏置电压. 根据(11)式可知, 为了平衡等效结电容的容值差异, 可以采用偏置电压调节的方法, 通过向光电二极管两端施加不同的偏置电压改变其耗尽层的宽度, 从而实现结电容的相互匹配. 其中偏置电压支持±3 V至±12 V连续可调, 且输出稳定在mV量级. 这种方案可以有效补偿不同二极管结电容的差异, 提高光电二极管元件的匹配精度.

      如图3所示, 为同步解决光电二极管的结电容失配与串联电阻差异导致共模噪声的问题, 可通过在两个光电二极管之间构建差分微调电路. 首先通过标称阻值相等的电阻元件R1, R2使运算放大器输入端上下支路实现初级阻抗匹配; 其次再通过调节高精度微调电位器P1来实现阻抗的动态修正, 从而确保放大器输入端上下支路串联电阻严格相等. 实验表明, 通过使用差分微调电路与偏置补偿技术, 能够有效提高对共模信号的抑制能力.

      除了增加补偿电路之外, 电路稳定性也值得关注. 为避免TIA电路的自激振荡和保持电路的稳定性, 通过使用反馈电容${C_{\text{f}}}$来优化放大器频率响应特性, 其容值大小由以下表达式确定[36]:

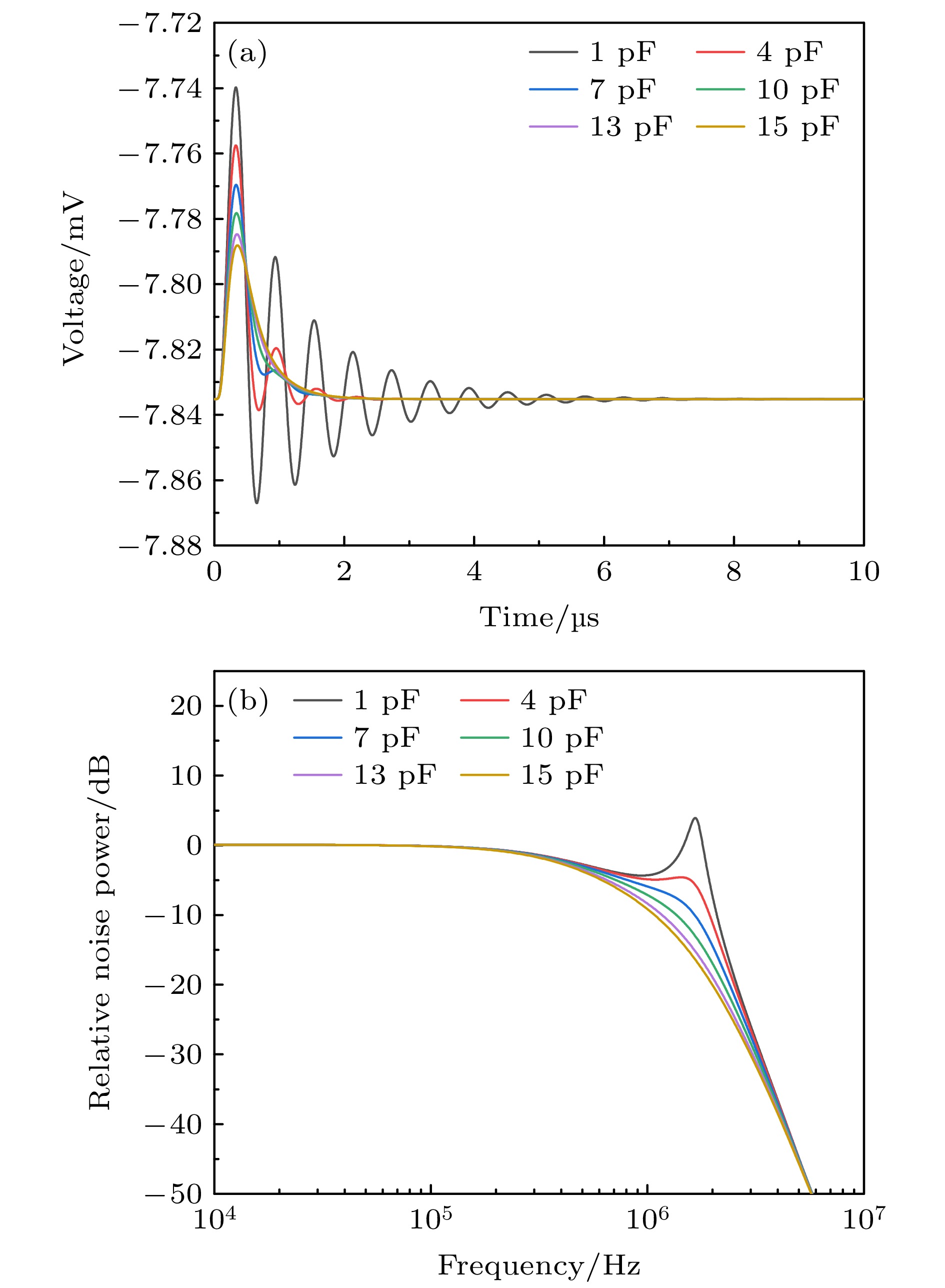
      其中${C_{\text{i}}}$为输入的总电容值, 其中包括二极管结电容、PCB板布线产生的寄生电容、运算放大器的输入电容. 由于改变偏置电压可引起二极管结电容的改变, 所以使用可调电容${C_{\text{f}}}$来匹配输入电容${C_{\text{i}}}$的变化, 从而确保电路的频率响应特性.

      在低频压缩态光场探测实验中, 系统首先需要在高频段(1 MHz量级)实现相位及压缩角的精确锁定, 确保系统锁定至最佳状态后再通过切换频率至低频段进行量子噪声测量. 上述探测方案对平衡光电探测器提出了双重性能要求, 不仅要求在低频段需要良好的噪声性能, 同样需要在MHz频段具有良好的频率响应特性. 针对平衡光电探测器在MHz频段的频率响应研究, 我们使用LTspice仿真软件模拟了不同反馈电容${C_{\text{f}}}$对电路时域和频域的影响, 实验结果如图4所示. 我们使用100 ns的脉冲宽度的光信号, 设置光电流的上升时间和下降时间为50 ns, 即${T_{\text{R}}}$与${T_{\text{F}}}$设定为50 ns; ${I_1}$设置为10 nA, 来模拟光电二极管的暗电流, 光电流${I_2}$设置为5 μA, 扫描时间设置为10 μs. AC端输出结果时域图如图4(a)所示, 反馈电容${C_{\text{f}}}$取值分别为1, 4, 7, 10, 13和15 pF. 由图4(a)分析可知, 随着补偿电容${C_{\text{f}}}$容值从1 pF增加到15 pF, 输出脉冲的幅度呈现显著衰减趋势. 频域如图4(b)所示, 当反馈电容为1 pF时, 在较高频段(约1.8 MHz处)放大器产生响应尖峰, 导致响应曲线的不平坦. 随着补偿电容增大, 高频增益尖峰逐渐平缓, 说明可通过补偿电容调节来有效抑制高频极点的不稳定性, 综合考虑信号跨阻增益与频率响应曲线, 最终选择使用10 pF的可调电容进行后续实验.

      综上所述, 该平衡探测器使用光电流自减的设计结构, 同时采用可调偏置电压模块与差分微调电路, 该设计结构能减小电子元器件之间性能的微小差异从而提升共模信号的抑制能力. 该探测器供电模块使用±12 V锂电池为基准电压芯片供电, 能有效降低电源噪声对其探测系统的干扰. 信号处理部分采用两级放大结构: 前级基于AD797芯片构成跨阻运放电路, 该器件具备较低输入噪声和低失调电压漂移, 配合10 kΩ低温漂精密电阻与可调补偿电容构成的反馈网络, 并通过LTspice电路仿真软件分析了不同补偿电容容值对电路频率响应特性的影响, 成功地消除高频响应尖峰; 后级电路采用AD8671运算放大器构建同相比例放大器, 进一步实现微小信号的二级放大, 该芯片具有0.3 V/℃的低漂移特性和在低频处较低的输入噪声, 既能保证系统能够在长时间保持稳定工作, 又能实现对微小信号的二级放大. 电子学噪声基底是决定探测器测量精度的核心参数, 通过TIA理论建模, 分析其跨阻放大器中的噪声来源, 通过选择使用低温漂、高精度的电阻和电容等精密元件以及电路结构的优化, 使系统整体电子学噪声降低至10–5量级, 最终实现了噪声性能优化及长期稳定性的提升.

    3.   平衡光电探测器性能测试及表征

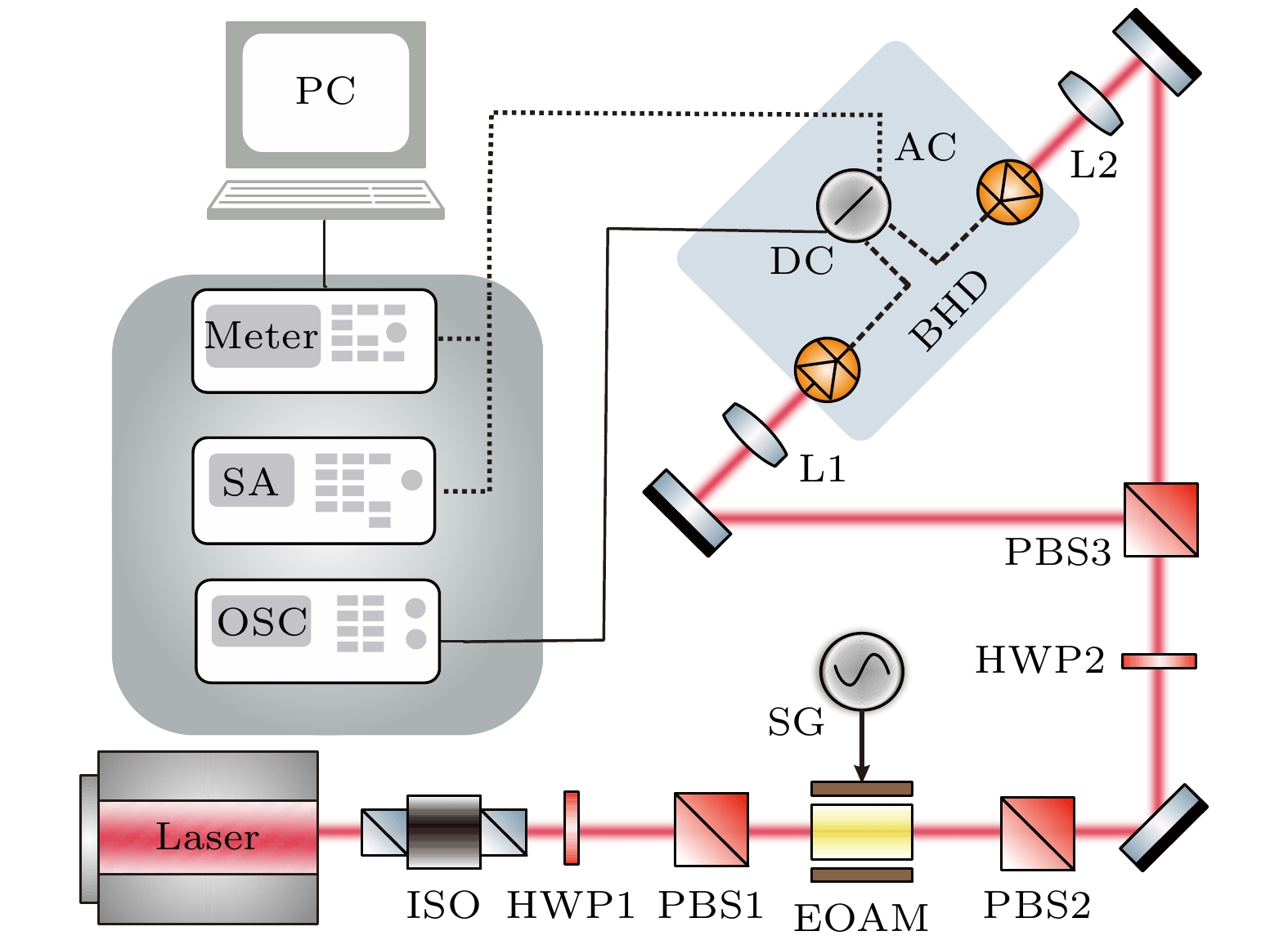
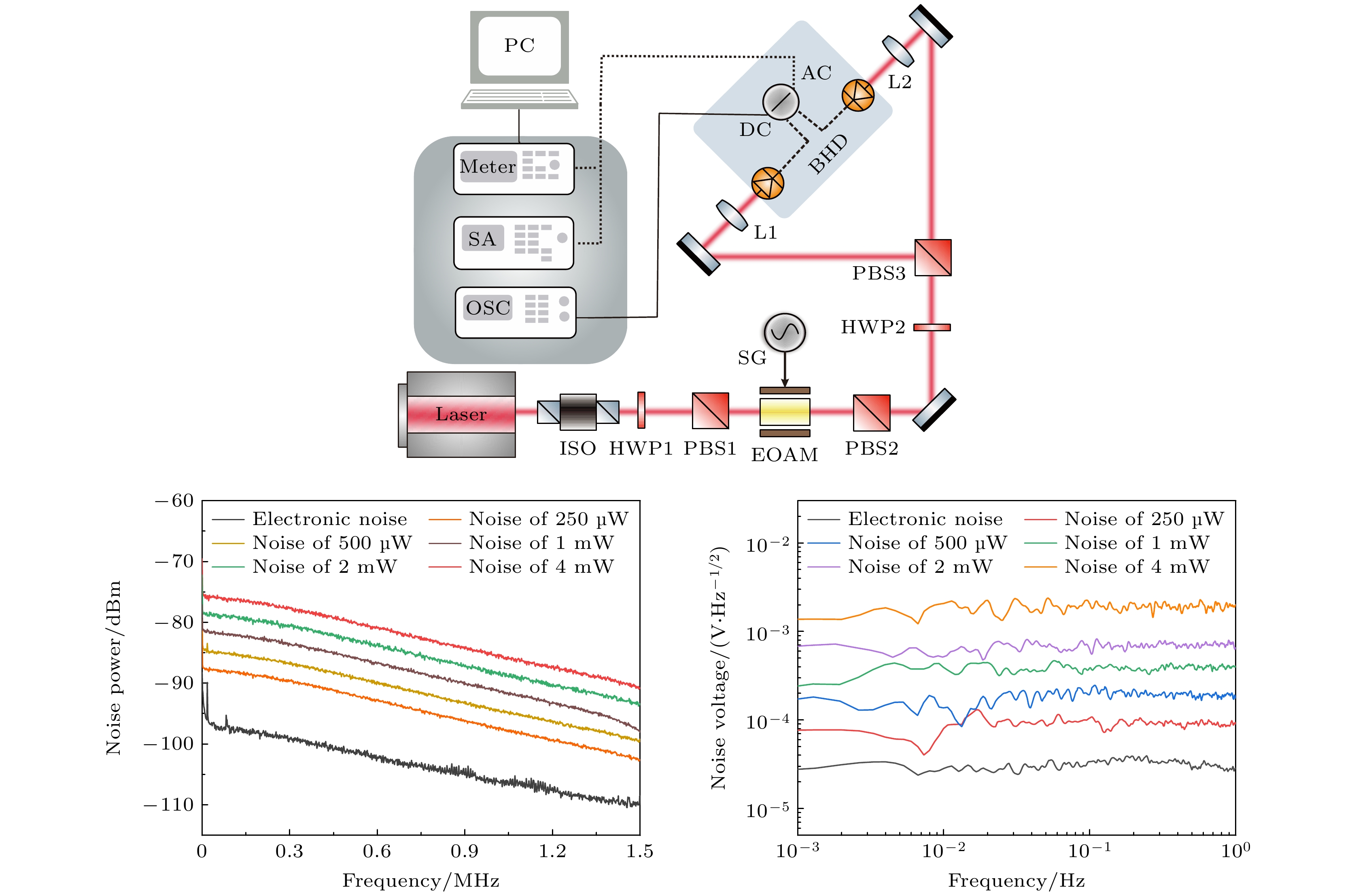
    • 平衡光电探测器的性能测试装置如图5所示, 激光器采用国产Nd:YVO4单频激光器(1064 nm波长, 2 W最大功率), 其输出光束经过隔离器后再经过由HWP1与PBS1组成的偏振调节系统实现功率调节, 经PBS1后的输出光束通过电光幅度调制器(EOAM)和PBS2, 其中EOAM由信号发生器SG驱动, 实现光强振幅分量的精确调制. 在光功率平衡调节方面, 由HWP2与PBS3构成的可调分束系统实现了双路的光功率平衡, 其光束经过透镜后入射到平衡探测器的两个PD中. 该PD采用两个同型号的InGaAs (FD 300W)光电二极管作为光电转化模块, 确保良好的一致性. 平衡光电探测器采用交直流双路输出结构, 直流分量(DC)接入数字示波器(OSC)实时监测双PD光功率平衡度, 交流信号(AC)接入频谱分析仪(RS: FSW-8)进行噪声功率谱测量. 值得注意的是, 对于更低频段的测量, 目前低频商用谱仪无法对其进行精准评估测量, 因此需要对更低频段的噪声进行评估与表征. 在实验中, 使用高精度数字万用表(Keithley: 3706A)对电压进行时域采集, 再结合LPSD算法[40]对时域采集信号进行处理并获得噪声谱分析结果.

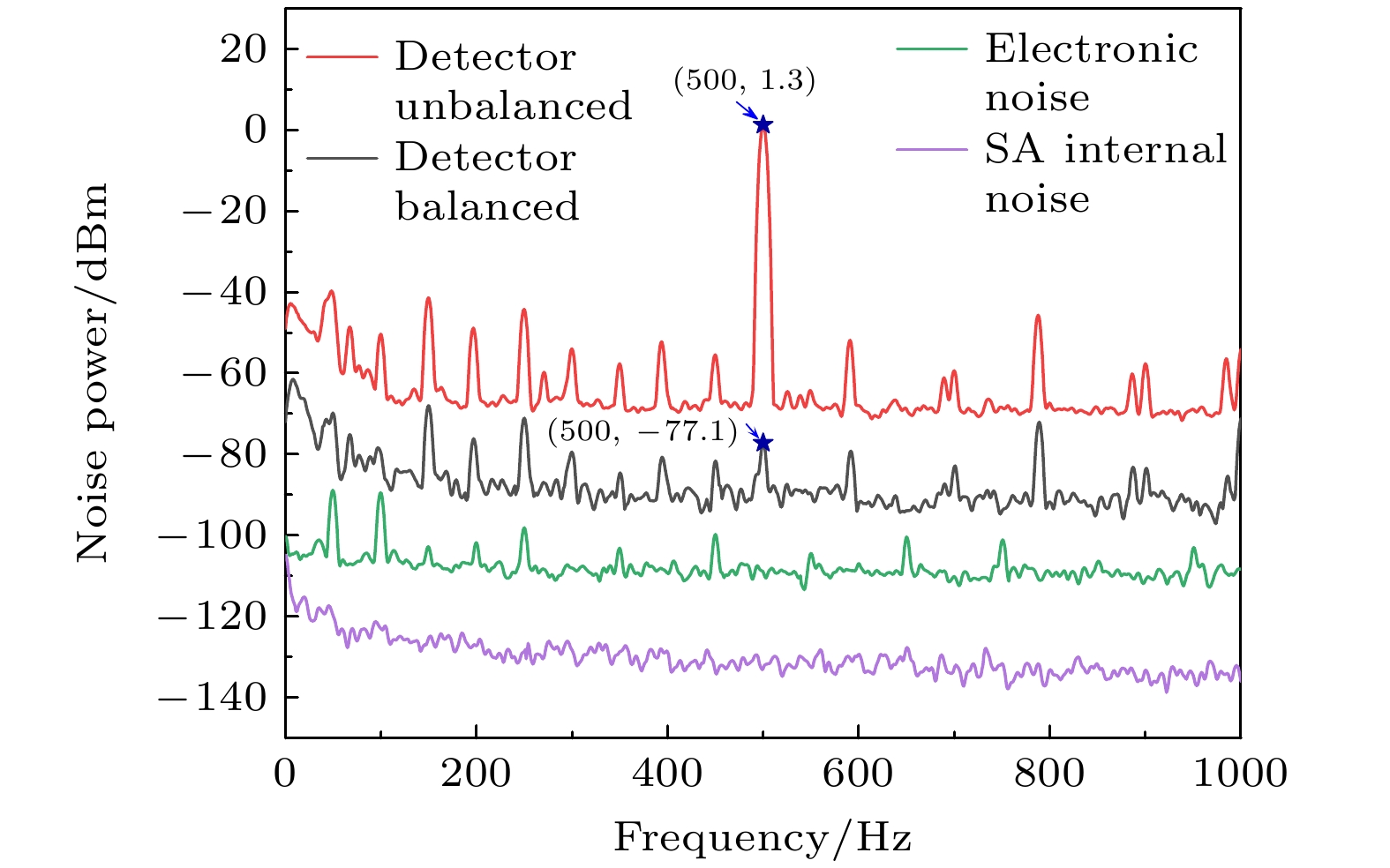
      图6展示的是由频谱分析仪(RS:FSW-8)测试平衡探测器共模抑制比的噪声功率谱分布曲线, 红色曲线对应为不平衡工作状态(单路遮光处理, 另一路由500 μW光功率驱动), 共模噪声谱线(红色曲线)在500 Hz处出现明显谱峰, 对应于EOAM的调制频率, 此时输入总功率稳定在1 mW. 在差模工作状态下(双路均入射500 μW光功率), 对应噪声谱线由黑色曲线所示. 绿色曲线和紫色曲线分别为对应为本底电子学噪声(双路遮光处理)和频谱分析仪内部噪声. 平衡探测器共模抑制比为单路遮挡条件下探测器响应功率与双路均入射光状态下的功率比值, 如图6所示, 在500 Hz频点处系统CMRR达到78 dB, 该特性可明显减小系统误差, 能有效地抑制光场技术噪声, 从而提高压缩度测量的准确性[29].

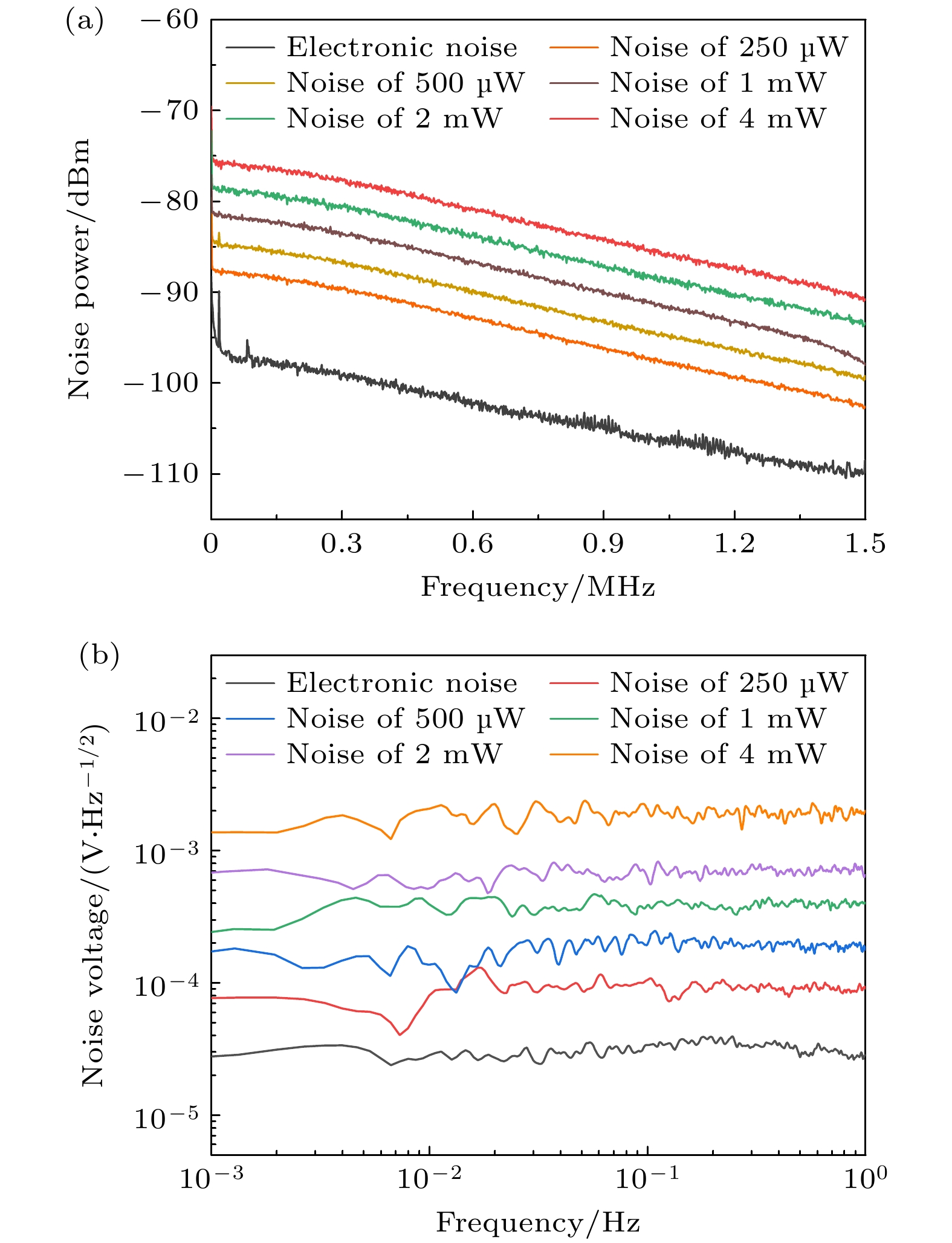
      针对空间引力波探测等量子精密测量需求, 不同探测频段应采用不同的仪器进行频率响应与噪声特性表征. 首先在大于1 kHz频段 (1 kHz—1.5 MHz), 利用RS FSW-8频谱分析仪实测平衡探测器的噪声分布曲线, 其中频谱分析仪分辨率带宽(RBW)设置为100 Hz, 视频分辨率带宽(VBW)设置为10 Hz. 首先在遮光处理下测量电子学噪声, 初始调节平衡探测器入射本底光功率为250 μW, 随后成倍地增加入射的本底光功率, 得到如图7(a)所示的曲线. 当4 mW光功率入射时, 其增益达到20 dB以上, 满足压缩态光场的探测需求. 对于极低频段(1 mHz—1 Hz)平衡光电探测器的性能评估[40], 我们使用了高精度数字万用表(Keithley: 3706A)对该探测器的AC端时域信号进行采集, 采样时长为1200 s, 采样率设置为2 S/s, 并进一步通过LPSD算法转化为相对应的频域信号. 如图7(b)所示, 在1 mHz—1 Hz频段内, 我们设计的平衡光电探测器电子学噪声在3.5 × 10–5 V/Hz1/2以下, 优于空间引力波探测计划中对于激光强度噪声要 求(1 × 10–4 V/Hz1/2). 与当前商用的平衡探测器 (New Focus, 2117)相比[30], 我们设计的平衡光电探测器在1—100 mHz频段具有更低的电子学噪声特性.

      基于上述差分放大电路的设计架构, 目前已经实际应用到压缩态光场探测系统中. 针对极低频段(1 mHz—10 Hz)量子噪声测量的技术挑战, 通过系统性地分析压缩态光场制备过程中的噪声传递机制, 结合本文中低噪声高增益的平衡光电探测器, 最终成功地实现了毫赫兹频段8.0 dB真空压缩态光场的直接探测[28], 为极低频段量子噪声的高效精确评估奠定了基础.

    4.   结　论

    • 本研究基于光电流自减原理的差分放大电路架构, 通过等效电路建模与噪声频谱分析, 分析了平衡光电探测器电子学噪声的主要构成及来源. 在电子元器件选择方面, 选用低噪声、低失调电压输入运放以及低温度漂移金属箔电阻, 并构建二级运放电路, 进一步提高增益. 为提高电路对共模信号的抑制能力, 设计使用差分微调电路和采用可调偏置电压模块分别对等效输入电容和电阻失配进行补偿, 实测在500 Hz频点处共模抑制比达78 dB. 针对放大器频率响应优化, 设计可调反馈电容网络, 通过使用LTspice电路仿真软件, 补偿输入电容变化带来的影响, 来维持系统稳定性. 在数据采集处理方面, 针对1 mHz—1 Hz频段, 使用高精度数字万用表(Keithley: 3706A), 结合基于LabVIEW程序编写的LPSD算法程序实现了对1 mHz—1 Hz的噪声强度的表征, 测量得到电子学噪声达3.5 × 10–5 V/Hz1/2以下, 并且低于空间引力波探测计划对于激光强度噪声的要求(1 × 10–4 V/Hz1/2); 在大于1 kHz频段, 使用商用频谱分析仪(RS:FSW-8)测量评估了该探测器的增益、共模抑制比、线性度等性能, 满足宽频带探测需求, 能够为下一代空间引力波探测以及更低频段压缩态光场的探测提供关键技术方案.

    参考文献 (40)

目录

/

返回文章
返回