MD方法以牛顿第二运动定律为主要控制方程，首先根据所研究的具体问题以及所涉及材料的晶体结构、晶格常数等信息，得到原子初始坐标、初始速度等，并确定计算模拟体系的加载方式等初始条件和边界条件，再结合计算模拟体系的原子间相互作用势函数，求解单个原子的运动方程，得到每个原子的坐标、速度等物理量的时空演化规律。基于这些计算模拟数据，采用统计力学分析方法，获得关于体系演化的温度、压力、密度、扩散系数、径向分布函数等大量有用信息。另外，MD模拟总是在一定的系综条件下进行，常见的系综有NVE系综（原子总数、体积和总能量不变）、NPT系综（原子总数、压强和温度不变）、NVT系综（原子总数、体积和温度不变）等。针对不同的系综，常常需要对计算模拟体系的温度和压力进行控制，常用的控温方法有直接速度标定法、Berendesen控温热浴法、Gaussian控温法、Nose-Hoover控温方法等^[2]。其中，Nose-Hoover控温法的基本思想是引入一个反映真实系统与外部热浴相互作用的广义变量，将真实系统与热浴作为统一的扩展系统来考虑。该方法可以把任何数量的原子与热浴耦合，消除局域的相关运动，模拟系统温度涨落现象。MD计算模拟中压力的控制主要通过改变体积来实现，常见的压力控制方法有直接体积标定法、Berendesen控压法、Andersen控压法等^[2]。Andersen控压法假定系统与外部活塞耦合，当内外压强产生较大差异时，通过活塞运动使系统收缩或膨胀，从而达到内外压强一致的目的，此后的各种控压方法都是基于该思想发展起来的。关于温度和压力控制方法的更多细节可以在文献[2]中找到。积分算法是MD计算模拟的重要步骤，积分算法的计算效率和准确性直接决定MD计算模拟所需的时间及模拟结果的可靠性。迄今为止，已经发展了Verlet算法、Leap-frog算法、Velocity Verlet算法等，这些算法各有优缺点。在综合考虑计算效率和准确性的基础上，目前MD最常用的是Velocity Verlet算法，它可以在不牺牲精度的情况下，同时给出位置、速度和加速度。

MD计算模拟中，原子间作用力由原子间相互作用势函数计算得到，因此原子间相互作用势对MD计算模拟至关重要。就相互作用势的类型而言，当前MD使用的相互作用势主要包括兰纳-琼斯势（Lennard-Jones，LJ）、嵌入原子势（Embedded-Atom Method，EAM）、改进分析性嵌入原子势（Modified Analytic Embedded-Atom Method，MAEAM）等。LJ相互作用势在计算两个原子之间的相互作用时，不考虑其他原子的影响，属于对势的一种。其势函数模型十分简单，计算量小，主要用于描述简单金属和惰性气体等的相互作用^[3–4]。EAM是Daw和Baskes^[5]于1983年提出来的，其基本思想是将体系中每个原子都看作是嵌在其他所有近邻原子产生的电子云背景中。EAM势函数的表达式如下

式中：r_ij表示原子距离，ρ_i表示电子密度；等号右侧第1项为原子间的相互作用能；第2项为原子嵌到背景电子云中的嵌入能，嵌入能可表示为电荷密度的泛函。EAM势函数在金属模拟中^[6]取得很大成功，但是最初的EAM理论中并没有给出其具体的解析形式，大大限制了EAM势的理论应用。张邦维等^[7]提出了MAEAM，考虑到电子密度对非球对称分布的偏离所带来的影响，在EAM势中添加一个能量修正项进行弥补，同时也避免了在模拟过程中因计算角度而加大计算量的问题。采用MAEAM计算的体系晶格能量为

相比（1）式，（2）式增加了一项M（p_i），代表新加入的能量修正项，其中p_i是电子密度非球对称所引起的能量贡献。由于该势函数是基于EAM势函数的改进，因此也常用于金属材料的MD计算模拟^[8–9]。通常来说原子间相互作用势函数中各项的具体函数形式未知，实际应用中常使用经验或半经验的方法给出带参数的泛函形式，然后再根据材料物性参数等信息进行具体优化求解，最终得到相互作用势的具体函数形式^[10]。确定相互作用势参数的方法主要有3种：（1）通过实验测得的晶格常数、弹性常数、振动谱等材料参数进行拟合，（2）通过蒙特卡罗方法确定，（3）通过基于量子力学得到的各种微观信息确定。势函数的选择没有统一的评判标准，需要结合具体的研究内容进行选择，关键是所选择的势函数能够准确描述所研究的材料性质，同时尽可能地兼顾计算效率。

MD计算模拟的直接输出通常是包含单个原子的坐标、速度、受力等海量数据，这些数据蕴含了整个原子体系的动力学演化过程及规律。如何从这些原始数据中分析提取表征体系演化规律的物理参量和微结构等信息，是MD计算模拟中十分重要的问题。目前，MD计算所采用的重要的数据分析处理方法有中心对称方法、公共近邻分析方法（Common Neighbor Analysis，CNA）、最近邻法、径向函数法、位错提取算法等。

（1）中心对称方法

简立方、面心立方（fcc）和体心立方（bcc）等晶体结构具有中心对称性，即以一个原子为中心，在其相反的两个方向上，等距离存在两个原子，因此该中心原子与其所有近邻原子位置矢量之和为零。中心对称参数的计算公式为^[11]

式中：CSP代表中心对称参数，N表示原子的最近邻原子数，R_m和R_n代表从中心原子到其相反的两个近邻位置的矢量。对于具有中心对称结构的晶体，（3）式计算的CSP为零。如果原子的局域结构为非中心对称结构，CSP非零。一般而言，原子的热运动会导致CSP偏离理想值，但影响不会很大；而计算体系中存在的缺陷将严重破坏原子结构的中心对称性，使CSP为较大的非零值。因此利用CSP的具体数值，可以将完整晶格与晶体缺陷区分开来，在使用过程中需要首先选择合适的阈值区分缺陷原子和完美晶格。高温下，完美晶体中CSP值的分布变得更宽，并且可能开始与晶体缺陷的特征范围重叠。CSP的主要优点是受弹性变形的影响小。

（2）公共近邻分析方法

不同晶体结构，本质上是原子周围拓扑结构不同。公共近邻分析方法^[12]是根据原子共同近邻成键情况判断原子的局域结构，通过计算与特定原子相关的4个参数，区分不同的晶体结构。其中：第1个参数用来表示该对原子能否成键，先设置一个截断距离r_cut用以判断相邻原子间能否成键，若两个原子之间的距离小于截断距离，则能成键，用1表示，否则用2表示，在分析结构过程中一般只考虑成键原子对；第2个参数是所分析的一对原子的公共近邻原子个数；第3个参数表示该原子对公共近邻原子中成键的原子对数；第4个参数是在前3个参数相同的情况下区分该原子对公共近邻原子成键的几何构型，该参数没有特定的要求，只需用一个值代表一种构型即可。对于不同的晶体结构，由于其原子排列不同，导致这4个参数的值不同，例如：对于fcc结构，这4个参数值分别为1、4、2、1；对于正二十面体结构，参数值分别为1、5、5、1。与中心对称分析方法相比，公共近邻方法能更有效地区分不同的晶体结构，但缺点是计算过程比较耗时。

（3）其他方法

除了上述两种处理方法之外，MD中还可以采用最近邻分析法、径向分布函数法、位错提取算法等数据分析方法^[13–14]。最近邻分析法通过计算原子的最近邻原子数区分原子结构，如bcc铁的初始结构中最近邻原子数为8，冲击加载发生相变后其最近邻原子数变为12，因此通过统计最近邻原子数即可得到相变等信息。径向分布函数法是对原子的空间分布进行统计分析，对晶体结构而言，原子分布在特定的位置，反映在径向分布函数上为一系列峰值，通过分析峰位等信息，可以获取关于晶体结构的信息。位错提取算法基于位错定义，通过对弹性位移场的Burgers环路积分识别部分位错与界面位错，该分析方法用连续的线表示计算模拟中产生的位错形态，也可用来分析位错结等位错反应产物。

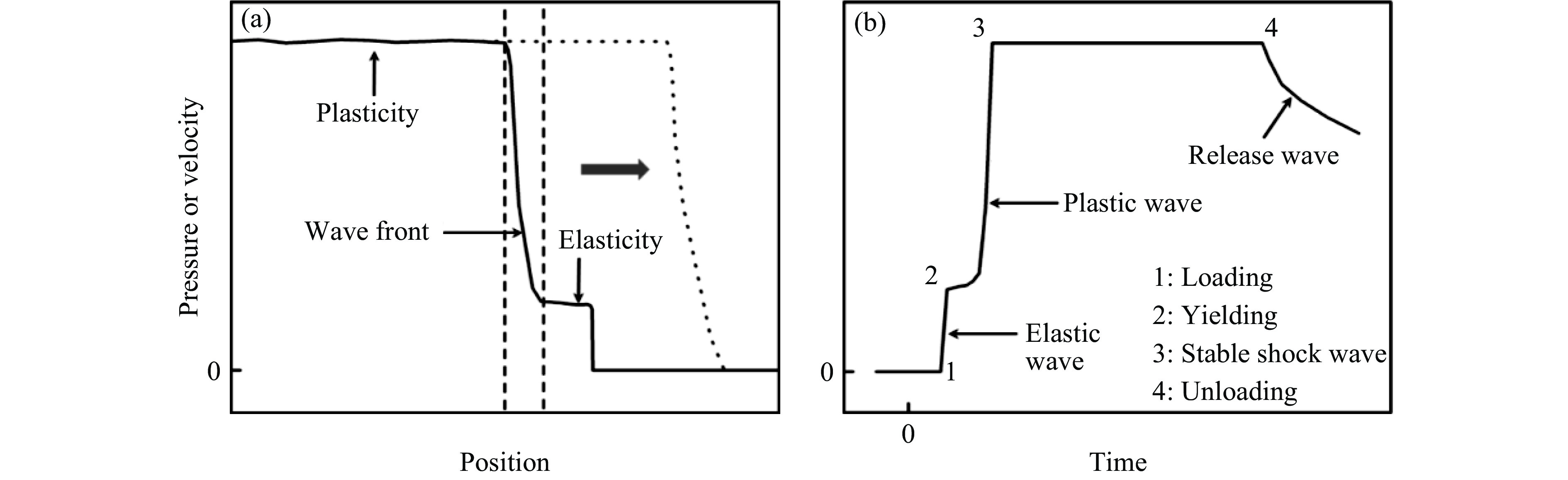
冲击加载下，金属材料首先经历弹性压缩，然后屈服，产生不可逆的塑性变形，最后进入应力、温度和密度均匀稳定的波后状态。图1（a）为典型的弹塑性双波结构示意图，前面是弹性先驱波，后面是塑性波。如果塑性波速高于弹性波速，塑性波将超过弹性波，形成单波结构，如图1（a）中虚线所示。金属材料的冲击塑性一直是冲击波物理和材料科学的研究热点，长期以来，人们进行了大量的相关实验。实验研究中，一般通过测量样品沿加载方向的应力剖面或自由面速度历史剖面（图1（b））反推材料的冲击响应状态，难以直接获得样品中的波传播结构和详细的塑性变形微观过程。得益于MD的高时空分辨率特性，其不仅可以获得精细的波传播结构，还可以对金属材料的冲击塑性变形过程进行原位、实时的观察，因此MD方法在金属材料的冲击塑性变形研究中得到了广泛的应用。

位错的成核与生长是金属在动态加载下的常见塑性变形机制。位错扩展源于滑移面上原子的滑动，滑移面通常为晶体的密排面，如面心立方金属的{111}面。滑移启动与否由滑移面上分解的剪切应力决定，因此完美单晶中的冲击塑性行为具有明显的方向依赖性。Germann等^[15]比较了单晶铜中沿[100]、[111]晶向加载的冲击塑性行为，从微观机制上定性地解释了沿不同晶向冲击塑性的差异。当冲击波沿[100]晶向传播时，仅领先不全位错（Leading Partial Dislocation）被激发，形成快速扩展的不全位错环，经过的区域留下堆垛层错（Stacking Fault）并产生一个高速的塑性波，使得沿[100]晶向无弹性先驱波；而沿[111]晶向冲击时，样品中激发出领先型和滞后型（Trailing Partial Dislocation）两种类型的不全位错，它们相互作用形成全位错环，全位错环通过复杂的交滑移过程扩展，运动速度相对较慢，形成典型的弹塑性双波结构；弹塑性双波结构也存在于沿[110]、[221]晶向的冲击加载中。除波结构的差异外，加载晶向还会对材料的雨贡纽弹性极限产生影响。研究表明，单晶铜在沿[100]、[110]和[111]晶向加载下的雨贡纽弹性极限（$u_{\rm p}^{\rm HEL} $）分别约为0.75、0.75和1.2 km/s^[16]。而且MD计算模拟结果显示，在一定温度范围内初始温度对材料的雨贡纽弹性极限几乎没有影响^[17]。

变形孪晶是另外一种重要的塑性变形机制。孪生是指晶体中的一部分相对另一部分做整体滑动，需要的能量一般比位错扩展高，因此通常在低温、高应变率和滑移系较少的情况下发生^[18–19]。单晶材料的变形孪晶同样具有强烈的晶向依赖性，如单晶钽的气炮实验结果表明，沿[110]晶向加载后样品中的孪晶比例明显较高。Ravelo等^[20]模拟了单晶钽的冲击塑性行为，重现了与实验一致的依赖加载晶向的变形机制。当冲击粒子速度低于1.2 km/s（冲击压力约100 GPa）时，沿[110]方向冲击的塑性变形机制以变形孪晶为主（见图2），但计算模拟中沿[111]晶向加载时，塑性变形并非以孪晶变形为主，该现象与前述实验结果存在差别。当速度进一步增加时，波阵面上虽有孪晶成核，但不会长大，造成样品中的孪晶密度降低。变形孪晶的这种晶向依赖性可能源于母体与孪晶晶格的择优取向。变形孪晶并非独立存在，伴随着孪晶的形成，孪晶区之间将会出现位错成核与增殖，进一步释放残余的剪切应力。

当单晶中存在缺陷时，其冲击塑性行为将发生改变。Holian等^[17]通过改变加载活塞表面平整度的方式模拟材料中的非均匀性，指出预先存在的缺陷会导致材料雨贡纽弹性极限的降低。最近人们通过在体系中引入空位的方式考察了点缺陷对冲击塑性行为的影响^[21–22]。如Luo等^[21]发现：在粒子速度为0.5 km/s的冲击强度下，空位浓度C_v≤0.375%时，样品处于纯弹性压缩状态；而当C_v>0.375%时，样品中开始出现位错成核；随着空位浓度的增加，样品的冲击塑性逐渐增强。计算不同空位浓度下样品的Von-Mises剪切流动强度（假设均发生塑性变形）时发现，当空位浓度从零增加到2%时，Von-Mises剪切流动强度从4.6 GPa降低到3.2 GPa，降低幅度约30%。跟踪样品中的塑性变形过程发现，空位（包括单空位、双空位和三空位）为滑移提供了成核点。另外空位的引入导致样品的自由能和自由体积增加，降低了局部剪切的势垒，有助于滑移扩展，因此当空位存在时，材料的冲击塑性更容易发生。虽然研究的空位浓度远高于常温常压下材料中的空位浓度，但是这些研究给出的材料冲击塑性行为随空位浓度的变化趋势仍具有重要的指导意义。此外，粒子辐照、薄膜生长、快速淬火等也可能在材料中形成较高的空位浓度。

金属材料中通常含有大量的晶界，晶界的存在对金属材料的冲击响应（如冲击波结构、位错运动等）具有显著影响。冲击加载下，晶界为塑性变形提供成核点，促进塑性变形的发生。为了揭示晶界对金属材料冲击塑性行为的影响机理，人们开展了大量金属双晶的冲击响应模拟。双晶模型具有结构简单、便于获取清晰的塑性变形详细过程而不被复杂的晶界变形干扰的优点。

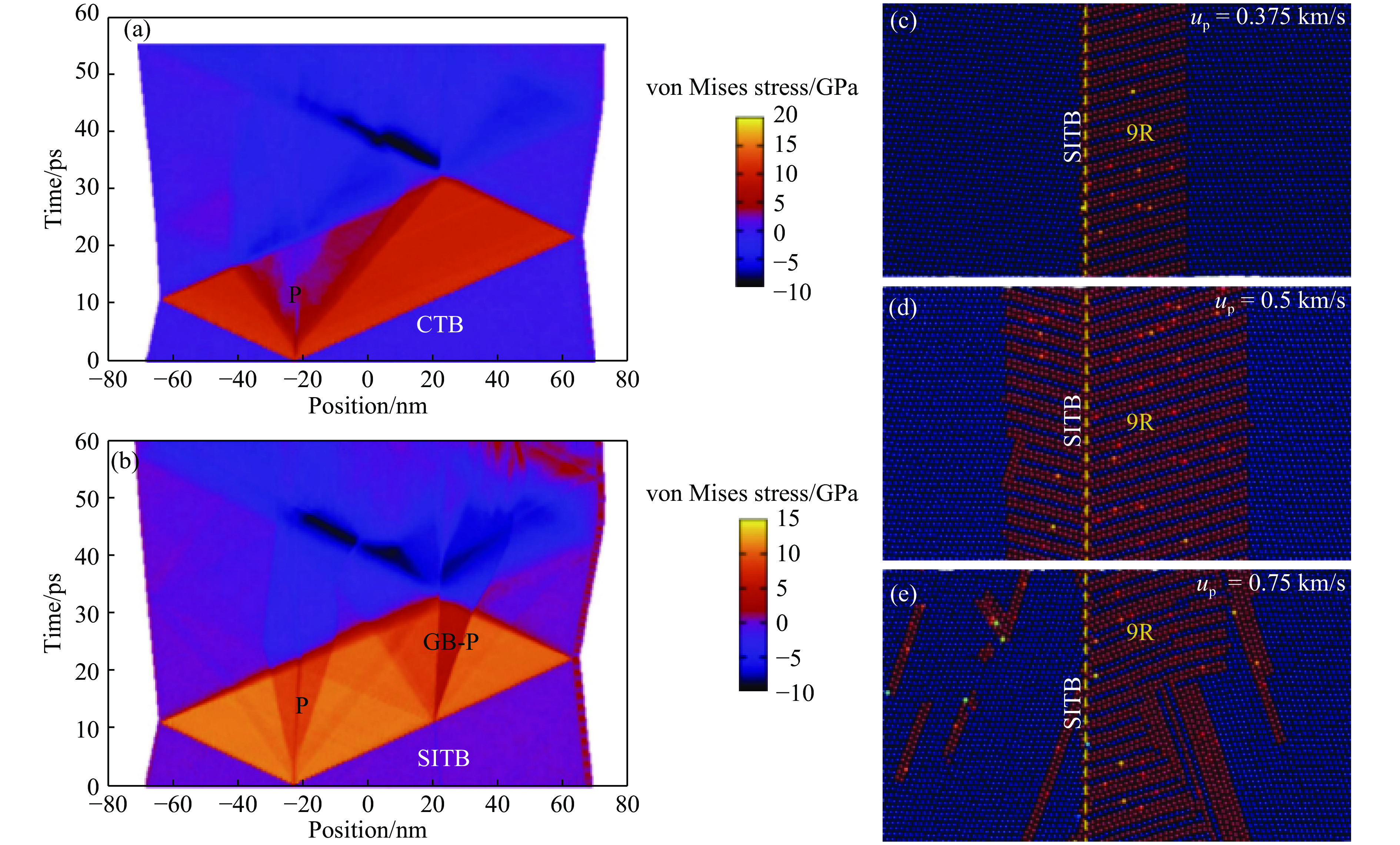
晶界能量是影响双晶塑性变形行为的重要参数。晶界能量越高，结构畸变越严重，塑性变形就越容易发生。Han等^[23]开展了金属铜中$\varSigma $3{111}共格孪晶界（Coherent Twin Boundary, CTB）和$\varSigma $3{112}非共格对称孪晶界（Symmetric Incoherent Twin Boundaries, SITB）的冲击塑性研究（见图3）。在孪晶生长过程中，CTB和SITB经常成对出现，是影响纳米孪晶材料力学性能的主要因素之一。CTB和SITB的晶界能量分别为22.2 mJ/m²和591.9 mJ/m²，位于$\varSigma $3晶界能量谱的低、高端。冲击加载下，CTB结构保持良好，即使塑性波经过，也仅形成少量的晶界台阶；并且冲击波传过CTB前后，其特征也无明显变化，如图3（a）所示。这是由于CTB的结构畸变较小，与单晶差异较小。与之相对，SITB表现出明显的晶界塑性行为。即使是弹性前驱波传过SITB，也可能在SITB中引发塑性变形，从而在晶界前端晶粒中形成反射弹性波，后端晶粒中形成塑性波（见图3）。

SITB晶界可表示为一簇{111}面上的肖克莱不全位错的重复排列。外力作用下，这簇不全位错将发生分裂形成9R结构。冲击加载下，SITB的晶界塑性行为与加载强度相关。弹性前驱波强度较低时（如粒子速度u_p=0.375 km/s），组成SITB的一部分不全位错被激活，在后端晶粒中引发塑性变形；当粒子速度u_p增加到0.5 km/s时，组成SITB的所有不全位错均被激活，晶界塑性向两边晶粒扩展；当u_p进一步增加到0.75 km/s时，加载面传来的塑性波会抑制晶界塑性在前端晶粒传播，使其仅在后端晶粒中扩展。另外，加载面产生的塑性波与晶界塑性相互作用，导致其他滑移面上的滑移系启动。

晶界的塑性行为将导致冲击波强度减弱。冲击加载下，长度为1.5 μm、包含53个SITB的样品的x-t-p图出现了粗糙的三波结构：一个狭窄的弹性波E和两个塑性P₁和P₂，其中P₁源于SITB的晶界塑性行为。随着传播距离的增加，弹性波的强度逐渐减弱，从初始的10.7 GPa减小到2.18 GPa，衰减幅度约为80%。弹性波强度的衰减曲线分为两个阶段，其中第2阶段的衰减速率降低。该现象是由于SITB的晶界塑性从晶界两边扩展转变为单边扩展，因而导致冲击波强度的衰减效率降低。SITB同样会造成塑性波强度衰减，但需要更长的衰减距离，超过MD的模拟能力。晶界对冲击波的衰减特性可应用于抗冲击超材料的设计。当晶界是非对称晶界时，金属双晶的冲击响应将出现左右加载方向依赖性。在粒子速度u_p=0.5 km/s的加载强度下，含(111)//(112)$\left\langle\right.\!110\!\left. \right\rangle$非对称晶界的铜双晶表现出明显的左右加载方向依赖性：两种加载方式均能激发出晶界塑性，但左向加载的晶界塑性仅向另外一个晶粒扩展，而右向加载的晶界塑性可同时在两个晶粒内扩展^[24]。

真实的金属材料常以多晶形式存在，多种类型晶界同时存在于材料中，形成不同的晶界交叉点。冲击压缩下，多晶材料的塑性变形更加复杂，包含位错滑移、孪生、晶界迁移和晶粒旋转等多种塑性变形模式。晶界不仅可以促进塑性变形的产生，还可能阻挡部分塑性变形从一个晶粒传入另一个晶粒，从而抑制塑性变形的扩张。

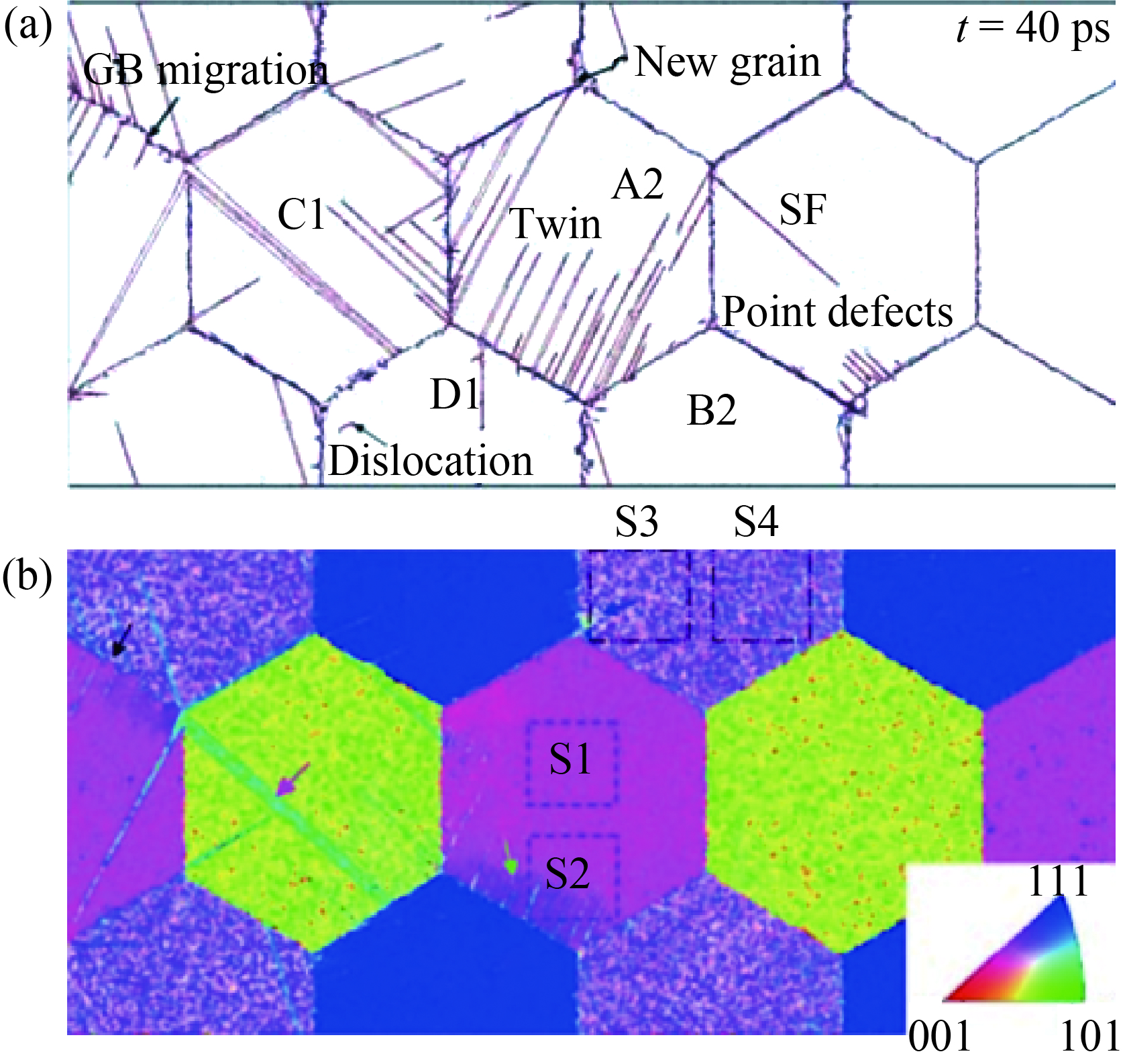
柱状多晶铝的冲击响应研究发现：冲击压缩下，层错优先在晶界或晶界交叉点成核，并向晶粒内部传播^[25]。由于塑性变形的晶向依赖性，不同晶粒中激活的滑移系具有明显差异，这种变形差异将导致晶界迁移。当一系列相邻的(111)面发生连续的1/6[112]不全位错滑移时，孪晶开始形成并扩展。铝是一种高层错能金属，其中的变形孪晶现象十分罕见^[26]。该结果说明晶界对变形孪晶具有促进作用。伴随位错、层错、孪晶的发展，晶粒中的部分区域发生晶格旋转，如图4中箭头所示绿色区域，近似从[113]取向旋转到[212]取向。晶粒的局部旋转将导致亚晶粒的形成。当层错传过晶粒内部到达另一边晶界时，滑移被晶界阻止而导致层错终止，体现出晶界抑制塑性变形传播的作用。

马文等^[27]研究非规则形状纳米多晶铝的冲击响应时发现：它首先发生晶界主导的塑性变形，晶界滑移；然后发生位错主导的塑性变形，位错发射。晶界滑移表现为原子拖拽和应力辅助的自由体积迁移。这两种不同塑性变形机制的转变将导致应力剖面出现拐折。观察到晶界滑移的前提条件是晶粒尺寸足够小，同时冲击加载强度适中。另外，晶界滑移和位错发射等微观塑性机制还与材料物性参数相关，模拟结果发现在层错能较低的金属铜中，位错发射现象并不一定需要很大的应力集中和晶界变形，因此在纳米多晶铜中通常无明显的晶界滑移现象。

物质在一定的温度和压力下会发生物相转变，这种现象称为相变^[28]。1956年，Minshall等^[29]采用炸药爆轰冲击压缩铁的实验方法，发现铁在约13 GPa的冲击压力下发生 $\alpha $（体心立方，bcc）到 $\varepsilon $ （六角密排，hcp）的同质异构相变现象^[28]。由于铁存在体心立方、面心立方和六角密排等丰富的相结构，因此对铁的冲击相变进行研究，既能丰富冲击相变实验数据，又能加深冲击相变的理解和认识；同时，铁的冲击相变对地球物理也具有重要意义。因此铁的冲击相变现象受到人们的高度重视。早期的实验研究主要通过波剖面结构分析间接获取关于相变动力学的有关信息^[29–30]。2005年，Kanlantar等^[31]利用X射线衍射技术首次实现了铁的冲击相变的原位动态测量。Yaakobi^[32]采用X射线吸收精细结构方法，研究了激光辐照下铁的冲击相变，进一步证实了铁的 $\alpha $→$\varepsilon $ 相变。

MD方法具有原子尺度的分辨能力，因而在冲击相变的微观过程和机理研究方面广泛使用。例如：Kauda等^[33]进行了铁冲击相变的MD计算模拟，利用Voter-Chen提出的铁的EAM势，研究了沿不同晶向冲击加载下铁的相变动力学过程及其相变的阈值压力，模拟结果表明，沿着[001]、[011]、[111]晶向进行冲击加载时，发生相变的临界压力分别为15、17和20 GPa。崔新林等^[34–35]也对铁的冲击相变问题展开MD研究，重点关注铁中孔洞尺寸和剪切应力等对相变的影响，发现：铁的冲击相变包含压缩和滑移两个阶段，相变产物沿着{011}$\left\langle\right.\!01-1\!\left. \right\rangle$方向发展，其中剪切应力发挥着重要作用；孔洞不会改变铁相变的微观机制，但会明显降低相变的阈值压力，同时也会影响相变的初始成核位置及后续的相变成核速率。邵建立等^[36–38]也对含缺陷的铁的冲击相变问题展开研究，MD计算模拟结果表明：含孔洞的铁样品发生非均匀相变，相变时间受冲击压力的影响，并且相变产物沿着{111}晶面生长。他们还进一步研究了准等熵压缩过程中单晶铁结构相变的微观过程，揭示了弹性压缩、晶格软化、相变、超应力松弛和高压相弹性压缩5个动态过程。综合实验和数值模拟研究，铁相变的“压缩穿插”机制得以确认，即bcc结构铁首先沿[001]晶向被压缩18.4%，然后在(110)晶面之间彼此滑动$a/(3\sqrt 2) $，最后在(110)晶面上形成hcp结构^[39]。

在MD中广泛使用的Voter-Chen相互作用势对铁的相变压力拟合效果较好，但却对铁塑性变形相关性质的描述较差。这些问题导致MD计算中没有观察到冲击加载下铁的塑性变形现象，因此无法揭示塑性和相变二者如何相互影响及协同演化^[40–42]。多晶铁的冲击试验表明，其波剖面为典型的三波结构，即弹性压缩、弹塑性转变、相变^[43–44]。然而，前期的MD计算结果显示，无论是单晶铁还是多晶铁，均为纯弹性压缩和相变的二波结构^[45]。同时计算模拟过程中出现的bcc→fcc相变与第一性原理计算及实验结果不符^[46]。

Wang等^[8–9]、Gunkelmann等^[24]采用不同的原子间相互作用势，利用MD成功模拟出相变之前晶粒边界位错发射现象，得到了弹性压缩、塑性变形和相变3个过程。如Wang等^[8]重新构建了铁的相互作用势，该势函数重现了相变前的塑性变形，又避免了计算过程中虚假的fcc结构（见图5）。利用该势函数，他们研究了斜波加载下铁相变对准等熵性的影响，结果表明：相变会导致温度升高，是影响准等熵性的关键因素；并且加载波形的上升时间越长，温升越不明显。对比单晶铁和多晶铁的研究结果发现：多晶铁可以同时出现应力援助和应变诱导的相变耦合模式，而单晶铁中只有应力援助的相变耦合模式^[8–10]。最近，Amadou等^[47]利用MD方法对铁相变和塑性相关问题进行了进一步研究，采用冲击和斜波加载手段对单晶铁的动态响应进行数值模拟，结果显示单晶铁在12 GPa的冲击压力下发生孪晶形式的塑性屈服，同时铁的bcc→hcp相变过程与塑性变形历史紧密相关。

近年来，常温常压下hcp结构的金属材料的相变吸引了人们的注意，典型材料有Ti、Zr等。当压力增加时，它们会发生 $\alpha $→$\omega $ 相变^[48]。由于相变的发生会影响材料的力学性能，因而在实际使用过程中需要考虑其相变问题。MD计算模拟发现Ti单晶的冲击相变有很强的方向依赖性^[49]。尽管Zr和Ti的相图类似，但却显示出不同的相变机制。为深入理解这一现象，最近人们采用基于机器学习的相互作用势，对Zr的相变问题展开研究，发现Zr单晶 $\alpha $→$\omega $ 冲击相变的发生是间接的，相变过程中观察到bcc结构，这些结果还需要精密的冲击相变实验加以验证^[50]。

冲击加载下，由于稀疏波相互作用在材料内部产生拉伸应力，一定条件下材料在该拉伸应力作用下发生破坏，该现象称为层裂。层裂是材料在动态加载下一种典型的失效模式。对延性金属材料而言，1976年Seaman等^[51–52]通过对冲击加载样品的显微分析，对层裂产生机制进行了研究。现在人们已经意识到，冲击加载下延性金属材料的层裂过程包括微孔洞的成核、增长和贯通3个阶段。通常认为，当拉伸应力大于材料的拉伸强度时，孔洞开始成核，随后孔洞在拉伸应力作用下通过位错发射增长，同时材料内部还可能出现孪晶、相变等过程。当单个孔洞增长到一定程度，孔洞之间可能相互作用而贯通，孔洞贯通之后材料内部的损伤演化加速，直至最后材料出现完全断裂。因此，研究冲击加载下延性材料中微孔洞演化的相关问题是理解金属材料层裂现象的关键。传统的冲击加载实验通常通过测量自由面速度和回收样品对层裂问题展开研究^[53–54]，难以得到层裂发生和演化的动态过程。MD方法能够得到原子尺度的孔洞演化信息^[55–57]，是金属材料层裂研究的重要工具之一。

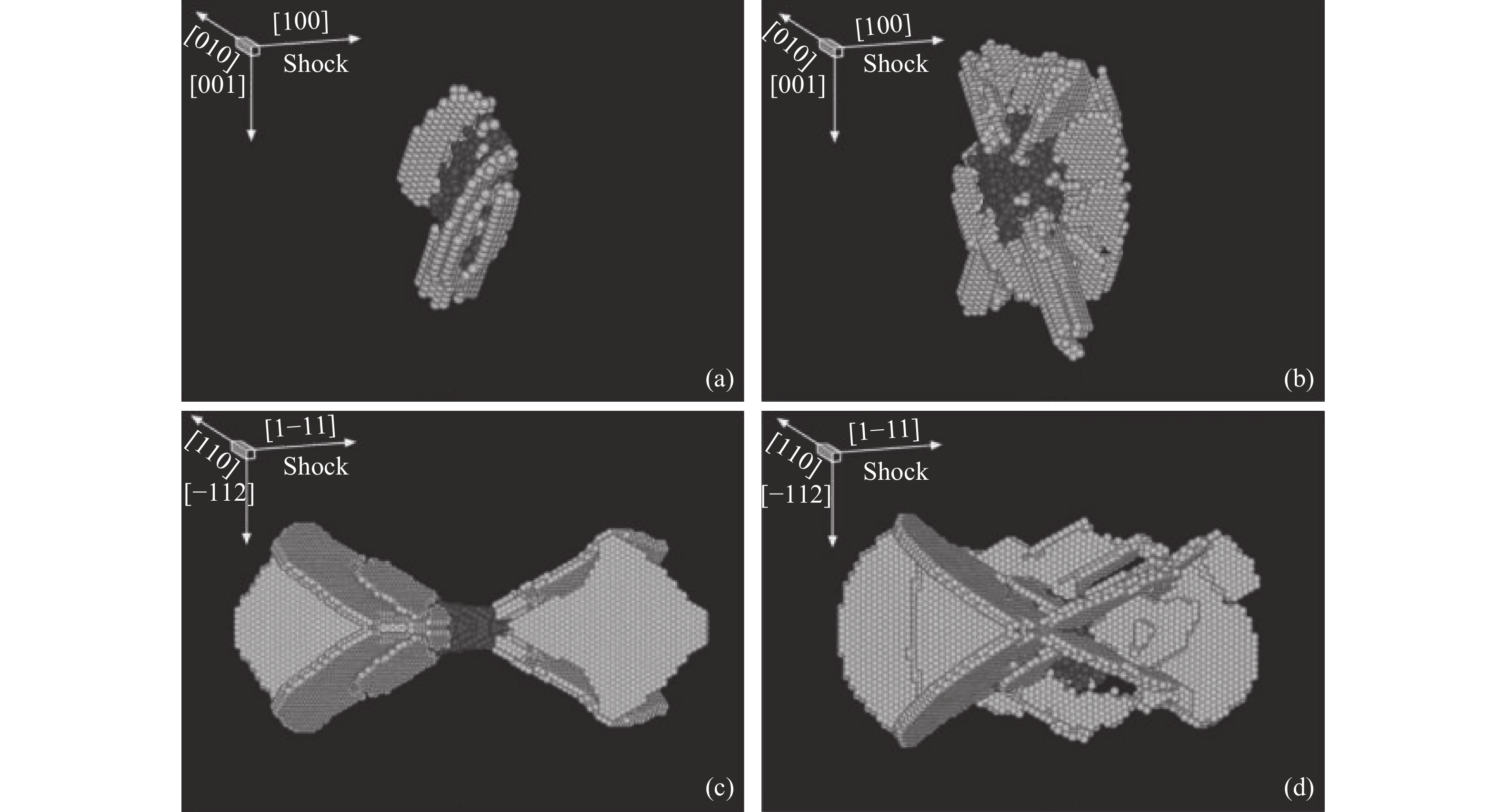
祝文军等^[58–59]利用MD方法，对冲击加载下金属铜中的单孔洞演化和双孔洞贯通问题进行了研究，结果显示：在较低的冲击压力下，孔洞仅受到弹性的压缩和拉伸，在孔洞周围未观察到塑性变形；而当活塞速度为350～500 m/s时，在压缩阶段观察到孔洞塌缩，并在周围出现位错成核和运动现象。他们还分析了活塞速度对孔洞半径增长速度的影响，认为在相同活塞速度下，孔洞半径恒定增长，并且随着活塞速度的增加，孔洞半径的增长速度加大。沿着不同晶向加载时，孔洞演化呈现不同的特征：当沿[100]晶向加载时，位错首先在沿着垂直冲击加载方向的孔洞表面区域成核和运动；当沿[1–11]晶向冲击加载时，位错首先在沿着冲击加载方向的孔洞表面附近区域成核和运动（见图6）。邓小良等^[60]在孔洞贯通方面的研究表明：在[100]加载方向下，孔洞塌缩和增长的原因是周围剪切型位错环发射，在加载的初始阶段，孔洞各自增大到变形区，然后交叠并相互作用，最后两个孔洞贯通，这种贯通方式与实验上通过显微镜观察的结果一致。他们在研究孔洞之间的夹角对贯通的影响时认为，在相同的冲击加载强度下，当两个孔洞的中心连线与冲击加载方向成60°时，孔洞之间更容易出现相互贯通，该现象与孔洞周围的位错发射过程紧密相关。该模拟与实验相互验证，从微观角度对特定情况的研究有助于更深入的探索以及对实验现象的进一步认识。

层裂方式也与晶体本身的结构相关，对于金属锡等强度较低的材料，层裂发生时材料由于冲击或卸载出现熔化现象，称之为微层裂^[61]。Liao等^[61]使用MD研究了锡的微层裂过程，模拟结果表明：经典层裂和微层裂行为产生孔洞的数量和分布有所不同；与经典层裂相比，微层裂过程中成核的孔洞数目更多，分布也更加集中，孔洞的体积尺寸分布符合幂函数规律。在冲击压缩过程中，结构会不断破坏而产生位错、孪晶等缺陷，Agarwal等^[62]通过MD模拟对其进行了深入的研究，模拟结果显示[001]方向上的层裂强度高于[111]方向，因此认为在层裂过程中这些缺陷发挥的作用不可忽视，这为材料层裂强度提供了更多的判断依据。由于锡和铅具有低熔点、低强度的特点，在较低压强下就能够发生卸载熔化，因此人们对其开展了大量实验^{[16, 19–20, 23]}与模拟研究^[63–65]：Soulard^[65]在使用MD模拟层裂破碎时发现，熔融状态下材料的层裂强度会显著降低；向美珍等^[63–64]模拟了铅的层裂过程，认为前期损伤中空穴占据主因；陈永涛等^[66–67]利用改进的Asay窗技术，研究了爆轰加载下金属锡和铅的微层裂现象，发现自由面附近的物质密度明显小于初始密度，且不同颗粒之间存在明显的速度梯度。当冲击加载强度增加时，金属样品表面可能出现熔化，从而导致不同的实验现象：当样品本身还是固体时，只产生传统的微喷射现象；当样品处于部分熔化或完全熔化时，样品表面除形成传统微喷射外，还会出现孔洞成核、破碎断裂等行为，使得自由面附近形成大面积“微层裂”破碎区。这些工作为深刻认识微层裂产生及动态演化提供了至关重要的信息。

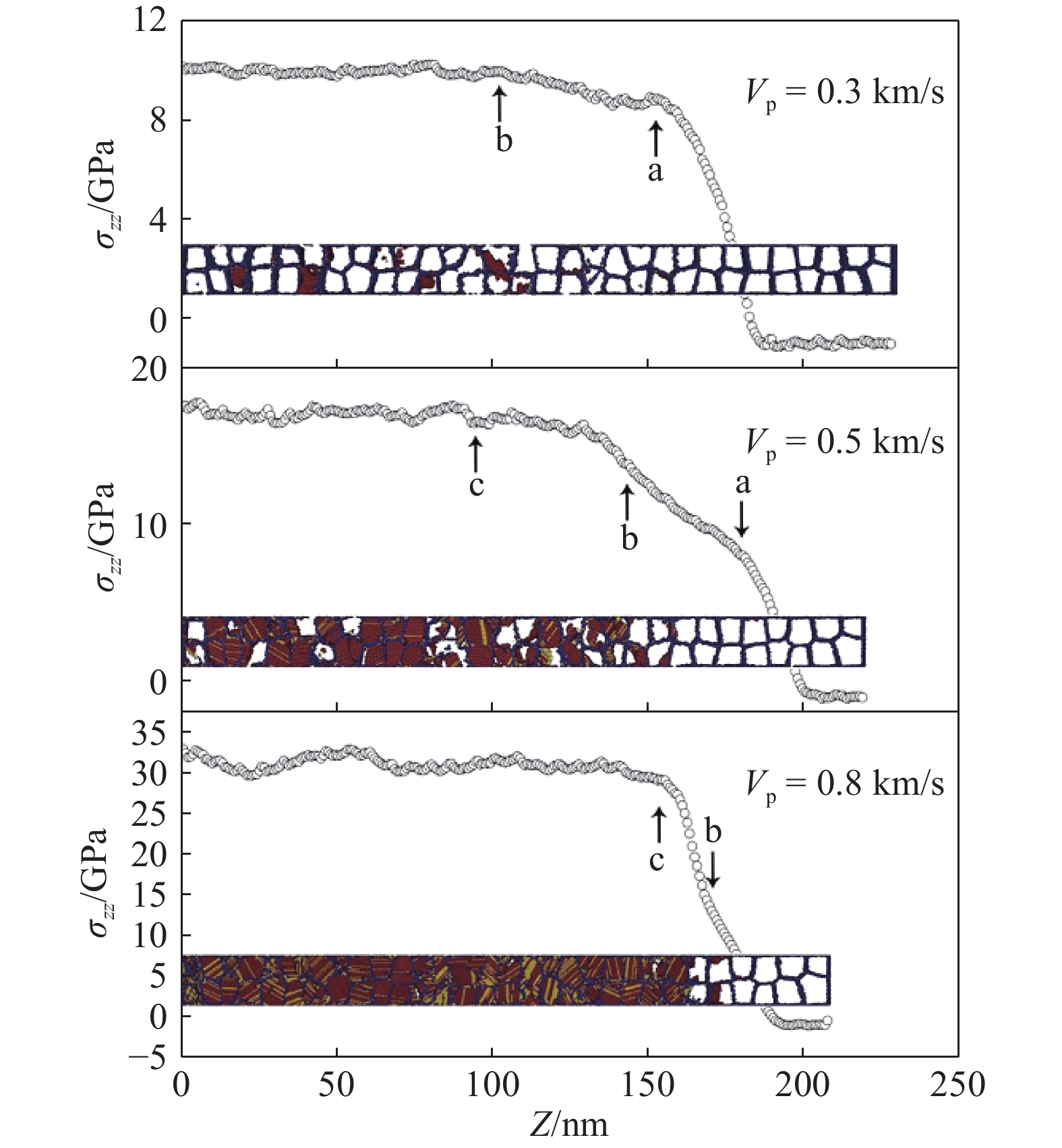
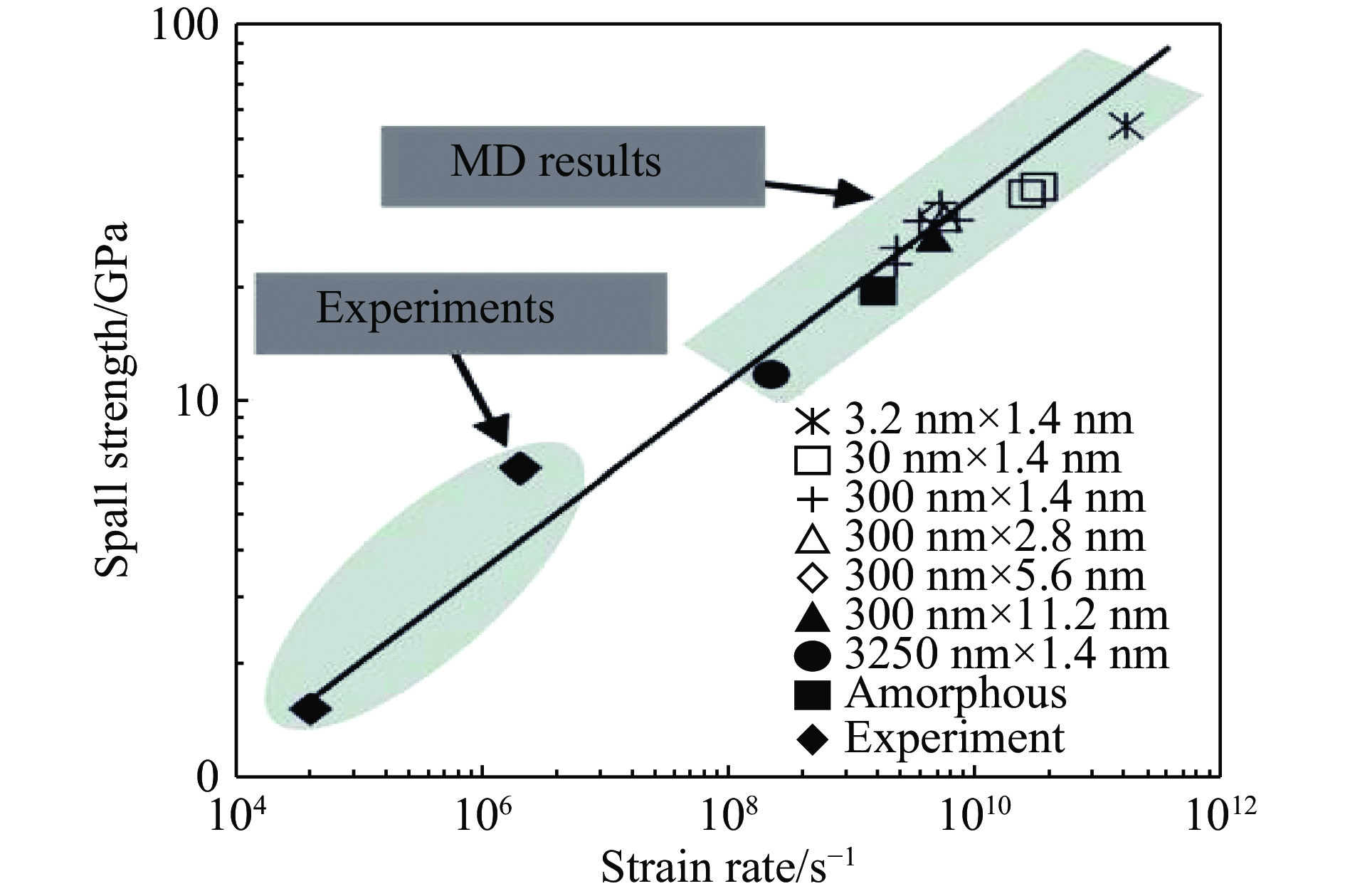
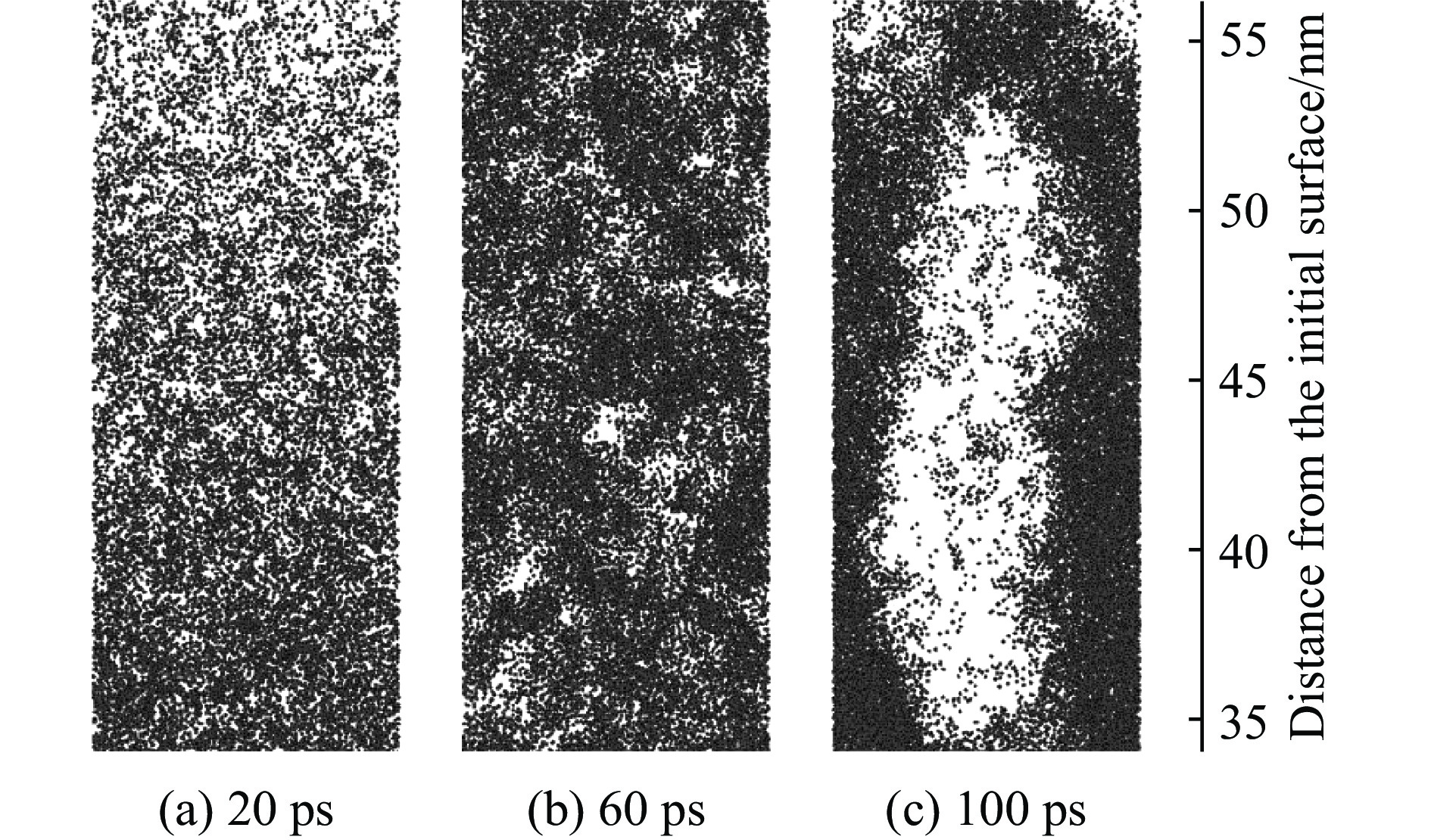
金属材料的层裂过程还受加载应变率的影响。大量实验和理论工作显示，材料层裂强度随加载应变率的增加而增加^[68–70]。最近人们对金属坦在冲击加载下的层裂问题进行了MD数值计算模拟^[71–73]，结果表明：金属坦的层裂强度随着拉伸应变率的增加而增加，最后在超高应变率下达到饱和值；层裂强度的最大值与原子之间的结合能（将晶格上的原子相互分开所需的能量）相关。并且对多晶坦的MD模拟和实验结果^[74]显示，晶界附近的多处滑移为孔洞的形成提供了先决条件，孔隙在晶界生长所需的能量小于晶内，因此单晶比多晶具有更高的破碎强度。MD计算结果与实验结果吻合较好，预测了多晶层裂过程中晶界的分离以及层裂强度随应变速率的增加而增加。图7为多晶钽层裂图。

Srinivasan等^[75]用MD模拟Ni在冲击下发生的层裂时发现：温度和应力等宏观性质与样品的横截面积无关，但冲击引起的微结构随着样品横截面积的变化而显著变化，因此为得到微结构演化的本质规律和特征，增大横截面积十分必要；剪切应力在1 ps时可以忽略不计，但在30 ps时，由于大量微观断裂结构形成，剪切应力不能忽略；温度和应力对层裂的影响大于初始微结构，层裂强度（${\sigma ^*}$）与应变率（${\varepsilon ^*}$）存在对应关系，可以表示为 ${\sigma ^*}$=0.11${\varepsilon ^{*1/4}}$，如图8所示。

以上所述都是平板冲击下延性材料的动态断裂损伤。当前，激光加载成为研究材料动态力学行为的重要手段，其加载应变率与MD模拟更加接近，因此MD方法也被广泛用于研究激光加载下材料的行为。辛建婷等^[76]在MD中使用Z分层方法模拟铝的激光烧蚀现象，结果表明金属铝表面严重烧蚀，形成孔洞，表面结构经历了熔化再结晶现象，结晶后的结构不再是以前的规则晶体，表明形成多孔层。分层模型能够产生与激光加载实验较为接近的冲击波形状和速度，这种泰勒冲击波于层裂而言是一个较好的研究方向。激光与材料的相互作用是当前实验研究的热门领域，我国对激光辐照延性材料的动态损伤MD计算较少，国外却已经对此进行了大量研究。采用双温模型研究飞秒激光对铜的脉冲损伤时发现^[77]，单晶铜开始产生缺陷时即形成小孔洞，随后缺陷增多，孔洞增大贯通直至出现层裂现象。Hatomi等^[78]在研究激光烧蚀金属铂的过程中发现：在不同的激光通量条件下，激光的烧蚀过程不同；当使用低通量时，金属铂出现体积大但数量少的孔洞，并出现层裂现象；使用高通量时，则产生体积非常小的孔洞。短脉冲激光照射金属靶时，可触发一系列高度非平衡过程，从而形成各种实际应用中感兴趣的独特表面结构。Wu等^[79–81]模拟研究了飞秒激光脉冲辐照下的银靶，发现其表面产生200 nm长的冻结纳米尖峰，这种表面结构与层裂过程中液桥（层裂两边被部分熔化原子连接的结构）过冷现象相关。发生层裂时，阻碍了热量从表面（激光辐照部分）向靶固体部分扩散，由于靶固体部分的温度低，使得靠近靶固体部分的液桥发生凝固再结晶现象，形成冻结的纳米尖峰。因此，该层裂导致的过冷现象为靶固体部分的外延再生长与均匀成核之间的竞争奠定了基础。Abou-Saleh等^[82]在实验中也观察到相似的现象，如图9所示，并且发现实验中不同晶体表面取向的样品有不同的反应。为了揭示该现象，Abou-Saleh等^[82]通过MD模拟获得了激光诱导产生层裂过程以及由此导致的纳米尺度表面粗糙度的详细图像，其特征是具有与实验观察到的尺寸相似的细长冻结纳米针和纳米颗粒，并解释了该现象是由于第一次激光脉冲所导致的表面粗糙。

Cuq-Lelandais等^[83]模拟了激光对钽的冲击层裂过程，观察到激光产生的泰勒冲击波到达自由面后反向传播，当冲击波穿过先前冲击波产生的位错场时，缺陷区产生大量空隙，空隙逐渐聚集，形成大规模的延性破坏，出现层裂现象，这与实验和有限元模拟得到的现象相符。Leveugle等^[84]在研究激光辐照下材料层裂的微观机制时发现，当激光能量接近碎裂阈值时，孔洞的体积分布可用幂律$N\left( V \right) \sim {V^{ - \tau }}$较好地描述（N(V)指体积为V的孔洞数目，$\tau $为幂指数），且指数随时间逐渐增大。Zhigilei等^{[13, 85–87]}采用双温模型研究激光辐照金属时发现：在低激光通量条件下，表面出现热解吸现象，解吸率表现为对激光通量的阿伦尼乌斯型依赖关系；当激光通量超过一定值，出现多层喷射或烧蚀现象，但是当能量密度达到某临界值时，烧蚀深度不再增加。基于该现象，他们采用不同的能量密度对Cr进行加载，发现低能量密度时出现熔化再结晶现象，不断提高能量密度后，熔化区向层裂区转变，层裂区向相爆炸区转变，并讨论了转变的物理条件。相爆炸如图10所示，相爆炸状态下层裂降低了烧蚀效率，这是由于层裂中断了材料表面的热传导，导致最大熔化深度和熔化持续时间急剧下降，而层裂区向相爆炸区转变却又增加了熔化深度和熔化持续时间。这些模拟为我们充分认识实验现象具有十分重要的意义。虽然MD在激光与材料相互作用的诸多研究中取得了令人瞩目的成果，但是依旧面临很多困难，例如：双温模型中并无实际电子存在，而是通过传热方式来近似电子与声子的相互作用，这种方式显然是对激光能量沉积过程的简化处理。为了更合理地描述激光与材料的相互作用，Lorazo等^[88]采用蒙特卡罗（Monte Carlo，MC）和MD耦合的计算方法，模拟激光光子能量吸收过程。更精细的能量沉积模型需要考虑原子电离效应，包含离子实与电子之间的相互作用^[89]。未来需要通过不断改进模型以考虑实验中的更多因素及复杂过程，从而使模拟结果更接近实验结果，以此帮助理解实验现象。总而言之，MD方法已经在激光加载下材料的层裂研究方面取得了一些进展，但现阶段仍面临很多挑战。

通过MD计算模拟能够得到冲击加载下材料在原子尺度的动态演化物理过程，计算模拟结果包含了加载条件下材料内部微结构演化过程和机制的重要信息。对这些信息的综合分析和提取，可大大强化分析和解读实验结果的能力，加深对材料动态响应的理解和认识，从而为构建基于微观信息的物理模型提供支撑。当前，MD方法已经在冲击塑性、冲击相变、动态损伤与断裂等领域得到许多应用。这些研究结果一方面能够验证某些实验现象，增强对实验结果的理解和认识。另一方面，MD计算结果也能够为新的实验方案设计提供思路，牵引更深入的实验研究工作。

然而，正如所有计算模拟方法都有其局限性一样，MD计算模拟方法也有其自身的问题，在未来的金属材料动态响应相关研究中需要重点关注和解决。

（1）计算模拟的时间和空间尺度问题。材料的动态响应问题是复杂的多尺度问题，原子尺度上的缺陷演化和原子移动并非必然导致宏观尺度上的材料失效。因此，通常不能将小尺度MD计算模拟结果直接外推至宏观尺度，因此开展大尺度MD计算模拟有其现实需求。目前，典型的MD计算模拟时间尺度为皮秒（10^–12 s），空间尺度为纳米（10^–9 m）。虽然千亿（10¹¹）、万亿（10¹²）原子体系的MD计算模拟结果已有报道^[90–91]，但这种规模的计算模拟消耗巨大计算资源为代价。如美国劳伦斯利弗莫尔国家实验室（Lawrence Livermore National Laboratory，LLNL）的Germann等^[89]利用蓝色基因（BlueGene/L）超级计算机（212 992个中央处理器和72 TB内存）展示了利用MD方法直接在三维空间进行微米尺度计算的模拟能力；虽然其空间尺度达到了微米（2.56 μm），但是时间尺度仅为皮秒量级，与宏观的实验尺度相比仍然很小。因此，如何在MD计算模拟过程中降低其时间或空间尺度的限制，获得具有普适意义的规律性认识是需要关注的问题。

（2）MD方法与其他计算方法的耦合。当前多尺度计算模拟是计算力学领域快速发展的方向之一，由于每种方法都有其局限性，将不同计算模拟方法相互耦合，可克服每种方法自身的缺点和不足，从而拓展其应用范围。例如，根据每18个月计算能力翻倍的趋势，如果在工程尺度上进行全原子分辨的计算模拟（假设空间尺度和时间尺度分别为2.5 cm和1 ms），还需要一百年时间^[91]。因此，探索如何将MD与近场动力学^[92]、有限元^[93]等方法结合，实现不同尺度计算方法的无缝衔接，并将其应用于冲击加载下材料损伤断裂、界面不稳定性等领域是今后值得努力的方向。

（3）MD方法和实验研究的结合。当前，以X射线自由电子激光为代表的先进诊断技术飞速发展，实验上已具备了超快时间分辨、超高空间分辨的诊断能力，为探索材料动态响应的微观机理提供了有力工具^[94]。利用先进诊断技术获得的实验结果一方面对MD计算模拟研究提出了挑战，另一方面也为MD计算模拟的相关研究指引了方向。这需要从事MD计算模拟的科研人员重点关注利用先进诊断技术发现的新现象和新问题，然后进行针对性的物理建模和计算模拟，为这些现象和问题提供机理性的理解和认识。

相信未来随着计算模拟能力的不断提升，及其与实验研究的紧密结合，MD方法必将极大地推动人们对金属材料动态响应微观过程和机理的理解和认识。