高级搜索

杆式钨合金弹超高速撞击薄靶的能量损耗

,  ,  ,  , 

downloadPDF

上一篇

下一篇

孙欢腾, 李名锐, 周刚, 马坤, 舒孝鸿. 杆式钨合金弹超高速撞击薄靶的能量损耗[J]. 高压物理学报, 2019, 33(6): 064106-1. doi: 10.11858/gywlxb.20190732
引用本文: 孙欢腾, 李名锐, 周刚, 马坤, 舒孝鸿. 杆式钨合金弹超高速撞击薄靶的能量损耗[J]. 高压物理学报, 2019, 33(6): 064106-1. doi: 10.11858/gywlxb.20190732
shu
Huanteng SUN, Mingrui LI, Gang ZHOU, Kun MA, Xiaohong SHU. Energy Dissipation of Tungsten Alloys Cylindrical Rods Hypervelocity Impacting Thin Steel Target[J]. gaoyawli, 2019, 33(6): 064106-1. doi: 10.11858/gywlxb.20190732
Citation: Huanteng SUN, Mingrui LI, Gang ZHOU, Kun MA, Xiaohong SHU. Energy Dissipation of Tungsten Alloys Cylindrical Rods Hypervelocity Impacting Thin Steel Target[J]. gaoyawli, 2019, 33(6): 064106-1. doi: 10.11858/gywlxb.20190732
shu

杆式钨合金弹超高速撞击薄靶的能量损耗

  • 1.

    湘潭大学，湖南 湘潭　411105

  • 2.

    西北核技术研究所，陕西 西安　710024

  • 3.

    中南大学粉末冶金研究院，湖南 长沙　410083

    • 作者简介: 孙欢腾（1994－），男，博士研究生，主要从事超高速撞击能量研究. E-mail：780519755@qq.com .
    通讯作者: 周　刚（1964－），男，研究员，主要从事爆炸与冲击动力学研究. E-mail：gzhou@nint.ac.cn; 

  • 中图分类号: O385

Energy Dissipation of Tungsten Alloys Cylindrical Rods Hypervelocity Impacting Thin Steel Target

  • 1.

    Xiangtan University, Xiangtan 411105, China

  • 2.

    Northwest Institute of Nuclear Technology, Xi’an 710024, China

  • 3.

    Powder Metallurgy Research Institute, Central South University, Changsha 410083, China

    • Corresponding author: Gang ZHOU, gzhou@nint.ac.cn ; 

  • MSC: O385

  • 摘要: 超高速撞击过程伴随着复杂的物理过程。为分析杆式圆柱形钨合金弹超高速撞击薄钢靶时的物理过程，采用AUTODYN/SPH数值仿真计算方法获得了撞击过程模型及每个光滑粒子流体动力学信息，并通过广度搜索破片识别程序识别每个破片所含粒子，利用MATLAB编程对破片粒子数据信息进行统计分析，获得弹靶撞击过程的变化特性、弹靶破片数量、相关能量随撞击时间的变化规律。通过分析发现：随着弹体撞击速度的增加，剩余弹体被严重侵蚀，且弹体能量损耗增加，弹体损失的能量主要转变为弹靶破片动能；计算得到了撞击20 ${\text{μ}}{\rm{s}}$时的能量损耗直方图，同时分析了发生撞击时靶板的能量变化过程，并简要描述了该过程。
    Abstract: The complex physical process is always accompanied with hypervelocity impact. In this paper, the physical process of rod-shaped cylindrical tungsten alloy bomb impact thin steel target has been studied. The impact process model and fluid dynamic information of every particle were obtained by means of AUTODYN/SPH method and the fragment particles were identified through range search and fragment identification program. Some information of the elastic target change process, the number of the target fragment, the change of the relative energy with the time during the impact were obtained by MATLAB. It is found that with the increase of impact speed, the residual body is eroded seriously, and the energy loss of missile body is increased, and the energy of the body loss is mainly converted into the kinetic energy of the bomb target. The energy loss histogram of the impact at the time of 20 μs and energy change process for the target plate impacted have been analyzed.
  • 加载中

  • 图 1  弹体撞击靶板示意图

    Figure 1.  Diagrammatic sketch of projectile impact target plate

    下载: 全尺寸图片 幻灯片

    图 2  仿真结果与实验结果对比

    Figure 2.  Comparison between simulation and experimental results

    下载: 全尺寸图片 幻灯片

    图 3  不同时刻弹体的侵蚀

    Figure 3.  Erosion of projectile at different time

    下载: 全尺寸图片 幻灯片

    图 4  不同长度弹体以不同速度撞击时产生的弹体破片数量

    Figure 4.  Fragments’ number of projectile with different velocities and lengths

    下载: 全尺寸图片 幻灯片

    图 5  不同长度弹体的撞击结果

    Figure 5.  Impact results of projectiles with different lengths

    下载: 全尺寸图片 幻灯片

    图 6  不同长度的弹体撞击形成的破片云长度和宽度

    Figure 6.  Debris length and width of projectiles with different lengths

    下载: 全尺寸图片 幻灯片

    图 7  能量耗散图

    Figure 7.  Image of energy dissipation

    下载: 全尺寸图片 幻灯片

    图 8  耗散的能量损失与剩余弹体速度降低量

    Figure 8.  The dissipation of energy and the decline of projectile velocity

    下载: 全尺寸图片 幻灯片

    图 9  耗散的总塑性功与内能

    Figure 9.  The dissipation of total plastic energy and internal energy

    下载: 全尺寸图片 幻灯片

    图 10  靶板获能过程

    Figure 10.  The gain energy of target plate

    下载: 全尺寸图片 幻灯片

    图 11  剩余弹体动能

    Figure 11.  Kinetic energy of residual projectile

    下载: 全尺寸图片 幻灯片

    表 1  状态方程参数

    Table 1.  Parameters of equation of state

    MaterialSC0/(m·s–1)${\varGamma}$${{\rho _0}/\left( {{\rm kg}\cdot {{\rm m}^{-3}}} \right)}$
    Tungsten alloy1.234 0401.6717.6
    Q345 Steel1.494 5692.177.83
    下载: 导出CSV

    表 2  钨合金的Steinberg-Guinan强度模型参数

    Table 2.  Steinberg-Guinan strength model parameters of tungsten alloy

    ${{G_0}/{\rm GPa}}$${{Y_0}/{\rm GPa}}$${ {T_{\rm m}}/{\rm{K} } }$${ {G'_p} }$${ {G_T'}/({ {\rm{MPa} }\cdot{\rm K}^{ - 1} } })$${\,\beta }$${n}$${ {Y'_p} }$
    1321.44 5201.794–401.30.10.019 027
    下载: 导出CSV

    表 3  Q345钢的Johnson-Cook强度模型参数

    Table 3.  Johnson-Cook strength model parameters of Q345 steel

    ${A/{\rm GPa}}$${B/{\rm GPa}}$${n}$${C}$${m}$${{T_{{\rm{melt}}}}/{\rm K}}$T0/KG/GPa
    0.3740.795 70.454 50.015 860.885 61 75930080.47
    下载: 导出CSV

    表 4  实验与数值仿真结果

    Table 4.  Results of simulation and experiment

    MethodResidual projectile’s
    kinetic energy/(km·s–1)    		Residual projectile’s
    length/mm
    Experiment2.94512.510
    Simulation2.95211.823
    下载: 导出CSV
  • [1] 武强, 张庆明, 孙浩勇, 等. 超高速撞击下PTFE/Al含能材料薄板的载荷特性分析 [J]. 航天器环境工程, 2017, 34(1): 1–7. doi: 10.3969/j.issn.1673-1379.2017.01.001 WU Q, ZHANG Q M, SUN H Y, et al. The loading characteristics of PTFE/Al energetic materialsunder hypervelocity impact [J]. Spacecraft Environment Engineering, 2017, 34(1): 1–7. doi: 10.3969/j.issn.1673-1379.2017.01.001
    [2] 迟润强, 庞宝君, 何茂坚. 球形弹丸超高速正撞击薄板破碎状态实验研究 [J]. 爆炸与冲击, 2009, 29(3): 231–236. doi: 10.3321/j.issn:1001-1455.2009.03.002 CHI R Q, PANG B J, HE M J. Experimental investigation for deformation and fragmentation of spheres penetrating sheets at hypervelocity [J]. Explosion and Shock Waves, 2009, 29(3): 231–236. doi: 10.3321/j.issn:1001-1455.2009.03.002
    [3] 曲广吉, 韩增尧. 空间碎片超高速撞击动力学建模与数值仿真技术 [J]. 中国空间科学技术, 2002(5): 26–30. doi: 10.3321/j.issn:1000-758X.2002.05.005 QU G J, HAN Z Y. Dynamical modeling and numerical simulation of hypervelocity space debris impact [J]. Chinese Space Science and Technology, 2002(5): 26–30. doi: 10.3321/j.issn:1000-758X.2002.05.005
    [4] 张伟, 庞宝君, 贾斌, 等. 弹丸超高速撞击防护屏碎片云数值模拟 [J]. 高压物理学报, 2004, 18(1): 47–52. doi: 10.3969/j.issn.1000-5773.2004.01.009 ZHANG W, PANG B J, JIA B, et al. Numerical simulation of debris cloud produced by hypervelocity impact of projectile on bumper [J]. Chinese Journal of High Pressure Physics, 2004, 18(1): 47–52. doi: 10.3969/j.issn.1000-5773.2004.01.009
    [5] 童宗保, 王金相, 彭楚才. 2~3km/s初速下球形破片对金属薄靶的侵彻效应分析 [J]. 科学技术与工程, 2014, 14(33): 215–219. doi: 10.3969/j.issn.1671-1815.2014.33.040 TONG Z B, WANG J X, PENG C C. Analysis of the effect of the circle fragment penetration the tine metal target with the initial velocity between 2km/s and 3km/s [J]. Science Technology and Engineering, 2014, 14(33): 215–219. doi: 10.3969/j.issn.1671-1815.2014.33.040
    [6] FA W K, JIE H. Test study on the performance of shielding configuration with stuffed layer under hypervelocity impact [J]. Acta Astronautica, 2016(127): 553–560.
    [7] SHI C L, YI L. Research on the technique of identifying debris and obtaining characteristic parameters of large-scale 3D point set [J]. International Journal of Impact Engineering, 2013(56): 27–31.
    [8] 唐恩凌, 徐名扬, 张庆明. 超高速撞击厚靶过程的能量分配研究 [J]. 固体力学学报, 2016, 37(2): 152–160. TANG E L, XU M Y, ZHANG Q M. Study on partitioning of energy in hypervelocity impact on thick target [J]. Chinese Journal o f Solid Mechanics, 2016, 37(2): 152–160.
    [9] Thomson W T. An approximate theory of armor penetration [J]. Journal of Applied Physics, 1955, 26: 80–82. doi: 10.1016/0734-743X(95)00023-4
    [10] WOODWARD R L. The penetration of metal targets by conical projectiles [J]. International Journal of Mechanical Sciences, 1978, 20: 349–359. doi: 10.1016/0020-7403(78)90038-3
    [11] WIERZBICKI T. Petalling of plates under explosive and impact loading [J]. International Journal of Impact Engineering, 1999, 22: 935–954. doi: 10.1016/S0734-743X(99)00028-7
    [12] WANG B, XIONG J. Energy absorption efficiency of carbon fiber reinforced polymer laminates under high velocity impact [J]. Materials and Design, 2013(50): 140–148.
    [13] 汪庆桃, 吴克刚, 陈志阳. 圆柱形长杆超高速正碰撞薄板结构破碎效应 [J]. 振动与冲击, 2017, 36(5): 53–60. WANG Q T, WU K G, CHEN Z Y. Fragmentation effect of a long cylindrical rod with a hypervelocity normally impacting a thin plate structure [J]. Journal of Vibration and Shock, 2017, 36(5): 53–60.
    [14] 汪庆桃, 吴克刚, 李必红, 等. 球形弹丸超高速碰撞破碎特性 [J]. 振动与冲击, 2014, 33(22): 46–50. WANG Q T, WU K G, LI B H, et al. Fragmentation properties of spherical projectiles impacting at hypervelocity [J]. Journal of Vibration and Shock, 2014, 33(22): 46–50.
    [15] 陈鸿, 周智炫, 黄洁. 带迎角钨杆斜侵彻铝板数值仿真研究 [J]. 实验流体力学, 2014, 28(2): 85–89. doi: 10.11729/syltlx2014pz29 CHEN H, ZHOU Z X, HUANG J. Numerical simulation study on tungsten rod oblique penetrating aluminum plate with attack angle [J]. Journal of Experiments in Fluid Mechanics, 2014, 28(2): 85–89. doi: 10.11729/syltlx2014pz29
    [16] 王芳, 李磊, 金俊. 空间碎片超高速碰撞的数值方法研究 [J]. 中国安全科学学报, 2006, 16(5): 26–30. doi: 10.3969/j.issn.1003-3033.2006.05.005 WANG F, LI L, JIN J. Study on numerical simulation of hypervelocity impact of debris in outer space [J]. China Safety Science Journal, 2006, 16(5): 26–30. doi: 10.3969/j.issn.1003-3033.2006.05.005
  • 加载中
图( 11) 表( 4)
计量
  • 文章访问数:  2771
  • HTML全文浏览数:  2771
  • PDF下载数:  33
  • 施引文献:  0
出版历程
  • 收稿日期:  2019-03-04
  • 刊出日期:  2019-12-01

杆式钨合金弹超高速撞击薄靶的能量损耗

    通讯作者: 周　刚（1964－），男，研究员，主要从事爆炸与冲击动力学研究. E-mail：gzhou@nint.ac.cn; 
    作者简介: 孙欢腾（1994－），男，博士研究生，主要从事超高速撞击能量研究. E-mail：780519755@qq.com
  • 1. 湘潭大学，湖南 湘潭　411105
  • 2. 西北核技术研究所，陕西 西安　710024
  • 3. 中南大学粉末冶金研究院，湖南 长沙　410083
  • 收稿日期:  2019-03-04

摘要: 超高速撞击过程伴随着复杂的物理过程。为分析杆式圆柱形钨合金弹超高速撞击薄钢靶时的物理过程，采用AUTODYN/SPH数值仿真计算方法获得了撞击过程模型及每个光滑粒子流体动力学信息，并通过广度搜索破片识别程序识别每个破片所含粒子，利用MATLAB编程对破片粒子数据信息进行统计分析，获得弹靶撞击过程的变化特性、弹靶破片数量、相关能量随撞击时间的变化规律。通过分析发现：随着弹体撞击速度的增加，剩余弹体被严重侵蚀，且弹体能量损耗增加，弹体损失的能量主要转变为弹靶破片动能；计算得到了撞击20 ${\text{μ}}{\rm{s}}$时的能量损耗直方图，同时分析了发生撞击时靶板的能量变化过程，并简要描述了该过程。

English Abstract

    全文HTML

  • 半个世纪以来，人们对于超高速撞击的研究主要应用于反卫反导、航天器空间碎片防护、轻质装甲与反装甲设计、陨石坑以及动能武器等领域。西北核技术研究所、哈尔滨工业大学、北京理工大学、清华大学、中国科学技术大学、国防科学技术大学、北京航空航天大学、西北工业大学、中国科学院、中国工程物理研究院流体物理研究所、北京卫星环境工程研究所等众多研究单位陆续开展了超高速撞击问题的相关研究工作。我国在超高速撞击方面的研究多见于空间碎片对航天器的毁伤及其对空间防护结构的影响，例如：武强等[1]进行了超高速撞击下含能材料防护板的载荷分析；迟润强等[2]进行了球形弹丸超高速撞击薄板的实验研究；曲广吉等[3]进行了空间碎片超高速撞击的动力学建模并进行了仿真模拟；张伟等[4]介绍了超高速加载技术，并且通过SPH（Smooth Particle Hydrodynamics）数值模拟方法研究了弹丸超高速撞击空间碎片防护屏时，弹丸厚度和形状、撞击速度以及材料模型等对碎片云的影响；童宗保等[5]研究了弹丸以2～3 km/s的速度撞击靶板时的主要侵彻效应，对弹丸撞击后的变形、弹丸尺寸、弹孔形貌进行了测量，并与低速撞击进行对比。Fa等[6]通过实验研究了防护结构对超高速撞击的影响；Shi等[7]采用SPH数值模拟结合破片搜索方法分析了破片特征及分布。关于超高速撞击能量的研究多集中于中低速撞击、厚靶撞击、吸能材料等，如：唐恩凌等[8]研究了铝弹丸以2.61 km/s的速度撞击2A12铝厚靶板的能量分配，发现铝厚靶板在受到撞击时会产生反向迸溅破片，且有靶板成坑现象，不同于超高速撞击薄靶板过程中出现的携带大量动能的弹靶破片，说明其主要能量分配形式不同；Thomson[9]考虑靶板的破坏模式，改进了Taylor模型，建立了薄板模型；Woodward[10]考虑靶板的局部塑性弯曲耗能，建立了靶板的简化模型；Wierzbicki[11]利用能量原理建立了穿孔模型。超高速撞击条件下，Wang等[12]通过实验与数值模拟相结合的方法研究了碳纤维增强聚合物复合板在高速撞击下的能量吸收效率问题。在长杆弹超高速撞击薄板研究方面，汪庆桃等[13-14]对圆柱形长杆超高速正碰撞薄板结构的破碎规律以及球形弹丸超高速碰撞破碎特性进行解读，给出了弹体破碎长度随弹靶材料特性、弹靶尺寸及初始撞击速度变化的关系式。

    综上所述，我国对超高速撞击的研究多集中在空间碎片防护方面，其特点为撞击速度更高（7 km/s以上），弹体材质以轻质材料居多。有关碰撞能量的研究则多针对中低速撞击下的弹道极限及对厚靶的撞击。超高速碰撞与低速碰撞、中速碰撞的区别在于其物理现象不同。低速碰撞时，所研究的问题属于结构动力学问题，局部侵彻与结构总体变形效应紧密地耦合在一起。中低速撞击时，从毁伤模式上看，大部分为剪切冲塞、靶板花瓣破坏、撕裂变形等形式破坏，弹体基本为刚性侵彻，所以撞击后形成的弹靶材料破片少，弹体损失的能量主要转化为塞块动能、靶板撕裂变形能、内能以及靶板的整体变形能等。关于长杆弹撞击薄板的研究报道较少，为此本研究以杆式圆柱形钨合金弹2.5～4 km/s速度撞击薄钢靶的数值仿真结果为基础，对撞击过程的能量损耗进行统计分析，研究结果对撞击机理研究具有重要的参考价值。由于杆式圆柱形钨合金弹超高速撞击薄钢靶具有复杂性和多样性等特点，通过实验手段研究超高速撞击能量的变化过程较为困难，数值仿真方法是分析超高速撞击能量变化过程的有效手段之一，考虑到数值仿真结果不可直接用于弹靶破片数及相关能量统计，因而需要进行数据结果的统计分析[5]。

    本研究通过AUTODYN/SPH方法模拟杆式圆柱形钨合金弹体超高速撞击薄钢靶过程，将仿真得到的剩余弹体速度、长度与实验图像处理后的结果进行对比，以验证模型参数的合理性；然后利用该模型参数进行数值仿真实验，对仿真结果进行广度破片识别搜索，通过MATLAB统计分析，获得破片数量、剩余弹体以及靶板的相关能量。

1.   数值仿真

    1.1.   模型参数

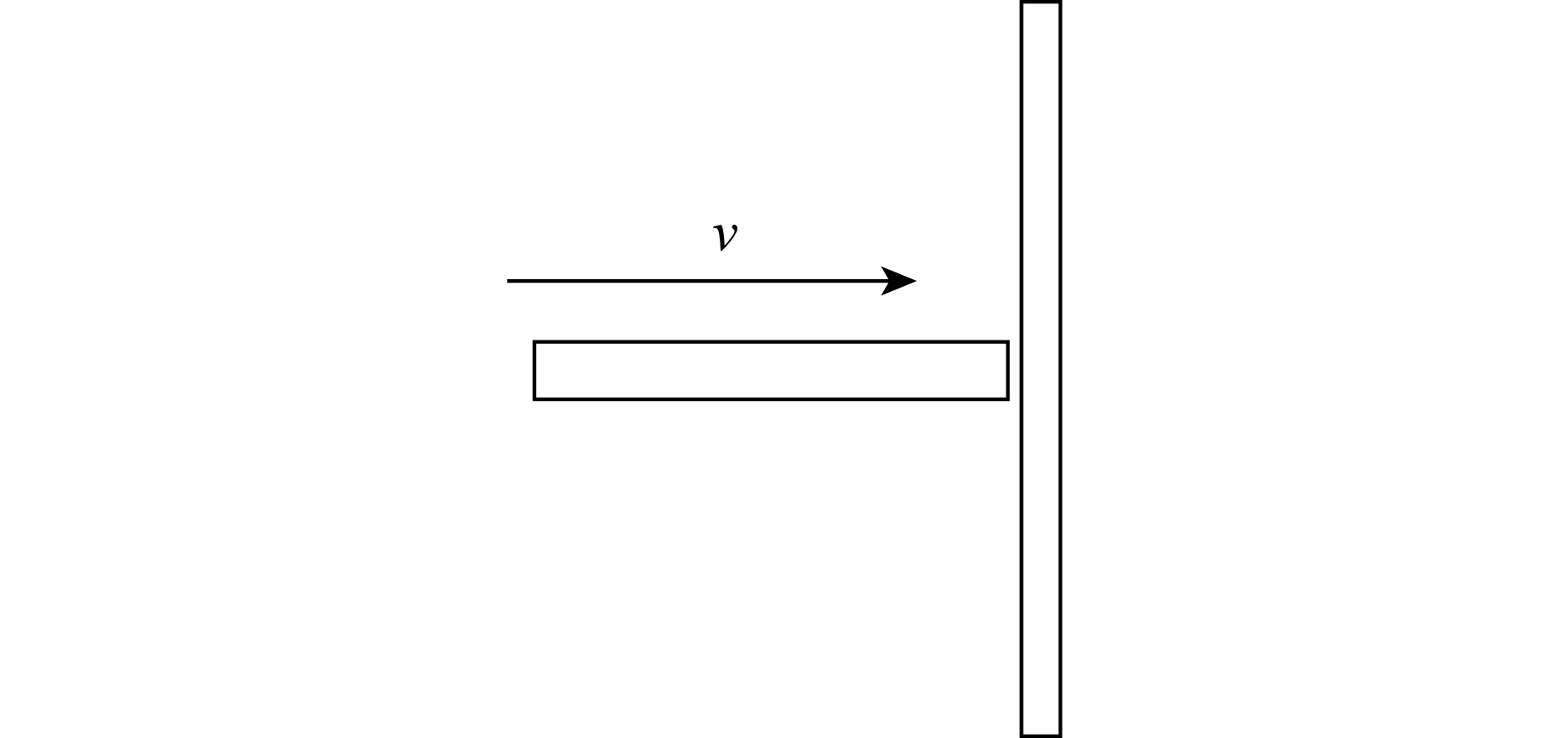
  • 在数值仿真计算过程中，初始条件、边界条件及材料模型参数的设定对数值仿真结果具有重要影响，合适的参数可以使计算结果更接近实际情况；同时，利用合适的参数通过数值仿真得到规律性结论，可以进一步指导实验方案的制定[4]。本研究采用AUTODYN/SPH方法进行超高速撞击的数值仿真计算，弹体选用钨合金弹体，靶板选用Q345钢。选取速度初始条件作为模拟初始条件，靶板固定，弹靶材料的光滑粒子长度均取0.1 mm，考虑到弹体的撞击速度为2.5～4 km/s，可以忽略冲击相变的影响。弹靶均采用Shock状态方程，弹体采用Steinberg-Guinan强度模型，靶板采用Johnson-Cook强度模型，详细信息见文献[15-16]。具体的模型参数见表1、表2和表3，弹体撞击圆柱形钢靶板的仿真模型如图1所示。表1中：S为参数，C0为零压体积声速，Γ为格临爱森因子，ρ0为初始密度。表2中：G0为初始剪切模量，Y0为初始屈服应力，Tm为熔化温度，β为硬化常数，n为硬化指数，$ Y'_p$为应力关于压力的一阶偏导数，$G'_p $、$G'_T $分别为剪切模量关于压力和温度的一阶偏导数。表3中：A为初始屈服应力，B为硬化常数，n为硬化指数，C为应变率常数，m为温度软化指数，Tmelt为熔化温度，T0为室温，G为剪切模量。

    • 1.2.   模拟结果与实验结果对比

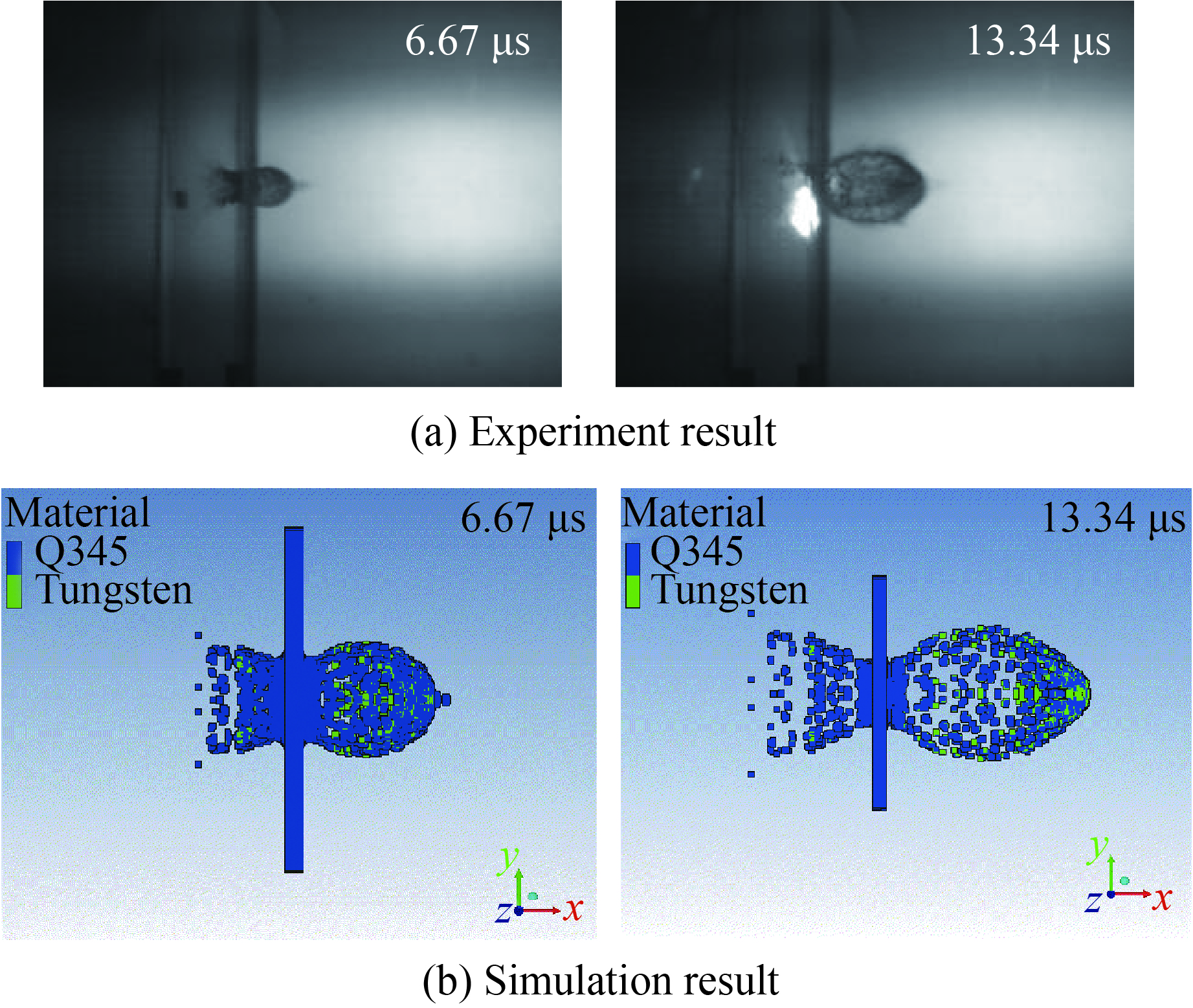
  • 采用该模型参数进行与实验条件相同的数值仿真计算，撞击条件为：直径2.92 mm、长14.6 mm的钨合金圆柱形弹体以2.99 km/s的速度撞击1.5 mm厚的Q345薄钢靶板。采用1.5×105帧每秒的高速摄影机拍摄的实验结果如图2（a）所示，利用多幅图像识别剩余弹体，根据剩余弹体位置变化和时间间隔得到剩余弹体速度和剩余弹体长度；根据数值仿真结果，利用破片识别程序识别剩余弹体，并根据剩余弹体包含的粒子信息计算剩余弹体的平均速度和长度，模拟结果如图2（b）所示。

    如表4所示，计算结果与实验结果符合较好，验证了模型选取的合理性。本研究将以此模型参数为基础，进行数值仿真计算。每个时间点的所有粒子点信息结果均可导出.dat格式的数据文件，从而得到每个破片的粒子信息，再通过MATLAB对粒子信息进行广度破片识别搜索[7]。

    将模拟空间划分成若干长度为L0的方格，考虑材料的拉伸变形作用，L0取1.1～1.3倍光滑粒子长度r0。如果L0取值太小，则在破片云未充分扩展时，程序将错误识别破片云内某个破片中粒子的归属，错误认为其属于同一破片，而实际上，当破片云充分扩展时，此粒子属于不同的破片；如果L0取值过大，则会错误认为不同破片的粒子属于同一破片。具体判定条件：若结果中的两个粒子点距离小于L0，则认为两个粒子点属于同一破片，并且认为此两点连接在一起，因此识别两个粒子点是否属于同一破片的问题转化为判定两个粒子点的距离是否小于L0。具体判定操作：利用各方向尺寸略小于L0的方格将数据分布区域网格化；然后选取随机点Ai作为识别起始点；访问未访问的本方格和相邻方格的未被访问点B1，B2，B3，···，Bn；以B1，B2，B3，···，Bn中距离小于L0的点分别作为起点；重复上述步骤，直到Ai的破片粒子全部被访问；如果能够一次找完所有点，则粒子点群属于同一个破片，否则找寻其他随机点Ai+1作为起始点；重复上述步骤，直至找完所有粒子点，统计分析后可得到弹、靶破片的数量以及相关的能量结果。为减少仿真过程的计算量，根据对称性，将弹体和靶板设置为半圆柱模型，以此进行弹体超高速撞击薄钢靶仿真计算。

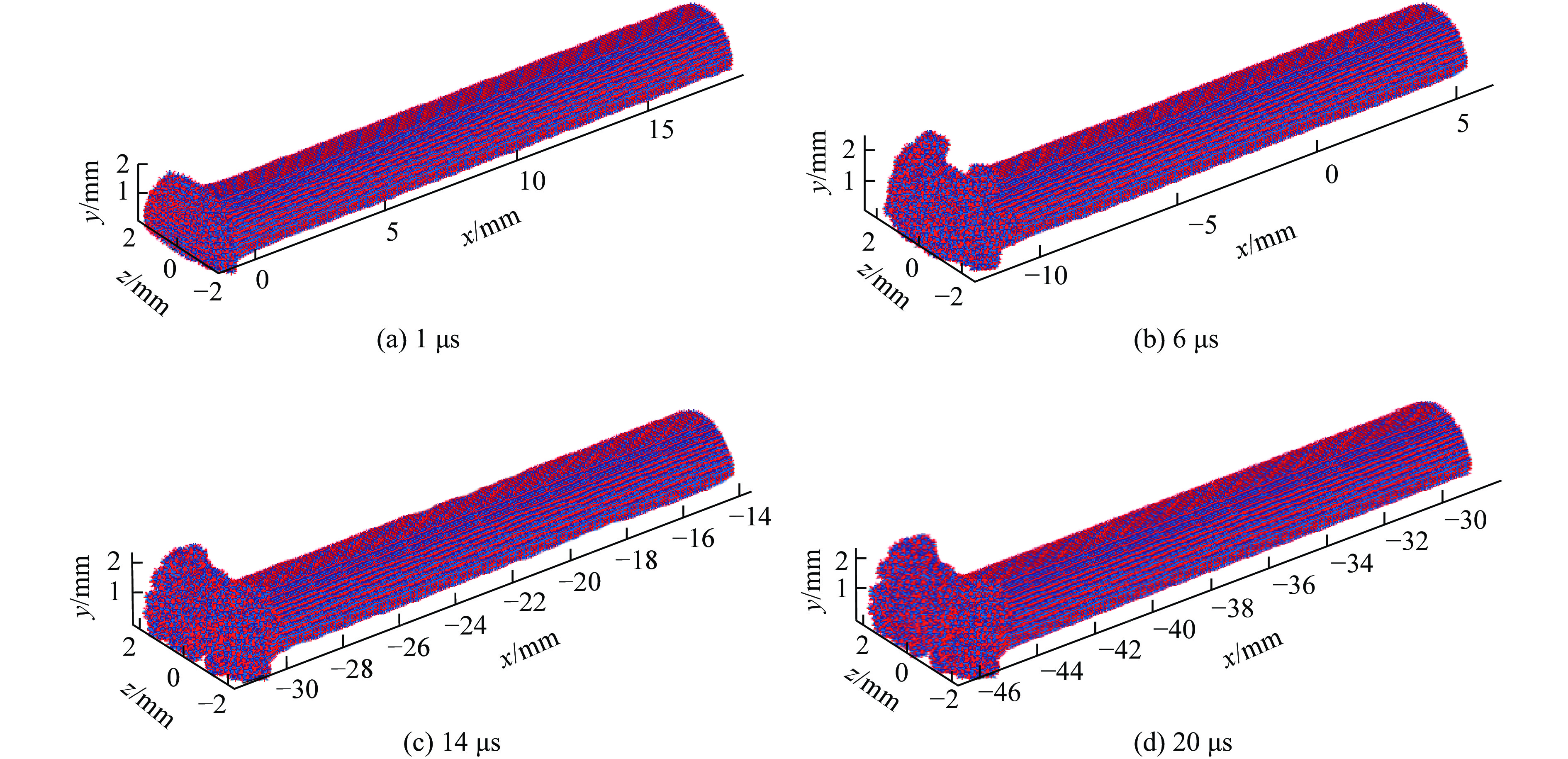
    破片识别程序识别的剩余弹体经过MATLAB重构后的结果见图3。直径2.6 mm、长度20.8 mm的钨合金弹体以速度2.5 km/s撞击1.5 mm厚钢靶时，不同时刻剩余弹体的形貌变化如图3所示。

2.   结果与分析

    2.1.   超高速弹靶撞击

  • 与中低速度撞击不同，在超高速撞击过程中，由于撞击瞬间弹靶之间产生了冲击波，冲击波压力远大于材料强度，导致弹靶发生破裂，并且在反射稀疏波的作用下不断拉伸破碎，形成弹靶破片，破片数量对毁伤效果具有重要影响。

    • 2.1.1.   弹体破片数

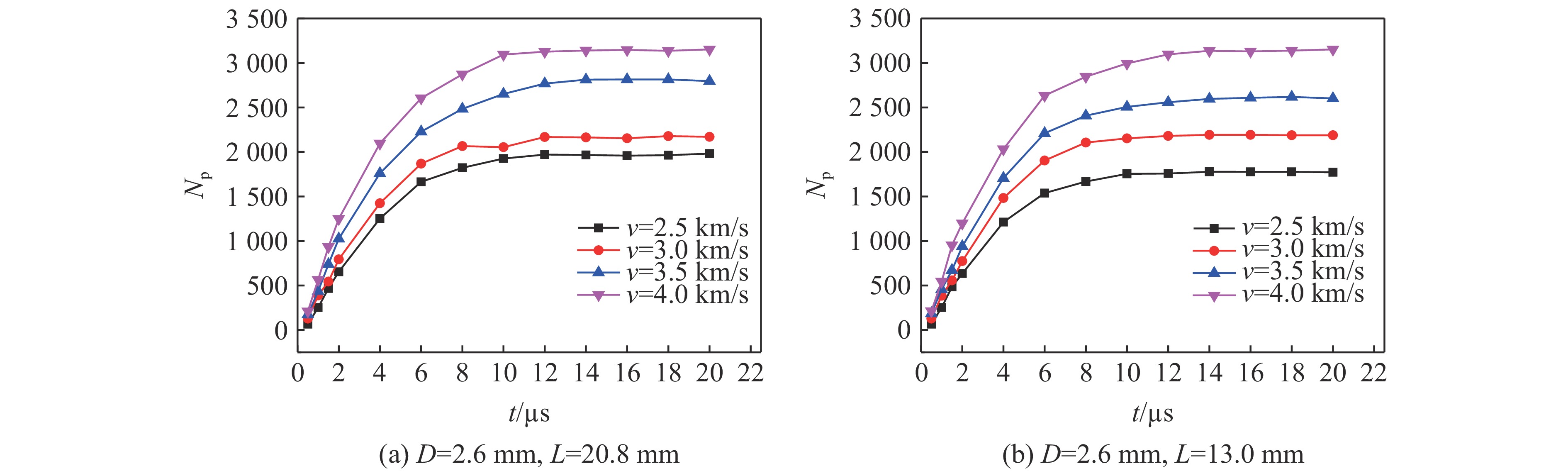
  • 直径2.6 mm、长度为20.8 mm和13.0 mm的弹体分别以2.5、3.0、3.5和4.0 km/s的速度撞击1.5 mm厚钢靶板，其弹体破片数量Np随时间的变化曲线见图4。对比图4(a)和图4(b)可以看出，在撞击12 ${\text{μ}}{\rm{s}}$左右时破片生成过程基本结束。固定靶板参数和弹靶撞击速度，当弹体长度不同时，撞击后产生的弹体破片数相差不大；随着撞击时间的增加，弹体破片数量不再上升后，由于弹体长度变化产生的破片数差异在10%以内，即在其他条件一定时，弹体长度超过某一长度后，其对超高速撞击产生破片数的影响较小。同时可以看出，随着撞击速度的增加，弹体破碎越来越严重，产生的破片数量增多。靶板的破片数与弹体破片数类似，这里不再赘述。

    • 2.1.2.   临界长度分析

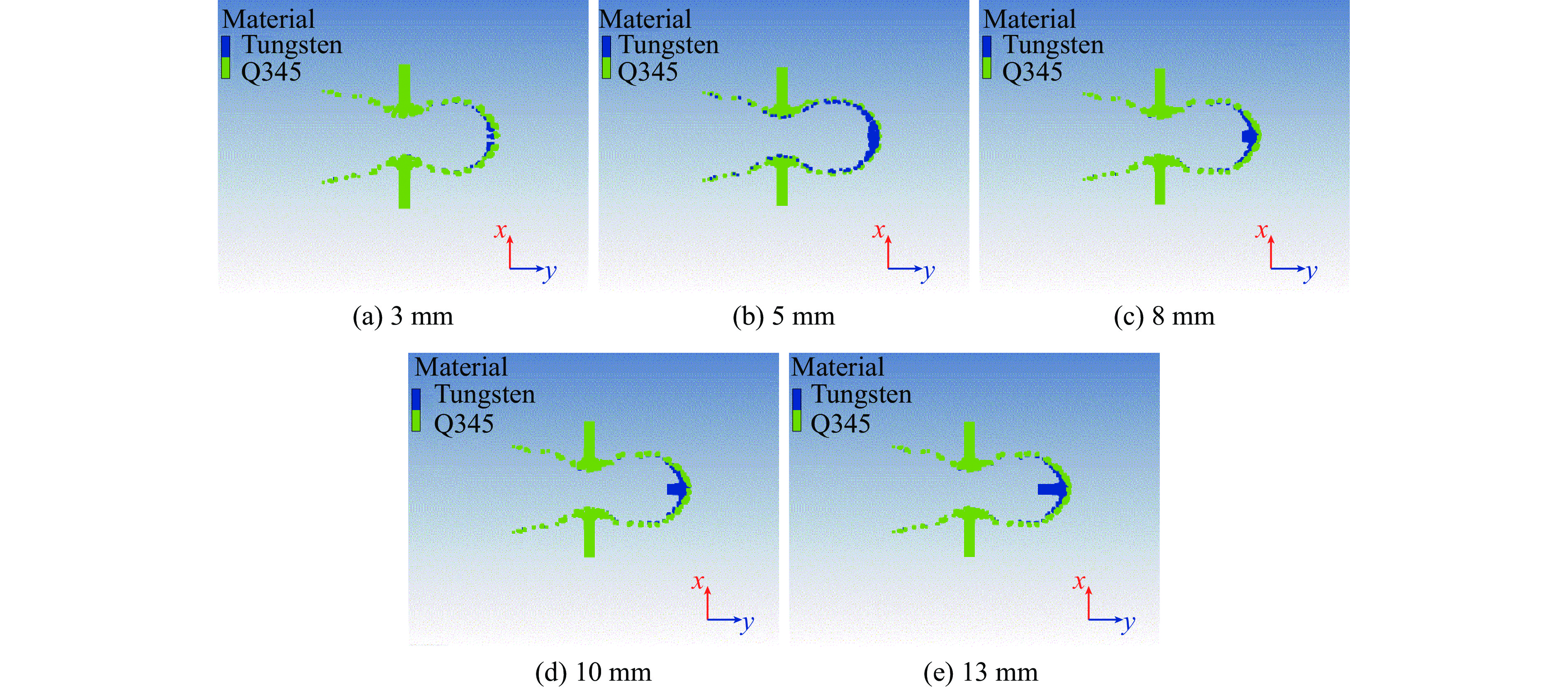
  • 计算了弹体长度13 mm、直径2.6 mm的钨合金弹以2.5 km/s速度撞击厚度为2.5 mm的靶板，初始状态为弹体头部距离靶板13.5 mm，撞击结果如图5(e)所示。

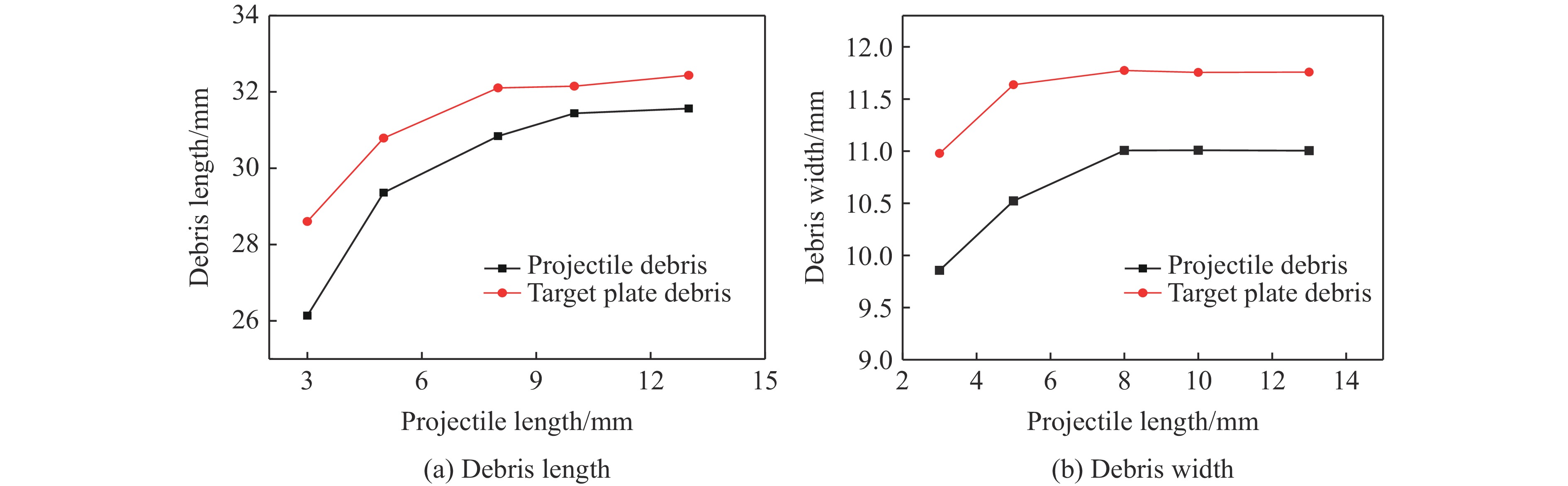
    本文对临界长度的定义是从数值模拟结果为出发点，通过测量弹体穿靶后的侵蚀长度与光滑粒子的塑形变形区长度，两者之和可以认为是弹体的临界长度。本例中撞击完成后，弹体长度被侵蚀掉3.88 mm，考虑到被侵蚀头部的塑性影响区长度为4.75 mm，因此撞击时弹体的影响区长度为8.63 mm。设计并计算弹体直径为2.6 mm，长度分别为3、5、8、10和13 mm的钨合金弹以2.5 km/s的速度撞击厚度为2.5 mm的靶板，计算结果如图5和图6所示。

    分析计算结果发现：当弹体长度超过8 mm后，在相同撞击条件下（与13 mm弹体撞击时条件相同），弹体在相同时刻产生的破片云特征相似，所以基本确定其临界长度处于8～10 mm之间。

    • 2.2.   弹靶撞击过程的能量耗散分析

  • 本研究所统计的能量信息均根据AUTODYN输出的SPH粒子信息进行统计计算整合分析得到。弹体撞击靶板过程的每一时刻都存在弹体初始动能向其他形式能量的转化。在撞击时弹体损失的初始能量转化为弹体破片动能、靶板破片动能、弹靶材料的塑性能、内能以及穿靶过程引起的靶板振动耗能、电磁闪光辐射等。研究能量的转化形式以及转化量为撞击过程的机理分析提供了重要依据。

    式中：Ed为弹体总能损失，E1为弹体破片动能，E2为靶板破片动能，E3为弹靶总塑性能，E4为弹靶总内能，E5为靶板的振动能，E6为电磁辐射能。根据唐恩凌等[8]关于电磁辐射能的计算结果，电磁辐射能在耗能损失中占比极小，因此本研究的统计计算结果中不考虑撞击过程的电磁辐射能。

    • 2.2.1.   弹靶耗能分析

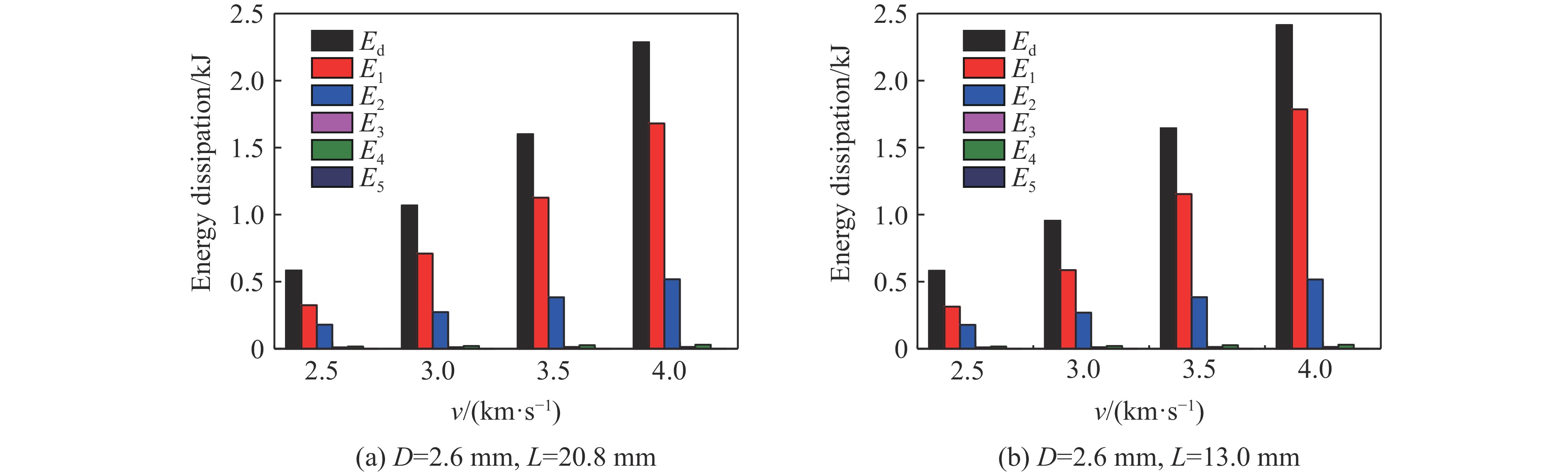
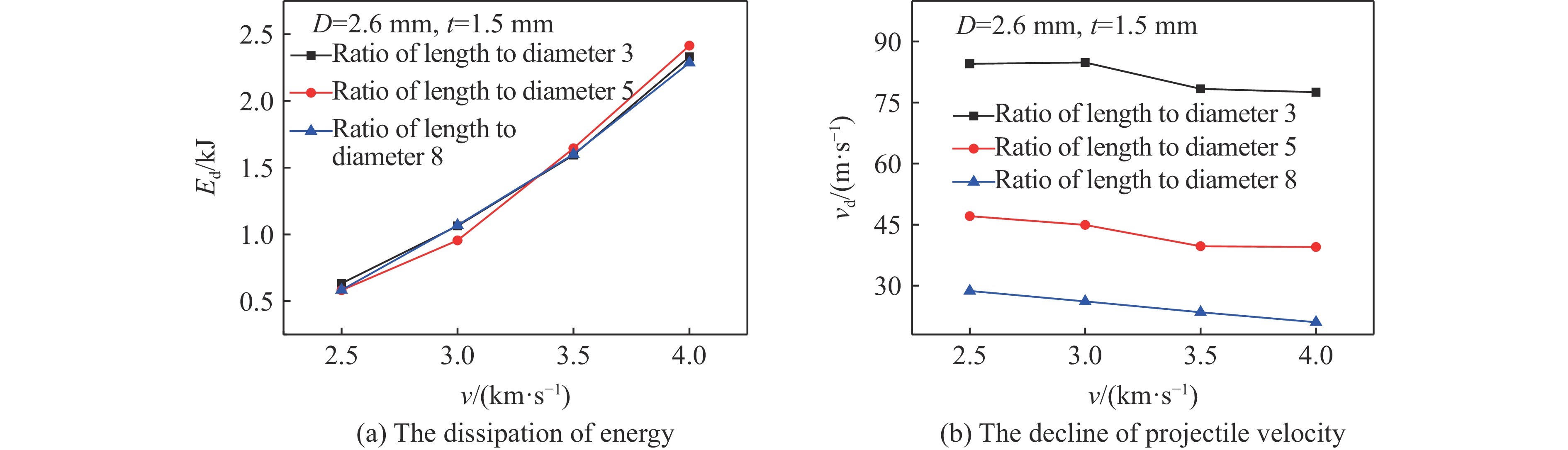
  • 图7和图8显示了直径为2.6 mm、长度为20.8、13.0和7.8 mm的弹体分别以2.5、3.0、3.5、4.0 km/s的速度撞击1.5 mm厚钢靶板在20 ${\text{μ}}{\rm{s}}$时的能量耗散。图8(b)的纵坐标vd为弹体的初始速度值与撞击后剩余的弹体速度值之差，即剩余弹体速度降低量。从图8可以明显看出，总能量损失Ed大部分转换为弹体的破片动能E1，其次是靶板的破片动能E2，并且弹靶破片动能占总能损失的80%以上，而其他形式能量所占比重较小。说明弹靶材料破碎形成空间破片是超高速撞击薄钢靶的主要耗能形式。当其他条件一定、弹体长度不同时，其能量耗散分布近似。

    • 2.2.2.   弹体总能量损失

  • 由图8(a)看出，当弹体直径为2.6 mm、板厚为1.5 mm时，随着撞击速度的提高，弹体在撞击过程的能量损失越发严重，结合图7分析可知，这是因为弹体头部与靶板材料撞击时，弹体头部破碎转化为弹体破片导致的；弹体长度为变量，且固定撞击速度和弹体直径，当弹体长度大于临界长度的弹体贯穿相同厚度薄钢靶所损耗的弹体动能可近似为恒定值。

    由图8(b)可见，当弹体直径、撞击速度相同时，大长度弹体撞击薄钢靶后剩余弹体降速缓慢，主要由于能量耗散近似固定，大长度弹体的剩余弹体质量大，需要剩余弹体速度降低较小量从而达到近似固定能耗。

    • 2.2.3.   塑性功与内能

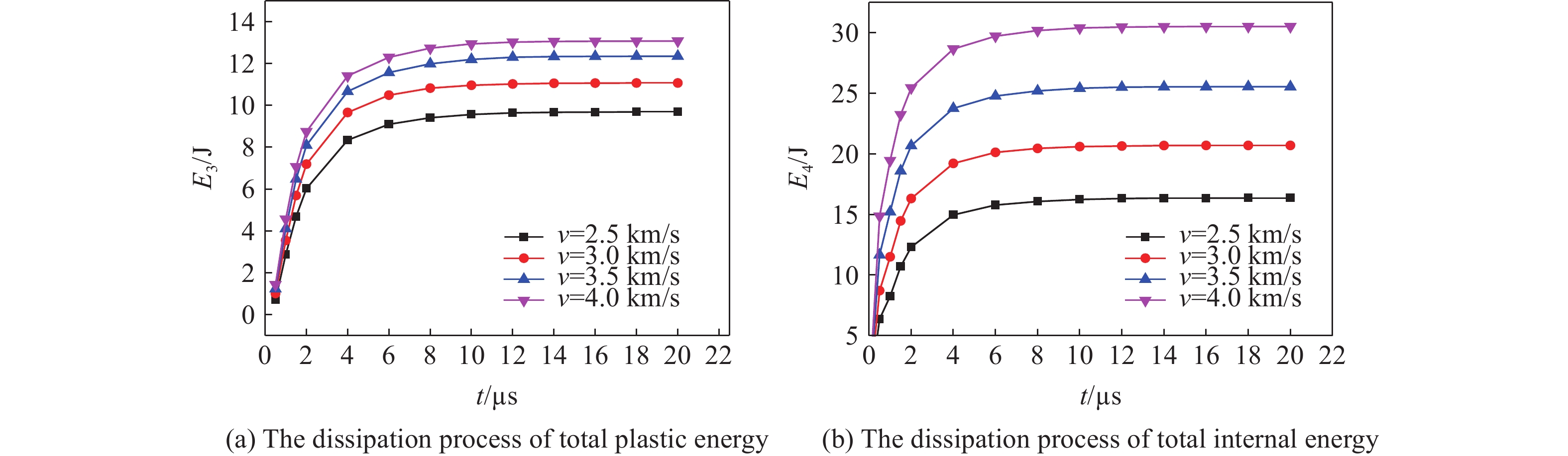
  • 图9为直径2.6mm、长度20.8mm的弹体分别以2.5、3、3.5、4km/s的速度撞击1.5mm钢靶板的不同时刻总塑形功和内能情况，可见能量耗散中塑性功E3和内能E4所占比例较少。在超高速撞击过程中，此部分能量集中在撞击表面接触处以及发生塑性变形的影响区，且作用区域较小，所以当此能量作用在弹靶材料影响区时，材料会发生状态改变。

    • 2.2.4.   靶板穿孔及振动过程分析

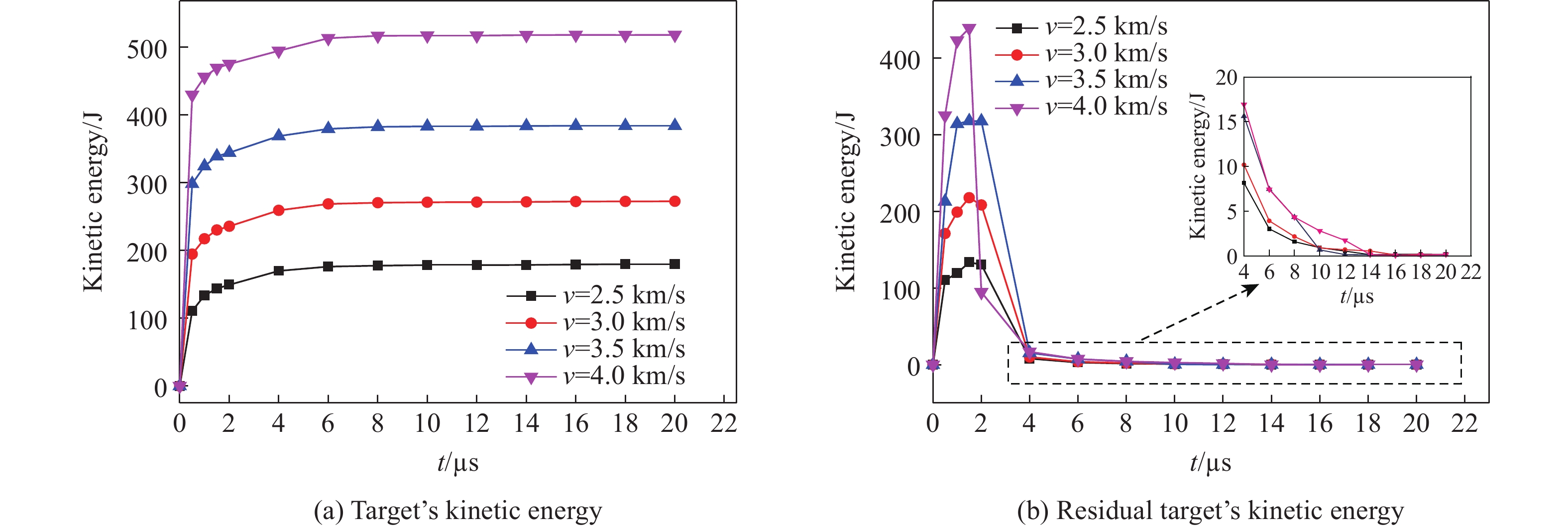
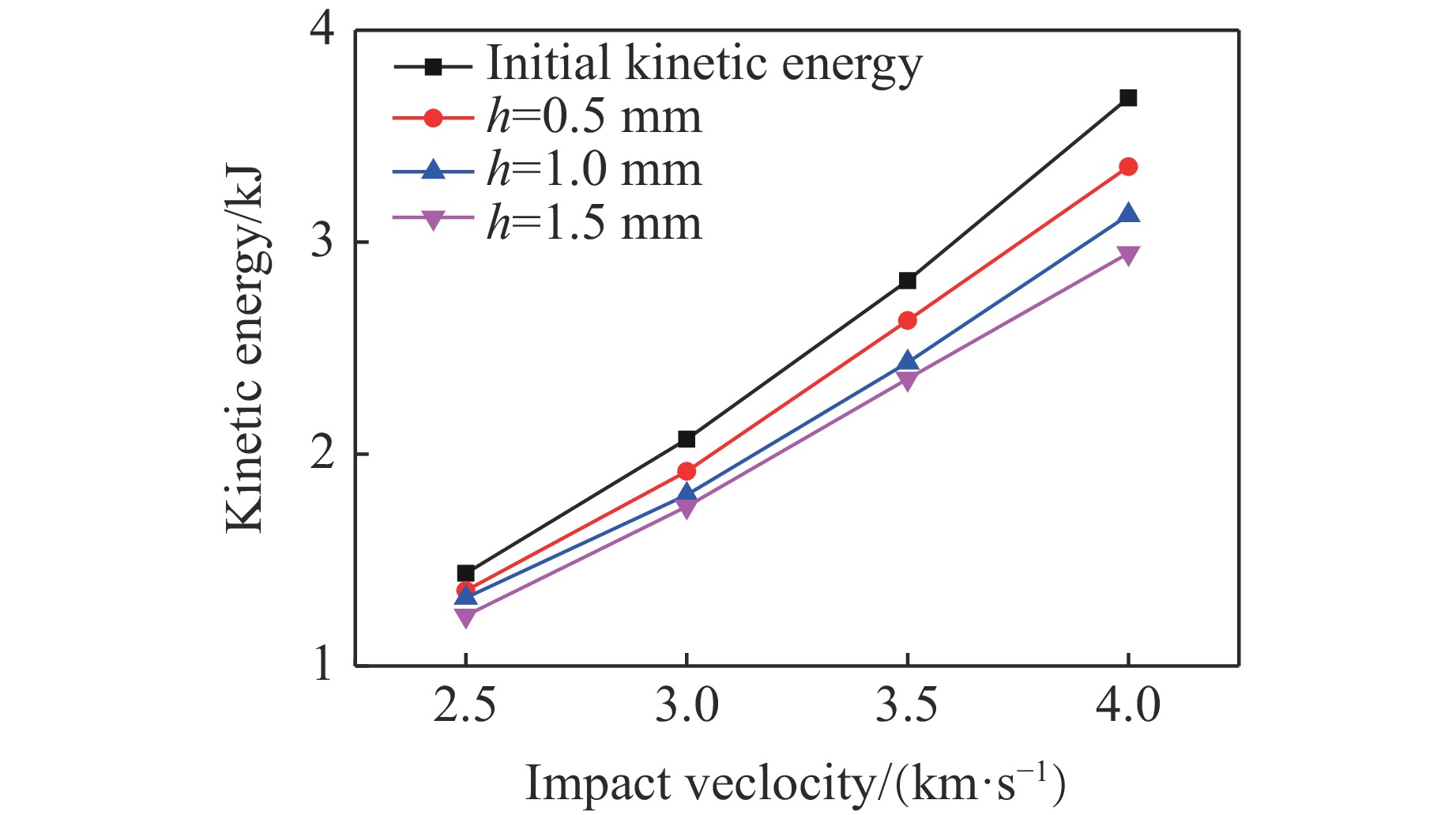
  • 图10(a)描述了靶板（包括剩余靶板和靶板破片）撞击过程的动能变化，以整个靶板的SPH粒子为研究对象，进行撞击过程靶板动能统计；图10(b)展示了剩余靶板的动能随时间变化曲线。靶板在0～2 ${\text{μ}}{\rm{s}}$获得能量积累，此时靶板伴有破片反溅耗能、开坑塑性形变耗能以及内能等形式耗散，靶板动能积累远大于能量耗散；2～4 ${\text{μ}}{\rm{s}}$靶板产生大量破片，靶板积累的能量开始大量转化为靶板破片的动能等，由于此时剩余弹体速度与靶板破片速度存在差异，两者依然相互作用，所以存在靶板总动能继续累积的过程，但耗散转化过程远大于能量累积过程；4～12 ${\text{μ}}{\rm{s}}$弹体基本完全穿透靶板，剩余弹体与头部弹靶破片逐渐分离，但仍存在轻微的相互作用，因此靶板材料总动能依然略微增加。此时存在剩余靶板以振动形式耗散；12 ${\text{μ}}{\rm{s}}$以后，剩余弹体与靶板材料几乎无相互作用，靶板材料所获动能总量基本不变，剩余弹体能量耗散基本趋于稳定，撞击过程基本完成。

    本研究还模拟了直径为1.6 mm、长度为13.0 mm的钨合金弹以2.5～4.0 km/s的速度撞击厚度（h）为0.5～1.5 mm的钢靶板，结果如图11所示。

    从图11可以看出，当钨合金弹体在相同条件下撞击不同厚度的靶板时，随着弹体撞击速度增加，弹体初始动能与剩余弹体动能之间的差值变大，即能量损失量增加，验证了本研究结论的合理性。

3.   结　论

  • (1) 数值仿真破片识别所得到的剩余弹体速度和长度结果与实验图像处理得到的结果差别较小，验证了所选用数值仿真参数的合理性。

    (2) 弹体超高速撞击薄钢靶时，弹体损失的能量中占比最多的为形成弹靶材料破片的动能，而弹靶塑性能、内能以及靶板振动能等形式损耗的能量占比较小。

    (3) 在其他条件一定的情况下，超高速撞击中，随着撞击速度的增加，弹靶破碎产生的破片量增大，弹体能量损失越多；弹体长度越长，撞击后弹体剩余速度与初始速度相比，其降低值越小。

参考文献 (16)

目录

/

返回文章
返回