对于非均匀准脆性材料，其内部所具有的微裂纹、孔隙以及黏结界面的随机分布使材料力学性能的分布也随之变化。因此，很多学者认为，岩石、混凝土材料的准静态强度可以用Weibull分布表征^{[13, 16-19]}。与准静态不同的是，在动态载荷作用下，由于应变率效应，准脆性材料内部单元强度也发生改变。因此，在动态拉伸载荷下，必须充分考虑应变率带来的影响。

与在准静态拉伸载荷作用下类似^[13]，假设材料内部的准静态拉伸强度满足Weibull分布^[19]，具体表达式为

式中：${{\sigma _{\rm{s}}}}$为材料的准静态拉伸强度，m和$\lambda $为形状和尺度参数，f为材料拉伸强度的密度函数。同时，材料的均值E(${{\sigma _{\rm{s}}}}$)表示为

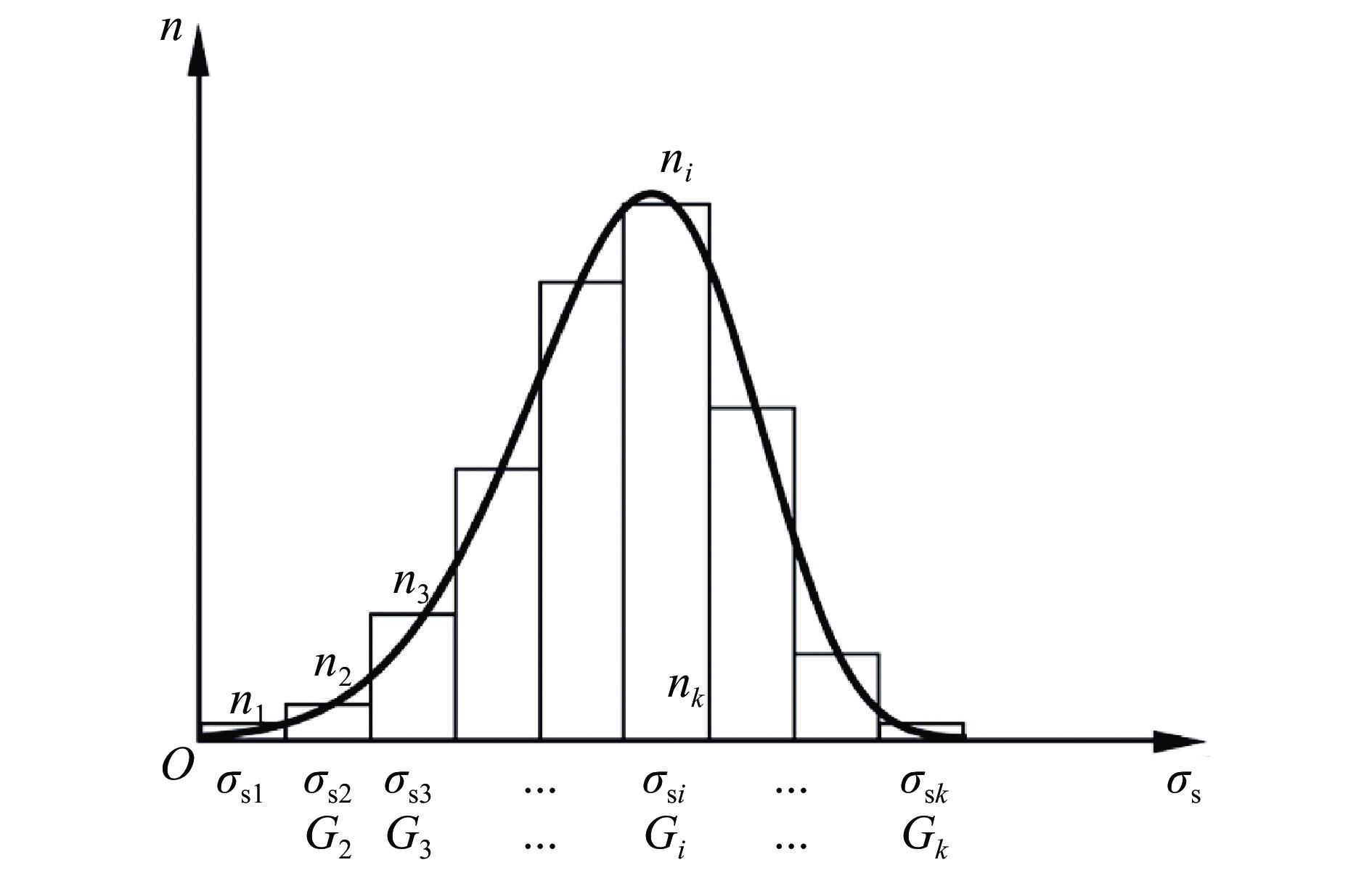
式中：$\varGamma $为Gamma函数，给定材料强度均值E(${{\sigma _{\rm{s}}}}$)和形状参数m以后，就可以得到尺度参数$\lambda $和Weibull分布的具体形式。

由Weibull分布函数可以得到材料的准静态强度的数量分布，如图1所示，横轴表示材料的准静态拉伸强度，将强度按一定间隔均匀划分，就可以由(1)式积分得到每种强度对应的数量，再将其随机分配到计算域中，把这称为材料强度的随机分布。如Li等^[13]所述，主要步骤如下：首先，将计算域划分为N个均匀且各向同性的单元；然后，将这N个单元划分为k个组G₁,G₂,···,G_k，每组包含n₁, n₂,···, n_k个单元，并且满足n₁ + n₂ + ··· + n_k = N；其次，将强度从小到大分为k组${\sigma \rm_{s1}},\;{\sigma \rm_{s2}},\; \cdots \;,\;{\sigma \rm_{sk}}$，每组的数量和计算域中k个组相对应，此外，为了保证单元拉伸强度的数量满足Weibull分布，需要满足${n_i}/N = f({\sigma _{{\rm{s}}i}})$；最后，对于计算域中的给定单元，其对应的强度需要使用一个随机数p∈(0,1)来确定，随机数由Monte Carlo随机数生成法获得。

考虑到材料强度的率相关性，Ou等^[15]认为材料动态失效强度不是材料的內禀特性，其应变率效应只是材料的一种结构响应，动态失效强度应称为动态承载能力。Petrov等^[20]提出了有限结构-时间准则，认为材料的失效存在一个孕育过程而非瞬间完成的。在此基础上，Ou等^[15]得到了脆性材料动态拉伸承载能力关于应变率的解析表达式

式中：${\sigma _{\rm{d}}}$为材料的动态拉伸承载能力，E为杨氏模量，${\dot \varepsilon }$为局部应变率，$\tau $为孕育时间。为了便于计算，假定材料中的加载波不会随时间衰减，并且裂尖处的局部应变率与边界应变率相同。

此外，为了描述应变率对裂纹扩展的影响，引入临界应变率作为判定条件。定义临界应变率为每一个裂纹扩展单元所需的最低应变率，临界应变率的拟合关系式^[21]为

式中：${{\dot \varepsilon }\rm _c}$为单元临界应变率，$\beta $为材料常数，一般取材料压缩强度与准静态拉伸强度之比的4%～10%^[22]。

由(3)式和(4)式可以得到材料中每一个单元的动态拉伸承载能力和临界应变率，其中，动态拉伸承载能力的随机分布如图2所示，L和H分别为模型的长度和高度。给定模型的尺寸后，将模型划分为一系列具有相同尺寸的单元，不同的明暗程度代表着不同的动态拉伸承载能力，颜色越暗的单元，其动态拉伸承载能力越强。在模型左侧中点处，预置一条长度为a的水平初始裂纹。

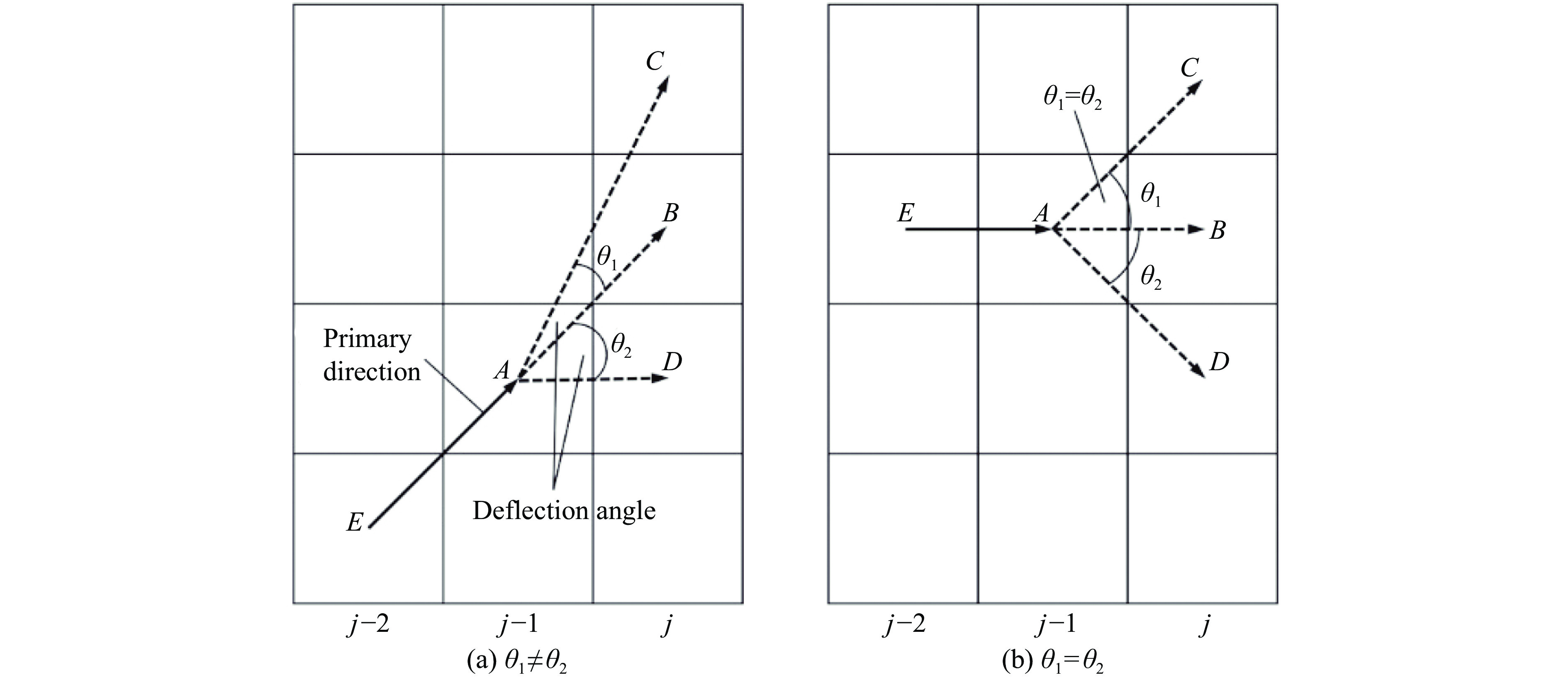
考虑到在动态拉伸载荷作用下，裂纹扩展模式与准静态的不同，本研究基于(3)式和(4)式提出两个扩展准则。第一个为应力准则，$\sigma \geqslant {\sigma \rm _d}$，当外载荷大于或者等于当前裂纹扩展单元动态拉伸承载能力时，该单元满足裂纹扩展的首要条件；第二个为应变率准则，$\dot \varepsilon \geqslant {{\dot \varepsilon }\rm _c}$，当局部应变率大于或者等于当前裂纹扩展单元临界应变率时，裂纹可以从该单元传递。

在数值计算过程中，由以上两个裂纹扩展准则就可以确定所有的裂尖单元（裂纹扩展路径上的单元），然后裂纹可以由所有裂尖单元连线生成。为了确定裂尖单元，将计算域分为p行q列的单元格。在本计算中，只考虑单一裂纹的扩展情况，也就是每一列中只有一个裂尖单元。为了确定裂纹扩展路径，引入裂纹主向^[13]对裂纹扩展做出判定。对于第j–1列的裂尖单元，其裂纹主向为j–1列裂尖单元和j–2列裂尖单元的连线，如图3(a)所示，EA则为第j–1列的裂纹主向。值得注意的是，本研究假设在动态载荷作用下，裂纹的扩展不再沿着能量耗散最小的方向传递，而是由裂纹主向所主导。这也是本研究动态裂纹扩展与准静态裂纹扩展最根本的不同之处。

在确定第j–1列中的裂尖单元以后，对于第j列中的裂尖单元，其确定方法如下。

（1）在第j列的p个单元中，找出满足应力准则的p₁（p₁≤p）个单元，将其作为裂纹可能传递的单元，构成集合S₁。如果${S_1} = \varnothing $，则第j列单元不满足裂纹扩展条件，材料在当前外载条件下不会发生断裂。如果${S_1} \ne\varnothing$，那么执行下一步。

（2）从第j列的p₁个单元中继续挑选满足应变率准则的单元p₂（p₂≤p₁），将这p₂个单元组成集合S₂，如果${S_2} =\varnothing $，则表明局部应变率太小使得裂纹以类似准静态条件下传递，即沿着最小能量耗散的方向传递。如果${S_2} \ne \varnothing$，那么执行下一步。

（3）如果p₂=1，意味着第j列中只有一个单元满足动载下裂纹扩展条件，那么这个单元就可以选择为这一列的裂尖单元。如果p₂>1，那么执行下一步。

（4）对于p₂>1时，意味着第j列中不止一个单元可以成为裂尖单元。因此，引入偏转角${\theta _i} (i = 1,2, \cdots, {p_2})$作为选择条件，定义偏转角为第j列中S₂集合中的单元与第j–1列中的裂尖单元连线与第j–1列中的裂纹主向的夹角。如图3(a)所示，比较S₂中所有的偏转角，如果S₂集合中只有一个最小偏转角，那么这个单元就会成为这一列的裂尖单元。如果不止一个最小偏转角，那么执行下一步。

（5）如图3(b)所示，如果第j列中有两个相同的呈对称状的最小偏转角，就从这两个最小偏转角中随机选择一个作为第j列的裂尖单元。

本研究所有的数值计算都在MATLAB软件中实现。对于动载下的泛形裂纹扩展模型，可以预见的是，给定满足材料断裂所需的外载荷以后，局部应变率越高，生成的裂纹轮廓线越平滑。因此，当局部应变率足够高，高于所有单元的临界应变率的时候，裂纹扩展路径会成为一条直线，此时的泛形复杂度C=1；相反，如果局部应变率特别低，低于所有单元的临界应变率的时候，裂纹扩展和准静态相同。

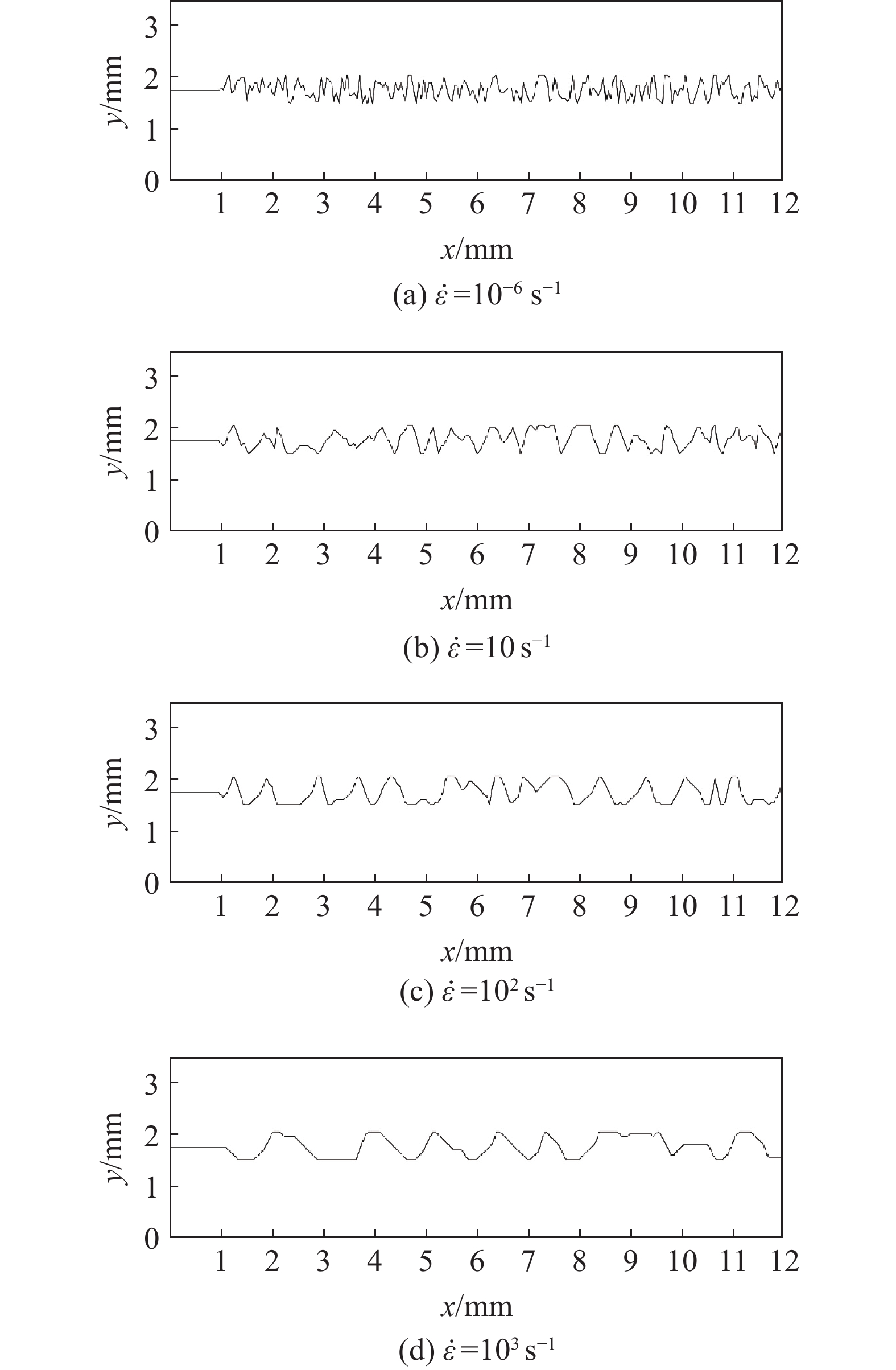
为了得到动态载荷下准脆性材料的裂纹扩展，选择常见的大理石作为研究对象。如图2所示，模型的长度和高度分别为L=12.0 mm，H=3.5 mm，并且，初始裂纹a=1.0 mm。计算过程中大理石所需相关参数有：杨氏模量E=34.65 GPa^[23]，拉伸强度均值为$E\left( {{\sigma \rm _s}} \right)$=7.52 MPa^[23]，压缩强度为37 MPa^[24]，准静态的拉伸强度可以由Weibull分布得到，形状参数m取为5^[16]，尺度参数由(2)式可得，$\lambda $=8.19 MPa，孕育时间$\tau $=51 μs^[24]。

由以上参数可以计算得到在不同应变率下的大理石拉伸断裂产生的裂纹轮廓图，如图4所示。可以明显看出，局部应变率越大，生成的裂纹轮廓线越平滑。

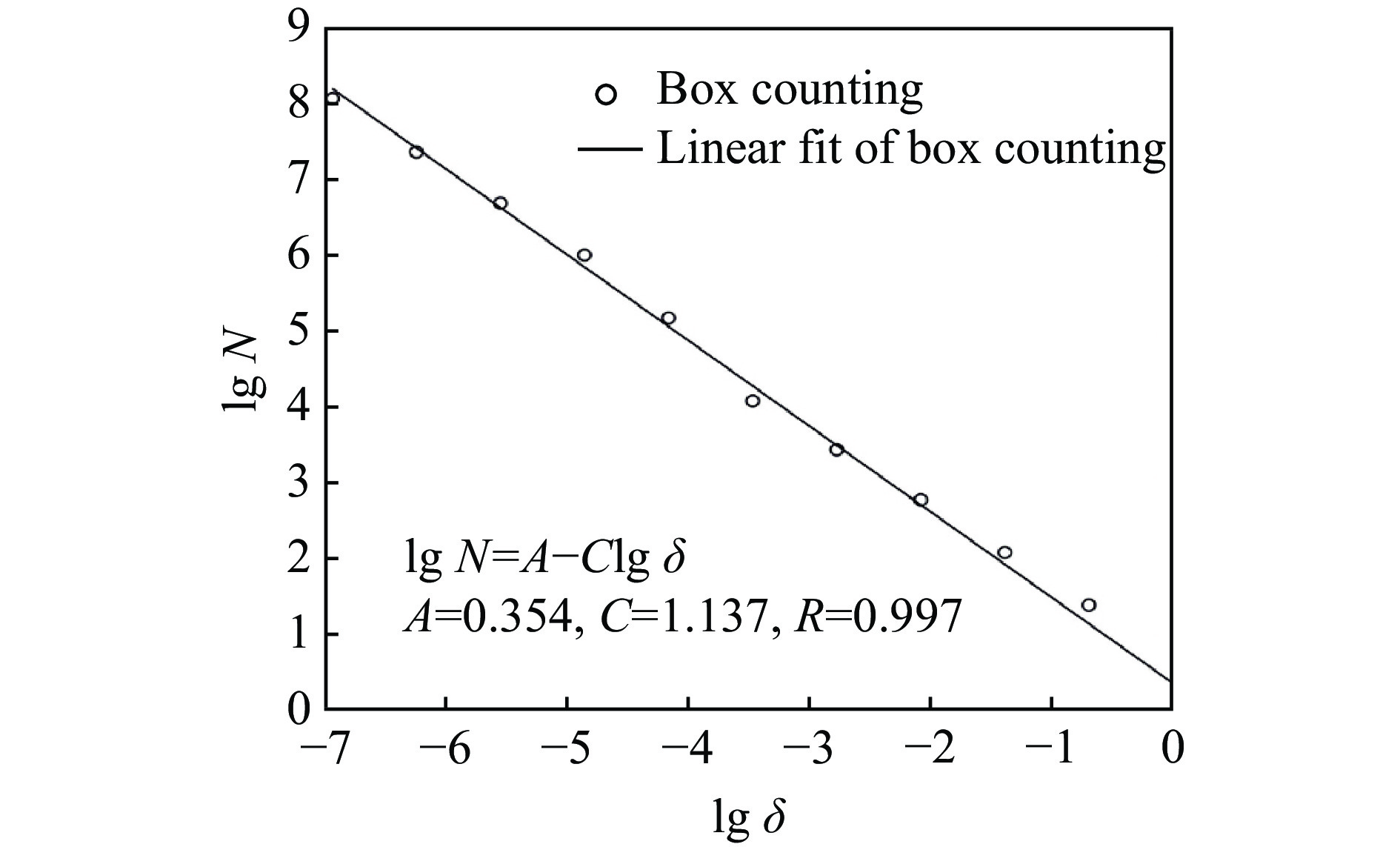
采用计盒维数法计算裂纹的泛形复杂度，其核心思想是计算覆盖裂纹所用的边长为$\delta $的盒子个数N($\delta $)，其拟合关系式为

当局部应变率为10³ s^–1时，泛形裂纹复杂度C=1.137，如图5所示，相关系数R=0.997。

为了研究动态载荷下应变率的变化对复杂度的影响，选取了5组不同空间分布的样本S1、S2、S3、S4、S5作为对比。其中，5组样本的Weibull分布参数相同，在不同应变率下的复杂度如表1所示。从表中可以看出，随着应变率的增加，复杂度随之降低，通过对比已有的实验数据，岩石材料裂纹复杂度在1.087～1.525^[25-26]之间变化。并且，由图4可以发现，裂纹轮廓线随着应变率的增加而趋于平滑。这就表明，随着应变率的增加，裂纹的扩展可能沿着裂纹主向上强度较大的单元而不是强度最小的单元。同时，在选择混凝土作为研究对象时也发现了这一规律，并且已有实验数据表明，混凝土材料的拉伸断裂面形貌随着应变率的增加而变得平直^{[5, 27]}。因此，本研究的模拟结果与实验基本一致，说明所构建的动载下准脆性材料的泛形裂纹扩展模型是合理的。

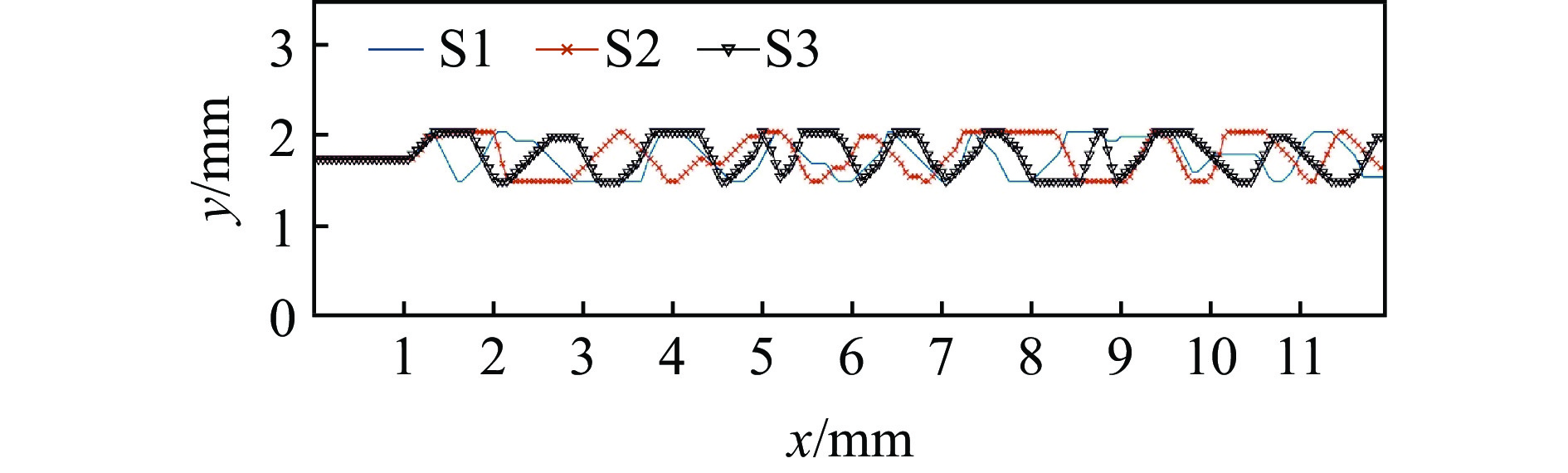
考虑到材料动态拉伸承载能力的随机分布对裂纹的影响，对比表1中的5组样本在相同局部应变率下的泛形复杂度。可以看出，在不同应变率下，5组样本的复杂度基本一致，并且都呈现出随应变率增大而减小的趋势。为了进一步分析动态拉伸承载能力的空间随机分布对裂纹构形的影响，选择3组样本S1、S2和S3在局部应变率为10³ s^–1时的裂纹轮廓线进行对比。如图6所示，尽管裂纹构形有所不同，但是裂纹的曲折程度近似。也就是说，具有相同参数但不同分布的准脆性材料，其动态拉伸承载能力的空间随机分布与复杂度无关，这也是动态载荷下裂纹扩展可以用泛形表征的基础。

在Weibull分布函数中，m作为形状参数影响着分布函数的具体形貌^[19]。也就是说，在不同的形状参数下，动态拉伸承载能力分布的均匀程度也有所不同。为了研究形状参数m的变化对裂纹扩展的影响，选取6组具有不同形状参数m的计算结果作为对比。保持其他参数不变，当临界应变率为10³ s⁻¹时，计算所得泛形复杂度如表2所示。

由表2可以看出，随着形状参数m的增大，泛形复杂度逐渐减小。考虑到Weibull分布函数的具体形貌，当m变大时，由Weibull分布函数表征的力学参数变得更加集中，即力学参数的分布就越均匀。这就意味着动态拉伸承载能力的分布随着m的增加趋于均匀，材料的均匀性越好，生成裂纹形貌也就越光滑，因此，泛形复杂度就越小。

本研究建立了非均匀准脆性材料动载下的泛形裂纹扩展模型，以大理石为研究对象，得到了大理石在动态载荷下的泛形裂纹构形，并通过计盒维数法得到泛形复杂度，和已有实验结果相比基本一致，证实了动态拉伸载荷下的裂纹扩展路径是泛形的。

（1）动态载荷作用下，随着局部应变率的提高，裂纹形貌越平滑，裂纹的复杂度越低，从本质上反映出在高应变率下，裂纹扩展可以通过裂纹主向上强度较大的单元，而不是朝着强度最小的单元，说明本研究假设动态载荷下裂纹扩展由裂纹主向所主导是合理的。

（2）复杂度与材料动态拉伸承载能力的空间随机分布无关，即在相同Weibull参数的条件下，材料强度空间分布的不同会影响裂纹的构形，但不会影响裂纹的曲折程度，而这也正是非均匀准脆性材料的裂纹扩展可以使用泛形表征的基础。

（3）复杂度随着Weibull分布形状参数m的增大而减小。形状参数m影响了材料动态拉伸承载能力分布的均匀程度，材料越均匀，生成裂纹就越平滑。