-
热辐射是一种基本的物理过程, 由于带电粒子的热运动, 从温度高于绝对零度的物体自发地辐射电磁能量. 传统的热辐射是宽带、非极化和非相干的, 这也导致红外波段的大部分能量不能有效利用, 降低了辐射效率. 因此, 实现合理的波长选择热辐射对于各种热管理应用是必不可少的. 在过去的20年里, 随着纳米光子学和纳米制造技术的快速发展, 对波长或亚波长尺度上的纳米结构的探索为调节热辐射带来了突破. 近年来, 超构表面[1–3]已经被广泛研究用于调节热辐射[4–10]. 由共振元原子组成的各种超构表面已被提出来实现窄带热辐射[11–14], 通过锥形超表面[15–17]或在超构表面中加入多共振原子[18–22]可以实现宽带热辐射. 二维亚波长纳米结构的超构表面由于其超薄的厚度, 可以提供空间可调谐的辐射率, 更适合于红外器件的集成和小型化.
另一方面, 合成维度方法为设计各种人工微结构材料提供了全新的视角[23,24]. 在物理学领域, 超越传统三维体系之外的系统[25,26]中存在丰富的物理, 特别是丰富的拓扑物理[27,28]. 尽管从理论上讲三维物理现象可以在完整的三维结构中得到探索, 但实际上构建这样的结构可能会遇到重大挑战[23,24]. 相比之下, 研究一维或二维系统中的这些物理效应显得更为可行且高效. 合成维度作为光子学中的一个新兴概念, 在其他物理系统中也得到了广泛研究, 如光学晶格中的冷原子[29,30]和超导量子元[31]. 而合成维度在光子学中具有独特之处. 一方面, 光子具有多个内禀自由度, 在选择光子态来构造人工晶格时, 可以利用光子系统中不同的频率[32–34]、角动量[35–37]或者空间模式[38,39]等. 例如在光子谐振环内通过引入频率维度研究多维能带结构[33]或布洛赫振荡[32,34], 又或是将角动量之间的耦合作为新的维度, 从而研究非厄米系统中的奇异点[37]. 另一方面, 可以通过系统的结构或者物理参数引入合成维度, 从而在低维度的系统中研究诸如外尔奇异环[40]或合成外尔点[41–48]的高维物理. 相应地, 合成空间的构造也为在光子系统中操控这些内在自由度提供了可能, 其中也涵盖了对热辐射的操控[49].
本文以超构表面上集成的一维光子晶体阵列为基础, 通过巧妙融合两个光子晶体阵列的几何结构参数与布洛赫动量维度, 成功构筑了三维合成空间, 并在超构表面结构中实现了合成外尔锥. 基于结构色散在合成空间中的灵活性和可操作性, 我们利用角分辨热辐射谱(ARTES)设备, 对合成外尔锥进行了全面的热辐射表征. 分析结果表明, 所提出的结构具有作为波长选择热发射器件的潜力. 论文结构安排如下: 第2节详尽阐述了基于超晶格结构实现合成外尔点的原理和方法; 第3节展示了合成外尔锥的热辐射实验表征成果; 第4节基于实验数据进行深入讨论, 并阐释了通过调整合成参数来实现特定波长选择性热辐射的机制; 第5节对全文进行了总结, 并讨论了该研究在未来可能的应用前景.
-
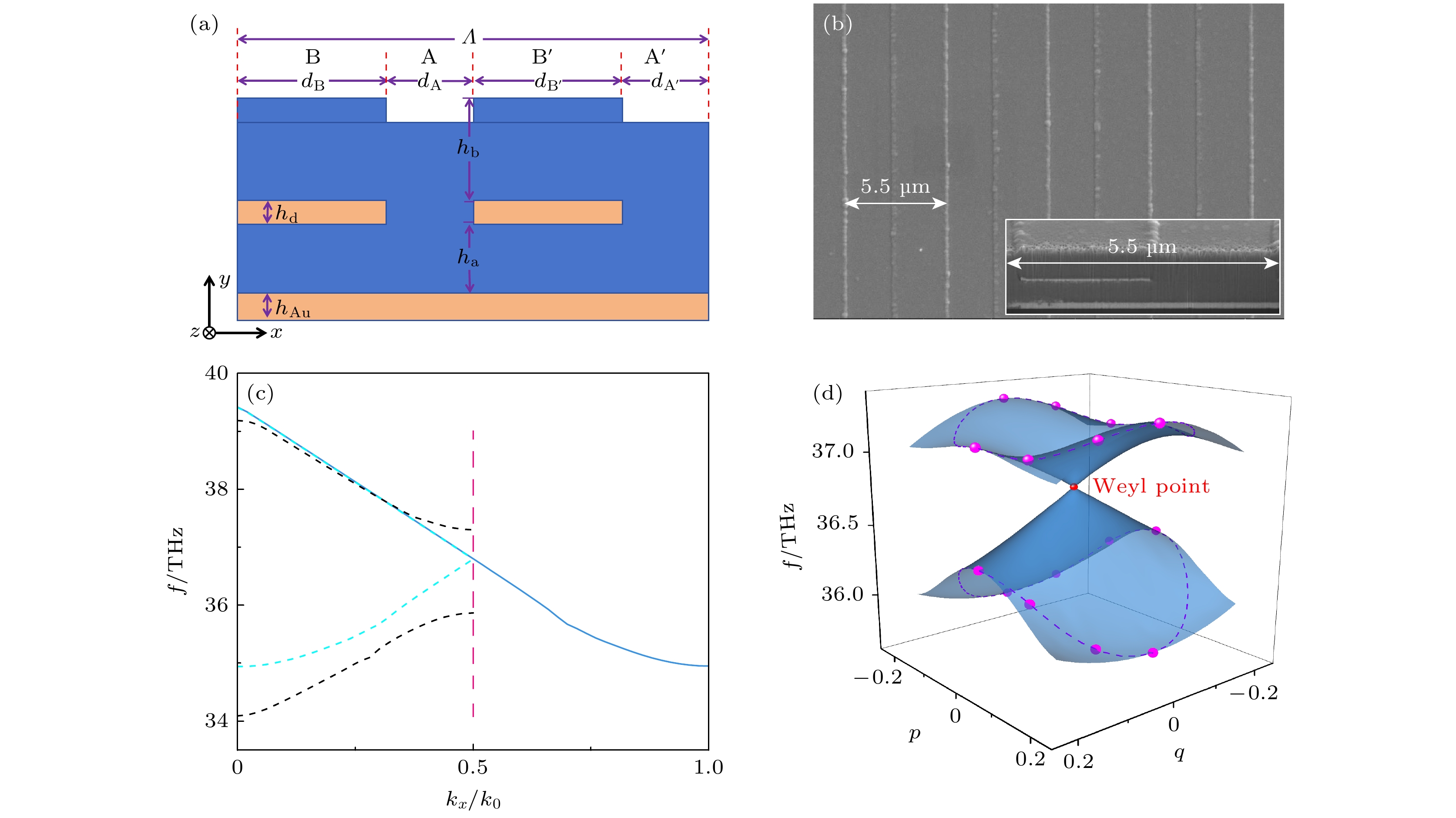
本工作首先讨论了可以灵活调节结构参数的超晶格的设计. 图1(a)展示了一维金属/介质/金属结构的光子晶体阵列的原胞结构. 其中蓝色部分代表金属锗(Ge), 黄色部分代表金属金(Au). 在这个原胞内部, 嵌入了4个多层结构. 根据结构的不同特点, 这些多层结构被标记为
$\rm A(A') $ 和$\rm B(B') $ . A和A' 由5层结构堆叠而成, 其顺序为Au/Ge/Au/Ge/Air; 而B和$\rm B' $ 则由3层结构组成, 顺序为Au/Ge/Air. 对于具有多层结构的元晶体, 通过调整金光栅和锗层的相应几何参数可以实现多层结构有效折射率的变化, 从而控制锗层内的TE模式(Ez)的色散. 由于结构中多层介质的等效折射率的虚部微乎其微, 这一现象揭示了在中红外波段, 该结构的损耗很小[49]. 基于这一认识, 本文并未将结构的非厄米性质纳入考量范围. 光子晶体阵列的宽度定义为:下面的所有计算中, 参数均取db = 2.5 μm, da = 3 μm. 相比于3层结构A和A', 5层结构B和B'的宽度略窄. 锗层的厚度分别为ha = 0.58 μm, hb = 0.73 μm, 金光栅的高度hd = 70 nm. 结构底层有一层厚度为hAu = 200 nm的金层.
(1)式中p和q是两个特意引入的独立结构参数, 其取值范围限定在(–1, 1)之间. 这两个参数分别用于调节多层结构A(A')和B(B')的宽度. 根据(1)式, 可得知5层结构A和A'的总宽度为2da, 同样地, 3层结构B和B'的总宽度为2db, 这意味着原胞的总宽度Λ是一个固定值, 即
$ \varLambda = 2\left({d}_{{\mathrm{a}}}+{d}_{{\mathrm{b}}}\right) $ . 每一个(p, q)组合都代表了一种特定的光子晶体阵列配置, 而一系列这样的(p, q)组合共同构成一个二维的合成参数空间. 此外, 光子晶体阵列在x方向的周期性质使其拥有一维的布洛赫波矢kx. 当这3个维度结合在一起时, 它们形成了一个三维的合成参数空间(p, q, kx).为了充分验证所提出的结构设计的有效性, 本研究设计了一系列具有代表性的样品, 并对其进行系统的测量实验. 图1(b)是结构参数为(p, q) = (0, 0)的样品对应的电子显微镜扫描图(SEM), 右下角插图中展示了一个周期单元的侧视图扫描电镜图. 在可见光和紫外光的频率较高的情况下, 由于金的等离子频率较高, 这些高频电磁波能够激发金属中的自由电子, 导致金属对这些频率的电磁波是透明的. 但对于红外波段的光来说, 其频率较低, 不足以穿透金属的等离子层, 因此适当厚度的金层可以隔绝红外波段的光. 在工艺流程初始阶段, 采用电子束蒸发镀膜技术(EBE)于硅片表面沉积一层200 nm厚的金层及一层厚度为ha的锗层. 该金层的厚度确保了中红外波段的光无法穿透, 而在后面的热辐射测试中, 该层材料能有效地屏蔽硅片自身的热辐射信号, 确保所探测的热辐射仅源自于设计的结构. 继而, 通过紫外光刻技术制备中间的金光栅, 其线宽精度可达1.5 μm, 满足样品的制备需求. 光刻处理后的样品再次经过EBE技术在表面沉积一层厚度为hd的金层, 随后再覆盖一层锗层, 从而完成了样品的整体制备.
-
从2.1节出发, 本文专注于图1(a)展示的结构中锗层内的导模, 因此后续所有的色散计算均只考虑锗层内的TE模式. 图1(c)展示了利用商业仿真软件COMSOL Multiphysics计算的该模型的色散, 我们选用了处于中红外波段且频率为37 THz附近的色散.
该模型中存在一个比较特殊的情况, 即参数(p, q) = (0, 0), 这种情况下原胞的参数可以简化成
$ {d}_{{\mathrm{A}}}={d}_{{{\mathrm{A}}}'}={d}_{{\mathrm{a}}}{, d}_{{\mathrm{B}}}={d}_{{{\mathrm{B}}}'}={d}_{{\mathrm{b}}} $ . 注意到原本具有周期Λ的原胞会退化成周期为Λ/2的原胞, 而布里渊区的宽度相应地变为原来的2倍. 然而, 当参数(p, q)偏离原点(0, 0)时, 原胞的周期重新变回原来的Λ. 在图1(c)中, 蓝色实线和青色虚线代表参数设置为(p, q) = (0, 0)时的色散曲线. 横轴中k0被定义为$ {k}_{0}={\mathrm{\pi }}/\left({d}_{{\mathrm{a}}}+{d}_{{\mathrm{b}}}\right) $ , 反映了布里渊区的基本周期. 值得注意的是, 青色虚线所代表的色散曲线是由于人工加倍原胞周期而产生的能带折叠现象所致, 它在布里渊区的X点(由红色虚线所标示)呈现出一个简并点. 另一方面, 黑色虚线则对应于(p, q) = (0, 0.2)时的色散情况, 通过将其与青色虚线进行比较, 我们可以观察到在kx = 0.5k0的位置上, 原本的简并点成功分离并出现带隙. 这一变化揭示了参数(p, q)微小变动对色散特性的显著影响.为了深入探究合成空间内的色散特性, 图1(d)展示了利用COMSOL软件计算所得的(p, q)空间能带色散图. 在此过程中, 所有计算所采用的波矢均取自布里渊区的X点, 即kx = 0.5k0. 在p和q均为零的条件下, 色散曲线呈现简并状态. 然而, 当(p, q)偏离坐标原点, 由于能带折叠现象, 色散曲线的简并度得到提升, 从而形成了带隙. 此外, 随着合成参数p和q数值的增长, 带隙亦呈现出扩大的趋势. 显然, 在简并点邻近区域, 模式的色散特性在各个维度上都表现出接近线性的特点. 图中的色散轨迹在三维合成空间内描绘出两个交叉的锥形曲面轮廓, 其形状类似狄拉克锥, 两个锥面的交点即为外尔点[41].
-
合成外尔锥在结构设计中具有天然的参数灵活性, 这一特性使得其在设计和构建超构表面时具有极大的自由度, 从而便于样品的制作, 并预示着在当前及未来应用中的便捷性. 此外, 合成外尔锥对于精准管理结构色散方面有卓越的能力, 包括调控色散带隙的开启与闭合, 结构中能带的拓扑性质也围绕中心的外尔点发生变化. 得益于这种可操作性, 其在色散调控以及色散相关的领域有很大的研究价值. 在此背景下, 我们制作了多个样品, 对第2节中设计的合成外尔锥进行了热辐射表征.
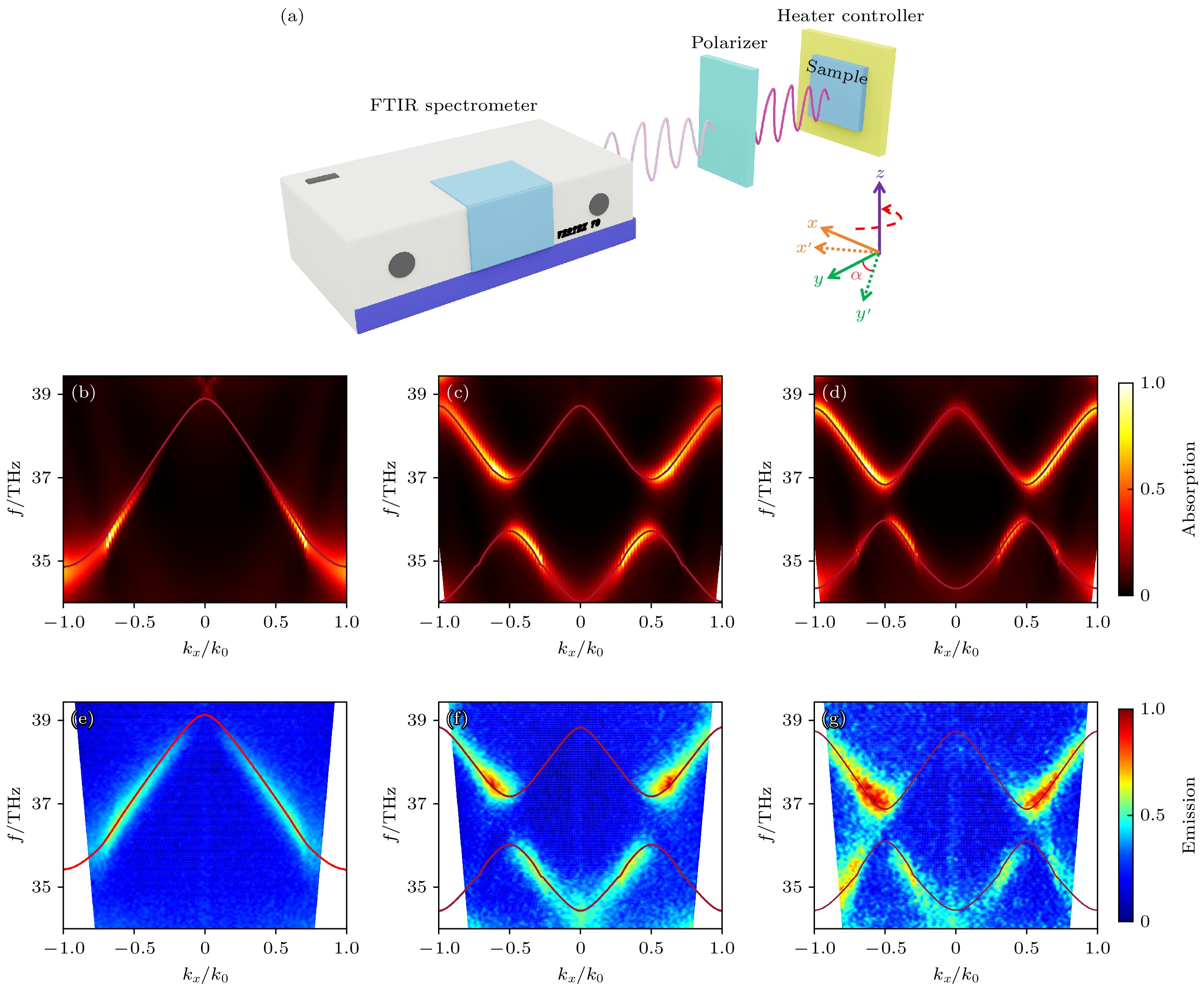
热辐射实验测量系统如图2(a)所示, 其中包括将样品安置于一个Linkam FTIR600加热器中, 确保在整个测试过程中样品温度恒定为100 ℃, 且温度波动控制在0.1 ℃以内, 保证了实验条件的稳定性. 样品被嵌置于旋转台之上, 其最小旋转步距精细至0.2°. 实验时通过围绕z轴旋转样品, 并透过加热器窗口捕捉样品的热辐射信号. 样品与探测器之间保持大约1 m的距离, 相较于波长而言, 这样的距离有助于确保获得较高的角度分辨率. 热辐射信号通过傅里叶变换红外光谱分析仪(FTIR: Bruker Vertex 70)在不同角度下进行分析, 期间应用偏振器来筛选信号, 确保FTIR光谱仪仅对TE模式的电磁波(Ez)敏感, 从而实现了对特定偏振状态的精确探测.
根据基尔霍夫辐射定律, 光吸收与热辐射过程互为逆过程, 通过计算模型中的光吸收强度可以来验证实验数据的准确性. 因此除了对样品进行热辐射性能的测试之外, 吸收光谱的计算可以用来验证实验结果.
除了对合成外尔点的表征, 实验上沿着
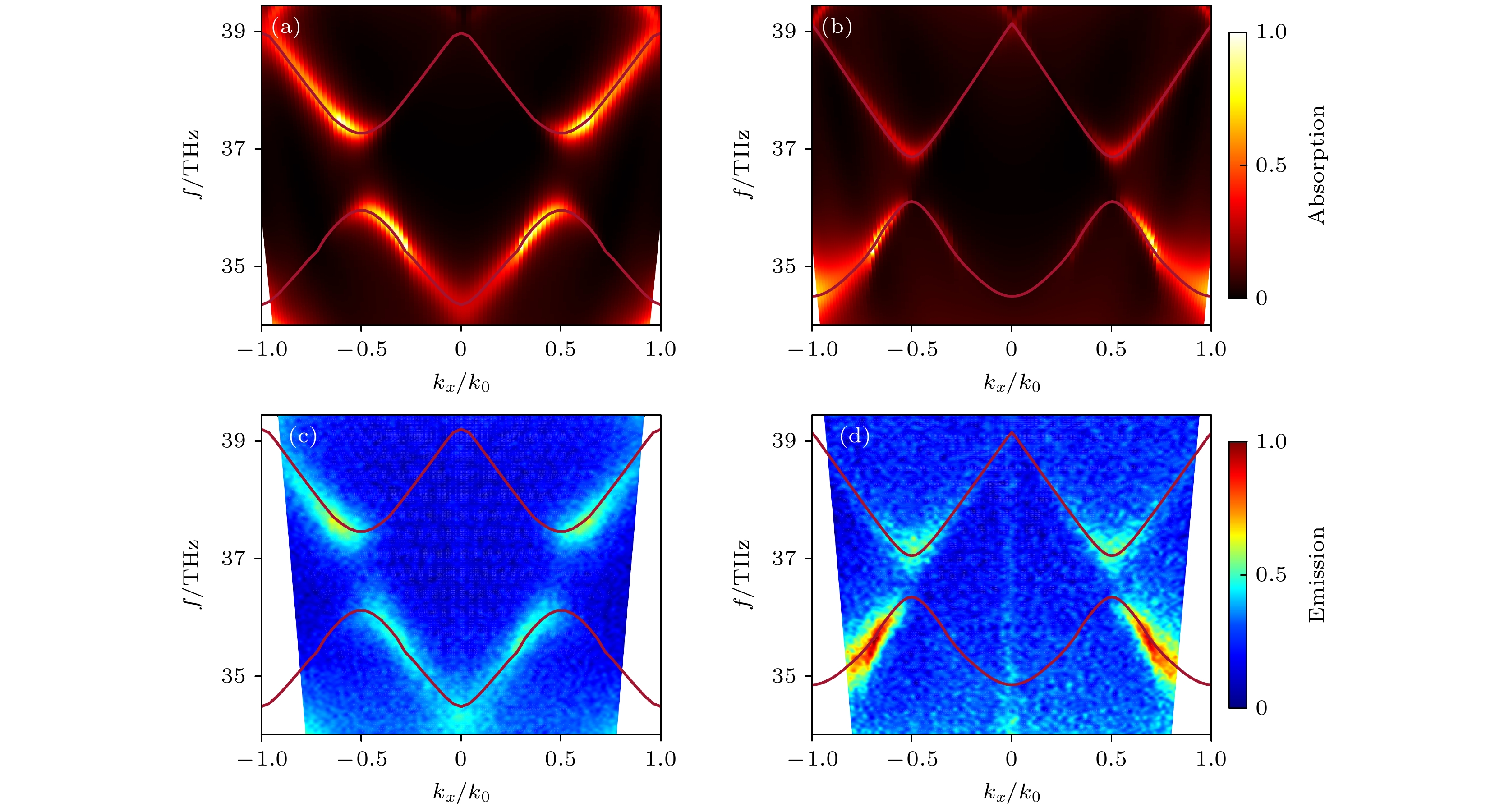
$ {p}^{2}+ {q}^{2} = 0.{2}^{2} $ 的参数回路设计并测量了另外4个数据, 如图1(d)所示. 紫红色圆点标记了进行实验表征的数据点, 图中外尔锥表面的紫色虚线标出参数的回路, 由于(p, q)与(–p, –q)对应相同的结构, 因此对应在外尔锥上相当于测量了9个点. 为了方便说明, 定义了一个参数空间的旋转角度θ, 它与参数(p, q)满足关系:$ p=0.2{\mathrm{s}}{\mathrm{i}}{\mathrm{n}}\theta , q=0.2{\mathrm{c}}{\mathrm{o}}{\mathrm{s}}\theta $ . 图2(b), (e)展示了参数为$ \left(p, q\right)=\left(0, 0\right) $ 的COMSOL, FDTD和热辐射实验测量结果. 图2(b)为FDTD仿真模拟的超晶格吸收谱, 结果是一个密度图, 旁边的颜色棒代表吸收的相对强度, 图中暗红色的实线是COMSOL的计算结果, 两者符合得很好. 图2(e)为利用角分ARTES表征的热辐射谱测量结果, 结果也是一个密度图, 右边的颜色棒代表热辐射的相对强度, 理论模拟与实验测量一致. 同样, 图2(c), (f)是对应参数$ \theta ={\mathrm{\pi }}/6 $ [对应合成参数(p, q) = (0.1, 0.1732)] 时, 理论模拟与实验测量的对比, 图2(d), (g)对应参数$ \theta ={\mathrm{\pi }}/3 $ [对应合成参数(p, q) = (0.1732, 0.1)] 时, 理论模拟与实验测量的对比, 实验结果与理论都符合得很好. 另外两个参数的数据对应$ \theta =0 $ [对应合成参数(p, q) = (0, 0.2)]和$ \theta ={\mathrm{\pi }}/2 $ [对应合成参数(p, q) = (0.2, 0)], 其模拟和测量结果在附录A中给出. -
在进行样品测量过程中, 样品被安置于旋转台上, 以便进行细致的角度调节. 通过绕z轴旋转样品, 并通过加热器窗口来检测样品的热辐射信号. 这里将样品的旋转角度
$ \alpha $ 定义为围绕z轴的旋转角, 如图2(a)右下角的插图所示. 特别地,$ \alpha =0^\circ $ 对应样品的表面与偏振片平行时z轴的旋转角, 此时探测器捕获的中红外表面波波矢与样品表面垂直, 并且探测到的中红外光波信号的波矢对应于$ {k}_{x}=k\cdot {\mathrm{s}}{\mathrm{i}}{\mathrm{n}}\alpha =0 $ . 所有样品的热辐射测试结果覆盖了$ \alpha \in \left[-40^\circ, 40^\circ\right] $ 的角度范围内的信号, 并以1°为探测步长进行细致扫描.在图2的测试结果中, 合成角度θ的变化对热辐射强度的影响显而易见. 尽管COMSOL模拟计算得到的色散线型的整体趋势保持相对稳定, 但热辐射的强度分布却随θ的变化而明显改变. 按照COMSOL的计算结果,
$ \alpha $ 和合成角度θ取任何数值都有对应的色散存在, 但是热辐射测量结果却只能与部分色散结果重合. 以图2(f), (g)为例, 这两个结果分别代表了合成角度为$ \theta ={\mathrm{\pi }}/6 $ 和$ \theta ={\mathrm{\pi }}/3 $ 的情况. 从色散线型的角度来看, 图2(f)显示低能带的热辐射强度峰值主要集中在第一布里渊区, 而图2(g)的低能带的最大热辐射强度却能覆盖第一和第二布里渊区. 对于单一样品的测量结果来说, 在k空间中, 波矢的扫描是通过改变热辐射角度 来实现的, 当波矢由
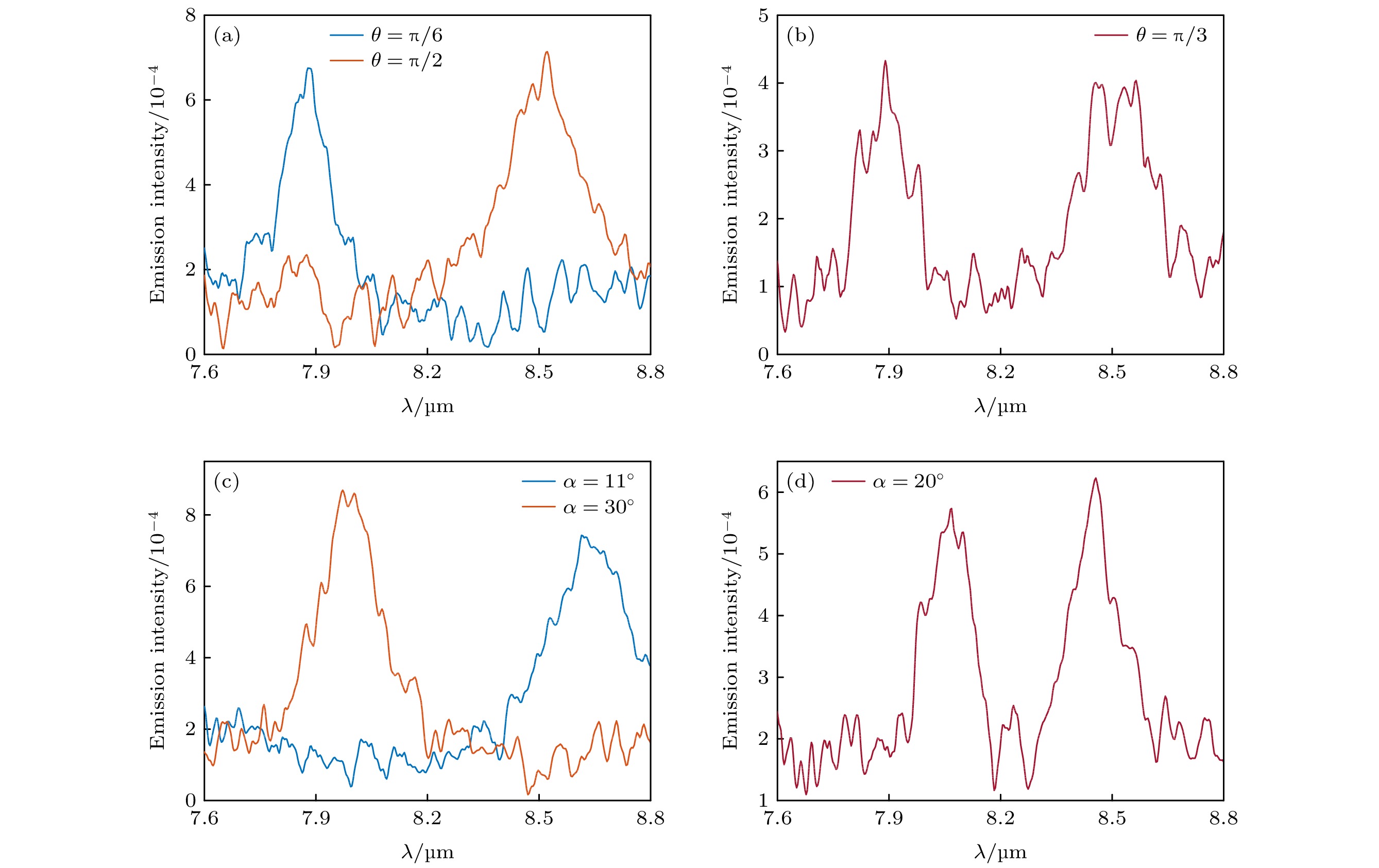
来实现的, 当波矢由$ {k}_{x}=0 $ 增至$ {k}_{x}={k}_{0} $ , 这个过程中辐射角度由$ \alpha =0^\circ $ 逐步增至$ \alpha =40^\circ $ , 而随着$ \alpha $ 的改变, 其热辐射峰的频率或者说热辐射峰的波长也发生改变. 这一现象揭示了合成角度θ的变化和辐射角度$ \alpha $ 的变化, 共同导致了热辐射强度的变化, 或者更准确地说, 是辐射波长的变化.热辐射强度受两个角度的调制现象由图3给出, 测量数据中出现的信号抖动是由于探测器测量波动所致. 图3(a), (b)给出了
$ \alpha =35^\circ $ 时, 不同合成角度下的热辐射谱. 当$ \alpha $ 固定时, 合成角度$ \theta ={\mathrm{\pi }}/6 $ 对应的辐射峰出现在7.9 μm的位置, 而在8.5 μm附近的辐射峰则被抑制, 如图3(a)中的蓝色实线所示. 然而, 当θ增至π/3时, 原本被抑制的在8.5 μm波段的热辐射峰被激发, 因此同时存在两个辐射峰, 如图3(b)中的红色实线所示. 当合成角度继续增至$ \theta ={\mathrm{\pi }}/2 $ 时, 原本位于7.9 μm位置的辐射峰被抑制而消失, 而在8.5 μm附近的辐射峰保留, 如图3(a)中的橙色实线所示. 热辐射波长也可以通过热辐射角度 来调制. 图3(c), (d)展示了当
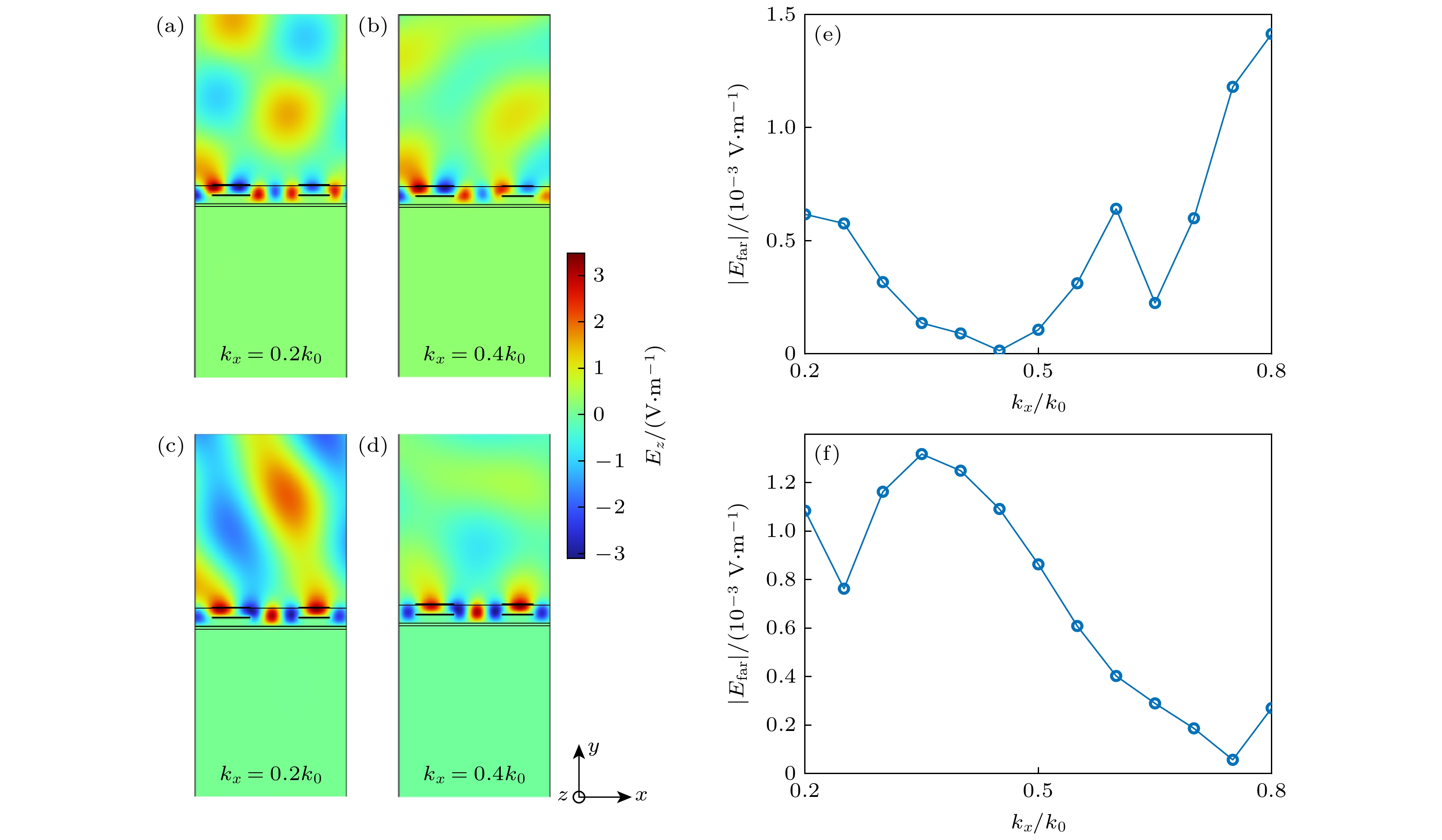
来调制. 图3(c), (d)展示了当$ \theta ={\mathrm{\pi }}/6 $ 时, 在不同热辐射角度($ \alpha =11^\circ, 20^\circ,\; 30^\circ $ )下的实验测试的结果. 当辐射角度设定为$ \alpha =11^\circ $ 时, 波长为8.5 μm处的辐射峰被激发, 而7.9 μm附近的辐射峰受到抑制, 如图3(c)中的蓝色实线所示. 当角度调整为$ \alpha =20^\circ $ 时, 位于7.9 μm和8.5 μm波段的热辐射峰都能够被激发, 这时在目标波段可以看到有两个辐射峰, 如图3(d)所示. 当辐射角度增至$ \alpha =30^\circ $ 时, 结果与$ \alpha =11^\circ $ 时截然相反, 波长为8.5 μm处的辐射峰被抑制, 而7.9 μm附近的辐射峰被激发.实验上对于超晶格色散的测量, 实际上是由热辐射激发超晶格的本征模式, 从而产生远场辐射. 两条色散对应着超晶格的两种本征模式, 不同波矢下两种模式的模场在附录B中给出. 超晶格本征模式的远场热辐射强度实际上与该模式的模场对称性有很大的关系. 以θ = π/6为例, 当kx = 0.2k0时和kx = 0.4k0时低频率的本征模式中存在明显且强度较大的近似对称模式, 如图B1(c), (d)所示, 这种模式能够产生较强的远场辐射. 而高频率的本征模式仅存在近似反对称模式或者存在强度较弱的近似对称模式, 如图B1(a), (b)所示, 这导致它无法向远场辐射. 但是随着辐射角度改变, 这种情况截然相反, 近似反对称模式能够在更大角度下向远场辐射(第二布里渊区), 而近似对称模式在更大的辐射角度下则被抑制. 为了让结果更加直观, 我们计算了θ = π/6时动量空间中的远场TE模式的电场模, 由图B1(e), (f)给出. 从趋势中也可以明显看出, 这种远场辐射随着波矢的变化趋势, 对于具有近似对称模式的低频率色散在较小的波矢下向远场辐射, 与此相反的高频率色散在较大的波矢下向远场辐射, 这就是在不同辐射角度下, 辐射峰波长会变化的原因.
另一方面, 随着合成角度改变, 结构的拓扑 相也在绕着中心的外尔点改变, 其对应的就是能带对称性的改变. 所以当合成角度从0变化到2π 时, 能带对称性的改变就会导致辐射峰从上下两条能带之间交换. 从实验结果来看, 当θ由0逐渐增至π/2, 能带对称性的改变导致两个模式产生远场辐射的角度发生改变. 实验中低频率的模式, 其可以进行远场辐射的波矢从短波矢逐渐向长波矢移动, 而高频率的模式, 其可以进行远场辐射的波矢则从长波矢逐渐向短波矢移动. 因此辐射角度一定时, 即在波矢不变的情况下, 合成角度改变导致的能带对称性的变化会使得辐射峰的波长发生变化.
-
本文通过对合成外尔点的操控实现了对热辐射波长的精细调节. 研究设计了一个由光子晶体阵列组成的拓扑超晶格, 成功在参数空间中构建出一个外尔锥. 随后, 基于合成外尔锥在结构设计中的参数灵活性以及在色散调控时的可操作性, 通过对合成外尔锥进行热辐射表征, 验证了实验结果与理论预测的高度一致性. 最后阐明了如何运用合成参数θ以及热辐射角度
$ \alpha $ 来精确控制热辐射波长选择性发射. 近年来, 研究者们通过使用超材料、超表面和光子晶体等结构, 设计出了新颖的波长选择热发射器. 而当前研究的各种波长选择热发射器, 通常只能在单一的结构参数下或者特定辐射方向上实现波长选择热辐射. 我们提出的波长选择性热发射器, 通过引入热辐射角度和结构的合成角度, 可以在辐射方向和结构参数两个维度上更为灵活地实现热辐射波长调控, 该结果可以作为高效、低成本的红外辐射源, 对于实际的红外应用, 如热光伏和热管理领域, 有广阔的应用前景. 这一发现不仅丰富了合成维度物理学的内涵, 还为设计和实现新型高效热辐射器件提供了重要的实验依据和技术路线.
基于合成维度拓扑外尔点的波长选择热辐射超构表面
Wavelength-selective thermal emission metasurfaces based on synthetic dimensional topological Weyl points
-
摘要: 黑体辐射通常具有覆盖整个红外波长范围的宽带光谱, 导致红外波段的大部分能量不能有效利用, 降低了辐射效率. 近年来, 具有二维亚波长人工纳米结构的超构表面因其在调节光学特性方面的灵活性而得到广泛研究, 这为调控热辐射提供了一个理想的平台. 在超构表面中, 采用合成维度方法为热辐射的精细调控开辟了新路径, 尤其突显了超越传统三维体系的物理特性和丰富的拓扑物理. 相比于在三维系统中探索物理现象, 研究一维或二维系统更为可行和高效. 合成维度的方法通过引入系统的结构或物理参数, 为操控光子系统中的内在自由度提供了可能性. 本文研究了利用合成维度方法实现波长选择热辐射. 首先在超晶格模型中构建合成拓扑外尔点, 通过角分辨热辐射谱(ARTES)对合成外尔锥进行实验表征, 在实现了合理的波长选择热辐射的同时能够尽可能地抑制其他波长的辐射, 对于实际的红外应用, 如热光伏和热管理装置, 是必不可少的.Abstract: Blackbody emission such as the emission from incandescent sources usually possesses a broadband emission spectrum covering the whole infrared wavelength range. Most of emission energy goes into the unwanted infrared range and consequently causes low emission efficiency. Recently, metasurfaces with two-dimensional subwavelength artificial nanostructures have been widely studied due to their flexibility in modulating optical properties, thus providing an ideal platform for controlling thermal emission. The use of synthetic dimension methods in metasurfaces has opened up new avenues for fine-tuning thermal emission, especially highlighting the physical properties beyond traditional three-dimensional systems and rich topological physics. Although it is theoretically possible to explore physical phenomena through complete three-dimensional structures, such structures are difficult to construct in practice. In contrast, studying one-dimensional system or two-dimensional system is more feasible and efficient. The synthetic dimension approach introduces the possibility of manipulating intrinsic degrees of freedom in photon systems by introducing structural or physical parameters. In this work, we propose utilizing synthetic dimension methods to achieve wavelength-selective thermal emission. Firstly, we construct synthetic Weyl point in a superlattice model and validate it theoretically. Subsequently, experimental characterization of synthetic Weyl cones is conducted by using angle-resolved thermal emission spectroscopy (ARTES). The experimental results demonstrate that we can achieve reasonable wavelength-selective thermal emission while suppressing emission at other wavelengths as much as possible. This is essential for practical infrared applications such as thermalphotovoltaics and thermal management devices.
-
Key words:
- thermal emission /
- metasurfaces /
- superlattices /
- synthetic dimensions .
-

-
图 1 (a)超晶格的结构示意图; (b)参数为(p, q) = (0, 0)的实验样品对应的SEM扫描图; (c)不同参数下的超晶格色散, 红色虚线标出了超晶格的第一布里渊区边界, 蓝色实线和青色虚线代表参数设置为(p, q)=(0, 0)时的色散曲线, 青色虚线是由于人工加倍原胞周期而产生的能带折叠现象, 黑色虚线是参数(p, q) = (0, 0.2)对应的色散; (d)合成空间中的外尔锥, 紫色虚线是参数空间中对应
$ {p}^{2}+{q}^{2}=0.{2}^{2} $ 的回路, 紫红色圆点是已表征的实验数据点Figure 1. (a) Schematic structure of the superlattice; (b) SEM picture corresponding to the experimental sample with the parameter (p, q) = (0, 0); (c) dispersion of the superlattice with different parameters, the red dashed line marks the boundary of the first Brillouin zone of the superlattice, the blue solid line and cyan dashed line represent the dispersion curves when the parameter is set to (p, q) = (0, 0), and the folding of the bands resulting from the artificial doubling of the unitcell period is marked by the cyan dashed line, and the black dashed line is the dispersion corresponding to the parameter (p, q) = (0, 0.2); (d) Weyl cones in the synthetic space, the purple dashed line is the loop in the parameter space corresponding to
$ {p}^{2}+{q}^{2}=0.{2}^{2} $ , and the fuchsia dots are the experimental data points that have been characterized.图 2 (a) ARTES测量装置及测量光路图; 由FDTD solutions计算的超晶格吸收谱(b)—(d)以及由ARTES测量的样品热辐射谱(e)—(g); (b), (e) 合成参数
$ \left(p, q\right)=\left(0, 0\right) $ ; (c), (f)合成参数$ \theta =\pi /6 $ ; (d), (g) 合成参数$ \theta =\pi /3 $ , 图片右边的颜色棒代表归一化吸收/辐射强度, 图中的暗红色实线来自COMSOL的仿真结果Figure 2. (a) ARTES measurement device and measurement optical path diagrams. The superlattice absorption spectra (b)–(d) calculated by FDTD and the thermal emission spectra (e)–(g) of the sample measured by ARTES: (b), (e) Correspond to the synthesis parameter (p, q) = (0, 0); (c), (f) correspond to the synthesis parameter θ = π/6; (d), (g) correspond to the synthesis parameter θ = π/3; colorbar on the right side of the picture represents the normalized absorbed/radiated intensity, and the dark red solid line in the diagram is from the COMSOL multiphysics simulation results.
图 3 不同参数下的热辐射谱 (a)热辐射角
$ \alpha =35^\circ $ 时, 不同$ \theta $ 角对应的热辐射谱; (b) 热辐射角$ \alpha =35^\circ $ 时,$ \theta ={\mathrm{\pi }}/3 $ 对应的热辐射谱; (c)热辐射角$ \theta ={\mathrm{\pi }}/6 $ 时, 不同$ \alpha $ 角对应的热辐射谱; (d) 热辐射角$ \theta ={\mathrm{\pi }}/6 $ 时,$ \alpha =20^\circ $ 对应的热辐射谱Figure 3. Thermal emission spectra with different parameters: (a) Thermal emission spectrum for different θ at thermal emission angle α = 35°; (b) thermal emission spectrum corresponding to θ = π/3 at thermal emission angle α = 35°; (c) thermal emission spectrum corresponding to θ = π/6 at different thermal emission angle α; (d) thermal emission spectrum corresponding to α = 20° for thermal emission angle θ = π/6
图 B1 合成角度θ = π/6, 当波矢为 (a) kx = 0.2k0, (b) kx = 0.4k0时高频率本征模式的模场分布以及当波矢为(c) kx = 0.2k0, (d) kx = 0.4k0时低频率本征模式的模场分布; (e) 合成角度θ = π/6时高频率色散对应的TE模式的远场辐射强度; (f) 合成角度θ = π/6时低频率色散对应的TE模式的远场辐射强度
Figure B1. Mode-field distributions of the high-frequency eigenmodes at synthetic angle θ = π/6 when the wave vectors are (a) kx = 0.2k0, (b) kx = 0.4k0 and the low-frequency eigenmodes when the wave vectors are (c) kx = 0.2k0, (d) kx = 0.4k0; (e) the far-field radiation intensity of the TE modes corresponding to the high-frequency dispersion at synthetic angle θ = π/6; (f) the far-field radiation intensity of the TE mode corresponding to the low-frequency dispersion at synthetic angle θ = π/6.
图 A1 由FDTD计算的超晶格吸收谱(a), (b)以及由ARTES测量的样品热辐射谱(c), (d); (a), (c) 合成参数
$ \theta =0 $ ; (b), (d) 合成参数$ \theta ={\mathrm{\pi }}/2 $ ; 图片右边的颜色棒代表归一化吸收/辐射强度, 图中的暗红色实线来自COMSOL的仿真结果Figure A1. Superlattice absorption spectra (a), (b) calculated by FDTD and thermal emission spectra (c), (d) of the sample measured by ARTES: (a), (c) Synthesis parameter θ = 0; (b), (d) synthesis parameter θ = π/2; colorbar on the right side of the picture represents normalized absorption/emission intensity, and the dark-red solid line in the picture is from COMSOL simulation result.
-
[1] Chu Q Q, Zhong F, Shang X H, Zhang Y, Zhu S N, Liu H 2024 Nanophotonics 13 1279 doi: 10.1515/nanoph-2023-0754 [2] Li A B, Singh S, Sievenpiper D 2018 Nanophotonics 7 989 doi: 10.1515/nanoph-2017-0120 [3] Chen H T, Taylor A J, Yu N F 2016 Rep. Prog. Phys. 79 076401 doi: 10.1088/0034-4885/79/7/076401 [4] Diem M, Koschny T, Soukoulis C M 2009 Phys. Rev. B 79 033101 doi: 10.1103/PhysRevB.79.033101 [5] Doiron C F, Naik G V 2019 Adv. Mater. 31 1904154 doi: 10.1002/adma.201904154 [6] Zhang X, Liu H, Zhang Z G, Wang Q, Zhu S N 2017 Sci. Rep. 7 41858 doi: 10.1038/srep41858 [7] Zhang X, Zhang Z G, Wang Q, Zhu S N, Liu H 2019 ACS Photonics 6 2671 doi: 10.1021/acsphotonics.9b00024 [8] Chu Q Q, Zhang F Y, Zhang Y, Qiao T, Zhu S N, Liu H 2022 Nanophotonics 11 4263 doi: 10.1515/nanoph-2022-0328 [9] Chu Q Q, Zhang F Y, Zhang Y, Zhu S N, Liu H 2023 Opt. Express 31 39832 doi: 10.1364/OE.504375 [10] Zhong F, Zhang Y, Zhu S N, Liu H 2021 Opt. Express 29 35216 doi: 10.1364/OE.439729 [11] Makhsiyan M, Bouchon P, Jaeck J, Pelouard J L, Haïder R 2015 Appl. Phys. Lett. 107 251103 doi: 10.1063/1.4937453 [12] Li J Y, Yu B W, Shen S 2020 Phys. Rev. Lett. 124 137401 doi: 10.1103/PhysRevLett.124.137401 [13] Kudyshev Z A, Kildishev A V, Shalaev V M, Boltasseva A 2020 Appl. Phys. Rev. 7 021407 doi: 10.1063/1.5134792 [14] Streyer W, Feng K, Zhong Y, Hoffman A J, Wasserman D 2015 Appl. Phys. Lett. 107 081105 doi: 10.1063/1.4929432 [15] Argyropoulos C, Le K Q, Mattiucci N, D'Aguanno G, Alù A 2013 Phys. Rev. B 87 205112 doi: 10.1103/PhysRevB.87.205112 [16] Kong A, Cai B Y, Shi P, Yuan X C 2019 Opt. Express 27 30102 doi: 10.1364/OE.27.030102 [17] Liu G Q, Liu X S, Chen J, Li Y Y, Shi L L, Fu G L, Liu Z Q 2019 Sol. Energy Mater. Sol. Cells 190 20 doi: 10.1016/j.solmat.2018.10.011 [18] Chen C, Liu Y H, Jiang Z Y, Shen C, Zhang Y, Zhong F, Chen L S, Zhu S N, Liu H 2022 Opt. Express 30 13391 doi: 10.1364/OE.447783 [19] Xu C L, Qu S B, Pang Y Q, Wang J F, Yan M B, Zhang J Q, Wang Z L, Wang W J 2018 Infrared Phys. Technol. 88 133 doi: 10.1016/j.infrared.2017.08.017 [20] Zhou J R, Zhan Z G, Zhu F D, Han Y G 2023 ACS Appl. Mater. Interfaces 15 21629 doi: 10.1021/acsami.3c01452 [21] Zhu Y, Hou G Z, Wang Q Y, Zhu T, Sun T, Xu J, Chen K J 2022 Nanoscale 14 10816 doi: 10.1039/D2NR02299K [22] Zou C J, Ren G H, Hossain M M, et al. 2017 Adv. Opt. Mater. 5 1700460 doi: 10.1002/adom.201700460 [23] Yuan L Q, Lin Q, Xiao M, Fan S H 2018 Optica 5 1396 doi: 10.1364/OPTICA.5.001396 [24] Liu H, Yan Z W, Xiao M, Zhu S N 2021 Acta Opt. Sin. 41 0123002 doi: 10.3788/AOS202141.0123002 [25] Zhang S C, Hu J P 2001 Science 294 823 doi: 10.1126/science.294.5543.823 [26] Qi X L, Hughes T L, Zhang S C 2010 Phys. Rev. B 81 159901 doi: 10.1103/PhysRevB.81.159901 [27] Ozawa T, Price H M, Amo A, Goldman N, Hafezi M, Lu L, Rechtsman M C, Schuster D, Simon J, Zilberberg O, Carusotto I 2019 Rev. Mod. Phys. 91 015006 doi: 10.1103/RevModPhys.91.015006 [28] Tang G J, He X T, Shi F L, Liu J W, Chen X D, Dong J W 2022 Laser Photon. Rev. 16 2100300 doi: 10.1002/lpor.202100300 [29] Kraus Y E, Zilberberg O 2012 Phys. Rev. Lett. 109 116404 doi: 10.1103/PhysRevLett.109.116404 [30] Mei F, Zhu S L, Zhang Z M, Oh C H, Goldman N 2012 Phys. Rev. A 85 013638 doi: 10.1103/PhysRevA.85.013638 [31] Tsomokos D I, Ashhab S, Nori F 2010 Phys. Rev. A 82 052311 doi: 10.1103/PhysRevA.82.052311 [32] Yuan L Q, Fan S H 2016 Optica 3 1014 doi: 10.1364/OPTICA.3.001014 [33] Cheng D L, Lustig E, Wang K, Fan S H 2023 Light-Sci. Appl. 12 158 doi: 10.1038/s41377-023-01196-1 [34] Englebert N, Goldman N, Erkintalo M, Mostaan N, Gorza S P, Leo F, Fatome J 2023 Nat. Phys. 19 1014 doi: 10.1038/s41567-023-02005-7 [35] Wang B, Chen T, Zhang X D 2019 Annual Conference of Chinese-Society-of-Optical-Engineering(CSOE)-Quantum Information Technology (AOPC) Beijing, China, July 07–09, 2019 [36] Cardano F, D'Errico A, Dauphin A, Maffei M, Piccirillo B, de Lisio C, De Filippis G, Cataudella V, Santamato E, Marrucci L, Lewenstein M, Massignan P 2017 Nat. Commun. 8 15516 doi: 10.1038/ncomms15516 [37] Yang M, Zhang H Q, Liu Z H, Zhou Z W, Zhou X X, Xu J S, Han Y J, Li C F, Guo G C 2023 Sci. Adv. 9 eabp8943 doi: 10.1126/sciadv.abp8943 [38] Bell B A, Wang K, Solntsev A S, Neshev D N, Sukhorukov A A, Eggleton B J 2017 Optica 4 1433 doi: 10.1364/OPTICA.4.001433 [39] Zhang F X, Feng Y M, Chen X F, Ge L, Wan W J 2020 Phys. Rev. Lett. 124 053901 doi: 10.1103/PhysRevLett.124.053901 [40] Liu J J, Li Z W, Chen Z G, Tang W Y, Chen A, Liang B, Ma G C, Cheng J C 2022 Phys. Rev. Lett. 129 084301 doi: 10.1103/PhysRevLett.129.084301 [41] Wang Q, Xiao M, Liu H, Zhu S N, Chan C T 2017 Phys. Rev. X 7 031032 [42] Yan Z W, Wang Q, Xiao M, Zhao Y L, Zhu S N, Liu H 2021 Phys. Rev. Lett. 127 013901 doi: 10.1103/PhysRevLett.127.013901 [43] Song W E, Wu S J, Chen C, Chen Y X, Huang C Y, Yuan L Q, Zhu S N, Li T 2023 Phys. Rev. Lett. 130 043803 doi: 10.1103/PhysRevLett.130.043803 [44] Fan X Y, Xia T Z, Qiu H H, Zhang Q C, Qiu C Y 2022 Phys. Rev. Lett. 128 216403 doi: 10.1103/PhysRevLett.128.216403 [45] Deng W M, Chen Z M, Li M Y, Guo C H, Tian Z T, Sun K X, Chen X D, Chen W J, Dong J W 2022 Light-Sci. Appl. 11 134 doi: 10.1038/s41377-022-00821-9 [46] Xia S, Lei S, Song D, Lauro L D, Alamgir I, Tang L, Xu J, Morandotti R, Buljan H, Chen Z J A P 2024 Adv. Photon. 6 026005 doi: 10.1117/1.AP.6.2.026005 [47] Yang B, Guo Q H, Tremain B, Liu R J, Barr L E, Yan Q H, Gao W L, Liu H C, Xiang Y J, Chen J, Fang C, Hibbins A, Lu L, Zhang S 2018 Science 359 1013 doi: 10.1126/science.aaq1221 [48] Wang Q, Ding K, Liu H, Zhu S N, Chan C T 2020 Opt. Express 28 1758 doi: 10.1364/OE.381700 [49] Zhong F, Ding K, Zhang Y, Zhu S N, Chan C T, Liu H 2020 Phys. Rev. Appl. 13 014071 doi: 10.1103/PhysRevApplied.13.014071 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: