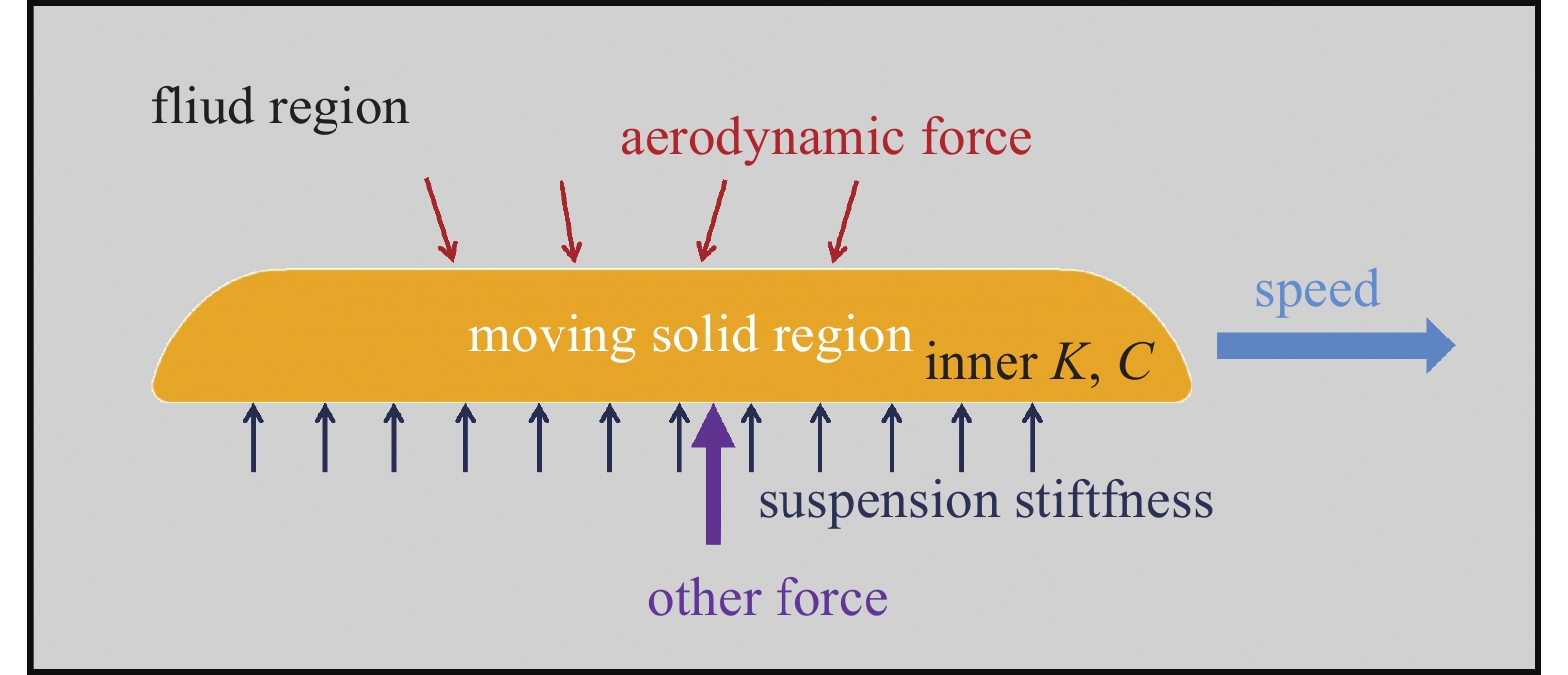
真空管道磁悬浮列车流固耦合效应研究需要在真空管道磁悬浮列车空气动力学研究中进一步融合考虑列车自身系统动力学响应对管道内流场产生的影响。如图1所示，在真空管道磁悬浮列车的空气动力学分析中引入了列车动力学参数，设置列车作为具有六自由度的运动物体，列车受到的气动在和作为车辆动力学分析的载荷参数，同时利用动力学理论分析列车姿态的变化。为实现两种力学理论的融合，利用欧拉描述对流体进行分析，拉格朗日描述对固体运动力学进行分析，将两种描述相结合形成任意拉格朗日-欧拉（Arbitrary Lagrangian-Eulerian, ALE）方法，可以实现了流固耦合分析中需要的空气动力学和运动力学分析的统一^[27]。利用该方法将列车动力学响应下的列车姿态变化融入流场分析理论中，形成了空气动力学−车辆动力学的大系统动力学研究理论。

首先对于流体分析，流体的质量守恒方程：

动量守恒方程：

式中ρ_f为流体密度、t为时间、f_f为流体体积力矢量。u_f为流体速度矢量、τ_f为剪切力张量。其中τ_f可表示为：

式中，p为流体压力，μ为动力粘度，e为速度应力张量，e可表示为：

由牛顿第二定律导出固体部分的守恒方程：

其中，ρ_s为固体密度、σ_s为柯西应力张量、f_s为固体体积矢量、u_s为固体域当地速度矢量，T为温度。

在列车和空气相互作用过程中，满足交界面上的流体和固体的速度守恒，因此满足：

$ {\boldsymbol{u}}_{\text{f}}^{\text{i}} $为流体在在耦合交界面上的速度，$ {\boldsymbol{u}}_{\text{s}}^{\text{i}} $为固体在耦合交界面上的速度，$ {\boldsymbol{\sigma }}_{\text{f}}^{\text{i}} $和$ {\boldsymbol{\sigma }}_{\text{s}}^{\text{i}} $分别表示流体和固体在耦合交界面上的应力，n为相互作用的交界面上的外法向量^[27]。

在满足交界面i上速度守恒的同时，交界面上的应力也同时需要满足守恒定律，实现应力平衡。但是交界面上的流体和固体节点并非完全重合，因此需要将将流体的应力映射到固体的节点上，从而实现两种计算域的应力有效传递，计算出固体节点力$ {\boldsymbol{F}}_{\text{s}}^{\text{i}} $：

$ {\left( {{{\boldsymbol{H}}^{\text{s}}}} \right)^{\text{T}}} $是流体到固体域的应力传递插值矩阵。

在传递节点应力的同时，需要利用固体的节点位移和节点位移传递插值矩阵计算出流体域的节点位移$ {\boldsymbol{X}}_{\text{f}}^{\text{i}} $：

$ {\left( {{{\boldsymbol{H}}^{\text{f}}}} \right)^{\text{T}}} $是固体到流体域的位移传递插值矩阵，$ {\boldsymbol{x}}_{\text{s}}^{\text{i}} $为交界面上的固体节点位移。

对于流体力学和固体力学分别采用欧拉和拉格朗日进行描述，本构方程为：

欧拉描述———流体流动方程：

式中，ρ为流体密度，t为时间，u_f为流体速度矢量，μ为流体动力黏度，T为温度，F为外力，p为压力，I为单位矩阵。

拉格朗日描述———运动力学方程：

式中，v_s为固体速度向量，σ为应力。

需要基于流体运动公式（9）和（10）计算得到的流场的流速u_f，进一步计算得到运动物体所受到的流体产生的载荷f：

式中，p为压力，μ为流体粘度，T为温度，I为特征矩阵。

本文中运动物体受到的流体产生的载荷为气动载荷。利用气动载荷f及网格单元的空间框架和材料框架的缩放因子dv和dV，可以进一步计算出运动物体受到的气动力矩阵F_f：

同时耦合效应需考虑物体刚性运动的速度$ {\boldsymbol{u}}_{\text{s}}^{\text{r}} $：

其中，$ {\boldsymbol{X}}_{\text{s}}^{\text{r}} $为运动物体的刚体位移矩阵。运动物体的刚体运动位移和变形量共同决定了流固耦合交界面上的固体节点位移$ {\boldsymbol{x}}_{\text{s}}^{\text{i}} $。

主要运动力学方程为：

其中，M_s为运动物体的质量矩阵，C_s为运动物体的阻尼矩阵，K_s为运动物体的刚度矩阵，F_a为气动载荷以外的其他外界载荷。

基于上述真空管道磁悬浮列车流固耦合理论，利用COMSOL多场分析软件的流体力学分析模块、多体动力学分析模块以及流固耦合分析器，构建出真空管道磁悬浮列车空气动力学−车辆动力学的联合仿真计算环境，实现了列车空气动力学分析和多体动力学分析实时联系，形成兼顾计算精度和计算效率的真空管道环境下列车流固耦合动力学分析计算方法。建立了考虑空气动力学−车辆动力学耦合效应的真空管道磁悬浮列车实时在线流固耦合数值计算模型。

真空管道磁悬浮列车分析模型采用二维模型，分析中采用单节车的结构，管道直径6 m，列车高度0.9 m，阻塞比为0.3，车体与管道地面的间隙为1 m。基于低真空管道仿真模型结构，设置列车为运动固体域，设置低真空管道内其余部分为流体域，建立低真空管道仿真模型。为实现340 m/s的运行速度，流场压力设置为0.1个大气压对应的密度，湍流模型设置为RANs的k-ω模型，温度为293.15 K。

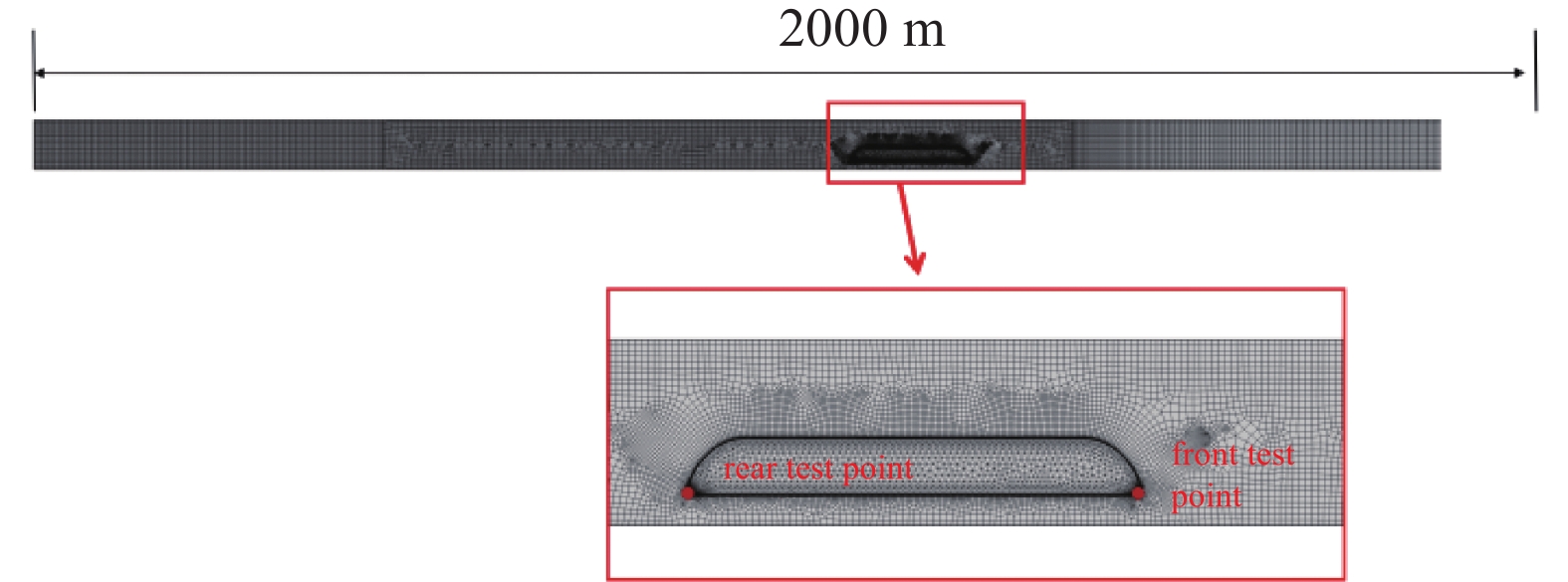
网格划分时，对运动域附近的网格设置为动网格，跟随运动域以相同速度运行，并将这部分网格进行细化。在远离运动域的部分，采用较粗的网格进行划分，降低整体网格数量，网格划分后如图2所示。其中在列车表面的网格需要相对较小，采用了最小10 mm的网格尺寸，在远离列车位置的网格，则采用渐变式网格，距离列车位置越远网格尺寸越大，网格最大为1000 mm。此外为了准确模拟列车表面附面层效果，对列车周围流场区域设置了边界层网格，总共设置了8层边界层，总网格数为112526个。

建立用于为列车提供悬浮力的悬浮力模拟单元。分析时采用了弹簧基座模型对悬浮力进行模拟。弹簧基座模型是一种可以定义与运动物体和固定地面之间相互作用的力元模型，该模型可以定义各向刚度和阻尼，同时可以定义该力元随运动物体以相同的速度运动。弹簧基座模型可以定义为沿运动物体表面均布的弹簧力元，可以实现较为均匀的悬浮特性模拟，对于电动悬浮这种电磁力特性具有较好的模拟效果。

设置列车运动速度曲线和流场边界条件。设置列车运动速度曲线，为模拟列车的高速运行，设置列车运行速度为先加速后匀速，其中为了保证计算的收敛性，定义列车在0.1 s内从静止加速到340 m/s，随后一直匀速运行至4.0 s。设置低真空管道流体域进出口为压力出口，相对压力为0。管道壁面边界为固定壁面，列车为低真空管道流体域的内部运动边界。其中管道顶部与底部均采用无滑移壁面处理。

基于空气动力学−车辆动力学的大系统动力学研究理论，利用提出列车流固耦合动力学分析计算方法和列车流固耦合数值计算模型，对真空管道磁悬浮列车在多种运行条件下的管道内空气流场分布特性和列车气动及运动特性进行了研究。对比研究了不同悬浮刚度以及固定姿态运行下列车流场特性，基于相关模型电磁力学分析结果，设置悬浮刚度为30，300，3000 kN/m三种等级，模型总质量为4.8 t，计算总时间为4 s。

从图3和图4的不同悬浮刚度下列车周围压力分布图可以看出，列车后部均存在多道反射波、斜激波。同时在刚度为300 kN/m、3000 N/m和固定姿态运行时，列车顶部与管道壁面间形成了多道反射波，而在悬浮刚度为30 kN/m时，列车顶部则没有出现这种反射波。此外，列车在30 kN/m悬浮刚度时，列车头部顶端出现了一个明显的低压区域。在低悬浮刚度下，列车周围的流场分布会与较高悬浮刚度下的流场分布出现明显差别，表明悬浮运行的列车的悬浮刚度会对气动特性产生明显影响，且悬浮刚度越低，流固耦合效应越明显。

图5为4 s时刻不同悬浮刚度下列车周围速度及流线分布。从该图可以看出30 kN/m的悬浮刚度下，列车尾部出现了两个明显的且非常靠近的高流速区域，而悬浮刚度越大的工况，车尾顶部的高流速区域表现越弱。主要原因是列车运行姿态变化更加大后，导致流场分布明显变化，列车尾部流速出现升高。在30 kN/m的悬浮刚度下，列车顶部的流线分布比较均匀，相反在悬浮刚度较大和固定工况下，由于车顶反射波的存在，列车顶部流线出现曲折分布。当悬浮刚度逐渐增大后，流场分布于列车固定姿态运行的流场分布特性逐渐接近。因此，列车悬浮运行工况下，悬浮刚度较小会导致流场与固定姿态运行的流场特性出现明显差异，列车尾部和列车顶部的流场分布均与固定姿态运行工况存在较大差异，较小的悬浮刚度会导致流固耦合效应突显。

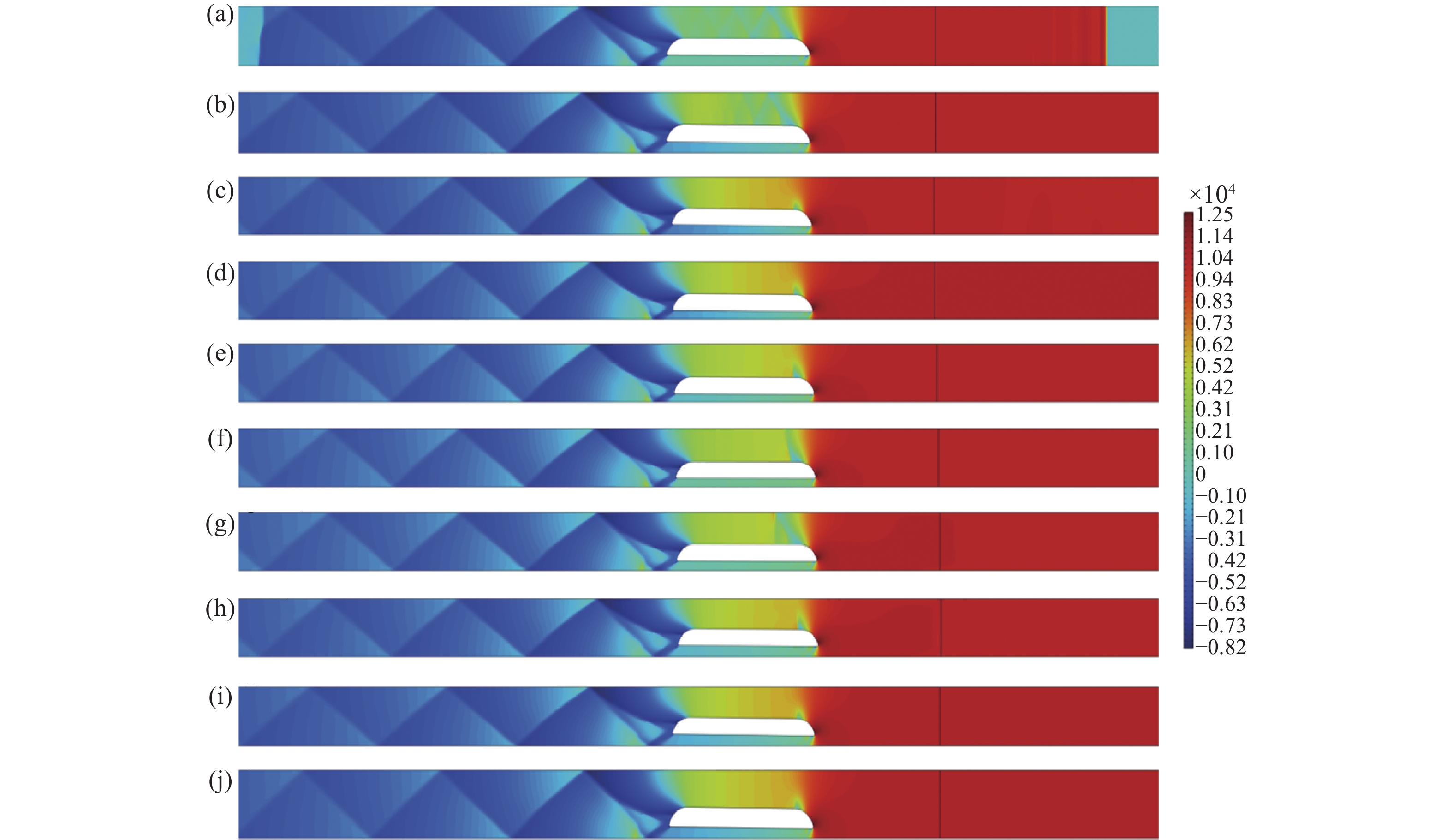
图6为流场悬浮刚度为30 kN/m工况下，不同时刻列车周围压力，可以从0.5 s和1 s时刻列车列车顶部也出现了固定姿态运行工况下的反射波，但是在1.5 s时刻，列车顶部反射波消失，并且在之后的时刻中不再出现。此外，列车头部的上方在1.5 s出现一个低压区域，1.5 s～3.5 s该区域逐渐增大，而3.5 s～5 s该区域逐渐减小，该低压区域面积随着列车运行呈现周期性变化。从0.5 s～5 s时刻列车周围的压力分布可以看出，列车尾部流场较为复杂，存在多道斜激波和反射波，但是随着列车的运行相对较为稳定，而列车顶部和头部的波系相对更加简单，但是会随着列车运行发生明显的变化。总结可知，列车的悬浮运行会导致列车存在非稳定流场中，尤其是列车顶部和头部流场变化明显。

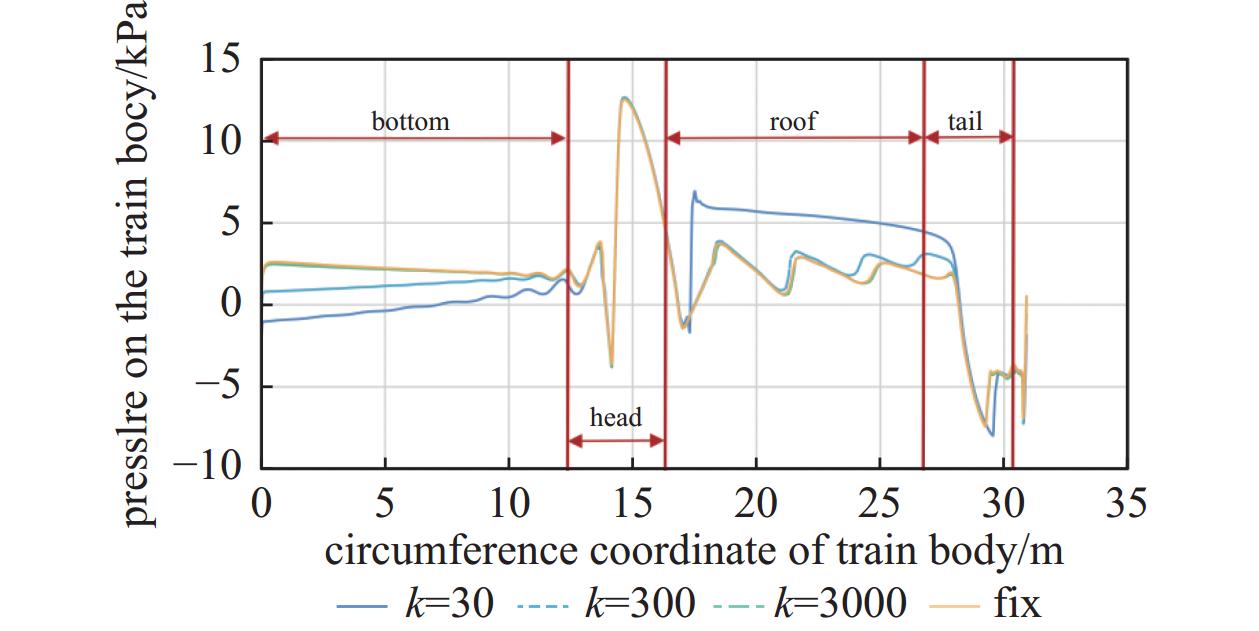
图7所示4 s时刻不同悬浮刚度下列车车身压力分布，其中车头和车尾部分的压力分布均相对较为接近，二在车底和车顶的压力分布则存在明显的差别。其中车底压力分布为，悬浮刚度越低压力越低。悬浮刚度30 kN/m工况下，车顶的压力远高于其他三种工况的压力分布，这一特性在前文中的压力分布图也可以看出，车顶未出现明显的反射波，且压力较高。因此，不同的悬浮刚度会导致列车周围的压力分布存在明显差别，对列车受到的气动载荷也会产生相应的影响。

为进一步分析真空管道磁悬浮列车在非定常气动环境下列车的运行特性，利用空气动力学−车辆动力学真空管道磁悬浮列车流固耦合数值计算模型，对多种悬浮刚度条件下的列车运动力学特性进行数值计算分析，重点关注列车的气动载荷变化特征。

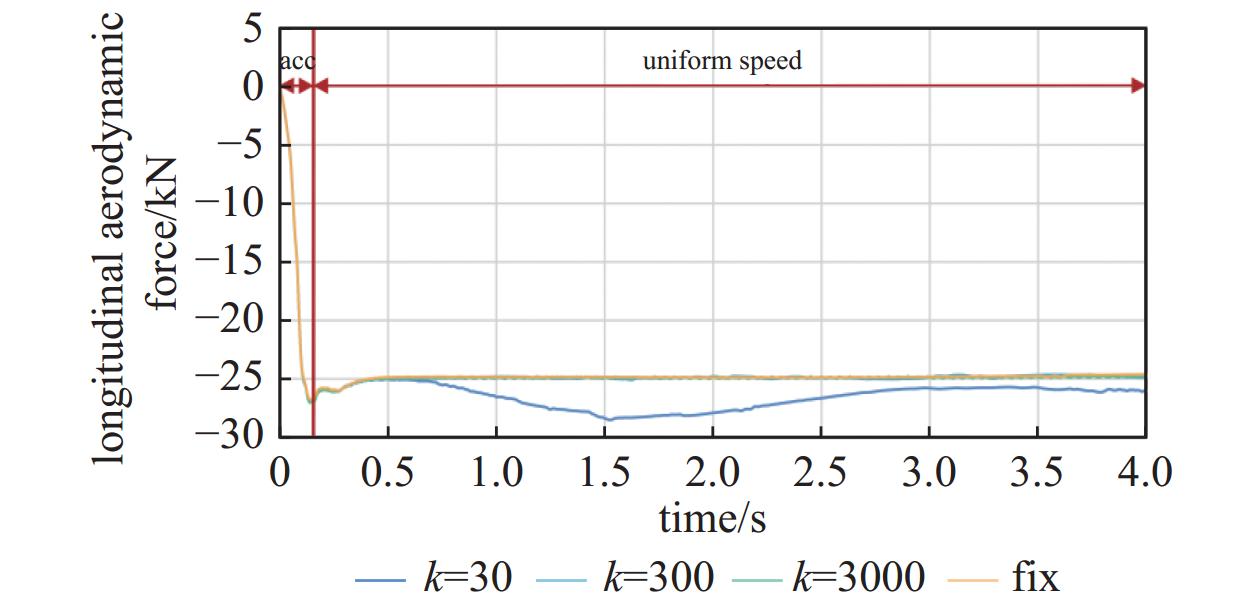
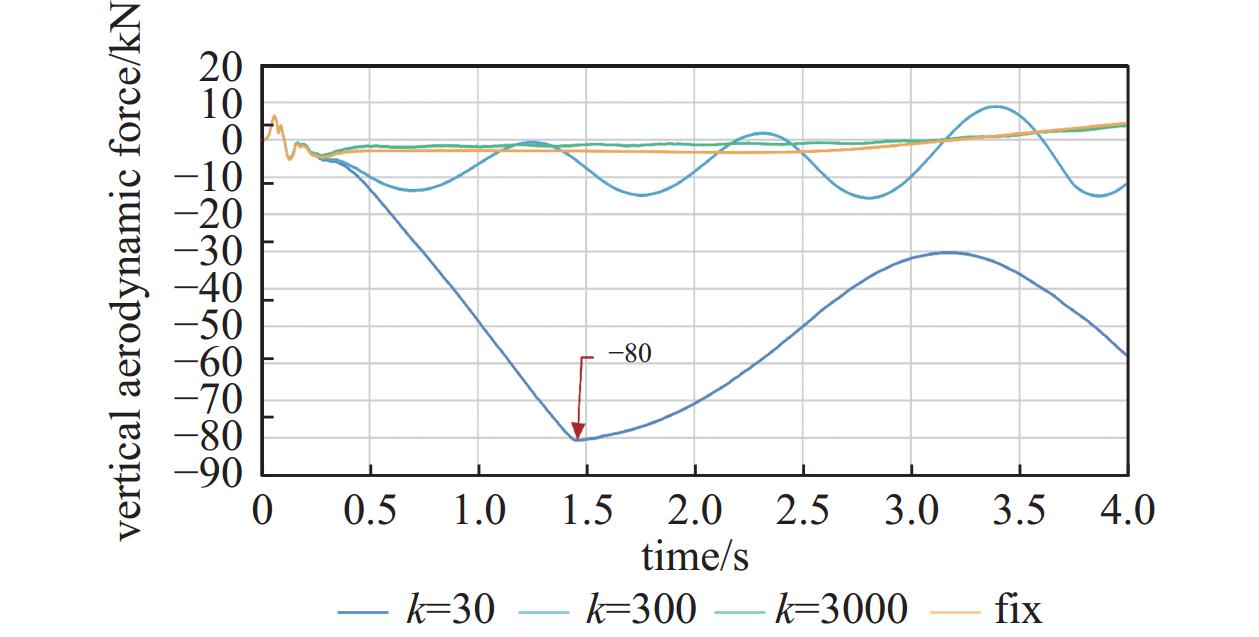
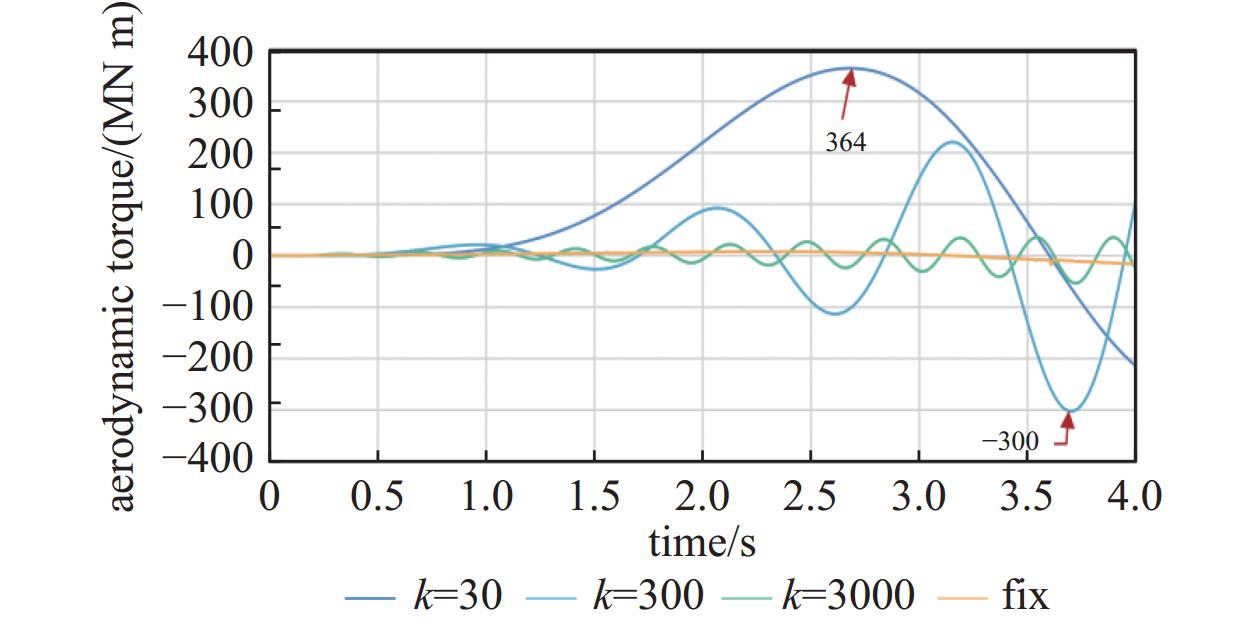
如图8所示，列车在不同悬浮刚度下受到的纵向气动载荷均在运行速度达到340 m/s的0.1 s时刻达到一个峰值，悬浮刚度为300 kN/m、3000 kN/m和固定姿态运行工况下列车纵向气动载荷逐渐回落至一个较为稳定的值。而悬浮刚度30 kN/m工况下，气动载荷在1.5 s左右时刻又出现一个峰值，从而导致纵向气动载荷最大值明显高于其他三种工况。图9中列车受到的垂向气动载荷则体现出一定的振荡变化特性，其中悬浮刚度为300 kN/m工况下，列车垂向气动载荷呈现幅值增大的周期性变化。相对而言，悬浮刚度为3000 kN/m工况和固定姿态运行下，列车受到的气动垂向气动载荷较为接近。而悬浮刚度为30 kN/m工况下，列车受到的垂向气动载荷远高于其他三种工况，其变化也呈现出一定的周期性。气动载荷的周期性变化在图10中体现地更加明显。悬浮运行的三种工况下，列车受到气动力矩均呈现出一定的周期性并且振荡的幅值均呈现增大趋势。列车受到垂向气动载荷和气动力矩最大值均随悬浮刚度的减小而增大。由于悬浮刚度不同导致列车姿态变化频率的不同，气动载荷变化频率随悬浮刚度减小而减小。

实时在线流固耦合仿真结果显示列车受到的气动载荷和悬浮力均呈低频周期性变化。悬浮刚度的减小会导致列车受到的气动载荷幅值增加，频率下降。随着时间推移，列车受到的气动载荷呈现振荡幅值增大的态势，表明流固耦合效应会不断增强，如果没有有效地克服列车受到的气动载荷，抑制列车的振动，列车运行将逐渐受到更大的影响。

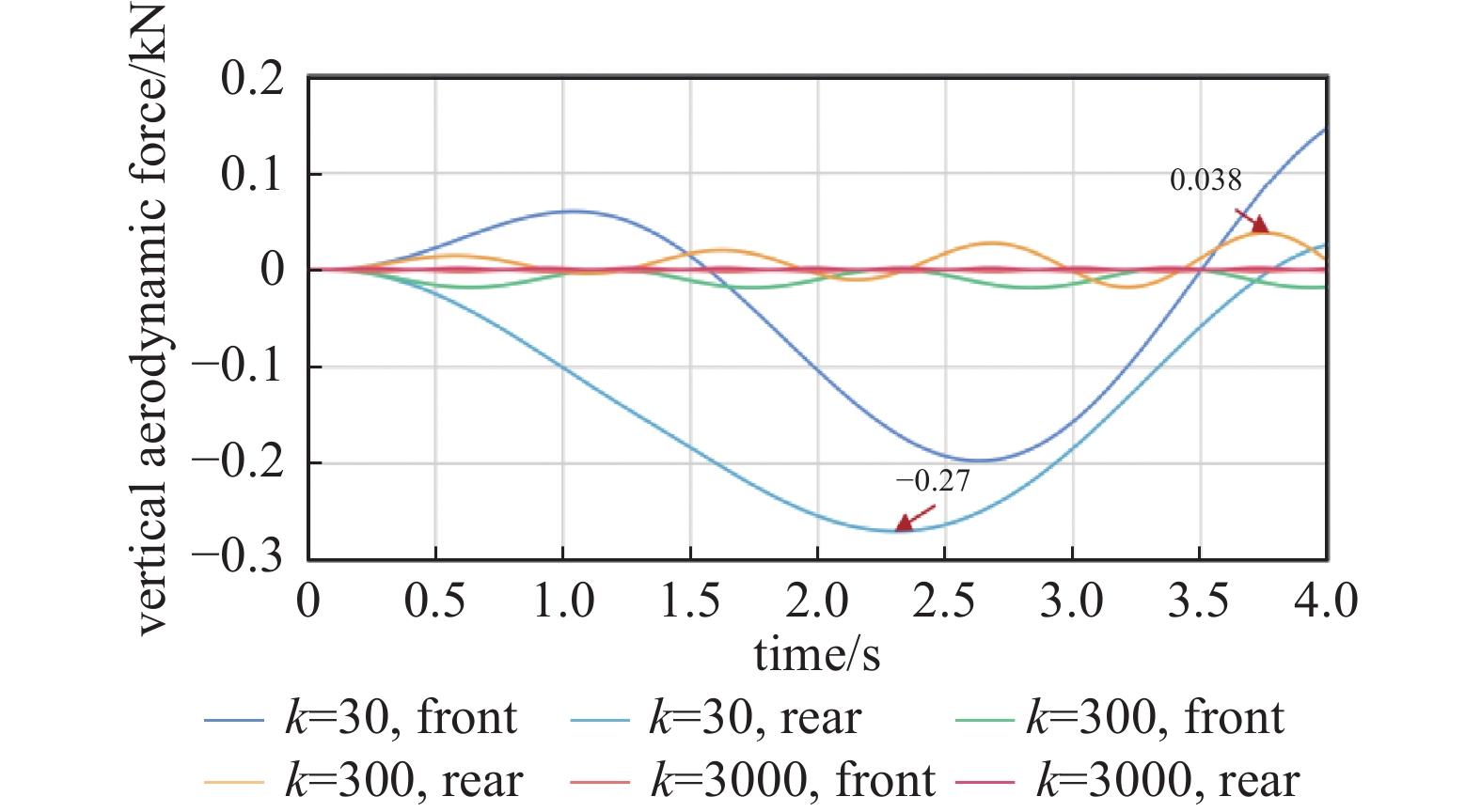
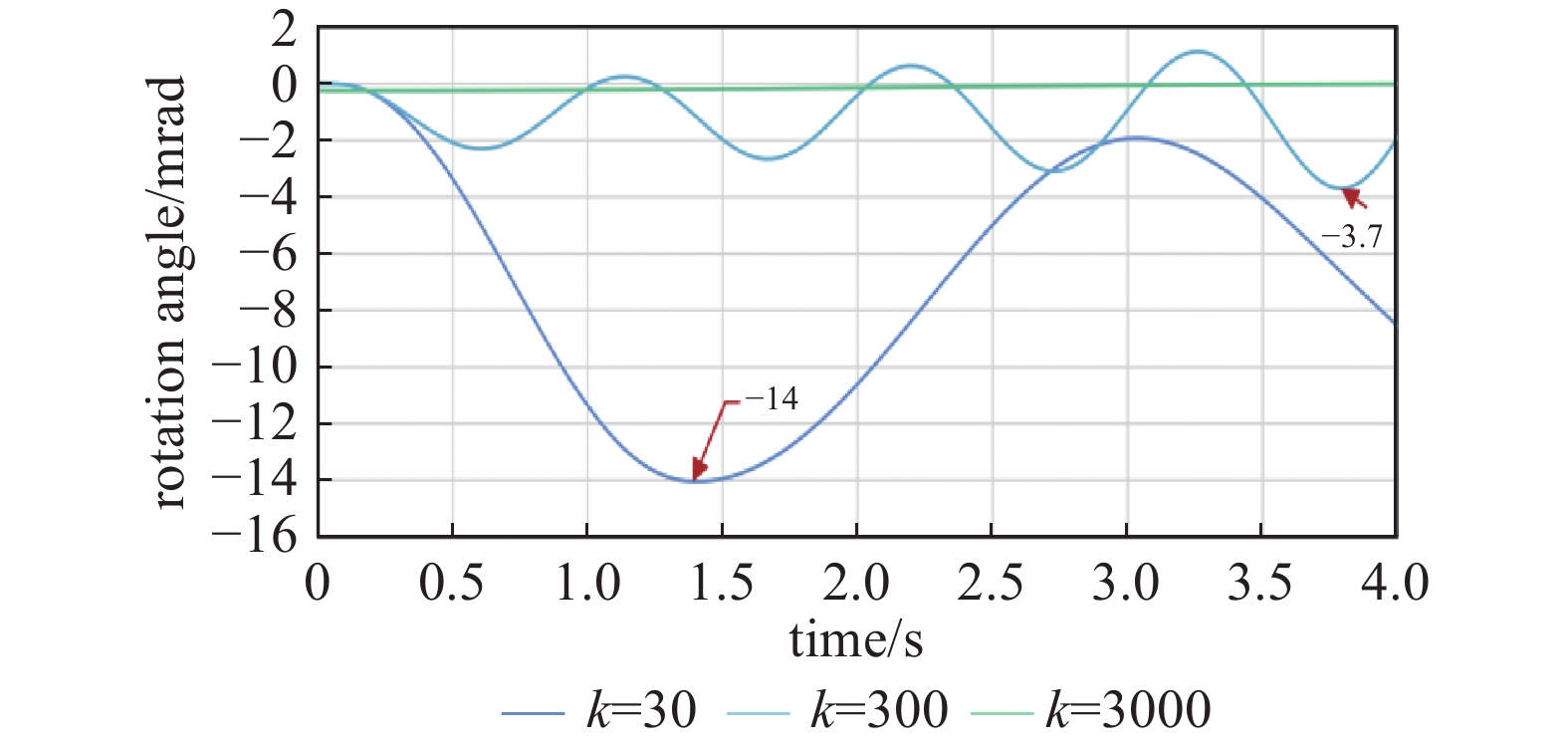
图11为列车前后测点的垂向位移。在悬浮刚度为30 kN/m和300 kN/m两种悬浮刚度下，列车的垂向位移较大，最大幅值可达约270 mm和38 mm，而悬浮刚度为3000 kN/m时，列车测点位移最大幅值仅为2 mm左右。图12中列车的点头转动角度也是在这两种悬浮刚度下呈现较大的振荡幅值，其最大幅值可达14 mrad和3.7 mrad。表明在这两种悬浮刚度下，列车会在气动载荷的作用下产生严重的振动，流固耦合效应尤为明显。由于气动载荷随着时间的推移呈现的幅值增大的特性也导致了列车的垂向位移及旋转角度呈现出了相似的特性。随着列车的运行，流固耦合效应将对悬浮列车的运行姿态影响越来越明显，对列车的运行安全性影响极大。

针对真空管道磁悬浮列车悬浮运行时，列车与管道内流场间存在严重的流固耦合效应，提出了真空管道磁悬浮列车流固耦合动力学理论，并建立了真空管道磁悬浮列车实时在线流固耦合数值计算模型，分析真空管道磁悬浮列车的车辆流固耦合特性。研究发现：

(1)列车悬浮运行列车尾部流场较为复杂，存在多道斜激波和反射波，但是随着列车的运行相对较为稳定，而列车顶部和头部的波系相对更加简单，但是会随着列车运行发生明显的变化。

(2)实时在线流固耦合仿真结果显示列车受到的气动载荷均呈低频周期性变化。悬浮刚度的减小会导致列车受到的气动载荷幅值增加，频率下降。随着时间推移，列车受到的气动载荷呈现振荡幅值增大的态势，表明流固耦合效应会不断增强。

(3)列车悬浮运行工况下，悬浮刚度较小会导致流场与固定姿态运行的流场特性出现明显差异，流固耦合效应突显。在30 kN悬浮刚度下，列车的位移和转动幅值可以达到270 mm和14 mrad，并且随着时间推移，列车受到的气动载荷呈现振荡幅值还有增大的态势。

这些研究结果表明悬浮运行的真空管道磁悬浮列车随着运行时间的增加流固耦合效应会不断增强，如果无法有效克服变化的气动载荷，会导致列车运行姿态的变化不能受到有效的抑制，行车安全将可能受到影响。