-
2004 年英国曼彻斯特大学的 Andre Geim和Konstantin Novoselov 等[1]通过机械剥离的方法成功分离出了单层石墨烯,开启了二维量子材料领域研究的大门。自此以后,越来越多的二维材料开始进入研究人员的视野,其中典型的二维材料包括过渡金属二硫族化合物(Transition Metal Dichalcogenides, TMDs)和六方氮化硼(Hexagonal Boron Nitride, h-BN)。这些原子级厚度的材料对磁场、电场和应力场等外部环境极其敏感,物理性质极易受到这些外场的调控。同时,随着二维范德瓦尔斯异质结制备技术的不断发展,研究人员发现二维材料以不同的旋转角度和堆叠次序组成异质结时,由于受到晶格常数和层间旋转角度的影响,会形成超晶格结构,并带来了一系列空间结构及电子能带结构的变化。随着研究的不断深入,Cao等[2-3]发现,在层间相对旋转角为1.1°时,石墨烯的平带整数填充时出现了关联绝缘态及其附近的超导态。这一发现掀起了近几年对二维量子材料超晶格结构中强关联效应研究的热潮。本文主要围绕着超晶格结构导致的能带变化及强关联效应所带来的新奇物性展开讨论,并展望了未来可能的发展方向。
-
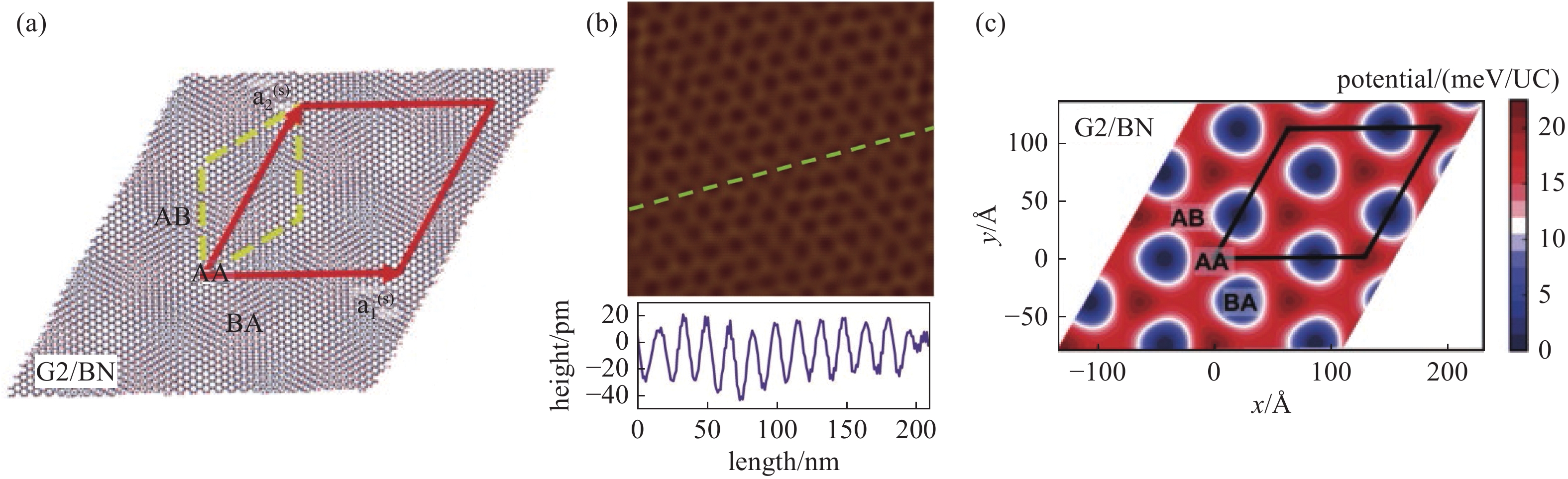
当两个具有相似周期的二维量子材料堆叠在一起时,晶格常数的不同和层间旋转角度会使体系产生新的超晶格结构。虽然超晶格结构是由相似晶格结构堆叠而成的,但并不是所有的超晶格都具有可公度性。例如转角双层石墨烯(Twisted Bilayer Graphene,TBG)在旋转角度为30°时,会形成像准晶一样只具有旋转对称性而没有平移对称性的非公度结构[2,4-5],此外在石墨烯与氮化硼形成的异质结中也会发生可公度与非公度结构之间的转变[6]。当超晶格具有可公度性时,会形成周期性莫尔条纹,这种超晶格也被称为莫尔超晶格,如图1(a)所示。从结构上来讲,这种超晶格来源于晶格结构的失配。当堆叠晶格之间的晶格常数不同或具有相对旋转角度时,会导致晶格失配,进而产生超晶格结构,主要分为同质结和异质结两种莫尔超晶格结构,下面作者按照这两种情况分别进行讨论。
首先,在同质结构中,由于材料具有相同的晶格常数,超晶格的形成只能通过调节层间旋转角来实现。最典型的代表是TBG,它的旋转角度被定义为上下两层晶格矢量之间的夹角,超晶格基矢可以分别设为
$ {\boldsymbol{t}}_1=i{\boldsymbol{a}}_1+(i+1){\boldsymbol{a}}_2 $ 和$ {\boldsymbol{t}}_2=-\left(i+1\right){\boldsymbol{a}}_1+\left(2i+1\right){\boldsymbol{a}}_2 $ ,其中$ {\boldsymbol{a}}_1 $ 、$ {\boldsymbol{a}}_{2} $ 分别为石墨烯的基矢,因此,旋转角度可以表示为[7]:则超晶格的晶格周期为
$ L=\sqrt{3{i}^{2}+3i+1}{a}_{0} $ ,$ {a}_{0}=0.246 $ nm为单层石墨烯的晶格常数,当$ i $ =0时,该转角体系变为AA堆叠的双层石墨烯。而在异质结构中,由于两种材料的晶格常数不同,例如氮化硼与石墨烯无需旋转角度就可形成超晶格结构,同时也可以通过改变旋转角度的方式对超晶格进行调制,如果同时考虑晶格失配
$ \delta $ (石墨烯和氮化硼的晶格失配$ \delta =1.8\% $ )与旋转角度$ \theta $ ,则超晶格的莫尔周期$ L $ 为[8]:可以得出,当旋转角度
$ \theta $ 为零,即氮化硼和石墨烯对齐时其超晶格具有最大的莫尔周期,约为13.9 nm。这里需要说明的是,当晶格失配δ为零时,(2)和(1)本质上为均为反应转角与周期之间关系的同一种公式,利用关系$ L=\sqrt{3{i}^{2}+3i+1}{a}_{0} $ 替换掉式(1)中的 i 即可得到式(2)。莫尔超晶格不仅会对晶格空间结构产生调制,还会显著影响其能带结构。根据堆叠情况的不同,莫尔超晶格的元胞内部根据原子的堆叠序不同可以分成不同的区域,如通过外延生长而成的石墨烯/氮化硼超晶格,不同区域之间的起伏可以达到约20 pm (图1(b))[9],由于层与层之间通过范德瓦尔斯力相结合,并且该力受距离的影响,当石墨烯与氮化硼的距离越近时,作用力会越强。因此空间周期性的起伏可以导致如图1(c)所示的周期性莫尔晶格势,该周期势同时会调制转角体系的能带结构。
本文将从以下几部分介绍由于莫尔超晶格在空间与能带结构方面的影响而产生的新奇物理现象。
-
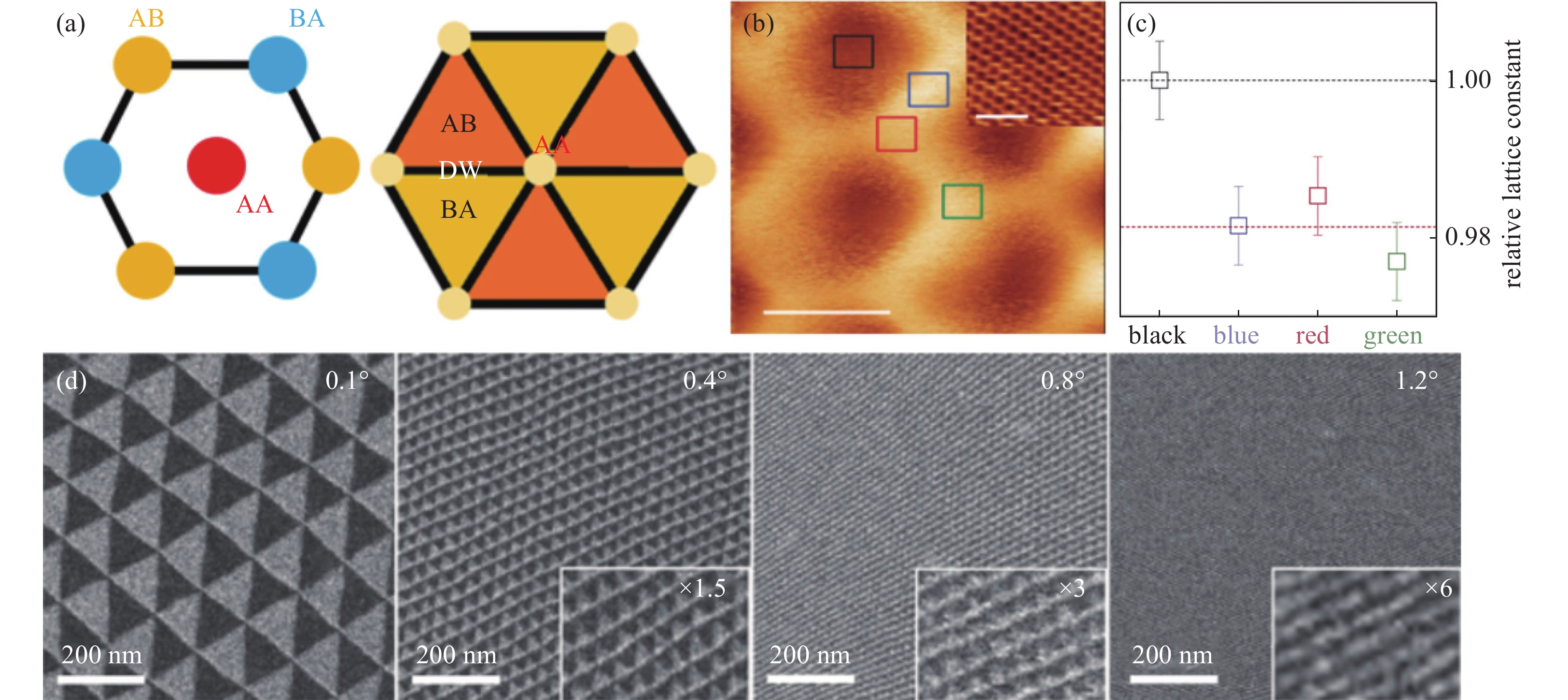
最近的研究表明,通过层间耦合可以诱导原子在接近0°的转角下发生重构,从而产生离散的对称域[6,10-12]。以TBG为例,其中AA堆叠能量最高,BA堆叠次之,AB堆叠能量最低,所以为了使整体能量最低,表面会发生原子重构。AB和BA堆叠的区域会扩展形成一个三角形区域,中间由畴壁隔开,畴壁交叉处为AA堆垛,最终形成AB堆垛和BA堆垛交替出现的周期性结构。其中,每个AB堆叠区域都被三个相邻的BA堆叠区域包围(反之亦然)。图2(a)中展示了原子重构前(左图)后(右图)TBG的堆叠情况。而且,Yoo等[13]发现当转角角度增加时,发生原子重构的区域逐渐减小,对比度明显减弱,最终变得接近单向条纹(如图2(d)所示)。这一趋势表明,重构强度、域内的对比度,都会随着转角的减小而增加。除了层间耦合之外,层间平移也可以产生原子重构。Alden等[12]发现在双层石墨烯中,当其中一层石墨烯在某个方向上相对于另一层石墨烯移动了原子尺度的距离时,也可以观察到上述原子重构的现象。而且这种情况也会发生在MoSe2/WSe2等由TMDs构成的异质结中[10]。
除此之外,覆盖在氮化硼上层的石墨烯也会根据氮化硼的周期做出其他微小的应力调整[6,11],进而产生原子重构。石墨烯和氮化硼的晶格常数差约为0.05 Å。当不考虑重构现象时,石墨烯和氮化硼沿着相同的晶向排列最大周期为12.04 nm。但因为石墨烯晶格上的跃迁会减小石墨烯和氮化硼堆叠区域的晶格失配,产生原子重构,因此实际上当石墨烯和氮化硼沿着相同的晶向排列时最大周期可以达到13.9 nm。而且,有实验表明,原子重构会显著影响畴壁的原子结构[6,14-15]。Woods等[6]发现单层石墨烯/氮化硼中畴壁区域的相对晶格常数小于均匀区域的相对晶格常数(如图2(b)和2(c)所示),这表明畴壁区域的晶格很有可能是被压缩过的,这也有力的证明了原子重构的存在。
-
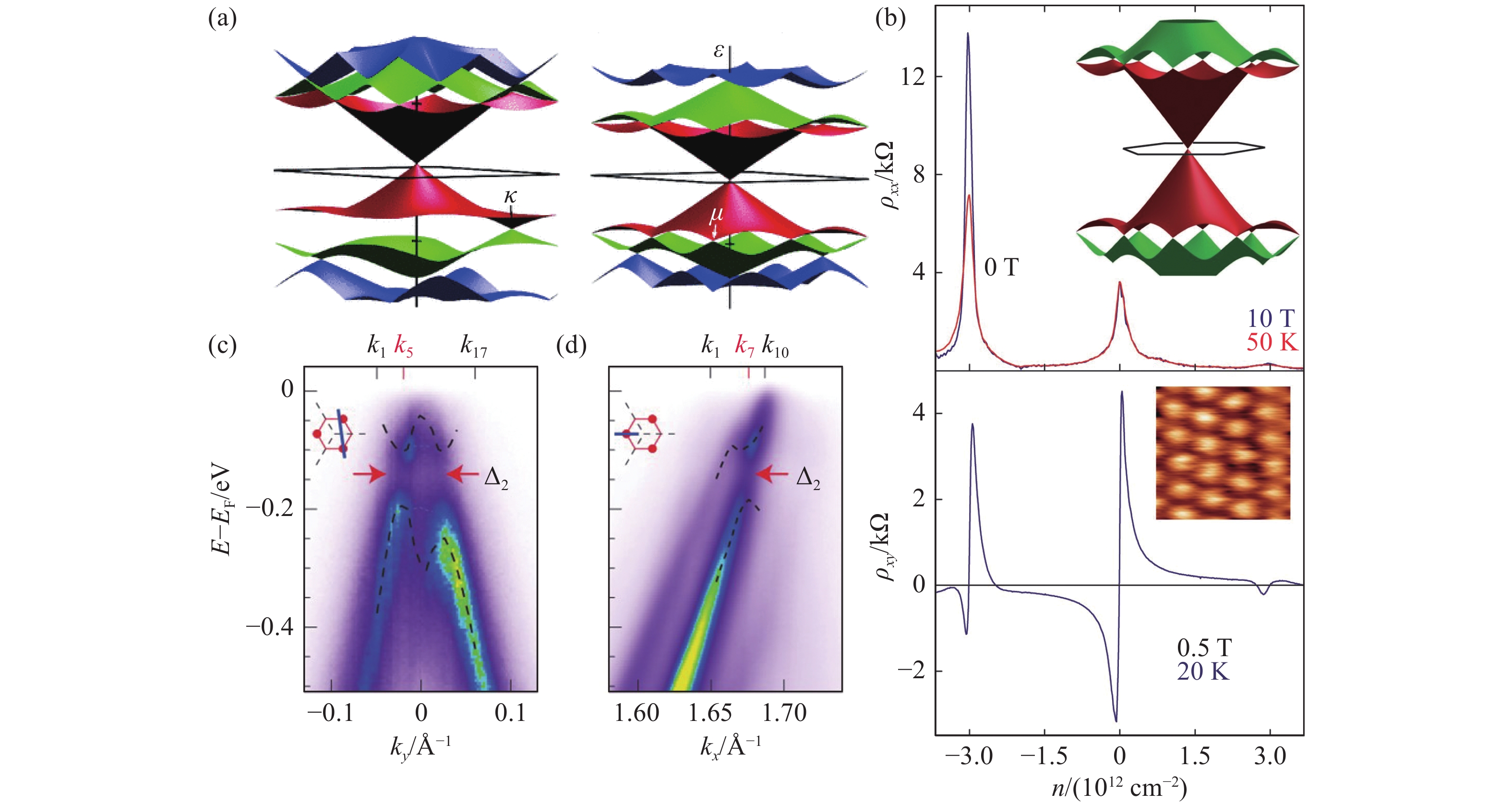
超晶格狄拉克点(superlattice Dirac Points,SDP)是莫尔超晶格势使石墨烯能带结构发生改变的典型现象。理论认为,在莫尔晶格势的调制下,在布里渊区的边界将会出现类似于石墨烯狄拉克点的色散关系,这些点被称为超晶格狄拉克点[16-19]。这一现象产生的原因可以用衬底对石墨烯中狄拉克电子的微扰来解释,根据衬底的不同,微扰可以分为反演对称部分和非反演对称部分,对于相同原子的衬底晶格来说后一部分可以不用考虑,但对于像氮化硼这种具有两种原子的衬底晶格来说,由于氮原子和硼原子的Pz轨道的占据不同,这会导致其中一个原子会比另一个原子更强地影响石墨烯电子,因此在考虑反演对称部分的同时也要考虑非反演对称部分。虽然纯粹的反演对称部分扰动会产生无间隙的主狄拉克点和超晶格狄拉克点,但考虑到有限的反演不对称分量则会在两者上打开间隙。此外,在考虑莫尔周期势调制的基础上,还要考虑三个影响因素,分别是静电势中的对称部分与非对称部分,以及最近邻碳−碳跳跃振幅的空间调制[20]。根据超晶格狄拉克点在倒空间出现位置及数量,可以将其大致分为四种情况[21]:(a) κ点出现一个孤立的SDP;(b) −κ点出现一个孤立的SDP;(c) μ点出现三个孤立的SDP;(d) 无SDP出现。图3(a)为对石墨烯κ点附近电子能带结构的数值计算。
实验上SDP的观测可以在石墨烯/氮化硼超晶格上实现。SDP可以通过多种手段直接或间接的观测到,例如利用扫描隧道显微镜(Scanning Tunneling Microscope,STM)可以在测得的扫描隧道谱(Scanning Tunneling Spectroscopy,STS)中看到主狄拉克点(谱线的最小值)的两侧存在极小值,证明在石墨烯的主狄拉克点所对应能量的两侧还存在由于超晶格调制而产生的SDP[8]。此外,STM的测量还发现石墨烯上的石墨烯摩尔纹图案可以提供微弱的周期电位,从而也可以导致超晶格狄拉克点的出现[22]。
输运测量也是常用的SDP观测方式之一,可以将异质结做成霍尔棒结构,并在改变载流子浓度的同时测量其纵向电阻和霍尔(横向)电阻[23],结果如图3(b)所示,在主狄拉克点和SDP处纵向电阻率会增加,同时霍尔电阻率会改变符号。另外,狄拉克点在磁场下会产生朗道能级,因此也可以利用磁输运测量,根据朗道扇形的出现来证明SDP的存在。同样也是通过调节栅压来调节载流子浓度,增加磁场来诱导朗道能级的产生,在朗道能级被完全填充时电导率会下降,从这些测量结果中均可以看出主狄拉克点的两侧都存在SDP[24]。通常,人们会通过电学输运和磁输运实验相结合的方式对SDP进行探究的,例如在适当的载流子掺杂和磁场作用下,在石墨烯/氮化硼异质结构中发现了二次以及三次狄拉克点[25],以及发现石墨烯与氮化硼之间的旋转角度对SDP的能隙大小存在调制作用[26]等。
角分辨光电子能谱(Angle Resolved Photoelectron Spectroscopy ,ARPES)也是研究SDP的常用研究手段之一。由于计算时所考虑的参数不同,有些理论认为SDP不存在能隙[17,19],有些则认为SDP是存在能隙的[28-29]。由于ARPES具有极高动量和能量分辨率,可以清晰的找到SDP动量空间所在的位置以及获得能隙大小,同时该测量手段对石墨烯/氮化硼样品质量的要求非常高,周期均匀区域的尺寸至少需要50 以上,传统的机械剥离转移法很难满足样品的尺寸条件,但成熟的外延生长技术解决了这一问题。图3(c)和3(d)是利用ARPES技术在外延技术生长出来的石墨烯/氮化硼样品,并观测到了SDP上所具有约100 meV大小的能隙,并证明了反演对称性的破缺会使主狄拉克点及SDP产生能隙[27]。
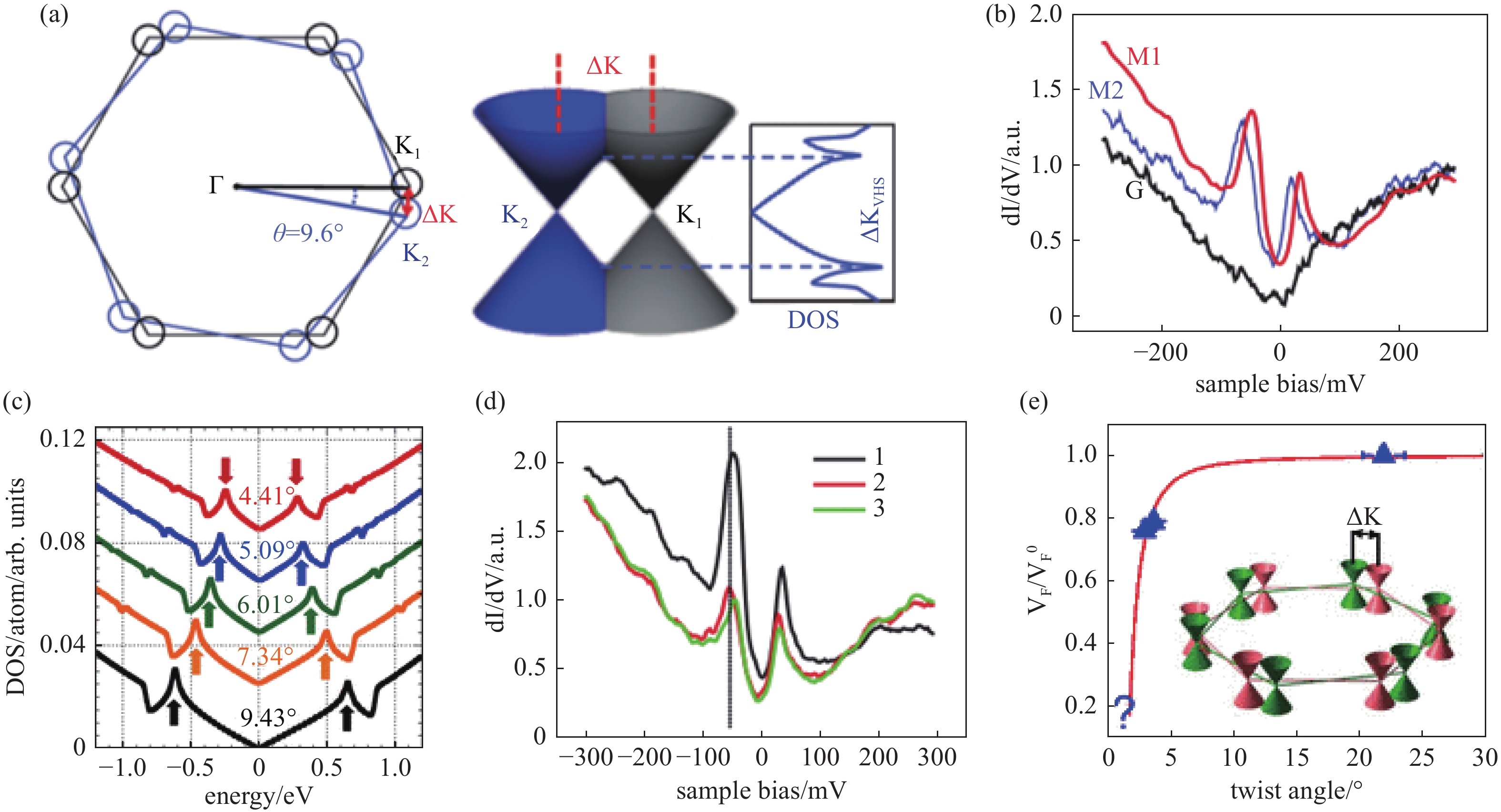
范霍夫奇点是超晶格结构对能带调制产生的另一种现象,是指电子结构中具有发散态密度的点[30],电子能带结构中的鞍点、极大值或极小值点都有可能成为范霍夫奇点。在转角体系中,范霍夫奇点一般由能带结构中的鞍点产生,早在石墨烯/氮化硼超晶格发现之前,人们就已经在外延生长而成的TBG中发现了这一现象。图4(a)为范霍夫奇点形成的示意图,当上下两层石墨烯发生相对旋转时,其布里渊区也将发生旋转,致使上下两层的狄拉克锥在倒空间发生分离[31-32],两个狄拉克锥的偏移量可由式(3)算出[7]:
式中
$ K $ 为倒晶格矢量,$ \theta $ 为上下两层实空间相对旋转角度。这样的分离必然会导致在两个狄拉克锥相交的地方产生鞍点,该点沿着锥分离方向是极大值,在正交的方向上是极小值。从理论上来讲范霍夫奇点一般会成对出现,并且与旋转角度和层间耦合强度有关,一对范霍夫奇点之间的能量差$ \mathrm{\Delta }{E}_{\mathrm{V}\mathrm{H}\mathrm{S}} $ 可以由式(4)粗略估计[33]:式中
$ v_{\mathrm{F}} $ 为重整费米速度,$ {t}_{\theta } $ 为层间耦合系数。最初的范霍夫奇点是利用STM的STS谱,在通过化学气相沉积方式生长出来的TBG上测得的(图4(b))[34]。众多的研究表明,范霍夫奇点的位置和能量差
$ \mathrm{\Delta }{E}_{\mathrm{V}\mathrm{H}\mathrm{S}} $ 随相对旋转角度$ \theta $ 的变化大致可以分为三个阶段。当角度大于10°时,鞍点能量足够远离狄拉克点,层间电子倾向于解耦,低能带结构看起来像是单层石墨烯狄拉克锥的简单叠加[33,39-41]。当角度介于2°到10°之间时,$ \mathrm{\Delta }{E}_{\mathrm{V}\mathrm{H}\mathrm{S}} $ 值会随着角度$ \theta $ 的减小而减小[36,39],但两个范霍夫奇点的能量对称中心几乎不随角度发生改变[35],如图4(c)所示。当角度小于2°时,范霍夫奇点在空间分布中出现局域化现象[34,36-37,42],从图4(d)中可以看出态密度分开始向AA堆叠区域聚集[36],因此当费米能量进一步接近范霍夫奇点能量时,会出现一个强局部化的电荷密度波[34]。STM之所以能成为研究范霍夫奇点的首选工具,不仅是因为它能够通过形貌像中的莫尔周期推断出TBG的旋转角度,同时它还可以测得空间某点的局域电子态密度,以及测得磁场下的朗道能谱,从而获得电子的费米速度和层间耦合强度。一定磁场下无质量狄拉克费米子的朗道能谱满足如下关系[37]:
其中
$ E_{\mathrm{D}} $ 是狄拉克点的能量,$ v\mathrm{_F} $ 是费米速度,B是外加磁场的大小。只要测得一系列能级能量与$ \left(\right|n|B{)}^{1/2} $ 之间的依赖关系,便可根据斜率得到费米速度的大小。当角度$ \theta $ 略大于3°时,又可以通过重整费米速度公式来得到层间耦合强度$ {t}_{\theta } $ 的大小[7]:利用该公式求出的费米速度与实验结果吻合(图4(e))[37-38]。可见重整费米速度的大小是否与角度
$ \theta $ 有关,受层间耦合强度的影响[33],当层间耦合足够小时,费米速度与角度$ \theta $ 无关[38,42]。除了上面的结论之外,围绕范霍夫奇点还有很多其他的物性研究。例如通过静电掺杂调节TBG中的费米面位置,当费米面接近范霍夫奇点能量时,体系会出现多体量子现象[43]。在光学领域,当激发光子能量与范霍夫奇点能量差
$ \mathrm{\Delta }{E}_{\mathrm{V}\mathrm{H}\mathrm{S}} $ 相匹配时,拉曼光谱中的G模声子振幅会大幅增强[44]。此外,还可以通过对TBG施加压力或对三层石墨烯施加垂直电场的方式产生高阶范霍夫奇点[45]。 -
1976年,霍夫斯塔特预言:当二维电子气同时处于周期性的电场和磁场中时,会产生分形能谱[46],因此该能谱也被称为霍夫斯塔特蝴蝶能谱。只有当与电子回旋运动有关的磁长度
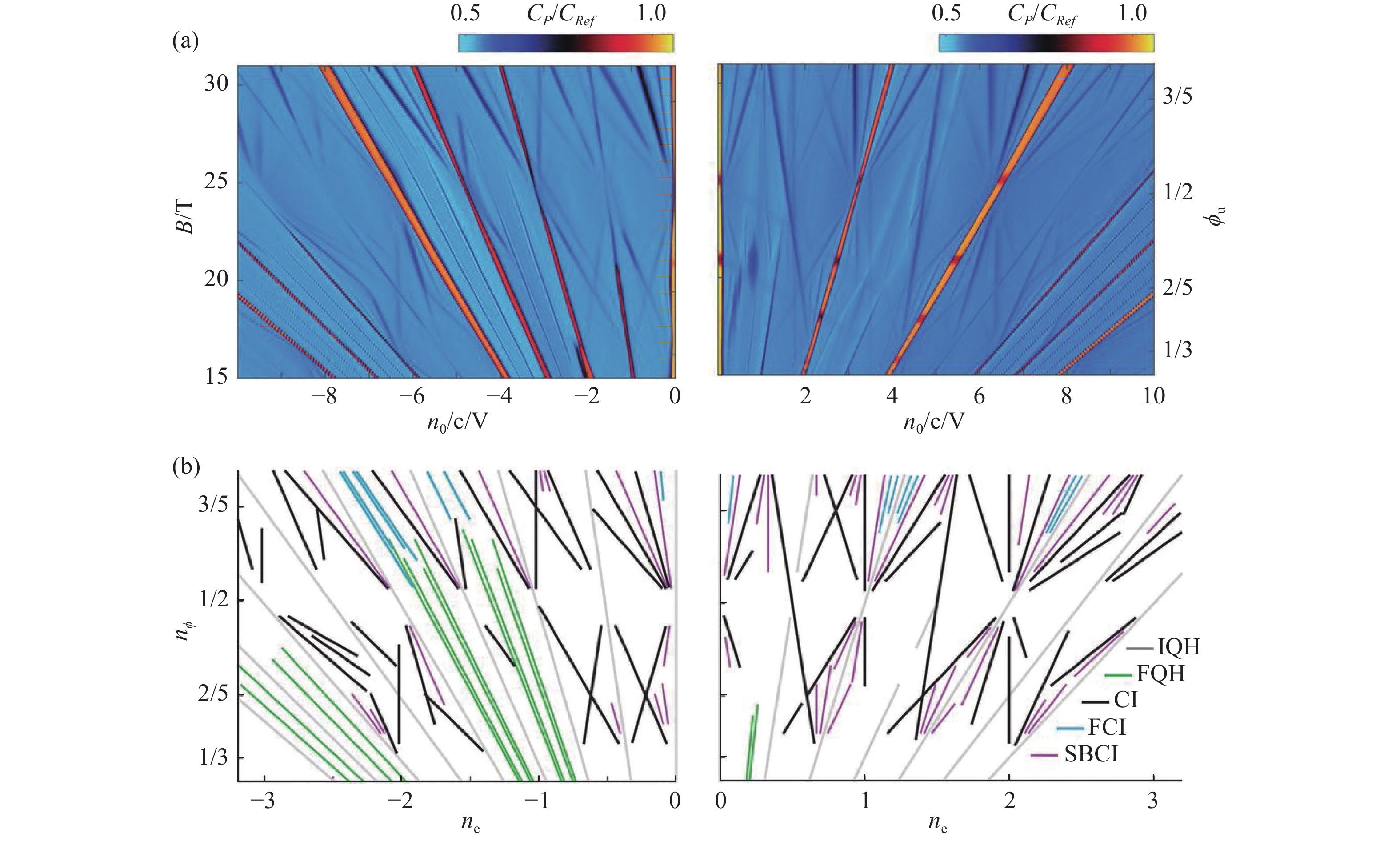
$ {l}_{B} $ ($ {l}_{B}=\sqrt{\hslash /eB} $ ,B为磁场大小)和与电子布洛赫波有关的周期势波长$ \lambda $ 大小相近时,才能呈现出清晰的分形能谱,因此在常规晶格尺寸上实现霍夫斯塔特蝴蝶能谱通常是十分困难的,对于小于1 nm的晶格,所需要的磁场大小要超过10000 T。在实验室条件下实现该能谱最简单的方式是构造周期远大于普通晶格的超晶格结构,早期的实验主要是在GaAs/AlGaAs异质结上进行的,该异质结的超晶格周期约为100 nm,可以在较低的磁场下观察到霍夫斯塔特能谱[47],但由于载流子掺杂能力较差,无法得到完整的能谱。二维材料的出现使这一问题得到更好的解决,二维材料不仅能够通过转移的方法较为方便的形成二维异质结,而且可以通过改变相对旋转角度和晶格失配度可以实现对超晶格周期的调控,最重要的是由二维材料组成的范德瓦尔斯异质结构更易于实现载流子掺杂,从而观测到更完整的霍夫斯塔特蝴蝶能谱。在二维材料的范德瓦尔斯异质结中对霍夫斯塔特能谱的观测首先是在石墨烯/氮化硼异质结上实现的[23-24,48]。从图5(a)中可以看出这些由超晶格产生的能谱是具有递归性且自相似的,如果将能谱看作是电阻关于磁场和载流子浓度的函数,所有的轨迹都为直线且满足如下关系:
其中
$\dfrac{n}{{n}_{0}}$ 为单位超晶格的载流子浓度,t为该轨迹所对应霍尔电导率$ {\sigma }_{xy}=t{e}^{2}/h $ 的系数,s为布洛赫能带填充指数。当单位超晶格的磁通量$\phi$ 满足$\phi /{\phi }_{0}=p/q$ (其中$ p $ ,$ q $ 都为整数,${\phi }_{0}=h/e$ )时这些轨迹将会产生新的分形,这时该系统可以等价成一个被置于零磁场中具有不同周期的超晶格结构。如图5(b)所示,根据式中t和s的取值不同,能谱中的轨迹大致可以分为五类[49]。当s=0且t为整数时,所对应的轨迹被称为整数量子霍尔效应(Integer Quantum Hall,IQH),二维电子气在外磁场的作用下会产生一系列朗道能级。当费米面到达某个朗道能级时,纵向电阻会降至最小值,而霍尔电导率将会到达一个稳定的数值
$ t{e}^{2}/h $ 。对于石墨烯/氮化硼体系来说,理论上t可以取4 m+2 (m为整数),其中4代表自旋与谷的简并,当空间反演对称性被氮化硼破坏,谷简并消失时,t将会变为4 m[28],这些已经在实验中得到了验证[50]。当s=0且t为分数时,所对应的轨迹被称为分数量子霍尔效应(Fractional Quantum Hall,FQH),该效应一般出现在质量较高的器件中。在这些器件中,电子之间的相互作用会变得更强,导致电子出现集体激发行为。与IQH一样,FQH同样会出现一个霍尔电导平台,但数值是$ {e}^{2}/h $ 的分数倍[50-51]。当s和t均为非零整数时对应的状态是霍夫斯塔特陈绝缘体(Hofstadter Chern Insulators,HCI),由于s对应的是布洛赫能带的填充指数,晶格的变化会导致电子能带结构发生改变,因此非零的s值通常来源于晶格的调制。对于石墨烯/氮化硼体系,由于超晶格的存在,电子能带结构出现了超晶格狄拉克点,因此在磁场下会出现$ s=\pm 4 $ 的HCI态[23-24]。分数的s和整数的t对应对称破缺陈绝缘体(Symmetry-Broken Chern Insulators,SBCI),该状态中的分数s源于电子相互作用导致的自发超晶格对称性破缺[49],超晶格单元将会发生重构,使得每个单元能容纳更多的电荷[52-53]。对于TBG来说,调节旋转角度将会改变其能带结构,在特定角度下将会有平带产生。平带具有自旋、谷以及亚晶格有关的八重简并,无论是通过与下层氮化硼对齐打破C2z对称性,还是通过电子之间的相互作用打破时间反演对称性,都会使平带的简并消除,形成一系列具有非零陈数的平带,在磁场下产生s和t为非零整数的HCI态,但破坏不同的对称性会产生不同的s和t的值[52-54]。当s和t均为分数时,所对应的状态是分数陈绝缘体(Fractional Chern Insulators,FCI)。该态出现的前提是该系统具有非零陈能带且具有足够强的电子相互作用,例如对于双层石墨烯,当电子之间的库仑能和周期势能的相对大小处于电荷密度波和可压缩态之间时会出现FCI态[49]。霍夫斯塔特能谱中的五类轨迹蕴含着丰富的物理现象,所以仍然需要更多的研究去理解这些丰富的物理特性。 -
激子是受激电子和空穴由于库仑相互作用而形成的束缚态复合体。在半导体中,当一个电子从满的价带激发到空的导带上的时候,会在价带内产生一个空穴,在导带内产生一个电子。它们因受到库仑力而互相吸引,在一定条件下会在空间中束缚在一起,这样形成的复合体称为激子[55]。而莫尔超晶格中面内超晶格势会对范德华异质结构中电子特性产生显著影响[56],由于这些影响而发生变化的激子被称为莫尔激子。虽然莫尔激子主要受电子-空穴相互作用和莫尔晶格势影响,受电子-电子间的强关联效应的影响较小,但强关联效应依然会影响电子和空穴之间的相互作用,从而对莫尔激子的物理性质和稳定性产生影响。
目前,对于超晶格结构的研究主要集中在转角石墨烯和转角TMD中。与石墨烯相比,TMD具有较大的带隙,这使得转角TMD具有较好的热稳定性和光发射能力,并存在稳定的开关行为[57]。其次,TMD中较强的自旋−轨道耦合为拓扑带的调控和自旋/谷的光学控制提供了可能。最后,双层转角TMD中可以形成平带的“魔角”范围很大,并且可以连续调节。相比于转角石墨烯中离散的魔角,更容易在实验中实现。因此,在研究莫尔激子的时候,通常选择如MoSe2和WSe2等TMD材料。
受到莫尔超晶格影响的激子种类有很多,如下表1所示(“CVD”表示材料系统通过化学气相沉积制备)[58]。其中层间激子作为复合准粒子,受到莫尔超晶格的影响最强烈。Tran等[59]在小转角的MoSe2/WSe2异质结中观察到的具有正或负圆极化发射的多个层间激子共振,并且认为这些共振源于限制在莫尔势内的激子基态和激发态。除此之外,层内激子也会受到莫尔超晶格的影响。Zhang等[56]报告了MoSe2/MoS2异质结中莫尔超晶格对激子的影响。根据理论预测,莫尔超晶格会产生周期性调制的电势,其中层内激子和层间激子的能量最低,形成一个量子点阵,其中不同位置原子限制势的变化导致层内跃迁和层间跃迁的能量分裂。研究人员通过光致发光光谱(Photoluminescence Spectroscopy,PL谱)测量成功地观察到了MoSe2/MoS2异质结构中层内激子和三激子的能量分裂,观测到的分裂峰之间的能量差与理论预测结果一致。
此外,带杂化[67] 和畴重构[63]等来自外界的干扰也可能会改变莫尔激子的行为。Hsu等[67]研究了异质双层(WSe2/MoSe2,WS2/MoS2)和在K点具有不同堆叠结构的同质双层(MoS2/MoS2)结构的层间价带杂化对激子结构的影响。通过这种杂化产生的激子由一个层杂化空穴和一个限制在独立层中的电子组成,具有较大的光偶极矩,同时在平面外方向具有一个较大的电偶极矩,结合了层内激子和层间激子的优点。最后,研究人员还讨论了杂化的起源,并证明了此杂化是由层间跳跃积分决定的。Sung等[63]也探讨了转角MoSe2同质双层异质结中晶体重构畴的对称性对激子性质的影响。研究发现斯塔克斜率会突然改变符号,以及激子峰反射光谱会避免与新的光谱特征交叉,这些都表明AB和BA堆叠中激子的电偶极矩方向发生了改变,密度泛函理论(Density Functional Theory,DFT)的计算结果进一步证实了这一推论。
-
在早期对范霍夫奇点的研究中,对于电子在小角度TBG(< 2°)下的行为,不同的理论往往会得出不同的结果。有的理论认为电子的费米速度不会随角度发生进一步改变[7],但有的理论认为随着角度的减小,电子的费米速度会继续随之降低[68]。
由于电子的费米速度依赖于上下层之间的层间耦合强度与转角大小[69]。当处于大角度情况时,层间耦合强度可以用微扰理论进行处理;当处于小角度情况时,层间耦合强度无法再被看作微扰来处理,电子性质变得越来越复杂。基于这两个因素,MacDonald和Bistritzer构建了一个由两个单层哈密顿量和一个与层间耦合相关的隧穿项三部分组成的连续体模型哈密顿量,并用该模型预测了电子费米速度在一组离散角度下消失的现象(图6(a)),即平带的产生。除此之外研究人员还预测在小角度下层间的相对平移几乎不会改变电子的性质[69]。但由于层间电子隧穿受层间原子的相对位置的影响,不同莫尔区域的电子之间会存在差异,理论表明电子波函数在近似AA堆叠的区域倾向于局部化[41],这些性质在后续的实验中也得到了证实[70-72]。
虽然在连续体模型中并没有考虑到电子−电子相互作用,但由于平带上的电子费米速度接近于零,并且在超晶格中局域化,因此电子之间的相互作用能
${V}_{\mathrm{C}}={e}^{2}/\left(4\pi \varepsilon d\right)$ ($ d $ 为电子之间的有效距离,与莫尔晶格周期$ \lambda $ 具有相同尺度)要远大于电子的动能,成为影响该区域物理性质的主要因素,使得该区域的物理性质产生显著的改变。后续的很多实验都证实了此电子之间的强关联效应的影响,例如在STS谱中,由于平带的存在导致能量在零附近的局域电子态密度变大,因此当平带全填充或全未填充时, STS谱表现为一个尖峰,对应单粒子行为。但当平带被部分填充时,STS谱中对应的尖峰会发生展宽,并且会产生明显的能带劈裂[71,73-74]。这是由于较强的电子−电子相互作用导致的对称性破缺,使简并的平带分裂出子带,是强关联引起的多体行为。在下面几部分中将介绍由于电子之间强关联有关的新奇的物理现象。
-
自从魔角石墨烯被成功制备,其中形成的关联绝缘态和超导性一直备受关注。该现象最初是在TBG上被观测到的,Cao等通过改进“撕裂与堆叠”制备技术,在2018年制备出了转角在最大魔角(~1.1°)附近的TBG[2],之后将样品通过微纳加工制成场效应晶体管结构,通过调节栅极电压对载流子浓度进行调控,可以得到不同平带填充情况下的电学性质。由于TBG的平带具有与谷和自旋相关的四重简并度,因此满填充时平均每个莫尔单元中有8个电子,填充超晶格中一个平带所需的电子数密度
${n}_{\mathrm{S}}\approx {2.7\times 10}^{12}\,\,{{\rm{cm}}}^{-2}$ 。当平带完全被电子或空穴占据时,即载流子浓度n=$ \pm {n}_{\mathrm{S}} $ 时,该体系电导将为0,处于绝缘态,Cao等的测量结果也证明了这一点。但是在单粒子图像中,在本应该处于金属态的平带半填充(n=$ \pm {n}_{\mathrm{S}}/2 $ ,填充因子$ \nu =2 $ )处却观测到了绝缘态的产生(图6(b))。这是因为魔角附近的异质结,由于平带的产生,电子的动能接近于零,远小于电子之间的库仑相互作用能,这时体系四重简并的平带将会分裂成两支,形成类似于莫特绝缘体的绝缘态[75]。并且由于轨道效应和塞曼效应对不同方向磁场响应的不同,发现分裂后的能带为自旋单重态。除了在半填充(
$ \nu =2 $ )处存在绝缘态之外,有很多实验在$ \nu =0,\pm 1,\pm 3 $ 处也观测到了绝缘态[76-81]。$\nu = 0$ 处绝缘态的出现是由于TBG与氮化硼衬底在零角度对齐时打破了$ {C}_{2} $ 对称性,使该系统导带和价带之间的狄拉克点张开,形成平坦的陈带。在其他整数填充处出现绝缘态是由于电子之间的相互作用可以破坏系统的$ {C}_{2}\mathrm{T} $ 对称性,产生自旋和谷极化的平带,因此在所有$ \nu $ 为整数值处都会有相互作用诱导的绝缘态[82]。$ {C}_{2}\mathrm{T} $ 对称性的打破和能隙的产生,与转角的角度和相互作用强度有着密切的联系,即使在魔角附近,绝缘态仍然只在特定的相互作用范围内才会出现。虽然$ {C}_{2} $ 和$ \mathrm{T} $ 对称性的打破都可以产生平坦的陈带,但由于破坏$ {C}_{2} $ 对称性会导致谷陈数符号反转,而破坏$ \mathrm{T} $ 对称性则不会,因此产生平带的陈数会有所不同[54,78,83]。TBG中的超导性也是Cao等在2018年首次观测到的[3]。当调节TBG中的载流子浓度n使其稍微偏离关联绝缘态(n=
$ \pm {n}_{\mathrm{S}}/2 $ )时,将会有最高超导转变温度为1.7 K的超导态的出现,类似圆顶形状的超导相出现在半填充状态的每一侧,如图6(c)所示,在外加磁场的情况下临界磁场随载流子浓度产生很大变化。除此之外,临界磁场的依赖性与金兹堡-朗道理论较为吻合,并且在相图中还出现了由于样品不均匀形成的约瑟夫森结阵列结构导致的震荡现象,这些都进一步证明了超导态的存在。和绝缘态相同,后续的实验中同样也观测到了在其他整数填充附近出现的超导相[76-77,79-80]。与其他超导体相比,二维异质结材料更便于通过调节角度和压力等参数来对电子相互作用强度进行调制[26,89],并且具有清洁的层间界面,载流子浓度的调节也十分便捷,是研究超导现象的理想平台。虽然很多实验都在TBG中观测到了关联绝缘态与超导态,但关于TBG中超导产生的原因以及超导相和关联绝缘相之间的关系一直存在争议。一些观点认为TBG中的关联绝缘态是超导态产生的前提条件,通过掺杂莫特绝缘体产生超导电性,类似于铜基超导体[90]。TBG中超导与高温超导体具有很多相似之处,最直观的一点就是TBG中随载流子浓度的变化,超导态出现在关联绝缘态的两侧,与铜基超导体的相图极其相似[90-91]。同时由于强电子相互作用,TBG中超导的转变温度与费米温度的比值较大,超出了传统超导体所在的范围[3]。并且通过对掺杂水平在
$ \pm {n}_{\mathrm{S}}/2 $ 附近的TBG进行变温电阻测量,发现在该掺杂范围内存在奇异金属态[92-93]。其电阻随温度变化曲线大致可以分为三部分:低温下的曲线具有超导特性,在超导转变温度附近电阻值骤降,随着温度的升高超导态逐渐转变为关联绝缘态,曲线也呈现出了绝缘态的性质,电阻随温度升高而降低,但到了一定温度后,曲线开始呈现奇异金属态,即电阻与温度满足简单的线性关系$ \rho \left(T\right)\sim AT $ (A为常数)。铜氧化物超导体的电阻和温度同样也成线性关系[94]。除此之外,在对TBG的STM测量中发现,当平带处于部分填充状态时,STS中与平带相关的峰发生劈裂,出现了一个赝能隙,并且两峰的权重随空间位置而变化,这种现象的产生意味着电荷在空间中并不是均匀分布的,而是形成了一个条纹电荷序,打破了莫尔晶格的C6对称性[71-72]。同样的现象也在外加不同方向磁场下的输运测量中得到证实,纵向电阻对面内磁场具有各向异性的响应[81]。这些条纹电荷序在高温超导体中也经常出现[95-96]。但同时也有很多证据支持TBG中的超导并不是高温超导,而是由电声耦合产生的常规超导,与关联绝缘态不是共存而是竞争关系。在用于输运测量的器件中,当TBG与底部石墨烯栅极之间的氮化硼厚度小于莫尔周期大小时,栅极石墨烯中的极化电荷将屏蔽该尺度上的库仑相互作用[79]。绝缘态的产生需要电子之间的库仑相互作用大于带宽,但超导体主要受到费米能级上的态密度影响,因此库仑相互作用的屏蔽将会影响绝缘态的形成但不影响超导态的形成。所以当绝缘态消失时,超导态仍然存在,并且会占据原来属于绝缘态的位置[79-80]。在氮化硼与TBG之间添加单层WSe2绝缘层或者添加双层Bernal石墨烯也可以在不产生绝缘态的情况下生成超导态,并且超导态可以出现在比魔角小得多的角度中[77,80]。库仑相互作用减小会稳定超导性的现象支持了TBG中超导体起源于电声耦合的假设,这是因为对于电声耦合,库仑斥力越弱,电子之间越容易形成库珀对,超导序参量越稳定。但对于高温超导来说序参量随着库仑相互作用的增加而增强。同时对于电阻随温度线性变化的奇异金属态,还有一种理论认为是高温下的电子-声子散射导致的,在温度上也会线性演化,并且斜率与电子-声子耦合强度有关[93,97-98]。对于TBG中超导起源及性质的问题目前还没有定论,仍然需要大量的探索。
另一方面,随着范德瓦尔斯异质结制备技术的成熟和对转角角度控制能力的提升,越来越多的其他转角体系也逐渐受到研究,双层转角石墨烯(Twisted Double Bilayer Graphene,TDBG)就是其中之一。与TBG不同的是,TDBG的能带继承了双层Bernal堆叠石墨烯的电场可调节性[84],因此TDBG不仅可以通过改变相对旋转角和层间耦合来对电子相互作用强度进行调节,同样也可以通过改变电场对平带进行调节[84-85,99-102],如图6(d)所示。这使得TDBG的平带可以在较大的转角范围内出现,而不像TBG一样只局限在1.1°附近的小范围内。当不加外电位移场时,两平带之间具有较小的能隙,而平带上方和下方具有较大的能隙。当电位移场增大时,平带之间的能隙迅速变宽,而平带上方和下方的能隙变小并最终消失[84-85]。和TBG一样,TDBG的整数填充处都曾经观测到关联绝缘态[95,99-102],但STM的实验表明TDBG中的电子波函数并不像TBG中在某个堆叠区域发生局域化,而是非定域的,并且由强关联导致的局域态密度谱线劈裂出现在所有堆叠区域,因此TDBG中
$ \nu =2 $ 的绝缘态可能来自于非局域交换相互作用[103]。除此之外,通过对TDBG的自旋塞曼效应的观测发现g因子约为2,表明与TBG在$ \nu =2 $ 处的谷极化不同,TDBG在$ \nu =2 $ 处为自旋极化[95,99,101]。除了关联绝缘态之外,在TDBG中也观测到了疑似超导的证据,但也有可能是由于绝缘态的铁磁转变中载流子散射过程被铁磁序抑制所导致的电阻率下降行为[101],TDBG中超导态是否存在还需要进一步的实验证明。转角三层石墨烯(Twisted Trilayer Graphene,TTG)与TBG一样具有电场可调节性。TTG由三个单层石墨烯组成,顶层与中间层之间相对旋转角的角度为
$ \theta $ ,中间层和底层之间的为$ -\theta $ ,保持了垂直镜像平面对称性。其能带结构可以看出是由单层石墨烯的狄拉克锥与TBG平带共同组成[86,104-105],并且它们之间的杂化可以由电位移场D调节[86],因此由于独立的狄拉克锥的存在,TTG在D=0时任何填充下都不会表现出较强的绝缘行为[104]。从图6(e)所示的结果中不难发现,和TBG一样,TTG在整数填充附近也观测到了超导态的存在[86,104-106]。对于自旋单重态的超导体,由于塞曼效应,超导行为在平行磁场达到某一特定值时消失,该上限值称为泡利极限。但如果电子之间通过自旋三重态配对形成超导体,这时外加磁场不会加大库珀对中的两个电子的能量差而对库珀对产生破坏作用,因此自旋三重态配对产生的超导体可以在较高的磁场中保持超导性。TTG的超导并不受泡利极限的限制,可以在高达10 T的磁场下存在,并且随着磁场增加会观测到第二个超导相,两个超导相可能通过一阶相变相连[86](图6(f)与6(g))。这些现象表明TTG中的超导电子可能是自旋三重态。除此之外,还发现范霍夫奇点上的发散态密度并不会诱导或增强TTG中的超导序,并且超导态可以在玻色-爱因斯坦凝聚交叉点附近调谐[105],具有强耦合的性质,因此TTG中的超导性不太可能与传统的弱电声耦合一致。在TTG中同样也有人通过加入双层石墨烯的方式来调节TTG中的电子相互作用强度,结果与TBG一致,超导可以在没有关联绝缘态出现的情况下存在,与电子相互作用形成竞争关系[106]。但针对这一实验结果,也有理论认为超导性来源于具有相反陈数的斯格明子对通过反铁磁耦合形成的扩展库珀对,对于该机制来说,绝缘态的存在并不是必要的[107]。虽然TTG中超导性的起源仍然存在争议,但越来越多的研究表明转角体系中C2Z对称性对超导态的存在起着至关重要的作用[105,107-108]。除了上述提到的高对称性转角体系之外,具有较低晶体对称性的转角单层-双层石墨烯(Twisted Monolayer-Bilayer Graphene,tMBG)也开始逐渐受到关注。tMBG由单层石墨烯和双层Bernal堆叠石墨烯组成,由于组成tMBG异质结的石墨烯具有不同的层数,因此tMBG既没有镜面反射对称性,同时也不具备TBG、TTG所具有的C2Z对称性,晶体对称性较低。这导致了tMBG在
$ D > 0 $ 和$ D < 0 $ 时的相图差异很大,但也具有高度电场可调性[87,109-110],如图6(h)所示。从总体上看,两个电阻峰值出现在平带满填充($ \nu =\pm 4 $ )处,并且电位移场D可以使平带之间打开间隙,电阻率随D的绝对值增加而增加。但在$ D > 0 $ 时,电位移场的方向为单层指向双层,其相图类似于TDBG,在$ \nu =2 $ 处相互作用将四重简并的平带导带分裂成自旋极化的陈数为0的平带,出现了关联绝缘行为[111-112]。此外,在磁场下的$ \nu =1 $ 和$ \nu =3 $ 填充处发生了谷极化,也有陈数为2的陈绝缘态出现[109,111-112]。并且在$ D > 0 $ 时也观察到了与TDBG类似的平带密度电子态在实空间均匀分布的特征[113]。而在$ D < 0 $ 时,tMBG的相图与TBG更加相似,但由于tMBG的带宽比TBG更大,因此只在整数填充处观测到了具有金属行为的关联态,但施加垂直磁场会使其由金属态转变为绝缘态[110]。同时与TBG类似,tMBG在$ D < 0 $ 时也会出现平带电子态局域化的情况,集中于ABB堆叠区域[113]。由于tMBG不但具有关联态,同时还具有非零陈数的平带的特性[114],因此tMBG是研究关联态和拓扑态相互作用的理想平台。除了转角石墨烯之外,转角TMD也受到了越来越多的关注。Lei Wang 等[115]在转角双层WSe2中平带半填充时,发现了一个可随转角和电位移场变化的关联绝缘体。在温度低于3 K,转角为5.1°时,远离半填充的位置观察到了零电阻区域,这表明该绝缘态存在过渡到超导状态的可能性。Yang Xu等[88]通过一种新的光学传感技术,在WSe2/WS2莫尔晶格的分数填充下观察到近二十多个关联绝缘态。该技术基于WSe2单层半导体中激子激发态对介电环境的敏感性。这种材料会与光发生强烈的相互作用,形成激子,即束缚的电子-空穴对[116]。而且这种激子的激发态(2s、3s等)对介电环境十分敏感[117]。这样就可以利用传感器测量激子激发态的共振能量和强度,以光学方式探测TMD莫尔超晶格中的绝缘态。观察到的绝缘态以及相应的共振能量如图6(i)所示,这样的结果表明,电子填充和空穴填充的超晶格都存在绝缘态,并且还存在许多较弱的绝缘态,特别是在分数填充的情况下。Xiong Huang等[118]在WS2/WSe2莫尔异质结构中的分数填充下也观察到了一系列关联绝缘态。而且研究人员在其中一个样品中发现,n=±1/3和±2/3填充处产生的关联绝缘态在120 K的温度下依然可以存在,并且在n= −8/9、−5/6、−7/9、+5/9和+6/7等分数填充处也观察到了关联绝缘态,这表明该样品中还存在理论预测之外的其他强相互作用。
-
通常情况下,像硅和铝这样的半导体金属能够以电子的形式导电,在材料中产生电流。但是,在极低温下,因为没有足够的能量来激发电子的运动,所以这些金属中的电子几乎会停止运动。而带负电荷的电子自然地相互排斥,因此对于处于极低温下密度较低的电子,它们之间的相互排斥力起到了类似支架的作用,将电子固定在原地,以相等的间隔隔开,形成由电子组成的类似晶体的结构。这种可以将金属从导体变成绝缘体的刚性结构,被称为电子晶体,这个概念是1934年由美籍匈牙利物理学家Eugene Paul Wigner首次提出的,因此也被称为威格纳晶体(Wigner crystal)[119]。
电子晶体的概念提出之后,许多研究组都对其产生了浓厚的兴趣。1971年,Grimes等[120]提出,液氦自由表面上形成的非简并二维电子气,在低温下可能会具有电子晶体的特性。不久之后,Chaplik等[121]研究了位于半导体反转层中的电子形成维格纳晶体的可能性。虽然各个研究组都在理论上预言了电子晶体的存在,但是它真正在实验中被观测到是在1988年。Andrei等[122]在极低温强磁场下的二维电子气中首次观察到二维电子晶体的特征。电子在低密度下,简并的朗道能级可以将电子的动能猝灭,进而自发的进行排列,形成高度有序的电子晶体。
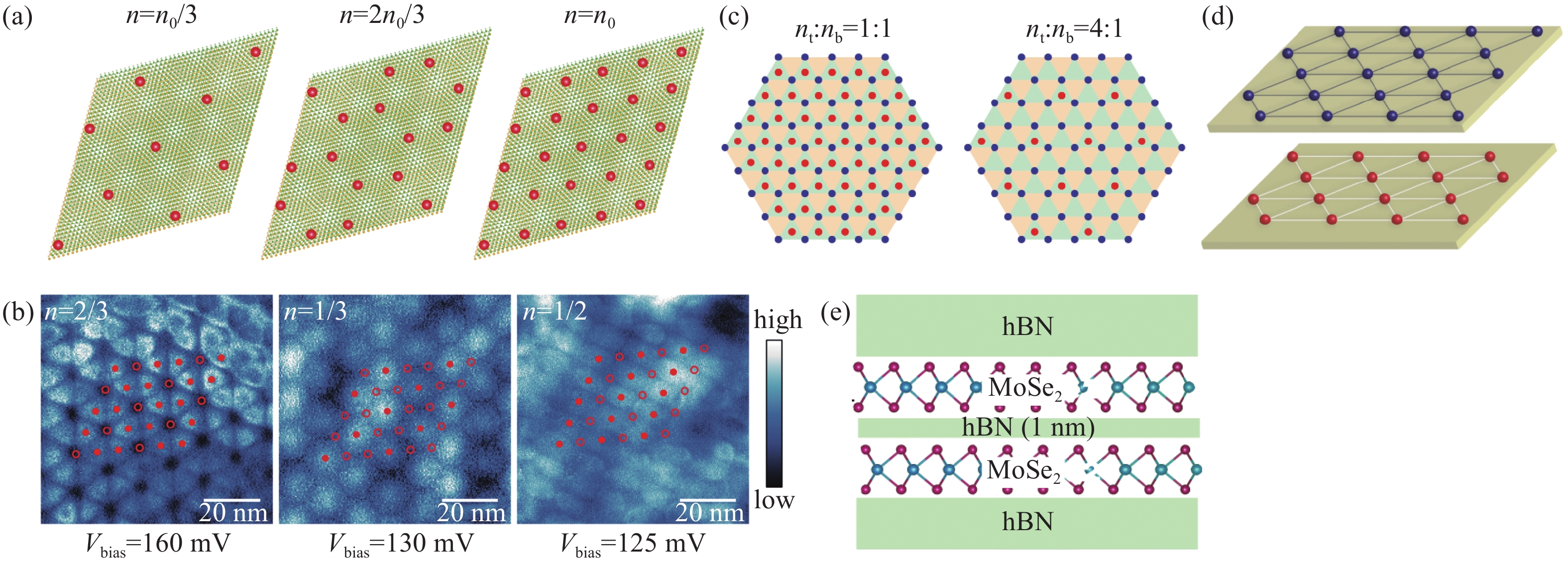
Wang等[123]利用最新的光学检测电阻和电容技术,在半导体WSe2/WS2莫尔超晶格的底层晶格上观察到了广义维格纳晶体。这种维格纳晶体与Andrei等[122]在二维电子气中观察到的维格纳晶体不同,不仅由电子−电子间的相互作用产生,还受到了莫尔超晶格的影响,是由电子关联效应和莫尔周期势共同作用形成的。研究人员发现,WSe2/WS2的莫尔异质结构在n=1、n=1/3和n=2/3电子填充时的绝缘态(n为每个位点的电子数)[124-125],具有较低的态密度和较大的电阻,而这些特征从来没有在大转角WSe2/WS2异质结构中出现过。
n=1填充时的绝缘状态通常被认为是莫特绝缘态[124],同时也可以理解为相互作用导致的维格纳晶体[119,125-128]或电荷转移绝缘体[129]。因为TMD异质结构的简并度为2,来自自旋谷锁定[130],所以这种状态对应于莫尔微带的半填充。类似的关联绝缘态在转角双层石墨烯和ABC三层石墨烯/氮化硼异质结中形成的莫尔超晶格中也可以观测到[2-3,131-132]。由于在其他莫尔超晶格系统中,没有发现过如n=1/3和n=2/3等晶格位点为分数的填充状态,同时这种状态也不能被描述为莫特绝缘态或只有原位排斥相互作用的哈伯德模型,因此研究人员认为,n=1/3和n=2/3填充时的绝缘态对应广义维格纳晶体[119,125-128]。图7(a)展示了猜想的广义维格纳晶体实空间结构。这样的广义维格纳晶体结构表明,位点间(长程)相互作用能大于莫尔微带带宽,可以证明TMD莫尔异质结构中强关联特性,Huang等[118]的实验也证明了这一点。
为了获得维格纳晶体的实空间图像,Wang等的课题组利用扫描隧道显微镜,成功实现了在n=2/3、n=1/2和n=1/3填充的 WSe2/WS2莫尔异质结的实空间成像[133]。二维维格纳晶体的实空间成像对测量技术的要求十分苛刻,它必须同时具有高空间分辨率、高单电子灵敏度和低电子晶格扰动等特点。扫描隧道显微镜具有出色的空间分辨率和电荷灵敏度,可以满足上述实验要求。但是高灵敏度的测量不可避免的会对电子晶格产生较大的扰动,因此研究人员设计了一种新颖的扫描隧道显微镜测量方案,在保持高单电子灵敏度的情况下尽可能抑制了晶格扰动。在n=1/3和n=2/3时,观测到的广义维格纳晶体实空间图像如图7(b)所示,这与之前的预测结果[123]相符,证实了广义维格纳晶体态的存在。在n=1/2时,莫尔超晶格自发地产生C3对称性破缺,电子交替填充,产生的广义维格纳晶体高度简并,多个电子晶格结构仅在最近邻相互作用的影响下具有相同的能量[134]。
Smoleński等[135]利用单层TMD材料在磁场B=0的情况下也观察到了维格纳晶体。根据量子蒙特卡罗计算[136],在外部磁场B=0时,维格纳晶体想要成为二维电子系统的基态,库仑相互作用与动能的比值rs不能小于30。rs正比于有效电子质量me,反比于介电常数ϵ和电子密度ne,而单层TMD材料的相关参数可以很好的满足上述要求[137]。根据观测到的高能激子umklapp共振与莫特绝缘态下电子电荷排列[138],研究人员得出结论,维格纳晶体是由低ne的电子形成的。
Zhou等[139]在无磁场或莫尔周期的薄夹层双层MoSe2异质结中观察到了双层维格纳晶体。该异质结的结构示意图如图7(e)所示,两个MoSe2单层的旋转角度为0°,中间用1 nm厚的六方氮化硼隔开。在低温条件下,双层MoSe2在电子对称填充(nt:nb=1:1)和不对称填充(nt:nb=3:1、4:1和7:1)下会表现出与关联绝缘态有关的光学特征,如图7(c)所示,研究人员认为这些特征与双层维格纳晶体密切相关。双层维格纳晶体的结构如图7(d)所示,由对称互锁的三角形电子晶格组成,依靠层间相互作用达到稳定的状态[140]。
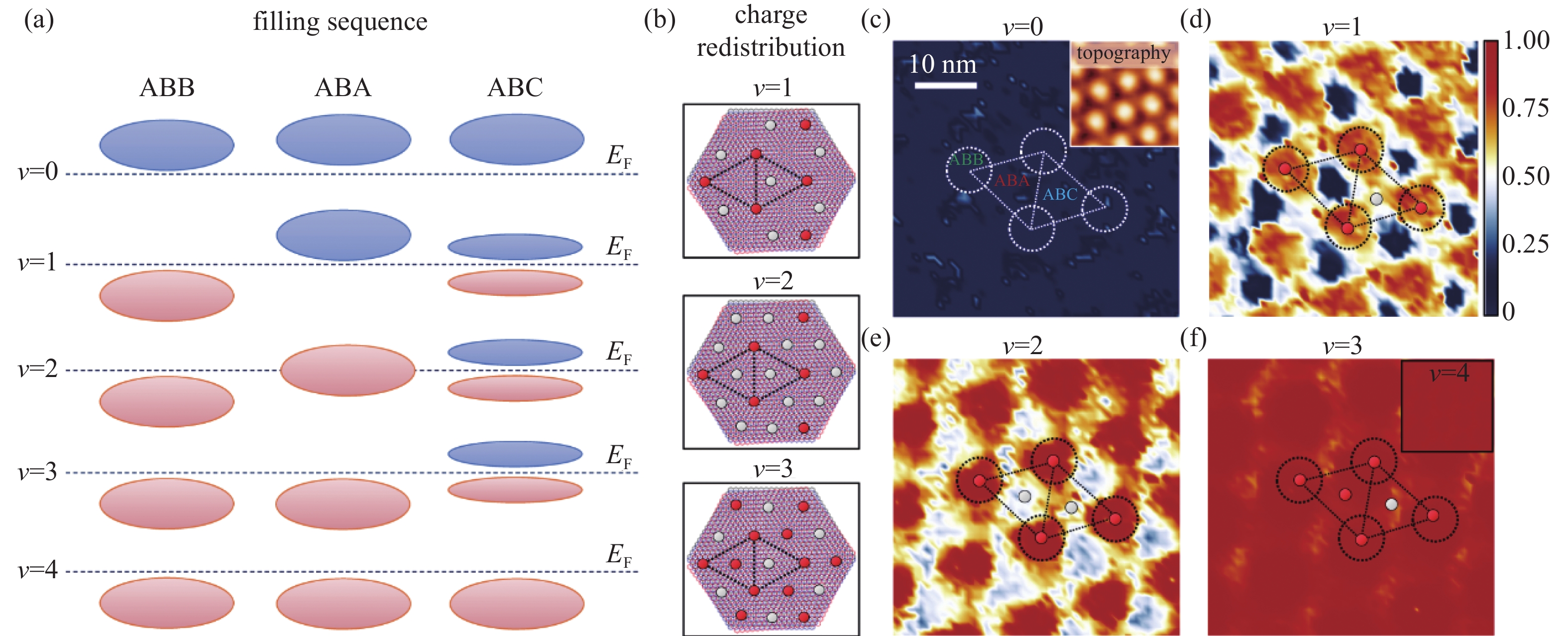
Li等[141]利用ABB、ABA和ABC区域dI/dV随掺杂水平(Vg)变化的图像推导了莫尔单元的填充序列(如图8(a)所示),并设想了以电子晶体结构作为填充因子的函数。当ν=0时,整个样品中没有电子,局部填充率为零(如图8(c)所示)。在ν=1时(如图8(d)所示),ABB区域首先收集大部分掺杂电子(红色三角形区域),形成电子晶格结构。在ν=1、2、3时,随着填充因子增加(如图8(e)-(f)所示),ABA区域逐渐实现完全填充。而ABC区域始终保持部分填充,直到v=4时到达完全填充(如图8(f)的插图所示)。研究人员利用在EF附近的dI/dV图,逐点积分计算各点导平带(Conductance Flat Band,CFB)的局部填充系数R,得到的在固定的全局填充ν下提取的局部填充率的颜色轮廓(如图8(c)-(f)所示)与推测的结果相匹配,证实了电子晶体的存在。同时,在电子晶体形成过程中,CFB的局部填充受到调制,电子晶体的电荷密度调制与局域能带填充的协同作用产生了整体金属−绝缘体转变。而且由于电子晶体提供了空间调制的平带填充,这意味着它可以在莫尔晶格内诱导实空间陈数变化。因此,在两个具有不同局部陈数[142-143]的区域边界处,会出现拓扑保护的边界态。陈数的周期实空间调制会产生一个无间隙拓扑界面态的周期晶格,在实空间中形成周期性的拓扑态圆环。为了进一步确认圆环态的拓扑起源,研究人员在没有强电子关联或实空间电子聚集的对照样品上进行了相同的测试,并没有观察到环面结构。因此,可以得出结论电子强关联效应、实空间电荷密度调制以及非平庸拓扑态与拓扑环面态的形成密切相关。
-
材料中的磁性通常来源于电子的自旋以及电子的轨道运动,分别形成自旋磁矩和轨道磁矩。对于二维电子气来说,外加磁场会使其中的电子做回旋运动,形成平直的朗道能级,并且回旋运动所导致的电流环将会产生轨道磁矩。若忽略子晶格内的莫尔势,TBG中的平带可近似看作朗道能级,平带中的八个自由度所产生的价带都可看做零阶赝朗道能级[144-145]。当TBG处于整数填充时,电子之间的相互作用会使体系倾向于通过谷、自旋和子晶格之间的极化或耦合的方式使自旋或谷对称性发生破坏[145-146]。同时由于电子之间的长程库仑相互作用的交换作用,八重简并中被电子占据的平带与未被占据的平带间将会产生能隙,若平带具有非零陈数,则在莫尔超晶格原胞内将会出现实空间中的环路电流,导致轨道磁化[147-148]。
在TBG中,每个谷的两条平带具有类似于二维Z2拓扑绝缘体的特性,对于每个自旋和谷所对应的两条平带可以看做二维Z2拓扑绝缘体中陈数相反(
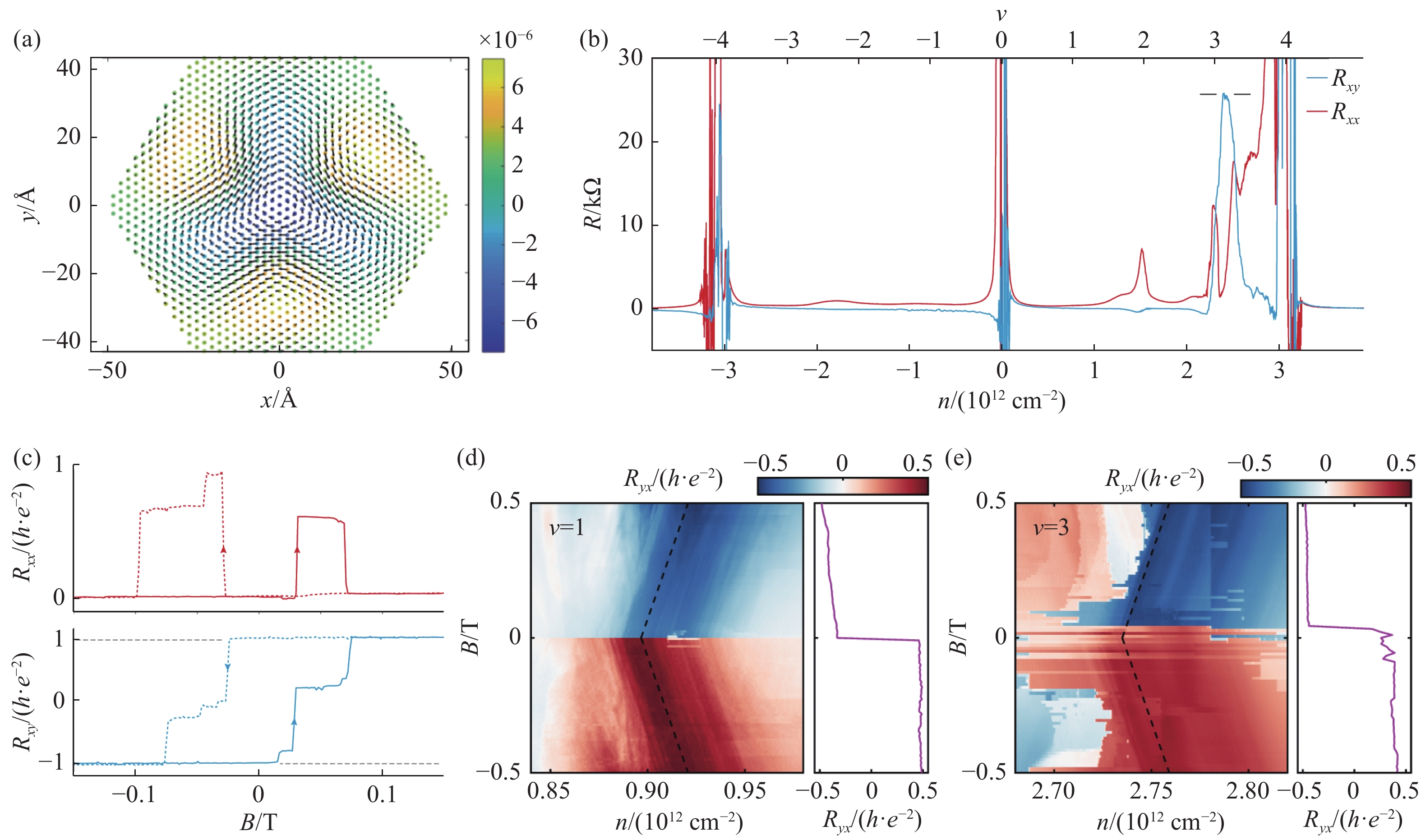
$ \pm 1 $ )的两个赝自旋分量,其威尔逊环矩阵的本征值与自旋分量奇数缠绕的本征值完全相同,因此在TBG中的平带具有非平庸的拓扑特征[147]。因此当氮化硼衬底与石墨烯以相同空间取向进行排列时,由于子晶格势的存在导致C2Z对称性被破坏,在$ {K}^{\mathrm{\text{'}}} $ 和$ K $ 处完全简并的两条平带之间将会被能隙隔开,每条平带具有非零谷陈数[148,149]。当平带处于整数填充时,强电子−电子相互作用将会破坏时间反演对称性,导致自旋和谷的对称性受到破坏[82,150],得到的谷极化态将是一个如图9(a)所示的由围绕AA堆叠区域的环路电流产生的轨道铁磁态[147]。转角体系中的轨道铁磁态与拓扑带的存在使得反常量子霍尔效应的出现成为可能。对于普通的磁性材料来说,产生反常量子霍尔效应首先需要通过打破自旋的时间反演对称性,导致自旋极化,之后通过较强的自旋-轨道耦合将时间反演对称性的破缺传递到轨道[151-153]。然而石墨烯中的自旋-轨道耦合非常弱,直接破坏的轨道时间反演对称性会产生较明显的反常量子霍尔效应。如图9(b)和9(c)所示,在对TBG的输运测量中发现在
$ \nu =3 $ 处纵向电阻Rxx接近于零,霍尔电阻Rxy出现了一个以h/e2为在TBG中出现的反常量子霍尔效应,在tMBG中施加
$ D > 0 $ 的电位移场时同样也会出现。图9(d)与9(e)所示的结果表明在$ \nu =1 $ 和$ \nu =3 $ 填充处自旋和谷对称性发生破缺,出现了陈数为2的反常量子霍尔效应[87,109,111]。除此之外,通过施加磁场,在氮化硼衬底与石墨烯未对齐的TBG中其他整数填充处也观测到了平带陈数从零到非零的转变[80,155]。未对齐的tMBG的$ \nu =\pm 1 $ 填充处同样在外磁场的诱导下出现了非零陈数以及回滞现象[76]。平带在外磁场下的拓扑转变表明普通绝缘态和陈绝缘态之间可能存在竞争关系。在转角TMD中同样也观测到了铁磁态的出现。Yanhao Tang等[156]研究了相对旋转角为0°的WSe2/WS2异质结,并通过测量其光学响应对外磁场和栅极调控载流子浓度的依赖性,来探测系统的电学和磁学性能。在能带半填充的情况下,研究人员观察到了具有反铁磁性Curie–Weiss行为的关联绝缘态,这与理论上强相互作用状态下的哈伯德模型预期的相同[157-160]。当填充因子接近0.6时,反铁磁性状态出现了向弱铁磁性状态转变的趋势。
-
前几章的描述中,由于平带非平庸的拓扑性质,石墨烯转角体系的绝缘态会具有非零陈数。对于一个由M和N层石墨烯组成的魔角石墨烯来说,当上下两层为手性相同地叠加时,每个谷的两个平带的总陈数为
$ \pm (M-N) $ ,当上下两层为手性相反地叠加时,每个谷的两个平带的总陈数为$ \pm (M+N-2) $ ,并且由于平带与高能带之间存在较大的能隙,两个平带的总陈数具有较强的稳定性[161]。但对于每个平带的陈数而言,其陈数值容易受到转角角度、库伦相互作用强度以及外部磁场强度等多方面因素的影响[76]。并且其陈数值还与对称性破缺的方式有关,如3.1节所述,通过石墨烯与氮化硼对齐堆叠打破C2z对称性或通过外加磁场打破时间反演对称性的方式均可以使平带简并度下降并在其之间打开能隙,产生具有非零陈数的能带(图10(a))。在掺杂的过程中,随着载流子浓度的增加,CFB中的所有四种自旋和谷能带理论上应该被均匀填充,但在达到整数填充前会发生级联相变,交换作用将所有的载流子全部转移到某一能带,并将其他三条能带推至更高的能量(图10(b))[162-163]。对于TBG来说,在磁场下的陈绝缘体往往显示出时间反演对称性破缺的特征[54],即在填充数为
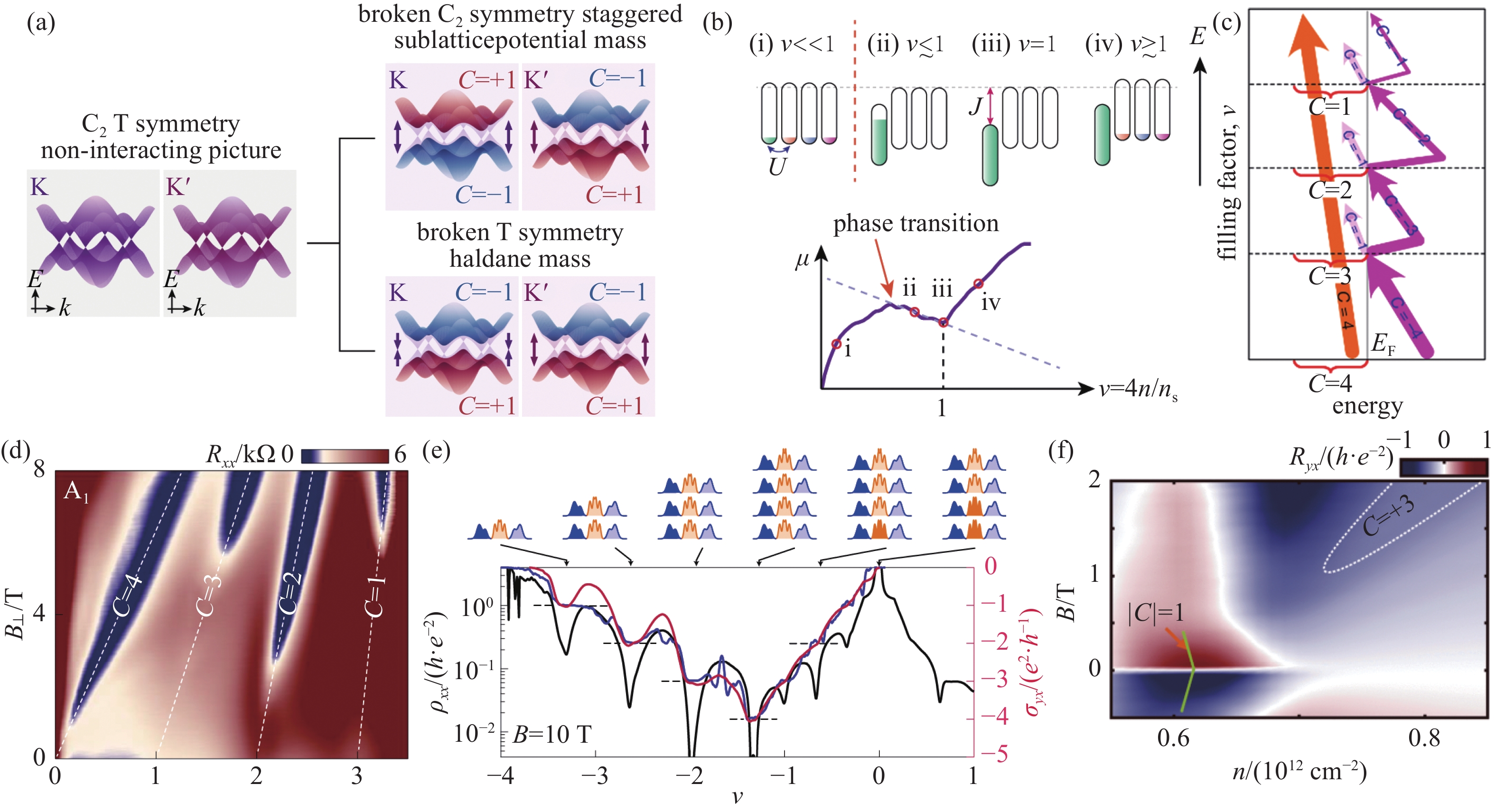
$ \nu =\pm 1,\pm 2,\pm \mathrm{3,0} $ 时,对应的陈数分别为$C=\pm 1,\pm 2, \pm 3,\pm 4$ ,其填充原理如图10(c)所示,图10(d)为在实验中测得的结果。此外,TBG在不同填充处的热激活能隙$ \Delta $ 对外加磁场的响应不同。当$ \nu =2 $ 时,$ \Delta $ 会随着磁场的增加而减小,而$ \nu =\mathrm{1,3} $ 时情况则相反,这说明$ \nu =2 $ 时TBG处于谷极化或谷间相干态,$ \nu =\mathrm{1,3} $ 时处于自旋极化态[164]。除了TBG之外,其他的转角体系也观测到了具有非零陈数的陈绝缘体,例如,根据能隙在拓扑上被强制闭合的磁场值与陈数的关系推断出了TDBG中存在$ C=2 $ 的绝缘态[99],通过调节电位移场使ABC堆叠的三层石墨烯在$ \nu =-1 $ 时出现陈数为2的绝缘态[165]。作为打破时间反演对称性的常用手段,磁场不仅可以诱导陈绝缘体的产生,也可以产生朗道能级,导致平带的重建。例如在图10(e)所示的TBG中,零朗道能级会演化为C=2的陈带,同时为了保持总陈数为零,C=2陈带的上下两侧平带的陈数为−1,因此对于每个自旋和谷来说,磁场将两个平带重建为三个子平带[53]。此外,在磁场的作用下,不同的陈绝缘体之间会存在相互竞争的关系。在没有磁场的情况下,在整数填充处的基态为多体简并的基态,各个基态具有不同的陈数,在忽略手征扰动的情况下,陈数较小的态具有优势,但磁场的出现会降低较大陈数态的能量,使其与较低陈数态竞争时更具优势。例如,在实验中观测到了
$ \nu =0.8 $ 附近的TBG在磁场为0.5 T左右时陈数绝对值由1到3的转变(图10(f))[166]。空间对称性破缺对于陈绝缘体的状态非常重要。除了上述的C2z对称性,在电子相互作用的影响下,电荷密度的调制会使能量在布里渊区中分布不均,使得该体系发生平移对称性破缺并通过将布里渊区折叠的方式来降低体系的能量。对于TBG,由于贝利曲率主要集中于
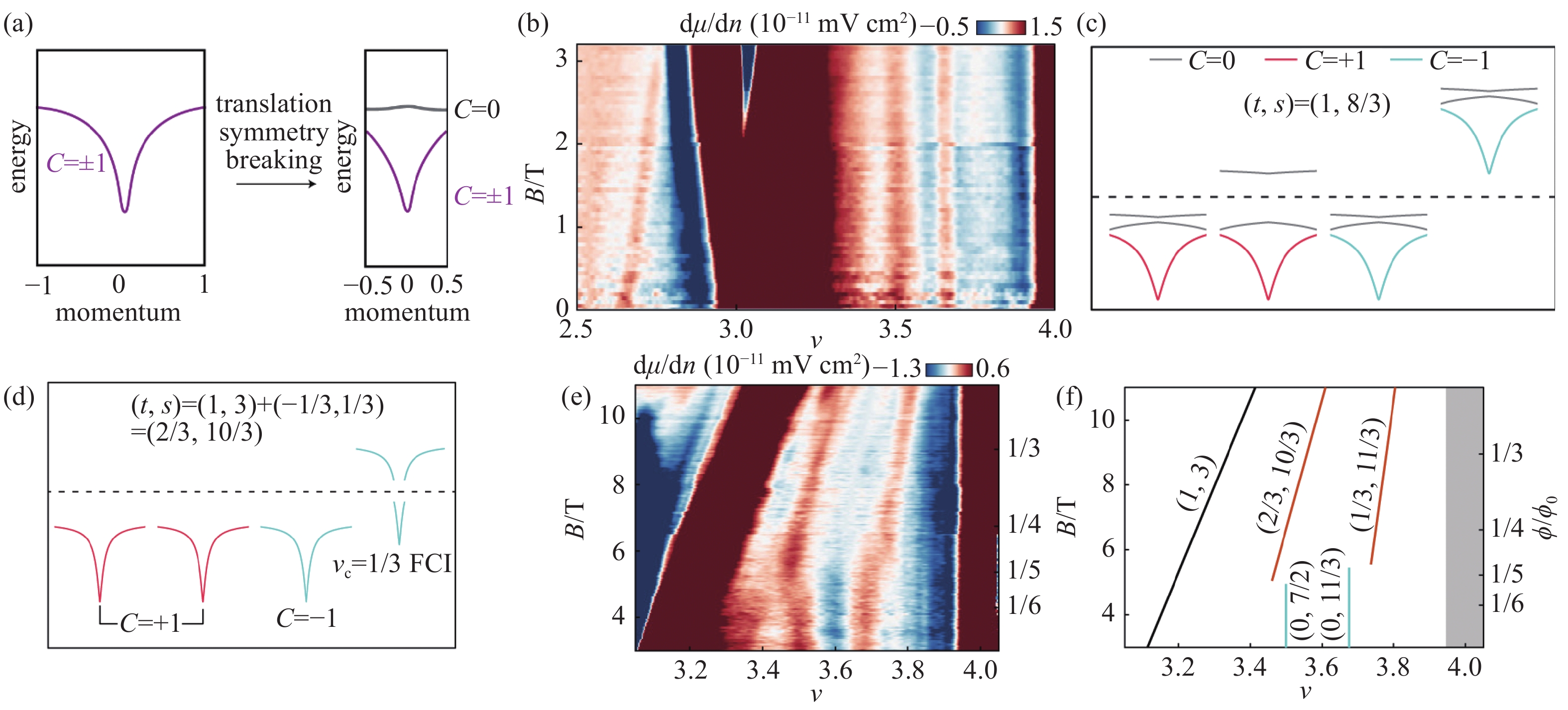
$ \mathrm{\Gamma } $ 点,因此布里渊区的折叠会产生一条陈数为零的新能带,导致总能带数翻倍(图11(a)),在不同的填充下会有新的陈绝缘态产生[167]。平移对称性的破缺也可以使布里渊区发生更高倍的折叠,例如在实验中观测到了三倍折叠而形成的SBCI态,如图11(b)与11(c)所示。利用该理论同样可以解释FCI态的转变,例如图11(d)中的陈数和填充数分别为2/3和10/3的FCI态(2/3,10/3)可以看作上一个(1,3)的陈绝缘态和(−1/3,1/3)的FCI态的叠加[168]。同时从图11(e)与11(f)中可以看出CDW态与FCI态存在竞争关系,但由于磁场会提高布里渊区内贝利曲率分布的均匀性,布里渊区不易发生折叠,从而有利于FCI态的形成[169-170],因此随着磁场的增加CDW态逐渐演变为FCI态。除此之外,在WSe2衬底上的TBG也观察到了由于布里渊区二倍折叠导致的(−4,−0.5)的SBCI态[171]。这些都说明了对称性破缺的重要性。 -
二维量子材料的莫尔超晶格中存在着丰富的物理现象,同时由于其可以通过角度、压强、垂直电位移场以及磁场等方式进行调节,是研究各种新奇物性的理想结构。本文主要介绍了超晶格结构所带来的各种新奇的物理性质。首先从超晶格结构所带来的晶格空间结构以及能带结构的变化出发,介绍了超晶格狄拉克点、霍夫斯塔特蝴蝶能谱、莫尔激子、范霍夫奇点和原子重构。接着,在出现平带的超晶格结构中,我们重点介绍了关联绝缘态、超导、电子晶体和轨道磁性等与电子之间强关联现象有关的内容。而且超晶格结构还可以为多种物理现象之间的关联研究提供理想的平台。例如TBG、TTG中出现的超导现象极有可能为探究非常规超导现象开辟新的道路,即使该超导和关联绝缘等状态的起源尚且存在争议。除此之外,同时具有拓扑非平庸的平带与较强的电子相互作用的超晶格结构更是探究拓扑与强关联效应相互作用的绝佳体系。
虽然超晶格结构中蕴藏着如此丰富的物理现象,但是有限的测量手段在一定程度上制约了对其中新奇物性的探索。常见的测量手段各有所长。输运测量最大的优势是可以较直观的获得样品整体的特性,例如对超导态和关联绝缘态的测量。STM测量则具有高精度的空间与能量分辨率,能为其他测量结果提供更微观的解释,可以很好的应用于对电子晶体、原子重构和关联绝缘态的探索。但是这两种测量探究手段都无法得到具有动量分辨信息的电子能带结构,无法直观地获得范霍夫奇点、SDP等的测量结果,很大程度上限制了其对TMD的探索。而ARPES具有较高的动量分辨,可以提供更多的电子结构信息,但对样品的质量有较高的要求。因此,改进制备方法并提高样品质量或许可以突破各种测量手段自身的局限性,进一步开拓超晶格结构的研究领域。目前成熟的转移技术主要分为干法转移和湿法转移两种[172]。湿法转移最大的特点是可以在室温下转移CVD生长的大面积二维材料。但由于湿法转移不可避免的会与液体接触,因此样品表面往往会产生大量褶皱和裂纹[173-174],并吸附各种杂质[175-176]。而干法转移可以最大限度避免溶液吸附和毛细作用力对样品的影响,同时可以在手套箱中操作,对一些性质不稳定、只能保存在惰性气体环境中的TMD样品较为友好。但是,干法转移的操作通常较为复杂[177],而且转移时受应力的干扰较为明显[178],需要丰富的转移经验才能制备出质量较高的样品。当然,在制备方法不断发展的过程中,其中一些问题已经得到了解决,例如通过在真空或惰性气体环境下退火可以有效的去除样品表面吸附的杂质;在干法转移中利用热膨胀代替接触式按压可以很大程度上减少应力的干扰。因此我们有理由相信,随着异质结样品制备方法的逐步改进,制备出来的样品能更好的适用于各种测量方法,研究人员对超晶格结构的认识将会更进一步,在其中发现更多有趣的物理现象。
超晶格结构在二维转角异质结中产生的新奇物态
Novel States Induced by Superlattice Structures in Twisted Two-Dimensional Heterostructures
-
摘要: 二维量子材料由于其展现出的许多新奇特质而受到了普遍关注。当二维量子材料组成同质结或异质结时,晶格常数和层间旋转角度会使体系产生新的超晶格结构,从而导致一系列电子能带结构和物理性质的变化。文章首先围绕着超晶格结构所带来的晶格空间结构以及能带结构的变化展开讨论,主要介绍了由此产生的超晶格狄拉克点、莫尔激子和原子重构等新奇物性。除此之外,超晶格结构会使电子的费米速度在一组特定的旋转角度下消失,产生平带。这会导致该区域的物理性质由电子之间的相互作用能主导,从而产生显著地改变。这些由电子之间强关联现象所引起的新奇物性,成为了近些年凝聚态物理等研究领域的前沿课题之一。在这里,文章主要围绕着关联绝缘态、超导、电子晶体和轨道磁性等介绍了与电子之间强关联现象有关的内容,并在最后对超晶格结构未来的发展方向进行了展望。Abstract: Two-dimensional quantum materials have attracted widespread attention due to their manifestation of numerous novel and unique characteristics. When two-dimensional quantum materials are stacked to form homojunctions or heterojunctions, variations in lattice constants and interlayer rotation angles give rise to new superlattice structures, consequently leading to a series of changes in the electronic band structures and physical properties. In this article, the discussion begins by focusing on the alterations in the lattice spatial structure and band structure resulting from the presence of the superlattice structure, such as superlattice Dirac points, Moiré excitons, and atomic reconstructions. Moreover, at specific rotation angles, the Fermi velocity of electrons will diminish at discrete angles due to the influence of the superlattice structure, giving rise to the creation of flat bands. This will cause a significant change in the physical properties of this region as they are predominantly governed by the interaction energy between electrons. These novel physical properties, arising from strong electron-electron correlations, have become one of the forefront topics in the field of condensed matter physics. Here, the article primarily focuses on subjects pertaining to strong electron-electron correlations, such as correlated insulators, superconductivity, electron crystals, and orbital magnetism. And it offers a forward-looking perspective on the future development directions of superlattice structures.
-
Key words:
- Two-dimensional quantum material /
- Moiré superlattice /
- Flat band /
- Strong correlation effect .
-

-
图 1 超晶格。(a)通过层间旋转形成的石墨烯/氮化硼超晶格示意图,硼和氮原子分别用蓝色和红色表示,碳原子用灰色表示,超晶格内部具有不同的堆叠区域。(b)上图为石墨烯/氮化硼在AFM表征下的形貌像,下图为沿着绿线的高度起伏。(c)石墨烯/氮化硼超晶格的层间相互作用势在空间中的分布[6-7]
Figure 1. Superlattice. (a) Schematic diagram of graphene/boron nitride superlattice formed by interlayer rotation, with boron and nitrogen atoms represented in blue and red, and carbon atoms in gray. Different stacking regions are present within the superlattice. (b) The upper part shows the morphology image of graphene/boron nitride characterized by AFM, while the lower part represents the height variations along the green line. (c) Spatial distribution of the interlayer interaction potential in the graphene/boron nitride superlattice [6-7]
图 2 原子重构。 (a)未重构的转角双层石墨烯(左)和重构的转角双层石墨烯(右)堆垛类型示意图。(b) 样品的扫描隧道显微镜(Scanning Tunneling Microscope,STM)图像及其局部放大图像(如右上角插图所示),比例尺为10 nm。正方形区域的大小为3 nm × 3 nm。插图:黑色正方形区域的放大图,原子结构清晰可见。比例尺为1 nm。(c)( b)中图像内不同颜色区域的相对晶格常数,颜色与(b)中的相互对应。(d)通过选择TBG中的石墨烯衍射峰获得的透射电子显微镜暗场图像,转角分别为0.1°、0.4°、0.8°和1.2°[6,10-13]
Figure 2. Atomic reconstruction. (a) Schematic diagram depicting the stacking types of unreconstructed twisted bilayer graphene (left) and reconstructed twisted bilayer graphene (right). (b) Scanning Tunneling Microscope (STM) images of the sample and their local magnifications (as shown in the upper-right inset), with a scale bar of 10 nm. The size of the square region is 3 nm × 3 nm. Inset: A magnified view of the black square region, showing clear atomic structures with a scale bar of 1nm. (c) Relative lattice constants of different color regions within the images in (b), corresponding to the colors in (b). (d) Dark-field transmission electron microscope images obtained by selecting graphene diffraction peaks in TBG, with twist angles of 0.1°, 0.4°, 0.8°, and 1.2°, respectively[6,10-13]
图 3 超晶格狄拉克点。(a)氮化硼上石墨烯κ点附近电子能带结构,左图价带对应于κ点出现一个孤立的SDP的情况,右图对应μ点出现SDP的情况。 (b)上图:纵向电阻率随载流子浓度变化曲线,在SDP处电阻率出现峰值,并具有很强的温度依赖性。下图:霍尔电阻率随载流子浓度变化曲线,霍尔电阻率在SDP处符号发生改变。 (c)和(d) ARPES观测到的具有能隙的主狄拉克点(c)和SDP(d)[21,23,27]
Figure 3. Superlattice Dirac points. (a) The electronic band structure of graphene near the κ point on boron nitride. In the left image, there is an isolated saddle point (SDP) in the valence band at the κ point. In the right image, there is an SDP at the μ point. (b) Upper image: Longitudinal resistivity as a function of carrier concentration, exhibiting a peak in resistivity at the SDP with a strong temperature dependency. Lower image: Hall resistivity as a function of carrier concentration, showing a change in sign of the Hall resistivity at the SDP. (c) and (d) ARPES (Angle-Resolved Photoemission Spectroscopy) observations of gapped main Dirac point (c) and SDP (d)[21,23,27]
图 4 范霍夫奇点。 (a)范霍夫奇点形成的示意图,左侧为布里渊区的相对旋转导致狄拉克锥的分离,右侧为在两狄拉克锥之间形成了范霍夫奇点,在奇点处具有较高的电子态密度。(b) G为单层石墨烯的STS曲线,M1和M2为转角双层石墨烯的STS曲线,可以明显看到狄拉克点两侧有范霍夫奇点出现。(c)当角度介于2°与10°之间时,
$ \mathrm{\Delta }{E}_{\mathrm{V}\mathrm{H}\mathrm{S}} $ 值会随着角度$ \theta $ 的减小而减小,但两个范霍夫奇点的能量对称中心几乎不随角度发生改变。(d)1为AA堆叠处的STS谱线,2和3为其他堆叠处的STS谱线,虽然所有光谱都显示两个峰,但1处的电子态密度明显比其他位置高。(e)重整费米速度随层间转角的变化关系,红色曲线为根据式 (6) 得到的拟合曲线,蓝色三角对应于实验上测出的数据,随着角度减小在问号~1.16°处出现文中提到的AA处局域化的现象[31-32,34-38]Figure 4. Van Hove singularities. (a) Schematic diagram illustrating the formation of Van Hove singularities (VHS). On the left, relative rotation in the Brillouin zone leads to the separation of Dirac cones. On the right, VHS forms between the two Dirac cones, resulting in a higher electron density at the singularity point. (b) STS (Scanning Tunneling Spectroscopy) curves for graphene. G represents the STS curve for a single-layer graphene, while M1 and M2 represent STS curves for twisted bilayer graphene, where VHS is clearly observed on both sides of the Dirac point. (c) When the angle is between 2° and 10°, the
$ \mathrm{\Delta }{E}_{\mathrm{V}\mathrm{H}\mathrm{S}} $ value decreases as the angle θ decreases, but the energy center of the two VHS points remains almost unchanged with varying angles. (d) STS spectra, where 1 corresponds to the AA-stacked region, and 2 and 3 correspond to other stacking regions. While all spectra display two peaks, the electron density at position 1 is significantly higher than at other positions. (e) Relationship between the reorganized Fermi velocity and the interlayer twist angle. The red curve represents the fitted curve obtained from formula (6), while the blue triangles correspond to experimentally measured data. The localization phenomenon at the AA-stacked position occurs around a twist angle of approximately 1.16° as mentioned in the text[31-32,34-38]图 5 霍夫斯塔特蝴蝶能谱。(a)电子掺杂侧的霍夫斯塔特蝴蝶能谱,横轴反应了单位超晶格中载流子数密度,纵轴代表单位超晶格中磁通量的大小,
$ C\mathrm{_p} $ 为穿透场电容,它与参考电容$ C_{\mathrm{Ref}} $ 的比值区分了有能隙和无能隙状态。(b)根据(a)图得到的五类霍夫斯塔特蝴蝶能谱线[49]Figure 5. Hofstadter butterfly energy spectrum. (a) The Hofstadter butterfly energy spectrum on the electron-doped side, where the horizontal axis reflects the carrier density per unit superlattice, and the vertical axis represents the magnitude of the magnetic flux per unit superlattice.
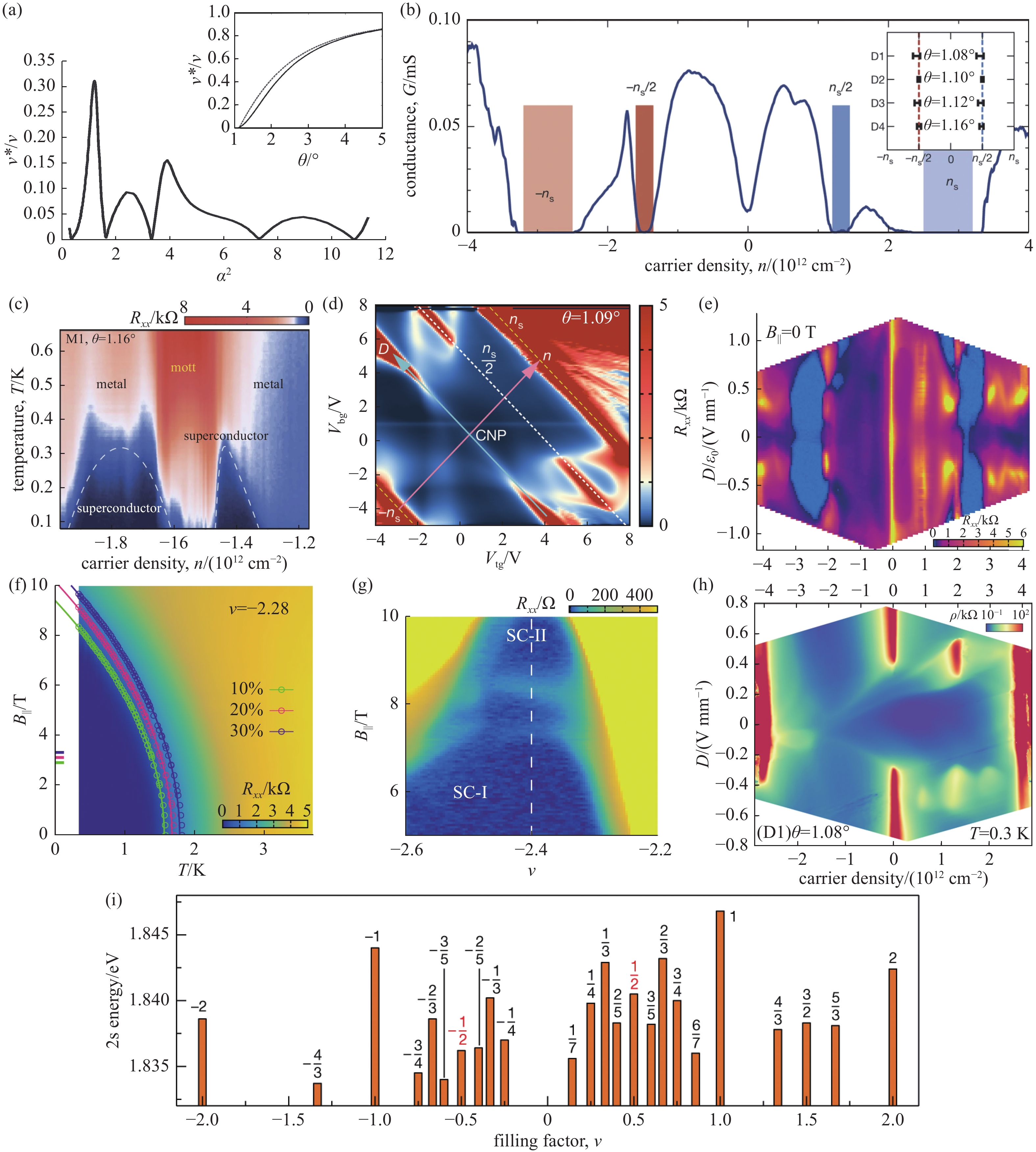
$ C\mathrm{_p} $ represents the tunneling field capacitance, and it distinguishes between gapped and gapless states based on its ratio to the reference capacitance$ C\mathrm{_{Ref} } $ . (b) The five distinct classes of Hofstadter butterfly energy spectra obtained based on the graph in (a)[49]图 6 关联绝缘态和超导。(a)在某些
$ \alpha $ 所对应的角度下,重整费米速度为零,有平带产生。(b) TBG中电导率随载流子浓度变化曲线,在半填充$ \nu =2 $ 处出现了绝缘态。(c) TBG$ \nu =2 $ 附近的相图,在载流子浓度稍微偏离半填充的两侧出现了超导相。(d)通过调节TDBG的顶栅和底栅电压实现对电位移场和载流子浓度的调节。在电场的调节下,电子半填充处可以观察到有关联绝缘态的产生。(e) TTG关于载流子浓度与电位移场的相图,在整数填充附近有超导态的存在。(f) 在TTG的$ \nu =-2.28 $ 处,纵向电阻随温度和平行磁场的变化,可以看出TTG的超导并不受泡利极限的限制,可以在高达10 T的磁场下存在。(g)TTG中纵向电阻随填充数和平行磁场的变化,随着磁场增加会观测到第二个超导相的出现,两个超导相可能通过一阶相变相连,这些现象表明TTG中的超导电子可能是自旋三重态。(h) tMBG关于载流子浓度与电位移场的相图,tMBG在D>0和D<0的相图具有很大的不同,具有较强的电场可调性。(i) 所有绝缘态的激子共振能量,顶部的数字显示了绝缘状态的填充因子[2,3,69,75,84-88]Figure 6. Correlated insulating states and superconducting states. (a) At certain angles corresponding to α, the reorganized Fermi velocity becomes zero, leading to flat bands. (b) The conductivity in TBG as a function of carrier concentration, exhibiting an insulating state at half-filling ν=2. (c) Phase diagram near ν=2 in TBG, showing superconducting phases slightly away from half-filling on both sides of the carrier concentration. (d) Adjustment of the electric displacement field and carrier concentration in TDBG by tuning the top and bottom gate voltages. Under electric field tuning, the emergence of correlated insulating states is observed at the electron half-filling. (e) Phase diagram of TTG concerning carrier concentration and electric displacement field, with the presence of superconducting states near integer fillings. (f) Longitudinal resistivity in TTG at ν=−2.28 as a function of temperature and parallel magnetic field, showing that TTG’s superconductivity is not limited by the Pauli limit and can exist under magnetic fields as high as 10 T. (g) Longitudinal resistivity in TTG as a function of filling and parallel magnetic field. As the magnetic field increases, the appearance of a second superconducting phase can be observed, possibly connected by a first-order phase transition, indicating that superconducting electrons in TTG may be of spin-triplet nature. (h) Phase diagram of tMBG concerning carrier concentration and electric displacement field. tMBG exhibits significant tunability with strong differences in phase diagrams for D>0 and D<0. (i) Exciton resonance energies for all insulating states, with the top numbers indicating the filling factor of the insulating state[2,3,69,75,84-88]
图 7 过渡金属二硫族化合物中的电子晶体。(a)WSe2/WS2莫尔超晶格中广义维格纳晶体(n=1/3和n=2/3填充)和莫特绝缘态(n=1填充)的示意图。(b)广义维格纳晶体在n=2/3、n=1/3和n=1/2电子填充下的dI/dV图像。在实空间图像中,被电子填充的位置用实心红点表示,未被填充的位置用空心的红圈表示。(c)电子对称填充(nt:nb=1:1)和不对称填充(nt:nb=3:1、4:1和7:1,以4:1为例)的双层维格纳晶体堆叠示意图。其中 nt 和nb分别表示顶部和底部的电子密度。(d)双层维格纳晶体的示意图。(e)夹BN层的双层MoSe2异质结截面示意图。两个MoSe2单层以0°角对齐,由1 nm厚的六方氮化硼隔开。然后将MoSe2/hBN/MoSe2结构封装在15~20 nm厚的六方氮化硼中[123,133,139]
Figure 7. Wigner crystals in TMDs. (a) Schematic diagrams of the generalized Wigner crystal (n=1/3 and n=2/3 filling) and Mott insulating state (n=1 filling) in the WSe2/WS2 moiré superlattice. (b) dI/dV images of the generalized Wigner crystal at electron fillings of n=2/3, n=1/3, and n=1/2. In the real-space images, filled positions are represented by solid red dots, and unfilled positions are indicated by hollow red circles. (c) Schematic diagram of bilayer Wigner crystal stacking with electron symmetric filling (nt:nb=1:1) and asymmetric filling (nt:nb=3:1, 4:1, and 7:1, using 4:1 as an example). Here, nt and nb denote the electron densities in the top and bottom layers, respectively. (d) Schematic representation of a bilayer Wigner crystal. (e) Cross-sectional schematic of a thin-film bilayer MoSe2 heterostructure. Two MoSe2 monolayers are aligned at a 0° angle, separated by a 1nm-thick hexagonal boron nitride spacer. This MoSe2/hBN/MoSe2 structure is then encapsulated within 15~20 nm-thick hexagonal boron nitride[123,133,139]
图 8 转角双层石墨烯中的电子晶体。(a)显示了全局填充ν从0−4变化时,ABB、ABA和ABC区域的填充顺序。虚线表示每个填充因子下的费米能级。红色椭圆形表示平带存在电子填充,蓝色表示没有。(b)预测的电子晶体晶格结构。红色圆圈表示电子完全填充的位置,灰色表示部分填充。(c)-(f)从不同填充因子ν=0 (c)、ν=1 (d)、ν=2 (e)、ν=3 (f)和ν=4(f的插图)的dI/dV谱线中提取局部填充比[141]
Figure 8. Wigner crystals in TBG. (a) The sequence of filling in ABB, ABA, and ABC regions is depicted as global filling ν varies from 0 to 4. Dashed lines represent the Fermi level for each filling factor. Red ellipses represent the presence of flat bands with electron filling, while blue indicates their absence. (b) Predicted electronic crystal lattice structure. Red circles denote positions with complete electron filling, and gray represents partial filling. (c)-(f) Extraction of local filling ratios from dI/dV spectra at different filling factors ν=0 (c), ν=1 (d), ν=2 (e), ν=3 (f), and an inset for ν=4 (inset of (f))[141]
图 9 轨道磁性。(a) 有子晶格势存在时K谷平带对应的实空间电流分布,黑色箭头为电流方向,颜色反应了诱导的磁场强度,(b) TBG在
$ \nu =3 $ 时,$ {R}_{xy} $ 达到$ h/{e}^{2} $ ,$ {R}_{xx} $ 接近于零,出现了反常量子霍尔效应。(c)纵向电阻与霍尔电阻随磁场的变化,曲线有明显的回滞现象。(d)和(e)分别为tMBG在D>0时的$ \nu =1与\nu =3 $ 观测到了陈数为2的反常量子霍尔效应[109,147,154]Figure 9. Orbital magnetism. (a) Real-space current distribution of the flat bands at the K valley in the presence of sublattice potential, where black arrows represent the direction of current and the colors indicate the induced magnetic field strength. (b) In TBG at ν=3,
$ {R}_{xy} $ reaches$ h/{e}^{2} $ , while$ {R}_{xx} $ approaches zero, resulting in the emergence of the anomalous quantum Hall effect. (c) Changes in longitudinal resistance and Hall resistance with magnetic field, showing noticeable hysteresis in the curves. (d) and (e) Observations of the anomalous quantum Hall effect with Chern number 2 in tMBG at ν=1 and ν=3, respectively, when D>0[109,147,154]图 10 陈绝缘体与时间反演对称性。(a)对于每个平带的陈数而言,其陈数值与对称性破缺的方式有关。图中为TBG分别打破C2Z与时间反演对称性,所对应的能带陈数的变化。(b)上半部分为TBG中级联填充的示意图,下部分为对应的化学势随填充数的变化关系,在达到整数填充前会发生级联相变,交换作用将所有的载流子全部转移到某一能带,并将其他三条能带推至更高的能量。(c)在打破时间反演对称性的情况下,体系陈数随级联相变转化示意图。(d)实验中测得的在各个填充数下的陈绝缘态,在填充数为
$ \nu =\pm 1,\pm 2,\pm \mathrm{3,0} $ 时,对应的陈数分别为$ C=\pm 1,\pm 2,\pm 3,\pm 4 $ ,满足时间反演对称性破缺所对应的陈数变化。(e)在磁场诱导平带重建情况下的纵向电阻和霍尔电导随填充数的变化,上半部分为重建能带填充示意图。(f)$ \nu =0.8 $ 附近的TBG在磁场为0.5 T左右时陈数绝对值由1到3的转变[53-54,161-163]Figure 10. Chern insulator and time-reversal symmetry. (a) The Chern numbers for each flat band depend on the way symmetry is broken. The figure shows the changes in band Chern numbers for TBG when breaking C2Z and time-reversal symmetry. (b) The upper part illustrates cascaded filling in TBG, while the lower part shows the corresponding relationship between chemical potential and filling. A cascade phase transition occurs before reaching integer fillings, where exchange interactions move all carriers to one band and push the other three bands to higher energies. (c) Schematic representation of the system's Chern numbers transitioning during a cascade phase transition when breaking time-reversal symmetry. (d) Experimentally measured Chern insulators at various fillings, where at fillings ν=±1,±2,±3,0, the corresponding Chern numbers are C=±1,±2,±3,±4, consistent with the Chern number changes associated with breaking time-reversal symmetry. (e) Changes in longitudinal resistance and Hall conductance with filling for flatband reconstruction induced by a magnetic field. The upper part illustrates the filled reconstructed bands. (f) Near ν=0.8, TBG undergoes a transition from a Chern number with an absolute value of 1 to 3 at a magnetic field of around 0.5 T[53-54,161-163]
图 11 陈绝缘体与空间对称性。(a)由于平移对称性破缺导致的布里渊区的折叠示意图,产生一条陈数为零的新能带,导致总能带数翻倍。(b)B=0 T~3 T时,ν=2.5~4之间的局部逆压缩系数,可以看出具有陈数t为1,填充因子s为8/3的SBCI态。(c)(b)图中观测到的(t,s)=(1,8/3)的SBCI态的形成示意图,图中布里渊区发生了三重折叠。(d)B=3 T~11 T时,ν=3和4之间的局部逆压缩系数。(e)(d)图测量结果的Wannier图,随着磁场的增加,出现了CDW态向FCI态的转化。(f) (t,s)=(2/3,10/3)的FCI态的形成示意图,可以看作上一个(1,3)的HCI和(−1/3,1/3)的FCI态的叠加[167-170]
Figure 11. Chen insulators and spatial symmetry. (a) Schematic illustration of the Brillouin zone folding due to the breaking of translational symmetry, leading to the emergence of a new band with a Chern number of zero and a doubling of the total number of bands. (b) Local inverse compressibility coefficients between B=0 T and 3 T for fillings ν=2.5 to 4, showing the presence of a SBCI state with (t,s)=(1,8/3) at ν=8/3. (c) Schematic representation of the formation of the SBCI state with (t,s)=(1,8/3) observed in (b), with a tripling of the Brillouin zone. (d) Local inverse compressibility coefficients between B=3 T and 11 T for fillings ν=3 and 4, illustrating the presence of different states. (e) Wannier diagrams obtained from measurements in (d), showing the transition from a charge-density wave (CDW) state to a fractional Chern insulator (FCI) state with increasing magnetic field. (f) Schematic depiction of the formation of the FCI state with (t,s)=(2/3,10/3), which can be considered as a superposition of the previous (1,3) HCI and (−1/3,1/3) FCI states[167-170]
-
[1] Novoselov K S, Geim A K, Morozov S V, et al. Electric field effect in atomically thin carbon films[J]. Science,2004,306(5696):666−669 doi: 10.1126/science.1102896 [2] Cao Y, Fatemi V, Demir A, et al. Correlated insulator behaviour at half-filling in magic-angle graphene superlattices[J]. Nature,2018,556(7699):80−84 doi: 10.1038/nature26154 [3] Cao Y, Fatemi V, Fang S, et al. Unconventional superconductivity in magic-angle graphene superlattices[J]. Nature,2018,556(7699):43−50 doi: 10.1038/nature26160 [4] Yao W, Wang E, Bao C H, et al. Quasicrystalline 30° twisted bilayer graphene as an incommensurate superlattice with strong interlayer coupling[J]. Proceedings of the National Academy of Sciences of the United States of America,2018,115(27):6928−6933 [5] Koren E, Duerig U. Superlubricity in quasicrystalline twisted bilayer graphene[J]. Physical Review B,2016,93(20):201404 doi: 10.1103/PhysRevB.93.201404 [6] Woods C R, Britnell L, Eckmann A, et al. Commensurate–incommensurate transition in graphene on hexagonal boron nitride[J]. Nature Physics,2014,10(6):451−456 doi: 10.1038/nphys2954 [7] dos Santos J M B L, Peres N M R, Castro Neto A H. Graphene bilayer with a twist: electronic structure[J]. Physical Review Letters,2007,99(25):256802 doi: 10.1103/PhysRevLett.99.256802 [8] Yankowitz M, Xue J M, Cormode D, et al. Emergence of superlattice Dirac points in graphene on hexagonal boron nitride[J]. Nature Physics,2012,8(5):382−386 doi: 10.1038/nphys2272 [9] Yang W, Chen G R, Shi Z W, et al. Epitaxial growth of single-domain graphene on hexagonal boron nitride[J]. Nature Materials,2013,12(9):792−797 doi: 10.1038/nmat3695 [10] Rosenberger M R, Chuang H J, Phillips M, et al. Twist angle-dependent atomic reconstruction and Moiré patterns in transition metal dichalcogenide heterostructures[J]. ACS Nano,2020,14(4):4550−4558 doi: 10.1021/acsnano.0c00088 [11] Woods C R, Withers F, Zhu M J, et al. Macroscopic self-reorientation of interacting two-dimensional crystals[J]. Nature Communications,2016,7(1):10800 doi: 10.1038/ncomms10800 [12] Alden J S, Tsen A W, Huang P Y, et al. Strain solitons and topological defects in bilayer graphene[J]. Proceedings of the National Academy of Sciences of the United States of America,2013,110(28):11256−11260 [13] Yoo H, Engelke R, Carr S, et al. Atomic and electronic reconstruction at the van der Waals interface in twisted bilayer graphene[J]. Nature Materials,2019,18(5):448−453 doi: 10.1038/s41563-019-0346-z [14] Lin J H, Fang W J, Zhou W, et al. AC/AB stacking boundaries in bilayer graphene[J]. Nano Letters,2013,13(7):3262−3268 doi: 10.1021/nl4013979 [15] Butz B, Dolle C, Niekiel F, et al. Dislocations in bilayer graphene[J]. Nature,2014,505(7484):533−537 doi: 10.1038/nature12780 [16] Park C H, Yang L, Son Y W, et al. New generation of massless Dirac fermions in graphene under external periodic potentials[J]. Physical Review Letters,2008,101(12):126804 doi: 10.1103/PhysRevLett.101.126804 [17] Park C H, Yang L, Son Y W, et al. Anisotropic behaviours of massless Dirac fermions in graphene under periodic potentials[J]. Nature Physics,2008,4(3):213−217 doi: 10.1038/nphys890 [18] Wolf T M R, Zilberberg O, Levkivskyi I, et al. Substrate-induced topological minibands in graphene[J]. Physical Review B,2018,98(12):125408 doi: 10.1103/PhysRevB.98.125408 [19] Ortix C, Yang L P, van den Brink J. Graphene on incommensurate substrates: trigonal warping and emerging Dirac cone replicas with halved group velocity[J]. Physical Review B,2012,86(8):081405 doi: 10.1103/PhysRevB.86.081405 [20] Wallbank J R, Mucha-Kruczyński M, Chen X, et al. Moiré superlattice effects in graphene/boron-nitride van der Waals heterostructures[J]. Annalen der Physik,2015,527(5−6):359−376 doi: 10.1002/andp.201400204 [21] Wallbank J R, Patel A A, Mucha-Kruczyński M, et al. Generic miniband structure of graphene on a hexagonal substrate[J]. Physical Review B,2013,87(24):245408 doi: 10.1103/PhysRevB.87.245408 [22] Yan H, Chu Z D, Yan W, et al. Superlattice Dirac points and space-dependent Fermi velocity in a corrugated graphene monolayer[J]. Physical Review B,2013,87(7):075405 doi: 10.1103/PhysRevB.87.075405 [23] Ponomarenko L A, Gorbachev R V, Yu G L, et al. Cloning of Dirac fermions in graphene superlattices[J]. Nature,2013,497(7451):594−597 doi: 10.1038/nature12187 [24] Hunt B, Sanchez-Yamagishi J D, Young A F, et al. Massive Dirac fermions and Hofstadter butterfly in a van der Waals heterostructure[J]. Science,2013,340(6139):1427−1430 doi: 10.1126/science.1237240 [25] Chen G R, Sui M Q, Wang D M, et al. Emergence of tertiary Dirac points in graphene Moiré superlattices[J]. Nano Letters,2017,17(6):3576−3581 doi: 10.1021/acs.nanolett.7b00735 [26] Finney N R, Yankowitz M, Muraleetharan L, et al. Tunable crystal symmetry in graphene-boron nitride heterostructures with coexisting Moiré superlattices[J]. Nature Nanotechnology,2019,14(11):1029−1034 doi: 10.1038/s41565-019-0547-2 [27] Wang E Y, Lu X B, Ding S J, et al. Gaps induced by inversion symmetry breaking and second-generation Dirac cones in graphene/hexagonal boron nitride[J]. Nature Physics,2016,12(12):1111−1115 doi: 10.1038/nphys3856 [28] Moon P, Koshino M. Electronic properties of graphene/hexagonal-boron-nitride Moiré superlattice[J]. Physical Review B,2014,90(15):155406 doi: 10.1103/PhysRevB.90.155406 [29] Jung J, DaSilva A M, MacDonald A H, et al. Origin of band gaps in graphene on hexagonal boron nitride[J]. Nature Communications,2015,6(1):6308 doi: 10.1038/ncomms7308 [30] Van Hove L. The occurrence of singularities in the elastic frequency distribution of a crystal[J]. Physical Review,1953,89(6):1189−1193 doi: 10.1103/PhysRev.89.1189 [31] He W Y, Su Y, Yang M D, et al. Creating in-plane pseudomagnetic fields in excess of 1000 T by misoriented stacking in a graphene bilayer[J]. Physical Review B,2014,89(12):125418 doi: 10.1103/PhysRevB.89.125418 [32] He W Y, Chu Z D, He L. Chiral tunneling in a twisted graphene bilayer[J]. Physical Review Letters,2013,111(6):066803 doi: 10.1103/PhysRevLett.111.066803 [33] Yin L J, Qiao J B, Wang W X, et al. Landau quantization and Fermi velocity renormalization in twisted graphene bilayers[J]. Physical Review B,2015,92(20):201408 doi: 10.1103/PhysRevB.92.201408 [34] Li G H, Luican A, dos Santos J M B L, et al. Observation of Van Hove singularities in twisted graphene layers[J]. Nature Physics,2010,6(2):109−113 doi: 10.1038/nphys1463 [35] Cherkez V, de Laissardière G T, Mallet P, et al. Van Hove singularities in doped twisted graphene bilayers studied by scanning tunneling spectroscopy[J]. Physical Review B,2015,91(15):155428 doi: 10.1103/PhysRevB.91.155428 [36] Brihuega I, Mallet P, González-Herrero H, et al. Unraveling the intrinsic and robust nature of van Hove singularities in twisted bilayer graphene by scanning tunneling microscopy and theoretical analysis[J]. Physical Review Letters,2012,109(19):196802 doi: 10.1103/PhysRevLett.109.196802 [37] Luican A, Li G H, Reina A, et al. Single-layer behavior and its breakdown in twisted graphene layers[J]. Physical Review Letters,2011,106(12):126802 doi: 10.1103/PhysRevLett.106.126802 [38] Miller D L, Kubista K D, Rutter G M, et al. Observing the quantization of zero mass carriers in graphene[J]. Science,2009,324(5929):924−927 doi: 10.1126/science.1171810 [39] Wong D, Wang Y, Jung J, et al. Local spectroscopy of Moiré-induced electronic structure in gate-tunable twisted bilayer graphene[J]. Physical Review B,2015,92(15):155409 doi: 10.1103/PhysRevB.92.155409 [40] Yan W, Meng L, Liu M X, et al. Angle-dependent van Hove singularities and their breakdown in twisted graphene bilayers[J]. Physical Review B,2014,90(11):115402 doi: 10.1103/PhysRevB.90.115402 [41] de Laissardière G T, Mayou D, Magaud L. Localization of dirac electrons in rotated graphene bilayers[J]. Nano Letters,2010,10(3):804−808 doi: 10.1021/nl902948m [42] Yan W, Liu M X, Dou R F, et al. Angle-dependent van Hove singularities in a slightly twisted graphene bilayer[J]. Physical Review Letters,2012,109(12):126801 doi: 10.1103/PhysRevLett.109.126801 [43] Nandkishore R, Levitov L S, Chubukov A V. Chiral superconductivity from repulsive interactions in doped graphene[J]. Nature Physics,2012,8(2):158−163 doi: 10.1038/nphys2208 [44] Kim K, Coh S, Tan L Z, et al. Raman spectroscopy study of rotated double-layer graphene: misorientation-angle dependence of electronic structure[J]. Physical Review Letters,2012,108(24):246103 doi: 10.1103/PhysRevLett.108.246103 [45] Yuan N F Q, Isobe H, Fu L. Magic of high-order van Hove singularity[J]. Nature Communications,2019,10(1):5769 doi: 10.1038/s41467-019-13670-9 [46] Hofstadter D R. Energy levels and wave functions of Bloch electrons in rational and irrational magnetic fields[J]. Physical Review B,1976,14(6):2239−2249 doi: 10.1103/PhysRevB.14.2239 [47] Albrecht C, Smet J H, Weiss D, et al. Fermiology of two-dimensional lateral superlattices[J]. Physical Review Letters,1999,83(11):2234−2237 doi: 10.1103/PhysRevLett.83.2234 [48] Dean C R, Wang L, Maher P, et al. Hofstadter's butterfly and the fractal quantum Hall effect in Moiré superlattices[J]. Nature,2013,497(7451):598−602 doi: 10.1038/nature12186 [49] Spanton E M, Zibrov A A, Zhou H X, et al. Observation of fractional Chern insulators in a van der Waals heterostructure[J]. Science,2018,360(6384):62−66 doi: 10.1126/science.aan8458 [50] Yang W, Lu X B, Chen G R, et al. Hofstadter butterfly and many-body effects in epitaxial graphene superlattice[J]. Nano Letters,2016,16(4):2387−2392 doi: 10.1021/acs.nanolett.5b05161 [51] Wang L, Gao Y D, Wen B, et al. Evidence for a fractional fractal quantum Hall effect in graphene superlattices[J]. Science,2015,350(6265):1231−1234 doi: 10.1126/science.aad2102 [52] Cheng B, Pan C, Che S, et al. Fractional and symmetry-broken Chern insulators in tunable Moiré superlattices[J]. Nano Letters,2019,19(7):4321−4326 doi: 10.1021/acs.nanolett.9b00811 [53] Saito Y, Ge J Y, Rademaker L, et al. Hofstadter subband ferromagnetism and symmetry-broken Chern insulators in twisted bilayer graphene[J]. Nature Physics,2021,17(4):478−481 doi: 10.1038/s41567-020-01129-4 [54] Das I, Lu X B, Herzog-Arbeitman J, et al. Symmetry-broken Chern insulators and Rashba-like Landau-level crossings in magic-angle bilayer graphene[J]. Nature Physics,2021,17(6):710−714 doi: 10.1038/s41567-021-01186-3 [55] Ye Z L, Waldecker L, Ma E Y, et al. Efficient generation of neutral and charged biexcitons in encapsulated WSe2 monolayers[J]. Nature Communications,2018,9(1):3718 doi: 10.1038/s41467-018-05917-8 [56] Zhang N, Surrente A, Baranowski M, et al. Moiré intralayer excitons in a MoSe2/MoS2 heterostructure[J]. Nano Letters,2018,18(12):7651−7657 doi: 10.1021/acs.nanolett.8b03266 [57] Huang D, Choi J, Shih C K, et al. Excitons in semiconductor Moiré superlattices[J]. Nature Nanotechnology,2022,17(3):227−238 doi: 10.1038/s41565-021-01068-y [58] Liu Y P, Zeng C, Yu J, et al. Moire superlattices and related Moiré excitons in twisted van der Waals heterostructures[J]. Chemical Society Reviews,2021,50(11):6401−6422 doi: 10.1039/D0CS01002B [59] Tran K, Moody G, Wu F C, et al. Evidence for Moiré excitons in van der Waals heterostructures[J]. Nature,2019,567(7746):71−75 doi: 10.1038/s41586-019-0975-z [60] Seyler K L, Rivera P, Yu H Y, et al. Signatures of Moiré-trapped valley excitons in MoSe2/WSe2 heterobilayers[J]. Nature,2019,567(7746):66−70 doi: 10.1038/s41586-019-0957-1 [61] Scuri G, Andersen T I, Zhou Y, et al. Electrically tunable valley dynamics in twisted WSe2/WSe2 bilayers[J]. Physical Review Letters,2020,124(21):217403 doi: 10.1103/PhysRevLett.124.217403 [62] Andersen T I, Scuri G, Sushko A, et al. Excitons in a reconstructed Moiré potential in twisted WSe2/WSe2 homobilayers[J]. Nature Materials,2021,20(4):480−487 doi: 10.1038/s41563-020-00873-5 [63] Sung J, Zhou Y, Scuri G, et al. Broken mirror symmetry in excitonic response of reconstructed domains in twisted MoSe2/MoSe2 bilayers[J]. Nature Nanotechnology,2020,15(9):750−754 doi: 10.1038/s41565-020-0728-z [64] Alexeev E M, Ruiz-Tijerina D A, Danovich M, et al. Resonantly hybridized excitons in Moiré superlattices in van der Waals heterostructures[J]. Nature,2019,567(7746):81−86 doi: 10.1038/s41586-019-0986-9 [65] Jin C H, Regan E C, Yan A M, et al. Observation of Moiré excitons in WSe2/WS2 heterostructure superlattices[J]. Nature,2019,567(7746):76−80 doi: 10.1038/s41586-019-0976-y [66] Jin C H, Regan E C, Wang D Q, et al. Identification of spin, valley and Moiré quasi-angular momentum of interlayer excitons[J]. Nature Physics,2019,15(11):1140−1144 doi: 10.1038/s41567-019-0631-4 [67] Hsu W T, Lin B H, Lu L S, et al. Tailoring excitonic states of van der Waals bilayers through stacking configuration, band alignment, and valley spin[J]. Science Advances,2019,5(12):eaax7407 doi: 10.1126/sciadv.aax7407 [68] Suárez Morell E, Correa J D, Vargas P, et al. Flat bands in slightly twisted bilayer graphene: tight-binding calculations[J]. Physical Review B,2010,82(12):121407 doi: 10.1103/PhysRevB.82.121407 [69] Bistritzer R, MacDonald A H. Moiré bands in twisted double-layer graphene[J]. Proceedings of the National Academy of Sciences of the United States of America,2011,108(30):12233−12237 [70] Choi Y, Kemmer J, Peng Y, et al. Electronic correlations in twisted bilayer graphene near the magic angle[J]. Nature Physics,2019,15(11):1174−1180 doi: 10.1038/s41567-019-0606-5 [71] Jiang Y H, Lai X Y, Watanabe K, et al. Charge order and broken rotational symmetry in magic-angle twisted bilayer graphene[J]. Nature,2019,573(7772):91−95 doi: 10.1038/s41586-019-1460-4 [72] Kerelsky A, McGilly L J, Kennes D M, et al. Maximized electron interactions at the magic angle in twisted bilayer graphene[J]. Nature,2019,572(7767):95−100 doi: 10.1038/s41586-019-1431-9 [73] Xie Y L, Lian B, Jäck B, et al. Spectroscopic signatures of many-body correlations in magic-angle twisted bilayer graphene[J]. Nature,2019,572(7767):101−105 doi: 10.1038/s41586-019-1422-x [74] Kim K, DaSilva A, Huang S Q, et al. Tunable Moiré bands and strong correlations in small-twist-angle bilayer graphene[J]. Proceedings of the National Academy of Sciences of the United States of America,2017,114(13):3364−3369 [75] Mott N. On metal-insulator transitions[J]. Journal of Solid State Chemistry,1990,88(1):5−7 doi: 10.1016/0022-4596(90)90201-8 [76] Lu X B, Stepanov P, Yang W, et al. Superconductors, orbital magnets and correlated states in magic-angle bilayer graphene[J]. Nature,2019,574(7780):653−657 doi: 10.1038/s41586-019-1695-0 [77] Arora H S, Polski R, Zhang Y R, et al. Superconductivity in metallic twisted bilayer graphene stabilized by WSe2[J]. Nature,2020,583(7816):379−384 doi: 10.1038/s41586-020-2473-8 [78] Nuckolls K P, Oh M, Wong D, et al. Strongly correlated Chern insulators in magic-angle twisted bilayer graphene[J]. Nature,2020,588(7839):610−615 doi: 10.1038/s41586-020-3028-8 [79] Saito Y, Ge J Y, Watanabe K, et al. Independent superconductors and correlated insulators in twisted bilayer graphene[J]. Nature Physics,2020,16(9):926−930 doi: 10.1038/s41567-020-0928-3 [80] Stepanov P, Das I, Lu X B, et al. Untying the insulating and superconducting orders in magic-angle graphene[J]. Nature,2020,583(7816):375−378 doi: 10.1038/s41586-020-2459-6 [81] Cao Y, Rodan-Legrain D, Park J M, et al. Nematicity and competing orders in superconducting magic-angle graphene[J]. Science,2021,372(6539):264−271 doi: 10.1126/science.abc2836 [82] Xie M, MacDonald A H. Nature of the correlated insulator states in twisted bilayer graphene[J]. Physical Review Letters,2020,124(9):097601 doi: 10.1103/PhysRevLett.124.097601 [83] Shen C, Ying J H, Liu L, et al. Emergence of Chern insulating states in non-magic angle twisted bilayer graphene[J]. Chinese Physics Letters,2021,38(4):047301 doi: 10.1088/0256-307X/38/4/047301 [84] Adak P C, Sinha S, Ghorai U, et al. Tunable bandwidths and gaps in twisted double bilayer graphene on the verge of correlations[J]. Physical Review B,2020,101(12):125428 doi: 10.1103/PhysRevB.101.125428 [85] Cao Y, Rodan-Legrain D, Rubies-Bigorda O, et al. Tunable correlated states and spin-polarized phases in twisted bilayer-bilayer graphene[J]. Nature,2020,583(7815):215−220 doi: 10.1038/s41586-020-2260-6 [86] Cao Y, Park J M, Watanabe K, et al. Pauli-limit violation and re-entrant superconductivity in Moiré graphene[J]. Nature,2021,595(7868):526−531 doi: 10.1038/s41586-021-03685-y [87] Chen S W, He M H, Zhang Y H, et al. Electrically tunable correlated and topological states in twisted monolayer–bilayer graphene[J]. Nature Physics,2021,17(3):374−380 doi: 10.1038/s41567-020-01062-6 [88] Xu Y, Liu S, Rhodes D A, et al. Correlated insulating states at fractional fillings of Moiré superlattices[J]. Nature,2020,587(7833):214−218 doi: 10.1038/s41586-020-2868-6 [89] Yankowitz M, Chen S W, Polshyn H, et al. Tuning superconductivity in twisted bilayer graphene[J]. Science,2019,363(6431):1059−1064 doi: 10.1126/science.aav1910 [90] Lee P A, Nagaosa N, Wen X G. Doping a Mott insulator: physics of high-temperature superconductivity[J]. Reviews of Modern Physics,2006,78(1):17−85 doi: 10.1103/RevModPhys.78.17 [91] Keimer B, Kivelson S A, Norman M R, et al. From quantum matter to high-temperature superconductivity in copper oxides[J]. Nature,2015,518(7538):179−186 doi: 10.1038/nature14165 [92] Codecido E, Wang Q Y, Koester R, et al. Correlated insulating and superconducting states in twisted bilayer graphene below the magic angle[J]. Science Advances,2019,5(9):eaaw9770 doi: 10.1126/sciadv.aaw9770 [93] Polshyn H, Yankowitz M, Chen S W, et al. Large linear-in-temperature resistivity in twisted bilayer graphene[J]. Nature Physics,2019,15(10):1011−1016 doi: 10.1038/s41567-019-0596-3 [94] Bruin J A N, Sakai H, Perry R S, et al. Similarity of scattering rates in metals showing T-linear resistivity[J]. Science,2013,339(6121):804−807 doi: 10.1126/science.1227612 [95] Comin R, Sutarto R, He F, et al. Symmetry of charge order in cuprates[J]. Nature Materials,2015,14(8):796−800 doi: 10.1038/nmat4295 [96] Mukhopadhyay S, Sharma R, Kim C K, et al. Evidence for a vestigial nematic state in the cuprate pseudogap phase[J]. Proceedings of the National Academy of Sciences of the United States of America,2019,116(27):13249−13254 [97] Wu F C, Hwang E, Das Sarma S. Phonon-induced giant linear-in-T resistivity in magic angle twisted bilayer graphene: ordinary strangeness and exotic superconductivity[J]. Physical Review B,2019,99(16):165112 doi: 10.1103/PhysRevB.99.165112 [98] Sharma G, Yudhistira I, Chakraborty N, et al. Carrier transport theory for twisted bilayer graphene in the metallic regime[J]. Nature Communications,2021,12(1):5737 doi: 10.1038/s41467-021-25864-1 [99] Burg G W, Zhu J H, Taniguchi T, et al. Correlated insulating states in twisted double bilayer graphene[J]. Physical Review Letters,2019,123(19):197702 doi: 10.1103/PhysRevLett.123.197702 [100] He M H, Li Y H, Cai J Q, et al. Symmetry breaking in twisted double bilayer graphene[J]. Nature Physics,2021,17(1):26−30 doi: 10.1038/s41567-020-1030-6 [101] Liu X M, Hao Z Y, Khalaf E, et al. Tunable spin-polarized correlated states in twisted double bilayer graphene[J]. Nature,2020,583(7815):221−225 doi: 10.1038/s41586-020-2458-7 [102] Shen C, Chu Y B, Wu Q S, et al. Correlated states in twisted double bilayer graphene[J]. Nature Physics,2020,16(5):520−525 doi: 10.1038/s41567-020-0825-9 [103] Zhang C X, Zhu T C, Kahn S, et al. Visualizing delocalized correlated electronic states in twisted double bilayer graphene[J]. Nature Communications,2021,12(1):2516 doi: 10.1038/s41467-021-22711-1 [104] Hao Z Y, Zimmerman A M, Ledwith P, et al. Electric field-tunable superconductivity in alternating-twist magic-angle trilayer graphene[J]. Science,2021,371(6534):1133−1138 doi: 10.1126/science.abg0399 [105] Park J M, Cao Y, Watanabe K, et al. Tunable strongly coupled superconductivity in magic-angle twisted trilayer graphene[J]. Nature,2021,590(7845):249−255 doi: 10.1038/s41586-021-03192-0 [106] Liu X X, Zhang N J, Watanabe K, et al. Isospin order in superconducting magic-angle twisted trilayer graphene[J]. Nature Physics,2022,18(5):522−527 doi: 10.1038/s41567-022-01515-0 [107] Khalaf E, Chatterjee S, Bultinck N, et al. Charged skyrmions and topological origin of superconductivity in magic-angle graphene[J]. Science Advances,2021,7(19):eabf5299 doi: 10.1126/sciadv.abf5299 [108] Fischer A, Goodwin Z A H, Mostofi A A, et al. Unconventional superconductivity in magic-angle twisted trilayer graphene[J]. npj Quantum Materials,2022,7(1):5 doi: 10.1038/s41535-021-00410-w [109] Polshyn H, Zhu J, Kumar M A, et al. Electrical switching of magnetic order in an orbital Chern insulator[J]. Nature,2020,588(7836):66−70 doi: 10.1038/s41586-020-2963-8 [110] Xu S G, Al Ezzi M M, Balakrishnan N, et al. Tunable van Hove singularities and correlated states in twisted monolayer–bilayer graphene[J]. Nature Physics,2021,17(5):619−626 doi: 10.1038/s41567-021-01172-9 [111] Polshyn H, Zhang Y, Kumar M A, et al. Topological charge density waves at half-integer filling of a Moiré superlattice[J]. Nature Physics,2022,18(1):42−47 doi: 10.1038/s41567-021-01418-6 [112] He M H, Zhang Y H, Li Y H, et al. Competing correlated states and abundant orbital magnetism in twisted monolayer-bilayer graphene[J]. Nature Communications,2021,12(1):4727 doi: 10.1038/s41467-021-25044-1 [113] Tong L H, Tong Q J, Yang L Z, et al. Spectroscopic visualization of flat bands in magic-angle twisted monolayer-bilayer graphene: coexistence of localization and delocalization[J]. Physical Review Letters,2022,128(12):126401 doi: 10.1103/PhysRevLett.128.126401 [114] Li S Y, Wang Z W, Xue Y C, et al. Imaging topological and correlated insulating states in twisted monolayer-bilayer graphene[J]. Nature Communications,2022,13(1):4225 doi: 10.1038/s41467-022-31851-x [115] Wang L, Shih E M, Ghiotto A, et al. Correlated electronic phases in twisted bilayer transition metal dichalcogenides[J]. Nature Materials,2020,19(8):861−866 doi: 10.1038/s41563-020-0708-6 [116] Wang G, Chernikov A, Glazov M M, et al. Colloquium: excitons in atomically thin transition metal dichalcogenides[J]. Reviews of Modern Physics,2018,90(2):021001 doi: 10.1103/RevModPhys.90.021001 [117] Raja A, Chaves A, Yu J, et al. Coulomb engineering of the bandgap and excitons in two-dimensional materials[J]. Nature Communications,2017,8(1):15251 doi: 10.1038/ncomms15251 [118] Huang X, Wang T M, Miao S N, et al. Correlated insulating states at fractional fillings of the WS2/WSe2 Moiré lattice[J]. Nature Physics,2021,17(6):715−719 doi: 10.1038/s41567-021-01171-w [119] Wigner E. On the interaction of electrons in metals[J]. Physical Review,1934,46(11):1002−1011 doi: 10.1103/PhysRev.46.1002 [120] Grimes C C, Adams G. Crystallization of electrons on the surface of liquid helium[J]. Surface Science,1980,98(1−3):1−7 doi: 10.1016/0039-6028(80)90465-3 [121] Chaplik A V. Possible crystallization of charge carriers in low-density inversion layers[J]. Soviet Journal of Experimental and Theoretical Physics,1972,35:395−398 [122] Andrei E Y, Deville G, Glattli D C, et al. Observation of a magnetically induced Wigner solid[J]. Physical Review Letters,1988,60(26):2765−2768 doi: 10.1103/PhysRevLett.60.2765 [123] Regan E C, Wang D Q, Jin C H, et al. Mott and generalized Wigner crystal states in WSe2/WS2 Moiré superlattices[J]. Nature,2020,579(7799):359−363 doi: 10.1038/s41586-020-2092-4 [124] Mott N F. The basis of the electron theory of metals, with special reference to the transition metals[J]. Proceedings of the Physical Society. Section A,1949,62(7):416−422 doi: 10.1088/0370-1298/62/7/303 [125] Padhi B, Phillips P W. Pressure-induced metal-insulator transition in twisted bilayer graphene[J]. Physical Review B,2019,99(20):205141 doi: 10.1103/PhysRevB.99.205141 [126] Wu C J, Bergman D, Balents L, et al. Flat bands and Wigner crystallization in the honeycomb optical lattice[J]. Physical Review Letters,2007,99(7):070401 doi: 10.1103/PhysRevLett.99.070401 [127] Padhi B, Setty C, Phillips P W. Doped twisted bilayer graphene near magic angles: proximity to Wigner crystallization, not Mott insulation[J]. Nano Letters,2018,18(10):6175−6180 doi: 10.1021/acs.nanolett.8b02033 [128] Hubbard J. Generalized Wigner lattices in one dimension and some applications to tetracyanoquinodimethane (TCNQ) salts[J]. Physical Review B,1978,17(2):494−505 doi: 10.1103/PhysRevB.17.494 [129] Zhang Y, Yuan N F Q, Fu L. Moiré quantum chemistry: charge transfer in transition metal dichalcogenide superlattices[J]. Physical Review B,2020,102(20):201115 doi: 10.1103/PhysRevB.102.201115 [130] Xiao D, Liu G B, Feng W X, et al. Coupled spin and valley physics in monolayers of MoS2 and other group-VI dichalcogenides[J]. Physical Review Letters,2012,108(19):196802 doi: 10.1103/PhysRevLett.108.196802 [131] Chen G R, Jiang L L, Wu S, et al. Evidence of a gate-tunable Mott insulator in a trilayer graphene Moiré superlattice[J]. Nature Physics,2019,15(3):237−241 doi: 10.1038/s41567-018-0387-2 [132] Chen G R, Sharpe A L, Gallagher P, et al. Signatures of tunable superconductivity in a trilayer graphene Moiré superlattice[J]. Nature,2019,572(7768):215−219 doi: 10.1038/s41586-019-1393-y [133] Li H Y, Li S W, Regan E C, et al. Imaging two-dimensional generalized Wigner crystals[J]. Nature,2021,597(7878):650−654 doi: 10.1038/s41586-021-03874-9 [134] Jin C H, Tao Z, Li T X, et al. Stripe phases in WSe2/WS2 Moiré superlattices[J]. Nature Materials,2021,20(7):940−944 doi: 10.1038/s41563-021-00959-8 [135] Smoleński T, Dolgirev P E, Kuhlenkamp C, et al. Signatures of Wigner crystal of electrons in a monolayer semiconductor[J]. Nature,2021,595(7865):53−57 doi: 10.1038/s41586-021-03590-4 [136] Drummond N D, Needs R J. Phase diagram of the low-density two-dimensional homogeneous electron gas[J]. Physical Review Letters,2009,102(12):126402 doi: 10.1103/PhysRevLett.102.126402 [137] Zarenia M, Neilson D, Partoens B, et al. Wigner crystallization in transition metal dichalcogenides: a new approach to correlation energy[J]. Physical Review B,2017,95(11):115438 doi: 10.1103/PhysRevB.95.115438 [138] Shimazaki Y, Kuhlenkamp C, Schwartz I, et al. Optical signatures of periodic charge distribution in a Mott-like correlated insulator state[J]. Physical Review X,2021,11(2):021027 doi: 10.1103/PhysRevX.11.021027 [139] Zhou Y, Sung J, Brutschea E, et al. Bilayer Wigner crystals in a transition metal dichalcogenide heterostructure[J]. Nature,2021,595(7865):48−52 doi: 10.1038/s41586-021-03560-w [140] Świerkowski L, Neilson D, Szymański J. Enhancement of Wigner crystallization in multiple-quantum-well structures[J]. Physical Review Letters,1991,67(2):240−243 doi: 10.1103/PhysRevLett.67.240 [141] Li S Y, Wang Z, Xue Y, et al. Imaging topological and correlated insulating states in twisted monolayer-bilayer graphene[J]. Nat Commun, 2022, 13(1): 4225 [142] Tong Q J, Yu H Y, Zhu Q Z, et al. Topological mosaics in Moiré superlattices of van der Waals heterobilayers[J]. Nature Physics,2016,13(4):356−362 [143] Huang S Q, Kim K, Efimkin D K, et al. Topologically protected helical states in minimally twisted bilayer graphene[J]. Physical Review Letters,2018,121(3):037702 doi: 10.1103/PhysRevLett.121.037702 [144] Liu J P, Liu J W, Dai X. Pseudo Landau level representation of twisted bilayer graphene: band topology and implications on the correlated insulating phase[J]. Physical Review B,2019,99(15):155415 doi: 10.1103/PhysRevB.99.155415 [145] Po H C, Zou L J, Vishwanath A, et al. Origin of Mott insulating behavior and superconductivity in twisted bilayer graphene[J]. Physical Review X,2018,8(3):031089 doi: 10.1103/PhysRevX.8.031089 [146] Bultinck N, Khalaf E, Liu S, et al. Ground state and hidden symmetry of magic-angle graphene at even integer filling[J]. Physical Review X,2020,10(3):031034 doi: 10.1103/PhysRevX.10.031034 [147] Liu J P, Dai X. Orbital magnetic states in Moiré graphene systems[J]. Nature Reviews Physics,2021,3(5):367−382 doi: 10.1038/s42254-021-00297-3 [148] Bultinck N, Chatterjee S, Zaletel M P. Mechanism for anomalous hall ferromagnetism in twisted bilayer graphene[J]. Physical Review Letters,2020,124(16):166601 doi: 10.1103/PhysRevLett.124.166601 [149] Zhang Y H, Mao D, Senthil T. Twisted bilayer graphene aligned with hexagonal boron nitride: anomalous Hall effect and a lattice model[J]. Physical Review Research,2019,1(3):033126 doi: 10.1103/PhysRevResearch.1.033126 [150] Chatterjee S, Bultinck N, Zaletel M P. Symmetry breaking and skyrmionic transport in twisted bilayer graphene[J]. Physical Review B,2020,101(16):165141 doi: 10.1103/PhysRevB.101.165141 [151] Liu C X, Qi X L, Dai X, et al. Quantum anomalous hall effect in Hg1- yMn yTe quantum wells[J]. Physical Review Letters,2008,101(14):146802 doi: 10.1103/PhysRevLett.101.146802 [152] Xu S Y, Neupane M, Liu C, et al. Hedgehog spin texture and Berry’s phase tuning in a magnetic topological insulator[J]. Nature Physics,2012,8(8):616−622 doi: 10.1038/nphys2351 [153] Chang C Z, Zhang J S, Feng X, et al. Experimental observation of the quantum anomalous Hall effect in a magnetic topological insulator[J]. Science,2013,340(6129):167−170 doi: 10.1126/science.1234414 [154] Serlin M, Tschirhart C L, Polshyn H, et al. Intrinsic quantized anomalous Hall effect in a Moiré heterostructure[J]. Science,2019,367(6480):900−903 [155] Tomarken S L, Cao Y, Demir A, et al. Electronic compressibility of magic-angle graphene superlattices[J]. Physical Review Letters,2019,123(4):046601 doi: 10.1103/PhysRevLett.123.046601 [156] Tang Y H, Li L Z, Li T X, et al. Simulation of Hubbard model physics in WSe2/WS2 Moiré superlattices[J]. Nature,2020,579(7799):353−358 doi: 10.1038/s41586-020-2085-3 [157] Merino J, Powell B J, McKenzie R H. Ferromagnetism, paramagnetism, and a Curie-Weiss metal in an electron-doped Hubbard model on a triangular lattice[J]. Physical Review B,2006,73(23):235107 doi: 10.1103/PhysRevB.73.235107 [158] Li G, Antipov A E, Rubtsov A N, et al. Competing phases of the Hubbard model on a triangular lattice: insights from the entropy[J]. Physical Review B,2014,89(16):161118 doi: 10.1103/PhysRevB.89.161118 [159] Rohringer G, Hafermann H, Toschi A, et al. Diagrammatic routes to nonlocal correlations beyond dynamical mean field theory[J]. Reviews of Modern Physics,2018,90(2):025003 doi: 10.1103/RevModPhys.90.025003 [160] Zheng W H, Singh R R P, McKenzie R H, et al. Temperature dependence of the magnetic susceptibility for triangular-lattice antiferromagnets with spatially anisotropic exchange constants[J]. Physical Review B,2005,71(13):134422 doi: 10.1103/PhysRevB.71.134422 [161] Liu J P, Ma Z, Gao J H, et al. Quantum valley hall effect, orbital magnetism, and anomalous hall effect in twisted multilayer graphene systems[J]. Physical Review X,2019,9(3):031021 doi: 10.1103/PhysRevX.9.031021 [162] Choi Y, Kim H, Peng Y, et al. Correlation-driven topological phases in magic-angle twisted bilayer graphene[J]. Nature,2021,589(7843):536−541 doi: 10.1038/s41586-020-03159-7 [163] Park J M, Cao Y, Watanabe K, et al. Flavour Hund's coupling, Chern gaps and charge diffusivity in Moiré graphene[J]. Nature,2021,592(7852):43−48 doi: 10.1038/s41586-021-03366-w [164] Wu S, Zhang Z Y, Watanabe K, et al. Chern insulators, van Hove singularities and topological flat bands in magic-angle twisted bilayer graphene[J]. Nature Materials,2021,20(4):488−494 doi: 10.1038/s41563-020-00911-2 [165] Chen G R, Sharpe A L, Fox E J, et al. Tunable correlated Chern insulator and ferromagnetism in a Moiré superlattice[J]. Nature,2020,579(7797):56−61 doi: 10.1038/s41586-020-2049-7 [166] Stepanov P, Xie M, Taniguchi T, et al. Competing zero-field Chern insulators in superconducting twisted bilayer graphene[J]. Physical Review Letters,2021,127(19):197701 doi: 10.1103/PhysRevLett.127.197701 [167] Pierce A T, Xie Y L, Park J M, et al. Unconventional sequence of correlated Chern insulators in magic-angle twisted bilayer graphene[J]. Nature Physics,2021,17(11):1210−1215 doi: 10.1038/s41567-021-01347-4 [168] Xie Y L, Pierce A T, Park J M, et al. Fractional Chern insulators in magic-angle twisted bilayer graphene[J]. Nature,2021,600(7889):439−443 doi: 10.1038/s41586-021-04002-3 [169] Ledwith P J, Tarnopolsky G, Khalaf E, et al. Fractional Chern insulator states in twisted bilayer graphene: an analytical approach[J]. Physical Review Research,2020,2(2):023237 doi: 10.1103/PhysRevResearch.2.023237 [170] Abouelkomsan A, Liu Z, Bergholtz E J. Particle-hole duality, emergent Fermi liquids, and fractional Chern insulators in Moiré flatbands[J]. Physical Review Letters,2020,124(10):106803 doi: 10.1103/PhysRevLett.124.106803 [171] Bhowmik S, Ghawri B, Leconte N, et al. Broken-symmetry states at half-integer band fillings in twisted bilayer graphene[J]. Nature Physics,2022,18(6):639−643 doi: 10.1038/s41567-022-01557-4 [172] Liao J Y, Wu J X, Dang C H, et al. Methods of transferring two-dimensional materials[J]. Acta Physica Sinica,2021,70(2):028201 doi: 10.7498/aps.70.20201425 [173] Schneider G F, Calado V E, Zandbergen H, et al. Wedging transfer of nanostructures[J]. Nano Letters,2010,10(5):1912−1916 doi: 10.1021/nl1008037 [174] Wang Y, Zheng Y, Xu X F, et al. Electrochemical delamination of CVD-grown graphene film: toward the recyclable use of copper catalyst[J]. ACS Nano,2011,5(12):9927−9933 doi: 10.1021/nn203700w [175] Dean C R, Young A F, Meric I, et al. Boron nitride substrates for high-quality graphene electronics[J]. Nature Nanotechnology,2010,5(10):722−726 doi: 10.1038/nnano.2010.172 [176] Li H, Wu J, Huang X, et al. A universal, rapid method for Clean transfer of nanostructures onto various substrates[J]. ACS Nano,2014,8(7):6563−6570 doi: 10.1021/nn501779y [177] Pizzocchero F, Gammelgaard L, Jessen B S, et al. The hot pick-up technique for batch assembly of van der Waals heterostructures[J]. Nature Communications,2016,7(1):11894 doi: 10.1038/ncomms11894 [178] Castellanos-Gomez A, Buscema M, Molenaar R, et al. Deterministic transfer of two-dimensional materials by all-dry viscoelastic stamping[J]. 2D Materials,2014,1(1):011002 doi: 10.1088/2053-1583/1/1/011002 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: