-
量子秘密共享(quantum secret sharing, QSS)的发展起源于Hillery等[1]的开创性工作, 他们提出了一种基于GHZ (Greenberger-Horne-Zeilinger)态[2]的方案, 用于在多个参与者之间共享秘密. 这种方案支持对量子秘密的完美重构[3]. 这项研究确立了量子秘密共享作为一个新的研究领域, 并随后催生了众多QSS方案及其变体[4–15]. 目前, QSS研究的主要关注点集中在提高方案的效率 、增强安全性以及QSS协议的实用性[5,9–13]. 研究人员正在积极探索新技术, 以增强QSS的能力[6,16–20]. 其中Shen等[13]提出了一种改进的测量设备无关(measurement-device-independent, MDI) QSS 协议, 该协议通过空间复用技术, 能够在至少10个通信方的网络中打破速率——距离限制, 提高了密钥生成速率, 并延长了传输距离. Li等[18]在量子网络上实现三用户量子拜占庭协议(quantum byzantine agreement, QBA)的实验研究, 为量子网络中的共识问题提供了一种经济实惠且实用的解决方案, 并为量子互联网的发展铺平了道路. 这些努力不仅推动了QSS技术的发展, 也为量子信息学领域带来了新的理解和应用可能性.
近年来, W态作为一种涉及多比特纠缠态的应用, 在量子信息学中显现出极大的前景. W态的独特之处在于其多比特纠缠特性, 这使得W态与GHZ态表现出明显的差异. 例如, 一个典型的对称W态可表示为1/(|001
$\rangle $ + |010$\rangle $ + |100$\rangle $ ), 这种态展现了成对的纠缠, 并且不可能通过本地操作和经典通信(local operations and classical communication, LOCC)转换为GHZ态[21]. 这表明与GHZ态相比, W态在物理特性上具有独特性[21]. Joo等[22]提出了一种利用三比特对称W态的部分量子秘密共享(partial quantum secret sharing, PQSS)方案. 然而, 现有的PQSS方案存在安全性问题, 即任何一个代理在没有其他代理帮助的情况下都能恢复秘密. 为了增强PQSS的安全性, Liu等[16]提出了一种多方量子秘密共享(multipartite quantum secret sharing, MQSS)方案, 该方案采用了Tsai和Hwang[17]提出的编码方法. 研究已经证明, 无论是通过理想的还是有噪声的量子信道, 这种MQSS方案都能保证安全. 这些进展不仅展示了W态在量子秘密共享中的潜力, 也为量子通信的安全性和效率提供了新的思路.不幸的是, 现有的对称W态的量子秘密共享方案在提供完美安全性的同时忽略了共享比特规模. 但是, 即使对于单调访问结构(对于访问结构A, 如果参与者集合p
$\in $ A意味着任何超集Q⊃P也属于A, 它就是单调的), 现有的方案需要指数级的共享比特规模. 相比之下, 在经典情景下, 任何单调访问结构都可以通过多项式大小的秘密共享方案来实现. 存在一类重要的秘密共享方案提供了完美安全性. 当且仅当任何子集p$\notin $ A对秘密一无所知时, 秘密共享方案被称为完美的. 当一个参与者所持有的共享长度等于秘密长度时, 秘密共享被称为理想的. 在量子情景下, 目前的量子秘密共享方案在传输成本和安全性方面存在局限. 为了缓解这些限制, 基于现有的工作[23–29], 本文研究W态的纠缠属性与其矩阵乘积态(matrix product state, MPS)表示之间的关系.量子优势体现在量子份额的大小显著小于秘密本身的大小. 本研究首先聚焦于基于W态的MPS表示, 这种表示能够确定W态在量子态秘密共享(QSS)中实现量子优势的关键条件. 优势的程度依赖于压缩光子的W态与秘密分发者和秘密恢复者之间关联矩阵的相关性. 我们还深入探讨不同相关矩阵的潜在应用. 通过分析不仅检验了矩阵乘积态与秘密共享技术之间的兼容性, 还为我们构建的QSS方案赋予了对抗外部和内部攻击的能力, 同时确保了秘密恢复过程的高度安全性. 此外, 通过不同量子通道传输的压缩态增强了秘密重构过程的非局域性, 从而提高了安全性. 本文的方案利用MPS进行信息编码, 实现了量子资源的最小化使用. 此外, 它还促进了量子份额与共享量子态(即秘密)之间的非唯一映射, 从而使参与者的动态添加和删除成为可能, 这增强了方案的灵活性和多功能性. 总体而言, 本文的主要贡献在于探索了矩阵乘积压缩态在QSS方案中的潜在优势, 并引入了新的互操作性和动态特性. 本文方案不仅提高了秘密共享协议的效率、灵活性和成本效益, 还为QSS在各种应用场景中的实际部署铺平了道路.
本文的其余部分组织如下. 第2节介绍了多体态、MPS和Pauli矩阵的定义. 第3节详细描述了基于矩阵乘积压缩态的QSS方案. 性能和安全性分析则在第4节中进行阐述. 第5节对论文进行总结.
-
本节主要介绍协议用到的多体态、MPS和Pauli算子/矩阵的定义.
假设存在一个一维晶格系统. 那么多体态的希尔伯特空间可以表示为n晶格希尔伯特空间的张量积:
其中每个子系统Hi, i = 1, 2, ···, n的维度是d.
其中
$ {{\boldsymbol{C}}_{{i_1}, {i_2}, \cdots {\text{ }}, {i_n}}} $ 是多体态的系数,${s_i}$ (i = 1, 2, ···, n)是物理指标,$ {s_i} \in {{\{ 0, 1\} }} $ .定义1 (多体量子态[26]) n个量子比特的多体量子态表示为
其中波函数
$ \psi (s) $ 是n个二元变量$ {s_i} \in \{ 0, 1\} $ 构成的复函数, 其中$ s \equiv ({s_1}, {s_2}, \cdots , {s_n}) $ . MPS具有特定的纠缠结构, 适用于描述量子多体系统的基态[25,26].定义2 (矩阵乘积态(MPS) [23]) 多体态的MPS表示式为
式中含n个指标的系数
$ {C_{{i_1}, {i_2}, \cdots {\text{ }}, {i_n}}} $ (n阶张量)转化成了n个矩阵$ {\boldsymbol{A}}_{{s_1}:}^{(1)}{\boldsymbol{A}}_{{s_2}:}^{(2)} \cdots {\boldsymbol{A}}_{{s_n}:}^{(n)} $ 的乘积, 其中$ {\boldsymbol{A}}_{{s_1}:}^{(1)}, {\boldsymbol{A}}_{{s_n}:}^{(n)} $ 分别是行向量和列向量, 且这些矩阵的乘积是一个数. 注意对应于多体态$ \left| \psi \right\rangle $ 的MPS表示不是唯一的[23].定义3 (Pauli矩阵[26]) Pauli矩阵定义如下:
当Pauli矩阵作用于态
$ \left| 0 \right\rangle $ 和$ \left| 1 \right\rangle $ 时, 结果如下: -
本节探讨利用MPS对纠缠态进行表征的方法, 该方法能精确揭示与概率振幅紧密相关的纠缠特性. 通过MPS的表征, 不仅能够将W态压缩为单个光子与一个二阶矩阵, 而且这种压缩技术还开辟了一种创新的技术路径. 更重要的是, 它实现了量子份额与共享量子态之间的非一对一映射关系, 这为量子信息的编码和传输提供了一种更高效和灵活的新方法.
本研究展示了一种动态的量子信息处理方式, 可以根据实际需求轻松地添加或移除参与者, 从而更好地适应参与者需求的变化. 这种方法不仅提高了QSS方案的实用性和适应性, 而且在实际应用场景中, 其还展现出了更高的灵活性和扩展性. 我们的目标是开发一种动态可扩展的量子秘密共享方案, 旨在减少通信和存储开销, 同时提高整体的安全性. 通过这种方法, 期望能够为量子通信领域带来一种既高效又安全的解决方案, 满足未来量子网络不断增长的需求.
与任何经典秘密共享一样, 主要角色包括秘密分发者Alice, 参与者表示为
$ P = \left\{{P}_{1}, {P}_{2}, \cdots , {P}_{n}\right\} $ , 以及秘密恢复者. Alice生成量子秘密份额, 通过量子通道分发给参与者(见图1). 参与者保留他们的份额, 直到一组参与者想要恢复秘密(量子态)的时候. 在恢复阶段, 参与者把他们的量子份额集合起来, 然后Alice选择一个参与者$ {P_j}, j = 1, 2, \cdots , n $ 充当半可信的(量子信道是不安全的, 经典信道是认证的)验证者和秘密恢复者, 以恢复共享的MPS. 如果参与者集属于访问结构(此处访问结构的定义为需要合作才能访问秘密的特定参与者子集), 则秘密恢复者被成功选择. 同时, 因为我们提出的量子秘密共享方案中量子份额与共享的量子态(秘密)之间映射的是非唯一性的, 所以在秘密恢复阶段, 秘密恢复者需要在根据测量结果恢复秘密(共享的量子态)之前检查测量结果的准确性. -
假设秘密(共享的量子态)是一个MPS, 形式为
其中系数为
$ \alpha _1^2 + \alpha _2^2 + \cdots + \alpha _n^2 = 1 $ .$ \left| \varphi \right\rangle $ 的系数为$ X = \left( {{X_1}, {X_2}, \cdots , {X_n}} \right) $ . 以下定理有助于找到MPS的系数.定理1 给定的n个多体态
$\cal{A} $ 1$ \in {R^{{I_1} \times {I_2} \times \cdots \times {I_N}}} $ ,$\cal{A} $ 2$ \in {R^{{I_1} \times {I_2} \times \cdots \times {I_N}}} $ , ···,$\cal{A} $ n$ \in {R^{{I_1} \times {I_2} \times \cdots \times {I_N}}} $ , 将这n个态相加得到$\cal{A} $ =$\cal{A} $ 1+$\cal{A} $ 2+···+$\cal{A} $ n (证明见附录A).给定
$n \geqslant 3$ , Alice与参与者P1, P2,$ \cdots $ , Pn之间共享的秘密(量子态为W态)被提出. 介绍方案时将首先展示$n = 3, 4, 5, 6$ 时的情况, 然后推广到$n$ .首先, 列出三光子W态的MPS表达式:
这里m表示光子的序列. 请注意, 以下表达式表示了三光子态
${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}}}$ 的不同排列组合:而且,
${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}}}$ 也可以表示为如下形式:也就是说, 存在着
$2 \times 3! = 12$ (!表示阶乘)种不同的三光子$W$ 态.四光子W态的MPS表达式如下:
类似地, 存在
$2 \times 4!$ 种不同的四光子W态. 我们还列出五到六光子W态的MPS表达式(见 附录B). 最后,$n$ 光子$W$ 态的MPS表示如下:同样地, 有2n! 种不同的
$n$ 光子$W$ 态.此外, 上面列出的
$W$ 态可以全部表示为MPS. 例如, (11)式可以用MPS的形式表示为[25](10)式可以用MPS的形式表示为
需要注意的是, 根据文献[23], 与所有上述
$W$ 态对应的MPS表示并不唯一, 其中所有态系数(即概率振幅)
${1}/{{\sqrt n }}$ 可写成$n$ 个矩阵的乘积.本文的QSS方案描述如下.
步骤1 本文的QSS适用于
$n$ 个参与者$\{ {P_1}, {P_2}, \cdots , {P_n}\} $ 的情况. 整体结构如图1所示. 其访问结构$\mathbb{A}$ 很简单, 只有完整的参与者群体属于$\mathbb{A}$ . 任何包含$(n - 1)$ 个或更少参与者的群体不属于$\mathbb{A}$ . 根据参与者数量$n$ , Alice选择一个适当的$W$ 态集合, 这个$W$ 态可以表示为MPS的形式. 需要注意的是, 有2n!种不同的$n$ 光子$W$ 态, 它们的MPS有无限多种形式. 接下来, Alice对$W$ 态进行压缩. 使用Pauli矩阵对压缩后的态进行加密, 并通过量子信道分发给参与者P1, P2,$ \cdots $ , Pn (见图1).矩阵乘积态压缩技术的数学原理 作为示例, 考虑(10)式, 用于描述三光子W态的MPS压缩过程. 此时共享MPS可以写成如下形式:
注意, 光子1和光子2是纠缠的. 所使用的符号表示法如下:
${\boldsymbol{A}}_{2\mid 1:1}^1$ 表示第1个光子为态$|1\rangle $ 和第2个光子为态$|1\rangle $ , 对应的矩阵为$\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right)$ ;${\boldsymbol{A}}_{2\mid 1:1}^0$ 表示第1个光子为态$|1\rangle $ 和第2个光子为态$|0\rangle $ , 对应的矩阵为$ \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right) $ ;${\boldsymbol{A}}_{2\mid 1:0}^1$ 表示第1个光子为态$|0\rangle $ 和第2个光子为态$|1\rangle $ , 对应的矩阵为$ \left( {\begin{array}{*{20}{c}} 0&0 \\ 0&1 \end{array}} \right) $ .观察到下式的第3项是根据前两个光子的状态展开得到, 即:
以下是对符号的解释:
${\boldsymbol{A}}_{3\mid 1:1, 2:1}^1$ 表示第1, 2, 3个光子态分别为$|1\rangle $ ,$|1\rangle $ 和$|1\rangle $ , 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 1&0 \\ 0&0 \end{array}} \right)$ ;${\boldsymbol{A}}_{3\mid 1:1, 2:1}^0$ 表示第1, 2, 3个光子态分别为$|1\rangle $ ,$|1\rangle $ 和$|0\rangle $ , 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 1&0 \\ 0&1 \end{array}} \right)$ ;${\boldsymbol{A}}_{3\mid 1:1, 2:0}^1$ 表示第1, 2, 3个光子态分别为$|1\rangle $ ,$|0\rangle $ 和$|1\rangle $ , 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 1&0 \\ 1&1 \end{array}} \right)$ ;${\boldsymbol{A}}_{3\mid 1:0, 2:1}^1$ 表示第1, 2, 3个光子态分别为$|0\rangle $ ,$|1\rangle $ 和$|1\rangle $ , 对应的矩阵为$ \left( {\begin{array}{*{20}{c}} 0&0 \\ 0&1 \end{array}} \right) $ .注意, (13)式的第4项是根据前3个光子的状态展开来写的, 因此:
符号的解释如下:
${\boldsymbol{A}}_{4\mid 1:1, 2:1, 3:1}^0$ 表示光子1、光子2、光子3和光子4分别处于态$|1\rangle $ ,$|1\rangle $ ,$|1\rangle $ 和$|0\rangle $ 时, 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 1 \\ 0 \end{array}} \right)$ ;${\boldsymbol{A}}_{4\mid 1:1, 2:1, 3:0}^1$ 表示光子1、光子2、光子3和光子4分别处于态$|1\rangle $ ,$|1\rangle $ ,$|0\rangle $ 和$|1\rangle $ 时, 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 1 \\ 0 \end{array}} \right)$ ;${\boldsymbol{A}}_{4\mid 1:1, 2:0, 3:1}^1$ 表示光子1、光子2、光子3和光子4分别处于态$|1\rangle $ ,$|0\rangle $ ,$|1\rangle $ 和$|1\rangle $ 时, 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 0 \\ 1 \end{array}} \right)$ ;${\boldsymbol{A}}_{4\mid 1:0, 2:1, 3:1}^1$ 表示光子1、光子2、光子3和光子4分别处于态$|0\rangle $ ,$|1\rangle $ ,$|1\rangle $ 和$|1\rangle $ 时, 对应的矩阵为$\left( {\begin{array}{*{20}{l}} 0 \\ 1 \end{array}} \right)$ .MPS可以很容易描述整个态的纠缠性质. MPS表示与冯·诺伊曼熵形成鲜明对比, 后者“量化”了纠缠程度. 根据(10)式和(16)式, 仅通过第3个纠缠光子及其匹配矩阵, Alice和指定参与者就能恢复正确的纠缠关系, 即:
方案的可行性
1) 技术实现的深度探讨. 通过MPS表征纠缠态, 不仅在理论上提供了一种精确的方法来描述量子态的概率振幅和纠缠特性, 而且在实践中实现了量子态的有效压缩. 这种压缩技术简化了量子信息的编码, 同时为量子态的恢复提供了一种更为经济的存储方案.
2) 创新性的强调. 本文方案中, 量子态的恢复能力是一个突出的创新点. 所有讨论的量子态都能够通过特定的纠缠光子和匹配矩阵来精确恢复, 这一点在量子信息的编码和传输中开辟了新的可能性, 增加了量子通信操作的灵活性和动态性.
3) 非唯一映射关系的利用. 本文观察到的非唯一映射关系, 即相同的压缩光子及其匹配矩阵能够解压缩成多种不同的量子态, 这一点在QSS方案中提供了额外的操作空间, 允许更灵活地管理和调整量子信息.
4) 安全性和效率的提升. 本文的QSS方案通过MPS压缩技术, 在减少通信和存储需求的同时, 提高了安全性. 这种平衡是量子通信领域中一个重要的进展, 因为其直接回应了实际应用中的效率和安全需求.
5) 动态性和可扩展性的论证. 方案的动态性和可扩展性是其另一个关键优势. 本文的QSS方案能够根据需求轻松添加或移除参与者, 这不仅提高了方案的实用性, 也展示了其在不断变化的通信环境中的适应能力.
MPS压缩是一种强大的技术, 它通过减少所需量子比特的数量来有效表示和处理量子态. 以下是对MPS压缩的物理机制的定性解释.
1) 量子态的表示. 量子态的波函数是量子力学中描述系统状态的核心, 它包含了所有可能状态的概率振幅. 这为我们提供了一个全面的框架来理解量子系统的演化和测量结果.
2) MPS的引入. MPS提供了一种优雅的解决方案, 用于高效地表示一维量子系统的量子态. 通过将复杂的量子态分解为一系列较小的、易于管理的局部矩阵(或“矩阵块”), MPS简化了量子信息的编码和处理.
3) 压缩的概念. 量子信息的压缩旨在减少表示和传输量子态所需的资源. 在MPS框架下, 压缩通过减少局部矩阵的数量或它们的维度来实现, 从而降低了系统的复杂性.
4) 物理实现. 在物理实现中, MPS压缩可以通过精确控制的量子门操作来完成, 这些操作能够精确地调整量子比特的状态. 通过这种方式, 我们能够以更少的量子资源来编码相同的信息量.
5) 压缩过程. 压缩过程精心选择并编码了量子态的关键特征, 同时排除了对当前任务不相关的信息. 在MPS中, 这意味着我们专注于那些对整体量子态有显著贡献的矩阵元素及其对应的量子态, 而忽略其他元素.
6) 解压缩. 解压缩是压缩过程的逆操作, 它可从压缩的MPS恢复出原始的量子态. 这一步骤涉及到对压缩后的矩阵执行逆操作, 从而恢复系统的全局性质和纠缠结构.
基于这些事实, 我们可以压缩MPS (即
$W$ 态)并提出一个与现有方案不同的QSS[1,4–15].步骤2 根据步骤1介绍的MPS态压缩原理和参与者数量, 假设有
$n$ 个参与者, 表示为P1, P2,$ \cdots $ , Pn, Alice首先使用在I或X之间均匀随机选择的Pauli矩阵对压缩后的光子进行加密. 然后, Alice通过量子通道将加密后的压缩态分别传输给P1, P2,$ \cdots $ , Pn. 这里, 参与者不知道其接收到的加密压缩态所对应的$|{\varPsi _i}{\rangle _{{1_m}{2_m} \cdots {n_m}}}$ 中的$i$ .为了说明步骤2, 以
${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}{4_m}}}$ 为例, 根据(16)式, Alice将秘密份额$\left( {\begin{array}{*{20}{c}} {{1}/{2}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right)\times \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)|1110\rangle $ 压缩为$|1\rangle $ 和$\left( {\begin{array}{*{20}{l}} 1&0 \\ 0&0 \end{array}} \right)$ , 并使用Pauli矩阵X对$|1\rangle $ 进行加密, 得到$|0\rangle $ . 她在压缩加密态$|0\rangle $ 中加入诱骗态一起通过量子通道发送给P1. Alice将秘密份额$\left( {\begin{array}{*{20}{c}} {{1}/{2}}&0 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1&0 \\ 0&0 \end{array}} \right)\times \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 1 \\ 0 \end{array}} \right)|1101\rangle $ 压缩为$|0\rangle $ 和$\left( {\begin{array}{*{20}{l}} 1&0 \\ 0&1 \end{array}} \right)$ , 并使用Pauli矩阵I对$|0\rangle $ 进行加密, 得到$|0\rangle $ . 同时, 她在压缩加密态$|0\rangle $ 中加入诱骗态一起通过量子通道发送给P2. Alice将秘密份额$\left( {\begin{array}{*{20}{c}} 0&{{1}/{2}} \end{array}} \right)\times \left( {\begin{array}{*{20}{c}} 1&0 \\ 0&1 \end{array}} \right)\;\;\left( {\begin{array}{*{20}{c}} 1&0 \\ 1&1 \end{array}} \right)\;\;\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)|1011\rangle $ 压缩为$|1\rangle $ 和$\;\left( {\begin{array}{*{20}{l}} 1&0 \\[-1pt] 1&1 \end{array}} \right)$ , 使用Pauli矩阵I对$|1\rangle $ 进行加密, 得到$|1\rangle $ . 此外, 她在压缩加密态$|1\rangle $ 中加入诱骗态一起通过量子通道发送给P3. Alice将秘密份额$\left( {\begin{array}{*{20}{c}} 0&{{1}/{2}} \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0&0 \\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0&0 \\ 0&1 \end{array}} \right)\left( {\begin{array}{*{20}{c}} 0 \\ 1 \end{array}} \right)|0111\rangle $ 压缩为$|1\rangle $ 和$\left( {\begin{array}{*{20}{l}} 0&0 \\ 0&1 \end{array}} \right)$ , 使用Pauli矩阵I对$|1\rangle $ 进行加密, 得到$|1\rangle $ . 她还在压缩加密态$|1\rangle $ 中加入诱骗态一起通过量子通道发送给P4.注意, 匹配矩阵、Pauli矩阵以及
$|{\varPsi _i}{\rangle _{{1_m}{2_m} \cdots {n_m}}}$ 中的$i$ 对应着接收到的加密压缩态, 它们通过安全经典信道传输给指定参与者P$_j, j = 1, 2, \cdots , n$ . 通过量子信道传输压缩态时, 采用诱骗态进行保护. 详细信息见步骤3.步骤 3 参与P1, P2,
$ \cdots $ , Pn和Alice执行一个窃听检测会话, 以确定Eve在秘密份额分发过程中是否存在干扰. 为此, Alice为随机选择的基${B_z} = \{ |0\rangle , |1\rangle \} $ 和${B_x} = \{ | + \rangle , | - \rangle \} $ 制备诱骗态, 其中$| \pm \rangle = (|0\rangle \pm |1\rangle )/\sqrt 2 $ . 随后, 诱骗态被随机地插入到加密压缩的光子中, 记录下粒子位置和初始态. 一旦参与者P1, P2,$ \cdots $ , Pn确认接收到这些态, Alice宣布诱骗态的位置, 并告知参与者应该使用哪组基来测量诱骗态.在测量完成后, 参与者P1, P2,
$ \cdots $ , Pn通过经过认证的广播信道向Alice通知他们的测量结果. Alice通过比较诱骗态的初始态与Bob的测量结果来计算错误率. 如果观测到的错误率超过预先约定的阈值, 从$2{\text{%}} $ 到$8.9{\text{%}} $ [30–33], 他们将中止协议以防止攻击危害秘密的分享. 否则, 他们将继续进行下一步.步骤4 在以后的某个时间, 参与者可能决定从存储的量子份额中恢复出秘密(量子态). 指定秘密恢复者P
$_i$ 在确认量子份额可用后, 收集由Alice发送的量子份额和矩阵, 以及$|{\varPsi _i}{\rangle _{{1_m}{2_m} \cdots {n_m}}}$ 中的$i$ 对应于他们收到的加密压缩态. 根据压缩的原理, 他恢复出共享的$W$ 态. 如果他找不到相应的矩阵乘积态, 则这个秘密态分享失败. 否则, 秘密态分享成功.为了说明步骤4, 考虑恢复秘密
$|\varPsi {\rangle _{{1_m}{2_m}{3_m}{4_m}}}$ 所需的步骤. 指定秘密恢复者P$_2$ 拥有来自参与者的压缩光子和相应的矩阵, 他首先使用Pauli矩阵I或X解密加密压缩光子, 然后恢复出最后, 他根据收到的加密压缩态中的
$i$ , 恢复出秘密态$|{\varPsi _i}{\rangle _{{1_m}{2_m} \cdots {n_m}}}$ , 结合前面的例子, 即恢复出: -
本节将探讨QSS的安全性问题. 通过将W态压缩为单个光子和一个简洁的矩阵, 实现了量子份额与共享量子态之间的非一对一映射关系, 从而为量子信息的编码和传输提供了一种更高效和灵活的方法. 这种新方法不仅增强了QSS的安全性, 而且引入了许多新特性, 例如允许注册新的参与者、注销旧的参与者以及更新共享的MPS, 从而增强了系统的动态性和适应性.
-
通过测量攻击, 窃听者Eve可以对量子通道进行攻击. 这表明Eve测量了发送的光子. 根据秘密共享方案的步骤3 (见第3节), 发送的光子由诱骗态保护. 在传输过程中, 诱骗态与用于秘密共享光子随机交错. 因此, Eve无法区分诱骗态和秘密共享光子. 如果Eve决定窃听, 那么她需要测量光子并随机选择两个基和两个Pauli矩阵中的一个进行加密. 正确猜测的概率为
$1/2 \times 1/2 = 1/4$ , 错误率为$1 - {({1}/{4})^n}$ . 根据当前的量子技术, 典型量子通道中的噪声率在2%—8.9%之间[30–33]. 这个结果远低于预期值$1 - {({1}/{4})^n}$ , 因此Eve的测量可以很容易被检测出来. -
假设攻击者Eve具有强大的计算能力, 仅受限于量子力学的原理. Eve能够拦截在量子通道中传输的压缩粒子, 或者重新发送她伪造的粒子, 并尝试从拦截的粒子中提取有意义的信息. 假设Eve拦截了由Alice发送给参与者的压缩光子, 并试图将伪造的压缩光子传输给参与者, 以逃避Alice和合法参与者在量子通道上的窃听检测. 由于压缩光子中加入了m对诱骗粒子, 并且这些诱骗粒子在本地无法区分, 如果Eve想要正确测量这些诱骗粒子的量子态, 就需要知道每对诱骗粒子的位置并执行正确的基础测量. 然而, Eve并不知道诱骗粒子对的位置. 如果Eve随机选择一个拦截到的粒子, 那么这个粒子是诱骗粒子的概率是
$\dfrac{m}{{1 + m}}$ . 对于$m$ 对诱骗粒子, Eve错误地识别这些诱骗粒子对的概率是${p_{\text{e}}} = 1 - {\Big(1 - \dfrac{m}{{1 + m}}\Big)^n} = 1 - {\Big(\dfrac{1}{{1 + m}}\Big)^n}$ . 随着诱骗粒子对数量$m$ 的增加,${p_{\text{e}}}$ 趋近于1. Eve通过对诱骗粒子进行基础测量引入错误的概率也趋近于1. 因此, 诱骗粒子与原始粒子不同的概率也趋近于1. 在第3节步骤3中, P1, P2,$ \cdots $ , Pn可以检测到这个错误.另一方面, 即使Eve的测量无法被检测到, 她也无法得到
$W$ 态. 这是因为她不知道加密矩阵和与检测到的光子相对应的$|{\varPsi _i}{\rangle _{{1_m}{2_m} \cdots {n_m}}}$ 中的$i$ . 即使她获得了加密矩阵, 也很难恢复出相应的态, 这是因为存在2n!个不同的$n$ 光子$W$ 态, 并且猜对的概率为${1}/{{2 n!}}$ , 当$n$ 足够大时, 获得正确的$W$ 态的概率可忽略不计. 其次, 同一个压缩光子和匹配矩阵有许多不同的解压方式. 更糟糕的是, 根据压缩原则和$W$ 态的MPS构造, 对应矩阵具有无限个不可能性. 因此, 本文方案对于拦截重发攻击是安全的. -
串谋攻击是指多个不诚实参与者合作, 以获取其他诚实参与者的共享信息, 并旨在未涉及这些诚实参与者的情况下恢复共享的量子态. 本节考虑以下关于串谋攻击的假设: 除指定参与者外, 所有参与者都进行串谋攻击, 以恢复共享的量子态. 在这种情况下, 因为匹配矩阵和用于这些参与者的压缩态的加密矩阵仅由指定参与者知道, 他们只能以
${\left[ {{1}/{{2(n - 1)}}} \right]^{n - 1}}$ 的概率猜测自己接收到的压缩态的匹配矩阵, 也就是说, 当$n$ 足够大时, 获得正确结果的概率是可以忽略的. 在更糟糕的情况下, 不诚实参与者们不知道$|{\varPsi _i}{\rangle _{{1_m}{2_m} \cdots {n_m}}}$ 中对应于Alice检测到的光子的$i$ , 并且存在2n!种不同的$n$ 光子$W$ 态, 猜测正确的概率是${1}/{{2 n!}}$ , 对于足够大的n来说, 获得正确的$W$ 态的概率可以忽略. 在最坏的情况下, 根据$W$ 态压缩原则, 对应的矩阵有无限的不可能性. 因此, 在这种情况下, 不诚实参与者们的串谋攻击将以极高的概率失败. -
参与者之一提供虚假的份额信息是可能发生的情况, 但我们的方案可以检测到这种攻击. Alice和用于恢复共享量子态的指定参与者可以检测到这种攻击. 也就是说, 如果恢复的量子态与Alice确定地知道态的不同, 其他参与者们可以检测到这种攻击. 例如, 在第3节步骤4的例子中, 如果
${P_2}$ 提供的虚假份额是$|1\rangle $ 而不是$|0\rangle $ ,${P_1}$ 根据Alice通知的Pauli矩阵首先将$|1\rangle $ 解密为$|1\rangle $ , 然后${P_1}$ 根据$|1\rangle $ 和他接收到的矩阵$\bigg( {\begin{array}{*{20}{l}} 1&0 \\[-1pt] 0&1 \end{array}} \bigg)$ , Alice发现在(16)式中没有匹配信息. 因此, 我们的方案对参与者攻击是安全的. -
在本文QSS方案中, 分享的秘密是MPS. 我们知道秘密可以由所有参与者恢复. 假设
$n - 1$ 个参与者利用他们的份额, 并试图确定秘密${\left| \varPsi \right\rangle _{{1_m}{2_m} \cdots {n_m}}}$ . 注意, 匹配和加密矩阵只对指定秘密恢复者是已知的, 因此该参与者集需要猜测它们. 正确猜测的概率是${\left[ {{1}/{{2(n - 1)}}} \right]^{n - 1}}$ , 对于足够大的$n$ 来说, 这是可以忽略的. 在最糟糕的情况下, 存在$2 n! $ 种不同的$n$ 光子$W$ 态, 正确猜测的概率是${1}/{{2 n!}}$ , 对于足够大的$n$ 来说, 获得正确的$W$ 态的概率可以忽略. 在最坏情况下, 根据$W$ 态的压缩原则, 相应的矩阵有无限的不可能性. 因此, 未授权集无法实现秘密恢复. -
一个共享的MPS通常是以流式方式动态生成的. 通过观察(9)式、(10)式、(B3)式、(B4)式给出的部分态和由(16)式、(C1)式、(C2)式确定的压缩操作, 很明显当原有参与者离开并有新的参与者加入时, Alice可以轻松地更新共享的MPS. 这是因为
$W$ 态的MPS表示并不唯一. 为了阐明这一观点, 示例如下:需要注意的是,
${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}{4_m}}}$ 的MPS由(13)式给出, 其被转换成(16)式. (17)式给出的压缩被转换成(18)式: -
当前所有已知的QSS方案普遍只适用于一个在其整个生命周期中保持固定的参与者群体. 与此相反, 我们提出的QSS方案打破了这种局限, 允许根据需求加入新成员, 并在不再需要时撤销旧成员. 因此, 我们的方案展现了显著的动态性和参与者群体规模的可扩展性. 这种灵活性的实现依赖于我们的技术创新, 能够将不同的光子态有效地压缩到同一个光子和匹配的矩阵中. 这项技术在保证安全性和效率的同时, 能够灵活调整参与者群体.
此特性赋予了本文QSS方案在应对现实世界中秘密共享场景的动态和多变需求时更强的适应性和实用性. 通过这种方式, 本文QSS方案不仅提高了操作的灵活性, 还为量子秘密共享的领域开辟了新的发展路径, 展示了量子通信在现实应用中的广泛潜力.
-
在本方案中, 群组成员可以轻松地接受新的参与者. 要加入一个新成员, 只需生成一个新的份额, 而不影响其他成员的份额即可. 这一能力源于
$W$ 态在压缩方面的对称性. 为了验证这一点, 比较${\left| \varPsi \right\rangle _{{1_m}{2_m} \cdots {{(n - 1)}_m}}}$ 和${\left| \varPsi \right\rangle _{{1_m}{2_m} \cdots {n_m}}}$ 的结果, 参考(16), (17)式. 显然, 该方案允许招募许多新的参与者.例如, 根据第3节, 在本文的方案中, 采用态
${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}{4_m}}}$ . 通过应用(18)式和(C1)式, 本文可以将其扩展为${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}{4_m}{5_m}}}$ . 这可以由Alice来完成, 她将秘密份额${1}/{2}|11110{\rangle _{{1_m}{2_m}{3_m}{4_m}{5_m}}}$ 压缩为$|1\rangle $ 和系数矩阵为$\left( {\begin{array}{*{20}{l}} 1&0 \\ 0&0 \end{array}} \right)$ . 她还将诱骗态与压缩加密后的光子混合后通过量子通道发送给P$_5$ . 矩阵$\left( {\begin{array}{*{20}{l}} 1&1 \\ 0&0 \end{array}} \right)$ 被通过经典通道发送给P$_1$ . 需要注意的是, 其他参与者可以保持他们的信息不变. 因此, 我们证明了在仅需最小工作量的条件下, 参与者群体能够有效地为新成员生成秘密份额. -
在本文的方案中, Alice有能力轻松地移除不再需要的参与者. 当需要从系统中移除一个旧参与者时, Alice可以简单地删除该参与者的份额, 而无需更改其他参与者的份额. 这表明, 本文QSS方案具有灵活的成员管理能力, 能够通过移除一个或多个参与者来实现轻量级的调整.
例如, 正如第3节所述, 态
${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}{4_m}{5_m}}}$ 可以通过删除某个参与者的信息来缩减为${\left| \varPsi \right\rangle _{{1_m}{2_m}{3_m}{4_m}}}$ , 同时允许其余参与者保持他们的信息不变. 这种灵活性在实际应用中非常有价值, 它使得QSS方案可以根据具体情况和需求, 轻松调整参与者的构成. -
本文在MPS与秘密共享之间发现了新的互操作性, 这为减少量子传输和存储的开销提供了一种有效方法. 具体来说, 我们的协议能够将复杂的
$W$ 态压缩成单个简化的态. 这一操作显著降低了需要传输和存储的量子比特(qubit)数量. 为实现这一目标, 我们采用了特定的矩阵.值得注意的是, 与量子传输和存储相比, 经典传输和存储的开销要低得多. 因此, 本文的QSS方案在量子传输和存储方面具有显著的成本优势, 详见表1. 这不仅提高了QSS方案的效率, 还使其在实际应用中更为可行和经济.
-
本文介绍了一种新颖的QSS方案, 可以让一组参与者共同分享一个量子态秘密. 这是通过分发携带量子信息的单光子和包含经典信息的匹配矩阵来实现的. 本文QSS方案的访问结构非常简单, 为了恢复秘密的量子态, 所有参与者都需要提供他们的份额. 这种简洁性是我们协议的优点之一. 另一个优点是
$W$ 态的类别可以通过它们的MPS来表示. 此外, 这些MPS可以压缩成由$|0\rangle $ 或$|1\rangle $ 表示的单个态.QSS方案最吸引人的特点之一是其能够将多个不同的量子态(由光子表示)压缩成由单个光子表示的单一态. 这个特性使得我们的方案具有可扩展性和动态性, 意味着根据参与者的特定需求, 参与者组可以轻松扩大或缩小. 新增参与者的添加由Alice负责, 她负责管理量子态份额的分发. 另一方面, 当一个参与者离开组时, 在秘密的量子态恢复过程中可以简单地忽略他们的旧份额. 通过这种策略, 我们能够在保持高效纠缠利用的同时, 满足系统的多元需求, 包括但不限于通信安全性、数据传输率和系统的可扩展性. 此研究还为量子信息科学领域提供了新的视角和可能性, 对于推动该领域的发展可能具有重要影响.
在未来工作中, 我们计划研究更多
$W$ 态的压缩类别, 并探索它们在QSS中的应用. 这将涉及探索不同类型的量子态, 以及考虑QSS在保护秘密量子态以外的其他潜在用途. -
基于矩阵乘积态分解的张量加法定义如下:
式中
$({X_1}, {X_2}, \cdots , {X_n}) = ({\mathcal{C}_1}\left( {{i_1}} \right), {\mathcal{C}_2}\left( {{i_2}} \right), \cdots , {\mathcal{C}_N}\left( {{i_N}} \right))$ .证明 依据
令
${\cal A} = X\left( {{i_1}, {i_2}, \cdots , {i_n}} \right) $ ,${\cal A}1 = X_1^1({i_1})X_1^2({i_2}) \cdots X_1^{n - 1}({i_{n - 1}})X_1^n({i_n}) $ ,${\cal A}2 = X_2^1({i_1})X_2^2({i_2}) \cdots X_2^{n - 1}({i_{n - 1}})\times X_2^n({i_n}) $ ,${\cal A} n = X_n^1({i_1})\times X_n^2({i_2}) \cdots X_n^{n - 1}({i_{n - 1}})X_n^n({i_n}) $ , 则有${\cal A} ={\cal A}1 + {\cal A} 2 +\cdots+{\cal A} n $ .证明过程是从已知出发, 使用了一系列矩阵乘法的计算步骤, 得到了求和结果的表达式.
-
${\left| {{\varPsi _i}} \right\rangle _{{1_m}{2_m}{3_m}{4_m}{5_m}}}$ 的MPS的压缩形式为${\left| {{\varPsi _i}} \right\rangle _{{1_m}{2_m}{3_m}{4_m}{5_m}{6_m}}}$ 的MPS的压缩形式为
基于矩阵乘积压缩态的动态可扩展秘密共享方案
Dynamic and scalable secret sharing schemes based on matrix product compressed states
-
摘要: 目前, 基于纠缠态的量子秘密共享(quantum secret sharing, QSS)方案未充分利用纠缠态的概率振幅潜力. 然而, 纠缠态的概率振幅是量子信息学的一个关键特性, 在量子计算和量子通信等领域有着广泛的应用潜力. 值得注意的是, 纠缠态可以通过矩阵乘积态(matrix product state, MPS)有效表达. 利用MPS对纠缠态进行表征, 能够准确地揭示与概率振幅相关的纠缠特性. 本研究证明利用MPS表征纠缠态, 可以将一个W态压缩为一个单光子和一个矩阵, 展示一种新的技术路径. 此外, 本研究还提出MPS与秘密共享方案之间的创新互操作性, 即通过压缩允许量子份额与共享的量子态之间形成非一对一的映射关系. 这种方法可能提供一种更高效的方式来实现量子信息的编码和传输, 对于量子秘密共享尤为重要. 同时, 我们提出的QSS方案具有动态特性, 能够根据需要轻松地添加或移除参与者, 以更好地适应参与者需求的变化, 并在实际应用场景中展现出更高的实用性和适应性. 本文的方案能够在保持高效纠缠利用的同时, 满足系统的多元需求, 包括但不限于通信安全性、数据传输率和系统的可扩展性.Abstract:
Currently, quantum secret sharing (QSS) schemes based on entangled states have not yet fully utilized the potential of the probability amplitude of entangled states. However, the probability amplitude is a key characteristic of quantum information science and possesses significant application prospects in the fields of quantum computing and quantum communication. It is worth noting that entangled states can be effectively represented by matrix product states (MPSs). The representation of entangled states using MPS can precisely reveal the entanglement characteristics closely related to the probability amplitude. This study first focuses on the representation of the W state by using MPS, an approach that allows us to determine the key conditions for W state to achieve quantum advantage in QSS. Subsequently, this research demonstrates that by representing entangled states with MPS, a W state can be compressed into a single photon state and a simplified matrix form, presenting an innovative technical path. Moreover, one of the most attractive features of our proposed QSS scheme is its ability to compress multiple different quantum states (represented by photons) into a unified state represented by a single photon. This characteristic endows our scheme with scalability and flexibility, meaning that the group of participants can be easily expanded or reduced according to their specific needs. The addition of new participants is managed by Alice, who is responsible for the distribution of quantum state shares. On the other hand, when a participant leaves the group, their old quantum state share can be simply ignored in the process of recovering the secret's quantum state, thereby simplifying the management process. Through this strategy, we can not only make effective use of entangled resources but also meet the various requirements of the system, including but not limited to communication security, data transfer rates, and system scalability. This research provides new perspectives and possibilities for the field of quantum information science and may have a significant influence on the development of the field. -

-
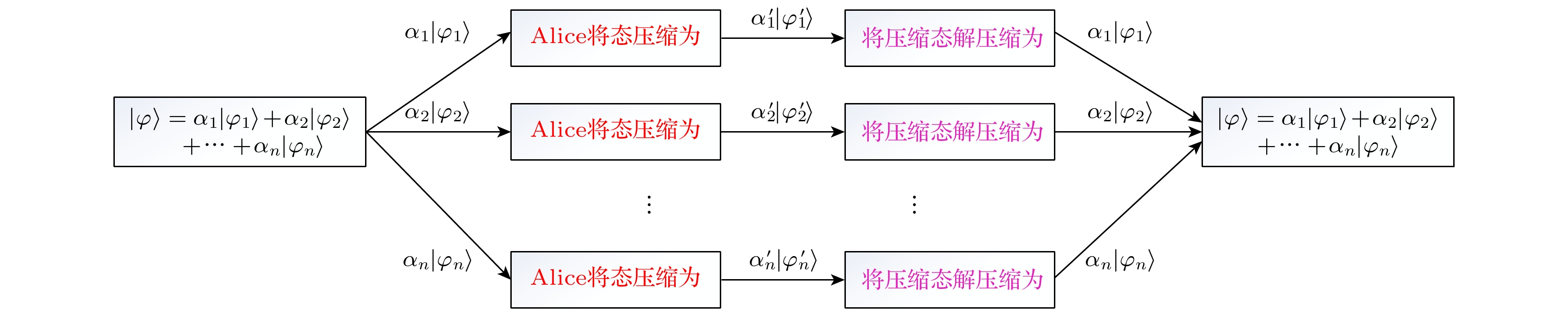
图 1 压缩量子态秘密共享示意图, 即一个特定的MPS被分解为多个部分, 每一部分都被压缩成一个单光子和一个矩阵, 并分别发送给各个参与者, 参与者在接收到这些部分后, 可以将其解压缩回原始的特定矩阵乘积态
Figure 1. Diagram of compressed quantum state secret sharing: A specific MPS is divided into several parts, each of which is compressed into a single photon and a matrix, and then sent to individual participants. Upon receiving these parts, participants can decompress them back into the original matrix product state.
-
[1] Hillery M, Bužek V, Berthiaume A 1999 Phys. Rev. A 59 1829 doi: 10.1103/PhysRevA.59.1829 [2] Greenberger D M, Horne M A, Zeilinger A 1989 Bell's Theorem, Quantum Theory and Conceptions of the Universe (Dordrecht: Springer) pp69–72 [3] Tittel W, Zbinden H, Gisin N 2001 Phys. Rev. A 63 042301 doi: 10.1103/PhysRevA.63.042301 [4] Xiao L, Long G L, Deng F G, Pan J W 2004 Phys. Rev. A 69 052307 doi: 10.1103/PhysRevA.69.052307 [5] Hsu J L, Chong S K, Hwang T, et al. 2013 Quantum Inf. Process. 12 331 doi: 10.1007/s11128-012-0380-0 [6] Singh S K, Srikanth R 2005 Phys. Rev. A 71 012328 doi: 10.1103/PhysRevA.71.012328 [7] Markham D, Sanders B C 2008 Phys. Rev. A 78 042309 doi: 10.1103/PhysRevA.78.042309 [8] Bagherinezhad S, Karimipour V 2003 Phys. Rev. A 67 044302 doi: 10.1103/PhysRevA.67.044302 [9] Gaertner S, Kurtsiefer C, Bourennane M, Weinfurter H 2007 Phys. Rev. Lett. 98 020503 doi: 10.1103/PhysRevLett.98.020503 [10] Bell B A, Markham D, Herrera-Martí D A, Marin A, Wadsworth W J, Rarity J G, Tame M S 2014 Nat. Commun. 5 5480 doi: 10.1038/ncomms6480 [11] Ampatzis M, Andronikos T 2022 Symmetry 14 1692 doi: 10.3390/sym14081692 [12] Lai H, Pieprzyk J, Pan L 2022 Phys. Rev. A 106 052403 doi: 10.1103/PhysRevA.106.052403 [13] Shen A, Cao X Y, Wang Y, Fu Y, Gu J, Liu W B, Weng C X, Yin H L, Chen Z B 2023 Sci. China Phys. Mech. Astron. 66 260311 doi: 10.1007/s11433-023-2105-7 [14] Singh P, Chakrabarty I 2023 arXiv: 2305.06062 [quant-ph] [15] Song X, Li C 2023 J. Electron. Inform. Technol. 46 1109 doi: 10.11999/JEIT230193 [16] Liu L L, Tsai C W, Hwang T 2012 Int. J. Theor. Phys. 51 2291 doi: 10.1007/s10773-012-1109-7 [17] Tsai C W, Hwang T 2010 Opt. Commun. 283 4397 doi: 10.1016/j.optcom.2010.06.039 [18] Li C L, Fu Y, Liu W B, Xie Y M, Li B H, Zhou M G, Yin H L, Chen Z B 2023 Phys. Rev. Res. 5 033077 doi: 10.1103/PhysRevResearch.5.033077 [19] Singh P, Chakrabarty I 2024 Phys. Rev. A 109 032406 doi: 10.1103/PhysRevA.109.032406 [20] Ma R H, Gao F, Cai B B, Lin S 2024 Adv. Quantum Technol. 7 2300273 doi: 10.1002/qute.202300273 [21] Dür W, Vidal G, Cirac J I 2000 Phys. Rev. A 62 062314 doi: 10.1103/PhysRevA.62.062314 [22] Joo J, Park Y J, Lee J, Jang J, Kim I 2005 J. Korean Phys. Soc. 46 763 [23] Pérez García D, Verstraete F, Wolf M M, Cirac J I 2007 Quantum Inf. Comput. 7 401 [24] Sutherland B 1971 J. Math. Phys. 12 246 doi: 10.1063/1.1665584 [25] Biamonte J 2020 arXiv: 1912.10049v2 [quant-ph] [26] Schollwöck U 2011 Ann. Phys. 326 96 doi: 10.1016/j.aop.2010.09.012 [27] Eisert J 2013 arXiv: 1308.3318 [quant-ph] [28] Islam R, Ma R, Preiss P M, Tai M E, Lukin A, Rispoli M, Greiner M 2015 Nature 528 77 doi: 10.1038/nature15750 [29] Lai H, Pieprzyk J, Pan L, Li Y 2023 Quantum Inf. Process. 22 235 doi: 10.1007/s11128-023-03990-7 [30] Hughes R J, Nordholt J E, Derkacs D, Peterson C G 2002 New J. Phys. 4 43 doi: 10.1088/1367-2630/4/1/343 [31] Jennewein T, Simon C, Weihs G, Weinfurter H, Zeilinger A 2000 Phys. Rev. Lett. 84 4729 doi: 10.1103/PhysRevLett.84.4729 [32] Stucki D, Gisin N, Guinnard O, Ribordy G, Zbinden H 2002 New J. Phys. 4 41 doi: 10.1088/1367-2630/4/1/341 [33] Beveratos A, Brouri R, Gacoin T, Villing A, Poizat J P, Grangier P 2002 Phys. Rev. Lett. 89 187901 doi: 10.1103/PhysRevLett.89.187901 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: