量子通信由于其量子信息传递的绝对安全和高效性, 近年来一直作为国际学术竞争中的焦点领域. 而长距离的纠缠分布对于量子网络^[1,2]的构建和量子通信^[3–7]的实现具有至关重要的作用. 目前基于光纤传输的直接纠缠分布距离受到传输损耗(>0.16 dB/km)和退相干效应(纠缠度变化)的影响被限制在500 km^[8,9]. 量子中继方案^[4]为解决该类问题提供了可能. 即将长距离的纠缠分布通道划分为不同的短距离子链路, 通过光子直接传输在短距离链路节点间建立纠缠并通过相邻节点间纠缠交换实现长距离纠缠分发. 量子中继节点的构建常利用原子系综作为基本单元, 即利用DLCZ (Duan-Lukin-Cirac-Zoller )过程, 通过自发拉曼(Raman)散射产生一对斯托克斯(Stokes)光子和相应的自旋波激发^[10,11]量子记忆纠缠态构建量子中继节点. 但即使在理想的量子态保真度、存储寿命、读出效率等前提下纠缠产生速率依旧太慢, 为此量子存储被要求具有大尺度的多模存储(多路复用)能力. 近年来在固态和气态原子系综中, 利用时间^[12–14]、空间^[15–17]、光谱^[18,19]多模的DLCZ型量子存储取得显著进展. 目前基于冷原子系综的量子复用存储方案主要表现为空间、时间复用方面, 例如2017年Pu等^[15]实验演示了一种新型的可独立访问225个存储单元的DLCZ型量子存储器. 同年Tian等^[16]通过在多空间方向(模式)对Stokes光子的采集实现六路空间复用的光与原子纠缠界面的设计. 而时间复用的量子存储, 是一个自由度不同于空间复用的量子存储方案, 其仅通过单一光学采集通道实现多个可分辨量子存储模式(量子光场)的探测, 具有极强的吸引力. 近年来研究者们分别通过将多束激光脉冲序列沿单一(固定)的空间方向^[20,21]和不同空间方向^[12–14]作用于冷原子系综、可控的移相技术(梯度回声技术和光学频率梳技术)、或对冷原子系综磁场进行反转控制^[22]等方式实现时间复用的DLCZ型量子存储实验研究.

在目前已实现的时间复用量子存储方案中, 在不使用光学腔和大光学厚度的情形下普遍存在读出效率偏低的问题, 例如在时间多模存储方案^[12–14]中读出效率仅约16%. 而读出效率的值对量子中继的成功与否至关重要, 读出效率每提高1%纠缠分布率将能够提高7%—18%^[23,24]. 本文通过合理选择能级结构并利用声光调制器设计可扩展型脉冲光制备技术实现对时间复用存储方案进行进一步的优化. 在不使用光学腔和大光学厚度的情形下实现高效率时间复用量子存储的研究, 实现纠缠源纠缠产生概率5.83倍的增强, 同时读出效率约38%, 对应Bell参数约为2.35. 本文方案具有操作简单、兼容性强等优点, 例如在我们实验结果的基础上可进一步通过光学腔增强Stokes光子与anti-Stokes光子耦合提高读出效率^[13,25–27], 或通过实验设计实现多模存储中的背景噪声抑制^[14,28], 达到大模式数高保真度时间复用的目的. 本文测量结果为打破时间复用量子存储无法大规模扩展的局限性, 推动量子通信的发展奠定基础.

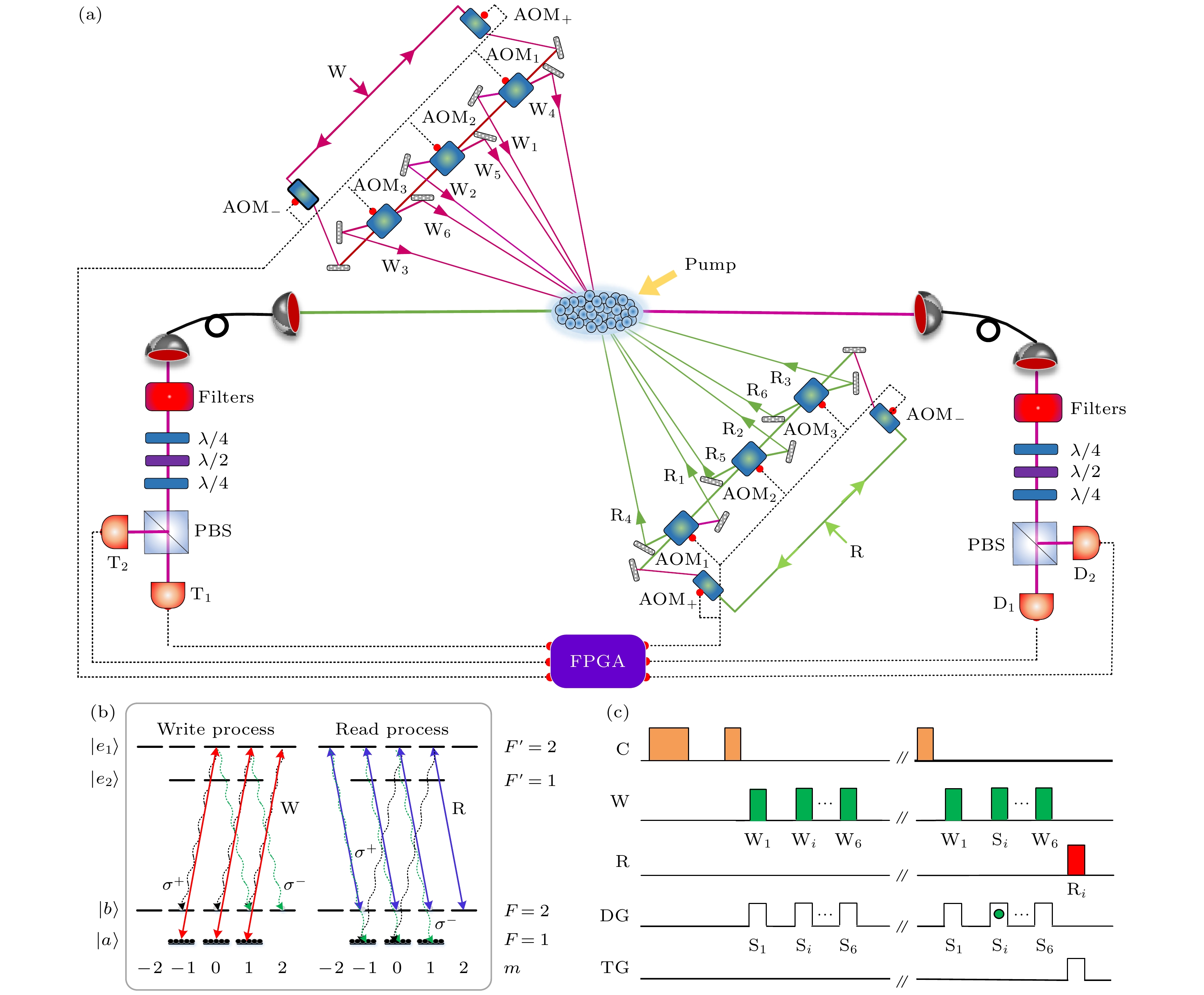
图1(a)所示为制备六路时间复用量子存储的实验装置, 以⁸⁷Rb冷原子作为存储介质. 俘获原子团的尺寸约为5 mm $ \times $2 mm $ \times $2 mm, 测量光学厚度为8—9. 图1(b)所示为原子能级结构, 图1(c)所示为实验时序图. 实验正式开始前通过两束左旋和右旋圆偏振频率共振于能级跃迁$\left| b \right\rangle \leftrightarrow \left| {{e_2}} \right\rangle $ $(\left| b \right\rangle \leftrightarrow \left| {{e_1}} \right\rangle ) $的泵浦光(清洁光)制备原子到基态能级$\left| {a, {m_{\text{F}}} = 0, \pm 1} \right\rangle $. 实验首先由FPGA (field-programmable gate array)程序操控写光网络产生6束右旋圆偏振频率为$\left| a \right\rangle \to \left| {{e_1}} \right\rangle $正失谐20 MHz的写激光脉冲(W₁—W₆)沿不同空间方向作用于原子系综, 设置每束写光功率约20 μW, 脉宽80 ns且相邻脉冲光时间间隔400 ns. 为保证时间复用存储器具有较长的存储寿命, 实验上使用近共线配置^[29,30], 其要求6路写(读)光束相对于采集方向的空间夹角非常小, 实验选择角度均小于$ 0.3^\circ $. 采用单光子探测器D₁ (D₂)探测每路写光作用后对应的光场时间模式S_i中情形, 此过程在第i路写光W_i作用下可能产生一个任意圆偏振(左旋或右旋)的Stokes光子, 定义为${\left| R \right\rangle _i}$(${\left| L \right\rangle _i}$), 在量子存储模式M_i中必然存在一个与该光子具有对应关系的自旋波激发, 定义为$\left| 1 \right\rangle _{{{\text{M}}_i}}^ + $($\left| 1 \right\rangle _{{{\text{M}}_i}}^ - $). 此时在写脉冲W_i作用下构建原子-光子共同态表示为$ \rho _{{\text{ap}}}^i = {\left| 0 \right\rangle ^i}{}^i\left\langle 0 \right| + {\chi _i}\left| \varPhi \right\rangle _{{\text{ap}}}^i{}_{{\text{ap}}}^i\left\langle \varPhi \right| $, 其中${\left| 0 \right\rangle ^i} = {\left| 0 \right\rangle _{{{\text{S}}_i}}}{\left| 0 \right\rangle _{{{\text{M}}_i}}}$表示不同量子模式下的真空状态, ${\chi _i}$表示第i路写激发率, $ \left| \varPhi \right\rangle _{{\text{ap}}}^i = (\cos \theta \left| 1 \right\rangle _{{{\text{M}}_i}}^ + {\left| R \right\rangle _i} + \sin \theta \left| 1 \right\rangle _{{{\text{M}}_i}}^ - {\left| L \right\rangle _i}) $表示过程中自旋波-光子纠缠态(第i个时间模式), $\cos \theta $$ (\sin \theta ) $是与C-G (Clebsch-Gordan )系数相关的参数. 定义$ {{{X}}_\alpha }({{{m}}_{{a}}}) = {{C}}_{{{{m}}_{{a}}}, 1, {{{m}}_{{a}}} + 1}^{{{{F}}_{{a}}}, 1, {{{F}}_{{{{e}}_1}}}}{{C}}_{{{{m}}_{{a}}} + 1, \alpha , {{{m}}_{{a}}} + \alpha + 1}^{{{{F}}_{{{{e}}_1}}}, 1, {{{F}}_{{b}}}} $为能级$ \left| {{a}} \right\rangle \to \left| {{{{e}}_1}} \right\rangle $和$ \left| {{{{e}}_1}} \right\rangle \to \left| {{b}} \right\rangle $跃迁C-G系数的乘积, 其中$ \alpha = \pm 1 $表示不同的圆偏振方向, $ {{{m}}_{{a}}} $表示Zeeman子能级, C表示跃迁C-G系数, F_a ($F_{e_1} $)表示基态(激发态)能级$ \left| {{a}} \right\rangle $($ \left| {{{{e}}_1}} \right\rangle $). 因此总跃迁概率表示为$ {{X}}_\alpha ^2 = {{X}}_\alpha ^2({{{m}}_{{a}}} = 1) + {{X}}_\alpha ^2({{{m}}_{{a}}} = 0) + {{X}}_\alpha ^2({{{m}}_{{a}}} = - 1) $. 所以权重参数

假设在写脉冲光W_i作用下探测到Stokes光子, 经设定的时间间隔FPGA将由前馈控制读光网络开启相应的读脉冲光束R_i, 其频率共振于$\left| b \right\rangle \to \left| {{e_1}} \right\rangle $能级跃迁且反向于W_i, 每束读光功率约2 mW, 脉宽90 ns. 该过程实现自旋波信息到anti-Stokes光子的转换. 双光子的纠缠态$\left| \varPhi \right\rangle _{{\text{ap}}}^i$表示为$ \left| \varPhi \right\rangle _{{\text{pp}}}^i = \big(\cos \theta {\left| H \right\rangle _{{\text{AS}}}}{\left| H \right\rangle _{{{\text{S}}_i}}} + \sin \theta {\left| V \right\rangle _{{\text{AS}}}}{\left| V \right\rangle _{{{\text{S}}_i}}} \big) $, 其中$ {\left| H \right\rangle _{{\text{AS}}}} ( {\left| H \right\rangle _{{{\text{S}}_i}}}) $和$ {\left| V \right\rangle _{{\text{AS}}}} ( {\left| V \right\rangle _{{{\text{S}}_i}}}) $分别为在anti-Stokes以及Stokes光场模式下水平(H )和竖直(V )偏振的光子. Stokes (anti-Stokes)光子在对应的采集通道中依次经单模光纤、光学滤光片Filters、偏振分束器PBS后送入单光子探测器D₁ (T₁)和D₂ (T₂).

本文将着重介绍利用可扩展型脉冲光技术设计写、读光网络系统制备所需6路空间异向的写-读激光脉冲序列. 目前已实现时间多模存储过程 中产生多个不同方向脉冲常见的方式主要有两种. 一种利用声光偏折器, 该法优点为单个声光偏折器可能产生超十束空间各异的激光脉冲, 但脉冲产生速率过低, 例如产生单一时间模式所需时间便达到μs量级, 对系综寿命有较高的要求. 另一种利用声光调制器, 单个声光调制器产生一束激光脉冲, 该法优点为脉冲识别、产生速率高, 脉宽压至几十ns量级, 但装置复杂、空间利用率较低. 我们设计的可扩展型脉冲光制备技术, 即利用光路的可逆性由激光双向穿透声光调制器产生两路写-读光脉冲, 实验利用3个声光调制器的串联实现时间复用量子存储中6路写读脉冲光的制备. 由于写-读光网络具有相同的结构, 以写脉冲光制备过程为例进行说明, 如图1(a)所示. 写光网络主要由两部分构成, 即主光路(声光调制器AOM₊、AOM_–)和实验光路(声光调制器AOM_1–3). 其中主光路通过声光调制器AOM₊、AOM_–的通断实现写光方向的控制, 实验光路通过声光调制器AOM_1–3产生实验所需的写光脉冲. 主光路和实验光路d 声光调制器具有相同的衍射频率, 但主光路选择+1级衍射, 实验光路选择–1级衍射. 实验过程写光W经偏振分束棱镜或光纤等方式分为两路, 由FPGA控制开启AOM₊ (关断AOM_–)产生单一方向的写光脉冲, 依次开断声光调制器AOM_1–3产生图示W₁—W₃写光脉冲; 此时关断AOM₊ (开启AOM_–), 同理将产生W₄—W₆写光脉冲. 相比于声光偏折器方案, 我们能够产生一系列脉宽为80 ns、脉冲间隔为400 ns, 甚至更窄的激光脉冲序列. 相比于声光调制器方案^[12], 本工作提高空间利用率, 降低实验成本, 后续将在此基础上探索通过实时改变声光调制器的衍射频率实现多通道信号可控输出, 实现由单一声光调制器实现更多路输出的可扩展型脉冲光.

我们定性分析实验中的能级选择, 在已实现的时间复用量子存储实验中^[12–14]读出效率约16%, 写光频率作用于$ \left| a \right\rangle \to \left| {{e_1}} \right\rangle $能级跃迁, 读光频率作用于$\left| b \right\rangle \to \left| {{e_2}} \right\rangle $能级跃迁. 选择相同的写光跃迁能级$\left| a \right\rangle \to \left| {{e_1}} \right\rangle $, 故而写光与原子发生作用产生的自旋波信息是完全相同的. 实验改变读光能级跃迁频率为$\left| b \right\rangle \to \left| {{e_1}} \right\rangle $, 如图1(b)所示, 当该频率读光作用的时候, 能够读出存储的全部自旋波激发. 而在读光能级跃迁频率为$\left| b \right\rangle \to \left| {{e_2}} \right\rangle $时, 将浪费部分存储的自旋波信息从而导致读出效率的降低. 此外能级跃迁概率受C-G系数影响, 实验选用跃迁频率为$\left| b \right\rangle \to \left| {{e_1}} \right\rangle $的读光相比于跃迁频率为$\left| b \right\rangle \to \left| {{e_2}} \right\rangle $的读光作用于原子时具有更高的C-G系数. 但跃迁频率为$\left| b \right\rangle \to \left| {{e_1}} \right\rangle $的读光作用原子时, 激发态子能级向下跃迁时C-G系数是不等且不平均的, 导致光子与原子纠缠转化为$ \left| {{H}} \right\rangle $和$ \left| {{V}} \right\rangle $间光子纠缠时是不平均的, 最终导致Bell参数值相比于读光跃迁频率为$\left| b \right\rangle \to \left| {{e_2}} \right\rangle $时发生一定程度的降低.

简述该计算过程, ⁸⁷Rb原子与近共振光作用可以通过偶极矩阵表示为$ \left\langle {F{m_{\text{F}}}} \right|er\left| {F'{{m}'_{\text{F}}}} \right\rangle $, 其是两个超精细子能级基态$ \left\langle {F{m_{\text{F}}}} \right| $和激发态$ \left| {F'{{m}'_{\text{F}}}} \right\rangle $耦合结果, 利用Wigner-Eckart理论计算该偶极矩阵, 该矩阵将简化成C-G系数和简化矩阵乘积的形式:

其中q是球坐标中标记r分量的指数, 双杠表示矩阵元素的减少. 利用Wigner3-j符号表示(1)式为

(2)式约化矩阵元能够利用F, $ {{F'}} $间的联系进一步简化成Wigner6-j符号, 新约化矩阵元只依赖于L, S, I和J量子数:

同理(3)式进一步可以分解为另一个Wigner6-j符号和仅涉及一个只包含量子数L的约化矩阵元:

利用(3)式得出的偶极矩阵, 即可计算出两子能级间跃迁概率. 利用文献[28]给出的能级跃迁概率, 最终计算得出读光能级为$\left| b \right\rangle \to \left| {{e_1}} \right\rangle $时读出效率约为33%, 相比于读光能级为$ \left| b \right\rangle \to \left| {{e_2}} \right\rangle $时读出效率约为15%, 因此理论计算我们选择的读光能级会将读出效率提升1倍左右^[31].

实验首先在存储时间$ \tau \approx 0.2 {\text{ μs}} $测量单路纠缠源的读出效率, 分别测量在6个不同写脉冲W_i作用下的读出效率. Stokes和anti-Stokes采集通道单光子总探测效率${\eta _{\text{S}}} \approx 30{\text{%}} , {\eta _{{\text{AS}}}} \approx 30{\text{%}} $ (单模光纤80%、滤波器组80%、多模光纤95%、单光子探测器60%). 定义第i路写光激发率$ \chi _{{i}} $:

其中$N$为FPGA发出总写脉冲数, ${N_{\text{S}}}$为该过程采集到的Stokes光子数. 在此基础上定义单路纠缠源读出效率$ {\gamma _{{i}}} $:

其中${N_{{\text{AS}}}}$为该过程采集到的anti-Stokes光子数. 实验结果如表1所列, 可以看出单路纠缠源读出效率最高达到39%, 平均恢复效率约为37%.

随后通过测量6路时间复用量子存储中单路纠缠源的Bell参数S来表征纠缠质量, 定义Bell参数S为

其中${\theta _{\text{S}}}$和${\theta _{{\text{AS}}}}$分别表示Stokes和anti-Stokes光场偏振基下的旋转角, 实验中选择${\theta _{\text{S}}}$, ${\theta _{{\text{AS}}}}$, $ {\theta '_{\text{S}}} $, $ {\theta '_{{\text{AS}}}} $分别为${0^ \circ }, {22.5^ \circ }, {45^ \circ }, {67.5^ \circ }$. 偏振关联函数定义为

其中$ C({\theta _{\text{S}}}, {\theta _{{\text{AS}}}}) $, $ C(\theta _{{\text{S}} + {{\text{π}} /2 }},\theta _{{\text{AS}} + {{\text{π}} / 2}}) $, $ C({\theta _{{\text{S}} + {{\text{π}} / {2}}}}, \theta {}_{{\text{AS}}}) $, $ C({\theta _{\text{S}}}, {\theta _{{\text{AS}} + {{\text{π}} / {2}}}}) $分别表示单光子探测器D₁-T₁, D₂-T₂, D₂-T₁, D₁-T₂之间的符合计数. 在存储时间$ \tau \approx 0.2 {\text{ μs}} $分别测量6路纠缠源Bell参数, 结果如表2所列, 可以看出, 单路纠缠源的Bell参数值平均水平约为2.48.

基于此建立起6路时间复用的量子存储, 首先分析6路时间复用纠缠源和单路纠缠源纠缠产生速率的关系, 通过Stokes光子的探测概率来表示自旋波-光子纠缠产生概率. 实验中单路纠缠源激发率均为$ \chi _{i} = 1{\text{%}} $. 由(1)式可知, 单路纠缠源探测到Stokes光子概率表示为

其中$P_{\text{S}}^1 = P_{{{\text{S}}_{1}}}^{1} + P_{{{\text{S}}_{2}}}^{1}$, $P_{{{\text{S}}_{1}}}^1$和$P_{{{\text{S}}_{2}}}^{1}$分别表示单通道D₁和D₂单光子探测器探测到Stokes光子的概率, ${\eta _{\text{S}}}$表示Stokes采集通道总探测效率. 当$\chi {\eta _{\text{S}}} < 1$时m路时间复用纠缠源的Stokes光子探测概率表示为^[12]

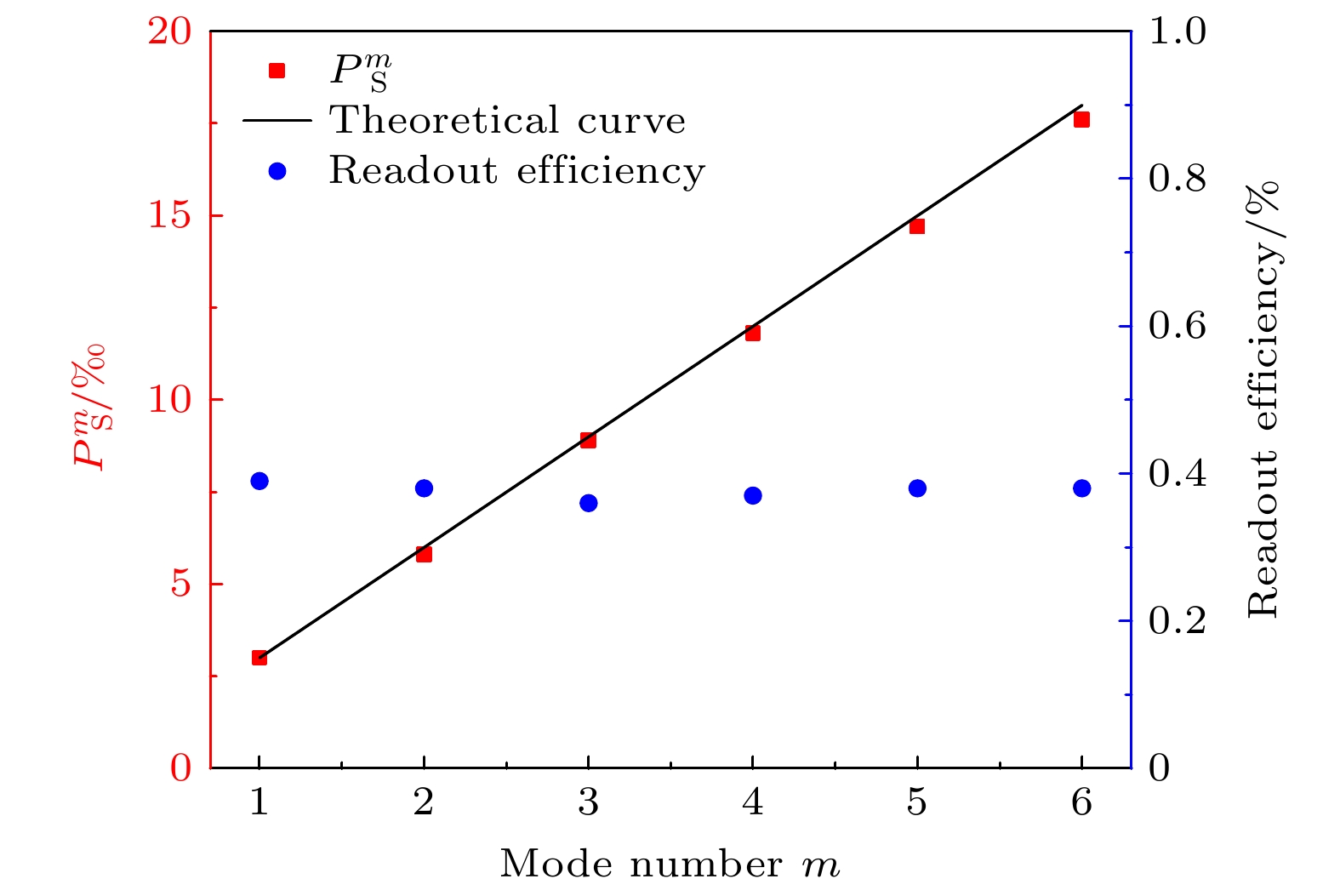
理论计算m路时间复用的量子存储, 其纠缠产生的概率即Stokes光子产生的概率相比单模情况增加m倍, 故监测$P_{\text{S}}^m$与时间模式数m间的关系, 即可反馈出时间复用量子存储纠缠产生概率变化情况. 实验结果如图2所示, 测量在不同时间模式数m下Stokes光子数量并推导出$P_{\text{S}}^m$与时间模式数m间的关系, 同时测量不同时间模式数m下对应的读出效率. 其中红色方块点为实际测量得到的Stokes光子的探测概率$P_{\text{S}}^m$, 黑色实线为由(7)式拟合的理论曲线, 蓝色的圆点表示读出效率的值. 结果表明随着时间模式数m的增大. Stokes光子的探测概率呈线性变化, 通过计算${{P_{\text{S}}^{6}} / {P_{\text{S}}^{1}}} = 5.83$. 实验证明相比较单模纠缠源, 我们设计6路时间复用的纠缠源Stokes光子产生的概率增大5.83倍, 与理论计算结果一致. 读出效率基本稳定在38%, 约为时间复用存储实验^[12–14]的2倍.

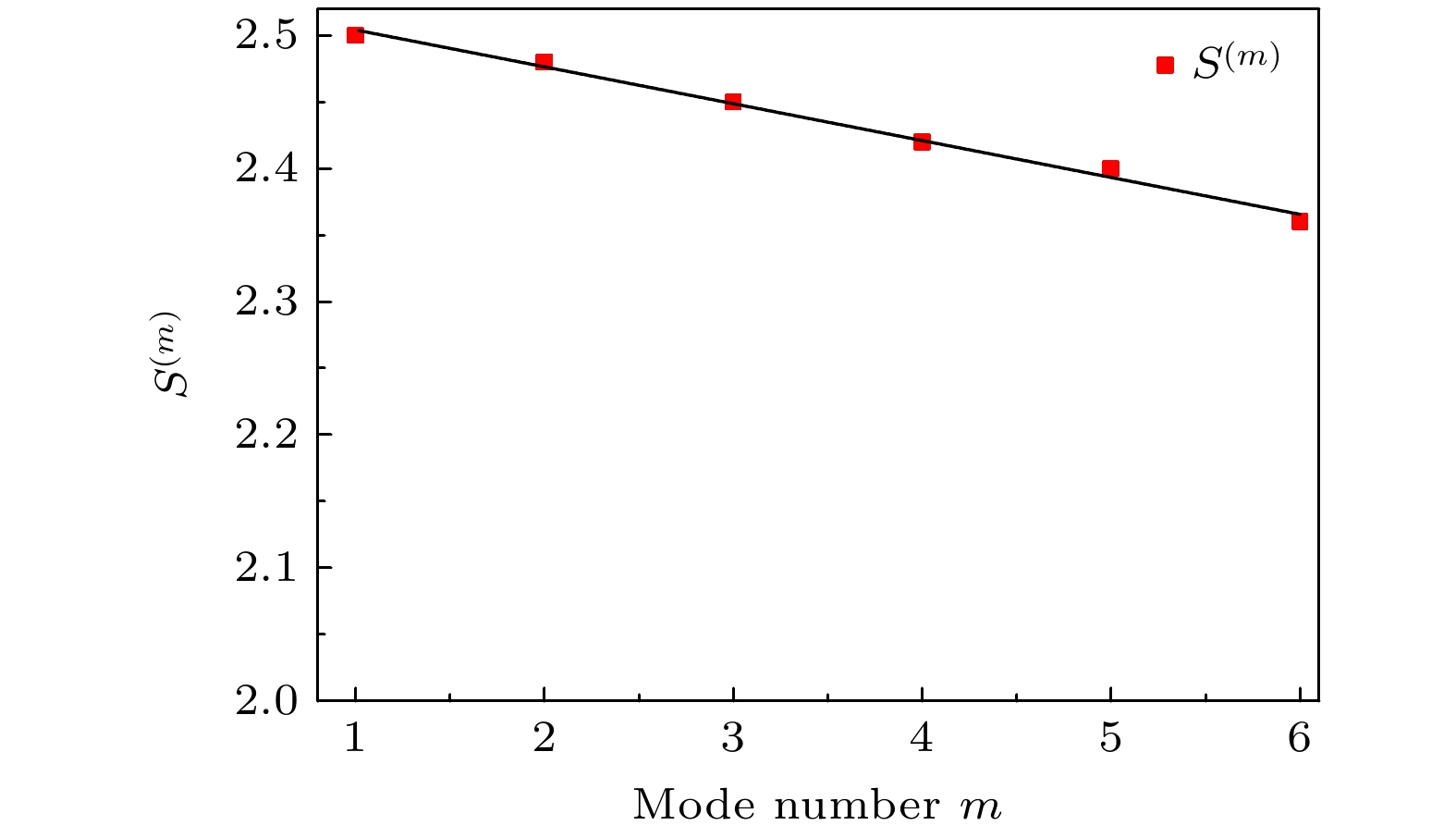
随后在存储时间$ \tau \approx {0}{.2} {\text{ μs}} $测量6路时间复用纠缠源Bell参数S ^(m)随着时间模式数m的变化, 实验结果如图3所示, 图中红色矩形点分别表示在不同的时间模式数m时测量的Bell参数S ^(m). 当时间模式数为1时测得Bell参数约为2.48, 当时间模式数m增大到6时Bell参数为2.35. 这是由于量子存储过程中背景噪声(荧光噪声)所导致的. 下面进行简单分析, 当模式数m为1时认为不受荧光噪声的影响, 而在时间复用存储方案中, 假设每次触发有m个不同方向的写脉冲作用到原子系综, 每一路写光将概率性地产生沿空间不同的方向的Stokes光子并且存储其对应的自旋波模式在原子系综中; 假设在写探测方向探测到第i路写光产生的Stokes光子, 当读取的时候, 除第i路写光, 由其他m – 1路写光存储在原子系综中的自旋波信息转换成的anti-Stokes光子是沿空间各个方向, 均认为是荧光噪声, 因此降低时间复用源的纠缠度. 背景噪声可以通过合适的光学腔设计实现较大的抑制^[28], 同样假设写探测方向探测到第i路上写光产生的Stokes光子, 那么其他m – 1路上产生的荧光都将得到抑制, 只有在采集方向荧光得到增强, 当读取的时候, 这些方向荧光转化的anti-Stokes光子减少, 从而抑制了荧光噪声的产生. 在此基础上能大幅度提高时间复用量子存储的Bell参数值.

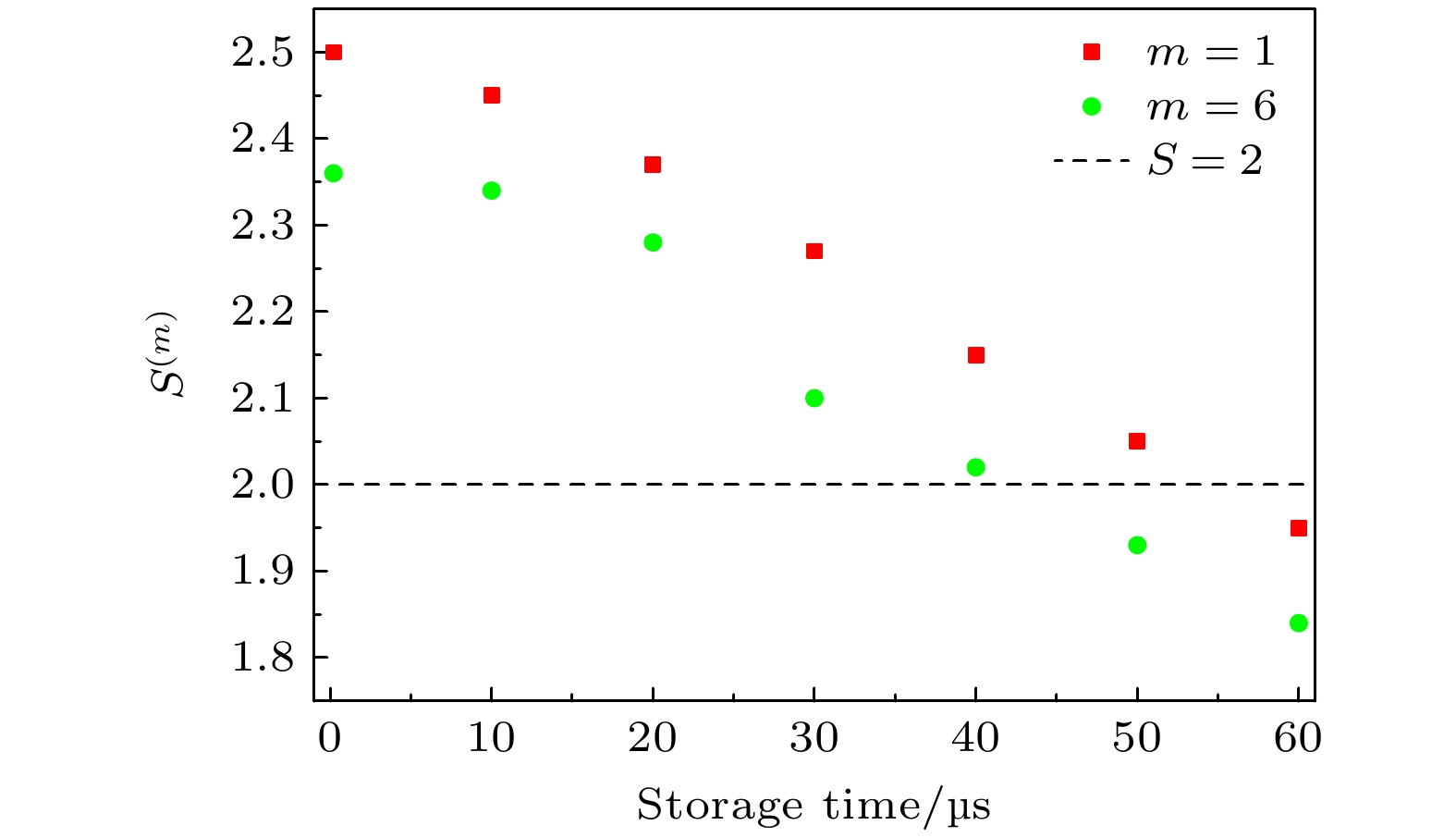
最后为验证时间复用量子存储的多模存储能力, 在单路纠缠源激发率$ {\chi _{{i}}} = 1{\text{%}} $时分析单路和6路时间复用纠缠源Bell参数S(S ⁽⁶⁾)随存储时间$ \tau $的函数关系. 实验结果如图4所示, 在不同存储时间下6路时间复用和单模存储的Bell参数值用绿色圆形点和红色正方形点表示, 临界值Bell参数S = 2用黑色虚线表示. 在近零存储时间($\tau = 200 {\text{ ns}}$) 6路时间复用纠缠源Bell参数值S ⁽⁶⁾约为2.35, 同理当$\tau = 40 {\text{ μs}}$时, Bell参数值S ⁽⁶⁾约为2.02.

我们在冷原子系综中演示了一种基于DLCZ过程的6路时间复用高读出效率的光学量子存储方案. 通过可扩展型脉冲光制备技术极大的降低装置的复杂性, 为多路时间复用的实现奠定实验基础, 通过合理选择读光能级实现高效率的读出. 在不使用光学腔和较低光学厚度的情形下通过相比于常见的时间复用量子存储方案^[9–11], 我们将读出效率提高到约38%, 并伴随有2.35的Bell参数. 同时实现自旋波-光子纠缠产生概率增加5.83倍. 在时间复用量子存储中, 考虑到随着时间模式数的增大, 背景噪声的存在严重限制时间模式数, 而在真正的量子通信过程中可能需要做到存储几十甚至上百个时间模式, 因此对于背景噪声的处理至关重要, 常见高效的解决方法为设计光学腔保证Stokes光子在腔内共振, anti-Stokes光子无作用可实现时间模式数的显著增大. 因此凸显出时间复用量子存储在无光学腔条件下高读出效率的重要性. 实验中可以通过改变光学厚度、优化光脉冲等方式实现读出效率的进一步提升. 我们的研究具有兼容性强的特点, 为实现高效率、超多模式的时间复用量子存储、长距离高效量子纠缠分发提供有效方法和实验基础.