自20世纪80年代以来, 随着超快激光技术的发展, 基于皮秒、飞秒光源的超快泵浦探测技术得到了蓬勃发展, 在光学与电子学之间构筑起一道桥梁, 为研究探测微观粒子的动力学行为提供了有力的手段^[1,2]. 然而, 对于原子内部更快的电子运动过程, 如电子在玻尔轨道上绕原子核旋转的动力学过程, 则需要脉宽更短的阿秒脉冲激光作探针. 2001年, 研究者们首次在实验上测量得到了孤立阿秒脉冲, 由此超快研究进入了阿秒时代^[3]. 经过二十多年的发展, 阿秒脉冲的世界纪录不断被刷新, 至今实验所能获得的最短脉冲宽度被推进到43 as^[4-6], 孤立阿秒脉冲的重复频率也被提高到100 kHz^[7]. 此外利用相干控制技术, 将多路不同波段的超快激光分别精确控制色散及相位后合成, 也可实现高能量的可见光阿秒脉冲激光输出^[8]. 上述这些工作的进展, 意味着人们在实验上开展阿秒时间尺度分辨能力的电子动力学探测已成为可能.

随着高次谐波(high-order harmonic generation, HHG)和阿秒激光技术的不断发展, 不断涌现的探测技术也为超快动力学的研究探测提供了强有力的工具, 冷靶反冲动量谱仪(cold target recoil ion momentum spectroscopy, Coltrims)^[9,10]、速度成像谱仪(velocity map imaging, VMI)^[11,12]让单原子尺度下的电子离子解离动力学的研究得以实现; 角分辨光电子能谱仪(angle resolved photoemission spectroscopy, ARPES)^[13–15]、飞行时间谱仪(time of flight, TOF)^[16]使得观测固体材料内部丰富的电子动力学过程成为可能, 如带内跃迁、带间跃迁及晶格声子动力学过程的探测.

开展上述实验, 面临的一个重要问题是激光光源系统, 即驱动光源要有良好的稳定度, 对传输光路系统也需要有极高的延时稳定性和高精度的延时扫描能力. 因此, 除了需要对光学器件的振动与实验室环境的变化进行严格控制外, 还需要额外引入一套主动稳定系统, 用以对上述因素所致的延时漂移做出反馈. 2019年, 江昱佼等^[17]使用双层辅助光路快速傅里叶变化算法, 实现了延时抖动仅4.1 as的锁定结果; 同年Vaughan等^[18]结合了迈克耳孙干涉仪提高锁定精度, 也实现了锁定精度小于10 as的结果; 2023年, Li等^[19]将辅助光与主激光同轴传输, 在臂长3 m、采样频率15 Hz的条件下得到了锁定精度小于20 as的结果; 同年, Luo等^[20]直接利用驱动激光实现了对延时抖动的锁定, 在60 ms的积分时间下得到了13 as的锁定精度. 然而, 上述实验均为对固定臂长的锁定, 并未考虑改变臂长特别是长距离臂长对锁定精度的影响. 为此本文基于已有的研究进展和基础, 开发了一种可以实现对延时锁定精度进行快速预测的装置. 本文将在分析介绍长距离阿秒泵浦-探测光路中臂长与延时锁定精度的关系上, 报道我们实现的阿秒锁定结果.

在泵浦-探测实验系统中, 两路激光共同构成了一个马赫-曾德干涉仪. 当频率为$\omega $的平面波:

通过泵浦-探测系统后, 干涉平面的电场分布可表示为

其中, $ {{\boldsymbol{E}}_1} $和$ {{\boldsymbol{E}}_2} $分别为两路激光的矢量场, $ \tau $是两路激光的延时差. 合成场的光强分布可表示为

其中, $ \theta $是$ {{\boldsymbol{k}}_{1}} $和$ {{\boldsymbol{k}}_2} $的夹角, $ \Delta \varphi $是$ \theta $, $ \tau $的函数. 进一步, 该公式可表示为

其中, $ {I_1} $, $ {I_2} $分别为两束激光的直流非相干叠加项, 而$ f(\theta , \tau ) $是激光相干叠加后产生的干涉项. 当系统处于相对稳定的状态时, 两路激光的指向可视为保持不变, 即$ \theta $保持不变, 此时干涉条纹变化的来源是激光的相对延时$ \tau $的抖动. 因此, 干涉条纹在空间上的抖动可以反映出激光相对延时的抖动状态, 通过分析条纹可以实现对激光延时的反馈锁定.

一组相对稳定的干涉条纹可以表示为某一时刻下的一维数组$f(x, {\text{ }}{\varphi _x}, {\text{ }}t)$, 也可表示为不同频率成分在$t$时刻对$\omega $的积分:

为了实现对干涉条纹的稳定, 需要避免无关项的干扰, 对主要信息成分进行分析. 利用傅里叶变换将一个由时间变化的干涉条纹$ f\left( {x, {\text{ }}{\varphi _x}, {\text{ }}t} \right) $变换成$ F\left( {\omega , {\text{ }}{\phi _\omega }, {\text{ }}t} \right) $, 从而得到随时间变化的功率谱(实部)及相位谱(虚部). 在实验中, 选择高信噪比的一级频率成分为信息频率可以有效避免零级项(直流)及杂散项(背景噪声)对反馈运算的干扰, 保证锁定精度. 此时, 一级频率成分的傅里叶逆变换为$ {f_1}\left( {x, {\text{ }}{\varphi _{{x}}}, {\text{ }}{\omega _1}, {\text{ }}t} \right) $, $ {\omega _1} $为一级中心频率. 根据上述方程, 可以通过干涉条纹所在的空间位置变化精确给出两束激光的相位差(延时)变化, 并以此为依据指导精密电机控制臂长变化.

若需要处理的离散信号个数为N, 使用离散傅里叶变换及逆变换的时间复杂度为N². 在实际使用中采样点数量通常较多, 较大的时间复杂度会极大的降低运算效率, 造成数据堆积, 并最终影响反馈锁定精度. 1965年, Cooley和Tukey^[21]利用傅里叶变化的周期对称性, 使用蝴蝶操作进行展开项合并, 将时间复杂度降低为$2 N{\log _2}N$量级, 大幅提高了运算效率, 被称为快速傅里叶算法. 该算法已在Labview等软件中得到广泛使用, 本文所述结果均基于快速傅里叶变换算法的主动反馈稳定系统.

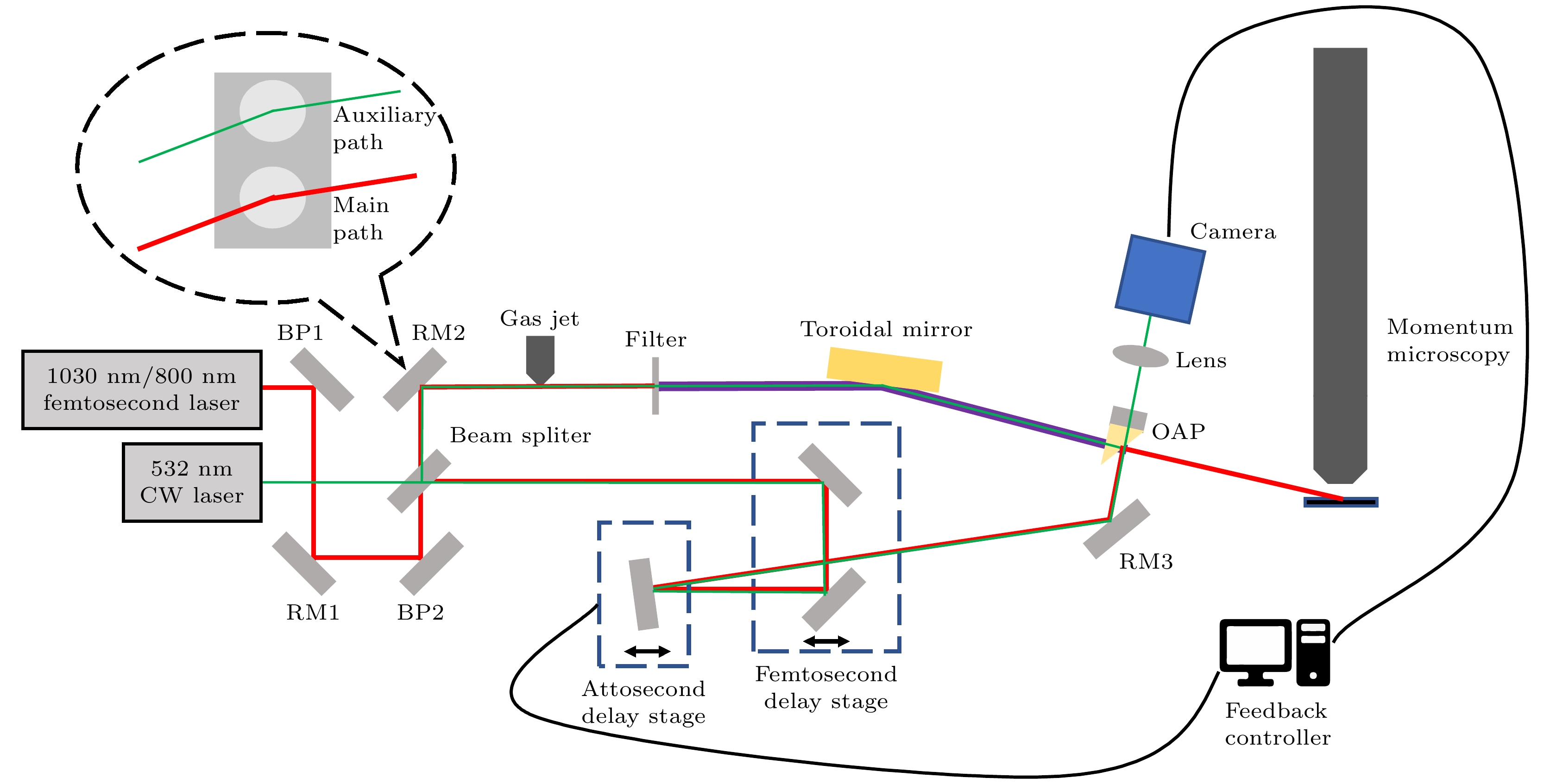
本实验开展于中国科学院物理研究所综合极端条件实验装置(synergetic extreme condition user facility, SECUF)阿秒激光实验站的时间分辨光电子显微镜终端, 图1为该终端系统的示意图. 所用驱动光源为一套高重频飞秒光学参量啁啾脉冲放大器(optical parametric chirped pulse amplification, OPCPA), 为满足不同的实验需求可选择输出中心波长850 nm、平均功率10 W、脉冲宽度10 fs、CEP稳定性优于200 mrad的飞秒激光或中心波长1030 nm、重复频率100 kHz、平均功率40 W、脉冲宽度250 fs的飞秒激光. 激光经过光束指向性锁定系统后, 被分束镜分为两路, 其中较强的一路作为探测光用来产生HHG, 使用金属膜过滤残留的基频光后由轮胎镜将HHG聚焦至样品处; 较弱的一路作为泵浦光用来激发待测样品, 激光经过定位精度分别为微米的直线位移台和亚纳米量级的压电陶瓷位移台(PZT)调节臂长, 可精确实现飞秒及亚阿秒量级的延时控制, 最终通过开孔的离轴抛物面镜(off-axis parabolic mirror, OAP)与HHG复合. 在上述泵浦探测系统中, 我们额外引入了平均功率50 mW、中心波长532 nm的连续光作为辅助激光, 用以实现泵浦光路与探测光路的精确锁定. 我们设计了一组光学元件夹持器, 将参考光路、主光路所需的各种光学元件分别上下放置并一同安装在镜架上, 使主激光及参考光在经过器件反射后基本保持平行, 从而实现参考光路与主光路在水平面上的投影完全重合, 仅在高度上与主激光光路分离. 在此状态下, 主激光与参考光可视为在同一光学元件的不同部位传输, 二者具有相同的光程抖动状态. 参考光在分束镜上方使用分束比为5∶5的分光片分为两束, 在主光路各器件的上层传输, 最终在OAP上方使用合束镜合束并反射出真空腔体.

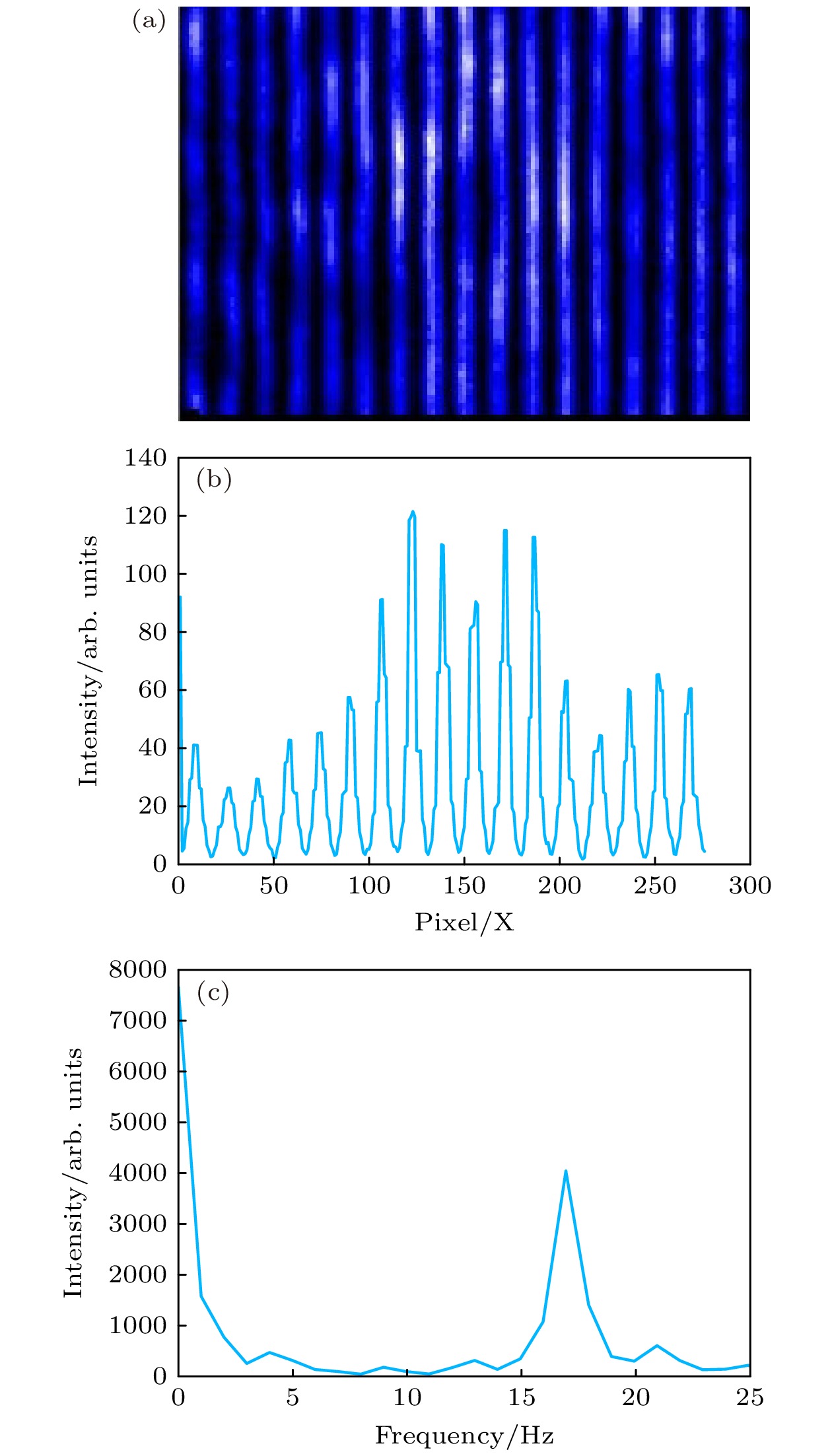
在真空腔外, 使用透镜将两束激光聚焦以保证两束光干涉, 在焦平面附近放置CCD实时采集干涉条纹图像, 并由计算机对采集到的图像信息进行快速处理. 对干涉条纹做纵向积分得到随时间变化的一维数组$f(x, {\text{ }}{\varphi _x}, {\text{ }}t)$, 使用快速傅里叶变换算法分析条纹抖动代表的相位差信息$\Delta {\varphi _x}$, 将该信息输入比例-积分-微分算法(proportion integration differentiation, PID)模块和PZT控制模块即可控制泵浦光路延迟线移动的距离. 通过优化干涉条纹选取区域、一级频率选取范围以及PID算法参数, 即可实现对相对延时的长时间锁定, 干涉条纹采集与反演结果如图2所示. 通过改变相位差$\Delta {\varphi _x}$的目标值可以实现阿秒量级的延时扫描功能, 由于这是直接以相位差为依据驱动PZT移动, 在实际实验中可以避免因PZT定位误差造成的延时变化误差, 从而获得更高的延时扫描精度.

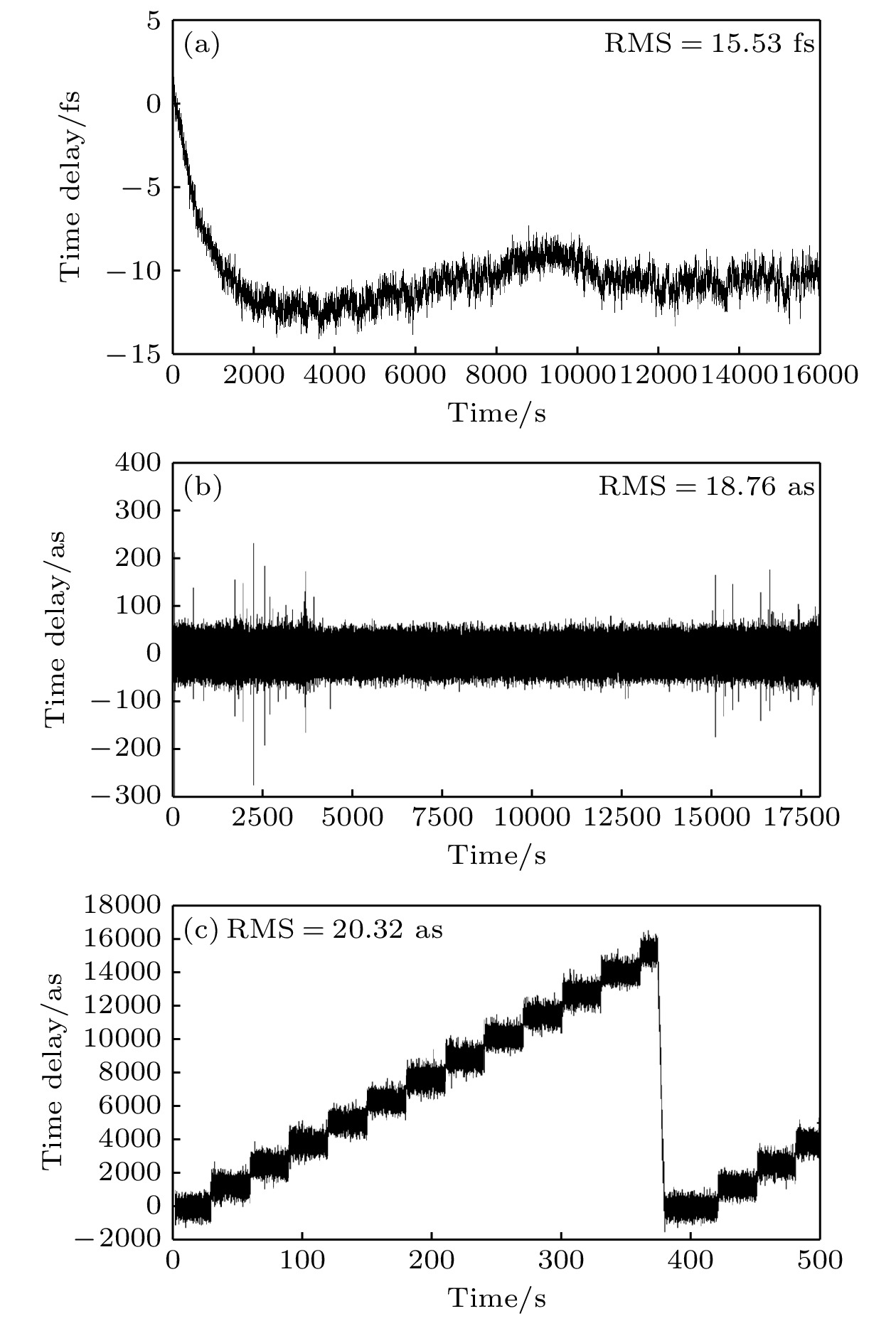
本系统在采集图像时使用尽可能短的积分时间以保证探测的准确性与反馈的及时性, 但受限于所用计算机(i5-8300h, Inter, USA)的性能、相机(OSG030-815UM, YVSION, CHN)的采集速度、PZT(P-752, PI, USA)的运动频率以及控制器(E-625, PI, USA)的相应时间, 反馈系统的工作频率最终设置为80 Hz. 在系统臂长为5 m的条件下, 图3(a)展示了未开启锁定时的延时抖动情况, 其延时抖动量可达15.53 fs; 图3(b)展示了开启锁定后的延时抖动情况, 在5 h的时间里其延时抖动量仅为18.76 as; 图3(c)展示了进行扫描时的延时抖动情况, 其延时抖动量仅为20.32 as, 且能实现高精度重复扫描. 该结果表明, 本文方案实现了臂长为5 m的泵浦-探测光路的阿秒量级稳定精度, 保障了高精度超快探测实验的可信度与准确性.

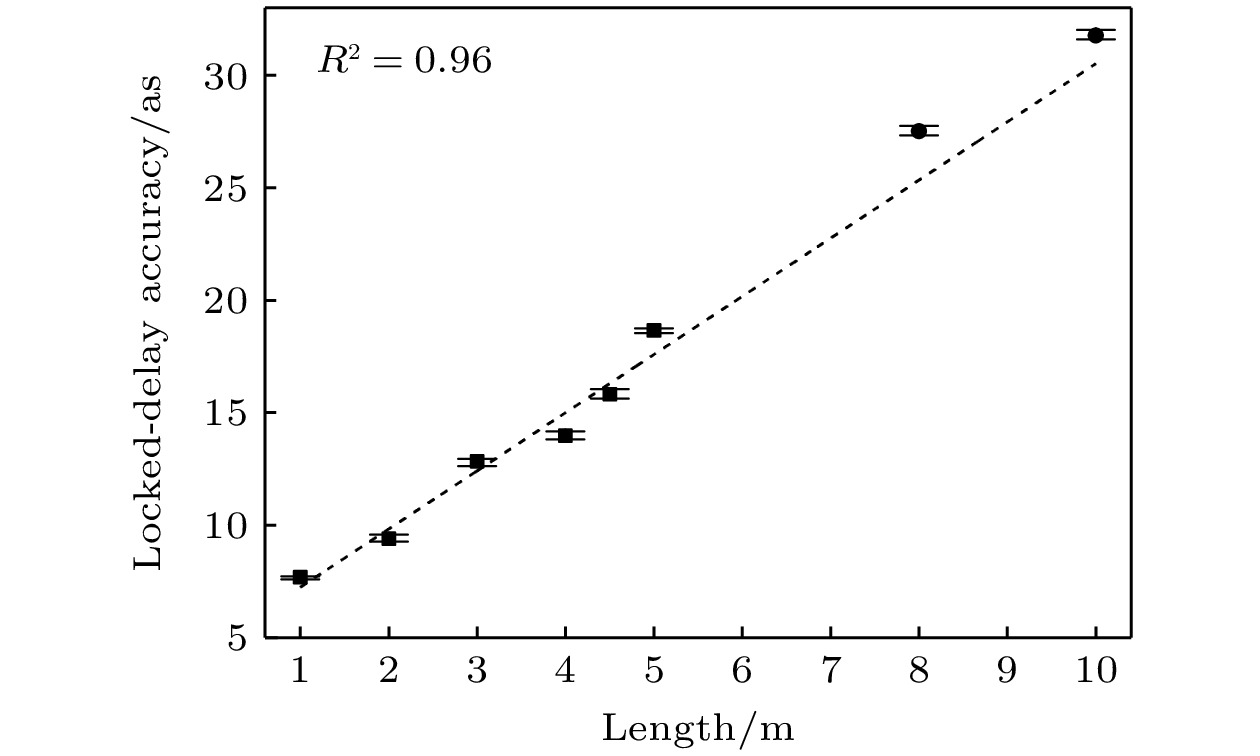
为了研究锁定精度与臂长的关系, 我们在相同实验条件下, 改变泵浦探测光路的臂长, 分别在臂长1 m, 2 m, 3 m, 4 m, 4.5 m及5 m条件下各进行了12次重复实验, 各臂长结果的均值如图4方形点所示, 极差由误差棒给出. 将不同臂长实验结果的均值进行锁定精度-臂长的拟合, 结果发现二者呈明显的线性相关, 线性拟合决定数R² = 0.96. 为了进一步验证上述结果, 以臂长分别为8 m, 10 m泵浦探测光路的锁定结果作为验证集与拟合公式进行对比, 锁定结果如图4圆形点所示, 极差由误差棒给出. 根据拟合公式推测, 当臂长为8 m, 10 m时, 锁定精度分别为25.36 as和30.53 as; 根据实验结果计算, 当臂长为8 m, 10 m时, 锁定精度均值分别为27.50 as和31.76 as. 这进一步印证了锁定精度与臂长之间存在线性相关——即在相同环境条件下, 使用短臂干涉光路得到的拟合曲线, 在长臂干涉光路上依旧适用. 因此, 在相同实验条件下使用短臂干涉仪可以实现对目标臂长锁定精度的预测, 也可作为探测器实现对环境因素影响锁定精度程度的快速检测.

本文发展了一种双层光路结构的泵浦探测光路, 通过对辅助光532 nm连续激光在泵浦探测光路中形成的干涉条纹抖动数据进行快速傅里叶变换, 计算出相对延时的相位抖动量, 使用自行编写的Labview程序反馈控制PZT位移, 快速准确 地补偿了阿秒泵浦探测系统中因机械震动、环境变化以及位移台回程差等因素引起相对延时的抖动, 最终在臂长5 m的泵浦探测系统中实现了工作频率80 Hz、延时锁定精度为18.76 as的锁定结果, 保证了泵浦探测实验结果的准确性与可信度; 在 此基础上改变泵浦探测光路的臂长, 通过对比臂长1—5 m的锁定结果, 发现锁定精度-臂长呈决定系数R² = 0.96的强线性相关关系, 且在臂长8 m, 10 m的对比实验中得到较好的验证.

上述结果表明, 利用快速傅里叶变换算法的延时反馈控制装置具有响应速度快、控制精度高的优点, 可以实现阿秒量级的相对延时稳定性, 这对于原子尺度的阿秒时间分辨电子动力学过程探测具有重要意义. 本文验证了利用短臂长干涉仪得到的锁定结果可以实现对长臂长干涉仪的较高精度预测, 可以对在当前环境下实现目标精度的可行性做快速预估, 有利于在大科学装置中长距离泵浦探测光束线的建设.