-
自旋电子学同时利用了电子的电荷和自旋, 在过去的几十年中, 由于其低能耗、高运算速度和高存储密度引起了人们的广泛关注[1-3]. 二维多铁材料由于其低功耗、高集成、高信息密度、可调控磁弹性等特性, 对下一代自旋电子器件的微型化与功能化具有重要意义[4-7]. 然而, Mermin-Wagner定律表明在有限温度下热扰动将导致低维材料磁有序退化[8], 即二维材料中不可能存在长程磁有序. 2017年Huang等[9]首次使用机械剥离法在实验上成功制备了范德瓦耳斯铁磁单层CrI3, 并且证明了磁晶各向异性能可以抵消热扰动带来的无序性, 在二维材料中实现了长程磁有序[10]. 这一发现激发了人们预测及合成更多二维磁体的研究热情. 需要注意的是, 大多数二维铁磁材料的居里温度极低, 单层CrI3为45 K[9], 双层Cr2Ge2Te为30 K[11], 这严重限制了二维铁磁材料在实际器件中的应用. 另外, 二维铁磁材料自旋方向的调控同样重要, 研究者们通常通过外部条件实现调控, 如引入外部电场与应力场、界面耦合、介电屏蔽等[12-15], 这些操作都不利于降低能耗.
多铁性集成了两种或多种主要铁性[16], 包括铁电性[17]、铁磁性/反铁磁性[18-20]和铁弹性[14], 提供了通过改变一种类型铁性来操纵另一种类型铁性的独特机会, 为调控二维铁磁材料的自旋方向提供了新机制. 根据d0规则, 铁磁性/反铁磁性经常与部分填充的d/f轨道相关, 而铁电性需要空的d/f轨道. 因此, 结合铁磁性/反铁磁性和铁电性的多铁性材料很少被报道. 幸运的是, 铁弹性不需要空的d轨道, 其与铁磁性/反铁磁性完全兼容. 整合铁弹性与铁磁性会导致磁弹耦合, 应力诱导平面内晶格结构90°旋转, 即铁弹性切换, 可用于操纵平面内易磁化轴的方向[21]. 同时具有铁磁性、铁电性与铁弹性的多铁单分子层MnOF[5], 可以实现铁磁、铁弹、铁电的相互耦合控制. 多铁耦合机制使得材料在机械开关、形状记忆与非易失性存储器件中具有重要的应用价值.
层状三元过渡金属卤化物具有丰富的物理性质, NiOX (X = Cl, Br)[22]具有铁磁性与铁弹性; CrOCl[23]被成功制备, 且具有显著光学各向异性的反铁磁体; VSeF是双极铁磁半导体[24]; VSCl[25]同时具有铁磁性与谷极化特性[25]; VOF是具有铁磁性和铁电性的多铁半导体材料[26]; MnOX (X = Cl, Br)[27], MnNX (X = F, Cl, Br, I)[28], CrSCl[29]被证明同时表现出铁磁性和铁弹性, 并且具有磁弹耦合效应; MnOF[5]和CrNCl[30]是结合三种铁性的多铁材料, 包括铁磁性、铁电性和铁弹性; Zeng等[31]通过化学气相沉积方法成功制备的FeOCl是具有显著面内磁晶各向异性的二维反铁磁半导体; Gu等[32]证明了剥离的少层CrOCl能保持反铁磁性且拥有磁弹耦合效应. 以上研究证实了层状三元过渡金属卤化物作为多铁材料的潜力. 同时, 二维四方结构的CrOCl的成功制备[23]也使得其他同结构材料具有成功制备的可能. 由此激发了在二维四方结构中寻找本征磁弹耦合材料的兴趣, 我们对MnOF母体进行了元素替换, 得到的单分子层MoTeX (X = F, Cl, Br, I)具有自发结构极化, 且Mo元素半填充的3d轨道使其具有大磁矩, 是潜在的具有磁弹耦合性质的二维材料.
本文通过第一性原理计算深入地研究了单分子层MoTeX (X = F, Cl, Br, I)的稳定性、电子结构、铁磁性以及铁弹性. 计算结果表明单分子层MoTeX是同时具有铁磁性和铁弹性的多铁半导体. MoTeF, MoTeCl, MoTeBr, MoTeI的磁各向异性能分别为0.782 meV, 0.613 meV, 0.430 meV, 0.447 meV, 面内磁晶各向异性显著. 较高的磁晶各向异性能表明MoTeX能抵抗一定温度下热扰动引起的磁无序性, 保持长程磁有序. MoTeX较高的居里温度有利于之后实验研究的开展. 此外, 证明了铁弹性转换将反转MoTeX的平面内易磁化轴方向. 我们的发现不仅为应变可控磁性纳米器件的应用提供了新的候选材料, 并且为寻找二维多铁性材料提供了新途径.
-
本工作中所有的第一性原理计算均使用基于密度泛函理论和投影增强波(projected augmented wave, PAW)[33]方法的VASP[34]软件进行. 使用Perdew-Burke-Ernzerhof (PBE)[35]版的广义梯度近似方法描述电子交换关联相互作用. 为了减少自交互误差, 本工作采用了有效的Hubbard U 修正值(Ueff = 4 eV). 使用13×9×1 Monkhorste-Pack[36]对第一布里渊区进行采样. 截断能设置为500 eV, 能量和力的收敛标准分别设置为10–7 eV和0.01 eV/Å. 另外, 增加厚度为20 Å的真空层以消除层与层之间的相互作用. 利用密度泛函微扰理论(density-functional perturbation theory, DFPT)计算声子色散以研究晶体结构的动力学稳定性, 该理论使用Phonopy程序包中实现[37,38]. 从头算分子动力学模拟(ab initio molecular dynamics, AIMD)采用正则系综, 使用Nosé-Hoover温控机制, 在300 K温度下模拟退火5 ps 来研究热力学稳定性. 基于Mcsolve软件对32×32×1的超胞进行了蒙特卡罗(Monte Carlo, MC)模拟, 以获得基于海森伯模型的居里温度.
-
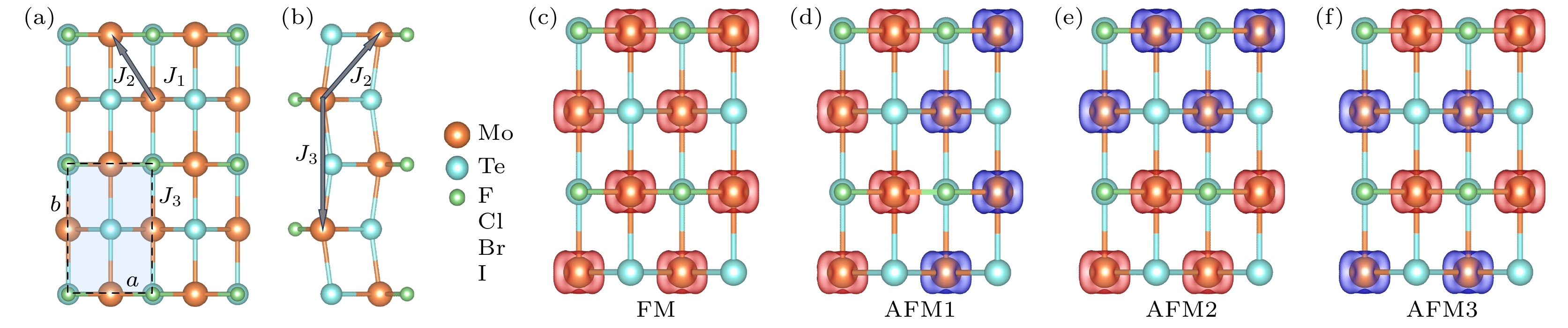
图1(a)展示了几何结构优化后单分子层MoTeX (X = F, Cl, Br, I)的原子结构. MoTeX属于Pmmn (No. 49)空间群, 单胞内有6个原子. 其晶体结构与MnOF, CrOCl, CrSBr, NiOBr等二维材料的结构类似, MoTe组成的网格状结构被夹在两层卤素原子X之间. MoTeX的晶格常数与键长如表1所列, 沿x方向的晶格常数小于沿y方向的晶格常数, 表明MoTeX有自发结构极化的潜力.
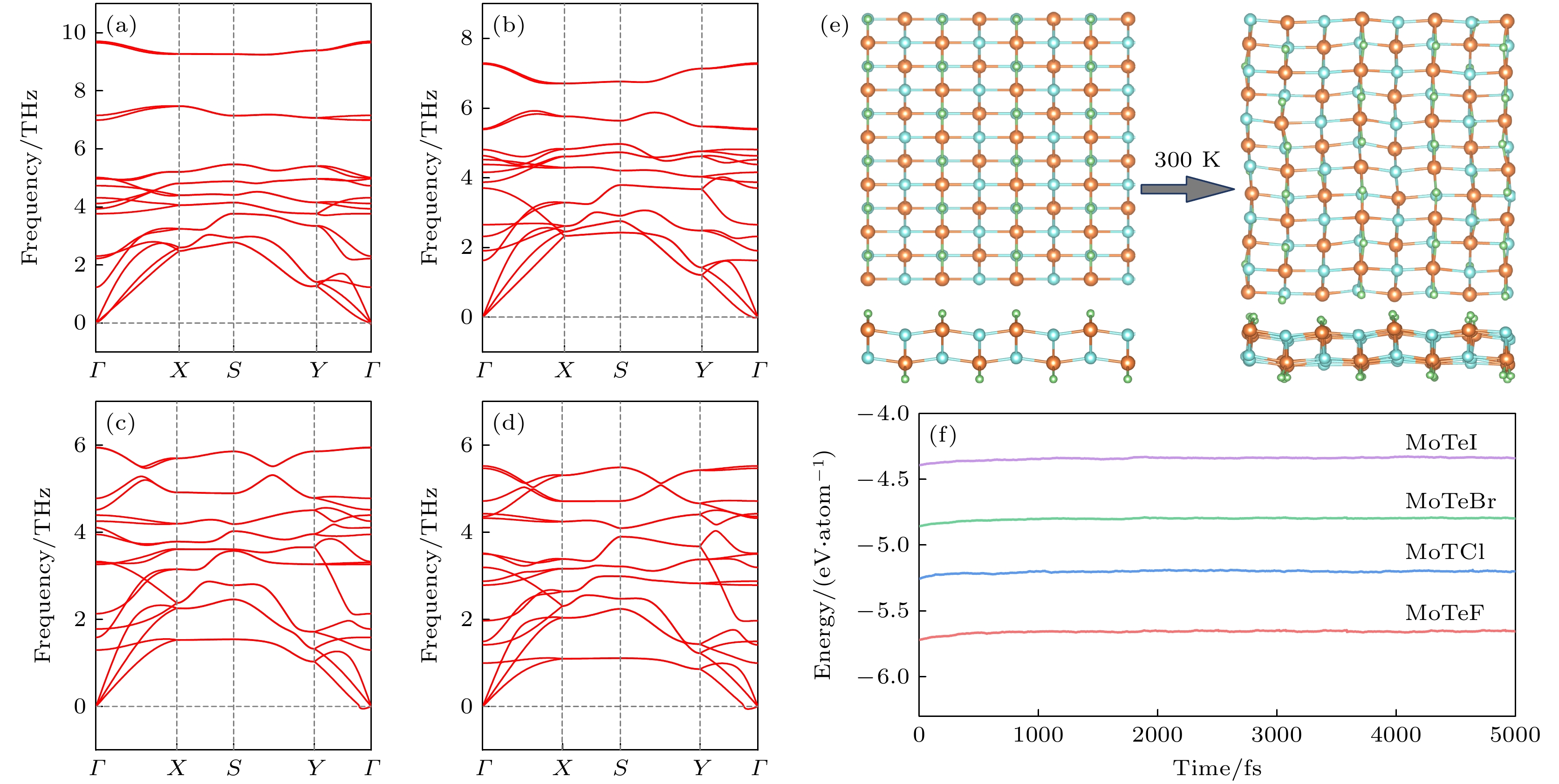
为了验证单分子层MoTeX的动力学稳定性以及力学稳定性, 计算了MoTeX的声子谱和弹性常数. 如图2(a)—(d)所示, MoTeF与MoTeCl的声子谱在整个布里渊区内没有虚频, MoTeBr与MoTeI的声子谱仅在Γ点附近出现极小虚频, 以上计算结果证实了MoTeX的动力学稳定性. 为了进一步验证其热稳定性, 构建了32×32×1的超胞, 对其进行AIMD模拟. 从图2(e)可以看出, 模拟过程中MoTeX的化学键没有断裂, 也没有发生几何重构现象. 另外, MoTeX的能量在模拟过程中稳定波动. 以上结果表明单分子层MoTeX具有优异的热力学稳定性.
此外, 通过计算单分子层MoTeX的弹性常数以考察其机械稳定性, 计算结果如表2所列. 所有MoTeX的弹性常数均满足Born-Houng力学稳定性判据[39], 即
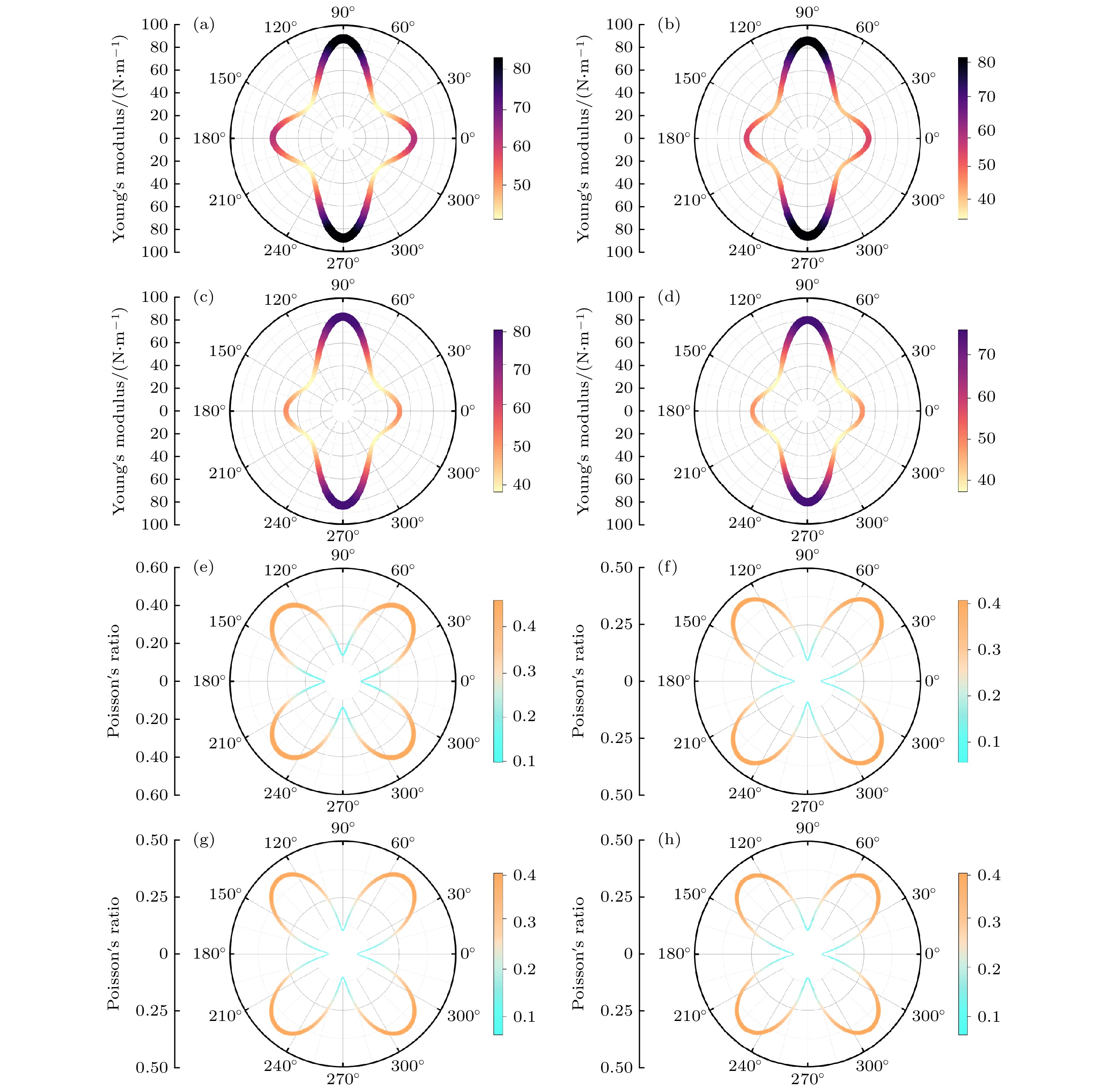
$ {C}_{11} > 0 $ ,$ {C}_{22} > 0 $ ,$ {C}_{66} > 0 $ ,$ {C}_{11}{C}_{22}- {C}_{12}^{2} > 0 $ , 表明MoTeX具有力学稳定性. 二维弹性模量可描述单分子层MoTeX力学性质的各向异性. 面内杨氏模量与泊松比作为面内角度θ(相对于x正方向的角度)的函数可以描述为其中,
$ \varDelta = {C_{11}}{C_{22}} - C_{12}^2 $ ,$ c= \cos\theta $ ,$ s=\sin\theta$ [39].图3展示了MoTeX的杨氏模量与泊松比随θ的变化. 从图3可以看出, MoTeX的杨氏模量和泊松比在整个平面内均具有显著的各向异性, 且[010]方向的杨氏模量明显大于[100]方向. 另外, 依据泊松比, MoTeX最脆性的方向为[100]方向, 而最韧性的方向为[110]方向. 杨氏模量与泊松比的极值可参考表2. 根据以上计算, 单分子层MoTeX具有高动力学稳定性、热稳定性和机械稳定性, 且力学性能优异.
-
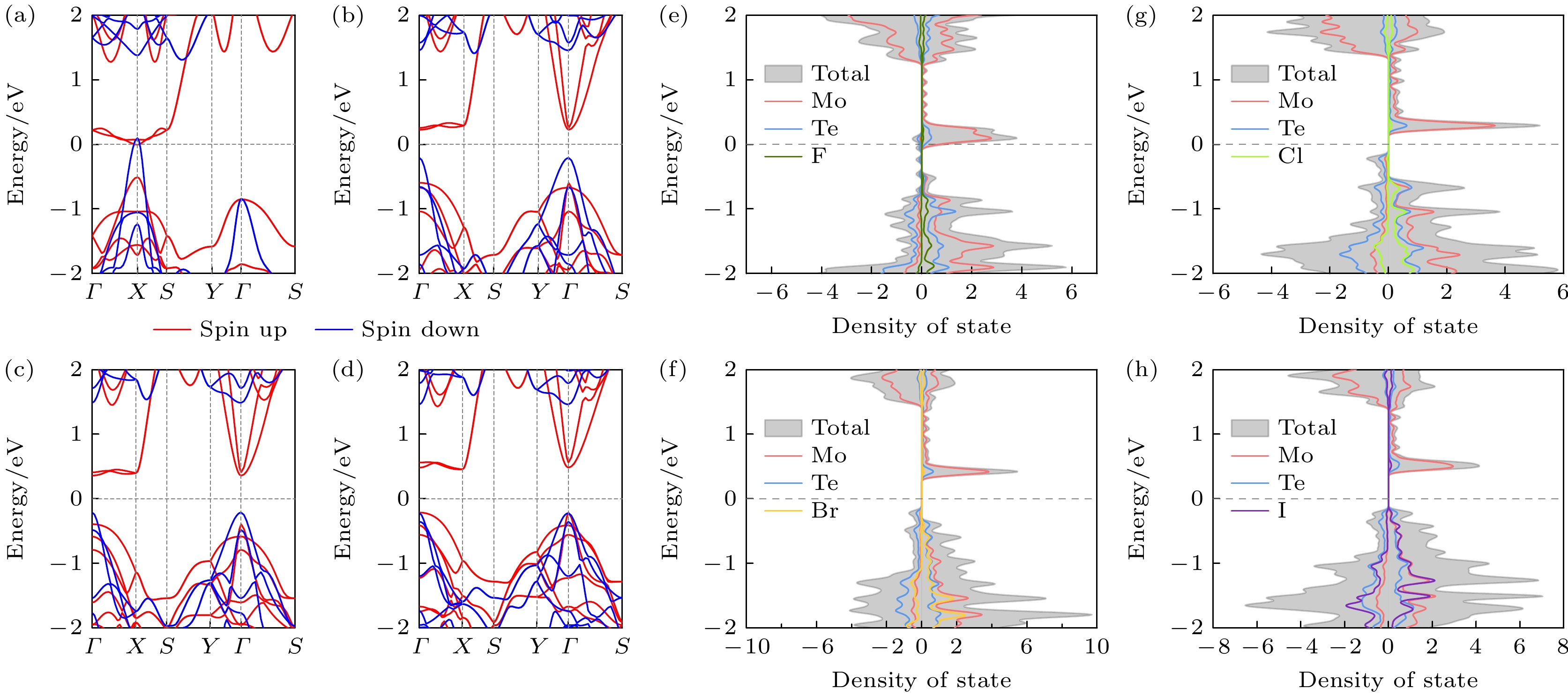
为了探究单分子层MoTeX的电子性质, 计算了其自旋极化能带结构. 图4(a)—(d)展示了基于PBE+U (U = 3.0 eV)方法计算得到的MoTeX的电子能带结构. 除了MoTeF表现出金属特征外, MoTeCl, MoTeBr, MoTeI均为半导体. 另外, MoTeCl, MoTeBr, MoTeI自旋向上通道的带隙为0.823 eV(直接带隙), 0.752 eV(直接带隙), 0.679 eV(间接带隙), 自旋向下通道的带隙则为1.622 eV, 0.702 eV, 1.685 eV. 自旋向上与自旋向下通道带隙之间存在显著差别, 可以提供长距离的自旋极化电流且可以有效地防止自旋翻转, 是自旋注入的理想材料.
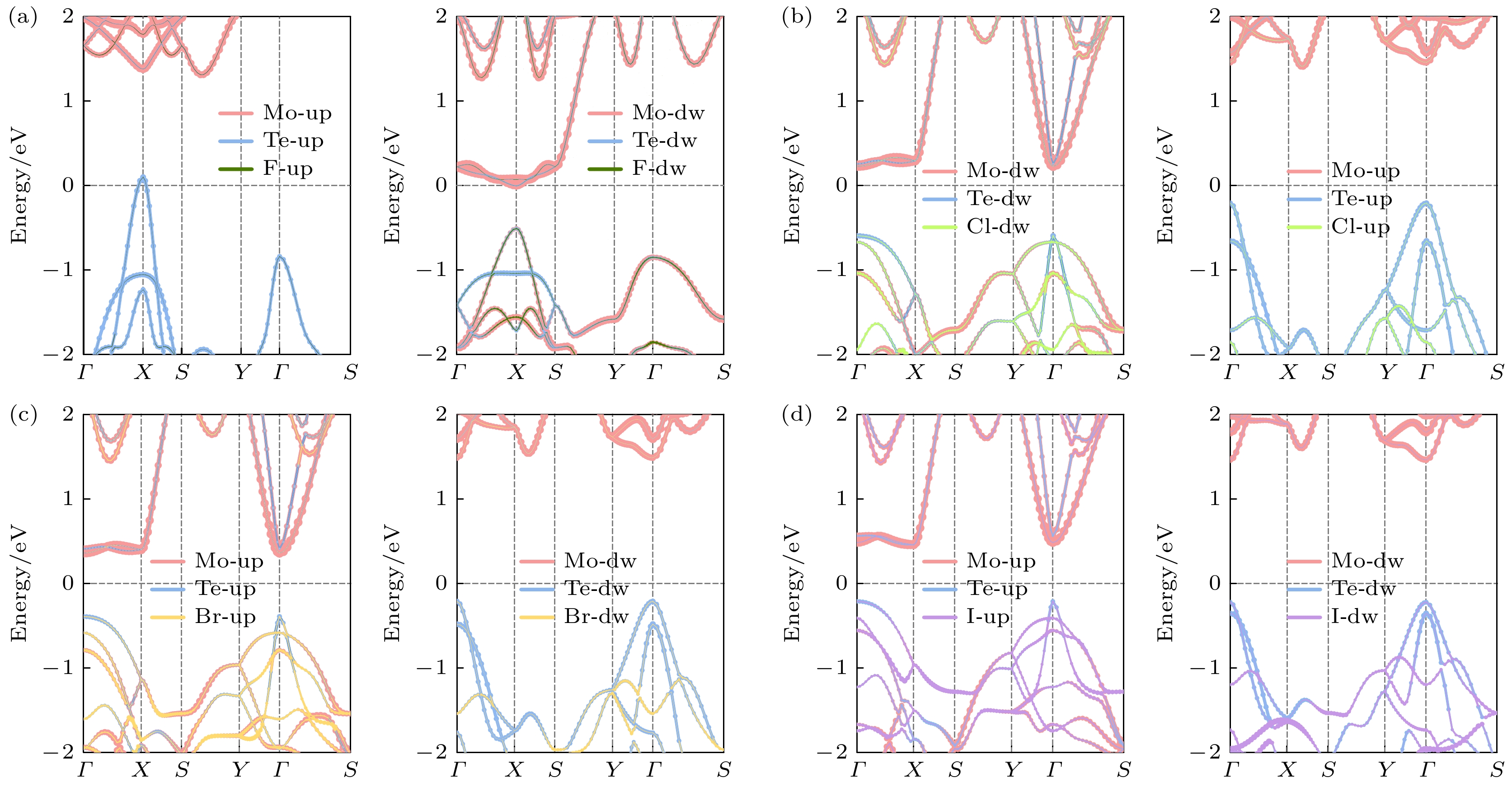
图4(e)—(g)中展示了单分子层MoTeX的态密度图, 以MoTeF为例, 左侧为自旋向下态密度, 右侧为自旋向上态密度. 费米能级之上存在明显局域化现象, 该部分态密度主要来自于Mo原子的4d轨道, Te原子的p轨道对这部分态密度同样有贡献, 且二者存在明显的耦合现象, 以上结果表明Te原子参与了Mo原子之间的磁交换作用. 同时自旋向上与自旋向下的态密度明显不对称, 再次说明MoTeX拥有铁磁性. 图5(a)—(d)展示了MoTeX的投影态密度图, 同样可以看出Mo原子与Te原子的态密度局域在在费米能级附近. 研究结果表明, 单分子层MoTeX是自旋电子器件的理想候选材料, 如自旋过滤器和自旋阀.
-
首先计算MoTeX的磁基态. 如图1(c)—(f)所示, 采用2×2×1超胞构建了四种不同的磁构型, 包括铁磁构型和三种反铁磁构型. 计算结果表明, 相比于反铁磁构型, 铁磁构型的总能量最低, 因此MoTeX的磁基态为铁磁态. 另外, MoTeX的磁矩主要由Mo(4d55s1)原子提供, 每个Mo原子可提供3μB的磁矩. 当Mo原子与Te原子成键时, Mo原子失去三个电子变成具有4d3电子的Mo3+, 三个电子占据不同的d轨道, 使得Mo原子的磁矩为3μB.
根据 Goodenough-Kanamori-Anderson规则[40,41], 利用超交换相互作用来分析单分子层MoTeX的磁交换机理, 解释其磁性起源. 最近邻Mo原子的距离为3.70—4.12 Å, 因此直接交换作用不能被忽略. 从表3中可以看出, MoTeX中Mo—Te—Mo的夹角均接近于90°, 有利于MoTeX中的铁磁超交换耦合. 直接交换作用使得两个磁性原子的磁矩反平行, 超交换作用则使它们倾向于平行排列. 随着磁性原子之间距离的增加, 直接交换作用的衰减速度要快于超交换作用, 因此
$ {J}_{2} $ >$ {J}_{1} $ . 第三近邻的Mo与Te原子间存在180°的夹角, 交换作用结果使得两个Mo原子的磁矩反平行排列.采用基于Heisenberg模型的MC模拟来获取单分子层MoTeX的TC. 自旋哈密顿量可以表示为
其中
$ {J}_{1} $ ,$ {J}_{2} $ 和$ {J}_{3} $ 分别表示第一、第二和第三近邻Mo原子的磁交换常数;$ {S}_{i} $ 和$ {S}_{j} $ 分别表示i和j位置处Mo原子的自旋磁矩; D为单个Mo离子的 磁各向异性能;$ {S}_{i}^{{\mathrm{e}}} $ 为沿易磁轴的自旋力矩. 为了 确定磁交换常数, 将上述四种磁构型的总能量表示为式中,
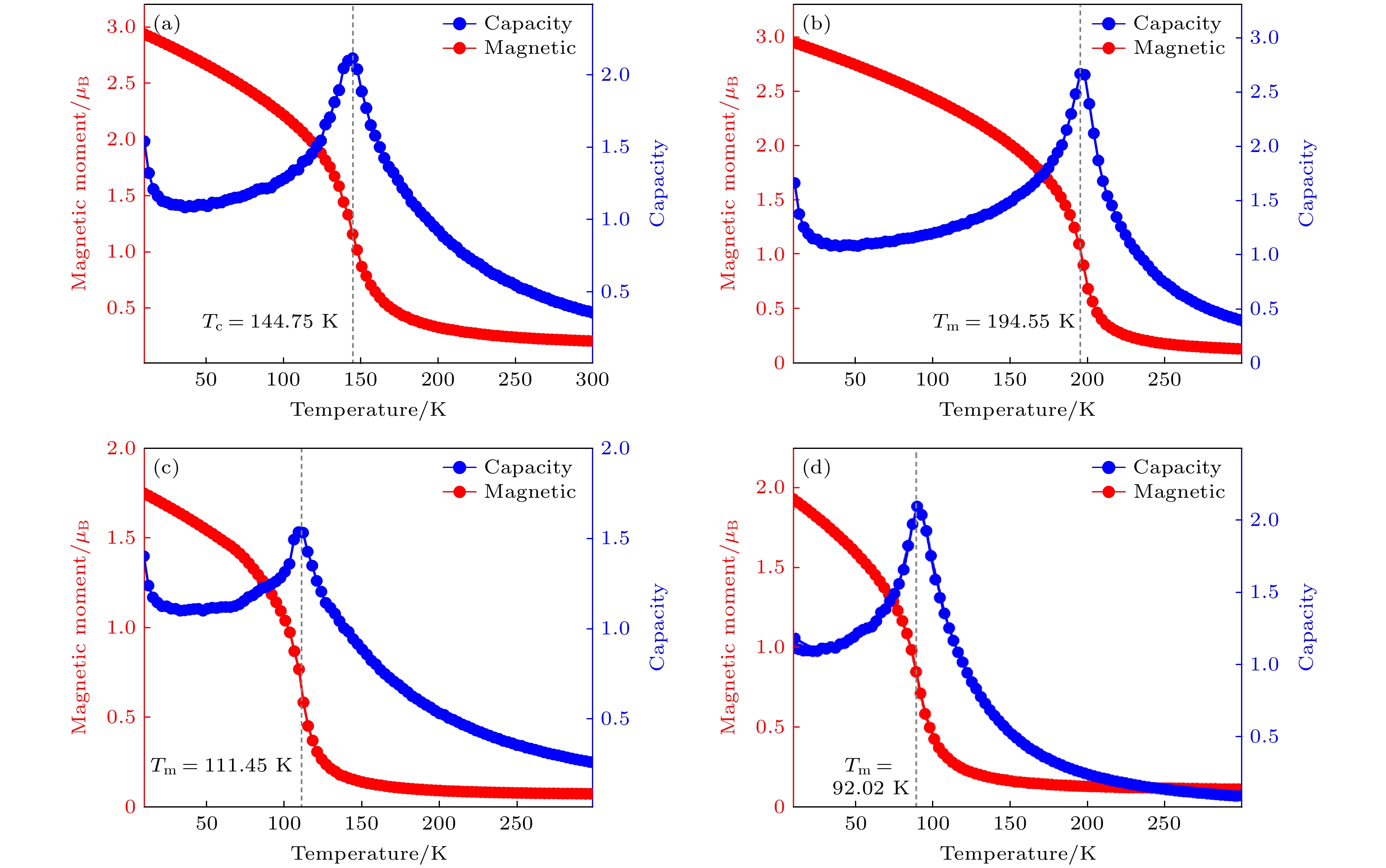
$ {E}_{0} $ 是基态能量, 不依赖于磁构型. 通过求解(4)式—(7)式, 得到了MoTeX的三个磁交换耦合参数$ {J}_{1} $ ,$ {J}_{2} $ 和$ {J}_{3} $ , 如表4所列. 其中$ {J}_{1} $ ,$ {J}_{2} $ 均为正值, 且各自的绝对值明显大于$ {J}_{3} $ , 表明MoTeX的铁磁性.图6(a)—(d)展示了MoTeX的磁矩和比热容随温度的变化. 当磁矩和比热容接近峰值位置时, 此时的温度为居里温度(TC). 我们的计算表明, MoTeX (X = F, Cl, Br, I)的居里温度分别为144.75 K, 194.55 K, 111.45 K, 92.02 K, 远远高于 CrI3单层(45 K)[9], Cr2Ge2Te6双层(30 K)[11], Fe3GeTe2单层(130 K)[42], CrOCl单层 (160 K)[43]. 较高的TC证明了MoTeX的铁磁基态能在有限温度下保持稳定, 放宽了实验验证及实际应用的条件.
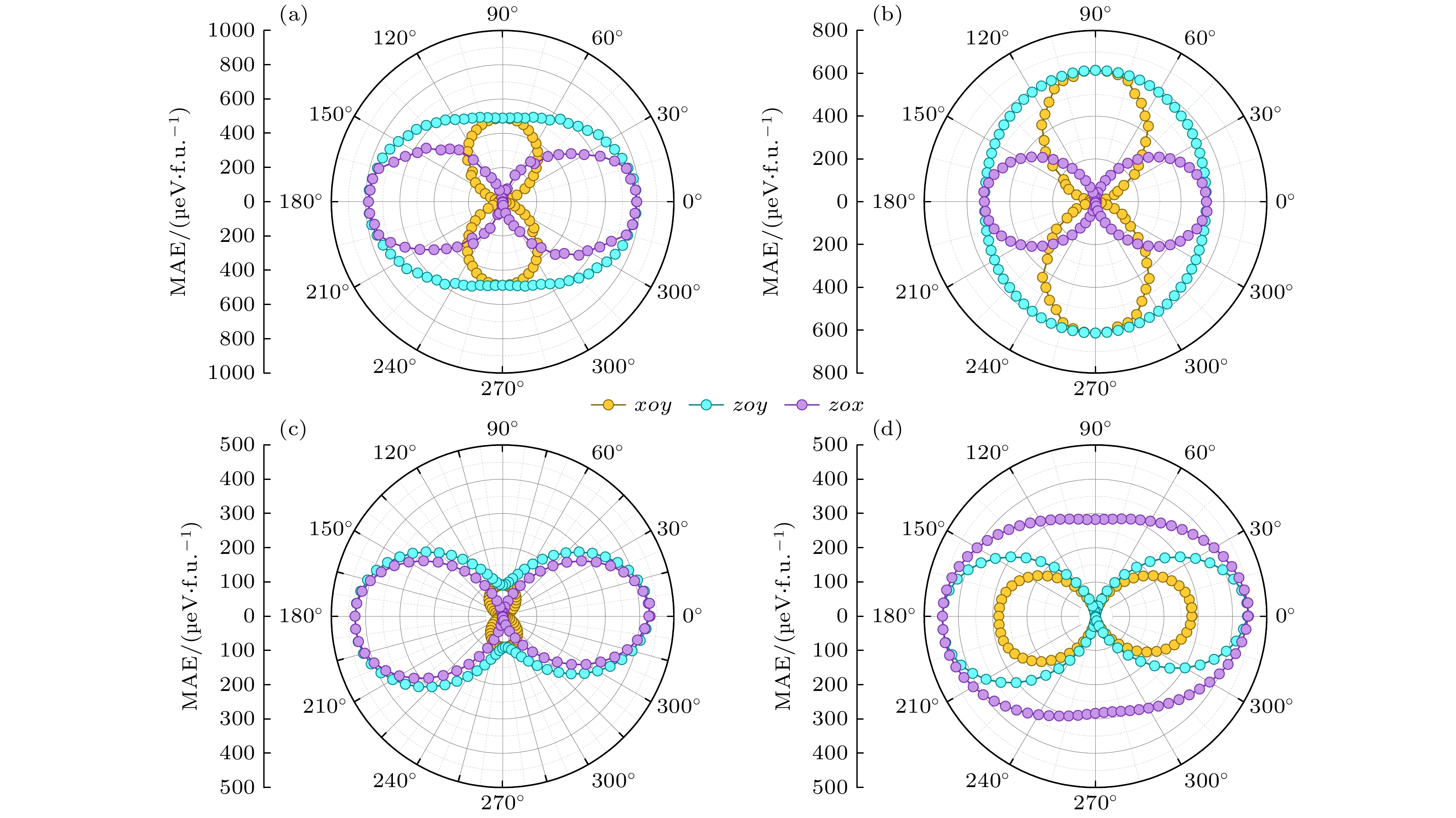
磁晶各向异性能(magnetic anisotropy energy, MAE)是影响二维磁性材料长程磁序稳定性的重要参数. MAE由自旋轨道耦合(spin-orbit coupling, SOC)效应导致, 具有强SOC效应的材料通常具有较高的MAE, 例如含有重金属元素的二维磁性材料EuGe2[44], 其MAE为3.62 meV/f.u. 我们考虑了自旋-轨道耦合效应, 计算了MoTeX单层的MAE. 图7展示了MoTeX单层的MAE相对于沿着xoy平面的极角φ以及沿着yoz和zox平面的方位角θ的变化. MoTeF, MoTeCl以及MoTeBr的易磁化轴沿[100]方向, 而MoTeI的易磁化轴沿[010]方向. 另外, 如表4所列, MoTeX (X = F, Cl, Br, I)的MAE分别为0.782, 0.613, 0.430与0.282 meV/atom, 这远高于MnOF (0.118 meV/atom)[5]和CrSCl (0.097 meV/atom)[29]. MoTeX较大的MAE有助于抵抗热波动, 保持铁磁有序性. 另外, 较大的面内MAE也为通过控制铁弹相切换来旋转面内易磁化轴提供了可能性.
-
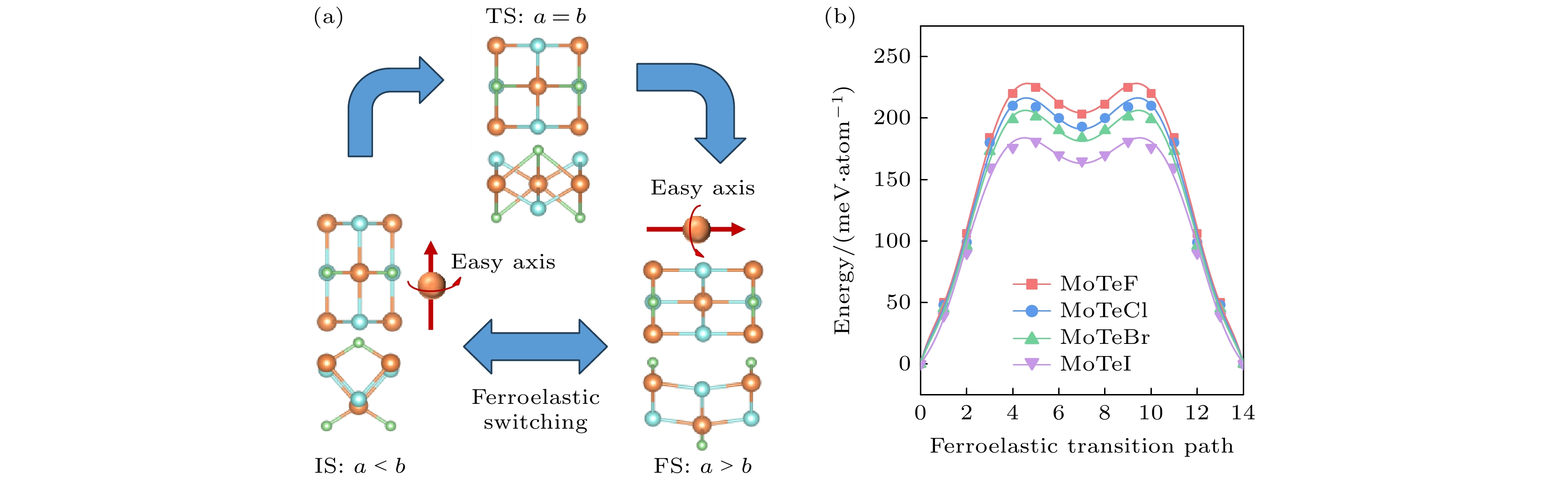
由于四重旋转对称的破缺, 单分子层MoTeX(X = F, Cl, Br, I)在xy平面上表现出各向异性以及二维铁弹性. 为了研究MoTeX的铁弹相变, 采用Cl-NEB方法[45,37]计算了相变路径和能垒. 如图8(a)所示, 初始态 (initial state, IS)在xy平面上旋转90°转变为终态(final state, FS), 其晶格常数同时旋转90°. 在整个铁弹相变过程中, 我们首先对IS施加沿y轴的压缩应变和沿x轴的拉伸应变, 使其转变为中间态, 即具有四重旋转对称性的方形过渡态(transition state, TS). 对TS继续沿y轴施加压缩应变和沿x轴施加拉伸应变, TS转换为FS, 相当于使IS结构旋转90°. 如图8(b)所示, MoTeX (X = F, Cl, Br, I)的铁弹相变能垒分别为0.180, 0.200, 0.209与0.226 eV/atom. MoTeX的铁弹势垒低于二维铁弹体BP5 (0.32 eV/atom)[46], 同时又高于FeO2H (54 meV/atom)[16], TcOBr (77 meV/atom)[47], 与GaTeCl(159 meV/atom)[48]. 该中等铁弹能垒为室温下可逆铁弹转变提供了可能性. 此外, 还计算了MoTeX的可逆铁弹应变, 定义为
$ \left|a\right|/\left|b\right|-1\times 100{\text{%}}$ . 计算结果表明, MoTeX的可逆铁弹性应变分别为54.58%, 46.32%, 43.06%与38.12%, 与BP5 (41.1%)[46]和磷烯(37.9%)相近.在Green-Lagrange应变张量[49]的基础上, 铁弹相变的变换应变矩阵可表示为
其中I为2 × 2的单位矩阵,
$ {\boldsymbol{H}}_{{\mathrm{I}}} $ 和$ {\boldsymbol{H}}_{{\mathrm{T}}} $ 分别为始态IS和中间态TS的弹性状态矩阵. 以MoTeI为例, MoTeI单层的$ {\boldsymbol{H}}_{{\mathrm{I}}} $ 和$ {\boldsymbol{H}}_{{\mathrm{T}}} $ 分别为$ \left( \begin{array}{c}4.62\\0\end{array}\right.\left.\begin{array}{c}0\\4.62\end{array} \right) $ 和$ \left( \begin{array}{c}4.12\\0\end{array}\right.\left.\begin{array}{c}0\\5.69\end{array} \right) $ .计算得到MoTeI的
$ \boldsymbol{\eta } $ 为$ \left(\begin{array}{c}-0.10\\0\end{array}\right.\left.\begin{array}{c}0\\0.25\end{array}\right) $ , 表明始态IS相比于中间态TS在a方向产生了10%的压缩应变, b方向产生了25%的拉伸应变. MoTeF, MoTeCl, MoTeBr的弹性转换矩阵分别为$ \left( \begin{array}{c}-0.11\\0\end{array}\right. \left.\begin{array}{c}0\\0.42\end{array} \right), \left( \begin{array}{c}-0.08\\0\end{array}\right. \left.\begin{array}{c}0\\0.38\end{array} \right), \left( \begin{array}{c}-0.11\\0\end{array}\right. \left.\begin{array}{c}0\\0.28\end{array} \right) $ , 在外加应变作用下, MoTeX可以在两种磁弹态之间发生可逆转换. MoTeX体系具有本征铁磁性与铁弹性, 且两个铁弹态的易磁化轴在xoy面内相互垂直, 外力作用下两个铁弹态之间发生转换时, 易磁化轴也会相应旋转. 意味着可以通过外部应变来调制MoTeX的易磁化轴方向. 这一特性可被用于设计新型磁性存储器, 可通过施加应变而非传统的电流或磁场来实现数据的写入和读取, 从而降低功耗, 提升存储密度. -
本文基于第一性原理计算研究了二维本征多铁性半导体MoTeX (X = Cl, Br, I)的稳定性、电子结构、铁磁性与铁弹性. MoTeX (X = F, Cl, Br, I)的居里温度分别为144.75, 194.55, 111.45 K, 其磁晶各向异性能表明MoTeX能在有限温度下维持长程磁有序. MoTeX适中的铁弹能垒为室温下的可逆铁弹转换提供了可能性. 另外, MoTeX在铁弹转变过程中表现出具有相同幅度但符号相反的平面内磁各向异性能, 意味着面内易磁化轴随铁弹态的转换旋转了90°, 表现出磁弹耦合性质. 该工作为研究二维多铁材料提供了新途径, 并为下一代应变可控磁性纳米器件提供了新候选材料.
具有磁弹耦合的本征多铁半导体: 单分子层MoTeX (X = F, Cl, Br, I)
Intrinsic multiferroic semiconductors with magnetoelastic coupling: two-dimensional MoTeX (X = F, Cl, Br, I) monolayers
-
摘要: 同时具有铁磁性与铁弹性的二维材料为磁性控制提供了全新机制, 即通过切换材料的铁弹态控制磁化方向. 源自半填充3d轨道的大磁矩和自发结构极化, 使单分子层MoTeX (X = F, Cl, Br, I)成为潜在的磁弹性多铁材料. 本文基于第一性原理计算, 系统地研究了单分子层MoTeX (X = F, Cl, Br, I)的铁磁性、铁弹性以及磁弹耦合性质. 计算结果表明单分子层MoTeX为本征半导体, 同时具有铁磁性和铁弹性. 单分子层MoTeX的面内磁晶各向异性能显著, 较高的磁晶各向异性能表明其具有抵抗热扰动的能力, 能在有限温度下维持长程磁有序. 另外, 单分子层MoTeX的易磁化轴均沿着平面内方向. 单分子层MoTeX在铁弹性转变过程中表现出相同幅度但符号相反的平面内磁各向异性能, 意味着面内易磁化轴随铁弹态的转换旋转了90°. 另外, 其铁弹转换势垒(0.180—0.226 eV/atom)适中, 表明单分子层MoTeX在室温下的可逆铁弹性转换和平面内易磁化轴的可逆转换. 本文提出了一种二维本征多铁半导体材料, 为多功能自旋电子器件提供了新候选材料.Abstract: Two-dimensional materials with both ferromagnetism and ferroelasticity present new possibilities for developing spintronics and multifunctional devices. These materials provide a novel method for controlling the direction of the magnetization axis by switching the ferroelastic state, achieving efficient and low-power operation of magnetic devices. Such properties make them a promising candidate for the next generation of non-volatile memory, sensors, and logic devices. By performing the first-principles calculations, the ferromagnetism, ferroelasticity, and magnetoelastic coupling in MoTeX (X = F, Cl, Br, I) monolayers are systematically investigated. The results indicate that the MoTeX monolayers are intrinsic semiconductors holding both ferromagnetism and ferroelasticity. The pronounced in-plane magnetic anisotropy suggests that the MoTeX monolayers can resist thermal disturbances and maintain long-range magnetic order. The Curie temperatures of MoTeX monolayers are 144.75 K, 194.55 K, 111.45 K, and 92.02 K, respectively. Our calculations show that the four MoTeX monolayers possess two stable ferroelastic states, with their easy magnetization axes perpendicular to each other. The ferroelastic transition barriers between the two ferroelastic states of MoTeF, MoTeCl, MoTeBr, MoTeI monolayers are 0.180 eV/atom, 0.200 eV/atom, 0.209 eV/atom, and 0.226 eV/atom, respectively, with their corresponding reversible strains of 54.58%, 46.32%, 43.06%, and 38.12%. These values indicate the potential for reversible magnetic control through reversible ferroelastic transition at room temperature. Owing to their unique magnetoelastic coupling properties, MoTeX monolayers exhibit the ability to control reversible magnetization axis at room temperature, laying the foundation for the development of highly controllable and stable spintronic devices.
-

-
图 1 MoTeX (X = F, Cl, Br, I)单层膜的顶视图(a)和侧视图(b). J1, J2和J3分别是最邻近的第一、第二和第三个Mo原子之间的层内磁交换参数; (c)铁磁(FM)俯视图; (d)— (f) MoTeX单层膜的三种反铁磁(AFM)构型. 橙色、蓝色和绿色的球分别代表Mn, O和X原子
Figure 1. (a) Top and (b) side views of the MoTeX (X = F, Cl, Br, I) monolayers. J1, J2 and J3 are the intralayer magnetic exchange parameters between the first, second and third nearest neighboring Mo atoms, respectively; (c) top views of ferromagnetic (FM); (d)–(f) three antiferromagnetic (AFM) configurations of MoTeX monolayers. The orange, blue and green balls represent Mn, O and X atoms, respectively.
图 2 单层MoTeX (X = F, Cl, Br, I)的声子谱 (a) MoTeF; (b) MoTeCl; (c) MoTeBr; (d) MoTeI. (e) 分子动力学模拟开始和结束时原子结构的俯视图和侧视图. (f) MoTeF, MoTeCl, MoTeBr和MoTeI单层膜在300 K, 5 ps下的AIMD模拟过程中总能量的波动
Figure 2. Phonon spectra of MoTeX (X = F, Cl, Br, I) monolayers: (a) MoTeF; (b) MoTeCl; (c) MoTeBr; (d) MoTeI. (e) Top and side views of atomic structures at the start and end of molecular dynamics (MD) simulation. (f) Evolution of total energies of MoTeF, MoTeCl, MoTeBr and MoTeI monolayers during AIMD simulation at 300 K for 5 ps.
图 3 (a) MoTeF, (b) MoTeCl, (c) MoTeBr, (d) MoTeI单层膜杨氏模量随面内角的变化; (e) MoTeF, (f) MoTeCl, (g) MoTeBr, (h) MoTeI单层膜泊松比随面内角的变化
Figure 3. Variations of Young’s modulus of (a) MoTeF, (b) MoTeCl, (c) MoTeBr, and (d) MoTeI monolayers with respect to the in-plane angle. Variations of Poisson’s ratio of (e) MoTeF, (f) MoTeCl, (g) MoTeBr and (h) MoTeI monolayers with respect to the in-plane angle.
图 4 单层MoTeX (X = F, Cl, Br, I)的能带结构与态密度图 (a) MoTeF; (b) MoTeCl; (c) MoTeBr; (d) MoTeI. 费米能级用0 eV的虚线表示. 红色和蓝色曲线分别表示自旋向上和自旋向下通道. 单层MoTeX (X = F, Cl, Br, I)的总态密度(TDOS)和投影态密度 (e) MoTeF; (f) MoTeCl; (g) MoTeBr; (h) MoTeI
Figure 4. Electronic band structures of MoTeX (X = F, Cl, Br, I) monolayers: (a) MoTeF; (b) MoTeCl; (c) MoTeBr; (d) MoTeI. Fermi level is denoted by the dashed line at 0 eV. Red and blue curves represent the spin up and spin down channels, respectively. Total density of states (TDOS) and project density of states of MoTeX (X = F, Cl, Br, I) monolayers: (e) MoTeF; (f) MoTeCl; (g) MoTeBr; (h) MoTeI monolayers.
图 8 (a) MoTeX (X = F, Cl, Br, I)单层的铁弹性转换和磁弹性耦合示意图, 铁弹性开关将使易磁化轴旋转90º, 如红色箭头所示; (b) MoTeX单层膜沿铁弹性过渡路径的相对能量
Figure 8. (a) Schematic diagram showing the ferroelastic switching and coupling between magnetism and ferroelasticity for the MoTeX (X = F, Cl, Br, I) monolayers, the ferroelastic switching will rotate the easy magnetization axis by 90º, as illustrated by the red arrows; (b) relative energy of the MoTeX monolayers along the ferroelastic transition path.
表 1 MoTeX (X = F, Cl, Br, I)的晶格常数、可逆应变、反铁磁构型相对铁磁构型的能量
Table 1. Lattice constant, reversible strain and the relative energies of FM and possible AFM configurations of MoTeX monolayers. The energy of FM configuration is a reference.
ML a/Å b/Å (|b|/|a|–1)×100% EFM/(meV·Mo–1) EAFM1/(meV·Mo–1) EAFM2/(meV·Mo–1) EAFM3/(meV·Mo–1) MoTeF 3.704 5.726 54.58 0 283 270 552 MoTeCl 3.906 5.715 46.31 0 306 301 509 MoTeBr 3.992 5.710 43.04 0 361 334 453 MoTeI 4.124 5.696 38.11 0 390 378 397 表 2 MoTeX (X = F, Cl, Br, I)单层膜的弹性模量和力学性能
Table 2. Elastic modulus and mechanical properties of MoTeX (X = F, Cl, Br, I) monolayers.
ML C11/(N·m–1) C12/(N·m–1) C22/(N·m–1) C66/(N·m–1) Ymax/(N·m–1) Ymin/(N·m–1) μmax μmin MoTeF 63.412 8.814 89.320 13.750 88.095 41.059 0.504 0.099 MoTeCl 54.424 5.000 86.926 13.809 86.467 39.404 0.448 0.058 MoTeBr 50.724 5.294 84.128 13.564 83.576 38.237 0.436 0.063 MoTeI 49.090 5.157 81.298 13.273 80.756 37.283 0.432 0.063 表 3 MoTeX (X = F, Cl, Br, I)单层膜交换作用路径参数. d1, d2和d3是第一, 第二和第三近邻Mo原子之间的距离, θ1, θ2和θ3是第一, 第二和第三近邻Mo原子与Te原子之间的夹角
Table 3. Parameters along the exchange interaction path of MoTeX (X = F, Cl, Br, I) monolayers. d1, d2 and d3 are the distances between the first, second and third nearest neighboring Mo atoms, and θ1, θ2 and θ3 are the angles formed between the first, second and third nearest neighboring Mo atoms and Te atoms.
ML d1(Mo-Mo)/Å d2(Mo-Mo)/Å d3(Mo-Mo)/Å θ1(Mo-Te-Mo) θ2(Mo-Te-Mo) θ3(Mo-Te-Mo) MoTeF 3.70 4.24 5.72 81.94 95.85 164.47 MoTeCl 3.90 4.29 5.71 87.06 96.79 161.32 MoTeBr 3.99 4.29 5.71 89.18 96.83 160.74 MoTeI 4.12 4.28 5.69 92.40 97.05 159.54 表 4 MoTeX (X = F, Cl, Br, I)单层的磁交换常数与磁晶各向异性能
Table 4. Magnetic exchange constant and magnetocrystalline anisotropy energy of MoTeX (X = F, Cl, Br, I) monolayer
ML $ {J}_{1} $ /eV$ {J}_{2} $ /eV$ {J}_{3} $ /eVE[100]/(μeV·atom–1) E[010]/(μeV·atom–1) E[001]/(μeV·atom–1) Tc/K MoTeF 0.14 7.72 –0.22 0 487 782 114 MoTeCl 1.85 6.65 –1.70 0 613 518 195 MoTeBr 3.79 6.25 –5.31 0 91 430 111 MoTeI 4.76 6.08 –3.93 0 –282 165 92 -
[1] Fert A 2008 Rev. Mod. Phys. 80 1517 doi: 10.1103/RevModPhys.80.1517 [2] Felser C, Fecher G H, Balke B 2007 Angew. Chem. Int. Ed. 46 668 doi: 10.1002/anie.200601815 [3] Wolf S A, Awschalom D D, Buhrman R A , Daughton J M, Molnar S V, Roukes M L, Chtchelkanova A Y, Treger D M 2001 Science 294 1488 doi: 10.1126/science.1065389 [4] Song Q, Occhialini C A, Ergecen E, Ilyas B, Amoroso D, Barone P, Kapeghian J, Watanabe K, Taniguchi T, Botana A S, Picozzi S, Gedik N, Comin R 2022 Nature 602 601 doi: 10.1038/s41586-021-04337-x [5] Xu S, Jia F, Yu X, Hu S, Gao H, Ren W 2022 Mater. Today Phys. 27 100775 doi: 10.1016/j.mtphys.2022.100775 [6] Spaldin N A, Fiebig M 2005 Science 09 391 doi: 10.1126/science.1113357 [7] Hu T, Kan E 2019 Wiley Interdiscip. Rev. - Comput. Mol. Sci. 9 e1409 doi: 10.1002/wcms.1409 [8] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133 doi: 10.1103/PhysRevLett.17.1133 [9] Huang B, Clark G, Navarro-Moratalla E, Klein D R, Cheng Ran, Seyler K L, Zhong D, Schmidgall E, McGuire M A, Cobden D H, Yao W, Xiao D, Jarillo-Herrero P, Xu X 2017 Nature 546 270 doi: 10.1038/nature22391 [10] Mosendz O, Pisana S, Reiner J W, Stipe B, Weller D 2012 J. Appl. Phys. 111 07B729 doi: 10.1063/1.3680543 [11] Gong C, Li L, Li Z, Ji H, Stem A, Xia Y, Cao T, Bao W, Wang C, Wang Y, Qiu Z Q, Cava R J, Louie S G, Xia J, Zhang X 2017 Nature 546 265 doi: 10.1038/nature22060 [12] Xu S, Jia F, Cheng X, Ren W 2021 J. Mater. Chem. C 9 17152 doi: 10.1039/D1TC04705A [13] Wenisch J, Gould C, Ebel L, Storz J, Pappert K, Schmidt M J, Kumpf C, Schmidt G, Brunner K, Molenkamp L W 2007 Phys. Rev. Lett. 99 077201 doi: 10.1103/PhysRevLett.99.077201 [14] Cenker J, Sivakumar S, Xie K, Miller A, Thijssen P, Liu Z, Dismukes A, Fonseca J, Anderson E, Zhu X, Roy X, Xiao D, Chu J, Cao T, Xu X 2022 Nat. Nanotechnol. 17 256 doi: 10.1038/s41565-021-01052-6 [15] Hu J M, Nan C W 2009 Phys. Rev. B 80 224416 doi: 10.1103/PhysRevB.80.224416 [16] Shen S Y, Xu X L, Huang B BA, Kou L Z, Dai Y, Ma Y D 2021 Phys. Rev. B 103 144101 doi: 10.1103/PhysRevB.103.144101 [17] Weston A, Castanon E G, Enaldiev V, Ferreira F, Bhattacharjee S, Xu S, Corte-Leon H, Wu Z, Clark N, Summerfield A, Hashimoto T, Gao Y, Wang W, Hamer M, Read H, Fumagalli L, Kretinin A V, Haigh S J, Kazakova O, Geim A K, Falko V, Gorbachev R 2022 Nat. Nanotechnol. 17 390 doi: 10.1038/s41565-022-01072-w [18] Abdullahi Y Z, Vatansever Z D, Ersan F, Akinci U, Akturk O U, Akturk E 2021 Phys. Chem. Chem. Phys. 23 6107 doi: 10.1039/D0CP05802E [19] Akgenc B, Vatansever E, Ersan F 2021 Phys. Rev. Mater. 5 83403 doi: 10.1103/PhysRevMaterials.5.083403 [20] Abdullahi Y Z, Ersan F, Vatansever Z D, Akturk E, Akturk O U 2020 J. Appl. Phys. 128 113903 doi: 10.1063/5.0009558 [21] Vaclavkova D, Delhomme A, Faugeras C, Potemski M, Bogucki A, Suffczynski J, Kossacki P, Wildes A R, Gremaud B, Saul A 2020 2D Mater. 7 035030 doi: 10.1088/2053-1583/ab93e3 [22] Xiao G, Xiao W Z, Feng Y X, Rong Q Y, Chen Q 2023 Nanoscale 15 17963 doi: 10.1039/D3NR03119E [23] Guo Z, Liu Y, Jiang H, Zhang X, Jin L, Liu C, Liu G 2023 Mater. Today Phys. 36 101153 doi: 10.1016/j.mtphys.2023.101153 [24] Li Y H, Deng J, Zhang Y F, Jin X, Dong W H, Sun J T, Pan J B, Du S X 2023 npj Comput. Mater. 9 50 doi: 10.1038/s41524-023-01005-8 [25] Yang H, Song M, Li Y, Guo Y, Han K 2022 Physica E 143 115341 doi: 10.1016/j.physe.2022.115341 [26] Xu S, Jia F, Zhao G, Wu W, Ren W 2021 J. Mater. Chem. C 9 9130 doi: 10.1039/D1TC02238E [27] Feng Y, Wang Z, Liu N, Yang Q 2023 Nanoscale 15 4546 doi: 10.1039/D2NR05764F [28] Hu M, Xu S, Liu C, Zhao G, Yu J, Ren W 2020 Nanoscale 12 24237 doi: 10.1039/D0NR06268E [29] Xu B, Li S C, Jiang K, Yin J, Liu Z G, Cheng Y C, Zhong W Y 2020 Appl. Phys. Lett. 116 052403 doi: 10.1063/1.5140644 [30] Sun H, Qu Z, Li A, Wan Y, Wu F, Huang C, Kan E 2023 Appl. Phys. Lett. 123 042901 doi: 10.1063/5.0157258 [31] Zeng Y, Gu P, Zhao Z, Zhang B, Lin Z, Peng Y, Li W, Zhao W, Leng Y, Tan P, Yang T, Zhang Z, Song Y, Yang J, Ye Y, Tian K, Hou Y 2022 Adv. Mater. 34 2108847 doi: 10.1002/adma.202108847 [32] Gu P, Sun Y, Wang C, Peng Y, Zhu Y, Cheng X, Yuan K, Lyu C, Liu C, Tan Q, Zhang Q, Gu L, Wang Z, Han Z, Watanabe K, Taniguchi T, Yang J, Zhang J, Ji W, Tan P, Ye Y 2022 Nano Lett. 22 1233 doi: 10.1021/acs.nanolett.1c04373 [33] Blochl P 1994 Phys. Rev. B 50 17953 doi: 10.1103/PhysRevB.50.17953 [34] Kresse G, Furthumller J 1996 Phys. Rev. B 54 11169 doi: 10.1103/PhysRevB.54.11169 [35] Blochl P E, Forst C J, Schimpl J 2003 Bull. Mater. Sci. 26 33 doi: 10.1007/BF02712785 [36] Monkhorst H J, Pack J D 1976 Phys. Rev. B 13 5188 doi: 10.1103/PhysRevB.13.5188 [37] Togo A, Oba F, Tanaka I 2008 Phys. Rev. B 8 134106 doi: 10.1103/PhysRevB.78.134106 [38] Togo A, Tanaka I 2015 Scr. Mater. 108 1 doi: 10.1016/j.scriptamat.2015.07.021 [39] Cadelano E, Palla P L, Giordano S, Colombo L 2010 Phys. Rev. B 82 235414 doi: 10.1103/PhysRevB.82.235414 [40] Kanamori J 1960 J. Appl. Phys. 31 S14 doi: 10.1063/1.1984590 [41] Goodenough J B 1955 Phys. Rev. 100 564 doi: 10.1103/PhysRev.100.564 [42] Dang N T, Kozlenko D P, Lis O N, Kichanov S E, Lulin Y V, Golosova N O, Savenko B N, Duong D L, Phan T L, Tran T A, Phan M H 2023 Adv. Sci. 10 2206842 doi: 10.1002/advs.202206842 [43] Miao N, Xu B, Zhu L, Zhou J, Sun Z 2018 J. Am. Chem. Soc. 140 2417 doi: 10.1021/jacs.7b12976 [44] Gao Z, Wang Y, Gao J, Cui Z, Zhang X, Shi J, Fan X 2022 Comput. Mater. Sci. 213 111611 doi: 10.1016/j.commatsci.2022.111611 [45] Henkelman G, Uberuaga B P, Jonsson H 2000 J. Chem. Phys. 113 9901 doi: 10.1063/1.1329672 [46] Wang H, Li X, Sun J, Liu Z, Yang J 2017 2D Mater. 4 045020 doi: 10.1088/2053-1583/aa8abd [47] Pang Z, Ji W, Zhang C, Wang P, Li P 2021 Chem. Phys. Lett. 763 138163 doi: 10.1016/j.cplett.2020.138163 [48] Zhang S, Liu B 2018 Nanoscale. 10 5990 doi: 10.1039/C7NR09588K [49] Li W, Li J 2016 Nat. Commun. 7 10843 doi: 10.1038/ncomms10843 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: