首页
登录
注册
下载:
-
近年来, 太赫兹(THz)技术在诸多方面已取得了长足的发展, 尤其是随着大功率太赫兹源[1]、高灵敏度太赫兹探测器[2]的技术突破, 以及各种高性能、高集成度的太赫兹功能器件研究, 如滤波器[3]、波导[4]、隔离器[5]、二向色镜等, 在很大程度上打破了太赫兹技术的应用限制, 并对成像[6]、安防[7]、传感[8]、雷达[9]等多个应用领域产生了重大影响. 特别是太赫兹雷达探测技术, 因太赫兹波具有低能量、高分辨率、穿透性、光谱信息丰富等优点, 更受到了全世界多国的重点关注. 由于水蒸气对太赫兹波的强烈吸收[10], 使得太赫兹波一般难以在近地大气中进行较远距离的有效传输, 但在临空高层大气或近距离条件下则仍具有明显优势. 临空高速飞行器在飞行过程中往往会产生高温激波、尾焰、尾迹以及等离子鞘套, 会严重干扰红外探测, 而太赫兹波有着对红外热辐射不敏感的特性[11,12], 可以很好地透过红外干扰对目标本体进行探测. 因此, 可以说红外和太赫兹复合探测能弥补各自的缺点, 实现对该类目标更精确的探测.
在多模复合探测系统中, 分光器件作为关键器件之一, 其性能会严重影响系统的光学性能. 在太赫兹波段, 由于材料响应和加工工艺等问题导致传统二向色镜等器件反射效率减低、插入损耗增大, 目前尚缺乏高效的分光器件, 相关研究成果也罕见报道. 刘闯[13]利用传统光学镀膜技术制备的太赫兹与红外二向色镜, 其中红外光透射率可达98%. 然而, 其在太赫兹频段的反射率最高仅为76%, 还有很大的性能提升空间, 远未能满足高效复合探测系统对高效分光器件的要求. 近年来, 被称为“超材料”或“超表面”的人工微结构材料, 以其在太赫兹波段的强电磁响应和易于人为调控的特点显示出巨大的应用前景. 超表面是一种亚波长结构的二维阵列, 其特性可以通过单元格的几何形状和尺寸来设计, 以调制入射太赫兹波的振幅、相位和偏振, 是操纵电磁波的一种有效方法. 目前, 基于超表面技术的滤波及减反增透理论实现任意单一波段的高反或者高透已经有若干文献的报道[14,15]. 然而, 利用超表面同时实现太赫兹波高透与中长波红外光高反的器件设计还未见报道.
本文提出了一种基于双层金属加双层介质基底单元结构的太赫兹红外超表面二向色镜设计. 在入射光45°入射时, 此超表面可以在1.1 THz附近实现大于97%的透射系数; 在中波红外3—5 μm和长波红外8—14 μm实现大于98%的反射系数, 并且具有偏振不敏感和0°—60°入射角度不敏感的特性. 该设计可作为太赫兹与红外复合成像系统的关键分光器件, 为各种场景下的太赫兹和红外高效分光提供了有价值的设计参考. 此外, 本研究还可以为其他光谱范围寻求高效分光提供一种有效的技术思路和解决方案.
-
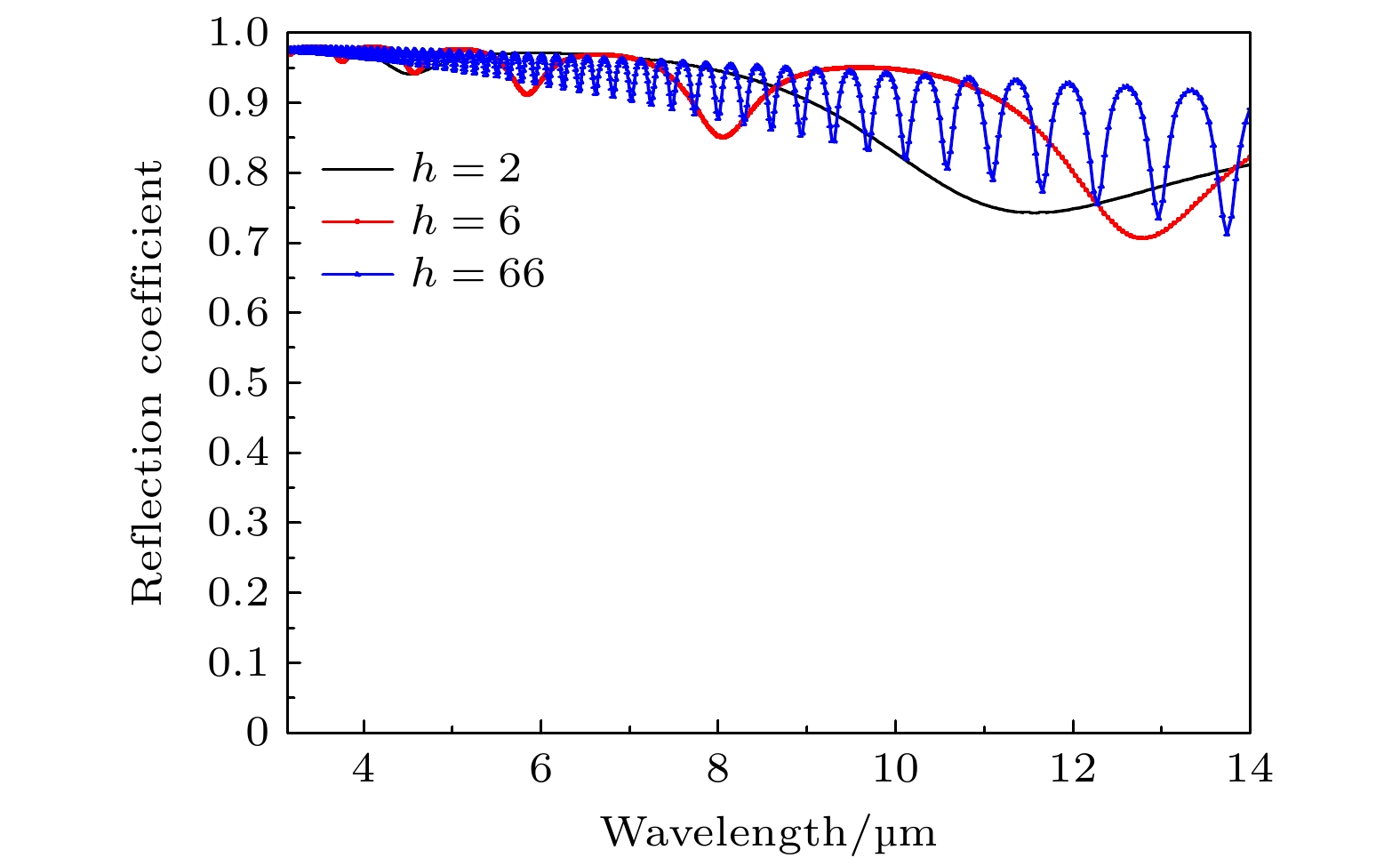
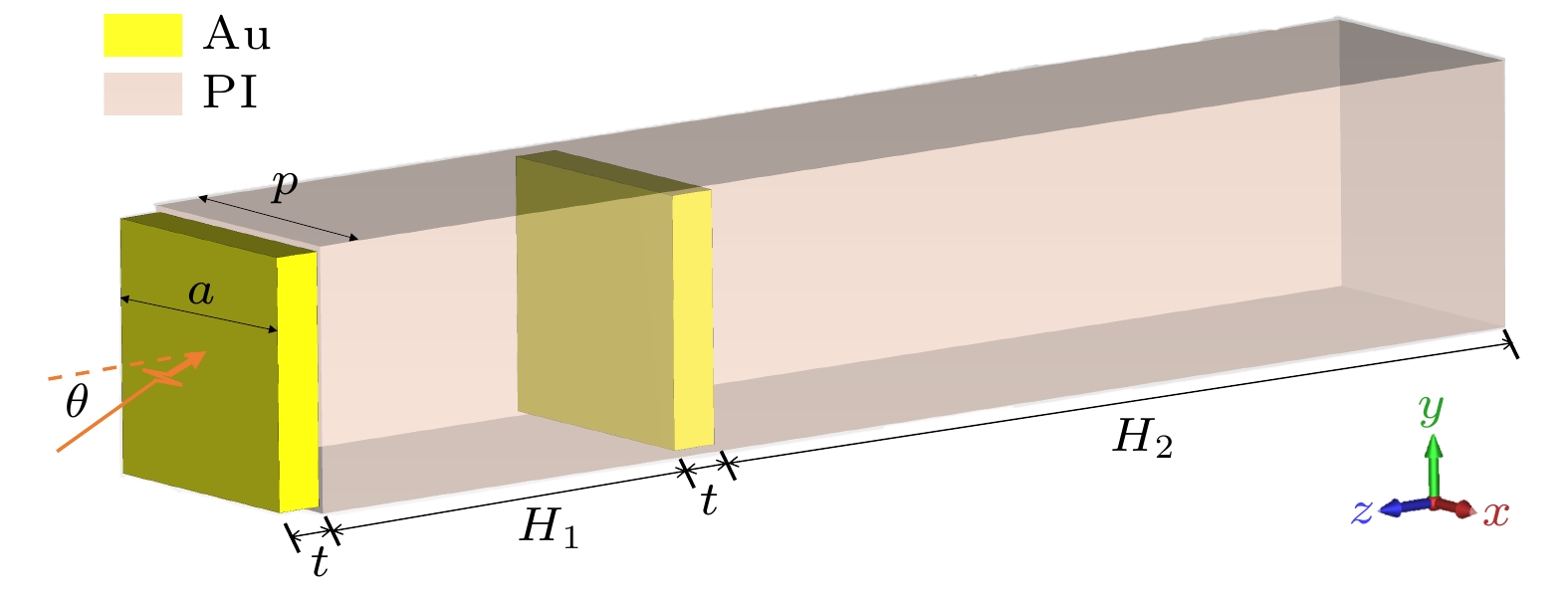
所设计的超表面单元结构如图1所示, 在两层介质结构上嵌入两层方型金属图案. 介质材料为柔性材料聚酰亚胺(PI), 红外和太赫兹波段相对介电常数为3.5, 损耗正切函数为0.0027[16]; 在太赫兹波段, Au的电导率为4.56 × 107 S/m, 在中长波红外波段, Au采用文献[17]中的数据进行拟合. 金属层的厚度为单层t = 0.20 μm, 两层PI层厚度分别为H1 = 1.80 μm, H2 = 64 μm, 即PI总厚度h = 66 μm. 单元结构周期长度为p = 1.10 μm, 方形金属单元边长为a = 1.05 μm. 入射角θ表示光波入射方向与-z方向之间的夹角. 仿真采用时域有限差分法(FDTD)方法进行数值模拟计算, 其中x, y方向分别采用周期边界条件, z方向采用开放边界条件或完全匹配层(PML).
-
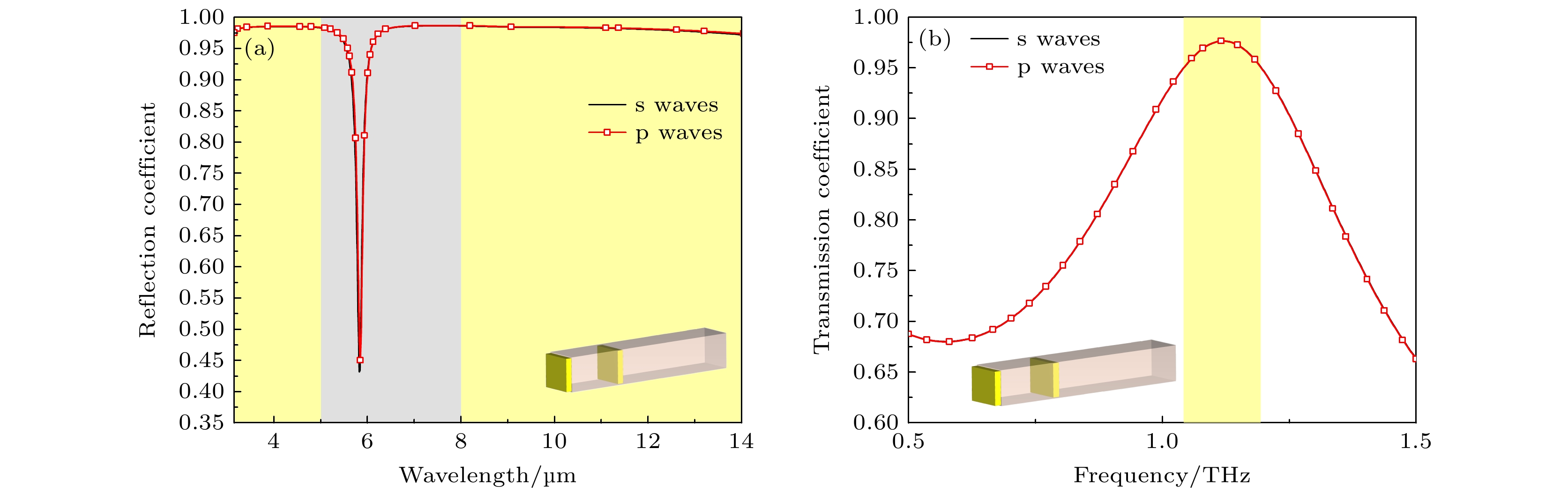
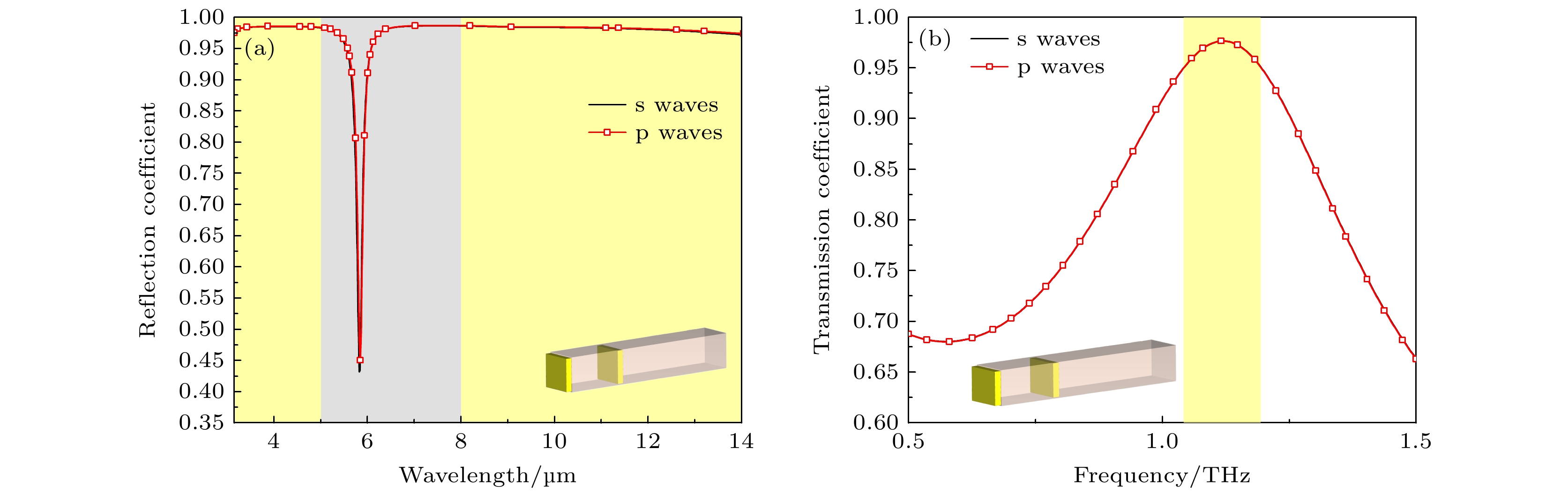
在入射角θ为45°时, 该超表面的红外反射系数与太赫兹透射系数如图2所示, 不同偏振状态的s波和p波完全重合(由于任意偏振态入射光可以分解为两正交的线偏振光, 因此s波和p波的分析具有一般性). 从图2可以看到, 该超表面的双层方形金属单元结构, 在入射红外激光激发下形成谐振, 中心谐振波长位于5.8 μm, 反射系数最小为0.43; 在入射太赫兹波激发下, 在1.10 THz频率处出现透射系数峰值, 最大为0.97. 以上结果表明, 该超表面设计可以实现中心频率1.10 THz附近、透射系数95%以上带宽152 GHz的太赫兹波、中波3—5 μm和长波8—14 μm、反射系数98%以上的有效透射和反射分光.
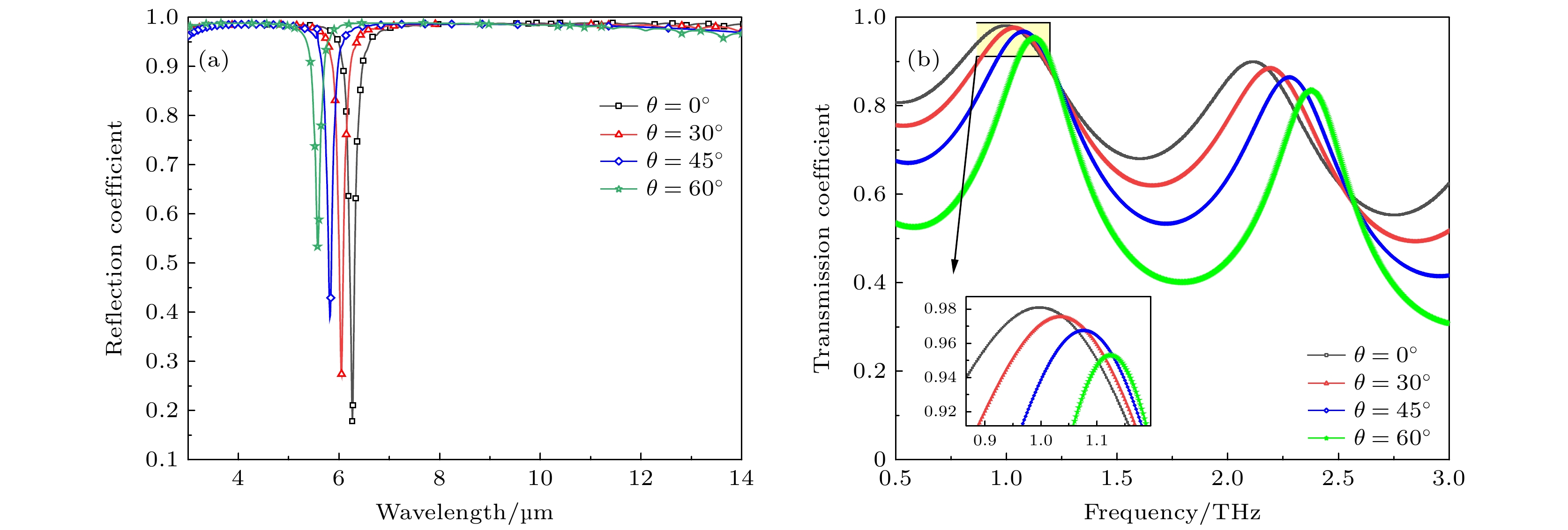
此外, 在不同入射角θ的条件下, 该超表面在0°—60°超入射角范围内, 红外中心谐振波长从6.3 μm平移到5.6 μm, 而太赫兹波段谐振透射峰频率从1.00 THz平移到1.12 THz, 其双波段透反射特性保持较稳定不变, 仿真结果如图3所示. 考虑入射角度变化时对应金属单元结构在入射方向上的投影面积变化, 0°—60°范围的入射角度变化可以等效为正入射情况下的金属间距和基底厚度的变化, 因此表现为如图3所示的红外共振吸收峰和太赫兹透射峰的微小频移. 而随着入射角度的增大, 太赫兹透射峰值小幅下降则满足菲涅耳透射公式中透射幅值和角度的关系, 见(1)式和(2)式[18]. 推论可知, 正入射在1.00 THz透射系数最大, 模拟结果显示可以达到0.98.
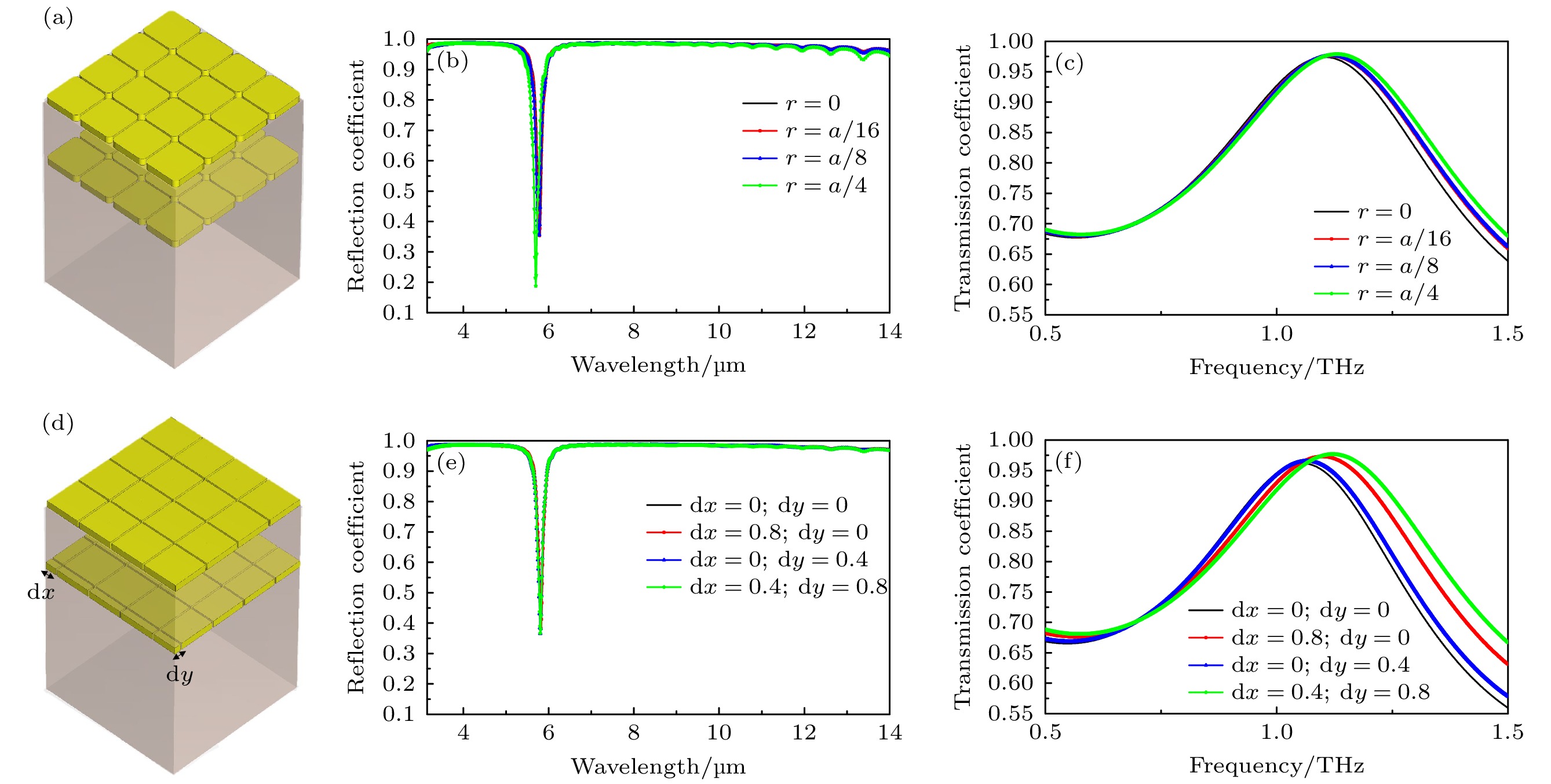
考虑到该超表面设计的单元尺寸和线宽尺度, 介于极紫外光刻(EUV)和电子束光刻(EBL)的加工工艺精度边界, 在实际加工过程中极易产生加工误差, 往往会导致结构倒圆角、小倍率缩放和层间错位等问题. 因此, 为了分析加工精度和误差对器件透反射性能的影响, 本文还对超表面单元结构的倒圆角、上下单元结构错位、小倍率缩放、基底厚度变化、边长变化的情况进行了模拟. 图4(a)—(c)为超表面结构的四角存在半径为r的倒圆角情况下, 结构示意图和红外、太赫兹波段的透反射系数曲线; 图4(d)—(f)为上下两层超表面结构错位未对齐情况下的示意图和透反射系数曲线, 其中 dx 和 dy 分别表示双层金属沿着 x 和 y 方向的相对偏移量. 从模拟计算结果可以看出, 倒圆角和层间错位误差对该超表面单元结构设计的透反射曲线影响较小.
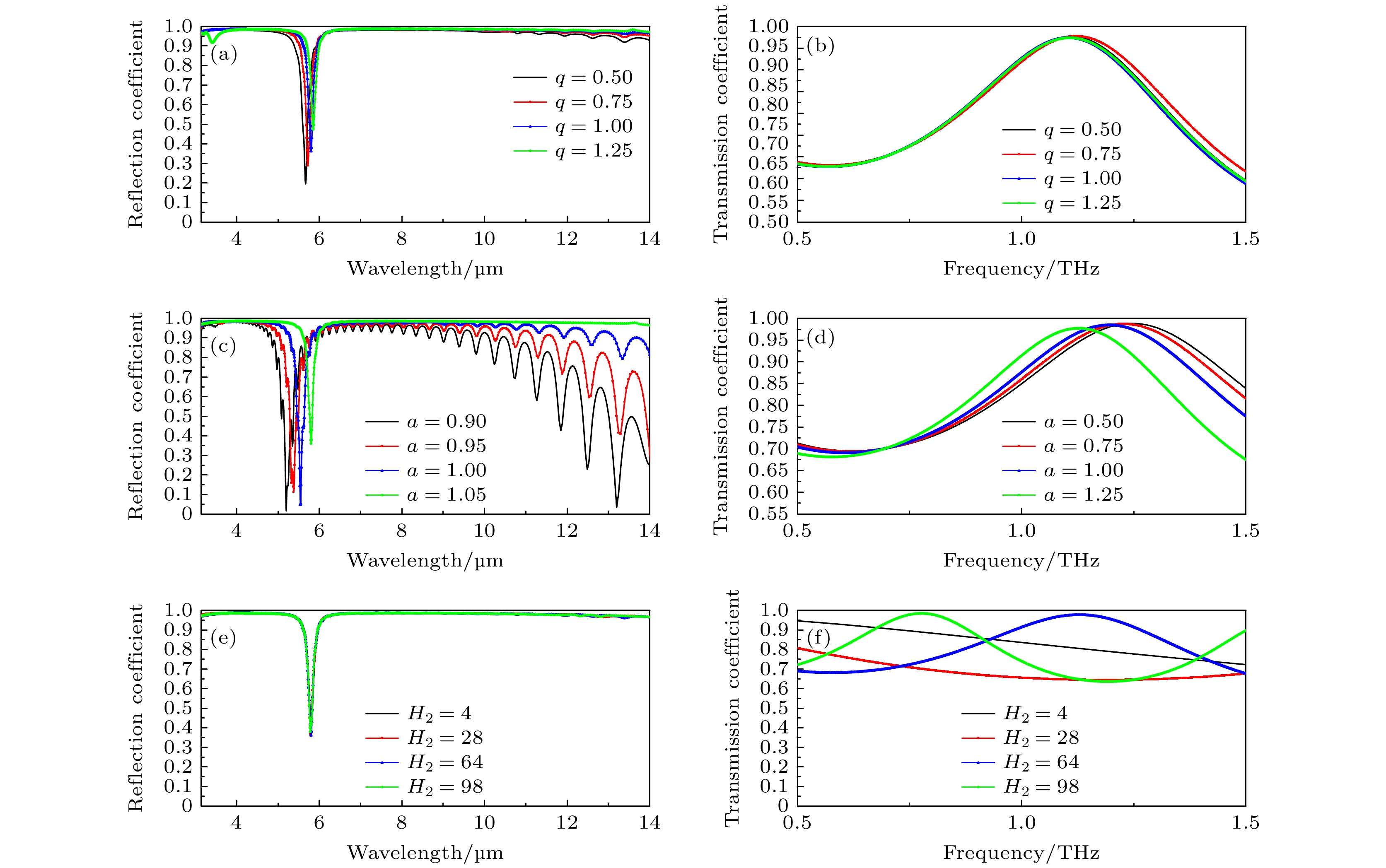
此外, 当存在小倍率缩放、超表面单元边长变化、基底厚度变化3种加工误差情况下, 超表面太赫兹、红外波段的透反射曲线分别如图5(a), (b)、图5(c), (d)、图5(e), (f)所示, 其中 q 表示缩放倍率. 从图5(c)可以看出, 超表面单元边长变化对长波红外反射影响较大, 随着边长的减小, 长波红外反射系数明显下降; 图5(f)显示, 基底厚度变化对太赫兹透射影响明显, 其原因是介质基底在入射波条件下会构成法布里-珀罗(F-P)谐振腔, 随着厚度的变化, 谐振光波的透射峰值变化明显; 而图5中其他情况下的透反射曲线则相对稳定.
-
对于该超表面单元结构在太赫兹波段的中心谐振频率附近的高透过率, 可以适用巴比涅定理进行解释: 当导电屏为理想导体并且厚度为无限薄的情形, 通常要求导电屏的厚度应该小于
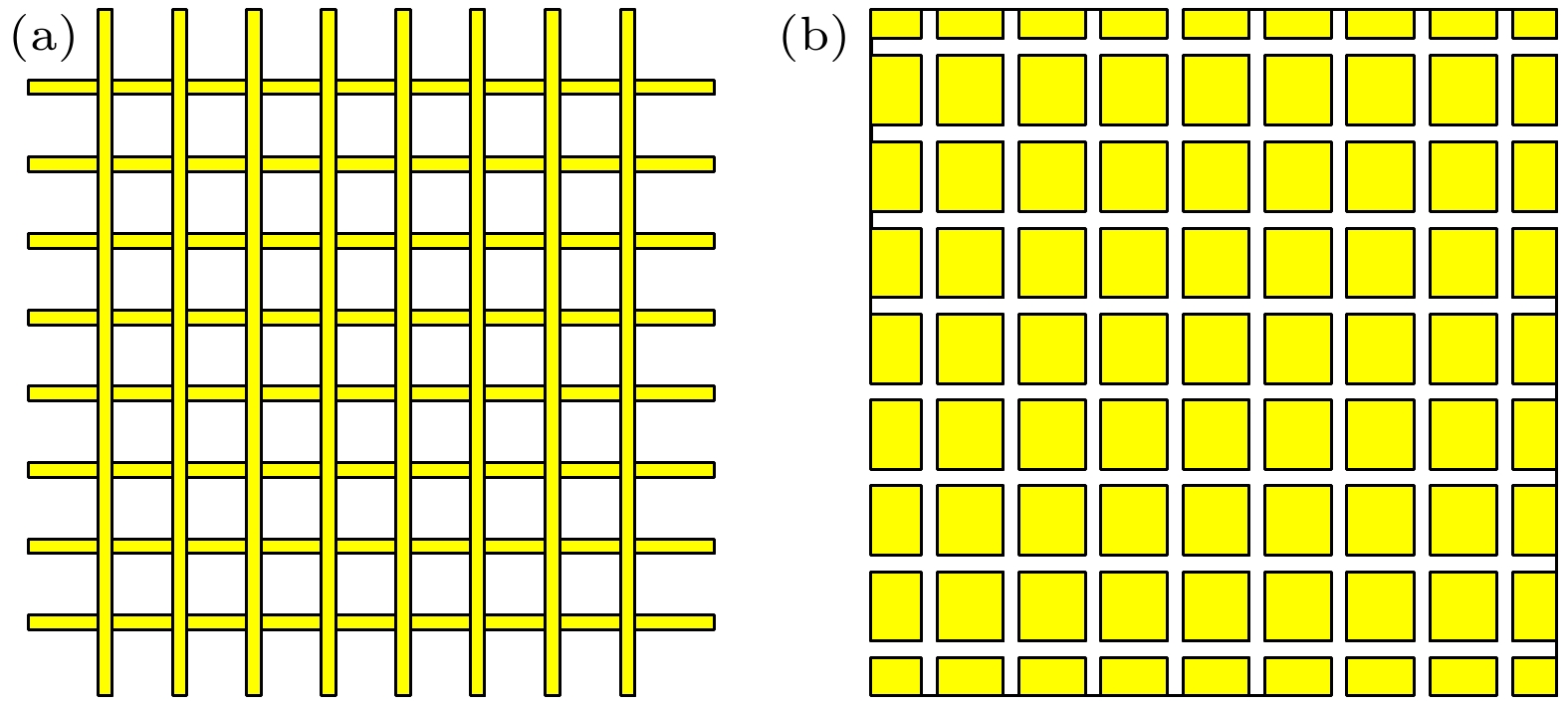
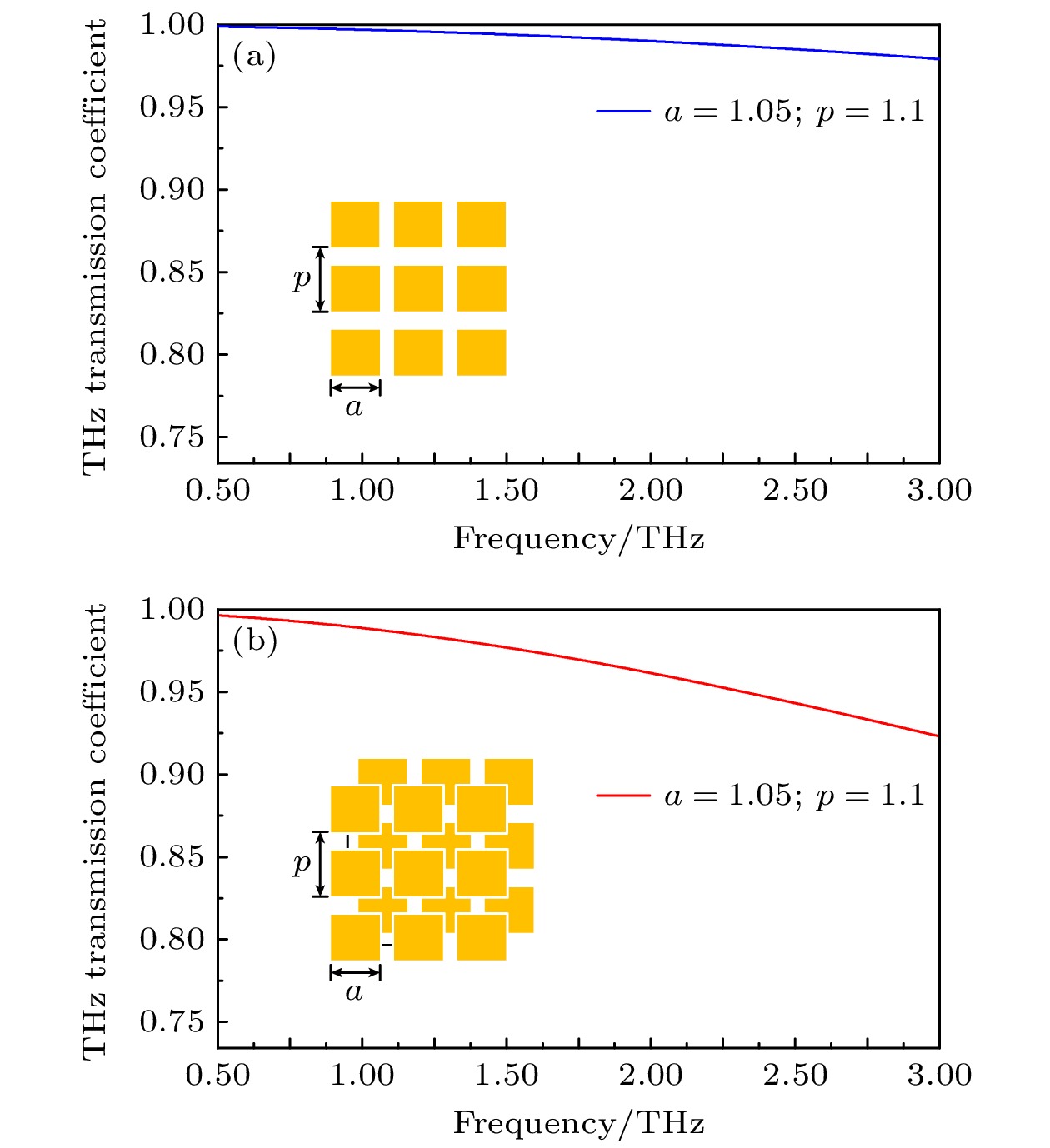
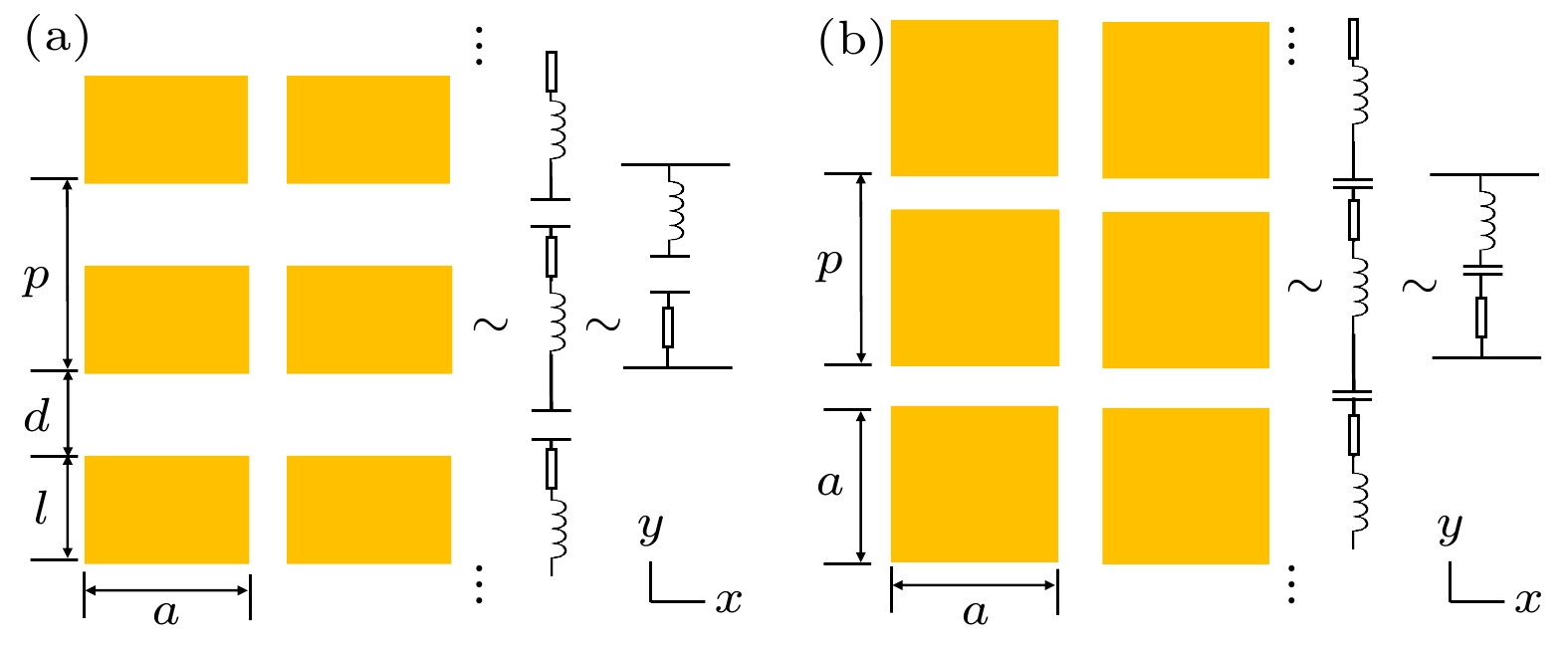
$ \lambda /1000 $ , 则一个阵列的镜面反射系数等于其互补阵列的传输系数[19]. 当入射波长远大于图6(a)中金属网栅间距时, 此时金属网栅可看成高反屏, 则根据巴比涅定理, 其互补屏图6(b)的金属方块阵列对入射波构成高透屏. 本文所设计的单层超表面结构, 金属层厚度t = 0.20 μm与1 THz附近对应的波长满足上述关系, 对单层金属超表面的太赫兹透射仿真结果见图7(a); 而双层超表面电尺寸间距远小于波长, 可以看成集总元件, 没有干涉效应, 可以简单地看成两个单层超表面透射系数相乘, 仿真结果如图7(b)所示, 因此双层超表面整体依然保持高透射特性. 另一方面, 由于介质基底厚度与波长可比拟, 其透射特性还受到F-P振荡的调制, 因而形成图3(b)中准周期振荡并维持高透射系数的曲线. 这也同时解释了上文中考虑几种加工误差单元结构的仿真结果, 只要等效基底厚度变化较小, 太赫兹透射曲线就会保持不变.而对于中长波红外, 此时的超表面金属层厚度相对于波长不满足无限薄近似条件, 因此巴比涅定理不再适用, 但可以通过等效电路模型对中长波红外窗口的宽带高反进行分析. 如图8(a)所示, 考虑y方向极化的电磁波入射情况, 金属块阵列可视为带阻滤波器, 且谐振波长与金属块y方向长度的关系可表示为
$ l \approx \lambda /2 $ , 与金属块a无关, 可以通过插入电容或导体的办法使其变得稍大或稍小[19]. 此时, 可将图8(a)结构等效为RLC串联电路(R, L, C分别表示电阻、电感和电容), 其谐振角频率的表达式如 (3) 式所示. 为了定性分析, 在y方向上厚度为t的金属块可以简化为匝数为1的线圈模型, 如(4)式所示; 而两相邻金属块可以简化为平板电容, 如(5)式所示, 其中A为y方向金属块截面面积. 当金属块y方向长度l逐渐增大到a时, 如图8(b)所示, 即为本文所设计超表面上层结构.根据品质因子Q定义(6)式可知, Q越高, 曲线谐振峰越尖锐, 反射带宽(WB)越窄; Q越低, 谐振曲线越平坦, WB越宽[20]. 而Q由R, L, C共同决定, 图8中只有l和d变化, 将(4)式、(5)式、(7)式代入(6)式, 其中(7)式为电阻决定式, 得到
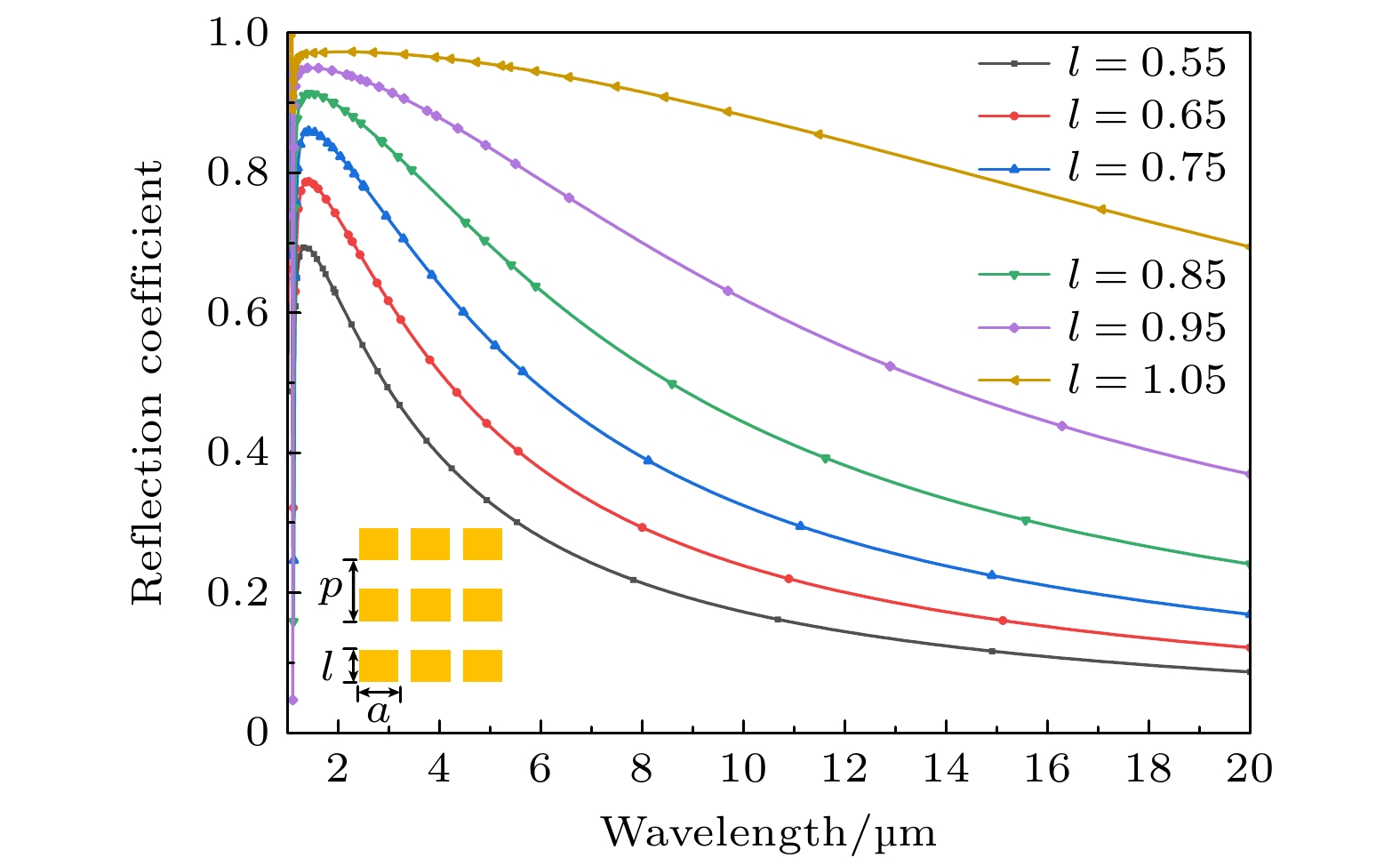
$ Q \propto \sqrt {d/{l^3}} = \sqrt {(p - l)/{l^3}} $ , 品质因数Q随l的变大而减小, 因此在谐振频点及更大波长光谱范围内, 存在宽带高反射响应特性, 仿真结果如图9所示.但是随着波长逐渐增大, 单层金属超表面结构的反射系数逐渐降低, 而且会受到基底介质材料F-P谐振的影响, 如图10所示. 有研究表明, 多层超表面级联可以减缓反射系数的降低, 进一步增大带宽[19]. 本文双层结构超表面可以等效为两个阻抗ZL串联, 由终端反射系数(8)式可知当负载阻抗ZL远大于特性阻抗Z0时, 表现为高反射, ZL越大, 反射系数越大, 从而增大反射带宽. 因此设计双层超表面会更利于中长波红外保持高反, 而且还能屏蔽介质基底厚度变化的影响, 本文结构随基底厚度的模拟结果如图5(e)所示.
-
本文设计了一种简单高效的二向色镜超表面. 在45°入射角工作时, 此二向色镜超表面可以在1.1 THz附近实现大于97%的透射系数, 在中波红外3—5 μm和长波红外8—14 μm实现大于98%的反射系数, 并具有偏振不敏感的特性. 通过仿真验证, 对本文结构中的金属图案进行倒角、小倍率缩放、层间错位等模拟结构失配和加工误差的情况, 红外反射和太赫兹透射都有很好的鲁棒性, 并通过巴比涅定理和等效电路模型做出合理解释. 该研究结果主要应用于太赫兹与红外波段的多波长复合成像系统中的分光器件, 此外还可以应用于多波段红外隐身、激光器中激光与泵浦光的分离等, 为各种场景下的太赫兹和红外高效分光提供了有价值的设计参考.
基于超表面的太赫兹与中长波红外高效分光器件
Metasurfaces based terahertz and mid- and long-wave infrared high-efficiency beam splitting devices
-
摘要: 多模复合成像技术结合了不同传感器的优势, 具有图像质量高、信息获取能力强、目标检测和识别能力高、对复杂环境的强适应能力、系统的稳定性和鲁棒性高等优点. 其中, 太赫兹和红外复合成像技术结合了太赫兹波段和红外波段的特点, 具有宽频谱覆盖、高分辨率、穿透性强的优点, 有广阔的应用前景. 作为共口径复合成像系统的关键器件之一的太赫兹和红外波段的高效分光器目前仍然缺少, 性能亟待提升. 本文提出了一种结构简单、性能高效的双层金属加介质基底结构二向色超表面. 作为分光器件使用, 当入射角度为45°时, 其在中心频率1.1 THz附近实现大于97%的透射系数, 在中波红外3—5 μm和长波红外8—14 μm波长范围均实现大于98%的反射系数. 该设计对层间结构错位、结构倒圆角、小倍率缩放等结构失配和加工误差都具有很好的鲁棒性, 并且具有偏振不敏感特性. 而当入射角度在0°—60°内变化时, 器件依然保持优异的分光特性. 基于巴比涅定理和等效电路模型, 对该超表面的电磁响应特性进行理论分析, 分析结果与模拟仿真结果相吻合. 该研究结果证明了超表面作为分光器件应用于太赫兹与红外波段的多波长复合成像系统中的可行性, 并为未来新型复合成像探测技术的研究提供了支撑.Abstract: The multi-mode composite imaging technology integrates the advantages of different sensors, and thus has the advantages of high image quality, strong information acquisition capability, high target detection and recognition ability, strong adaptability to complex environments, and high stability and robustness of the system. Among them, the terahertz and infrared composite imaging technology combines the characteristics of terahertz band and infrared band, has the advantages of wide spectrum coverage, high resolution and strong penetration, and has broad application prospects. As one of the key components of the common aperture composite imaging system, the efficient optical splitters in terahertz and infrared band are still lacking at present, and their performance needs to be improved urgently. In this paper, a kind of dichroic metasurface with a simple structure and high performance is proposed by combining simulation experiment and theoretical explanation. When used as a spectroscopic device at an incident angle of 45°, it achieves a transmission coefficient greater than 97% near the center frequency of 1.1 THz, and a reflection coefficient greater than 98% in a wavelength range of 3–5 μm for medium-wave infrared and 8–14 μm for long-wave infrared. The design has good robustness to structural mismatches and machining errors such as structural misalignment, structural fillet, small magnification scaling, and polarization insensitivity. When the incident angle changes in a range of 0–60°, the device still maintains excellent spectral characteristics. In this paper, based on Babinet theorem and equivalent circuit model, the electromagnetic response characteristics of the metasurface are analyzed theoretically, and the analysis results are in agreement with the simulation results. The results of this study prove the feasibility of metasurface as a spectral device in the multiwavelength composite imaging system of terahertz and infrared bands, and provide support for future studying new composite imaging detection technology. In addition, the metasurface structure described in this paper has broad application prospects in many fields such as multi-band infrared stealth, laser and pump light separation in lasers, and provides a valuable reference for designing terahertz and infrared spectroscopy in various scenarios. In the following figure, for S wave and P wave at an incident angle of 45°, panel (a) shows the reflection coefficients varying with the wavelength of metasurface and panel (b) displays terahertz transmission coefficient changing with frequency.
-
Key words:
- metasurface /
- dichroic mirror /
- equivalent circuit model /
- Babinet theorem .
-
-
图 2 在45°入射的超表面透反射系数曲线 (a) 红外反射系数; (b) 太赫兹透射系数
Figure 2. Transmission and reflection coefficient of this metasurface at 45° incident angle: (a) Infrared reflection coefficient; (b) terahertz transmission coefficient.
图 3 不同入射角度的红外反射系数(a)和太赫兹透射系数曲线(b)
Figure 3. Infrared reflection coefficient (a) and terahertz transmission coefficient (b) at different incidence angles.
图 4 在45°入射的超表面透反射系数曲线 (a)—(c) 金属结构倒圆角; (d)—(f) 金属结构层间错位
Figure 4. Transmission and reflection coefficient of this metasurface at 45° incident angle: (a)–(c) Metal structure chamfer; (d)–(f) dislocation between layers of metal structures.
图 5 在45°入射的超表面透反射系数曲线 (a), (b) 结构横向缩放; (c), (d) 金属方块边长变化; (e), (f) 介质基底变化
Figure 5. Transmission and reflection coefficient of this metasurface at 45° incident angle: (a), (b) Horizontal scaling of structure; (c), (d) metal square side length changes; (e), (f) dielectric basement change.
图 6 巴比涅定理互补结构示意图 (a) 单层金属网栅; (b) 单层金属方块阵列
Figure 6. Diagram of complementary structure of Babinet’s theorem: (a) Single layer metal grid; (b) single layer metal cube array.
图 7 超表面太赫兹透射系数 (a) 单层超表面; (b) 双层超表面
Figure 7. Terahertz transmission coefficient of metasurface: (a) Single layer metasurface; (b) double layer metasurface.
图 8 等效电路模型示意图 (a) 金属块; (b) 超表面金属方块
Figure 8. Equivalent circuit model diagram: (a) Metal block; (b) metasurface metal cube.
图 9 正入射的单层超表面红外反射系数随金属长度变化曲线
Figure 9. Reflection coefficient of this single layer metasurface at normal incident angle varies with the length of metal.
图 10 在45°入射的单层超表面反射曲线
Figure 10. Reflection coefficient of single layer metasurface at 45° incident angle.
-
[1] Koulouklidis A D, Gollner C, Shumakova V, Fedorov V Y, Pugžlys A, Baltuška A, Tzortzakis S 2020 Nat. Commun. 11 292 doi: 10.1038/s41467-019-14206-x [2] Burford N M, El-Shenawee M O 2017 Opt. Eng. 56 010901 doi: 10.1117/1.OE.56.1.010901 [3] Liu Z M, Gao E D, Zhang X, Li H J, Xu H, Zhang Z B, Luo X, Zhou F Q 2020 New J. Phys. 22 053039 doi: 10.1088/1367-2630/ab83d5 [4] Fan F, Zhang X Z, Li S S, Deng D C, Wang N, Zhang H, Chang S J 2015 Opt. Express 23 27204 doi: 10.1364/OE.23.027204 [5] Shalaby M, Peccianti M, Ozturk Y, Morandotti R 2013 Nat. Commun. 4 1558 doi: 10.1038/ncomms2572 [6] Wade C G, Šibalić N, Melo N R, Kondo J M, Adams C S, Weatherill K J 2017 Nat. Photonics 11 40 doi: 10.1038/nphoton.2016.214 [7] Cheng Y Y, Qiao L B, Zhu D, Wang Y X, Zhao Z 2021 Opt. Lett. 46 1233 doi: 10.1364/OL.418497 [8] Singh R J, Cao W, Ibraheem A N, Cong L Q, Withawat W, Zhang W L 2014 Appl. Phys. Lett. 105 171101 doi: 10.1063/1.4895595 [9] Cooper K B, Dengler R J, Llombart N, Thomas B, Chattopadhyay G, Siegel P H 2011 IEEE Trans. Terahertz Sci. Technol. 1 169 doi: 10.1109/TTHZ.2011.2159556 [10] Yang Y H, Mandehgar M, Grischkowsky D 2014 Opt. Express 22 4388 doi: 10.1364/OE.22.004388 [11] 耿兴宁, 徐德刚, 李吉宁, 陈锴, 钟凯, 姚建铨 2020 强激光与粒子束 32 78 doi: 10.11884/HPLPB202032.190291 Geng X N, Xu D G, Li J N, Chen K, Zhong K, Yao J Q 2020 High Power Las. Part. Beams 32 78 doi: 10.11884/HPLPB202032.190291 [12] 陈锴, 耿兴宁, 李吉宁, 钟凯, 徐德刚, 蒋山亚, 张景川, 姚建铨 2020 航天器环境工程 37 421 doi: 10.12126/see.2020.05.001 Chen K, Geng X N, Li J N, Zhong K, Xu D G, Jiang S Y, Zhang J C, Yao J Q 2020 Spacecraft Environ. Eng. 37 421 doi: 10.12126/see.2020.05.001 [13] 刘闯 2016 博士学位论文 (哈尔滨: 哈尔滨工业大学) Liu C 2016 Ph. D. Dissertation(Harbin: Harbin Institute of Technology [14] Chen H T, Zhou J F, Hara J F, Chen F, Azad A K, Taylor A J 2010 Phys. Rev. Lett. 105 073901 doi: 10.1103/PhysRevLett.105.073901 [15] 姚尧, 沈悦, 郝加明, 戴宁 2019 物理学报 68 147802 doi: 10.7498/aps.68.20190702 Yao Y, Shen Y, Hao J M, Dai N 2019 Acta Phys. Sin. 68 147802 doi: 10.7498/aps.68.20190702 [16] Sun K, Li J N, Sun J Y, Ge L, Xu D G, Zhong K, Yao J Q 2022 Results Phys. 33 105183 doi: 10.1016/j.rinp.2022.105183 [17] Olmon L R, Slovick B, Johnson W T, Shelton D, Oh S H, Boreman G D, Raschke M B 2012 Phys. Rev. B 86 235147 doi: 10.1103/PhysRevB.86.235147 [18] 郁道银, 谈恒英 2015 工程光学(第4版) (北京: 机械工业出版社) 第318页 Yu D Y, Tan H Y 2015 Engineering Optics (Vol. 4) (Beijing: China Machine Press) p318 [19] 本A明克 著 (侯新宇 译) 2009 频率选择表面理论与设计(北京: 科学出版社) 第110—113页 Munk B A (translated by Hou X Y) 2009 Frequency Selective Surfaces Theory and Design (Beijing: Science Press) pp4–8 [20] 张肃文 2009 高频电子线路 (第5版) (北京: 高等教育出版社) 第17—19页 Zhang S W 2009 High-Frenquency Electronic Circuit (Vol. 5) (Beijing: Higher Education Press) pp17–19 -
计量
- 文章访问数: 168
- HTML全文浏览数: 168
- PDF下载数: 9
- 施引文献: 0