-
卫星通信系统中,天线的设计往往受航天器上装载、部署等物理空间的限制,因此使用共口径多波束反射面天线是实现混合有效载荷、天线轻量化及提高天线通信效率的较优选择[1]。赋形反射面天线对复杂的覆盖区域具有高效率、高增益、低交叉极化的特性,是卫星通信系统中固定轮廓波束的最具吸引力的方法[2]。因此本文研究共口径多波束赋形反射面天线对同时进行多个卫星通信业务(卫星固定、移动、卫星广播等业务)具有重要意义[3]。例如实现两个轮廓波束用于固定服务区通信并附加点波束用于应急通信(森林火灾、海上救援等)是卫星通信发展的现实需求,但目前还未实现该需求。
传统的赋形反射面天线是通过单偏置反射面天线或偏置格里高利型天线实现平顶波束[4]、余割平方波束[5]、赋形波束及点波束[6-7]等,但是只能实现一种波束或一个赋形波束加附加点波束,所以卫星通信天线的反射面利用率低。研究人员对该方向进行了一些深入的研究,文献[6]采用口径大小为2.2 m×2 m的双馈源单偏置反射面天线实现了一个赋形波束和一个点波束,其中一个馈源置于焦点处实现印度国土的赋形波束,另一个馈源利用焦平面共轭场匹配的方法来补偿赋形反射面的口径相位差以实现高增益点波束覆盖安达曼群岛,这种方法只有一个反射面作为基础结构进行赋形操作,难以实现第二个赋形波束及扫描波束。李建军等[8]采用以格里高利型天线为基础的双偏置双馈源反射面天线技术(口径大小为2.2 m×2 m)实现了一个赋形波束和一个点波束,焦点处的馈源结合Zernike多项式作为主反射面赋形的形变基函数,并采用差分进化算法优化基函数系数实现赋形波束;另一个馈源结合最小二乘法对赋形反射面进行拟合,利用拟合后的形面结合射线追踪法对副反射面进行赋形,补偿馈源偏焦和反射面形变引入的口径相位差实现点波束,该方法实现点波束后副反射面固定,难以实现第二个轮廓波束。文献[3]与文献[8]技术路线相同,实现了一个赋形波束、一个点波束和扫描波束,文献[3]的优点在于可以实现C/Ku/Ka波段三种波束共同通信。万继响等[9]采用口径为1.2 m×1.2 m的双馈源双偏置反射面结构,同时对两个反射面进行赋形,馈源位置采用经验公式估算,实现了两个简单轮廓波束。该方法简单且效率高,实测与仿真相差仅0.2 dB,但赋形区域不能同时通信,当赋形较复杂轮廓将导致波束的增益和交叉极化鉴别比(XPD)降低,并且未实现点波束。可见双馈源单偏置结构以及副反射面用于实现点波束的双馈源双偏置反射面结构难以实现两个轮廓波束加一个点波束,为了运用口径为1.1 m×1.1 m实现相比文献[9]更复杂的两个轮廓波束以及附加一个点波束,本文将在文献[9]的基础架构上添加一个馈源并且在赋形方法上改进以实现目标。
本文采用Zernike多项式与Cubic B-splines函数共同作为反射面形变量先后叠加到主反射面和副反射面,并采用主反射面共用和极化隔离的方法,实现了中心频点为12.5 GHz和14.25 GHz的两个轮廓波束同时通信;保持赋形反射面不变,运用Snell定律和射线追踪法寻找固定点波束较优馈源位置,实现了固定点波束;将点波束馈源在xOy平面横向偏焦实现有限扫描点波束;最终实现了两个轮廓波束一个点波束。两个赋形波束的增益面积(GAP)范围为
6000 ~18000 ,表明了该天线系统的有效性和可行性。 -
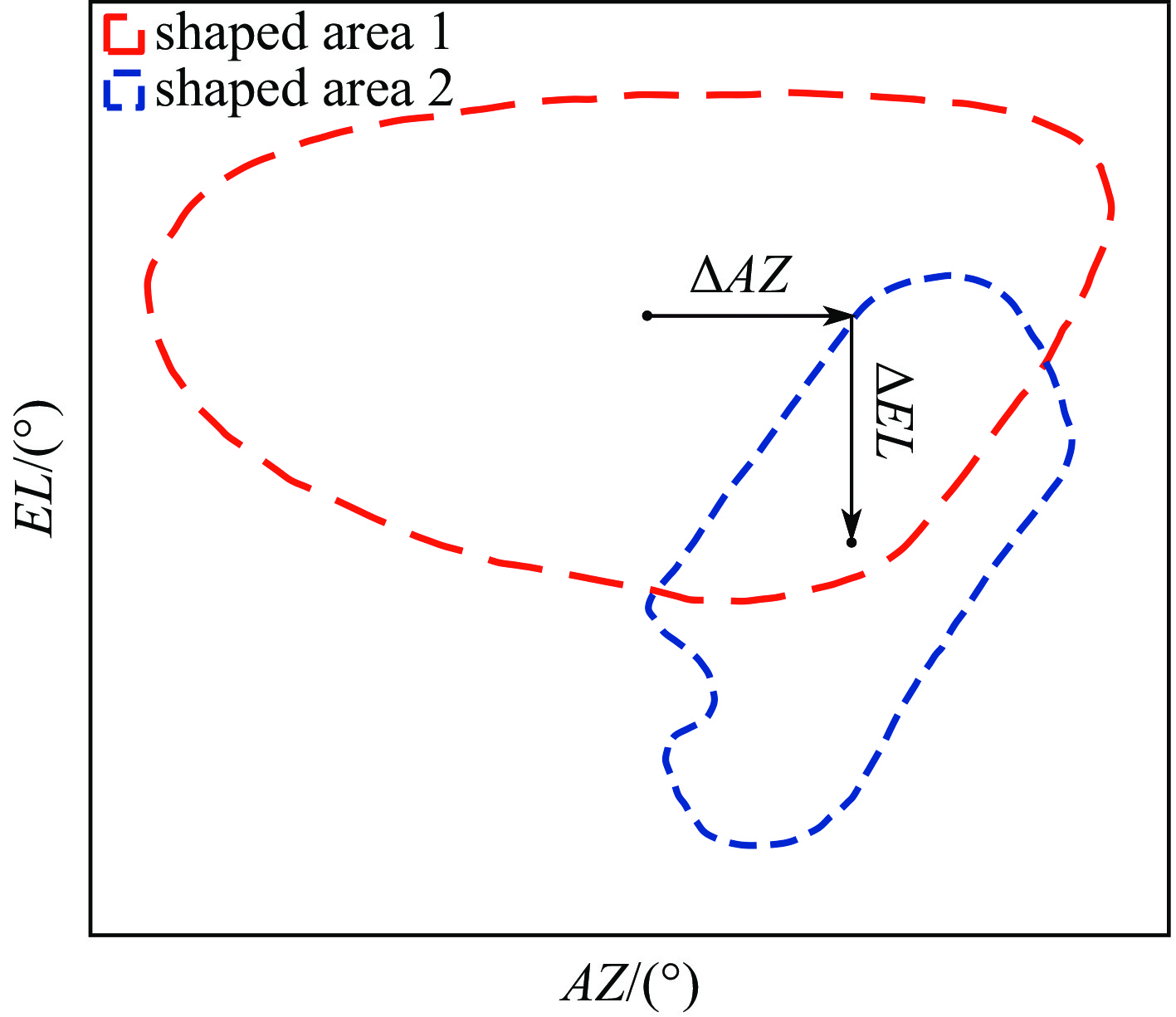
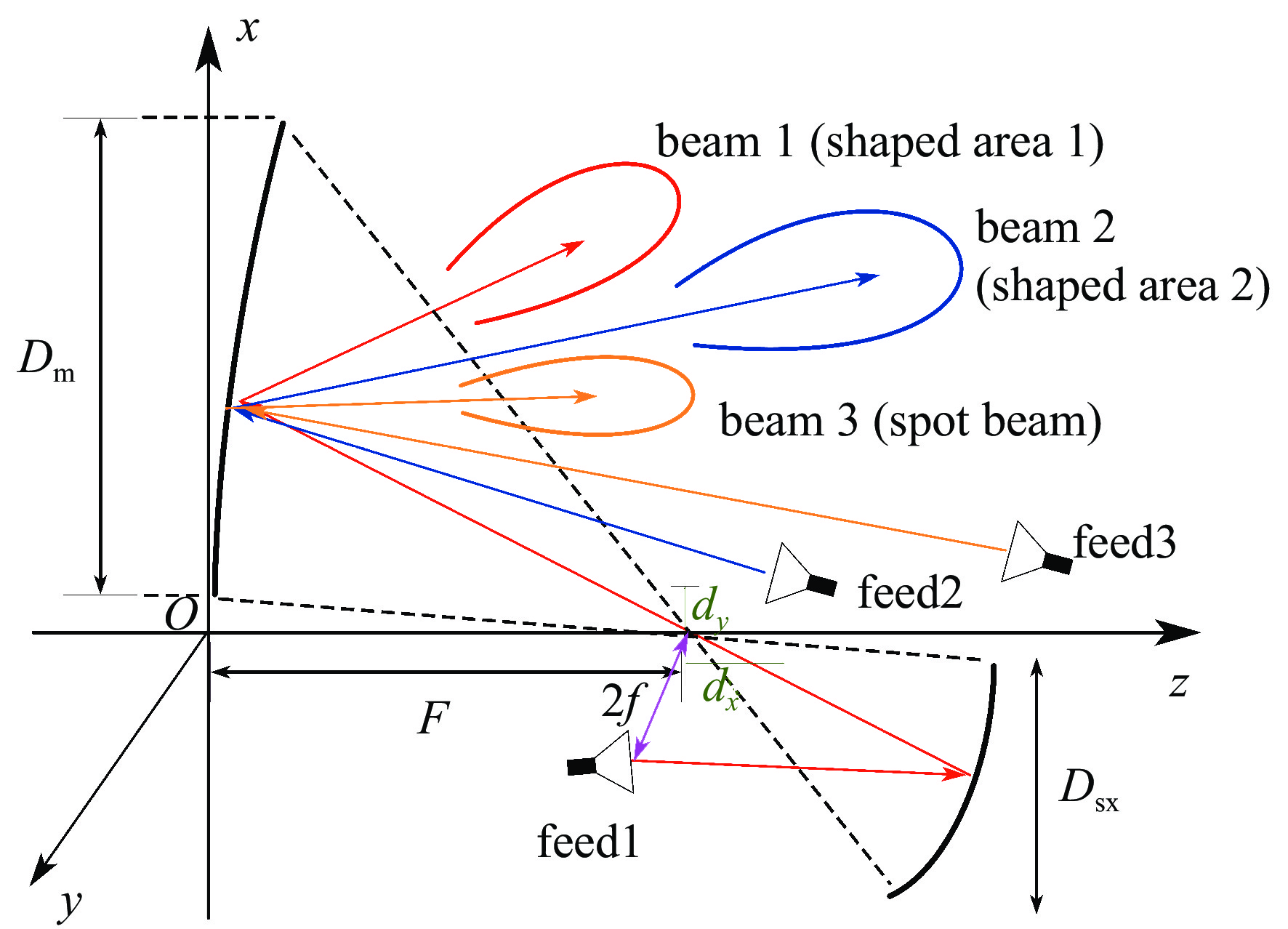
本文采用的是双偏置多馈源反射面天线(DMRA)结构,如图1所示。天线的结构是以满足Mizuguchi条件的格里高利型天线为基础[10],feed1馈源与主反射面(MR)和副反射面(SR)形成双偏置格里高利型天线以实现红色赋形区域1,feed2馈源和MR形成单偏置反射面天线以实现蓝色赋形区域2,如图2所示。Feed3馈源和MR也形成单偏置反射面天线以实现固定点波束,将feed3馈源偏焦实现有限扫描点波束。其中Dm为MR口径大小,Dsx为SR口径大小,F为MR焦距,
$ {\theta }_{0} $ 为MR偏置角度。 -
对于共口径反射面天线而言,最重要的三个参数是主反射面口径大小、主反射面焦距F以及馈源位置。赋形波束方向性系数G与赋形区域的面积、周长、口径与波长比有关。最小的方向性系数可表示为
式中:S代表覆盖区域的等效面积;C代表覆盖区域的等效周长;Dλ为口径与波长的比值。
Feed2馈源相对焦点的距离可表示为
式中:
$ \Delta EL $ 、$ \Delta AZ $ 表示两个赋形区域中心相对位置,如图2所示。从式(2)[9]可以看出feed2馈源位置根据两个赋形区域相对中心位置和主焦距决定(dx、dy单位为m)。详细天线结构参数见表1。通过仿真分析可知馈源位置对波束的影响:当馈源只在x方向移动时,波束在方位角方向移动;当馈源在y方向移动时,波束在俯仰方向移动;当馈源在z方向移动时,波束在俯仰方向和方位角方向均有移动,限于篇幅这里不展开分析。
-
赋形波束工作频点分别为14.25 GHz、12.5 GHz,用于覆盖两个交叠的异形区域以提供固定轮廓波束;固定点波束工作频点分别为17.9 GHz、17.5 GHz,为其中一个赋形区域内提供用于应急通信的高性能点波束;扫描波束在点波束附近实现有限范围扫描。收发波束进行极化隔离,实现不同波束同时工作且互相无干扰,指标见表2。
-
本文反射面天线系统设计可以分为三大步骤:首先通过先后优化Zernike多项式的系数和双三次B样条的控制点,对初始反射面叠加形变面进行反射面赋形设计,实现两个轮廓波束;然后保持赋形曲面不变,运用射线追踪法求解点波束的较优馈源位置;最后选取一个固定点波束进行深入研究,将馈源进行偏焦实现一定范围内的点波束扫描。
-
赋形波束是指将原有的笔形波束改变为与覆盖区域形状相同的轮廓波束。反射面天线实现赋形波束有两种方法:一是赋形反射面,将反射面运用基函数展开,通过优化基函数系数达到赋形效果,常用的基函数有Zernike多项式、双三次B样条(Cubic B-splines)、贝塞尔函数等;二是使用馈源阵列,根据服务区形状排列馈源,改变阵列馈源的激励系数实现赋形波束。第二种方法馈源网络设计复杂、成本高,本文采用第一种方法。
-
工程应用中常用的两种基函数是Zernike多项式和双三次B样条。Zernike多项式拟合曲面表达式为
式中:N、M是Zernike多项式最大拟合阶数;Cmn、Dmn是反射面展开后的Zernike系数;
$ \boldsymbol{R}_n^m(\rho) $ 是径向多项式,具体为根据实际应用需求,修改N、M阶数并改变Zernike系数Cmn和Dmn,在MR和SR上叠加Zernike表示的形面扰动量,以调节初始反射面形状进而修改口径场上的幅相分布,达到赋形的效果。由于Cmn和Dmn任意一个改变都会引起整体形面扰动量的改变,所以Zernike多项式影响反射面全局赋形。
-
B样条函数拟合曲面是由两个节点矢量A={a0, a1,…, ak+p+1}、B={b0, b1,…, br+q+1}和(k+1)×(r+1)个控制点Ci,j阵列构成的p×q次张量积曲面,可表示为[11]
式中:Ni,p(a)和Nj,q(b)是样条函数的基函数。由de Boor-Cox递推法则[12]可知,p次的基函数Ni,p(a)可以通过前p−1次进行递推获得,可表示为
因为样条曲面是由无数条A、B方向的曲线进行构成的,在赋形反射面时每个控制点只影响反射面局部形变,所以样条函数具有局部控制的能力。本文采用p、q均为3的基函数构造双三次B样条曲面,由于使用了19×19的Ci,j控制矩阵,所以需要将Ci,j矩阵细分为多个4×4的矩阵再进行处理。
-
为了实现两个复杂轮廓赋形,并达到任务指标,本文采用两种基函数混合使用的方法[13],将全局优化和局部优化的性能结合以实现抑制旁瓣、交叉极化并提高增益的目的。方法是采用Minimax优化算法对Zernike多项式的Cmn、Dmn系数和双三次B样条的Ci,j矩阵进行分步优化,在优化过程不断调整赋形区域增益和交叉极化以实现EOC gain、XPD的折衷。Minimax优化算法是一种数学规划的方法,该算法对于初始天线性能较好的结构优化时能实现快速收敛,并且优化用时小于进化算法。具体程序步骤如下。
Step1:初始化双偏置格里高利型天线。
Step2:加入Zernike多项式表示的形面扰动量,主要改善EOC gain和XPD。
Step3:加入双三次B样条函数表示的形面扰动量,主要改善旁瓣电平以及提高EOC gain。
-
固定点波束主要与MR形变程度及feed3馈源位置有关。本文采用射线追踪法求解feed3馈源较优位置[14]。
假设反射面上一点Pi,该点的输入向量为Si、反射向量为Sr、法向量为n,它们之间的关系为
假设
$ P(x,y,{\textit{z}}) $ 点为较优feed3馈源位置,P到Pi的距离平方为$ {\delta _i}^2 $ ,其可以表示为若P点到反射面上所有点的均方距离表示为
$ T(x,y,{\textit{z}}) $ (令$ {\delta _i}^2 $ =$ {d_i} $ ),则$ T(x,y,{\textit{z}}) $ 和$ {d_i} $ 之间的关系为最后对
$ T(x,y,{\textit{z}}) $ 求一阶偏导可求出极值点,便可推算出feed3馈源位置。 -
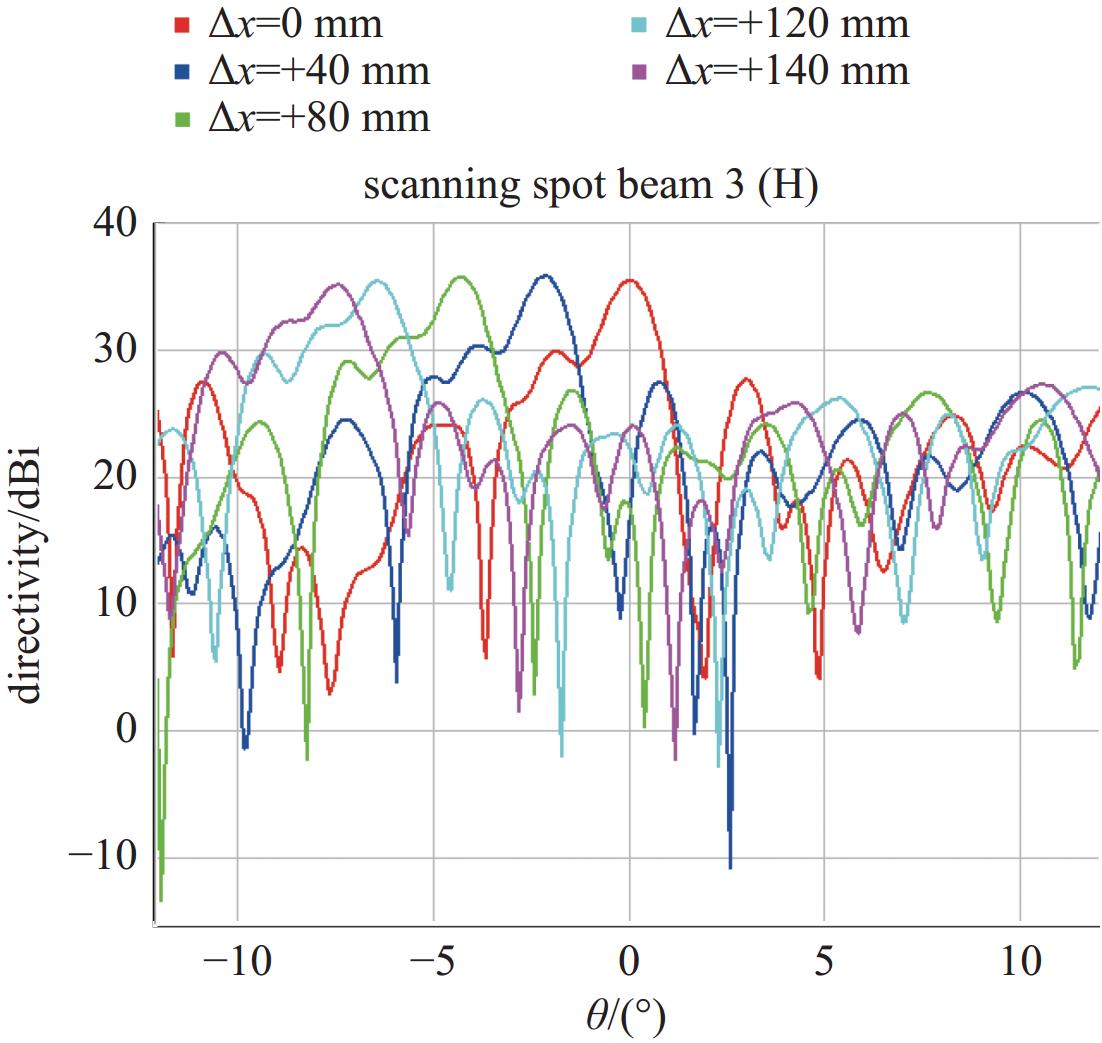
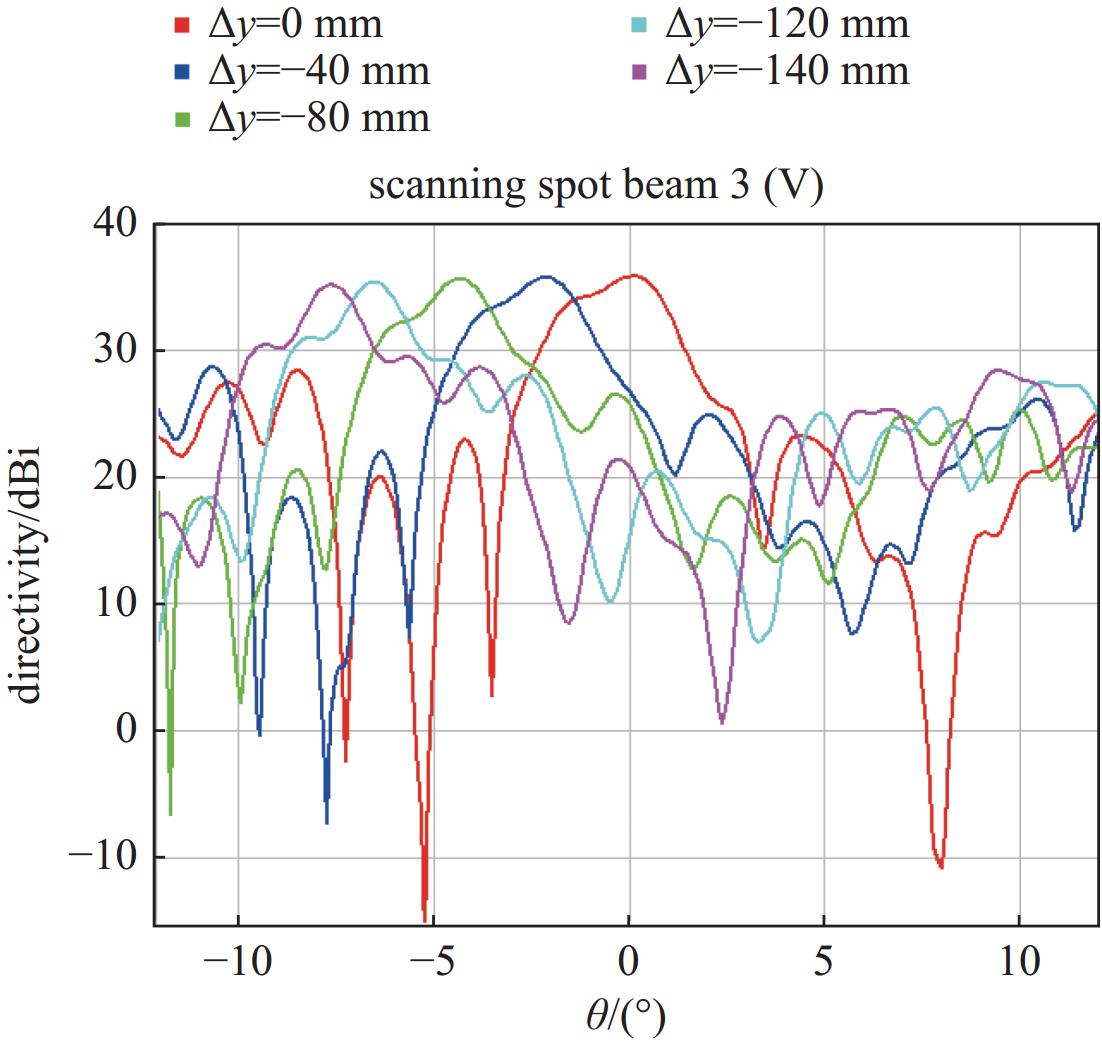
本文的有限扫描点波束是在固定点波束的基础上构造。得到feed3较优馈源位置后,将feed3馈源在xOy平面偏焦,分别考虑x方向、y方向偏焦,观察馈源在移动过程中点波束的增益以及旁瓣恶化情况,以及增益不低于35 dBi时的扫描角度。
-
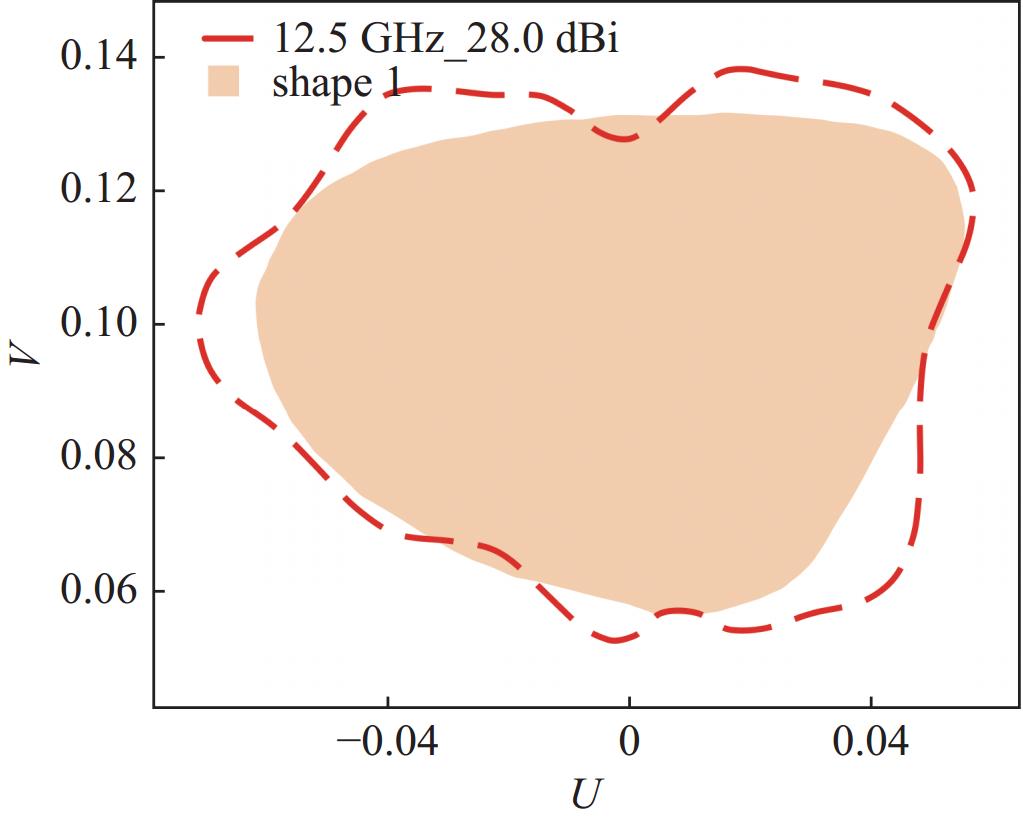
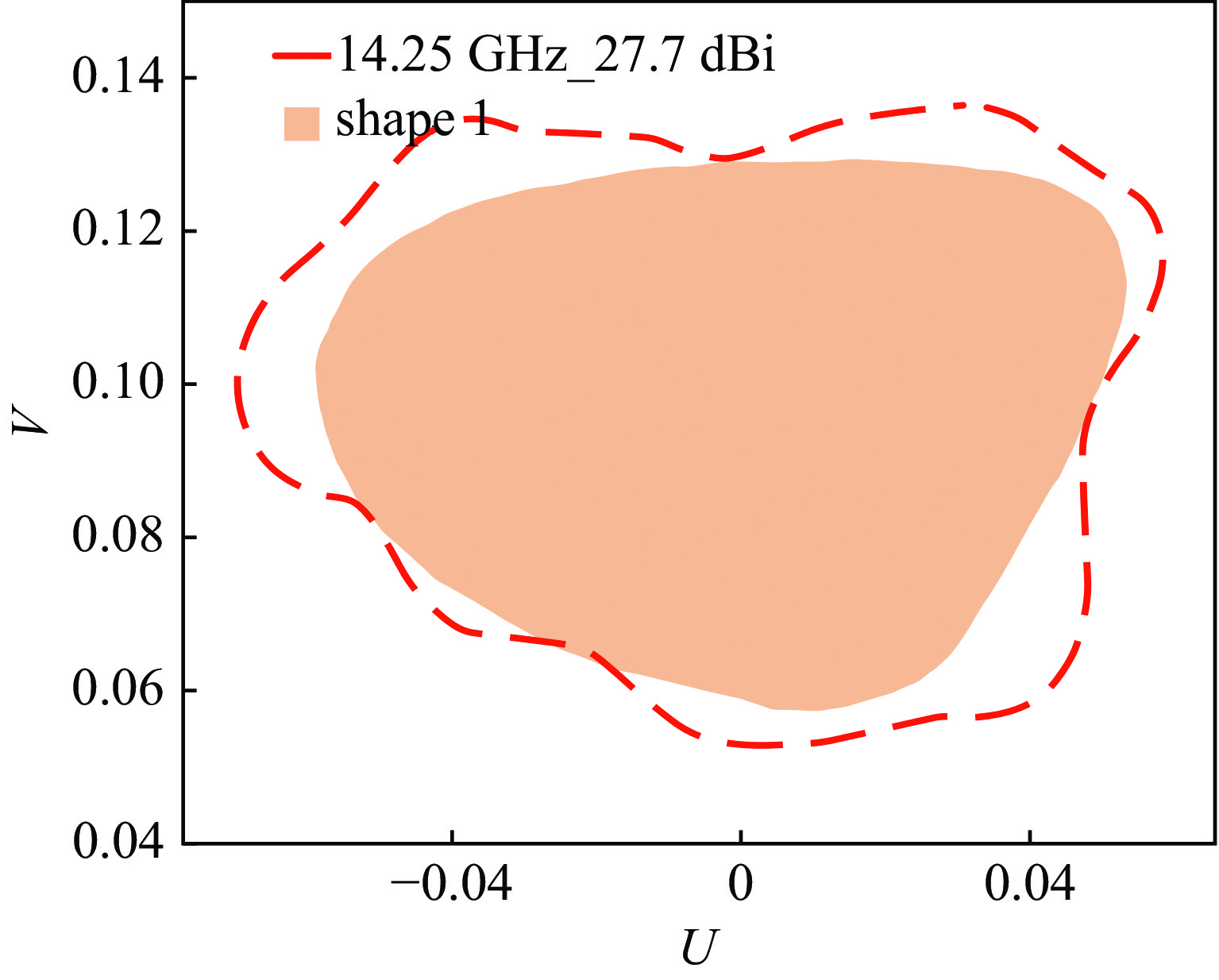
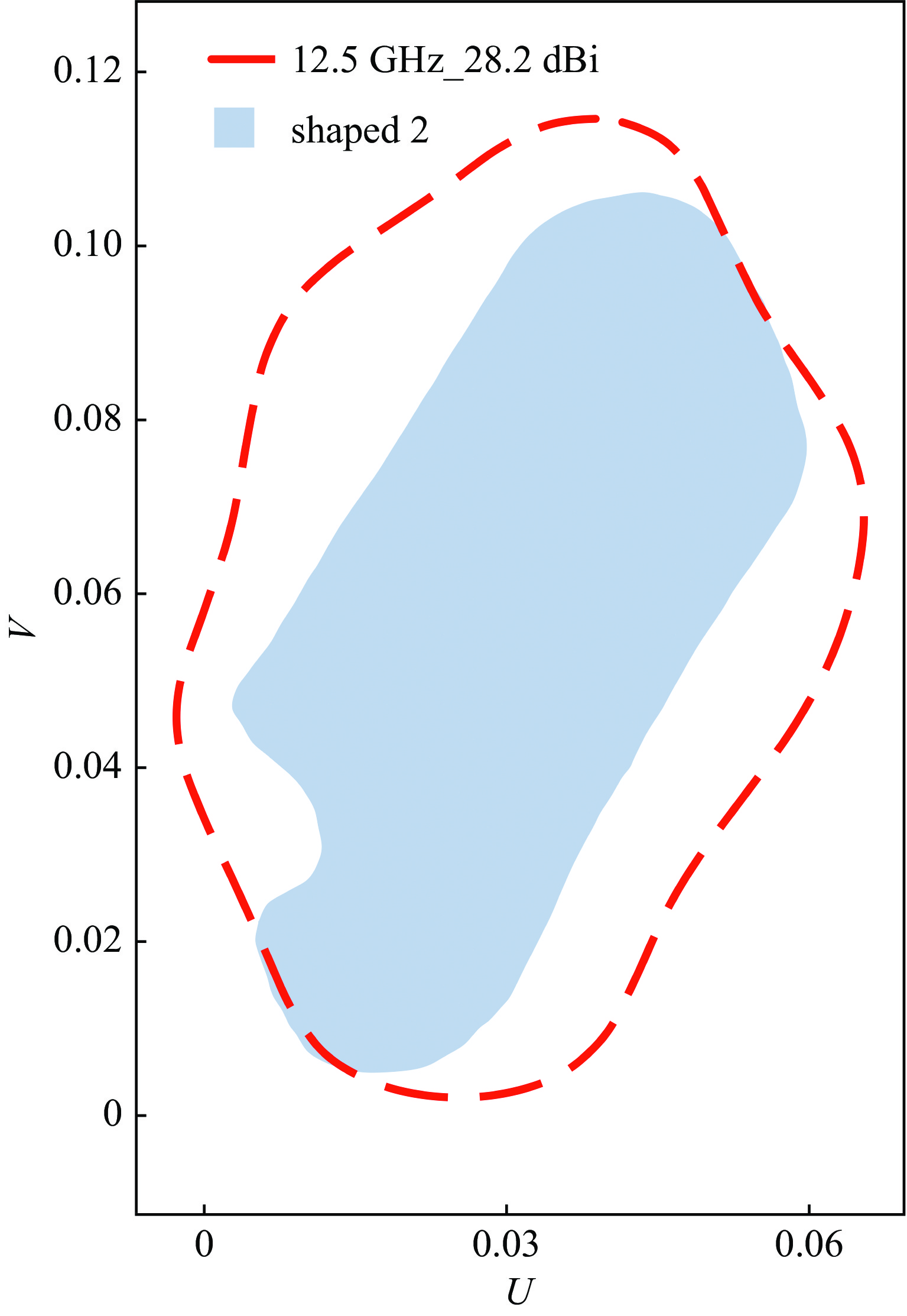
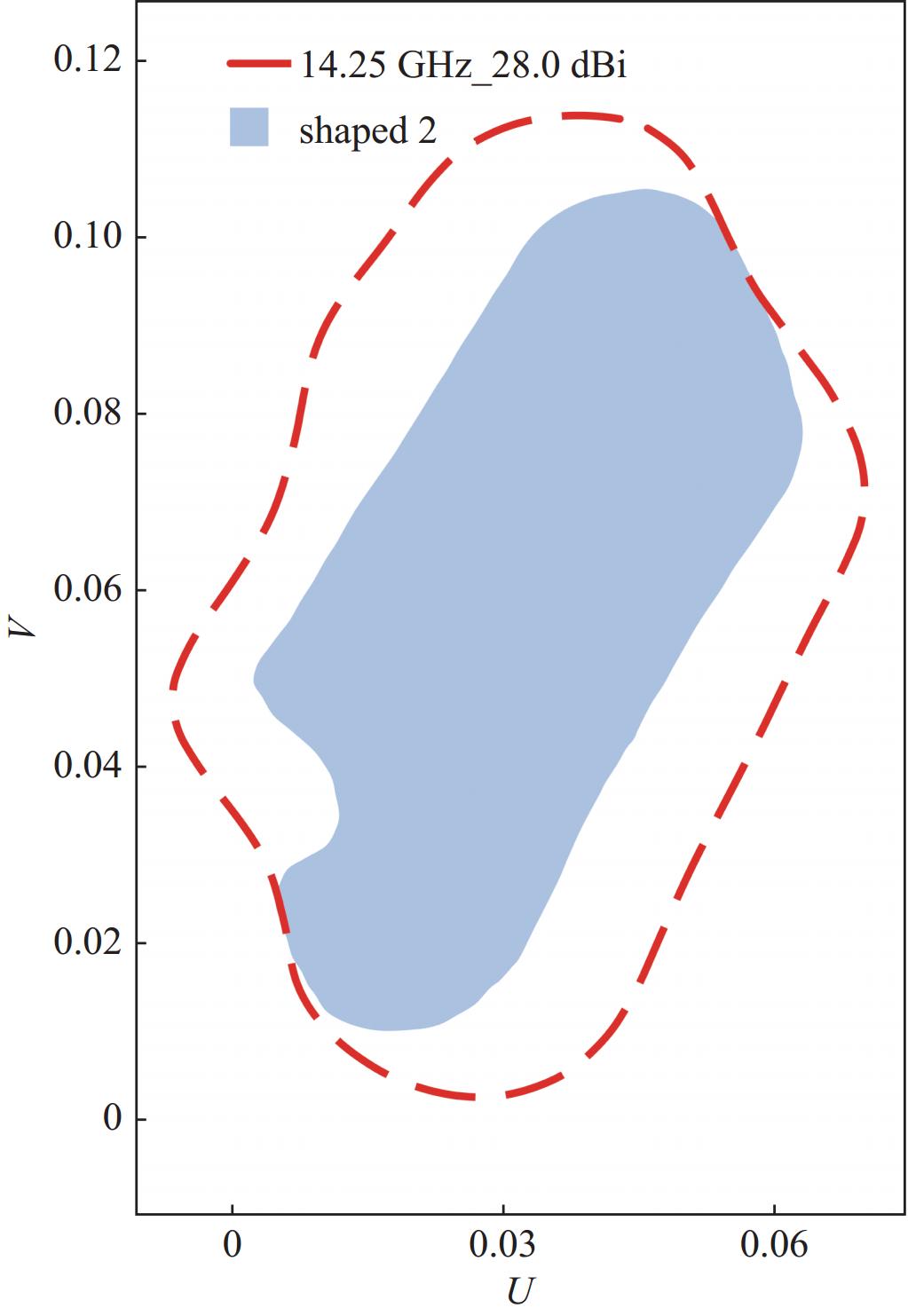
由图2可知,主要赋形区域是shape 1,次要赋形区域是shape 2,如图3至图6所示。Feed1、feed2馈源为横向槽波纹喇叭,锥削角度分别为23.7°和30°,边缘照射锥削电平选择−18 dB。运用TICRA Tools中的物理光学法、物理绕射理论(PO/PTD)和矩量法(MOM)为基本分析方法,并考虑散射、衍射、馈源遮挡、副反射面遮挡等影响,主要区域赋形方向性系数等值线效果见图3和图4,次要区域赋形方向性系数等值线效果见图5和图6。可见,无论是发射频率还是接收频率,每个赋形波束形状匹配较好,主赋形波束EOC gain不小于27.7 dBi,次赋形波束EOC gain不小于28 dBi,详细数据见表3。其中赋形波束使用(U,V)(注:文中所有赋形波束坐标U、V意义相同)坐标系可表示为
主要区域是通过feed1馈源、MR和SR形成的双偏置反射面天线进行赋形,次要区域是通过feed2馈源和MR形成单偏置反射面天线进行赋形,可以发现双反射面结构的交叉极化优于单反射面结构的交叉极化。
对于轮廓波束天线,常使用增益面积(GAP)[15-16]来表示波束品质因数。GAP的典型值约为
18000 ,其值随着赋形区域形状及面积的变化而变化,通常为6000 ~25000 (Dλ>25)[17]。由表4可知,两个赋形波束收发频段GAP估计值为6404 ~9149 ,表明该反射面天线具有良好的口径效率和可实用性。 -
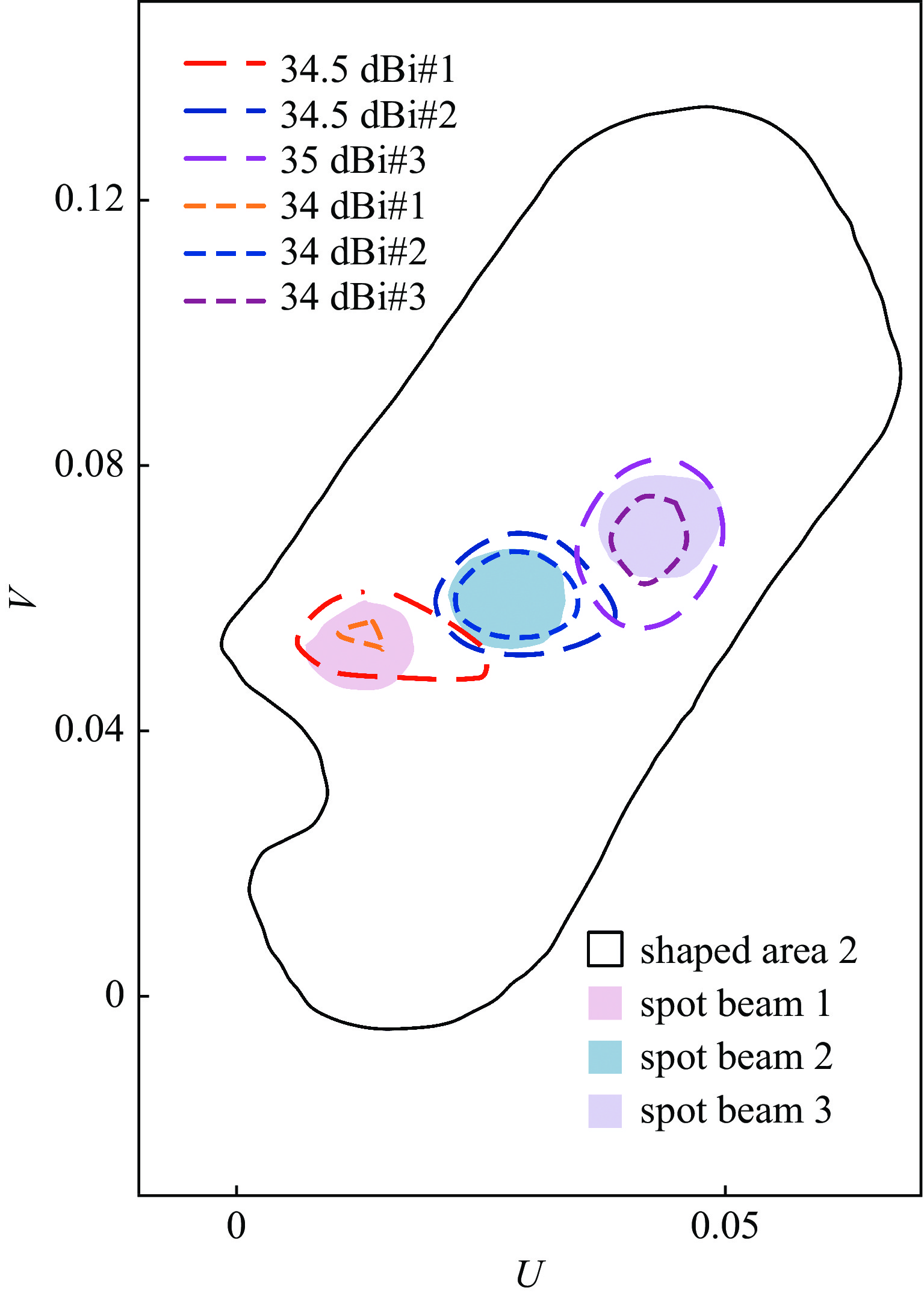
固定点波束收发中心频点为17.9 GHz和17.5 GHz,为了在保持主赋形波束运行的同时,在指定位置添加固定点波束与主赋形波束同时工作。本文运用射线追踪法通过式(7)至式(9)求解较优馈源位置。这里我们指定三个中心位置:(#1)spot beam 1,U=0.015,V=−0.037 ;(#2)spot beam 2,U=0.030,V=−
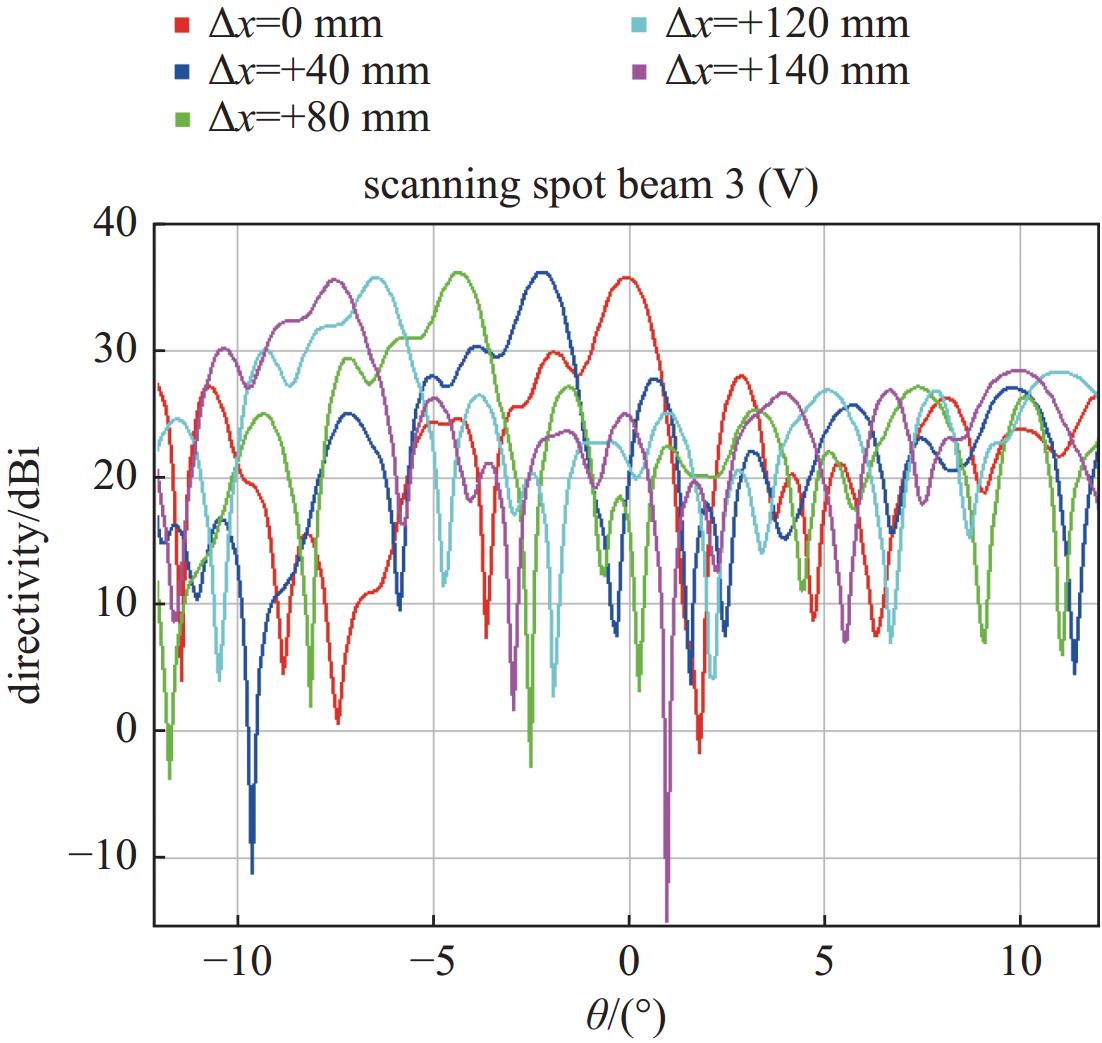
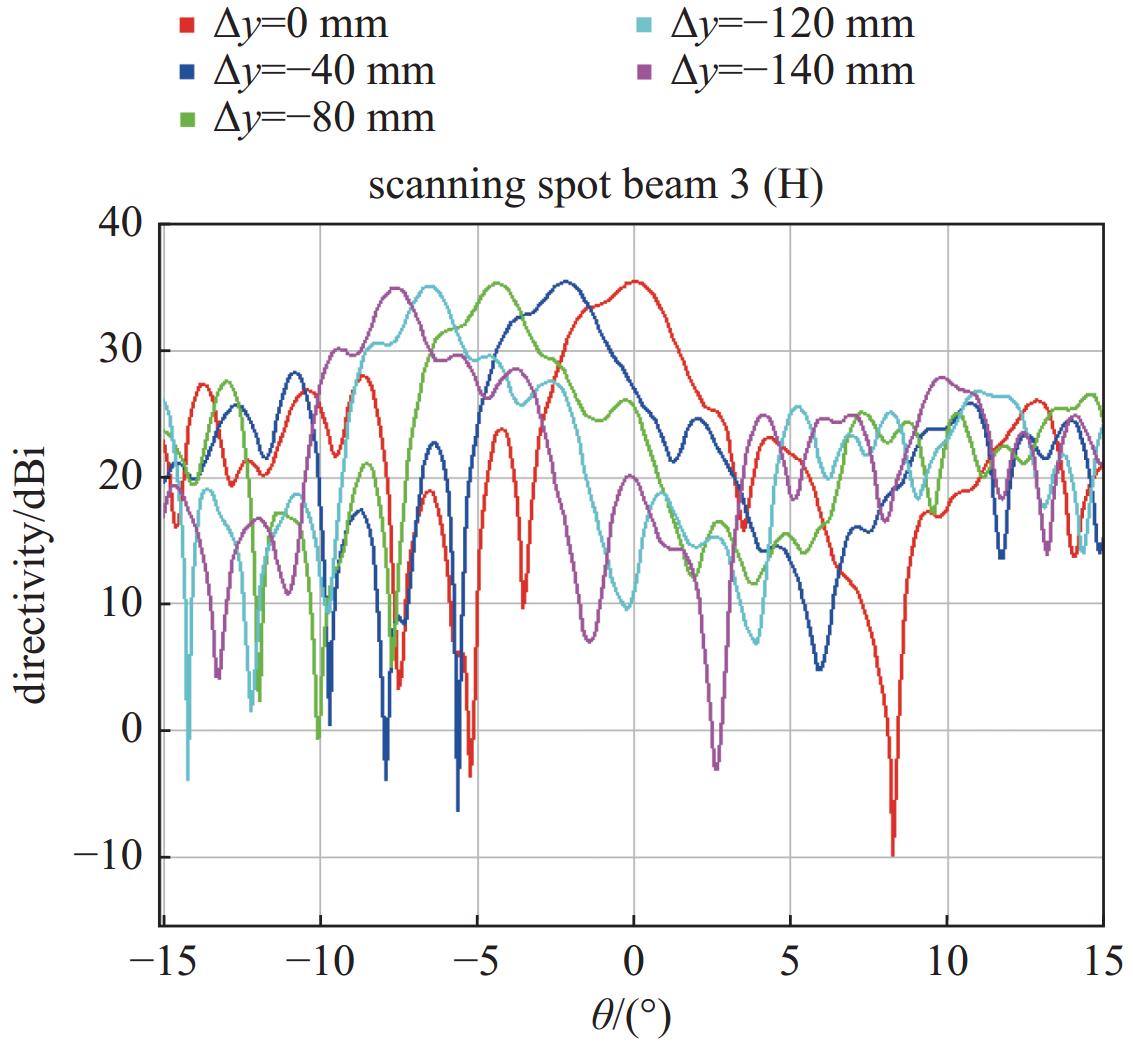
0.031 ;(#3)spot beam 3,U=0.043,V=−0.023。为了实现有限范围内的扫描波束,选取中心位置为第三个固定点波束,在该点波束的x向和y向进行一定偏焦,观察其效果。选取
$ \varphi $ 为0(x 方向)和90°(y 方向)时的切面进行扫描观察,如图9至图12所示。限于篇幅,这里仅展示当∆x、∆y分别变化时水平极化(17.5 GHz)的扫描数据,见表6。 -
在卫星通信系统中,有效载荷的设计往往受航天器装置、部署等物理空间的限制,因此有效利用物理空间、减少有效载荷的重量、降低天线设计成本是未来卫星通信系统发展的趋势。本文设计了一个新型共口径多波束反射面天线,实现了两个轮廓波束和一个点波束,该系统实现了任务指标,在设计过程中将主反射面共用,提高了反射面的利用率,减少了反射面天线有效载荷的物理空间和体积,结果表明主要赋形区域增益大于27.5 dBi,次要赋形区域增益大于28.0 dBi,两者赋形区域的GAP均在
6000 ~18000 范围内,因此该反射面天线系统具有良好的口径效率和可实用性。在实际应用中,还需要考虑馈源支柱对波束带来的影响;在寻找馈源位置时需要适当轴向偏焦来减少波束的遮挡;馈源的金属外壁引起的波束反射和衍射可以考虑添加吸波材料来减少。
星载共口径多波束赋形反射面天线设计
Design of common aperture multi-beam shaped reflector antenna for satellite communications
-
摘要: 为了满足星载通信中多任务并行需求,提出了一种由格里高利型反射面和三个馈源喇叭天线组成的共口径多波束反射面天线,该天线能够产生两个固定轮廓波束和一个点波束。天线设计是采用射线追踪法确定点波束馈源位置以建立天线基础结构,并通过Zernike多项式和Cubic B-splines函数共同对主、副反射面进行赋形优化来完成。为了验证该方法的有效性,对口径为1.1 m的天线进行仿真设计,结果表明两个赋形轮廓波束在Ku收、发频段边缘增益(EOC gain)分别为27.7、28.0、28.0、28.2 dBi,固定点波束在服务区EOC gain不低于34 dBi并且在0~6.5°范围内的扫描波束增益不低于35 dBi。
-
关键词:
- 星载天线 /
- 赋形波束 /
- Zernike多项式 /
- Cubic B-splines函数 /
- 射线追踪法
Abstract: To meet the requirement of multiple tasks in parallel in spaceborne communication, this paper proposes a common aperture multi-beam reflector antenna composed of a Gregorian reflector and three feed-horn antennas, which can generate two contoured beams and one spot beam. The antenna is designed using ray tracing method to determine the optimal spot beam feed position for establishing the antenna infrastructure, and employing Zernike polynomials and cubic B-splines function to optimize the shape of both the main and secondary reflectors. To validate the efficacy of the method, simulation experiments were conducted on 1.1 m diameter antenna. The results demonstrate that the edge of coverage gain for both shaped contour beams in Ku receiving and transmitting bands are 27.7 dBi, 28.0 dBi, 28.0 dBi and 28.2 dBi, respectively. The spot beam exhibits a minimum service EOC gain of not less than 34 dBi, while the scanning beam gain within the range of 0 to 6.5° is not less than 35 dBi.-
Key words:
- space-borne antenna /
- shaped beam /
- Zernike polynomials /
- cubic B-splines function /
- ray tracing method .
-

-
表 1 天线设计参数
Table 1. Design parameters for antenna
Dm/m F/m Dsx/m f/m feed1 position/m feed2 position/m feed3 position/m SR eccentricity 1.1 0.88 0.278 0.15 (−0.13,0,0.076) (0.035,0.055,0.92) (0.045,−0.043,0.84) 0.25 表 2 任务指标
Table 2. Task metrics
item EOC gain/dBi XPD/dB shaped beam 1 27.5 29 shaped beam 2 28.0 25 spot beam 34.0 30 EOC gain: edge-of-coverage gain; XPD: cross-polarization discrimination 表 3 赋形波束数据
Table 3. Date of shaped beam
shaped data transmitted form frequency/GHz linear polarization EOC gain/dBi XPD/dB EOC gain/dBi[10] shaped beam 2 TX 12.50 H 28.2 25 27.3 RX 14.25 V 28.0 25 27.1 shaped beam 1 TX 12.50 V 28.0 29 26.1 RX 14.25 H 27.7 29 26.1 H: horizontal ; V: vertical ; TX: transmit ; RX: receive 表 4 赋形波束GAP
Table 4. GAP of shaped beam
shaped data transmitted form Dλ GAP shaped beam 2 TX 45.83 6706 RX 52.25 6404 shaped beam 1 TX 45.83 9149 RX 52.25 8538 表 5 点波束增益
Table 5. Gain of spot beam
spot beam transmitted form gain/dBi XPD/dB #1 TX 34.58 30 RX 34.78 30 #2 TX 35.04 32 RX 35.27 31 #3 TX 35.38 33 RX 35.77 33 表 6 点波束增益
Table 6. Gain of spot beam
$ \Delta x/\mathrm{m}\mathrm{m} $ 

$ \Delta y/\mathrm{m}\mathrm{m} $ 

$ \theta$ /(°)

gain/dBi $ \Delta x/\mathrm{m}\mathrm{m} $ 

$ \Delta y/\mathrm{m}\mathrm{m} $ 

$ \theta $ /(°)

gain/dBi 40 0 −2.1 35.74 0 −40 −2.2 35.35 80 0 −4.3 35.67 0 −80 −4.3 35.27 120 0 −6.4 35.32 0 −120 −6.5 35.04 140 0 −7.4 35.07 0 −140 −7.6 34.80 -
[1] Rao S, Hsu C C, Wang J. Common aperture satellite antenna system for multiple contoured beams and multiple spot beams[C]//2010 IEEE Antennas and Propagation Society International Symposium. 2010: 1-4. [2] Pinsard B, Renaud D, Diez H. New surface expansion for fast PO synthesis of shaped reflector antennas[C]//Tenth International Conference on Antennas and Propagation. 1997: 25-29. [3] 李建军, 尹鹏飞, 赵现斌. 一种星载通信混合反射面天线的设计方法[J]. 电子与信息学报, 2020, 42(11):2621-2628 doi: 10.11999/JEIT190564 Li Jianjun, Yin Pengfei, Zhao Xianbin. A synthesis method of hybrid reflector antenna for satellite communications[J]. Journal of Electronics & Information Technology, 2020, 42(11): 2621-2628 doi: 10.11999/JEIT190564 [4] 潘昱旭, 王梓丞, 郭庆功. K波段平顶波束赋形反射面天线设计[J]. 四川大学学报(自然科学版), 2021, 58:043004 Pan Yuxu, Wang Zicheng, GUO Qinggong. Design of a K-band flat-top contoured-beam reflector antenna[J]. Journal of Sichuan University (Natural Science Edition), 2021, 58: 043004 [5] Dastranj A, Abiri H, Mallahzadeh A. Design of a broadband cosecant squared pattern reflector antenna using IWO algorithm[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(7): 3895-3900. doi: 10.1109/TAP.2013.2254439 [6] Mahajan M, Jyoti R, Sood K, et al. A method of generating simultaneous contoured and pencil beams from single shaped reflector antenna[J]. IEEE Transactions on Antennas and Propagation, 2013, 61(10): 5297-5301. doi: 10.1109/TAP.2013.2271492 [7] Lee J J, Parad L I, Chu R S. A shaped offset-fed dual-reflector antenna[J]. IEEE Transactions on Antennas and Propagation, 1979, 27(2): 165-171. doi: 10.1109/TAP.1979.1142056 [8] 李建军, 尹鹏飞, 赵现斌, 等. 双馈源双偏置结构星载通信多波束天线[J]. 微波学报, 2018, 34(4):10-15 Li Jianjun, Yin Pengfei, Zhao Xianbin, et al. Multi-beam antenna with double feeds and dual-offset configuration for space-borne communication[J]. Journal of Microwaves, 2018, 34(4): 10-15 [9] Wan Jixiang, Yan Tao, Wang Feng. A hybrid reflector antenna for two contoured beams with different shapes[J]. IEEE Antennas and Wireless Propagation Letters, 2018, 17(7): 1171-1175. doi: 10.1109/LAWP.2018.2836927 [10] Granet C. Designing classical offset Cassegrain or Gregorian dual-reflector antennas from combinations of prescribed geometric parameters[J]. IEEE Antennas and Propagation Magazine, 2002, 44(3): 114-123. doi: 10.1109/MAP.2002.1028736 [11] Li Tiansong, Shi Xinling, Chen Jianhua, et al. The global double cubic B-spline surface interpolation based on particle swarm optimization[C]//2013 IEEE International Conference on Signal Processing, Communication and Computing (ICSPCC). 2013: 1-5. [12] Piegl L, Tiller W. The NURBS book [M]. 2nd ed. Berlin: Springer, 1997. [13] Gupta R C, Sagi S K, Raja K P, et al. Shaped prime-focus reflector antenna for satellite communication[J]. IEEE Antennas and Wireless Propagation Letters, 2017, 16: 1945-1948. doi: 10.1109/LAWP.2017.2689800 [14] Krichevsky V, DiFonzo D. Optimum beam scanning in offset single and dual reflector antennas[J]. IEEE Transactions on Antennas and Propagation, 1985, 33(2): 179-188. doi: 10.1109/TAP.1985.1143547 [15] Rao S, Shafai L, Sharma S. Handbook of reflector antennas and feed systems Volume I: theory and design of reflectors[M]. Boston: Artech House, 2013. [16] Rao S, Shafai L, Sharma S. Handbook of reflector antennas and feed systems volume III: applications of reflectors[M]. Boston: Artech House, 2013. [17] Rao S K. Advanced antenna technologies for satellite communications payloads[J]. IEEE Transactions on Antennas and Propagation, 2015, 63(4): 1205-1217. doi: 10.1109/TAP.2015.2391283 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: