全文HTML
-
近些年,随着加速器技术的发展[1−3],越来越多的原子核能级被观测到,核数据越发完善,这为研究原子核结构方面相关问题提供了新机会。特别地,幻数
$ N=28 $ 附近pf壳层核结构问题引起了的广泛关注[4],例如壳结构的演化[5],张量力的作用[6],中子和质子旋磁比之间的线性关系[7],中子和质子配对作用对基态形成的影响[8],原子核形状共存[9]以及恒星系统的演化[10]等。对于幻数$ N=28 $ 附近核素,随着中子数目的增加,其结构不仅受到pf壳影响,甚至某些核素会受到$ 1g_{9/2} $ 轨道影响[11−12],从而导致幻数$ N=28 $ 附近壳结构出现能级反转等特殊现象。因此,讨论和研究围绕幻数$ N=28 $ 附近pf壳结构演化规律及其特点具有重要的意义。目前,对于
$ N=28 $ 附近Mn和Ni同位素壳结构,已经有了广泛的讨论。其中,对于质子数$ Z=28 $ 的Ni同位素,早在1967年便有文献对其壳结构进行了深入研究[4]。随后,又采用蒙特卡罗壳方法(Monte Carlo Method)对56Ni附近的核素进行计算,解释了双幻核中球形与形变共存的现象[9]。而在质子数$ Z=26 $ 的Mn同位素,文献[11, 13]通过熔合-蒸发反应观测到57−60Mn的高自旋数据;近期,又利用壳模型对奇A核49−57Mn同位素的低激发态进行系统研究,揭示并讨论了基态反转和基态自旋序列的集体性[14]。位于Ni和Mn之间质子数$ Z=27 $ 的Co同位素,虽然实验数据相对丰富[15−21],但该同位素的系统研究仍然存在空白。因此,本文旨在对围绕$ N=28 $ 附近的奇A核Co同位素的壳结构问题展开讨论。为了进一步深入研究
$ N=28 $ 附近Co同位素的能级,理论计算至关重要。壳模型是目前应用最广泛的原子核微观理论模型之一,已经成功应用于轻质量数和幻数附近原子核结构性质研究[13, 22−35]。对于某一模型空间,哈密顿量可利用球形基矢与有效相互作用进行对角化。因此,在壳模型的框架下,Co同位素的集体性质和准粒子激发都可以在确定的模型空间中被描述。本文结构如下,第1节为壳模型理论方法简介,第2节给出了奇A核Co同位素壳模型计算结果与讨论,第3节为总结展望。 -
壳模型计算就是精确求解原子核的多体薛定谔方程,原子核的薛定谔方程[36−37]中哈密顿量可写为
其中:
$ H_0 $ 为无微扰哈密顿量;$ H_1 $ 为微扰哈密顿量;T为核子动能;U为选取的合适的单体势;V为核子-核子之间的相互作用,选取模型空间P空间以及被排除的Q空间[38]:D为模型空间的维数,可以得到模型空间内的薛定谔方程[38]:
考虑模型空间P以及模型外空间Q,可以定义在模型空间内的有效哈密顿量[38]:
使用多体微扰理论可以将有效相互作用写为
式中:
$ H_0 $ 为哈密顿量的非微扰部分;ω为非微扰部分能量,第一项为哈密顿量单体部分,最后两项代表哈密顿量剩余相互作用部分。在壳模型计算中,通常仅分析费米面附近核子的关联效应,冻结满壳层下的核子,将计算空间限制在少量的价核子以及一个较小的有效价空间内。在大多数情况下,选择两个幻数之间的价空间是合适的,并可以在价空间内构建两体或多体相互作用[39]。
-
为了更深入地理解
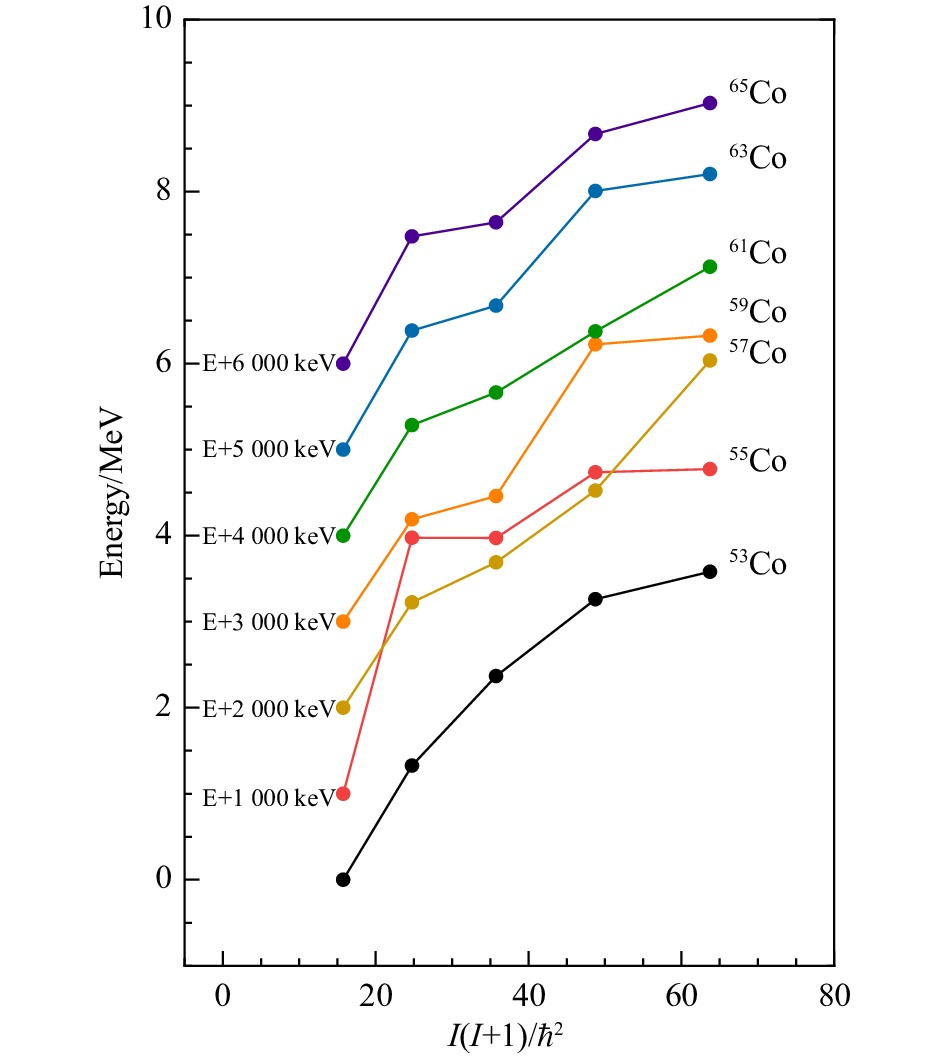
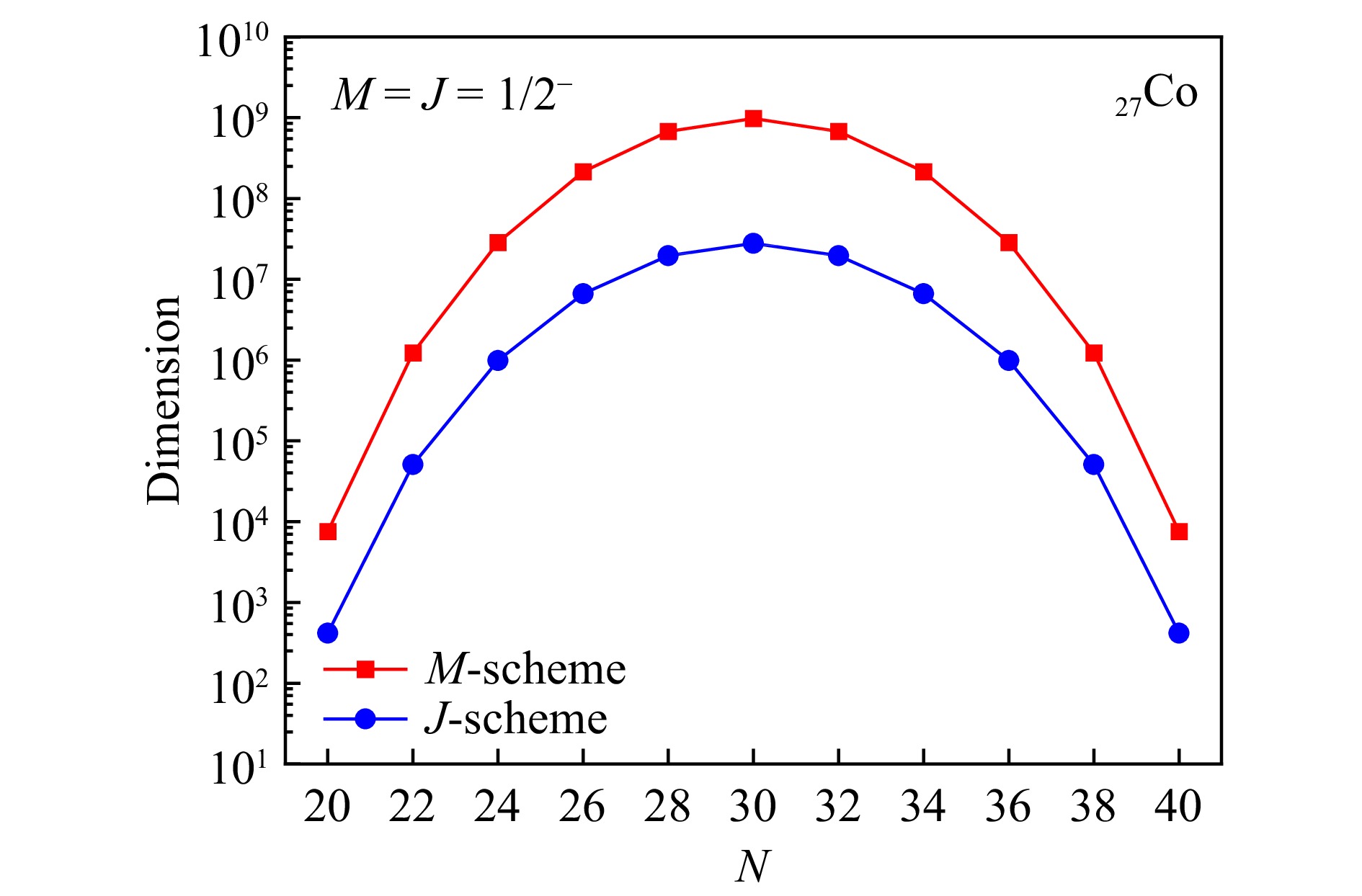
$ N=28 $ 附近Co原子核的微观结构,本文首先对奇A核53−65Co[15−21, 40−45]晕态即自旋宇称序列$ 7/2^-、9/2^-、11/2^-、13/2^-、15/2^- $ 实验结果进行了系统学研究;然后基于壳模型程序ANTOINE[46],使用GXPF1A相互作用[47]计了其能量、磁矩、电四极矩、质子中子平均占据数及组态,研究其结构性质。此时,将40Ca视为核芯,剩余核子限制在pf壳模型空间,即模型空间由四个质子轨道($ 1f_{7/2},\, 2p_{3/2},\, 1f_{5/2},\, 2p_{1/2} $ )和四个中子轨道($ 1f_{7/2},\, 2p_{3/2},\, 1f_{5/2},\, 2p_{1/2} $ )构成。计算中选取标准有效电荷($ e_{\mathrm{p}}=1.5,\, e_{\mathrm{n}}=0.5 $ )和自由g因子($ g_{s}^{\pi}=5.586 $ ,$ g_{l}^{\pi}=1.000 $ ,$ g_{s}^{v}=-3.826 $ ,$ g_{l}^{v}=0 $ )。图1展示了pf壳模型空间下,奇A核Co同位素链$ 1/2^{-} $ 态在M-scheme和J-scheme下分别对应的壳模型计算的维数。从图1中可以看出,M-scheme下55, 57, 59Co的计算维数接近$ 10^9 $ ,达到了程序的计算极限。为避免维数过大所带来的计算困难,对这三个核素的质子模型空间作了截断。考虑到质子$ f_{7/2} $ 轨道与$ p_{3/2} $ 、$ f_{5/2} $ 、$ p_{1/2} $ 轨道之间能隙较大,质子波函数的主要组态为$ \pi (1f_{7/2})^{7} $ ,因此,仅允许最多三个质子从$ f_{7/2} $ 轨道向上激发,中子激发未限制。图2展示了奇A核53−65Co同位素负宇称晕态实验能量[48]随
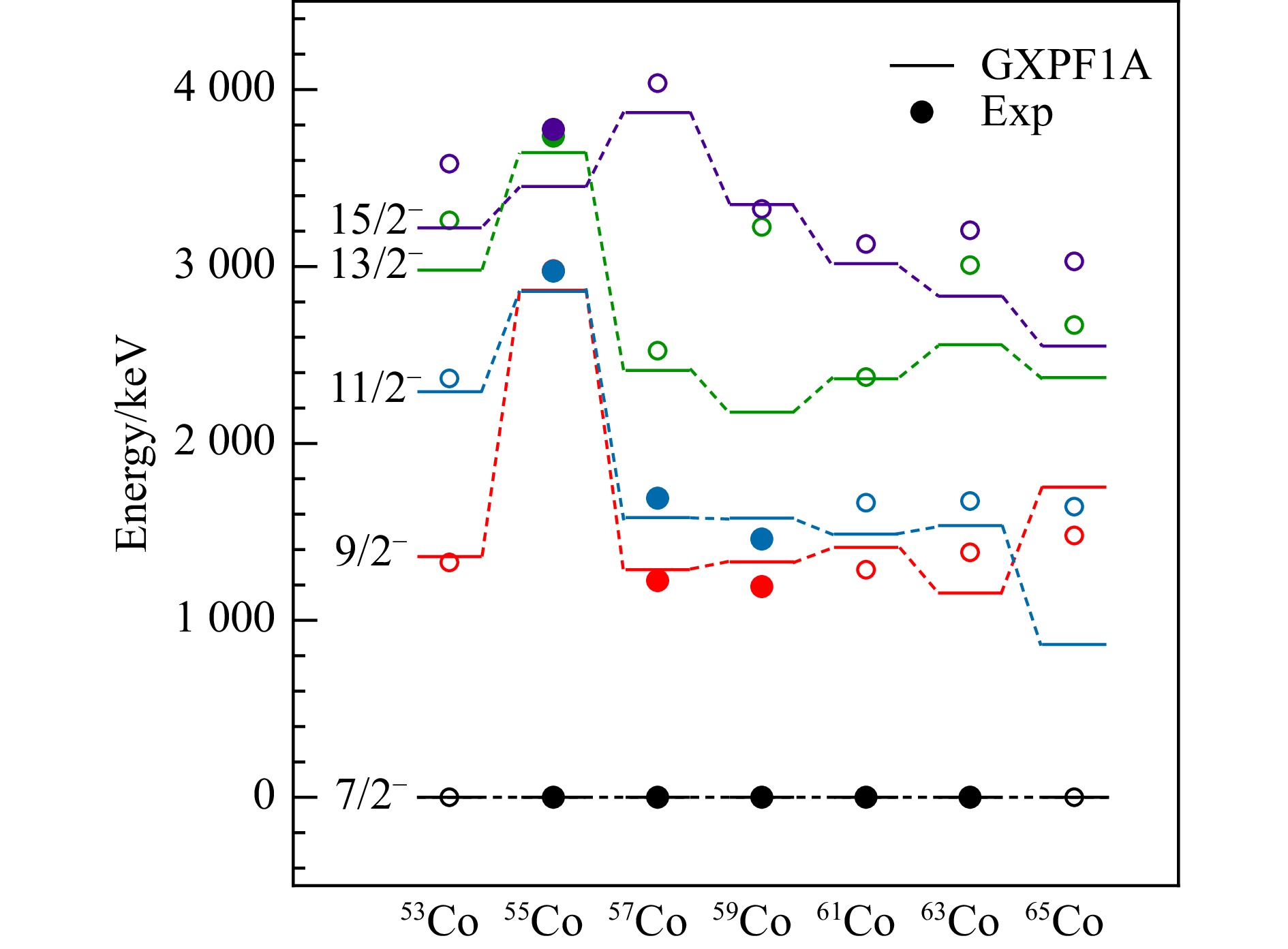
$ I(I+1) $ 的变化趋势。为了更清楚地观察演化趋势,对图2中核素的激发能进行垂直方向的平移。从图中能够观察到53Co激发能与$ I(I+1) $ 近似呈线性关系,表明其可能具有集体转动效应,这与49Cr[49]和49Mn[14]中激发能随自旋变化相类似。对于超过$ 15/2^- $ 的激发态,由于激发能随自旋变化曲线存在明显振荡,且相关文献[50]中指出,超过$ 15/2^- $ 的自选值可能存在单准粒子和三准粒子之间的组态竞争,因此本文仅针对自旋低于$ 15/2^- $ 的激发态进行讨论。随着中子数增加,特别是55, 59Co出现较大的能量波动,激发能与$ I(I+1) $ 的线性关系不明显,表明了可能存在较强的单粒子激发。奇A核53−65Co相应实验上的激发能[15−21]的系统对比如图3所示(其中实验上确定数据用实心圆表示,不确定数据用空心圆表示)。从图3中的实验值可以发现,55Co的激发能与其他核表现出了明显的差异;
$ 9/2^- $ ,$ 11/2^- $ 与$ 13/2^- $ 的能级能量都比其他核明显高。$ 9/2^- $ 的能级能量表现出了异常的高,以至于与$ 11/2^- $ 能级出现了轻微的反转。对于整体而言,对于自旋$ 9/2^- $ ,$ 11/2^- $ 与$ 13/2^- $ 的能级,这些核有着相似的趋势,即在55Co处出现峰值后出现相对大的剧减,除了自旋$ 13/2^- $ 在63Co出现微小的涨幅外,在最后大致趋于平缓。而对于自旋$ 15/2^- $ 的能级,这些核的能级呈现大概抛物线的趋势,在55Co处出现峰值。为了解释奇A核53−65Co以上系统性的特点,基于GXPF1A相互作用[47],计算得到的激发能(短线)如图3。从图中可以看出,GXPF1A基本再现了这些核的
$ 9/2^- $ 、$ 11/2^- $ 、$ 13/2^- $ 和$ 15/2^- $ 的能级和演化趋势。具体来说,除了65Co的计算的能级与实验值有较大的差异之外,其他核计算的能级与实验值符合得比较好。对于使用的GXPF1A相互作用,它的拟合的核素范围为A = 47~65,因此对于65Co的中子接近相互作用拟合采用的核素范围的边界,这可能是导致计算结果与实验值具有较大差异的原因。此时模型空间可能要考虑$ g_{9/2} $ 轨道[12, 51],未来可以进一步研究$ g_{9/2} $ 轨道的贡献。表1列出了壳模型计算得到的奇
$ A $ 核53−65Co基态自旋7/2−,激发态9/2−、11/2−、13/2−和15/2−质子和中子的平均占据数及组态成分最大的两组组态。其中,组态成分由左至右依次为1$ f{_{7/2}} $ 、2$ p{_{3/2}} $ 、1$ f{_{5/2}} $ 和2p1/2轨道。如表1所列,55Co基态中质子在$ \pi(1f_{7/2}) $ 轨道上的占据数为6.7,相比其他核素一般为6.5的占据数而言更接近于7,说明55Co其基态$ 7/2^- $ 组态较稳定。此外,55Co在$ 9/2^- $ 以及$ 11/2^- $ 态中,$ \pi(1f_{7/2}) $ 的轨道占据数为6.1,相比其他同位素6.4的占据数,55Co质子在$ 9/2^- $ 与$ 11/2^- $ 态更容易被激发,因此55Co 的$ 9/2^- $ 以及$ 11/2^- $ 态激发能要远高于其他同位素。从表1中可以看出,55Co的基态
$ 7/2^- $ 中,$ \pi\left(1f_{7/2}\right)^7\otimes \nu\left(1f_{7/2}\right)^8 $ 组态占主导,占比为66%,其占比明显高于其他同位素中占据主导的组态。因此,从组态占比上同样能够观测到55Co基态$ 7/2^- $ 的组态较稳定。55Co的激发态$ 9/2^- $ 中概率最高的两组组态为$ 25 {\text{%}} \pi\left(1f_{7/2}\right)^6\left(2p_{3/2}\right)^1\otimes \nu\left(1f_{7/2}\right)^8+23 {\text{%}} \pi\left(1f_{7/2}\right)^7\otimes\nu\left(1f_{7/2}\right)^7{\left(2p_{3/2}\right)}^1 $ ,二者占据概率相当,质子激发与中子激发概率几乎一致。而在$ 11/2^- $ 态下概率最高的两组组态为$ 23 {\text{%}} \pi\left(1f_{7/2}\right)^7\otimes\nu\left(1f_{7/2}\right)^7{\left(2p_{3/2}\right)}^1+ 13 {\text{%}} \pi\left(1f_{7/2}\right)^6\left(2p_{3/2}\right)^1\otimes\nu\left(1f_{7/2}\right)^8 $ ,其中子激发占优。分析可知这两种组态的占比大小在$ 9/2^- $ 与$ 11/2^- $ 态中恰好相反,且两激发态内这两种组态的占比差别较小,从而导致两个激发态的能级差距较小。这反映出在55Co中$ 9/2^- $ 和$ 11/2^- $ 态质子激发与中子激发存在竞争关系,导致$ 9/2^- $ 与$ 11/2^- $ 态之间发生能级反转,而其余的Co的同位素中占据主导的质子组态均为$ \pi\left(1f_{7/2}\right)^7 $ ,主要以中子激发为主,表明这些核素中质子很难跨壳激发。为进一步验证计算得到的波函数的有效性,我们将壳模型计算得到的奇
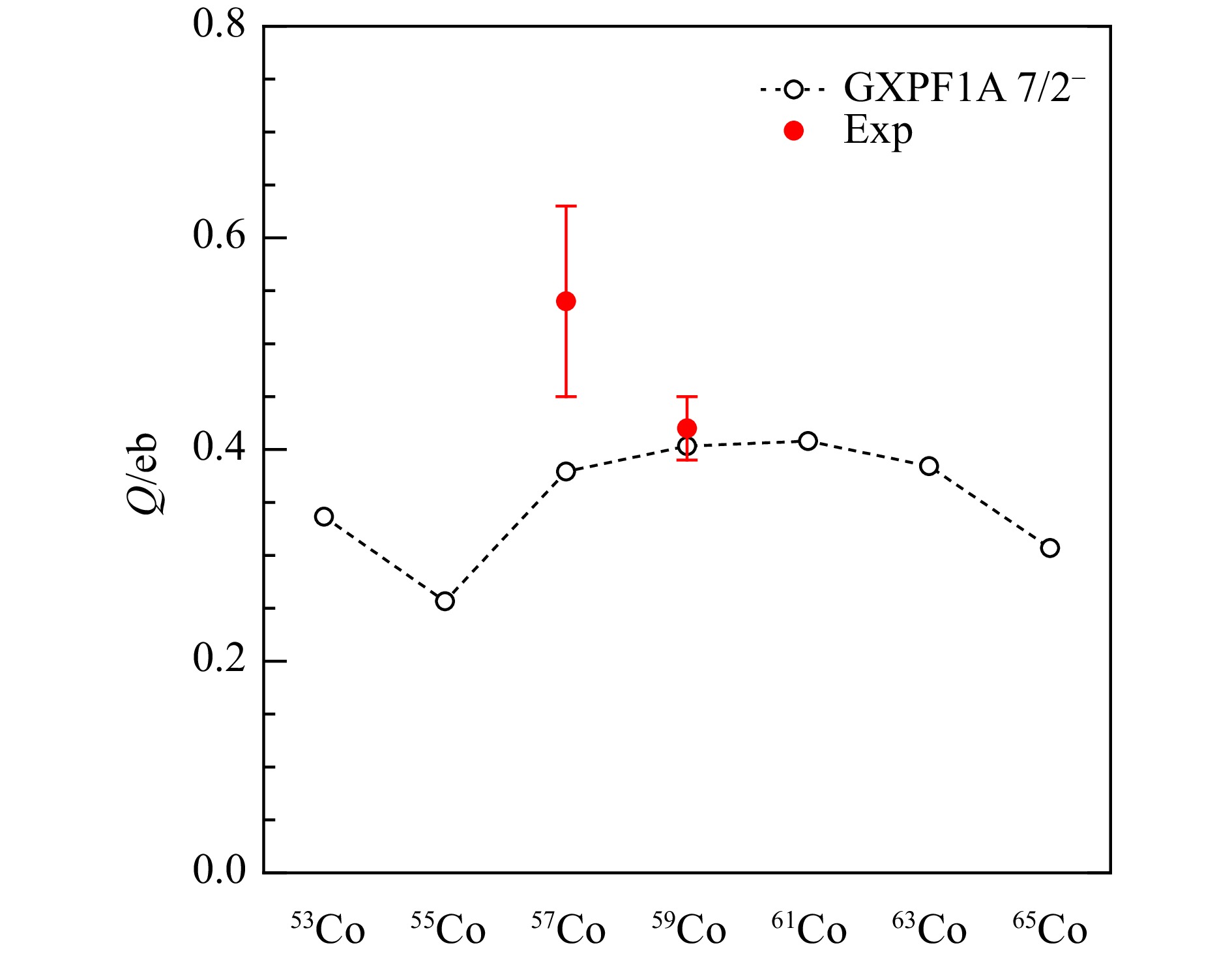
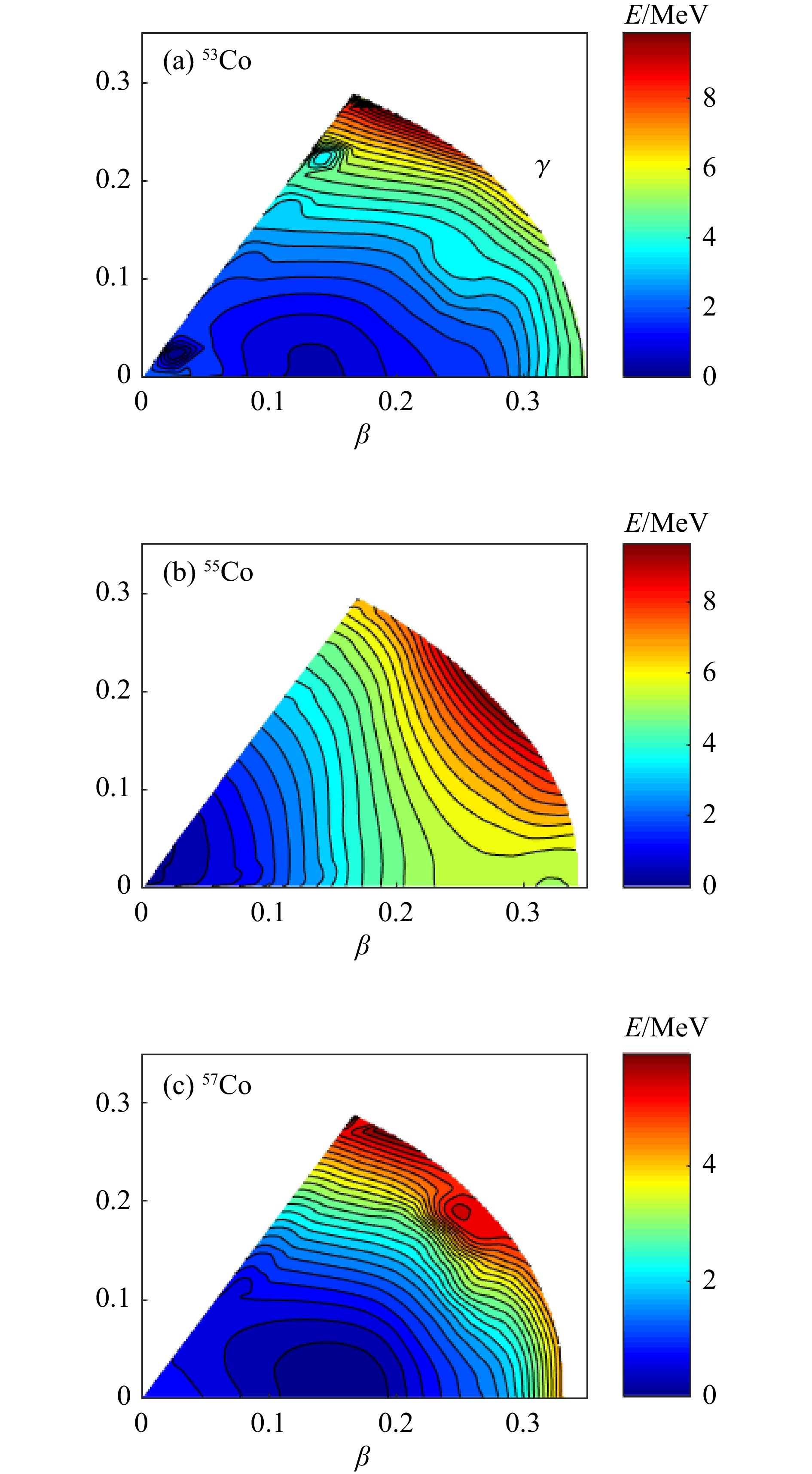
$ A $ 核53−65Co基态($ 7/2^- $ )磁矩与实验值[52−54, 55]进行对比,结果如表2所列。通过壳模型计算得到的这些核的基态磁矩与已有的55, 57, 59Co的实验磁矩十分接近,表明计算得到的波函数是合理的。此外还理论预言了其他几个核的基态磁矩。图4也将理论计算的这些核的基态电四极矩与已有的实验电四极矩[53, 56]进行了对比,从图可以看到,59Co的基态电四极矩与实验值相吻合,而57Co计算值偏小。除此之外,从图4可以观察到55Co基态$ 7/2^- $ 的电四极矩突然下降,说明55Co在基态情况下形变较小,这与图5得到的55Co形变结果一致。本文的壳模型计算中取40Ca为核芯,核芯为球形,且核芯中的核子激发被冻结,故核芯对Co同位素形变的影响可以忽略。在现有的模型空间下,基于GXPF1A相互作用,利用CHF方法[57]计算得到53, 55, 57Co自旋
$ I=7/2 $ 时的等势能面如图5所示。图5中53, 57Co的位能面极小处$ \beta $ 形变为0.13,呈现出近球形核趋势;这可能是导致53, 57Co在自旋$ 7/2^-、9/2^-、11/2^-、13/2^- $ 和$ 15/2^- $ 中的激发能呈现出具有集体转动效应的原因。而55Co位能面极小处$ \beta $ 形变为0,因此中子数$ N=28 $ 的55Co应呈现出明显的球形核特征,1$ f{_{7/2}} $ 轨道质子不易激发,从而导致55Co激发态能相较于其他同位素更高。 -
综上,本文首先对奇A核53−65Co同位素链实验的低激发态
$ 7/2^-、9/2^-、11/2^-、13/2^- $ 和$ 15/2^- $ 进行了系统的研究,通过对激发能与自旋的变化趋势分析得到53, 57Co可能存在集体转动效应,CHF方法计算得到的等势能面也反映出了这两个核的确存在弱的四极形变。此外也揭示了$ N=28 $ 附近Co同位素的特殊现象,指出了55Co能级突变及反转、能级序列的集体性等显著特点。基于GXPF1A有效相互作用的壳模型计算能够比较好地再现了奇A核53−65Co已有的实验上电四极矩和磁矩,也比较好地再现了低激发态的能级。计算结果表明,基态自旋$ 7/2^- $ 质子主要组态成分为$ \pi\left(1f_{7/2}\right)^7 $ ,中子数$ N=28 $ 的55Co中,基态情况下组态较稳定,在$ 9/2^- $ 与$ 11/2^- $ 的激发态中55Co质子和中子激发之间存在竞争,因此质子激发占优的$ 9/2^- $ 与中子激发占优的$ 11/2^- $ 态能级相近,从而导致$ 9/2^- $ 与$ 11/2^- $ 态之间发生能级反转。再者通过CHF方法得到中子数$ N=28 $ 的55Co应呈现出明显的球形核特征,1$ f{_{7/2}} $ 轨道质子不易激发,从而导致55Co激发态能相较于其他同位素更高。需要指出的是,目前计算结果依然存在不足之处,由于计算的Co同位素链在pf壳价核子数目较多,对角化时产生大量Lanzcos矢量,所以本研究对55, 57, 59Co三个同位素原子核采取冻结部分核子在轨道上的截断方式进行壳模型计算。此外,本文仅采用GXPF1A相互作用对于低激发态进行研究,并未采用其他的相互作用与计算方法进行计算并相互印证,也并未考察较高激发态的组态以及能级情况,这些都是接下来工作需要完善的地方。

 首页
首页 登录
登录 注册
注册




 下载:
下载: