高级搜索

辐照效应对于掺镱光纤放大器模式不稳定阈值影响的理论研究

,  ,  ,  ,  ,  , 

downloadPDF

上一篇

下一篇

曹涧秋, 周尚德, 刘鹏飞, 黄值河, 王泽锋, 司磊, 陈金宝. 辐照效应对于掺镱光纤放大器模式不稳定阈值影响的理论研究[J]. 物理学报, 2024, 73(20): 204202-1. doi: 10.7498/aps.73.20240816
引用本文: 曹涧秋, 周尚德, 刘鹏飞, 黄值河, 王泽锋, 司磊, 陈金宝. 辐照效应对于掺镱光纤放大器模式不稳定阈值影响的理论研究[J]. 物理学报, 2024, 73(20): 204202-1. doi: 10.7498/aps.73.20240816
shu
Jian-Qiu Cao, Shang-De Zhou, Peng-Fei Liu, Zhi-He Huang, Ze-Feng Wang, Lei Si, Jin-Bao Chen. Theoretical study on radiation effect on threshold of transverse mode instability of Yb-doped fiber amplifiers[J]. Acta Physica Sinica, 2024, 73(20): 204202-1. doi: 10.7498/aps.73.20240816
Citation: Jian-Qiu Cao, Shang-De Zhou, Peng-Fei Liu, Zhi-He Huang, Ze-Feng Wang, Lei Si, Jin-Bao Chen. Theoretical study on radiation effect on threshold of transverse mode instability of Yb-doped fiber amplifiers[J]. Acta Physica Sinica, 2024, 73(20): 204202-1. doi: 10.7498/aps.73.20240816
shu

辐照效应对于掺镱光纤放大器模式不稳定阈值影响的理论研究

  • 1.

    国防科技大学前沿交叉学科学院, 长沙　410073

  • 2.

    国防科技大学南湖之光实验室, 长沙　410073

  • 3.

    国防科技大学高能激光技术湖南省重点实验室, 长沙　410073

    • 作者简介: 曹涧秋.E-mail: jq_cao@126.com .
    通讯作者: E-mail: kdchenjinbao@aliyun.com.

  • 中图分类号: 42.55.Wd, 42.88.+h, 42.65.Sf, 42.60.Lh

Theoretical study on radiation effect on threshold of transverse mode instability of Yb-doped fiber amplifiers

  • 1.

    College of Advanced Interdisciplinary Studies, National University of Defense Technology, Changsha 410073, China

  • 2.

    Nanhu Laser Laboratory, National University of Defense Technology, Changsha 410073, China

  • 3.

    Hunan Provincial Key Laboratory of High Energy Laser Technology, National University of Defense Technology, Changsha 410073, China

    • Corresponding author: E-mail: kdchenjinbao@aliyun.com.

  • MSC: 42.55.Wd, 42.88.+h, 42.65.Sf, 42.60.Lh

  • 摘要: 光纤放大器在辐照环境中具有良好的应用前景, 而模式不稳定(transverse mode instability, TMI)效应则是制约光纤放大器功率提升的重要因素. 因此, 针对辐照效应对于掺镱光纤放大器TMI阈值的影响, 开展了理论研究. 通过将辐致损耗引入光纤放大器的TMI理论模型, 率先给出了考虑辐照效应的TMI阈值表达式, 探讨了TMI阈值随辐射剂量的变化规律, 研究表明: 辐照效应对于TMI阈值的影响, 不仅与光纤的抗辐照性能有关, 还与光纤放大器的增益系数有关. 增益系数的增大, 会减缓TMI阈值随辐射剂量的衰减, 但也会导致TMI阈值的整体下降. 通过对比辐照效应对于TMI阈值和输出功率的影响, 结果发现, TMI阈值随辐致损耗衰减更快. 这也使得TMI效应成为辐照条件下光纤放大器输出功率的限制因素. 相关研究结果, 对于辐射条件下光纤放大器的设计及应用研究具有指导意义.
    Abstract: Yb-doped fiber amplifiers and their applications in radiation environments have become more and more attractive in recent years. However, the radiation effect will cause damage to the Yb-doped fibers, which can give negative effect on the output properties of Yb-doped fiber amplifiers. In this work, the influence of radiation effect on the transverse mode instability (TMI) of Yb-doped fiber amplifier is studied. TMI can couple the single light from the fundamental mode to high-order mode, thereby degenerating the beam quality of fiber amplifier. TMI is considered a key limitation of power up-scaling of fiber amplifiers.In this work, the radiation effect on the TMI is studied theoretically, and a formula of TMI threshold is presented by taking the radiation-induced attenuation (RIA), the most important radiation effect for the TMI, into account. The formula is deduced by introducing the loss of signal light induced by RIA into the formerly reported TMI-threshold formula which can be obtained by the linear stability analysis of the numerical model studying the TMI. Then, the relationship between the TMI and radiation dose is also given with the help of Power-Law describing the relationship between the RIA and radiation dose.With the formula, the variations of TMI threshold with the radiation dose and RIA are studied. It is found, as expected, that the TMI threshold decreases monotonically with the increase of RIA or radiation dose. Nevertheless, it is unexpectedly found that, to some extent, the gain coefficient of fiber amplifiers will also affect the radiation effect on TMI threshold. The results reveal that the increase of gain coefficient will lower the sensitivity of TMI threshold to the radiation dose. However, it is also implied that the gain coefficient cannot be too large because it can also make the TMI threshold lowered. Therefore, in order to maintain a high TMI threshold in a radiation environment, sufficient radiation resistance of Yb-doped fiber is essential.Because the RIA can affect not only the TMI threshold but also the output power or efficiency of Yb-doped fiber amplifier, the comparison between two effects of RIA is also discussed. It is found that the threshold of TMI is more sensitive to the radiation than to the output power or efficiency (see the figure attached below), which means that the TMI can exist in the irradiated Yb-doped fiber amplifier, although the output power is reduced because of RIA. This result can be verified by the experimental observation reported formerly. As a result, TMI can become a key limitation to the output power of Yb-doped fiber amplifier in radiation environments. The relevant results can provide significant guidance for the applications of Yb-doped fiber amplifiers in radiation environments.
  • 加载中

  • 图 1  归一化TMI阈值随辐射剂量D、系数C1和f的变化, 泵浦光和信号光波长分别为976 nm和1080 nm, 增益系数gsat为2 dB/m, f取值分别为0.5 (a), 0.7 (b), 0.9 (c), 1.1 (d)

    Figure 1.  Variation of normalized TMI threshold with radiation dose D, coefficients C1 and f, the pump wavelength and signal wavelength are 976 nm and 1080 nm, respectively, and the gain coefficient gsat is 2 dB/m. The value of coefficient f are 0.5 (a), 0.7 (b), 0.9 (c), and 1.1 (d), respectively.

    下载: 全尺寸图片 幻灯片

    图 2  归一化TMI阈值随辐射剂量D、系数C1和f的变化, 泵浦光和信号光波长分别为976 nm和1080 nm, 系数f为0.7, 增益系数取值分别为1 dB/m (a), 3 dB/m (b), 5 dB/m (c), 10 dB/m (d)

    Figure 2.  Variation of normalized TMI threshold with radiation dose D, coefficients C1 and f. The pump wavelength and signal wavelength are 976 nm and 1080 nm respectively, and the coefficient f is 0.7. The value of gain coefficient are 1 dB/m (a), 3 dB/m (b), 5 dB/m (c), and 10 dB/m (d), respectively.

    下载: 全尺寸图片 幻灯片

    图 3  不同增益系数对应的TMI阈值随D的变化　(a) C1 = 0.002, f = 0.5; (b)C1 =0.012, f = 0.9, 纤芯直径为30 μm

    Figure 3.  Variation of TMI threshold with D corresponding to various gain coefficient: (a) C1 = 0.002, f = 0.5; (b) C1 = 0.012, f = 0.9, the core diameter is 30 μm.

    下载: 全尺寸图片 幻灯片

    图 4  归一化TMI阈值(实线、虚线和点划线)及输出功率比值(空心圆点)随辐致损耗的变化　(a)光纤长度为20 m; (b)光纤长度为10 m

    Figure 4.  Variation of normalized TMI threshold (solid, dashed, and dotted) and output power ratio (hollow dots) with RIA: (a) Yb-doped fiber length is 20 m; (b) Yb-doped fiber length is 10 m.

    下载: 全尺寸图片 幻灯片

    图 5  TMI阈值与输出功率随辐致损耗的变化

    Figure 5.  Variation of TMI threshold and output power with RIA.

    下载: 全尺寸图片 幻灯片
    下载: 全尺寸图片 幻灯片
  • [1] Girard S, Kuhnhenn J, Gusarov A, Brichard B, Uffelen M V, Ouerdane Y, Boukenter A, Marcandella C 2013 IEEE Trans. Nucl. Sci. 60 2015 doi: 10.1109/TNS.2012.2235464
    [2] Girard S, Morana A, Ladaci A, Robin T, Mescia L, Bonnefois J J, Boutillier M, Mekki J, Paveau A, Cadier B, Marin E, Ouerdane Y, Boukenter A 2018 J. Optics-UK 20 093001 doi: 10.1088/2040-8986/aad271
    [3] Henschel H, Kohn O, Schmidt H U, Kirchof J, Unger S 1998 IEEE Trans. Nucl. Sci. 45 1552 doi: 10.1109/23.685238
    [4] Rose T S, Gunn D, Valley G C 2001 J. Lightw. Technol. 19 1918 doi: 10.1109/50.971685
    [5] Faustov A V, Gusarov A, Wuilpart M, Fotiadi A A, Liokumovich L B, Zolotovskiy I O, Tomashuk A L, Schoutheete T D, Mégret P 2013 IEEE Trans. Nucl. Sci. 60 2511 doi: 10.1109/TNS.2013.2273273
    [6] Ma J, Li M, Tan L Y, Zhou Y P, Yu S Y, Ran Q W 2009 Opt. Express 17 15571 doi: 10.1364/OE.17.015571
    [7] Girard S, Ouerdane Y, Tortech B, Marcandella C, Robin T, Cadier B, Baggio J, Paillet P, Ferlet-Cavrois V, Boukenter A, Meunier J P, Schwank J R, Shaneyfelt M R, Dodd P E, Blackmore E W 2009 IEEE Trans. Nucl. Sci. 56 3293 doi: 10.1109/TNS.2009.2033999
    [8] Fox B P, Simmons-Potter K, Thomes W J, Kliner D A V 2010 IEEE Trans. Nucl. Sci. 57 1618 doi: 10.1109/TNS.2010.2043854
    [9] Duchez J B, Mady F, Mebrouk Y, Ollier N, Benabdesselam M 2014 Opt. Lett. 39 5969 doi: 10.1364/OL.39.005969
    [10] Xing Y B, Zhao N, Liao L, Wang Y B, Li H Q, Peng J G, Yang L Y, Dai N L, Li J Y 2015 Opt. Express 23 24236 doi: 10.1364/OE.23.024236
    [11] Chen Y S, Xu H Z, Xing Y B, Liao L, Wang Y B, Zhang F F, He X L, Li H Q, Peng J G, Yang L Y, Dai N L, Li J Y 2018 Opt. Express 26 20430 doi: 10.1364/OE.26.020430
    [12] Tao M M, Chen H W, Feng G B, Luan K P, Wang F, Huang K, Ye X S 2020 Opt. Express 28 10104 doi: 10.1364/OE.384980
    [13] Tan S, Li Y, Zhang H S, Wang X W, Jin J 2022 Chin. Phys. B 31 064211 doi: 10.1088/1674-1056/ac43a8
    [14] Shao C Y, Ren J J, Wang F, Ollier N, Xie F H, Zhang X Y, Zhang L, Yu C L, Hu L L 2018 J. Phys. Chem. B 122 2809 doi: 10.1021/acs.jpcb.7b12587
    [15] Kher S, Chaubey S, Oak S M, Gusarov A 2013 IEEE Photonic. Technol. Lett. 25 2070 doi: 10.1109/LPT.2013.2281200
    [16] Fernandez A F, Brichard B, Berghmans F 2003 IEEE Photonic. Technol. Lett. 15 1428 doi: 10.1109/LPT.2003.818247
    [17] Eidam T, Wirth C, Jauregui C, Stutzki F, Jansen F, Otto H-J, Schmidt O, Schreiber T, Limpert J, Tünnermann A 2011 Opt. Express 19 13218 doi: 10.1364/OE.19.013218
    [18] Beier F, Möller F, Sattler B, Nold J, Liem A, Hupel C, Kuhn S, Hein S, Haarlammert N, Schreiber T, Eberhardt R, Tünnermann A 2018 Opt. Lett. 43 1291 doi: 10.1364/OL.43.001291
    [19] Dong L 2013 Opt. Express 21 2642 doi: 10.1364/OE.21.002642
    [20] Tao R M, Wang X L, Zhou P 2018 IEEE J. Sel. Topics in Quant. Elect. 24 0903319 doi: 10.1109/JSTQE.2018.2811909
    [21] Dong L 2022 J. Lightw. Technol. 40 4795 doi: 10.1109/JLT.2022.3165394
    [22] Xia N, Yoo S 2020 J. Lightw. Technol. 38 4478 doi: 10.1109/JLT.2020.2986981
    [23] Zervas M N 2017 Proc. of SPIE 10083 100830M doi: 10.1117/12.2252435
    [24] Zervas M N 2018 APL Photonic. 4 022802 doi: 10.1063/1.5050523
    [25] Zervas M N 2019 Opt. Express 27 19019 doi: 10.1364/OE.27.019019
    [26] Dong L, Ballato J, Kolis J 2023 Opt. Express 31 6690 doi: 10.1364/OE.483808
    [27] Cao J Q, Chen M N, Huang Z H, Wang Z F, Chen J B 2024 Opt. Express 32 12892 doi: 10.1364/OE.516692
    [28] Kelson I, Hardy A A 1998 IEEE J. Quant. Elect. 34 1570 doi: 10.1109/3.709573
    [29] Jiang Z, Marciante J R 2008 J. Opt. Soc. Am. B 25 247 doi: 10.1364/JOSAB.25.000247
    [30] Richardson D J, Nilsson J, Clarkson W A 2010 J. Opt. Soc. Am. B 27 B63 doi: 10.1364/JOSAB.27.000B63
    [31] Snyder A W, Love J D 1983 Optical Waveguide Theory (London: Chapman and Hall) pp254-255
    [32] Huang Z M, Shu Q, Luo Y, Tao R M, Feng X, Liu Y, Lin H H, Wang J J, Jing F 2021 J. Opt. Soc. Am. B 38 2945 doi: 10.1364/JOSAB.436225
    [33] Lezius M, Predehl K, Stower W, Turler A, Greiter M, Hoeschen C, Thirolf P, Assmann W, Habs D, Prokofiev A, Ekstrom C, Hansch T W, Holzwarth R 2012 IEEE Trans. Nucl. Sci. 59 425 doi: 10.1109/TNS.2011.2178862
    [34] 黄宏琪, 赵楠, 陈瑰, 廖雷, 刘自军, 彭景刚, 戴能利 2014 物理学报 63 200201 Huang H Q, Zhao N, Chen G, Liao L, Liu Z J, Peng J G, Dai N L 2014 Acta Phys. Sin. 63 200201
    [35] Fox B P, Schneider Z V, Simmons-Potter K, Thomes W J, Meister D C, Bambha R P, Kliner D A V 2008 IEEE J. Quant. Elect. 44 581 doi: 10.1109/JQE.2008.919873
    [36] Fox B P, Simmons-Potter K, Thomes W J, Meister D C, Bambha R P, Kliner D A V 2008 Proc. of SPIE 7095 70950B
    [37] Hecht J 2009 Laser Focus World 45 53
    [38] Wang Y S, Peng W J, Liu H, Yang X B, Yu H M, Wang Y, Wang J, Feng Y J, Sun Y H, Ma Y, Gao Q S, Tang C 2023 Opt. Lett. 48 2909 doi: 10.1364/OL.489289
  • 加载中
图( 6)
计量
  • 文章访问数:  189
  • HTML全文浏览数:  189
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-06-09
  • 刊出日期:  2024-10-20

辐照效应对于掺镱光纤放大器模式不稳定阈值影响的理论研究

    通讯作者: E-mail: kdchenjinbao@aliyun.com.
    作者简介: 曹涧秋.E-mail: jq_cao@126.com
  • 1. 国防科技大学前沿交叉学科学院, 长沙　410073
  • 2. 国防科技大学南湖之光实验室, 长沙　410073
  • 3. 国防科技大学高能激光技术湖南省重点实验室, 长沙　410073
  • 收稿日期:  2024-06-09

摘要: 光纤放大器在辐照环境中具有良好的应用前景, 而模式不稳定(transverse mode instability, TMI)效应则是制约光纤放大器功率提升的重要因素. 因此, 针对辐照效应对于掺镱光纤放大器TMI阈值的影响, 开展了理论研究. 通过将辐致损耗引入光纤放大器的TMI理论模型, 率先给出了考虑辐照效应的TMI阈值表达式, 探讨了TMI阈值随辐射剂量的变化规律, 研究表明: 辐照效应对于TMI阈值的影响, 不仅与光纤的抗辐照性能有关, 还与光纤放大器的增益系数有关. 增益系数的增大, 会减缓TMI阈值随辐射剂量的衰减, 但也会导致TMI阈值的整体下降. 通过对比辐照效应对于TMI阈值和输出功率的影响, 结果发现, TMI阈值随辐致损耗衰减更快. 这也使得TMI效应成为辐照条件下光纤放大器输出功率的限制因素. 相关研究结果, 对于辐射条件下光纤放大器的设计及应用研究具有指导意义.

English Abstract

    全文HTML

    1.   引　言

    • 随着近衍射极限光纤放大器功率水平的不断提升, 其应用领域也在不断拓展, 现阶段在工业加工、材料处理、生物医疗等领域已得到广泛应用. 不仅如此, 光纤放大器还具有结构紧凑、抗干扰能力强、操控灵活等优势, 使其在特殊复杂环境中也有很好的应用前景. 现阶段, 光纤放大器在辐照环境下的应用已经受到广泛关注[1,2].

      为了揭示辐照效应对于光纤放大器的影响, 已有研究机构针对不同掺杂的光纤及光纤放大器开展了研究[3–13]. 现有研究表明, 辐照效应之所以会对光纤放大器产生影响, 主要是因为作为增益介质的掺杂光纤对于辐照效应较为敏感. 关于辐照影响掺杂光纤的微观机理, 当前研究认为: 掺杂光纤在辐照射线影响下产生了色心, 从而影响掺杂光纤的传输特性[14]. 对于掺镱光纤来说, 在辐照射线的作用下, 三价镱离子会转变为二价镱离子, 同时导致色心的产生[14]. 这一过程与掺镱光纤的共掺元素(如铝、磷等)有关, 因此, 通过共掺元素的优化设计, 可以在一定程度上削弱辐照射线对于掺镱光纤的影响[14].

      辐照效应对于掺杂光纤传输特性的影响主要体现在两个方面, 即辐致损耗(radiation-induced attenuation, RIA)和辐致折射率变化[2,15,16]. 两者之中, 对于光纤放大器的影响占主导地位的是辐致损耗(特别是在辐照剂量不高时)[12], 因为辐致损耗既可导致光纤激光器的腔内损耗增大, 降低激光器的输出功率; 还会导致热量的产生, 从而加剧热效应对于光纤激光器的影响. 现阶段研究表明: 辐致损耗是由于辐照产生的色心引起的[2,14]. 色心会对光场产生吸收, 进而导致光场的衰减. 色心对于光场的吸收与波长有关, 而且, 不同共掺元素产生的色心, 对应的吸收谱线也是不同的[2,14]. 对于掺镱光纤来说, 铝元素相关的色心在1 μm波段具有较强的吸收峰[14], 因此, 该色心导致的辐致损耗对于掺镱光纤放大器(主要为1 μm波段)输出特性的影响较为显著.

      光纤放大器中的热效应之一, 就是模式不稳定(transverse mode instability, TMI)效应[17–24]. 研究发现, 当光纤放大器的输出功率达到一定阈值(即TMI阈值)时, 纤芯中产生的热量所导致的折射率变化, 会使得光场的能量在基模和高阶模式之间产生耦合, 从而使得输出光场的模式(横模)无法保持稳定的基模输出, 这就是TMI效应. TMI效应会导致光纤放大器的光束质量恶化. 现阶段, TMI效应已被看作是限制近衍射极限光纤放大器功率提升的关键因素[25–27], 在高功率光纤激光器的研究中备受关注.

      由于TMI效应与纤芯中的热量有关, 而辐致损耗又会导致纤芯中热量的增大, 因此, 辐照效应必然会对光纤激光器中的TMI产生影响. 文献[11]的实验研究表明, 与未经辐照的掺镱光纤相比, 辐照后的掺镱光纤会导致光纤放大器的TMI阈值显著下降, 进而在较低功率下出现TMI效应. 文献[12]还通过数值计算掺镱光纤的平均热负载, 初步探讨了辐照效应对于TMI阈值的影响, 数值结果表明, 在低辐射剂量的条件下, TMI阈值会随着辐射剂量的增大而迅速下降, 这也再次表明辐照效应对于TMI阈值的影响不容忽视. 不过, 遗憾的是, 相关研究有限, TMI阈值随辐照效应的变化规律有待进一步研究.

      因此, 本文针对辐照效应对于掺镱光纤放大器的TMI阈值的影响开展理论研究, 通过将辐照效应引入到现有光纤放大器TMI理论, 推导了考虑辐照效应的TMI阈值的解析表达式, 并利用该表达式, 探讨了辐照效应对于掺镱光纤放大器TMI阈值的影响, 并将相关结果与辐照效应对于输出功率的影响进行对比研究.

    2.   理论推导

    • 如前所示, TMI是光纤放大器中的一种模式耦合现象, 该现象是放大器增益、热传导、热光效应以及模式特性等多物理因素共同作用的结果, 因此, TMI研究的理论模型较为复杂, 一般由信号光传输方程、热传导方程和描述放大器增益的速率方程等3组方程组成[20–24], 对该模型进行解析处理的难度很大. 不过, 幸运的是, 文献[24]在相关研究方面做出了重要进展. 通过采用线性稳态分析(linear stability analysis)的方法, 对于TMI理论模型进行了解析研究, 成功给出了TMI阈值的解析表示式. 下文简要介绍相关研究方法.

      在该研究中, 将光纤放大器中信号光的高阶模式看作是微扰[23,24], 这也就意味着信号光的能量主要是集中在基模的. 该假设和绝大多数的实验研究是吻合的, 因为在TMI出现前, 均需保持光纤放大器的稳定基模输出[17,18,22]. 因此, 该模型的稳态解就可以由基模决定. 这里需要说明的是, 该稳态解表示的是光纤放大器基模稳定连续输出的状态, 因此, 适用于连续光放大器, 对于脉冲光放大器不适用. 在该基模稳态解的基础上, 引入与高阶模式相对应的微扰项, 就可以得到微扰项满足的微分方程, 通过分析微扰项的增益, 当增益大于零时, 就意味着微扰项的影响会被放大, 从而使得系统的状态不再稳定(即出现TMI效应), 由此可以得到TMI的阈值. 由于在高功率光纤激光器中, 信号光的功率很强, 由此产生增益饱和效应较为严重, 在此情况下, TMI阈值可由下述解析表达式给出[23,24], 即

      其中, k和dn/dT分别表示石英光纤的热传导率和热光系数, 这两个系数均与石英光纤的材料特性有关; λs为信号光波长, dco为掺镱光纤的纤芯直径. 系数A1由信号光的模式特性决定, 现有实验研究表明, 由于TMI效应, 与基模(LP01模)产生能量耦合的高阶模式为LP11模[17–22], 因此, 系数A1可以表示为

      其中, U01和U11分别由LP01模和LP11模的传播常数决定, neff则为基模(LP01模)的有效折射率, 这些参数与光纤的结构(纤芯直径和数值孔径)有关. 但文献[27]的研究表明, 对于相同的归一化频率(V值), 当纤芯直径大于10 μm时, 系数A1可以近似看作常数. 参数α’则与掺镱光纤的损耗和增益有关, 可以表示为

      其中, gsat表示的是考虑了饱和效应的增益系数(区别于小信号增益系数), 由粒子在两个能级上的稳态分布决定, 而粒子在能级上的稳态分布只与基模有关(因为如前所述, 稳态解是由基模决定的). 同时, 还需要注意的是, 该增益系数并不是净增益系数, 因此, 与光纤的损耗无关. λp表示泵浦光波长, 因此, (3)式中的第2项表示量子亏损的影响, 这是因为量子亏损会导致热量的产生, 进而影响TMI阈值[18–22].

      (3)式中的α0表示的掺镱光纤的背景损耗, 如果不考虑辐照效应, 由于光纤的背景损耗往往很小, 其影响可以忽略不计. 但是, 如果考虑辐照效应, 由于辐照效应会导致光纤的背景损耗显著增大(即辐致损耗), 这一项的影响就不能忽略, 因此, 辐照效应对于TMI阈值的影响, 通过辐致损耗产生. 不过, 需要说明的是, 辐照效应对于光纤的掺杂区域(纤芯)和非掺杂区域(内包层)均有影响, 均会导致这些区域的背景损耗增大, 不过, 现有研究表明, 掺杂区域对于辐照更加敏感, 该区域的辐致损耗要远大于非掺杂区域的辐致损耗[7,9,11,12]. 因此, 本文忽略内包层辐致损耗, 仅考虑纤芯区域的辐致损耗.

      还需要注意的是, 纤芯的辐致损耗不仅会影响信号光, 还会影响泵浦光, 不过, 由于泵浦光被约束在内包层中, 与纤芯的交叠因子较小(约为纤芯包层面积比[28,29]), 特别是考虑在高功率光纤激光器中, 为了保证泵浦光的耦合能力, 往往采用内包层较大的双包层光纤[30], 纤芯包层面积比较小, 这使得泵浦光与纤芯的交叠因子往往远小于信号光(信号光基模交叠因子一般为0.8—1[28,31], 具体数值由归一化频率V决定)[18,30,32], 考虑到辐致损耗在1 μm波段随波长变化不大[7,12], 这就使得纤芯辐致损耗对于泵浦光的影响与信号光相比, 可以忽略不计, 因此, 本文只考虑纤芯辐致损耗对于信号光的影响, 则(3)式可以表示为

      其中, αRIA表示纤芯的辐致损耗, 可由Power-Law定理给出(见最后一个表达式的第1项)[3,7,9,12], 该公式为经验公式, D表示辐射剂量, C1和f为两个拟合系数, 可通过拟合辐致损耗的实验数据得到. 现有研究表明[12,33,34], C1的取值通常在1—10 dB/(km·Gy)量级, 而f的取值在0.7—1.0之间, 具体的取值与光纤的结构、掺杂方式等因素有关. 这里需要说明的是, 除了辐照剂量, 辐照剂量率也是影响辐致损耗的因素之一[35,36]. 不过, 现有研究表明, 在辐照剂量率较低的情况下(如空间辐照环境[2]), 辐照剂量对于辐致损耗的影响远比辐照剂量率显著[4,35,36]. 因此, 本文仅考虑辐照剂量对于辐致损耗的影响. 将(4)式代入(1)式, 就可得到考虑辐照效应的TMI阈值表达式(1)式.

    3.   结果与讨论

    • 从(1)式和(4)式可以看出, 辐照效应产生的辐致损耗, 会导致TMI阈值下降, 而且, 由于系数C1和f均为正数, 因此, 随着辐射剂量的增大, TMI阈值会单调下降. 不过, 仅仅了解定性的变化趋势还是不够的, 相关的定量分析更具有指导意义. 因此, 本节将定量讨论辐照效应对于TMI阈值的影响.

      首先, 本文将讨论辐照效应对于归一化TMI阈值的影响. 归一化TMI阈值$ P_{{\text{th}}}^{{\prime}} $定义为辐照前后TMI阈值的比值, 即: (Pth/Pth0), 其中, Pth为辐照后的TMI阈值, Pth0为辐照前的TMI阈值. 讨论归一化TMI阈值的原因为: 该值能给出辐照效应影响下, TMI阈值下降的比例, 从而能有效反映辐照效应对于TMI阈值影响的剧烈程度; 由(1)式可以发现, 在归一化TMI阈值的表达式中, 除了与辐致损耗相关的α’外, 其他各项都可以消掉, 因此, 归一化TMI阈值与光纤结构和材料参数无关, 换言之, 由此得到的规律, 并不依赖于光纤结构和材料的限制, 对于所有结构的光纤都应该是适用的. 利用(1)式可得到归一化TMI阈值的表达式为

      由此可见, 当辐射剂量D足够小, 以至于辐致损耗与分母中的第2项(即量子亏损项)相比, 可以忽略不计的话, 此时就无需考虑辐照效应对于TMI阈值的影响. 不过, 对于掺镱光纤放大器, 其泵浦光波长和信号光波长较为接近(如常见的976 nm和1080 nm), 量子亏损较小(约为10%). 同时, 在高功率放大器中, 信号光的放大倍率为10—100倍, 相应的增益系数gsat为1—2 dB/m(掺镱光纤的长度按照10 m量级估算). 按此推算, 当辐致损耗达到0.01 dB/m时, 其数值已经达到量子损耗项的1/10, 此时辐致损耗的影响已不能忽略(TMI阈值将降为无辐照时的91%). 不过, 对于掺镱光纤, 仅需要1—10 Gy量级的辐射剂量, 即可达到同等量级的辐致损耗[7,9,12]. 由此可见, TMI阈值对于辐照效应非常敏感. 图1给出的计算结果也可证明.

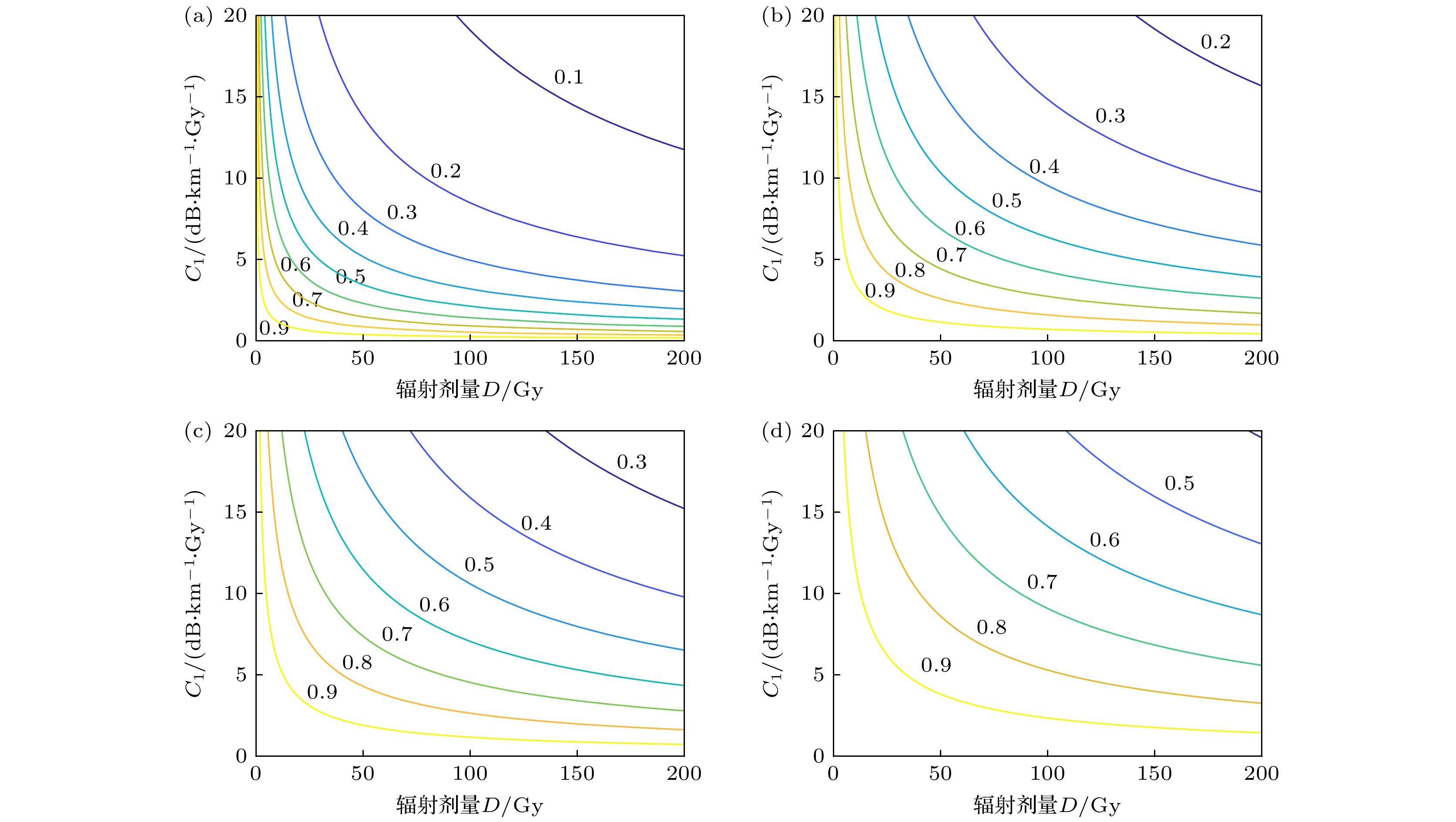
      图1给出了系数C1和f对于归一化TMI阈值的影响, C1和f表征掺镱光纤的抗辐照性能, 其值越小, 相同辐射剂量产生辐致损耗越小, 光纤的抗辐照性能越好. 从图1可以看出, 当TMI阈值下降特定比例时, 辐射剂量与系数C1和f之间的关系. 以TMI阈值下降10%, 即归一化TMI阈值为0.9为例, 从图1(a)可以看出, 当辐射剂量小于25 Gy时, 系数C1的取值随辐射剂量迅速减小至2.5 dB/(km·Gy); 当辐射剂量大于50 Gy时, 系数C1的变化则显著变缓, 随着辐射剂量增至200 Gy, 系数C1的取值仅由1.5 dB/(km·Gy)降低至约1 dB/(km·Gy). 该结果表明: 当系数C1的值大于2.5 dB/(km·Gy)时, TMI阈值对于辐射剂量会非常敏感, 25 Gy的辐射剂量, 就会使TMI阈值降低10%以上; 若要减低辐照的敏感程度, 需要将系数C1降低至1.5 dB/(km·Gy)以下. 本质上讲, 这对于光纤抗辐照性能给出了明确的要求.

      上述结果讨论对应的是系数f为0.5的情况, 随着f的增大, TMI阈值随着辐射剂量的衰减也会更加剧烈. 当f增至0.7时(见图1(b)), 若要在25 Gy剂量的辐照下, 归一化TMI阈值达到0.9以上, 则需要系数C1小于1.2 dB/(km·Gy); 如果将系数f进一步增至0.9和1.1时, 系数C1的取值则分别要小于0.7 dB/(km·Gy)和0.3 dB/(km·Gy). 由此可见, 随着系数f的增大, 系数C1的取值也会显著减小. 一般地, 如果要求在D0剂量的辐照下, TMI阈值的下降比例小于R0, 则系数C1和f之间的关系可以由下式估算, 即

      从图1还可以看出, 随着归一化TMI阈值的减小, 对应的辐射剂量或者系数C1和f的取值就越大, 这也是很好理解的: 如果允许的TMI阈值下降幅度增大, 对于光纤的抗辐照需求就会下降. 因此, 在提升掺镱光纤抗辐照性能的同时, 最大程度提升无辐照条件下的TMI阈值, 从而提升应用场景所能够容忍的TMI阈值下降比例, 也是非常重要的.

      在上文讨论中, 均假设增益系数gsat为2 dB/m, 下文将讨论gsat对于TMI阈值的影响. 图2给出了不同gsat条件下, 归一化TMI阈值随辐射剂量的变化, 假设f为0.7. 由图2可以看出, 随着gsat的增大, TMI阈值下降相同比例(对应于相同的归一化TMI阈值), 所需要的辐射剂量D或系数C1也随之增大. 这表明增益系数的增大, 有利于抑制辐照效应对于归一化TMI阈值的影响. 这也是可以理解的, 因为从(5)式可以看出, 增益系数的增大, 会导致相同辐射剂量下, 辐致损耗在分母中的占比减小, 从而导致归一化TMI阈值增大.

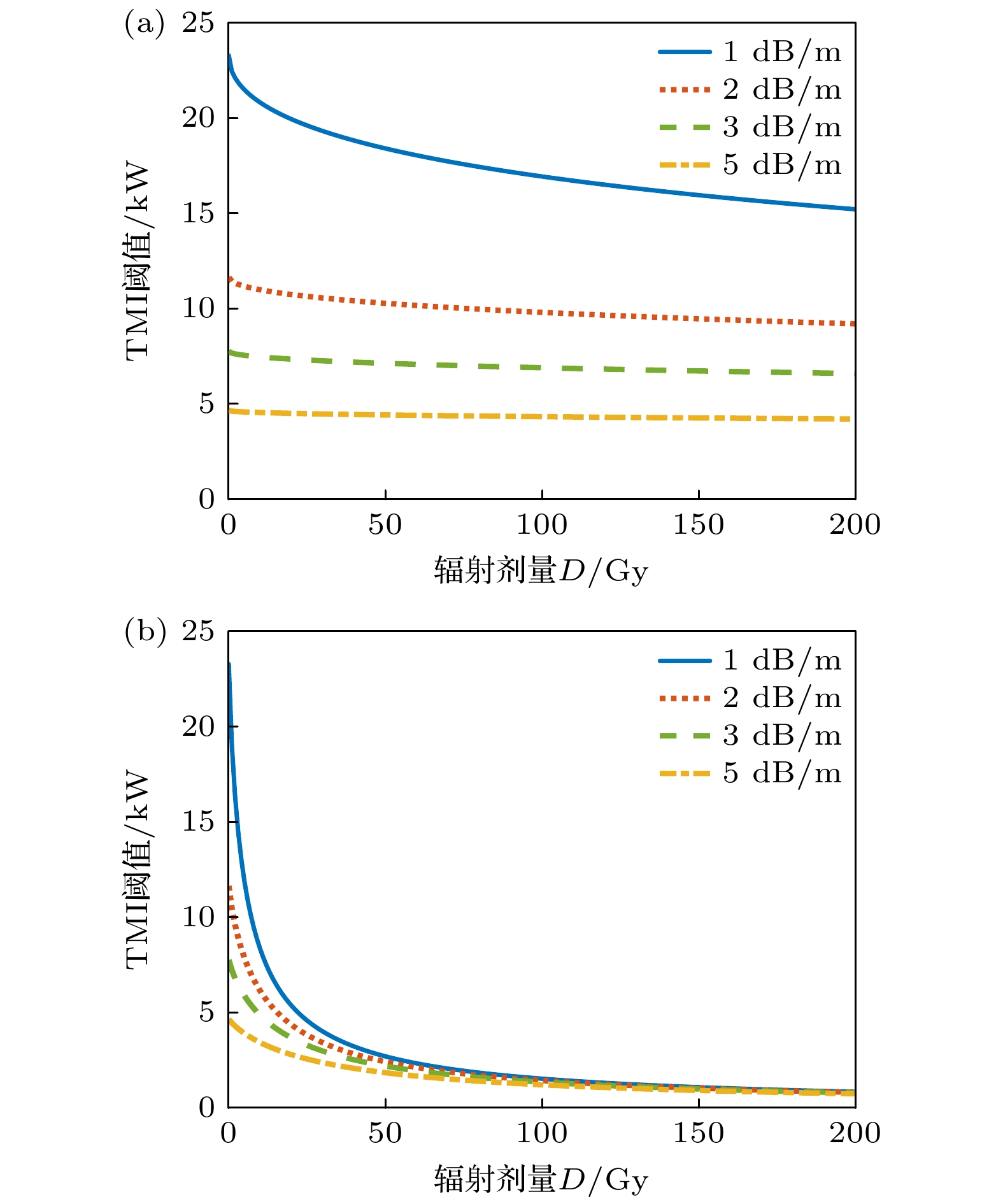
      从(1)式还可以看出, 增益系数gsat的增大, 虽然有利于归一化TMI阈值的提升, 但是, 会导致TMI阈值的下降. 为了进一步明确增益系数的影响, 图3给出了不同增益系数对应的TMI阈值随辐射剂量D的变化. 这里假设掺镱光纤的纤芯直径为30 μm, 归一化频率V为3, 相应地, 系数A1应为23.7(计算过程详见文献[27]的附录A). 此时, 该光纤包含LP01和LP11两个模式, 相应的无辐照条件下的TMI阈值公式已得到实验验证[23,27](实验中, TMI阈值可通过测量光束质量[17]或输出功率稳定性[11,18]的变化得到). 从图3可以明显看出, 增益系数gsat的增大虽然可以减缓TMI阈值随辐射剂量的衰减速率, 但是, 代价是TMI阈值的整体下降; 而且, 掺镱光纤的抗辐照性能越好(即系数C1和f的值越小), TMI阈值随gsat的下降就越明显. 这也表明增大增益系数, 并不是理想的抑制辐照效应的方法.

      如果增益系数较小, TMI阈值会随着辐射剂量的增大而迅速衰减, 特别是在辐照初期(对应于图3中辐射剂量较小的情况). 而且, 对于抗辐照性能较差的光纤(系数C1和f较大, 见图3(b)), TMI阈值随辐射剂量的衰减非常剧烈, 以至于gsat对于TMI阈值的影响不再明显. 从图3(b)可以看出, 在无辐射条件下, 当增益系数gsat由1 dB/m增至3 dB/m, TMI阈值则由23.3 kW降低至7.76 kW; 但是, 当辐射剂量增至20 Gy, TMI阈值仅由5.37 kW降至3.67 kW. 该结果是可以理解的, 从(4)式可以看出, 随着辐致损耗的增大, 增益系数的影响就会相对减弱, 如果辐致损耗项远大于增益系数项, 增益系数的影响就可以忽略不计(见图3(b)辐射剂量D大于100 Gy的情况). 图3表明要在辐照条件下获得较高的TMI阈值, 需要同时保证较低的增益系数和较好的光纤抗辐照能力, 此外, 结合应用场景的辐射剂量, 适当预留TMI阈值的下降空间, 也是非常必要的.

      至此, 本文主要讨论了辐照效应对于TMI阈值的影响. 除了TMI阈值外, 辐照产生的辐致损耗还会导致光纤放大器输出功率的下降. 对于光纤放大器, 输出功率可以表示为

      其中, P0表示种子光功率; L为掺镱光纤长度; G为总增益, 可由增益系数gsat对掺镱光纤长度积分得到, 由于增益系数考虑了饱和效应, 而饱和效应与信号光功率有关, 因此, 信号光功率的变化会对增益G产生一定的影响. 不过, 这里假设信号光功率很强, 以至于辐致损耗导致的功率衰减, 不会对增益G产生显著影响. 此时, 辐照前后光纤放大器输出功率的比值可以近似表示为

      其中, $ P_{{\text{out}}}' $表示的是辐照后的光纤放大器输出功率. (8)式表明, 辐致损耗对于输出功率的影响与掺镱光纤的长度有关. 在相同辐照条件(辐致损耗系数相同)下, 掺镱光纤长度越长, 辐照导致的光纤总损耗越大, 输出功率下降越剧烈.

      图4所示为功率比值Rp与归一化TMI阈值的变化. 这里需要说明的是: 输出功率比值与辐致损耗和光纤长度有关(见(8)式), 图4给出的是输出功率下降至相同比例(50%)时, 不同光纤长度的归一化TMI和输出功率比值的对比(因此选择了不同的辐致损耗取值范围). 同时, 考虑到高功率光纤放大器的总增益一般为10—30 dB[32,37,38], 因此, 针对不同的光纤长度, 增益系数取值也有所区别. 此外, 图4(a)中还给出了2 dB/m的增益系数对应的结果(对应于20 m光纤长度, 总增益则为40 dB), 以便与图4(b)中相同增益系数的结果进行对比.

      从图中可以看出, 对应于相同增益系数的归一化TMI阈值的变化曲线相同, 这是因为归一化TMI阈值与光纤长度无关(见(4)式). 同时, 从图中还可以看出, 光纤长度越长, 输出功率比值随辐致损耗下降越快; 这也表明: 掺镱光纤越长, 辐致损耗对于输出功率的影响越显著. 因此, 为了抑制辐致损耗对于输出功率的不利影响, 应尽量缩短掺镱光纤的长度. 不过, 如前所述, 光纤长度还与光纤放大器的总增益有关, 若要在保证总增益的前提下, 缩短掺镱光纤长度, 就需要增大增益系数, 但增大增益系数又不利于TMI阈值的提升(见图3). 由此可见, 对光纤长度、增益系数和总增益的优化设计, 有助于有效抑制辐照效应的影响.

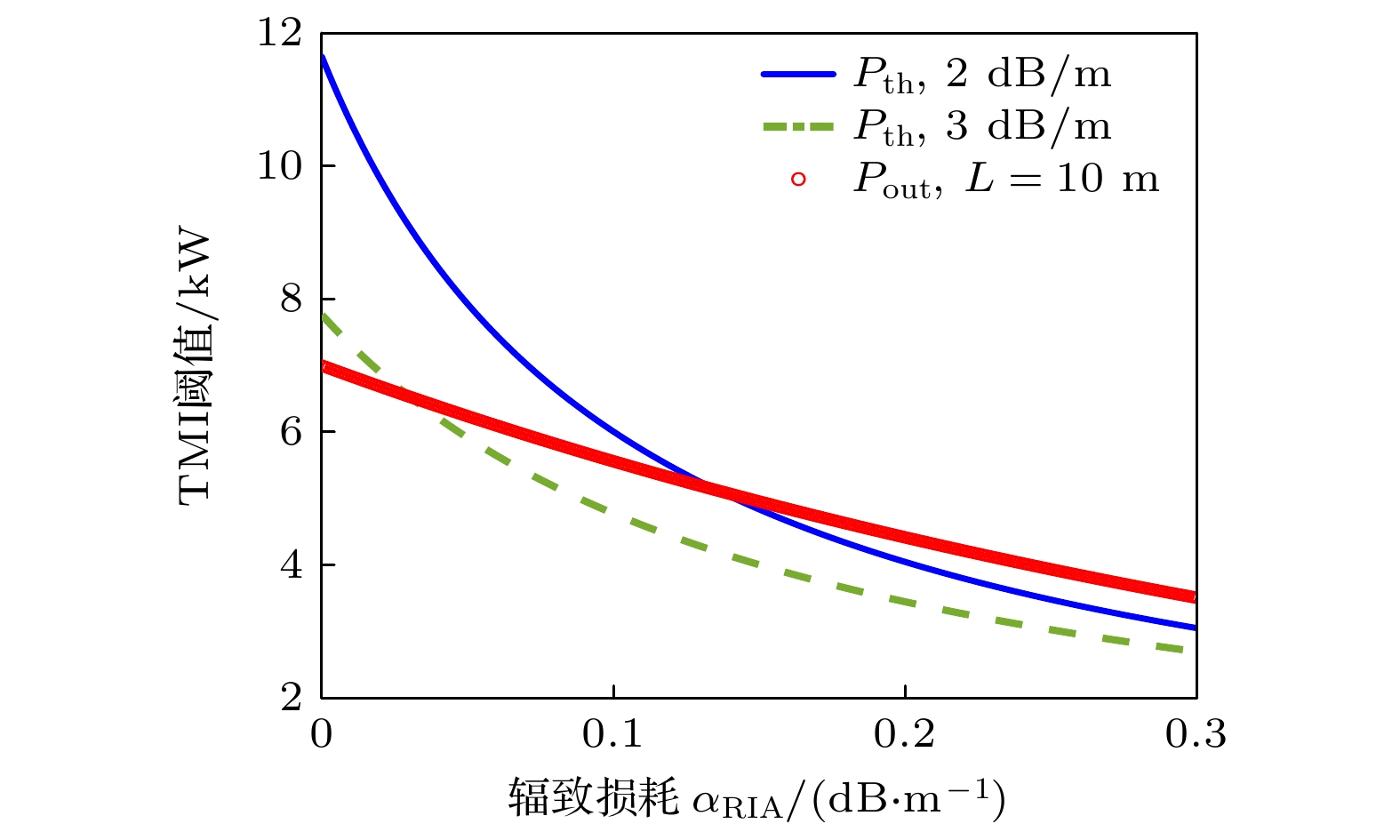
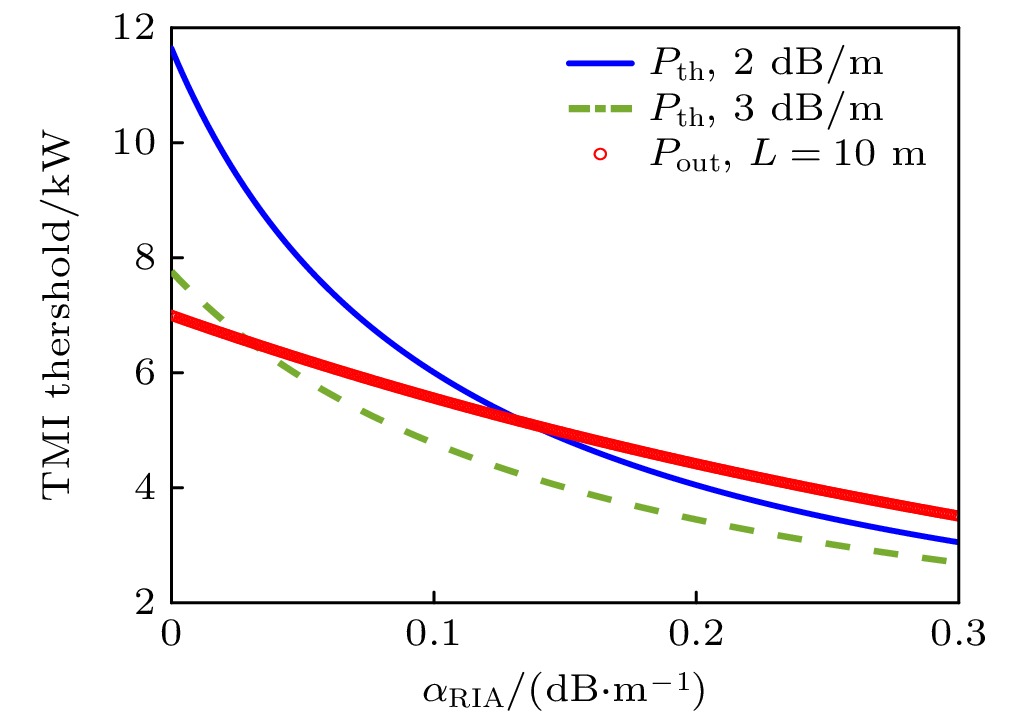
      图4结果还表明, 归一化TMI阈值随辐致损耗的衰减速率, 要大于输出功率的衰减速率. 这表明TMI阈值对于辐照效应更为敏感. 这就可能带来这样一个结果(如图5所示), 即在无辐照条件下, 光纤放大器的功率小于TMI阈值, 但是, 随着辐射剂量的增加, 辐致损耗会使得TMI阈值快速下降, 其减小幅度大于功率下降幅度, 进而使得TMI阈值小于同辐射剂量下的输出功率, 导致TMI效应的出现. 事实上, 文献[11]也报道了类似的实验结果, 辐照效应不仅导致了输出功率的下降, 还导致了TMI效应的出现. 通过上述分析可以看出: 该实验结果应该是由于辐照效应导致的TMI阈值快速下降而产生的.

      还需要注意的是, 尽管gsat的增大能够减缓TMI阈值下降速率(见图2), 但是, 由于gsat的增大会导致TMI阈值的整体下降, 从而使得TMI效应更容易出现. 从图5可以看出, 当gsat从2 dB/m增至3 dB/m时, 由于TMI阈值的整体下降, 使得TMI阈值在较弱的辐照效应下(仅需RIA大于0.03 dB/m), 就小于输出功率, 此时, 光纤放大器将出现TMI现象, 输出功率也将由TMI阈值决定, 这也再次体现了TMI效应研究对于光纤放大器在辐照条件下应用的重要意义.

    4.   结　论

    • 本文针对光纤放大器在辐照环境(空间辐照环境等低辐照剂量率环境)下的应用, 理论研究了辐照效应对于掺镱光纤放大器TMI阈值的影响. 通过将辐致损耗引入连续光光纤放大器的TMI理论模型, 率先给出了考虑辐照效应的TMI阈值表达式, 揭示了辐照效应对于TMI阈值的影响. 通过研究归一化TMI阈值随辐射剂量的变化规律, 揭示了光纤的抗辐照性能对于TMI阈值的影响, 研究还发现: 光纤放大器的增益系数也会对TMI阈值产生影响, 增益系数的增大, 会减缓归一化TMI阈值随辐射剂量的减小, 但是, 会导致TMI阈值的整体下降. 通过将TMI阈值的变化规律与输出功率的衰减进行比较, 发现TMI阈值对于辐照效应更为敏感, 当辐致损耗(或辐射剂量)达到一定程度时, TMI阈值会小于输出功率, 从而导致TMI效应的出现, 这一结果也得到了已发表实验结果的验证. 这也表明TMI效应是限制辐照条件下光纤放大器输出功率的重要因素. 不过, 较为遗憾的是, 由于现阶段相关实验研究非常有限, 也为本文理论结果的进一步验证带来了困难. 虽然本文理论研究采用的TMI阈值公式((1)式)和Power-Law定理((4)式)均有良好的实验基础[3,7,9,12,23,27,33,34], 但是, 更加深入的实验验证和理论研究工作仍亟待进一步开展. 尽管如此, 本文仍为辐照条件下掺镱光纤放大器TMI阈值的预测提供了理论方法, 对于不同类型的掺镱光纤, 通过实验测量不同辐照剂量下的辐致损耗, 利用Power-Law定理就可以拟合出辐致损耗随辐射剂量的变化规律, 然后, 利用(1)式和(4)式, 就可以预测掺镱光纤放大器TMI阈值随辐照剂量的变化, 进而为掺镱光纤放大器在辐照环境中的应用提供指导. 该理论研究同样可以为其他稀土掺杂光纤放大器的辐照效应研究提供参考. 因此, 本文研究对于辐射条件下光纤放大器的设计及应用研究具有重要意义.

    参考文献 (38)

目录

/

返回文章
返回