高级搜索

基于分子模拟方法的纳米气泡溃灭过程分析

,  ,  , 

downloadPDF

上一篇

下一篇

张雪松, 范振忠, 仝其雷, 付沅峰. 基于分子模拟方法的纳米气泡溃灭过程分析[J]. 物理学报, 2024, 73(20): 204701-1. doi: 10.7498/aps.73.20241105
引用本文: 张雪松, 范振忠, 仝其雷, 付沅峰. 基于分子模拟方法的纳米气泡溃灭过程分析[J]. 物理学报, 2024, 73(20): 204701-1. doi: 10.7498/aps.73.20241105
shu
Xue-Song Zhang, Zhen-Zhong Fan, Qi-Lei Tong, Yuan-Feng Fu. Analysis of nanobubble collapse process by molecular simulation method[J]. Acta Physica Sinica, 2024, 73(20): 204701-1. doi: 10.7498/aps.73.20241105
Citation: Xue-Song Zhang, Zhen-Zhong Fan, Qi-Lei Tong, Yuan-Feng Fu. Analysis of nanobubble collapse process by molecular simulation method[J]. Acta Physica Sinica, 2024, 73(20): 204701-1. doi: 10.7498/aps.73.20241105
shu

基于分子模拟方法的纳米气泡溃灭过程分析

  • 东北石油大学, 提高油气采收率教育部重点实验室, 大庆　163318

    • 作者简介: 张雪松. E-mail: zxs1127@stu.nepu.edu.cn .
    通讯作者: E-mail: fanzhenzhong@163.com.; 

  • 中图分类号: 47.55.dd, 47.11.Mn, 47.40.-x

Analysis of nanobubble collapse process by molecular simulation method

  • Key Laboratory of Enhanced Oil and Gas Recovery, Ministry of Education, Northeast Petroleum University, Daqing 163318, China

    • Corresponding author: E-mail: fanzhenzhong@163.com.; 

  • MSC: 47.55.dd, 47.11.Mn, 47.40.-x

  • 摘要: 采用分子动力学模拟方法研究纳米气泡逐渐凹陷并发展至溃灭的过程, 本文主要研究冲击速度和气泡尺寸对纳米气泡溃灭的动力学特性影响机制. 结果表明: 纳米气泡溃灭大体上经历三个阶段. 首先是气泡外侧水分子压缩阶段, 然后是冲击波导致液膜稳定结构被破坏阶段, 最终发展至气泡完全溃灭阶段; 在冲击速度较大时, 较小尺寸气泡在更强的冲击效果作用下, 气泡溃灭时间更短; 纳米气泡溃灭后高速射流后在速度等高线右端形成凸起, 随着气泡尺寸和冲击速度增大, 凸起程度就越大, 水分子向气泡中心汇集, 在气泡上方和下方形成涡旋结构, 有效的增强了流体内部传质作用; 随着气泡尺寸和冲击速度的增大, 气泡周围密度也逐渐增大, 气泡完全时溃灭时局部密度可达1.5 g/cm3附近; 当气泡体系衰减至一半时, 出现水锤冲击效应, 随着气泡尺寸和冲击速度的增大, 水锤冲击作用愈发明显, 对于up = 3.0 km/s, D = 10 nm的纳米气泡结构塌陷后射流水锤冲击所形成的局部压强可达30 GPa.
    Abstract: This study employs molecular dynamics simulations to investigate the process of nanobubble gradual indentation and eventual collapse. The research primarily focuses on the mechanisms by which impact velocity and bubble size influence the dynamic characteristics of nanobubble collapse. The results indicate that nanobubble collapse generally proceeds through three stages. Initially, there is a compression phase of water molecules surrounding the bubble, followed by a phase where the shock wave disrupts the stable structure of the liquid film, and finally, the complete collapse of the bubble. At higher impact velocities, smaller bubbles collapse more rapidly due to stronger shock effects. Post-collapse, a high-speed jet forms a protrusion on the right end of the velocity contour. The degree of protrusion increases with bubble size and impact velocity. Water molecules converge towards the bubble center, forming vortex structures above and below the bubble, effectively enhancing internal mass transfer. As bubble size and impact velocity increase, the density around the bubble gradually rises, reaching approximately 1.5 g/cm³ in localized areas upon complete collapse. When the bubble system decays to half its original size, a water hammer effect occurs. This effect becomes more pronounced with increasing bubble size and impact velocity. For a nanobubble structure with up = 3.0 km/s and D = 10 nm, the local pressure formed by the water hammer impact of the jet after collapse can reach 30 GPa.
  • 加载中

  • 图 1  纳米气泡冲击过程示意图

    Figure 1.  Schematic diagram of nanobubble impact process.

    下载: 全尺寸图片 幻灯片

    图 2  纯水体系在不同冲击速度条件下沿z轴一维密度分布　(a) 1.0—2.0 km/s; (b) 2.5—3.0 km/s

    Figure 2.  One-dimensional density distribution along the z-axis in the pure water system under different impact velocities:(a) 1.0–2.0 km/s; (b) 2.5–3.0 km/s.

    下载: 全尺寸图片 幻灯片

    图 3  纯水体系在不同冲击速度条件下沿z轴一维密度分布曲线　(a) 1.0 km/s; (b) 1.5 km/s; (c) 2.0 km/s; (d) 2.5 km/s; (e) 3.0 km/s

    Figure 3.  One-dimensional density distribution curves along the z-axis in the pure water system under different impact velocities: (a) 1.0 km/s; (b) 1.5 km/s; (c) 2.0 km/s; (d) 2.5 km/s; (e) 3.0 km/s.

    下载: 全尺寸图片 幻灯片

    图 4  up-us的Hugoniot冲击压缩图

    Figure 4.  Hugoniot shock compression diagram of up-us.

    下载: 全尺寸图片 幻灯片

    图 5  纳米气泡体积归一化Ω(t)随冲击时间变化关系曲线　(a) 不同冲击速度; (b) 不同气泡尺寸

    Figure 5.  Normalized Ω(t) curves of nanobubble volume as a function of impact time: (a) Different impact velocitys; (b) different nanobubble sizes.

    下载: 全尺寸图片 幻灯片

    图 6  不同时刻下的纳米气泡结构变化情况(D = 10 nm, up = 3.0 km/s)

    Figure 6.  Changes in nanobubble structure at different times (D = 10 nm, up = 3.0 km/s).

    下载: 全尺寸图片 幻灯片

    图 7  纳米气泡溃灭前后的z 方向速度分布情况　(a) 不同冲击速度; (b) 不同气泡尺寸

    Figure 7.  z-direction velocity distribution before and after the collapse of the nanobubble: (a) Different impact velocities; (b) different bubble sizes.

    下载: 全尺寸图片 幻灯片

    图 8  1.4—3.0 ps纳米气泡外层液膜的运动轨迹曲线(单位: km/s)

    Figure 8.  Motion trajectory curve of outer liquid film of 1.4–3.0 ps nanobubble (unit: km/s).

    下载: 全尺寸图片 幻灯片

    图 9  up = 3.0 km/s, D = 10 nm纳米气泡二维流场(y-z平面)速度矢量分布　(a) 1.3 ps; (b) 2.2 ps; (c) 2.8 ps; (d) 3.4 ps (单位: km/s, 由于比例问题, 气泡呈椭圆形)

    Figure 9.  Velocity vector distribution of two-dimensional flow field (y-z plane) of nanobubble with up = 3.0 km/s and D = 10 nm: (a) 1.3 ps; (b) 2.2 ps; (c) 2.8 ps; (d) 3.4 ps (unit: km/s, due to proportional issues, the bubble is elliptical in shape).

    下载: 全尺寸图片 幻灯片

    图 10  不同气泡尺寸及冲击速度大小的气泡流场速度分布　(a) 不同气泡尺寸; (b) 不同冲击速度

    Figure 10.  Velocity distribution of the bubble flow field at different bubble sizes and impact velocities: (a) Different bubble sizes; (b) different impact velocities.

    下载: 全尺寸图片 幻灯片

    图 11  不同冲击速度下的体系势能PE (a)和动能KE (b)沿z轴一维分布曲线(3.3 ps)

    Figure 11.  One dimensional distribution curves of system potential energy PE (a) and kinetic energy KE (b) along the z-axis at different impact velocities (3.3 ps).

    下载: 全尺寸图片 幻灯片

    图 12  纳米气泡周围水分子质量密度沿z轴一维分布曲线

    Figure 12.  One dimensional distribution curve of water molecule mass density around nanobubble along the z-axis.

    下载: 全尺寸图片 幻灯片

    图 13  纳米气泡周围水分子质量密度的y-z平面二维云图　(a) 不同气泡尺寸; (b) 不同冲击速度

    Figure 13.  Two dimensional cloud map of y-z plane of water molecule mass density around nanobubble: (a) Different nanobubble sizes; (b) different impact velocities.

    下载: 全尺寸图片 幻灯片

    图 14  纳米气泡射流前沿x-y平面(径向)二维云图(单位: km/s)

    Figure 14.  Two dimensional cloud map of the front x-y plane (radial) of the nanobubble jet (unit: km/s).

    下载: 全尺寸图片 幻灯片

    图 15  纳米气泡射流产生局部压强的y-z平面二维云图　(a) 不同气泡尺寸; (b) 不同冲击速度

    Figure 15.  Two dimensional cloud map of y-z plane generated local pressure by nanobubble jet: (a) Different nanobubble size; (b) different impact velocity.

    下载: 全尺寸图片 幻灯片

    表 1  SPC/E刚性分子模型势能参数

    Table 1.  Potential energy parameters of SPC/E rigid molecular model.

    type ε/(kcal·mol–1) σ/Å q/e
    O 3.166 0.15535 –0.8476
    H 0 0 0.4238
    下载: 导出CSV

    表 2  不同条件下的粒子速度和冲击速度对应结果

    Table 2.  Corresponding results of particle velocity and impact velocity under different conditions.

    up/(km·s–1) us1 us2 us3 uexp usim ε/%
    1.0 3.21 3.26 3.17 3.57 3.61 9.8
    1.5 4.06 4.14 4.16 4.40 4.30 6.4
    2.0 5.07 5.06 5.16 5.25 5.18 2.9
    2.5 5.89 5.93 5.99 5.93 5.51 0.6
    下载: 导出CSV

    表 3  不同粒子速度和尺寸下的纳米气泡破裂时间

    Table 3.  Breakdown time of nanobubble at different particle velocities and sizes.

    粒子速度
    up/(km·s–1)    		 气泡尺寸
    D/nm    		 气泡破裂时间 τ/ps
    MD Rayleigh 差值
    1.0 8 3.3 3.8 0.5
    10 4.2 4.7 0.3
    12 4.6 5.7 1.0
    1.5 8 2.2 2.5 0.3
    10 2.7 3.1 0.4
    12 3.4 3.7 0.3
    2.0 8 1.8 2.1 0.3
    10 2.2 2.3 0.1
    12 2.6 2.8 0.2
    2.5 8 1.4 1.5 0.1
    10 1.9 1.8 0.1
    12 2.1 2.2 0.1
    3.0 8 1.2 1.1 0.1
    10 1.6 1.4 0.2
    12 1.9 1.7 0.2
    下载: 导出CSV

    表 4  MD模拟和Rankine–Hugoniot计算冲击压力结果

    Table 4.  MD simulation and Rankine-Hugoniot calculation of impact pressure results.

    粒子速度up/(km·s–1) 冲击速度us/(km·s–1) 冲击压力 Ps/GPa
    MD Rankine–
    Hugoniot    		 差值
    1.0 3.22 3.09 3.20 0.11
    1.5 4.12 6.16 6.18 0.02
    2.0 5.09 10.19 10.18 0.01
    2.5 5.93 14.96 14.82 0.14
    3.0 6.80 20.63 20.40 0.23
    下载: 导出CSV
  • [1] 马艳, 吴俊, 周维 2024 环境工程技术学报 14 1141 doi: 10.12153/j.issn.1674-991X.20240200 Ma Y, Wu J, Zhou W 2024 J. Environ. Eng. Technol. 14 1141 doi: 10.12153/j.issn.1674-991X.20240200
    [2] 杨丽, 廖传华, 朱跃钊, 陈海军, 金勤芳 2012 化工进展 31 1333 Yang L, Liao C H, Zhu Y Z, Chen H J, Jin Q F 2012 Chem. Ind. Eng. Prog. 31 1333
    [3] 张立娟, 郑晋, 文博, 胡钧 2024 中国科学: 化学 54 85 doi: 10.1360/SSC-2023-0193 Zhang L J, Zheng J, Wen B, Hu J 2024 Sci. Sin. Chem. 54 85 doi: 10.1360/SSC-2023-0193
    [4] 张敏, 宋昭峥, 孙珊珊, 张志勇, 穆红岩, 赵立平, 李永峰, 张忠智 2016 环境工程学报 10 599 doi: 10.12030/j.cjee.20160214 Zhang M, Song Z Z, Sun S S, Zhang Z Y, Mu H Y, Zhao L P, Li Y F, Zhang Z Z 2016 Chin. J. Environ. Eng. 10 599 doi: 10.12030/j.cjee.20160214
    [5] 翟伟哲, 王永刚, 王旭, 董婧, 王恒嘉 2018 环境科学与管理 43 95 doi: 10.3969/j.issn.1673-1212.2018.05.024 Zhai W Z, Wang Y G, Wang X, Dong J, Wang H J 2018 Environ. Sci. Manage. 43 95 doi: 10.3969/j.issn.1673-1212.2018.05.024
    [6] 李恒震, 胡黎明, 辛鸿博 2015 岩土工程学报 37 115 doi: 10.11779/CJGE2015S2023 Li H Z, Hu L M, Xin H B 2015 Chin. J. Geotech. Eng. 37 115 doi: 10.11779/CJGE2015S2023
    [7] Cook S S 1928 Proc. R. Soc. London, Ser. A 119 481 doi: 10.1098/rspa.1928.0107
    [8] Obara T B, Bourne N K, Field J E 1995 Wear 186 388
    [9] 詹胜鹏 2022 博士学位论文 (北京: 机械科学研究总院) Zhan S P 2022 Ph. D Dissertation (Beijing: Academy of Machinery Science and Technology
    [10] 王小峰, 陶钢, 徐宁, 王鹏, 李召, 闻鹏 2021 物理学报 70 134702 doi: 10.7498/aps.70.20210058 Wang X F, Tao G, Xu N, Wang P, Li Z, Wen P. 2021 Acta Phys. Sin. 70 134702 doi: 10.7498/aps.70.20210058
    [11] Rawat S 2023 Phys. Fluids 35 097114 doi: 10.1063/5.0158192
    [12] Vedadi M H, Haas S 2011 Appl. Phys. Lett. 99 154105 doi: 10.1063/1.3650695
    [13] Zhou Y, Cao D, Zhang X 2022 Nanomaterials 12 2654 doi: 10.3390/nano12152654
    [14] Nan N, Si D, Hu G 2018 J. Chem. Phys. 149 074902 doi: 10.1063/1.5037643
    [15] Wang X F, Tao G, Wen P, Ren B X, Pang C Q, Du C X 2020 J. Phys. Chem. B 124 9535 doi: 10.1021/acs.jpcb.0c06077
    [16] Lu X, Yuan B, Zhang X, Yang K, Ma Y 2017 Appl. Phys. Lett. 110 023701 doi: 10.1063/1.4973592
    [17] Thompson A P, Aktulga H M, Berger R, Bolintineanu D S, Brown W M, Crozier P S, In ’T Veld P J, Kohlmeyer A, Moore S G, Nguyen T D, Shan R, Stevens M J, Tranchida J, Trott C, Plimpton S J 2022 Comput. Phys. Commun. 271 108171 doi: 10.1016/j.cpc.2021.108171
    [18] Stukowski A 2010 Modell. Simul. Mater. Sci. Eng. 18 015012 doi: 10.1088/0965-0393/18/1/015012
    [19] Berendsen H J C, Grigera J R, Straatsma T P 1987 J. Phys. Chem. 91 6269 doi: 10.1021/j100308a038
    [20] Zhou Y, Huang M, Tian F, Shi X, Zhang X 2024 J. Phys. Chem. 160 054109 doi: 10.1063/5.0189490
    [21] Rybakov A P, Rybakov I A 1995 Eur. J. Mech. B Fluids 14 323
    [22] Vedadi M, Choubey A, Nomura K, Kalia R K, Nakano A, Vashishta P, Van Duin A C T 2010 Phys. Rev. Lett. 105 014503 doi: 10.1103/PhysRevLett.105.014503
    [23] Hołyst R, Litniewski M, Garstecki P 2010 Phys. Rev. E 82 066309 doi: 10.1103/PhysRevE.82.066309
    [24] Zhang A M, Cui P, Wang Y 2013 Exp. Fluids 54 1602 doi: 10.1007/s00348-013-1602-7
    [25] Zhang H, Lu Z, Zhang P, Gu J, Luo C, Tong Y, Ren X 2021 Opt. Laser Technol. 138 106606 doi: 10.1016/j.optlastec.2020.106606
    [26] Zhan S, Duan H, Pan L, Tu J, Jia D, Yang T, Li J 2021 Phys. Chem. Chem. Phys. 23 8446 doi: 10.1039/D1CP00406A
  • 加载中
图( 15) 表( 4)
计量
  • 文章访问数:  371
  • HTML全文浏览数:  371
  • PDF下载数:  3
  • 施引文献:  0
出版历程
  • 收稿日期:  2024-08-06
  • 刊出日期:  2024-10-20

基于分子模拟方法的纳米气泡溃灭过程分析

    通讯作者: E-mail: fanzhenzhong@163.com.; 
    作者简介: 张雪松. E-mail: zxs1127@stu.nepu.edu.cn
  • 东北石油大学, 提高油气采收率教育部重点实验室, 大庆　163318
  • 收稿日期:  2024-08-06

摘要: 采用分子动力学模拟方法研究纳米气泡逐渐凹陷并发展至溃灭的过程, 本文主要研究冲击速度和气泡尺寸对纳米气泡溃灭的动力学特性影响机制. 结果表明: 纳米气泡溃灭大体上经历三个阶段. 首先是气泡外侧水分子压缩阶段, 然后是冲击波导致液膜稳定结构被破坏阶段, 最终发展至气泡完全溃灭阶段; 在冲击速度较大时, 较小尺寸气泡在更强的冲击效果作用下, 气泡溃灭时间更短; 纳米气泡溃灭后高速射流后在速度等高线右端形成凸起, 随着气泡尺寸和冲击速度增大, 凸起程度就越大, 水分子向气泡中心汇集, 在气泡上方和下方形成涡旋结构, 有效的增强了流体内部传质作用; 随着气泡尺寸和冲击速度的增大, 气泡周围密度也逐渐增大, 气泡完全时溃灭时局部密度可达1.5 g/cm3附近; 当气泡体系衰减至一半时, 出现水锤冲击效应, 随着气泡尺寸和冲击速度的增大, 水锤冲击作用愈发明显, 对于up = 3.0 km/s, D = 10 nm的纳米气泡结构塌陷后射流水锤冲击所形成的局部压强可达30 GPa.

English Abstract

    全文HTML

    1.   引　言

    • 纳米气泡通常是指直径小于1 μm的气泡. 与传统气泡相比, 纳米气泡具有比表面积大, 表面Zeta电位高、稳定性强, 能够产生自由基、传质效率高等特点[1,2], 纳米气泡按形成机制分为表面纳米气泡和体相纳米气泡, 表面纳米气泡形成在固体表面, 而体相纳米气泡分散在水相中, 相比而言, 有着数量和分布更加均匀的优势. 纳米气泡技术基于上述优点在污水处理、生物医疗、工业清洁、水体养殖、颗粒浮选等领域具有较好的应用场景[3], 近年来逐渐成为科学研究的热点. 对于水处理领域中一系列难降解难度大、处理周期长且成本高的有机污染物[4-6], 可通过纳米气泡技术实现低成本且无害化处理, 当纳米气泡收缩塌陷后形成高温高压的极限环境, 促使有机物发生降解, 因此气泡溃灭的动力学特性直接影响到纳米气泡在实际应用效果, 然而纳米气泡易受到尺寸效应, 内部扰流或外部冲击等多种作用影响, 导致纳米气泡溃灭过程较为复杂, 难以进行清晰合理的解释, 因此开展纳米气泡的溃灭机制研究, 有助于纳米气泡技术在实际应用中的优化和改进提供理论基础和实验指导.

      1915年由Cook[7]首次提出了“水锤效应”是导致叶片或是螺旋桨高速运转会导致机器冲蚀损伤的重要原因. 1928年Obara等[8]设计了水射流撞击固体表面实验, 冲击应力波的形成与衰减过程, 水射流在固体表面射流产生冲击波并形成气泡, 气泡的溃灭导致短时间内局部压强的急剧上升, 这是关于气泡溃灭产生水锤冲击现象的早期解释. 但由于纳米气泡的尺寸较小, 以及气泡溃灭过程十分短暂, 一般发生在数皮秒(10–12 s)内, 采用一般宏观电镜表征手段和连续介质的有限元模拟方法难以捕捉这一物理化学耦合过程, 然而借助于分子动力学模拟方法能够较大程度还原这一微观过程, 基于牛顿第二运动定律并结合统计平均方法, 在纳米尺度上能够更为精确、定量地实现对纳米气泡溃灭过程的研究. 利用国内学者通过分子模拟技术开展了一系列的纳米气泡溃灭的相关研究, 纳米尺寸的气泡溃灭特征研究[9,10], 包括冲击速度、气体尺寸和气体类型(如氮气、二氧化碳和氧气等)等因素对射流速度和气泡溃灭后局部压强的影响. 一些国外学者还对纳米气泡溃灭后体系内物质反应机制进行了研究, 通过ReaxFF反应动力学模拟, 根据原子间动态键级, 判断气泡溃灭后气体介质以及有机分子产物分布情况[11–13]. 一些学者还对纳米气泡传质机制进行研究, 气泡破裂后的高速射流会改变膜的通透性[14,15], 或是利用气泡破灭后产生的能量将物质定向传递到某个位置发挥其能效[16].

      尽管许多学者通过分子动力学(MD)模拟技术研究了纳米气泡溃灭过程, 但很少有学者进行纳米气泡溃灭时间、冲击速度和气泡尺寸建立响应并讨论差异与联系, 对纳米气泡结构溃灭后的流场分布规律进行研究. 本文研究采用全原子力场进行计算, 建立了具有不同半径和冲击速度的真空纳米气泡模型. 本文首先通过冲击速度定义法、Rankine公式和质心位置法验证了MD冲击过程模拟的适应性和准确性, 然后采用动量镜法重点研究了不同冲击速度和气泡尺寸条件下的气泡溃灭时间、流场速度分布、能量和密度等参数变化规律, 最后对纳米气泡溃灭后的径向射流和水锤冲击作用机制进行了分析.

    2.   计算方法

    • 分子动力学模拟是通过Lammps[17]程序实现, 水分子结构可视化及部分冲击过程分析是采用OVITO[18]软件. 水分子采用Lennard-Jones 相互作用的SPC/E[19]刚性模型, 因为它在计算水的密度、扩散系数和黏度方面与实验结果非常吻合. 各项势能参数如表1所列, 其中ε表示势阱深度, σ表示粒子平衡距离, q表示电荷量.

      采用谐波方法计算键和键角能量, 如(1)式和(2)式所示, 其中r为键长, 平衡键长r0 = 1.0 Å, θ为键角, 平衡键角θ0 = 109.47°, kb为键伸缩强度参数, kθ为键角弯曲强度参数, Eb 和Eθ 分别键能和键角能.

      • 2.1.   初始模型构建

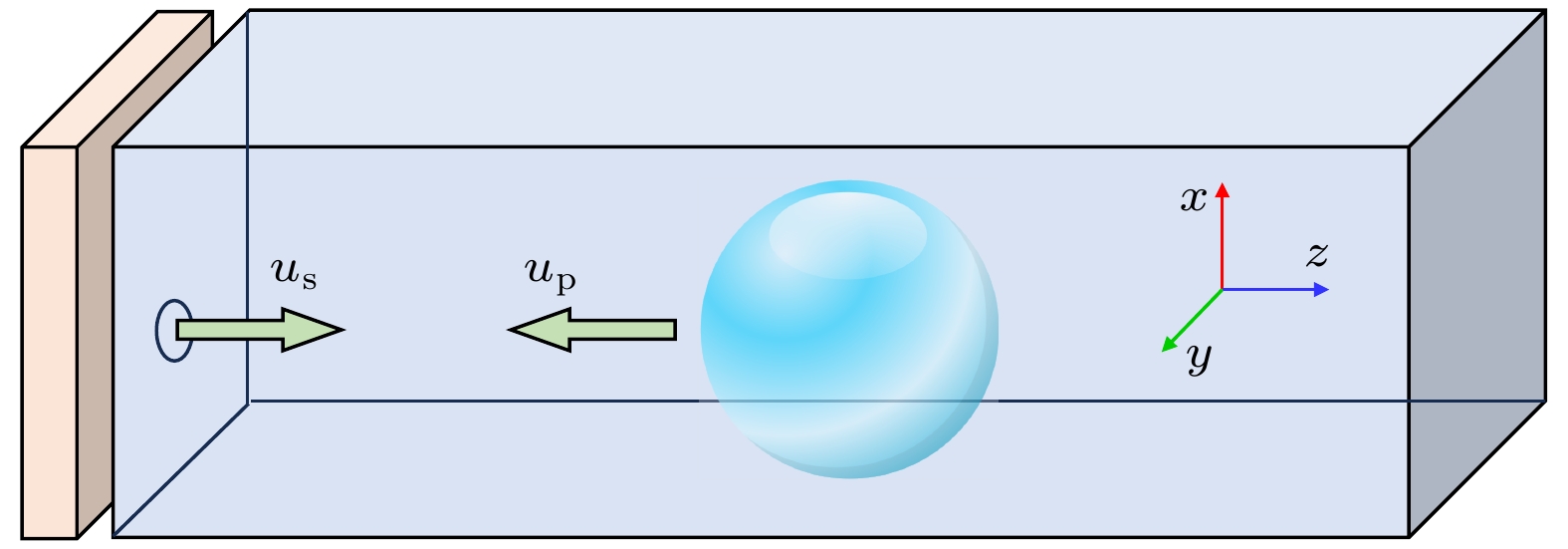
    • 图1表示纳米气泡冲击过程示意图. 浅蓝色球形区域表示纳米气泡, 左侧黄色区域表示动量镜, 深蓝色区域表示水相环境. 同时为了验证SPC/E模型进行冲击模拟过程的可行性, 构建了纯水体相模型, 与纳米气泡冲击模型相比, 仅有水分子数量有所不同. 尽管真空纳米气泡可能不是一个真实的场景, 然而这是许多学者进行MD模拟工作中采取的标准, 另外真空纳米气泡消除了气泡内部溶解气体和高拉普拉斯压力的影响, 这种模型能够更方便地解释纳米气泡塌陷溃灭过程[20].

      • 2.2.   冲击模拟设置

    • 冲击波的产生是由动量镜法实现. 所谓动量镜法是指初始粒子(所有水分子)以up的速度朝着–z方向运动, 当粒子无限接近于动量镜时, 速度up大小保持不变, 速度方向改变为+z [9,10]. 该过程实际上相当于有一个无限大的活塞将水分子初始设置速度up沿着+z方向推动并反射接触的粒子, 当+z与–z两个方向的水分子接触后, 速度发生跳跃式改变并产生一个冲击波平面, 冲击波面向+z方向的纳米气泡传递的过程为波的传播方向, 其速度大小为us. 为了避免初始状态下水分子与动量镜发生不良相互作用, 因此将动量镜放置在水相左侧2 nm处.

      初始时刻所有水分子冲击模拟在NVE系综下进行, x和y方向均采用周期性边界条件, z方向采用非周期边界条件, 时间积分步长为1.0 fs. 粒子速度up分别设置为1.0, 1.5, 2.0, 2.5和3.0 km/s.

    3.   模拟结果讨论与分析

      3.1.   SPC/E模型可行性验证

    • 为了验证SPC/E水分子模型在冲击过程模拟的适应性和准确性, 模拟了纯水冲击动量镜的过程, 并通过冲击速度定义法、Rankine-Hugoniot公式法和质心位置法共三种方法分别计算了冲击速度, 并与其他学者的实验和模拟结果进行了比较分析.

      • 3.1.1.   冲击速度定义法

    • 根据冲击速度的定义可知:

      其中us是冲击速度; up是粒子速度; ud是沿着冲击方向z轴密度不连续处的速度.

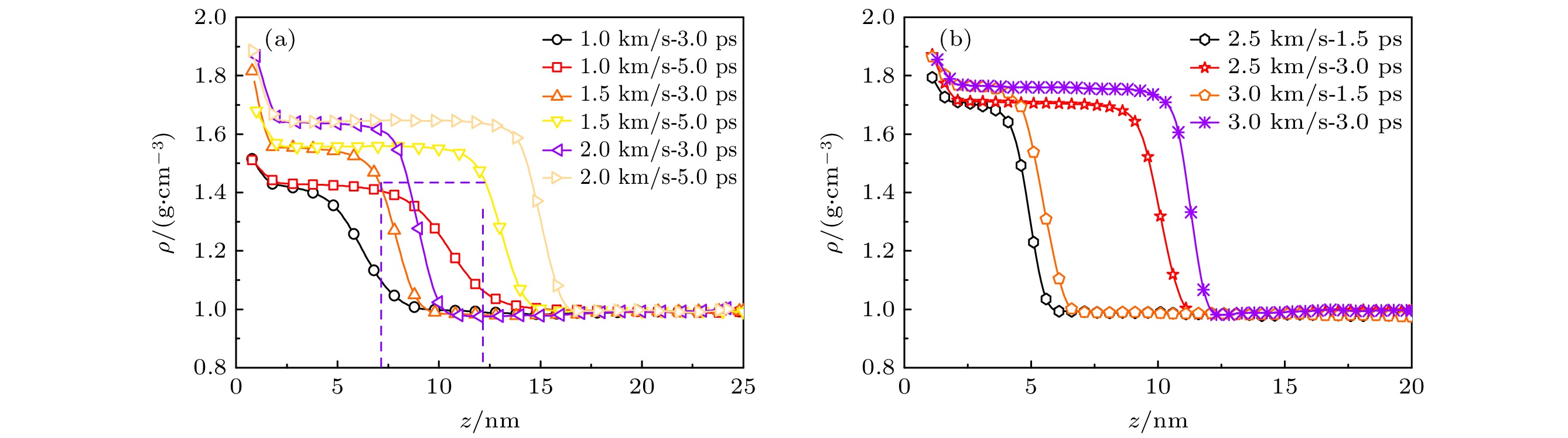
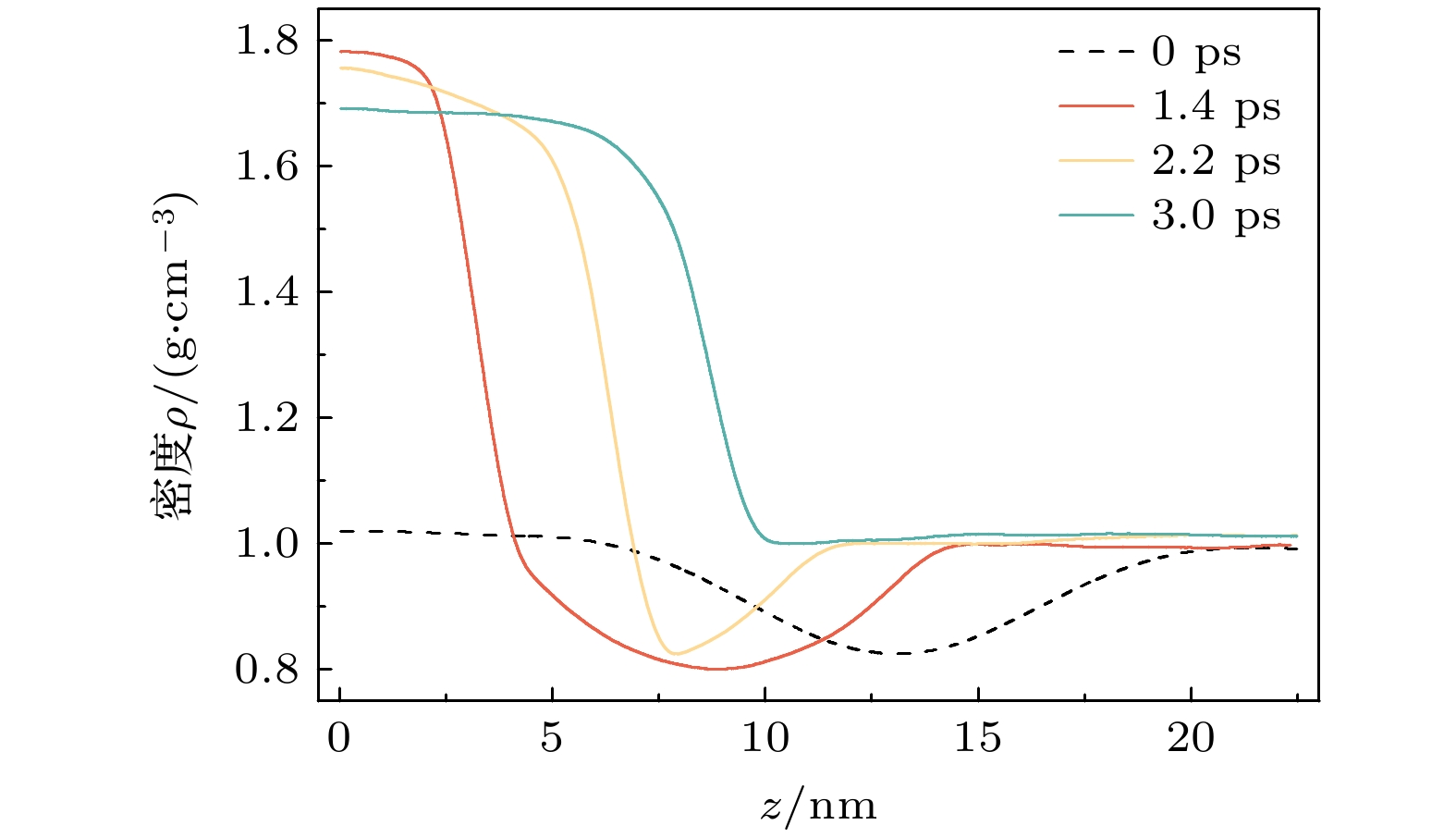
      通过图2纯水体系在不同冲击速度条件下沿z轴一维密度分布曲线, 首先取冲击波前沿处一点在不同时刻(此处取1.5, 2.0, 3.0和5.0 ps时)的位置, 计算区间平均速度得到ud, 并代入(3)式得到冲击速度us.

      • 3.1.2.   Rankine–Hugoniot 公式法

    • 由Rankine–Hugoniot 公式可知:

      其中ρ是冲击后的水的局部密度; ρ0是未经冲击的水的体相密度.

      • 3.1.3.   质心位置法

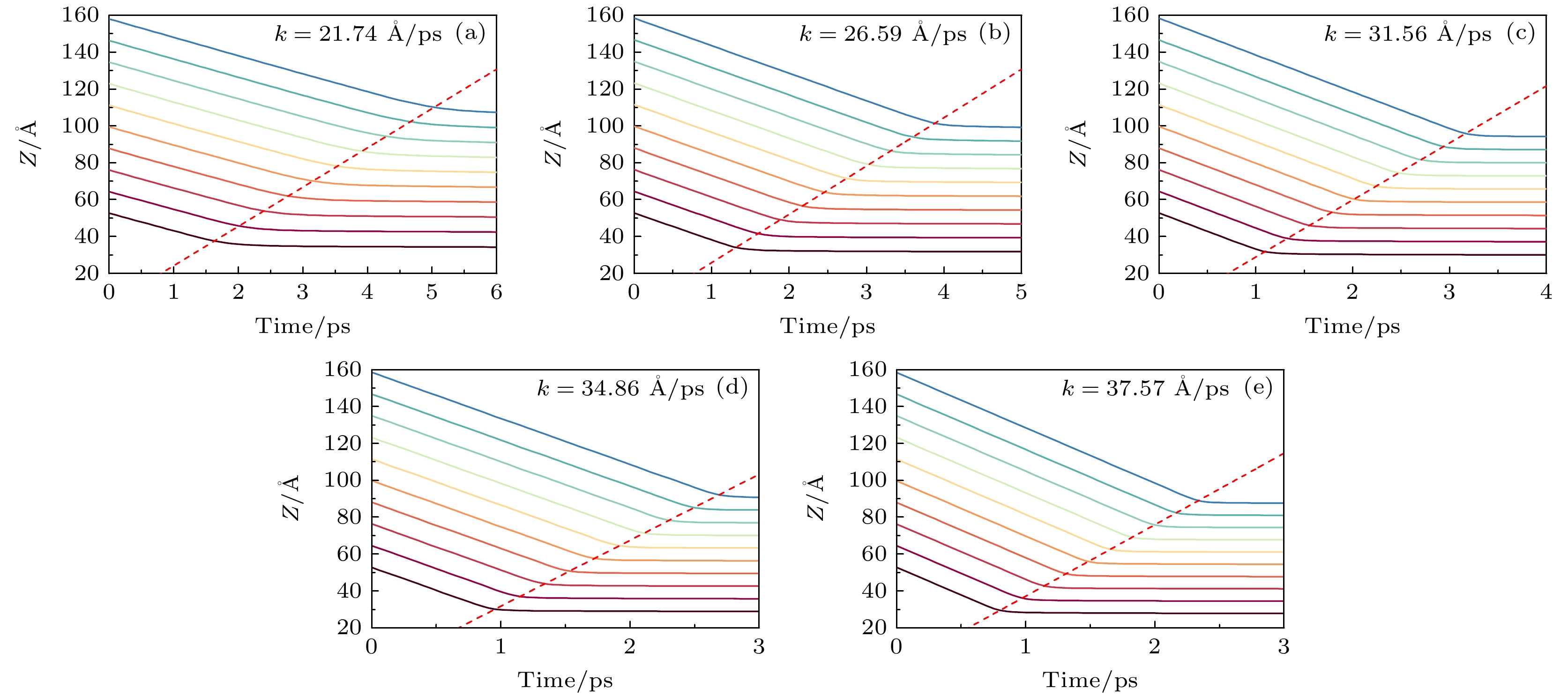
    • 将纳米气泡及周围部分水分子沿着z轴划分网格, 首先通过计算冲击过程不同时间内的各网格分子质心位置高度, 然后通过拟合曲线拐点拟合出水分子的质心速度, 最后代入(5)式计算冲击速度, 如图3所示. 本文设置网格宽度为1 nm, 为了避免边界处的网格对计算结果的影响, 取气泡中心两侧共10个网格进行计算.

      其中ucmp是拟合的体相水分子质心速度.

      • 3.1.4.   SPE模型模拟冲击过程可行性分析

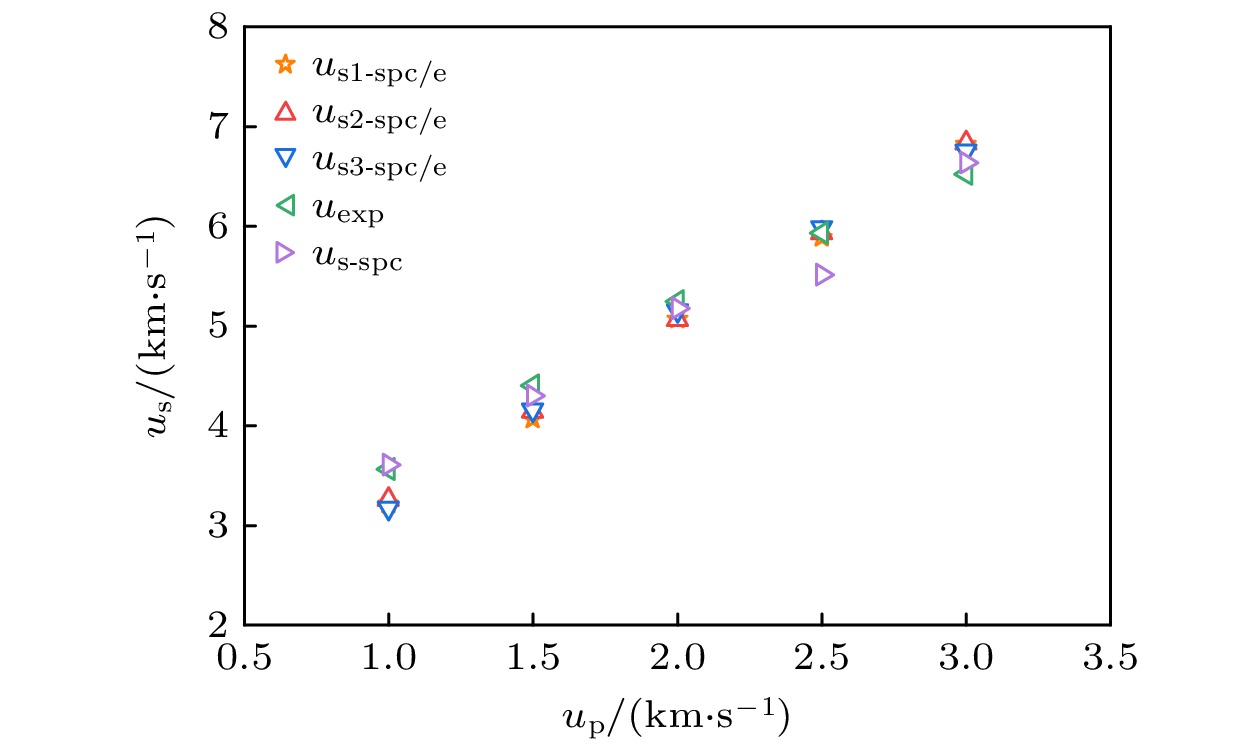
    • 根据三种验证方法绘制了图4粒子速度和冲击速度up-us的Hugoniot冲击压缩图, 计算了三种验证方法与实验结果的平均误差, 如表2所列. 在不同粒子速度情况下, 三种验证方法的冲击速度us与Rybakov实验结果平均误差ε均小于10%, 说明本文的模拟结果与Rybakov和Rybakov[21]实验结果以及Vedadi等[22]模拟结果具有良好的一致性, 采用SPC/E水分子模型模拟纳米气泡溃灭过程是可行的.

      • 3.2.   气泡溃灭时间

      3.2.1.   冲击速度和气泡尺寸的影响

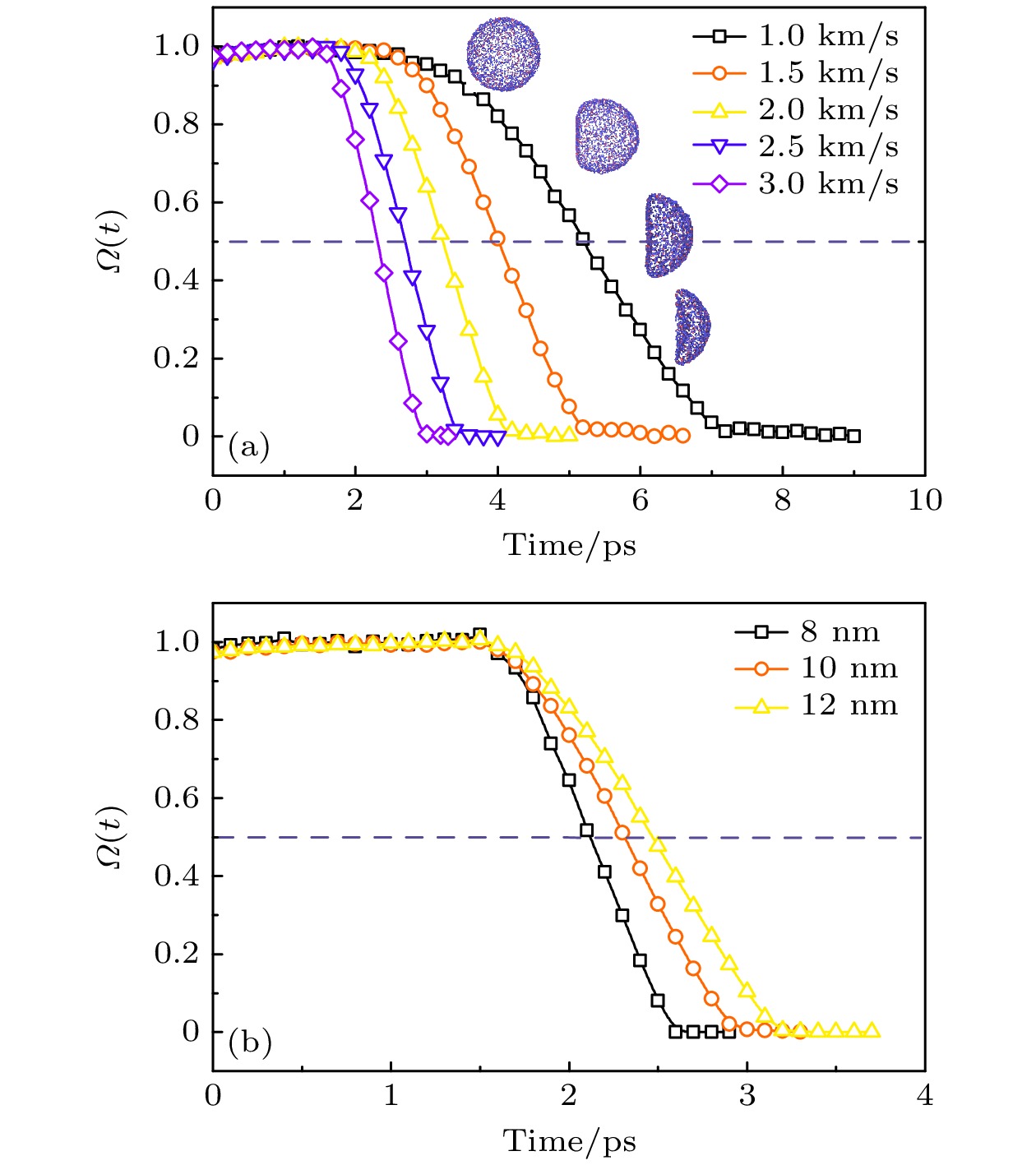
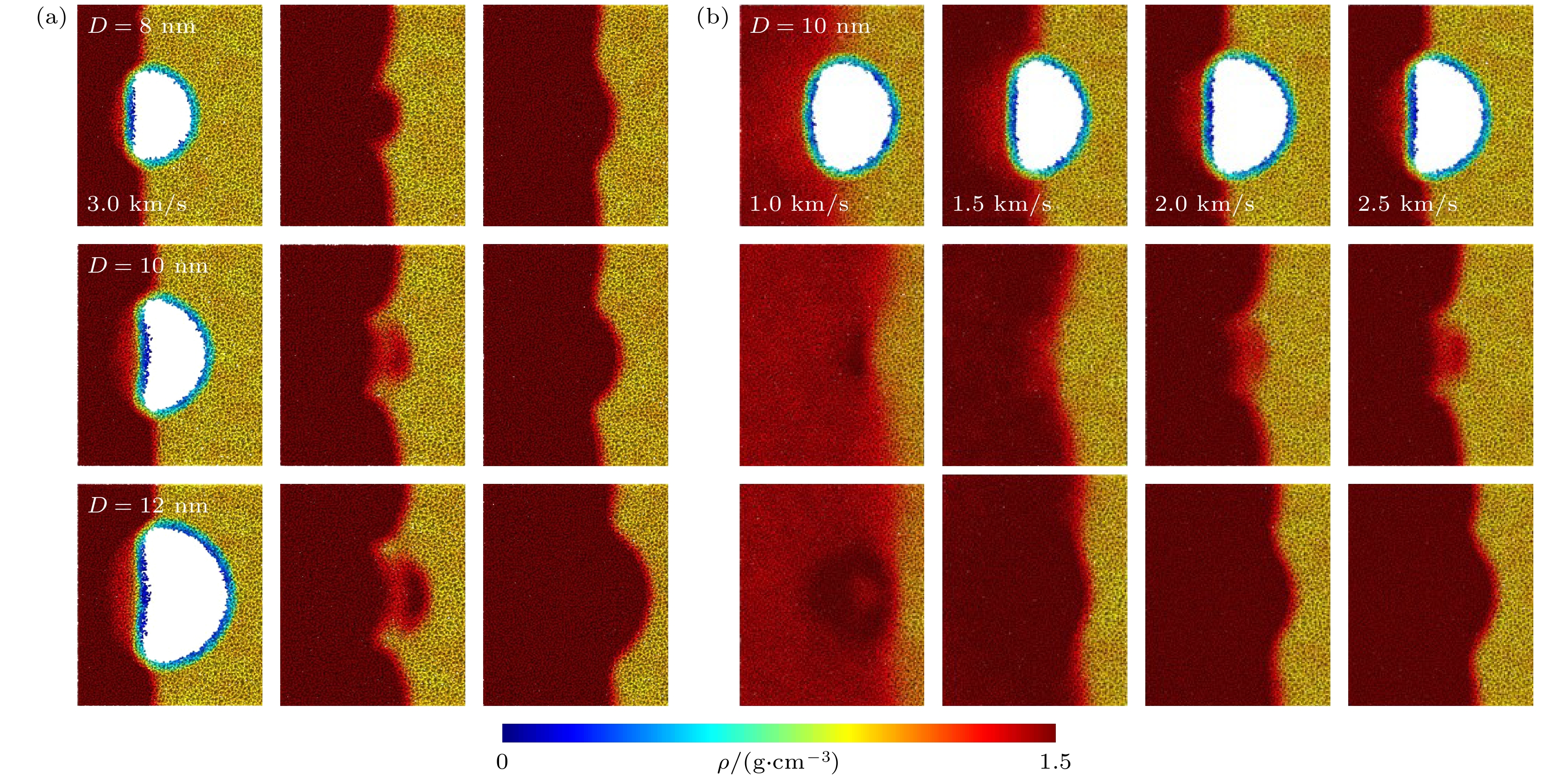
    • 由于冲击速度和气泡尺寸的不同, 纳米气泡溃灭时间存在差异. 不同冲击速度下和气泡尺寸下的纳米气泡溃灭前后的体系快照如图5所示, 当气泡尺寸减小、冲击速度增大时, 气泡越容易发生溃灭, 一方面较高的冲击速度能够使水分子经动量镜反射到纳米气泡附近的时间缩短, 另一方面较高的冲击速度拥有更强的冲击效果, 促使纳米气泡周围水分子加快向中心气泡收缩, 并且当气泡尺寸减小时, 气泡可压缩空间减小, 气泡更容易收缩. 需要值得说明的是, 气体分子的存在会影响气泡的稳定性. 气泡内部气体与外部水分子间形成液膜, 膜内外存在物质交换, 气体和水分子不断进出液膜, 液膜也会随着气体和水分子数量的变化进行收缩和扩大导致气泡尺寸发生变化, 而真空纳米气泡由于没有填充气体, 尺寸则一直保持相对恒定, 不会产生较大变化. 因此两种纳米气泡模型的体积变化还是存在一定差异的.

      如表3所列示, 统计了不同尺寸的纳米气泡溃灭前后的时间信息, 当冲击速度up为3.0 km/s, 直径D在8, 10和12 nm对应的气泡溃灭时间分别为1.4, 1.6和1.9 ps, 而根据Rayleigh[23]公式($ \tau = 0.45 D\sqrt {{\rho {/ } {\Delta P}}} $, 其中ρ是质量密度, P表示压强, D是气泡直径)进行估算, 气泡溃灭时间逐渐延长, 分别为1.1, 1.4和1.7 ps.

      MD模拟结果与理论计算所得的气泡溃灭时间值所体现的差异, 一方面是由于Rayleigh公式所描述的气泡环境是在稳定均匀的流体内, 为气泡的自溃灭行为, 而MD冲击模拟过程中密度和压强在短时间发生剧烈变化, 另一方面与MD模拟不同, 该公式未考虑不同原子间相互作用引起的粘度和表面张力效应. 根据表3不同粒子速度和尺寸下的纳米气泡破裂时间结果可知, 当气泡尺寸逐渐增大, 气泡破裂时间延长, 而当冲击速度逐渐增大, 气泡破裂时间缩短, 另外值得注意的是, 当气泡尺寸和冲击速度较高时, 气泡破裂时间的MD模拟结果和Rayleigh公式推导值较为吻合, 推测是由于大尺寸气泡在高速冲击时, 粘度效应和表面张力作用效果降低.

      • 3.2.2.   气泡溃灭阶段

    • 尽管不同冲击速度和尺寸下的纳米气泡溃灭的时间有所不同, 但纳米气泡溃灭过程类似, 大体上经历三个阶段, 不同时刻下的纳米气泡结构变化情况如图6所示. 反应最初阶段, 纳米气泡及周围的水分子向–z方向移动, 此过程没有外部冲击作用, 气泡体积基本没有变化; 随后水分子与动量镜发生接触后反弹, 速度方向发生改变, 形成向+z方向移动的冲击波, 当冲击波移动至气泡附近, 气泡在冲击波作用下液膜稳定结构被破坏, 气泡发生形变并且体积迅速减小; 最终阶段, 水分子挤压液膜阻力增大, 导致纳米气泡体积减小速度放缓, 最终发展至纳米气泡完全溃灭.

      • 3.3.   气泡溃灭流场速度分布

      3.3.1.   气泡溃灭前后速度变化

    • 随着冲击速度和气泡尺寸的增大, 气泡高速射流区域面积逐渐增大, 如图7所示. 尽管初始粒子冲击速度up 大小存在差异, 且部分up小于3.0 km/s(1.0—2.5 km/s), 但当气泡完全溃灭时所产生的射流速度仍能达到3.0 km/s 以上. 当冲击波经动量镜反射到达气泡左侧边缘时, 冲击波面处于同一位置, 但当气泡完全溃灭时, 气泡上下边缘的冲击波速度要小于气泡中部, 造成中间部分的冲击波面向前凸起, 且高速射流范围越大凸起现象越为明显.

      • 3.3.2.   纳米气泡溃灭射流验证

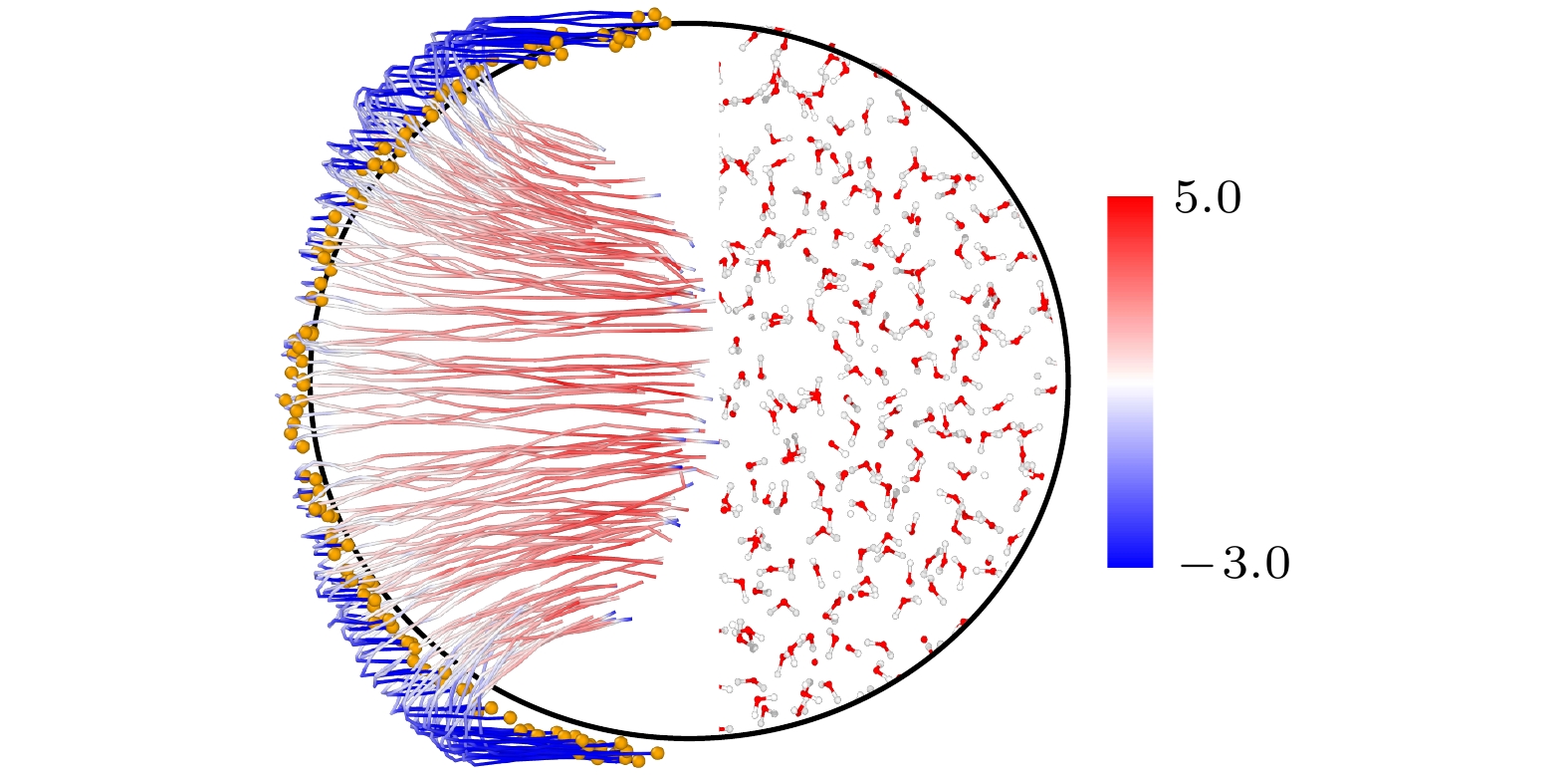
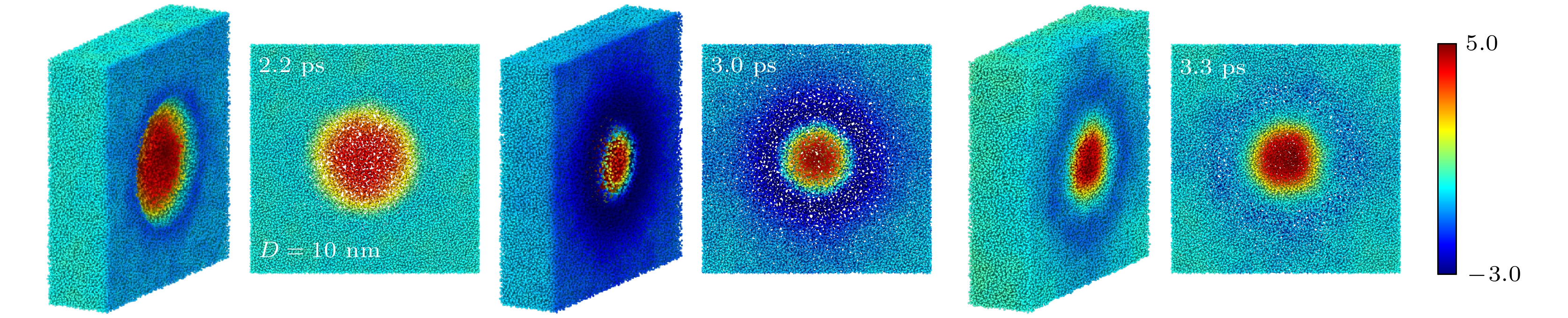
    • 为了进一步验证纳米气泡射流这一现象, 绘制了D = 10 nm, up = 3.0 km/s, 时间在1.4—3.0 ps内(纳米气泡从完整到溃灭的时间段)气泡外层左半部分的液膜运动轨迹, 如图8所示, 黄色小球表示纳米气泡外层液膜水分子中的氧原子, 曲线对应原子的运动轨迹, 曲线颜色对应原子处于该点位置时z轴方向的速度分量, 由图8像可知, 氧原子速度首先逐渐衰减, 速度方向改变后向气泡内中心汇聚, 射流速度大小逐渐增大至5.0 km/s. 由于可见, 气泡溃灭过程中伴随着高速射流现象的产生. Zhang等[24]通过高速摄像机也同样捕捉到了气泡溃灭时的射流现象, 进一步验证了模拟工作的准确性. 需要值得说明的是, 气体分子的存在会影响也气泡的射流程度. 由于真空气泡内部没有气体, 射流主要由外部液体决定, 但含气纳米气泡的射流是由内部气体和外部液体共同决定的, 另外也受到气体含量和种类的控制, 例如王小峰等[10]在纳米气泡完全塌陷过程的模拟工作中指出, 低含量二氧化碳和氧气的纳米气泡在溃灭时产生的射流速度大于真空纳米气泡.

      • 3.3.3.   二维速度矢量分布

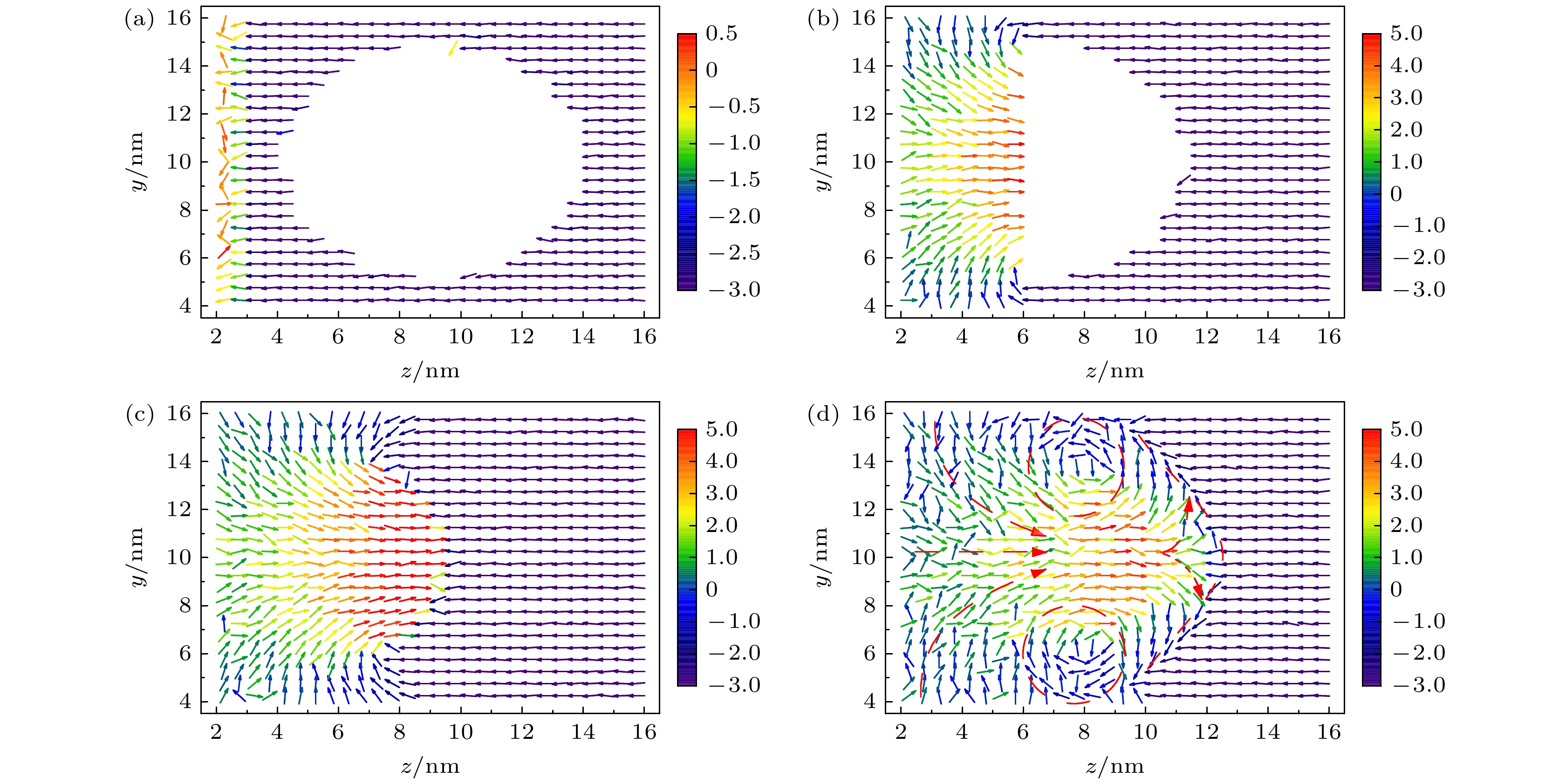
    • 纳米气泡溃灭后会造成周围的流场速度分布不均匀, 为了研究纳米气泡溃灭过程前后周围流场分布情况, 以及气泡尺寸及冲击速度大小对流场速度分布的影响, 以长度为0.5 nm进行网格划分, 绘制了气泡周围的流场(y-z平面)速度矢量分布图, 如图9和图10所示, 其中, 图9箭头的方向表示网格内水分子的速度方向, 箭头的颜色映射网格内水分子在z轴方向的速度大小分量, 中间球状区域代表真空纳米气泡, 图10所示, 箭头的颜色映射网格内水分子在XYZ坐标轴下合速度大小.

      首先对不同时刻下气泡流场变化进行了研究, 由图9可知, 时间为1.4 ps (图9(a))时, 冲击波运动至气泡左侧边缘处, 左侧水分子速度发生衰减, 部分水分子速度改变为+z方向, 但右侧水分子速度基本不受影响, 气泡维持球形结构; 随后冲击波继续移动, 在2.2 ps (图9(b))时处于气泡中心处附近, 气泡溃灭体积接近一半, 液膜逐渐收缩导致气泡体积减小, 气泡左半部分真空区域被冲击波挤压的水分子所填充, 水分子有向气泡中心汇集的趋势, 气泡内部靠近几何中心的水分子速度最高达5.0 km/s; 当时间为2.8 ps (图9(c))时, 能够观察到呈圆锥状向右移动的冲击波, 真空区域消失, 此时气泡完全发生溃灭, 高射流的水分子形成连续性区域. 当时间为3.3 ps (图9(d) )时气泡完全溃灭, 周围水分子向中心射流的程度最为明显, 在水分子射流的水锤冲击作用下, 产生了强烈的冲击力和剪切力, 原有气泡层流流场的状态被改变, 在上方和下方形成了紊流涡旋结构, 有效的增强了流体内部传质作用, 射流前端速度发生衰减并形成弧形剖面, 如图9(d)红线标记所示.

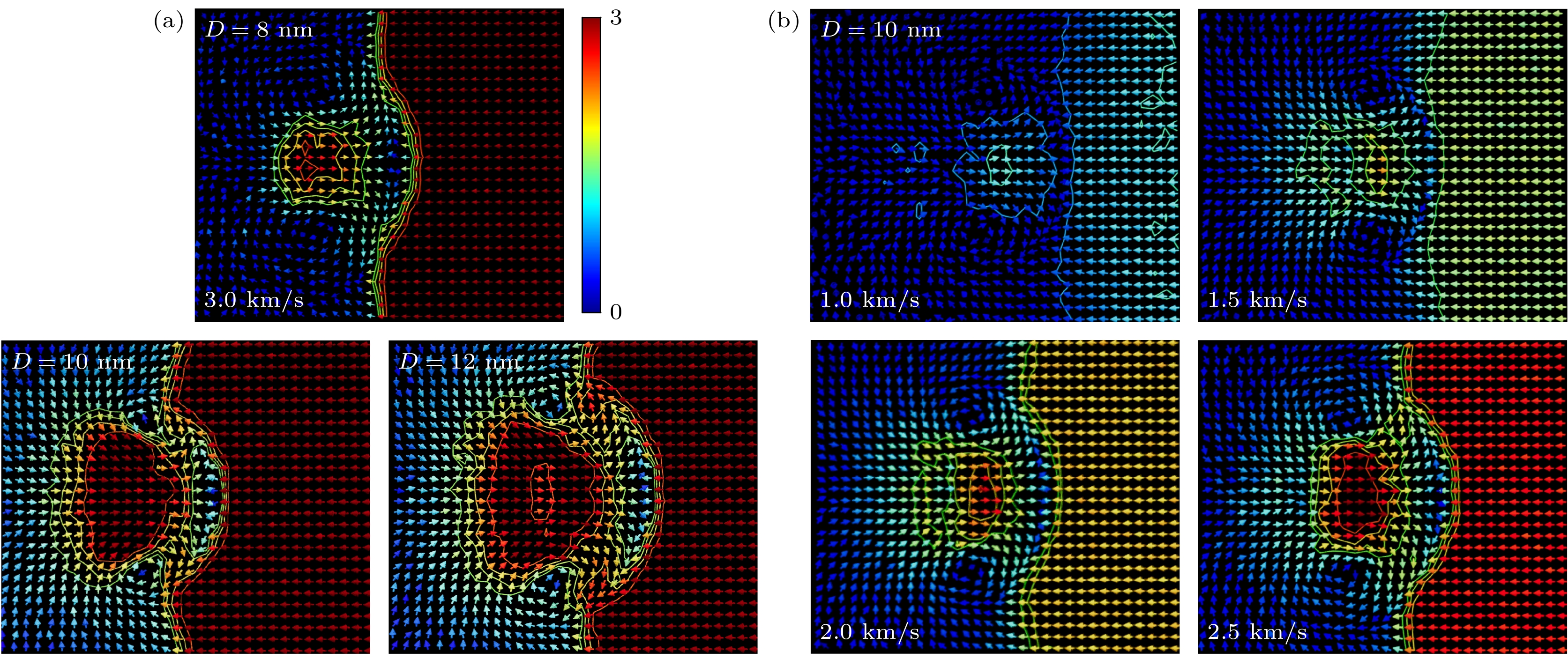
      同样也考虑了气泡尺寸及冲击速度大小对气泡的影响, 如图10所示. 纳米气泡完全溃灭时, 气泡上方和下方水分子会发生方向改变, 其平均分子速度指向气泡中心. 在右侧水分子冲击影响下, 纳米气泡射流速度由气泡中部向上下两侧逐渐衰减, 由于中心位置射流速度较大, 因此在速度等高线位置处形成向右的凸起, 并且随着气泡尺寸和冲击速度增大, 凸起程度就越大, 当等高线左侧的水分子沿等高线向两侧运动, 逐渐向气泡中心汇集时, 在气泡上方和下方形成涡旋结构. 等高线左侧区域的水分子运动范围主要受到气泡尺寸的影响, 气泡尺寸越大, 水分子向两侧延伸的程度就越大. 另外凸起位置与高速射流之间的区域内速度大小, 体系能量和密度(3.4节中进行讨论)存在呈跳跃式变化, 因此证明了纳米气泡在溃灭时产生了二次冲击波. Zhang等[25]通过水听器检测到的空化气泡产生的声信号, 气泡溃灭时产生的射流强度与等离子体冲击波的能量大小成正比, 在60 mJ激光能量的条件下, 检测到了空化气泡溃灭时产生的冲击波, 与本文模拟结果基本保持一致.

      • 3.4.   气泡溃灭能量和密度分析

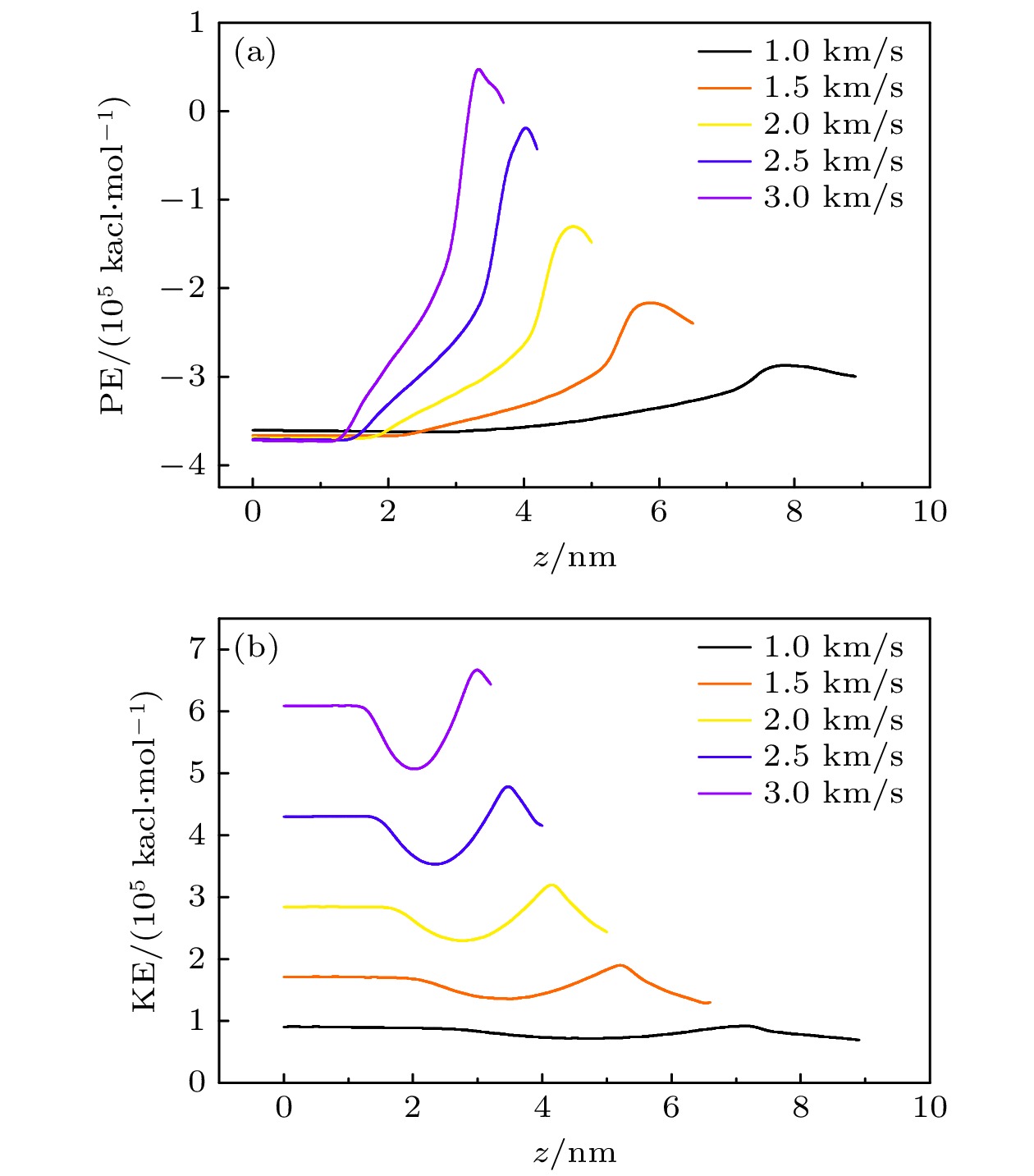
    • 高速冲击作用下纳米气泡溃灭后导致局部水分子被压缩和运动轨迹发生被改变, 体系的能量和密度在短时间内也随之发生剧烈变化. 由于不同尺寸的纳米气泡模型中的删除掉了不同数量的水分子, 导致计算能量和密度时粒子数量基准存在差异, 因此只讨论了D = 10 nm条件下, 不同冲击速度下的纳米气泡溃灭能量(动能和势能)和密度变化规律, 如图11所示, 以及y-z平面的密度分布曲线云图, 如图12和图13所示.

      • 3.4.1.   气泡溃灭能量分析

    • 从图11体系势能和动能沿z轴一维分布曲线, 当冲击波未到达纳米气泡附近时, 冲击波以稳定的速度向+z方向运动, 势能和动能基本保持不变, 但由于粒子速度up不同, 造成各组动能差异较为明显; 当冲击波作用纳米气泡发生部分塌陷后, 液膜附近水分子向中心产生射流聚集造成分子间距减小, 分子间作用力以排斥力为主(势能为正), 因此势能逐渐增大, 而动能呈现出先减小后增大的趋势, 一方面由于冲击波在到达纳米气泡位置后, 传播介质由液相-真空相-液相, 而冲击波的传播速度在真空环境下要远小于液体环境下, 因此该过程动能相较于未冲击时发生一定程度的衰减, 另一方面由于本文的研究对象为真空纳米气泡, 初始时刻气泡内部没有粒子填充导致气泡内部区域的速度未能被统计, 该部分能量损失大小与冲击波接触长度成正比, 当冲击波运动至气泡中心位置处时(气泡塌陷一半), 此时冲击波接触长度对应气泡直径, 因此气泡中心位置处的体系动能最小, 随着初始up冲击速度的增大, 动能和势能的变化愈发明显; 最终在水分子撞击右侧壁面, 在水锤冲击作用下体系能量产生耗散, 势能和动能发生下降.

      • 3.4.2.   气泡溃灭密度分析

    • 由图12 纳米气泡溃灭前后周围密度的沿z轴一维分布曲线可知, up = 3.0 km/s, D = 10 nm, 0 ps时气泡质心位于13 nm处, 这是由于真空气泡内没有粒子存在, 因此气泡周密度呈减小后增大至不变的趋势, 这一现象与气泡动能变化规律类似; 由于体系向-z方向的动量镜处移动, 气泡质心位置向左发生偏移, 但随着冲击波到达纳米气泡左端逐渐推动纳米气泡质心向右发生移动, 原有位置的真空体积被气泡射流水分子占据造成密度增大; 动量镜位置与气泡左侧之间的密度迅速下降, 但随着冲击时间的增大, 密度下降速率也逐渐放缓, 最终气泡完全破裂在+z方向的10 nm位置附近接近正常水相密度.

      由图13 纳米气泡周围质量密度的y-z平面二维云图可知, 随着气泡尺寸和冲击速度的增大, 气泡周围密度也逐渐增大. 初始时刻, 由于纳米气泡未溃灭时周围粒子较少, 因此密度较低, 但在冲击波持续作用下水分子剧烈挤压气泡内部空间, 气相迅速释放到周围液体中, 并且由于动量镜反射作用, 边界和气泡周围密度逐渐增大, 此过程涉及由气相向液相的转变, 最终在纳米气泡完全时溃灭时局部密度可达1.5 g/cm3附近.

      • 3.5.   径向射流和水锤冲击作用分析

    • 水锤冲击作用是指纳米气泡受外部环境影响, 气泡体积迅速变化至溃灭时气泡周围流速和压强的急剧变化现象. 本文对纳米气泡溃灭产生射流速度径向剖面的变化情况和水锤冲击作用范围进行了讨论, 绘制了D = 10 nm, up = 3.0 km/s体系在2.2—3.3 ps的x-y平面冲击波前沿的速度分布云图, 如图14所示, 以及不同尺寸和冲击速度下的y-z平面的压强分布云图, 如图15所示, 以气泡附近高压区域(黑色区域)大小表征纳米气泡水锤冲击作用波及范围.

      • 3.5.1.   径向射流作用

    • 纳米气泡射流速度随时间呈先增大后减小的趋势, 纳米射流区域随时间的增大逐渐减小, 当冲击波到达气泡中心附近(2.2 ps), x-y平面波前沿活动空间范围最大, 水分子在此处向四周扩散导致射流区域较大, 射流速度由中心向四周辐射逐渐减小, 随着气泡右侧体积的减小, 水分子运动空间受限, 因此射流区域逐渐减小, 射流速度随时间逐渐增大, 直至气泡完全溃灭并(3.0 ps)射流速度达到最大, 当向动量镜方向 –z移动的水分子对冲碰撞时(3.3 ps)射流速度有所减小.

      • 3.5.2.   水锤冲击作用

    • 根据Rankine–Hugoniot跳跃条件$ {P_{\text{s}}} = {\rho _0}{u_{\text{s}}}{u_{\text{p}}} $ 计算可以得到冲击压力, 其中ρ0 是系综中的水分子密度, 将3.1节中的三种方法计算结果取平均值得到冲击速度us , 代入公式可以得到不同粒子速度条件下的冲击压力Ps计算值, 如表4所列, 不同粒子速度下的MD模拟和Rankine-Hugoniot计算冲击压力结果基本吻合, 进一步证明了采用SPC/E水分子模型对冲击压力描述的准确性.

      图15中分别表示绘制了气泡溃灭50%, 气泡完全溃灭以及气泡完全溃灭0.5 ps后的局部压强分布情况. 局部压强是指气泡发生塌陷时周围的部分水分子压强贡献值. 随着气泡尺寸和冲击速度的增大, 水锤冲击作用愈发明显. 当气泡溃灭约50%时, 水锤作用范围较小, 但直至气泡完全溃灭后射流区域内部逐渐产生大范围的水锤冲击作用, 并且随着时间的延长高压作用区域逐渐增大, 水锤冲击的波及范围也逐渐增大, 因此水锤冲击作用相对于纳米气泡射流现象具有一定的滞后性, 并且水锤冲击作用范围和大小在气泡溃灭后一段时间内持续积累. 对于up = 3.0 km/s的纳米气泡结构塌陷后射流水锤冲击所形成的局部压强可达30 GPa以上, 该数值与Zhan等[26]的模拟结果具有良好的一致性.

    4.   结　论

    • 本文运用分子动力学方法研究了纳米气泡逐渐凹陷并发展至溃灭的过程, 冲击速度和气泡尺寸对纳米气泡溃灭的动力学特性影响机制, 通过构建水分子粒子速度和冲击速度up-us的Hugoniot冲击压缩曲线, 验证了采用SPC/E水分子模型模拟纳米气泡高速冲击溃灭过程可行性. 纳米气泡溃灭主要经历三个阶段, 体系变化速率逐渐增大后最终放缓, 冲击速度的减小和气泡尺寸的增大都会延长气泡溃灭时间. 纳米气泡溃灭时间的分子模拟结果与Rayleigh理论公式结果存在一定差异, 主要是受流体的稳定程度以及黏度和表面张力效应作用的影响, 气泡尺寸和冲击速度较大时吻合程度较高. 纳米气泡溃灭后高速射流后在速度等高线右端形成凸起, 随着气泡尺寸和冲击速度增大, 凸起程度就越大, 水分子向气泡中心汇集, 在气泡上方和下方形成涡旋结构, 有效的增强了流体内部传质作用. 纳米气泡溃灭过程中, 传播介质由液相过渡到真空相, 造成冲击速度衰减, 体系动能产生损耗, 随着气泡尺寸和冲击速度的增大, 气泡周围密度也逐渐增大, 水分子射流剧烈挤压气泡内部空间造成体系密度增大, 局部密度可达1.5 g/cm3. 纳米气泡溃灭过程中伴随着高速射流现象的产生, 产生强烈的冲击力和剪切力促使紊流涡旋结构的形成, 有效增强了流体内部传质作用, 纳米气泡(up = 3.0 km/s, D = 10 nm)塌陷水锤冲击所形成的局部压强可达30 GPa以上.

    参考文献 (26)

目录

/

返回文章
返回