随着社会经济的发展和城市化进程的推进, 城市人口不断增加, 城市中经常出现大型的、行人高度聚集的社会活动, 在地下交通枢纽、地下商业设施等大型地下综合体内经常出现大规模人群. 一旦发生火灾、恐怖袭击、爆炸等突发公共安全事件, 易发生视野受限的紧急情况, 将导致人群恐慌, 可能因疏散行为或应急管理策略不当造成大量的人员伤亡和财产损失^[1]. 同时, 在出行活动中, 结伴行为日益普遍. 在发生意外情况需要疏散时, 由于结伴行人之间的相互作用关系, 可能出现结伴行人寻找同伴的现象, 且结伴群体会占据更大空间, 结伴行为会对人群疏散过程产生重要影响^[2]. 在视野受限条件下, 结伴人群疏散过程中个体间的相互作用关系变得更加复杂, 人员伤亡的风险更加严峻^[3–6]. 因此, 视野受限条件下结伴人群的安全疏散问题引起了国内外研究人员的广泛关注.

近年来, 学者们采用可控实验^[7]和建模仿真^[8]的方法对结伴行人的疏散问题展开了一系列的研究. Wei等^[9]通过问卷调查和实地观测研究了结伴行人的群组大小、空间位置、速度调整、信息传递等因素对结伴群体运动过程的影响, 发现结伴群体的等待行为对疏散过程具有重要影响. Gorrini等^[10]通过对比分析结伴行人和单个行人的运动速度, 发现结伴行人为了保持结伴队形以及互相交谈, 运动速度比单个行人的运动速度降低30%. Chen等^[11]通过疏散实验和模型仿真研究了儿童结伴行为对疏散过程的影响, 发现儿童结伴行为对疏散效率产生了负面影响. Cuesta等^[12]通过疏散实验对比分析了火灾条件下单个行人和不同规模结伴群体的疏散过程, 发现大规模结伴群体的疏散效率高于小规模结伴群体和单个行人的疏散效率. Ren等^[13]通过疏散实验研究了结伴群体的行为模式对人群疏散效率的影响, 发现结伴群体的存在降低了人群疏散效率. 霍非舟等^[4]考虑结伴行为构建了行疏散仿真模型, 仿真结果表明行人疏散时间随结伴比例的增大呈现先延长后缩短的趋势. 从以上研究可以发现, 在正常视野条件下, 行人结伴行为通常会对人群疏散过程产生负面影响. 但是, 在不良视野(零视野和有限视野)条件下, 行人只能从周围环境中获取有限的信息, 行人运动行为与正常视野条件下的行人运动行为有很大差异, 进而影响疏散效率和安全. Xie等^[14,15]通过可控实验对比分析了不同能见度条件下个体和结伴群体的疏散效率, 发现随着能见度的降低, 结伴群体的疏散效率逐渐提高, 而个体的疏散效率逐渐降低. Was等^[16]通过组织烟雾环境中的隧道疏散实验, 发现结伴群体在烟雾环境中的疏散速度低于正常视野条件下的疏散速度. Xue等^[17]通过疏散实验和模型仿真研究了有限视野条件下行人在疏散过程中的沿墙行为和冲突解决过程. Zeng等^[18]通过组织零视野条件下隧道内的个体和结伴群体疏散实验, 发现零视野条件下结伴群体的移动速度高于个体移动速度, 结伴行为可以提高疏散效率. 从以上研究可以发现, 在正常视野条件下, 结伴行人之间的交流和互动对人群疏散效率产生阻碍作用; 在视野受限条件下, 结伴行人之间的信息交流使行人获得更多周围环境信息, 对人群疏散效率产生促进作用. 虽然学者们针对视野受限条件下行人疏散特性、结伴疏散效率已开展初步探讨, 但行人结伴行为具有异质性, 针对零视野条件下行人结伴疏散的研究还不充分.

实际上, 行人在疏散过程中会受到多种因素的干扰^[19,20], 结伴行人并不总是以整体的形式进行运动, 结伴行人之间可能出现分离的情况. 在正常视野条件下, 行人可以通过视觉寻找同伴或者疏散路径; 但在零视野条件下, 行人的视野信息完全缺失, 需要依靠声音信息寻找同伴^[21]. 然而, 现有零视野条件下考虑结伴行为的行人疏散研究中主要探讨结伴群体作为整体的疏散情况, 未考虑到结伴行人分开时的结伴过程对疏散过程的影响. 因此, 本文通过组织零视野条件下行人的结伴疏散实验, 获取结伴行人在零视野疏散过程中的运动行为特征; 考虑结伴行为、沿墙行为、听觉引导行为, 构建零视野条件下行人疏散模型; 利用实验数据对提出的模型进行验证, 仿真研究零视野条件下结伴行为对疏散过程的影响. 本文的理论贡献和创新性主要包括以下两个方面: 首先, 通过可控实验发现了零视野疏散过程中结伴行人的听觉引导行为、沿墙行为和结伴疏散模式, 揭示了个体行为对疏散过程的影响机理; 其次, 考虑不同结伴模式下行人的运动行为特征对疏散过程的影响机制, 构建了基于元胞自动机的零视野条件下行人疏散模型, 探讨了零视野条件下结伴行为对疏散过程的影响, 为制定零视野条件下行人应急疏散预案与管理策略提供了理论支持.

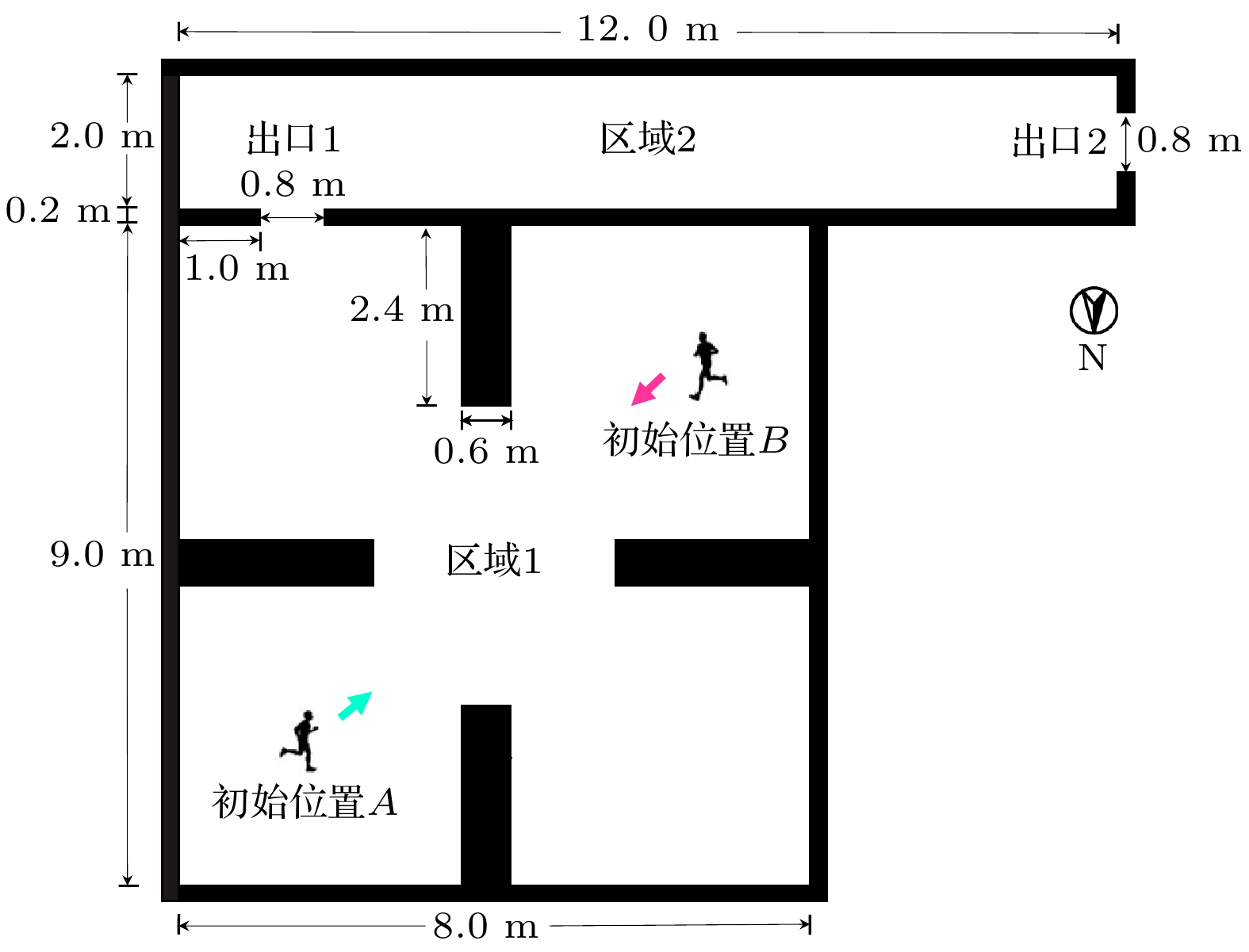
零视野条件下行人的疏散实验在图1所示场景内进行. 实验场景由区域1和区域2组成, 区域1长度为9 m, 宽度为8 m; 区域2长度为12 m, 宽度为2 m. 在两个区域分别有一个出口, 两个出口的宽度均为0.8 m, 出口1位于区域1南侧边界, 距离东侧边界1 m; 出口2位于区域2西侧边界. 在区域1有四个障碍物, 分别位于区域1的东侧、南侧、西侧和北侧的中间位置, 障碍物的长度为2.4 m, 宽度为0.6 m, 高度为0.74 m. 在图1中, 黑色矩形代表障碍物和边界, 边界宽度为0.2 m. 在实验场地旁边楼宇的顶层安置一台摄像机, 用来记录行人疏散的过程.

疏散实验的参与人员均为在校大学生, 共234人, 平均年龄为22岁, 其中男生132人, 女生102人, 所有参与人员被分为117个两人小组. 小组内两个行人是具有同学、朋友或者恋人等社会关系的组合, 用来模拟现实情况中行人结伴出行的情景.

疏散实验的目的是研究零视野条件下两个具有社会关系的行人在出现分离情况后的紧急疏散过程, 小组内的两个行人分别被称为行人1和行人2. 疏散实验规则如下:

1)在疏散过程中, 行人需要全程佩戴不透明眼罩, 用来模拟零视野情景.

2)疏散实验开始后, 两个行人应采取自己认为最快的方式离开疏散区域.

3)疏散实验开始后, 两个行人之间可以通过语言、敲击障碍物、触摸等任何方式进行交流.

4)当两个行人一起从出口2离开时, 疏散实验结束.

疏散实验以组为单位进行, 具体实验流程如下:

1)进入实验区域前, 工作人员告知参与人员实验规则和注意事项, 同时为行人1和行人2分别佩戴青色帽子和红色帽子, 用于提取行人轨迹.

2)进入实验场地后, 工作人员带领参与人员熟悉疏散空间环境, 然后为其佩戴不透明眼罩.

3)佩戴不透明眼罩后, 工作人员告知参与人员将被带到实验场地的一个随机位置.

4)两位工作人员分别带领两位参与人员在原地顺时针旋转3圈和逆时针旋转3圈, 然后在场地内无序行走, 随机走到某一位置后再次在原地顺时针或者逆时针旋转3圈, 最后将两位参与人员带到指定初始位置, 等待实验开始. 行人1和行人2的初始位置分别为初始位置A和初始位置B (见图1), 青色和红色箭头方向代表两位参与人员的初始朝向. 该步骤是使行人无法获知自己的初始位置.

5)工作人员发出实验开始指令后, 两位参与人员开始移动, 并采取自己认为最快的方式离开疏散区域.

6)两位参与人员一旦一起从出口2离开, 该组疏散实验结束.

疏散实验中设置两个行人的起点为初始位置A和B的原因是: (i)为了更好地观察行人的结伴疏散过程, 两个行人的初始位置需要有较远的距离; (ii)为了防止行人快速地找到出口或者墙壁, 两个行人的初始位置不能离出口和墙壁太近; (iii)为了排除行人初始位置到出口距离不同对疏散过程的影响, 两个行人的初始位置到出口的距离需要大致相同.

在疏散过程中, 所有两人小组均发生了结伴行为, 他们通过声音信息的传递和相互触碰, 从初始的分离状态变为结伴状态, 一起寻找出口. 这是因为实验中两个行人具有一定社会关系, 在完全黑暗的极端环境中, 行人希望获取心理上的安全感和行动上的支持, 这促使行人倾向于结伴疏散. 此外, 实验规则要求当两个行人一起从出口2离开时, 疏散实验结束. 这条规则虽然没有要求行人必须以结伴的形式进行疏散, 但也在一定程度上驱动或者强化了行人之间的结伴行为. 在结伴形成后, 结伴行人通过协商对疏散路径进行决策, 行人之间采用拉手或触碰对方的方式维持结伴状态.

不同结伴小组的结伴行为在时间和空间上具有差异性. 在时间上, 结伴行为可以分为疏散开始阶段的结伴行为和疏散过程中的结伴行为; 在空间上, 结伴行为可以分为区域1内部的结伴行为和出口1附近的结伴行为. 在117个两人小组中, 114个小组的结伴疏散过程表现出明显的规律性. 根据结伴行为的时空差异, 可以将114组结伴行人的结伴模式分为3类, 具体如下.

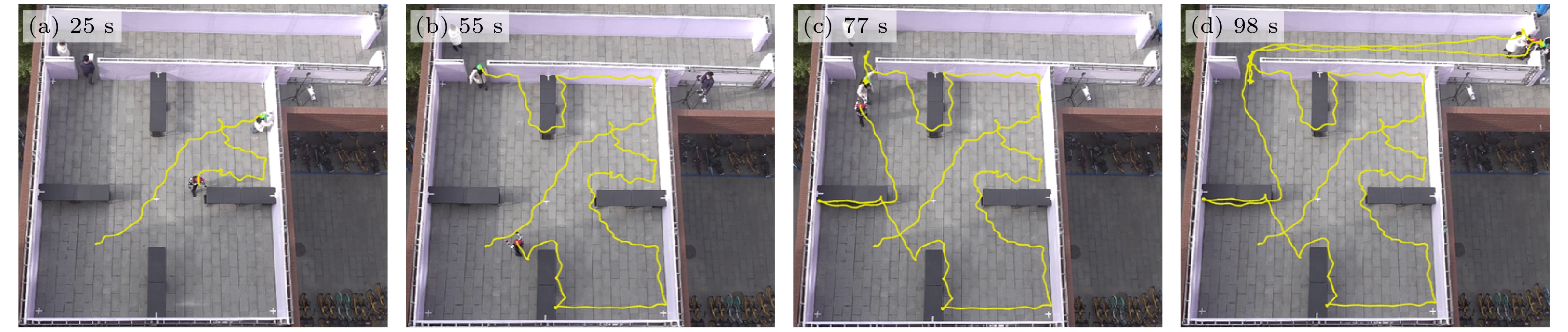
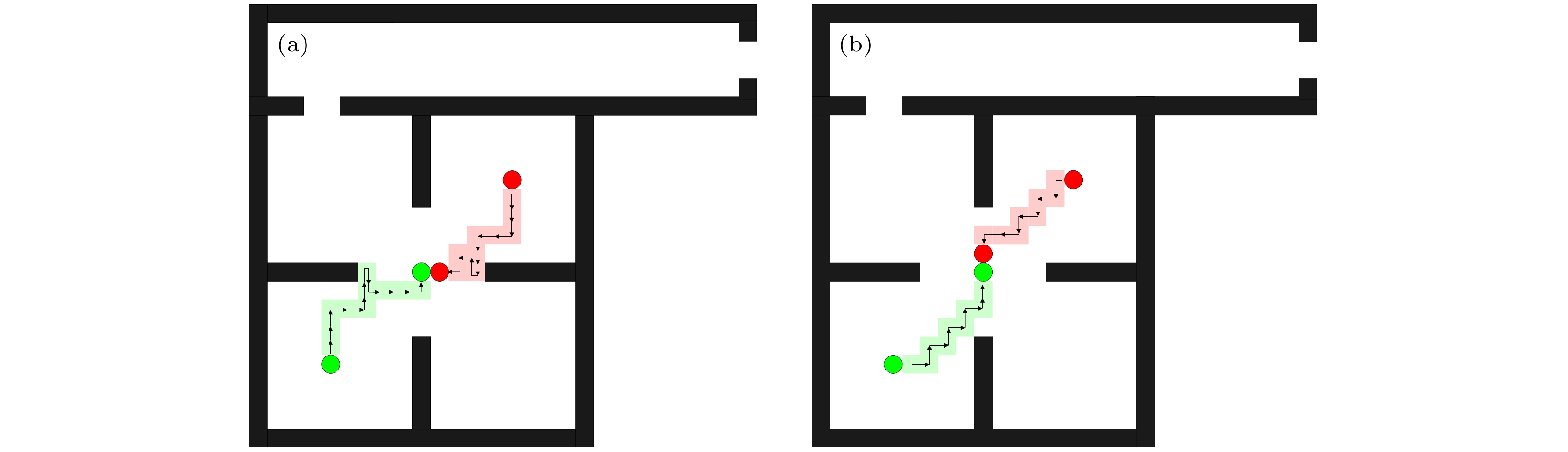
结伴模式I: 在疏散实验开始后, 两个行人首先寻找对方进行结伴, 汇合后两个行人一起寻找出口. 结伴模式I的疏散过程画面如图2所示.

结伴模式II: 在疏散实验开始后, 两个行人经过沟通分别寻找出口, 期间即使相遇也依旧按照自己的决策寻找出口. 当其中一个行人找到出口1后, 会发出声音信息(如呼喊、拍手、击打边界等)引导另一个行人向出口1行进. 此时, 接收到声音信息的行人会停止寻找出口, 开始向同伴所在位置运动. 在出口1附近汇合后, 两个行人进入区域2, 一起寻找出口2. 结伴模式II的疏散过程画面如图3所示.

结伴模式III: 在疏散实验开始后, 两个行人经过沟通分别寻找出口, 但如果两个行人相遇或者相距较近, 两个行人会进行结伴, 然后一起寻找出口. 结伴模式III的疏散过程画面如图4所示.

在结伴疏散过程具有规律性的114个两人小组中, 64个小组的结伴行为是结伴模式I, 占结伴小组总数的56%; 17个小组的结伴行为是结伴模式II, 占结伴小组总数的15%; 33个小组的结伴行为是结伴模式III, 占结伴小组总数的29%.

在其他3个两人小组中, 行人的结伴疏散行为没有明显的规律性, 无法将他们的结伴疏散过程归纳成特定的结伴模式. 我们将这3个两人小组称为无规律小组1、无规律小组2和无规律小组3. 图5给出了3个无规律小组的行人运动轨迹. 在无规律小组1中, 两个行人在区域1内先结伴进行疏散, 但在进入区域2后分开, 两个行人分别向出口2的方向移动一段距离后, 又向相反方向行进, 直到触碰到区域2内的东侧墙壁后, 两个行人再次结伴, 一起向出口2方向移动. 因此, 如图5(a)所示, 无规律小组1在区域2内有多条重复的运动轨迹. 在无规律小组2中, 两个行人在区域1内首先进行结伴并一起寻找出口, 但结伴移动一段距离后, 两个行人便分开寻找出口, 之后出现多次结伴后分开的情形, 直到进入区域2后, 两个行人一直结伴向出口2移动. 如图5(b)所示, 无规律小组2在区域1的局部区域形成密集的运动轨迹. 在无规律小组3中, 两个行人在区域1内先分别进行疏散, 相遇后结伴寻找出口, 但在结伴疏散过程中, 行人1的速度明显更快, 两个行人无法保持结伴队形, 行人1离开行人2独自寻找疏散出口. 行人1找到出口1后, 引导行人2向出口1处移动. 两个行人从出口1结伴进入区域2后又再次分开, 分别向出口2移动. 如图5(c)所示, 在区域1内, 两个行人的运动轨迹存在较大差异.

相比于114个具有规律性的疏散小组, 3个无规律小组中行人的疏散行为表现出较强的随机性, 行人的疏散路线十分混乱, 需要更多的时间才能离开疏散区域. 为了更好地归纳零视野条件下行人在结伴疏散过程中的运动规律, 在后续的结果分析和建模仿真中, 我们将剔除3个无规律小组, 只探讨其余114组行人的结伴疏散过程.

在零视野条件下, 行人无法通过视觉获取周围信息, 但是听觉不会受到影响. 在结伴过程中行人通过“声音传递信息、听觉接收信息”的方式确定彼此的位置. 图6给出了听觉引导行为发生的情景. 这种听觉引导行为一般在以下两种情景中发生.

1)在疏散实验开始阶段, 结伴行人首先寻找同伴, 如图6(a)所示. 此时行人之间进行沟通, 确定两个人的疏散策略, 通过声音判断同伴的位置, 并向对方位置移动.

2)在疏散过程中, 分离状态的结伴行人中的一个行人发现出口1时, 如图6(b)所示. 此时行人通过呼喊或拍击边界等方式发出声音, 引导同伴向自己移动.

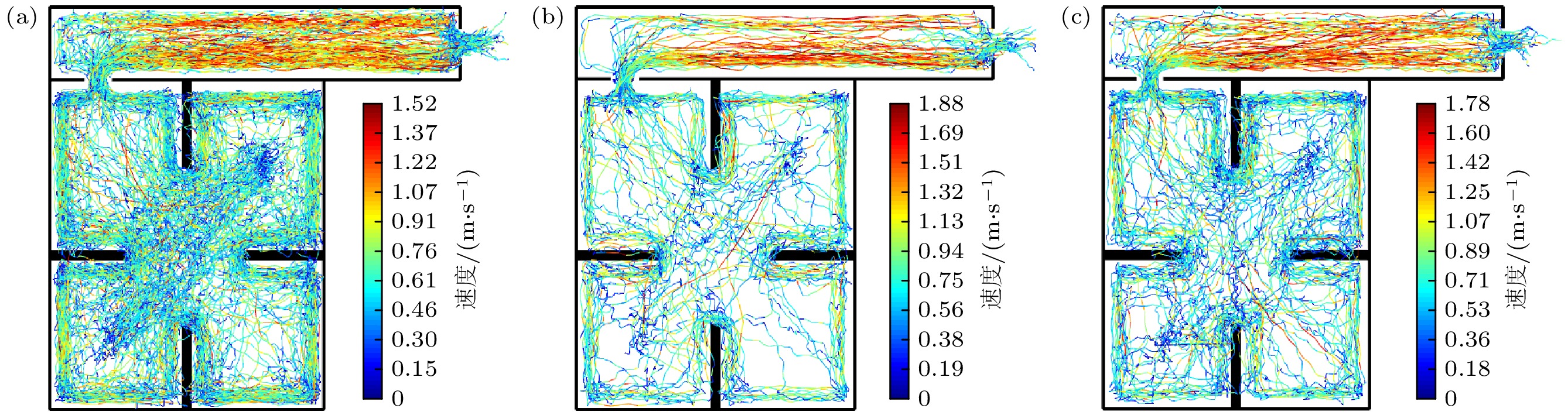
在疏散过程中, 行人的运动速度是衡量行人疏散效率的重要指标. 图7(a)—(c)分别是结伴模式I、结伴模式II和结伴模式III下结伴行人的运动轨迹, 颜色代表行人运动速度的大小, 单位是m/s. 从图7可以看出, 结伴行人在不同空间位置的运动速度具有差异性.

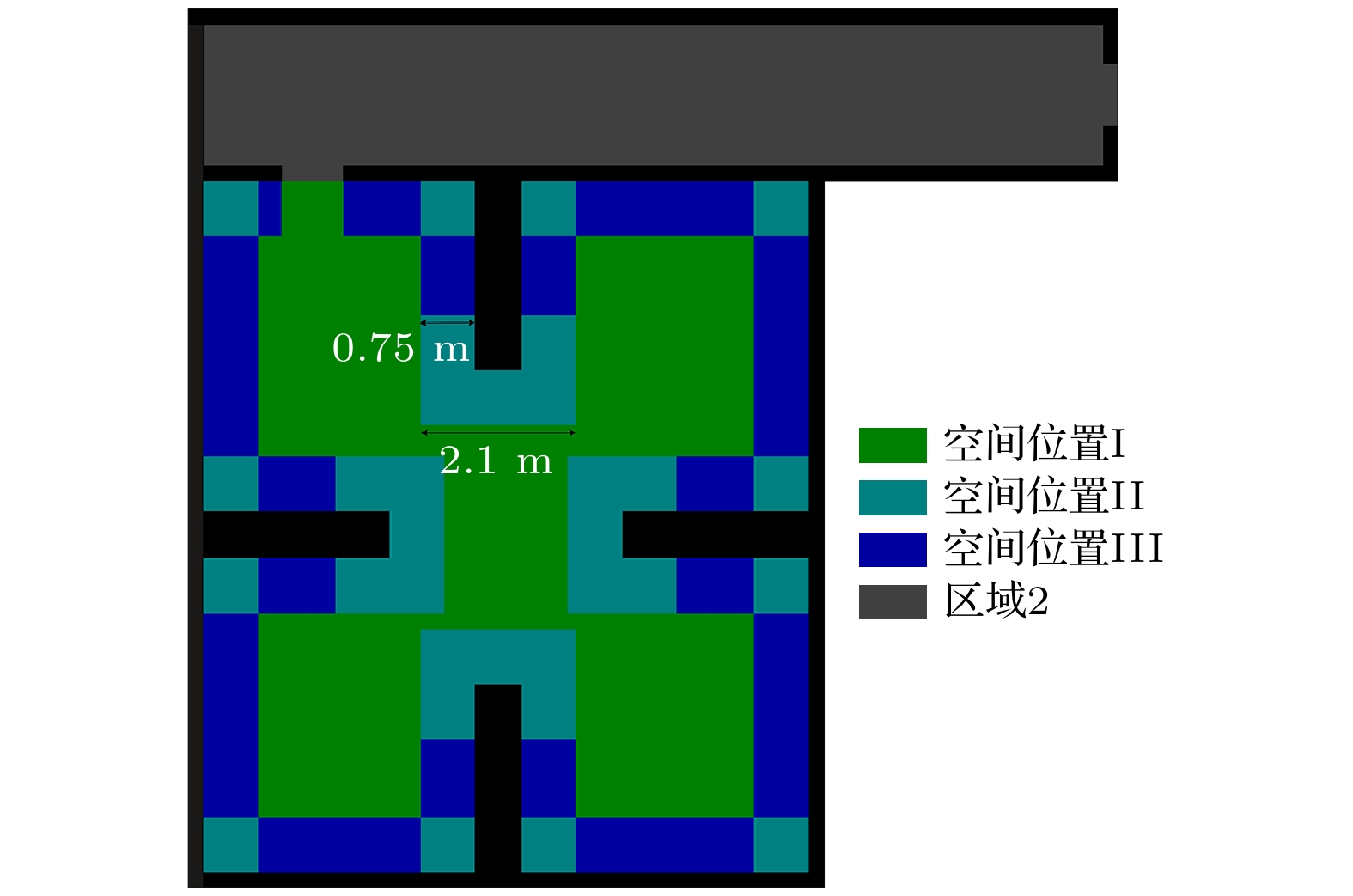
为进一步探究零视野条件下行人运动速度的规律, 将区域1的空间位置分为3类, 具体为: 空间位置I是指在疏散过程中, 行人不能接触到边界或者障碍物的运动区域; 空间位置II是指在沿墙行走过程中, 行人会改变运动方向的区域; 空间位置III是指在沿墙行走过程中, 行人不会改变运动方向的区域. 图8给出了疏散场景中不同空间位置划分示意图. 在图8中, 绿色区域代表空间位置I, 青色区域代表空间位置II, 蓝色区域代表空间位置III, 灰色区域代表区域2. 成年人的手臂加手长的长度约为0.733 m^[22]. 当行人与边界或者障碍物的距离小于此距离时, 认定行人已经触碰到边界或者障碍物. 因此, 设置空间位置II和空间位置III的宽度(即边界或障碍物与空间位置I的距离)为0.75 m.

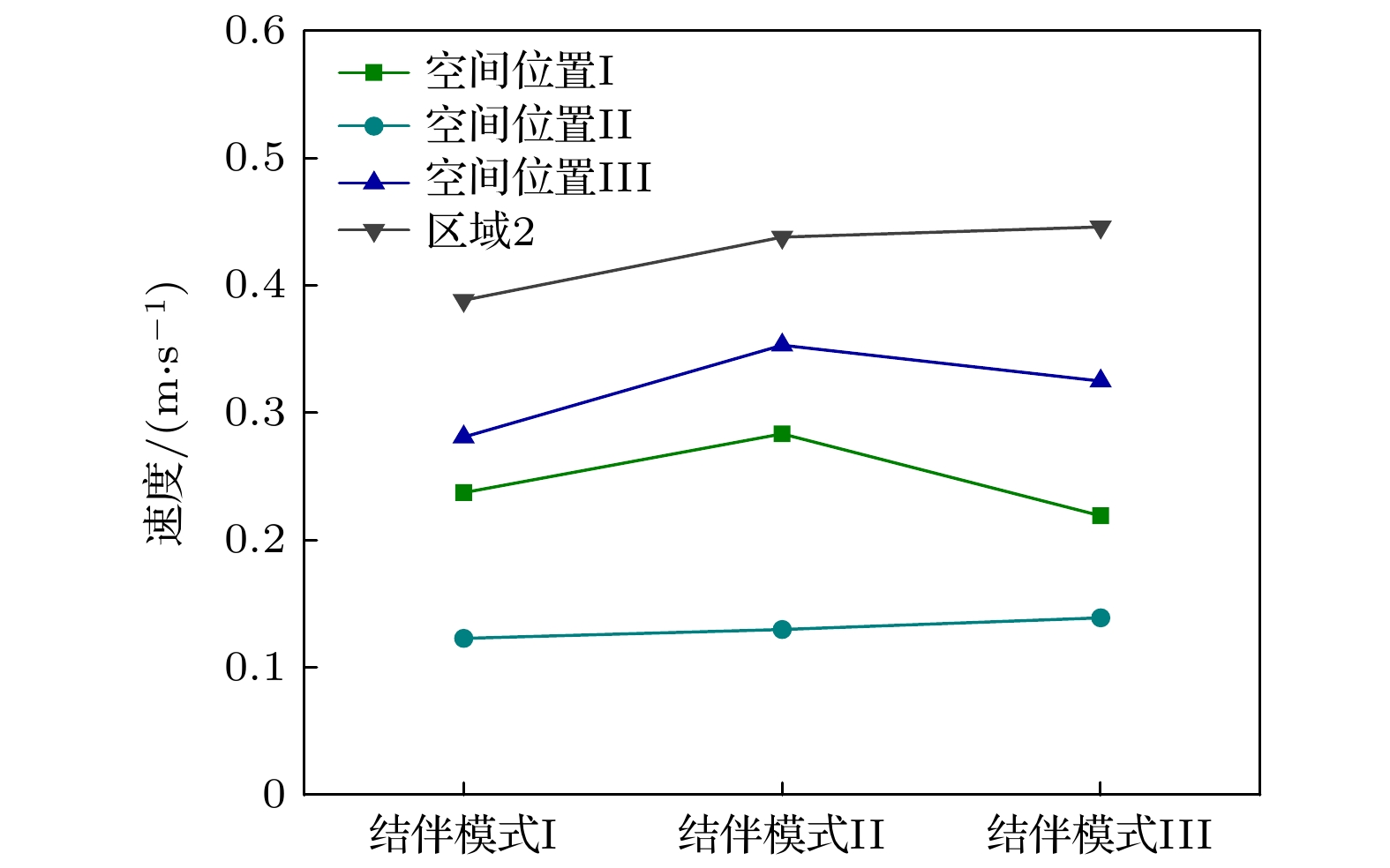
图9给出了不同结伴模式下行人在不同空间位置的平均运动速度. 结伴模式I、结伴模式II和结伴模式III的两人小组在空间位置I的平均速度分别是0.237, 0.281, 0.219 m/s, 在空间位置II的平均速度分别是0.123, 0.130, 0.139 m/s, 在空间位置III的平均速度分别是0.281, 0.353, 0.325 m/s, 在区域2的平均运动速度分别是0.389, 0.438, 0.446 m/s. 由图7和图9可知得以下结果.

1)行人在初始位置的运动速度较小. 这是因为疏散实验开始时, 行人需要对黑暗环境进行适应. 在行人没有接触到同伴或者依附物时, 从外界环境中感知到的有利于寻找出口的信息非常有限, 导致行人在初始位置的运动速度较小.

2)行人在障碍物和边界转角处的运动速度较小. 这主要有两个原因: 一是行人在沿墙行走的过程中碰到障碍物或者边界的转角时, 行人会与障碍物或边界发生碰撞, 使得行人速度下降; 二是在黑暗环境中, 行人期望依附障碍物行走, 为了不脱离依附物, 行人障碍物转角处需要降低运动速度.

3)在不改变运动方向时, 行人在沿墙过程中的运动速度高于寻墙过程中的运动速度. 这是因为行人在接触到依附物后, 依附物会对行人的疏散路径提供指引信息, 使行人的运动速度变大.

4)行人在区域2的运动速度高于在区域1的运动速度. 这是因为参与人员知道地形图, 但是区域1中障碍物的设置和可行走空间是对称的, 增加了参与人员判断出口1位置的难度, 而行人从出口1进入区域2后, 比较容易判断出口2的方向. 同时, 与区域1相比, 区域2是一个狭长的走廊区域, 没有障碍物阻碍行人的行进路线. 因此, 行人进入区域2后, 为了尽快离开疏散区域, 行人运动速度变快.

5)行人在区域2的运动轨迹并不总是沿墙行走. 这是因为结伴行人具有前后结伴和左右结伴两种结伴形态. 当结伴行人在区域2中以左右结伴行为移动时, 其中一个行人在运动过程中将不会接触到墙壁, 那么其运动轨迹便不会沿墙行走.

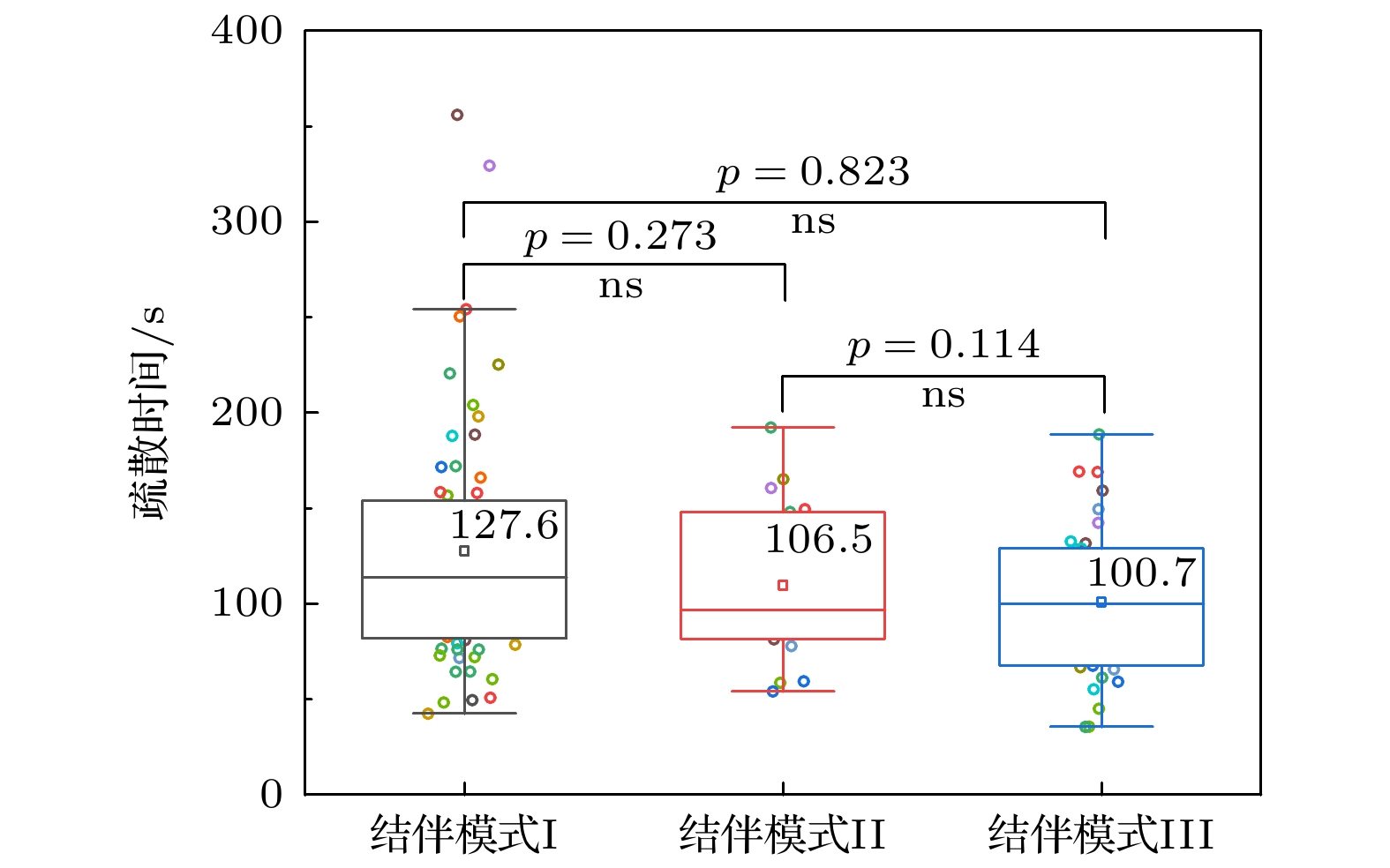
行人的疏散时间是指从发出疏散指令开始到两个行人一起从出口2离开疏散区域的时间. 图10给出了不同结伴模式下每个小组的疏散时间及其分布. 在疏散实验中, 结伴模式I、结伴模式II和结伴模式III的两人小组的平均疏散时间分别为127.6, 106.5, 100.7 s. 配对样本t检验结果显示不同结伴模式下行人的疏散时间没有显著性差异.

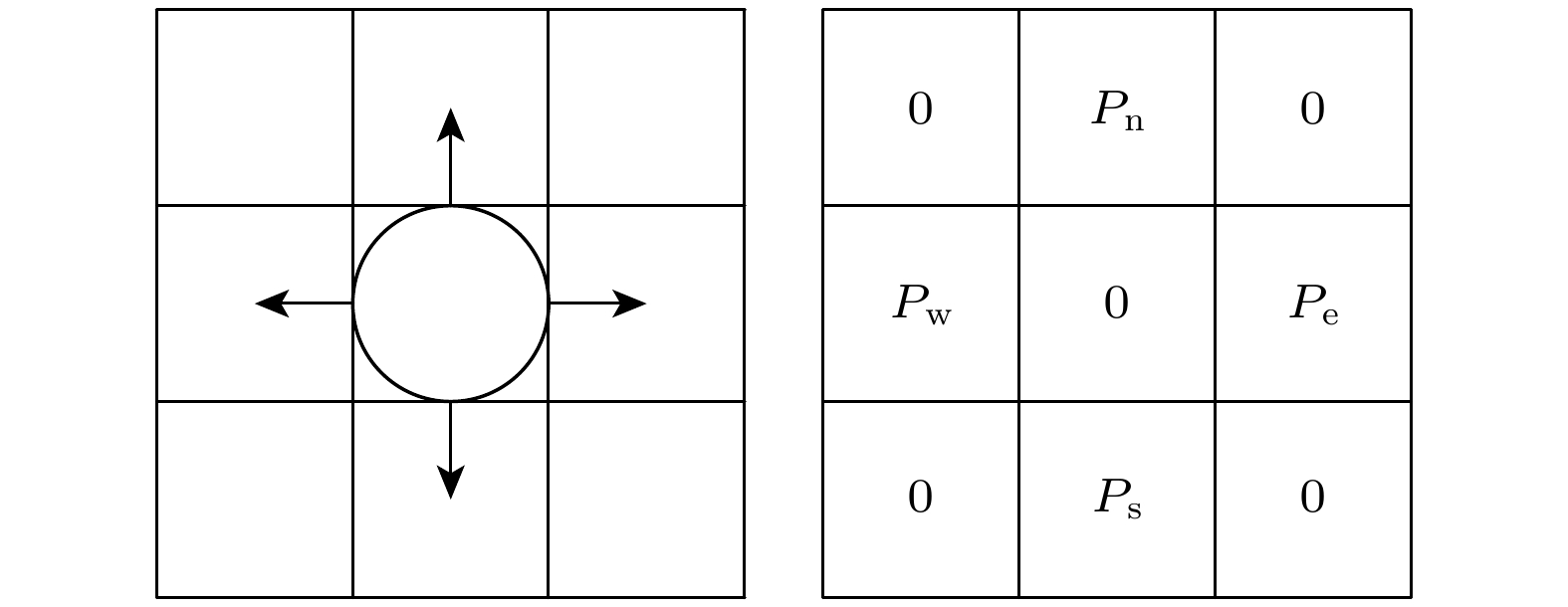
疏散场景的地面结构由二维网格表示. 每个网格代表一个元胞, 一个元胞可能被墙壁、障碍物或者行人占据, 也可能为空. 每个行人可以用圆来表示, 成年人的半径是$ (0.255 \pm 0.035){\text{ m}} $ ^[23]. 因此, 每个圆的半径设置为0.25 m. 根据行人所占据空间的大小, 将每一个元胞的大小设置为0.5 m×0.5 m.

每一个时间步, 疏散空间内的行人可以向北、东、南、西4个方向移动一个元胞. 行人的移动方向由转移概率决定, 在移动方向上的转移概率越大, 行人更偏向于选择该方向运动. 如果行人移动方向上的相邻元胞被墙壁、障碍物或者其他行人占据, 则行人无法向该方向移动. 如果四个方向都不能移动, 则行人的位置不变. 图11给出了行人可以移动的方向以及相邻元胞的转移概率.

根据疏散实验的结果, 行人的疏散过程可以分为3个阶段, 分别是发生结伴行为前阶段、结伴完成前阶段和结伴完成后阶段. 发生结伴行为前阶段是指疏散开始后, 行人没有寻找同伴, 单独寻找出口的过程. 结伴完成前阶段是指行人与同伴开始进行结伴到两个行人汇合的过程. 结伴完成后阶段是指从结伴行人汇合到结伴行人从出口2离开的过程. 在疏散实验中, 结伴模式I的两个行人首先寻找同伴, 不存在发生结伴行为前阶段, 只存在结伴完成前阶段和结伴完成后阶段; 结伴模式II和结伴模式III下的两个行人均存在单独寻找出口和结伴寻找出口的过程, 都存在3个疏散阶段. 下面分别对不同阶段的行人疏散过程进行建模.

在发生结伴行为前的疏散过程中, 单独寻找出口的行人将会出现寻墙行为和沿墙行走行为. 模拟行人寻墙行为和沿墙行为的步骤如下:

第1步　确定寻墙方向. 疏散开始后行人可以随机选择北、东、南、西4个方向中的一个方向作为寻墙方向, 选择每一个方向的概率相等, 均为${P_{\text{f}}}$.

第2步　向寻墙方向移动一个元胞的距离.

第3步　检查行人是否触墙. 如果行人的相邻元胞被障碍物或者墙壁占据, 则寻墙过程结束, 执行第4步; 否则, 执行第2步.

第4步　确定沿墙行走方向. 选择顺时针方向沿墙行走的概率为${P_{\text{w}}}$, 选择逆时针沿墙行走的概率为$ {P'_{\text{w}}} = 1 - {P_{\text{w}}} $.

第5步　向沿墙行走方向移动一个元胞的距离.

第6步　判断行人是否感知到另一个行人. 如果另一个行人在感知范围内, 对于结伴模式II的行人, 不会产生结伴行为, 执行第5步; 对于结伴模式III的行人, 产生结伴行为, 发生结伴行为前阶段结束. 否则, 执行第7步.

第7步　判断行人是否到达出口. 如果行人的相邻元胞被出口占据, 行人发出声音信息指引另一个行人疏散, 产生结伴行为, 发生结伴行为前阶段结束. 否则, 执行第五步.

以上算法基于两人小组的结伴模式, 设置寻墙方向、沿墙方向的确定规则以及结伴行人之间的交互规则, 能够模拟在发生结伴行为前的疏散过程中, 行人单独寻找出口时寻墙行为和沿墙行为.

在结伴过程中, 行人依靠听觉和触觉判断同伴的位置. 模型中将行人感知到同伴所发出声音信息的最大距离称为结伴感知距离. 当两个行人的距离小于或等于结伴感知距离时, 结伴行人将会做出与同伴结伴行动的决策. 当两个行人的距离小于或等于结伴感知距离但未完成结伴时, 行人处于结伴完成前疏散阶段. 3种结伴模式的两人小组在疏散过程中均存在结伴完成前疏散阶段. 行人的移动方向由转移概率决定, 用${P_{\text{n}}}$, ${P_{\text{e}}}$, ${P_{\text{s}}}$, ${P_{\text{w}}}$分别代表行人向北、东、南、西方向的转移概率, 其计算公式如下:

其中, $ N = {1}/[{{{a_{\text{n}}}{{\text{e}}^{ - {f_{\text{n}}}}} + {a_{\text{e}}}{{\text{e}}^{ - {f_{\text{e}}}}} + {a_{\text{s}}}{{\text{e}}^{ - {f_{\text{s}}}}} + {a_{\text{w}}}{{\text{e}}^{ - {f_{\text{w}}}}}}}] $. ${f_{\text{n}}}$, ${f_{\text{e}}}$, ${f_{\text{s}}}$, ${f_{\text{w}}}$分别代表行人北、东、南、西方向的相邻元胞的势能值. ${a_{\text{n}}}$, ${a_{\text{e}}}$, ${a_{\text{s}}}$, ${a_{\text{w}}}$分别代表行人北、东、南、西方向的相邻元胞是否被墙壁、障碍物或者其他行人占据. 例如, 如果与行人东面相邻的元胞没有被障碍物占据, 那么该行人可以向东移动, ${a_{\text{e}}} = 1$; 否则, ${a_{\text{e}}} = 0$. 在疏散过程中, 行人向势能值较小的方向移动的概率较大.

由于行人失去视觉, 在依靠听觉判断同伴位置时可能会产生误差^[24]. 在模型中, 行人会误认为与同伴相邻的某个元胞为同伴所在的元胞, 该元胞被称为“误差元胞”. 行人选择同伴所在元胞和“误差元胞”的偏好是不同的, 用${\alpha _d}(d = 0, 1, 2, \cdots , 8)$表示行人选择同伴所在元胞和“误差元胞”的偏好强度. 在结伴过程中, 行人最终选择的同伴所在元胞称为目标元胞. 目标元胞$(i', j')$可能是同伴所占据的元胞, 也可能是“误差元胞”. 确定目标元胞的步骤如下:

第1步　分别计算行人所在元胞$\left( {x, y} \right)$与同伴所在元胞的8个相邻元胞$\left( {{x_k}, {y_k}} \right)$的距离${D_k}( k = 1, 2, \cdots , 8 )$, 计算公式如下:

第2步　将所有${D_k}$按照从小到大的顺序排列. 如果${D_m} = {D_n}$$(m = 1, 2, \cdots , 8,n = 1, 2, \cdots , 8$且$m \ne n)$, 则随机排序.

第3步　设置同伴所占据元胞具有最大的偏好强度${\alpha _0}$, 第$k$小的${D_k}$所对应的元胞$\left( {{x_k}, {y_k}} \right)$具有第$k$大的偏好强度${\alpha _k}$, ${\alpha _k} \ne 0$.

第4步　目标元胞$(i', j')$的确定由${p_{\left( {i', j'} \right)}}$决定, ${p_{\left( {i', j'} \right)}}$的计算公式如下:

其中, $d = 0, 1, 2, \cdots , 8$.

上述算法考虑行人根据声音信息判断同伴位置时产生的误差, 通过“误差元胞”来表示行人因听觉误差选择的目的地, 能够模拟结伴行为完成前阶段中行人依靠听觉引导行为判断同伴位置的过程.

行人主要依靠声音信息寻找同伴, 能够对彼此之间的距离做出判断. 因此, 模型中元胞的势能值由两行人之间的距离决定. ${f_{\left( {i, j} \right)}}$代表元胞$(i, j)$的势能值, ${f_{\left( {i', j'} \right)}}$代表目标元胞$(i', j')$的势能值, ${f_{\left( {i, j} \right)}}$和${f_{\left( {i', j'} \right)}}$是无量纲的参数, 计算结伴完成前疏散阶段中行人使用的元胞势能值的步骤如下:

第1步　当元胞被墙壁或障碍物占据时, ${f_{\left( {i, j} \right)}} = + \infty $; 当元胞被确定为目标元胞时, $ {f_{\left( {i', j'} \right)}} = 0 $.

第2步　将目标元胞$ \left( {i', j'} \right) $放进一个有序队列中, 该队列的顺序按元胞的势能值升序排列.

第3步　选择有序队列中势能值最小的元胞$\left( {{i_0}, {j_0}} \right)$, 并将其从有序队列中移除, 检查其相邻的4个元胞, 若元胞的势能值还未计算, 则该元胞的势能值计算公式如下:

第4步　将第3步计算得到势能值的元胞$\left( {i, j} \right)$添加到有序队列之中.

第5步　若所有元胞的势能值均已计算完毕, 则停止计算, 否则, 执行第3步.

以上算法中, ${d_{i, j}}$表示相邻元胞$\left( {i, j} \right)$与$\left( {{i_0}, {j_0}} \right)$的距离, ${d_{i, j}} = 1$. 模型中利用该算法得到的元胞势能值计算行人的转移概率, 行人在选择运动方向时综合考虑与同伴之间的距离和结伴过程中通过声音判断同伴位置时所产生的误差的影响. 在每个时间步, 以上算法执行一次, 元胞势能值可以根据行人的运动状态进行动态更新.

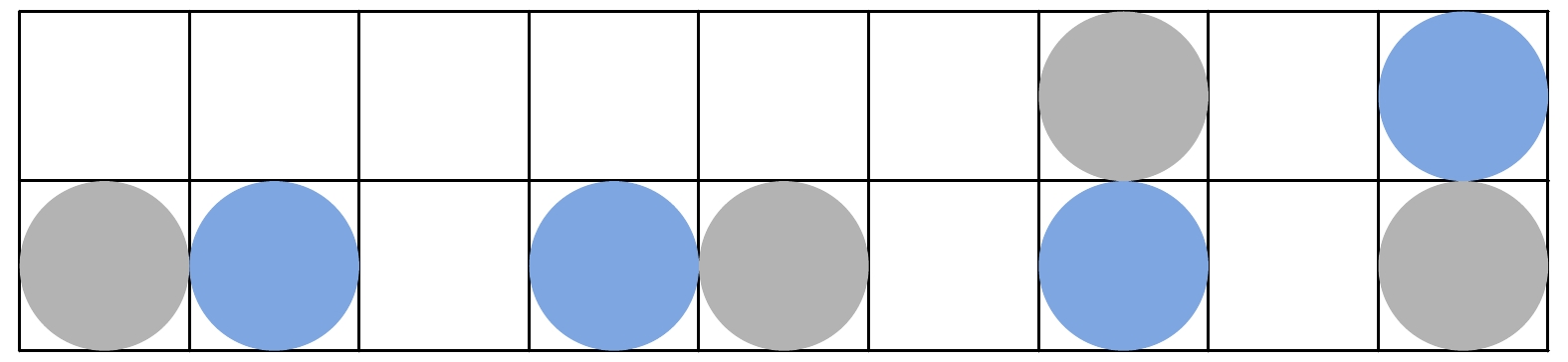
行人结伴后, 形成一个整体, 继续寻找出口, 直到从出口2离开. 图12给出了两人小组结伴完成后的结伴形态. 模型中假设结伴行人在运动过程中具有整体性, 且不会变换结伴形态. 在图12中, 灰色圆和浅蓝色圆分别代表领导者和跟随者.

模拟结伴行人寻墙行为和沿墙行为的步骤与模拟单人寻墙行为和沿墙行为的步骤类似, 但在判断相邻元胞被占据状态时不同. 在结伴完成后, 结伴行人占据两个元胞, 有10个相邻元胞; 单个行人占据一个元胞, 有8个相邻元胞. 在判断行人触墙状态时, 结伴行人需要判断10个方向上的相邻元胞是否被障碍物占据, 单个行人需要判断8个方向上的相邻元胞是否被障碍物占据. 完成结伴的行人在疏散过程中不需要再判断同伴的位置, 单个行人在寻墙过程和沿墙过程中需要判断同伴的位置是否在结伴感知距离内, 来确定是否与同伴进行结伴.

不同结伴模式下行人在不同空间位置的平均运动速度不同. 根据3种结伴模式下不同空间位置处行人的平均运动速度计算模型中时间步的大小. 结伴模式m下的时间步$\Delta {t_m}$的计算公式如下:

其中, l代表元胞的实际长度, $ v_{\max }^m $代表结伴模式m下行人在不同空间位置的最大速度. 为了便于模拟结伴行人在不同空间位置处的速度差异, 在空间位置I、空间位置II、空间位置III和区域2, 将结伴模式I下行人的平均运动速度分别设置为0.25, 0.10, 0.30, 0.40 m/s; 将结伴模式II下行人的平均运动速度分别设置为0.30, 0.15, 0.35, 0.45 m/s; 将结伴模式I下行人的平均运动速度分别设置为0.20, 0.15, 0.35, 0.45 m/s. 因此, $ \Delta {t_1} = 1.25 $ s, $ \Delta {t_2} = 1.11 $ s, $ \Delta {t_3} = 1.11 $ s. 对于其他参数, 设置${\alpha _0} = 9$, ${\alpha _k} = {\alpha _0} - k$$(k = 1, 2, \cdots , 8)$, ${P_{\text{f}}} = 0.25$, ${P_{\text{w}}} = 0.5$, 行人之间的结伴感知距离$\gamma = 8$. 仿真结果取30次仿真结果的平均值.

通过行人在结伴过程中的运动轨迹验证模型可以刻画零视野条件下听觉引导误差对行人结伴过程影响. 图13(a)给出了考虑听觉引导误差时行人结伴过程的运动轨迹, 图13(b)给出了不考虑听觉引导误差时行人结伴过程的运动轨迹. 在图13中, 箭头表示行人在下一个时间步的移动方向. 由图13可知: 不考虑听觉引导误差时, 行人的运动路线比较流畅; 考虑听觉引导误差时, 行人的运动路线出现徘徊现象. 这是因为在模型中考虑听觉引导误差后, 行人在寻找同伴的过程中可能会错误地判断同伴的位置, 导致行人的运动方向发生改变.

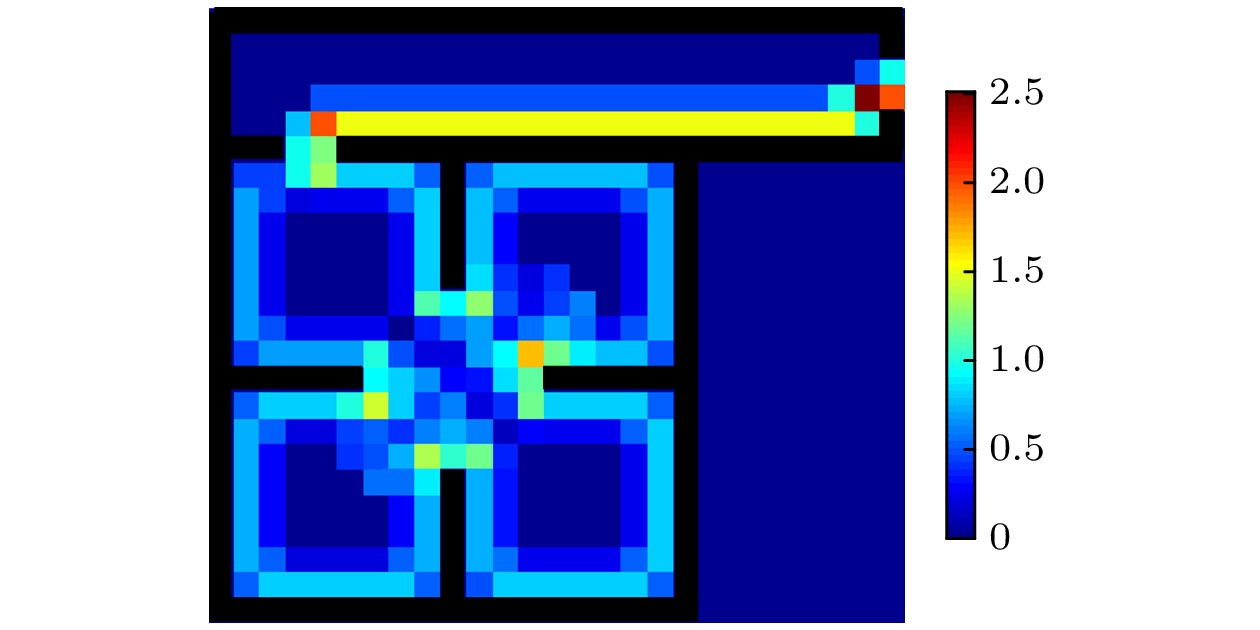
图14—图16分别给出了不同结伴模式下行人在每一个元胞的平均停留时间步数. 由图14—图16可知:

1)在结伴模式I的疏散过程中, 行人在边界和障碍物附近以及中心区域停留步数较多(见图14). 这是因为在结伴模式I中, 疏散开始后行人先去寻找同伴而不是寻找依附物, 结伴行为多发生在区域1的中间区域. 结伴完成后, 两个行人寻找墙壁并沿墙行走, 最终从出口2离开. 从实验中结伴模式I下行人的运动轨迹(见图2)可以看出, 两个行人的运动轨迹在区域1的中心区域汇合, 然后两个行人在墙壁和障碍物附近的运动轨迹几乎重叠在一起. 通过对比仿真和实验中行人的运动轨迹, 可以验证该模型能够再现结伴模式I下行人的结伴疏散行为.

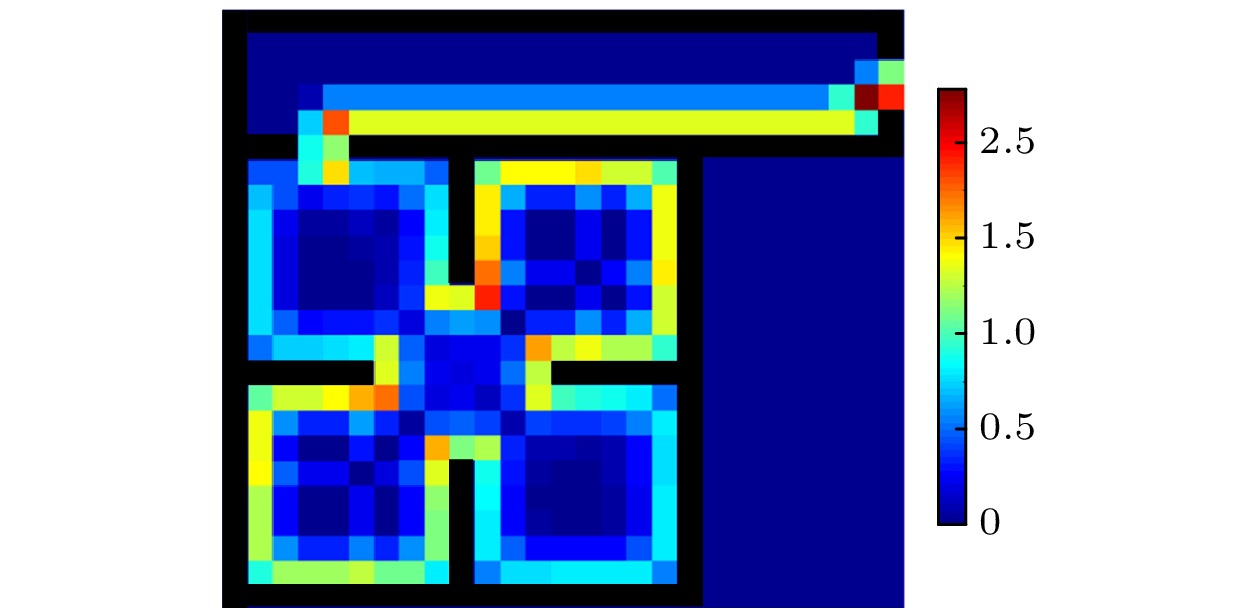
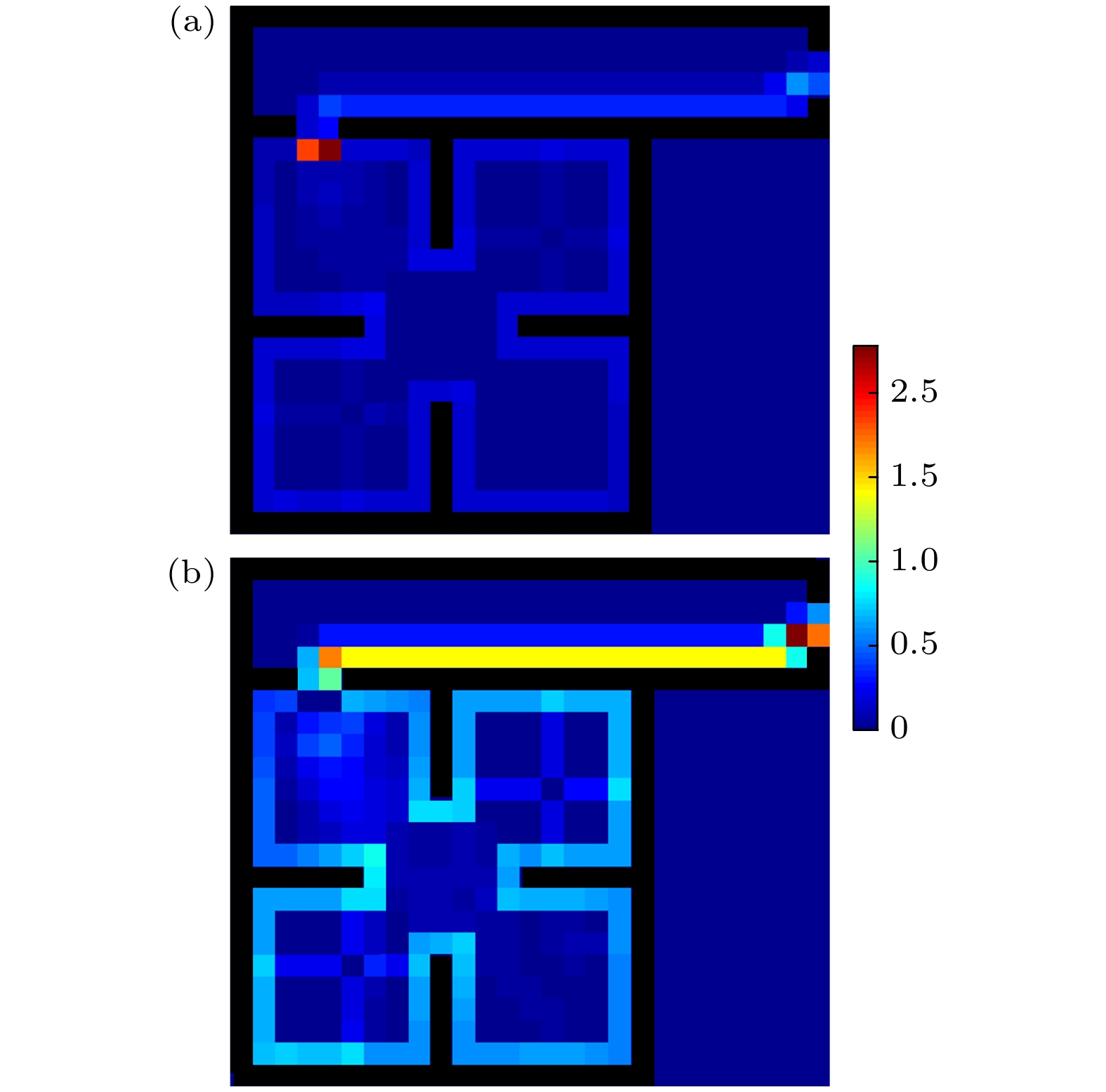
2)在结伴模式II的疏散过程中, 行人在门口1附近的平均停留步数显著大于其他区域的平均停留步数(见图15(a)). 这是因为在结伴模式II中, 行人分别寻找出口, 当其中一个行人找到出口1后, 会在原地等待同伴, 导致等待位置的平均停留步数值较高. 图15(b)给出了去除等待位置后其他位置的平均停留步数. 由图15(b)可知, 行人在区域1内的轨迹主要分布在与边界与障碍物相邻的第一层元胞和出口附近. 这是因为在疏散过程中, 两个行人先去寻找墙壁并沿墙行走, 当其中一人到达出口1后向同伴传递出口位置信息, 此时同伴会停止寻找墙壁或者沿墙行走的过程, 开始向同伴行进, 最终在出口1附近完成结伴过程. 从实验中结伴模式II下行人的运动轨迹(见图3)可以看出, 两个行人在区域1内的运动轨迹都是单独沿障碍物和墙壁行走, 并且其中一个行人存在直接前往出口1的运动轨迹. 在区域2内, 两个行人在墙壁附近的运动轨迹同时存在, 结伴前往出口2. 通过对比仿真和实验中行人的运动轨迹, 可以验证该模型能够再现结伴模式II下行人的结伴疏散行为.

3)在结伴模式III的疏散过程中, 行人除了在边界和障碍物附近停留步数较多, 在区域1其他位置的平均停留步数也比较多. 这是因为在结伴模式III中, 两个行人首先单独寻找边界和出口, 行人的沿墙行为使边界相邻元胞平均停留时间步数增加. 在疏散过程中, 如果分离的两个行人处于结伴感知距离内, 行人会脱离依附物发生结伴行为, 使得边界和障碍物等依附物之间的轨迹较为明显. 从实验中结伴模式III下行人的运动轨迹(见图4)可以看出, 两个行人在运动轨迹开始阶段就存在沿墙行走过程. 当运动轨迹比较接近后, 两条运动轨迹在墙壁和障碍物附近同时出现, 两个行人结伴前往出口2. 通过对比仿真和实验中行人的运动轨迹, 可以验证该模型能够再现结伴模式III下行人的结伴疏散行为.

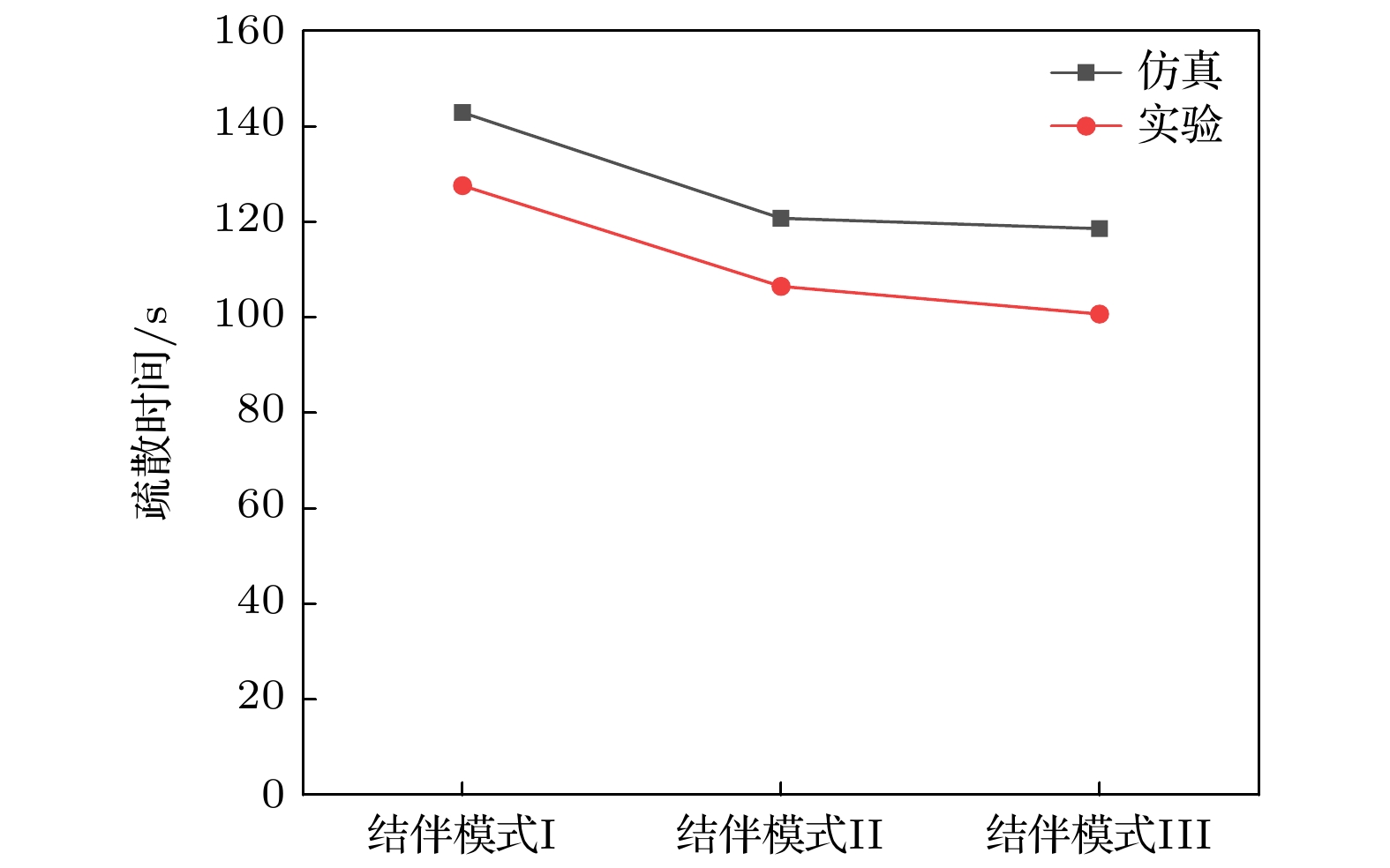
首先, 通过对比仿真和实验中不同结伴模式下行人的疏散时间验证该模型具有刻画零视野条件下结伴行人疏散过程的能力. 图17给出了仿真和实验中不同结伴模式下行人的疏散时间. 由图17可知, 在结伴模式I下行人的疏散时间最长, 在结伴模式III下行人的疏散时间最短. 这与实验中行人疏散时间变化趋势一致. 此外, 我们可以发现仿真中得到的疏散时间与实验中得到的疏散时间有一定差异. 这主要是因为行人的疏散行为非常复杂, 单一的模型无法完全刻画行人的疏散行为.

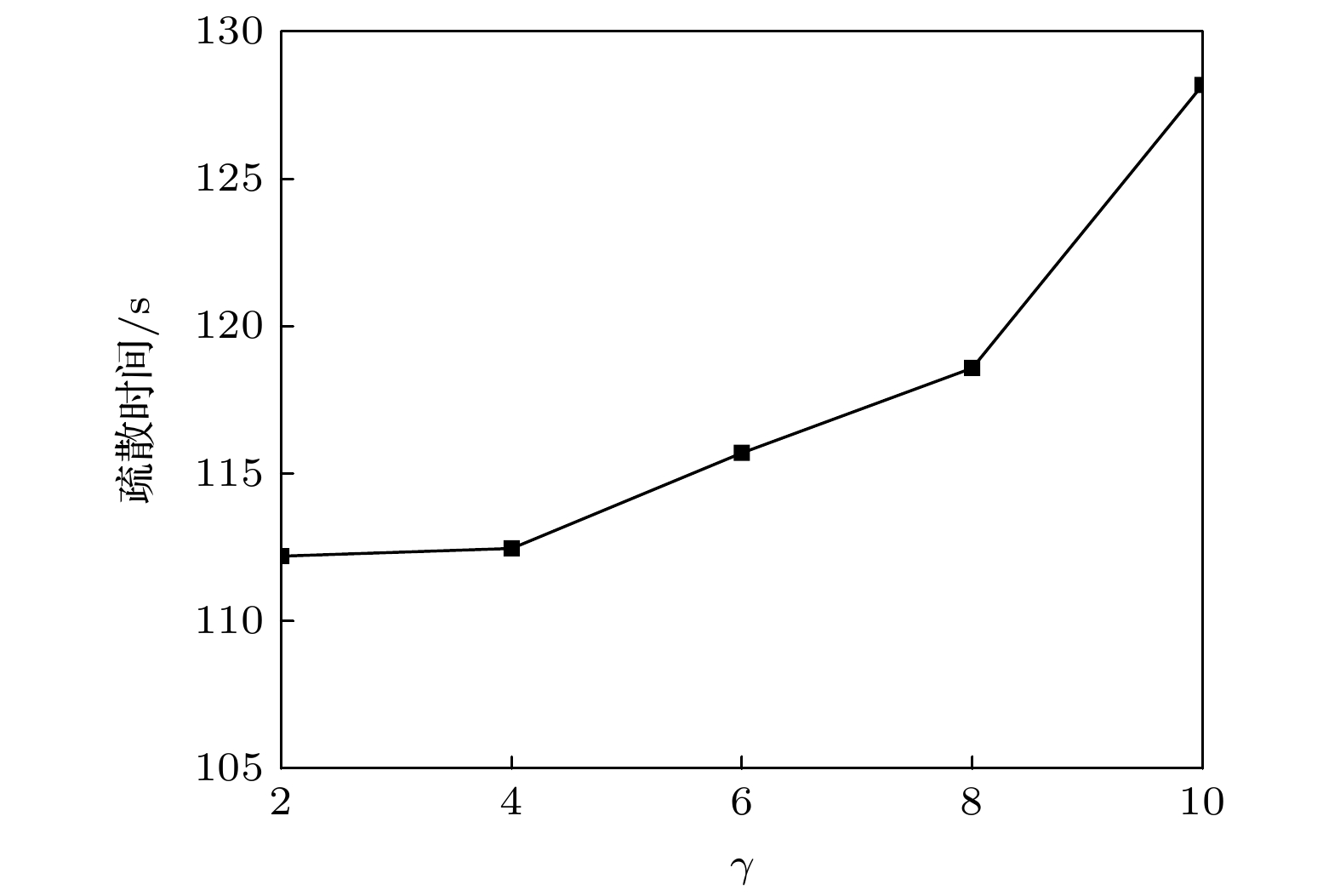
然后, 分析结伴感知距离$\gamma $对疏散时间的影响. 图18给出了在结伴模式III下结伴感知距离对行人疏散时间的影响. 由图18可知, 随着$\gamma $的增大, 行人的疏散时间逐渐上升. 这是因为当结伴感知距离较小时, 行人在障碍物之间不能感知到同伴位置, 两个行人在出口附近或沿墙行走相遇时才发生结伴行为, 受到同伴发出声音信息的影响较小. 当$\gamma $逐渐增大时, 行人能够感知同伴的距离增大, 受到同伴发出声音信息的影响增大, 结伴行为发生的概率上升. 行人结伴行为会增加两人小组的疏散时间. 如果结伴完成时两个行人所处位置不在边界或者障碍物处, 两人小组还将重新寻找边界进行沿墙行走, 这也进一步增加了行人疏散时间.

本文针对零视野条件下结伴行人的疏散过程展开深入研究, 采用可控实验的研究方法, 提取零视野条件下行人结伴疏散过程中的运动行为特征, 建立可以有效刻画零视野条件下考虑结伴行为的行人疏散模型, 揭示了各种自组织现象的形成机理, 分析了结伴行为对零视野条件下行人疏散效率的影响. 本文的主要结论如下:

1)通过行人疏散实验, 发现了零视野环境中行人的结伴行为、听觉引导行为和沿墙行为等典型疏散行为特征. 在结伴过程中, 行人之间依靠声音信息来相互引导同伴进行结伴.

2)行人结伴行为可以分为3种模式. 通过对比分析不同结伴模式下行人的运动速度和疏散时间, 发现零视野条件下结伴行为会降低疏散效率, 沿墙行走行为可以提高疏散效率.

3)考虑不同结伴模式下行人的疏散行为特征以及沿墙行为、听觉引导行为在结伴疏散过程中的影响机制, 构建了零视野条件下考虑结伴行为的行人疏散模型. 通过对比分析仿真过程和实验过程的行人运动轨迹和疏散时间, 验证了该模型能够有效再现零视野条件下行人的结伴疏散过程.

4)在疏散过程中, 行人结伴感知距离越大, 行人发生结伴行为的概率越高, 行人形成结伴群体的时间越早, 疏散效率降低, 即零视野条件下结伴行为对行人的疏散过程具有负面影响. 但是, 在文献[14, 18]中零视野条件下的行人疏散实验中, 结伴行为可以提高行人的疏散效率. 这是因为本研究与文献[14, 18]的实验目的和研究对象不同. 本研究以分离的结伴行人为研究对象, 探讨结伴行人分开时的结伴过程对疏散过程的影响. 当发生结伴行为时, 行人需要在零视野条件下与同伴汇合, 结伴过程会消耗大量时间, 并且结伴完成后行人才会继续开始寻找出口的过程. 当行人结伴感知距离越小时, 行人发生结伴行为的概率越低, 行人形成结伴群体的时间越晚, 两个行人分别寻找出口的时间越多, 在结伴完成后越容易判断出出口位置, 进而提升疏散效率. 文献[14, 18]以结伴群体为研究对象, 主要研究结伴行人作为整体的疏散过程. 当结伴群体中的行人发现出口后, 其他结伴行人便获悉了出口所在位置, 整个群体的疏散效率也随之提高.

以上研究结果可为类似场景中行人疏散策略和方案的制定提供科学依据. 但是, 本文未考虑结伴行人对密集人群疏散过程的影响. 下一步研究工作将致力于扩大结伴行人数量, 考虑疏散过程中不同结伴行人之间的冲突行为, 提高模型的泛化能力. 此外, 现实中的疏散场景里有限视野的情况更多, 有限视野条件下的疏散实验可以更接近现实场景. 因此, 未来的研究将继续扩展至有限视野的实验, 进一步探讨不同能见度条件下行人结伴行为对疏散过程的影响.