首页
登录
注册
-
固体氧化物燃料电池(solid oxide fuel cell, SOFC)作为第四代燃料电池技术, 是一种可以将化学能直接转化为电能的高效清洁的能量转换技术, 具有比能量高、效率高、噪声低、污染小、燃料选择灵活等优点, 不仅可以广泛应用于固定式电站、分布式家庭电源、紧急电源等固定设备领域, 也可以拓展到水面舰艇、水中兵器、无人平台、航天航空、单兵电源、移动电源等移动设施领域[1–6], 是最具发展前景的新型能源. 但由于SOFC各部件具有不同的热膨胀系数, 导致其在工作过程中产生较大的热应力, 从而引起电池内部萌生微裂纹进而扩展甚至发生脱层, 使电池性能下降甚至失效, 这将严重影响电池的寿命. 因此, SOFC的电极裂纹问题严重制约了其商业化应用的进程.
为了提高燃料电池的稳定性和耐久性, 延长其工作寿命, 研究人员对SOFC的电极裂纹问题进行了多方面的探索. Shao等[7,8]建立了SOFC的能量转换和裂纹扩展的数学模型, 采用扩展有限元方法研究了温度梯度对阳极支撑电池的预裂纹扩展路径的影响. 结果表明, 裂纹的扩展路径不仅与初始方向有关, 而且与预先存在的裂纹相对于SOFC界面的位置有关. Joulaee等[9]对典型SOFC单电池的裂纹扩展进行了建模, 基于各层及其界面的力学性能, 采用裂纹长度函数的能量准则来预测裂纹扩展的可能性, 分析了界面裂纹挠度与层间裂纹渗透之间的竞争关系. Nguyen等[10]建立了预测SOFC材料损伤和断裂的离散和连续模型, 使用改进的边界层建模方法对内部裂纹和不同材料之间的界面裂纹进行了分析. 结果表明, 该方法可以直接估计SOFC材料的断裂韧性和抗裂性能, 是一种高效实用的方法. Li等[11]建立阳极微结构相场断裂数值模型, 模拟了微结构在不同状态下的热应力分布和断裂过程的裂纹演化, 对比研究了微观结构、边界条件、载荷作用方式对电极断裂的影响规律. 结果表明, Ni的存在增加了材料的刚度和强度, 对于裂纹的扩展起到了抑制的作用. Bouhala等[12]通过采用无网格法研究了界面位置对平板型SOFC的裂纹萌生和扩展路径的影响. 结果表明, 电池的初始裂纹在阳极产生, 并逐渐扩展到阳极与电解质的界面. Pitakthapanaphong和Busso[13]研究了在电池冷却过程中由热残余应力引起的界面裂纹的断裂行为, 并确定了界面裂纹的能量释放率. 此外, 对于所有类型的裂纹而言, 在LSCoO(La0.82Sr0.18CoO3)层和基底之间引入La0.8Sr0.2Mn O3 (LSM)层可以降低界面裂纹的能量释放率. 进一步, Kim等[14]分析了平板型SOFC在高温下的裂纹萌生机理, 并对阳极-电解质界面的裂纹萌生进行了研究.
目前, 大部分研究对SOFC裂纹的影响因素考虑得不够全面, 对预裂纹的几何特征分析得不够充分. 基于此, 本文建立了含有预裂纹的SOFC的三维模型, 利用扩展有限元法从工作温度、材料属性、预裂纹角度、预裂纹位置等方面出发, 以电池应力分布、裂纹扩展路径等作为判据分析各因素对预裂纹扩展行为的影响, 提出基于材料优化和结构优化的提高电池稳定性的方案.
-
扩展有限元法(extended finite element method, XFEM)是一种求解不连续力学问题的数值方法, 在模拟界面、裂纹生长、复杂流体等不连续问题时特别有效. 它所使用的网格与结构内部的几何或物理界面无关, 克服了在诸如裂纹尖端等高应力和变形集中区进行高密度网格剖分所带来的困难, 模拟裂纹生长时也无需对网格进行重新剖分[15].
基于扩展有限元法可以判定裂纹的扩展条件以及确定裂纹的扩展方向. 根据裂纹界面的相对位移和载荷作用的方式, 可以将裂纹间断区域的变形特征分为三类[16], 包括张开型(I型)、滑移型(II型)和撕开型(III型)裂纹. 在实际的工程应用中, 由于结构受到的载荷非常复杂, 裂纹的类型并非单一出现, 而是由几种裂纹类型叠加而成, 即以复合型裂纹的形式存在. 燃料电池内部裂纹通常为I-II型复合型裂纹. 目前复合型裂纹的断裂准则有最大周向应力准则[17]、最大切向应变准则[18]、最大能量释放率准则[19]等, 本文采取的是最大周向应力准则. 最大周向应力准则也称为最大应力准则, 在I-II型复合型裂纹问题中, 裂纹尖端附近的应力场采用极坐标可表示为
其中r和θ为以裂纹尖端为坐标原点建立的极坐标参数, K为应力强度因子.
最大应力准则的基本假设为: 裂纹开裂沿最大周向应力方向, 当最大周向应力强度因子超过临界值时裂纹将扩展. 根据下列关系:
可以得到裂纹的开裂方向, 即裂纹开裂角θ0为
θ0以逆时针方向为正. 因此, 定义Kmax为最大应力强度因子, 可判定裂纹的开裂条件, 表示为
其中KIC为材料的平面应变断裂韧性.
-
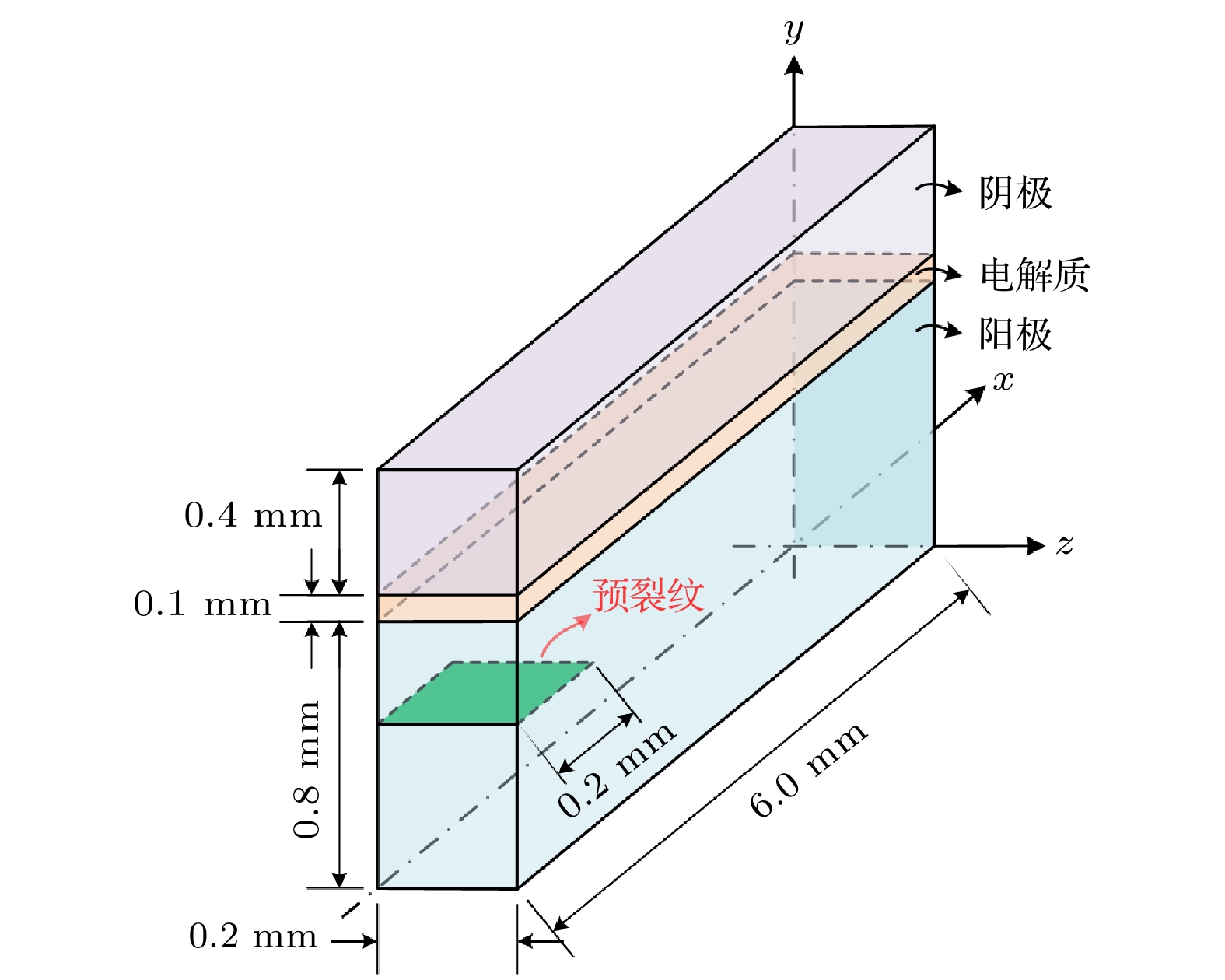
典型的平板式SOFC是由阳极、阴极和电解质组成的三明治结构, 阴极、阳极与电解质之间的界面均为平面界面, 其几何模型示意图如图1所示. 电池的长度L = 6.0 mm, 宽度W = 0.2 mm, 阳极、电解质和阴极的厚度分别为0.8, 0.1和0.4 mm. 为了研究不同条件对阳极裂纹扩展情况的影响, 在阳极的左端边界处设置一条长度为0.2 mm、宽度为0.2 mm的预裂纹, 且预裂纹的位置位于阳极厚度1/2处, 如图1所示.
模拟过程中对电池的边界进行约束, 即在电池右侧x = 6 mm处约束其x方向位移, 同时约束x = 6 mm, y = 0处y, z方向的位移. 对模型施加均匀的温度场, 使其从工作温度(1073 K)降到室温(298 K). 为简便起见, 本文仅考虑静态情况下电池在冷却过程中的温度差, 不考虑动态情况下冷却速率对电池应力分布及裂纹情况的影响. 此外, 本文的模拟不考虑制备过程中的残余热应力, 且假设阳极-电解质界面和阴极-电解质界面在整个分析过程中结合良好.
在SOFC模型中, 分别采用镍基合金钇稳定氧化锆(Ni-YSZ)和掺锶的锰酸镧(LSM)作为电池的阳极和阴极. 电解质则采用氧化钇稳定的氧化锆(YSZ), 其具有离子电导率高、电子电导率低、致密性好、热相容性好、材料强度高等特点. 所有材料均采用各向同性线弹性模型和均质化模型. 电极和电解质的材料属性包括弹性模量Eφ、泊松比μφ和热膨胀系数αφ(φ为Ni-YSZ, YSZ和LSM)都与温度相关, 具体数值如表1所列.
-
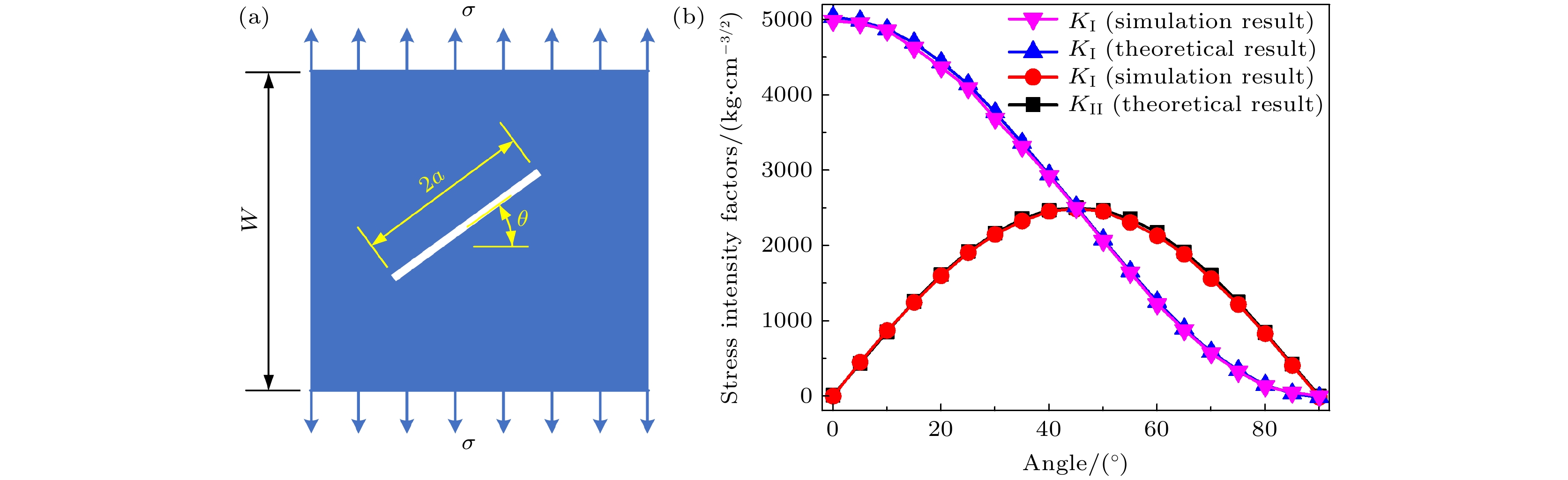
为了验证有限元模型的有效性, 通过计算一个内部含有倾斜裂纹的无限大平板受到均布拉力作用下的应力强度因子, 并与理论解析解进行对比. 平板宽度为W = 100 cm, 裂纹的长度2a = 2 cm, 平板宽度W与裂纹长度a的比值W/(2a) = 50, 裂纹与水平方向的夹角为θ, 平板的弹性模量为E = 210 GPa, 泊松比μ = 0.3, 板上下边受到均布拉力σ = 200 MPa. 该问题在真实状态下的第I型和第II型的应力强度因子的理论解析解分别表示为[28]
图2给出了应力强度因子随倾斜角θ变化的数值计算结果与理论解析解的对比情况. 由图2中可以看出, 应力强度因子KI随倾斜角θ的增大而逐渐减小, 这与解析解中系数
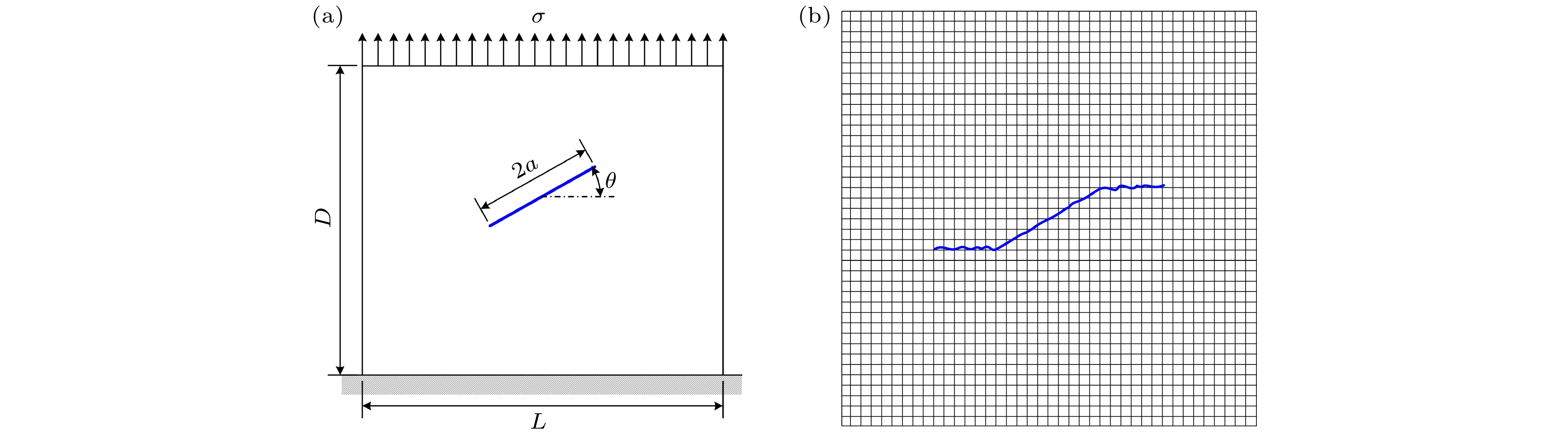
${\cos ^2}\theta $ 的变化相一致. 应力强度因子KII则随倾斜角θ先增大后逐渐减小, 这也与系数$\cos \theta \sin \theta $ 的变化相符, 同时也可看出本方法得出的结果与解析解十分接近.此外, 对裂纹扩展路径的正确性进行验证. 考察内部含有倾斜裂纹的有限正方形板, 对其在受到均匀拉力作用下的裂纹扩展路径进行分析. 正方形板尺寸为L×D = 10 cm×10 cm, 裂纹的长度2a = 3.0 cm, 裂纹与水平方向的夹角为θ = 30º, 板的弹性模量为E = 190 GPa, 泊松比μ = 0.305, 板上边受到均匀拉力σ = 10 MPa, 下边受到位移约束. 网格密度采用40 × 40, 开裂步长为Δa = 0.25, 扩展步数为6步, 如图3所示. 表2和表3给出了开裂后左右两端裂尖的应力强度因子和开裂角. 从表2和表3中可得出, 左端裂尖的应力强度因子小于右端裂尖的应力强度因子, 并且随着扩展步的增加, 右端裂尖的扩展角明显大于左端裂尖开裂角, 这可能与没考虑裂尖间的相互影响有关系, 本文得到的裂纹扩展路径和分析结果与文献[29,30]的研究结果一致. 所以, 当前的有限元模型是可以进行应力强度因子计算和模拟裂纹扩展的.
-
SOFC的工作温度通常在873 至1273 K之间, 这个范围内的高温有利于促进电极和电解质材 料的离子传导和电子传导, 从而提高电池的效率. 此外, 高温还有助于减少催化剂和电解质材料的极化损失. 但为保护电池组件, 其升温速率不能太快, 因此高温工作环境会导致电池的启动时间较长. 此外, 温度过高可能使电池材料萌生裂纹. 综合考虑以上因素, 本文确定了符合SOFC设计要求的四种工作温度(923, 973, 1023, 1073 K), 将其分别作为热载荷施加在电池的有限元模型上, 研究SOFC从工作温度冷却至室温后阳极预裂纹的扩展情况.
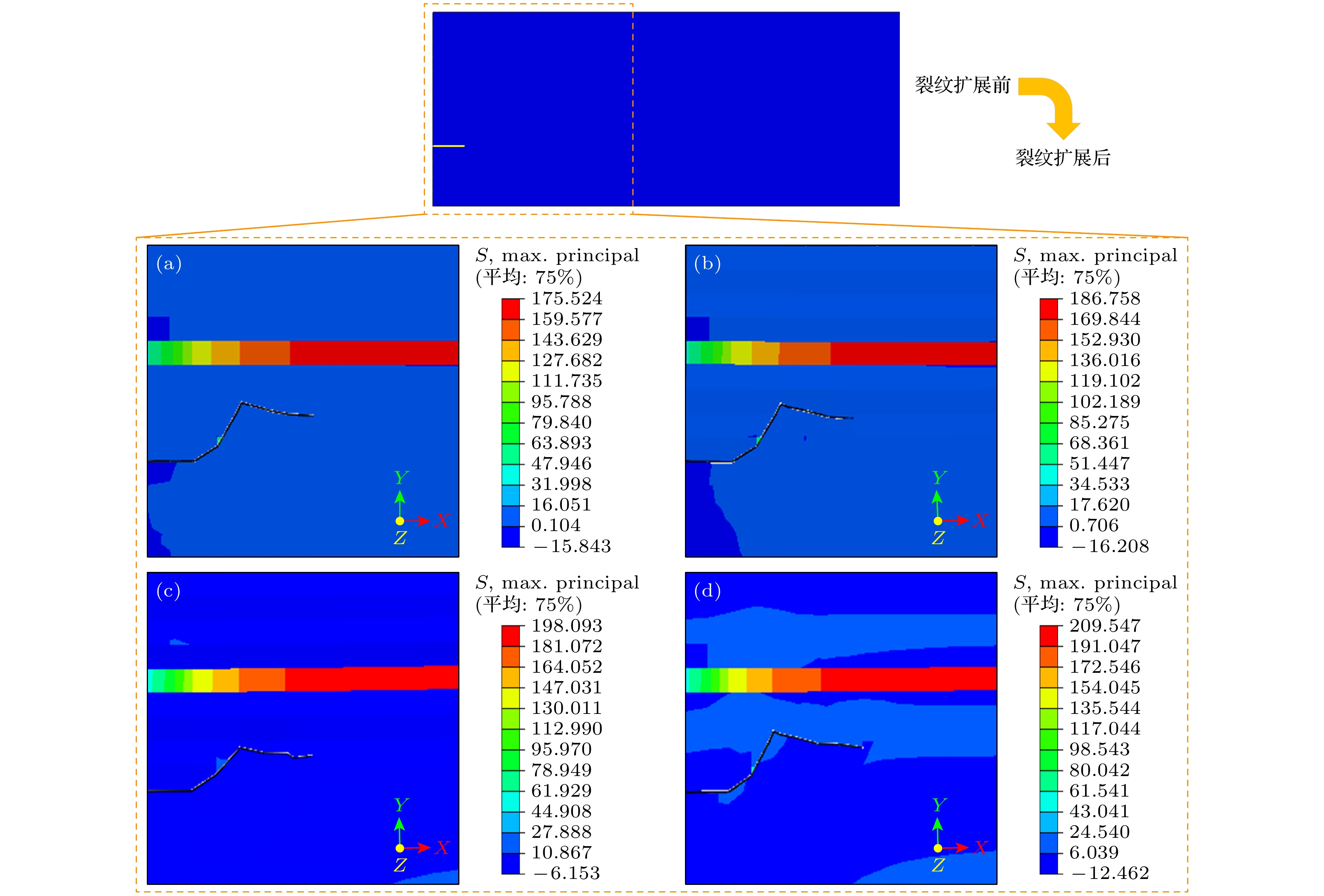
图4给出了不同工作温度下SOFC阳极预裂纹扩展后的应力云图, 为便于观察裂纹扩展情况, 仅显示了电池z方向的二维视图. 从图4中可以看出, 在电池冷却过程中其最大应力主要集中在电解质处, 且随着工作温度的增加, 电池的最大拉应力逐渐增大. 具体来看, 当工作温度为1073 K时, 电解质处的应力最大约为210 MPa, 而电解质的断裂应力在300 MPa左右[31], 故阳极的裂纹扩展不会造成电解质的断裂. 此外, 电池在1073 K下的最大拉应力相比于923 K增加了19.4%, 因此工作温度的升高会增大电池内部的热应力, 但由于最大拉应力主要分布在电解质处且电解质的断裂韧性较高, 因此温度变化对其不构成影响, 故工作温度的选择还需要从其他方面进行考虑.
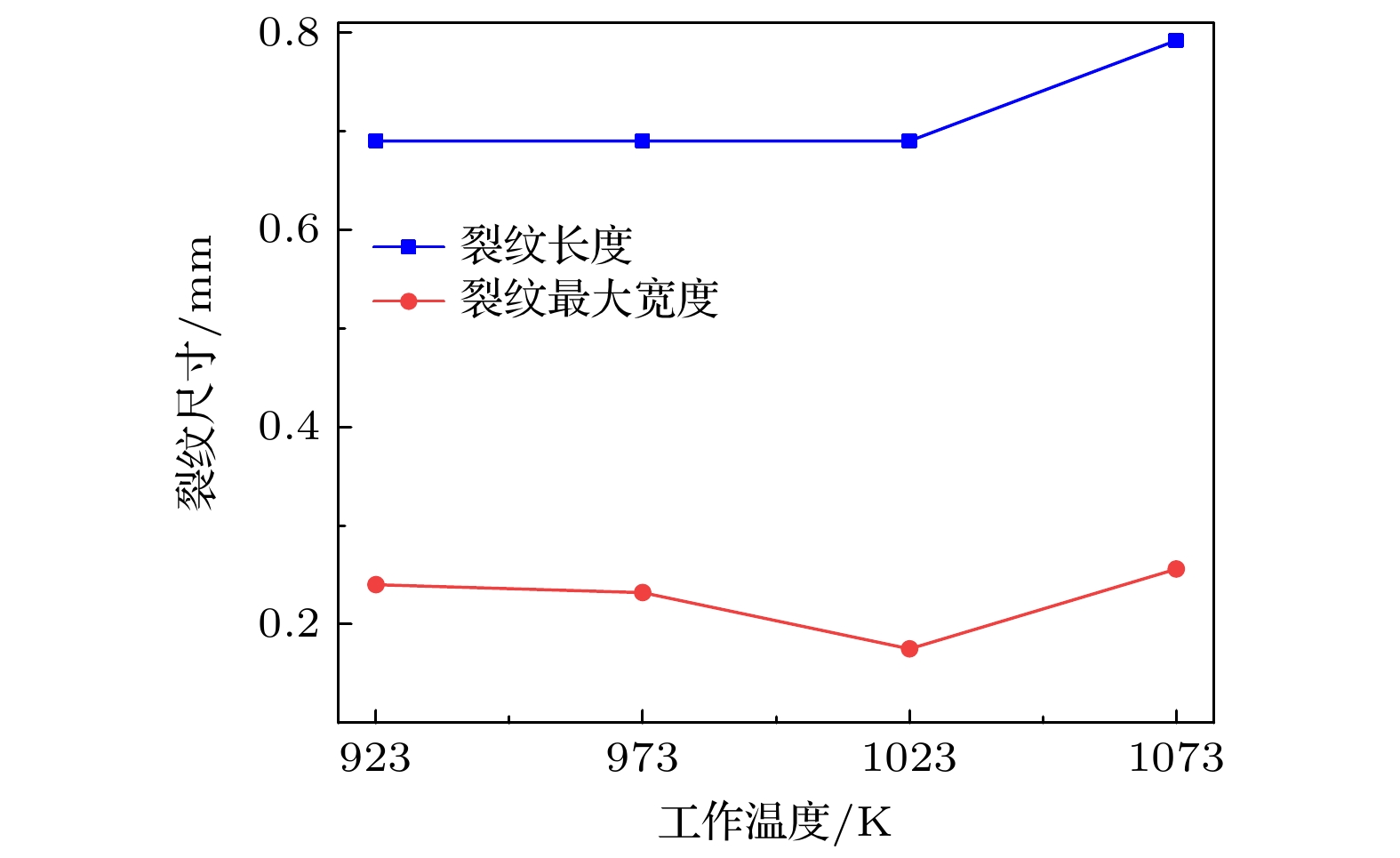
图5给出了阳极预裂纹扩展后的裂纹长度和最大宽度随电池工作温度的变化情况. 结合图4可以看出, 随着工作温度的增加, 裂纹扩展后的长度逐渐增加, 且增加幅度逐渐加大. 尤其当工作温度从1023 K升高至1073 K时, 裂纹长度大幅度增加. 而裂纹扩展后的最大宽度却随着温度的增加出现明显波动. 当工作温度由923 K升高到973 K时, 裂纹最大宽度基本不变; 但当工作温度升高至1023 K时, 裂纹最大宽度出现明显下降; 随后当工作温度升高到1073 K时, 裂纹最大宽度又增大, 且略高于973 K时的裂纹最大宽度.
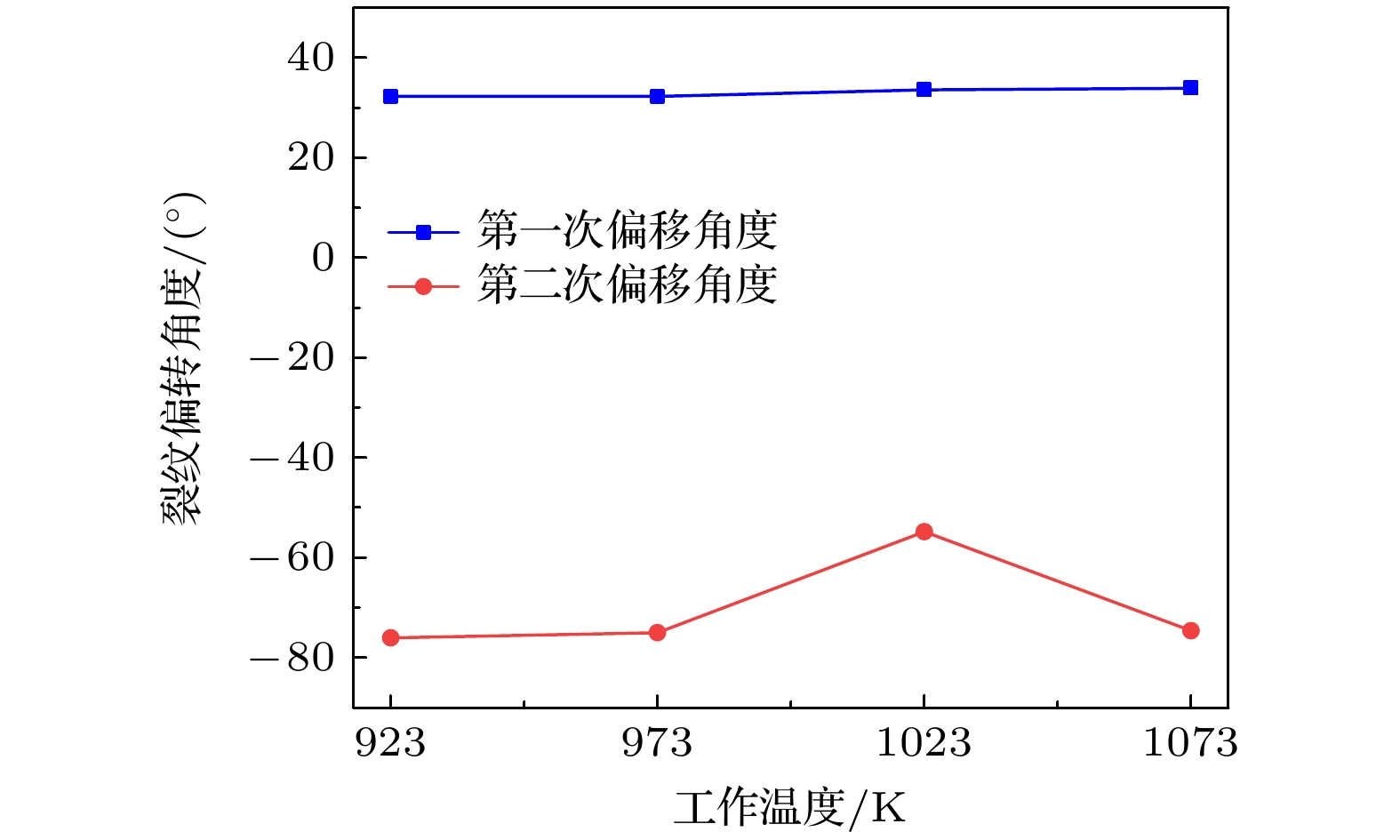
图6给出了阳极预裂纹扩展后的裂纹偏转角度随电池工作温度的变化情况, 偏转角度以逆时针为正, 顺时针为负. 结合图4可以看出, 随着温度的升高, 裂纹的第一次偏转角度基本保持不变, 为逆时针偏转33°左右. 而第二次偏转角度随着工作温度的升高出现明显波动, 即在工作温度为923, 973和1073 K时, 第二次偏转角度保持在顺时针偏转76°左右; 而在工作温度为1023 K时, 第二次偏转角度大幅下降至顺时针偏转54.8°. 因此, 结合阳极预裂纹扩展后的裂纹长度、最大宽度和两次偏转角度可以看出, 当电池的工作温度为1023 K时电池受裂纹影响的范围最小.
-
SOFC阳极的材料为由Ni和YSZ复合而成的金属陶瓷Ni-YSZ, 其材料属性受Ni的含量、孔隙率、制备温度等方面的影响. 实验研究发现[32,33], 随着孔隙率的不同, Ni-YSZ的弹性模量在32到75 GPa之间变化; 随着Ni含量的不同, Ni-YSZ的热膨胀系数在10.2×10–6 K–1和13.5×10–6 K–1之间变化. 而当Ni-YSZ材料属性变化时, 阳极预裂纹在冷却过程中的裂纹扩展情况也随之发生变化. 因此, 有必要研究能够抑制裂纹扩展的阳极材料属性的方案. 以阳极的热膨胀系数为变量, 其所选数值如表4所列, 研究阳极预裂纹随热膨胀系数的变化情况.
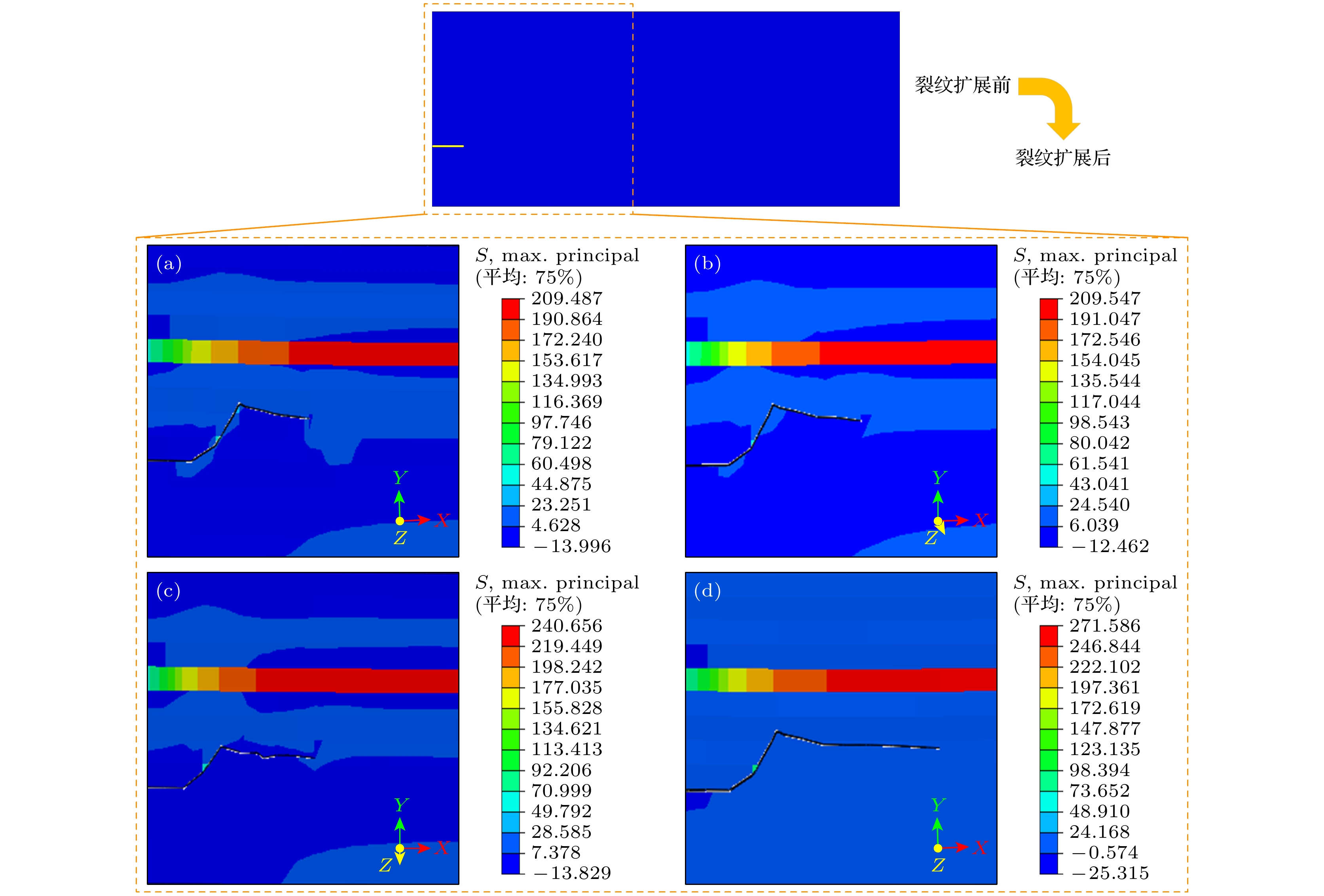
图7给出了不同方案的热膨胀系数下SOFC阳极预裂纹扩展后的应力云图. 从图7中可以看出, 电池的最大应力位于电解质处, 当阳极热膨胀系数为13.00×10–6 K–1时, 最大应力为271 MPa, 小于电解质的断裂应力, 故阳极裂纹扩展不会引起电解质的断裂. 此外, 随着阳极热膨胀系数的增大, 电池的最大热应力值也随之增大. 尤其当阳极热膨胀系数为13.00×10–6 K–1时, 其相应的电池最大拉应力与其他方案相比增幅非常明显, 最高增加了29.64%; 而阳极所受到的最大压应力也急剧升高, 最高增加了近一倍左右. 因此, 从热应力的角度 分析, 当阳极热膨胀系数增加至13.00×10–6 K–1时, 电池的稳定性较差.
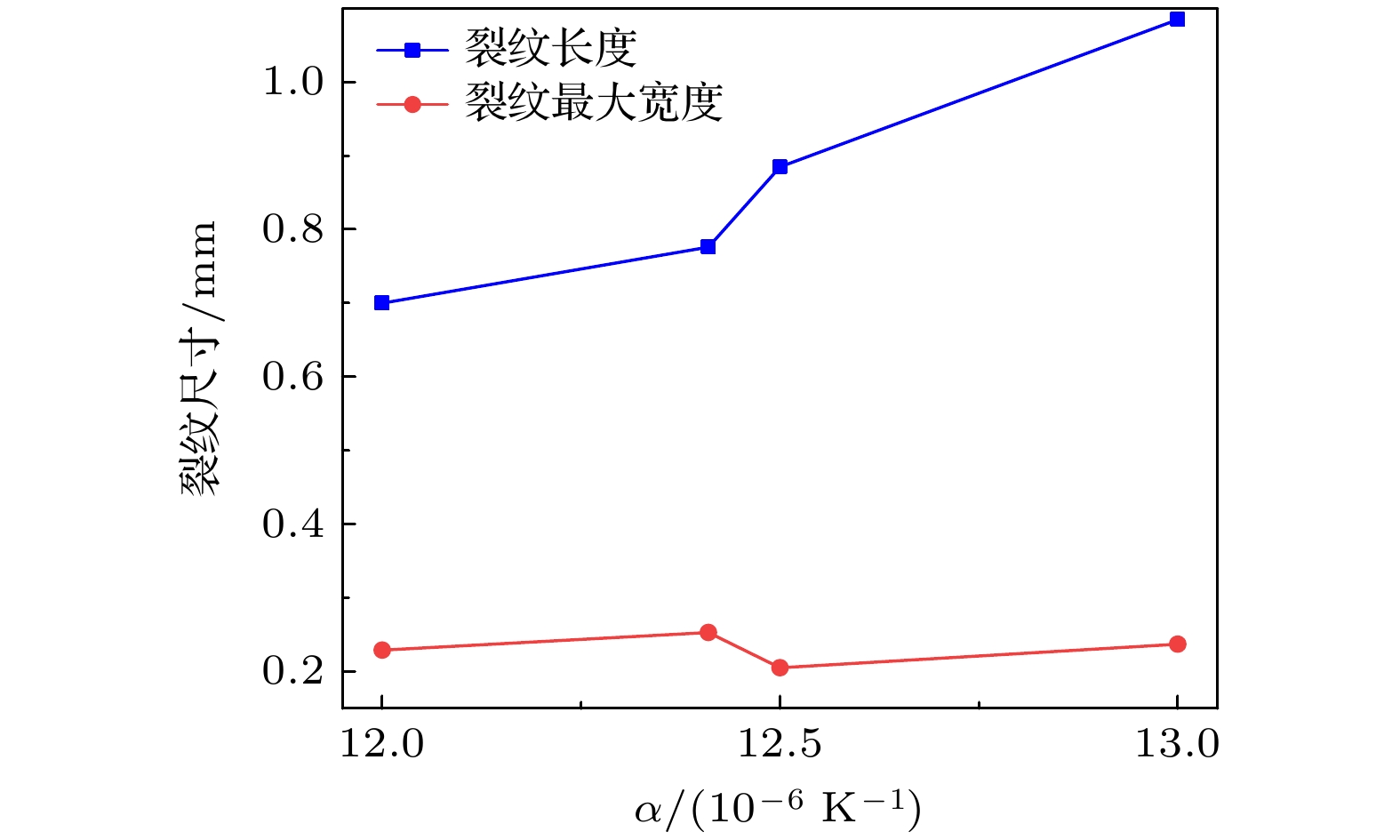
图8给出了阳极预裂纹扩展后的裂纹长度和最大宽度随阳极热膨胀系数的变化情况. 结合图7可以看出, 随着阳极热膨胀系数数值的增加, 裂纹扩展后的长度逐渐增加. 尤其当热膨胀系数由12.50×10–6 K–1增加至13.00×10–6 K–1时, 裂纹长度增加了22.6%, 增幅较大. 而对于裂纹扩展后的最大宽度而言, 其随阳极热膨胀系数变化不是很明显, 基本在0.2 mm左右波动. 因此, 从裂纹扩展的程度而言, 当阳极热膨胀系数增至13.00×10–6 K–1时, 电池的稳定性较差.
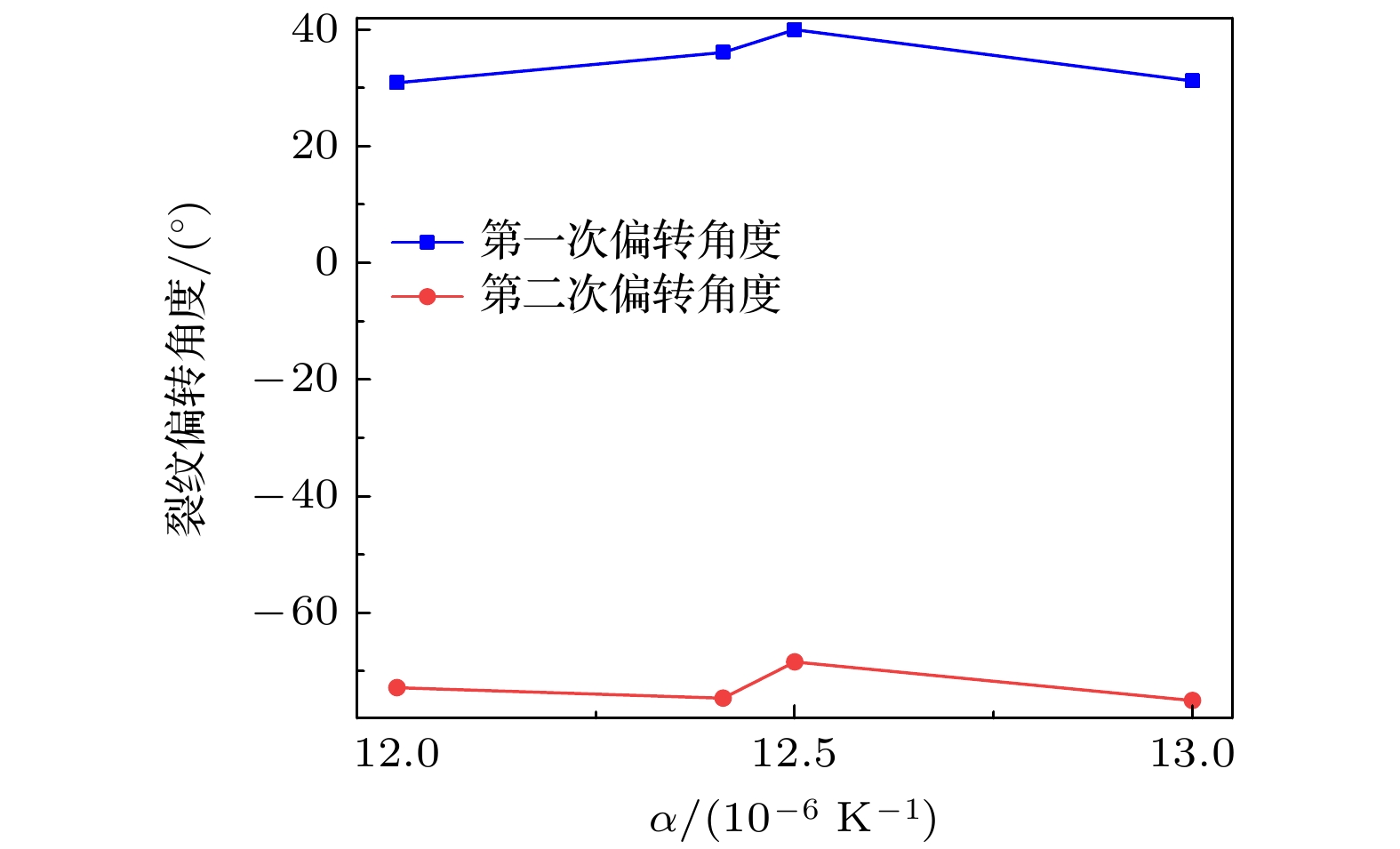
图9给出了阳极预裂纹扩展后的裂纹偏转角度随阳极热膨胀系数的变化情况. 结合图7可以看出, 随着阳极热膨胀系数的变化, 裂纹的两次偏转波动不大, 仅当阳极热膨胀系数为12.50×10–6 K–1时略有增加, 但相比于偏转角度最小时增幅也仅为9°左右. 因此, 裂纹偏转角度对阳极热膨胀系数的选择指导意义较小.
综合电池热应力、预裂纹扩展后的长度和最大宽度以及裂纹两次偏转角度可以看出, 为保证电池的稳定性, 阳极热膨胀系数的选择应小于12.50×10–6 K–1.
-
预裂纹倾斜的角度通常选择为裂纹扩展的预期方向. 确定预裂纹倾斜角度的原则有很多, 比如可以根据材料的断裂韧性和裂纹扩展的方式(如剪切、拉伸等)来选择合适的角度. 另外, 可以通过有限元分析方法对应力场进行分析, 选择使裂纹尖端受到应力最大的方向作为预裂纹的方向, 以便更好地模拟裂纹扩展时的应力集中效应. 再者, 可以根据材料的微观结构等因素, 选择预裂纹倾斜角度以适应材料的断裂行为. 此外, 还需要根据具体的工程应用需求来确定预裂纹倾斜角度[34,35].
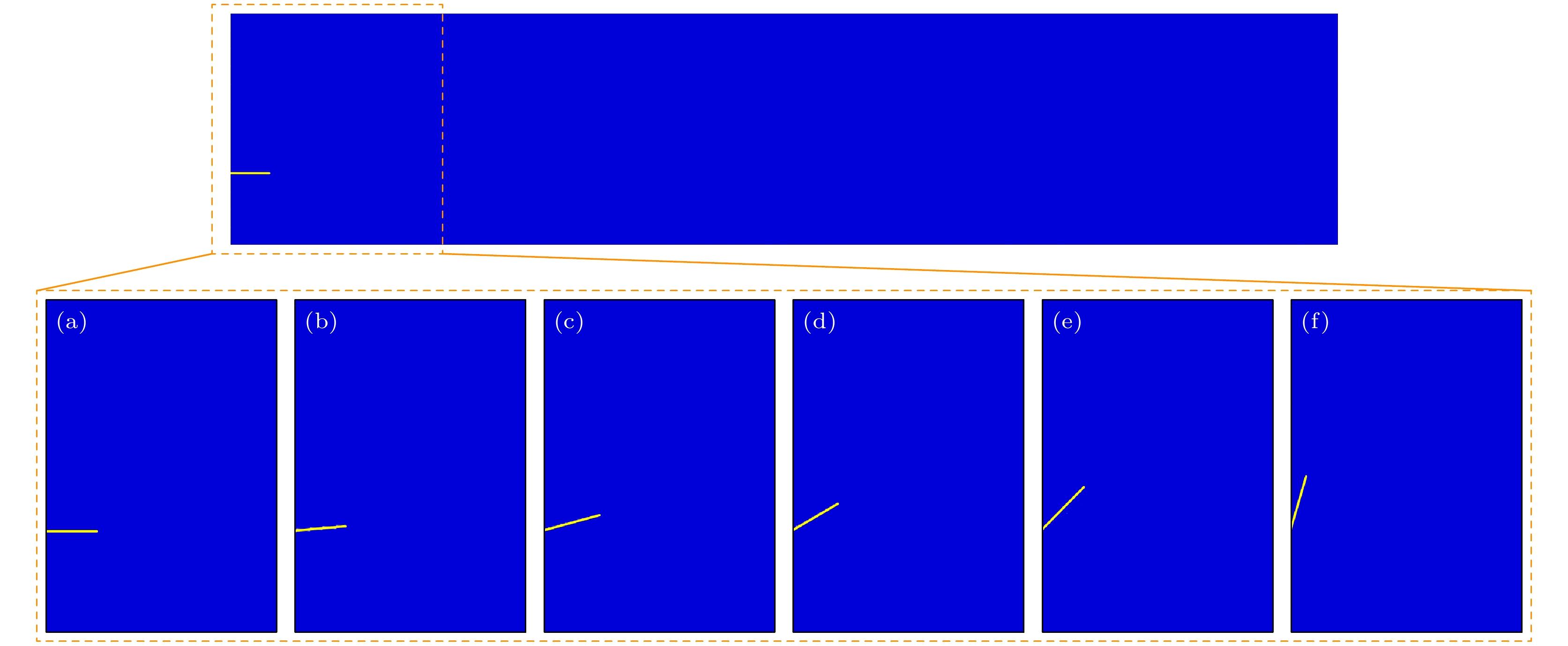
综合考虑以上因素, 本文确定了符合SOFC设计要求的六种裂纹倾斜角度来研究预裂纹角度对电池阳极裂纹扩展行为的影响, 如图10所示, 其中图10(a)—(f)分别代表的预裂纹倾斜角度为0°, 5°, 15°, 30°, 45°和75°.
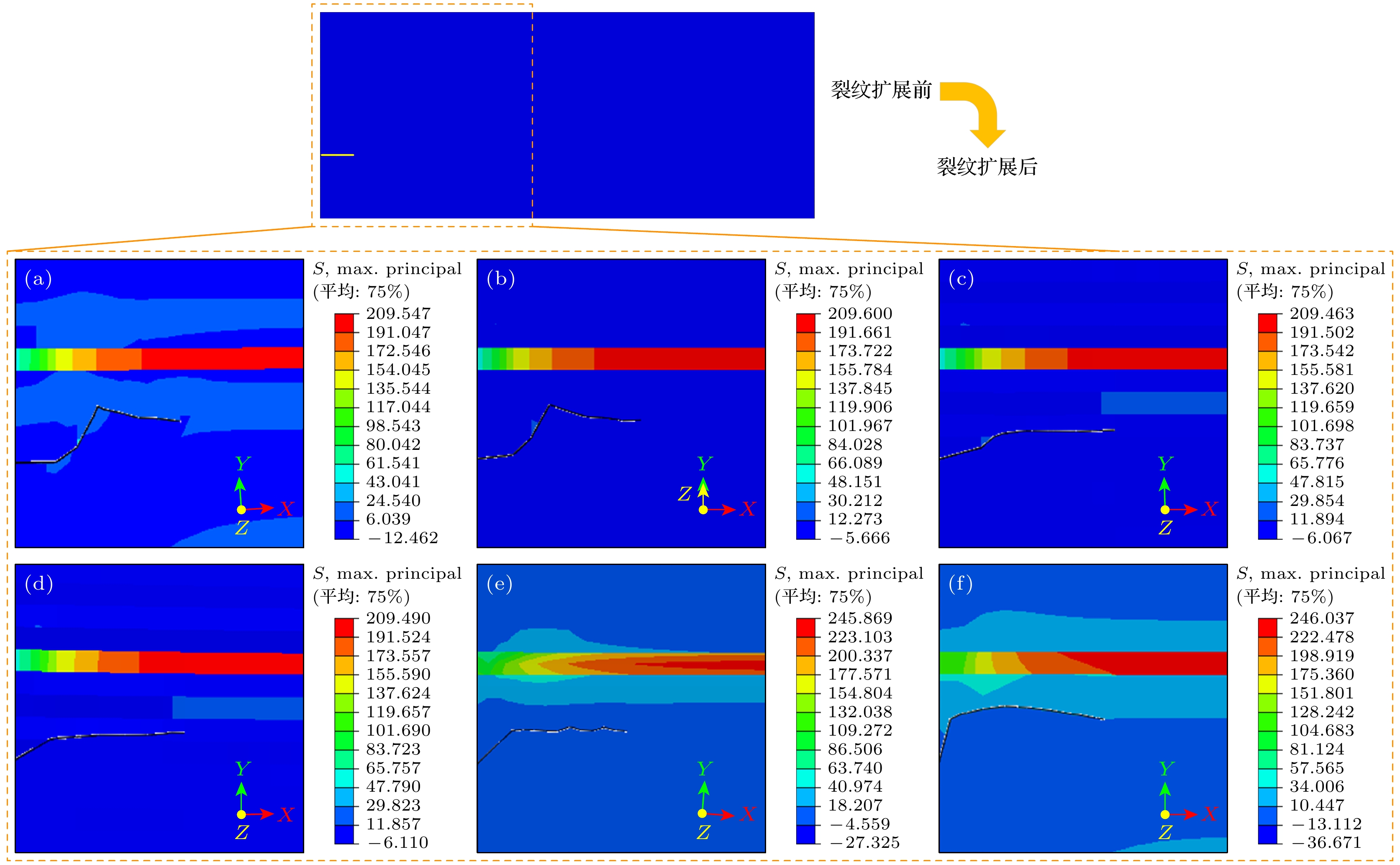
图11给出了不同预裂纹倾斜角度下SOFC阳极预裂纹扩展后的应力云图. 从图11中可以看出, 当预裂纹倾斜角度小于45°时, 电池的最大热应力值和整体热应力分布情况均变化不大; 而当倾斜角度增加至45°时, 电池的最大热应力增加了17%; 当倾斜角度继续增大时, 电池最大热应力值的变化幅度很小. 由此可以看出, 预裂纹倾斜角度为45°时是电池应力增大的临界点.
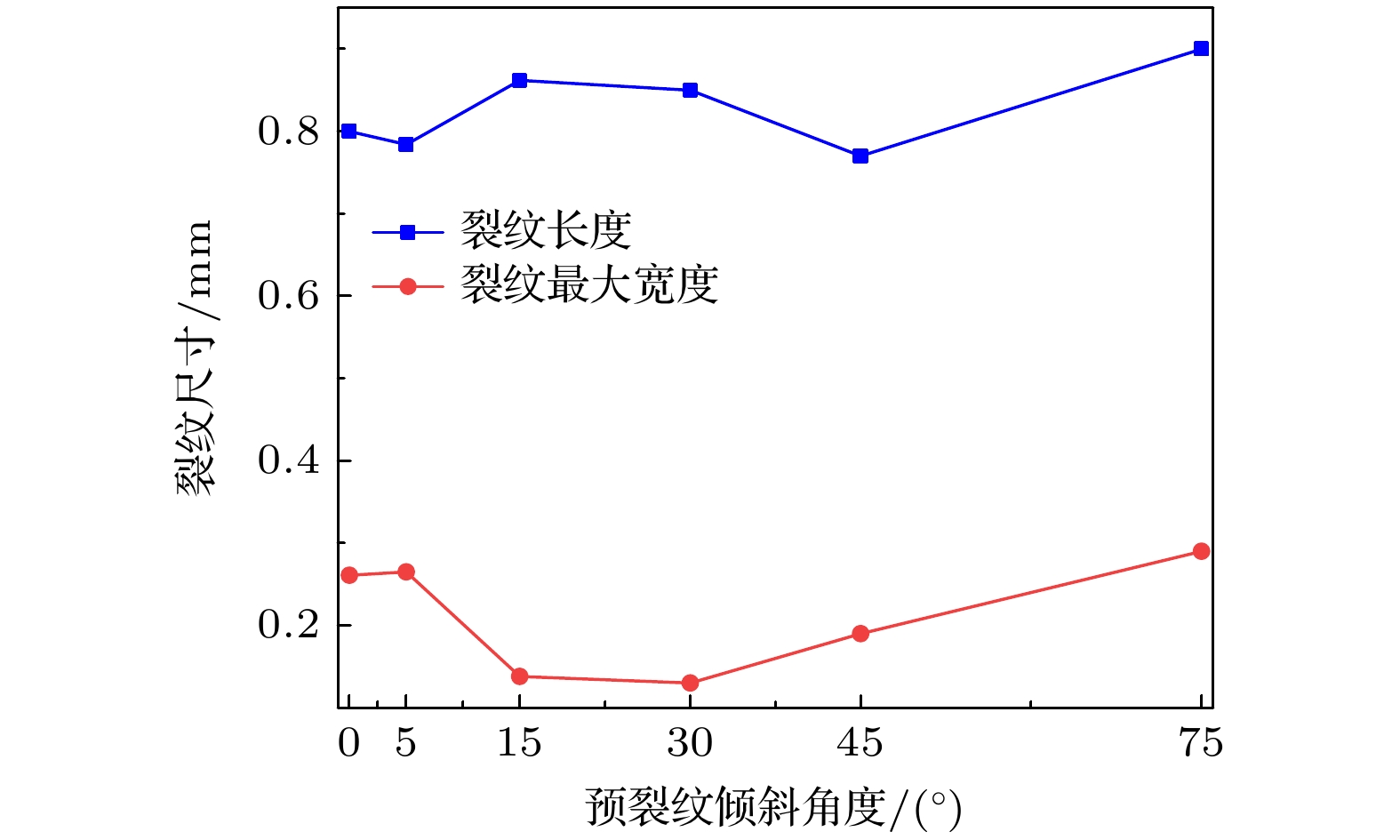
图12给出了阳极预裂纹扩展后的裂纹长度和最大宽度随预裂纹倾斜角度的变化情况. 结合图11可以看出, 随着预裂纹倾斜角度的增加, 裂纹扩展后的长度振荡变化. 具体来说, 当预裂纹倾斜角度为45°时, 裂纹扩展长度最短; 当预裂纹倾斜角度为75°时, 裂纹扩展长度最长. 另一方面, 随着预裂纹的倾斜角度的增加, 扩展后的裂纹最大宽度呈现先减小后增大的趋势. 从图12中可以看出, 裂纹最大宽度首先随着预裂纹倾斜角度的增大而减小, 尤其当倾斜角度从5°增加到15°时, 裂纹最大宽度减小了92%. 随后当倾斜角度从30°增加到75°时, 裂纹宽度基本呈线性增加的趋势; 且当倾斜角度为75°时, 裂纹宽度达到最高, 比倾斜角度为5°时还提高了9.4%. 因此, 从扩展后的裂纹尺寸来看, 在所选范围内, 当预裂纹倾斜角度为45°时, 裂纹扩展后的长度和宽度相对较低、电池受裂纹影响的范围最小, 电池稳定性较高.
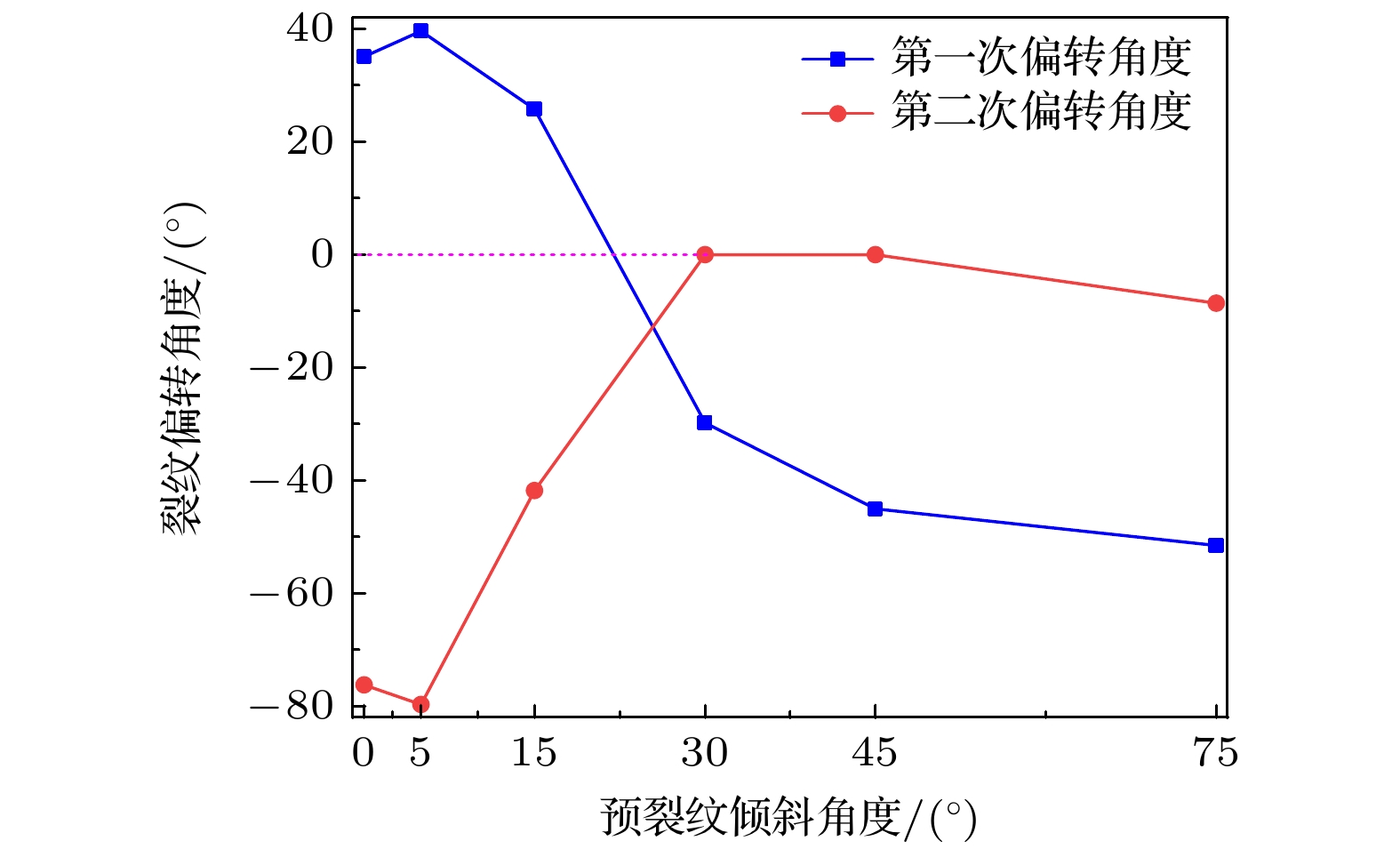
图13给出了阳极预裂纹扩展后的裂纹偏转角度随预裂纹倾斜角度的变化情况. 结合图11可以看出, 随着预裂纹倾斜角度的变化, 裂纹的两次偏转角度变化非常明显, 第一次偏转角度随预裂纹角度的增加基本呈现先减小后增大的趋势, 而第二次偏转角则基本呈现一直减小的趋势. 值得注意的是, 当预裂纹角度较小(小于15°)时, 裂纹在扩展过程中发生两次明显偏转; 而当预裂纹角度较大(大于30°)时, 裂纹仅发生一次偏转. 这主要是由于裂纹最终的扩展方向接近水平方向, 而当预裂纹角度大于30°时, 裂纹尖端在温度载荷的作用下已经处于阳极的最大应力范围内, 根据裂纹扩展的最大应力原则, 则没有发生二次偏转.
综合电池热应力、预裂纹扩展后的长度和最大宽度以及裂纹两次偏转角度可以看出, 为保证电池的稳定性, 预裂纹角度为45°时电池的稳定性最高, 裂纹扩展的路径最为简单.
-
由于电池阳极的厚度相对较厚, 预裂纹可能出现的范围也较大, 比如靠近电解质一侧或靠近电池底部等. 不同位置的预裂纹扩展后的路径有所不同, 对电池的影响程度也不同. 因此, 本文设定了四种不同的预裂纹初始位置, 令其距x轴(电池底部)的距离为hα (α = 1, 2, 3, 4), 其中h1 = 0.30 mm, h2 = 0.35 mm, h3 = 0.40 mm, h4 = 0.45 mm, 以研究预裂纹位置对SOFC阳极裂纹扩展行为的影响.
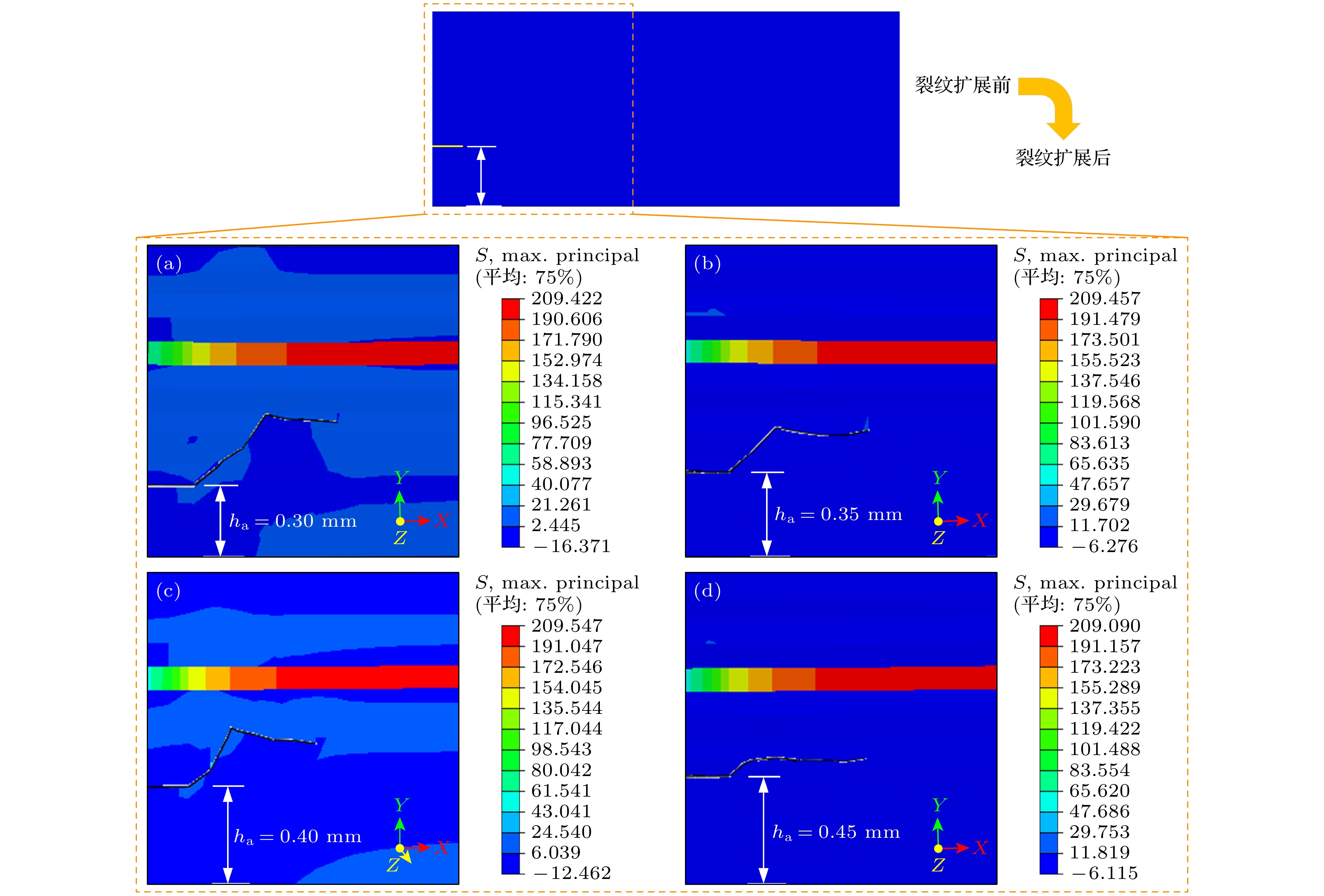
图14给出了不同预裂纹位置下SOFC阳极预裂纹扩展后的应力云图. 从图14中可以看出, 随着预裂纹位置的变化, 电池的最大热应力值和整体热应力分布情况均变化不大. 由此可以看出, 预裂纹位置对电池的应力影响不大, 故预裂纹位置的选择还需要从其他方面进行考虑.
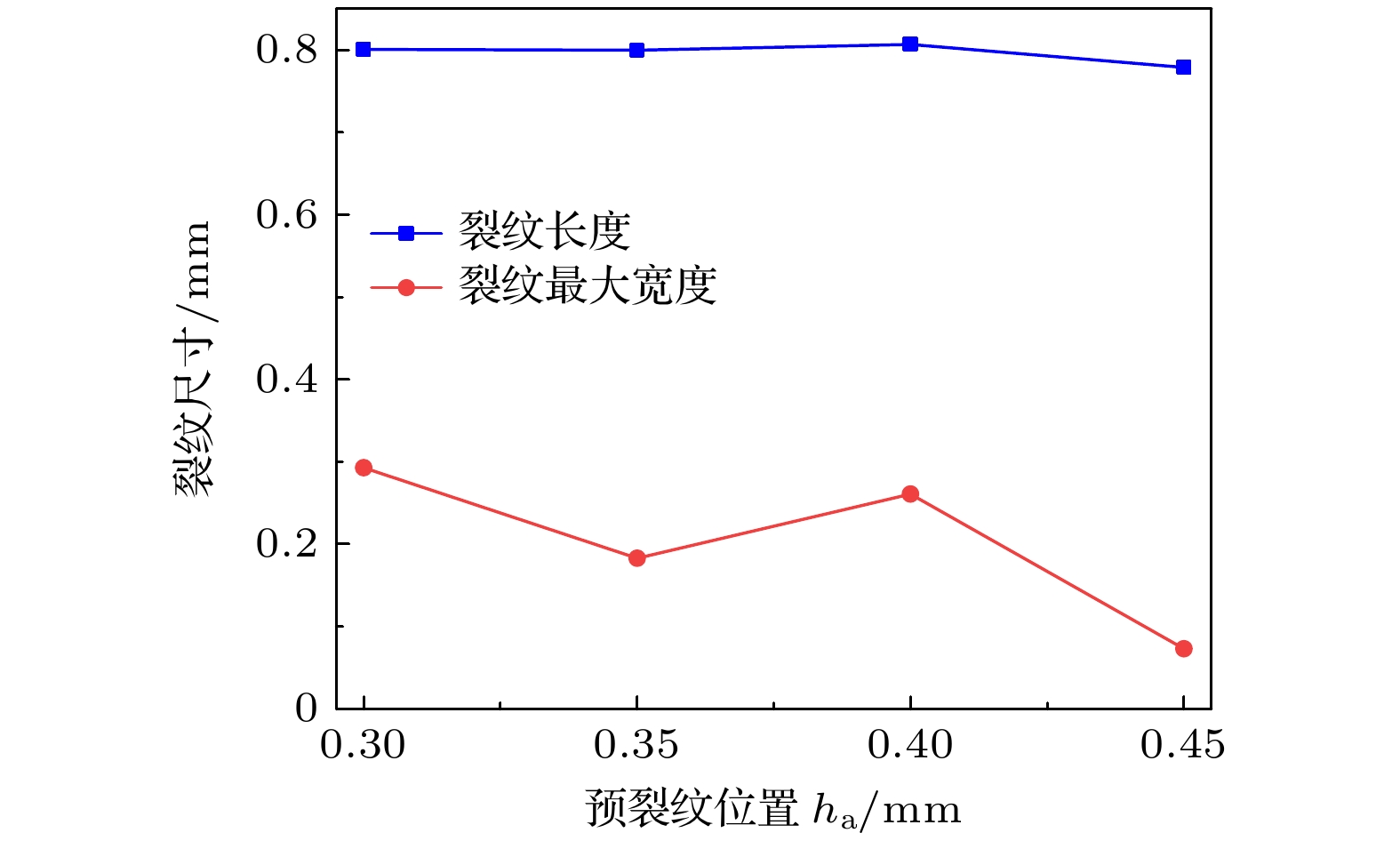
图15给出了阳极预裂纹扩展后的裂纹长度和最大宽度随预裂纹位置的变化情况. 结合图14可以看出, 随着预裂纹与x轴距离的增加, 裂纹扩展后的长度基本保持不变, 仅当距x轴0.45 mm时略有减小, 但减小幅度仅为3%左右. 而对于扩展后的裂纹最大宽度而言, 其随预裂纹位置振荡下降且程度明显. 具体来说, 当ha = 0.45 mm时, 预裂纹扩展后的最大宽度仅为ha = 0.30 mm时的1/4. 由此可见, 裂纹位置对预裂纹扩展后的裂纹长度影响不大, 但对裂纹最大宽度影响明显. 在所选数据范围内, 距离x轴最远时即ha = 0.45 mm时电池受裂纹的影响范围最小.
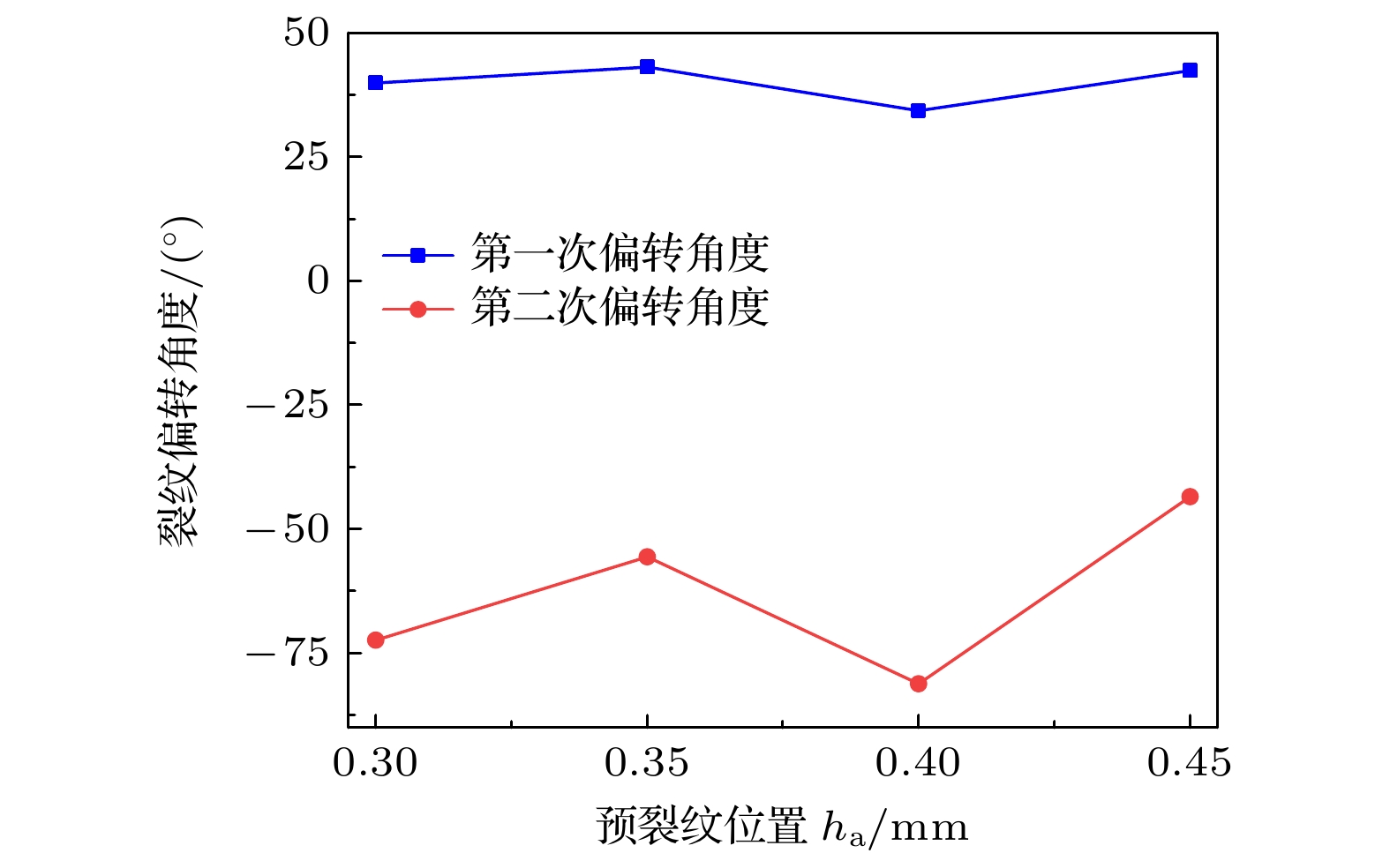
图16给出了阳极预裂纹扩展后的裂纹偏转角度随预裂纹位置的变化情况. 结合图14可以看出, 随着预裂纹与x轴距离的增加, 裂纹第一次偏转角度变化不大, 而第二次偏转角度变化比较明显. 值得注意的是, 当预裂纹距离x轴0.45 mm时, 裂纹在扩展的过程中先逆时针偏转42.4°继而顺时针偏转43.5°, 即裂纹扩展的最终方向基本与预裂纹方向一致. 由此可见, 当预裂纹距离x轴0.45 mm时裂纹偏转程度最小且最易预测裂纹扩展方向.
-
对含有预裂纹的SOFC的冷却过程进行有限元分析, 研究工作温度、阳极材料属性、预裂纹几何特征对电池热应力分布和阳极预裂纹扩展情况的影响, 从电池热应力分布、裂纹扩展后的长度和最大宽度以及裂纹的偏转角度等方面来探究抑制裂纹扩展的电池优化方案以保证电池的稳定性.
1)在所选温度范围内, 当电池的工作温度为1023 K时, 电池受裂纹影响的范围略小, 但程度不明显. 而保证SOFC的电化学效率需要较高的温度, 因此电池的工作温度不应低于1023 K.
2)电池的热应力和阳极裂纹扩展程度随阳极热膨胀系数的增大而增加, 尤其当阳极热膨胀系数为13.00×10–6 K–1时增幅最大, 因此需要通过调节阳极Ni的含量使其热膨胀系数小于12.50×10–6 K–1.
3)预裂纹的倾斜角度和初始位置对电池的热应力分布和裂纹扩展长度影响不大, 但裂纹最大宽度受其影响明显. 在所选范围内, 当预裂纹倾斜角度为45°时或预裂纹距x轴0.45 mm时, 裂纹扩展后的最大宽度最小, 且扩展方向最易预测, 此时电池受裂纹影响的范围最小、稳定性最高.
含有预裂纹的固体氧化物燃料电池的电极裂纹扩展分析
Analysis of electrode crack propagation in solid oxide fuel cell with pre-crack
-
摘要: 为了降低固体氧化物燃料电池在冷却过程中的裂纹扩展程度, 提高电池的稳定性和耐久性, 对含有预裂纹的固体氧化物燃料电池的三维模型进行有限元分析. 从工作温度、材料属性、预裂纹角度、预裂纹位置等方面出发, 以电池应力分布、裂纹扩展后的长度、最大宽度和偏转角度等作为判据, 探究各因素对预裂纹扩展行为的影响, 提出基于材料优化和结构优化的提高电池稳定性的方案. 研究结果表明, 在所选参数范围内, 为了抑制裂纹扩展程度, 电池的工作温度不应低于1023 K, 阳极的热膨胀系数应小于12.50×10–6 K–1. 此外, 当预裂纹倾斜角度为45°或预裂纹距阳极底部0.45 mm时, 裂纹扩展后的最大宽度最小, 且扩展方向最易预测, 此时电池受裂纹影响的范围最小, 稳定性最高. 该研究工作为抑制固体氧化物燃料电池的裂纹扩展, 提高燃料电池的使用寿命, 促进燃料电池的商业化进程提供了依据.Abstract: The mechanical performance of solid oxide fuel cell is one of the main factors limiting its commercialization process. In order to reduce the degree of crack propagation in the cooling process and improve the stability and durability of the cell, the finite element analysis is conducted on a three-dimensional model of solid oxide fuel cell containing pre-crack. Utilizing the extended finite element method (XFEM) and fracture theory, and considering the stress distribution, length and maximum width after crack propagation and deflection angle of crack as criteria, this paper investigates the influence of various parameters, including working temperature, material properties, pre-crack angle, and pre-crack location, on pre-crack propagation behavior and proposes a solution based on material optimization and structural optimization to improve the stability of the cell. A pre-crack is set at the left boundary of the anode to analyze the influence of different operating conditions on the propagation of anode cracks in the cell. The correctness of finite element simulation is verified by comparing the simulation results with theoretical results of crack stress intensity factors in the same model. From the comprehensive analysis of the thermal stress of the cell, the crack length and maximum width after pre-crack propagation, and the two deflection angles of crack propagation, it can be seen that within the selected parameters, in order to ensure the stability of the cell and inhibit the degree of crack propagation, the operating temperature of the cell should not be lower than 1023 K, and the thermal expansion coefficient of anode should be less than 12.50×10–6 K–1. In addition, when the pre-crack angle is 45° or 0.45 mm away from the bottom of anode, the maximum width after crack propagation is the smallest, and the propagation path is the most predictable. In this case, the cell is affected by the smallest crack range and the highest stability. This research provides a guidance for suppressing crack propagation in solid oxide fuel cell, improving the lifetime and promoting the commercialization process of fuel cell.
-
Key words:
- solid oxide fuel cell /
- pre-crack /
- crack propagation /
- thermal stress .
-
-
图 1 含预裂纹的平板式SOFC几何模型示意图
Figure 1. Schematic diagram of the geometric model of planar SOFC with pre-crack.
图 2 应力强度因子随倾斜角变化的数值计算结果与理论解析解的对比图 (a) 无限大平板几何模型和边界条件; (b) 应力强度因子对比曲线
Figure 2. The comparison between the numerical result and theoretical analytical solution of stress intensity factor with the inclination angle : (a) The infinite plate geometric model and boundary conditions; (b) stress-intensity factor contrast curve.
图 3 倾斜裂纹扩展路径数值模拟图 (a) 正方形板几何模型和边界条件; (b) 裂纹扩展数值模拟图
Figure 3. Numerical simulation diagram of inclined crack propagation path: (a) Geometric model and boundary conditions of a square plate; (b) numerical simulation diagram of crack propagation.
图 4 不同工作温度下SOFC阳极预裂纹扩展后的应力云图(Z-方向视图) (a) 923 K; (b) 973 K; (c) 1023 K; (d) 1073 K
Figure 4. Stress nephogram of SOFC anode pre-crack propagation at different operating temperatures (Z-direction view): (a) 923 K; (b) 973 K; (c) 1023 K; (d) 1073 K
图 5 阳极预裂纹扩展后的裂纹长度和最大裂纹宽度随电池工作温度的变化情况
Figure 5. The change of the crack length and maximum crack width with the SOFC operating temperature after anode pre-crack propagation.
图 6 阳极预裂纹扩展后的裂纹偏转角度随电池工作温度的变化情况
Figure 6. The variation of crack deflection angle after anode pre-crack propagation with SOFC operating temperature.
图 7 不同热膨胀系数下SOFC阳极预裂纹扩展后的应力云图(Z-方向视图) (a) 12.00×10–6 K–1; (b) 12.41×10–6 K–1; (c) 12.50×10–6 K–1; (d) 13.00×10–6 K–1
Figure 7. Stress nephogram of SOFC anode pre-crack propagation under different thermal expansion coefficients (Z-direction view): (a) 12.00×10–6 K–1; (b) 12.41×10–6 K–1; (c) 12.50×10–6 K–1; (d) 13.00×10–6 K–1
图 8 阳极预裂纹扩展后的裂纹长度和最大裂纹宽度随阳极热膨胀系数的变化情况
Figure 8. The change of crack length and the maximum crack width with the thermal expansion coefficient of anode after the anode pre-crack propagation.
图 9 阳极预裂纹扩展后的裂纹偏转角度随阳极热膨胀系数的变化情况
Figure 9. Variation of crack deflection angle with thermal expansion coefficient of anode after anode pre-crack propagation.
图 10 预裂纹倾斜角度示意图(Z-方向视图) (a) 0°; (b) 5°; (c) 15°; (d) 30°; (e) 45°; (f) 75°
Figure 10. Schematic diagram of pre-crack inclination angle (Z-direction view): (a) 0°; (b) 5°; (c) 15°; (d) 30°; (e) 45°; (f) 75°.
图 11 不同预裂纹倾斜角度下SOFC阳极预裂纹扩展的应力云图(Z-方向视图) (a) 0°; (b) 5°; (c) 15°; (d) 30°; (e) 45°; (f) 75°
Figure 11. Stress nephogram of SOFC anode pre-crack propagation under different pre-crack inclination angles (Z-direction view): (a) 0°; (b) 5°; (c) 15°; (d) 30°; (e) 45°; (f) 75°
图 12 阳极预裂纹扩展后的裂纹长度和最大裂纹宽度随预裂纹倾斜角度的变化
Figure 12. Variation of crack length and maximum crack width after anode pre-crack propagation with the inclination angle of the pre-crack.
图 13 阳极预裂纹扩展后的裂纹偏转角度随预裂纹倾斜角度的变化
Figure 13. Variation of crack deflection angle with pre-crack inclination angle after anode pre-crack propagation.
图 14 不同预裂纹位置下SOFC阳极预裂纹扩展的应力云图(Z-方向视图) (a) ha = 0.30 mm; (b) ha = 0.35 mm; (c) ha = 0.40 mm; (d) ha = 0.45 mm
Figure 14. Stress nephogram of SOFC anode pre-crack propagation at different pre-crack locations (Z-direction view): (a) ha = 0.30 mm; (b) ha = 0.35 mm; (c) ha = 0.40 mm; (d) ha = 0.45 mm.
图 15 阳极预裂纹扩展后的裂纹长度和最大裂纹宽度随预裂纹位置的变化
Figure 15. Variation of crack length and maximum crack width with the pre-crack position after anode pre-crack propagation.
图 16 阳极预裂纹扩展后的裂纹偏转角度随预裂纹位置的变化
Figure 16. Variation of crack deflection angle with pre-crack position after anode pre-crack propagation.
材料属性 阳极
Ni-YSZ电解质
YSZ阴极
LSM弹性模量
E/GPa298 K 72.5 196.3 41.3 1073 K 58.1 148.6 48.3 泊松比 μ 298 K 0.36 0.31 0.33 1073 K 0.36 0.31 0.33 热膨胀系数
α/(10–6 K–1)298 K 12.41 10.0 9.8 1073 K 12.60 10.5 11.8 
下载: 导出CSV
表 2 裂纹开裂后左端裂尖的应力强度因子和开裂角
Table 2. Stress intensity factor and cracking angle at the left crack tip after crack propagation.
步数 KI/(MPa· $ \sqrt {\text{m}} $ )KII/(MPa· $ \sqrt {\text{m}} $ )θ/(º) 前人结果[29] 本文结果 误差/% 前人结果[29] 本文结果 误差/% 前人结果[29] 本文结果 误差/% 初始 1.7394 1.7380 0.08 1.000 1.002 0.20 –0.7528 –0.7530 0.03 1 2.1129 2.1131 0.02 –0.6982 –0.6985 0.04 0.5442 0.5445 0.05 2 4.2294 4.2294 0 0.7843 0.7845 0.03 –0.5365 –0.5365 0 3 4.2843 4.2845 0.07 –0.6983 –0.6988 0.07 0.4596 0.4601 0.10 4 4.2254 4.2254 0 0.7370 0.7374 0.05 –0.4498 –0.4498 0 5 4.2779 4.2784 0.01 –0.5585 –0.5590 0.09 0.3123 0.3123 0 6 4.2528 4.2533 0.01 0.4764 0.4768 0.08 –0.2526 –0.2527 0.04
下载: 导出CSV
表 3 裂纹开裂后右端裂尖的应力强度因子和开裂角
Table 3. Stress intensity factor and crack angle of right end crack tip after crack propagation.
步数 KI/(MPa· $ \sqrt {\text{m}} $ )KII/(MPa· $ \sqrt {\text{m}} $ )θ/(º) 前人结果[29] 本文结果 误差
/%前人结果[29] 本文结果 误差
/%前人结果[29] 本文结果 误差
/%初始 1.7803 1.7805 0.01 0.9857 0.9857 0 –0.7393 –0.7393 0 1 2.1168 2.1168 0 –0.7279 –0.7282 0.04 0.5593 0.5588 0.08 2 2.4731 2.4736 0.02 0.7963 0.7963 0 –0.5344 –0.5340 0.07 3 2.6760 2.6757 0.01 –0.8094 –0.8099 0.06 0.5110 0.5110 0 4 2.9802 2.9805 0.01 0.8856 0.8856 0 –0.5044 0.5048 0.08 5 3.3000 3.3000 0 –0.9070 0.9073 0.03 0.4759 0.4759 0 6 3.6713 3.6709 0.01 0.9229 0.9233 0.04 0.4441 0.4435 0.13
下载: 导出CSV
表 4 不同方案的阳极热膨胀系数
Table 4. The thermal expansion coefficient of anode in different schemes.
参 数 298 K 1073 K 阳极热膨胀系数/(10–6 K–1) 12.00 12.60 12.41 12.60 12.50 13.13 13.00 13.65
下载: 导出CSV
-
[1] Minh N Q, Takahashi T 1995 Science and Technology of Ceramic Fuel Cells. (Amsterdam: Elsevier Science) p147 [2] Singhal S C, Kendall K 2002 Mater. Today 5 55 doi: InternationalJournalofHeatandMassTransfer [3] 申双林, 张小坤, 万兴文, 郑克晴, 凌意瀚, 王绍荣 2022 物理学报 71 164401 doi: 10.7498/aps.71.20220031 Shen S L, Zhang X K, Wan X W, Zheng K Q, Ling Y H, Wang S R 2022 Acta Phys. Sin. 71 164401 doi: 10.7498/aps.71.20220031 [4] 徐晗, 张璐, 党政 2020 物理学报 69 098801 doi: 10.7498/aps.69.20191697 Xu H, Zhang L, Dang Z 2020 Acta Phys. Sin. 69 098801 doi: 10.7498/aps.69.20191697 [5] 李凯, 李霄, 李箭, 谢佳苗 2019 无机材料学报 34 611 doi: 10.15541/jim20180398 Li K, Li X, Li J, Xie J M 2019 J. Inorg. Mater. 34 611 doi: 10.15541/jim20180398 [6] Su Y, Zhu D Y, Zhang T T, Zhang Y R, Han W P, Zhang J, Ramakrishna S, Long Y Z 2022 Chin. Phys. B 31 057305 doi: 10.1088/1674-1056/ac3baa [7] Shao Q, Fernández-González R, Ruiz-Morales J, et al. 2015 Int. J. Hydrogen Energy 40 16509 doi: 10.1016/j.ijhydene.2015.10.016 [8] Shao Q, Bouhala L, Fiorelli D, Fahs M, Younes A, Núñez P, Belouettar S, Makradi A 2016 Int. J. Solids Struct. 78–79 189 doi: 10.1016/j.ijsolstr.2015.08.026 [9] Joulaee N, Makradi A, Ahzi S, Khaleel M A, Koeppel B K 2009 Int. J. Mech. Mater. Des. 5 217 doi: 10.1007/s10999-009-9095-5 [10] Nguyen B N, Koeppel B J, Ahzi S, Khaleel M A, Singh P 2006 J. Am. Ceram. Soc. 89 1358 doi: 10.1111/j.1551-2916.2005.00874.x [11] Li Q Q, Xue D X, Feng C Y, Zhang X W, Li G J 2022 J. Electrochem. Soc. 169 073507 doi: 10.1149/1945-7111/ac7c3f [12] Bouhala L, Belouettar S, Makradi A, Rémond Y 2010 Mater. Des. 31 1033 doi: 10.1016/j.matdes.2009.10.002 [13] Pitakthapanaphong S, Busso E P 2005 Model Simul. Mater. Sci. Eng. 13 531 doi: 10.1088/0965-0393/13/4/004 [14] Kim S J, Choi M B, Park M, Kim H, Son J W, Lee J H, Kim B K, Lee H, Kim S G, Yoon K 2017 J. Power Sources 360 284 doi: 10.1016/j.jpowsour.2017.06.004 [15] 李录贤, 王铁军 2005 力学进展 35 5 doi: 10.6052/1000-0992-2005-1-J2004-054 Li L X, Wang T J 2005 Adv. Mech. 35 5 doi: 10.6052/1000-0992-2005-1-J2004-054 [16] 王自强, 陈少华 2009 高等断裂力学(北京: 科学技术出版社) 第87页 Wang Z Q, Chen S H 2009 Advanced Fracture Mechanics (Beijing: Science and Technology Press) p87 [17] Ergodan F, Sih G C 1963 J. Basic Sci. Eng. 85 520 [18] Chang K J 1981 Eng. Fract. Mech. 14 107 doi: 10.1016/0013-7944(81)90021-7 [19] Hussain M A, Pu S L, Underwood J H 1974 Strain Energy Release Rate for a Crack under Combined Mode I and Mode II (West Conshohocken: ASTM International) p35 [20] Mori M, Yamamoto T, Itoh H, Inaba H, Tagawa H 1998 J. Electrochem. Soc. 145 1374 doi: 10.1149/1.1838468 [21] Sameshima S, Ichikawa T, Kawaminami M, Hirata Y 1999 Mater. Chem. Phys. 61 31 doi: 10.1016/S0254-0584(99)00109-1 [22] Nakajo A, Mueller F, Brouwer J, Favrat D 2012 Int. J. Hydrogen Energy 37 9249 doi: 10.1016/j.ijhydene.2012.03.043 [23] Nakajo A, Mueller F, Brouwer J, Favrat D 2012 Int. J. Hydrogen Energy 37 9269 doi: 10.1016/j.ijhydene.2012.03.023 [24] Petruzzi L, Cocchi S, Fineschi F 2003 J. Power Sources 118 96 doi: 10.1016/S0378-7753(03)00067-3 [25] Nakajo A, Kuebler J, Faes A, et al. 2012 Ceram. Int. 38 3907 doi: 10.1016/j.ceramint.2012.01.043 [26] Chatterjee A, Sharma G, Varshney J, Neogy S, Singh R N 2017 Mater. Sci. Eng. 684 626 doi: 10.1016/j.msea.2016.12.052 [27] Nakajo A, Stiller C, Harkegard G, Bolland O 2006 J. Power Sources 158 287 doi: 10.1016/j.jpowsour.2005.09.004 [28] Tada H, Paris P C, Irwin G R 1973 The Stress Analysis of Cracks Handbook (New York: ASME Press) p30 [29] 朱传锐 2010 硕士学位论文 (郑州: 河南理工大学) Zhu C Y 2010 M. S. Thesis (Zhengzhou: Henan Polytechnic University [30] 陈浩 2022 博士学位论文 (兰州: 兰州大学) Chen H 2022 Ph. D. Dissertation (Lanzhou: Lanzhou University [31] Junya K, Hirohisa S, Katsuhiro K, Toshio N 2004 J. Alloys Compd. 365 253 doi: 10.1016/S0925-8388(03)00640-6 [32] Pihlatie M, Kaiser A, Mogensen M 2009 J. Eur. Ceram. Soc. 29 1657 doi: 10.1016/j.jeurceramsoc.2008.10.017 [33] Biswas S, Nithyanantham T, Saraswathi N, Bandopadhyay S 2009 J. Mater. Sci. 44 778 doi: 10.1007/s10853-008-3141-9 [34] Chen T, Yao C, Hu L, Huang C, Li X 2019 Thin Wall. Struct 143 143106196 [35] El-Emam M H, Salim A H, Sallam M E H 2016 J. Struct. Eng. 143 04016229 -
计量
- 文章访问数: 143
- HTML全文浏览数: 143
- PDF下载数: 2
- 施引文献: 0