首页
登录
注册
-
石墨烯自发明以来, 以其高迁移率、高导热性和高机械强度等优异的性能而受到高度关注[1–3]. 并且石墨烯场效应晶体管(graphene field effect transistors, GFET)因其优异的性能, 在器件和电路中都具有巨大的应用潜力. 所以一些关于GFET的理论问题和实际问题一直被研究[4,5], 其中GFET的可靠性问题是一个研究重点. 石墨烯材料是单层原子层, 具有非常高的比表面积, 并且电荷都在其表面, 非常容易受到外界环境的影响[6,7]. 最显著的表现就是狄拉克电压(VDirac)的移动, VDirac代表了石墨烯的导带和价带相交的狄拉克点的电压值, 当VG＞VDirac时, 石墨烯中的载流子为电子, 当VG＜VDirac时, 石墨烯中的载流子为空穴. 因此VDirac的位置是GFET非常重要的信息之一, 所以哪些因素会影响GFET的VDirac的移动一直是人们非常关注的问题[8].
近年来, 研究人员对GFET的可靠性进行实验研究. 2014年, Feng等[9]研究了温度和栅极扫描范围对背栅结构GFET的电学特性的影响, 发现, 石墨烯的狄拉克电压VDirac随着温度的上升逐渐由正向0 V移动. 并且随着温度和栅极电压扫描范围的增大, GFET的回滞曲线和VDirac的位置都出现了滞后的现象. 他们把原因归结于温度和栅极电压的共同影响, 背栅结构的GFET中界面陷阱电荷的产生, 以及石墨烯/氧化层表面的氧化还原反应和氧化层中离子位移产生的结果. 2017年, Zhang等[10]研究了埋栅结构的GFET转移特性对栅压的依赖, 实验结果表明, 在测试GFET的转移特性曲线时, 栅压连续的正向或负向扫描会增大狄拉克点电压值. 并且转移特性曲线测试前, 栅极电压保持的时间增长会使得转移特性曲线测试中的狄拉克电压逐渐向正方向漂移. 指出狄拉克电压的大小与栅极电压的大小和保持的时间有关, 并把原因归结于电子注入衬底的陷阱中所造成的.
综上所述, GFET可靠性研究对于顶栅结构的GFET器件在不同偏置电压条件下的电应力实验研究不足. 因此本文针对顶栅结构的GFET器件在不同偏置电压条件下进行电应力实验, 研究GFET的电学性能的退化规律. 在此基础上结合TCAD数值模拟研究其损伤机制.
-
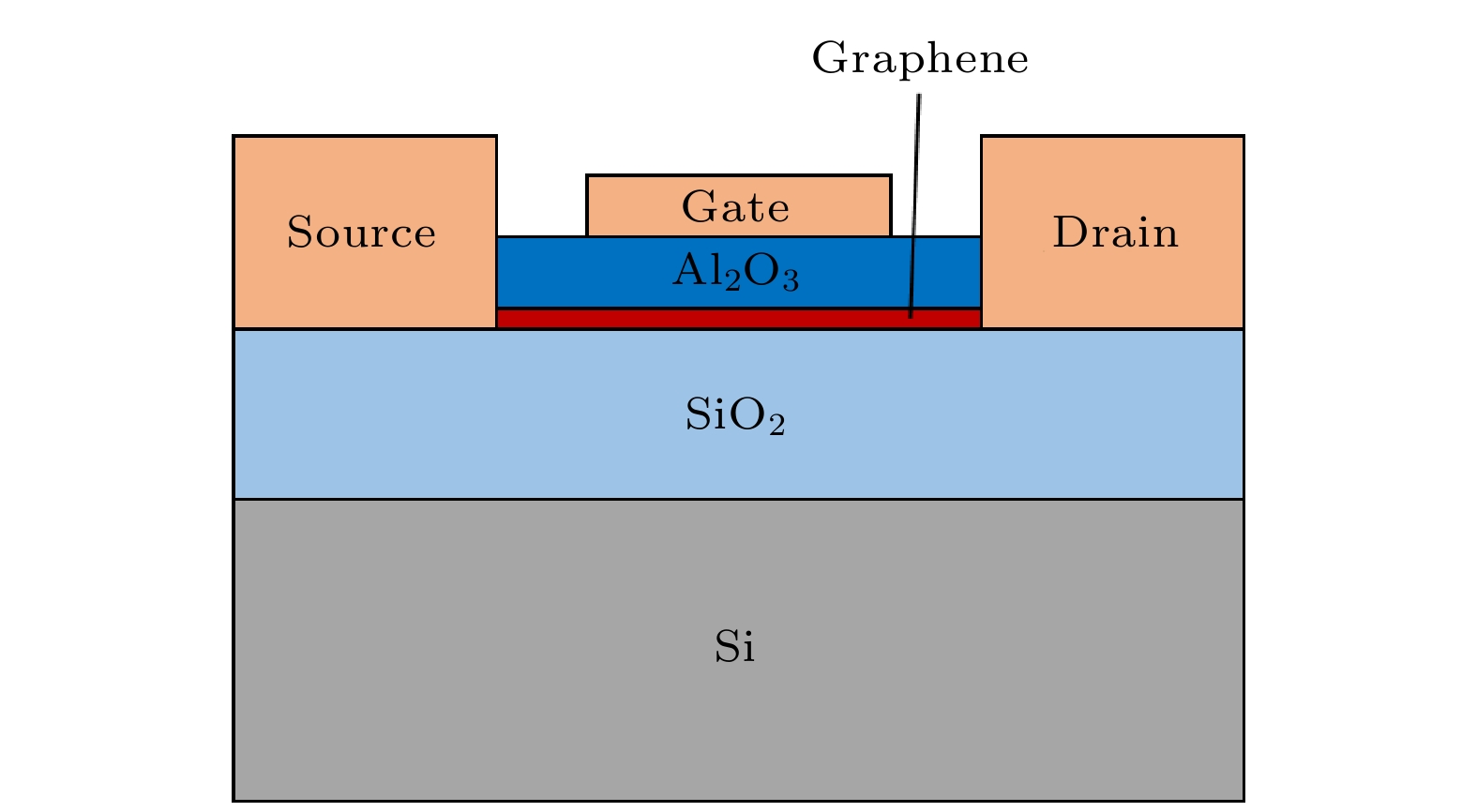
研究对象是顶栅结构的石墨烯场效应晶体管. 器件结构如图1所示, GFET的石墨烯尺寸为100 μm×100 μm, 栅极氧化层是20 nm厚的Al2O3, 衬底是由P型Si和90 nm厚的SiO2构成. 单层石墨烯采用化学气相沉积(chemical vapor deposition, CVD)和聚合物辅助转印进行生长、转移.
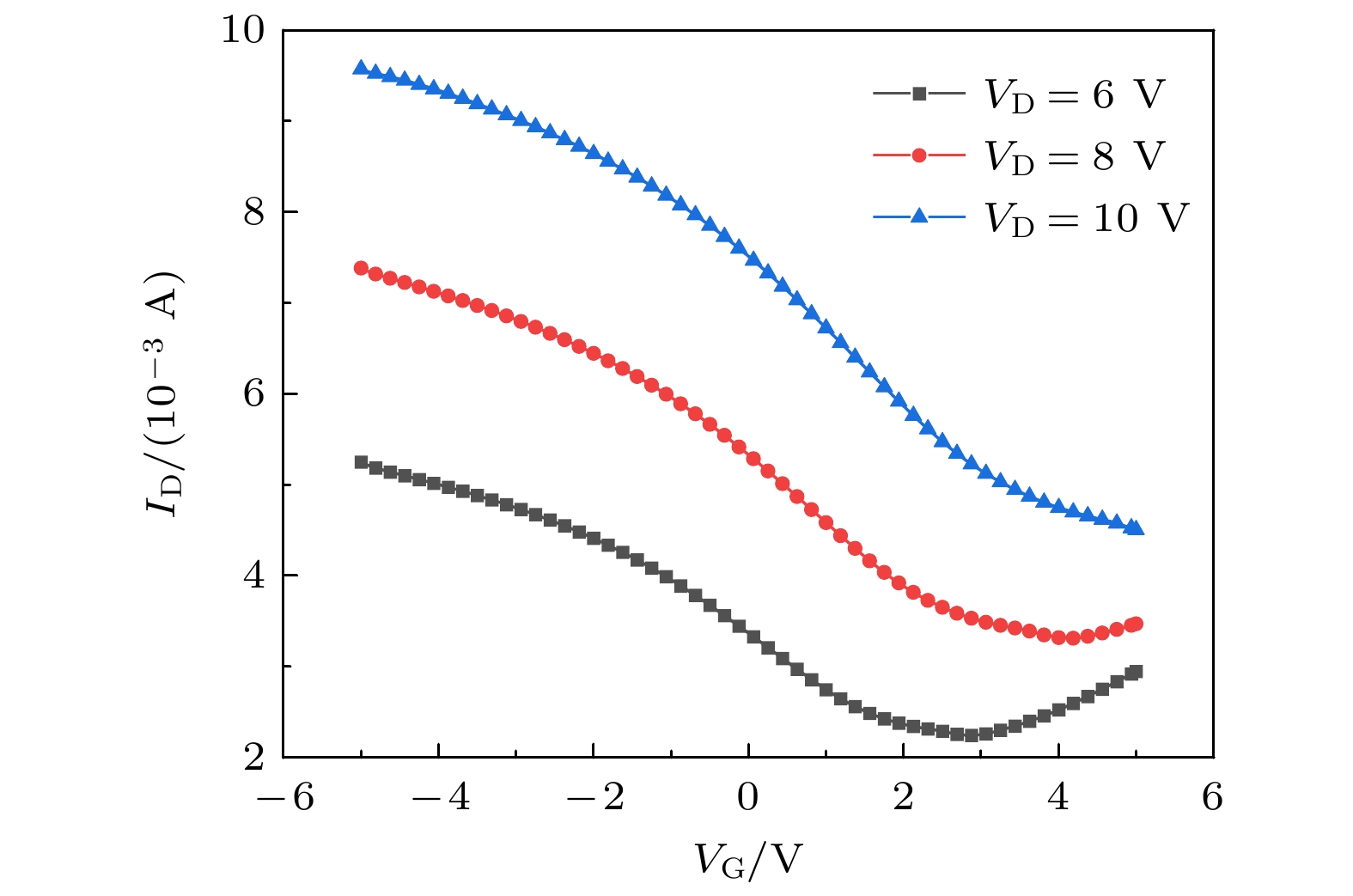
电应力实验及电参数测试采用B1500半导体分析仪进行. 对GFET进行多次转移特性曲线测试. 转移特性曲线测试的条件为: 栅极电压VG扫描范围为–5—+5 V, 源极电压VS接地, 漏极电压VD则从20 mV逐渐增大. 如图2所示, 随着漏极电压的逐渐增大, GFET的VDirac逐渐向正方向漂移, 这表明空穴掺杂逐渐增强, P型掺杂逐渐增强, N型掺杂逐渐减弱[11,12]. GFET的电流逐渐增大, 因为逐渐增大的电压产生越来越强的电场, 增强的电场给电子足够大的能量, 使得电子能挣脱石墨烯的束缚, 逃逸出石墨烯, 导致器件中的空穴掺杂增强, 载流子浓度增大, 电流增大[13,14]. 而增大的电流会导致石墨烯温度上升, 晶格的振动越来越剧烈, 也会导致逃逸的电子数量增多[15,16], 使得石墨烯的空穴掺杂增强, 载流子浓度增加, 电流增大.
电应力实验的偏置电压条件共分为3组, 分别为栅极电应力(VG = –10 V, VD = 0 V, VS = 0 V)、漏极电应力(VG = 0 V, VD = –10 V, VS = 0 V)、栅极与漏极电压同时施加的电应力(VG = –10 V, VD = –10 V, VS = 0 V). 电应力实验总共持续时长为1000 s, 电应力期间包含5个测试点. 当电应力累积时间达到测试点时, 半导体分析仪就会自动在设置好的转移特性曲线测试条件下测试一次GFET的转移特性曲线, 并保存数据. 电应力实验测试条件如表1所示.
-
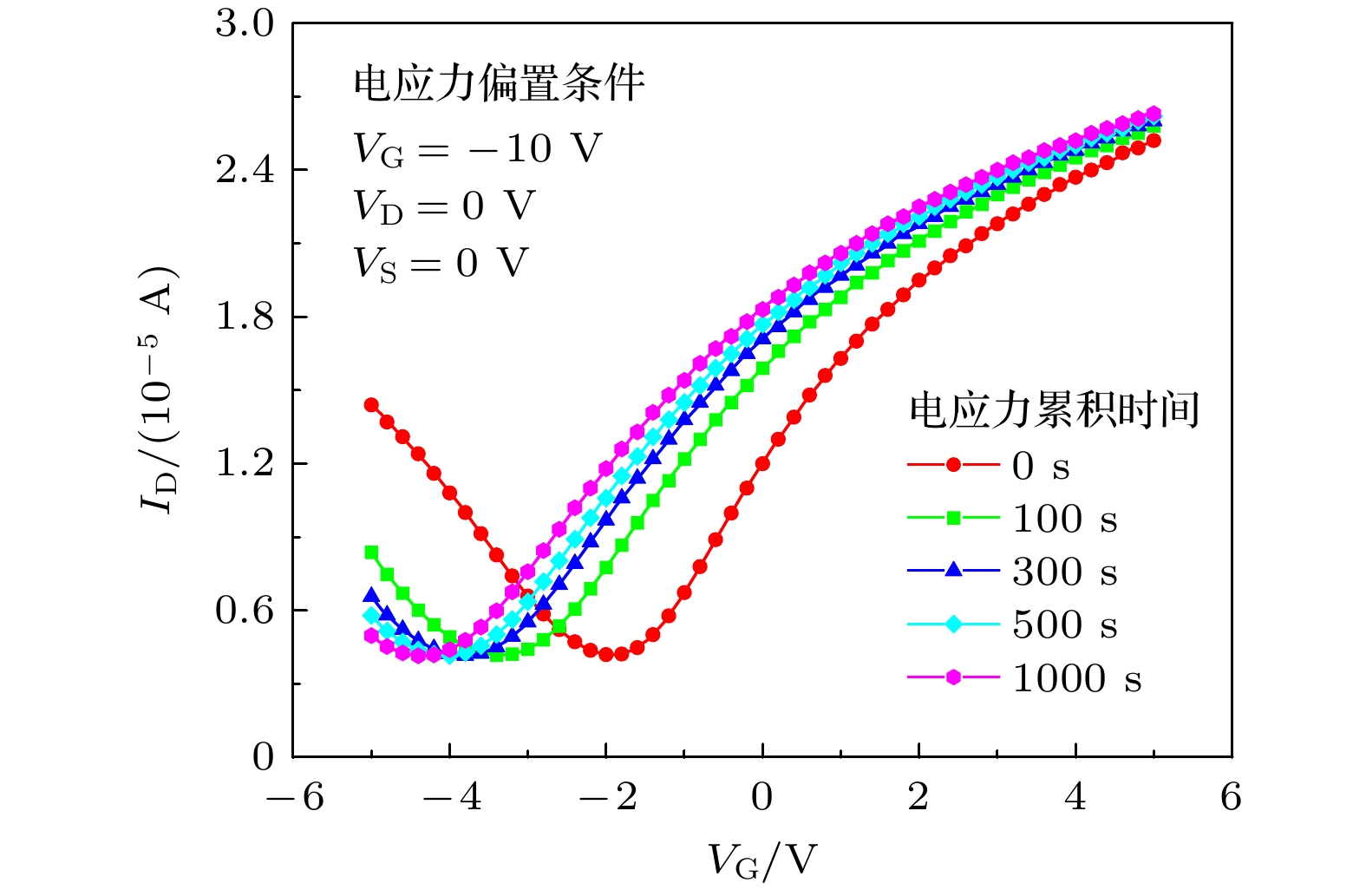
图3—图5分别为GFET在3种不同偏置电压条件下, 器件的转移特性曲线随电应力累积时间到1000 s的变化趋势. 如图3所示, GFET在栅极电应力(VG = –10 V, VD = 0 V, VS = 0 V)作用下, 随着电应力时间的逐渐累积, 器件的转移特性曲线逐渐向负方向移动. VDirac向负方向漂移, 电应力测试前为–2 V, 电应力测试后为–4.46 V, 变化量为2.46 V.
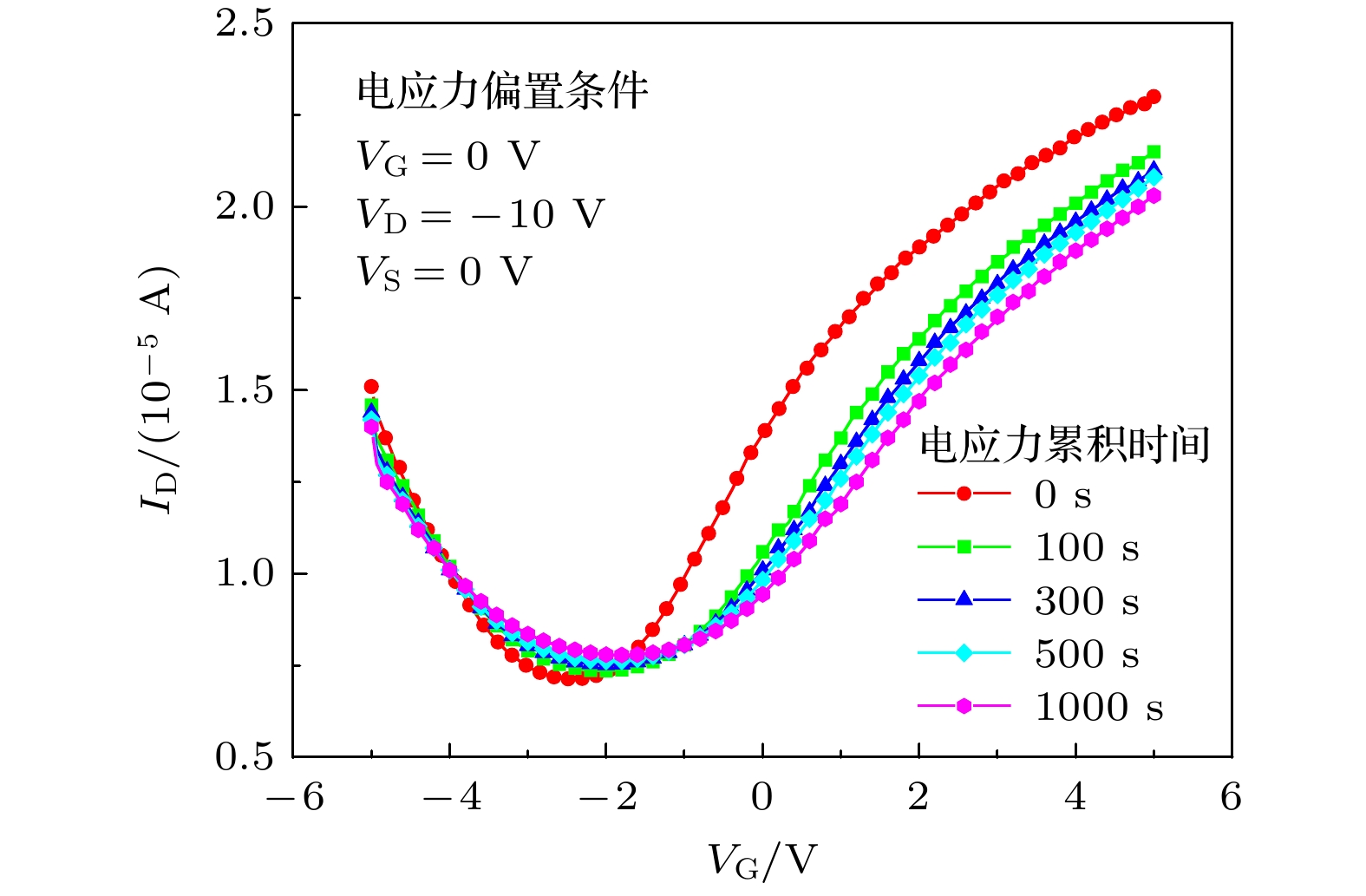
如图4所示, GFET在漏极电应力(VG = 0 V, VD = –10 V, VS = 0 V)作用下, 转移特性曲线逐渐向正方向移动. VDirac向正方向漂移, 电应力测试前为–2.48 V, 电应力测试后为–1.94 V, 变化量为0.54 V. GFET器件VDirac的漂移方向与栅极电应力条件的漂移方向相反. 分析原因可能是不同电压偏置条件下的电应力产生陷阱电荷的带电类型差异所造成的结果.
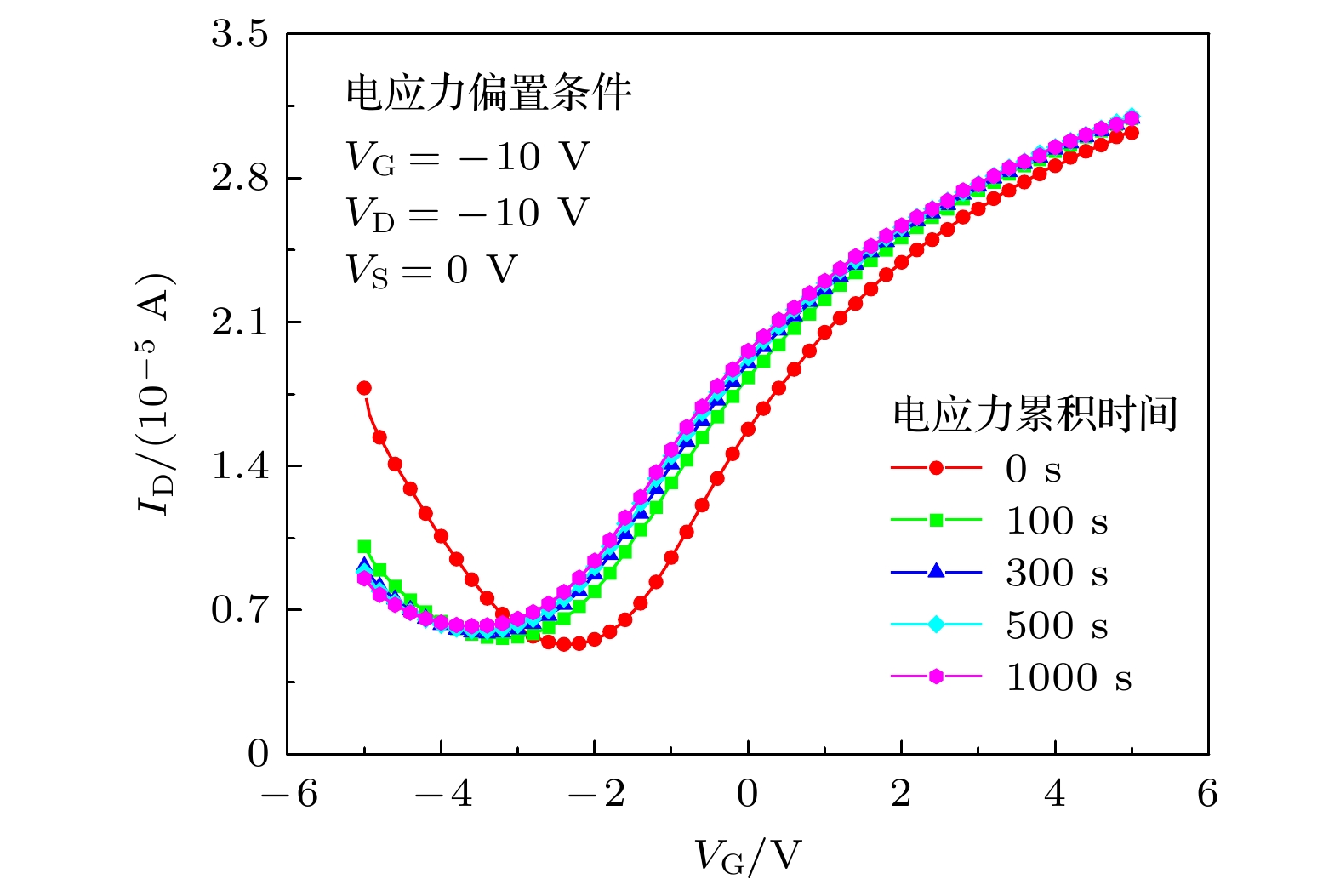
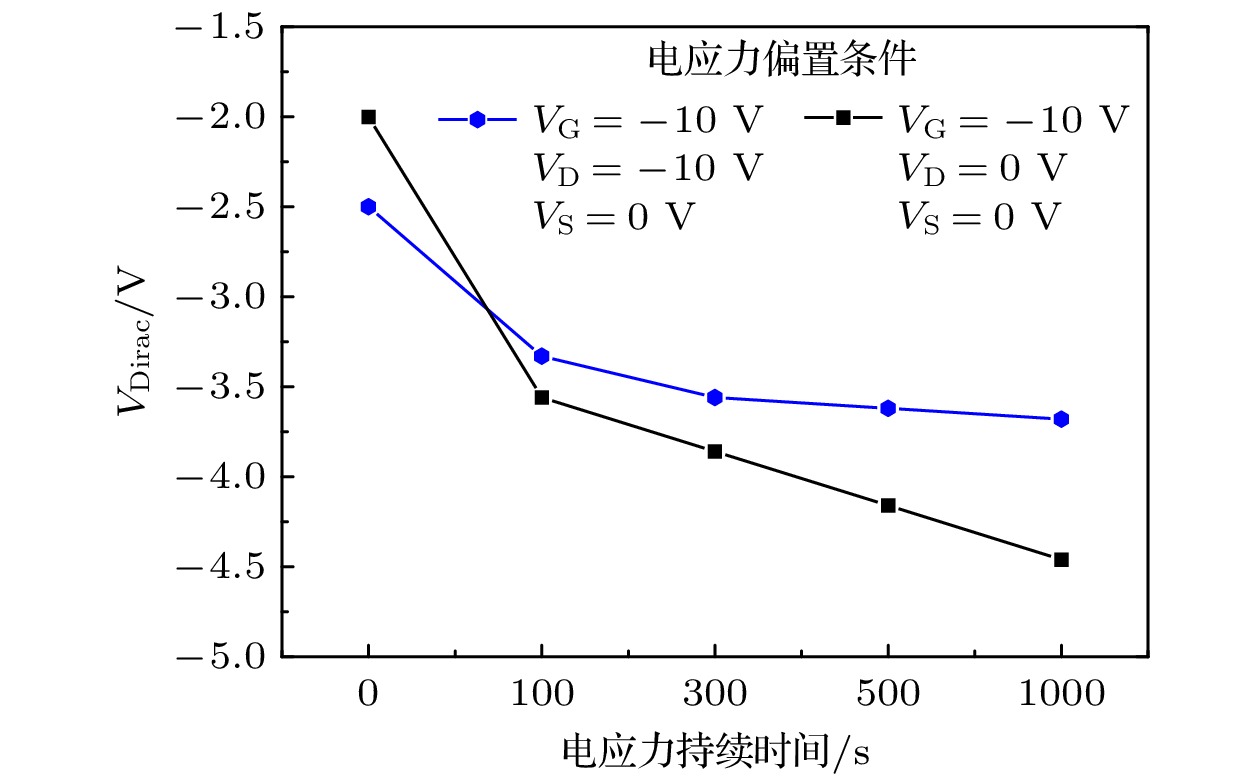
如图5所示, GFET在栅极和漏极电压同时 施加的电应力(VG = –10 V, VD = –10 V, VS = 0 V)作用下, 转移特性曲线逐渐向负方向移动. VDirac向负方向漂移, 电应力测试前为–2.5 V, 电应力测试后为–3.68 V, 变化量为1.18 V, 对比发现变化量明显要小于栅极电应力条件下的变化量.
图6给出了GFET的VDirac在两种不同的偏置电压条件下(栅极电应力、栅极和漏极电压同时施加的电应力)随电应力累积时间的变化趋势. 对比GFET在两种不同的偏置电压条件下VDirac的变化量, 发现栅极电应力诱导器件VDirac的退化趋势更加明显. 这可能是因为在栅极和漏极电压同时施加的电应力实验中产生的两种带电类型的陷阱电荷, 引起VDirac的漂移, 产生相互抵消的作用, 导致VDirac退化程度减小.
计算GFET在不同偏置电压条件下的电应力实验中, 每个时间测试点对应的载流子迁移率. GFET的跨导Gm与载流子迁移率的关系如(1)式所示[17,18]:
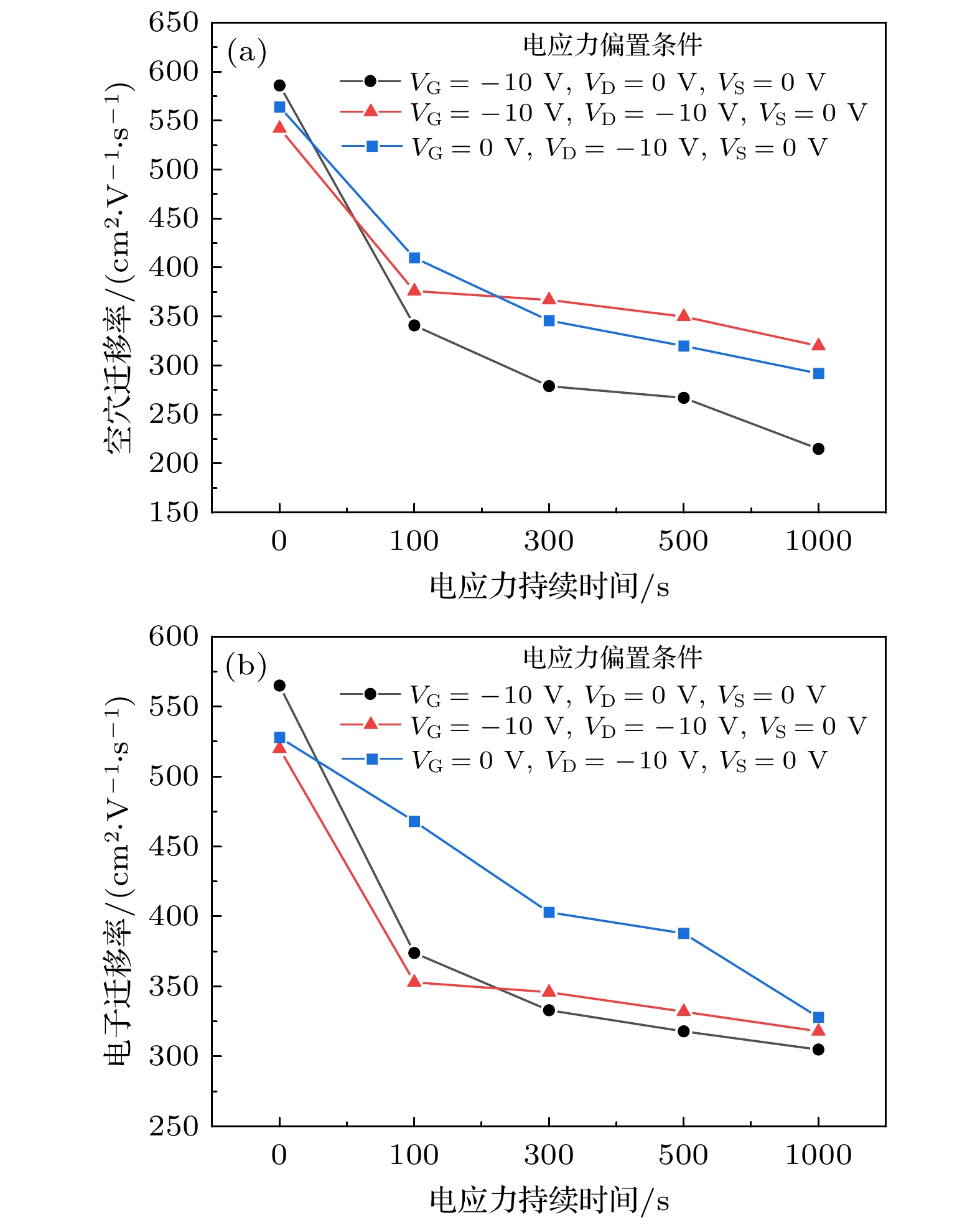
其中, μ为载流子迁移率, L/W为长宽比, CG为栅介质的电容, VD为漏极电压, 跨导Gm为转移特性曲线的斜率. 详细计算参数L/W长宽比为1, CG栅介质电容为3.54×10–7 F/cm2, VD漏极电压为20 mV. 如图7所示, 不同偏置电压条件下的电应力实验中, GFET的空穴迁移率和电子迁移率均随着电应力累积时间的延长而逐渐降低. 载流子迁移率与氧化物陷阱电荷之间的关系为[19]:
其中, μc为受库仑散射作用的载流子迁移率, Not为氧化物陷阱电荷, μSR为受短程散射影响的载流子迁移率, Qgc为电荷密度, Eeff为有效电场强度, α, β, N0, Q0为拟合参数. 由(2)式和(3)式可以得出, 载流子迁移率的退化是由于在电应力实验中产生了氧化物陷阱电荷, 增加了散射位点, 导致库仑散射作用增强, 载流子迁移率降低[17–20].
其中μ为实验后的载流子迁移率,
$ \Delta {N}_{{\mathrm{i}}{\mathrm{t}}} $ 为新产生的界面陷阱电荷, μ0为实验前的载流子迁移率. 由(4)式得出, 新产生的界面陷阱电荷导致载流子迁移率的降低.GFET在不同偏置电压条件下的电应力实验中, 产生了氧化物陷阱电荷和界面陷阱电荷, 增加了散射位点, 其库仑散射增强. 导致GFET的电子迁移率和空穴迁移率均随着电应力累积时间的延长而逐渐降低.
-
对于栅极电应力, 栅极电压为负, 电场方向垂直于沟道并指向栅极, 使得石墨烯沟道中的空穴浓度增大, 同时在负栅压的作用下, 空穴会隧穿经过石墨烯/栅极氧化层的界面并进入栅极氧化层中, 被材料里的缺陷俘获, 形成带正电荷的氧化物陷阱电荷. 并且沟道中的空穴受电场的影响会累积在石墨烯/栅极氧化层的界面处, 导致界面陷阱更容易俘获空穴, 形成带正电荷的界面陷阱电荷. 产生的陷阱电荷的带电类型一致, 对器件产生叠加效果, 导致GFET的VDirac向负方向漂移量更大, 退化程度更加明显[23–25].
对于漏极电应力, 漏极一端电压为负, 存在由沟道指向漏极的电场方向, 使得石墨烯沟道中的电子浓度增大, 导致石墨烯/氧化层界面处的陷阱更容易俘获电子[10,24], 形成带负电荷的界面陷阱电荷, 导致GFET的VDirac向正方向移动. 栅极电应力与漏极电应力产生的陷阱电荷带电类型不同, 因此造成GFET的VDirac漂移方向相反.
对于栅极和漏极电压同时施加的电应力, 在器件中既有垂直于沟道并指向栅极的电场, 也存在由沟道指向漏极的电场. 使得器件沟道中的空穴浓度和电子浓度均有所增大, 同时在电场的作用下, 空穴会隧穿进入栅极氧化层中形成带正电荷的氧化物陷阱电荷, 在石墨烯/栅极氧化层的界面形成带正电荷的界面陷阱电荷. 电子更容易被石墨烯/氧化层界面处的陷阱俘获, 形成带负电荷的界面陷阱电荷. 因此产生的陷阱电荷所带电类型不同, 对GFET的VDirac的漂移具有相互抵消的效果. 所以在栅极和漏极电压同时施加的电应力作用下, GFET的VDirac的漂移量小于栅极电应力条件下的漂移量, 退化程度减小.
为了更好地解释陷阱电荷带电类型的差异会对顶栅GFET器件VDirac的漂移方向和退化程度产生不同的影响. 结合TCAD仿真工具研究陷阱电荷对GFET的影响, 在TCAD仿真工具中建立顶栅GFET器件的二维结构模型, 石墨烯沟道长度为100 μm, 石墨烯材料则是通过修改多晶硅的材料参数完成代替[26,27]. 仿真过程中, 在GFET的石墨烯/氧化层界面处加入带正电荷的固定陷阱电荷和带负电荷的固定陷阱电荷, 用来模拟在不同偏置电压条件下, 电应力产生陷阱电荷带电类型的差异对GFET的VDirac退化影响.
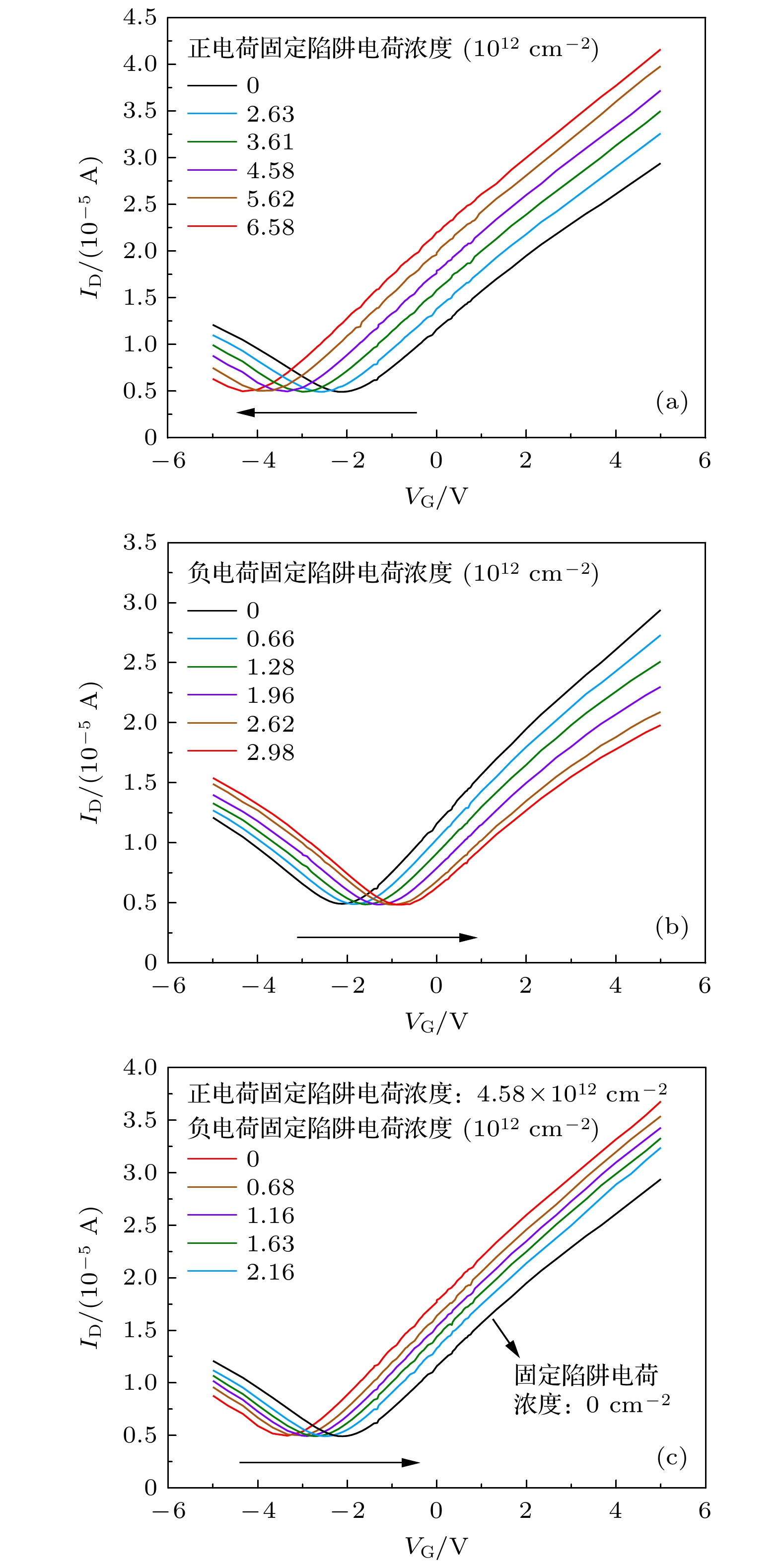
图8为TCAD仿真结果, 给出了带不同电性的固定陷阱电荷对GFET的转移特性曲线的影响. 如图8(a)所示, 随着带正电荷的固定陷阱电荷浓度的升高, 器件的转移特性曲线逐渐向负向移动, VDirac也逐渐向负方向漂移. 如图8(b)所示, 随着带负电荷的固定陷阱电荷浓度的升高, 器件的转移特性曲线逐渐向正方向移动, VDirac也逐渐向正方向漂移. 对比TCAD仿真结果, 证明陷阱电荷带电类型的差异是导致GFET的VDirac向不同的方向漂移的原因. 为了验证带不同电性的陷阱电荷会对GFET的VDirac漂移量有抵消的效果, 图8(c)中最右边的黑色转移特性曲线未添加固定陷阱电荷, 其余的转移特性曲线添加了相同浓度的带正电荷的固定陷阱电荷. 随着带负电荷的固定陷阱电荷浓度从0 cm–2逐渐增大, 图中的转移特性曲线逐渐向正方向移动, 逐渐靠近未添加固定陷阱电荷的转移特性曲线. 通过TCAD仿真结果发现, 在带正电荷的固定陷阱电荷和带负电荷的固定陷阱电荷共同作用下, GFET的VDirac漂移量逐渐减小. 证明带不同电性的陷阱电荷对GFET的VDirac漂移量会产生抵消作用.
-
本文研究了顶栅结构的GFET器件在不同的电应力条件作用下, 器件电学性能的退化规律. 发现GFET的载流子迁移率随着电应力累积时间的延长不断退化, 但不同偏置电压条件的电应力作用下, GFET的VDirac的漂移方向和退化程度不同. 分析认为, 不同偏置电压条件的电应力作用会在GFET中产生不同方向的电场, 影响沟道中载流子浓度和分布. 在电场方向的作用下, 空穴和电子隧穿进入氧化层, 被材料中的缺陷俘获, 形成氧化物陷阱电荷, 并且还会促使石墨烯/氧化层界面处的陷阱俘获空穴和电子, 形成界面陷阱电荷, 这是造成GFET的载流子迁移率和VDirac退化的主要原因. 同时产生的陷阱电荷所带电类型的差异, 是导致GFET的VDirac的漂移方向和退化程度不同的主要原因. 结合TCAD仿真模拟表明, 带正电荷的陷阱电荷导致GFET的VDirac向负方向漂移, 而带负电荷的陷阱电荷会导致GFET的VDirac向正方向漂移, 并且当两种陷阱电荷同时存在时, 会对GFET的VDirac漂移量产生抵消作用, 证明陷阱电荷的带电类型差异对GFET的VDirac产生不同的退化影响, 为GFET在实际应用中提供参考和帮助.
石墨烯场效应晶体管在不同偏置电压条件下的电应力可靠性
Electrical stress reliability of graphene field effect transistor under different bias voltages
-
摘要: 本文以顶栅结构的石墨烯场效应晶体管(graphene field effect transistors, GFET)为研究对象, 开展了不同偏置电压条件下的电应力可靠性研究. 实验结果表明, 在不同偏置电压条件的电应力作用下, GFET的载流子迁移率随着电应力时间的延长均不断退化, 而不同偏置电压条件的电应力对狄拉克电压(VDirac)的漂移方向和退化程度的影响不同; 栅极电应力与漏极电应力造成器件的VDirac漂移方向相反, 且栅极电应力要比栅极和漏极电压同时施加的电应力导致GFET的VDirac退化程度更加明显. 分析原因表明, 不同偏置电压条件下的电应力实验在器件中产生的电场方向不同, 从而会影响载流子浓度和移动方向. 诱导沟道中的电子和空穴隧穿进入氧化层, 被氧化层中缺陷和石墨烯/氧化层界面处的陷阱俘获, 形成氧化物陷阱电荷和界面陷阱电荷, 从而导致GFET的载流子迁移率降低. 而电应力产生陷阱电荷的带电类型差异是造成VDirac漂移方向不同的主要原因. 论文结合TCAD仿真, 进一步揭示了电应力感生陷阱电荷对GFET的VDirac产生影响的仿真模型. 相关研究为石墨烯器件的实际应用提供了数据和理论支撑.Abstract: In this paper, graphene field effect transistors (GFETs) with the top-gate structure are taken as the research object. The electrical stress reliabilities are studied under different bias voltage conditions. The electrical pressure conditions are gate electrical stress (VG = –10 V, VD = 0 V, and VS = 0 V), drain electric stress (VD = –10 V, VG = 0 V, and VS = 0 V), and electrical stresses applied simultaneously by gate voltage and drain voltage (VG = –10 V, VD = –10 V, VS = 0 V). Using a semiconductor parameter analyzer, the transfer characteristic curves of GFETs before and after electrical stress are obtained. At the same time, the carrier migration and the Dirac voltage VDirac degradation are extracted from the transfer characteristic curves. The test results show that under different electrical pressures, the carrier mobility of GFETs degrades continuously with the increase of electric stress time. Different electrical pressure conditions have varying effects on the drift direction and degradation of VDirac: gate electrical stress and drain electrical stress cause VDirac drift of the device in opposite directions, and the gate electrical stress is greater than the electrical stress applied by both gate voltage and drain voltage, leading to VDirac degradation of GFETs. An analysis of the causes indicates that different electrical stresses produce different electric field directions in the device, which can affect the carrier concentration and movement direction. Electrons and holes in the channel are induced and tunnel into the oxide layer, and they are captured by trap charges in the oxide layer and at the interface between graphene and oxide, forming oxide trap charges and interface trap charges. This is the main reason for reducing carrier mobility of GFET. Different electric field directions under different electric stresses produce positively charged trap charges and negatively charged trap charges. The difference in the type of trap charge banding is the main reason for the different directions of VDirac drift in GFETs. When both trap charges coexist, they have a canceling effect on the VDirac drift of the GFETs. Finally, by combining TCAD simulation the simulation model of the influence of electrical stress induced trap charge on the VDirac generation of GFET is further revealed. The result demonstrates that the differences in the type of trap charge banding have different degradation effects on the VDirac of GFETs. The related research provides data and theoretical support for putting graphene devices into practical application.
-
Key words:
- graphene field effect transistors /
- electrical stress /
- VDirac /
- carrier mobility .
-
-
图 2 GFET的转移特性曲线在不同漏极电压下的变化趋势
Figure 2. The variations of the transfer characteristic curve of GFET under different drain voltages.
图 3 栅极电应力下, GFET的转移特性曲线随电应力累积时间的变化趋势
Figure 3. Variations of GFET transfer characteristic curve with the accumulation time of electrical stress under gate voltage bias condition.
图 5 栅极和漏极电压同时施加的电应力下, GFET转移特性曲线随电应力累积时间的变化趋势
Figure 5. Variations of GFET transfer characteristic curve with the accumulation time of electrical stress under the condition of electrical stress applied by both the gate and drain voltages.
图 4 漏极电应力下, GFET的转移特性曲线随电应力累积时间的变化趋势
Figure 4. Variations of GFET transfer characteristic curves with the accumulation time of electrical stress under drain voltage bias conditions.
图 6 VDirac随着电应力累积时间的变化趋势
Figure 6. The variations of VDirac with the accumulation time of electrical stress.
图 7 载流子迁移率随电应力累积时间的变化趋势 (a)空穴迁移率随电应力累积时间的变化趋势; (b)电子迁移率随电应力累积时间的变化趋势
Figure 7. The variations of carrier mobility with the accumulation time of electrical stress: (a) The variations of hole mobility with the accumulation time of electrical stress; (b) the variations of electron mobility with the accumulation time of electrical stress.
图 8 TCAD仿真结果 (a)带正电荷的固定陷阱电荷对GFET转移特性曲线的影响; (b)带负电荷的固定陷阱电荷对GFET转移特性曲线的影响; (c)带正电荷和带负电荷的固定陷阱电荷同时对GFET转移特性曲线的影响
Figure 8. TCAD simulation results: (a) Effect of a positively charged fixed trap charge on the transfer characteristic curve of GFET device; (b) effect of negatively charged fixed trap charge on the transfer characteristic curve of GFET device; (c) the effect of both positively charged and negatively charged fixed trap charges on the transfer characteristic curve of GFET devices.
表 1 电应力实验测试条件
Table 1. Electrical stress test conditions.
偏置电压条件 电应力测试时间点 转移特性曲线测试条件 栅极电应力(VG = –10 V, VD = 0 V, VS = 0 V) 0 s, 100 s, 300 s,
500 s, 1000 sVG 从–5 V扫到5 V,
VD 为20 mV, VS 接地漏极电应力 (VG = 0 V, VD = –10 V, VS = 0 V) 栅极电压与漏极电压同时施加的电应力
(VD = –10 V, VD = –10 V, VS = 0 V)
下载: 导出CSV
-
[1] Novoselov K S, Geim A K, Morozov S V, Jiang D, Zhang Y, Dubonos S V, Grigorieva I V, Firsov A A 2004 Science 306 666 doi: 10.1126/science.1102896 [2] 陈智, 王子欧, 李亦清, 李有忠, 毛凌锋 2012 微电子学与计算机 29 154 Chen Z, Wang Z O, Li Y Q, Li Y Z, Mao L F 2012 Microelectron. Comput. 29 154 [3] Radsar T, Khalesi H, Ghods V 2021 Superlattices Microstruct. 153 106869 doi: 10.1016/j.spmi.2021.106869 [4] Zhang Q W 2018 Ph. D. Dissertation(Chengdu: University of Electronic Science and Technology of China) (in Chinese)[张庆伟 2018 博士学位论文 (成都: 电子科技大学)] [5] Xu J, Gu Z Y, Yang W X, Wang Q L, Zhang X B 2018 Nanoscale Res. Lett. 13 311 doi: 10.1186/s11671-018-2736-6 [6] Yavari F, Kritzinger C, Gaire C, Song L, Gulapalli H, Borca-Tasciuc T, Ajayan P M, Koratkar N 2010 Small 6 2535 doi: 10.1002/smll.201001384 [7] Docherty C J, Lin C T, Joyce H J, Nicholas R J, Herz L M, Li L J, Johnston M B 2012 Nat. Commun. 3 1228 doi: 10.1038/ncomms2235 [8] Wang R, Wang S, Zhang D D, Li Z J, Fang Y, Qiu X H 2011 ACS Nano 5 408 doi: 10.1021/nn102236x [9] Feng T T, Xie D, Li G, Xu J L, Zhao H M, Ren T L, Zhu H W 2014 Carbon 78 250 doi: 10.1016/j.carbon.2014.07.001 [10] 张庆伟, 李平, 王刚, 曾荣周, 王恒, 周金浩 2017 微电子学与计算机 34 36 Zhang Q W, Li P, Wang G, Zeng R Z, Wang H, Zhou J H 2017 Microelectron. Comput. 34 36 [11] Ghosh S, Arroyo M 2013 J. Mech. Phys. Solids 61 235 doi: 10.1016/j.jmps.2012.07.002 [12] Zhao P, Chauhan J, Guo J 2009 Nano Lett. 9 684 doi: 10.1021/nl803176x [13] 陈卫 2017 博士学位论文 (长沙: 国防科技大学) Cheng W 2017 Ph. D. Dissertation (Chang Sha: National University of Defense Technology [14] Liu P, Wei Y, Jiang K L, Sun Q, Zhang X B, Fan S S, Zhang S F, Ning C G, Deng J K 2006 Phys. Rev. B 73 235412 doi: 10.1103/PhysRevB.73.235412 [15] Li J, Zhang Z H, Wang D, Zhu Z, Fan Z Q, Tang G P, Deng X Q 2014 Carbon 69 142 doi: 10.1016/j.carbon.2013.11.076 [16] Chiu H Y, Perebeinos V, Lin Y M, Avouris P 2010 Nano Lett. 10 4634 doi: 10.1021/nl102756r [17] 李济芳, 郭红霞, 马武英, 宋宏甲, 钟向丽, 李洋帆, 白如雪, 卢小杰, 张凤祁 2024 物理学报 73 058501 doi: 10.7498/aps.73.20231829 Li J F, Guo H X, Ma W Y, Song H J, Zhong X L, Li Y F, Bai R X, Lu X J, Zhang F Q 2024 Acta Phys. Sin. 73 058501 doi: 10.7498/aps.73.20231829 [18] Zhang Y F, Peng S Y, Wang Y H, Guo L X, Zhang X Y, Huang H Q, Su S H, Wang X W, Xue J M 2022 J. Phys. Chem. Lett. 13 10722 doi: 10.1021/acs.jpclett.2c02955 [19] Esqueda I S, Cress C D, Anderson T J, Ahlbin J R, Bajura M, Fritze M, Moon J S 2013 Electronics 2 234 doi: 10.3390/electronics2030234 [20] Kang C G, Lee Y G, Lee S K, Park E, Cho C, Lim S K, Hwang H J, Lee B H 2013 Carbon 53 182 doi: 10.1016/j.carbon.2012.10.046 [21] Petrosjanc K O, Adonin A S, Kharitonov I A, Sicheva M V 1994 Proceedings of 1994 IEEE International Conference on Microelectronic Test Structures 1994-03 pp126–129 [22] Galloway K F, Gaitan M, Russell T J 1984 IEEE Transactions on Nuclear Science 31 1497 doi: 10.1109/TNS.1984.4333537 [23] Jain S, Shinde V, Gajarushi A, Gupta A, Rao V R 2018 IEEE 13TH Nanotechnology Materials and Devices Conference (NMDC) New York, US October 14–17, 2018 pp353–356 [24] 谷文萍, 郝跃, 张进城, 王冲, 冯倩, 马晓华 2009 物理学报 58 511 doi: 10.7498/aps.58.511 Gu W P, Hao Y, Zhang J C, Wang C, Feng Q, Ma X H 2009 Acta Phys. Sin. 58 511 doi: 10.7498/aps.58.511 [25] Childres I, Jauregui L A, Foxe M, Tian J, Jalilian R, Jovanovic I, Chen Y P 2010 Appl. Phys. Lett. 97 173109 doi: 10.1063/1.3502610 [26] Ismail M A, Zaini K M M, Syono M I 2019 TELKOMNIKA (Telecommunication Computing Electronics and Control) 17 1845 doi: 10.12928/telkomnika.v17i4.12760 [27] Jeppson K 2023 IEEE Trans. Electron Devices 70 1393 doi: 10.1109/TED.2023.3239331 -
计量
- 文章访问数: 161
- HTML全文浏览数: 161
- PDF下载数: 3
- 施引文献: 0