-
近日, 中国科学技术大学研究团队[1]首次在三维超冷原子光晶格体系观测到费米-哈伯德模型(Fermi-Hubbard model)中的反铁磁相变, 文章在Nature发表并迅速引起广泛关注. 这项工作通过发展新型冷却技术、构建均匀的大尺寸三维光晶格(约8×105个格点)以及精确表征反铁磁结构因子, 展示了对体系中相互作用强度、温度和掺杂浓度的精确调控, 测量了反铁磁结构因子的相变临界标度行为, 成功观测到了费米-哈伯德模型中的反铁磁相变. 这项工作克服了量子模拟领域的多项世界级难题, 特别是在原子冷却方面取得了突破性进展. 鉴于费米-哈伯德模型在强关联电子体系中的重要性, 以及该模型中可能存在各种新奇的物态和低温物理性质[2,3], 这项工作无疑将促进对该模型更加广泛和深入的实验和理论研究, 为探索量子磁性与高温超导之间的联系提供了新的可能.
-
费米-哈伯德模型是研究强关联电子体系的“标准”模型, 其重要性可类比于统计物理学中的伊辛模型. 哈伯德模型最早由Hubbard, Kanamori和Gutzwiller在1963年提出[4–6], 用于描述过渡金属及其氧化物中的相互作用电子, 以及理解该体系中的磁性与金属-绝缘体转变等性质. 1986年铜基高温超导体的发现, 使得哈伯德模型开始受到研究者们的广泛关注: 铜基高温超导的母体为反铁磁莫特绝缘体, 也是半满填充的哈伯德模型(排斥相互作用)的基态; 同时, 基于铜基高温超导体的相图, 人们普遍认为掺杂的哈伯德模型有可能解释高温超导现象, 以及明晰量子磁性与高温超导机理之间的重要联系. 因而, 研究哈伯德模型的低温物理性质特别是自旋关联以及磁性性质被认为是破解高温超导谜题的关键.
单能带哈伯德模型的哈密顿量可表示为
其中,
$ i, j $ 为格点指标,$ \sigma =\uparrow , \downarrow $ 为自旋指标, 跃迁系数$ {t}_{ij} $ 包含最近邻(一般写为t)、次近邻等分量, U为在位库仑相互作用. 一般选择t作为能量单位, 因而哈伯德模型中的常见可调参数包括相互作用强度$ U $ 、次近邻跃迁系数t'和费米子填充数$ n $ . 在吸引相互作用($ U < 0 $ )下, 该模型在任意填充数都具有s波超导基态, 因而常被用于研究费米超流以及BCS (Bardeen-Cooper-Schrieffer)-BEC (Bose-Einstein condensation)渡越现象[7]. 在排斥相互作用($ U > 0 $ )时, 该模型在半满($ n=1 $ )、t' = 0以及二分晶格上存在反铁磁长程有序的基态: 其中对于类似三维简单立方晶格、无相互作用部分为金属(费米能级态密度为有限值或发散)的情形, 反铁磁长程序在无穷小$ U $ 就会出现; 而对于类似二维六角蜂窝晶格、无相互作用部分为半金属(费米能级态密度为0)的情形, 反铁磁长程序只在$ U $ 大于某个临界值才出现. 此外, 哈伯德模型在不同维度、不同晶格结构上的物理性质差异巨大. 例如,$ U > 0 $ 的哈伯德模型在三维存在由热涨落驱动的高温顺磁相到低温反铁磁长程有序(奈尔序)相的相变, 即反铁磁相变, 属于三维海森伯普适类[8]; 但是在二维体系由于更强的量子涨落, 该有限温相变不存在(即Mermin-Wigner定理[9]).自1990年代以来, 量子多体数值计算方法的发展和应用极大地促进了费米-哈伯德模型的理论研究[2,3]. 但是三维哈伯德模型的研究滞后于二维情形, 人们对该模型的完整相图(温度、次近邻跃迁、相互作用、填充数等)仍然知之甚少. 有多种数值计算方法研究过三维排斥哈伯德模型的有限温性质, 主要包括辅助场量子蒙特卡罗算法(AFQMC)[10–13]、动力学平均场理论(DMFT)及其扩展方法[14–17]和图形蒙特卡罗算法(DiagMC)[18–20]等. 这些研究工作主要集中于半满填充(
$ n=1 $ ), 且大部分都是研究该体系中的反铁磁相变, 也有研究体系单粒子谱学性质、热力学性质以及次近邻跃迁、质量不平衡、跃迁各向异性等因素对自旋关联性质的影响. 其中, 最新的AFQMC研究[13]得到了该模型中目前最准确的反铁磁转变温度的理论结果, 并通过结合热力学和动力学性质定出了该模型在顺磁相中金属-绝缘体渡越中3个不同区域(费米液体、渡越区、莫特绝缘体)的边界. 与之相对的, 偏离半满填充的理论研究则非常少. 已有的DMFT和$ {\mathrm{D}}{{\Gamma }}{\mathrm{A}} $ (DMFT的一种扩展算法) [16,17]和DiagMC[18]计算研究均表明三维哈伯德模型在半满附近具有类似于铜基高温超导相图中穹顶形状的长程磁有序区域, 且在偏高温和小掺杂区域为常见的奈尔序, 而在低温和较大掺杂区域则为非公度的自旋密度波序. 除此之外, 该体系在掺杂区域的热力学和动力学性质、是否存在赝能隙和奇异金属行为、基态是否存在超导长程序等基础而深刻的问题, 几乎没有任何可靠的理论和数值计算结果.值得关注的是, 在数值计算方面, 新的高精度算法的发展[19,21]极大地缓解了负符号问题的困扰, 从而让研究非半满哈伯德模型中基态和有限温的众多新奇物理现象成为可能. 例如, 近年来数值计算研究发现空穴掺杂下二维正方晶格哈伯德模型的基态存在自旋和电荷的条纹序[22], 以及d波超导长程序(仅在t' ≠ 0时)[23].
-
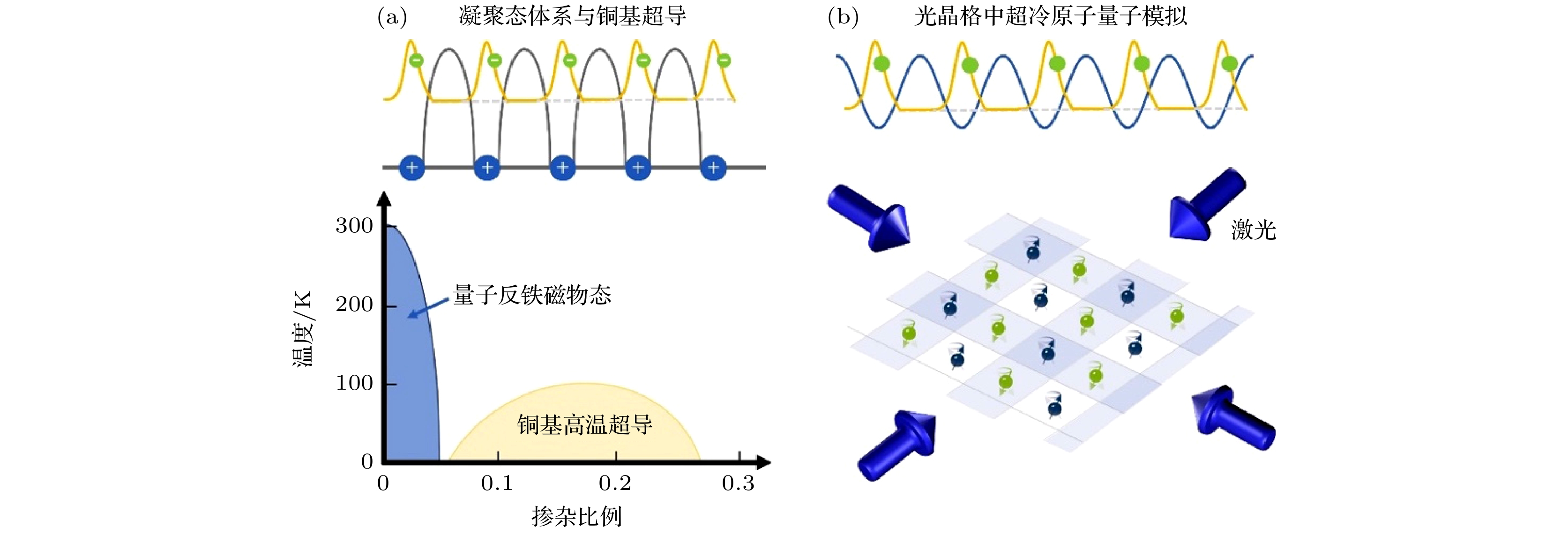
在费米-哈伯德模型的多体数值计算面临巨大挑战的背景下, 人们基于费曼提出的采用可控量子体系来“模拟”复杂量子多体问题的思路[24], 发展出采用超冷原子等效地模拟晶格中的电子、直接对费米-哈伯德模型进行实验研究的想法, 如图1所示. 针对该模型主导的强关联体系的量子模拟经历了多年的发展, 正在进入一个开始超越经典计算能力的临界区域.
1995年, 碱金属原子的玻色-爱因斯坦凝聚态被实验制备出来[25], 从而开启了冷原子物理领域的新纪元. 随后, 超冷原子的哈伯德模型体系被提出[26], 如图1所示, 该理论方案巧妙地将原子对应于凝聚态体系中的电子, 采用光学驻波的方式构建“光晶格”, 从而建立了强关联模型量子模拟的基础. 1999年, 实验首次实现了费米简并量子气体[27], 让费米-哈伯德模型的量子模拟成为可能. 2002年, 玻色-哈伯德模型主导的超流到莫特绝缘态的相变被观测到[28]. 经过几年的技术积累, 双组分费米子的莫特绝缘态也被实验实现[29,30]. 同时, 人们也意识到其实超冷原子还不够冷, 实现费米-哈伯德模型量子模拟的核心瓶颈就是降温. 随后几年, 人们从理论上提出了一系列的制冷方案[31].
直观来说, 量子模拟体系的温度相对于哈伯德模型中自旋交换相互作用的能量尺度还不够低. 以双组分半满填充的莫特绝缘态为例, 基态是一种量子反铁磁物态, 其中粒子间关联主要由超交换相互作用构建. 铜基超导体系中超交换相互作用的强度达到1500 K左右[32], 而冷原子体系中的超交换作用只有15 nK左右[33,34]. 这就是说, 在相同的哈伯德模型下, 如果高温超导的临界温度是100 K, 那么冷原子量子模拟体系的温度要达到1 nK左右. 然而, 在这个强关联区域, 要达到这样的等效温度实验上仍然存在困难. 针对费米-哈伯德模型量子模拟的等效温度过高的问题, 需要开发新的制冷方法和技术.
同时, 超冷原子体系的高精度表征技术极大的促进了降温技术的发展. 为了明晰哈伯德模型中费米子的微观行为, 人们发展了量子气体显微镜技术[35], 实现了采用光学显微的方式探测原子在晶格格点上的占据数和自旋态等信息. 随后, 费米子体系中这项显微技术也陆续被开发出来[36], 并被用于观测半满填充的莫特绝缘态[37]. 结合布拉格散射谱, 三维体系的反铁磁关联的信号也被探测到[38]. 2017年, 利用量子气体显微技术, 一种新的制冷方法被开发出来, 通过在原子团外围构筑热库的方式, 原子团的熵被吸收到热库中, 从而制备出温度为
$ 0.25 t $ (其中$ t $ 为哈伯德模型最近邻跃迁系数)的双组分反铁磁物态[39], 实验观测到强的反铁磁关联. 随后的几年里, 人们开展了一系列费米-哈伯德模型的量子模拟工作, 但是一直没能实现更低的温度. 值得关注的是, 利用玻色子初始温度低、易于调控的特点, 强关联玻色体系的深度冷却技术被开发出来[40]. 其核心理念是将超流态与莫特绝缘态交错排布, 进而利用超流态将莫特绝缘态的熵带出体系. 基于低熵的莫特绝缘态, 玻色子形成了反铁磁物态[41]. 这不仅为费米子体系的冷却提供了新的思路和方法, 还开辟了玻色子研究反铁磁物态的道路.2024年7月, 中国科学技术大学研究团队拓展了体系大小达8×105个格点, 发展了新型冷却技术, 从而降低了体系的温度达到
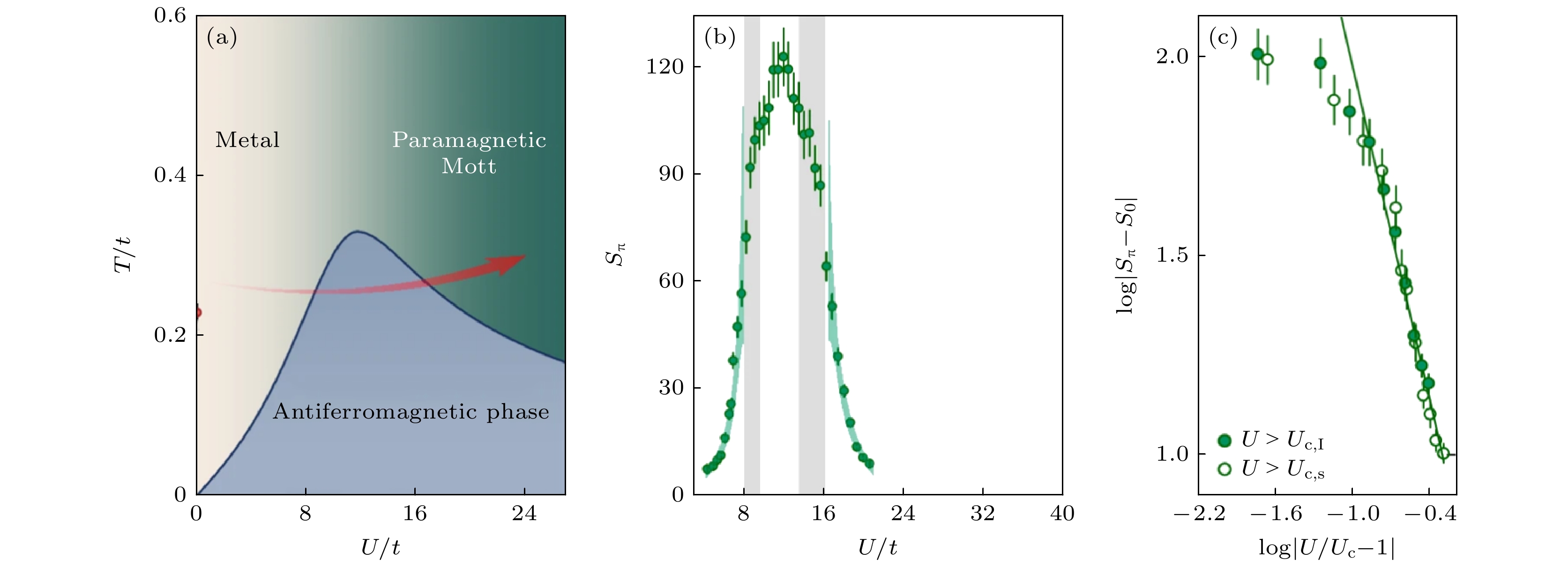
$ 0.23 t $ , 进而成功观测到费米-哈伯德模型中的反铁磁相变[1]. 该实验的技术创新点主要体现在3个方面. 1)低温的费米简并量子气体. 由于冷原子的蒸发冷却依赖于原子间的散射, 而同自旋态的费米子间没有有效的散射路径, 使得费米子的深度蒸发冷却一直是一个难题. 该实验中结合了多项前沿冷却技术, 制备了超低熵的费米简并气体. 2)均匀的三维外势场. 实验设计了新型三维盒子势, 从而制备出三维的空间均匀的费米量子气体, 这不仅防止了由于化学势不均匀带来的原子输运加热, 同时大大提升了调控掺杂浓度的精度, 精准地控制了体系所处的量子相区域, 例如反铁磁区域, 这也使得量子模拟更接近真实的材料体系. 3)以宏观观测量表征反铁磁相变. 实验采用布拉格散射的方法测量反铁磁结构因子, 并清晰地展示了实验测量结果的临界标度行为, 为反铁磁相变的表征提供了坚实可靠的依据. 如图2(b)所示, 这项实验中测量得到的反铁磁结构因子$ {S}_{\mathbf{\pi }} $ 最大值为120 (出现在相互作用$ U\approx 11.75 t $ 附近)[1], 是之前的实验结果[38]的60倍.实验中还确认了通过调节参数实现反铁磁相变的3种不同方式: 1)调控原子间的相互作用
$ U $ , 体系发生金属-反铁磁-顺磁莫特绝缘态的相变; 2)降低温度(减小初始单粒子熵), 体系发生顺磁-反铁磁的相变; 3)调控掺杂浓度, 体系发生顺磁-反铁磁-顺磁的相变. 在这3种实验中, 测量得到的$ {S}_{\mathbf{\pi }} $ 均在反铁磁相变附近展现出普适的临界标度行为, 即$ \left({S}_{\mathbf{\pi }}-{S}_{0}\right)\propto {\left|A/{A}_{{\mathrm{c}}}-1\right|}^{-\gamma } $ ($ {S}_{0} $ 为背景值), 其中$ A $ 代表相互作用$ U $ 、初始单粒子熵$ s $ 、填充密度$ n $ , 且$ \gamma =1.396 $ 为三维海森伯普适类的临界指数[8]. 图2(c)展示了通过调节$ U $ 实现的反铁磁相变过程中反铁磁结构因子$ {S}_{\mathbf{\pi }} $ 的临界标度行为[1].最激动人心的是, 这个实验为后续的费米-哈伯德模型的探索提供了新的思路. 基于该实验的降温方法和新型的盒子势, 再结合光晶格中的深度冷却技术, 可能会得到更低温的反铁磁莫特绝缘态; 结合已经发展的量子气体显微成像技术, 将有利于在二维体系中观测自旋和空穴的输运过程; 通过精确地控制掺杂比例, 进入可能存在的赝能隙、条纹相区域, 探测这些物相的微观特性; 结合纠缠的探测技术, 理解自旋的配对方式和机理等.
-
上述实验首次在费米-哈伯德模型的量子模拟中观察到完整的反铁磁相变, 此体系的深入研究还有望解决一系列的重要科学问题.
1)实验与数值计算的精确比对. 实验的相互作用调节过程中, 多个参量跟随改变, 与理论计 算的过程存在差异; 同时光晶格的有限大小与可 能存在的密度不均匀性, 导致在反铁磁相中实验测量的反铁磁结构因子是有限值, 不同于理论预期 的发散结果; 实验上反铁磁结构因子和反铁磁相变的最高温度在
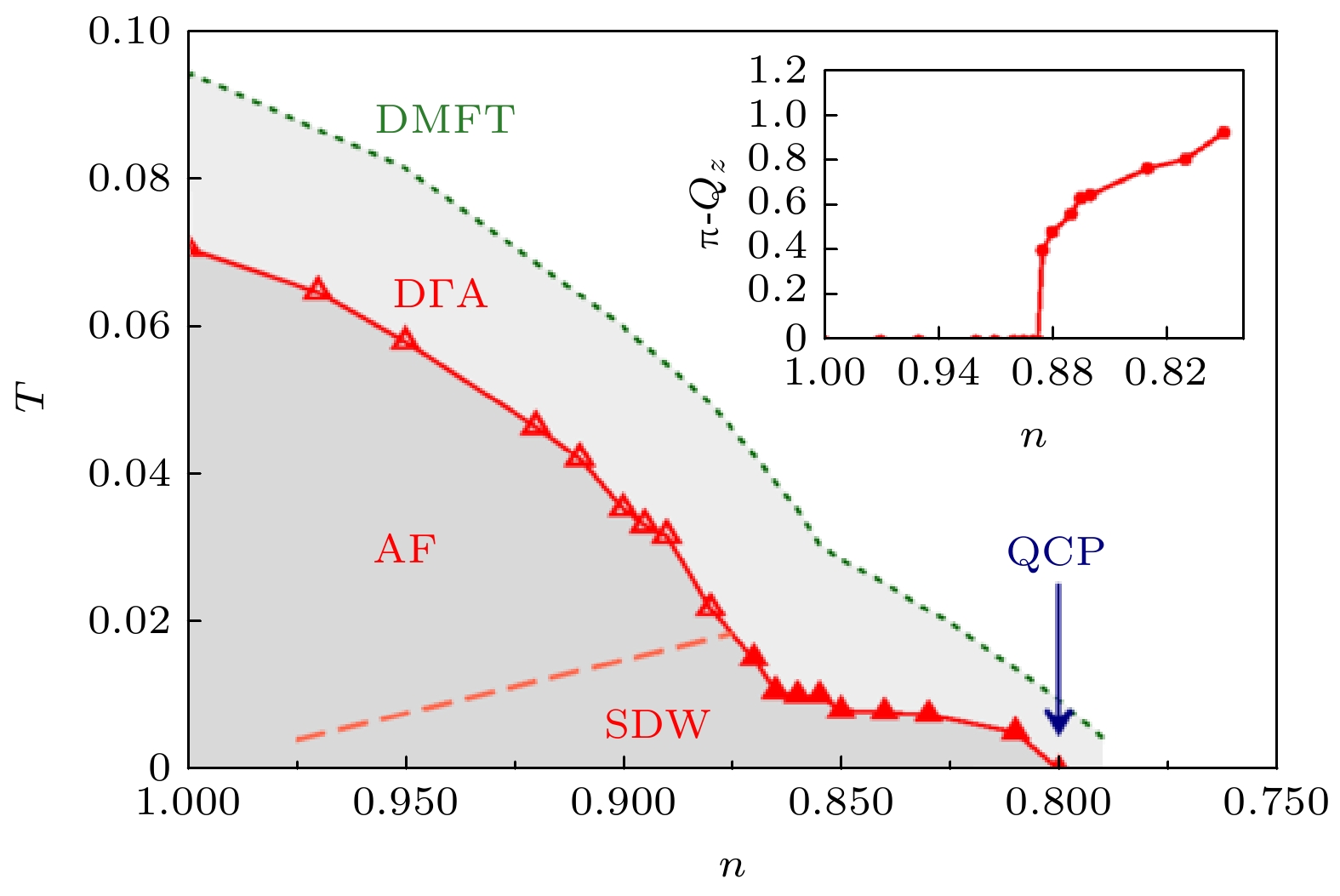
$ U\approx 11.75 t $ , 大于数值计算结果[13]的$ U\approx 8 t $ .2)掺杂的磁性相图. 虽然在小掺杂、较高温区、半满的奈儿反铁磁序的区域, 实验与理论结果一致; 然而在更低温区域, 数值计算结果[16–18]表明, 体系会出现非公度的自旋密度波序(spin density wave, SDW); 如图3所示, 其可能会在
$ n=0.80 $ 附近出现SDW相到顺磁相的量子相变.3)掺杂体系中的新奇物理. 是否存在赝能隙和奇异金属行为、d波超导态等, 受限于多体数值算法的计算能力和精度, 这些问题目前几乎没有任何可靠的定性或定量的理论结果. 这些问题将是实验和理论/数值研究共同的重要课题.
费米-哈伯德模型的超冷原子量子模拟实验已经开展了20余年, 虽然尚未能明晰其与高温超导机理之间的关系, 但是其中发现了大量新奇的物理现象, 也不乏众多创新的技术. 然而, 由于在极低温下, 任何小的扰动都可能会带来激发, 继续降温的任务极其艰巨, 这使得往往要经过数年的发展才能进一步降低一点温度. 尽管如此, 最新的实验进展, 在部分物理性质的探索上已经追平甚至超越了最前沿的理论和多体数值计算能力. 此次三维费米-哈伯德模型的量子模拟实验被称为是该领域的里程碑式的工作, 对后续进一步探索掺杂哈伯德模型的低温以及基态性质至关重要. 量子模拟将与同样高速发展的量子多体数值计算相结合, 相互促进, 有望携手解决费米-哈伯德模型中悬而未决的重大难题, 特别是量子磁性与高温超导机制之间的深刻联系.
基于哈伯德模型的超冷原子量子模拟研究进展
Recent research progress of ultracold-atom quantum simulation of Fermi-Hubbard model
-
摘要: 费米-哈伯德模型是描述凝聚态物理中关联电子体系的基础模型, 与高温超导现象具有深刻联系. 近年来, 超冷原子量子模拟已成为研究该模型的重要范式, 同时多体数值计算在该模型基础物理性质的研究方面也取得了重要进展. 特别地, 最近超冷原子实验观测到三维哈伯德模型中的反铁磁相变, 是费米-哈伯德模型量子模拟的重要一步, 为理解量子磁性与高温超导之间的联系奠定了基础. 本文回顾费米-哈伯德模型的理论与实验研究进展, 侧重于三维体系, 并讨论实验的发展历程和现状, 展望未来的发展趋势.Abstract:
Fermi-Hubbard model is a fundamental lattice model describing correlated electron systems in condensed matter physics and is closely related to high-temperature superconductivity. In recent years, cold-atom quantum simulations have become an important paradigm for studying the Fermi-Hubbard model, and advances in quantum many-body computations have contributed to our understanding of its fundamental properties. Notably, a recent ultracold-atom experiment achieving the well-known antiferromagnetic (AFM) phase transition in the three-dimensional (3D) Hubbard model represents a key step in quantum simulation, laying a foundation for exploring the link between the quantum magnetism and high-temperature superconductivity. In this paper, the experimental and theoretical research progress of Fermi-Hubbard model in 3D systems is reviewed, the development history and present status in this field are discussed, and the future development direction is also prospected. The paper is organized as follows. To begin with, recent progress of observing AFM phase transitions in the 3D Hubbard model is reviewed, focusing on an ultracold-atom experiment conducted by the research group at the University of Science and Technology of China (USTC). Next, a theoretical introduction to the fundamental properties of the 3D Hubbard model is provided, in which prior theoretical studies is summarized, the current research status is outlined, and some unresolved or under-explored problems are discussed. In Section 3, the quantum simulation of the Hubbard model using ultracold atoms in optical lattices is discussed, and the basic principle, historical developments and key challenges are outlined. The USTC team overcame these challenges through innovative techniques such as atom cooling, large-scale uniform box traps, and precise measurements of the AFM structure factor. Their work successfully confirms the AFM phase transition via the critical scaling analysis. Finally, the significance of this achievement is emphasized, and the future research prospects of the 3D Hubbard model are discussed, including experimental studies on the doped regions and related theoretical benchmarks. -

-
图 1 超冷原子模拟费米-哈伯德模型的示意图, 采用超冷原子等效于凝聚态体系中的电子, 而利用光学驻波构建出晶格结构, 可构筑哈伯德模型中的量子反铁磁物态, 进而通过调控体系的相互作用、温度和掺杂浓度等来研究反铁磁相变, 以及探究高温超导态的微观机理
Figure 1. Illustration of the ultracold atom simulation for the Fermi-Hubbard model, ultracold atoms serve as analogues of electrons in condensed matter systems, with optical standing waves forming lattice structures, this setup allows for the creation of the Hubbard antiferromagnetic (AFM) state, by controlling parameters such as interaction strength, temperature and doping, the system can be utilized to study AFM phase transitions and explore the microscopic mechanism of high-temperature superconductivity.
图 2 (a)半满填充下的费米-哈伯德模型大致相图[1]; (b)随着
$ U $ 增大实验测量的反铁磁结构因子结果[1]; (c)关于$ U $ 的临界标度行为[1]Figure 2. (a) Schematic phase diagram of the 3D half-filled Fermi-Hubbard model[1]; (b) experimental results of antiferromagnetic structure factor as a function of interaction strength
$ U $ [1]; (c) the critical scaling behavior of antiferromagnetic structure factor[1].图 3 使用DMFT和
$ {\mathrm{D}}{{\Gamma }}{\mathrm{A}} $ 算法得到的掺杂三维哈伯德模型在$ U=9.8 t $ 的磁性相图[16], 其中AF是奈儿反铁磁序, SDW是非公度的自旋密度波序, QCP是量子临界点Figure 3. Magnetic phase diagram for the 3D doped Hubbard model with
$ U=9.8 t $ , based on DMFT and$ {\mathrm{D}}{{\Gamma }}{\mathrm{A}} $ simulations[16], AF denotes the antiferromagnetic order, and SDW represents incommensurate spin density wave order, and QCP marks the quantum critical point. -
[1] Shao H J, Wang Y X, Zhu D Z, Zhu Y S, Sun H N, Chen S Y, Zhang C, Fan Z J, Deng Y, Yao X C, Chen Y A, Pan J W 2024 Nature 632 267 doi: 10.1038/s41586-024-07689-2 [2] Arovas D P, Berg E, Kivelson S A, Raghu S 2022 Annu. Rev. Conden. Ma. P. 13 239 doi: 10.1146/annurev-conmatphys-031620-102024 [3] Qin M, Schäfer T, Andergassen S, Corboz P, Gull E 2022 Annu. Rev. Conden. Ma. P 13 275 doi: 10.1146/annurev-conmatphys-090921-033948 [4] Hubbard J, Flowers B H 1963 Proc. R. Soc. Lond. Ser. A 276 238 doi: 10.1098/rspa.1963.0204 [5] Kanamori J 1963 Prog. Theor. Phys. 30 275 doi: 10.1143/PTP.30.275 [6] Gutzwiller M C 1963 Phys. Rev. Lett. 10 159 doi: 10.1103/PhysRevLett.10.159 [7] Chen Q J, Wang Z Q, Rufus Boyack, Yang S L, Levin K 2024 Rev. Mod. Phys. 96 025002 doi: 10.1103/RevModPhys.96.025002 [8] Campostrini M, Hasenbusch M, Pelissetto A, Rossi P, Vicari E 2002 Phys. Rev. B 65 144520 doi: 10.1103/PhysRevB.65.144520 [9] Mermin N D, Wagner H 1966 Phys. Rev. Lett. 17 1133 doi: 10.1103/PhysRevLett.17.1133 [10] Staudt R, Dzierzawa M, Muramatsu A 2000 Eur. Phys. J. B 17 411 doi: 10.1007/s100510070120 [11] Ibarra-García-Padilla E, Mukherjee R, Hulet R G, Hazzard K R A, Paiva T, Scalettar R T 2020 Phys. Rev. A 102 033340 doi: 10.1103/PhysRevA.102.033340 [12] Sun F, Xu X Y 2024 arXiv: 2404.09989 [cond-mat. str-el] [13] Song Y F, Deng Y, He Y Y 2024 arXiv: 2407.08603 [cond-mat. str-el] [14] Werner F, Parcollet O, Georges A, Hassan S R 2005 Phys. Rev. Lett. 95 056401 doi: 10.1103/PhysRevLett.95.056401 [15] Fuchs S, Gull E, Troyer M, Jarrell M, Pruschke T 2011 Phys. Rev. B 83 235113 doi: 10.1103/PhysRevB.83.235113 [16] Schäfer T, Katanin A A, Held K, Toschi A 2017 Phys. Rev. Lett. 119 046402 doi: 10.1103/PhysRevLett.119.046402 [17] Rampon L, Simkovic F, Ferrero M 2024 arXiv: 2409.08848 [cond-mat. str-el] [18] Kozik E, Burovski E, Scarola V W, Troyer M 2013 Phys. Rev. B 87 205102 doi: 10.1103/PhysRevB.87.205102 [19] Lenihan C, Kim A J, Simkovic F, Kozik E 2022 Phys. Rev. Lett. 129 107202 doi: 10.1103/PhysRevLett.129.107202 [20] Garioud R, Šimkovic F, Rossi R, Spada G, Schäfer T, Werner F, Ferrero M 2024 Phys. Rev. Lett. 132 246505 doi: 10.1103/PhysRevLett.132.246505 [21] He Y Y, Qin M P, Shi H, Lu Z Y, Zhang S W 2019 Phys. Rev. B 99 045108 doi: 10.1103/PhysRevB.99.045108 [22] Zheng B X, Chung C M, Corboz P, Ehlers G, Qin M P, Noack R M, Shi H, White S R, Zhang S W, Chan G K L 2017 Science 358 1155 doi: 10.1126/science.aam7127 [23] Xu H, Chung C M, Qin M P, Schollwöck U, White S R, Zhang S W 2024 Science 384 7691 doi: 10.1126/science.adh7691 [24] Feynman R P 1982 Int. J. Theor. Phys. 21 467 doi: 10.1007/BF02650179 [25] Anderson M H, Ensher J R, Matthews M R, Wieman C E, Cornell E A 1995 Science 269 198 doi: 10.1126/science.269.5221.198 [26] Jaksch D, Bruder C, Cirac J I, Gardiner C W, Zoller P 1998 Phys. Rev. Lett. 81 3108 doi: 10.1103/PhysRevLett.81.3108 [27] DeMarco B, Jin D S 1999 Science 285 1703 doi: 10.1126/science.285.5434.1703 [28] Greiner M, Mandel O, Esslinger T, Hansch T W, Bloch I 2002 Nature 415 39 doi: 10.1038/415039a [29] Jordens R, Strohmaier N, Gunter K, Moritz H, Esslinger T 2008 Nature 455 204 doi: 10.1038/nature07244 [30] Schneider U, Hackermuller L, Will S, Best Th, Bloch I, Costi T A, Helmes R W, Rasch D, Rosch A 2008 Science 322 1520 doi: 10.1126/science.1165449 [31] Ho T L, Zhou Q 2009 arXiv: 0911.5506 [cond-mat. quant-gas] [32] Lee P A, Nagaosa N, Wen X G 2006 Rev. Mod. Phys. 78 17 doi: 10.1103/RevModPhys.78.17 [33] Duan L M, Demler E, Lukin M D 2003 Phys. Rev. Lett. 91 090402 doi: 10.1103/PhysRevLett.91.090402 [34] Trotzky S, Cheinet P, Fölling S, et al. 2008 Science 319 295 doi: 10.1126/science.1150841 [35] Bakr W S, Gillen J I, Peng A, Folling S, Greiner M 2009 Nature 462 74 doi: 10.1038/nature08482 [36] Haller E, Hudson J, Kelly A, Cotta D A, Peaudecerf B, Bruce G D, Kuhr S 2015 Nat. Phys. 11 738 doi: 10.1038/nphys3403 [37] Greif D, Parsons M F, Mazurenko A, Chiu C S, Blatt S, Huber F, Ji G, Greiner M 2016 Science 351 953 doi: 10.1126/science.aad9041 [38] Hart R A, Duarte P M, Yang T L, Liu X X, Paiva T, Khatami E, Scalettar R T, Trivedi N, Huse D A, Hulet R G 2015 Nature 519 211 doi: 10.1038/nature14223 [39] Mazurenko A, Chiu C S, Ji G, et al. 2017 Nature 545 462 doi: 10.1038/nature22362 [40] Yang B, Sun H, Huang C J, Wang H Y, Deng Y J, Dai H N, Yuan Z S, Pan J W 2020 Science 369 550 doi: 10.1126/science.aaz6801 [41] Sun H, Yang B, Wang H Y, et al. 2021 Nat. Phys. 17 990 doi: 10.1038/s41567-021-01277-1 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: