首页
登录
注册
下载:
-
超导转子可用来制作高精度惯性器件. 超导材料具有零电阻效应和迈斯纳效应, 这些特性使得超导体在磁场环境中能够实现几乎零损耗的无接触支承. 超导材料铌的膨胀系数小、蠕变小[1–4], 极大地增强了超导转子的旋转稳定性, 使得磁场中的超导体可以实现几乎没有损耗的无接触支承, 确保了长期稳定且高精度的运行. 这些优势使得超导磁悬浮转子相较其他精密仪器在一些高精度的角位移和角速度测量领域具有更高的精度潜力[1,4].
超导转子极轴偏移的主要误差源是超导转子的质量偏心和球面误差[5]. 现在已有的内驱转子驱动结构[6], 采用力矩线圈定中和驱动线圈置于超导转子内开孔的方式对转子进行驱动, 其设计结构比较复杂, 实现高精度测量具有不小的难度. 张源等[7]提出的新型超导转子驱动电磁结构相较内驱转子驱动结构, 结构相对简单, 是一个完整对称的封闭结构, 且不存在理论质量偏心, 该悬浮系统电磁结构更加简化, 实现了电机线圈和力矩线圈功能一体化. 文献[7]虽然提出了完整球形超导转子的电磁驱动方法, 但并未对影响转子极轴偏移的干扰力矩进行分析, 本文主要分析了超导转子的动力学特性. 此前有文献[8]对内驱转子驱动结构进行了干扰力矩分析, 但未分析转子极轴运动轨迹, 并未考虑地球自转对超导转子极轴偏移的影响. 准确计算超导转子质球面误差产生的极轴漂移误差并进行补偿, 是实现超导转子磁悬浮装置高精度的关键步骤. 基于此, 开展了完整球形超导转子极轴偏移特性主要影响因素分析. 本文针对新型完整球形转子, 分析了影响转子极轴偏移的主要因素, 在考虑了地球自转的影响后, 计算出其极轴运动轨迹, 通过漂移误差结果对比分析, 为超导转子磁悬浮系统进行极轴漂移误差补偿可提供参考.
张源等[9]对超导磁悬浮支承系统的结构、原理和磁悬浮作用力等方面进行了分析和计算. 离心变形和加工误差属于影响磁支承干扰力矩的主要因素, 文献[8]虽分析过内驱转子的磁支承干扰力矩的计算公式, 但并未分析过离心变形和加工误差两个因素哪个对磁支承干扰力矩影响更大. 本文在此基础上对超导转子的球面误差产生的干扰力矩及其引起的漂移误差进行了研究, 得到了不同参数下转子漂移率的规律, 分析了两大影响因素对磁支承干扰力矩的影响权重, 为超导转子磁悬浮系统的设计、优化和超导转子承载能力的评估提供参考.
-
超导线圈通电时会产生磁场, 由于超导体的抗磁性, 悬浮线圈产生的磁通被迫进入超导转子和整形铌瓦之间的狭窄缝隙, 对超导转子产生磁压力, 即悬浮力. 当悬浮力大于重力时, 转子起浮.
超导体任意表面微元面ds的磁场力dF如下:
式中, B为微元面积ds处的磁场强度,
$ {\mu _0} $ 表示真空磁导率.基于(1)式, 求出超导转子表面磁场B分布即可计算超导转子的磁支承力. 依据超导电动力学 的原理, 可对超导转子表面磁场强度进行理论分 析[7–10], 但直接采用解析法进行分析, 边界条件较为复杂, 不易得到解析解, 本文主要通过数值方法来进行相关的模拟和分析.
本文采用有限元软件Ansys Maxwell 2023来计算悬浮线圈不同载流下的磁场分布. 模型建 立完成后将模型中的“超导材料”的电导率设置
$ 1 \times {10^7}\; {\text{S/m}} $ , 相对磁导率设置$ 1 \times {10^{ - 7}} $ , 然后划分网格, 施加激励条件, 并设置边界条件即可进行求解. 磁场B分布确定后, 依靠麦克斯韦方程确定超导体的电流密度分布:其外边界条件设置狄利克雷(Dirichlet)边界条件, 其他边界条件设置为自然边界条件.
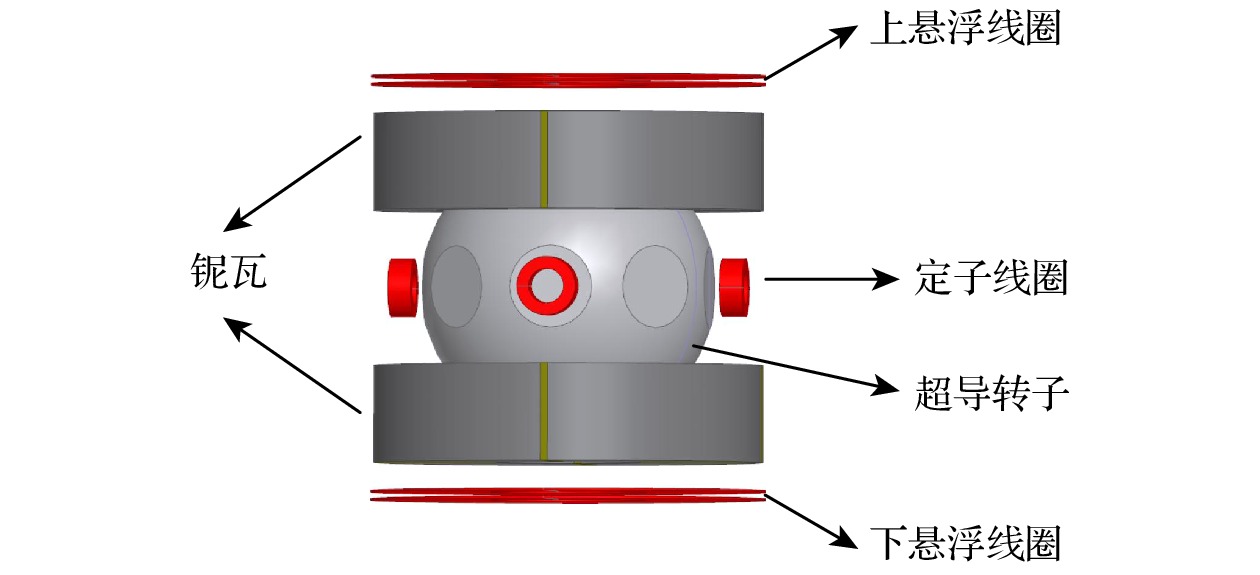
本文介绍的超导转子磁支承结构如图1所示, 主要包括完整球形超导转子、整形铌瓦、定子线圈和悬浮线圈. 完整球形超导转子由
$99.5{\text{%}} $ 的纯铌材料制作, 半径25 mm, 质量84 g, 是在赤道加厚了的薄壁铌球. 悬浮线圈和定子线圈均是铌钛线双绕绕制的盘形线圈. 定子双绕线圈分为两路, 一路负责定中, 一路负责驱动. 悬浮线圈的磁场只作用在超导转子的球面上, 而非球面部分没有磁场, 超导体表面的迈斯纳力垂直于超导体表面并向内, 作用在球面的迈斯纳力均过球心, 因此悬浮线圈磁场在超导球上不产生磁力矩, 如图2所示. 加转时, 超导转子被定中路线圈持续通电产生的磁力保持在竖直姿态; 同时, 超导转子被驱动路按照特定时序通电产生的磁力作用在超导转子切削平面上, 产生转矩, 实现驱动. -
磁悬浮超导球形转子受到的干扰力矩主要来源于两个方面, 主要分为与磁支承有关的干扰力矩和与磁支承无关的干扰力矩. 与磁支承有关的干扰力矩分为转子非球形因素引起的一次干扰力矩; 由转子失中度、装配误差引起的二次干扰力矩. 与支承无关的干扰力矩分为俘获磁通、伦敦磁矩.
-
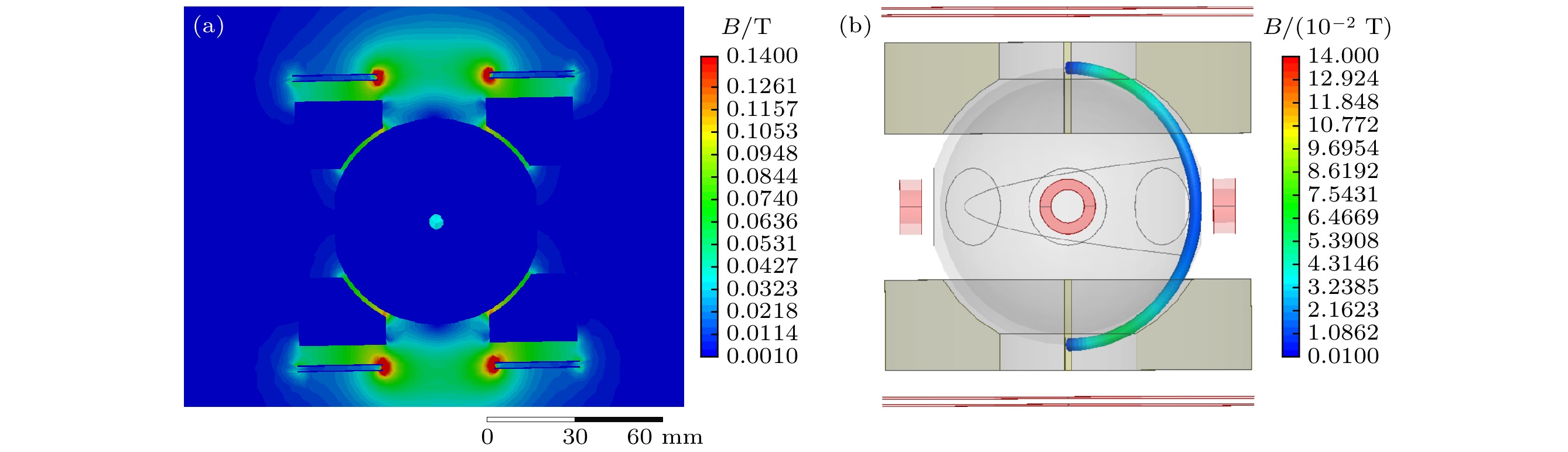
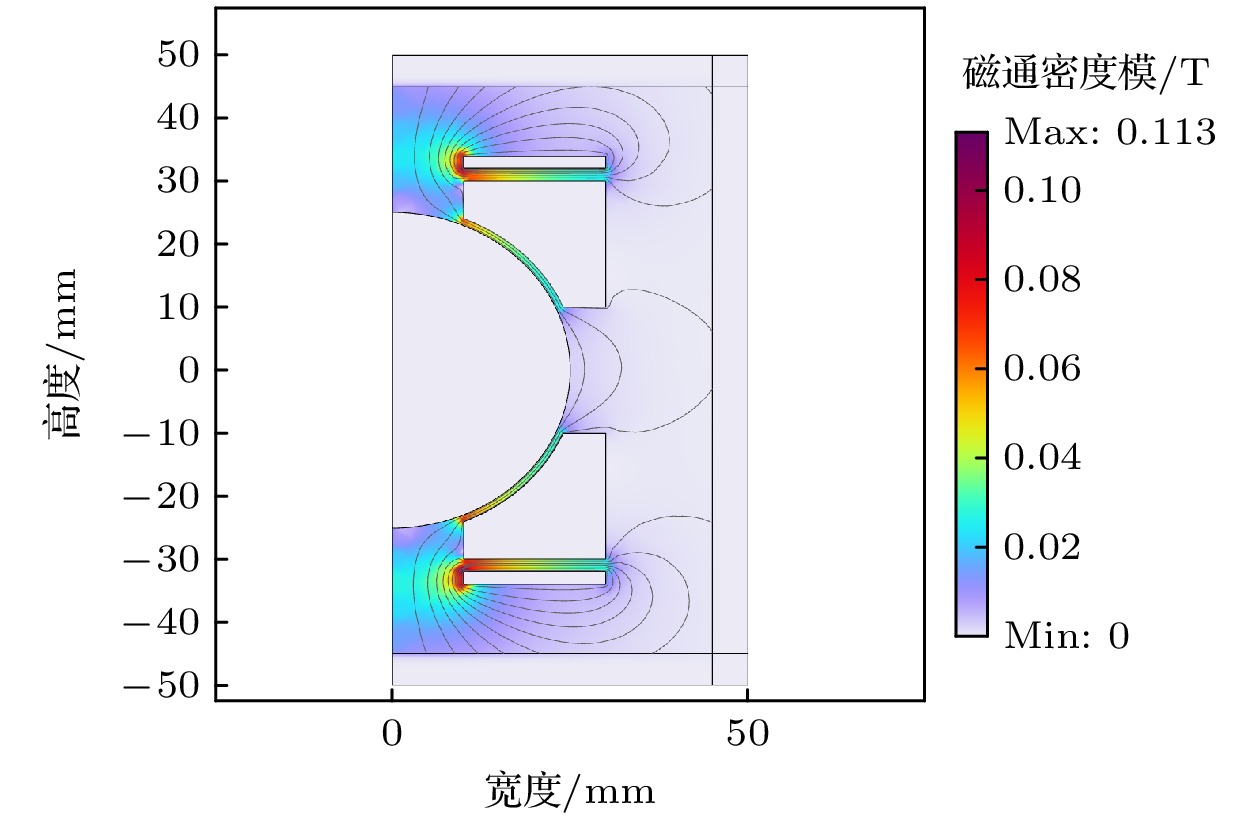
由于高速旋转的超导转子表面会发生离心变形, 其表面的磁场分布会发生变化, 磁通变化因此导致了悬浮线圈产生的磁悬浮力和磁支承力矩发生变化. 超导转子由铌制成, 其下临界磁场是0.14 T, 在超导转子悬浮时, 超导转子与整形铌瓦之间的狭窄缝隙中磁密最大, 为防止失超, 需要保证狭窄缝隙中的最大磁场小于0.14 T [4]. 悬浮线圈匝数为400匝, 图3是上线圈通电2.7 A, 下线圈通电3 A时, 悬浮在超导球腔中心位置的超导转子表面磁密分布. 在超导转子与整形铌瓦之间的狭窄缝隙内, 转子表面的磁场密度分布极不均匀, 形成了越靠近线圈位置磁密越大的分布特征.
此处仍对图1的模型进行超导转子的离心变形效应的分析, 参数也相同. 为简化计算, 对其进行以下假设, 超导转子为均匀各向同性的弹性体, 变形前壳体表面为理想球形; 壳体厚度变化相对极轴及赤道轴面都具有对称性; 壳体厚度与半径之比足够小, 充分接近薄膜应力状态[11]. 则超导转子的母线方程如下:
式中,
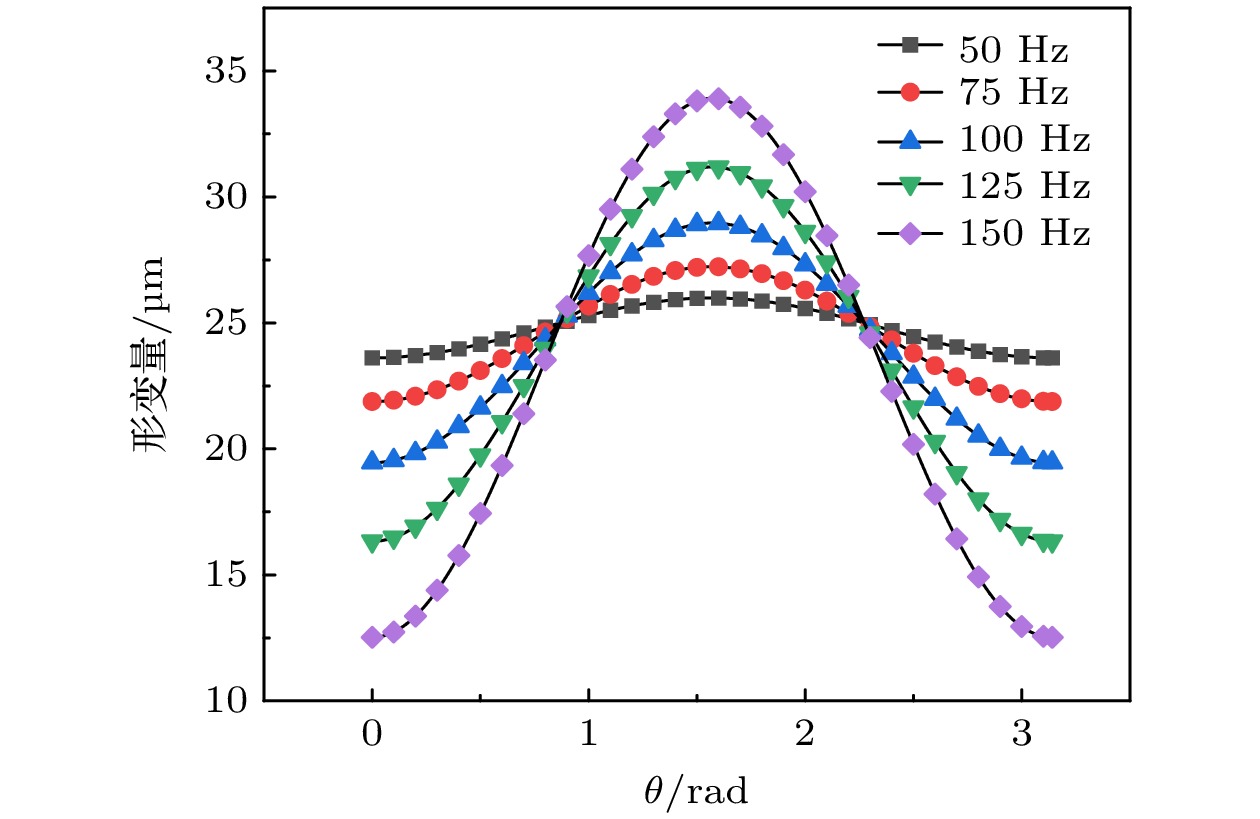
$\theta $ 是超导转子表面任一点与球心的连线与旋转轴的夹角,$\nu $ 是泊松比,$\rho $ 是材料密度,$\omega $ 是转子转速,${r_0}$ 是转速为零时的转子半径,$E$ 是材料弹性模量. 计算结果表明, 在赤道附近, θ (50°, 130°)超导转子表面在离心力的作用力下向外膨胀; 在θ (0°, 50°)和θ (130°, 180°)的范围内, 超导转子向内收缩, 如图4所示. -
式中,
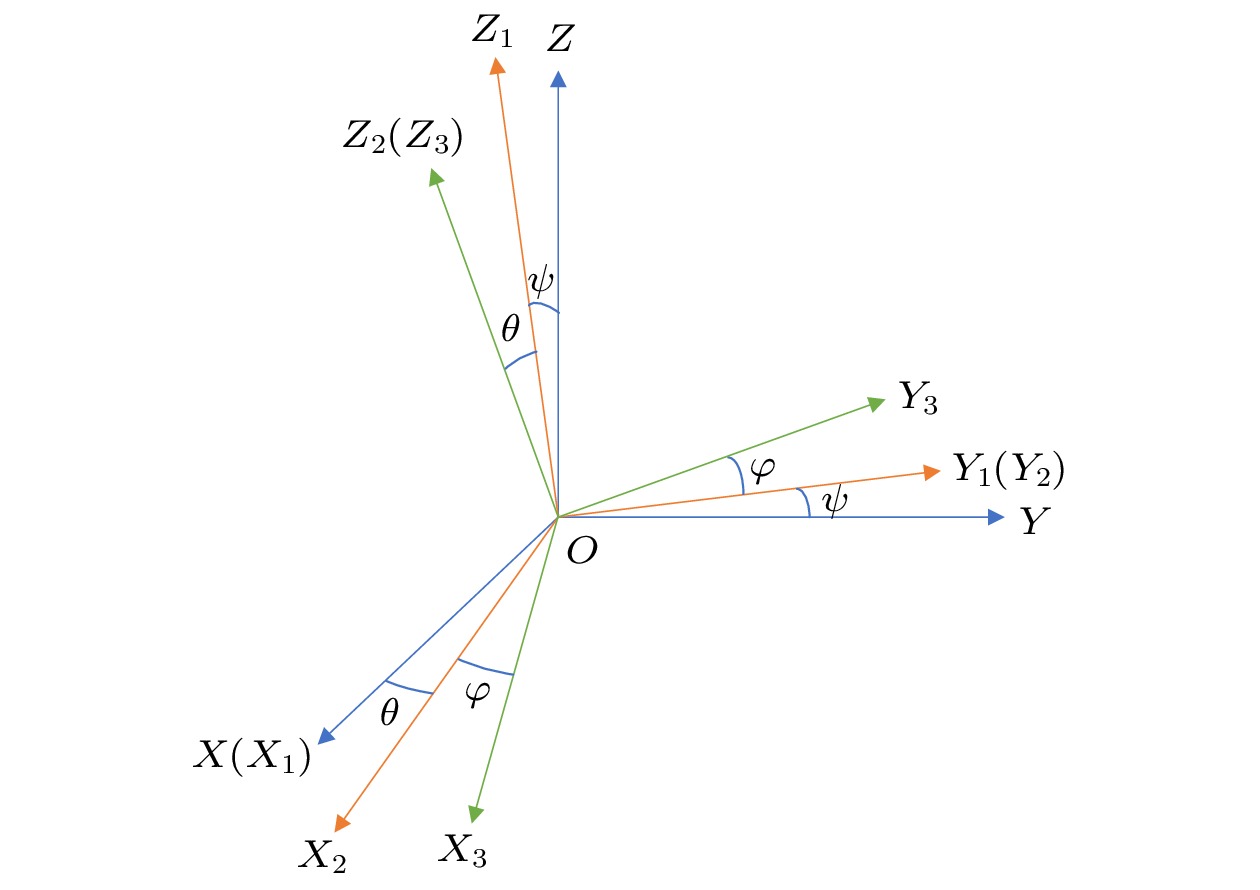
$\varPhi $ 为磁路磁通,$N$ 为线圈匝数,$I$ 为悬浮线圈电流,${R_{\text{m}}}$ 为磁路磁阻.首先, 建立3个坐标系, 如图5所示. 一是壳体坐标系
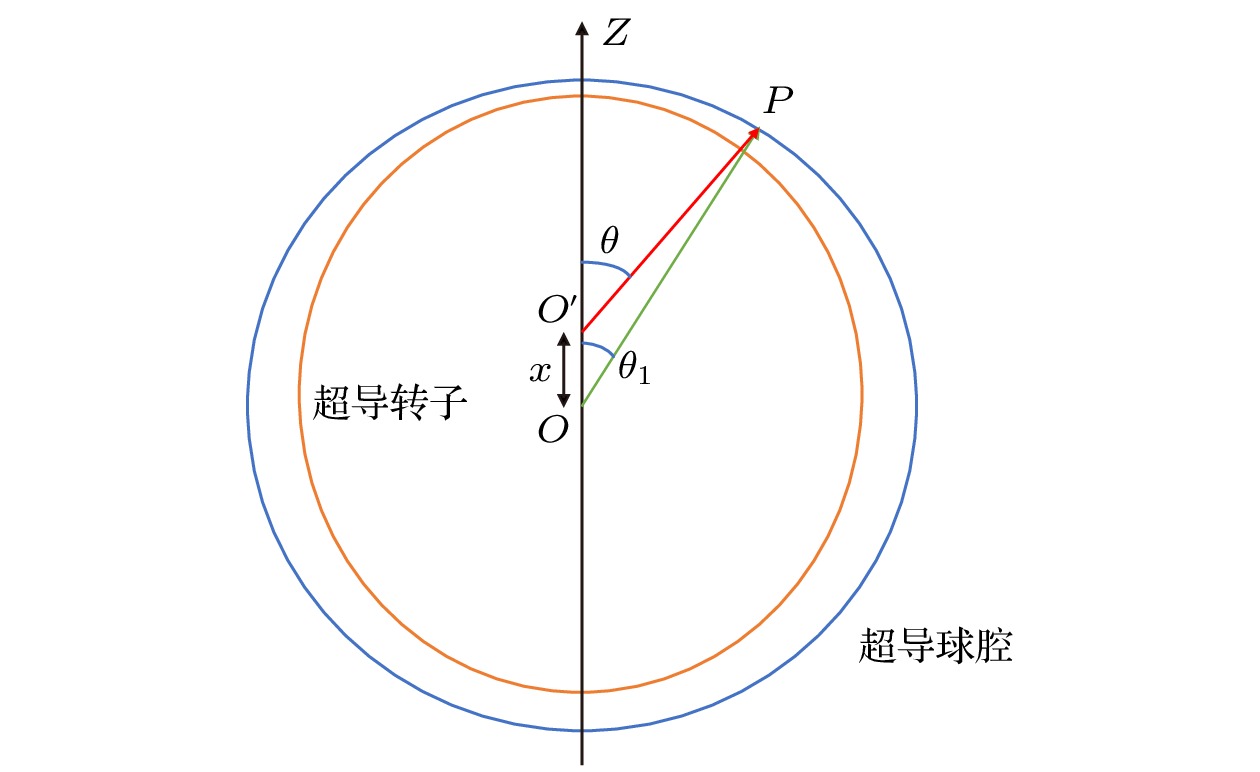
$ O{X_1}{Y_1}{Z_1} $ , 其中${Z_1}$ 与极轴方向悬浮磁场的对称轴方向一致, 即可视为惯性坐标系. 二是牵连坐标系$ O{X_2}{Y_2}{Z_2} $ ,${Z_2}$ 方向与转子极轴方向一致,${X_2}$ 和${Y_2}$ 轴位于转子赤道平面内, 但不参与转子绕极轴的转动. 三为转子坐标系$ O{X_3}{Y_3}{Z_3} $ ,${Z_3}$ 轴沿转子极轴方向,${X_3}$ 和${Y_3}$ 轴位于转子赤道平面内, 参与转子绕极轴的转动.转子表面的不球度可以由傅里叶级数表示, 将转子表面的母线展开为
$\theta $ 的余弦级数, 由勒让德多项式[14]表示为式中, r为转子表面上一点P的矢径, 其长度为质心到点P的距离,
${a_n}$ 为描述转子形状的谐波系数,$ {P_n}\left( {\cos {\theta _1}} \right) $ 为勒让德多项式级数,${\theta _1}$ 为矢径r与转子回转主轴的夹角. 一次谐波对应于刚体的轴向平移; 二次及以上的偶次谐波对应于转子的离心变形造成的赤道方向膨胀[11].勒让德多项式级数为[15]
其余各项可由递推公式计算[15]:
其中,
式中,
${a_2}$ 是转子的离心变形,${a_3}$ 是转子的加工误差.利用坐标变换[14]可得到:
式中,
$\theta $ 和$\psi $ 是卡尔丹角.式中
$r$ 是超导转子表面微元ds相对球心的径向长度,$ {{\boldsymbol{r}}^{0}} $ 是其对应的径向矢量,$ {{\boldsymbol{n}}^{0}} $ 是超导转子表面的法向向量.悬浮线圈产生的磁场磁路模式如图6所示, 则图中在狭窄缝隙内转子表面任意一点处的磁感应强度B为
由(3)式、(11)式—(13)式可进一步简化超导转子磁支承干扰力矩:
式中,
$ {\boldsymbol{O}}{{\boldsymbol{Z}}_{2}} $ 是超导转子极轴,$ {{\boldsymbol{r}}^{0}} $ 是超导转子表面任意一点的径向矢量.可以求得超导转子的离心变形产生的磁支承干扰力矩公式为
式中,
$r$ 是超导转子表面微元ds相对球心的径向长度,$ {{\boldsymbol{r}}^{0}} $ 是其对应的径向矢量,$ {\boldsymbol{O}}{{\boldsymbol{Z}}_{2}} $ 是超导转子极轴矢量,${\theta _0}$ 是转子表面微元ds与球腔坐标系$z$ 轴的夹角,${\theta _1}$ 是转子表面微元ds与转子坐标系$z$ 轴的夹角, I为悬浮线圈电流.根据文献[12, 16], 悬浮磁路磁阻可基于有限元方法求解. 由(3)式可知, 当求得磁通
$\varPhi $ 时, 通过计算转子和铌块间隙内面积即可求得超导转子表面的平均磁密分布. 代入实际参数, 进行拟合计算可求得当转速
$\omega $ 为10000 r/rad, a2 = 1 μm, a3 = 1 μm, I上 = 0.75 A, I下 = 2.65 A时, 干扰力矩为根据动量矩定理, 可以求得超导转子的极轴漂移速度[11]:
式中,
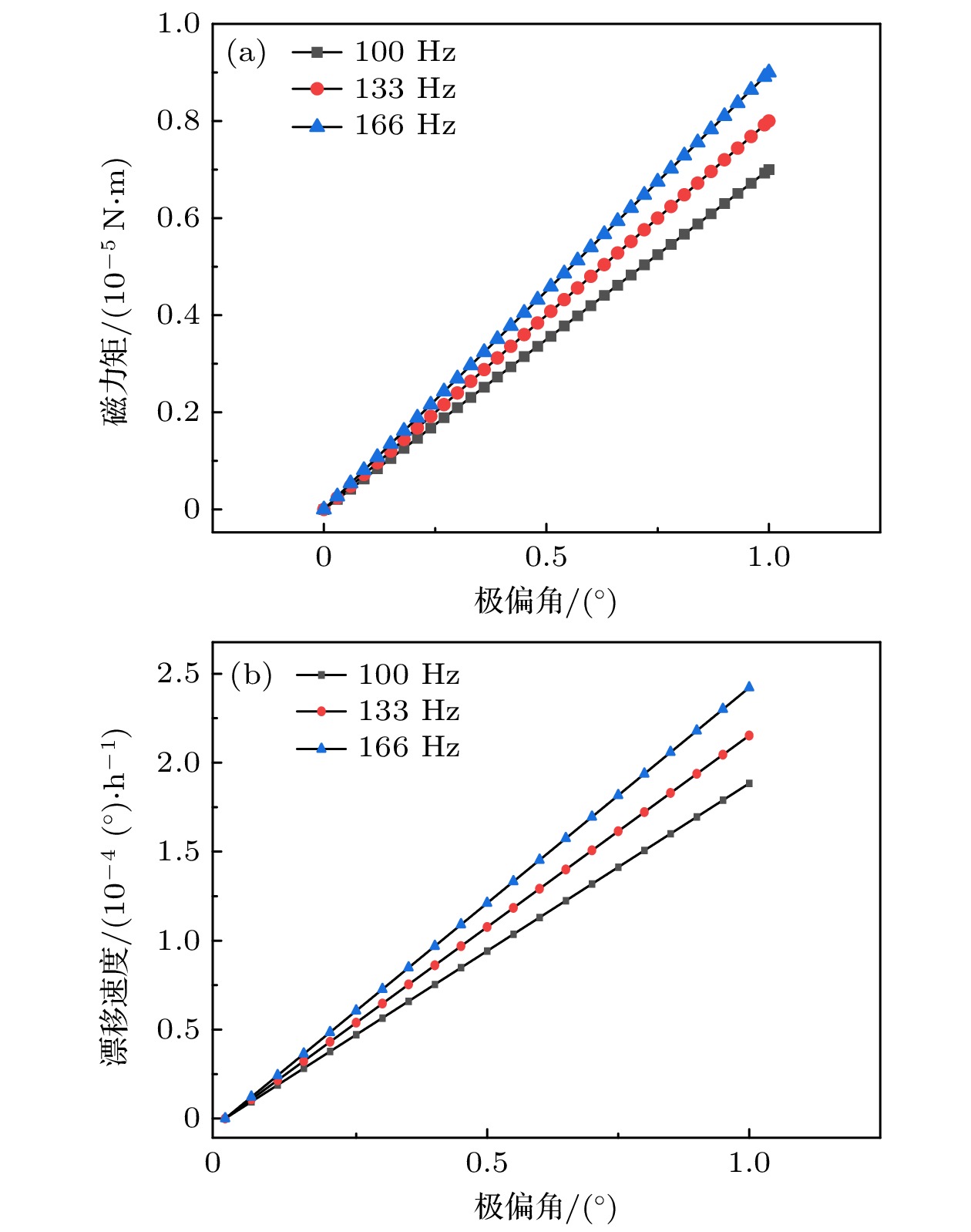
${\omega _{\text{d}}}$ 是超导转子漂移速度, H为超导转子动量矩, M是超导转子干扰力矩.图7为超导转子离心变形引起的磁支承干扰力矩及其产生的漂移速度, 离心变形导致的磁支承干扰力矩产生极轴漂移随转子转速增大而增大, 随超导转子极偏角的增大而增大.
在此分析两个影响因素产生的干扰力矩对磁支承干扰力矩影响更大. 根据 (8)式, 当转速
$\omega $ = 10000 r/rad, I上 = 2.73 A, I下 = 3.76 A时:a2 = 100 μm, a3 = 1 μm时, 可求得
a2 = 1 μm, a3 = 100 μm时, 可求得
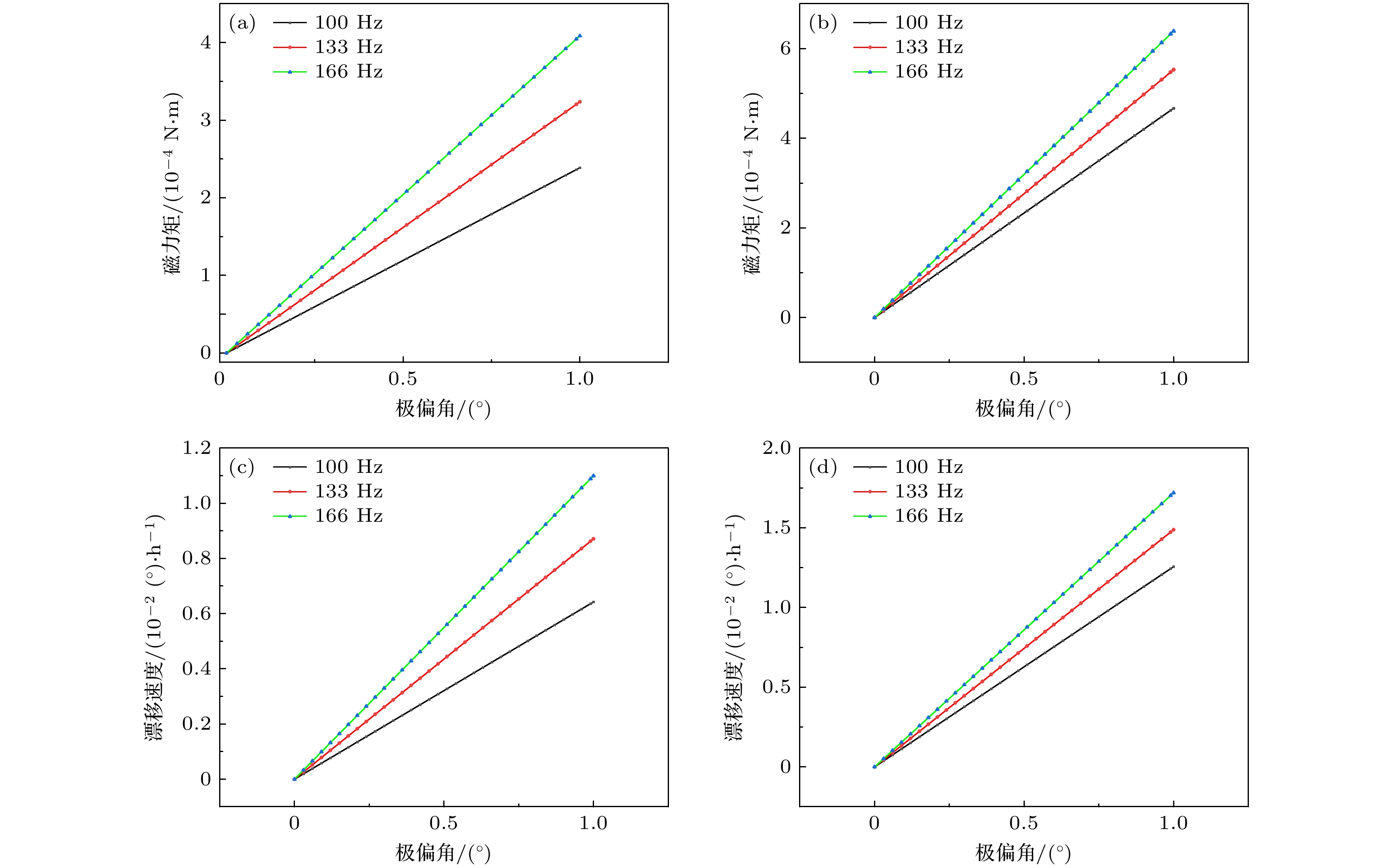
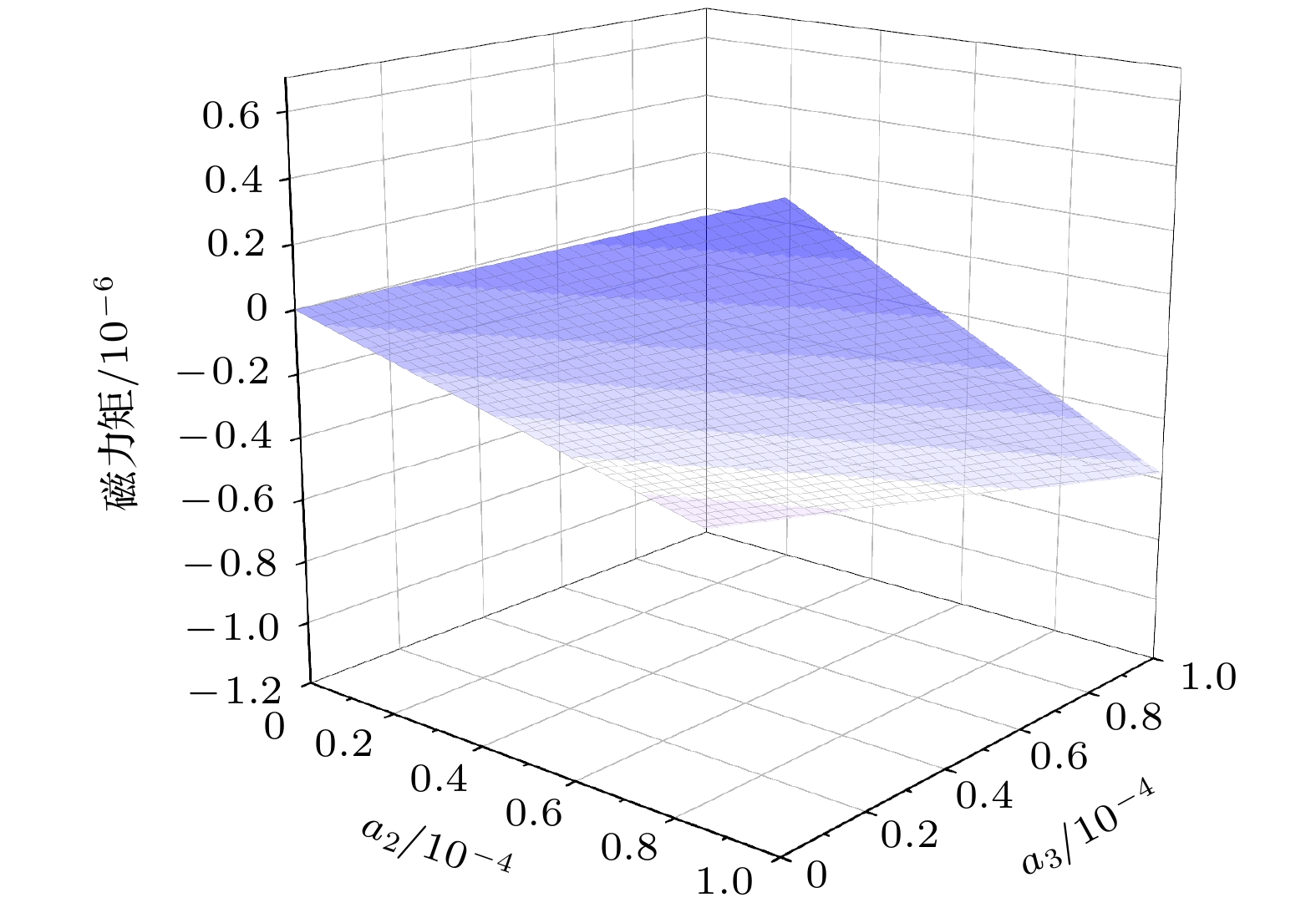
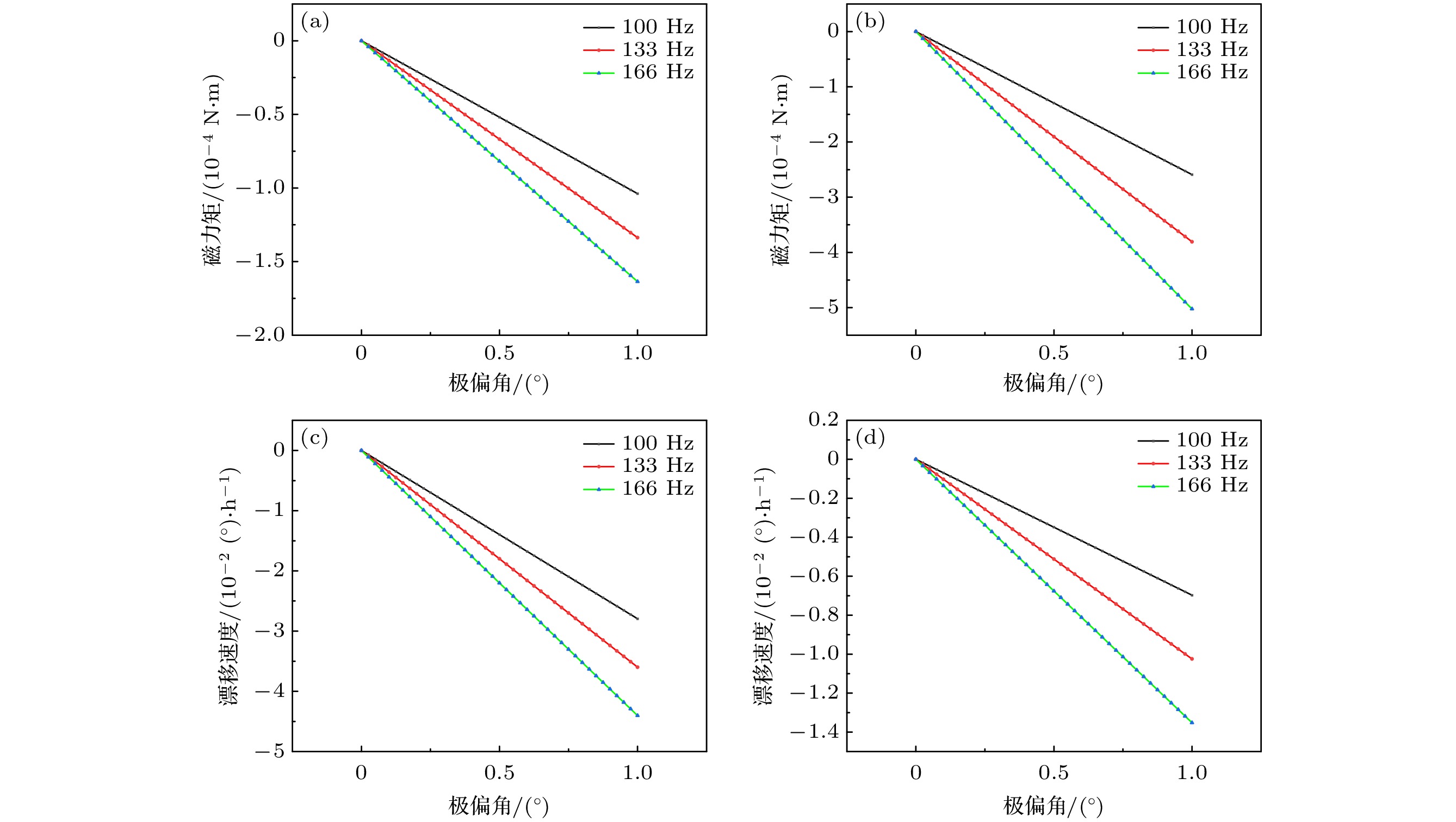
图8为改变加工误差和离心变形大小, 产生的磁支承干扰力矩及其产生的漂移速度, 超导转子的漂移率随转速增大而增大, 随超导转子极偏角的增大而增大. 由图9和(13)式可知, 加工误差
$ {a_3} $ 比离心变形${a_2}$ 产生的磁支承干扰力矩, 对超导转子极轴偏移的影响更大, 约高$27.3{\text{%}} $ . 因此, 为提高超导磁悬浮装置精度, 进一步优化转子结构, 与减小离心变形产生的干扰力矩相比, 可以优先减小加工误差, 以减少磁支承干扰力矩对转子极轴偏移的影响. -
磁支承干扰力矩的变化会导致磁悬浮力的变化, 磁悬浮力的变化会使超导转子的悬浮位置相对球腔中心位置的变化, 致使超导转子的极轴偏移, 产生干扰力矩[8]. 悬浮位置的漂移会产生额外的磁干扰力矩, 影响着超导转子的极轴偏移. 接下来讨论未悬浮在中心位置时, 磁支承干扰力矩对转子极轴偏移的影响, 此时超导转子干扰力矩由两部分组成[15], 由(24)式和(25)式可以得到:
1) 由非球形误差引起的干扰力矩, 即一次磁力矩:
2) 由转子非球形误差与转子-球腔间隙误差组合产生的干扰力矩-二次磁力矩. 产生转子失中度的主要原因是由于外力使转子偏移球腔中心:
式中, r是超导转子表面微元ds相对球心的径向长度,
$ {{\boldsymbol{r}}_0} $ 是其对应的径向矢量, OZ2是超导转子极轴矢量,${\theta _0}$ 是转子表面微元ds与球腔坐标系$z$ 轴的夹角,${\theta _1}$ 是转子表面微元ds与转子坐标系$z$ 轴的夹角,${a_2}$ 是转子的离心变形、${a_3}$ 是转子的加工误差.当在中心位置向下偏移0.1 mm时, 转子转速为166 Hz, a2 = 1 μm, a3 = 1 μm时:
当在中心位置向上偏移0.1 mm时, 转子转速为166 Hz, a2 = 1 μm, a3 = 1 μm时:
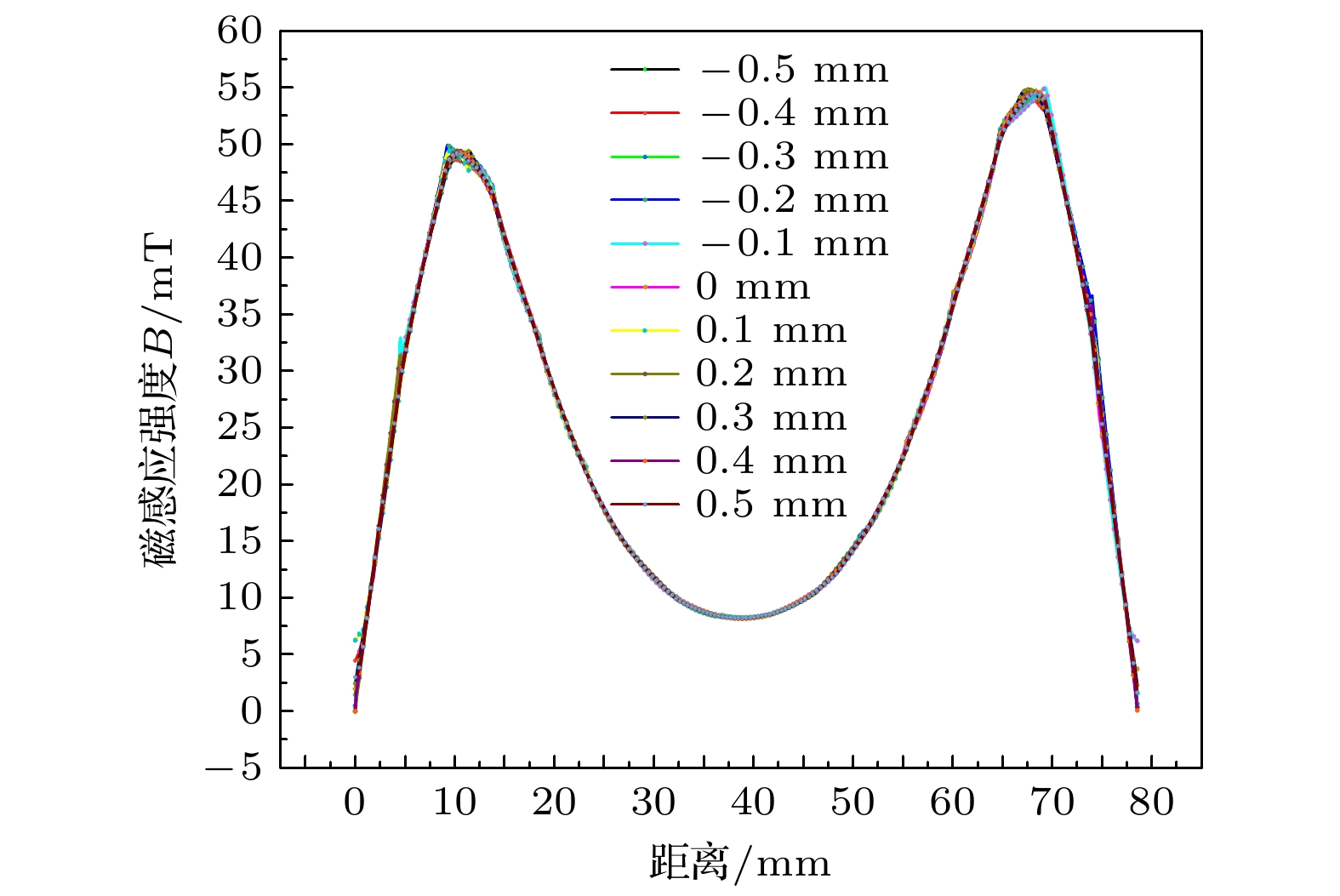
图10是超导转子中心位置偏移时引起的磁干扰力矩与漂移速度, 干扰力矩和漂移速度偏移距 离增大而增大, 随超导转子极偏角的增大而增大. 且超导转子向下偏移时, 产生的漂移速度大于向上偏移时产生的漂移速度. 图11是悬浮在不同位置时, 狭窄缝隙内的磁感应强度大小分布, 图中横坐标是以转子圆弧弧线上端为零点, 下端为终点的距离, 可以看到, 悬浮位置发生变化时, 并不会致使超过临界磁场导致超导转子失超, 在极轴和赤道附近, 磁感应强度大小小于中间位置, 且下半球的磁感应强度大于上半球. 本节建立的模型和分析方法, 可用来分析完整球形转子结构的超导磁悬浮装置, 在提高装置精度时, 对超导转子的磁支承干扰力矩进行考虑是十分有必要的.
-
超导转子在地球上转动, 若转子极轴与地球自转轴不平行, 产生的转矩会作用于转子, 不可避免的会受到地球自转的影响, 在实际实验时, 壳体会随地球自转运动, 而转子由于定轴性的存在, 始终保持初始方向[11].
-
超导转子极轴与地球自转平行时, 地球自转角速度方向与转动方向相同或相反, 不对超导转子极轴偏移产生影响.
-
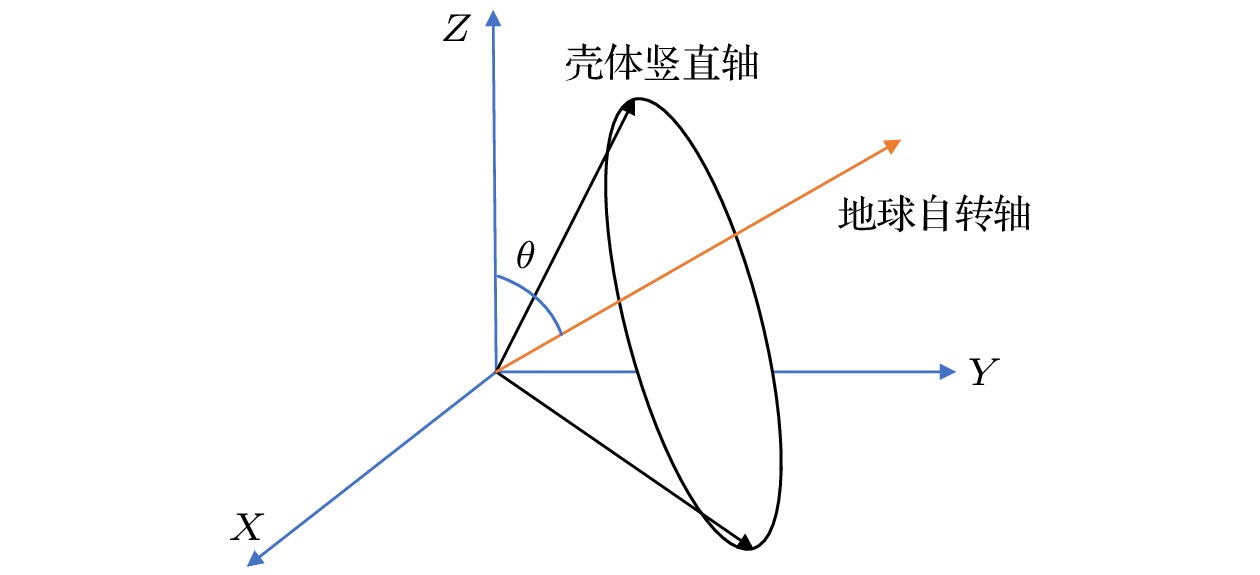
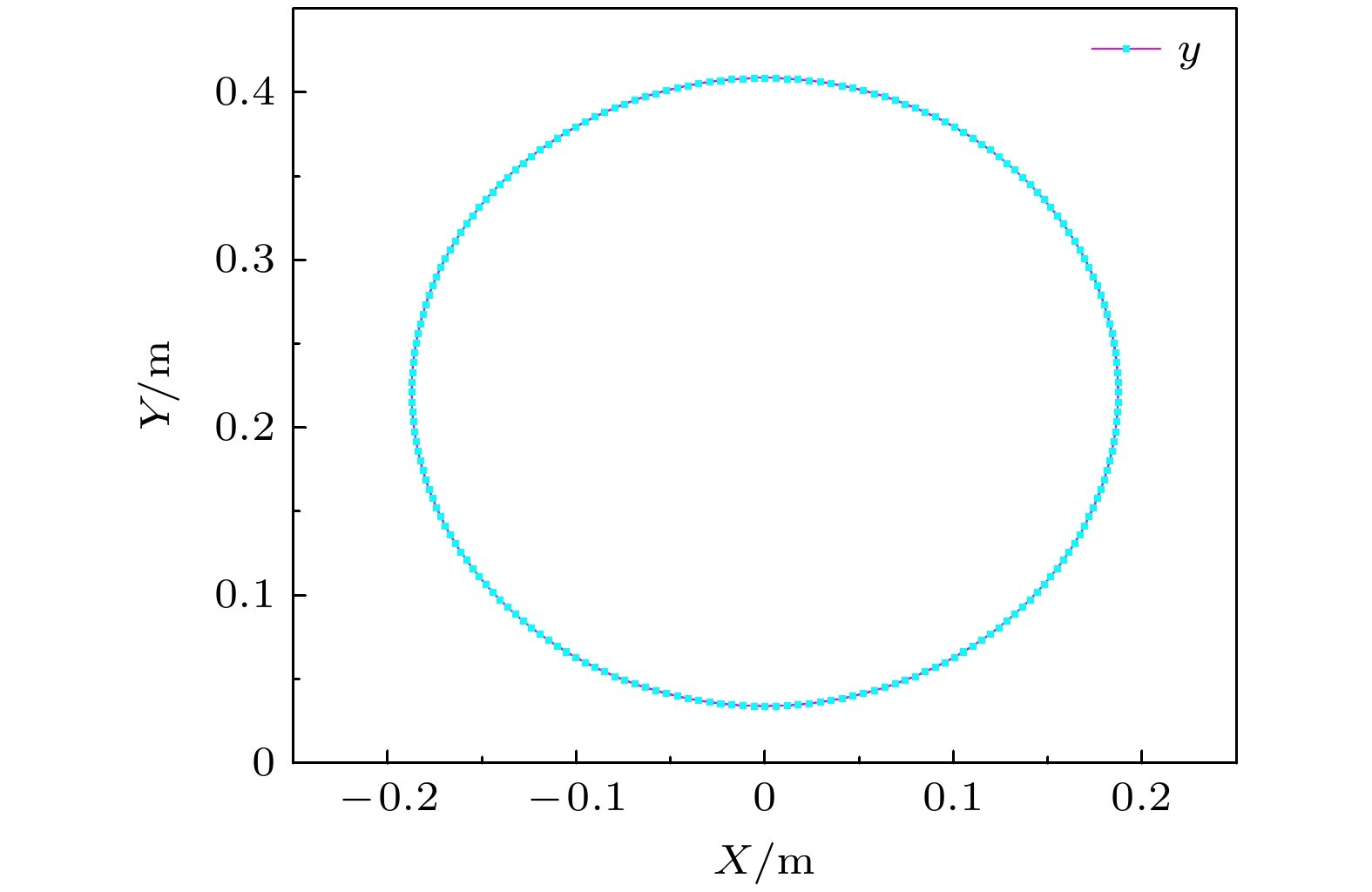
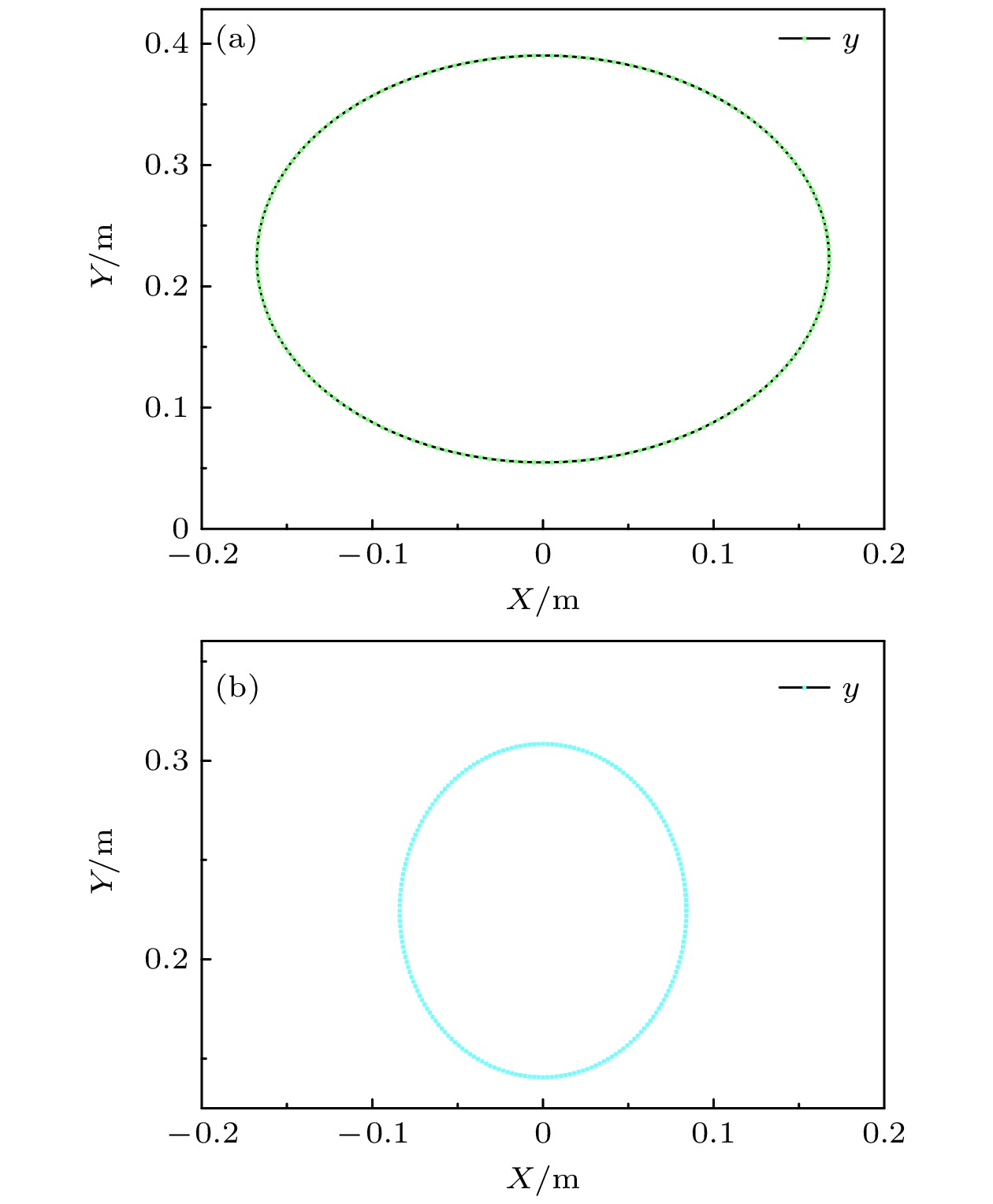
在地球自转的作用下, 超导转子的动量矩矢量H将绕当地水平坐标系竖直轴做小顶角的锥面运动, 经过几何分析, 可求得转子极轴绕罐体轴旋转的轨迹, 如图12所示. 圆心即罐底投影在XOY面的运动轨迹如图13所示.
圆心坐标
$ {O'}(0, {\text{ }}R\cos \theta \sin \theta , {\text{ }}R{\cos ^2}\theta ) $ ;圆函数方程为
式中, R为罐底到质心的距离,
$\theta $ 为当地纬度余角. -
当罐体初始角度发生变化时, 漂移测试方案与最终的漂移精度也会随之改变, 这对于我们提高装置精度, 完善漂移补偿机制是十分必要的[17].
此时, 转子的运动方程可表示为
式中, R为罐底到质心的距离,
$\theta $ 为当地纬度余角,$\varphi $ 为倾斜角度.在确定超导转子磁悬浮装置的漂移测试方案时, 需要考虑装置的倾倒角度[18–21]. 选择不同的初始角度, 需构建不同的漂移误差模型, 采取不同的漂移测试方案, 其能达到的漂移测试精度也不一样. 不同的初始角度, 锥形运动的轨迹是不同的, 如图14所示. 在构建漂移误差模型时, 地球自转对超导转子漂移测试的影响是不可忽略的. 通过改变不同的初始角度, 可以得到不同角度下的极轴运动轨迹, 并以此来标定出地球自转对转子极轴漂移的影响比重, 为后续漂移误差分析提供一定的参考.
-
本文对一种完整球形转子磁悬浮结构的极轴偏移特性进行了分析, 基于矢量磁势方程和超导电动力学, 利用有限元仿真软件对超导转子磁支承系统进行建模, 分析了转子在理想状态下(即悬浮于球腔中心位置)的磁场强度分布, 分析了磁场强度对磁支承力的影响.
基于完整球形转子的转子动力学方程, 分析了超导转子球面误差引起的磁支承干扰力矩及其漂移误差, 包括转子球面误差引起的一次干扰力矩、转子离心变形和失中度耦合产生的二次干扰力矩, 得到了不同参数下漂移率. 同时对离心变形和加工误差各自引起的磁支承干扰力矩大小进行了对比分析, 结果表明, 同一极偏角在相同转速时, 加工误差比离心变形对转子极轴偏移的影响更大, 约高
$27.3{\text{%}}$ . 结果为后续转子漂移误差分析, 进一步完善转子结构提供了一定参考.最后, 还分析了地球自转对转子漂移测试的影响, 通过理论分析得到其极轴运动轨迹, 推导出极轴运动轨迹方程. 研究结果为提升转子漂移精度, 进行误差补偿提供了一定参考. 以上分析结果可以为新型完整球形转子结果设计与优化以及系统评估提供一定的参考.
完整球形超导转子极轴偏移特性的主要影响因素
Main factors affecting polaraxis offset characteristics of intact spherical superconducting rotor
-
摘要: 超导转子凭借其独特的物理性质, 在精密测量领域具有巨大的应用潜力. 超导转子磁悬浮装置可制作高精度角速度传感器, 在外界干扰力矩作用下, 极轴偏移初始位置是引起超导转子极轴漂移误差的原因, 其中球面误差和地球自转属于主要误差源, 对超导转子球面误差引起的极轴研究结果为提升转子漂移精度、进行误差补偿提供了一定参考. 速度进行补偿是实现超导转子磁悬浮装置高精度的关键步骤. 基于此, 开展了完整球形超导转子球面误差和地球自转对超导转子极轴偏移特性的影响因素研究. 首先, 本文基于矢量磁势方程对超导转子磁支承结构进行建模, 分析了理想状态下(即悬浮于球腔中心位置)超导转子表面的磁场强度分布, 研究了磁支承力特性. 然后分析了球面误差引起的超导转子的磁支承干扰力矩, 并基于超导转子动力学方程, 建立了超导转子动力学模型, 给出了不同转子结构参数下超导转子极轴漂移误差的分布规律. 最后, 探讨了地球自转对超导转子漂移测试的影响. 研究结果为后续提升转子漂移精度、优化转子结构设计和漂移测试方法的完善提供了参考.Abstract: Superconducting rotor has great potential applications in the field of precision measurement due to its unique physical properties. The superconducting rotor magnetic levitation device can be used to fabricate high-precision angular velocity sensors. Under the action of external interference torque, the pole-axis deviation from the initial position is the cause of the superconducting rotor pole-axis drift error, in which the spherical surface error and the earth’s rotation belong to the main sources of error, and compensating for the pole-axis drift speed caused by the spherical surface error of the superconducting rotor is a key step in realizing the high-precision superconducting rotor magnetic levitation device. Based on this, the factors affecting the spherical surface error of a complete spherical superconducting rotor and the rotation of the earth on the pole-axis offset characteristics of a superconducting rotor are investigated. First, the magnetic support structure of the superconducting rotor is modeled based on the vector magnetic potential equation, the magnetic field strength distribution on the surface of the superconducting rotor in the ideal state (i.e. suspended in the center of the spherical cavity) is analyzed, and the magnetic support force characteristics are investigated. Then the magnetic support interference moment of the superconducting rotor caused by the spherical surface error is analyzed, and a superconducting rotor dynamics model is established based on the superconducting rotor dynamics equations, and the distribution law of the superconducting rotor pole-axis drift error under different rotor structural parameters is given. Finally, the influence of the earth’s rotation on the superconducting rotor drift test is investigated. The results provide a reference for subsequently improving rotor drift accuracy, optimizing rotor structure design and improving drift test methods.
-
-
图 2 (a) 悬浮线圈产生的磁场分布图; (b) 悬浮于中心位置时, 超导转子狭窄缝隙内磁感应强度分布图
Figure 2. (a) Distribution of magnetic field generated by suspension coils; (b) distribution map of magnetic induction intensity in the narrow gap of the superconducting rotor when suspended at the center position.
图 3 上下线圈同时通电2.7—3.0 A时超导磁悬浮系统磁密分布图
Figure 3. Magnetic density distribution diagram of superconducting maglev system when the lower coil is energized at 2.7–3.0 A simultaneously.
图 5 超导球形转子欧拉角示意图
Figure 5. Schematic diagram of Euler angle of superconducting spherical rotor.
图 6 超导转子磁感应强度计算模型
Figure 6. Calculation model for magnetic induction intensity of superconducting rotor.
图 7 (a)超导转子产生的磁支承干扰力矩; (b)磁支承力矩产生的漂移速度
Figure 7. (a) Magnetic support interference torque generated by superconducting rotor; (b) drift velocity generated by magnetic support torque.
图 8 (a) a2 = 100 μm, a3 = 1 μm, 超导转子产生的磁支承干扰力矩; (b) a2 = 1 μm, a3 = 100 μm, 超导转子产生的磁支承干扰力矩; (c) a2 = 100 μm, a3 = 1 μm, 超导转子磁支承干扰力矩产生的漂移速度; (d) a2 = 1 μm, a3 = 100 μm, 超导转子磁支承干扰力矩产生的漂移速度
Figure 8. (a) When a2 = 100 μm, a3 = 1 μm, the superconducting rotor generates magnetic support interference torque; (b) when a2 = 1 μm, a3 = 100 μm, the superconducting rotor generates magnetic support interference torque; (c) a2 = 100 μm, a3 = 1 μm, drift velocity generated by the interference torque of the superconducting rotor magnetic support; (d) a2 = 1 μm, a3 = 100 μm, drift velocity generated by the interference torque of the superconducting rotor magnetic support.
图 9 a2和a3连续变化时, 磁力矩变化情况
Figure 9. Changes in magnetic torque during a2 and a3 continuous variation.
图 10 (a)中心位置向下偏移0.1 mm时, 产生的磁支承干扰力矩; (b)中心位置向上偏移0.1 mm时, 产生的磁支承干扰力矩; (c)中心位置向下偏移0.1 mm时, 超导转子磁支承干扰力矩产生的漂移速度; (d)中心位置向上偏移0.1 mm时, 超导转子磁支承干扰力矩产生的漂移速度
Figure 10. (a) When the center position is shifted downwards by 0.1 mm, the magnetic support interference torque generated by the superconducting rotor; (b) when the center position is shifted upwards by 0.1 mm, the magnetic support interference torque generated by the superconducting rotor; (c) drift velocity caused by magnetic support interference torque of superconducting rotor when the center position is shifted downwards by 0.1 mm; (d) drift velocity generated by the interference torque of the superconducting rotor magnetic support when the center position is shifted upwards by 0.1 mm.
图 11 悬浮在不同位置时, 狭窄缝隙内的磁感应强度大小分布
Figure 11. Distribution of magnetic induction intensity in narrow gaps when suspended at different positions.
图 13 由于地球自转, 转子极轴绕罐体轴旋转的轨迹在
$XOY$ 面的投影Figure 13. Due to the rotation of the earth, the trajectory of the rotor’s polar axis rotating around the axis of the tank is projected onto the
$XOY$ plane. -
[1] 赵尚武 2010 博士学位论文 (北京: 中国科学院大学) Zhao S W 2010 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences [2] Christen D K, Kerchner H R, Sekula S T, Thorel P 1980 Phys. Rev. B 21 102 doi: 10.1103/PhysRevB.21.102 [3] 张裕恒 1997 超导物理(合肥: 中国科学技术大学出版社) 第11—12页 Zhang Y H 1997 Superconducting Physics (Hefei: University of Science and Technology of China Press) pp11–12 [4] 管惟炎, 李宏成, 蔡建华, 吴杭生 1981 超导电性物理基础(北京: 科学出版社)第47—51页 Guan W Y, Li H C, Cai J H, Wu H S 1981 The Physical Basis of Superconductivity (Beijing: Science Press) pp47–51 [5] Harding T H, Lawson D W 1968 AIAA J. 6 305 doi: 10.2514/3.4494 [6] Schoch K F, Darrel B 1967 Adv. Cryog. Eng. 12 657 [7] 张源, 胡新宁, 崔春艳, 崔旭, 牛飞飞, 黄兴, 王路忠, 王秋良 2024 物理学报 73 038401 doi: 10.7498/aps.73.20231455 Zhang Y, Hu X N, Cui C Y, Cui X, Niu F F, Huang X, Wang L Z, Wang Q L 2024 Acta Phys. Sin. 73 038401 doi: 10.7498/aps.73.20231455 [8] 崔春艳, 胡新宁, 程军胜, 王晖, 王秋良 2015 物理学报 64 018403 doi: 10.7498/aps.64.018403 Cui C Y, Hu X N, Chen J S, Wang H, Wang Q L 2015 Acta Phys. Sin. 64 018403 doi: 10.7498/aps.64.018403 [9] 张源, 胡新宁, 崔春艳, 崔旭, 牛飞飞, 黄兴, 王路忠, 王秋良 2023 物理学报 72 128401 doi: 10.7498/aps.72.20230328 Zhang Y, Hu X N, Cui C Y, Cui X, Niu F F, Huang X, Wang L Z, Wang Q L 2023 Acta Phys. Sin. 72 128401 doi: 10.7498/aps.72.20230328 [10] 杨再敏, 胡新宁, 崔春艳, 王秋良 2007 低温与超导 46 1 doi: 10.3969/j.issn.1001-7100.2007.01.001 Yang Z M, Hu X N, Cui C Y, Wang Q L 2007 Cryog. Superconduct. 46 1 doi: 10.3969/j.issn.1001-7100.2007.01.001 [11] 刘延柱 1979 静电陀螺仪动力学 (北京: 清华大学出版社) 第21—23页) Liu Y Z 1979 Electrostatic Gyroscope Dynamics (Beijing: Tsinghua University Press) pp21–23 [12] Lin Q R, Zhao Y M 1987 Magnetic Circuit Design Principle (Beijing: Machinery Industry Press) pp87–88 [林其壬, 赵佑民 1987 磁路设计原理(北京: 科学出版社)第87—88页] Lin Q R, Zhao Y M 1987 Magnetic Circuit Design Principle (Beijing: Machinery Industry Press) pp87–88 [13] 邹继斌, 刘宝庭, 崔淑海, 郑萍 1998 磁路与磁场(哈尔滨: 哈尔滨工业大学出版社)第 43—47 页) Zou J B, Liu B T, Cui S H, Zheng P 1998 Magnetic Circuit and Magnetic Field (Harbin: Harbin Institute of Technology Press) pp43–47 [14] 刘延柱 2009陀螺力学 (北京: 科学出版社) Liu Y Z 2009 Mechanics of Gyroscopes (Beijing: Science Press [15] 高钟毓 2004 静电陀螺仪技术 (北京: 清华大学出版社) 第21—23页) Gao Z Y 2004 Electrostatic Gyroscope Dynamics (Beijing: Tsinghua University Press) pp21–23 [16] 胡新宁, 赵尚武, 王厚生, 王晖, 王秋良 2008稀有金属材料与工程 37 436 Hu X N, Zhao S W, Wang H S, Wang H, Wang Q L 2008 Rare Metal Mater. Eng. 37 436 [17] 何川 2007 博士学位论文 (北京: 中国科学院大学) He C 2007 Ph. D. Dissertation (Beijing: University of Chinese Academy of Sciences [18] 崔春艳, 王秋良, 胡新宁, 赵尚武 2008稀有金属材料与工程 37 57 Cui C Y, Wang Q L, Hu X N, Zhao S W 2008 Rare Metal Mater. Eng. 37 57 [19] 王浩, 王秋良, 胡新宁, 崔春艳, 苏华骏, 何忠名 2018 低温与超导 46 1 Wang H, Wang Q L, Hu X N, Cui C Y, Su H J, He Z M 2018 Cryog. Superconduct. 46 1 [20] 汤继强 2005 博士学位论文(哈尔滨: 哈尔滨工程大学) Tang J Q 2005 Ph. D. Dissertation (Harbin: Harbin Engineering University [21] 刘建华, 王秋良, 严陆光, 李献 2010 电工技术学报 25 1 Liu J H, Wang Q L, Yan L G, Li X 2010 Transactions China Electrotech. So. 25 1 -
计量
- 文章访问数: 608
- HTML全文浏览数: 608
- PDF下载数: 1
- 施引文献: 0