首页
登录
注册
-
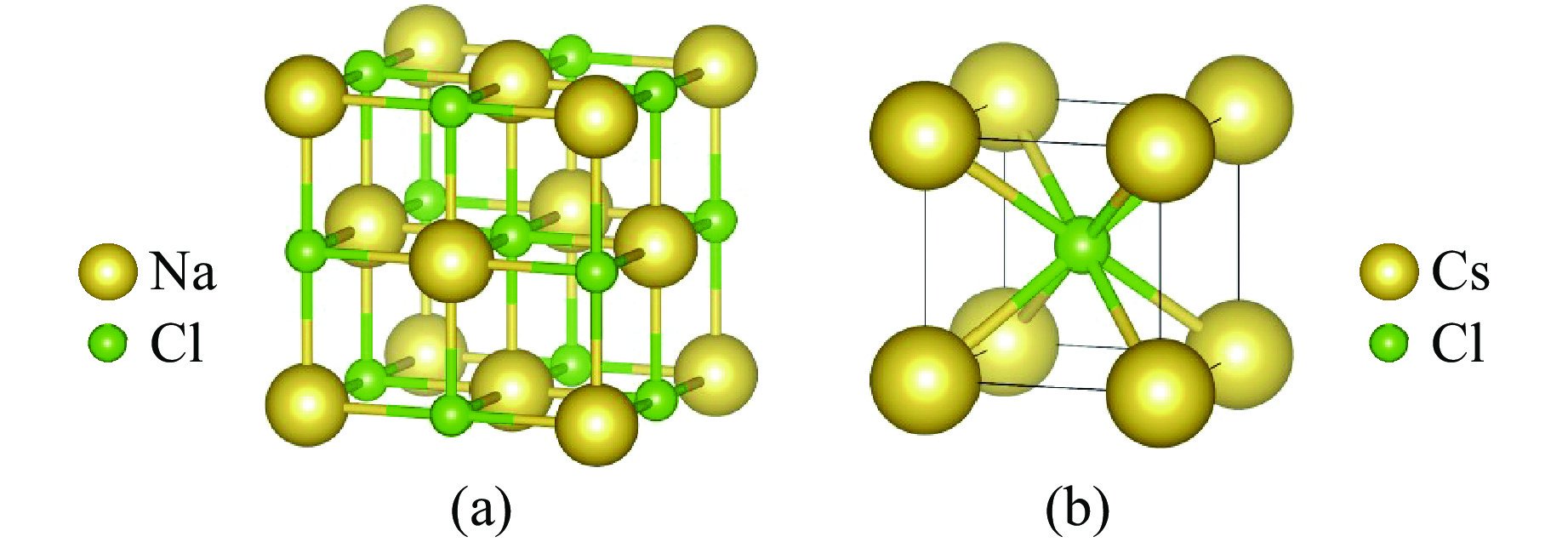
碱金属卤化物是由卤族元素和碱金属元素形成的离子化合物。如图1所示，它有2种基本结构：一种是面心立方结构，以NaCl为代表；另一种则是体心立方结构，以CsCl为代表。在标准大气压条件下，仅CsCl、CsBr和CsI这3种碱金属卤化物为CsCl型结构，其他成员皆为NaCl型结构。然而，在压力作用下，碱金属卤化物普遍会发生由NaCl结构到CsCl结构的转变。碱金属卤化物具有较宽的能量带隙、较低的熔点、高离子性、易形成稳定的离子晶体等物理化学特性，被广泛应用于电池材料、电解质、光电器件、催化剂以及核反应堆冷却剂等领域[1]。随着科技进步和全球可持续发展的不断推进，对碱金属卤化物的研究也朝着更深入的微观结构理解、更广泛的创新应用方向发展。例如：张程祥等[2]通过晶格动力学方法讨论了NaCl、KCl和NaF晶体的相Ⅰ、相Ⅱ结构的相变点及吉布斯函数，发现次近邻离子对之间存在较强的短程吸引作用，对上述晶体的高压结构相变起关键作用；孙力等[3]在2000年对Eu2+离子掺杂的KCl荧光粉的光存储性能进行了首次探索性研究，拓展了碱金属卤化物的研究路径；崔守鑫等[4]采用分子动力学方法探究了NaCl晶体在高温高压环境下的热物理特性。近年来，碱金属卤化物在新型储能技术、光电子学以及清洁能源技术等方面取得了显著进展。例如：郑东阳等[5]制备的KBr单晶展现出优越的光学性能；Jiang等[6]发现NaCl纳米晶作为癌症治疗药物成分，在有效摧毁癌细胞的过程中还展示出提升机体免疫力的额外优势，拓展了碱金属卤化物的医疗应用；Bangaru等[7–9]探究了3种碱金属卤化物（KCl、KBr和KI）在稀土元素（Tb、Ce）掺杂条件下的热释发光特性和光致发光特性，发现这类稀土掺杂的卤化物晶体适合作为高级辐射检测材料；Okada等[10]对Sm掺杂的KBr晶体中热释发光的动力学过程和光致发光现象进行了深入研究。可见，碱金属卤化物一直是众多科学领域的重要研究对象，而在诸多碱金属卤化物中，NaCl、KCl、KBr是最常见的研究对象。此外，深入研究碱金属卤化物的晶体结构、热力学性质、动力学行为有助于提高其性能，为设计更环保、更高效的产品提供帮助。相变能够改变物质的物理性质、结构和能量状态，研究碱金属卤化物的高压相变不仅能够阐明离子晶体相变的微观机制，还有助于优化功能材料属性。因此，本研究针对NaCl、KCl、KBr这3种最常见的碱金属卤化物，探究它们在高压相变过程中的晶体结构、力学性质以及电子性质的变化，判断其高压相变点，以期深入理解碱金属卤化物的高压相变的微观机理，同时探讨不同诊断方法对相变点判断的敏感性，为碱金属卤化物的系统研究提供理论依据。
-
基于密度泛函理论（density functional theory，DFT）的第一性原理方法，采用CASTEP代码[11]中的模守恒赝势，选用广义梯度近似（generalized gradient approximation，GGA）[12]中的Perdew-Burke-Ernzerh（PBE）泛函[13]进行计算。此外，引入Grimme的DFT-D方法来校正分子间的范德华力[14]。为了获得精确结果并保证计算的收敛性，NaCl和KCl的平面波截断能设为830 eV，KBr的截断能设为440 eV。对于NaCl的相Ⅰ和相Ⅱ、KCl的相Ⅱ和KBr的相Ⅱ，布里渊区k点网格设置为4×4×4；对于KCl的相Ⅰ和KBr的相Ⅰ，布里渊区k点网格设置为2×2×2。随后，进行迭代计算和结构优化，直到总能量收敛精度达到5.0×10−6 eV/atom，作用在每个原子上的力不超过0.1 eV/nm，最大应力不超过0.02 GPa，原子最大位移在5×10−4 Å以内。同时，采用CASTP代码对NaCl、KCl、KBr的相Ⅰ和相Ⅱ分别施加压力。因为NaCl、KCl、KBr从相Ⅰ（NaCl构型）转变到相Ⅱ（CsCl构型）的压强分别为30 GPa[15]、2.0 GPa[16]、2.2 GPa[17]，所以对NaCl晶体施加的压力区间为0～50 GPa，压力间隔为5 GPa，对KCl和KBr晶体施加的压力区间为0～5 GPa，压力间隔为0.5 GPa。
-
NaCl、KCl、KBr在高压下会发生从相Ⅰ（NaCl构型）至相Ⅱ（CsCl构型）的转变，为此，计算了3个碱金属卤化物的2种相在稳定压力区间内的晶体结构，即NaCl相Ⅰ在零压下及相Ⅱ在30.6 GPa下、KCl相Ⅰ在零压下及相Ⅱ在2.12 GPa下、KBr相Ⅰ在零压下及相Ⅱ在2.20 GPa下的晶格常数和原胞体积，并与实验值[15, 18–22]进行对比，结果如表1所示，其中：p为压强，a为晶格常数，V0为原胞体积。由表1可知，计算的NaCl、KCl、KBr的相Ⅰ、相Ⅱ的晶格常数a和原胞体积V0与实验值符合得较好，说明本研究所用的计算方法和模拟的结构较为精确。
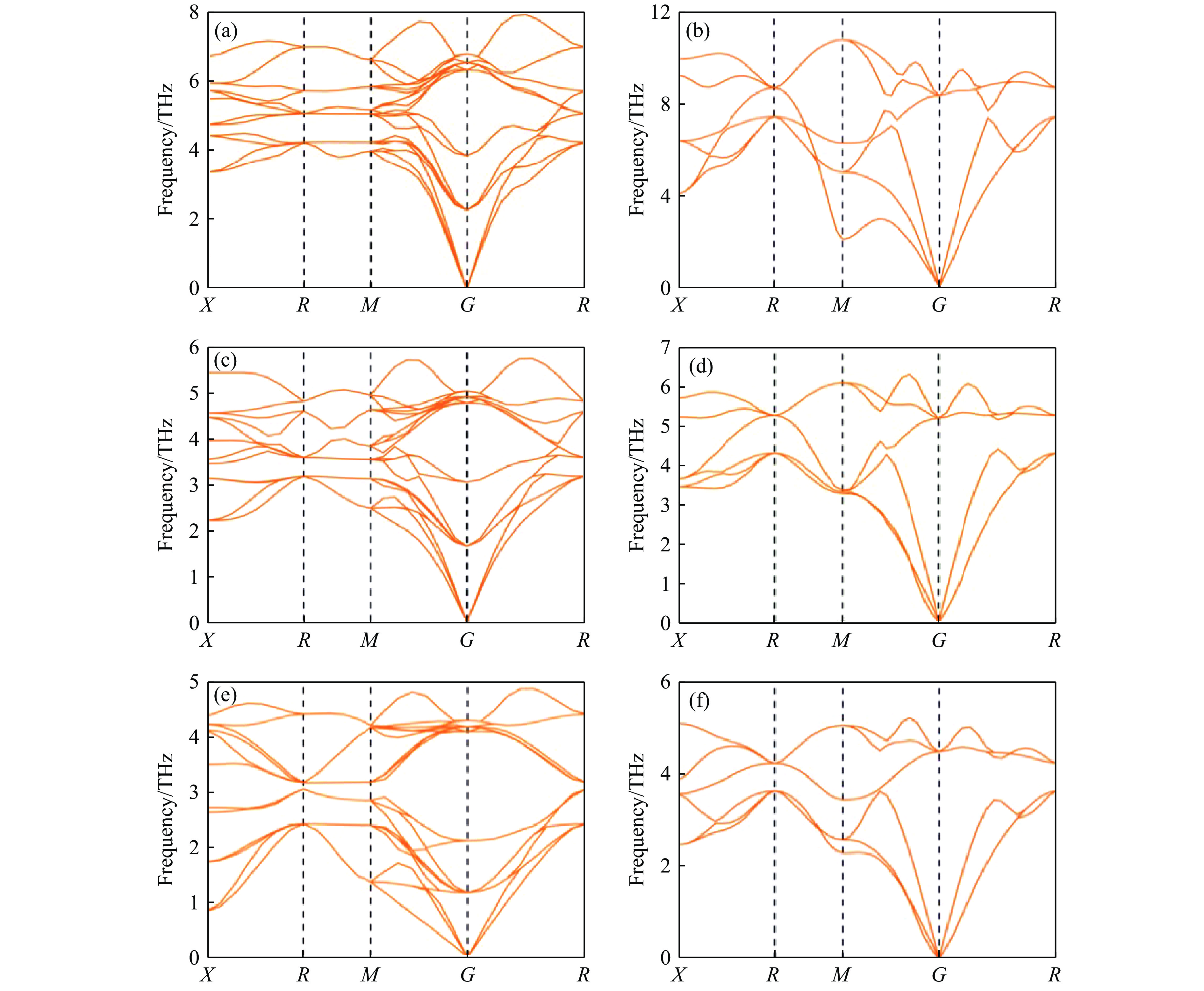
为了进一步验证所模拟结构的稳定性，计算了6种结构在稳定压力区间内的声子谱和弹性常数，结果如图2和表2所示。由图2可知，这6种结构的声子谱均未出现虚频，表明材料在所选压力区间内都是动力学稳定的，进一步说明了计算方法和模拟结构的准确性。此外，表2还列出了6种结构的独立弹性常数C11、C12、C44。依据立方晶系在压力下的力学稳定性判据[23–24]
可知，NaCl、KCl、KBr的相Ⅰ和相Ⅱ在稳定压力区间内也是力学稳定的。
-
相变过程会引起材料物理性质、结构和能量状态发生改变。通过对NaCl、KCl以及KBr的相Ⅰ和相Ⅱ分别加压，探究加压过程中材料的晶体结构、力学性能、电子性能、稳定性的变化，分析不同物理性质与相变点的相关性。
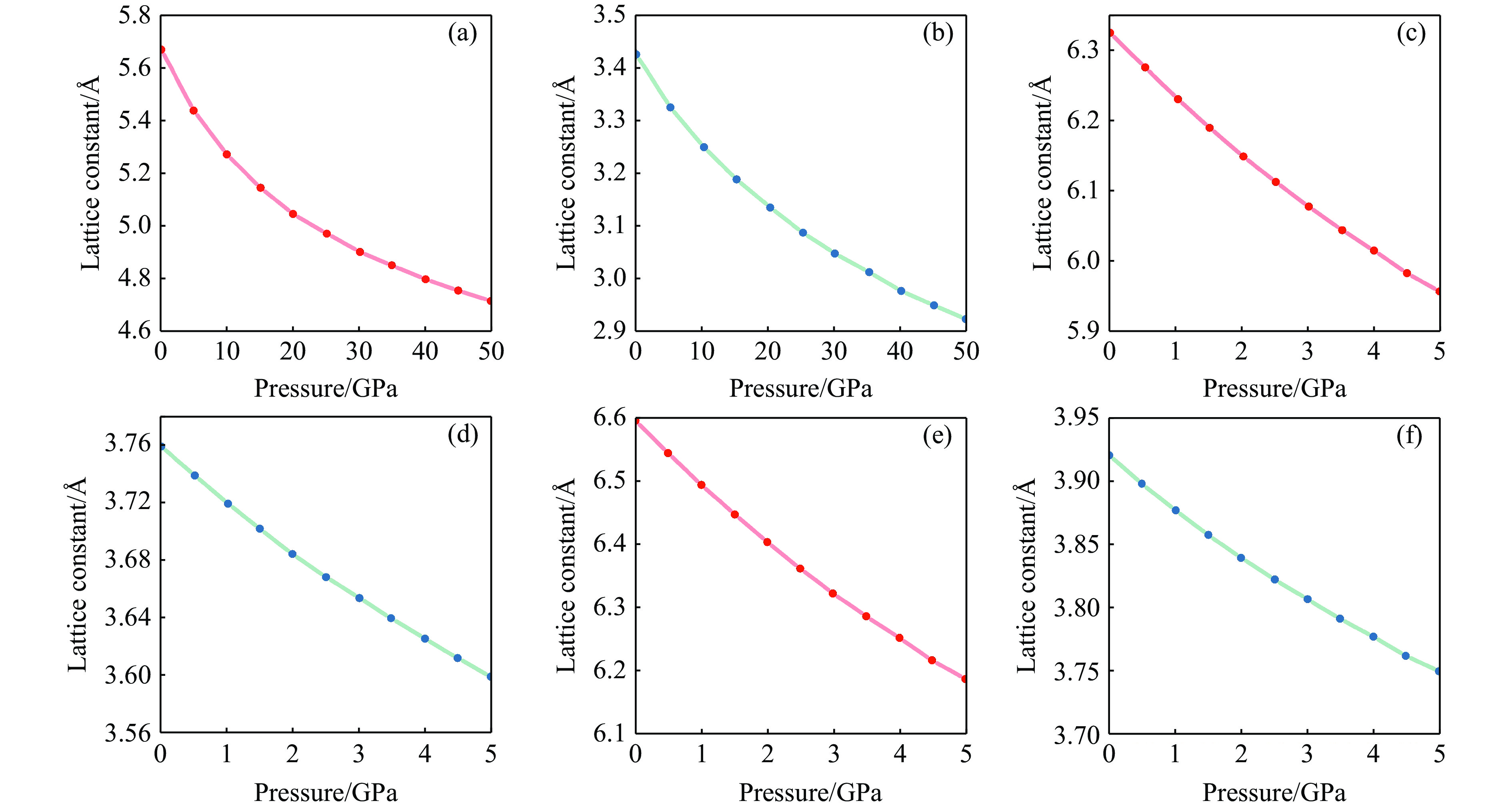
首先，讨论晶格常数与相变点的相关性。高压下6种结构的晶格常数变化如图3所示。由图3可知，对于NaCl、KCl、KBr晶体的相Ⅰ和相Ⅱ，随着压力的升高，晶格常数均减小，说明通过晶格常数不足以判断碱金属卤化物的相变点。不同构型的晶格常数对压力的响应程度存在一定的差异，其中：NaCl相Ⅰ的晶格常数压缩率为16.94%，相Ⅱ为14.80%；KCl相Ⅰ的晶格常数压缩率为5.83%，相Ⅱ为4.31%；KBr相Ⅰ的晶格常数压缩率为6.24%，相Ⅱ为4.38%。由此可知，碱金属卤化物晶体相Ⅰ构型的晶格常数对压力的响应更敏感。
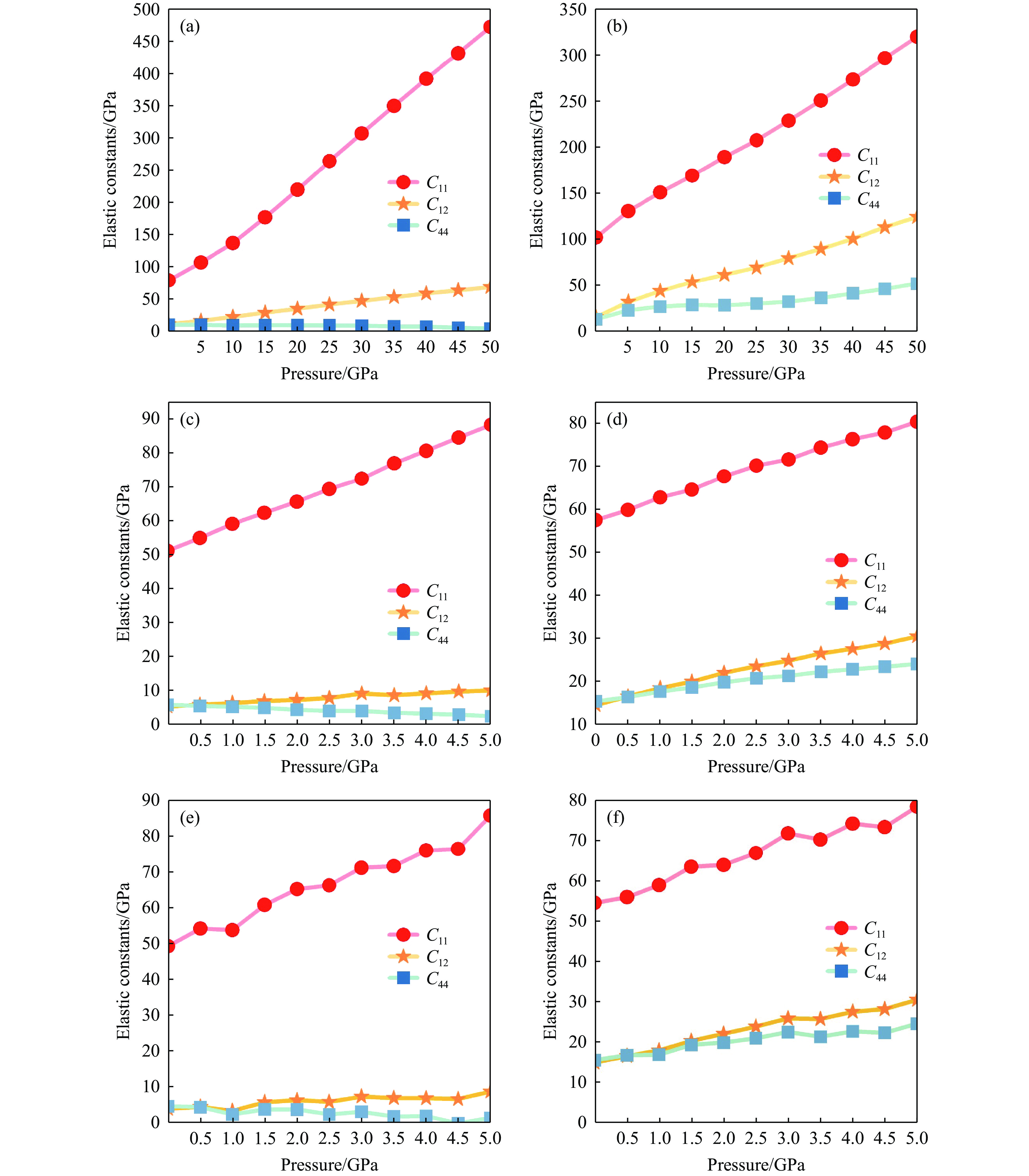
其次，讨论晶体稳定性与相变点的相关性。压力作用下6种结构的独立弹性常数变化如图4所示。根据立方晶系在压力下的力学稳定性判据[24]，NaCl的相Ⅰ和相Ⅱ在0～50 GPa内的力学性能表现为稳定，KCl和KBr的相Ⅰ、相Ⅱ在0～5 GPa内的力学性能也表现为稳定。随着压力的升高，NaCl、KCl和KBr晶体的相Ⅰ和相Ⅱ的C11均呈上升趋势，表明6种结构的抗压缩性能随着压力升高而增强；同时，观察到C44随压力的变化幅度较小，说明压力对这6种晶体结构的抗剪切能力的影响较小。虽然6种结构的弹性常数随压力的变化有细微的差异，但是总体变化趋势相同，上述结果表明，在所研究的压力范围内，6种碱金属卤化物结构都是力学稳定的。因此，无法仅仅通过力学稳定性来确定相变点。为了进一步研究晶体在不同压力下的动力学稳定性，计算了6种结构在不同压力下的声子谱，观察其是否出现虚频，统计结果如表3所示。由表3可知，NaCl的相Ⅰ在0～10 GPa压力区间未出现虚频，为动力学稳定状态，而在10～50 GPa区间出现虚频，为动力学不稳定状态。其他5种结构在所研究的压力区间都呈现出动力学稳定状态。
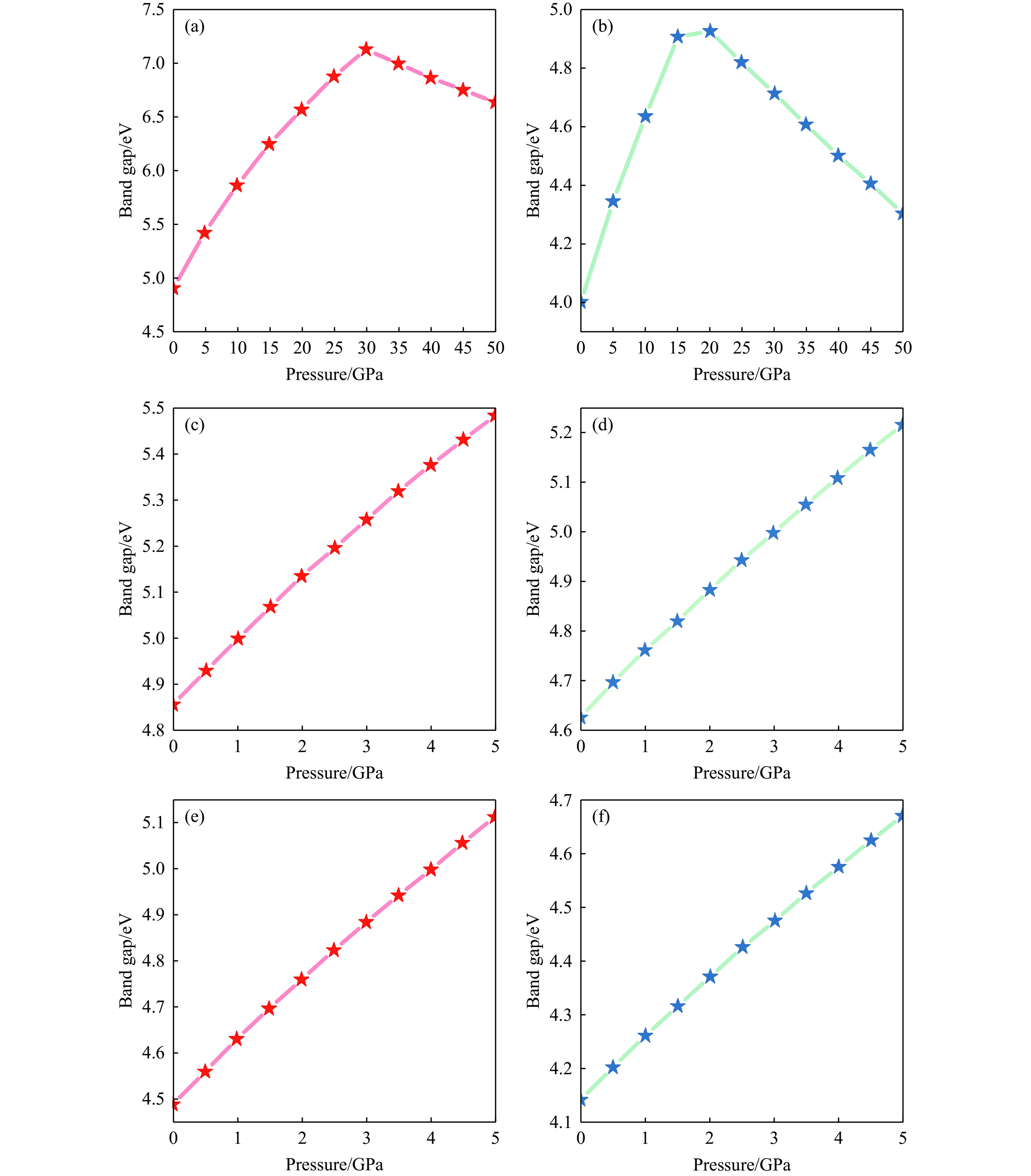
最后，讨论电子结构与相变点的相关性。压力下6种结构的带隙变化如图5所示。对于NaCl的相Ⅰ结构：在0～30 GPa压力区间，随着压力的升高，带隙不断增大，但是在30～50 GPa区间，带隙反而下降，30 GPa正位于NaCl相Ⅰ结构的相变点。对于NaCl的相Ⅱ结构：在0～15 GPa范围内，带隙随压力的升高而迅速增大；至15～20 GPa，带隙增长速度减缓；在20～50 GPa范围内，带隙快速减小。对于KCl和KBr的相Ⅰ及相Ⅱ结构，在0～5 GPa压力区间，带隙均随着压力的升高而不断增大。由NaCl相Ⅰ结构的带隙随压力的变化可知，根据电子结构对碱金属卤化物的相变点进行判断存在一定的可行性。
-
受外界条件的影响，物质总是朝着吉布斯自由能更小的方向转变。因此，可通过比较不同压力下两相的吉布斯自由能大小来确定两相的相变点。在准简谐近似下，吉布斯自由能为
式中：G为体系的吉布斯自由能，E、V分别为体系基态的总能量和体积，Fel和Fvib分别为电子热激发和原子振动对吉布斯自由能的贡献。由于所选化合物由相Ⅰ到相Ⅱ都是高压相变，且温度对吉布斯自由能的贡献主要体现在电子热激发Fel和原子振动Fvib两方面，只有在相对较高的温度下原子振动对吉布斯自由能的贡献才会更明显；同时，所研究的材料均为宽带隙半导体，需要很高的温度才会激发电子，因此，电子热激发对吉布斯自由能的影响很小。综上，暂不考虑温度对相变点的影响，则式(2)可改写为
式中：EZPE为晶体的零点振动能量。
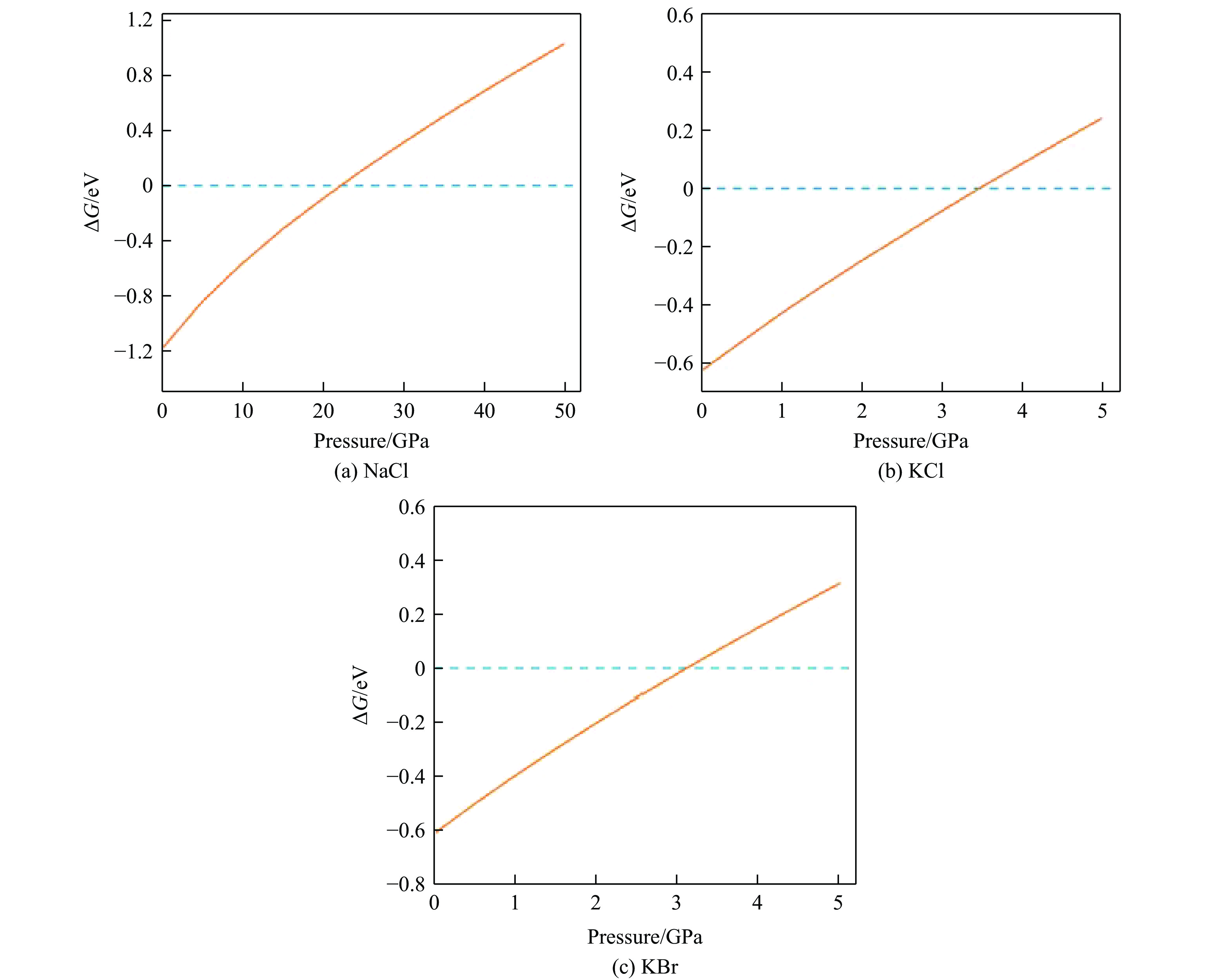
计算得到的NaCl、KCl、KBr晶体的相Ⅰ与相Ⅱ结构的吉布斯自由能之差（
$\Delta G$ ）随压力的变化如图6所示。$\Delta G$ <0 eV表示相Ⅰ的吉布斯自由能更低，此时相Ⅰ的结构更稳定；$\Delta G$ >0 eV则表示相Ⅱ结构的吉布斯自由能更低，此时相Ⅱ的结构更稳定；$\Delta G$ =0对应的压力为相Ⅰ与相Ⅱ的平衡点，也可看作相变点。从图6可以看出，根据吉布斯自由能，推断NaCl、KCl、KBr的相变点分别为22.26、3.47和3.11 GPa。 -
采用基于DFT的第一性原理计算方法，对3种典型碱金属卤化物NaCl、KCl和KBr进行了研究，通过计算不同压力范围内3种物质的相Ⅰ和相Ⅱ的晶体结构、电子结构以及力学性质，探讨了压力下这些性质的变化与相变点之间的关系，根据吉布斯自由能法对相变点进行推断，得到以下主要结论。
(1) 在晶体结构方面，随着压力的升高，6种结构的晶格常数均减小，但对压力的响应程度存在一定的差异，整体而言，相Ⅰ的晶格常数对压力的敏感程度大于相Ⅱ。通过晶体结构变化不足以判断碱金属卤化物的相变点。
(2) 在电子结构方面，NaCl相Ⅰ的带隙随着压力的升高先增大后减小，30 GPa为NaCl相Ⅰ结构的相变点，说明通过电子结构判断金属卤化物的高压相变点存在一定的可行性。
(3) 在稳定性方面，随着压力的升高，NaCl、KCl、KBr的相Ⅰ和相Ⅱ的力学性能均保持稳定，抗压缩能力逐渐增强，但抗剪切能力的变化幅度较小。此外，NaCl的相Ⅰ结构在10～50 GPa压力区间的声子谱出现虚频，说明在此压力区间其动力学不稳定。采用吉布斯自由能法计算出NaCl、KCl、KBr的相变点分别为22.26、3.47、3.11 GPa，计算结果所呈现的变化规律与实验结果较为符合。因此，利用吉布斯自由能法或压力下的电子结构判断金属卤化物的相变点具有一定的可行性。
典型碱金属卤化物高压相变的第一性原理研究
First-Principles Investigation of the High-Pressure Phase Transition in Representative Alkali Metal Halides
-
摘要: 基于密度泛函理论的第一性原理计算方法，研究了NaCl、KCl和KBr晶体在不同压力下相Ⅰ和相Ⅱ构型的几何、电子和力学性质，探讨了这些性质与相变点之间的关系，利用吉布斯自由能法对NaCl、KCl与KBr晶体的相变点进行判断。结果显示，对于NaCl的相Ⅰ结构，在0～30 GPa压力范围内，随着压力的升高，带隙不断增大；在30～50 GPa压力范围内，带隙随着压力的升高而下降，30 GPa正位于NaCl相Ⅰ结构的相变点。这表明根据电子结构判断金属卤化物在压力作用下的相变点具有一定的可行性。由高压下的晶体结构、声子谱以及力学稳定性无法对碱金属卤化物的相变点进行判断。通过吉布斯自由能法计算出了NaCl、KCl和KBr的相变点，分别为22.26、3.47和3.11 GPa。Abstract: Utilizing first-principles calculations based on density functional theory, this study investigates the geometric, electronic, and mechanical properties of NaCl, KCl, and KBr crystals in phase Ⅰ and phase Ⅱ structures under varying pressures. The relationships between these properties and the phase transition points are explored. Additionally, the Gibbs free energy method was employed to judge the phase transition points of NaCl, KCl, and KBr crystals. The results show that in the phase Ⅰ structure of NaCl, the band gap value increases with pressure from 0 to 30 GPa. However, in the range of 30−50 GPa, the band gap value decreases, indicating that 30 GPa is the phase transition point for NaCl phase Ⅰ. This suggests that pressure-induced changes in electronic structure can be indicative of metal halide phase transition points to some extent. However, pressure-induced alterations in crystal structure, phonon spectrum, and mechanical stability cannot reliably indicate alkali metal halide phase transition points. Furthermore, the phase transition points for NaCl, KCl and KBr calculated by Gibbs free energy method are 22.26, 3.47 and 3.11 GPa, respectively.
-
Key words:
- alkali halide /
- phase transition /
- first-principles /
- high pressure /
- band gap /
- Gibbs free energy .
-
-
图 1 (a) NaCl型结构，(b) CsCl型结构
Figure 1. (a) NaCl-type structure; (b) CsCl-type structure
图 2 6种结构在稳定压力区间的声子谱：(a) 零压下NaCl相Ⅰ，(b) 30.6 GPa下NaCl相Ⅱ，(c) 零压下KCl相Ⅰ，(d) 2.12 GPa下KCl相Ⅱ，(e) 零压下KBr相Ⅰ，(f) 2.20 GPa下KBr相Ⅱ
Figure 2. Phonon spectra for six structures in the stable pressure range: (a) NaCl phase Ⅰ at zero pressure; (b) NaCl phase Ⅱ at 30.6 GPa; (c) KCl phase Ⅰ at zero pressure; (d) KCl phase Ⅱ at 2.12 GPa; (e) KBr phase Ⅰ at zero pressure; (f) KBr phase Ⅱ at 2.20 GPa
图 3 压力下6种结构的晶格常数a的变化：(a) 0～50 GPa下NaCl的相Ⅰ，(b) 0～50 GPa下NaCl的相Ⅱ，(c) 0～5 GPa下KCl的相Ⅰ，(d) 0～5 GPa下KCl的相Ⅱ，(e) 0～5 GPa下KBr的相Ⅰ，(f) 0～5 GPa下KBr的相Ⅱ
Figure 3. Lattice parameter a changes for six structures under pressure: (a) NaCl phase Ⅰ at 0−50 GPa; (b) NaCl phase Ⅱ at 0−50 GPa; (c) KCl phase Ⅰ at 0−5 GPa; (d) KCl phase Ⅱ at 0−5 GPa; (e) KBr phase Ⅰ at 0−5 GPa; (f) KBr phase Ⅱ at 0−5 GPa
图 4 压力下6种结构的独立弹性常数：(a) 0～50 GPa下NaCl的相Ⅰ，(b) 0～50 GPa下NaCl的相Ⅱ，(c) 0～5 GPa下KCl的相Ⅰ，(d) 0～5 GPa下KCl的相Ⅱ，(e) 0～5 GPa下KBr的相Ⅰ，(f) 0～5 GPa下KBr的相Ⅱ
Figure 4. Independent elastic constants for six structures under pressure: (a) NaCl phase Ⅰ at 0−50 GPa; (b) NaCl phase Ⅱ at 0−50 GPa; (c) KCl phase Ⅰ at 0−5 GPa; (d) KCl phase Ⅱ at 0−5 GPa; (e) KBr phase Ⅰ at 0−5 GPa; (f) KBr phase Ⅱ at 0−5 GPa
图 5 压力下6种结构的能带带隙：(a) NaCl相Ⅰ，(b) NaCl相Ⅱ，(c) KCl相Ⅰ，(d) KCl相Ⅱ，(e) KBr相Ⅰ，(f) KBr相Ⅱ
Figure 5. Band gaps of six structures under pressure: (a) NaCl phase Ⅰ; (b) NaCl phase Ⅱ; (c) KCl phase Ⅰ; (d) KCl phase Ⅱ; (e) KBr phase Ⅰ; (f) KBr phase Ⅱ
图 6 NaCl、KCl和KBr的相Ⅰ与相Ⅱ的吉布斯自由能之差随压力的变化
Figure 6. Variations of Gibbs free energy difference of phase Ⅰ and phase Ⅱ structures of NaCl, KCl and KBr with pressure
表 1 NaCl、KCl、KBr的相Ⅰ和相Ⅱ结构的晶格常数和原胞体积
Table 1. Lattice constant and cell volumes for phase Ⅰ and phase Ⅱ structures of NaCl, KCl and KBr
Material Phase Space group p/GPa a/Å V0/Å3 Method NaCl Ⅰ $Fm\overline 3 m $ 0 5.672 45.637 This work 0 5.640 44.830 Experiment[18] NaCl Ⅱ $Pm\overline 3 m $ 30.6 3.043 28.186 This work 30.6 3.010 27.271 Experiment[15] KCl Ⅰ $Fm\overline 3 m $ 0 6.325 63.274 This work 0 6.294 62.333 Experiment[19] KCl Ⅱ $Pm\overline 3 m $ 2.12 3.681 49.864 This work 2.12 3.670 49.431 Experiment[20] KBr Ⅰ $Fm\overline 3 m $ 0 6.598 71.826 This work 0 6.586 71.418 Experiment[21] KBr Ⅱ $Pm\overline 3 m $ 2.20 3.833 56.293 This work 2.20 3.740 52.314 Experiment[22] 
下载: 导出CSV
表 2 NaCl、KCl、KBr的相Ⅰ（零压）和相Ⅱ（稳定压力）结构的独立弹性常数
Table 2. Independent elastic constants for phase Ⅰ (at zero pressure) and phase Ⅱ (at steady pressure) of NaCl, KCl and KBr
Material Phase C11/GPa C12/GPa C44/GPa NaCl Ⅰ 78.642 9.548 10.509 Ⅱ 230.431 79.373 31.849 KCl Ⅰ 51.087 5.107 5.587 Ⅱ 67.763 21.993 19.573 KBr Ⅰ 49.338 3.959 4.636 Ⅱ 65.451 22.265 19.708
下载: 导出CSV
表 3 NaCl、KCl、KBr的相Ⅰ和相Ⅱ结构的声子谱虚频统计
Table 3. Statistics of imaginary frequencies in the phase Ⅰ and phase Ⅱ phonon spectra for NaCl, KCl and KBr
Pressrue/GPa Imaginary frequency NaCl
(Phase Ⅰ）NaCl
(Phase Ⅱ)KCl
(Phase Ⅰ)KCl
(Phase Ⅱ)KBr
(Phase Ⅰ)KBr
(Phase Ⅱ)0 F F F F F F 0.5 F F F F F F 1.0 T F F F F F 1.5 T F F F F F 2.0 T F F F F F 2.5 T F F F F F 3.0 T F F F F F 3.5 T F F F F F 4.0 T F F F F F 4.5 T F F F F F 5.0 T F F F F F Note: “T” is imaginary frequency, while “F” is not imaginary frequency.
下载: 导出CSV
-
[1] NATTLAND D, HEYER H, FREYLAND W. Metal-nonmetal transition in liquid alkali metal-alkalihalide melts: electrical conductivity and optical reflectivity study [J]. Zeitschrift für Physikalische Chemie, 1986, 149(1): 1–15. doi: 10.1524/zpch.1986.149.1.001 [2] 张程祥, 吴绍曾, 吴姝妍, 等. NaCl、KCl和NaF晶体高压结构相变点的计算 [J]. 高压物理学报, 1993, 7(3): 233–237. doi: 10.11858/gywlxb.1993.03.011 ZHANG C X, WU S Z, WU S Y, et al. Calculations of the high pressure phase transition point of NaCl, KCl and NaF crystals [J]. Chinese Journal of High Pressure Physics, 1993, 7(3): 233–237. doi: 10.11858/gywlxb.1993.03.011 [3] 孙力, 王永生, 何志谊, 等. 电子俘获材料KCl: Eu2+的光存储特性研究 [J]. 激光与红外, 2000, 30(2): 117–118, 120. doi: 10.3969/j.issn.1001-5078.2000.02.016 SUN L, WANG Y S, HE Z Y, et al. Optical storage properties of electron trapping material KCl: Eu2+ [J]. Laser & Infrared, 2000, 30(2): 117–118, 120. doi: 10.3969/j.issn.1001-5078.2000.02.016 [4] 崔守鑫, 蔡灵仓, 胡海泉, 等. 氯化钠晶体在高温高压下热物理参数的分子动力学计算 [J]. 物理学报, 2005, 54(6): 2826–2831. doi: 10.7498/aps.54.2826 CUI S X, CAI L C, HU H Q, et al. Molecular dynamics simulation for thermophysical parameters of sodium chloride solids at high temperature and high pressure [J]. Acta Physica Sinica, 2005, 54(6): 2826–2831. doi: 10.7498/aps.54.2826 [5] 郑东阳, 刘贺, 李春, 等. 大截面溴化钾晶体生长工艺研究 [J]. 硅酸盐学报, 2015, 43(1): 60–64. doi: 10.14062/j.issn.0454-5648.2015.01.09 ZHENG D Y, LIU H, LI C, et al. Growth process of large section crystal of potassium bromide [J]. Journal of the Chinese Ceramic Society, 2015, 43(1): 60–64. doi: 10.14062/j.issn.0454-5648.2015.01.09 [6] JIANG W, YIN L, CHEN H M, et al. NaCl nanoparticles as a cancer therapeutic [J]. Advanced Materials, 2019, 31(46): 1904058. doi: 10.1002/adma.201904058 [7] BANGARU S, MURALIDHARAN G, BRAHMANANDHAN G M. Thermoluminescence and optical studies on X-irradiated terbium-doped potassium bromide crystals [J]. Journal of Luminescence, 2010, 130(4): 618–622. doi: 10.1016/j.jlumin.2009.11.005 [8] BANGARU S, RAVI D, SARADHA K. Comparison of luminescence property of gamma-ray irradiated Tb3+-doped and Ce3+ Co-doped potassium halide single crystals [J]. Luminescence, 2017, 32(3): 358–363. doi: 10.1002/bio.3187 [9] BANGARU S, SARADHA K, MURALIDHARAN G. Thermoluminescence and photoluminescence studies on γ-ray-irradiated Ce3+, Tb3+-doped potassium chloride single crystals [J]. Luminescence, 2016, 31(3): 649–653. doi: 10.1002/bio.3005 [10] OKADA G, FUJIMOTO Y, TANAKA H, et al. Dynamics of radio-photoluminescence and thermally-stimulated luminescence in KBr: Sm [J]. Journal of Materials Science: Materials in Electronics, 2017, 28(21): 15980–15986. doi: 10.1007/s10854-017-7496-z [11] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [J]. Physical Review Letters, 1996, 77(18): 3865–3868. doi: 10.1103/PhysRevLett.77.3865 [12] PERDEW J P, CHEVARY J A, VOSKO S H, et al. Erratum: atoms, molecules, solids, and surfaces: applications of the generalized gradient approximation for exchange and correlation [J]. Physical Review B, 1993, 48(7): 4978. doi: 10.1103/PhysRevB.48.4978.2 [13] PERDEW J P, BURKE K, ERNZERHOF M. Generalized gradient approximation made simple [Phys. Rev. Lett. 77, 3865 (1996)] [J]. Physical Review Letters, 1997, 78(7): 1396. doi: 10.1103/PhysRevLett.78.1396 [14] GRIMME S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction [J]. Journal of Computational Chemistry, 2006, 27(15): 1787–1799. doi: 10.1002/jcc.20495 [15] LIU L G, BASSETT W A. Compression of Ag and phase transformation of NaCl [J]. Journal of Applied Physics, 1973, 44(4): 1475–1479. doi: 10.1063/1.1662396 [16] PRABHAKAR N V K, SINGH R K, GAUR N K, et al. High-pressure phase transitions in some alkali halides [J]. Journal of Physics: Condensed Matter, 1990, 2(15): 3445–3449. doi: 10.1088/0953-8984/2/15/002 [17] RAMOLA Y, LOUIS C N, AMALRAJ A. Electronic band structure, density of states, phase transitions, metallization and superconducting transition of KBr under high pressure [J]. Orbital: the Electronic Journal of Chemistry, 2020, 12(2): 69–75. doi: 10.17807/orbital.v12i2.1401 [18] BASSETT W A, TAKAHASHI T, MAO H K, et al. Pressure-induced phase transformation in NaCl [J]. Journal of Applied Physics, 1968, 39(1): 319–325. doi: 10.1063/1.1655752 [19] COHEN A J, GORDON R G. Theory of the lattice energy, equilibrium structure, elastic constants, and pressure-induced phase transitions in alkali-halide crystals [J]. Physical Review B, 1975, 12(8): 3228–3241. doi: 10.1103/PhysRevB.12.3228 [20] LIVSHITS L D, RYABININ Y N, LARIONOV L V. Phase transitions of potassium chloride and its alloys with rubidium chloride at high pressures [J]. Soviet Physics Technical Physics, 1969, 14: 837. [21] LEIBSSLE H. Die piezooptischen eigenschaften einiger alkalihalogenide des steinsalz-typus [J]. Zeitschrift für Kristallographie: Crystalline Materials, 1960, 114(1): 457–467. doi: 10.1524/zkri.1960.114.16.457 [22] WEIR C E, PIERMARINI G J. Lattice parameters and lattice energies of high-pressure polymorphs of some alkali halides [J]. Journal of Research of the National Bureau of Standards A, 1964, 68A(1): 105–111. doi: 10.6028/jres.068A.009 [23] 高娟, 刘其军, 蒋城露, 等. 7大晶系的力学稳定性判据及其应用: 以SiO2为例 [J]. 高压物理学报, 2022, 36(5): 051101. doi: 10.11858/gywlxb.20220575 GAO J, LIU Q J, JIANG C L, et al. Criteria of mechanical stability of seven crystal systems and its application: taking silica as an example [J]. Chinese Journal of High Pressure Physics, 2022, 36(5): 051101. doi: 10.11858/gywlxb.20220575 [24] GAO J, LIU Q J, TANG B. Elastic stability criteria of seven crystal systems and their application under pressure: taking carbon as an example [J]. Journal of Applied Physics, 2023, 133(13): 135901. doi: 10.1063/5.0139232 -
计量
- 文章访问数: 249
- HTML全文浏览数: 249
- PDF下载数: 2
- 施引文献: 0