-
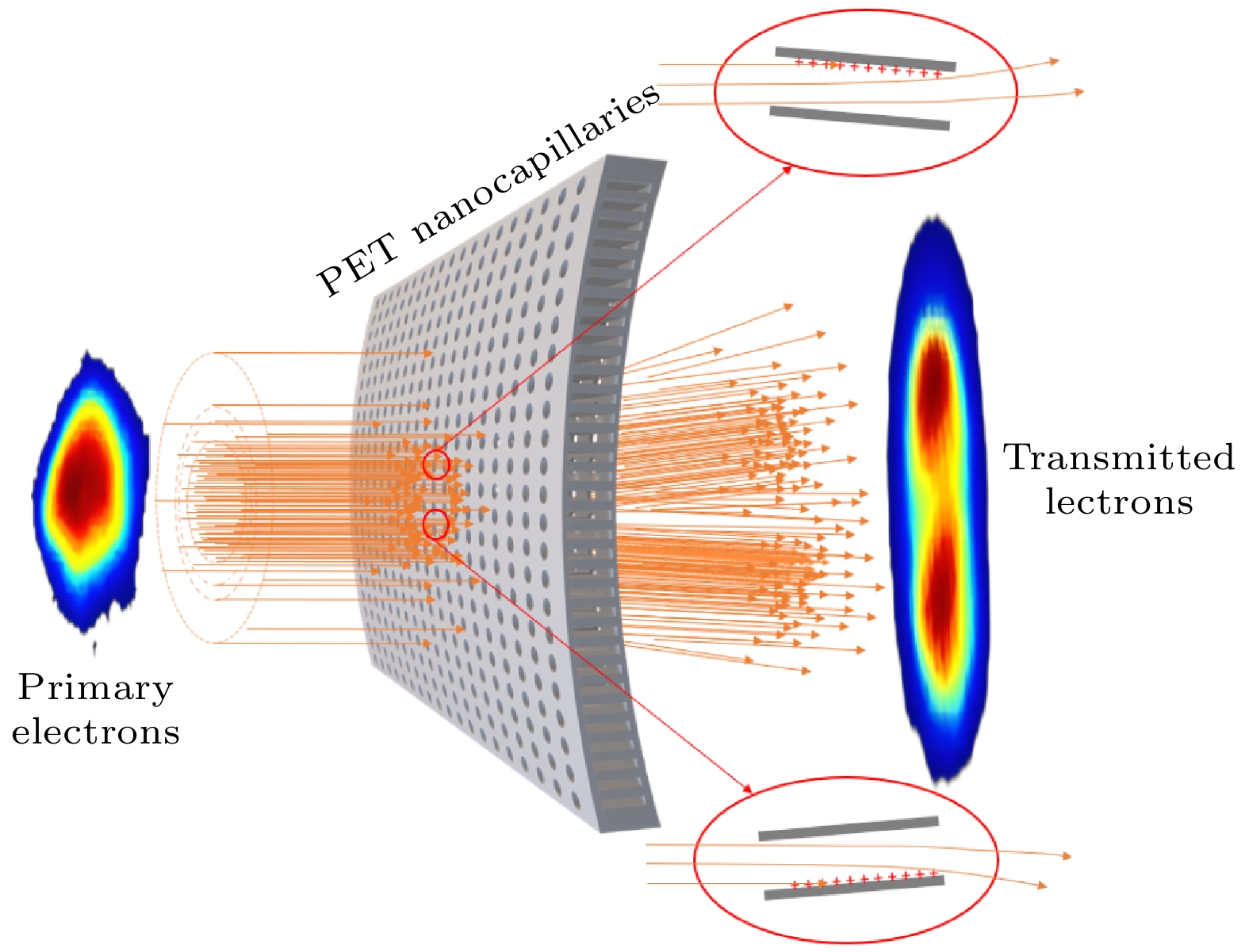
导向效应的发现始于2002年对带电粒子在绝缘纳米微通道中传输的研究[1]. 当慢速高电荷态离子(3 keV-Ne7+)在绝缘纳米聚对苯二甲酸乙二醇酯(polyethylene terephthalate, PET)微孔膜中传输时, 即使微孔膜平面的法线方向与入射离子束方向之间的夹角(被称为倾角)达到20°, 仍能保持大部分出射离子的能量和电荷态相对于初态不发生明显的改变. 这为荷电粒子束光学新技术的发展提供了一种可能性. 正离子在绝缘微孔膜和单根玻璃毛细管中传输的早期研究[1–19]揭示了导向效应的机制: 正离子与微孔相互作用会造成正电荷在微孔内壁沉积, 自组织形成电荷斑, 因而产生排斥后续入射离子的库仑场, 使后续的正离子可以不与微孔表面接触而沿着微孔轴线方向通过, 因此传输过程不发生电荷交换和能量损失[10,11].
目前, 正离子导向效应的物理机制已经被研究清楚[18–20]. 沉积电荷斑的库仑场、镜像电荷力和近表面散射等过程在传输中的作用也已经被揭示. 在Ne7+ 离子通过菱形和矩形孔的云母微孔膜的实验中发现了镜像电荷力[13,14]对离子束的整形作用. 在70 keV的Ne7+ 离子通过菱形孔的云母微孔膜的实验中观察到穿透中性粒子图像为香蕉状, 这表明对于能量较高的离子, 散射过程对离子传输起着重要作用[15].
然而, 带负电的粒子在绝缘纳米微孔膜中传输机制的研究仍存在一些争议[21–45]. 能量在10 keV以上的负离子穿越绝缘纳米微孔膜时[21–26], 散射过程与电荷交换过程均起主要作用. 穿透离子角分布呈现双峰结构, 即负离子沿初始束流方向分布形成一个峰, 而散射的中性离子和正离子沿微孔轴向分布形成另一个峰. 目前研究的负离子主要为能量大于10 keV的较高能量的负离子, 此时电荷沉积对粒子的偏转不起主要作用; 对于能量在10 keV以下较低能负离子, 基本没有实验数据, 其是否具有类似于正离子的导向效应也尚未得出结论. 与此同时, 研究人员开展了大量关于0.05—2 keV能量范围的低能电子在绝缘微孔中传输的研究 [27–45]. 低能电子穿透Al2O3纳米微孔膜的实验显示[27–29], 弹性散射电子沿微孔轴向出射, 电子穿透率随入射电荷量(充电时间)的累计而下降. 在低能电子穿透PET微孔膜的实验中[30–35], 只对具有初始能量的穿透电子的充电过程进行测量, 开始时几乎没有穿透电子, 沉寂一段时间后(几分钟至几十分钟), 穿透电子强度快速上升, 达到最高值后以缓慢速度下降, 短时间内可看作稳定不变. 穿透电子的质心能量在强度快速上升阶段快速振荡, 在强度平稳阶段维持在比初束能量略小的值上[32,33]. 对后者的理论模拟[31]表明, 该过程中电荷沉积并未起主要作用, 其主要的穿透特性是散射过程造成的. 对穿透率的计算表明, 随着入射电荷量的增大, 穿透率会下降, 这与低能电子穿透Al2O3微孔膜的实验结果一致[29], 但与PET微孔膜的实验结果不一致[32,33]. 在导电性能上, PET和Al2O3的体积电导率只有微小差异; 在膜结构上, 文献报道中使用的PET膜和Al2O3膜中, 微孔的参数也差别不大. 造成两者具有较大充电过程差异的因素还有待于研究.
上述带负电粒子的研究[25–30,32–40]在实验中采用一维静电能量分析器进行探测, 由于入口狭缝的限制, 其只能通过改变探测器的探测角度进行一维角分布测量, 无法测量充电过程中穿透粒子的二维全角分布随时间的演变. 为了研究电荷沉积如何影响低能电子在绝缘纳米微通道中传输的争议性的问题, 本文采用微通道板荧光屏二维位置灵敏探测器, 对2 keV电子穿越PET微孔的二维全角分布及其随充电的演变进行了全面精确的测量. 发现在垂直于倾角的观测方向上, 穿透电子角分布分裂为两个电子斑, 并随着倾角的增大两个电子斑相互靠近并最终重合. 对电子造成材料电荷沉积的模拟表明, 低能电子引起材料发射大量二次电子, 使材料表面1 nm内形成带正电的高密度空穴区, 同时入射电子有较大概率沉积在材料表面下几十纳米内, 形成负电荷沉积区, 两种极性相反的电荷沉积造成了电子复杂的充电现象. 本文还讨论了穿透电子角分布分裂的可能原因.
-
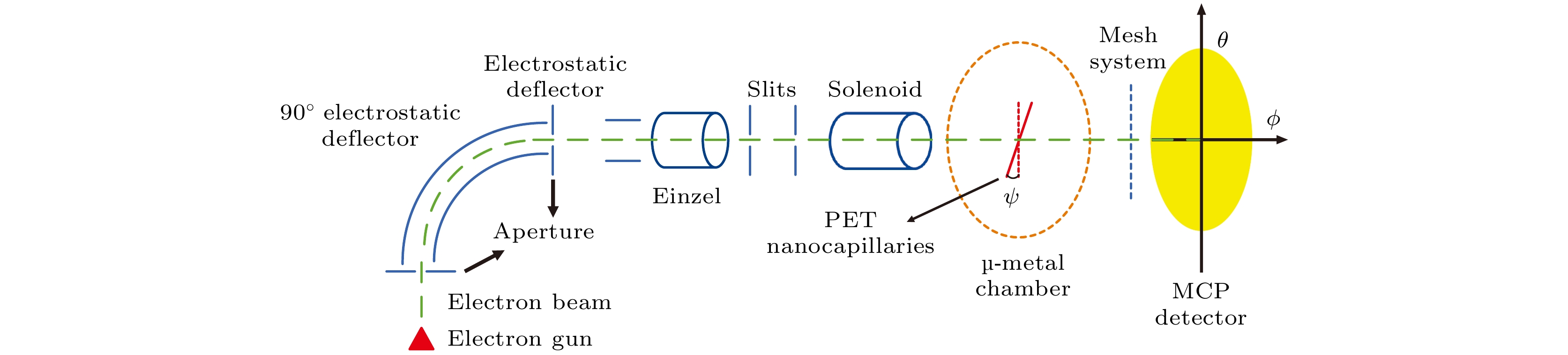
实验在兰州大学低能带电粒子束实验平台完成. 图1所示为实验装置的示意图. 电子束由LaB6电子枪产生. 为了避免微通道板(micro-channel plate, MCP)探测器收集到灯丝产生的光子, 使用90°静电偏转板对电子束进行偏转. 随后, 通过静电偏转板在水平和垂直方向上微调束流方向, 再由Einzel静电透镜聚焦, 最后通过一对可调狭缝和螺线管线圈相继准直后进入靶室. 靶室由μ金属制造, 能够有效屏蔽外部静磁场. PET微孔膜靶被安装在五维调节装置上, 可在3个空间维度上平移并在水平和竖直两个平面上旋转. 电子穿透微孔膜后经过由3层栅网组成的电子能量分析仪后被二维MCP-荧光屏探测器探测. 屏蔽线圈被放置在实验装置周围以抵消地磁场. 实验时靶室真空优于3×10–8 mbar (1 bar=105 Pa).
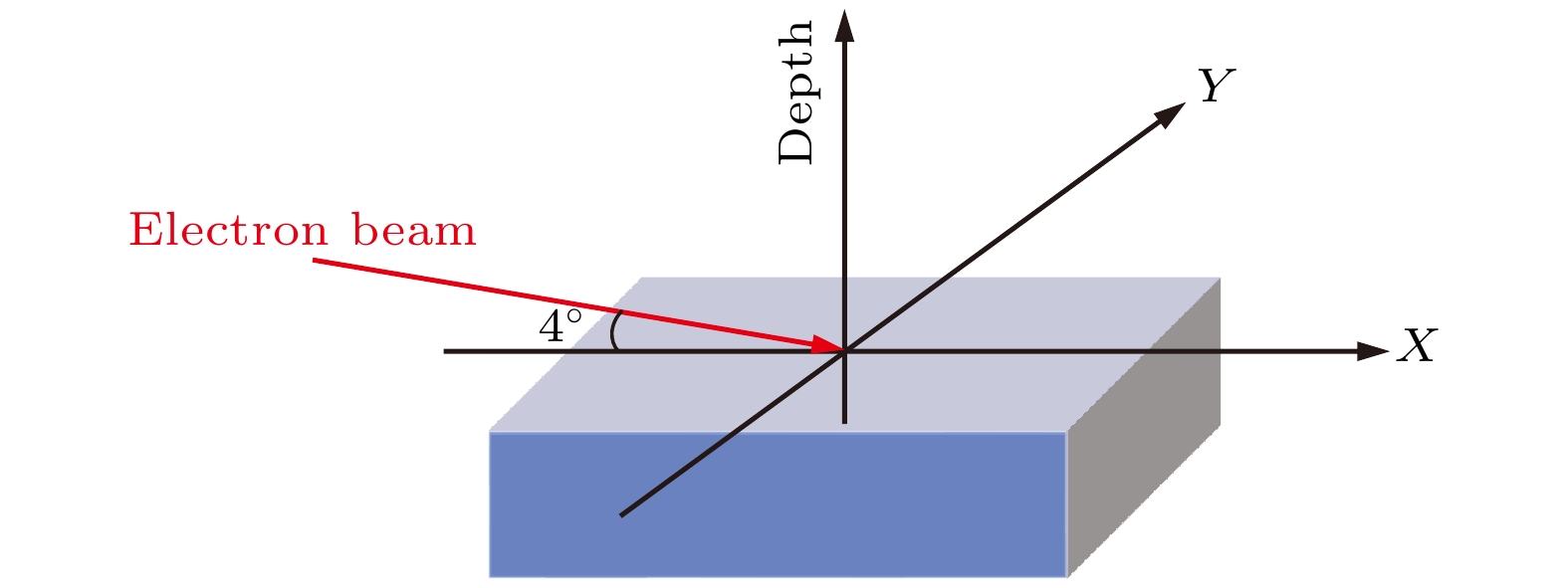
实验时, 通过在两个旋转维度上转动PET微孔膜找到穿透电子强度最大的角度, 定义该角度为0°, 此时微孔轴向与电子束入射方向相同. 微孔倾角ψ是指微孔轴向与初级电子束之间的角度. 观测角ϕ和θ相对于电子束入射方向给出, ϕ与ψ在同一旋转平面, θ在垂直于ψ的平面上.
PET薄膜被高能离子辐照后产生径迹, 再通过NaOH溶液蚀刻, 径迹变成微孔, 可以得到实验中使用的PET微孔膜. 膜厚度为10 μm, 微孔直径为800 nm, 由纵横比算出的相应的几何张角为4.6°. 膜中微孔的密度为2.4×107 mm–2, 微孔之间的平均间距为1.2 μm, 微孔的轴向发散角度小于0.5°, 相应的几何穿透率为12.3%. PET的体积电导率为1.0×10–16 Ω–1·m–1 [46], 表面电导率为1.0×10–18 Ω–1·m–2 [46], 介电常数约为3.3[46]. 膜的前后表面镀10 nm厚的金层, 防止电子束造成表面充电影响实验结果.
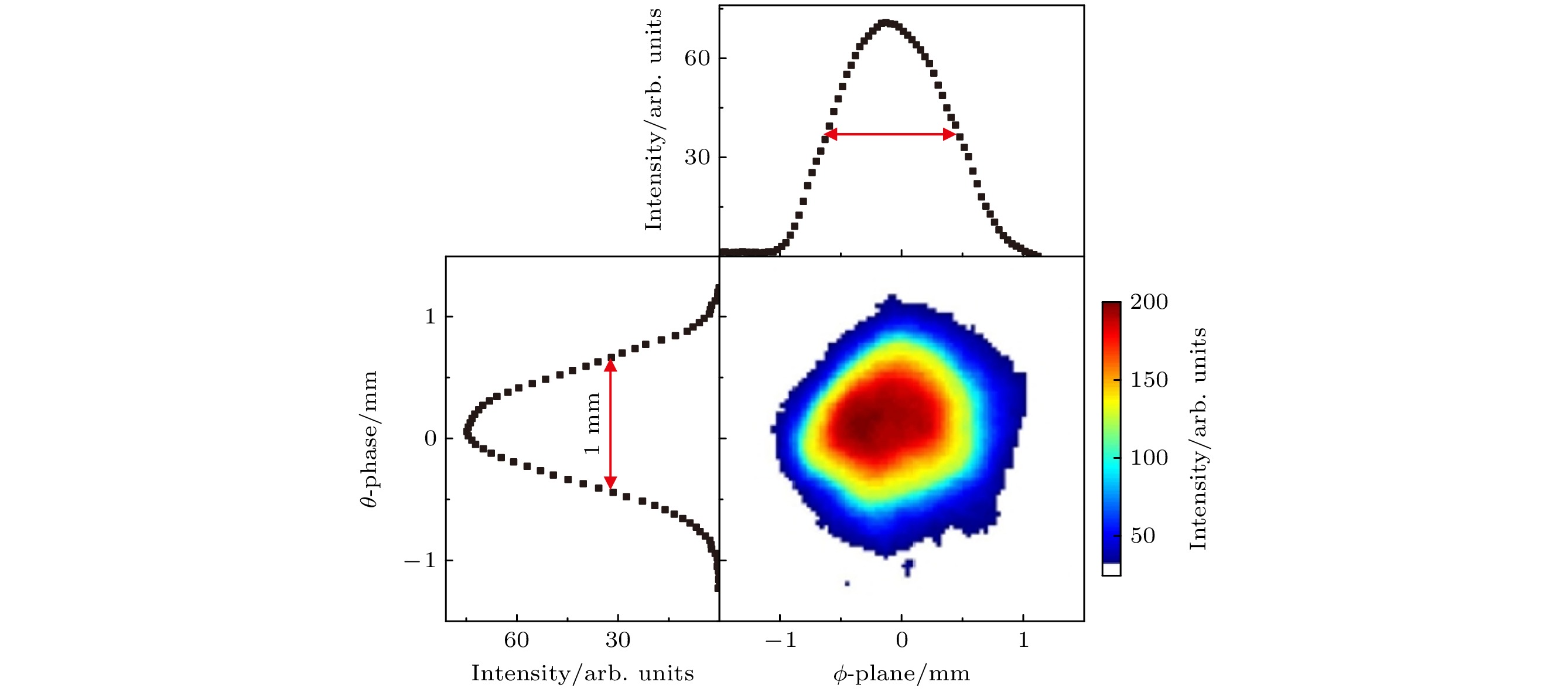
使用MCP探测器对2 keV电子束的初束进行测量. 保持传输束流的参数不变, 减小灯丝的加热功率, 使电子束强度保持在MCP探测器允许范围内. 图2展示了电子初束的二维角分布图像及其在ϕ和θ两个平面上的投影, 束斑尺寸为1.0 mm×1.0 mm. 使用靶架上的法拉第筒测量电子束参数. 升高灯丝加热功率将电子束强度增加到pA量级. 当束流达到稳态后, 法拉第筒测得束斑尺寸为2.0 mm×1.8 mm, 强度为–0.95 pA/mm2, 即每秒有3个电子进入单个微孔(3e/capillary). 根据靶架位置和探测器位置上的电子束直径计算电子束的发散角度小于0.3°. 对电子束穿透微孔膜的几何穿透角进行定义, 与我们之前的工作相同[24], 即:
$ \sigma_{\text{geot}} = \sqrt{\sigma_{\text{asp}}^2+\sigma_{\text{beam}}^2+\sigma_{\text{axis}}^2} $ , 其中$ \sigma_{\mathrm{asp}} $ ,$ \sigma_{\text{beam }} $ 和$ \sigma_{\text {axis }} $ 分别为微孔的几何张角(4.6°)、电子束散度(0.3°)和微孔的轴向散度(0.5°). 计算得到几何穿透角约为4.6°, 近似等于微孔几何张角. -
通过测量穿透电子的能量分布, 发现穿透电子的能量分布与入射电子的能量分布基本相同. 为了避免二次电子的影响(二次电子的来源比较复杂[24], 我们更关注的是具有入射能量的穿透电子), 在后续的测量中, 在中心栅网上施加–20 V电压, 以过滤掉低能二次电子.
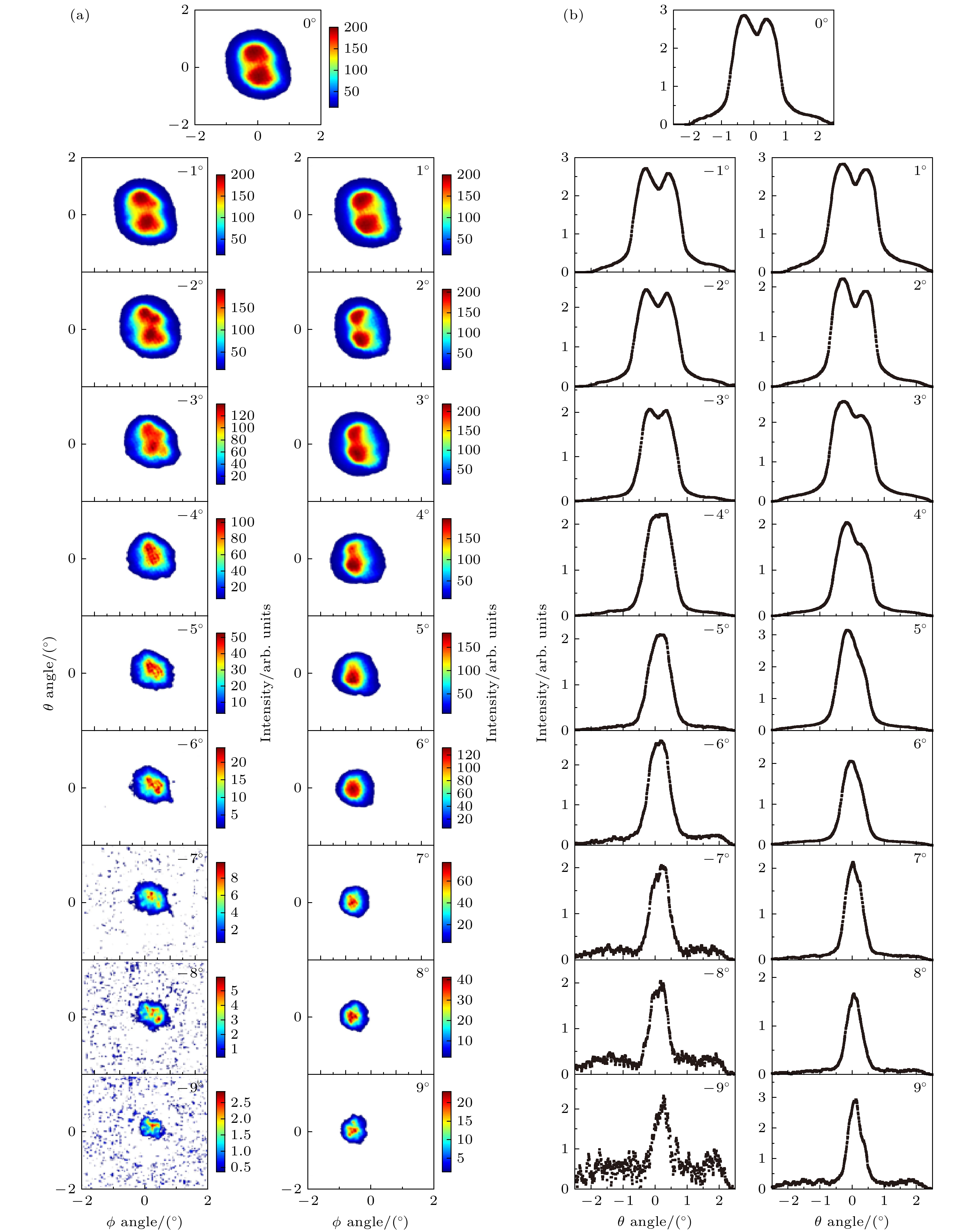
充电达到稳态时2 keV电子在不同倾角ψ下穿越PET纳米微孔的穿透电子二维角分布图像如图3所示. 每张图像由300e/capillary的入射电荷累积得到, 对应的时间长度为100 s. 在观测角ϕ上, 穿透电子角分布中心沿倾角有轻微的移动. 在几何张角内, 沿着观测角θ方向图像分裂为两个斑点. 随着倾角ψ远离0°, 这两个电子斑的大小和强度变小, 并向彼此靠近, 最终在倾角ψ约等于几何穿透角(±5°)时合并为一个电子斑. 倾角ψ继续向外移动, 穿透角分布图像上保持一个电子斑并继续收缩, 最终消失. 倾角向正角度移动, 穿透电子的角分布中心向观测角负向偏移; 倾角向负角度移动, 穿透电子的角分布中心向观测角正向偏移.
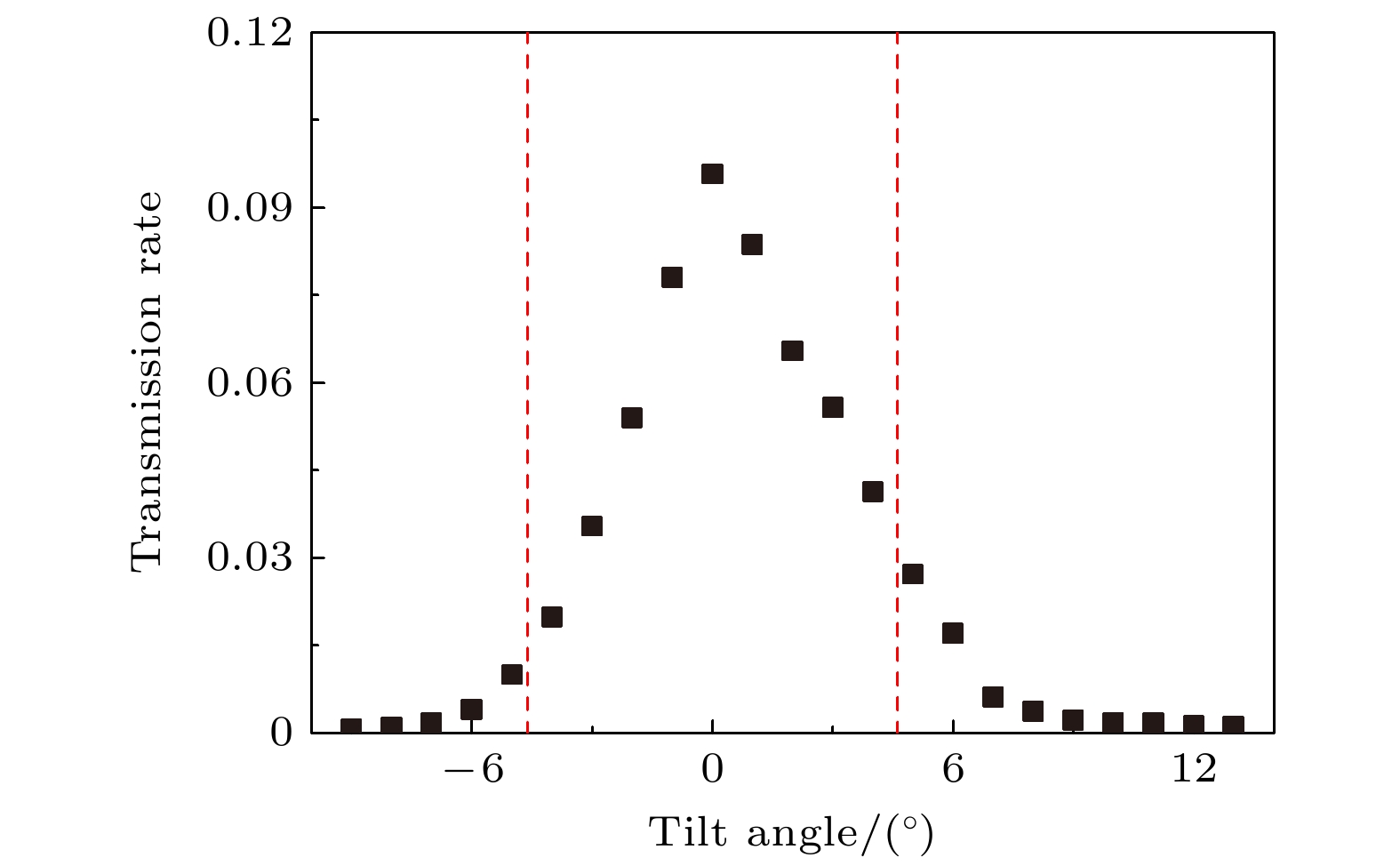
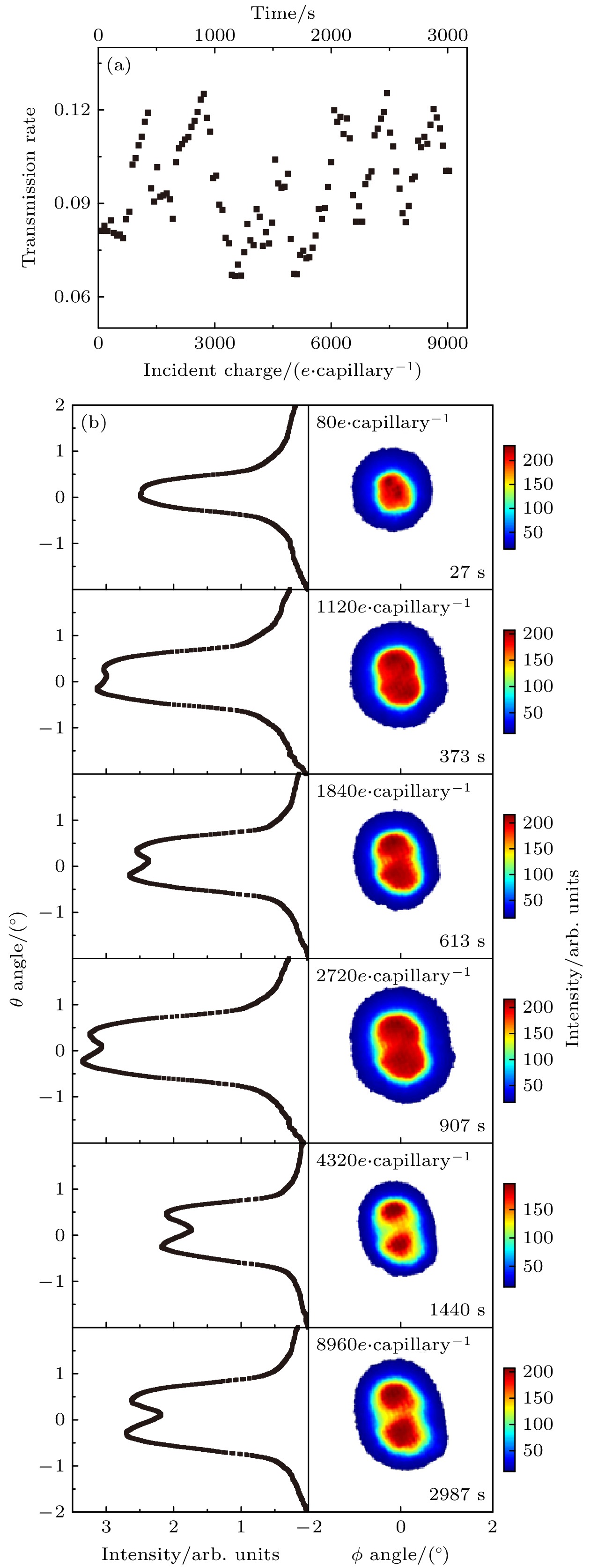
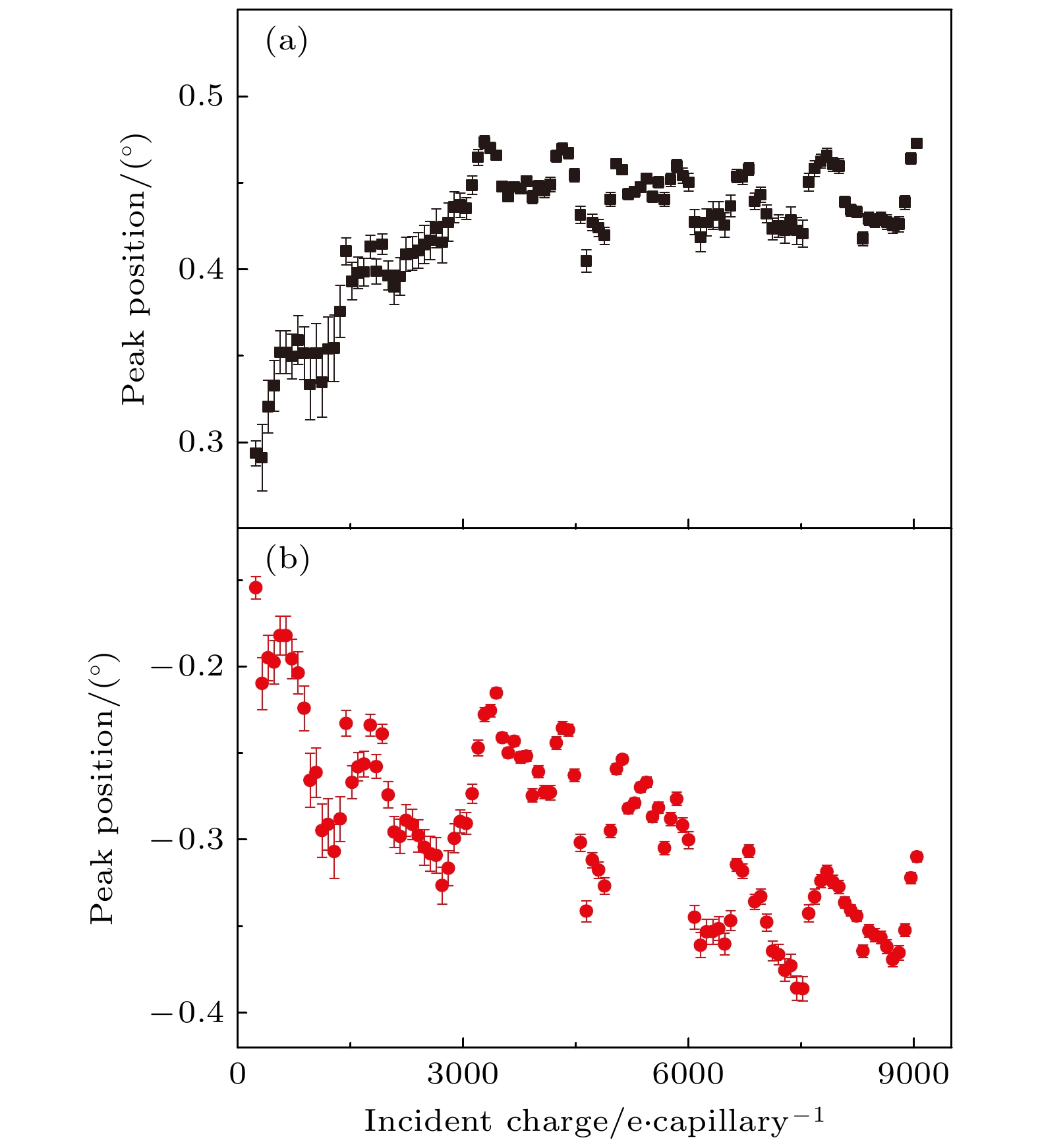
在充电达到稳态时, 2 keV电子的穿透率与倾角ψ的函数关系如图4所示. 红色虚线之间的角度表示几何穿透角. 倾角为0°时的电子穿透率可达10%. 倾角小于几何穿透角时, 电子穿透强度随倾角增加迅速下降; 倾角大于几何穿透角时, 穿透强度随倾角增加缓慢. 在倾角0°下, 对电子穿透PET纳米微孔膜的充电过程进行测量. 穿透电子全角分布的时间演化如图5(b)所示. 测量前, PET微孔膜完全放电. 图中每个图像对应的累积入射电荷量为80e/capillary, 对应的时间长度为27 s. 图像显示, 充电开始时只有一个穿透电子斑, 随着入射电荷量(充电时间)的积累, 电子斑开始沿着θ方向拉伸, 并逐渐分裂成两个穿透电子斑. 电子穿透率随充电时间变化的函数关系如图5(a)所示. 在充电过程中, 穿透率在9%左右振荡.
对ϕ和θ平面上穿透角分布的投影进行高斯拟合. 在ϕ平面上, 峰位移动和半高宽(full width at half maximum, FWHM)大小变化与穿透率同步振荡; 峰位从–0.12°开始, 振荡后接近0°, 同时FWHM振荡并展宽. 在θ平面上, 上峰位和下峰位的演变如图6(a), (b)所示. 随着充电累积, 上斑峰位移动到0.5°左右, 而下斑峰位移动到–0.3°左右. 两个峰值的相应FWHM在0.6°左右振荡. 同样地, 峰位移动和FWHM大小变化与穿透率同步振荡.
-
与正离子的导向效应不同, 电子在绝缘纳米通道中传输涉及更复杂的物理过程, 例如, 当倾角大于几何张角时, 电子的散射过程占主导地位. 而对于入射电子造成微孔内壁电荷沉积的过程, 仍存在许多争议[27–45]. 对不同绝缘材料的微孔通道, 电子穿透强度随时间演变的测量结果显示出不同的电荷沉积极性. 此外, 电子输运的理论模拟与实验结果也存在一定的差异[27–34]. 电子与微孔内壁碰撞会产生大量的二次电子, 这使得充电过程非常复杂. 为了研究电子在微孔内壁表面造成的电荷沉积, 考虑电子散射、二次电子激发和入射电子沉积等物理过程, 使用“CASINO”软件计算了2 keV电子造成PET材料上的电荷沉积及其空间分布[47–49].
CASINO在模拟中采用蒙特卡罗方法对电子进行详细的径迹计算, 其电子与样品之间作用的物理过程通过随机数取值与概率分布的方式实现[48]. 电子径迹追踪在电子从样品中出射后或者被样品俘获(及电子的能量小于某个阈值)后结束. 当对二次电子进行模拟时, 将样品的功函数作为阈值. 电子传输中每一步的能量损失包含等离子体激元的激发(the excitation of plasmons)、价带内外跃迁(inter-and intra-band transitions)和核心激发(core excitations). 当入射电子能量较低时, 可以通过改进的Bethe公式对电子在样品中的能量损失进行很好的描述[50]. 软件中的剩余能量损失(residual energy loss)作为可调参数对该改进的Bethe公式进行调节以对电子能量低于样品功函数的平均能量损失率进行补偿[51]. CASINO将样品中电离的价电子和等离子体激元激发产生的电子作为二次电子. 其中样品中电离的价电子部分可以通过Moller公式[52]进行计算.
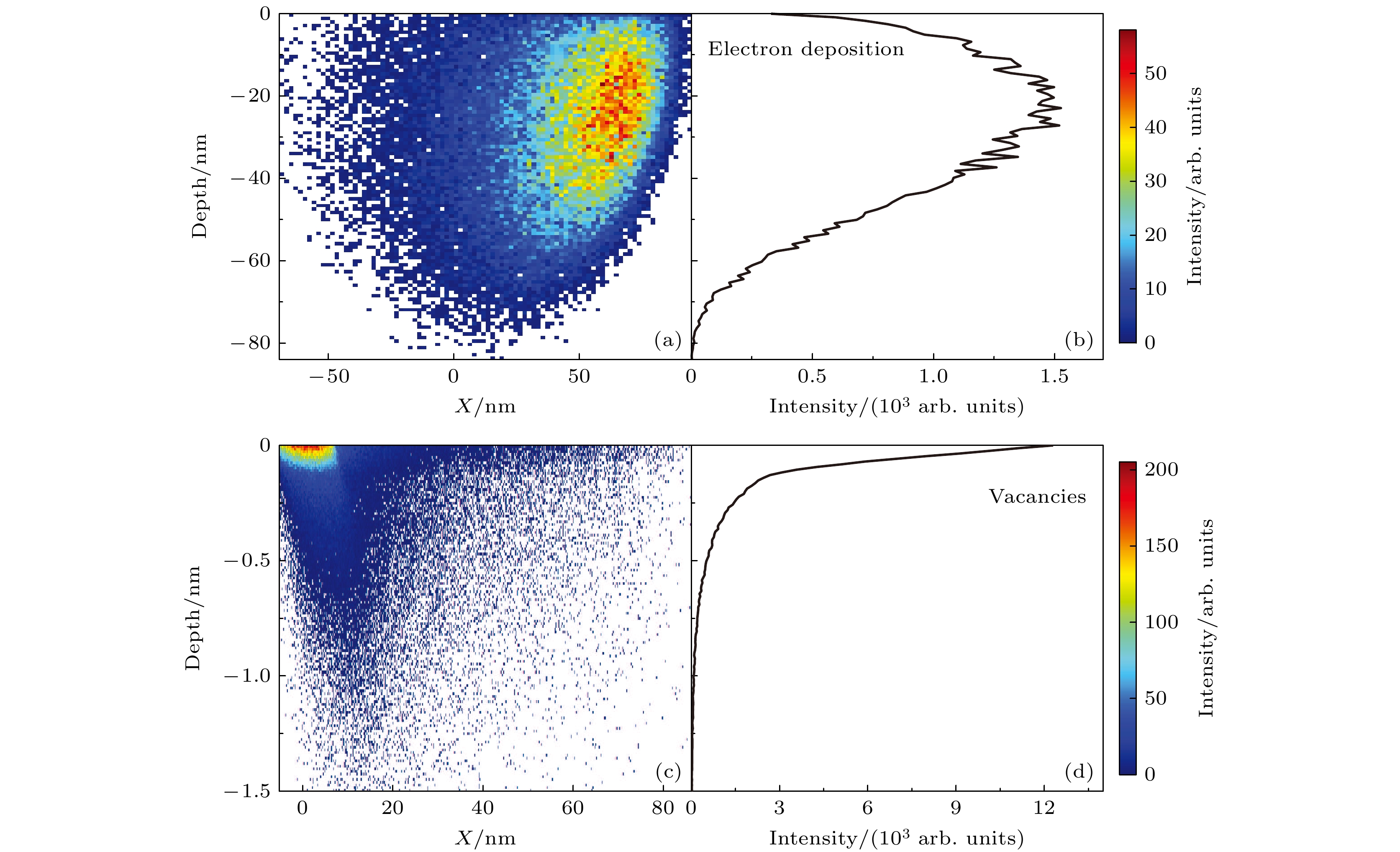
图7所示为CASINO中使用的PET样品的三维模型. 长度和宽度均为400 nm, 高度为100 nm. 电子束能量设置为2 keV, 入射角为4°, 角发散为0.3°. 由于CASINO软件中认为每个入射电子都是独立粒子, 不会互相影响. 因此束流的绝对流强在模拟中没有意义, 只需要设定模拟的电子数目即可. 为了统计性, 我们模拟的电子数目为100万个. 同样地, 模拟中使用的束斑直径对模拟结果也没有影响. 模拟时使用的束斑直径为1 nm. 计算结果如图8所示. 入射电子造成的电荷沉积由沉积的入射电子 (图8(a), (b))和激发的表面空穴 (图8(c), (d))组成. 入射电子沉积概率为32.6%, 位置基本在PET表面以下0—80 nm深度范围内, 其强度在深度上的投影分布如图8(b)所示, 其强度中心在30 nm左右处; 表面净空穴的激发概率为77.19%, 分布深度在0—1.5 nm范围内, 越靠近表面强度越大. PET表面大量空穴的存在, 使得电子与表面的碰撞区呈正电荷. PET内部入射电子的沉积, 使材料内部呈负电荷. 表面正电荷对入射电子的吸引造成低能电子在微孔中的穿透呈现几何穿透特征(图4), 同时在微孔的几何张角之外电子散射过程占主导地位[31], 使得电子传输无法像正离子那样形成导向效应. 这与我们目前的实验测量结果一致.
在观测角ϕ平面上穿透电子角分布中心的移动方向与微孔倾角移动方向相反(图3). 这是由于电子束直接碰撞那一侧微孔内壁表面存在正电荷斑, 吸引电子束造成. 0°倾角上充电时, 穿透束斑半高宽随充电累积而变宽(图5(b))也应该是内壁表面的正电荷吸引造成. 充电过程的振荡现象(图5(a)、图6)是表面正电荷与体内负电荷积累到一定强度后, 快速复合而后又再次积累, 并循环往复造成的. 内壁表面正电荷吸引入射电子进入表面减少其穿透概率并使穿透电子斑扩张, 而体内负电荷向外排斥进入表面的电子增加其出射概率并使穿透电子斑收缩, 两者互相竞争造成复杂的充电振荡现象.
对于观测到的穿透角分布沿θ方向分裂为两个电子斑的现象(图5(b)、图6), 分析认为: 由于PET微孔膜厚度只有10 μm, 在固定微孔膜时小角度弯曲不可避免. 如图9所示, PET纳米微孔膜存在θ平面上的小角度的弯曲, 导致电子束在θ角上以一定的入射角进入微孔. 对于上半部分的微孔, 电子入射导致微孔上表面充正电, 吸引电子向上偏转. 对于下半部分的微孔, 电子入射导致微孔下表面充正电, 吸引电子向下偏转. 随着充电时间的累积, 微孔上下表面正电荷逐渐累积, 对电子吸引效果逐渐增强, 上下电子斑逐渐变远, 直至充电达到稳定状态. 在转动角度后, 曲面上半部分的微孔内, 与上壁碰撞的电子变少, 与侧壁碰撞的电子变多; 曲面下半部分的微孔内, 与下壁碰撞的电子变少, 与侧壁(与上部分微孔为同一侧)碰撞的电子变多. 曲面上下两部分微孔内壁的充电电荷分布趋于一致, 因此又重新恢复成一个电子斑.
将薄膜做成的凹面结构可以对离子束进行聚焦, 而本文的结果表明, 同样的凹面结构可能对电子束形成分裂效果. 电子束与离子束相反的传输效果, 将是证明两者充电机制不同的最有力实验证据, 有望解决电子束充电机制上存在的争议. 作者将在后续严格设定θ平面上的弯曲角度, 进行电子束和离子束的对比实验, 验证本文的猜测, 并测量电子与离子充电现象的不同. 同时, 本文结果为发展电子的粒子束光学元件提供了数据和理论支撑.
-
本文展示了2 keV电子在直径为800 nm的PET纳米微通道中输运的测量结果. 充电达到稳态时的全角分布结果显示, 穿透电子角分布中心的移动方向与微孔倾角移动方向相反, 且没有观察到如正电子那样的导向效应. 0°倾角下充电演化的测量结果显示, 随着充电时间的积累, 穿透束斑半高宽变宽. 充电过程中存在振荡现象, 电子穿透束斑峰位及半高宽变化与穿透率同步振荡. 利用CASINO软件对电子在PET表面沉积电荷的情况进行了模拟, 模拟结果显示微孔表面被电子激发产生大量净空穴, 形成正电荷累积; 部分入射电子沉积于表面以下更深处, 形成负电荷层. 基于此, 对角分布中心移动特征解释为: 电子束与微孔内壁表面直接碰撞那一侧存在并积累正电荷斑, 吸引电子束. 入射电子被微孔表面正电荷吸引, 造成低能电子的穿透呈现几何穿透特征, 在微孔的几何张角之外电子散射过程占主导地位, 不利于导向效应的产生. 充电演化的穿透展宽特征是由微孔表面正电荷吸引电子, 使穿透电子扩张导致. 而其振荡特征是微孔表面正电荷吸引入射电子, 内部负电荷排斥入射电子, 并循环往复造成的. 对穿透电子角分布在θ平面上的分裂现象, 我们认为是由膜的弯曲造成的, 并据此提出验证电子与离子充电机制是否存在差异的新实验方法. 研究结果为利用绝缘微通道控制电子传输技术的发展提供了支撑.
低能电子在直径为800 nm的聚对苯二甲酸乙二醇酯纳米微通道中的输运过程
Transmission of low energy electrons through a polyethylene terephthalate 800-nm diameter nanocapillary
-
摘要: 研究了2 keV电子在直径为800 nm, 长度为10 μm的聚对苯二甲酸乙二醇酯(polyethylene terephthalate, PET)纳米通道中的输运过程. 结果表明, 当纳米微通道倾角为0°时, 穿透电子的穿透率可达10%, 而当倾角大于几何张角时, 穿透电子的透射率小于1%. 穿透电子角分布中心没有随微孔倾角的变化而移动, 因此没有如在正离子的情况下那样观察到绝缘微孔对电子的导向效应. 在充电达到稳态时, 当微孔倾角小于几何张角时, 电子分裂成上下两个电子斑. 穿透电子的全角分布的时间演化表明, 在充电开始时, 穿透电子为单电子斑. 随着入射电荷量(充电时间)的累积, 穿透电子被上下拉伸, 并逐渐分裂成两个电子斑. 当纳米微孔的倾角超过几何张角时, 穿透电子的分裂趋于消失. 对电子造成微孔内壁上的电荷沉积的模拟计算表明, 微孔表面被激发出大量空穴, 形成正电荷累积; 而部分入射电子沉积于表面以下更深处, 形成负电荷层, 因此不利于产生类似正离子的导向效应. 本文还讨论了造成穿透电子角分布上下分裂的可能原因, 并据此提出验证电子和离子充电机制不同的新的实验方法. 研究结果为利用绝缘微通道控制电子传输技术的发展提供了支撑.Abstract: The transmission of 2-keV electrons through a polyethylene terephthalate (PET) nanocapillary with a diameter of 800 nm and a length of 10 μm is studied. The transmitted electrons are detected using microchannel plate (MCP) with a phosphor screen. It is found that the transmission rate for the transmitted electrons with the incident energy can reach up to 10 % for an aligned capillary in the beam direction, but drops to less than 1% when the tilt angle exceeds the geometrical allowable angle. The transmitted electrons with the incident energy do not move with change of tilt angle, so the incident electrons are not guided in the insulating capillary, which is different from the scenario of positive ions. In the final stage of the transmission, the angular distribution of the transmitted electrons within the geometrical allowable angle splits into two peaks along the observation angle perpendicular to the tilt angle. The time evolution of the transmitted full angular distribution shows that when the beam turns on, the transmission profile forms a single peak. As the incident charge and time accumulate, the transmission profile starts to stretch in the plane perpendicular to the tilt angle and gradually splits into two peaks. When the tilt angle of the nanocapillary exceeds the geometrical allowable angle, this splitting tends to disappear. Simulation of the charge deposition in the capillary directly exposed to the beam indicates the formation of positive charge patches, which are not conducive to guidance, as seen in the case of positive ions. According to the simulation results, we can explain our data. Then, the possible reasons for the splitting the transmission angular profiles are discussed.
-
Key words:
- insulating nanocapillaries /
- low energy electrons /
- guiding effect .
-

-
图 3 不同倾角下2 keV电子在静止状态下通过PET纳米微孔的二维穿透角分布 (a)二维穿透角分布; (b) θ平面上的穿透角分布投影
Figure 3. Two-dimensional penetration angle distribution of 2 keV electrons through PET nanopores in a stationary state at different inclination angles: (a) Two-dimensional penetration angle distribution; (b) θ plane penetration angle distribution projection.
图 5 充电过程中2 keV电子在0°倾角下通过 PET 纳米微孔的穿透全角分布随时间的演变 (a)电子穿透率的演变; (b)二维穿透角分布图像及投影图
Figure 5. The time evolution of transmitted angular distributions of 2 keV electrons at the tilt angle of 0° through PET nanocapillaries during the charging process: (a) The evolution of electron transmission rates; (b) projections of the transmitted angular distributions.
图 8 2 keV电子在4°入射角下造成PET材料表面电荷沉积的计算结果 (a)入射电子沉积强度的二维分布图及其(b)在深度上的强度分布投影图; (c)表面空穴强度的二维分布图及其(d)在深度上的强度分布投影图
Figure 8. Calculated results of charge deposition on the surface of PET material caused by 2 keV electrons at an incidence angle of 4°: (a) The two-dimensional distribution of the intensity of the incident electron deposition and (b) its intensity distribution projection at depth; (c) the two-dimensional distribution of the surface hole intensity, and (d) its intensity distribution projection at depth.
-
[1] Stolterfoht N, Bremer J H, Hoffmann V, Hellhammer R, Fink D, Petrov A, Sulik B 2002 Phys. Rev. Lett. 88 133201 doi: 10.1103/PhysRevLett.88.133201 [2] Schiessl K, Palfinger W, Tökési K, Nowotny H, Lemell C, Burgdörfer J 2005 Phys. Rev. A 72 062902 doi: 10.1103/PhysRevA.72.062902 [3] Sahana M B, Skog P, Vikor G, Kumar R T R, Schuch R 2006 Phys. Rev. A 73 040901(R [4] Ikeda T, Kanai Y, Kojima T M, Iwai Y, Kambara T, Yamazaki Y, Hoshino M, Nebiki T, Narusawa T 2006 Appl. Phys. Lett. 89 163502 [5] Skog P, Soroka I L, Johansson A, Schuch R 2007 Nucl. Instr. Meth. Phys. Res. B 258 145 doi: 10.1016/j.nimb.2006.12.127 [6] Chen Y F, Chen X M, Lou F J, Xu J Z, Shao J X, Sun G Z, Wang J, Xi F Y, Yin Y Z, Wang X. A, Xu J K, Cui Y, Ding B W 2009 Chin. Phys. B. 18 2739 doi: 10.1088/1674-1056/18/7/019 [7] Cassimi A, Maunoury L, Muranaka T, Huber B, Dey K R, Lebius H, Lelièvre D, Ramillon J M, Been T, Ikeda T, Kanai Y, Kojima T M, Iwai Y, Yamazaki Y, Khemliche H, Bundaleski N, Roncin P 2009 Nucl. Inst. Meth. Phys. Res. B 267 674 doi: 10.1016/j.nimb.2008.11.016 [8] Nakayama R, Tona M, Nakamura N, Watanabe H, Yoshiyasu N, Yamada C, Yamazaki A, Ohtani S, Sakurai M 2009 Nucl. Inst. Meth. Phys. Res. B 267 2381 doi: 10.1016/j.nimb.2009.04.008 [9] Juhász Z, Sulik B, Rácz R, Biri S, Bereczky R J, Tőkési K, Kövér Á, Pálinkás J, Stolterfoht N 2010 Phys. Rev. A 82 062903 doi: 10.1103/PhysRevA.82.062903 [10] Skog P, Zhang H Q, Schuch R 2008 Phys. Rev. Lett. 101 223202 doi: 10.1103/PhysRevLett.101.223202 [11] Zhang H Q, Skog P, Schuch R 2010 Phys. Rev. A 82 052901 doi: 10.1103/PhysRevA.82.052901 [12] Stolterfoht N, Hellhammer R, Sulik B, Juhász Z, Bayer V, Trautmann C, Bodewits E, Hoekstra R 2011 Phys. Rev. A 83 062901 doi: 10.1103/PhysRevA.83.062901 [13] Zhang H Q, Akram N, Skog P, Soroka I L, Trautmann C, Schuch R 2012 Phys. Rev. Lett. 108 193202 doi: 10.1103/PhysRevLett.108.193202 [14] Zhang H Q, Akram N, Soroka I L, Trautmann C, Schuch R 2012 Phys. Rev. A 86 022901 doi: 10.1103/PhysRevA.86.022901 [15] Zhang H Q, Akram N, Schuch R 2016 Phys. Rev. A 94 032704 doi: 10.1103/PhysRevA.94.032704 [16] Giglio E, Guillous S, Cassimi A, Zhang H Q, Nagy G U L, Tőkési K 2017 Phys. Rev. A 95 030702(R [17] Giglio E, Guillous S, Cassimi A 2018 Phys. Rev. A 98 052704 doi: 10.1103/PhysRevA.98.052704 [18] Lemell C, Burgdörfer J, Aumayr F 2013 Prog. Surf. Sci. 88 237 doi: 10.1016/j.progsurf.2013.06.001 [19] Stolterfoht N, Yamazaki Y 2016 Phys. Rep. 629 1 doi: 10.1016/j.physrep.2016.02.008 [20] 万城亮, 潘俞舟, 朱丽萍, 李鹏飞, 张浩文, 赵卓彦, 袁华, 樊栩宏, 孙文胜, 杜战辉, 陈乾, 崔莹, 廖天发, 魏晓慧, 王天琦, 陈熙萌, 李公平, Reinhold Schuch, 张红强 2024 物理学报 73 104101 doi: 10.7498/aps.73.20240301 Wan C L, Pan Y Z, Zhu L P, Zhang H W, Zhao Z Y, Yuan H, Li P F, Fan X H, Sun W S, Du Z H, Chen Q, Cui Y, Liao T F, Wei X H, Wang T Q, Chen X M, Li G P, Schuch R, Zhang H Q 2024 Acta Phys. Sin. 73 104101 doi: 10.7498/aps.73.20240301 [21] Sun G Z, Chen X M, Wang J, Chen Y F, Xu J K, Zhou C L, Shao J X, Cui Y, Ding B W, Yin Y Z, Wang X A, Lou F J, Lv X Y, Qiu X Y, Jia J J, Chen L, Xi F Y, Chen Z C, Li L T, Liu Z Y 2009 Phys. Rev. A 79 052902 doi: 10.1103/PhysRevA.79.052902 [22] Chen L, Guo Y L, Jia J J, Zhang H Q, Cui Y, Shao J X, Yin Y Z, Qiu X Y, Lv X Y, Sun G Z, Wang J, Chen Y F, Xi F Y, Chen X M 2011 Phys. Rev. A 84 032901 doi: 10.1103/PhysRevA.84.032901 [23] Chen L, Lv X Y, Jia J J, Ji M C, Zhou P, Sun G Z, Wang J, Chen Y F, Xi F Y, Cui Y, Shao J X, Qiu X Y, Guo Y L, Chen X M 2011 Phys. B: At. Mol. Opt. Phys. 44 045203 doi: 10.1088/0953-4075/44/4/045203 [24] Zhang Q, Liu Z L, Li P F, Jin B, Song G Y, Jin D K, Niu B, Wei L, Ha S, Xie Y M, Ma Y, Wan C L, Cui Y, Zhou P, Zhang H Q, Chen X M 2018 Phys. Rev. A 97 042704 doi: 10.1103/PhysRevA.97.042704 [25] 哈帅, 张文铭, 谢一鸣, 李鹏飞, 靳博, 牛犇, 魏龙, 张琦, 刘中林, 马越, 路迪, 万城亮, 崔莹, 周鹏, 张红强, 陈熙萌 2020 物理学报 69 094101 doi: 10.7498/aps.69.20190933 Ha S, Zhang W M, Xie Y M, Li P F, Jin B, Niu B, Wei L, Zhang Q, Liu Z L, Ma Y, Lu D, Wan C L, Cui Y, Zhou P, Zhang H Q, Chen X M 2020 Acta Phys. Sin. 69 094101 doi: 10.7498/aps.69.20190933 [26] 刘中林, 哈帅, 张文铭, 谢一鸣, 李鹏飞, 靳博, 张琦, 马越, 路迪, 万城亮, 崔莹, 周鹏, 张红强, 陈熙萌 2021 原子核物理评论 38 95 doi: 10.11804/NuclPhysRev.38.2020050 Liu Z L, Ha S, Zhang W M, Xie Y M, Li P F, Jin B, Zhang Q, Ma Y, Lu D, Wan C L, Cui Y, Zhou P, Zhang H Q, Chen X M 2021 Nucl. Phys. Rev. 38 95 doi: 10.11804/NuclPhysRev.38.2020050 [27] Milosavljević A R, Víkor Gy, Pešić Z D, Kolarž P, Šević D, Marinković B P, Mátéfi-Tempfli S, Mátéfi-Tempfli M, Piraux L 2007 Phys. Rev. A 75 030901(R doi: 10.1103/PhysRevA.75.030901 [28] Milosavljević A R, Jureta J, Víkor G, Pešić Z D, Šević D, Mátéfi-Tempfli M, Mátéfi-Tempfli S, Marinković B P 2009 Europhys. Lett. 86 23001 doi: 10.1209/0295-5075/86/23001 [29] Milosavljević A, Schiessl K, Lemell C, Mátéfi-Tempfli M, Mátéfi-Tempfli S, Marinković B P, Burgdörfer J 2012 Nucl. Instr. Meth. Phys. Res. B 279 190. doi: 10.1016/j.nimb.2011.10.034 [30] Das S, Dassanayake B S, Winkworth M, Baran J L, Stolterfoht N, Tanis J A 2007 Phys. Rev. A 76 042716 doi: 10.1103/PhysRevA.76.042716 [31] Schiessl K, Tőkési K, Solleder B, Lemell C, Burgdörfer J 2009 Phys. Rev. Lett. 102 163201 doi: 10.1103/PhysRevLett.102.163201 [32] Dassanayake B S, Keerthisinghe D, Wickramarachchi S, Ayyad A, Das S, Stolterfoht N, Tanis J A 2013 Nucl. Instr. Meth. Phys. Res. B 298 1 doi: 10.1016/j.nimb.2012.12.017 [33] Keerthisinghe D, Dassanayake B S, Wickramarachchi S J, Stolterfoht N, Tanis J A 2013 Nucl. Instr. Meth. Phys. Res. B 317 105 doi: 10.1016/j.nimb.2013.01.047 [34] Keerthisinghe D, Dassanayake B S, Wickramarachchi S J, Stolterfoht N, Tanis J A 2016 Nucl. Instr. Meth. Phys. Res. B 382 67 doi: 10.1016/j.nimb.2016.04.037 [35] Keerthisinghe D, Dassanayake B S, Wickramarachchi S J, Stolterfoht N, Tanis J A 2015 Phys. Rev. A 92 012703 doi: 10.1103/PhysRevA.92.012703 [36] Vokhmyanina K A, Kubankin A S, Myshelovka L V, Zhang H Q, Kaplii A A, Sotnikova V S, Zhukova M A 2020 J. Instrum. 15 C04003 doi: 10.1088/1748-0221/15/04/C04003 [37] Dassanayake B S, Das S, Bereczky R J, Tőkési K, Tanis J A 2010 Phys. Rev. A 81 020701(R [38] Dassanayake B S, Bereczky R J, Das S, Ayyad A, Tökési K, Tanis J A 2011 Phys. Rev. A 83 012707 doi: 10.1103/PhysRevA.83.012707 [39] Wickramarachchi S J, Ikeda T, Dassanayake B S, Keerthisinghe D, Tanis J A 2016 Phys. Rev. A 94 022701 doi: 10.1103/PhysRevA.94.022701 [40] Stolterfoht N, Tanis J A 2018 Nucl. Instr. Meth. Phys. Res. B 421 32 doi: 10.1016/j.nimb.2018.02.015 [41] 万城亮, 李鹏飞, 钱立冰, 靳博, 宋光银, 高志民, 周利华, 张琦, 宋张勇, 杨治虎, 邵剑雄, 崔莹, Reinhold Schuch, 张红强, 陈熙萌 2016 物理学报 65 204103 doi: 10.7498/aps.65.204103 Wan C L, Li P F, Qian L B, Jin B, Song G Y, Gao Z M, Zhou L H, Zhang Q, Song Z Y, Yang Z H, Shao J X, Cui Y, Schuch R, Zhang H Q, Chen X M 2016 Acta Phys. Sin. 65 204103 doi: 10.7498/aps.65.204103 [42] 钱立冰, 李鹏飞, 靳博, 靳定坤, 宋光银, 张琦, 魏龙, 牛犇, 万城亮, 周春林, Arnold Milenko Müller, Max Dobeli, 宋张勇, 杨治虎, Reinhold Schuch, 张红强, 陈熙萌 2017 物理学报 66 124101 doi: 10.7498/aps.66.124101 Qian L B, Li P F, Jin B, Jin D K, Song G Y, Zhang Q, Wei L, Niu B, Wan C L, Zhou C L, Müller A M, Dobeli M, Song Z Y, Yang Z H, Schuch R, Zhang H Q, Chen X M 2017 Acta Phys. Sin. 66 124101 doi: 10.7498/aps.66.124101 [43] 李鹏飞, 袁华, 程紫东, 钱立冰, 刘中林, 靳博, 哈帅, 万城亮, 崔莹, 马越, 杨治虎, 路迪, Reinhold Schuch, 黎明, 张红强, 陈熙萌 2022 物理学报 71 074101 doi: 10.7498/aps.71.20212036 Li P F, Yuan H, Cheng Z D, Qian L B, Liu Z L, Jin B, Ha S, Wan C L, Cui Y, Ma Y, Yang Z H, Lu D, Schuch R, Li M, Zhang H Q, Chen X M 2022 Acta Phys. Sin. 71 074101 doi: 10.7498/aps.71.20212036 [44] 李鹏飞, 袁华, 程紫东, 钱立冰, 刘中林, 靳博, 哈帅, 张浩文, 万城亮, 崔莹, 马越, 杨治虎, 路迪, Reinhold Schuch, 黎明, 张红强, 陈熙萌 2022 物理学报 71 084104 doi: 10.7498/aps.71.20212335 Li P F, Yuan H, Cheng Z D, Qian L B, Liu Z L, Jin B, Ha S, Zhang H W, Wan C L, Cui Y, Ma Y, Yang Z H, Lu D, Schuch R, Li M, Zhang H Q, Chen X M 2022 Acta Phys. Sin. 71 084104 doi: 10.7498/aps.71.20212335 [45] 周鹏, 万城亮, 袁华, 程紫东, 李鹏飞, 张浩文, 崔莹, 张红强, 陈熙萌 2023 强激光与粒子束 35 026001 doi: 10.11884/HPLPB202335.220120 Zhou P, Wan C L, Yuan H, Cheng Z D, Li P F, Zhang H W, Cui Y, Zhang H Q, Chen X M 2023 High Pow. Laser Part. Beams 35 026001 doi: 10.11884/HPLPB202335.220120 [46] Data sheets of Mylar (http://www.dupontteijinfilms.com [47] Hovington P, Drouin D, Gauvin R. 1997 Scanning 19 1 doi: 10.1002/sca.4950190101 [48] Drouin D, Couture A R, Joly D, Taster X, Aimez V, Gauvin R 2007 Scanning 29 92 doi: 10.1002/sca.20000 [49] Demers H, Poirrier-Demers N, Couture A R, Joly D, Guilmain M, Jonge N D, Drouin D 2011 Scanning 33 135 doi: 10.1002/sca.20262 [50] Joy D C, Luo S 1989 Scanning 11 176 doi: 10.1002/sca.4950110404 [51] Lowney J R 1996 Scanning 18 301 doi: 10.1002/sca.1996.4950180406 [52] Reimer L 1998 Scanning Electron Microscopy (2nd Ed.) (Berlin: Springer) pp57–134 -


 首页
首页 登录
登录 注册
注册



 下载:
下载: