首页
登录
注册
-
硅基光电子芯片正朝着大规模集成和功能多样化发展[1–3], 然而, 更高的集成度和更多的功能器件往往伴随着更大的片上损耗. 光波导放大器作为硅基光电子芯片的一种重要元器件, 不仅可以有效补偿不同器件间的传输和耦合损耗, 而且是片上激光器的基础[4]. 由于铒离子(
$ {\rm{Er^{3+}}} $ )的发光中心(约$1.55\;{\rm{µm}}$ )恰好与常用的光通信波段匹配, 掺铒/铒镱共掺波导放大器(EDWA/EYCDWA)获得了国内外众多科研团队的广泛关注, 并在相关领域取得了丰硕的研究成果[5–10].EDWA/EYCDWA通常包括增益介质和信号/泵浦光波分复用器(WDM)两个部分[11]. 信号光和泵浦光经过WDM耦合后进入到增益介质中, 通过受激辐射过程产生和信号光同频的光子以实现信号光的放大. 作为EDWA最核心的部分, 增益介质的研究非常广泛, 近几年涌现了一批性能优秀的增益介质, 包括掺铒氮化硅[5,12,13]、掺铒氧化铝[7,8,14]、掺铒铌酸锂[9,10,15]、掺铒氧化钽[16,17]等. 和增益介质相比, 目前关于980 nm泵浦光/1550 nm信号光复用和解复用器件的研究较少[18–20]. 一方面在于之前的波导放大器并非全片上集成的, 通常使用光纤耦合器在片外进行980/1550 nm的耦合后, 再传输到掺铒波导中; 另一方面, 980 nm和1550 nm光谱分离得较远, 在较紧凑的芯片面积内实现信号光和泵浦光的高效低损耦合难度较大.
定向耦合器(directional coupler, DC)[21,22]、Y分支(Y branch, Y)[23–25]、马赫-曾德尔干涉仪(Mach-Zehnder interferometer, MZI)[26,27]及阵列波导光栅(arrayed waveguide grating, AWG)[28,29]等均可以实现不同波长光信号的复用和解复用. 和上述器件相比, MMI型复用/解复用器具有高工艺容差性、低插损、大带宽等优点, 被广泛用于片上不同波长的复用与解复用[30–32]. 但是, 目前大多数的片上MMI型波分复用/解复用器件主要是针对1310/1550 nm设计, 在绝缘体上硅平台(SOI)上实现的. 考虑到硅波导对980 nm的泵浦光有较强的吸收, 而泵浦光的耦合效率对光波导放大器的增益又十分关键, 有必要设计其他平台上的基于多模干涉效应的980/1550 nm波分复用/解复用器, 用于片上光波导放大器中的信号光和泵浦光的耦合. 目前, 已有基于
$ {{\rm{SiO_2}\text{-}\rm{SiON}}} $ 和$ {{\rm{Si_3 N_4}}} $ 的MMI型980/ 1550 nm波分复用/解复用器报道[18–20], 尽管实现了低于1 dB的插损和–20 dB左右的串扰, 但多模干涉波导的长度均超过450 µm, 整体尺寸较大.$ {{\rm{Ta_2}}{\rm{O_5}}} $ 是一种很有潜力的CMOS兼容材料, 具有较低的传输损耗[33]和覆盖$300\;{\rm{nm}}—10\;{\rm{µm}}$ 的超宽透明窗口, 已经有很多基于氧化钽材料的无源和有源器件相关工作发表[34–38]. 但是, 目前尚未有文献报道过基于$ {{\rm{Ta_2}}{\rm{O_5}}} $ 平台的波分复用/解复用器件.本文提出了一种紧凑的基于多模干涉效应的
$ {{\rm{Ta_2}}{\rm{O_5}}} $ 980/1550 nm波长复用/解复用器. 该器件采用分段级联的多模干涉波导结构, 通过一个基于对称型干涉机制和一个基于配对型干涉机制的MMI级联, 在不利用亚波长光栅等复杂结构调控泵浦光和信号光拍长的基础上, 极大地缩短了多模干涉波导的长度, 可以在约70 µm × 4.5 µm的干涉区域内实现980 nm和1550 nm波长光信号的分离. 采用时域有限差分(finite-difference time-domain, FDTD)工具对建立的模型进行分析和优化, 结果表明所设计的MMI双工器在980 nm处插损为0.4 dB, 在1550 nm处插损为0.8 dB, 并且两个波长的消光比均大于16 dB. 另外, 该双工器具有较大的1 dB带宽, 以1550和980 nm为中心波长的1 dB工作带宽分别为150和70 nm. 文中设计的分段级联MMI结构在性能上可以与先前报道的基于$ {{\rm{Si_3 N_4}}} $ 平台的980/1550 nm复用/解复用器媲美; 由于不需要严格满足泵浦光和信号光拍长的最小公倍数关系, 极大地缩小了980/ 1550 nm波分复用/解复用器的整体尺寸, 有望应用在片上集成的掺铒波导放大器和激光器领域. 此外, 这种分段的、不同多模干涉机制级联的思路降低了MMI器件的设计难度, 很适合用来分离两个中心波长相隔较远的光信号, 为通信波段和中红外波段波分复用/解复用器件的设计提供了参考. -
多模干涉器件基于多模波导的自映像效应, 即任一输入光场在多模波导中会周期性地出现输入光场的单个或多个像, 这是由输入光场在多模波导中激发出的不同模式的光场相互干涉导致的. 基模和一阶模的拍频长度
$ {L_{\text{π}}} $ 可以由下式[19]表示:其中,
$ \beta_{\rm{0}} $ 和$ \beta_{\rm{1}} $ 代表最低阶的两个模式的传播常数,$ W_{\rm{e}} $ 为多模波导的有效宽度. 根据入射光场的初始位置, 可以将MMI分为一般干涉型、配对干涉型和对称干涉型, 三种干涉机制对应的输入光场条件和成像位置如表1所列[39], 表中$ C_{\rm{\nu}} $ 和$ \nu $ 分别代表第$ \nu $ 阶模式的激励系数和模式的阶数. 从表1可以看出, 配对干涉和对称干涉具有更短的多模干涉区域长度, 第1重镜像出现的位置分别为$ {L_{\text{π}} } $ 和$ \dfrac{3}{4} {L_{\text{π}}} $ , 考虑到1 × 2 MMI波分复用器的实际需要和器件的整体尺寸大小, 本文选用对称型和配对型MMI级联完成后续的器件设计. -
本文采用400 nm厚的
$ {{\rm{Ta_2}}{\rm{O_5}}} $ 材料作为波导芯层, 为了实现泵浦光$ \lambda_{\rm{p}} $ = 980 nm和信号光$ \lambda_{\rm{s}} $ = 1550 nm的分离, 典型的多模干涉区域的长度$ L_{\rm{M}} $ 应该满足泵浦光和信号光拍长的最小公倍数关系, 即(2)式的关系[18]:其中, p为奇数(1, 3, 5, ···), q为偶数(2, 4, 6, ···), 泵浦光和信号光的拍长之比为
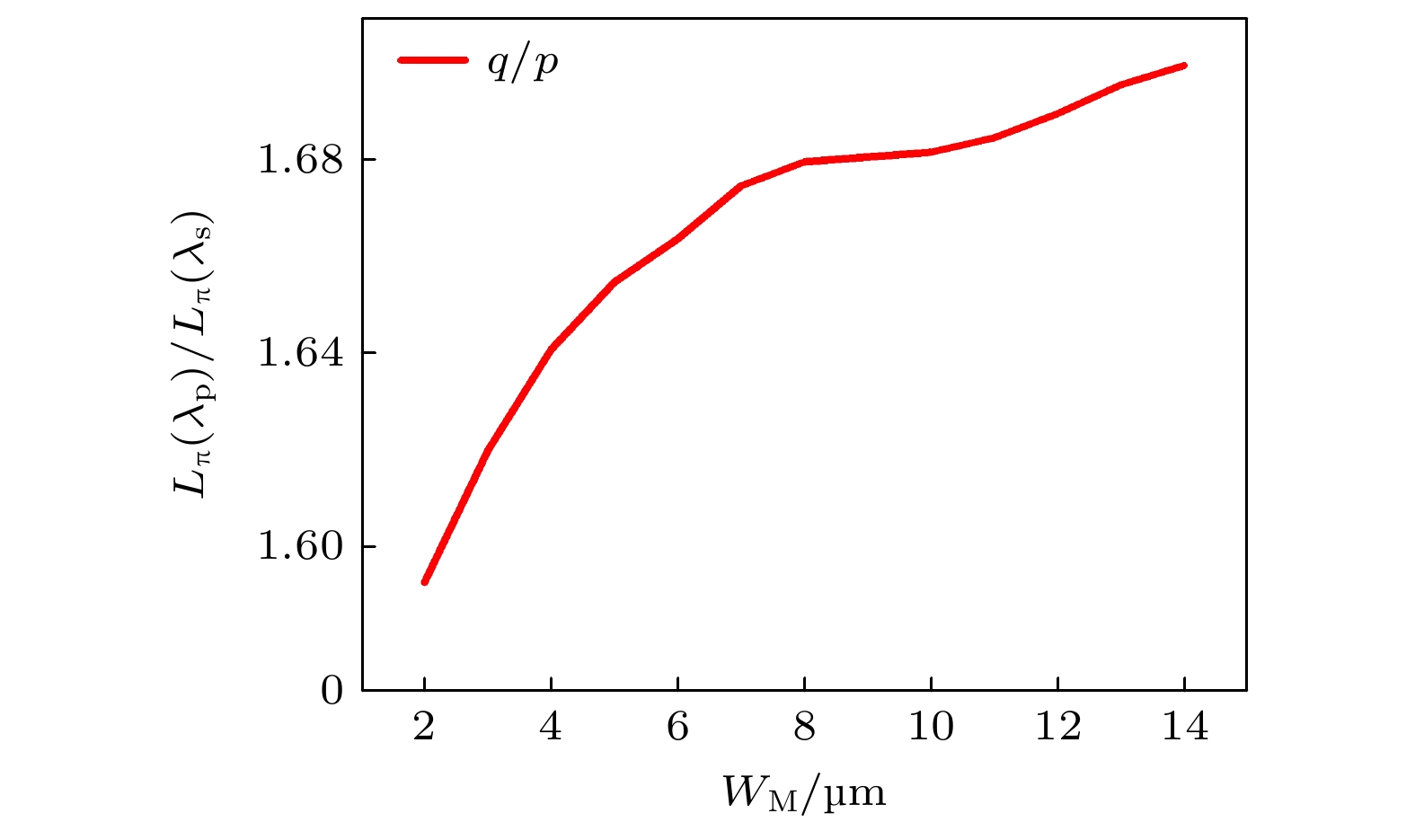
$ q/p $ . 理论上只要找到合适的q值和p值, 就能实现两个波长的分离.图1给出了利用EME仿真的不同多模波导宽度下对应的
$ q/p $ 值曲线图, 可以看出当多模波导宽度为$2—14\;{\rm{µm}}$ 时,$ q/p $ ≈1.6 = 8/5, 这意味着使用不分段的多模干涉区域至少需要8个信号光拍频长度才能将两个波长分开, 但显然这样的设计是不能够满足器件小型化和集成化的要求的. 因此, 如何通过简单的设计, 有效分离两个波长十分重要.在典型配对型多模干涉耦合器结构的基础上, 本文设计了对称型干涉和配对型干涉级联的多模干涉结构, 将多模波导一分为二. 如图2所示, 设计的分段MMI器件包括输入波导、多模干涉波导和输出波导三个部分. 其中输入、输出波导使用锥形波导结构, 主要原因在于锥形波导有利于降低插损, 但同时锥形波导会使得输出波导间隔太近, 导致串扰增强. 增大多模波导宽度可以有效降低串扰, 但会导致器件的整体尺寸变大. 因此, 需要合理设计多模波导的宽度以实现器件整体尺寸和插损、串扰等性能参数的权衡. 两级级联的多模干涉波导中, 第一段多模干涉波导(MMI 1)采用对称型多模干涉机制, 其长宽分别为
$ L_{{\rm{M1}}} $ 和$ W_{{\rm{M1}}} $ ; 第二段多模干涉波导(MMI 2)采用配对型多模干涉机制, 其长宽分别为$ L_{{\rm{M2}}} $ 和$ W_{{\rm{M2}}} $ . 从图2可以看出, 第一级MMI和第二级MMI首尾相连, 即MMI 1的输出位置与MMI 2的输入位置首尾重合. 如表1中不同干涉机制的输入和成像位置的描述, 对称型干涉输出位置在多模波导的正中, 而配对型干涉的输入位置在多模波导的±$ W_{\rm{e}}/6 $ 处, 也就是说, MMI 1和MMI 2的宽度关系满足下式:以信号光(
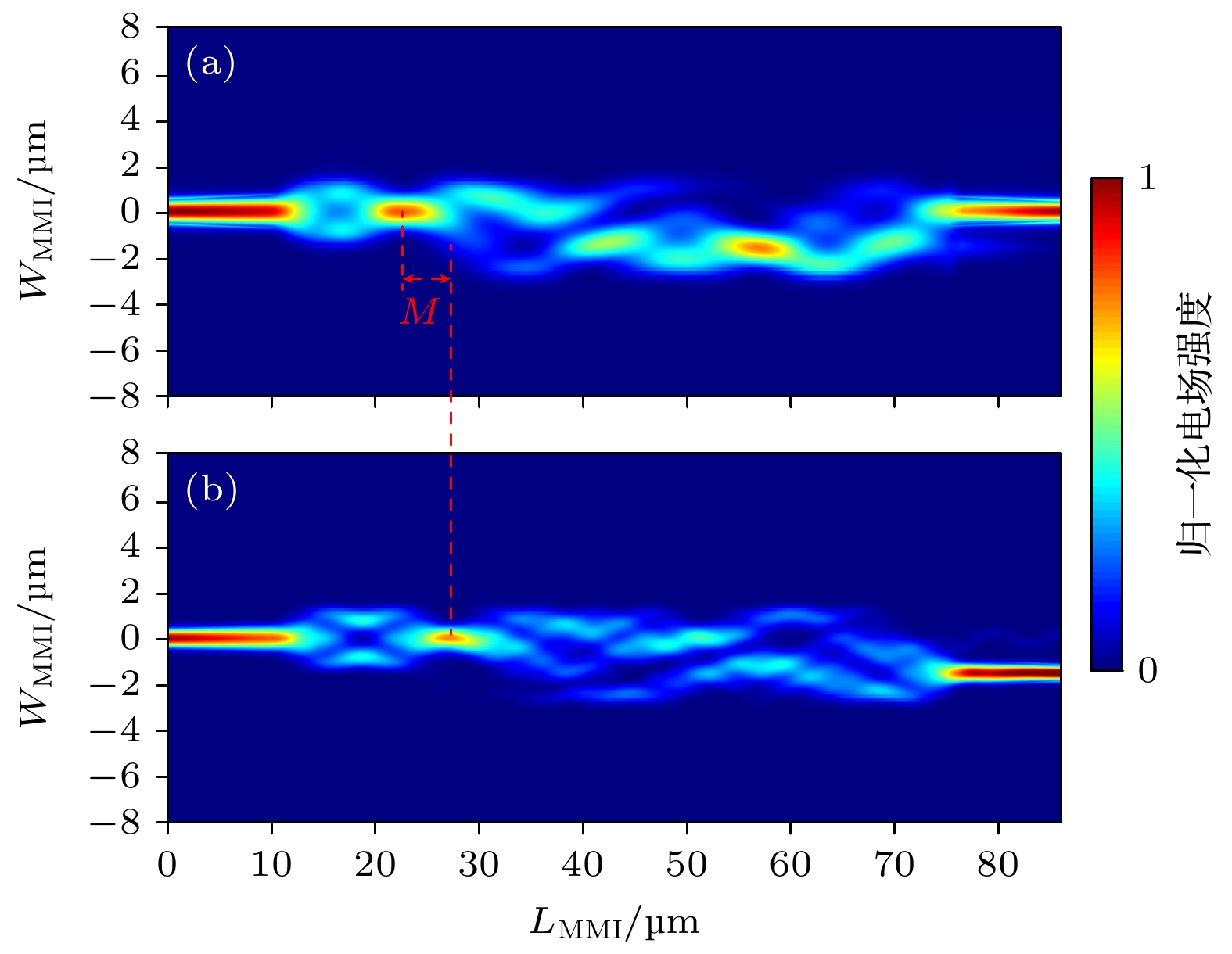
$ \lambda_{\rm{s}} $ )和泵浦光($ \lambda_{\rm{p}} $ )为例, 两级多模干涉波导的分割点位于长波长出现第一个单重像的位置, 输出位置为短波长在MMI 2中出现第一个单重像的位置, 即$ L_{{\text{π}}{\rm{-M1}}}(\lambda_{\rm{s}}) $ 处为MMI 1和MMI 2的分割点,$ L_{{\text{π}}{\rm{-M1}}}(\lambda_{\rm{p}}) + L_{{\text{π}}{\rm{-M2}}}(\lambda_{\rm{p}}) $ 处为最终输出位置.$ L_{{\text{π}}{\rm{-M1}}}(\lambda_{\rm{s}}) $ ,$ L_{{\text{π}}{\rm{-M2}}}(\lambda_{\rm{s}}) $ 和$ L_{{\text{π}}{\rm{-M1}}}(\lambda_{\rm{p}}) $ ,$ L_{{\text{π}}{\rm{-M2}}}(\lambda_{\rm{p}}) $ 分别代表信号光和泵浦光在MMI 1, MMI 2中的拍长, 它们之间应满足:(4)式中引入了一个新的变量M, 为分段级联多模干涉结构参数的优化提供了一个新的自由度. 通过调整MMI 1的长宽, 可以找到合适的M值, 使得信号光和泵浦光在输出位置上更接近, 以避免两个波长的拍长需要满足最小公倍数关系导致整体尺寸偏大. 当M值越大时, 泵浦光在进入第二级MMI时激发出的高阶模分量更多, 第二级MMI的长度越短, 器件整体长度越短. 而当M越小时, 泵浦光越接近基模(第1重镜像点)入射进第二级MMI, 整体长度更长. 但是M值的调整除了会影响器件长度外, 对性能也有一定的影响. 在实际的设计过程中, 我们以输出端的透过率为优化目标, 在确定MMI 1的长宽后, 通过调整第二段多模干涉区域的长度以及输入、输出端锥形波导的长宽, 可以获得更低的插损值. 信号光和泵浦光的输出位置位于±
$ W_{{\rm{M2}}}/6 $ 处. 使用FDTD对多模干涉区域结构参数进行优化后, 最终确定MMI 1和MMI 2宽度分别为3和4.5 µm, 长度分别为13和52 µm, M的长度为4.8 µm. 分段多模干涉波导结构的设计极大地缩短了器件的整体长度, 其长度不到普通配对型多模干涉器件的30% (约为250 µm缩短为70 µm), 并且整个器件没有引入复杂的结构, 很大程度上降低了器件的设计和加工难度. -
为了直观地判断分段级联多模干涉耦合器的波分复用和解复用效果, 使用FDTD仿真980 nm泵浦光和1550 nm信号光分别输入的光场分布图, 如图3所示. 从光场分布可以看出, 多模干涉区域分为两级, 第一级为对称型干涉区域, 第二级为配对型干涉区域. 输入模场经过锥形波导结构平稳过渡, 进入多模干涉区域激发出高阶模并发生多模干涉现象. 由于第一级干涉区域的长度为1550 nm的信号光出现第一个单重像的长度, 因此, 信号光以基模入射进第二级多模干涉区域; 而980 nm泵浦光由于拍长比信号光要长, 则以高阶模入射进第二级多模干涉区域. 在第二级多模干涉区域末端, 泵浦光和信号光分别通过输出端的锥形波导结构从cross端口和bar端口输出, 输出端较窄的直波导结构起到降低串扰和滤波的效果, 从而实现980 nm和1550 nm的高效分离.
-
对波分复用和解复用器来说, 衡量性能最重要的指标是插损(insertion loss, IL)和串扰(crosstalk, CT), IL和CT的定义如下[40]:
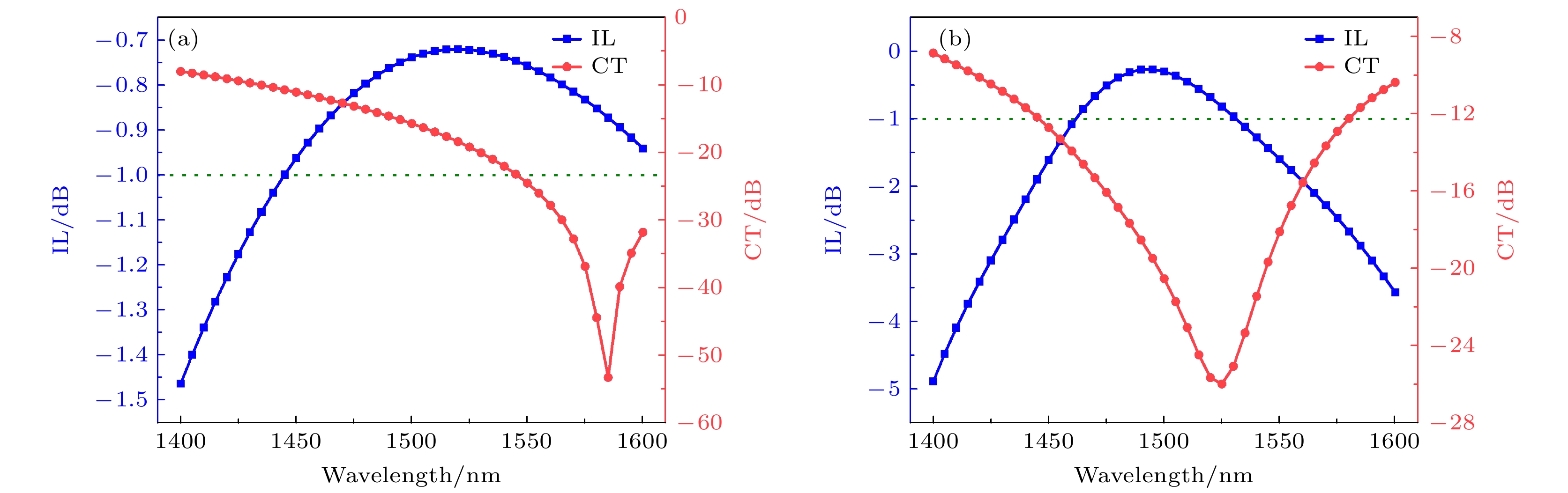
$ P_{{\rm{in}}} $ 是输入端口的功率,$ P_{{\rm{out1}}} $ 和$ P_{{\rm{out2}}} $ 分别是cross (bar)和bar (cross)端口的输出功率. 以980 nm泵浦光为例, 输出端口为cross端口, 则$ P_{{\rm{out1}}} $ 为bar端口的输出功率,$ P_{{\rm{out2}}} $ 为cross端口的输出功率. 对波导放大器来说, 我们希望不仅仅只是放大单个波长, 而是在一段较宽的频谱范围内都有放大. 因此, 对波长双工器来说, 需要考虑波长变化对器件性能的影响.图4为设计的多级MMI在1400—1600 nm和900—1100 nm波长范围内的传输谱线图, 其中图4(a)为信号光1550 nm波段对应的IL和CT; 图4(b)为泵浦光980 nm波段对应的IL和CT. 可以看出信号光的1 dB带宽高达150 nm以上, 1550 nm中心波长处插损低至0.75 dB, 对应的串扰小于23 dB. 泵浦光的1 dB带宽相对信号光较窄, 但仍有将近70 nm的频谱宽度, 并且980 nm中心波长处的损耗约为0.3 dB, 对应的串扰约为17 dB. 显然, 本文设计的分段干涉的MMI具有带宽大的优点, 可以在较宽的工作波长范围内保持较高的性能.
-
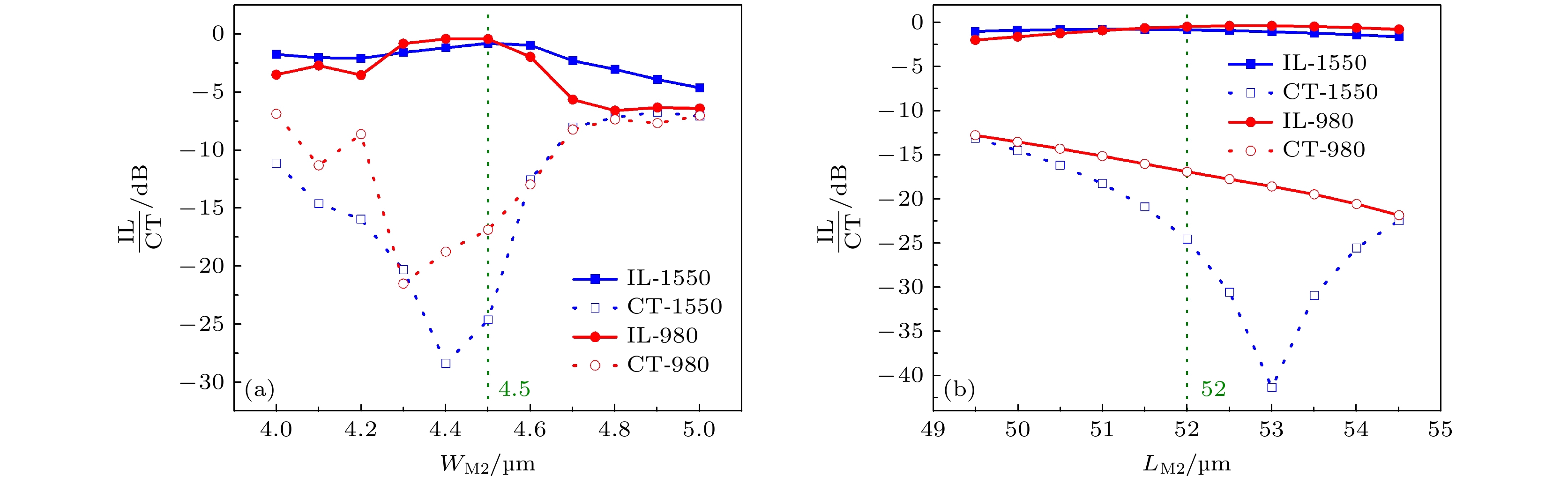
在分段多级干涉MMI的实际制备过程中, 由于所设计的结构均为一个高度, 因此只需要单步的刻蚀工艺就可以实现. 但是, 由于薄膜沉积的高度以及光刻产生的工艺误差不可避免, 需要评估所设计的MMI的工艺容差性, 主要包括薄膜厚度偏差(thickness)、第一级MMI的长度(
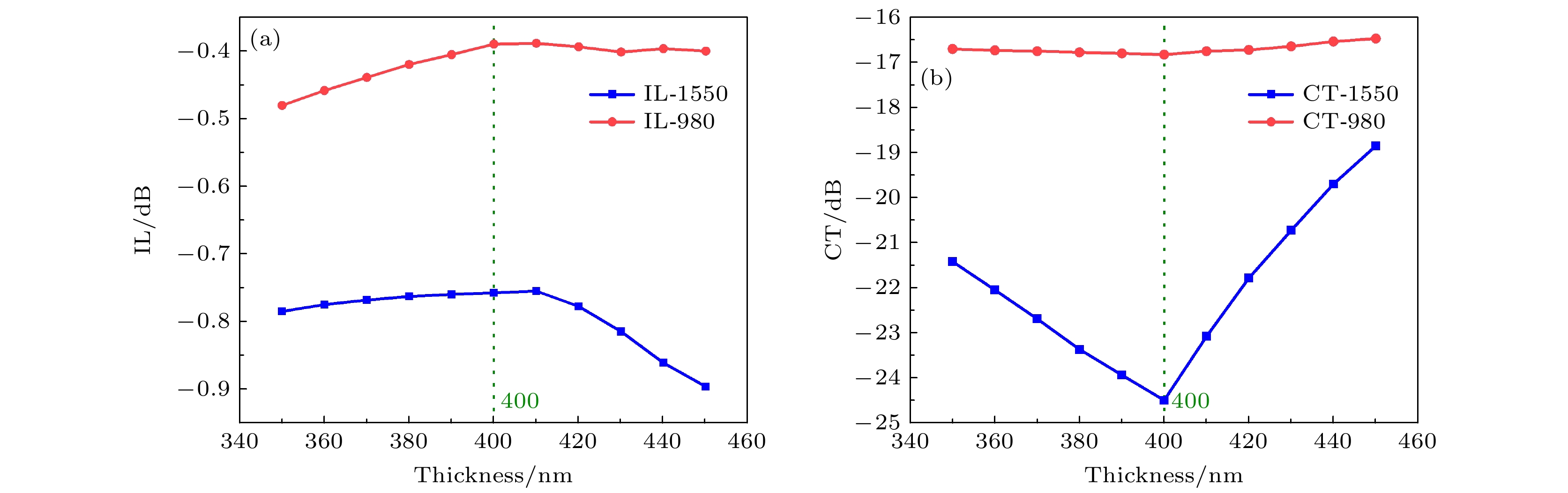
$ L_{{\rm{M1}}} $ )和宽度($ W_{\rm{M1}} $ )以及第二级MMI的长度($ L_{{\rm{M2}}} $ )和宽度($ W_{{\rm{M2}}} $ )对器件性能的影响.图5所示为薄膜厚度变化时, 对应MMI器件的插损和串扰变化情况. 从图中可以看出, 所设计的MMI器件对薄膜厚度的容差性较好, 当薄膜厚度在350—450 nm范围内时, 信号光和泵浦光的插损均小于1 dB, 并且较400 nm厚度中心值IL劣化不到0.2 dB. 在100 nm的厚度范围内, 信号光和泵浦光均保持较低的串扰, 其中信号光低于19 dB, 泵浦光低于16 dB.
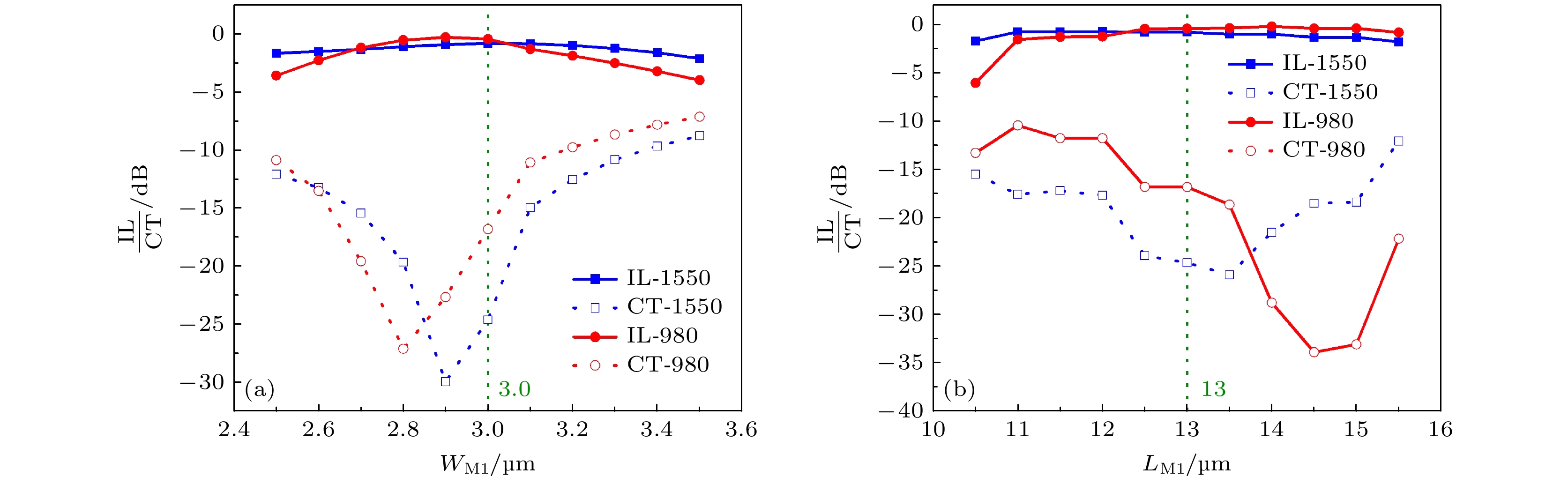
图6和图7所示为器件性能参数随第一级MMI结构参数和第二级MMI结构参数的变化. 其中, 图6(a)和图6(b)分别为第一级MMI的不同宽度和长度对器件IL/CT的影响, 图7(a)和图7(b)则分别表示在第二级MMI的不同宽度和长度下对应的器件的IL/CT值. 图6(a)和图7(a)中绿色虚线代表设计的两级MMI的宽度中心值: 3 µm和4.5 µm, 可以看出, 第一级MMI的宽度在偏离中心值± 0.2 µm的范围内, IL和CT的劣化较少, 尤其是信号光1550 nm几乎没有劣化; 而在距离中心值
$0.2—0.5\;{\rm{µm}}$ 范围内, 泵浦光980 nm的IL劣化较多, 并且信号光和泵浦光之间的串扰增强, 这主要是因为第一级MMI宽度$ W_{\rm{{M1}}} $ 变化较大, 导致第二级MMI的入射位置和第一级MMI的出射位置没有满足配对干涉$ \pm \dfrac{W_{\rm{{M2}}}}{6} $ 的入射条件, 造成了两级MMI的错位, 使性能劣化.同样, 在图7(a)中, 第二级MMI的宽度变化较大也会导致与第一级MMI的错位, 造成性能劣化. 在实际的加工过程中, 由于MMI 1和MMI 2是单次光刻, 不需要进行两级MMI结构的对准套刻, 实际上不会出现两级MMI在中间连接点之间的错位情况. 图6(b)和图7(b)中绿色虚线代表设计的两级MMI的长度中心值, 分别为13 µm和52 µm, 可以看出, 所设计的器件具有非常好的长度容差性, 在中心长度附近5 µm范围内, 信号光和泵浦光的IL均小于1 dB, 串扰均小于10 dB. 长度对串扰的影响较大, 主要是因为自镜像点有一定的宽度, 远离这个宽度自镜像点的成像质量较差, 并且有较大的串扰, 可以通过优化输入波导的宽度和MMI区域的宽度调节自镜像点的宽度和位置. 图6(b)中,
$ L_{\rm{{M1}}} = 10.5 $ µm时, 980 nm泵浦光IL较差, 主要原因是我们取信号光出现第一个单重像的长度(约$13\;{\rm{µm}}$ )作为第一段MMI的长度, 实际上这个点的长度本身是小于泵浦光出现第一个单重像长度(约$17\;{\rm{µm}}$ )的. 如果第一段MMI的长度进一步减小到10.5 µm, 会影响到泵浦光入射到第二段MMI的质量, 从而导致最终出射端的插损变大.从本节的分析可以看出, 对称干涉和配对干 涉级联的思路可以有效地缩小器件整体尺寸, 实现980 nm泵浦光和1550 nm信号光波长的高效分离. 此外, MMI器件在工艺容差性上优势比较 明显, 在一定加工误差范围内能保持较高的性能. 但是级联的思路使得对两级MMI的对准要求提升, 如果错位程度过大则会导致明显的性能劣化, 影响器件的正常使用. 在未来的设计中, 可以在两级MMI相连的位置设计特殊的结构, 使得多模干涉波导中的光场分布尽可能远离两级MMI相连的位置, 以减小拼接错位的影响.
-
本文提出一种基于
$ {{\rm{Ta_2}}{\rm{O_5}}} $ 平台的分段级联干涉的紧凑型980/1550 nm波长双工器, 在约70 µm × 4.5 µm的多模干涉区域内实现了980 nm波段和1550 nm波段光信号的高效分离. 仿真结果表明, 所设计的MMI双工器在980 nm处插损约0.4 dB, 在1550 nm处插损约0.8 dB, 并且两个波长的消光比均大于16 dB. 此外, 该双工器具有较大的工作带宽, 以1550和980 nm为中心波长的1 dB工作带宽分别为150和70 nm. 本文采用对称干涉和配对干涉级联的混合多模干涉机制, 无需严格满足泵浦光和信号光拍长的最小公倍数关系, 在不利用亚波长光栅等复杂结构调控泵浦光和信号光拍长的基础上, 将多模干涉波导的总长度缩短为相同宽度下普通配对型多模干涉波导的1/3. 文中设计的980/1550 nm波长双工器在片上掺铒/铒镱共掺波导放大器和激光器领域有潜在的应用价值, 并且这种分段的、混合级联干涉的设计思路极大地缩短了中心波长相隔较远的(解)波分复用器的设计难度, 为800/1310 nm, 1550/2000 nm等波段的复用和解复用器件的设计提供了参考.
基于分段级联多模干涉的Ta2O5 980/1550 nm波分复用/解复用器
Ta2O5 980/1550 nm wavelength multiplexer/demultiplexer based on segmented cascaded multimode interference
-
摘要: 提出一种紧凑的基于多模干涉效应的氧化钽($ {{\rm{Ta_2}} {\rm{O_5}}}$)波长双工器, 用于实现980和1550 nm波长的复用和解复用. 该器件采用对称干涉和配对干涉级联的混合多模干涉波导结构, 在不利用亚波长光栅等复杂结构调控泵浦光和信号光拍长的基础上, 将分段多模干涉波导的总长度缩短为普通配对型多模干涉波导结构的1/3. 采用三维有限时域差分(3D-FDTD)工具对建立的模型进行分析和优化, 结果表明所设计的MMI型双工器具有较低的插损和较高的工艺容差性, 在980 nm处插损为0.4 dB, 1550 nm处插损为0.8 dB, 消光比均优于16 dB. 该器件在1550 nm波长周围的1 dB带宽达150 nm, 在980 nm波长周围的1 dB带宽达70 nm. 文中设计的多级干涉结构极大地降低了MMI器件的设计难度并缩小了980/1550 nm波分复用/解复用器的整体尺寸, 有望应用在片上集成的掺铒波导放大器和激光器领域. 此外, 不同多模干涉机制级联的设计思路为分离两个中心波长相隔较远的光信号提供了技术参考, 在通信波段和中红外波段波分复用/解复用器件上具有潜在的应用价值.Abstract: On-chip erbium-doped/erbium-ytterbium co-doped waveguide amplifiers (EDWAs/EYCDWAs) have received extensive research attention in recent years. However, there has been relatively little research on integrated wavelength division multiplexing/demultiplexing devices for 980-nm pump light and 1550-nm signal light. This work aims to propose a compact Ta2O5 diplexer for 980/1550-nm wavelengths based on multimode interference effects. The device utilizes a structure that combines symmetric interference with a cascaded paired interference design, thereby reducing the total length of the segmented multimode interference waveguide to one-third that of a conventional paired multimode interference waveguide. This is achieved without using any complex structure, such as subwavelength gratings, to adjust the beat length of the pump and signal light. The three-dimensional finite difference time domain (3D-FDTD) tool is used to analyze and optimize the established model. The results demonstrate that the designed MMI diplexer has low insertion loss and high process tolerance, with an insertion loss of 0.4 dB at 980 nm and 0.8 dB at 1550 nm, and that the extinction ratios are both better than 16 dB. Moreover, the 1 dB bandwidth reaches up to 150 nm near the 1550 nm wavelength and up to 70 nm near the 980 nm wavelength. The segmented structure designed in this work greatly reduces both the difficulty in designing the MMI devices and the overall size of 980/1550 nm wavelength division multiplexers/demultiplexers. It is expected to be applied to on-chip integrated erbium-doped waveguide amplifiers and lasers. In addition, the segmented design method of cascading the hybrid multimode interference mechanism provides a technical reference for separating two optical signals with long center wavelengths such as 800/1310 nm and 1550/2000 nm, and has potential application value in communication and mid infrared diplexing devices.
-
Key words:
- multimode inteference /
- cascade /
- wavelength division multiplexing /
- Ta2O5 .
-
-
图 1 泵浦光和信号光的拍长比与多模波导宽度规律 曲线
Figure 1. Relationship curve between beat length ratio (
$ q/p $ ) and multimode waveguide width.
图 2 分段多模干涉耦合器结构示意图
Figure 2. Schematic diagram of two-section multimode interference coupler.
图 3 分段MMI的光场分布图 (a) 1550 nm; (b) 980 nm
Figure 3. The field distributions of the two-section MMI: (a) 1550 nm; (b) 980 nm.
图 4 分段MMI的传输谱线图 (a) 1550 nm波段的IL/CT; (b) 980 nm波段的IL/CT
Figure 4. Transmission spectrum of the two-section MMI: (a) IL/CT in 1550 nm band; (b) IL/CT in 980 nm band.
图 5 性能参数随薄膜厚度的变化 (a) IL; (b) CT
Figure 5. Performances with vary film thickness: (a) IL; (b) CT.
图 6 性能参数随第 1 级MMI结构参数的变化 (a)
$ W_{{\mathrm{M1}}} $ ; (b)$ L_{{\mathrm{M1}}} $ Figure 6. Performances with vary 1 st level MMI structural parameters: (a)
$ W_{{\mathrm{M1}}} $ ; (b)$ L_{{\mathrm{M1}}} $ .
图 7 性能参数随第 2 级MMI结构参数的变化 (a)
$ W_{{\mathrm{M2}}} $ ; (b)$ L_{{\mathrm{M2}}} $ Figure 7. Performances with vary 2 nd level MMI structural parameters: (a)
$ W_{{\mathrm{M2}}} $ ; (b)$ L_{{\mathrm{M2}}} $ .表 1 不同干涉机制MMI的输入条件和成像位置[39]
Table 1. Input conditions and imaging positions of MMI with different interference mechanisms[39].
一般干涉 配对干涉 对称干涉 输入 × 输出 N × N 2 × N 1 × N 第1个单重像位置 $ 3 L_{\text{π}} $ $ L_{\text{π}}$ $ 3L_{\text{π}}/4 $ 第1个N重像位置 $ 3 L_{\text{π}}/N $ $ L_{\text{π}}/N $ $ 3 L_{\text{π}}/(4 N) $ 限制条件 — $ C_{{\rm{\nu}}} = 0,~~ \nu = 2, 5, 8\cdots $ $ C_{{\rm{\nu}}} = 0, ~~\nu = 1, 3, 5\cdots$ 输入位置 任意 $ \pm W_{{\rm{e}}}/6 $ 0 
下载: 导出CSV
-
[1] Shekhar S, Bogaerts W, Chrostowski L, Bowers J E, Hochberg M, Soref R, Shastri B J 2024 Nat. Commun. 15 751 doi: 10.1038/s41467-024-44750-0 [2] Gao D S, Zhou Z P 2022 Front. Optoelectron. 15 27 doi: 10.1007/s12200-022-00030-7 [3] Zhou Z P, Chen W B, He X W, Ma D Y 2023 IEEE Photonics J. 16 0600109 [4] Wang B, Zhou P Q, Wang X J, He Y D 2022 Sci. China Inf. Sci. 65 162405 doi: 10.1007/s11432-021-3360-0 [5] Liu Y, Qiu Z R, Ji X R, Lukashchuk A, He J J, Riemensberger J, Hafermann M, Wang R N, Liu J Q, Ronning C, Kippenberg T J 2022 Science 376 1309 doi: 10.1126/science.abo2631 [6] Bonneville D B, Frankis H C, Wang R J, Bradley J D 2020 Opt. Express 28 30130 doi: 10.1364/OE.402802 [7] Rönn J, Zhang W W, Autere A, et al 2019 Nat. Commun. 10 432 doi: 10.1038/s41467-019-08369-w [8] Mu J F, Dijkstra M, Korterik J, Offerhaus H, García-Blanco S M 2020 Photonics Res. 8 1634 doi: 10.1364/PRJ.401055 [9] Liang Y T, Zhou J X, Liu Z X, Zhang H S, Fang Z W, Zhou Y, Yin D D, Lin J T, Yu J P, Wu R B, Wang M, Cheng Y 2022 Nanophotonics 11 1033 doi: 10.1515/nanoph-2021-0737 [10] Zhang Z H, Li S M, Gao R H, Zhang H S, Lin J T, Fang Z W, Wu R B, Wang M, Wang Z H, Hang Y, Cheng Y 2023 Opt. Lett. 48 4344 doi: 10.1364/OL.497543 [11] Kik P, Polman A 1998 MRS. Bull. 23 48 [12] Liu Y, Qiu Z R, Ji X R, Bancora A, Lihachev G, Riemensberger J, Wang R N, Voloshin A, Kippenberg T J 2024 Nat. Photonics 18 829 doi: 10.1038/s41566-024-01454-7 [13] Qiu Z R, Ji X R, Liu Y, Hafermann M, Kim T, Olson J C, Ning W R, Ronning C, Kippenberg T J 2024 Optical Fiber Communication Conference San Diego, March 24–28, 2024 pM4A.5 [14] Bonneville D B, Osornio-Martinez C E, Dijkstra M, García-Blanco S M 2024 Opt. Express 32 15527 doi: 10.1364/OE.516705 [15] Bao R, Fang Z W, Liu J, Liu Z X, Chen J M, Wang M, Wu R B, Zhang H S, Cheng Y 2024 Laser Photonics Rev. 19 2400765 [16] Zhang Z, Liu R X, Wang W, Yan K L, Yang Z, Song M Z, Wu D D, Xu P P, Wang X S, Wang R P 2023 Opt. Lett. 48 5799 doi: 10.1364/OL.499779 [17] Subramanian A Z, Murugan G S, Zervas M N, Wilkinson J S 2012 J. Lightwave Technol. 30 1455 doi: 10.1109/JLT.2012.2185925 [18] Mu J F, Vázquez-Córdova S A, Sefunc M A, Yong Y S, García-Blanco S M 2016 J. Lightwave Technol. 34 3603 doi: 10.1109/JLT.2016.2578463 [19] Paiam M, Janz C, MacDonald R, Broughton J 1995 IEEE Photonics Technol. Lett. 7 1180 doi: 10.1109/68.466583 [20] Han X Y, Pang F F, Cai H W, Qu R H, Fang Z J 2008 Optik 119 69 doi: 10.1016/j.ijleo.2006.07.010 [21] Yang Y D, Li Y, Huang Y Z, Poon A W 2014 Opt. Express 22 22172 doi: 10.1364/OE.22.022172 [22] He J H, Zhang M, Liu D J, Bao Y X, Li C L, Pan B H, Huang Y S, Yu Z J, Liu L, Shi Y C, Dai D X 2024 Nanophotonics 13 85 doi: 10.1515/nanoph-2023-0665 [23] Weissman Z, Nir D, Ruschin S, Hardy A 1995 Appl. Phys. Lett. 67 302 doi: 10.1063/1.115425 [24] Bucci D, Grelin J, Ghibaudo E, Broquin J E 2007 IEEE Photonics Tech. Lett. 19 698 doi: 10.1109/LPT.2007.895059 [25] Onestas L, Bucci D, Ghibaudo E, Broquin J E 2011 IEEE Photonics Tech. Lett. 23 648 doi: 10.1109/LPT.2011.2120603 [26] Chen S T, Fu X, Wang J, Shi Y C, He S L, Dai D X 2015 J. Lightwave Technol. 33 2279 doi: 10.1109/JLT.2015.2405510 [27] Sabri L, Nabki F, Ménard M 2024 Opt. Express 32 10660 doi: 10.1364/OE.514519 [28] Pathak S, Dumon P, Van Thourhout D, Bogaerts W 2014 IEEE Photonics J. 6 1 [29] Paśnikowska A, Stopiński S, Kaźmierczak A, Piramidowicz R 2023 J. Lightwave Technol. 42 2371 [30] Liu L, Deng Q Z, Zhou Z P 2017 IEEE Photonics Technol. Lett. 29 1927 doi: 10.1109/LPT.2017.2743109 [31] Zhang S C, Ji W, Yin R, Li X, Gong Z S, Lv L Y 2017 IEEE Photonics Technol. Lett. 30 107 [32] Han J L, Bao R, Wu R B, Liu Z X, Wang Z, Sun C, Zhang Z H, Li M Q, Fang Z W, Wang M, Zhang H S, Cheng Y 2024 Nanophotonics 13 2839 [33] Belt M, Davenport M L, Bowers J E, Blumenthal D J 2017 Optica 4 532 doi: 10.1364/OPTICA.4.000532 [34] Zhang C, Chen L, Lin Z L, Song J, Wang D Y, Li M X, Koksal O, Wang Z, Spektor G, Carlson D R, J Lezec H, Zhu W Q, Papp S B, Agrawal A 2024 Light Sci. Appl. 13 23 doi: 10.1038/s41377-023-01330-z [35] Black J A, Streater R, Lamee K F, Carlson D R, Yu S P, Papp S B 2021 Opt. Lett. 46 817 doi: 10.1364/OL.414095 [36] Dorche A E, Nader N, Stanton E J, Nam S W, Mirin R P 2023 Optical Fiber Communication Conference San Diego, March 05–09, 2023 pTu3C-6 [37] Bankwitz J R, Wolff M A, Abazi A S, Piel P M, Jin L, Pernice W H, Wurstbauer U, Schuck C 2023 Opt. Lett. 48 5783 doi: 10.1364/OL.499726 [38] Splitthoff L, Wolff M A, Grottke T, Schuck C 2020 Opt. Express 28 11921 doi: 10.1364/OE.388080 [39] 李赵一, 范作文, 丛庆宇, 周敬杰, 曾宪峰, 郑少南, 董渊, 胡挺, 钟其泽, 贾连希 2023 光通信研究 3 53 Li Z Y, Fan Z W, Cong Q Y, Zhou J J, Zeng X F, Zheng S N, Dong Y, Hu T, Zhong Q Z, Jia L X 2023 Study on Optical Communications 3 53 [40] 汪静丽, 陈子玉, 陈鹤鸣 2020 物理学报 69 054206 doi: 10.7498/aps.69.20191449 Wang J L, Chen Z Y, Chen H M 2020 Acta Phys. Sin. 69 054206 doi: 10.7498/aps.69.20191449 -
图( 7) 表( 1)
计量
- 文章访问数: 221
- HTML全文浏览数: 221
- PDF下载数: 4
- 施引文献: 0